Summary
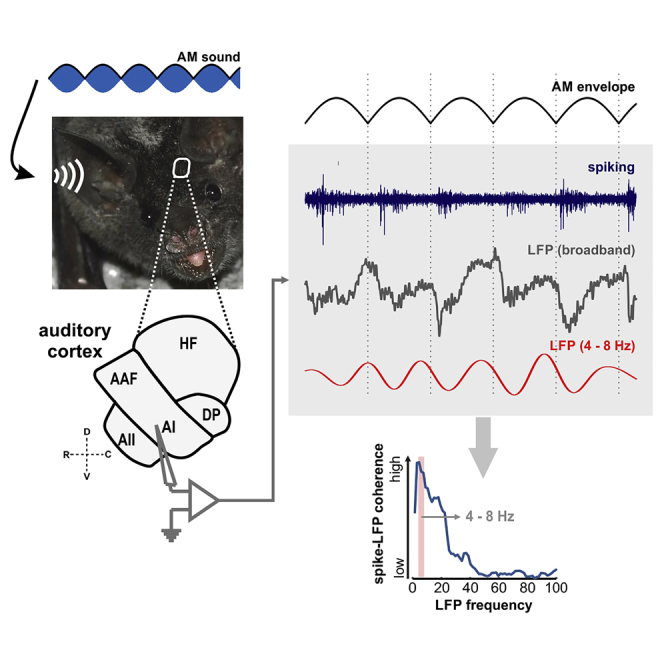
The extraction of temporal information from sensory input streams is of paramount importance in the auditory system. In this study, amplitude-modulated sounds were used as stimuli to drive auditory cortex (AC) neurons of the bat species Carollia perspicillata, to assess the interactions between cortical spikes and local-field potentials (LFPs) for the processing of temporal acoustic cues. We observed that neurons in the AC capable of eliciting synchronized spiking to periodic acoustic envelopes were significantly more coherent to theta- and alpha-band LFPs than their non-synchronized counterparts. These differences occurred independently of the modulation rate tested and could not be explained by power or phase modulations of the field potentials. We argue that the coupling between neuronal spiking and the phase of low-frequency LFPs might be important for orchestrating the coding of temporal acoustic structures in the AC.
Subject Areas: Neuroscience, Sensory Neuroscience, Model Organism
Graphical Abstract
Highlights
-
•
Auditory cortical neurons can track periodic sounds via synchronized spiking
-
•
Neuronal synchronization ability is well marked by theta-alpha spike-LFP coherence
-
•
Spike-LFP coherence patterns are independent of the stimulus' periodicity
-
•
Theta-alpha LFPs may orchestrate phase-locked neuronal responses to periodic sounds
Neuroscience; Sensory Neuroscience; Model Organism
Introduction
The timing of acoustic events is of great importance to animals that rely on acoustic information for communication and/or orientation. It is known that the temporal structure of sounds carries relevant information for a variety of complex behaviors, including communication call processing (Drullman et al., 1994, Kanwal et al., 1994, Shannon et al., 1995, Theunissen and Doupe, 1998, Koch and Grothe, 2000) as well as navigation and spatial cues detection (Middlebrooks, 2015, Suga, 2015, Wohlgemuth et al., 2016). Ethologically relevant sounds usually occur in well-structured temporal patterns that ultimately facilitate their neuronal processing. A typical example of acoustic structures in nature is amplitude modulation (AM), which characterizes a wide variety of vocalizations (Luo et al., 2007, Arnal et al., 2015, Slama and Delgutte, 2015).
Amplitude-modulated sounds are acoustic signals composed of one or more carrier frequencies whose amplitudes vary as a function of a modulating wave. Sinusoidal amplitude modulations (modulating wave is a sine function) have been extensively used to investigate how the brain processes acoustic events (Rhode and Greenberg, 1994, Krishna and Semple, 2000, Lu et al., 2001, Joris et al., 2004, Yin et al., 2011, Niwa et al., 2015). The periodicity of AM sounds is encoded along the auditory pathway via a synchronized discharge of auditory neurons to a certain phase of the stimulus (phase code), or by increasing the firing rate as a response to an increase in the modulation frequencies (rate code) (Lu and Wang, 2000, Lu et al., 2001, Joris et al., 2004, Yin et al., 2011, Johnson et al., 2012). It is known that the capacity of neurons to produce phasic responses deteriorates in higher hierarchical structures of the auditory pathway (Joris et al., 2004). In the auditory cortex (AC) of several mammals, the neuronal synchronization ability is already limited to modulation rates not higher than ∼35 Hz (Creutzfeldt et al., 1980, Schreiner and Urbas, 1988, Gaese and Ostwald, 1995, Fitzpatrick et al., 2009, Martin et al., 2017).
Although AM is a ubiquitous feature of natural sounds, how the mammalian AC processes amplitude envelopes is still not well understood. For example, most of the aforementioned studies focused on the encoding of the envelope's periodicity by cortical spike trains, but little is known about how other neuronal signals such as local-field potentials (LFPs, a slower component of the electrophysiological ensemble [Buzsaki et al., 2012]) are involved in the processing of AM stimuli. High-frequency oscillations of the LFPs are important for neural computations and attentional processes in sensory systems (Womelsdorf and Fries, 2007, Womelsdorf et al., 2007, Fries, 2009), whereas low-frequency fluctuations (typically <12 Hz) in cortical field potentials are associated with sensory selectivity (also linked to attention) and with the modulation of neuronal excitability (Schroeder and Lakatos, 2009, Stefanics et al., 2010, Palva and Palva, 2011, Henry and Obleser, 2012, Ng et al., 2012). In the AC, it has been shown that stimulus-evoked spiking synchronizes to low-frequency (<12 Hz) fluctuations (Lakatos et al., 2005), and that such synchronization could be important for neuronal coding (Kayser et al., 2009) and predictive timing (Arnal and Giraud, 2012). However, evidence linking slow LFPs with the coding of periodic (and thus predictive) stimuli by auditory cortical neurons in the mammalian brain is lacking.
In this study, we aimed to bridge this gap by investigating how the AC of the bat Carollia perscpicillata processes AM sounds, considering spiking responses, LFPs, and their interactions in terms of their synchronization to the stimulus and to each other. Because of the evidence suggesting that slow oscillations play an important role in organizing cortical responses, we hypothesized that low-frequency coherence between spikes and LFPs would differ between neurons that phase lock to the AM envelope and those that do not. Our data confirmed this hypothesis. We show that the ability of phase coding periodic stimuli in the AC is marked by significant differences in the phase coherence of spikes and LFPs in the theta–alpha range (4–12 Hz). That is, coherence between both neural signals is strongest when neurons are able to track the periodicity of the stimulus in a phasic manner. Such strong spike-LFP coherence is observed even at modulation frequencies beyond the tracking limits of the cortical spiking. Overall, our data suggest an involvement of theta-alpha LFPs in orchestrating temporally organized neuronal firing to periodic acoustic streams.
Results
Spiking Activity Synchronizes to Slow AM Stimuli
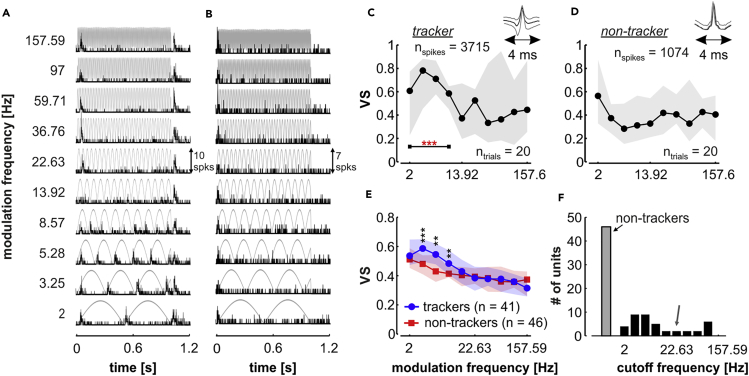
Cortical responses to AM sounds were recorded from 87 units in awake bats. Units were classified into two groups: trackers (showed significant phase synchronization to at least one modulation frequency) and non-trackers (were not significantly synchronized to any modulation rate). The phasic response of a typical tracker is depicted in the peri-stimulus time histogram (PSTH) shown in Figure 1A. This unit synchronized its discharge pattern to slow modulation frequencies, whereas it failed to do so to faster AM envelopes (>13.92 Hz). Note that the vector strength (VS) values calculated for the unit drop as the modulation frequency increases, as depicted in Figure 1C. The frequencies to which the unit was significantly synchronized, according to a “joint criterion” that includes both VS metrics and circular statistics (see Transparent Methods), are marked with red stars. Figure 1B shows the PSTH of a representative non-tracker, which failed to synchronize spikes to any modulation frequency tested. This unit did not fulfill the joint criterion for any of the presented stimuli (Figure 1D).
Figure 1.
Tracking and Non-tracking Units in the AC of C. perspicillata
(A and B) Peri-stimulus time histograms (1-ms bins) of a cortical tracker (A) and a non-tracker (B).
(C) Vector strength (VS) of the tracking unit depicted in (A), for all modulation frequencies tested. This unit was significantly synchronized (according to the joint criterion, see Transparent Methods) to modulation frequencies up to 8.57 Hz (red stars).
(D) VS of the non-tracking unit shown in (B). Solid black lines in (C and D) represent the median VS across trials; gray-shaded areas illustrate the interquartile range (IQR). Waveforms on top of VS curves represent the spike shape of each unit (C, tracker, n = 3,715 spikes; D, non-tracker, n = 1,074 spikes; all spikes are included to obtain the waveform).
(E) Vector strength of tracking (blue circles) and non-tracking (red squares) units; solid lines show median values, whereas shaded areas indicate the IQR. (* symbols indicate the results of FDR-corrected Wilcoxon rank-sum tests; **p < 0.01, ***p < 0.001).
(F) Distribution of cutoff frequencies in the population of trackers (black bars; non-trackers represented by the gray bar). The gray arrow indicates a cutoff frequency of 22.63 Hz.
At the population level, 47.13% of the units were classified as trackers (41/87), whereas 52.87% (46/87) were classified as non-trackers. Tracking units showed high VS values for low modulation frequencies (Figure 1E, blue), with the tracking ability deteriorating in response to higher modulation rates. The subpopulation of trackers had significantly stronger VS than the subpopulation of non-trackers only when the modulation frequency was higher than 2 Hz, but lower than 13.92 Hz (false discovery rate [FDR]-corrected Wilcoxon rank-sum test; corrected p ≤ 0.0093). Higher VS in trackers than in non-trackers is a consequence of the classification criterion (see Transparent Methods), but the fact that significant differences do not occur in response to rates above 13.92 Hz is also a sign of the deterioration of the tracking abilities with faster envelopes. To quantify the cortical phase-locking limits we defined, per unit, a modulation cutoff frequency representing the highest modulation rate to which the unit's spiking was significantly synchronized. Only a minority of the recorded units (10/87, 11.49%) were able to fire synchronously to AM envelopes faster than 22.63 Hz (Figure 1E), indicating that most cortical spiking could not follow rates higher than this value. Because of this, and based on the fact that most cortical phase coding responses across species occur at low modulation rates (see Joris et al., 2004), in the subsequent analyses we focused on tracking units whose cutoff frequency was not higher than 22.63 Hz (31 tracking units).
The existence of weak temporal organization in the response of a small number of non-tracking units was a possibility. In such cases, our approach would label these units as non-trackers, if their response patterns did not fulfill the classification criterion (see Transparent Methods). To explore the former, we considered pooled spiking responses from the group of trackers and non-trackers, per modulation frequency. We reasoned that if units in the AC synchronize to the same envelope phase for a given modulation rate (see Malone et al., 2007, Yin et al., 2011), pooled spikes across units could reveal the presence of (weak) temporal organization in the population response of non-trackers. Figure S1 shows pooled responses for the group of tracking and non-tracking units. The response of tracking units was well temporally organized, and spikes typically occurred at the same envelope phase across units, particularly in response to low modulation frequencies (Figure S1B). Importantly, pooled non-tracking responses still showed some temporal organization in their spiking, up to modulation rates of 13.92 Hz (note the circular spike-phase histograms in Figure S1C), which is in line with the idea that the definition of trackers and non-trackers is rather graded, and not strictly discrete. In addition, to evaluate to what extent the recorded units could overcome phase coding limitations to represent AM sounds, we quantified each unit's ability to encode the envelope's periodicity via a rate code, whereby a unit monotonically increases its firing rate in response to higher modulation frequencies. Although we observed rate coding responses in our data (see Figure S2), it was only in a minority of the population (13.79%, 12/87), comprising 14.63% of tracking (6/41) and 13.04% of non-tracking (6/46) units. Hence, we did not consider rate coding responses separately in further analyses.
Low-Frequency Spike-Field Coherence Is Strongest in Tracking Units
The spike-field coherence (SFC) metric was used to quantify differences between tracking and non-tracking units in terms of spike-LFP synchronization, across distinct frequency bands and modulation rates. In brief, the SFC is a normalized, frequency-dependent synchronization index that measures how well spikes lock to ongoing oscillations, by considering LFP windows related to the spiking activity. The value of the SFC in a certain frequency varies between 0 and 1, and it indicates the strength of the locking of spikes to that LFP frequency.
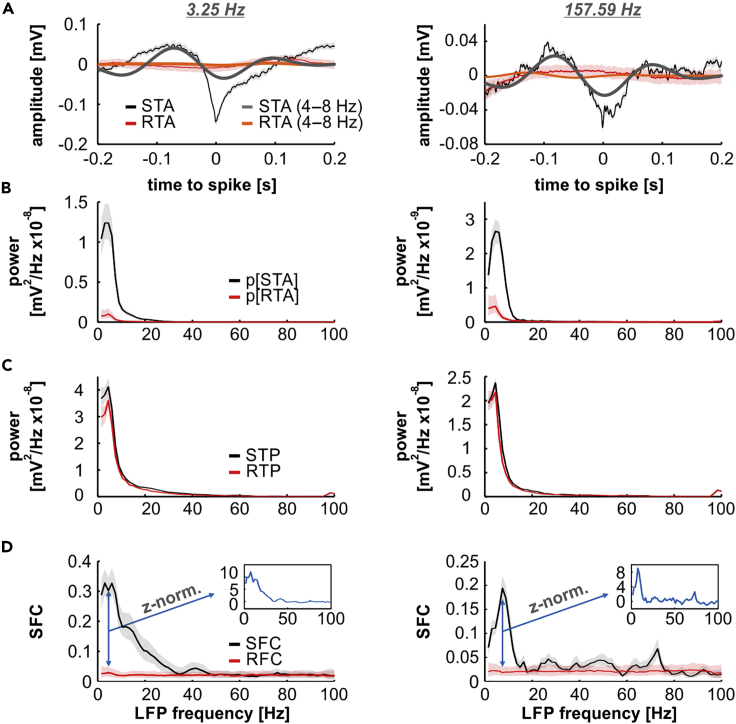
In tracking units, we observed that LFP segments centered at spike times typically carried strong slow oscillatory components, evidenced by the spike-triggered averages (STA; i.e., the average of the LFP segments associated to spikes; Figure 2A, black traces). Critically, such low-frequency components were not only present when the animals listened to slow AM envelopes (Figure 2A, left; modulation frequency of 3.25 Hz) but also appeared in response to modulation rates beyond the tracking ability of the cortical spiking (e.g., Figure 2A, right; modulation frequency of 157.69 Hz). The former implies that the presence of such slow fluctuations cannot be solely explained by separate entrainment of LFPs and spikes to the stimulus, since low-frequency LFPs would also not be phase locked to fast envelopes. Furthermore, if LFP segments were chosen at random time points and averaged (thus yielding the random-triggered average), the low-frequency oscillatory components considerably diminished in amplitude (red and orange traces in Figure 2A).
Figure 2.
Spike-Field Coherence in an Exemplary Tracking Unit
(A) Left: Spike-triggered averages (STAs; solid lines: median; shaded areas: IQR) obtained from a representative tracker (same shown in Figure 1A) in response to a modulation frequency of 3.25 Hz. Dark traces show the STA calculated with real spike times (thin black curve, raw median STA; thick gray curve, 4–8 Hz filtered median STA, shown for illustrative purposes). Red and orange traces represent the raw median STA calculated with randomly centered LFP windows (random-triggered average [RTA]; red trace, raw median RTA; thick orange curve, 4–8 Hz filtered median RTA). Right: same as in left, but obtained in response to a modulation frequency of 157.49 Hz.
(B) Power spectral density of the STAs (black) and RTAs (red) obtained from data shown in (A) (left, 3.25 Hz; right, 157.59 Hz).
(C) Average power of the LFP windows centered at spike times (spike-triggered power [STP], black traces), and at random time points (random-triggered power [RTP], red traces). Left and right columns follow above-described conventions.
(D) Spike-field coherence (SFC, black traces) and random-field coherence (RFC, red traces), at two modulation frequencies (left column, 3.25 Hz; right column, 157.59 Hz). Insets show the z-normalization of the median SFC with respect to the RFC (baseline). Data in the figure are shown as median (solid lines) and IQR (shaded areas) across repetitions (300 in total) in the coherence analysis (See Transparent Methods).
Coherence values were obtained after dividing the power of the STAs (Figure 2B) by the average power of the respective LFP segments (spike-triggered power; Figure 2C). The SFC of the example unit at two different modulation rates is depicted in Figure 2D (black trace). As a baseline, coherence was calculated using LFP windows chosen at random time points (red traces in Figure 2 depict data associated to randomly selected LFP segments), which resulted in the “random-field coherence” (RFC; Figure 2D, red). The RFC represents spike-LFP synchrony obtained if consistent phase relationships between spikes and LFPs are absent. To allow for comparisons between units in further analyses, the median SFC across repetitions (within a unit and modulation frequency, see Transparent Methods) was z-normalized to the corresponding distribution of RFC values. The insets in Figure 2D show the normalized SFC for the exemplary tracking unit in response to low and high modulation rates (3.25 Hz, left; 157.59 Hz, right). Note that high SFC values are clearly present in both cases in low-frequency bands of the LFP.
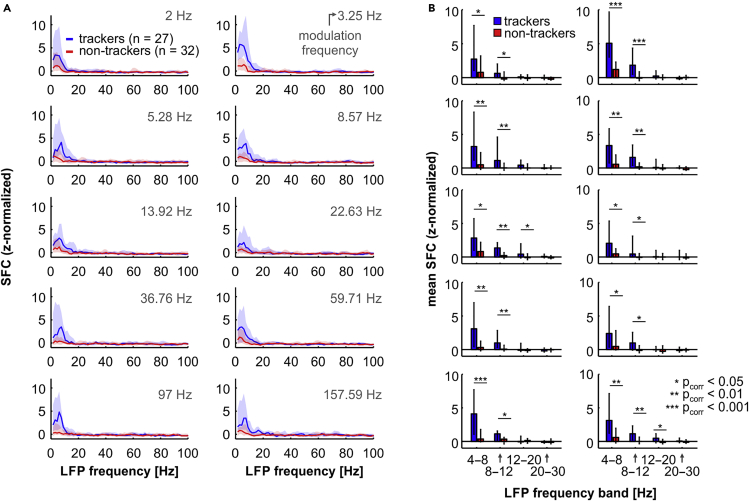
Spike-field coherence was compared between the subpopulations of tracking and non-tracking units using the z-normalized SFC (illustrated in Figure 2D). Because the SFC is affected by the number of spikes (and hence the number of LFP windows) used to calculate it (Grasse and Moxon, 2010), we considered only units that fired at least 40 spikes in response to every modulation frequency presented. Thus, a total of 27 trackers and 32 non-trackers were used. Population z-normalized SFC values obtained from trackers and non-trackers, across modulation rates, are shown in Figure 3A (blue, trackers; red, non-trackers). In line with the example unit shown in Figure 2, a peak in coherence can be readily seen for the subpopulation of trackers in low frequencies of the LFP, for every modulation rate analyzed (median SFC peak frequency across modulation rates: 5.96 Hz). The subpopulation of non-tracking units, on the other hand, exhibited weaker coherence than tracking units and no visible peak in low frequencies of the spectrum, particularly in response to fast AM sounds. Additionally, higher SFC values in tracking than in non-tracking units were only clearly observed at low LFP frequencies (<12 Hz).
Figure 3.
Theta-Alpha Spike-Field Coherence Is Strongest In Tracking Units across Modulation Frequencies
(A) z-normalized SFC across modulation frequencies (indicated in each sub-panel) in tracking (blue) and non-tracking units (red).
(B) Comparison, across modulation frequencies, of the average SFC in different LFP bands (theta, 4–8 Hz; alpha, 8–12 Hz; low beta, 12–20 Hz; and high beta, 20–30 Hz) in tracking (blue) and non-tracking (red) units. Each sub-panel shows the statistics for one modulation frequency; sub-panels are arranged as in (A). Data shown in the figure as median and 25th and 75th percentiles. Significance was assessed with FDR-corrected Wilcoxon rank-sum tests. All p values indicated in the figure are corrected for multiple comparisons. (∗ corrected p < 0.05; ∗∗ corrected p < 0.01; ∗∗∗ corrected p < 0.001).
To address the aforementioned differences in a quantitative way, we calculated the mean coherence values in canonical low-frequency LFP bands (theta, 4–8 Hz; alpha, 8–12 Hz; low beta, 12–20 Hz; high beta, 20–30 Hz) and compared them statistically between the two neuronal groups, across modulation rates (Figure 3B). There were significant differences between the mean theta- and alpha-band SFC in response to every modulation rate tested (FDR-corrected Wilcoxon rank-sum test; corrected p ≤ 0.045). In relatively higher frequency bands (i.e., low and high beta, 12–20 and 20–30 Hz, respectively) there were no consistent significant differences, and the z-normalized average SFC values were also not significantly different from 0 across modulation rates (FDR-corrected Wilcoxon signed rank test; corrected p > 0.05), with a few exceptions (for the low-beta band, at modulation rates of 5.28, 13.92, and 157.59 Hz; corrected p < 0.012). These results indicate that differences in coherence between tracking and non-tracking units in the AC occur in low-frequency bands (theta and alpha) of the LFP. Noteworthy, although tracking and non-tracking units also exhibited differences in their basic properties (e.g., the distribution of their best frequencies, see Figure S3), units tuned to low (<50 kHz) or high (≥50 kHz) sound frequencies did not significantly differ in their theta- or alpha-band SFC, either in the subpopulation of trackers or that of non-trackers (FDR-corrected Wilcoxon rank-sum tests, corrected p > 0.066 in both theta and alpha bands; data shown in Figure S4).
Considering that the definition of tracking and non-tracking units is not discrete, but to some extent graded (see previous section and Figure S1), we explored whether the strength of theta-band SFC, across modulation frequencies, would depend on the units' VS. We evaluated three conditions: one in which the considered VS of a unit was obtained in response to the specific modulation rate under consideration, a second condition in which the considered VS of a unit was obtained in response to a modulation frequency of 3.25 Hz, and a third condition in which the considered VS of a unit was calculated from responses to a modulation rate of 157.59 Hz. In these three cases, the units' SFC was grouped into four equipopulated subsets, where subset 1 contained units with the 25% lowest VS values, and subset 4, units with the 25% highest VS values. Figure S5 shows that, taking into account VS values at low modulation rates (i.e., <13.92 Hz), there was a clear relationship between the spiking synchronization strength and the SFC. Remarkably, this was true for the SFC across all modulation frequencies tested, considering VS values calculated in response to a modulation rate of 3.25 Hz (see Figure S5B), whereas no relationship was observed if the VS was computed from responses to an AM rate of 157.59 Hz (Figure S5C). The former strengthens the notion that theta-band SFC is a good marker for the coding of slow temporal envelopes in the AC.
Differences in SFC Are Not Explained by Differences in Amplitude or Phase Modulations of the LFP
We explored whether the observed differences in the SFC of trackers and non-trackers could be explained by differences in power modulations of ongoing oscillations, or by differences in LFP phase consistency across trials within a unit and modulation frequency. For that we used two approaches. First, to quantify power modulations in both groups, we calculated the phase-amplitude coupling (PAC [Tort et al., 2010]) between the LFP (same canonical bands as above) and the AM envelope across modulation frequencies. Second, to address phase consistency, we calculated the inter-trial phase coherence (ITC) of the LFP for each unit and modulation rate. Note that differences in the PAC or the ITC of tracking and non-tracking units would suggest that possible mechanisms behind the phase coding of periodic stimuli (i.e., the AM envelopes) in the AC go beyond low-frequency SFC and could also be attributed to differences in power or phase modulations of theta- or alpha-band oscillations. To be consistent, these analyses were performed on the same units used for SFC calculations (i.e., 27 trackers and 32 non-trackers).
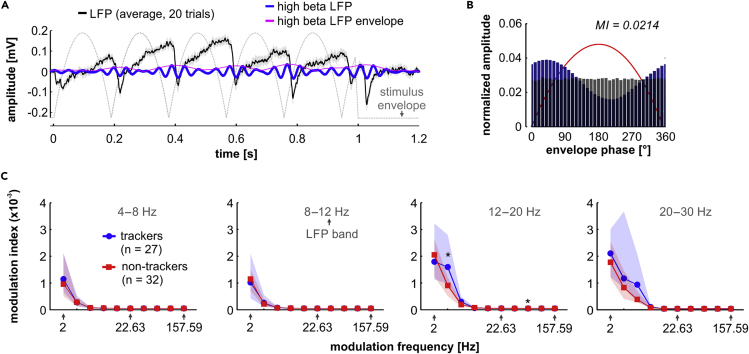
We observed power modulations in the LFP that were related to the phase of the stimulus' envelope. The effect is shown for illustrative purposes in the high-beta band (20–30 Hz) for an example tracking unit (Figures 4A and 4B; same tracking unit shown in previous figures), in response to a modulation rate of 5.28 Hz. We chose the high-beta band to illustrate PAC effects because power modulations were typically strongest in this frequency range (see Figure 4C and [Fujioka et al., 2012]). In the example unit, the amplitude distribution of high-beta LFPs was clearly non-uniform with respect to the AM envelope's phase (Figure 4B). This non-uniformity was measured with the modulation index (MI, indicated for the example in Figure 4B), which quantifies how strongly the envelope's phase modulates the amplitude of ongoing LFPs (see Transparent Methods for details).
Figure 4.
Phase-Amplitude Coupling in Tracking and Non-tracking Units
(A) Average LFP (black; solid line: mean; shaded area: SEM) of a tracking unit (same shown in Figure 1), in response to a modulation rate of 5.28 Hz (AM envelope shown as a dashed gray line). Average LFP filtered in high beta (20–30 Hz) is shown as a blue trace for illustrative purposes. Note the increases in amplitude at times close to the stimulus envelope's trough (the amplitude envelope of the beta-band LFP is shown in magenta).
(B) Amplitude distribution of the high-beta LFP in relation to the envelope's phase. The blue histogram shows the observed distribution of power across phases, whereas the gray histogram depicts a surrogate uniform distribution. The PAC modulation index (MI) for this unit and modulation frequency (5.28 Hz) had a value of 0.0214.
(C) Statistical comparisons (FDR-corrected Wilcoxon rank-sum tests; significance after corrected p < 0.05) of the PAC modulation index between tracking and non-tracking units, calculated at distinct LFP bands (indicated within the sub-panels), across modulation frequencies. There were no significant differences between the two subpopulations, except for the low-beta band (12–20 Hz), in response to modulation frequencies of 3.25 and 59.71 Hz. Units used in this analysis were the same used for SFC calculations (data is shown as median and IQR; *corrected p < 0.05).
When comparing MIs calculated for tracking and non-tracking units at the population level, we observed no significant differences (FDR-corrected Wilcoxon rank-sum test, corrected p > 0.09) between the two groups, at nearly every LFP frequency band and AM rate tested. The latter was so, except in the case of LFPs corresponding to the low-beta band (12–20 Hz) in response to modulation frequencies of 3.25 and 59.71 Hz (corrected p ≤ 0.045; Figure 4C). Lack of significant differences in the PAC between LFPs and AM envelopes was accompanied by lack of significant differences between the power of LFP bands of trackers and non-trackers, across modulation rates (FDR-corrected Wilcoxon rank-sum test, corrected p > 0.06; see Figure S6A). In addition, the modulation rate of the stimulus affected the power of the LFP bands in trackers and non-trackers (FDR-corrected Wilcoxon signed rank test; statistics summarized in Figure S6B; p < 0.02), in such a way that typically the power of theta, alpha, or (low and high) beta bands was higher in response to low modulation rates (≤ 22.63 Hz). However, such effects do not fully explain that MI values in the PAC analyses become negligible at high modulation rates (>30 Hz; see Figure 4C). Rather, this trend is mostly due to the fact that power modulations will not occur at frequencies higher than a certain LFP band (for example, theta-band LFPs cannot carry power modulations at frequencies >8 Hz). Overall, our results indicate that differences in the SFC occurring mainly at theta and alpha bands, between tracking and non-tracking units, are not fully accounted for by differences in power modulations (or by the power itself) of the same LFP bands in both neuronal subpopulations, particularly in response to stimuli with high modulation rates (>30 Hz).
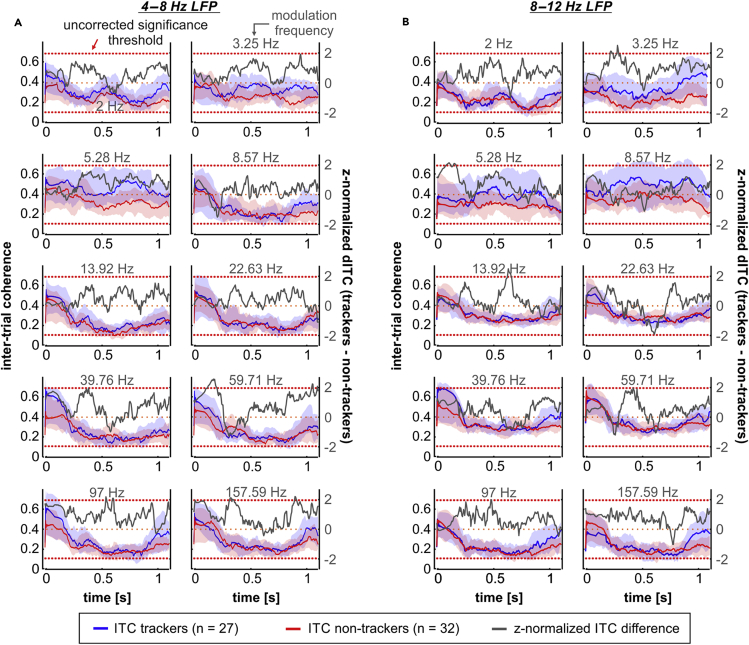
As mentioned in the preceding text, we also calculated the ITC from LFPs related to tracking and non-tracking units across modulation frequencies in the theta and alpha bands (where significant differences occurred in the SFC; Figure 5). Differences in the median ITC corresponding to trackers and non-trackers (dITC) were z-normalized to a null distribution in which the units' labels (“tracker” or “non-tracker”) were randomly assigned (see Transparent Methods). The resulting z-normalized dITC between trackers and non-trackers is depicted in Figure 5 as gray traces (associated y axis on the right of the sub-panels). We observed evidence of a reset in the phase of theta- and alpha-band LFPs across modulation rates, indicated by transiently high ITC values occurring around the stimulus onset. The former occurred considering LFPs related to either tracking or non-tracking units (Figures 5A and 5B). Moreover, ITC values in both groups were very similar (particularly in response to modulation frequencies >13.92 Hz), and the dITC between tracking and non-tracking units across modulation rates was not significantly different than what would be observed if the labels were randomly assigned. Note that the horizontal red dashed lines in Figure 5 depict an uncorrected significance threshold of z = 1.96. A z-score above 1.96 implies ITC in trackers significantly higher than in non-trackers, whereas z-scores lower than −1.96 indicate the opposite. Altogether, the results of the PAC and ITC analyses show that differences in the spike-LFP coherence at low frequencies, between tracking and non-tracking units, are not fully explained by power or phase modulations of the related LFPs in response to the stimulus.
Figure 5.
Inter-Trial Coherence in Tracking and Non-tracking Units
(A) Inter-trial coherence (ITC) of tracking (blue; n = 27) and non-tracking (red, n = 32; solid line, median; shaded area, interquartile range) units, across modulation frequencies (values associated to the y axis on the left), calculated with 4–8 Hz LFPs. Gray traces (associated to the y axis on the right) indicate a z-normalized (to a surrogate distribution, see Transparent Methods) difference in the median ITC of trackers and non-trackers (dITC). Horizontal red dashed lines depict an uncorrected significant threshold for the observed differences.
(B) Same as in (A), with ITC values obtained using 8–12 Hz LFPs. Units used in this analysis were the same used for SFC calculations. In every subpanel of the figure, the stimulus onset occurs at time 0.
Spike Phases Relative to Low-Frequency LFPs in Tracking Units Are Robust across Modulation Frequencies
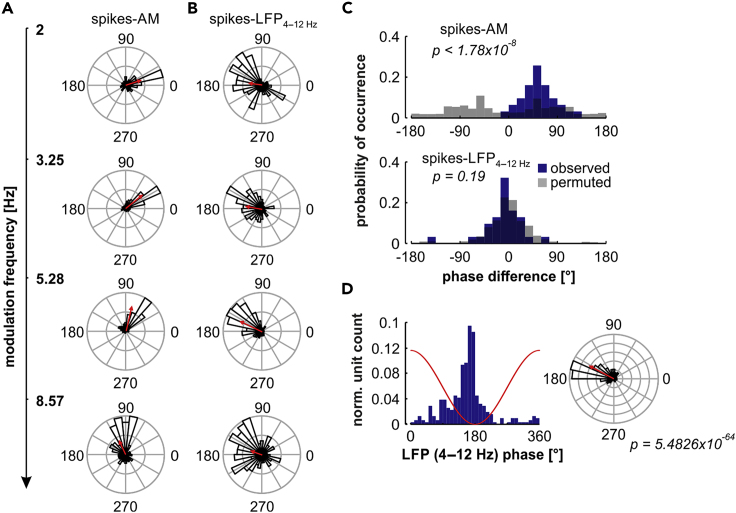
We systematically quantified the spike-phases relative to either the stimulus envelope or to low-frequency LFPs across modulation rates. This was done with the aim of evaluating the robustness of spike timing relative to the envelope, or to low-frequency oscillations, when changes in the temporal structure of the stimulus occurred. Only trackers were included in these analyses (n = 31; cutoff frequency ≤ 22.63 Hz, see Figure 1), because in non-trackers significant phase relationships between the stimulus' envelope and the spikes were inexistent. Remarkably, auditory cortical units showed phase differences across modulation rates that suggested a phase lag of spikes relative to the presented stimuli as the modulation rate increased. This phase lag was evidenced by a counterclockwise rotation of the units' preferred phase in response to rising AM rates (see Figure 6A for an exemplary unit, same shown in Figure 1A). We also calculated the preferred phase of the spikes relative to low-frequency LFPs (4–12 Hz, encompassing theta and alpha bands; a separate analysis for each band is shown in Figure S7). As the modulation frequencies increased, the preferred phase of spikes to low-frequency oscillations did not change predictably across stimuli (Figure 6B).
Figure 6.
Spike Phases Relative to the Stimulus (but Not to Low-Frequency LFPs) Are Affected by the Envelope's Rate
(A) Spike phases obtained from an exemplary tracking unit (same shown in Figure 1) relative to the AM envelope, for modulation frequencies to which the unit's spiking was significantly synchronized (i.e., 2–8.57 Hz). Red arrows indicate the mean vector of the phase distribution.
(B) Spike phases relative to low-frequency (4–12 Hz) LFPs. Note that the spikes here are the same spikes as in (A).
(C) Top: distribution of spike-phase differences between two consecutive modulation frequencies, when phases were calculated relative to the AM envelope. The observed distribution is shown in blue, whereas a surrogate (randomized differences across not-ordered modulation frequencies) distribution is shown in gray. There was a significant difference between the randomized and observed distribution (Fisher's circular mean test, p < 1.78 × 10−8). Bottom: Same conventions as data shown on top, but spike phases were calculated relative to low-frequency (8–12 Hz) LFPs. No significant differences occurred between the observed and the surrogate phase difference distributions (Fisher's circular mean test, p = 0.19).
(D) Histogram (left) and circular histogram (right) for the distribution of preferred spike phases (relative to low-frequency LFPs) in tracking units (n = 31), across all modulation frequencies tested (i.e., all preferred phases of trackers with a cutoff frequency ≤ 22.63 Hz are represented). The red trace in the left histogram illustrates the phase convention relative to the LFP; the red line in the circular histogram shows the mean vector of the phase distribution. Statistics showed that there was a significant directionality in the spike phases (Rayleigh test for non-uniformity, p = 5.48 × 10−64).
To test for reliability in the observed spike-envelope phase lag in the subpopulation of tracking units, we calculated for each unit the differences in preferred phase between pairs of low and high modulation frequencies, organized in an increasing order. The obtained distribution was then compared with a surrogate distribution in which the order of the modulation frequencies was randomized. At the population level, the recorded units reliably exhibited a phase lag that was represented in a clear above-zero spike-phase difference across pairs of modulation frequencies (Figure 6C, top; blue histogram). Significant differences between the observed and surrogate distributions (Figure 6C, top; gray histogram) were confirmed by a nonparametric circular median test (Fisher's circular median test, p < 1.78 × 10−8). In contrast, spike phases relative to low-frequency LFPs did not change predictably by increasing the modulation rate (Figure 6C, bottom; observed and surrogate differences in blue and gray, respectively), and there were no significant differences between observed and surrogate distributions (Fisher's circular median test, p = 0.19). The latter indicates that whereas the spikes change their stimulus-related phases (by lagging) as the envelopes' modulation rate increases, their synchronization to low-frequency oscillations is robust and independent of the stimulus modulation rate. In fact, by pooling all spike-to-LFP phases across all modulation rates, we observed that the preferred phase of spikes relative to low-frequency LFPs consistently occurred near the trough of the oscillations (Figure 6D; Rayleigh test, p = 5.4826 × 10−64; in the histograms, all preferred phases across tracking units and modulation frequencies are represented). This indicates a robust coupling between spikes and low-frequency cortical LFPs, and it is in line with the SFC results presented above.
Local-Field Potentials Phase Lock to AM Rates beyond the Spiking Synchronization Limits
We quantified the phase coherence between cortical oscillations and the AM stimuli, aiming to unravel whether recorded LFPs could represent amplitude envelopes to which the spiking activity did not synchronize. Coherence between LFPs and stimulus envelope, per modulation rate, was calculated using the stimulus-field coherence (StimFC) metric. The StimFC is a normalized, frequency-dependent synchronization index, which measures the strength of coherence between ongoing oscillatory activity and the auditory stimulus. The StimFC and SFC analyses are conceptually similar, but to evaluate phase locking between the AM envelopes and cortical oscillations, LFP windows were always defined in the range starting at 100 ms after stimulus onset and ending at the stimulus offset (i.e., windows were 900 ms long). Note that to obtain StimFC values, unit specificity was sacrificed to increase the robustness of coherence estimates. Thus, 300 LFP segments were chosen randomly, per modulation frequency, from a pool that included all trials from all units, depending on their classification as trackers or non-trackers. To reduce sampling biases, the procedure was repeated 500 times (see Transparent Methods for details).
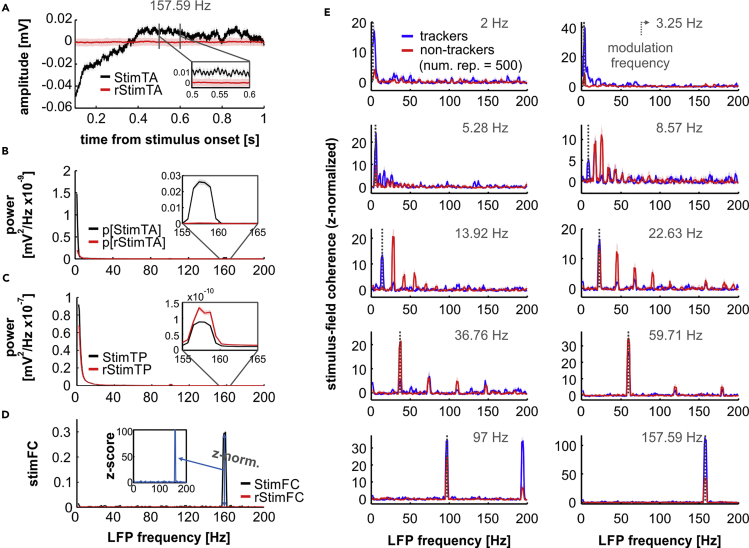
The stimulus-triggered averages (i.e., the mean of the LFP segments; StimTAs) revealed that, independently of the modulation frequency analyzed, oscillations in the AC were synchronized to the envelope's periodicity. Remarkably, we observed that even the highest modulation rate tested (157.59 Hz) entrained cortical field potentials, as depicted in Figure 7A. Note that the inset in the panel shows clear oscillatory activity in the LFP average, which matches the envelope's repetition rate. This entrainment did not occur when the phase consistency across trials was reduced to chance (red traces in the figure). Consequently, the spectra of the StimTAs clearly peaked at frequencies related to the modulation rate of the stimulus, which was not the case for the spectra of surrogate LFP averages (Figure 7B; black, observed; red, surrogate). Figure 7C shows the average spectrum of individual LFP windows used to obtain stimulus-triggered averages (also referred to as stimulus-triggered power, or StimTP). Spectral peaks were clearly present around frequencies related to the stimulus envelope in both observed and surrogate data (black and red traces in Figure 7C, respectively), which indicates that whereas the phase consistency was greatly reduced across trials for surrogate LFP windows, the power of individual segments was not equally affected. The StimFC (Figure 7D) was obtained after normalizing the power of the StimTA with the StimTP, and coherence values obtained from intact data were z-normalized to the distribution of coherence values obtained from surrogate data (z-normalized StimFC, shown in the inset of Figure 7D). Figure 7E depicts z-normalized StimFC values across modulation frequencies, for the population of trackers (blue) and non-trackers (red). Independently of the neuronal subgroup considered, LFPs in the AC were able to synchronize to AM envelopes with rates of at least 157.59 Hz, evidenced by the coherence peaks at frequencies related to the modulation rate under consideration, and at harmonics of such frequencies. The appearance of harmonics could be partly explained by nonlinearities in the processing of AM sounds along the auditory pathway (John and Picton, 2000, Prendergast et al., 2010).
Figure 7.
Local-Field Potentials Phase Lock to High-Frequency AM Envelopes
(A) Stimulus-triggered average (StimTA; black traces) related to tracking units, in response to a modulation frequency of 157.59 Hz (StimTAs over 500 repetitions). The StimTA preserves LFP components that are phase coherent to the stimulus (see Transparent Methods) and is obtained by averaging LFP windows (n = 300, randomly chosen a total of m = 500 times) associated to a particular time point (here, the 100-ms mark after stimulus onset). Randomized StimTAs are shown in red traces.
(B) Power of the StimTAs shown in A (black traces). Note that the StimTA spectrum peaks at frequencies related to the modulation rate of the stimulus, whereas the spectrum of surrogate StimTAs does not.
(C) Stimulus-triggered power (StimTP) of the LFP segments used to calculate StimTAs in (A). There is power in the LFP at frequencies around the modulation rate of the presented sounds, also when considering surrogate LFP segments (red trace).
(D) Stimulus-field coherence (StimFC; black) of recorded LFPs in response to a modulation frequency of 157.69 Hz. Calculated StimFC values were z-normalized to a baseline StimFC and are shown in the inset (light blue trace).
(E) z-normalized StimFC values across modulation rates (indicated in each sub-panel) for the subpopulations of tracking (blue) and non-tracking (red) units. Data in the figure are shown as median (solid lines) and quartiles (shaded areas).
Discussion
In this study, we investigated how LFPs interact with spikes for the representation of amplitude-modulated sounds. In a previous article we had already shown that, similar to other mammals, in the bat C. perspicillata the majority of cortical units cannot represent the temporal structure of fast (>22.63 Hz) AM sounds with a phase code (Martin et al., 2017). Here, using C. perspicillata as an animal model, we present three major findings that shed light onto the dynamics of temporal processing in the AC from an oscillatory coherence perspective. (1) SFC is stronger in units that elicit stimulus phase-locked responses (trackers) than in those that do not (non-trackers), even at modulation rates beyond their synchronization abilities. (2) AM envelopes modulate the amplitude and phase of low-frequency LFPs, but these modulations do not reliably account for differences in coherence between tracking and non-tracking units. (3) Spike phases relative to low-frequency LFPs (4–12 Hz) were robust across modulation rates, whereas spike phases relative to the stimuli were not. The implications of these findings are discussed below.
Neuronal Responses in the AC Exhibit Limited Tracking Capacities
The majority of recorded units had cutoff frequencies less than or equal to 22.63 Hz. Interestingly, we observed that cortical tracking units do not always synchronize to the same phase of the sound envelope across modulation rates; rather, spike phases relative to the envelope showed an increasing lag in response to faster envelopes (see Figures 6 and S1B). Similar phase differences have been observed in subcortical structures (Krishna and Semple, 2000), although not in the AC. The phase-locking threshold reported for auditory cortical units of C. perspicillata is consistent with results from previous studies showing that, in a variety of animal species, synchronized cortical responses have limiting modulation frequencies of around 25–35 Hz (Creutzfeldt et al., 1980, Schreiner and Urbas, 1988, Gaese and Ostwald, 1995, Fitzpatrick et al., 2009). Vocalizations of the bat species used in this study can carry AMs higher than 60 Hz (Hechavarria et al., 2016), and despite the reported phase-locking limitations such fast temporal structures can still be encoded in the bat's AC. The AC does not solely rely on a phase code to represent fast AM envelopes: rate coding is also a possible mechanism, whereby neurons alter their firing according to the stimulus' periodicity (Lu et al., 2001, Bendor and Wang, 2007, Gao et al., 2016, Tang et al., 2016). In a recent article, we reported that rate-coding neurons exist in the AC of C. perspicillata (Martin et al., 2017), which was corroborated in our present data (see Figure S2). Another possible way of representing fast envelopes in the AC is by means of fast trackers. Our data show that a small set of units phase-lock their spikes to envelopes above 30 Hz (see cutoff distribution in Figure 1F). These units were not considered in the analyses because their occurrence was rare (11.49% of the total recorded units), and our main interest lied in unraveling possible mechanisms underlying periodicity coding in the mammalian AC, by means of low-frequency LFPs. Nevertheless, note that neurons synchronized to modulation rates >30 Hz have also been reported in the AC of awake primates (Bieser and Muller-Preuss, 1996).
Local-Field Potentials in the Auditory Cortex Synchronize to Fast AM Rates
In contrast to the limited phase-locking abilities of the cortical spiking, LFPs were well synchronized to AM envelopes with modulation frequencies of at least 157.59 Hz (see Figure 7). The entrainment of high-frequency LFPs to fast temporal structures in the AC of C. perspicillata has also been reported in a previous study, in which cortical field potentials were shown to follow the syllabic rate of conspecific distress vocalizations, at frequencies >60 Hz (Hechavarria et al., 2016). However, phase synchronization of cortical oscillations to rates of at least 40 Hz is not an exclusive property of C. perspicillata's cortex, as oscillatory entrainment to fast-varying stimuli has also been reported in rats (Li et al., 2018, Wang et al., 2018). In humans, several electroencephalography and magnetoencephalography studies have shown auditory steady-state responses to AM envelopes with modulation frequencies as high as 80 Hz (Lins et al., 1995, John and Picton, 2000, Prendergast et al., 2010). In fact, the entrainment of gamma-band oscillations to fast-varying (>40 Hz) temporal structures in the AC is well documented as a mechanism for the cortical processing of the phonemic rate present in speech signals (Giraud and Poeppel, 2012).
It would be highly speculative to attribute the cause of high-frequency stimulus-coherent LFPs to a specific phenomenon along the auditory pathway. With our data, we cannot disentangle whether the observed oscillations are the result of potentials propagating passively in the conductive volume, or whether these cortical LFPs originate from synaptic inputs to the AC. Both possibilities are indeed feasible. In the AC of awake primates, subthreshold membrane potentials synchronize to AM sounds modulated at frequencies >30 Hz, which the spiking activity can no longer track in a phasic manner (Gao et al., 2016). Considering the fact that LFPs are affected by the membrane potentials (Buzsaki et al., 2012), it is possible that high-frequency LFP synchronization could be in part a consequence of synaptic potentials reflecting thalamic inputs (as the thalamus follows repetition rates of >100 Hz [Creutzfeldt et al., 1980, Rouiller et al., 1981]). On the other hand, previous studies in humans have shown that the sources of oscillatory responses to AM sounds depend on the modulation frequencies being heard: low frequencies are generated by cortical sources, whereas high frequencies (>40 Hz) are typically preferred by subcortical levels (Herdman et al., 2002, Farahani et al., 2017). Considering that neurons in subcortical auditory structures (e.g., the thalamus or the inferior colliculus) are able to phase lock to AM envelopes with frequencies >100 Hz (Joris et al., 2004), it is conceivable that potentials related to evoked activity in these structures propagate and reach the AC. However, we point out that these two phenomena (phase-locked subthreshold membrane potentials and passive propagation from lower order structures) are not mutually exclusive, and contributions from both might shape the dynamics of LFP coherence to fast varying acoustic streams.
Our data reveal LFP entrainment to AM rates of 36.76 and 59.71 Hz, two frequencies that fall within the canonical low-gamma range, spanning from 30 to 60 Hz. We note that it would be inaccurate to claim that these fluctuations in the gamma range subserve computational operations analogous to those typically described in the visual system, such as feature binding or neuronal communication (Fries et al., 2001, Womelsdorf et al., 2007, Fries, 2009, Fries, 2015, Singer, 2017). Rather, the oscillatory activity at those frequencies, in our data, represents a phase alignment strongly driven by the temporal structure of the AM envelope. Nevertheless, this does not imply that gamma oscillations do not participate in the encoding of sounds in the AC. An increase of gamma-band activity, linked to the processing of auditory stimuli, has been reported in humans (Pantev et al., 1991), non-human primates (Brosch et al., 2002), rats (Vianney-Rodrigues et al., 2011), and bats (Medvedev and Kanwal, 2008). Gamma-band oscillations in these studies (except for the one conducted on human subjects) were also correlated to some extent with neuronal spiking, something that we did not observe in our data (see Figures 2 and 3). We speculate the following main reasons for this disparity: (1) gamma oscillations, if temporally aligned to listened sounds, occurred in the early portion of short auditory stimuli, whereas our analyses were conducted in the range of 100 ms to 1s after stimulus onset; (2) induced gamma activity (i.e., not phase locked to specific portions of the stimulus) would have been masked by phase coherence analyses such as the SFC or StimFC; and (3) gamma-band LFPs might not be crucial for phase coding of slow temporal envelopes in the AC. In line with the last statement, tracking and non-tracking responses may instead be mediated by low-frequency oscillations, in the theta-alpha range. The possible contributions of low-frequency oscillations to periodicity coding in the cortex are addressed in the following section.
Roles of Low-Frequency Spike-LFP Coherence for Phase Coding in the AC
We showed that units in the AC capable to lock their spiking to the periodic temporal structure of AM envelopes (that is, trackers) synchronize more strongly to low-frequency LFPs than their non-tracking counterparts. In other words, the SFC of cortical tracking units in the theta-alpha range is higher than that in non-tracking units. Importantly, differences in low-frequency coherence between cortical trackers and non-trackers occurred well beyond the synchronization limits of neurons in the AC to AM sounds (up to modulation rates of 157.59 Hz; see Figures 1, 2, and 3). Moreover, neither PAC between the stimulus phase and the amplitude of low-frequency LFPs (Figure 4) nor the ITC of the units' LFPs across modulation rates (Figure 5) allowed to reliably separate trackers from non-trackers. A reliable classification (in terms of low-frequency LFP bands) was only possible when considering the SFC, mostly at theta (4–8 Hz) and alpha (8–12 Hz) bands. The former, together with the fact that spikes and slow oscillations maintain a robust phase relationship across modulation rates (see Figure 6), suggests that low-frequency waves might be important for periodicity coding.
The origins of theta and alpha oscillations in the AC remain somewhat unexplored. Evidence from in vivo experiments in the visual cortex suggests that oscillatory processes in the range of 5–10 Hz are generated by pacemaking pyramidal neurons located in infragranular layers of the cortical column, whose membrane temporal dynamics correspond with the aforementioned rhythms (Sun and Dan, 2009). In the auditory modality, Szymanski and colleagues observed that fast activations in the thalamo-recipient layers in the AC produce strong phase resets in ongoing low-frequency LFPs, which could explain, in part, their entrainment to sensory input (Szymanski et al., 2011). Although the resulting phase alignment in such scenario would be dependent on thalamic inputs (and therefore could be considered as evoked), there is strong evidence suggesting that cortical oscillatory activity also represents modulatory (as opposed to evoked) influences. For example, in the macaque brain, somatosensory inputs modulate the phase of delta- and theta-band oscillations in primary AC, which results in enhanced processing of acoustic stimuli (Lakatos et al., 2007). Importantly, these phase modulations occur not only during multimodal sensory processing but also as a consequence of attentional mechanisms, which could be regulated by higher order structures (Schroeder and Lakatos, 2009, Arnal and Giraud, 2012, Lakatos et al., 2013).
In the AC, low-frequency field potentials regulate the amplitude of faster oscillations, together with the neuronal excitability, in a hierarchical manner (Lakatos et al., 2005). These low-frequency oscillations can reliably entrain to periodic acoustic streams, whether the periodicity is present in the temporal (Lakatos et al., 2005, Lakatos et al., 2013, Luo et al., 2010, Arnal and Giraud, 2012, Giraud and Poeppel, 2012) or the spectral (Henry and Obleser, 2012) structure of the stimulus. For example, the phase patterns of theta oscillations are stable (and unique) enough to discriminate speech on a single trial basis (Luo and Poeppel, 2007). This implies that the phase of delta and theta bands might actively modulate the cortical spiking and the power of higher frequency LFPs according to the sensory input, such that a multiplexed cortical activity would enhance the representation of acoustic stimuli (Gross et al., 2013, Hyafil et al., 2015). Furthermore, there is strong evidence supporting the roles of entrained low-frequency oscillations in modulating behavioral performance during detection tasks (Ng et al., 2012, Lawrance et al., 2014). When there is entrainment of low-frequency oscillations (see Henry and Obleser, 2012, Lawrance et al., 2014), enhanced detection could be explained by the predictive coding framework. From the point of view of predictive coding, entrainment could allow sensory predictions (represented by the phase of low-frequency oscillations) to temporally align with relevant stimuli, and thus enhance their representation in the brain (Arnal and Giraud, 2012). Overall, the above indicates that low-frequency oscillations in the auditory domain play an important role for coordinating efficient neuronal responses to acoustic (and predictive) stimuli.
Our results resonate with the aforementioned views, showing that spike coherence to low-frequency LFPs is (at least) a fingerprint of periodicity coding in the AC. Based on our observations, we speculate that neurons whose spiking patterns are coupled to slow cortical oscillations profit from the phase relationship of these low-frequency waves with the periodicity of acoustic streams. On the contrary, neurons not phase synchronized to low-frequency LFPs do not profit from the aforementioned LFP-stimulus phase relationship, and do not elicit temporally organized spikes that track the rhythms of the AM envelopes. Altogether, our data suggest that low-frequency SFC could play an important role in orchestrating the phasic representation of rhythmic stimuli in the AC.
Methods
All methods can be found in the accompanying Transparent Methods supplemental file.
Acknowledgments
The German Research Council (DFG) funded this work (Grant No. HE 7478/1-1).
Author Contributions
F.G.R. and J.C.H. designed the study. F.G.R. collected the data. F.G.R. analyzed the data and wrote the manuscript. F.G.R., L.M.M., M.J.B., Y.C.C., M.K., and J.C.H. discussed the results and reviewed the manuscript.
Declaration of Interests
The authors declare no competing interests.
Published: November 30, 2018
Footnotes
Supplemental Information includes Transparent Methods and seven figures and can be found with this article online at https://doi.org/10.1016/j.isci.2018.10.009.
Contributor Information
Francisco García-Rosales, Email: garciarosales@bio.uni-frankfurt.de.
Julio C. Hechavarria, Email: hechavarria@bio.uni-frankfurt.de.
Supplemental Information
References
- Arnal L.H., Flinker A., Kleinschmidt A., Giraud A.L., Poeppel D. Human screams occupy a privileged niche in the communication soundscape. Curr. Biol. 2015;25:2051–2056. doi: 10.1016/j.cub.2015.06.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnal L.H., Giraud A.L. Cortical oscillations and sensory predictions. Trends Cogn. Sci. 2012;16:390–398. doi: 10.1016/j.tics.2012.05.003. [DOI] [PubMed] [Google Scholar]
- Bendor D., Wang X. Differential neural coding of acoustic flutter within primate auditory cortex. Nat. Neurosci. 2007;10:763–771. doi: 10.1038/nn1888. [DOI] [PubMed] [Google Scholar]
- Bieser A., Muller-Preuss P. Auditory responsive cortex in the squirrel monkey: neural responses to amplitude-modulated sounds. Exp. Brain Res. 1996;108:273–284. doi: 10.1007/BF00228100. [DOI] [PubMed] [Google Scholar]
- Brosch M., Budinger E., Scheich H. Stimulus-related gamma oscillations in primate auditory cortex. J. Neurophysiol. 2002;87:2715–2725. doi: 10.1152/jn.2002.87.6.2715. [DOI] [PubMed] [Google Scholar]
- Buzsaki G., Anastassiou C.A., Koch C. The origin of extracellular fields and currents–EEG, ECoG, LFP and spikes. Nat. Rev. Neurosci. 2012;13:407–420. doi: 10.1038/nrn3241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Creutzfeldt O., Hellweg F.C., Schreiner C. Thalamocortical transformation of responses to complex auditory stimuli. Exp. Brain Res. 1980;39:87–104. doi: 10.1007/BF00237072. [DOI] [PubMed] [Google Scholar]
- Drullman R., Festen J.M., Plomp R. Effect of reducing slow temporal modulations on speech reception. J. Acoust. Soc. Am. 1994;95:2670–2680. doi: 10.1121/1.409836. [DOI] [PubMed] [Google Scholar]
- Farahani E.D., Goossens T., Wouters J., van Wieringen A. Spatiotemporal reconstruction of auditory steady-state responses to acoustic amplitude modulations: potential sources beyond the auditory pathway. Neuroimage. 2017;148:240–253. doi: 10.1016/j.neuroimage.2017.01.032. [DOI] [PubMed] [Google Scholar]
- Fitzpatrick D.C., Roberts J.M., Kuwada S., Kim D.O., Filipovic B. Processing temporal modulations in binaural and monaural auditory stimuli by neurons in the inferior colliculus and auditory cortex. J. Assoc. Res. Otolaryngol. 2009;10:579–593. doi: 10.1007/s10162-009-0177-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fries P. Neuronal gamma-band synchronization as a fundamental process in cortical computation. Annu. Rev. Neurosci. 2009;32:209–224. doi: 10.1146/annurev.neuro.051508.135603. [DOI] [PubMed] [Google Scholar]
- Fries P. Rhythms for cognition: communication through coherence. Neuron. 2015;88:220–235. doi: 10.1016/j.neuron.2015.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fries P., Neuenschwander S., Engel A.K., Goebel R., Singer W. Rapid feature selective neuronal synchronization through correlated latency shifting. Nat. Neurosci. 2001;4:194–200. doi: 10.1038/84032. [DOI] [PubMed] [Google Scholar]
- Fujioka T., Trainor L.J., Large E.W., Ross B. Internalized timing of isochronous sounds is represented in neuromagnetic beta oscillations. J. Neurosci. 2012;32:1791–1802. doi: 10.1523/JNEUROSCI.4107-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaese B.H., Ostwald J. Temporal coding of amplitude and frequency modulation in the rat auditory cortex. Eur. J. Neurosci. 1995;7:438–450. doi: 10.1111/j.1460-9568.1995.tb00340.x. [DOI] [PubMed] [Google Scholar]
- Gao L., Kostlan K., Wang Y., Wang X. Distinct subthreshold mechanisms underlying rate-coding principles in primate auditory cortex. Neuron. 2016;91:905–919. doi: 10.1016/j.neuron.2016.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giraud A.L., Poeppel D. Cortical oscillations and speech processing: emerging computational principles and operations. Nat. Neurosci. 2012;15:511–517. doi: 10.1038/nn.3063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grasse D.W., Moxon K.A. Correcting the bias of spike field coherence estimators due to a finite number of spikes. J. Neurophysiol. 2010;104:548–558. doi: 10.1152/jn.00610.2009. [DOI] [PubMed] [Google Scholar]
- Gross J., Hoogenboom N., Thut G., Schyns P., Panzeri S., Belin P., Garrod S. Speech rhythms and multiplexed oscillatory sensory coding in the human brain. PLoS Biol. 2013;11:e1001752. doi: 10.1371/journal.pbio.1001752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hechavarria J.C., Beetz M.J., Macias S., Kossl M. Vocal sequences suppress spiking in the bat auditory cortex while evoking concomitant steady-state local field potentials. Sci. Rep. 2016;6:39226. doi: 10.1038/srep39226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henry M.J., Obleser J. Frequency modulation entrains slow neural oscillations and optimizes human listening behavior. Proc. Natl. Acad. Sci. U S A. 2012;109:20095–20100. doi: 10.1073/pnas.1213390109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herdman A.T., Lins O., Van Roon P., Stapells D.R., Scherg M., Picton T.W. Intracerebral sources of human auditory steady-state responses. Brain Topogr. 2002;15:69–86. doi: 10.1023/a:1021470822922. [DOI] [PubMed] [Google Scholar]
- Hyafil A., Fontolan L., Kabdebon C., Gutkin B., Giraud A.L. Speech encoding by coupled cortical theta and gamma oscillations. Elife. 2015;4:e06213. doi: 10.7554/eLife.06213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- John M.S., Picton T.W. Human auditory steady-state responses to amplitude-modulated tones: phase and latency measurements. Hear. Res. 2000;141:57–79. doi: 10.1016/s0378-5955(99)00209-9. [DOI] [PubMed] [Google Scholar]
- Johnson J.S., Yin P., O'Connor K.N., Sutter M.L. Ability of primary auditory cortical neurons to detect amplitude modulation with rate and temporal codes: neurometric analysis. J. Neurophysiol. 2012;107:3325–3341. doi: 10.1152/jn.00812.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joris P.X., Schreiner C.E., Rees A. Neural processing of amplitude-modulated sounds. Physiol. Rev. 2004;84:541–577. doi: 10.1152/physrev.00029.2003. [DOI] [PubMed] [Google Scholar]
- Kanwal J.S., Matsumura S., Ohlemiller K., Suga N. Analysis of acoustic elements and syntax in communication sounds emitted by mustached bats. J. Acoust. Soc. Am. 1994;96:1229–1254. doi: 10.1121/1.410273. [DOI] [PubMed] [Google Scholar]
- Kayser C., Montemurro M.A., Logothetis N.K., Panzeri S. Spike-phase coding boosts and stabilizes information carried by spatial and temporal spike patterns. Neuron. 2009;61:597–608. doi: 10.1016/j.neuron.2009.01.008. [DOI] [PubMed] [Google Scholar]
- Koch U., Grothe B. Interdependence of spatial and temporal coding in the auditory midbrain. J. Neurophysiol. 2000;83:2300–2314. doi: 10.1152/jn.2000.83.4.2300. [DOI] [PubMed] [Google Scholar]
- Krishna B.S., Semple M.N. Auditory temporal processing: responses to sinusoidally amplitude-modulated tones in the inferior colliculus. J. Neurophysiol. 2000;84:255–273. doi: 10.1152/jn.2000.84.1.255. [DOI] [PubMed] [Google Scholar]
- Lakatos P., Chen C.M., O'Connell M.N., Mills A., Schroeder C.E. Neuronal oscillations and multisensory interaction in primary auditory cortex. Neuron. 2007;53:279–292. doi: 10.1016/j.neuron.2006.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakatos P., Musacchia G., O'Connel M.N., Falchier A.Y., Javitt D.C., Schroeder C.E. The spectrotemporal filter mechanism of auditory selective attention. Neuron. 2013;77:750–761. doi: 10.1016/j.neuron.2012.11.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakatos P., Shah A.S., Knuth K.H., Ulbert I., Karmos G., Schroeder C.E. An oscillatory hierarchy controlling neuronal excitability and stimulus processing in the auditory cortex. J. Neurophysiol. 2005;94:1904–1911. doi: 10.1152/jn.00263.2005. [DOI] [PubMed] [Google Scholar]
- Lawrance E.L., Harper N.S., Cooke J.E., Schnupp J.W. Temporal predictability enhances auditory detection. J. Acoust. Soc. Am. 2014;135:EL357–EL363. doi: 10.1121/1.4879667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li S., Ma L., Wang Y., Wang X., Li Y., Qin L. Auditory steady-state responses in primary and non-primary regions of the auditory cortex in neonatal ventral hippocampal lesion rats. PLoS One. 2018;13:e0192103. doi: 10.1371/journal.pone.0192103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lins O.G., Picton P.E., Picton T.W., Champagne S.C., Durieux-Smith A. Auditory steady-state responses to tones amplitude-modulated at 80-110 Hz. J. Acoust. Soc. Am. 1995;97:3051–3063. doi: 10.1121/1.411869. [DOI] [PubMed] [Google Scholar]
- Lu T., Liang L., Wang X. Temporal and rate representations of time-varying signals in the auditory cortex of awake primates. Nat. Neurosci. 2001;4:1131–1138. doi: 10.1038/nn737. [DOI] [PubMed] [Google Scholar]
- Lu T., Wang X. Temporal discharge patterns evoked by rapid sequences of wide- and narrowband clicks in the primary auditory cortex of cat. J. Neurophysiol. 2000;84:236–246. doi: 10.1152/jn.2000.84.1.236. [DOI] [PubMed] [Google Scholar]
- Luo H., Liu Z., Poeppel D. Auditory cortex tracks both auditory and visual stimulus dynamics using low-frequency neuronal phase modulation. PLoS Biol. 2010;8:e1000445. doi: 10.1371/journal.pbio.1000445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo H., Poeppel D. Phase patterns of neuronal responses reliably discriminate speech in human auditory cortex. Neuron. 2007;54:1001–1010. doi: 10.1016/j.neuron.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo H., Wang Y., Poeppel D., Simon J.Z. Concurrent encoding of frequency and amplitude modulation in human auditory cortex: encoding transition. J. Neurophysiol. 2007;98:3473–3485. doi: 10.1152/jn.00342.2007. [DOI] [PubMed] [Google Scholar]
- Malone B.J., Scott B.H., Semple M.N. Dynamic amplitude coding in the auditory cortex of awake rhesus macaques. J. Neurophysiol. 2007;98:1451–1474. doi: 10.1152/jn.01203.2006. [DOI] [PubMed] [Google Scholar]
- Martin L.M., Garcia-Rosales F., Beetz M.J., Hechavarria J.C. Processing of temporally patterned sounds in the auditory cortex of Seba's short-tailed bat, Carollia perspicillata. Eur. J. Neurosci. 2017;46:2365–2379. doi: 10.1111/ejn.13702. [DOI] [PubMed] [Google Scholar]
- Medvedev A.V., Kanwal J.S. Communication call-evoked gamma-band activity in the auditory cortex of awake bats is modified by complex acoustic features. Brain Res. 2008;1188:76–86. doi: 10.1016/j.brainres.2007.10.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Middlebrooks J.C. Sound localization. Handb. Clin. Neurol. 2015;129:99–116. doi: 10.1016/B978-0-444-62630-1.00006-8. [DOI] [PubMed] [Google Scholar]
- Ng B.S.W., Schroeder T., Kayser C. A precluding but not ensuring role of entrained low-frequency oscillations for auditory perception. J. Neurosci. 2012;32:12268–12276. doi: 10.1523/JNEUROSCI.1877-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niwa M., O'Connor K.N., Engall E., Johnson J.S., Sutter M.L. Hierarchical effects of task engagement on amplitude modulation encoding in auditory cortex. J. Neurophysiol. 2015;113:307–327. doi: 10.1152/jn.00458.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palva S., Palva J.M. Functional roles of alpha-band phase synchronization in local and large-scale cortical networks. Front. Psychol. 2011;2:204. doi: 10.3389/fpsyg.2011.00204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pantev C., Makeig S., Hoke M., Galambos R., Hampson S., Gallen C. Human auditory evoked gamma-band magnetic fields. Proc. Natl. Acad. Sci. U S A. 1991;88:8996–9000. doi: 10.1073/pnas.88.20.8996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prendergast G., Johnson S.R., Green G.G. Temporal dynamics of sinusoidal and non-sinusoidal amplitude modulation. Eur. J. Neurosci. 2010;32:1599–1607. doi: 10.1111/j.1460-9568.2010.07423.x. [DOI] [PubMed] [Google Scholar]
- Rhode W.S., Greenberg S. Encoding of amplitude modulation in the cochlear nucleus of the cat. J. Neurophysiol. 1994;71:1797–1825. doi: 10.1152/jn.1994.71.5.1797. [DOI] [PubMed] [Google Scholar]
- Rouiller E., de Ribaupierre Y., Toros-Morel A., de Ribaupierre F. Neural coding of repetitive clicks in the medial geniculate body of cat. Hear. Res. 1981;5:81–100. doi: 10.1016/0378-5955(81)90028-9. [DOI] [PubMed] [Google Scholar]
- Schreiner C.E., Urbas J.V. Representation of amplitude modulation in the auditory cortex of the cat. II. Comparison between cortical fields. Hear. Res. 1988;32:49–63. doi: 10.1016/0378-5955(88)90146-3. [DOI] [PubMed] [Google Scholar]
- Schroeder C.E., Lakatos P. Low-frequency neuronal oscillations as instruments of sensory selection. Trends Neurosci. 2009;32:9–18. doi: 10.1016/j.tins.2008.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon R.V., Zeng F.G., Kamath V., Wygonski J., Ekelid M. Speech recognition with primarily temporal cues. Science. 1995;270:303–304. doi: 10.1126/science.270.5234.303. [DOI] [PubMed] [Google Scholar]
- Singer W. Neuronal oscillations: unavoidable and useful? Eur. J. Neurosci. 2018:1–10. doi: 10.1111/ejn.13796. [DOI] [PubMed] [Google Scholar]
- Slama M.C., Delgutte B. Neural coding of sound envelope in reverberant environments. J. Neurosci. 2015;35:4452–4468. doi: 10.1523/JNEUROSCI.3615-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stefanics G., Hangya B., Hernadi I., Winkler I., Lakatos P., Ulbert I. Phase entrainment of human delta oscillations can mediate the effects of expectation on reaction speed. J. Neurosci. 2010;30:13578–13585. doi: 10.1523/JNEUROSCI.0703-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suga N. Neural processing of auditory signals in the time domain: delay-tuned coincidence detectors in the mustached bat. Hear. Res. 2015;324:19–36. doi: 10.1016/j.heares.2015.02.008. [DOI] [PubMed] [Google Scholar]
- Sun W., Dan Y. Layer-specific network oscillation and spatiotemporal receptive field in the visual cortex. Proc. Natl. Acad. Sci. U S A. 2009;106:17986–17991. doi: 10.1073/pnas.0903962106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szymanski F.D., Rabinowitz N.C., Magri C., Panzeri S., Schnupp J.W. The laminar and temporal structure of stimulus information in the phase of field potentials of auditory cortex. J. Neurosci. 2011;31:15787–15801. doi: 10.1523/JNEUROSCI.1416-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang H.Z., Crain S., Johnson B.W. Dual temporal encoding mechanisms in human auditory cortex: evidence from MEG and EEG. Neuroimage. 2016;128:32–43. doi: 10.1016/j.neuroimage.2015.12.053. [DOI] [PubMed] [Google Scholar]
- Theunissen F.E., Doupe A.J. Temporal and spectral sensitivity of complex auditory neurons in the nucleus HVc of male zebra finches. J. Neurosci. 1998;18:3786–3802. doi: 10.1523/JNEUROSCI.18-10-03786.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tort A.B., Komorowski R., Eichenbaum H., Kopell N. Measuring phase-amplitude coupling between neuronal oscillations of different frequencies. J. Neurophysiol. 2010;104:1195–1210. doi: 10.1152/jn.00106.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vianney-Rodrigues P., Iancu O.D., Welsh J.P. Gamma oscillations in the auditory cortex of awake rats. Eur. J. Neurosci. 2011;33:119–129. doi: 10.1111/j.1460-9568.2010.07487.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y., Ma L., Wang X., Qin L. Differential modulation of the auditory steady state response and inhibitory gating by chloral hydrate anesthesia. Sci. Rep. 2018;8:3683. doi: 10.1038/s41598-018-21920-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wohlgemuth M.J., Luo J., Moss C.F. Three-dimensional auditory localization in the echolocating bat. Curr. Opin. Neurobiol. 2016;41:78–86. doi: 10.1016/j.conb.2016.08.002. [DOI] [PubMed] [Google Scholar]
- Womelsdorf T., Fries P. The role of neuronal synchronization in selective attention. Curr. Opin. Neurobiol. 2007;17:154–160. doi: 10.1016/j.conb.2007.02.002. [DOI] [PubMed] [Google Scholar]
- Womelsdorf T., Schoffelen J.M., Oostenveld R., Singer W., Desimone R., Engel A.K., Fries P. Modulation of neuronal interactions through neuronal synchronization. Science. 2007;316:1609–1612. doi: 10.1126/science.1139597. [DOI] [PubMed] [Google Scholar]
- Yin P.B., Johnson J.S., O'Connor K.N., Sutter M.L. Coding of amplitude modulation in primary auditory cortex. J. Neurophysiol. 2011;105:582–600. doi: 10.1152/jn.00621.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.