Abstract
The FEBio software suite is a set of software tools for nonlinear finite element analysis in biomechanics and biophysics. FEBio employs mixture theory to account for the multiconstituent nature of biological materials, integrating the field equations for irreversible thermodynamics, solid mechanics, fluid mechanics, mass transport with reactive species, and electrokinetics. This communication describes the development and application of a new “plugin” framework for FEBio. Plugins are dynamically linked libraries that allow users to add new features and to couple FEBio with other domain-specific software applications without modifying the source code directly. The governing equations and simulation capabilities of FEBio are reviewed. The implementation, structure, use, and application of the plugin framework are detailed. Several example plugins are described in detail to illustrate how plugins enrich, extend, and leverage existing capabilities in FEBio, including applications to deformable image registration, constitutive modeling of biological tissues, coupling to an external software package that simulates angiogenesis using a discrete computational model, and a nonlinear reaction-diffusion solver. The plugin feature facilitates dissemination of new simulation methods, reproduction of published results, and coupling of FEBio with other domain-specific simulation approaches such as compartmental modeling, agent-based modeling, and rigid-body dynamics. We anticipate that the new plugin framework will greatly expand the range of applications for the FEBio software suite and thus its impact.
Introduction
The FEBio project (1) was launched in 2007 to overcome the lack of a general purpose finite element (FE) software for solving problems in computational biomechanics. This deficiency hampered research progress, dissemination, and sharing of models and results. Commercial FE codes such as Ansys/Fluent (ANSYS, Canonsburg, PA), ABAQUS (Dassault Systèmes, Vélizy-Villacoublay, France), and Comsol Multiphysics (COMSOL, Burlington, MA) that were used historically for research in computational biomechanics are not specifically designed to serve the field, lack important simulation capabilities, are costly, and are closed source, which makes them difficult to verify and extend. These limitations led many researchers to develop custom FE codes for simulating domain-specific problems (2). Most of these custom codes were never distributed to the community.
The authors and many others in the research community felt there was a genuine need for a new FE simulation tool that would be designed by and for the biomechanics community. FEBio was designed around three pillars. First, it specifically targets the biomechanics community by focusing on simulation capabilities that are relevant in the field. This includes, for example, accurate constitutive relations for mechanical, transport, and electrokinetic properties of tissues and cells; the ability to easily model anisotropy and inhomogeneity; and the ability to prescribe boundary conditions and loading scenarios to model the complex interactions between biological structures. Second, both installation packages and the source code are freely available and designed such that it is easy for researchers to implement new algorithms (e.g., new constitutive models). This greatly reduced the need for new custom-written codes and overcame the problems with verification and repeatability of results. Third, we place substantial emphasis on thorough documentation, support, and outreach to the community, which has made it much easier than before for researchers to develop new ideas and share them with others.
Recently, we developed a plugin framework to allow users to extend the standard feature set of FEBio with less effort and to couple FEBio with other simulation codes. Although users can download and modify the FEBio source code directly, building the entire source code can be challenging, especially because of its dependency on third-party libraries. Further, disseminating custom modifications to the source code may be challenging because changes made by users may become incompatible with future releases of FEBio. The plugin framework overcomes these problems because plugins can be developed independently from the FEBio source code. In addition, the plugin framework facilitates dissemination and sharing because plugins can be distributed separately from the FEBio source code and installation packages (https://febio.org/plugins).
The objective of this communication is to introduce FEBio and the capabilities of the new plugin framework to the biophysics community. The exposition covers the modular framework of FEBio and its kernel mechanism, which were central to the development of the plugin framework. Several plugin examples illustrate the generality and versatility of the framework, including a material plugin based on a recent proposal for a novel constitutive model for describing a fibrous material with deformation induced anisotropy (3), an implementation of the hyperelastic warping algorithm for deformable image registration (4), a plugin that couples a discrete model of angiogenesis with FEBio to simulate the interactions between angiogenic microvessels and the ECM (5, 6, 7, 8), and a plugin for solving reaction-diffusion-convection problems.
Materials and Methods
Overview of FEBio
FEBio uses the FE method to discretize the equations for conservation of mass, linear momentum, and charge. The resulting equations allow fully coupled simulation of solid mechanics, solid-fluid mixtures (9), fluid mechanics (10), fluid-solid interactions, transport (11, 12), reaction and diffusion of neutral and charged species (12, 13), contact (11, 14, 15, 16, 17), prestrain (18), and growth and remodeling (13). The governing equations are formulated based on mixture theory. A mixture consists of any number of constituents α that may occupy the same region. The apparent mass density of constituent α is denoted by ρα. The complete set of governing equations can be summarized as follows:
| (1) |
| (2) |
| (3) |
| (4) |
and
| (5) |
Equation 1 represents the mass balance equation for constituent α with velocity vα. Equation 2 is the balance of linear momentum for each constituent, where aα is the acceleration, Tα is the Cauchy stress, bα is the body force, and is the internal momentum supply to constituent α due to interactions with all other mixture constituents. Equation 3 is the entropy inequality, which places constraints on the constitutive models. Here, Lα is the rate of deformation tensor, uα = vα − v, and v is the mixture velocity. The last term in this equation represents the rate form of the familiar constraint in chemical kinetics that reactions may proceed spontaneously only if they produce a net decrease in the mixture free energy. Electrokinetics is introduced by using Coulomb’s law as a body force acting on electrically charged constituents, Eq. 4, where zα is the charge number and Mα is the molar mass of constituent α, Fc is Faraday’s constant, and ψ is the electric potential in the mixture. To solve for ψ, we employ the electroneutrality condition, Eq. 5. FE discretization of Eqs. 1, 2, 3, 4, and 5 above results in a nonlinear system of equations that is solved using Newton-based methods, including quasi-Newton methods such as Broyden–Fletcher–Goldfarb–Shanno (BFGS) and Broyden’s method (19).
A more detailed overview of FEBio’s features can be found in the FEBio User Manual and the FEBio Theory Manual (https://febio.org/febio-help/). An overview of FEBio development and its features with historical context can be found in our recent publication (2).
Overview of the plugin mechanism
A plugin is essentially a “dynamically” linked library (also known as a shared object on some operating systems) that is linked to the executable at runtime. They differ from “static” libraries, which are linked to the executable at build time. The main advantage of dynamic libraries is that they are not required when building the executable and thus can be developed and maintained independently of the executable.
In FEBio, plugins can be used to add new features, such as new constitutive models, boundary loads, body loads, tasks, plot data, and log data. They can also be used to implement an entirely new physics module, as illustrated by the FEBioChem plugin described below. The main advantage of a plugin versus extending the source code directly is that plugins are loaded at runtime and can be developed and maintained outside of the FEBio source code. At runtime, FEBio parses a configuration file. This file contains a list of all plugins that the user wants to use, and FEBio loads each plugin file in this list. During this process, the plugin is given a chance to initialize itself. During this initialization step, it registers the new features with FEBio. For each feature, metadata are passed to FEBio, such as a textual name and a list of parameters that FEBio can use to allocate and modify the data of the plugin features. After the registration process, FEBio can use the new features in the plugin. For instance, after loading a new material plugin, the input module will be able to process the definition of the new material in the input file.
A more detailed explanation of the plugin framework can be found in the Supporting Materials and Methods. Detailed instructions on how to create plugins can be found in the FEBio Developer’s Manual (http://febio.org/support/). The specific plugins described below are available for download at the FEBio website (http://febio.org/plugins/).
Results
FEBio supports a number of different types of plugins, including material, plot data, callback, task, and solver plugins. These are described in more detail in the Supporting Materials and Methods. The following sections provide examples of material, nonlinear constraint, task, and solver plugins. Each type of plugin is demonstrated by a specific example application.
Material plugins
FEBio offers a rich library of constitutive models for representing the solid component of mixtures, including isotropic and anisotropic hyperelasticity, viscohyperelasticity (20), specialized materials for modeling fibrous tissues, damage mechanics, and growth and remodeling. Nevertheless, the development of novel constitutive models for describing the material response of biological tissues remains an active area of research as our understanding of how the intricate interactions between different physical scales affect the macroscopic material response continues to grow. As a result, the ability to add novel constitutive models to FEBio has been a high priority. Making this task easier for our users was the main initial impetus for the development of the plugin framework.
A new constitutive model can be implemented via a material plugin. Constitutive models are used to evaluate solution-dependent quantities, such as stress, permeability, diffusivity, etc. The quantities that need to be defined by the plugin depend on the particular physics module that the plugin extends. For instance, when implementing a new constitutive model for structural mechanics, the plugin must implement the evaluation of the second-order Cauchy stress tensor and the fourth-order spatial elasticity tensor. Implementation of the often complicated tensorial expressions for these quantities is greatly simplified by the extensive tensor classes in FEBio (see Supporting Materials and Methods).
As an illustration, we describe a material plugin that implements a constitutive model for representing fibrous ECMs as proposed by Wang et al. (3). The constitutive model is designed to reproduce experimental observations of long-range force transmission by cells in collagen gels due to realignment of collagen fibrils during loading. This is achieved by representing two fiber families. The first family aligns with the principal axes of the deformation, producing an increasingly anisotropic response as the deformation increases in magnitude, whereas the second family provides an isotropic background stress that opposes alignment.
The strain-energy density function of this constitutive model is given by:
| (6) |
Here, Wb captures the isotropic response:
| (7) |
where μ is the shear modulus, κ is the bulk modulus, is the first invariant of the deviatoric right deformation tensor , F is the deformation gradient, and J = det(F) is the volume ratio. Wf is the contribution from the aligned fibers:
| (8) |
where the λa are the principal stretch ratios. The particular form of f can be found in the Supporting Materials and Methods.
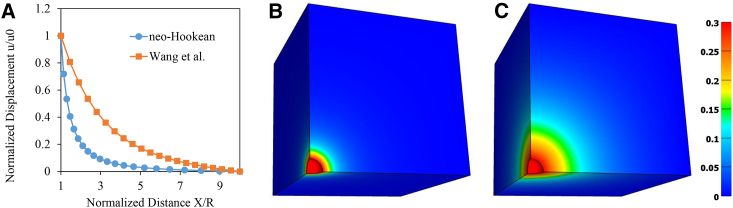
To illustrate the behavior of the material, an isotropically contracting sphere representing a contracting cell of radius R was positioned at the center of a cube of size L = 10 R. Cellular contraction was simulated by displacing the surface of the sphere toward its center to achieve a radial strain u0/R = 0.3. The resulting normalized displacement profiles as a function of normalized radial distance from the surface of the sphere demonstrate that the Wang et al. constitutive model produces greater matrix displacements and results in a longer range of influence of the simulated cellular traction forces than a standard neo-Hookean material (Fig. 1 A). This is visualized in space by examining the fringe plots of total matrix displacement (Fig. 1, B and C). These results are similar to those obtained by the authors for spherical cells in a cylindrical matrix (Fig. 2 in (3)). Please see the Supporting Materials and Methods for further details of the constitutive model and the material coefficients used in the simulations.
Figure 1.
Simulation of force transmission to the ECM due to cellular contraction using a neo-Hookean constitutive model and the Wang et al. constitutive model (3). A 1/8 symmetry model was used for the calculations, simulating a spherical, isotropically contracting cell of radius R centered in a cube of size L = 10R. (A) Normalized displacement u/u0 as a function of normalized distance X/R for a radial contractile strain of u0/R = 0.3. (B) A contour plot of displacement magnitude for the neo-Hookean matrix is sho febio.org/plugins wn. (C) A contour plot of the displacement magnitude for the fibrous matrix. The results illustrate that the fibrous constitutive model proposed by Wang et al. exhibits long-range force transmission. To see this figure in color, go online.
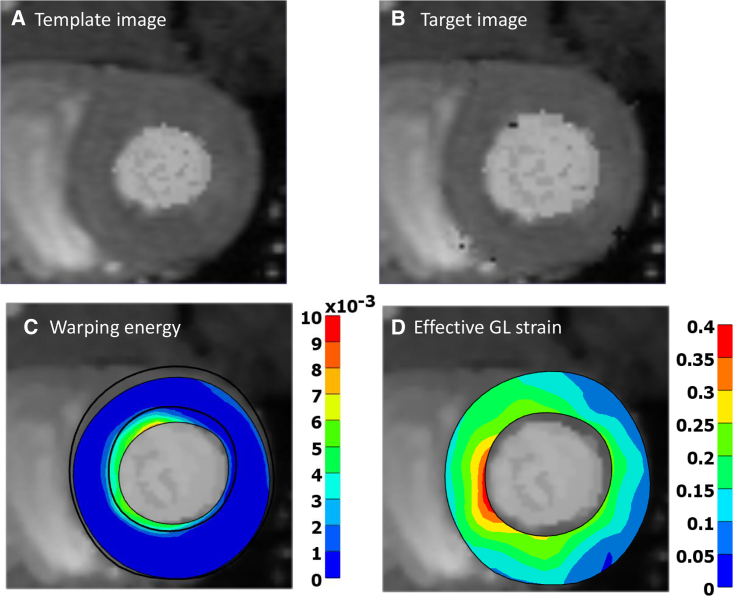
Figure 2.
Two-dimensional slice from a 3D warping analysis that tracks the deformation of the left ventricle during diastole. (A) The template image slice at start of diastole, (B) the target image slice at end of diastole, (C) and warping energy, measuring the mismatch between the template and the target image. The black contour shows the outline of the target geometry. (D) Effective Green Lagrange strain in the final, deformed state. To see this figure in color, go online.
Nonlinear constraint plugin
A nonlinear constraint enforces a nonlinear condition on field variables such as nodal displacements or concentrations. In FEBio, nonlinear constraints are enforced via an augmented Lagrangian method (21), which solves for the Lagrange multipliers using an iterative loop outside of the Newton nonlinear iterative loop. Contact between deformable bodies and incompressibility are typical examples of nonlinear constraints that are encountered in biomechanics simulation. Nonlinear constraint plugins allow users to easily implement additional nonlinear constraints.
The FEWarp plugin below is an example of a nonlinear constraint plugin. Hyperelastic Warping is a deformable image registration method that is used to find the deformation map that aligns a template image data set with a target image data set (4, 22, 23, 24, 25, 26, 27). This technique not only enables markerless strain measurement from sequences of images but in many cases can be used to predict the stress field as well and compensate for missing or incomplete boundary conditions (22). Two or more image data sets are used. The data set in the reference configuration is referred to as the template, and one or more data sets in different deformed configurations serve as the target. An FE discretization and interpolation of the template image data is deformed into alignment with the target. An energy functional is defined, consisting of an image-based term that measures alignment and a hyperelastic strain energy term that serves to regularize the problem. Minimization of the energy functional produces alignment of the deformed template image with the target image. If accurate stress calculations are desired, realistic constitutive models and material properties can be used. If the focus is on strain measurements from image data only, this is not necessary, in which case the image data are treated as a hard constraint, enforced using an augmented Lagrangian method (28). We use successive Gaussian blurring to evolve the solution from the level of coarse features to fine details in the image data. One of the strengths of this approach is that the deformation can be obtained without the specific knowledge of the applied loads and boundary conditions to the model. Because the method is based on continuum mechanics, the resulting deformation is guaranteed to be diffeomorphic. The method has been applied successfully to characterize the mechanics of tissues such as ligaments (22) and the left ventricle of the heart (29).
In the example illustrated in Fig. 2, the FEWarp plugin was used to track the deformation of the left ventricle during simulation of diastole. A three-dimensional (3D) MRI image was taken at the start of diastole. A forward FE analysis resulted in a deformed model that simulates the condition at the end of diastole. From this deformed configuration, a target image was generated. Then, the warping algorithm was applied to the template image and attempted to recover the deformed target image to validate the warping approach.
Task plugin
At the highest level, after parsing the input file, FEBio executes a single task. The default task solves the model defined by the FEBio input file, but other tasks can be executed as well. For instance, the optimization module in FEBio is implemented as a task that calls the default solver task repeatedly while minimizing an objective function by modifying model parameters. In essence, a task defines the outer loop that controls the work that FEBio performs. A task plugin allows the user to dictate how FEBio is used for a particular task at a high level.
The AngioFE plugin (7) is an example of a task plugin that illustrates how FEBio can be linked to other libraries via the plugin framework. It uses the “Angio” library, which simulates the growth, branching, and anastomosis of angiogenic microvessels embedded in a 3D collagen matrix (8, 30). During angiogenesis, growing neovessels deform the collagen matrix. In turn, deformation of the matrix directly affects the growth of the vessels through changes in matrix density and collagen fibril alignment. To couple the Angio growth library with FEBio, a task plugin was developed to allow the two codes to interact. The task plugin first seeds the matrix with parent microvessels using the Angio library and executes an initial growth step. The parent vessels are allowed to grow, governed by heuristics that control the growth rate, branching probability, and anastomosis. Then, the discrete model of the microvascular network is passed to FEBio, which solves for the matrix deformation. The mechanical interaction between the vessels and matrix is modeled as a spatially varying contractile stress that is centered at the tip of each microvessel sprout. The new, deformed configuration is then passed back to the Angio library, which calculates the next growth step in the deformed model (7).
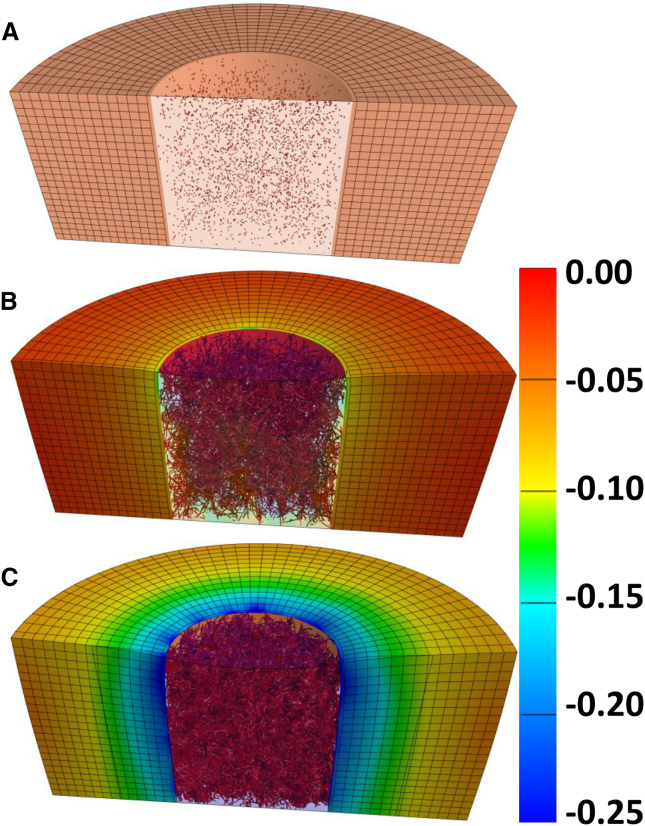
In the example application (Fig. 3), an in vitro model of neovessel growth is simulated using the AngioFE plugin. The simulation represents 6 days of growth in vitro. A cylindrical core of 3 mg/mL collagen is seeded with parent microvessels, and this core is surrounded by a field of avascular 3 mg/mL collagen (Fig. 3 A). A high-density interface forms between the core and field at the time of polymerization, and this density gradient is represented in the underlying model. The simulation geometry and parameters mimic an experimental model that is used to assess neovessel invasion across tissue interfaces. The high-density gradient that forms between the core and field is sufficient to prevent the angiogenic microvessels from crossing the interface into the field.
Figure 3.
Simulation of microvessel growth in an in vitro model of microvessel invasion across a tissue interface. (A) The initial geometry, illustrating the cores of collagen seeded with parent microvessels and the surrounding field of avascular collagen. The interface is too thin to be seen in this image. (B and C) At times X and Y during the simulation, microvessels grow into a dense vascular network, contracting the surrounding matrix as they grow. Vessels are unable to cross the interface because of the large density gradient. Fringe plots show Green-Lagrange deviatoric strain. To see this figure in color, go online.
Solver plugins
FEBio is a multiphysics solver that couples fluid and solid mechanics with growth, reaction-diffusion, and electrokinetic effects. This is embodied in the multiphasic mixture module, which solves the balance of linear momentum, mass balance, and diffusion equations simultaneously using a monolithic approach. At times, users may wish to solve governing equations with the FE method that are not supported within FEBio, or they may wish to focus on a subset of the physics supported by FEBio. For such cases, “solver plugins” can be developed.
As an illustration of this type of plugin, the FEBioChem plugin implements a nonlinear solver for the reaction-diffusion-convection equation. Using this plugin, users can solve for the concentrations of chemical species that diffuse, convect, and undergo chemical reactions in space and time. Although the multiphasic mixture module can address such problems, this plugin offers a simplified context that does not model solid matrix deformation or osmotic effects in the fluid solution, providing a simplified approach to modeling systems of chemical reactions. These simplifications result in a significant speedup compared to the analogous multiphasic model, as the additional displacement and pressure nodal degrees of freedom associated with the mixture framework are eliminated. In the future, we plan to add support for surface diffusion, biomolecular reactions between surface-bound molecules, and modeling reversible reactions with a single equation. The convection feature makes use of a user-defined velocity field.
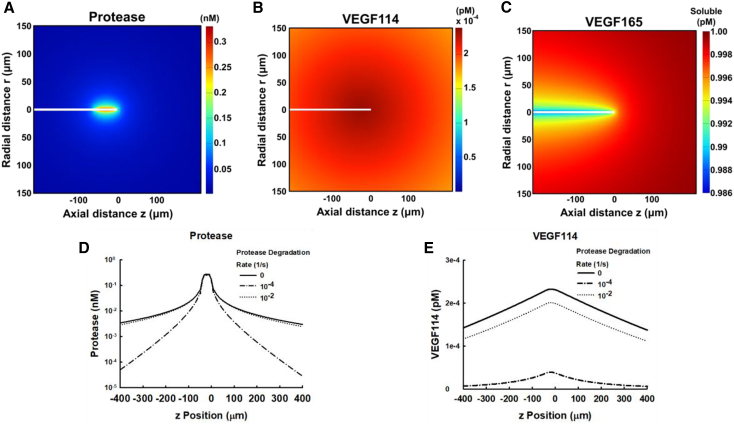
To illustrate the function and utility of the FEBioChem plugin, we reproduced the results of a computational study by Vempati et al. (31) that examined the proteolysis of vascular endothelial growth factor (VEGF) in the context of matrix metalloprotease secretion, VEGF-extracellular matrix (ECM) binding, VEGF proteolysis from VEGF165 to VEGF114, and VEGF receptor-mediated recapture (Fig. 4). The computational model simulates the stalk cells and tip cells of a capillary sprout, surrounded by a basement membrane within an ECM volume. Predicted concentrations of protease and VEGF were compared to those in the publications and most species agreed to within 1% (all species agreed within ∼5%; see Supporting Materials and Methods for further details). Furthermore, the spatial distributions showed excellent correspondence with the figures in the corresponding publication. FEBioChem’s simplified context can represent complex reaction networks, diffusion, and species production and degradation in porous media and materials.
Figure 4.
Reproduction of results in Vempati et al. (31) using FEBioChem. The panels in this figure correspond to Fig. 2, A–E in the publication. (A) A line of cells (white) extends from the left edge of the computational domain, surrounded by a thin basement membrane and ECM. The fringe plot shows predicted protease distribution produced by the tip (rightmost) cell, in equilibrium with flux and diffusion. (B) VEGF114 distribution near the tip partially governed by VEGF165 + Protease → VEGF114 + Protease. (C) The initial 1 pM concentration of VEGF 165 is slightly altered by protease activity. (D) Axial protease distributions. Protease degradation reduces the concentration of protease that is available to modify VEGF165. (E) Axial VEGF114 distribution. Protease degradation reduces conversion of VEGF165 to VEGF114. To see this figure in color, go online.
Discussion
The plugin framework is a powerful new capability that allows users to extend and customize FEBio to their specific needs. A large variety of plugin types are supported, including material, task, solver, body loads, boundary loads, initial conditions, nonlinear constraints, plot and log data, callback, and loadcurve plugins. Some of these plugins were illustrated in Results above, including a plugin to create a new constitutive model, a plugin that implements an image-based constraint, a plugin to link FEBio to an external library that simulates angiogenesis, and a plugin that adds reaction-diffusion modeling capabilities to FEBio. A description of the other available types of plugins can be found in the Supporting Materials and Methods. New types of plugins can be added easily as the need arises. The plugin approach in FEBio has been applauded by many of our users as flexible and easy to use. For instance, a recent publication implemented a new constitutive model in both FEBio and the commercial software ABAQUS (now called Simulia; Dassault Systèmes), and concluded that the plugin framework in FEBio made it far easier to implement the new constitutive model than the approach required for ABAQUS (32).
It is worth noting that the additional specialized xml-formatted input files required by some plugins need to be created in a text editor. PreView, our FE preprocessor that is used for setting up FEBio models, does not support the creation of these additional input files, although it does support the addition of user materials and the FEBioChem plugin capabilities (these plugins add features directly through FEBio’s “.feb” input file). This arrangement is intentional, as new plugins will have specific requirements for input that we cannot anticipate. For all the plugins that are developed by our lab and those that we distribute on behalf of outside developers, we provide detailed documentation of any additional input file formats that are needed by the plugin, and this information will always be up to date at https://www.febio.org.
To the best of our knowledge, there is no other freely available FE package that is designed specifically for simulation in biomechanics while offering such a wide variety of simulation capabilities. Nevertheless, it is informative to place FEBio in the context of other open-source software packages that serve the biomechanics community. OpenSim (http://opensim.stanford.edu/) is a modeling framework for simulation of human movement using forward and inverse rigid body dynamics. Muscles and tendons are modeled as discrete elements connected to rigid bodies. It is highly specialized for these applications and does not include any FE-based algorithms. FEBio has some rigid-body modeling capabilities and allows rigid-body dynamics to be coupled with FE analysis. Like FEBio, Artisynth (https://www.artisynth.org/Main/HomePage) supports the combined simulation of multibody and FE analysis. In this regard, it offers modeling capabilities that are similar to FEBio, but it focuses only on solid mechanics. SimVascular is focused on patient-specific blood flow analysis and includes capabilities for fluid mechanics and fluid-structure interaction. These capabilities overlap with FEBio, but SimVascular is limited to these types of physical simulations, caters to a much more specific group of users, and includes features that are specific to constructing models of blood flow in arteries that are not part of FEBio’s capabilities. Similarly, Continuity (https://continuity.ucsd.edu/) is an FE software that supports simulation of cardiac biomechanics, transport, and electrophysiology. It is tightly tailored to this application domain, and although some of the capabilities of Continuity exist in FEBio, it is once again focused on a highly specific group of users. In all of these cases, FEBio offers some functionality that overlaps with other software packages. This is not surprising, given that FEBio was developed to be a general-purpose FE software that targets a range of different types of simulations in biomechanics using mixture theory. That said, it is not our goal to replace the impressive and feature-rich software packages mentioned above. In fact, much of our current focus with application of the plugin framework is the integration of FEBio with other software packages so that users can take advantage of each software’s strengths. Through this approach, we hope to enable simulations that couple different modeling approaches and/or span different physical scales.
The FEBio software suite and the plugins discussed in this manuscript are available for download at https://www.febio.org.
Author Contributions
S.A.M. and J.A.W. conceived the project. S.A.M. wrote the plugin interface software. All authors participated in data analysis and interpretation. S.A.M., S.A.L., and J.A.W. drafted the manuscript. All authors edited the manuscript and gave final approval for publication.
Acknowledgments
Financial support from National Institutes of Health grant #R01EB015133 (S.A.M., G.A.A., and J.A.W.), National Institutes of Health grant #R01HL131856 (S.A.M. and J.A.W.), National Institutes of Health grant #R01AR069297 (S.A.M. and J.A.W.), and National Institutes of Health grant #R01GM104139 is gratefully acknowledged.
Editor: Vivek Shenoy.
Footnotes
Supporting Materials and Methods, five figures, three tables, and one data file are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)31069-5.
Supporting Material
References
- 1.Maas S.A., Ellis B.J., Weiss J.A. FEBio: finite elements for biomechanics. J. Biomech. Eng. 2012;134:011005. doi: 10.1115/1.4005694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Maas S.A., Ateshian G.A., Weiss J.A. FEBio: history and advances. Annu. Rev. Biomed. Eng. 2017;19:279–299. doi: 10.1146/annurev-bioeng-071516-044738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wang H., Abhilash A.S., Shenoy V.B. Long-range force transmission in fibrous matrices enabled by tension-driven alignment of fibers. Biophys. J. 2014;107:2592–2603. doi: 10.1016/j.bpj.2014.09.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rabbitt R.D., Weiss J.A., Miller M.I. Mapping of hyperelastic deformable templates. Proc. SPIE Int. Soc. Opt. Eng. 1995;2552:252–264. [Google Scholar]
- 5.Edgar L.T., Hoying J.B., Weiss J.A. Mechanical interaction of angiogenic microvessels with the extracellular matrix. J. Biomech. Eng. 2014;136:021001. doi: 10.1115/1.4026471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Edgar L.T., Hoying J.B., Weiss J.A. In silico investigation of angiogenesis with growth and stress generation coupled to local extracellular matrix density. Ann. Biomed. Eng. 2015;43:1531–1542. doi: 10.1007/s10439-015-1334-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Edgar L.T., Maas S.A., Weiss J.A. A coupled model of neovessel growth and matrix mechanics describes and predicts angiogenesis in vitro. Biomech. Model. Mechanobiol. 2015;14:767–782. doi: 10.1007/s10237-014-0635-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Edgar L.T., Underwood C.J., Weiss J.A. Extracellular matrix density regulates the rate of neovessel growth and branching in sprouting angiogenesis. PLoS One. 2014;9:e85178. doi: 10.1371/journal.pone.0085178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Todd J.N., Maak T.G., Weiss J.A. Hip chondrolabral mechanics during activities of daily living: role of the labrum and interstitial fluid pressurization. J. Biomech. 2018;69:113–120. doi: 10.1016/j.jbiomech.2018.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ateshian G.A., Shim J.J., Weiss J.A. Finite element framework for computational fluid dynamics in FEBio. J. Biomech. Eng. 2018;140 doi: 10.1115/1.4038716. 021001–021001-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ateshian G.A., Maas S., Weiss J.A. Solute transport across a contact interface in deformable porous media. J. Biomech. 2012;45:1023–1027. doi: 10.1016/j.jbiomech.2012.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ateshian G.A., Maas S., Weiss J.A. Multiphasic finite element framework for modeling hydrated mixtures with multiple neutral and charged solutes. J. Biomech. Eng. 2013;135:111001. doi: 10.1115/1.4024823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ateshian G.A., Nims R.J., Weiss J.A. Computational modeling of chemical reactions and interstitial growth and remodeling involving charged solutes and solid-bound molecules. Biomech. Model. Mechanobiol. 2014;13:1105–1120. doi: 10.1007/s10237-014-0560-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ateshian G.A., Maas S., Weiss J.A. Finite element algorithm for frictionless contact of porous permeable media under finite deformation and sliding. J. Biomech. Eng. 2010;132:061006. doi: 10.1115/1.4001034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ateshian G.A., Henak C.R., Weiss J.A. Toward patient-specific articular contact mechanics. J. Biomech. 2015;48:779–786. doi: 10.1016/j.jbiomech.2014.12.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Henak C.R., Anderson A.E., Weiss J.A. Subject-specific analysis of joint contact mechanics: application to the study of osteoarthritis and surgical planning. J. Biomech. Eng. 2013;135:021003. doi: 10.1115/1.4023386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Maas S.A., Ellis B.J., Weiss J.A. Finite element simulation of articular contact mechanics with quadratic tetrahedral elements. J. Biomech. 2016;49:659–667. doi: 10.1016/j.jbiomech.2016.01.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Maas S.A., Erdemir A., Weiss J.A. A general framework for application of prestrain to computational models of biological materials. J. Mech. Behav. Biomed. Mater. 2016;61:499–510. doi: 10.1016/j.jmbbm.2016.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Matthies H., Strang G. The solution of nonlinear finite element equations. Int. J. Numer. Methods Eng. 1979;14:1613–1626. [Google Scholar]
- 20.Ateshian G.A. Viscoelasticity using reactive constrained solid mixtures. J. Biomech. 2015;48:941–947. doi: 10.1016/j.jbiomech.2015.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Laursen T.A., Maker B.N. Augmented Lagrangian quasi-Newton solver for constrained nonlinear finite element applications. Int. J. Numer. Methods Eng. 1995;38:3571–3590. [Google Scholar]
- 22.Phatak N.S., Maas S.A., Weiss J.A. Strain measurement in the left ventricle during systole with deformable image registration. Med. Image Anal. 2009;13:354–361. doi: 10.1016/j.media.2008.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Phatak N.S., Sun Q., Weiss J.A. Noninvasive determination of ligament strain with deformable image registration. Ann. Biomed. Eng. 2007;35:1175–1187. doi: 10.1007/s10439-007-9287-9. [DOI] [PubMed] [Google Scholar]
- 24.Veress A.I., Gullberg G.T., Weiss J.A. Measurement of strain in the left ventricle during diastole with cine-MRI and deformable image registration. J. Biomech. Eng. 2005;127:1195–1207. doi: 10.1115/1.2073677. [DOI] [PubMed] [Google Scholar]
- 25.Veress A.I., Klein G., Gullberg G.T. A comparison of hyperelastic warping of PET images with tagged MRI for the analysis of cardiac deformation. Int. J. Biomed. Imaging. 2013;2013:728624. doi: 10.1155/2013/728624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Veress A.I., Weiss J.A., Rabbitt R.D. Strain measurement in coronary arteries using intravascular ultrasound and deformable images. J. Biomech. Eng. 2002;124:734–741. doi: 10.1115/1.1519279. [DOI] [PubMed] [Google Scholar]
- 27.Weiss J.A., Veress A.I., Rabbitt R.D. Strain measurement using deformable image registration. In: Holzapfel G.A., Ogden R.W., editors. Mechanics of Biological Tissue. Springer; 2006. pp. 489–501. [Google Scholar]
- 28.Veress A.I., Phatak N., Weiss J.A. Deformable image registration with hyperelastic warping. In: Suri J.S., Wilson D.L., Laxminarayanan S., editors. Handbook of Biomedical Image Analysis: Vol. 3, Registration Models (Part A) Kluwer Academic/Plenum Publishers; 2005. pp. 487–534. [Google Scholar]
- 29.Veress A.I., Weiss J.A., Gullberg G.T. Measuring regional changes in the diastolic deformation of the left ventricle of SHR rats using microPET technology and hyperelastic warping. Ann. Biomed. Eng. 2008;36:1104–1117. doi: 10.1007/s10439-008-9497-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Edgar L.T., Sibole S.C., Weiss J.A. A computational model of in vitro angiogenesis based on extracellular matrix fibre orientation. Comput. Methods Biomech. Biomed. Engin. 2013;16:790–801. doi: 10.1080/10255842.2012.662678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Vempati P., Mac Gabhann F., Popel A.S. Quantifying the proteolytic release of extracellular matrix-sequestered VEGF with a computational model. PLoS One. 2010;5:e11860. doi: 10.1371/journal.pone.0011860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Pierrat B., Murphy J.G., Gilchrist M.D. Finite element implementation of a new model of slight compressibility for transversely isotropic materials. Comput. Methods Biomech. Biomed. Engin. 2016;19:745–758. doi: 10.1080/10255842.2015.1061513. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.