Highly parallel, interferometric diffusing wave spectroscopy for monitoring cerebral blood flow dynamics

Abstract

Light-scattering methods are widely used in soft matter physics and biomedical optics to probe dynamics in turbid media, such as diffusion in colloids or blood flow in biological tissue. These methods typically rely on fluctuations of coherent light intensity, and therefore cannot accommodate more than a few modes per detector. This limitation has hindered efforts to measure deep tissue blood flow with high speed, since weak diffuse light fluxes, together with low single-mode fiber throughput, result in low photon count rates. To solve this, we introduce multimode fiber (MMF) interferometry to the field of diffuse optics. In doing so, we transform a standard complementary metal-oxide-semiconductor (CMOS) camera into a sensitive detector array for weak light fluxes that probe deep in biological tissue. Specifically, we build a novel CMOS-based, multimode interferometric diffusing wave spectroscopy (iDWS) system and show that it can measure ∼20 speckles simultaneously near the shot noise limit, acting essentially as ∼20 independent photon-counting channels. We develop a matrix formalism, based on MMF mode field solutions and detector geometry, to predict both coherence and speckle number in iDWS. After validation in liquid phantoms, we demonstrate iDWS pulsatile blood flow measurements at 2.5 cm source-detector separation in the adult human brain in vivo. By achieving highly sensitive and parallel measurements of coherent light fluctuations with a CMOS camera, this work promises to enhance performance and reduce cost of diffuse optical instruments.

1. INTRODUCTION

Fluctuations of scattered light can noninvasively probe the micro-scopic motion of scatterers in turbid media such as colloids, foams, gels, and biological tissue. Diffusing wave spectroscopy (DWS) uses intensity fluctuations of multiply scattered coherent light to infer the dynamics of a turbid medium (or sample) [1,2]. When informed by a light transport model that incorporates medium optical properties, illumination, and collection geometry, DWS can quantify particle dynamics. When DWS is applied to quantify blood flow in biological tissue by modeling transport with the correlation diffusion equation solution for a semi-infinite turbid medium [3], the term “diffuse correlation spectroscopy” (DCS) is often used [4–7]. Compared to singly scattered light dynamics, multiply scattered light dynamics can interrogate shorter time scales of motion [8] and probe deeper into turbid media such as the human head [4]. However, the available surface flux of diffuse light, which experiences many scattering events and penetrates deeply, is weak. DWS and DCS are homodyne methods, as they measure the intensity fluctuations formed by self-interference of changing light fields from various scattered sample paths. As single or few speckle collection is needed to measure these fluctuations, and light fluxes are low, single photon counting is required.

Heterodyne optical methods interfere a strong reference light field with the weak scattered sample field(s) to boost signal. Optical coherence tomography is a widespread optical heterodyne technique that forms images with quasi-ballistic back-reflected light, usually with a single-mode fiber (SMF) collector [9]. However, heterodyne interferometry is rarely applied to diffuse optical measurements such as DWS. Heterodyne interferometry with a single detector has been applied to study the transition from ballistic to diffusive transport in suspensions [10,11]. However, to date, deep tissue blood flow experiments have exclusively used homodyne DCS. The use of SMF or few-mode fiber (FMF) collectors in homodyne DCS limits achievable photon count rates at large source-detector (S-D) separations, making deep tissue, high-speed measurements challenging [4,5]. While time-of-flight-resolved methods enable deep tissue measurements at short S-D separations [12,13], their speed remains limited by the collection fiber throughput.

While multimode fibers (MMFs) improve throughput, MMFs are typically not used for collection in DWS and DCS. Conventional wisdom states that heterodyne interferometry should not be performed with MMF collection. Indeed, in heterodyne interferometry, multiple sample and reference modes interfering on a single detector reduce the mutual coherence, which negates the higher MMF throughput. Also, with coherent superposition of modes, one detector cannot measure more than one speckle (see Section 2.A). For these reasons, while MMFs are used occasionally in interferometers with single detectors [14–16], these systems cannot effectively utilize the high MMF throughput. Similarly, conventional wisdom states that homodyne interferometry (such as DCS) should not be performed with MMF collection. In homodyne interferometry, multiple modes on a single detector reduce the speckle contrast (coherence factor), which hinders measurements of intensity dynamics [17]. Thus, in the DWS/DCS literature, bundles of SMF or FMF collector(s) with dedicated single photon-counting detector(s) are typically employed to achieve high-throughput, multispeckle detection needed for high-speed, deep-tissue sensing [18,19]. However, avalanche photodiode arrays and associated electronics are expensive, limiting the number of possible channels. Multi-speckle systems with charge-coupled device cameras cannot currently capture rapid temporal dynamics [20,21], and camera noise may further degrade the performance of homodyne techniques.

To address these issues, we introduce interferometric DWS (iDWS), a heterodyne method that, contrary to conventional wisdom, uses a MMF collector along with a detector array to parallelize measurements, and show that it allows deep-tissue measurements without single-photon-counting detectors. We propose mutual coherence degree (MCD) and speckle number as two key figures of merit to optimize system design. We develop a statistical iDWS measurement model based on rigorous MMF mode field solutions and a transmission matrix formalism, applying it to investigate design tradeoffs. We show that an appropriate detector array can realize the benefits of MMF light throughput and multispeckle detection, while preserving coherence. Based on these results, we demonstrate an iDWS system with detection by a complementary metal-oxide-semiconductor (CMOS) line-scan camera. Though the camera is not scientific grade, heterodyne gain enables nearly shot-noise-limited performance. Finally, with this iDWS system, we demonstrate high-speed measurements of pulsatile blood flow in the human brain in vivo at a 2.5 cm S-D separation.

2. METHODS

A. Theory

1. Multimode Interference Transmission Matrix

To understand heterodyne detection by a MMF interferometer, we start from the intensity, I, formed by the superposition of two coherent fields in a Mach–Zehnder (M-Z) interferometer [22]:

$$I={\left|{\mathbf{E}}_S+{\mathbf{E}}_R\right|}^2={\left|{\mathbf{E}}_S\right|}^2+{\left|{\mathbf{E}}_R\right|}^2+2\mathrm{Re}\left\{{\mathbf{E}}_S^{\ast }·{\mathbf{E}}_R\right\},$$ (1)

where E_S and E_R are the vector electric fields of the sample and reference interferometer arms, respectively. In a MMF-based M-Z interferometer, where monochromatic input light with angular frequency, ω, splits between two arms with lengths, L_S and L_R, the corresponding electric fields, E_S and E_R, formed by excited core modes with different magnitudes and phases at the output are [23,24]

$${\mathbf{E}}_S\left(x,y\right)={\displaystyle \sum _m{a}_{S,m}{\mathbf{\Psi }}_m\left(x,y\right)\exp \left[i\left(\omega t-{\beta }_m{L}_S\right)\right]},$$ (2)

$${\mathbf{E}}_R\left(x,y\right)={\displaystyle \sum _n{a}_{R,n}{\mathbf{\Psi }}_n\left(x,y\right)\exp \left[i\left(\omega t-{\beta }_n{L}_R\right)\right]},$$ (3)

where a_S,_m and a_R,_n are the excitation coefficients, Ψ_m (x, y) and Ψ_n (x, y) form the normalized transverse core mode field bases, and β_m and β_n are the propagation constants of the mth and nth core modes in the sample and reference MMFs, respectively. Exemplary complex MMF field patterns, E_S and E_R, are shown in the top row of Fig. 1. By substituting Eqs. (2) and (3) into Eq. (1), the power measured by a sensor (i.e., spatial integral of intensity over an area p) is

$$\begin{gathered} P_p={{\displaystyle \int {\displaystyle {\int }_p\left|{\displaystyle \sum _m{A}_{S,m}{\mathbf{\Psi }}_m\left(x,y\right)}+{\displaystyle \sum _n{A}_{R,n}{\mathbf{\Psi }}_n\left(x,y\right)}\right|}}}^2\mathrm{d}x\mathrm{d}y \\ ={\displaystyle \int {\displaystyle {\int }_p\left[{\left|{\displaystyle \sum _m{A}_{S,m}{\mathbf{\Psi }}_m\left(x,y\right)}\right|}^2+{\left|{\displaystyle \sum _n{A}_{R,n}{\mathbf{\Psi }}_n\left(x,y\right)}\right|}^2+2\mathrm{Re}\left\{{\displaystyle \sum _m{\displaystyle \sum _n{A}_{S,m}^{\ast }{\mathbf{\Psi }}_m^{\ast }\left(x,y\right)·A_{R,n}{\mathbf{\Psi }}_n\left(x,y\right)}}\right\}\right]}}\mathrm{d}x\mathrm{d}y \\ =P_{S,p}+P_{R,p}+P_{\text{AC},p}, \end{gathered}$$ (4)

where A_S,_m and A_R,_n are complex amplitudes, including the magnitude and phase, of the mth and nth excited core modes in the sample and reference MMFs, respectively. Note that for fibers of interest, propagation over a distance of centimeters is sufficient to randomize the phases of excited core modes. Equation (1) [and therefore, Eq. (4)] consists of three terms corresponding to the sample intensity (power), P_S,_p, the reference intensity (power), P_R,_p, and a heterodyne term, P_AC,p, resulting from the coherent superposition of the two fields, as shown in Fig. 1 (bottom row). In practice, the intensity of the sample MMF speckle pattern is much lower than that of reference MMF speckle pattern. Therefore, the term in Eq. (4) most relevant to sample dynamics is the heterodyne term:

$$P_{\text{AC},p}=2\mathrm{Re}\left\{{\displaystyle \sum _m{T}_{p,m}·A_{S,m}^{\ast }}\right\},$$ (5)

where T_p,_m is a transmission coefficient, given by

Fig. 1.

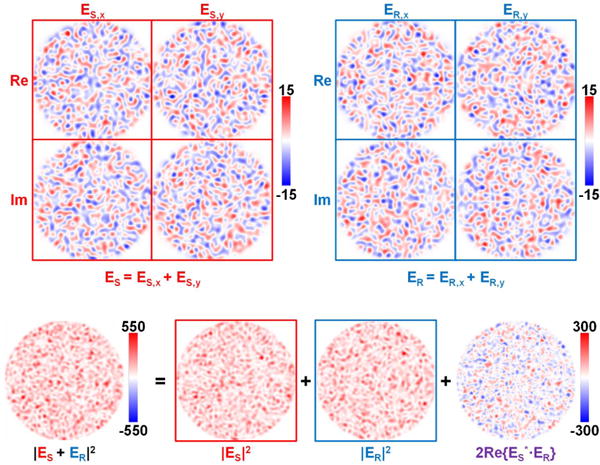
MMF interference pattern between E_S and E_R, formed by core modes with equal magnitudes and random phases. The vector electric field possesses two orthogonal transverse (x and y) components (top row). The resulting speckle pattern comprises a sample, reference, and heterodyne term (bottom row). In this example, sample and reference speckle patterns have equal power, maximizing the contrast of the heterodyne interference term (bottom right, purple text).

$$T_{p,m}={\displaystyle \int {\displaystyle {\int }_p{\displaystyle \sum _n{A}_{R,n}{\mathbf{\Psi }}_m^{\ast }\left(x,y\right)}}}·{\mathbf{\Psi }}_n\left(x,y\right)\mathrm{d}x\mathrm{d}y.$$ (6)

If the MMF interference pattern (Fig. 1) is detected by a sensor array, the collection of measured heterodyne signals is given by

$${\mathbf{P}}_{\text{AC}}=2\mathrm{Re}\left\{\mathbf{T}\times {\mathbf{A}}_S^{\ast }\right\},$$ (7)

where P_AC is a vector representing the heterodyne signals of P sensor elements, T is the P × M multimode interference transmission matrix (MMITM) with elements T_p,_m, and ${\mathbf{A}}_S^{\ast }$ is another vector related to the complex amplitudes of the M excited modes in the sample MMF.

Here, assuming that the sample MMF collects diffuse light emerging from a dynamic scattering medium, each core mode excited in the sample MMF would carry a temporal speckle (i.e., independent instance of the light field fluctuation). ${\mathbf{A}}_S^{\ast }$ in Eq. (7) can then be generalized as a delay time (t_d)-dependent vector ${\mathbf{A}}_S^{\ast }$ (t_d), where each element is a time series, ${\mathbf{A}}_{S,m}^{\ast }$ (t_d), that describes the fluctuations of one independent sample mode. Although the MMITM [T of Eq. (7)] depends on the complex amplitudes, A_R,_n, of excited reference modes, the MMITM is time independent if the reference arm MMF is static and the spatial profile and polarization of the input light are constant. Thus, based on Eq. (7), dynamics in ${\mathbf{A}}_S^{\ast }$ (t_d) induce temporal fluctuations in the observable heterodyne signal, P_AC (t_d), via the MMITM T. Three important points must be made here: 1. The heterodyne signals, P_AC (t_d), “reorganize” the sample mode fields through a weighted complex sum. 2. Although these heterodyne signals include only the component of the sample field oscillating in-phase with the reference field [due to taking the real part in Eq. (7)], accurate field autocorrelations can be still be determined (see Section S1 in Supplement 1). 3. The heterodyne signals of individual sensor elements, P_AC,p (t_d), achieve a speckle contrast of √2 (half speckle) [25], as they include the in-phase component. Hence, our heterodyne method, based on detecting a MMF interference pattern with a sensor array, theoretically achieves high-throughput, multispeckle detection of dynamically scattered light. As we will show in the next two sections, performance depends on two key parameters: signal-to-additive-noise ratio (SANR) and speckle number.

2. Mutual Coherence Degree and Signal-to-Additive-Noise Ratio

MCD can be defined as the normalized temporal or/and spatial correlation between two light fields [22]. For the dynamic multi-mode interference between a static polarized reference field and a fluctuating randomly polarized sample field, instantaneous MCD can vary between 0 and 1, from location to location across the multimode interference pattern. For a sensor array, we define the time- and sensor-element-averaged MCD between the two fields as

$${\overline{\gamma }}_{\mathit{SR}}=\sqrt{\frac{\langle \langle {\langle {\left|{\displaystyle \int {\displaystyle \int {\mathbf{E}}_S^{\ast }\left(x,y,t_d\right)·{\mathbf{E}}_R^{\ast }\left(x,y\right)\mathrm{d}x\mathrm{d}y}}\right|}^2\rangle }_p\rangle \rangle }{\langle \langle {\langle {\displaystyle \int {\displaystyle \int {\left|{\mathbf{E}}_S\left(x,y,t_d\right)\right|}^2\mathrm{d}x\mathrm{d}y}}\rangle }_p\rangle \rangle {\langle {\displaystyle \int {\displaystyle \int {\left|{\mathbf{E}}_R\left(x,y\right)\right|}^2\mathrm{d}x\mathrm{d}y}}\rangle }_p}},$$ (8)

where E_S (x, y, t_d) and E_R (x, y) are given by Eqs. (2) and (3), respectively, single brackets with subscript p indicate sensor element averaging, and double brackets indicate temporal averaging. The two terms in the denominator of Eq. (8) are time- and sensor-element-averaged powers of the sample ( ${\overline{P}}_S$) and reference ( ${\overline{P}}_R$) MMF speckle patterns.

In heterodyne detection, the dominant noise source is ideally shot noise in the reference photon number, which follows a Poisson distribution with equal mean and variance [26]. Thus, with increasing reference power, a limit is achieved where both mean-squared heterodyne signal and noise variance increase in proportion [Eq. (4)]. Shot-noise-limited performance of iDWS is verified in Section S7 of Supplement 1. Thus, it is reasonable to define SANR as

$$\text{SANR}=\frac{\langle \langle {\langle {\left[2\mathrm{Re}\left\{{\displaystyle \int {\displaystyle \int {\mathbf{E}}_S^{\ast }\left(x,y,t_d\right)·{\mathbf{E}}_R\left(x,y\right)\mathrm{d}x\mathrm{d}y}}\right\}\right]}^2\rangle }_p\rangle \rangle }{{\langle {\displaystyle \int {\displaystyle \int {\left|{\mathbf{E}}_R\left(x,y\right)\right|}^2\mathrm{d}x\mathrm{d}y}}\rangle }_p·E/t_e},$$ (9)

where t_e is the exposure time and E is the photon energy. SANR is simply the ratio of the mean-squared heterodyne signal to the reference power, ${\overline{P}}_R$, multiplied by a constant. Since ${\displaystyle \int {\displaystyle \int {\mathbf{E}}_S^{\ast }\left(x,y,t_d\right)}}·{\mathbf{E}}_R\left(x,y\right)\mathrm{d}x\mathrm{d}y$ for each sensor element is a complex, circularly symmetric, zero-mean, Gaussian random variable, the statistics of the real and imaginary parts are identical. Thus, Eq. (9) can be rewritten as

$$\text{SANR}=\frac{2\langle \langle {\langle {\left|{\displaystyle \int {\displaystyle \int {\mathbf{E}}_S^{\ast }\left(x,y,t_d\right)·{\mathbf{E}}_R\left(x,y\right)\mathrm{d}x\mathrm{d}y}}\right|}^2\rangle }_p\rangle \rangle }{{\langle {\displaystyle \int {\displaystyle \int {\left|{\mathbf{E}}_R\left(x,y\right)\right|}^2\mathrm{d}x\mathrm{d}y}}\rangle }_p·E/t_e}=2{\overline{\gamma }}_{\mathit{SR}}^2{\overline{N}}_S.$$ (10)

Thus, SANR depends only on the time- and sensor-element-averaged sample photon number, ${\overline{N}}_S={\overline{P}}_S{t}_e/E$, and MCD, ${\overline{\gamma }}_{\mathit{SR}}$.

An analogy can be made between our MMITM and the conventional mode transfer matrix of a MMF. Thus, squared singular values, ${\lambda }_i^2$, of the matrix, [Re{T}, Im {T}] [27], are analogous to transmission coefficients of “eigenchannels,” each mapping a linear combination of sample modes to a linear combination of sensor array elements [28–30]. The sum of the squared singular values is directly proportional to the sum of the squared heterodyne signals detected from all sensor elements. The SANR can thus be extracted directly from the MMITM,

$$\text{SANR}=\frac{2{\overline{N}}_S\left({\displaystyle \sum _i{\lambda }_i^2}\right)t_e}{M{\overline{N}}_{R}E},$$ (11)

where M is the excited sample mode number and ${\overline{N}}_R$ is the sensor-element-averaged reference photon number. SANRs estimated from simulations (with digitization) and Eq. (10) and determined directly from MMITMs [Eq. (11)] are compared in Section 3.A.1.

3. Speckle Number

Assuming that the diffuse light emerging from a scattering medium equally excites M modes in the sample MMF, the sample light field E_S can yield at most M speckles (M/2 each in in-phase and quadrature channels). From Eq. (7), the M speckles carried by the M excited sample modes, ${\mathbf{A}}_S^{\ast }$ (t_d), are mapped into P heterodyne signals, P_AC (t_d), through the MMITM, T. P real-valued measurements yield, at most, P/2 speckles if they are independent. In general, the effective speckle number, N_Speckle, in the P heterodyne signals, given in units of photon number [i.e., N_AC(t_d) = P_AC(t_d)t_e/E], is

$$N_{\text{Speckle}}={\left[\frac{\text{mean}\left({\displaystyle \sum _p{\mathbf{N}}_{\text{AC},p}^2}\right)}{\text{std}\left({\displaystyle \sum _p{\mathbf{N}}_{\text{AC},p}^2}\right)}\right]}^2=\frac{{\left({\displaystyle \sum _i{\lambda }_i^2}\right)}^2}{2{\displaystyle \sum _i{\lambda }_i^4}}.$$ (12)

The first expression for speckle number in Eq. (12) is the reciprocal of squared speckle contrast of the sum of ${\mathbf{N}}_{\text{AC},p}^2$. Alternatively, the second expression for speckle number [28–30] in Eq. (12) employs squared singular values, ${\lambda }_i^2$, [27]. The factor of 2 in the denominator accounts for the reduction in speckle number due to exclusion of the quadrature field component. Speckle numbers estimated from simulations (with digitization) and determined directly from MMTIMs [Eq. (12)] are compared in Section 3.A.2.

4. Detector Number in Multimode Interferometry

Here, we describe the inherent performance limitations of heterodyne interferometry with a single detector. Consider first a MMF interferometer supporting M = M_MMF core modes. With a single detector element, the sample photon number, ${\overline{N}}_{S,\text{MMF}}$, for the MMF is M_MMF/2 times higher than ${\overline{N}}_{S,\text{SMF}}$ for a SMF (which supports two perpendicularly polarized fundamental modes). However, while ${\overline{\gamma }}_{\mathit{SR}}^2$ is theoretically 1/2 between randomly polarized sample light and polarized reference light for the SMF [31], ${\overline{\gamma }}_{\mathit{SR}}^2$ is 1/M_MMF for the MMF with a single detector. According to Eq. (10), the SANR is $2{\overline{N}}_{S,\text{MMF}}/M_{\text{MMF}}={\overline{N}}_{S,\text{SMF}}$ for both the MMF and SMF. Furthermore, regardless of mode number, a single in-phase heterodyne measurement always yields half a speckle. Thus, a MMF collector with a single detector enhances neither SANR nor speckle number. The former effect is caused by the tradeoff between light collection and MCD [Eq. (10)], and the latter effect is caused by coherent superposition in heterodyne detection. However, with P > 1 sensor elements, both SANR and speckle number can be improved, per Eqs. (11) and (12), respectively. In theory, detecting all available speckles with optimal SANR requires P ≥ 2M sensor elements. Therefore, both SANR and speckle number can be enhanced by combining a MMF with a sensor array. The intuitive result that as many sensor elements as channels are needed to capture the information content of a speckle pattern is in line with prior work on homodyne speckle [23,24,32]. Moreover, as will be shown below, the spatial arrangement of sensor elements, encapsulated in the MMITM, is critical in determining the achievable performance improvement.

B. Multimode iDWS Design

Figure 2(a) shows the experimental multimode interferometric multispeckle detection system (i.e., multimode iDWS) for measuring coherent light-scattering dynamics. Long coherence length light at 852 nm from a distributed Bragg reflector (DBR) laser (D2-100-DBR-852-HP1, Vescent Photonics) is split into sample and reference arms of the M-Z interferometer by a fused SMF-28 fiber coupler. The collimated 50 mW sample beam with a spot size of 4 mm (below the American National Standards Institute maximum permissible exposure of 4 mW/mm²) is used for irradiating turbid media (e.g., human brain tissue). Diffusively reflected light from the sample is collected by a MMF at a distance ρ away (with a detection spot size of <1.5 mm) and combined with the reference light in a fiber-optic beam splitter (i.e., beam splitter-based MMF coupler, FOBS-22P-1111-105/125-MMMM-850-95/5-35-3A3A3A3A-3-1-NA=0.15, OZ Optics). The MMF coupler output is detected by a line-scan CMOS camera (spL4096-140km, Basler) with a 333 kHz line rate for 512 horizontal pixels, vertical pixel binning, and 4-tap/12-bit data acquisition. A set of cylindrical lenses projects the MMF output speckle pattern, with a diameter of 105 μm, onto the 512 by 2 camera pixel array with dimensions of 5120 by 20 μm (10 × 10 μm pixels).

Fig. 2.

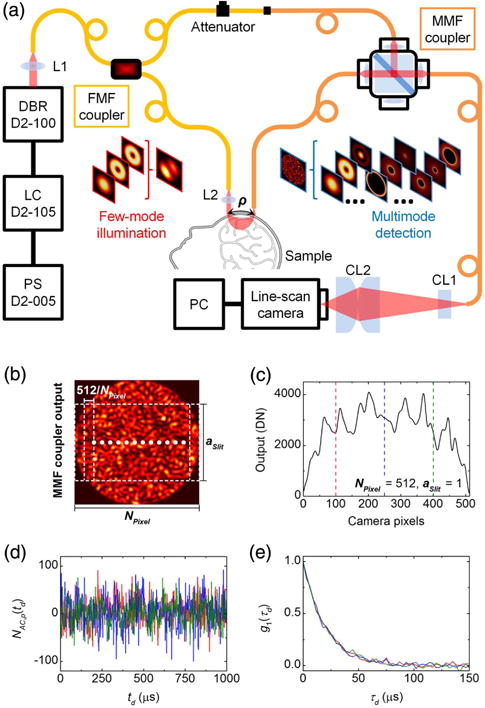
(a) Schematic of multimode iDWS system based on an M-Z interferometer built from two fiber couplers. The first SMF-28 fiber coupler supports the first six vectorial modes (HE₁₁ × 2, TE₀₁, HE₂₁ × 2, and TM₀₁) at 852 nm. In the reference arm, the SMF-28 output fiber connects to the MMF coupler via an APC mating sleeve, with a variable attenuator to avoid camera saturation. The splitting ratio of the MMF coupler is 95/5 (T/R). The core and cladding diameters of the step-index MMF are 105 μm and 125 μm, respectively, and the NA is 0.15. The light source is an 852 nm DBR (distributed Bragg reflector) laser with <1 MHz linewidth and >180 mW output power, modulated by a 500 mA LC (laser controller, D2-105-500, Vescent Photonics) with a PS (power supply, D2-005, Vescent Photonics). L1 and L2: spherical lens; CL1 and CL2: cylindrical lens; PC: personal computer. (b) The intensity pattern at the MMF coupler output is detected by a 512 pixel CMOS array. Pixels are binned horizontally to form N_Pixel binned pixels consisting of 512/N_Pixel pixels each, with fractional heights of a_Slit. (c) Instantaneous power measured by the pixel array with N_Pixel = 512 and a_Slit = 1. (d) Segments of heterodyne signal time courses (∼1 ms) extracted from the three pixels marked by vertical dashed lines in (c). (e) Normalized field autocorrelations calculated from full-time courses (∼100 ms) of the three heterodyne signals in (d).

As shown in simulations in Fig. 2(b), since a quasi-1D camera measures a 2D interference pattern, each pixel detects the power over a vertical rectangular region of a speckle pattern. The instantaneous power is shown in Fig. 2(c), with 512 pixels measuring the entire interference pattern (i.e., N_Pixel = 512, a_Slit = 1. Mean-subtracted power time courses yield heterodyne signals for each pixel. Thus, 512 pixels yield 512 heterodyne signals to estimate 512 field autocorrelations that contain information about sample dynamics. The correlation of these signals is investigated in Section 3.A.1. Based on the theoretical analysis in Section 2.A.4, we know that only an area-scan camera can possibly maximize the MCD and speckle number of multimode heterodyne signals. However, for in vivo monitoring of blood flow, a line-scan camera with a fast line rate (>100 kHz), manageable data volume, and low cost is chosen for the initial multi-mode iDWS system. Due to the mismatch between the 2D multimode interference pattern and quasi-1D sensor array, optimal SANR and speckle number cannot be achieved from the heterodyne signals, N_AC (t_d). Yet, relative to a single detector, sensor arrays improve achievable SANR and speckle number considerably. Given our practical sensor array choice, we next investigate the impact of three parameters: horizontal binned pixel number, N_Pixel, vertical fractional slit height, a_Slit, and excited reference mode number, N_Mode, on the performance of our multimode iDWS system.

3. RESULTS AND DISCUSSION

A. Simulations

Simulations are performed to investigate the effects of three parameters, N_Pixel, a_Slit, and N_Mode, on SANR and speckle number, and to optimize all parameters in the experimental setup (Fig. 2). 1. SANRs are estimated from statistical simulations of noise-added and digitized heterodyne signals using Eq. (10) and realistic photon numbers, and speckle numbers are estimated from statistical simulations of digitized heterodyne signals without additive noise using Eq. (12) (see simulated signals with and without additive noise in Visualization 1); 2. SANRs and speckle numbers are directly calculated from the MMITMs using Eqs. (11) and (12), respectively. Section S3 of Supplement 1 describes MMITM computation, statistical simulation, and other data processing in more detail.

1. Horizontal Pixel Binning

Due to correlations between adjacent camera pixels, horizontal pixel binning, or coherent summation, may improve heterodyne signal. To investigate the impact of horizontal pixel binning on SANR and speckle number, based on the methods described in Section S3 of Supplement 1, we generated 20 independent noise-added heterodyne signal time series, N_AC,N (t_d), where subscript “N” denotes noise, for each of four MMITMs with reference mode numbers, N_Mode, of 1702, 1300, 900, and 500. We then estimated field autocorrelations for 10 different binned pixel numbers, N_Pixel, ranging from 512 to 1. For the simulations in this section, we set a_Slit to 1. Exemplary normalized field autocorrelations with N_Mode of 1702 are shown in Fig. 3(a) for different values of N_Pixel, with corresponding exponential fits. The field autocorrelation noise appears to be minimized for N_Pixel ∼ 32–64. The minimum root mean-squared error (RMSE) for the fitted decay rate, estimated from 20 independent simulations, appears at N_Pixel ∼ 64 for all reference mode numbers [Fig. 3(b)]. Figure 3(c) shows SANRs, either estimated from simulating and fitting G₁ (τ_d) [i.e., A/B from Eq. (S7)] or calculated from MMITMs by Eq. (11), for different N_Mode and N_Pixel. Figure 3(d) shows speckle numbers, either estimated from simulations or calculated from MMITMs by Eq. (12). The slightly lower simulated SANRs and slightly higher simulated speckle numbers are the result of digitization in the simulation, which reduces heterodyne fluctuation amplitude [see panel (e) of Visualization 1].

Fig. 3.

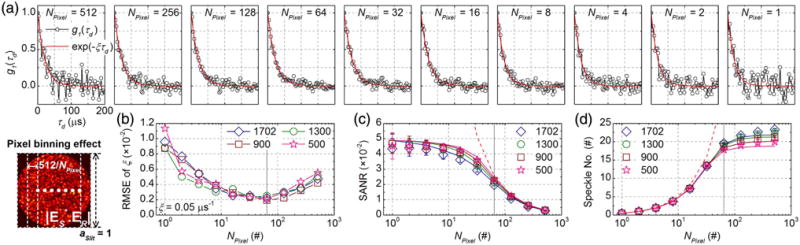
Optimization of horizontal pixel binning. (a) Simulated g₁ (τ_d) for N_Pixel ranging from 512 to 1 with a_Slit = 1 and N_Mode 1702, where total sample and reference photon numbers detected by the 512 camera pixels are set as ∼41 and ∼4.1 × 10⁶ per 3 μs exposure, respectively. (b) RMSE of decay rates versus N_Pixel for N_Mode of 1702, 1300, 900, and 500, estimated from 20 independent sets of simulations each. (c) SANR versus N_Pixel estimated from simulations with digitization (open symbols) and calculated from the corresponding MMITMs (solid lines). (d) Speckle number versus N_Pixel estimated from simulations with digitization (open symbols) and calculated from the corresponding MMITMs (solid lines). Red dashed curves in (c) and (d) indicate theoretical SANR for binning of fully correlated pixels and theoretical speckle number for binning of uncorrelated pixels, respectively. The optimal N_Pixel of 64 is indicated by vertical dotted lines in (b), (c), and (d).

Figures 3(c) and 3(d) clearly shows that horizontal pixel binning incurs a tradeoff between SANR and speckle number. To explain why N_Pixel 64 is optimal, we first note that the improvement in SANR from horizontal binning deviates from the theoretical improvement for fully correlated pixels [red dashed curve in Fig. 3(c)] for N_Pixel ≲ 64. It can be inferred that the heterodyne signals of ∼8 adjacent pixels remain highly correlated, so that binning over <8 pixels performs coherent summing for signal enhancement relative to noise. However, binning over >8 adjacent pixels results in summing partially correlated (and eventually, uncorrelated) pixels, resulting in less signal enhancement relative to noise. A similar conclusion can be also inferred from Fig. 3(d), where the speckle numbers drop for N_Pixel ≲ 64, also due to partially correlated (and eventually, uncorrelated) pixel binning. Finally, although 1702 “speckle” channels corresponding to 1702 sample modes are theoretically available, the maximal speckle number is ∼23 in Fig. 3(d). This occurs because each pixel covers multiple potential “speckle” channels in the vertical direction [Fig. 2(b)], resulting in a loss of dimensionality, as a 2D pattern is measured by a quasi-1D sensor array.

From Eq. (10), SANR is determined by the interplay between ${\overline{\gamma }}_{\mathit{SR}}^2$ and ${\overline{N}}_S$. To investigate further, we estimated ${\overline{\gamma }}_{\mathit{SR}}^2$ and SANRs while varying N_Pixel via Eqs. (8) and (10), respectively. Here, we generated 400 random sample MMF patterns with 1702 modes, and four fixed reference MMF patterns with N_Mode of 1702, 1300, 900, and 500. The simulated γ_SR distributions (based on a single sample pattern), shown in Figs. 4(a) and 4(b), clearly show enhanced coherence with reduced binning (smaller pixels). All γ_SR distributions are stretched to the same horizontal scale. In Fig. 4(c), as pixel size increases, sample photon number per pixel, ${\overline{N}}_S$, increases, but MCD, ${\overline{\gamma }}_{\mathit{SR}}^2$, decreases. The aforementioned tradeoff between ${\overline{\gamma }}_{\mathit{SR}}^2$ and ${\overline{N}}_S$ as N_Pixel varies leads to SANRs [Eq. (10)] shown in Fig. 4(d), which agree with Fig. 3(c).

Fig. 4.

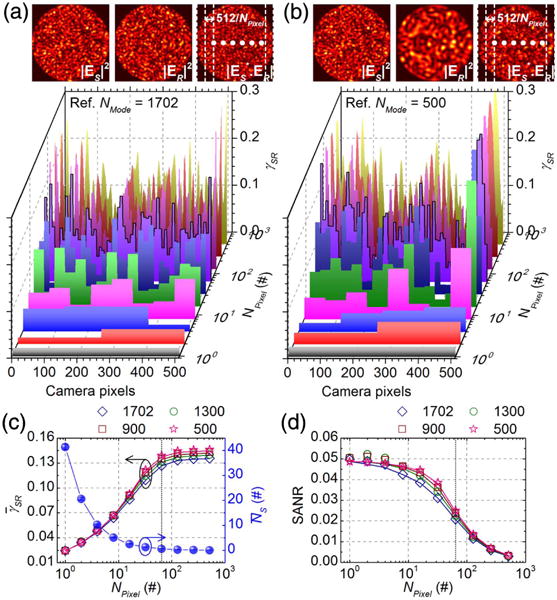
Tradeoff between coherence and pixel photon number incurred by binning. Distributions of instantaneous, local MCD values, γ_SR [Eq. (8) without time- or sensor-element-averaging], across pixels for different amounts of binning (N_Pixel), with a_Slit = 1 and 1702 random sample modes interfering with a fixed reference MMF pattern of either 1702 (a) or 500 (b) modes. (c) ${\overline{N}}_S$ and simulated ${\overline{\gamma }}_{\mathit{SR}}$ versus N_Pixel based on 400 random sample MMF patterns, with different N_Mode (open symbols). (d) SANRs calculated based on Eq. (10) from ${\overline{\gamma }}_{\mathit{SR}}$ and ${\overline{N}}_S$ shown in (c) (open symbols). Corresponding SANRs calculated from MMITMs are shown as solid lines in (c) and (d) for comparison.

2. Vertical Slit Height

Lost MMF “speckle” channels, caused by experimental losses, also increase coherence. This may offset the accompanying reduction in detected sample photons. To understand how experimental losses affect performance, we investigated the impact of vertical slit height on SANR and speckle number. For the simulations in this section, we set N_Pixel to its optimal value of 64. We created 12 random MMITMs based on normalized vertical slit heights, a_Slit, ranging from 1 to 0.02, for each of four reference mode numbers. We generated 20 independent noise-added heterodyne signal time series, N_AC,N(t_d), for each MMITM. Exemplary normalized field autocorrelations for N_Mode of 1702 and selected a_Slit values are shown in Fig. 5(a), with corresponding exponential fits. The field autocorrelation noise is noticeably worse for smaller a_Slit values. RMSEs for the fitted decay rates, estimated from 20 independent simulations, rise for a_Slit < 0.2 [Fig. 5(b)]. Figure 5(c) shows SANRs, either estimated from simulating and fitting G₁ (τ_d) [i.e., A/B from Eq. (S7)] or calculated from MMITMs by Eq. (11), for different N_Mode and a_Slit. Figure 5(d) shows speckle numbers, either estimated from simulations or calculated from MMITMs by Eq. (12). As in Figs. 3(c) and 3(d), the slightly lower simulated SANRs and slightly higher simulated speckle numbers are caused by reduced heterodyne fluctuation amplitude due to digitization.

Fig. 5.

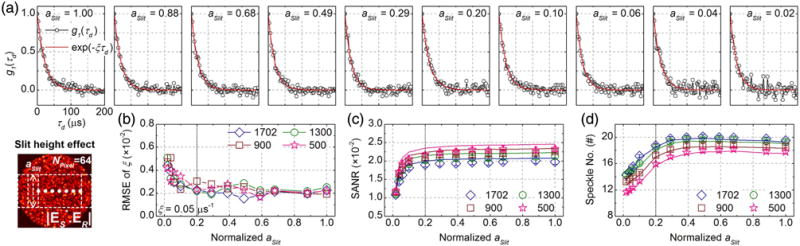
Optimization of fractional vertical slit height. (a) Simulated g₁ (τ_d) for different a_Slit with N_Pixel = 64 and N_Mode = 1702, where total sample and reference photon numbers detected by the 512 camera pixels are set as ∼41 and ∼4.1 × 10⁶ per 3 μs exposure for a_Slit = 1, respectively. (b) RMSE of decay rates versus a_Slit for N_Mode of 1702, 1300, 900, and 500, estimated from 20 independent sets of simulations each. (c) SANR versus a_Slit estimated from simulations with digitization (open symbols) and calculated from the corresponding MMITMs (solid lines). (d) Speckle number versus a_Slit estimated from simulations with digitization (open symbols) and calculated from the corresponding MMITMs (solid lines). Vertical dotted lines in (b), (c), and (d) mark an a_Slit threshold of 0.2, above which minimal changes in SANR and speckle number are observed.

Figures 5(c) and 5(d) clearly show that SANR and speckle number remain roughly constant for 0.2 ≲ a_Slit ≤ 1, and rapidly decline for a_Slit ≲ 0.2. To explain this behavior in terms of the tradeoff between mutual coherence and pixel photon number [Eq. (10)], we again performed simulations on 400 random sample MMF patterns with 1702 modes, and four fixed reference MMF patterns. The tradeoffs between ${\overline{\gamma }}_{\mathit{SR}}^2$ and ${\overline{N}}_S$, incurred by changing a_Slit, are investigated for the optimal N_Pixel of 64. The simulated γ_SR distributions, shown in Figs. 6(a) and 6(b), indicate coherence enhancement with decreasing a_Slit, with ${\overline{\gamma }}_{\mathit{SR}}$ approaching its maximum theoretical value of 0.707 [dotted red line in Fig. 6(c)]. The aforementioned tradeoff between ${\overline{\gamma }}_{\mathit{SR}}^2$ and ${\overline{N}}_S$ as a_Slit varies leads to SANRs [Eq. (10)] shown in Fig. 6(d), which agree with Fig. 5(c).

Fig. 6.

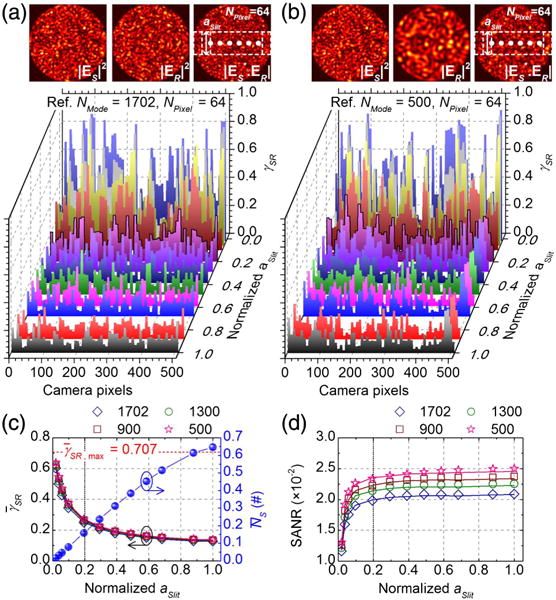
Tradeoff between coherence and pixel photon number incurred by changing slit height. Distributions of instantaneous, local MCD values, γ_SR, across pixels for different a_Slit, with N_Pixel = 64 and 1702 random sample modes interfering with a fixed reference MMF pattern of either 1702 (a) or 500 (b) modes. (c) ${\overline{N}}_S$ and simulated ${\overline{\gamma }}_{\mathit{SR}}$ versus a_Slit based on 400 random sample MMF patterns, with different numbers of reference modes N_Mode (open symbols). (d) SANRs calculated based on Eq. (10) from ${\overline{\gamma }}_{\mathit{SR}}$ and ${\overline{N}}_S$ shown in (c) (open symbols). Corresponding SANRs calculated from MMITMs are shown as solid lines in (c) and (d) for comparison.

Since the transformation a_Slit = 1/N_Pixel and N_Pixel = 1/a_Slit does not change binned pixel size, the connection between pixel binning and vertical slit results merits further comment. Regardless of a_Slit and N_Mode, SANRs begin to decrease for N_Pixel > 4 (Fig. S2), and speckle numbers deviate from theory for uncorrelated pixels for N_Pixel > 4 (Fig. S3). Thus adjacent binned pixels are partially correlated for N_Pixel > 4. If the multimode interference pattern had been measured by a 512 × 512 pixel 2D array, vertical pixel binning over every ∼102 pixels would yield ∼5 binned pixels in the vertical direction, where the central horizontal line of binned pixels corresponds to an a_Slit of 0.2 (i.e., 102/512). However, by the argument above, any further reduction in slit height would result in a loss of partially correlated fluctuations, explaining the loss of SANR for a_Slit < 0.2 [Fig. 5(c)].

3. Summary

The simulations provide several helpful guidelines for system design and optimization. First, since adjacent pixels in the line-scan camera measure similar combinations of “speckle” channels, their heterodyne signals are correlated, and horizontal pixel binning over 8 camera pixels improves SANR without degrading speckle number. Accordingly, ${\overline{\gamma }}_{\mathit{SR}}$ is enhanced from ∼0.024 [i.e., (1/1702)^1/2] for N_Pixel = 1 to ∼0.127 for N_Pixel = 64 [Fig. 4(c)]. Experimental results (Fig. S4) confirmed that N_Pixel 64 yielded the lowest noise autocorrelation estimates, and that there is a tradeoff between SANR and speckle number as N_Pixel is varied, as predicted by simulations. More specifically, experiments confirmed that N_Speckle ≈ 20 was achieved for N_Pixel = 64 [Fig. S4(m)]. Second, a vertical slit with a fractional height of 0.2 can be applied to the MMF interferometer output without appreciably degrading SANR or speckle number, while slit fractional heights of ≲0.2 degrade both. This confirms that detection of all light by the line-scan camera is not essential, and aberrations in our setup should not significantly degrade performance. Third, reference mode number does not play a major role in speckle number or SANR (see simulations for different N_Mode in Section S4 of Supplement 1). Thus, we conclude that excitation of every reference core mode is not required in our experimental setup.

B. Experiments

1. Phantom Measurements

For experimental validation of the multimode iDWS system (see Section S6 in Supplement 1), measurements of Brownian motion were performed for S-D separations ρ from 1 cm to 4 cm. The liquid phantom was made of Intralipid-20% (Fresenius Kabi, Uppsala, Sweden) diluted with water, providing reduced scattering ${{\mu }^{\prime }}_s$ of 6.0 cm⁻¹ and absorption μ_a of 0.05 cm⁻¹ (water) at 852 nm. For phantom measurements, both source and detector fibers were directly inserted ∼1 mm below the liquid surface. Based on the experimental setup in Fig. 2(a), the dynamic interference pattern for each S-D separation was recorded for 1 s. Then, N_Pixel individual autocorrelation estimates, from mean-subtracted temporal fluctuations of N_Pixel binned pixels, were summed to yield the field autocorrelation estimate, G₁ (τ_d, ρ), which was then fitted with a modified DCS model (see Section S5 in Supplement 1). Normalized field autocorrelations, g₁ (τ_d, ρ), for different S-D separations (at an optimized N_Pixel of 64) are shown in Fig. 7(a) (see experimental confirmation of optimal pixel binning in Section S6 of Supplement 1). The corresponding Brownian diffusion coefficients, D_B, of the liquid phantom, estimated by fitting G₁ (τ_d, ρ), are shown in Fig. 7(b). Across a wide range of S-D separations, the estimated D_B remains around 1.25 × 10⁻⁸ cm²/s. Our results are in agreement with the previously reported D_B value of 1.07 × 10⁻⁸ cm²/s for Intralipid at ∼18.5°C, estimated by conventional DCS [33], given our slightly higher temperature of 21°C and possible errors in optical properties.

Fig. 7.

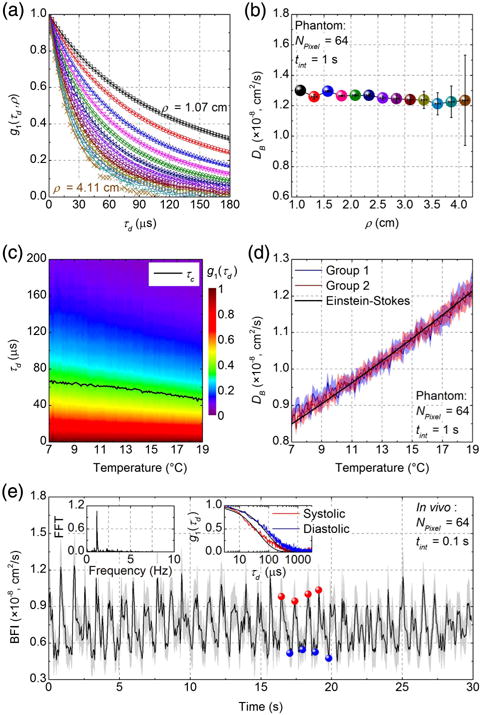
Multimode iDWS in experimental phantoms and in vivo. (a) Normalized field autocorrelations, g₁ (τ_d, ρ), of an Intralipid phantom at different S-D separations (symbols). Corresponding exponential fits are indicated by solid lines. (b) Diffusion coefficient (D_B) values estimated by fitting G₁ (τ_d, ρ) are independent of ρ. Error bars indicate 95% confidence intervals of D_B estimates. (c) Evolution of g₁ (τ_d) from 7°C to 19°C at an S-D separation of 2.5 cm. The decay time of g₁ (τ_d), τ_c, is indicated by black line. (d) Temperature-dependent diffusion coefficients, D_B, were estimated by fitting G₁ (τ_d) in two independent experiments. Shaded regions indicate 95% confidence intervals of D_B estimates. The black line is the fit of the Einstein–Stokes equation. (e) In vivo pulsatile blood flow index (BFI) measured from the human brain with a 2.5 cm S-D separation. Shaded regions indicate 95% confidence intervals of BFI estimates. The left inset of panel 7(e) shows the FFT spectrum of the BFI fluctuations, where a heart rate of ∼1.2 Hz is evident. The right inset shows field autocorrelations, g₁ (τ_d), averaged over four systolic maxima (red) and four diastolic minima (blue), respectively, with corresponding fits. Integration times t_int for estimating G₁ (τ_d) are 1 s and 0.1 s for the phantom and in vivo experiments, respectively. N_Pixel is 64 for all experiments.

For further validation of iDWS system, temperature dependence of Brownian motion in an Intralipid phantom was also investigated. The phantom was passively heated with an average rate of <0.14°C/min to avoid convection effects. With an S-D separation of 2.5 cm, the dynamic interference pattern was recorded for 1 s for every 0.1°C increase in temperature, as monitored by a thermometer (TMD-56, Amprobe). The temperature-dependent D_B was extracted from fitting the summed field autocorrelations, G₁ (τ_d) (N_Pixel = 64), with Eq. (S8). The evolution of the normalized field autocorrelation, g₁ (τd), for temperatures from 7°C to 19°C is shown in Fig. 7(c), where a decreased decay time, τ_c [g₁ (τ_c) = 1/e], indicates increased Brownian motion. Figure 7(d) shows D_B determined from Eq. (S8), in two independent experiments, as well as the fit of the Einstein–Stokes equation, assuming the temperature dependence of water viscosity [33,34]. An average Intralipid particle radius of 171.8 ± 0.4 nm is estimated, in agreement with the previously reported value of 196 nm [33]. The robustness of iDWS to ambient light is demonstrated in Fig. S6 at an S-D separation of 4.1 cm in the same Intralipid phantom (see Section S8 in Supplement 1).

2. In vivo Measurements

Taking advantage of the parallel multispeckle detection of our iDWS system, we monitored high-speed pulsatile blood flow dynamics in the human brain in vivo [18,19,34,35]. A healthy adult human subject sat on a chair with her head placed on a chin rest. Non-contact source and detector fibers were aimed at the subject’s forehead over the prefrontal cortex with an S-D separation of 2.5 cm, which provides sensitivity to brain blood flow with some superficial contamination in DCS [36]. All experimental procedures and protocols were reviewed and approved by the UC Davis Institutional Review Board (IRB), and safety precautions were implemented to avoid accidental eye exposure. A commercial fingertip pulse oximeter (SM-165, Santa Medical) for monitoring the heart rate was placed on the subject’s index finger. With the experimental setup of Fig. 2(a), the dynamic interference pattern was continuously recorded by the line-scan camera for 30 s. Then, summed field autocorrelations, G₁ (τ_d, ρ), were an estimated, with integration time, t_int, of 0.1 s and a sampling rate of 20 Hz (overlapping sampling window), from the mean-subtracted temporal fluctuations of the N_Pixel = 64 binned pixels. The blood flow indices (BFIs) were determined by fitting the measured field autocorrelations with Eq. (S8). Typical optical properties of ${{\mu }^{\prime }}_s=7.38$ cm⁻¹ and μ_a = 0.12 cm⁻¹ [35] were assumed for brain tissue. The estimated BFI time course in Fig. 7(e) clearly reveals the pulsatile nature of the blood flow. Although recovered absolute BFI values are impacted by assumptions about optical properties (particularly scattering) BFI fluctuations track pulsatile flow in deep tissue in vivo [33]. Cardiac rate is confirmed from the fast Fourier transform (FFT) of the BFI fluctuations [Fig. 7(e) left inset], where the peak at ∼1.2 Hz indicates a heart rate of ∼72 bpm, in agreement with the pulse oximeter. The repeatability of iDWS was investigated by measurements in two subjects, which yielded coefficients of variation of 4%–5% in half-minute sessions (see Section S9 in Supplement 1).

It may seem surprising that interferometry, which is highly sensitive to phase shifts caused by wavelength-scale motion, provides meaningful results with a non-contact measurement in vivo. However, our method requires phase stability only on the time scale of the intrinsic field decorrelation due to blood flow, which is a hundred microseconds for the measurements performed here. Changes in light coupling or in the probed tissue volume due to motion may also impact our results. In particular, the non-uniform pulsatile BFI peaks [Fig. 7(e)] could be caused by phase noise due to forehead motion. Finally, though we used non-contact iDWS for in vivo human brain measurements, contact iDWS measurements are also possible in vivo (see Section S10 in Supplement 1).

4. CONCLUSION

A novel MMF-based iDWS employing a CMOS line-scan camera is proposed and experimentally demonstrated. Unlike conventional heterodyne methods that employ a single detector, this system benefits from both MMF light throughput and multispeckle detection. We describe the iDWS system with a MMITM, built from vectorial modes of the MMF. We introduce SANR and speckle number, two key system parameters, and then use the MMITM to investigate the effect of horizontal pixel binning, vertical slit width, and reference mode number on system performance. We show that iDWS can measure Brownian motion in liquid phantoms at up to 4.1 cm S-D separation, and pulsatile blood flow in the human brain at 2.5 cm S-D separation. In the future, speckle number and S-D separation can be further enhanced in iDWS by larger core MMF or free-space collection, as well as detection by an area scan camera. By contrast, in conventional DCS, many SMF or FMF channels with costly single-photon-counting detectors are needed to improve performance.

More broadly, our work links the fields of DWS and DCS, which have relied on single photon counting detectors, to CMOS camera technology, which is rapidly advancing due to mobile phone and autonomous driving applications. Relative to conventional DWS and DCS, our approach introduces novel features, including sensitivity to optical phase, low cost, robustness against ambient light, and the potential for massively parallel multiple speckle detection without single-photon counting. The heterodyne interferometric approach thus represents an advance in diffuse optical sensing of tissue blood flow.