Simulating long-term human weight-loss dynamics in response to calorie restriction

ABSTRACT

Background

Mathematical models have been developed to predict body weight (BW) and composition changes in response to lifestyle interventions, but these models have not been adequately validated over the long term.

Objective

We compared mathematical models of human BW dynamics underlying 2 popular web-based weight-loss prediction tools, the National Institutes of Health Body Weight Planner (NIH BWP) and the Pennington Biomedical Research Center Weight Loss Predictor (PBRC WLP), with data from the 2-year Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy (CALERIE) study.

Design

Mathematical models were initialized using baseline CALERIE data, and changes in body weight (ΔBW), fat mass (ΔFM), and energy expenditure (ΔEE) were simulated in response to time-varying changes in energy intake (ΔEI) objectively measured using the intake-balance method. No model parameters were adjusted from their previously published values.

Results

The PBRC WLP model simulated an exaggerated early decrease in EE in response to calorie restriction, resulting in substantial underestimation of the observed mean (95% CI) BW losses by 3.8 (3.5, 4.2) kg. The NIH WLP simulations were much closer to the data, with an overall mean ΔBW bias of –0.47 (–0.92, –0.015) kg. Linearized model analysis revealed that the main reason for the PBRC WLP model bias was a parameter value defining how spontaneous physical activity expenditure decreased with caloric restriction. Both models exhibited substantial variability in their ability to simulate individual results in response to calorie restriction. Monte Carlo simulations demonstrated that ΔEI measurement uncertainties were a major contributor to the individual variability in NIH BWP model simulations.

Conclusions

The NIH BWP outperformed the PBRC WLP and accurately simulated average weight-loss and energy balance dynamics in response to long-term calorie restriction. However, the substantial variability in the NIH BWP model predictions at the individual level suggests cautious interpretation of individual-level simulations. This trial was registered at clinicaltrials.gov as NCT00427193.

INTRODUCTION

How much weight change is expected for a given intervention relating to diet or physical activity? This question has been investigated for decades. In the 1950s, the popular 3500-kcal/lb weight-loss rule originated from quantifying the average energy density of lost weight (1, 2). While weight-loss predictions were easily calculated using this rule of thumb, the predictions dramatically exaggerated expected weight losses because the simple calculation failed to account for dynamic changes in energy expenditure (EE) (3–7) and the fact that the energy density of lost weight depends on factors such as body fatness (8–10).

Accurate weight-loss predictions require mathematical models of human weight dynamics that account for adaptations of EE and energy partitioning, and several such models have been developed since the 1970s (11). However, mathematical models of human weight change were not regularly utilized in clinical practice or the nutrition or obesity research communities, possibly because the models were difficult to use. In recent years, the use of mathematical models of human body weight (BW) dynamics has been greatly facilitated by the implementation of models as web-based tools such as the NIH Body Weight Planner (NIH BWP; https://www.niddk.nih.gov/health-information/weight-management/body-weight-planner) and the Pennington Biomedical Research Center Weight Loss Predictor (PBRC WLP; http://www.pbrc.edu/research-and-faculty/calculators/weight-loss-predictor/). These tools have been used by millions of people since the mathematical models defining these simulators were published in 2011 (5, 12).

Although both the NIH BWP and PBRC WLP models have been validated and appear to provide similar predictions over the short term, the NIH BWP predicts greater long-term weight changes than the PBRC WLP for the same intervention (6, 13). Testing the relative long-term accuracy of the NIH BWP and PBRC WLP has been complicated by the lack of human studies that included accurate measures of energy intake (EI) over prolonged time periods. Recently, the results of a 2-year human calorie restriction study called Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy (CALERIE) were published (14) where EI was objectively measured using the intake-balance method (15). Here, we used the CALERIE study data to test the validity of the NIH BWP and PBRC WLP models for simulating long-term BW, body fat, and energy balance dynamics in response to caloric restriction using the measured time-varying EI time courses as common model inputs.

METHODS

The published NIH BWP (5) and PBRC WLP (12) models were initialized using the baseline values for age (A), sex, height (H), BW, and total EE measured in CALERIE. Both models used identical time-varying measured EI changes from baseline (ΔEI) to simulate time courses for BW, fat mass (FM), and EE to be compared with the CALERIE data. We implemented the published version of the PBRC WLP model (12) that did not account for the effect of aging on resting metabolic rate and body composition since these effects have negligible impact over the 2-year duration of the CALERIE intervention.

The process of implementing the PBRC WLP model revealed errors in the published model description (12). The equations relating fat-free mass (FFM) to FM, A, and H (10, 12) contained typographical errors and rounded numerical coefficients that did not reproduce the intended mathematical relations. The corrected equations (DM Thomas, Montclair State University, personal communication, 2014) were implemented in our model simulations (see Supplemental Materials). Another challenge we encountered when implementing the published equations for the PBRC WLP (12) was that initializing the model using baseline individual subject measurements in CALERIE often resulted in simulated weight-loss even when EI was set equal to the measured baseline EE. This occurred because the published initialization procedure for the PBRC WLP model specified setting an initial value for volitional physical activity (PA) of zero in the case where the other components of the initial modeled EE exceeded the measured baseline EE. Thus, non-PA components of the modeled EE exceeded the measured EE and weight-loss resulted when EI was set equal to measured baseline EE. To correct this problem, we specified that the initial value of spontaneous physical activity (SPA) expenditure should be lowered from its initial value of 32.6% of baseline EE (12) such that the modeled initial EE was equal to the measured baseline EE.

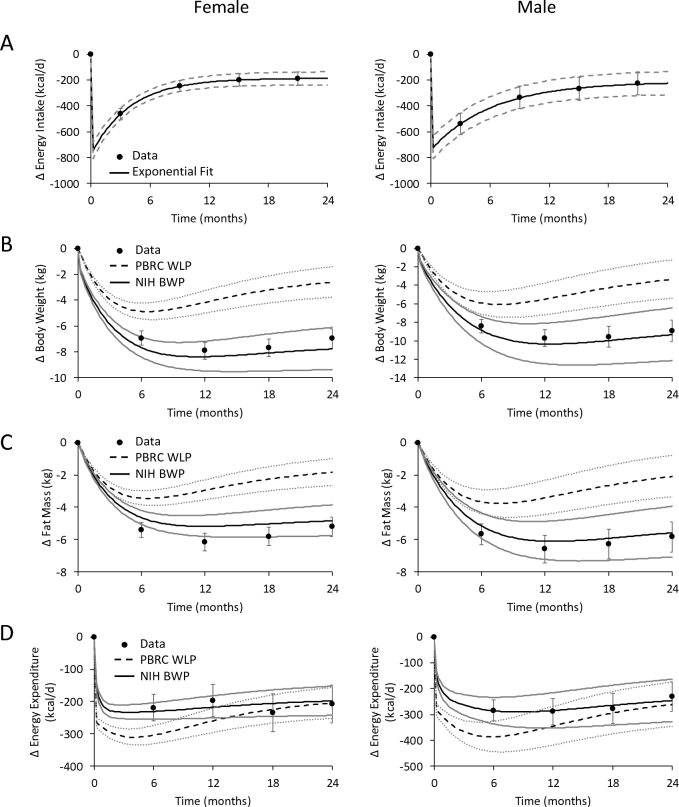
We compared the model predicted changes (Δ) in BW, FM, and EE with CALERIE data at both the individual level and the group level for men and women. Only the CALERIE subjects with complete data for EI, BW, FM, and EE were used. Despite the constant prescribed 25% calorie restriction, the intervention did not achieve a constant mean change in EI (14) and the group-level simulations used exponential functions to fit the measured average ΔEI time courses for CALERIE men and women (solid black curves in Figure 1A). We tested the sensitivity of the group-average model simulations to uncertainties in the measured mean ΔEI by simulating the response to ΔEI exponential time courses at the upper and lower ends of the measured 95% CI (dashed gray curves in Figure 1A). At the individual level, the measured ΔEI for each subject was simulated as step changes over each 6-month measurement period. There was substantial variability between subjects with respect to diet adherence (14).

FIGURE 1.

Mean data from female (n = 78, left column) and male (n = 35, right column) participants in the CALERIE study who had complete data (•) on (A) energy intake, (B) body weight, (C) fat mass, and (D) energy expenditure changes following 2 years of calorie restriction. The NIH BWP model (solid black curves) and PBRC WLP model (dashed black curves) simulations are depicted in response to time-varying mean energy intake measurements described by the best-fit exponential time course and its 95% CI (solid black curves and dashed gray curves in panel A, respectively). The simulated ranges for body weight, fat mass, and energy expenditure changes for the NIH BWP model are bounded by the solid gray curves, and the corresponding simulated PBRC model ranges are bounded by the gray dotted curves. Error bars are ±95% CI. CALERIE, Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy; NIH BWP, National Institutes of Health Body Weight Planner; PBRC WLP, Pennington Biomedical Research Center Weight Loss Predictor; Δ, change from baseline.

The objective EI measurements in CALERIE were performed using the intake-balance method (15) requiring multiple assessments of EE using the doubly labeled water (DLW) method along with estimates of changes in body energy stores obtained using repeated dual-energy X-ray absorptiometry (DXA) measurements. While the intake-balance method is the gold standard for objective measurement of free-living EI, the CALERIE study provided only a single estimate of EI over each 6-month period. Furthermore, the EE measurements were limited to the 2 weeks at the start and end of this period and may not truly reflect the average EE, especially in the early stages of calorie restriction (15). A systematic bias of the intake-balance method could possibly result from inaccurate assumptions of the DLW method (16) as well as systematic errors arising from DXA which is a 2-compartment body composition method that makes assumptions about hydration status that may be violated with weight-loss (17). We assumed that such systematic biases were negligible in the CALERIE study.

The precision of the intake-balance method is determined by the inherent measurement uncertainties of the DLW and DXA methods, with coefficients of variation of ∼5% (18) and ∼1% (19–21) for each EE and FM measurement, respectively. Therefore, propagation of DLW and DXA measurement errors results in a corresponding uncertainty in the ΔEI values calculated using the intake-balance method as previously described (22). To investigate the contribution of the ΔEI uncertainties to the observed variability at the individual subject level, we used the Monte Carlo method. Specifically, the NIH BWP model was used to perform 500 model simulations for each individual CALERIE subject with ΔEI over each 6-month interval being sampled from a normal distribution with measured mean ΔEI and the SD corresponding to the calculated ΔEI measurement uncertainties. The results of these Monte Carlo simulations provided estimates of the variability in ΔBW, ΔFM, and ΔEE time courses expected solely due to the ΔEI measurement uncertainties at the individual subject level. The SDs of these simulated ΔBW, ΔFM, and ΔEE values were compared with the SDs of the residuals between the NIH BWP simulations and CALERIE data to estimate the proportion of the model residuals at the individual level explained by the ΔEI measurement uncertainties.

Linearized versions of both models were derived (see Supplemental Materials) to examine differences between NIH BWP and PBRC WLP models on a common basis and thereby help explain discrepancies between the models. It is important to note that the linearized models of BW dynamics do not result in BW and FM solutions that are linear in time. Rather, for a constant ΔEI, linearized models result in an exponential time course as the system approaches a new steady state of energy balance. Mathematical models were implemented in Berkeley Madonna software (version 8.3), Berkeley, CA and MATLAB version R2017a (Mathworks Inc., Natick, MA). Statistical analyses were performed using SAS version 9.4 (SAS Institute Inc., Cary, NC). Simple paired t tests were conducted to compare the model simulations with the data and significance was declared at P < 0.05.

RESULTS

Similar to the previous report using the full CALERIE sample (14), the 78 women and 35 men with complete data for BW, FM, and EE did not restrict calories by a constant amount over time despite the intervention target of a constant 25% caloric restriction. Rather, the mean ΔEI time course exhibited a large early decrease that exponentially waned over time (solid black curves in Figure 1A). In response to the measured time-varying ΔEI model input, the NIH BWP simulated early weight-loss followed by a plateau and slight weight regain that closely matched the mean data in both women and men (solid black curves in Figure 1B). The NIH BWP model also accurately simulated the observed mean changes in FM (Figure 1C) and EE (Figure 1D). In contrast, the PBRC WLP substantially underestimated the observed mean BW and FM losses (dashed black curves in Figure 1B, C) and overestimated the early decreases in EE (Figure 1D).

Variations in the mean exponential ΔEI time course within its measured 95% CI (dashed gray curves in Figure 1A) resulted in a range of simulated ΔBW, ΔFM, and ΔEE trajectories for the NIH BWP and PBRC models bounded by the solid and dotted gray curves in Figure 1B, C, and D, respectively. Whereas the NIH BWP model simulation range overlapped the measured 95% CI for the mean values of all variables at all time points for both women and men, the PBRC WLP model simulation range was outside the measured 95% CI for all but the mean ΔEE during the second year.

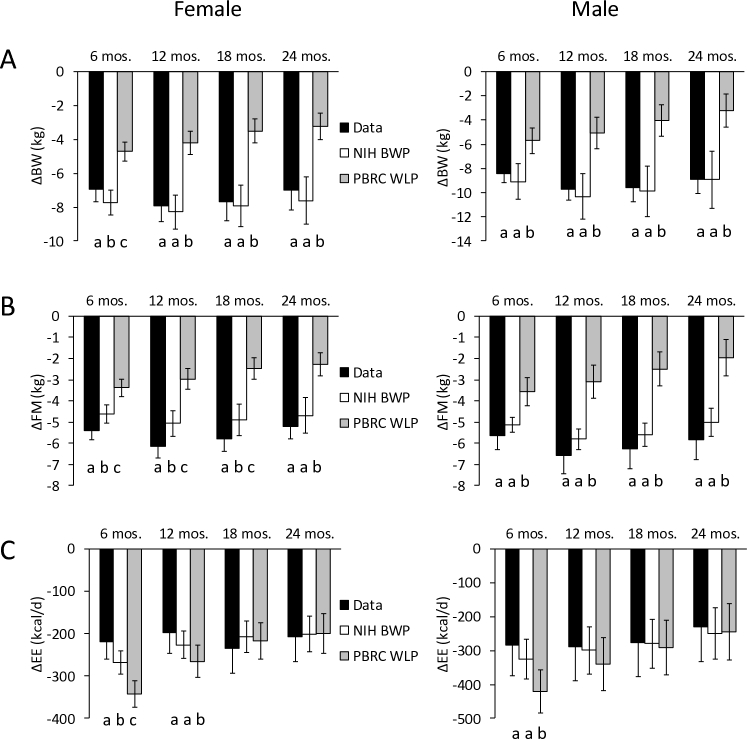
Figure 2 shows the simulation results for individual CALERIE subjects using both NIH BWP and PBRC WLP models. The NIH BWP model simulations provided much closer agreement to the data than the PBRC WLP model whose results were significantly different from the data for all variables at all time points except for ΔEE at months 18 and 24 for women and months 12, 18, and 24 for men. In contrast, the NIH BWP individual simulations were significantly different from the data only in women at 6 months for ΔBW, ΔFM, and ΔEE and at the 12- and 18-month time points for ΔFM.

FIGURE 2.

Individual female (n = 78, left column) and male (n = 35, right column) subjects in the CALERIE study were simulated using the NIH BWP model (open bars) and PBRC WLP model (gray bars) and compared to the data (black bars) for (A) ΔBW, (B) ΔFM, and (C) ΔEE for given ΔEI measured using the intake-balance method. Different letters indicate significant differences between models and data at each time point as determined by paired, 2-sided t tests. Error bars are ±95% CI. ΔBW, change in body weight; CALERIE, Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy; ΔEE, change in energy expenditure; ΔFM, change in fat mass; NIH BWP, National Institutes of Health Body Weight Planner; PBRC WLP, Pennington Biomedical Research Center Weight Loss Predictor.

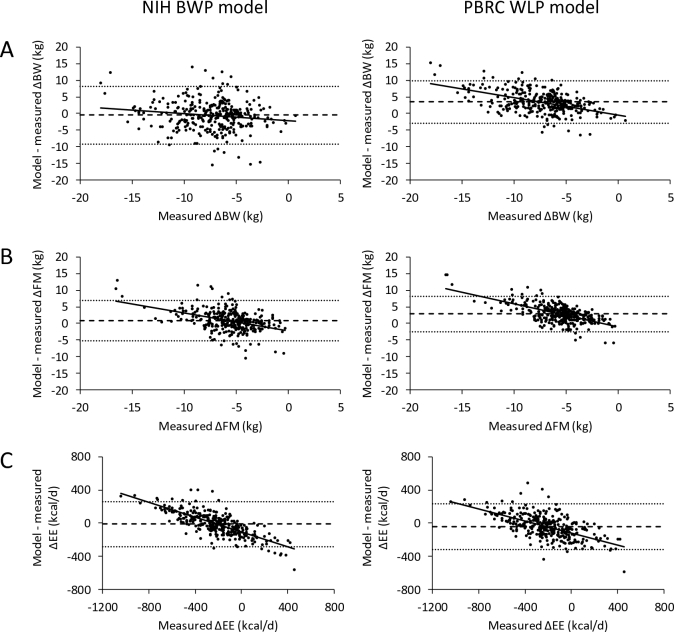
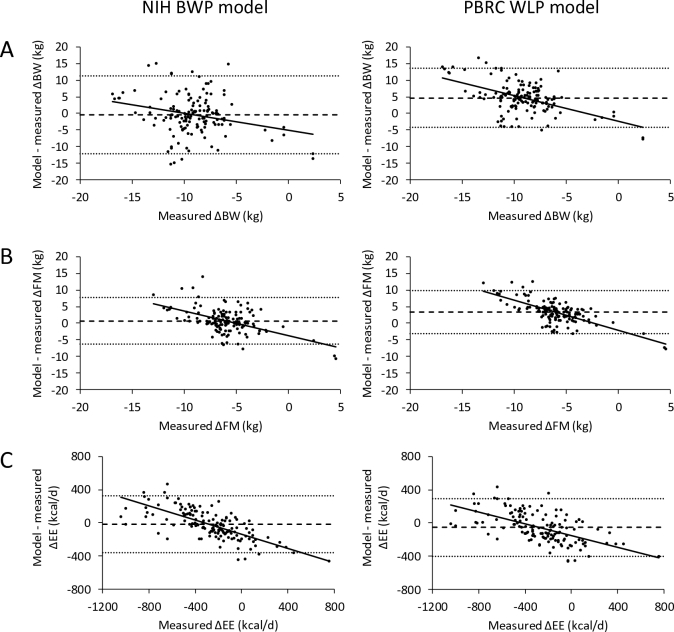
Figures 3 and 4 show the model residual plots at all time points for the individual NIH BWP and PBRC WLP model simulations of CALERIE women and men, respectively. Both models had relatively large limits of agreement (interval between the dotted horizontal lines) indicating the variable concordance of the model simulations with the data at the individual subject level. The NIH BWP resulted in significantly less average bias (horizontal dashed lines) compared to the PBRC WLP. The mean (95% CI) bias for the NIH BWP simulated ΔBW was –0.5 kg (–1.0, –0.011 kg) for women (P = 0.046), –0.40 kg (–1.5, 0.48 kg) for men (P = 0.43), and –0.47 kg (–0.92, –0.015 kg) overall (P = 0.043). For the PBRC WLP, the mean ΔBW bias was 3.5 kg (3.1, 3.8 kg) for women (P < 0.0001), 4.7 kg (2.7, 4.2 kg) for men (P < 0.0001), and 3.8 kg (3.5, 4.2 kg) overall (P < 0.0001). Mean bias for the NIH BWP simulated ΔFM was 0.82 kg (0.47, 1.2 kg) for women (P < 0.0001), 0.70 kg (0.23, 1.4 kg) for men (P = 0.02), and 0.78 kg (0.48, 1.1 kg) overall (P < 0.0001). For the PBRC WLP, the mean simulated ΔFM bias was 2.9 kg (2.6, 3.2 kg) for women (P < 0.0001), 3.3 kg (2.3, 3.4 kg) for men (P < 0.0001), and 3.0 kg (2.7, 3.3 kg) overall (P < 0.0001). Mean bias for the NIH BWP simulated ΔEE was –12 kcal/d (–27) for women (P = 0.14), –19 kcal/d (–41, 17 kcal/d) for men (P = 0.2), and –14 kcal/d (–28, 0.03 kcal/d) overall (P = 0.051). For the PBRC WLP, the mean simulated ΔEE bias was –41 kcal/d (–57, –26 kcal/d) for women (P < 0.0001), –54 kcal/d (–71, –12 kcal/d) for men (P = 0.0005), and –45 kcal/d (–60, –31 kcal/d) overall (P < 0.0001).

FIGURE 3.

Residuals between CALERIE study data in 78 women for individual NIH BWP model (left column) and PBRC WLP model (right column) simulations of (A) ΔBW, (B) ΔFM, and (C) ΔEE for given ΔEI measured over each 6-month period using the intake-balance method. The dashed horizontal line is the mean model residual bias, and the dotted horizontal lines indicate the limits of agreement (±1.96 × SD of the residuals). The solid line is the best fit linear regression line. The mean bias of the simulated ΔBW was –0.5 kg for the NIH BWP and 3.5 kg for the PBRC WLP. The mean bias of the simulated ΔFM was 0.82 kg for the NIH BWP and 2.9 kg for the PBRC WLP. The mean bias of the simulated ΔEE was –12 kcal/d for the NIH BWP and –41 kcal/d for the PBRC WLP. ΔBW, change in body weight; CALERIE, Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy; ΔEE, change in energy expenditure; ΔFM, change in fat mass; NIH BWP, National Institutes of Health Body Weight Planner; PBRC WLP, Pennington Biomedical Research Center Weight Loss Predictor.

FIGURE 4.

Residuals between CALERIE study data in 35 males for individual NIH BWP model (left column) and PBRC WLP model (right column) simulations of (A) ΔBW, (B) ΔFM, and (C) ΔEE for given ΔEI measured over each 6-month period using the intake-balance method. The dashed horizontal line is the mean model residual bias, and the dotted horizontal lines indicate the limits of agreement (±1.96 × SD of the residuals). The solid line is the best fit linear regression line. The mean bias of the simulated ΔBW was –0.4 kg for the NIH BWP and 4.7 kg for the PBRC WLP. The mean bias of the simulated ΔFM was 0.7 kg for the NIH BWP and 3.3 kg for the PBRC WLP. The mean bias of the simulated ΔEE was –19 kcal/d for the NIH BWP and –54 kcal/d for the PBRC WLP. ΔBW, change in body weight; CALERIE, Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy; ΔEE, change in energy expenditure; ΔFM, change in fat mass; NIH BWP, National Institutes of Health Body Weight Planner; PBRC WLP, Pennington Biomedical Research Center Weight Loss Predictor.

To estimate how much of the individual variability between measured and simulated ΔBW, ΔFM, and ΔEE was attributable simply to measurement uncertainties in the input ΔEI at the individual subject level, we used the NIH BWP to perform Monte Carlo simulations as described in the Methods. For women, the overall mean ΔEI uncertainty at the individual level was 137 kcal/d and the corresponding SDs for ΔBW, ΔFM, and ΔEE residuals were 2.6 kg, 1.5 kg, and 81 kcal/d, respectively. Therefore, the ΔEI measurement uncertainties in women explained ∼58%, ∼48%, and ∼58% of the observed individual variability between measured and simulated ΔBW, ΔFM, and ΔEE, respectively. For men, the overall mean ΔEI uncertainty at the individual level was 173 kcal/d and the corresponding SDs for ΔBW, ΔFM, and ΔEE residuals were 3.2 kg, 1.8 kg, and 106 kcal/d, respectively. Therefore, the ΔEI measurement uncertainties in men explained ∼55%, ∼48%, and ∼61% of the observed individual variability between measured and simulated ΔBW, ΔFM, and ΔEE, respectively.

The Supplemental Materials show that both NIH BWP and PBRC WLP models can be written in the following linear form that accurately reproduces the results of the full models:

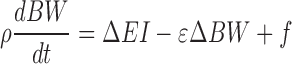(1)

Where ρ is an effective energy density, ε is a parameter that defines how EE depends on BW change, and f is a positive constant in the linearized PBRC WLP model when ΔEI < 0 and represents metabolic adaptation of resting EE in response to caloric restriction. In contrast, the linearized NIH BWP model results in f = 0 (see Supplementary Materials). For a fixed ΔEI, the linear models have solutions that follow an exponential time course approaching a steady state weight change given by (ΔEI + f)/ε.

When initialized to the average values for women and men in CALERIE, the linearized PBRC WLP model resulted in parameter values of ρ = 8860 and 8230 kcal/kg, f = 106 and 134 kcal/d, and ε = 38 and 43 kcal · kg^–1 · d^–1, respectively. The exponential time constant defining the rate that the model approaches steady state for constant ΔEI, τ = ρ/ε, was therefore calculated to be 230 d and 190 d in women and men, respectively. In contrast, the linearized NIH BWP model resulted in the parameters ρ = 9916 and 9383 kcal/kg, f = 0 and 0 kcal/d, ε = 24 and 28 kcal · kg^–1 · d^–1, and τ = 414 and 340 d for women and men, respectively. Therefore, for a given constant ΔEI, the PBRC WLP model results in a weight plateau more quickly than the NIH BWP model, and the magnitude of weight change at steady state is smaller.

The linear model analysis revealed that the biggest discrepancy between the NIH BWP and PBRC WLP models was due to differences in the parameter ε. The value of ε in the PBRC WLP model depended sensitively on how SPA expenditure changed with energy restriction. The PBRC BWP model assumed that two-thirds of the total EE change is a result of decreased SPA. However, if the value of this SPA parameter is decreased by 25%, such that half of the total EE change results from decreased SPA, then the PBRC WLP model more closely resembles the NIH BWP such that the revised values for ε in women and men are 23 and 26 kcal · kg^–1 · d^–1, respectively.

DISCUSSION

The PBRC WLP and NIH BWP models were developed using data from controlled feeding studies in humans, typically conducted over relatively short periods of several weeks or months. Here, we evaluated these models in comparison to long-term data from the human calorie restriction study CALERIE with objective measurements of time-varying ΔEI as model inputs. Because the CALERIE data were published several years after the NIH BWP and PBRC WLP were fully developed and parameterized, comparison of the model-simulated weight changes with the CALERIE data constitutes a true test of long-term model validity. We demonstrated that the NIH BWP performed substantially better than the PBRC WLP to accurately simulate mean changes in BW, FM, and EE in response to calorie restriction over 2 years.

The greater long-term accuracy of the NIH BWP model likely resulted from its origin as a tool to accurately simulate periods of long-term maintenance of lost weight using data from studies where participants had maintained a stable steady state weight change (23). In contrast, the PBRC WLP model was not developed using data from studies with long-term measurements or steady state weight changes. Nevertheless, the PBRC WLP model has been used on several occasions to perform long-term energy balance calculations (24–27). The biases revealed in the present report warrant careful reconsideration of any conclusions based on such long-term PBRC WLP model calculations.

Our analysis of the linearized models revealed that a key factor underlying the contrasting results between NIH BWP and PBRC WLP models involves their different assumptions about how caloric restriction affects physical activity. The NIH BWP model (5) makes no a priori assumptions about physical activity changes. Nevertheless, since physical activity expenditure was assumed to be weight-bearing, the overall physical activity expenditure in the NIH BWP model decreases in proportion to the weight lost even if the amount of physical activity is unchanged. In contrast, the PBRC WLP assumed that SPA expenditure decreases immediately and substantially following caloric restriction, including periods of subsequent weight stability following active weight-loss (12). However, the evidence in support of this assumption is mixed and a recent review suggested that restriction of EI does not generally lead to major reductions in overall physical activity (28).

Interestingly, we found that the PBRC model can be brought into closer alignment with the NIH BWP model by simply decreasing the SPA model parameter by 25%, such that about half of the overall EE change during underfeeding is due to reductions in physical activity EE. This value also represents the mean physical activity EE effect observed in 3 underfeeding studies, although the results are highly variable (29–31). We recommend that the PBRC WLP model be updated accordingly.

While the overall mean bias of the NIH BWP simulations was much lower than that of the PBRC WLP, the model did slightly underestimate loss of FM and overestimate the loss of BW, especially at the early time points in women. The greater BW loss was likely due to greater simulated body water losses very early in the simulations depicted in Figure 1B arising from an assumed reduction in dietary sodium and carbohydrate. The slight underestimation of FM loss by the NIH BWP may have been due to a systematic underestimation of the degree of early calorie restriction as measured by the intake-balance method. A previous study noted a rapid drop in EE upon induction of calorie restriction and failure to directly measure such an early drop in EE likely led to an overestimation of EI using the intake-balance method during the first 6 months of the CALERIE study (15). In other words, the actual EI was likely somewhat lower than the estimated EI that was used as a model input and therefore slightly less FM loss was simulated by the NIH BWP model than was observed.

We believe that the NIH BWP model can be used with reasonable confidence to accurately predict long-term changes in mean BW, body fat, and energy balance dynamics for groups of people in response to given changes in EI. For example, the NIH BWP model has been used at the population level to evaluate obesity interventions (32, 33) and investigate the relation between changes in a nation's food supply, obesity prevalence, and the progressive increase in food waste and its impact on natural resources and the environment (34, 35). The NIH BWP model has also been used to estimate mean compensatory increases in EI in response to diabetes treatment with sodium-glucose type 2 transport inhibitors (36) and thereby provide the first quantification of feedback control of human EI at the group level (37).

Despite the reasonable accuracy of the NIH BWP model at the group level, previous publications using the NIH BWP model emphasized the expected imprecision of model predictions for individual patients while also acknowledging that such individual-level simulations may have clinical utility (5, 38). In contrast, the originators of the PBRC WLP model claimed that it “provides accurate estimates for both group-level and individual-level data, demonstrating the ability to use the model to accurately predict individual patients weight-loss and objectively measure adherence to calorie prescriptions” (12). Our results suggest otherwise. Rather, individual-level model simulations are fundamentally limited by uncertainties in the measurement of free-living EE and EI, even when the best methods are employed.

As we previously demonstrated (22), the uncertainty of ΔEI measured using the intake-balance method at the individual level in the CALERIE study spans hundreds of kcal/d. Monte Carlo simulations using the NIH BWP demonstrated that variations in ΔEI within the measurement uncertainty at the individual level led to substantial variations in individual ΔBW, ΔFM, and ΔEE time courses that explained much of the observed variability between data and model simulations. The remaining variability was likely due to individual physiological and behavioral differences not captured by the NIH BWP model, such as variable degrees of metabolic adaptation or changes in physical activity.

In conclusion, data from the CALERIE study were used to demonstrate that the PBRC WLP model substantially underestimated loss of BW and FM primarily due to an exaggerated reduction in EE via decreased SPA with caloric restriction. In contrast, the CALERIE data provided long-term validation of the NIH BWP model at the group level, but the precision of the model predictions at the individual level was fundamentally limited by EI measurement uncertainties and suggests cautious interpretation of individual patient model simulations.

Notes

Supported by the Intramural Research Program of the NIH, National Institute of Diabetes and Digestive and Kidney Diseases.

Supplemental Materials are available from the “Supplementary data” link in the online posting of the article and from the same link in the online table of contents at https://academic.oup.com/ajcn/.

Abbreviations used: BW, body weight; CALERIE, Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy; DLW, doubly labeled water; DXA, dual-energy X-ray absorptiometry; EE, energy expenditure; EI, energy intake; FM, fat mass; NIH BWP, National Institutes of Health Body Weight Planner; PBRC WLP, Pennington Biomedical Research Center Weight Loss Predictor; SPA, spontaneous physical activity; Δ, change from baseline.