Environmentally Controlled Curvature of Single Collagen Proteins

Abstract

The predominant structural protein in vertebrates is collagen, which plays a key role in extracellular matrix and connective tissue mechanics. Despite its prevalence and physical importance in biology, the mechanical properties of molecular collagen are far from established. The flexibility of its triple helix is unresolved, with descriptions from different experimental techniques ranging from flexible to semirigid. Furthermore, it is unknown how collagen type (homo- versus heterotrimeric) and source (tissue derived versus recombinant) influence flexibility. Using SmarTrace, a chain-tracing algorithm we devised, we performed statistical analysis of collagen conformations collected with atomic force microscopy to determine the protein’s mechanical properties. Our results show that types I, II, and III collagens—the key fibrillar varieties—exhibit similar molecular flexibilities. However, collagen conformations are strongly modulated by salt, transitioning from compact to extended as KCl concentration increases in both neutral and acidic pH. Although analysis with a standard worm-like chain model suggests that the persistence length of collagen can attain a wide range of values within the literature range, closer inspection reveals that this modulation of collagen’s conformational behavior is not due to changes in flexibility but rather arises from the induction of curvature (either intrinsic or induced by interactions with the mica surface). By modifying standard polymer theory to include innate curvature, we show that collagen behaves as an equilibrated curved worm-like chain in two dimensions. Analysis within the curved worm-like chain model shows that collagen’s curvature depends strongly on pH and salt, whereas its persistence length does not. Thus, we find that triple-helical collagen is well described as semiflexible irrespective of source, type, pH, and salt environment. These results demonstrate that collagen is more flexible than its conventional description as a rigid rod, which may have implications for its cellular processing and secretion.

Introduction

Collagen is the predominant structural protein in vertebrates, for whom it represents more than one quarter of the total protein in our bodies (1, 2). It is widely used as a biomaterial and plays a vital physiological role in extracellular matrix and connective tissue mechanics. Collagen can assemble into many different higher-order forms, which fulfill distinct structural and mechanical roles.

Over 28 different types of human collagen have been identified (1, 2), of which the most prevalent are fibrillar collagens such as types I, II, and III. These collagens assemble to create highly ordered fibrils, which in turn are the building blocks for the extracellular matrix and for fibers, which act as load- and tension-bearing structures in connective tissues. Not surprisingly, changes in collagen’s composition are associated with a wide variety of diseases, including osteogenesis imperfecta (3) and Ehlers-Danlos syndrome (4). In addition to genetic mutations in collagen, physiological dysfunction can arise from alterations in post-translational modifications and aging via nonenzymatic glycation and cross-link formation (5). Such chemical changes at the protein level correlate with altered tissue structure and mechanics and pathologically affect human health. Because of the hierarchical nature of collagen structure, identifying the mechanisms by which chemical changes modify tissue mechanics requires understanding how they impact mechanics at the molecular level.

Collagen’s molecular structure is a right-handed triple helix (Fig. 1 A), ∼300 nm long and 1–2 nm in diameter (2). This triple helix comprises three left-handed polyproline-II-like helices (α-chains) with a characteristic (Gly-X-Y)_n repeat amino acid sequence. Although frequently proline or hydroxyproline, the X and Y amino acids are variable and provide the sequence diversity that defines individual collagen types. Different collagen types are also distinguished as homotrimeric (three identical α-chains) or heterotrimeric. Although the sequences of the different types of collagen are well established, their mechanical properties are not.

Figure 1.

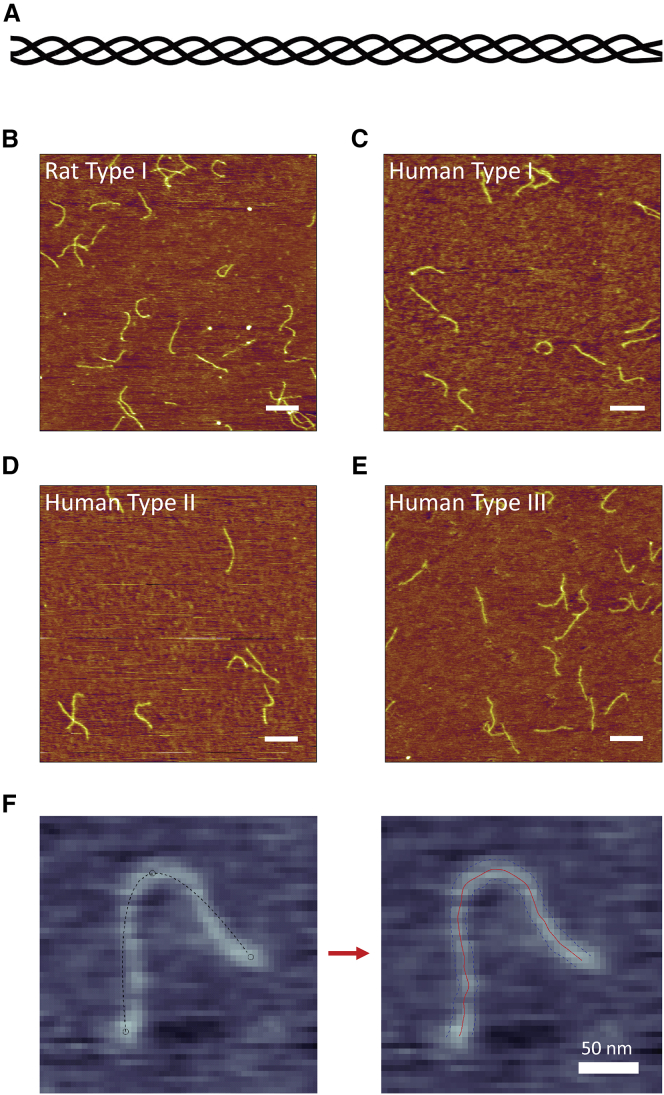
Imaging individual collagen proteins. (A) A schematic of triple-helical collagen. (B–E) Representative AFM images of each of the four collagen samples investigated in this work. For each sample, collagen was deposited from a solution of 100 mM KCl + 1 mM HCl. Scale bars, 250 nm. (B) Rat tail-derived type I collagen. (C) Recombinant human type I collagen. (D) Cartilage-derived human type II collagen. (E) Recombinant human type III collagen. (F) SmarTrace starts with user input points along a collagen chain (left image). Initial splines connecting the three input points (dashed lines) do not follow the chain. The SmarTrace algorithm identifies both the center line of the chain (red) and its width (blue—used for chain tracing but no further analysis), as shown in the right image. To view this figure in color, go online.

One property commonly used to describe the mechanical properties of chain-like biomolecules is the persistence length—the length over which the orientation of the chain remains correlated in the presence of thermal noise. Although the persistence lengths of other biological polymers such as DNA are well established and robust to experimental technique, this is not the case for collagen (Table 1). Early solution-based studies found that collagen’s triple helix should be considered semirigid, exhibiting a persistence length of p ≈ 130–180 nm (6, 7, 8). These values likely led to the conventional description of collagen as a possessing a stiff, rod-like structure (9, 10). However, most recent single-molecule experimental and simulation studies contradict this description, finding persistence lengths for collagen as short as p ≈ 10 nm (11, 12, 13, 14, 15, 16, 17). These values imply that collagen is highly flexible, adopting compact, coiled configurations in solution. Other experimental and simulation approaches have determined persistence lengths throughout this range, with another cluster of values around p ≈ 40–60 nm (14, 18, 19, 20). It is remarkable that this fundamental parameter of persistence length is so poorly established for a protein of such mechanical importance and ubiquity.

Table 1.

Literature Estimates of Persistence Length for Fibrillar, Molecular Collagens

Persistence Length, p (nm)	Collagen Type and Source	Solution Conditions	Method	Reference
10	57-residue segment of homotrimeric mouse type I	water, neutral pH	Molecular dynamics	(16)
12	Bovine dermis type I	water, pH ∼5	AFM imaging	(13)
13	45-residue segment of rat type I	10 mM NaCl, neutral pH	Molecular dynamics	(17)
11–15	Cell-derived human type I procollagen; recombinant human type II procollagen	>10 mM buffer, neutral pH	Optical tweezers stretching	(11, 12)
16	30-residue homotrimeric peptide	water, neutral pH	Steered molecular dynamics	(15)
22	57-residue segment of heterotrimeric mouse type I	water, neutral pH	Molecular dynamics	(16)
15–65	Recombinant human type II procollagen	>10 mM buffer, neutral pH	Optical tweezers stretching	(14)
40	Fetal bovine type III	50 mM acetic acid + equal volume glycerol	Electron microscopy	(18)
51	60-nm segment of human type I collagen	water, neutral pH	Coarse-grained molecular dynamics	(20)
57	Calf dermis type I	50 mM acetic acid + equal volume glycerol	Electron microscopy	(18)
130	Rat skin type I	>10 mM buffer, pH ∼5	Viscometry	(6)
135–165	Bovine dermis type I	>10 mM buffer, neutral pH	AFM imaging	(13)
161	Rat skin type I	0.3 M acetate + 6 mM NaCl, pH 4	Rheology	(7, 8)
160–165	Bovine dermis type I	1 mM HCl	Dynamic light scattering	(19)
167	Rat skin type I	>10 mM buffer, neutral pH	Rheology	(8)

Examination of Table 1 suggests that there is diversity not only in the approaches used to study collagen’s flexibility but also in the types of collagen, their sources, and solution conditions. A comparison of different tissue-derived collagen types was performed in (18), which determined the type I heterotrimer to be slightly more rigid than the type III homotrimer. A similar difference between homo- and heterotrimeric collagen sequences was found in recent molecular dynamics simulations (16). Collagen’s remodeling by MMP-1, a collagenase that unwinds the triple helix, has been suggested to depend on the source of collagen (e.g., recombinant, from cell culture, or from tissue) (21), implying that post-translational enzymatic and age-related nonenzymatic modifications may alter its mechanics at the molecular level. A recent study found that collagen’s flexibility is influenced by its solution environment, with collagen appearing flexible at low salt in acidic conditions and more rigid in high-ionic-strength, neutral pH buffers (13). This result runs counter to the expectations of the behavior of polyelectrolytes like DNA, which are expected to become more flexible as ionic strength is increased (22, 23). Understanding collagen’s response in different solution conditions is relevant not only to its mechanical role in distinct tissue environments but also to understanding its intracellular compactness as it traverses a pH gradient during cellular processing and secretion (24, 25).

In this work, we use atomic force microscopy imaging and characterization to investigate how composition, source, and chemical environment affect the flexibility of collagen’s triple helix. By comparing different fibrillar collagens (types I, II, and III; tissue-derived and recombinantly expressed; homo- and heterotrimeric triple helical structures), we find that molecular composition does not significantly impact collagen’s overall flexibility. In contrast, we find that both ionic strength and pH independently impact the apparent flexibility of collagen, providing estimates of persistence length that span the range from flexible to semirigid depending on solution environment. Careful consideration of polymer chain statistics shows, however, that treating collagen as a standard worm-like chain does not describe its properties in most of these chemical environments. Instead, we show that a curved worm-like chain model that includes inherent molecular curvature is a far more appropriate descriptor of the observed conformations of collagen on mica. With this model, collagen’s bending flexibility depends much less on solution conditions; instead, salt concentration and pH modulate its global curvature. We find that curvature does not depend strongly on the type or source of collagen, nor does the persistence length. To the best of our knowledge, these results constitute the first experimental analysis of curved worm-like chains and provide a new explanation for the conflicting reports on the flexibility of triple-helical collagen.

Materials and Methods

Collagen sources

Recombinant human type I and recombinant human type III collagen were expressed in yeast and obtained from FibroGen (San Francisco, CA) (generous gifts of Alexander Dunn, Stanford University), rat tail tendon-derived type I collagen (Cultrex 3440-100-01) was purchased from R&D Systems (Oakville, Canada), and human cartilage-derived type II collagen (CC052) was purchased from EMD Millipore (Burlington, MA). All stocks are of pepsin-treated collagen and are have a concentration between 2 and 5 mg/mL in 20 mM acetic acid.

Sample preparation

The desired solution conditions were obtained by solution exchange using Millipore Amicon Ultra-0.5 spin filters (50 kDa, UFC505096), then dilution to ∼1 μg/mL collagen before deposition. 50 μL was deposited onto freshly cleaved mica (Highest Grade V1 AFM Mica Discs, 10 mm; Ted Pella, Redding, CA) for 20 s. After deposition, samples were rinsed five times with 1 mL ultrapure water to remove unbound proteins, and the mica was dried under a flow of filtered compressed air. It is important to note that all collagen molecules were imaged in these dry conditions. Thus, solution conditions quoted refer to the condition under which collagen was deposited onto mica, at room temperature.

Atomic force microscopy imaging

Images of collagen adsorbed to mica were collected with an Asylum Research MFP-3D atomic force microscope (Asylum Research, Santa Barbara, CA) using tapping mode in air. AFM tips with a 325 kHz resonance frequency and 40 N/m force constant (MikroMasch, HQ:NSC15/AL BS) were used for image collection and were changed as necessary to preserve image quality.

Chain tracing

The SmarTrace algorithm used to trace collagen chains from AFM images was developed in MATLAB (26) and uses a graphical user interface adapted from (27). It is available from the authors upon request. A detailed description of the SmarTrace workflow and validation can be found in the Supporting Materials and Methods. Briefly, the algorithm uses cross-correlation analysis of a template cross section with the imaged chain to identify its center line and width. Continuity constraints on the local directionality and width enable the tracing of chains in noisy environments.

Data analysis

Traced chains were sampled using bootstrapping to extract statistics of the chain for flexibility determination. Following the method of Faas et al. (28), each chain was randomly divided into nonoverlapping segments of lengths drawn from a set of input values (here, s = 10, 20, 30, ..., 200 nm). The maximal segment length does not need to be the same as the chain contour length, so it allows the use of partially traced chains. This is particularly useful when ends of a molecule are not clear or chains intersect, as it allows subsections of the chain to be included in the analysis. $\langle R^2\left(s\right)\rangle$ and $\langle \cos \theta \left(s\right)\rangle$ were determined from all segments of each length s.

Resultant $\langle R^2\left(s\right)\rangle$ and $\langle \cos \theta \left(s\right)\rangle$ were fitted to equations derived from the inextensible two-dimensional worm-like chain (WLC) model with (Eqs. 3 and 4) or without (Eqs. 1 and 2) intrinsic curvature. Derivations for Eqs. 3 and 4 are presented in the Supporting Materials and Methods.

The kurtosis of each angular distribution was calculated at each segment length s as$n\left[{\sum }_i{\left({\theta }_i-\langle \theta \rangle \right)}^4\right]/{\left[{\sum }_i{\left({\theta }_i-\langle \theta \rangle \right)}^2\right]}^2$, for a distribution across n values of θ_i. The standard error of the kurtosis was determined using Eq. S19.

Values for p and κ_o presented in Table 2 are an average of the results from independent fits to $\langle R^2\left(s\right)\rangle$ and to $\langle \cos \theta \left(s\right)\rangle$. Reported errors, Δ, represent the propagated error of the 95% confidence intervals of the respective fit parameters or half of the difference between the $\langle R^2\left(s\right)\rangle$ and $\langle \cos \theta \left(s\right)\rangle$ fit parameters, whichever is larger. A full list of fitting parameters from all models and samples is provided in Table S1. The total length of collagen chains traced in each sample condition is also included in Table S1.

Table 2.

Summary of Fitting Parameters Determined in This Work

Collagen Type	Solvent Condition	Standard Model Fits		Curved Model Fits
		p (nm)	Δp (nm)	p (nm)	Δp (nm)	κo (nm−1)	Δκo (nm−1)
Rat I	water	59	17	102	21	0.015	0.003
Rat I	100 μM KCl	40	8	57	14	0.014	0.003
Rat I	1 mM KCl	70	15	105	21	0.011	0.001
Rat I	10 mM KCl	91	9	89	11	0.000	N/A
Rat I	100 mM KCl	120	22	120	46	0.000	N/A
Rat I	1 mM HCl	39	8	57	11	0.016	0.002
Rat I	10 mM KCl + 1 mM HCl	75	15	117	26	0.010	0.001
Rat I	100 mM KCl + 1 mM HCl	103	10	101	18	0.000	N/A
Human I	100 mM KCl + 1 mM HCl	86	8	88	14	0.000	N/A
Human II	100 mM KCl + 1 mM HCl	98	7	101	10	0.002	N/A
Human III	100 mM KCl + 1 mM HCl	84	7	83	11	0.001	N/A
Rat I	20 mM acetic acid	33	7	49	8	0.018	0.002
Human I	20 mM acetic acid	38	9	59	10	0.017	0.001
Human II	20 mM acetic acid	57	18	97	17	0.017	0.002
Human III	20 mM acetic acid	44	11	69	14	0.017	0.002

Fit parameters are averages of the values from independent $\langle R^2\left(s\right)\rangle$ and $\langle \cos \theta \left(s\right)\rangle$ fits of the data; errors, Δ, represent the error in these estimates. N/A indicates uncertainties that are unphysically large. The total contour lengths of collagen traced in each condition is provided along with a comprehensive list of fitting parameters and χ² values in Table S1.

Model selection used a likelihood-based approach, the Bayesian Information Criterion (BIC) (29). Details are provided in the Supporting Materials and Methods, with results provided in Table S2.

Validation tests

The performance of the SmarTrace algorithm and data analysis code was evaluated by tests on simulated polymers and on images of DNA. Details are provided in the Supporting Materials and Methods.

Results and Discussion

Atomic force microscopy (AFM) is a well-established tool for imaging the conformations of flexible biopolymers (30). We have used the technique to image collagens of different types and sources deposited from a range of solution conditions and have characterized how these parameters influence the flexibility of collagen’s triple helix.

Collagen type and source

To investigate how collagen’s flexibility depends on its source, we compared four different samples of collagen. These represent three types of fibrillar collagens (types I, II, and III) of either rat (type I) or human (all three) genetic origin. Although all of these samples are capable of self-assembly into highly ordered fibrils, they were imaged under sufficiently dilute conditions such that assembly did not occur. Type I collagen is a heterotrimer (α₁(I)₂α₂(I)₁), whereas types II and III are each homotrimeric (α₁(II/III)₃). Additionally, to explore how collagen’s source influences its flexibility, our samples encompass both tissue-derived (rat type I and human type II) and cell-derived (human types I and III) sources. The latter were recombinantly expressed in yeast and possess only prolyl hydroxylation as a post-translational modification (31). This contrasts with mammalian-produced collagens, which have extensive post-translational modifications including hydroxylation of prolines and lysines as well as O-glycosylation of hydroxylysines (14, 24).

Representative AFM images of each of the four collagen samples are shown in Fig. 1, B–E. Each image was obtained by depositing collagen from a room-temperature solution of 100 mM KCl + 1 mM HCl onto freshly cleaved mica, then rinsing with water and drying before imaging. For all four collagen samples, the chains appear semiflexible, with contour lengths of ∼300 nm, as expected (32). There are no obvious qualitative differences in flexibility among these samples.

To quantify the flexibility of each collagen type, the imaged chains were traced to provide backbone contours for conformational analysis. Existing chain-tracing algorithms proved problematic for many of our images, in some cases because of the background levels of noise (28) or in others from the sensitivity of the algorithm to the locations of user-input starting points (27). Hence, we developed a new chain-tracing program, dubbed SmarTrace. The algorithm incorporates pattern matching to identify the best centerline of a chain and refines an initial guess at this centerline by using direction and width continuity constraints. Required user input is minimal: backbone contours are identified from only a few clicks near the chain (see Fig. 1 F). Details of SmarTrace’s methodology and workflow are provided in the Supporting Materials and Methods.

From traced chains, we implemented tools of polymer physics to analyze the statistical properties of chain conformations and determine persistence lengths (33). To perform this analysis, chains were segmented randomly into nonoverlapping pieces of different contour lengths (e.g., s = 10, 20, …, 200 nm). This approach allows partially traced chains to be included in the analysis (28). For each segment, we calculated its squared end-to-end distance R²(s) and the change in orientation between its starting and ending tangent vectors $\hat{t}\left(s\right)\cdot \hat{t}\left(0\right)=\cos \theta \left(s\right)$; these quantities were then averaged over all segments of length s within the population. Length-dependent trends in mean-square end-to-end distance, $\langle R^2\left(s\right)\rangle ,$ and tangent vector correlation, $\langle \cos \theta \left(s\right)\rangle$, were compared with the predictions of the WLC model for polymers equilibrated in two dimensions:

$$\langle R^2\left(s\right)\rangle =4sp\left[1-\frac{2p}{s}\left(1-e^{-\frac{s}{2p}}\right)\right]$$ (1)

and

$$\langle \cos \theta \left(s\right)\rangle =e^{-\frac{s}{2p}}.$$ (2)

The validity of the SmarTrace chain-tracing algorithm and analysis approaches was established by testing their performance on AFM images of DNA and on simulated chains (see Supporting Materials and Methods; Figs. S1–S3).

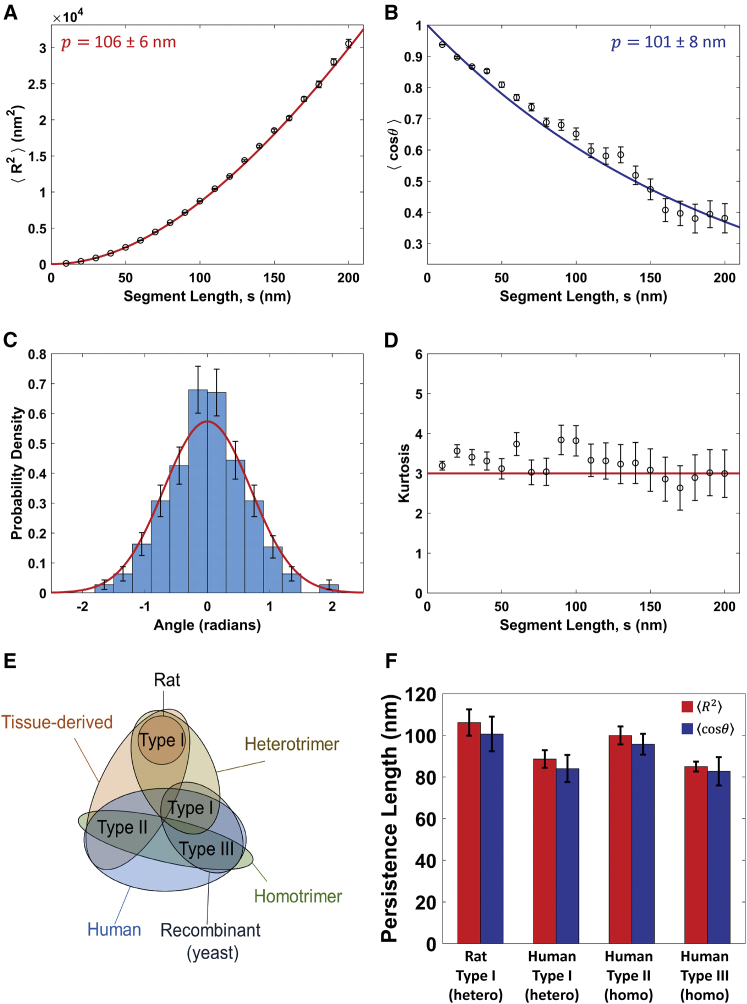
We first investigated whether collagen molecules are equilibrated on the mica and are well described by the WLC model. For type I collagen from rat deposited from 100 mM KCl + 1 mM HCl, both mean-square end-to-end distance $\langle R^2\left(s\right)\rangle$ and tangent vector correlation $\langle \cos \theta \left(s\right)\rangle$ are well described by the WLC model (Fig. 2, A and B). The agreement between persistence lengths from the fits to Eqs. 1 and 2, p = 106 ± 6 nm and p = 101 ± 8 nm, respectively, further suggest that collagen deposited from this solution condition behaves as an equilibrated two-dimensional WLC. This assumption is corroborated by Gaussian distributions of bending angles (Fig. 2 C). The kurtosis of the bending angle distribution is ∼3 (the value characteristic of a normal distribution) at all contour lengths (Fig. 2 D). These measures all indicate that the conformations of collagen on mica represent a sample equilibrated in two dimensions and that rat type I collagen has a persistence length of ∼100 nm.

Figure 2.

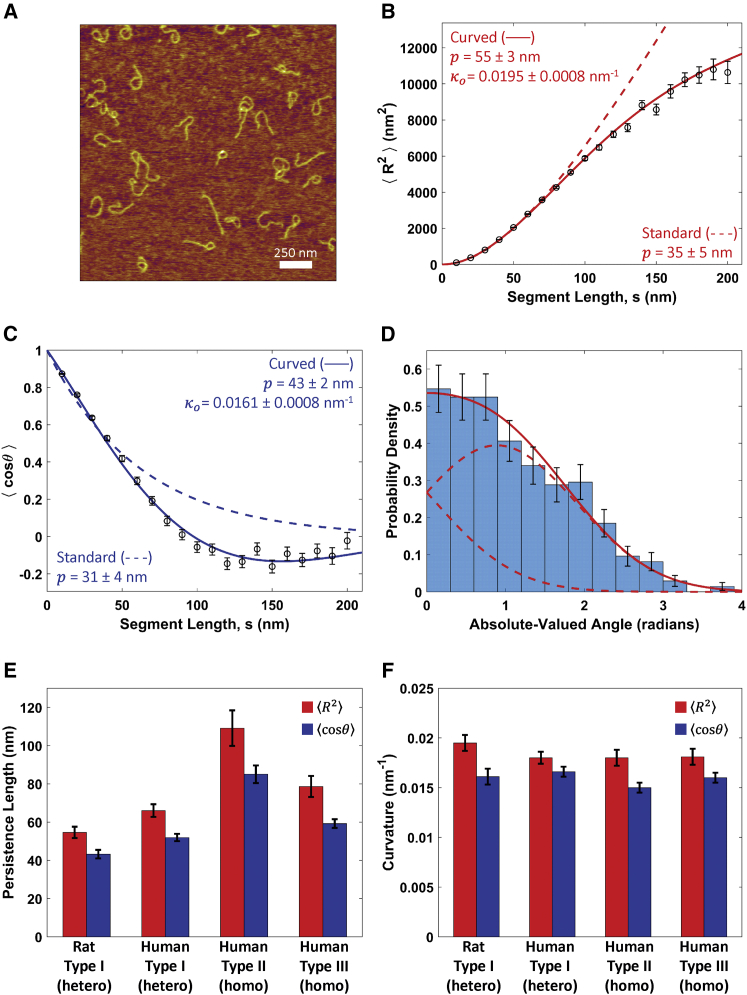
Determination of collagen’s persistence length using the standard worm-like chain (WLC) model. (A–D) Analysis for rat type I collagen deposited from a solution of 100 mM KCl + 1 mM HCl. (A) Mean-square end-to-end distance as a function of segment length, $\langle R^2\left(s\right)\rangle$. Points represent mean values determined at 10 nm segment-length intervals, with error bars representing standard errors of the mean. The red line is a fit with Eq. 1, yielding a persistence length of p = 106 ± 6 nm (error represents 95% confidence interval of the fit). (B) Tangent vector correlation as a function of segment length, $\langle \cos \theta \left(s\right)\rangle$. Points and errors are similarly represented as in (A). The blue line is a fit with Eq. 2, yielding p = 101 ± 8 nm. Fits to the WLC model in (A) and (B) capture the trends in the data and yield comparable persistence lengths. (C) An angular histogram for s = 50 nm segment lengths (blue bars). Error bars represent $\sqrt{N}$ counting error. This distribution agrees well with that expected for a WLC of persistence length p = 103 nm (the average of the results from (A) to (B)), which is a normal distribution with a mean of zero and a variance of s/p (red line). (D) Kurtosis of the angular distributions extracted from the traced collagens at different segment lengths is shown. Error bars represent the standard error in the kurtosis (Eq. S19). The kurtosis of the angular distributions is close to three (red line) for all segment lengths, indicating that the collagens behave as equilibrated Gaussian chains on the mica surface. (E) A Venn diagram illustrating the similarities and differences between the different collagen samples tested, including trimeric identity and source. (F) Persistence length for each collagen sample deposited from a solution of 100 mM KCl + 1 mM HCl, obtained using $\langle R^2\left(s\right)\rangle$ and $\langle \cos \theta \left(s\right)\rangle$ analyses. The similarity among these samples suggests that collagen type and source have little impact on the mechanical properties of collagen at the molecular level. To view this figure in color, go online.

The persistence lengths were similarly determined for the other collagen samples (Fig. 2 E). The data and fits are shown in Fig. S4, and persistence lengths are presented in Fig. 2 F. Table 2 provides a summary of the fit parameters, representing an average of the $\langle R^2\left(s\right)\rangle$- and $\langle \cos \theta \left(s\right)\rangle$-derived results; the complete summary of parameters from each fit is given in Table S1, along with reduced χ² values used to assess goodness of fit. All four collagen samples exhibit similar persistence lengths, within the range of 84–103 nm in these solution conditions. We do not observe significant differences in flexibility for homotrimeric (II, III) collagen versus heterotrimeric (I) collagen, in contrast with previous findings (18, 34). Tissue-derived collagens (rat I, human II) appear to be slightly more rigid than the yeast-expressed recombinant (human I, III) collagens, which correlates with their increase in post-translational modifications. However, these differences are small in the context of the wide range of values in the literature (Table 1). Thus, differences in type, source, and extent of post-translational modifications do not appear to cause substantial differences in molecular flexibility.

Influences of salt and pH

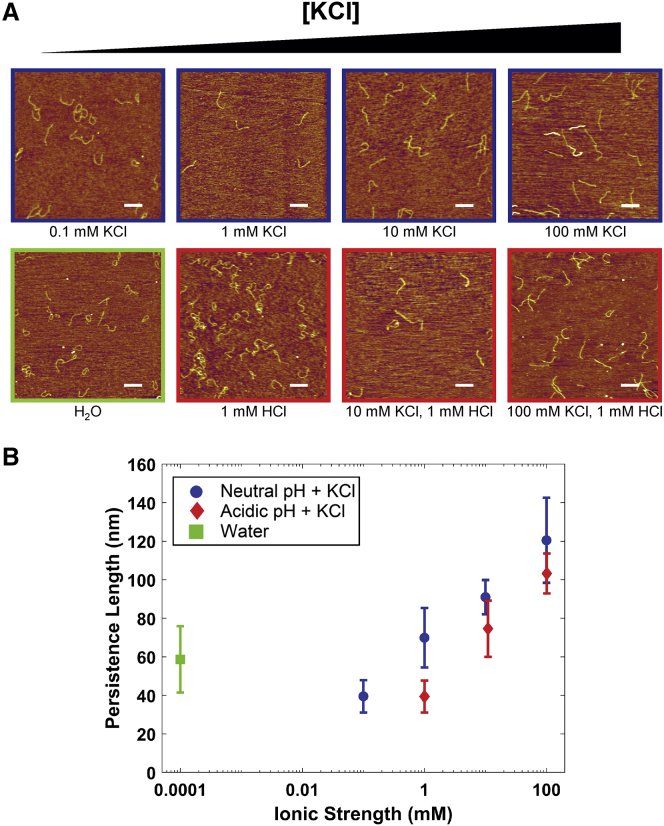
Given a previous report of significantly different collagen flexibility in buffers with high salt concentration and neutral pH, compared with low-ionic-strength, acidic solutions (13), we next investigated how pH and salt concentration independently impact the flexibility of collagen. Rat type I collagen was deposited onto mica from a range of different solution conditions in a controlled ionic environment. In one set of experiments, solutions contained only varying concentrations of potassium chloride, from 0 mM (water) to 100 mM KCl. In a second set of experiments, solutions again contained varying concentrations of KCl but were acidified to pH ≈ 3 by 1 mM HCl.

Images of collagen at different KCl concentrations and pH are shown in Fig. 3 A. It is immediately apparent that salt affects the conformations of collagen: the protein transitions from more compact structures at low ionic strength to much more extended conformations at high ionic strength. A similar trend is seen in the acidic conditions. Conformations were analyzed to obtain mean-square end-to-end distances and tangent correlations as a function of contour length and were fitted to Eqs. 1 and 2, respectively. This analysis finds persistence length to increase significantly with ionic strength at both neutral and acidic pH (Fig. 3 B; Table 2). Our results corroborate and elaborate on the previous findings of increased flexibility at low pH and salt compared with neutral pH and high salt (13).

Figure 3.

Effects of ionic strength on persistence length. (A) AFM images of rat type I collagen deposited from solutions covering a range of KCl concentration, for both neutral and acidic (∼3) pH. Scale bars, 250 nm. As salt concentration increases, the collagen chains appear to straighten. (B) Persistence lengths in these conditions. The reported values are the average of p extracted from fits to $\langle R^2\left(s\right)\rangle$ and to $\langle \cos \theta \left(s\right)\rangle$, and errors are the larger of the propagated error in this mean or half the separation between the two values of p. For the purposes of graphical representation, water was assumed to have an ionic strength of 10⁻⁷ M. Increasing the ionic strength causes a large increase in the apparent persistence length, an effect that is reduced slightly in the acidic condition for the same ionic strengths. To view this figure in color, go online.

The dependence of persistence length on salt concentration is striking. In neutral solutions, the determined persistence length increases approximately threefold as the KCl concentration is increased to 100 mM. In acidic solutions, persistence lengths are shorter but still increase, more than doubling as the concentration of KCl increases from 1 to 100 mM. Intriguingly, the range of persistence lengths exhibited here spans a significant portion of values reported and unreconciled in the literature (Table 1).

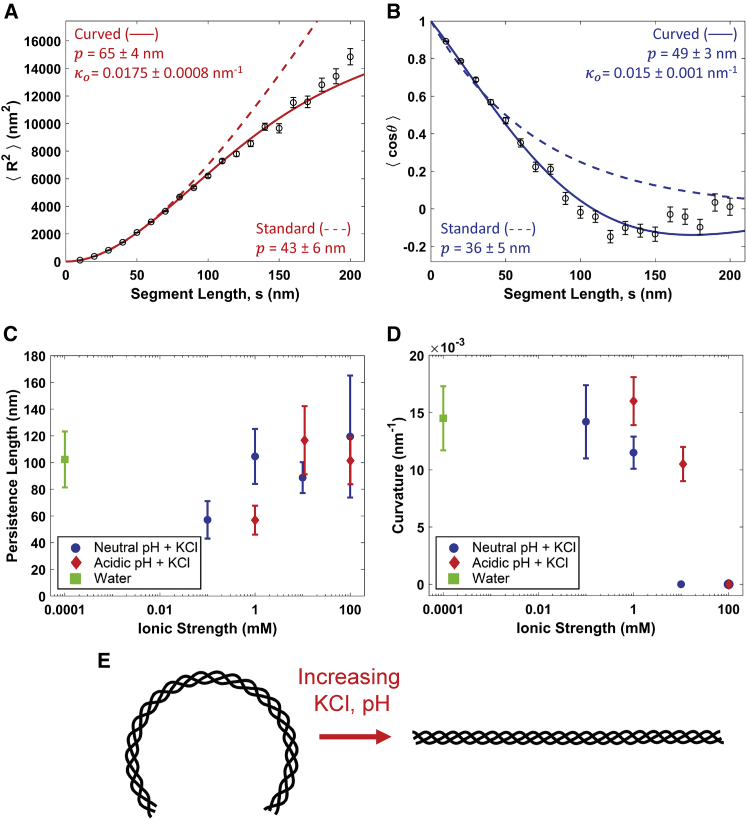
The trend of increasing stiffness with increasing ionic strength is unexpected, as it is opposite to predictions for polyelectrolytes and to observations for biopolymers such as DNA (22, 23). However, examination of the data and fits in some of the solution conditions, particularly at lower salt concentrations, reveals that the experimental data are not well described by the standard WLC model (e.g., Fig. 4; see also Figs. S5 and S6). For $\langle R^2\left(s\right)\rangle$, the agreement between model and data is reasonable at shorter segment lengths (e.g., s < 100 nm), but longer segments exhibit shorter-than-expected end-to-end distances. The disagreement with the standard WLC model is even more apparent when considering the $\langle \cos \theta \left(s\right)\rangle$ behavior. There appears to be an oscillatory modulation of the tangent vector correlation whereby chains maintain directionality at small segment lengths, reorient substantially at intermediate lengths, and in many cases, exhibit anticorrelated tangent vectors at longer contour lengths. These are not features of a well-equilibrated WLC. Instead, the oscillatory character of the tangent vector decorrelation suggests that curvature may play a role in the observed conformations of collagen.

Figure 4.

At low ionic strength, collagen is better described as a cWLC. (A) Fits of the mean-square end-to-end distance using both the standard (Eq. 1, dashed red line) and curved (Eq. 3, solid red line) WLC models to data extracted from rat tail type I collagen deposited from 1 mM HCl. (B) Corresponding fits of the standard (Eq. 2, dashed blue line) and curved (Eq. 4, solid blue line) WLC tangent vector correlation functions. The data are more accurately described by the curved model equations, as shown statistically by a significant improvement in reduced χ² values (see text). The standard WLC underestimates the persistence length of the collagens in this condition, presumably interpreting the induced curvature as additional fluctuation. (C) Persistence lengths for the different cosolute conditions presented in Fig. 3 Rather than the trend with ionic strength seen with the standard WLC fits, there is a less significant and less obviously monotonic variation in persistence length as a function of ionic strength. Instead, the observed systematic conformational changes are attributed to a variation in innate curvature, which drops as the ionic strength of the solution is increased (D). For the purposes of graphical representation, water was assumed to have an ionic strength of 10⁻⁷ M. Error bars on $\langle R^2\left(s\right)\rangle$ and $\langle \cos \theta \left(s\right)\rangle$ values are as described for Fig. 2, and error bars on p and κ_o are obtained as described for Fig. 3. (E) A schematic illustrating the transition of collagen from a molecule with a curved backbone at low ionic strength and pH ∼3 (left) to one with a straight backbone at higher ionic strength and neutral pH (right). The persistence length characterizes fluctuations about this lowest-energy conformation. To view this figure in color, go online.

Curved WLC

To describe an intrinsically curved WLC (cWLC), we assume that the lowest-energy conformation of the chain is curved (bent) rather than straight. The extent of angular fluctuations about this curved state is determined by the angular bending potential and the thermal energy of the system, which relate to persistence length as for the standard WLC. From this cWLC model, equations for the mean-square end-to-end distance and mean tangent vector correlation can be derived (see Supporting Materials and Methods):

$${\langle R^2\left(s\right)\rangle }_c=\frac{4sp}{{\left(1+4{\kappa }_o^2{p}^2\right)}^2}\left\{1-\frac{2p}{s}\left(1-4{\kappa }_o^2{p}^2\right)\left[1-\cos \left({\kappa }_{o}s\right)e^{-\frac{s}{2p}}\right]+\frac{4{\kappa }_o{p}^2}{s}\left[{\kappa }_{o}s-2\sin \left({\kappa }_{o}s\right)e^{-\frac{s}{2p}}\right]\right\}$$ (3)

and

$$\langle \cos \theta {\left(s\right)}_{\text{c}}\rangle =\cos \left({\kappa }_{o}s\right)e^{-\frac{s}{2p}}.$$ (4)

Here, κ_o represents the inherent curvature of the chain, which is the inverse of its inherent radius of curvature: ${\kappa }_o=R_o^{-1}$. Eqs. 3 and 4 describe the expected behavior of an intrinsically curved, inextensible WLC equilibrated in two dimensions and are two-dimensional versions of three-dimensional results derived previously (35). Of note, the cWLC model is distinct from approaches that assume a random local curvature (28): in the cWLC model, the lowest-energy conformation of the chain is globally curved, i.e., bends always in the same direction.

Fig. 4, A and B show fits of the cWLC model to the $\langle R^2\left(s\right)\rangle$ and $\langle \cos \theta \left(s\right)\rangle$ data from rat type I collagen deposited from 1 mM HCl. The cWLC captures trends in both $\langle R^2\left(s\right)\rangle$ and $\langle \cos \theta \left(s\right)\rangle$ significantly better than the standard model. Notably, the cWLC model captures the longer-length anticorrelation of the tangent vectors $\left(\langle \cos \theta <0\rangle \right)$, which under the standard WLC model is unphysical. Additionally, the cWLC fits provide a distinct interpretation of the compact structures observed at low ionic strength (Fig. 3): rather than being more flexible at lower salt concentration, collagen is instead more curved.

Salt-dependent trends in persistence length and curvature obtained from the cWLC model are shown in Fig. 4, C and D. In contrast to the monotonic increase in persistence length with increasing KCl concentrations found when using the standard WLC model (Fig. 3), the results from the cWLC fits indicate that persistence length varies only modestly over the range of concentrations used here (Fig. 4 C). Instead, the curvature depends strongly on ionic strength, decreasing from κ_o = 0.02 nm⁻¹ to 0 (i.e., straightening) as the concentration of KCl is increased (Fig. 4 D). This effect is shown schematically in Fig. 4 E.

Statistical considerations demonstrate that the cWLC is a better model than the WLC for collagen in almost all of the tested solution conditions. In lower-concentration KCl conditions, χ² is significantly lower when the data are fitted with the cWLC model than with the WLC model (Table S1). In contrast, the WLC model produces a lower χ² than the cWLC in only three conditions (10 mM KCl, 100 mM KCl, and 1 mM HCl + 100 mM KCl). In these three solution conditions, we find that fitting with the cWLC model gives the same persistence length and zero curvature, i.e., the cWLC model reduces to the same results as the standard WLC model. We further assessed these two models using the BIC, which uses likelihood analysis to assess the probability that one model is a better descriptor of the data than another. The BIC incorporates a stronger penalty for additional fit parameters than does χ² analysis (Eq. S29), thereby challenging more strongly the ability of a model with additional fit parameter(s) to describe the data. Even so, the BIC also indicates a strong preference for the cWLC model in the lower-salt conditions (Table S2).

Origins of collagen curvature

To determine whether the induction of curvature is ion specific, images of rat type I collagen deposited from 20 mM acetic acid were collected and analyzed with the standard and cWLC models (Fig. 5, A–D). Conformations of collagen deposited from acetic acid are better described by the cWLC model, consistent with observations at low ionic strengths of KCl. Again, naïve application of the standard WLC model results in persistence lengths smaller than those obtained from cWLC fits. To test for equilibration of the samples, we considered the distribution of bend angles. Because of chain curvature, these distributions should not be represented by a single Gaussian centered at θ(s) = 0. Rather, the distributions are expected to be described by two Gaussians, centered symmetrically about zero at an angle θ(s) = κ_os and with standard deviation $\sigma \left(s\right)=\sqrt{s/p}$ (Eq. S20). The experimental angular distribution is indeed well described by this bimodal function (Fig. 5 D). The agreement between predicted and measured angular distributions is strong evidence of collagen equilibration on the mica surface in this low-salt condition. The fit parameters in acetic acid (p = 49 nm, κ_o = 0.018 nm⁻¹) are similar to those from the 1 mM HCl solution (Table 2), which has comparable ionic strength and pH. Thus, at low ionic strength, there does not seem to be a strong effect of chloride versus acetate anions on collagen’s mechanical properties.

Figure 5.

Behavior of different collagen types in acetic acid. (A) A representative image of rat tail type I collagen deposited from 20 mM acetic acid. (B) Standard (Eq. 1, dashed red line) and curved (Eq. 3, solid red line) WLC model are shown fitted to the mean-square end-to-end distance, $\langle R^2\left(s\right)\rangle$. (C) Standard (Eq. 2, dashed blue line) and curved (Eq. 4, solid blue line) WLC models are shown fitted to the tangent vector correlation, $\langle \cos \theta \left(s\right)\rangle$. Data in both (A) and (B) are described more accurately by the cWLC model, as seen also by the reduced χ² values (Table S1) and the BIC (Table S2). (D) The absolute-valued angular distribution of the same collagen molecules at a segment length of s = 50 nm. The red line represents the expected distribution (Eq. S3) for a cWLC using a persistence length p = 51 nm and intrinsic curvature κ_o = 0.0182 nm⁻¹, the average values of each parameter extracted from the fits shown in (B) and (C). The dashed red lines are the two Gaussian components that make up this distribution, as discussed in the Supporting Materials and Methods. (E and F) Persistence lengths and curvatures, respectively, of different collagen types deposited from 20 mM acetic acid. As with the different collagen types deposited from 100 mM KCl + 1 mM HCl (Fig. 2F), there is only modest variation among the different samples, demonstrating that, also at lower ionic strength and different cosolute conditions, only minor mechanical differences exist between different collagen types and sources. To view this figure in color, go online.

It is possible that the observed curvature is an effect specific to heterotrimeric collagen. Because type I collagen has one α-chain which is different than the other two, a larger or smaller propensity for surface interactions with this chain could produce a surface-induced curvature to minimize its energy (36). To address this possibility, types I, II, and III human collagens were also imaged in 20 mM acetic acid and analyzed with the cWLC model (Fig. S7). The results of this analysis are shown in Fig. 5, E and F. Although the different types vary somewhat in their persistence lengths, their curvatures are nearly identical under these solution conditions, regardless of their trimeric identity. Thus, surface interactions with a unique chain in heterotrimeric collagen are not responsible for the observed curvature.

The curvature observed at low ionic strengths may nonetheless result from molecular interactions with the surface. Intrinsically straight, chiral semiflexible chains may adopt curved conformations at an interface (36). The extent to which the chain curves at an interface will be determined by a competition between the free energy of surface-molecular interactions and the torsional twist energy of the chain. Specifically, curvature in this model requires a chiral organization of sites on the chain that interact differentially at the interface compared with the rest of the chain sites. In the current context, these could be the side chains of the three individual α-chains of collagen, which are arranged in a right-handed superhelical structure about the central axis of the collagen molecule (2). If these sites interact strongly with the mica surface, the free energy gained by adhering to the surface could outweigh the energetic cost of altering the twist (local helical pitch) of the triple helix. In this scenario, the observed trends in curvature with salt concentration (Fig. 4 F) imply a salt dependence of collagen’s torsional stiffness and/or its interactions with the surface. Salt-dependent interactions with mica are well established for other biopolymers (e.g (33)) and could be expected to contribute here (37). In particular, K⁺ affects the interactions of self-assembling collagen with a mica surface (37, 38, 39).

Collagen’s stability in solution is also influenced by salt and pH. Collagen has a lower thermal stability at low ionic strength and acidic pH than at high ionic strength and neutral pH (40), and its thermal stability and helicity decrease at lower concentrations of KCl (41). The conditions found to destabilize collagen in solution are the same as those promoting increased curvature in our measurements. It is thus possible that this destabilization of the triple helix reduces the torsional stiffness of collagen, enabling it more easily to adopt curved conformations on mica.

In addition to the ionic-strength dependence of curvature, our images and conformational analysis demonstrate a dependence on pH: collagen appears more curved in acidic conditions (Fig. 4 F). At a pH of 3, collagen carries a net positive charge. At neutral pH, collagen instead has a roughly equal balance of positively and negatively charged residues. The increased curvature at acidic pH could result from stronger electrostatic affinity to the negatively charged mica surface (37). Alternatively, electrostatic repulsion between α-chains could destabilize the triple helix and reduce its torsional stiffness, particularly at low ionic strength when shielding from cosolute anions is weak (at 1 mM ionic strength, the Debye length ≈ 10 nm). At neutral pH, the potential for salt bridge formation could strengthen attractions between α-chains (41, 42), thereby increasing the torsional stiffness of the triple helix.

It is also possible that collagen itself is intrinsically bent, even in solution (43). Certainly within the fibrillar superstructure, collagen molecules display conformations that are locally bent (44). Studying how salt influences conformations in solution would be key to discriminating which interactions are surface specific in our study. A change in torsional stiffness and/or alteration of preferred twist angle at lower ionic strength would be expected to alter the average shape of collagen in solution. Light scattering or other solution-based techniques could be used to study how collagen’s compactness in solution depends on salt concentration and thereby determine how the triple helix itself responds to changes in ionic strength.

Comparison with other estimates of collagen flexibility

Taken together, our results indicate that collagen should be regarded as a semiflexible polymer at room temperature with a persistence length in the range of 50–120 nm. This is more flexible than solution-based estimates yet more rigid than found in almost all previous single-molecule approaches (Table 1). Inherent biases and assumptions built into data interpretation within each methodology may contribute to the range of results reported in the literature. Here, we describe possible reasons for the discrepancies.

With AFM imaging, one must play particular heed to molecule-surface interactions and to the possibility of kinetically trapping polymers in nonequilibrium configurations on the surface. In our measurements, the observed conformations appear well equilibrated in two dimensions (Figs. 2, C and D and 5 D). Furthermore, although electrostatic interactions with mica may play a role in the apparent curvature of collagen on the surface, we have found that the persistence length is not strongly affected.

In single-molecule stretching experiments, one source of bias is the underestimation of persistence length when the contour length L < 20p (45), as is the case for collagen. Any structural changes in the triple helix that occur during stretching may also modify the bending energy: such changes have been inferred from enzymatic cleavage assays of collagen under force (21, 46, 47, 48) and may contribute to softening of collagen’s force-extension response (14).

Many of the simulations of collagen have used steered molecular dynamics, which may not investigate its equilibrium flexibility. Additionally, the results of molecular dynamics simulations depend on the force fields used (49), which have been developed predominantly for globular proteins rather than the unique fold of collagen.

Interpretations of light-scattering data require a model (such as an ellipsoidal scatterer (19)), and it is possible to describe decay curves equally well assuming both compact and more extended molecular geometries (50). Furthermore, the effective size of the protein, as deduced from solution-based studies such as light scattering and rheology, is often affected by intermolecular interactions; thus, concentration-dependent studies are essential to determine the spatial extent of a given molecule in isolation (51). Given collagen’s propensity to self-associate (52, 53), intermolecular interactions may contribute to larger estimates of collagen’s size in solution. The rheological studies of (8) found that pH does not have a significant effect on collagen’s flexibility; however, to reach this conclusion, the authors had to assume that type I collagen exhibited a nonuniform flexibility at neutral pH, with ends considerably more flexible than the central region of the triple helix.

The two studies most similar to ours, which used AFM imaging (13) and electron microscopy (18) to analyze collagen’s flexibility, based their estimates of persistence length on the distance between the endpoints of the collagen chain. As we have shown (Figs. 4 and 5), naïve application of Eq. 1 can lead to significant underestimation of persistence length for curved chains. Consistently, our estimates of collagen’s persistence length are greater than theirs obtained at low ionic strength. At high ionic strength and neutral pH, our results and those of the previous AFM imaging study (13) are in reasonable agreement: in this condition, collagen is well described by the standard WLC model and curvature may be disregarded. In general, however, our findings demonstrate the importance of mapping the functional forms of $\langle R^2\left(s\right)\rangle$ and $\langle \cos \theta \left(s\right)\rangle$ and caution against determining persistence length by using only chain end-point separations.

In our description and analysis of collagen, we have made two major assumptions. First, neither the WLC nor cWLC model takes into account the helical nature of collagen. Thus, flexibility of the chain derives only from bending deformations. If the intrinsic curvature described by our model arises because of a surface-collagen interaction inducing altered twist in the protein, then torsional stiffness of the triple helix (54) is an important parameter, and twist-bend coupling (55) may be required to fully describe collagen’s flexibility.

Second, our analysis procedures treat collagen as an apolar, homogenous WLC. We are not able to discriminate between N → C and C → N directionality in the imaged chains. Furthermore, persistence lengths and curvatures reported in this work represent average values for the entire collagen sequence. In adopting this approach, we have implicitly assumed that the (Gly-X-Y)_n triple-helix-forming motif dominates collagen’s response, with local sequence variations (e.g., fraction of prolines occupying the X and Y positions) viewed as introducing only minor perturbations. The flexibility of fibrillar collagen triple helices appears approximately uniform in electron microscopy images (18), supporting this assumption. However, molecular dynamics simulations (56) and modeling of atomistic collagen structures (54) suggest that collagen possesses a sequence-dependent flexibility commensurate with the expected variations in pitch observed for different triple helical sequences (2, 44). It is interesting to speculate how a sequence-dependent mechanical signature may provide additional physical cues to interaction partners (48). Experimentally elucidating the detailed sequence-dependent flexibility of collagen is an exciting future prospect that will require higher-precision algorithms than applied thus far to this mechanically important protein.

Conclusions

Using AFM, we determined the persistence length of different types and sources of collagen in the presence of different cosolutes (K⁺, Cl⁻, acetate). Although collagens of different type and source exhibited only minor differences in persistence length, our initial findings implied that ionic strength and to a lesser extent pH modulate collagen’s flexibility. Closer inspection of these results, however, revealed this interpretation to be an artifact of the model used for analysis. Rather than behaving as an intrinsically straight WLC, collagen deposited in low salt conditions was found to adopt preferentially curved conformations on the mica surface. Statistical analysis of chain conformations demonstrates that this curvature is a thermodynamic property, with chains appearing equilibrated in two dimensions. The extent of curvature depends strongly on salt concentration and pH, with persistence length remaining roughly constant across all KCl conditions. Thus, collagen possesses an experimentally tunable curvature and is to our knowledge the first such example of a cWLC.

Our findings provide a possible explanation for the range of persistence lengths reported for collagen in the literature: rather than a direct modulation of its flexibility, the presence of certain cosolutes may induce curvature along the collagen backbone. Whether or not the curvature seen in our results is intrinsic to collagen or is caused by cosolute-dependent interactions with the imaging surface remains to be determined. If intrinsic, then the modulation of collagen’s conformation by salt and pH has potentially broad implications. The acidification experienced along the secretory pathway (25) may play a heretofore unexplored role in controlling collagen’s intracellular compactness. Changes in salt concentration experienced upon secretion may also contribute to extracellular self-assembly of fibrillar collagens; for example, chloride ions are essential for the distinct network assembly of type IV collagen (57). Such changes in pH and cosolute concentrations could therefore influence collagen self-assembly through modification of its conformational properties: collagen does not assemble into fibrillar structures at low pH or at low ionic strength (38, 58), precisely those conditions in which we observe its strongest curvature.

The strong agreement between measures of chain flexibility and the predictions of the cWLC model suggest that this formalism may be useful for interpreting the mechanical properties of other biological filaments. The intrinsic curvature of certain DNA sequences (59, 60, 61) is important for gene regulation (62), and amyloid fibrils (36) and coiled-coil proteins (63) have been found to exhibit preferentially curved conformations at interfaces. Applying the cWLC model to describe these systems and others is likely to provide further insight into their equilibrium structures and the energies governing their mechanical properties.

The datasets generated and analyzed during the current study are available from the corresponding author on request.

Author Contributions

N.R. and A.L. performed experiments. N.R. developed the SmarTrace algorithm and software. A.L. performed polymer chain simulations and derived the cWLC fitting equations. All authors contributed to the design of the project, data analysis, and writing of the manuscript.

Editor: Thomas Perkins.

Supporting Citations

References (64, 65, 66, 67, 68) appear in the Supporting Material.