Thermodynamic Modeling of the Statistics of Cell Spreading on Ligand-Coated Elastic Substrates

Abstract

Biological spread cells exist in a perpetually fluctuating state and therefore cannot be described in terms of a unique deterministic system. For modeling approaches to provide novel insight and uncover new mechanisms that drive cell behavior, a framework is required that progresses from traditional deterministic methods (whereby simulation of an experiment predicts a single outcome). In this study, we implement a new, to our knowledge, modeling approach for the analysis of cell spreading on ligand-coated substrates, extending the framework for nonequilibrium thermodynamics of cells developed by Shishvan et al. to include active focal adhesion assembly. We demonstrate that the model correctly predicts the coupled influence of surface collagen density and substrate stiffness on cell spreading, as reported experimentally by Engler et al. Low surface collagen densities are shown to result in a high probability that cells will be restricted to low spread areas. Furthermore, elastic free energy induced by substrate deformation lowers the probability of observing a highly spread cell, and, consequentially, lower cell tractions affect the assembly of focal adhesions. Experimentally measurable observables such as cell spread area and aspect ratio can be directly postprocessed from the computed homeostatic ensemble of (several million) spread states. This allows for the prediction of mean and SDs of such experimental observables. This class of cell mechanics modeling presents a significant advance on conventional deterministic approaches.

Introduction

There is no unique outcome for tissue development in nature. For example, examination of arterial tissue across several samples reveals nonhomogenous structures with nonuniform collagen fiber alignment, tissue thickness, and smooth muscle cell (SMC) morphology (1, 2, 3). The same is true in vitro, in which cells of the same phenotype exhibit a diverse range of spread shapes, area, stress-fiber (SF) alignments, and focal adhesion (FA) distributions. However, over large populations, the statistics of observables is highly reproducible. Several experimental studies have demonstrated that the microenvironment has a significant impact on cell behavior. Jacot et al. (4) show that sarcomere development and alignment in cardiomyocytes are dependent on substrate stiffness. A study by Arnold et al. (5) reveals that FA and SF formation are limited by ligand spacing on the substrate. Engler et al. (3) show that both the mean and standard error of SMC spread area depend on substrate rigidity and ligand density; with decreasing surface collagen density and decreasing substrate stiffness, the standard error reported for the experiment reduces.

It is therefore evident that to uncover the biomechanisms underlying such observations, a statistical mechanics approach to cell modeling is required. Typically, previous models have assumed the spread state as the reference configuration and simulate a single deterministic outcome (6, 7, 8, 9, 10, 11, 12). McEvoy et al. (13) recently implemented a framework whereby an initially unadhered cell deforms to a range of possible spread states, and the system free energy is computed for each configuration. It is demonstrated that cell spreading entails a competition between the increasing elastic free energy because of the stretching of passive cell components and the decreasing cytoskeletal free energy as contractile proteins assemble to form SFs. Such a competition allows for the identification of a low free-energy state, and it is shown that the predicted cell areas and SF alignments in these configurations are similar to reported experimental measurements (14). However, in the study of McEvoy et al. (13), a single low-energy spread state is identified. This deterministic approach neglects the fact that cells display a fluctuating response to their microenvironment in terms of observables such as SF alignment and spread area.

In this study, we implement a statistical mechanics framework for the homeostatic ensemble of spread cells, following the approach of Shishvan et al. (15). This methodology allows for the simulation of a large collection of spread microstates the cell-substrate system assumes while maintaining its homeostatic state. The framework incorporates mathematical models to describe SF formation and cell-substrate deformation. Here, we expand the model for the calculation of Gibbs free energy to include the free energy associated with the traction-dependent FA assembly. Simulations accurately predict the dependence of cell area and shape on surface collagen density and substrate stiffness, as reported in the experimental study of Engler et al. (3).

Methods

We aim to analyze the response of cells adhered to collagen-coated elastic substrates. This experimental system is responding to both mechanical and chemical cues from its environment, viz the stiffness of the substrate and the extracellular proteins (collagen) through which the cells adhere to the substrates. The response of this complex system is recorded through a range of observables, all of which exhibit large variations but with trends clearly emerging when the statistics of these observables are analyzed. This motivates our choice of a modeling framework, called homeostatic statistical mechanics (15), in which, just as in the experimental system, observables fluctuate, and trends (and understanding) emerge once these observables are viewed statistically. This framework has previously been shown to successfully capture a range of observations for SMCs seeded on elastic substrates in which perfect adhesion was assumed and the role of the extracellular matrix neglected. Here, we extend the framework to include an adhesion model and thus will first give a brief overview of the modeling framework (details in Supporting Materials and Methods, Section S1) and then focus on the adhesion model.

Overview of the homeostatic mechanics framework

The homeostatic mechanics framework recognizes that the cell is an open system that exchanges nutrients with the surrounding nutrient bath. These high-energy nutrient exchanges fuel fluctuations in cell responses associated with various intracellular biochemical processes (such nonthermal nutrient-fueled fluctuations are observed to be very large and occur over very long timescales, compared to conventional thermal fluctuations). However, these biochemical processes attempt to maintain the cell in a homeostatic state (i.e., the cell actively maintains its various molecular species at a specific average number over these fluctuations that is independent of the environment). This translates to the constraint on the average Gibbs free energy (16) of the cell. Employing the ansatz that biochemical processes such as actin polymerization and treadmilling provide the mechanisms to maximize the morphological entropy of the cell subject to the constraint that the cell maintains a homeostatic state, Shishvan et al. (15) obtained the distribution of states that the cell assumes in terms of the Gibbs free energy $G^{\left(j\right)}$ of the morphological state $\left(j\right)$ of the system as follows:

$$P_{\text{eq}}^{\left(j\right)}=\frac{1}{Z}\text{exp}\left(-\zeta G^{\left(j\right)}\right).$$ (1)

$Z\equiv \sum _j\text{exp}\left(-\zeta G^{\left(j\right)}\right)$ is the partition function of the morphological microstates, and the distribution parameter $\zeta$ follows from the following homeostatic constraint:

$$\frac{1}{Z}\sum _j{G}^{\left(j\right)}\text{exp}\left(-\zeta G^{\left(j\right)}\right)=G_{\text{S}},$$ (2)

where $G_{\text{S}}$ is equal to the equilibrium Gibbs free energy of an isolated cell in suspension (free-standing cell), that is, the homeostatic processes maintain the average biochemical state of the system equal to that of a cell in suspension. Thus, the distribution (Eq. 1) is characterized by a homeostatic temperature $1/\zeta$ that is conjugated to the morphological entropy of the cell. We employ Markov Chain Monte Carlo to construct a Markov chain that is representative of the homeostatic ensemble. This involves three steps: 1) a discretization scheme to represent morphological microstate $\left(j\right)$, 2) calculation of $G^{\left(j\right)}$ for a given morphological microstate $\left(j\right)$, and 3) construction of a Markov chain comprising these morphological microstates. Typical Markov chains comprised in excess of 2.5 million spread states (a detailed overview of the procedure is provided in Supporting Materials and Methods, Section S2.2).

Free energy ${\mathit{G}}^{\left(\mathit{j}\right)}$ of a morphological state

Much like conventional statistical mechanics frameworks that require a model for the energy of molecular systems, the homeostatic statistical mechanics framework requires a model for the Gibbs free energy $G^{\left(j\right)}$ of a morphological state $\left(j\right)$ of the system. Here, we employ a relatively simple model for the Gibbs free energy wherein the cell consists of a passive elastic nucleus within a cytoplasm that is modeled as comprising an active SF cytoskeleton and elements such as the cell membrane, intermediate filaments, and microtubules that are all lumped into a single passive-elastic contribution.

Details of the model, including the parameters used to characterize the SMCs, are given in Supporting Materials and Methods, Section S2. Here, we briefly describe the salient features of the model for SMCs on elastic substrates. The SMCs are modeled as two-dimensional bodies in the $x_1-x_2$ plane lying on the surface of an elastic substrate such that the out-of-plane Cauchy stress ${\sum }_{33}=0$. The substrates are modeled as linear elastic half spaces, whereas the cells are modeled using the approach of Vigliotti et al. (17) as modified by Shishvan et al. (15). The Vigliotti et al. (17) model assumes only two elements within the cell: 1) a passive elastic contribution from elements such as the cell membrane, intermediate filaments, and microtubules and 2) contractile actomyosin SFs that are modeled explicitly. The cell in its undeformed state is a circle of radius $R_0$ and, for a given morphological microstate $\left(j\right)$, the strain distribution within the cell is specified. This directly gives the elastic strain energy of the cell ${\hat{F}}_{\text{passive}}$ via a two-dimensional Ogden-type hyperelastic model for both the nucleus and cytoplasm. The passive hyperelastic behavior of the cytoplasm and nucleus has been characterized for several cell types using experimental techniques in which SFs are disrupted using Cytochalasin D (18, 19, 20). The SF cytoskeleton within the cytoplasm is modeled as a distribution of SFs such that at each location $x_i$ within the cell $\hat{\eta }\left(\phi \right)$ parameterizes the angular concentration of SFs over all angles $\phi$, whereas ${\hat{n}}^{ss}\left(\phi \right)$ denotes the number of functional units within each SF. Thus, at any $x_i$, there is a total concentration ${\hat{N}}_{\text{b}}$ of bound SF proteins obtained by integrating $\hat{\eta }{\hat{n}}^{ss}$ over all orientations $\phi$, and these bound proteins are in chemical equilibrium with the unbound SF proteins. The unbound proteins are free to diffuse within the cell, and thus, at equilibrium of a morphological microstate, the concentration ${\hat{N}}_{\text{u}}$ of these unbound SF proteins is spatially uniform. This chemical equilibrium condition along with the conservation of SF proteins within the cell provides the spatial and angular distributions of SFs from which the free energy of the cytoskeleton ${\hat{F}}_{\text{cyto}}$ is evaluated. The total normalized free energy of the cell’s morphological microstate $\left(j\right)$ then follows as ${\hat{G}}^{\left(j\right)}\equiv {\hat{F}}_{\text{passive}}^{\left(j\right)}+{\hat{F}}_{\text{cyto}}^{\left(j\right)}+{\hat{F}}_{\text{sub}}^{\left(j\right)}$, where ${\hat{F}}_{\text{sub}}^{\left(j\right)}$ is the elastic energy of the substrate $({\hat{G}}^{\left(j\right)}$ is the normalized value of $G^{\left(j\right)}$; see Supporting Materials and Methods (Section S2.4) for details of the normalizations).

In addition to the contributions to ${\hat{G}}^{\left(j\right)}$ from the passive elasticity and cytoskeleton of the cell, here we also include the contribution from the FAs between the cell and the collagen extracellular matrix laid on the elastic substrates on which the SMCs are seeded. Shishvan et al. (15) implicitly assumed an unlimited supply of adhesion proteins as well as extracellular proteins to form adhesion complexes and thereby neglected the contribution of adhesion to ${\hat{G}}^{\left(j\right)}$. Here, we extend the approach of Shishvan et al. (15) for the case of a finite quantity of both FA proteins and extracellular collagen and thus explicitly include an adhesion contribution to ${\hat{G}}^{\left(j\right)}$; that is, we write ${\hat{G}}^{\left(j\right)}$ as follows:

$${\hat{G}}^{\left(j\right)}\equiv {\hat{F}}_{\text{passive}}^{\left(j\right)}+{\hat{F}}_{\text{cyto}}^{\left(j\right)}+{\hat{F}}_{\text{sub}}^{\left(j\right)}+{\hat{F}}_{\text{adh}}^{\left(j\right)}.$$ (3)

We now proceed to make explicit this adhesion model.

Adhesion complexes between the cell and the extracellular collagen

The FA model proposed here is a modification to the model of McEvoy et al. (13) in which adhesion is assumed to be via integrins that exist in a single state. These integrins form complexes by binding to ligands that have a density $N_{\text{H}}$ per unit area on the surface of the elastic substrate. For a given morphological microstate $\left(j\right)$, the strain state of the cell is specified, and this implies that the tractions ${\text{T}}_i\left(x_i\right)$ that the cells exert on the substrate are also fixed from the cell model; see Supporting Materials and Methods, Section S2.1 (for the sake of brevity, here we have dropped the superscript $\left(j\right)$ to indicate that these are tractions for a given morphological microstate $\left(j\right))$. These tractions are transmitted to the substrate through the FA complexes, and here we explain the adhesion model with the tractions ${\text{T}}_i\left(x_i\right)$ specified.

When in local equilibrium at a location $x_i$ on the surface of the cell, the integrins with a local concentration $C_{\text{I}}\left(x_i\right)$ have a chemical potential at temperature $T$ in terms of the Boltzmann constant $k_{\text{B}}$:

$${\chi }_{\text{I}}\left(x_i\right)={\mu }_{\text{I}}\left(x_i\right)+k_{\text{B}}T\ln \left(\frac{\overline{C}\left(x_i\right)}{1-\overline{C}\left(x_i\right)}\right),$$ (4)

where ${\mu }_{\text{I}}$ is their enthalpy while $\overline{C}\left(x_i\right)\equiv C_{\text{I}}\left(x_i\right)/C_{\text{r}}$ in terms of the number of integrin sites per unit area $C_{\text{r}}$ on the cell membrane. The enthalpy of the integrins follows from recalling that each integrin molecule transmits a force $\mathcal{F}\left(x_i\right)$ related to the traction $\text{T}\left(x_i\right)\equiv \sqrt{{\text{T}}_1{\left(x_i\right)}^2+{\text{T}}_2{\left(x_i\right)}^2}$ on the cell surface via $\text{T}\left(x_i\right)=\mathcal{F}\left(x_i\right)N_{\text{H}}$. Then,

$${\mu }_{\text{I}}\left(x_i\right)=\mathit{\Phi }\left(\mathit{\Delta }\left(x_i\right)\right)-\mathcal{F}\left(x_i\right)\mathit{\Delta }\left(x_i\right),$$ (5)

where $\mathit{\Delta }$ is the stretch of the FA complex, and $\mathit{\Phi }$ the internal energy of the complex subjected to a stretch $\mathit{\Delta }$. Now, assuming linear behavior of the complex with a stiffness ${\kappa }_{\text{s}}$ such that $\mathcal{F}\left(x_i\right)\equiv {\kappa }_{\text{s}}\mathit{\Delta }\left(x_i\right)$, Eq. 5 reduces to ${\mu }_{\text{I}}\left(x_i\right)=-\mathcal{F}{\left(x_i\right)}^2/2{\kappa }_{\text{s}}$, and the chemical potential follows as such:

$${\chi }_{\text{I}}\left(x_i\right)=k_{\text{B}}T\ln \left(\frac{\overline{C}\left(x_i\right)}{1-\overline{C}\left(x_i\right)}\right)-\frac{\mathcal{F}{\left(x_i\right)}^2}{2{\kappa }_{\text{s}}}.$$ (6)

The integrins are mobile over the surface membrane, and at equilibrium, their chemical potentials are spatially uniform such that ${\chi }_{\text{I}}\left(x_i\right)={\chi }_{\text{C}}$. The equilibrium concentrations ${\overline{C}}_{\text{eq}}\left(x_i\right)$ then follow in terms of ${\chi }_{\text{C}}$ as follows:

$$\left(\frac{{\overline{C}}_{\text{eq}}\left(x_i\right)}{1-{\overline{C}}_{\text{eq}}\left(x_i\right)}\right)=\exp \left(\frac{{\chi }_{\text{C}}+\frac{\mathcal{F}{\left(x_i\right)}^2}{2{\kappa }_{\text{s}}}}{k_{\text{B}}T}\right).$$ (7)

However, ${\chi }_{\text{C}}$ is as yet unknown, and the conservation of integrins provides the additional constraint to determine ${\chi }_{\text{C}}$, viz given a spatially uniform surface density $C_0$ of integrins for a cell in suspension, the conservation statement reads as follows:

$$A_0{C}_0=C_{\text{r}}\underset{A}{\int }{\overline{C}}_{\text{eq}}\left(x_i\right)dA,$$ (8)

where $A_0$ is the surface area of the cell in suspension, and A is its area in the current configuration. The simultaneous solution of Eqs. 7 and 8 gives ${\chi }_{\text{C}}$, and the adhesion free energy of the cell is then given as $F_{\text{adh}}=A_0{C}_0{\chi }_{\text{C}}$.

The above analysis assumes the adhesion complexes can sustain any required force $\mathcal{F}\left(x_i\right)$ via the assumed linearity of the complex response. However, it has been demonstrated that complexes cannot support a force greater than a critical value ${\mathcal{F}}_{\text{max}}$ (21, 22, 23). Direct enforcement of the condition that no complex force exceeds ${\mathcal{F}}_{\text{max}}$ at the cell-substrate interface would require an iterative adjustment of spread state (as implemented for simplified microstates by McEvoy et al. (13)) and is therefore excessively computationally expensive in the context of the Monte Carlo simulations required for sampling the homeostatic ensemble. Here, we use the alternative approach of a penalty scheme to ensure that a very small number of spread states contain complexes with forces $\mathcal{F}>{\mathcal{F}}_{\text{max}}$. In summary, we define a penalty force as follows:

$${\mathcal{F}}^{\text{p}}=\underset{A}{\int }\mathit{\Delta }{\mathcal{F}}^{\text{p}}\left(x_i\right)dA,$$ (9)

where

$$\mathit{\Delta }{\mathcal{F}}^{\text{p}}\left(x_i\right)=\{\begin{array}{cc}\mathcal{F}\left(x_i\right)-{\mathcal{F}}_{\text{max}}& \mathcal{F}\left(x_i\right)>{\mathcal{F}}_{\text{max}}\\ 0& \text{otherwise}.\end{array}$$ (10)

A penalty energy is then defined as ${\chi }_{\text{p}}={\left({\mathcal{F}}^{\text{p}}\right)}^2/\left(2{\kappa }_{\text{p}}\right)$, where the parameter ${\kappa }_{\text{p}}$ has the units of stiffness and sets the magnitude of the penalty. The total FA free energy, including the penalty contribution, is then defined as follows:

$$F_{\text{adh}}=A_0{C}_0\left({\chi }_{\text{C}}+{\chi }_{\text{p}}\right),$$ (11)

with the normalized energy ${\hat{F}}_{\text{adh}}$ following from the definitions detailed in Supporting Materials and Methods (Section S2.4) along with the model parameters. To compare model predictions with the experimental results of Engler et al. (3), the number of ligands per unit area, $N_{\text{H}}$, can be expressed as surface collagen density ${\rho }_{\text{col}}$ through the following expression:

$${\rho }_{\text{col}}=N_{\text{H}}{M}_{\text{col}}/L,$$ (12)

where $M_{\text{col}}$ is the molar mass of collagen, and $L$ is Avogadro’s constant. We assume a uniform surface collagen distribution and substrate stiffness.

Results and Discussion

Spread dependence of cells on surface collagen density

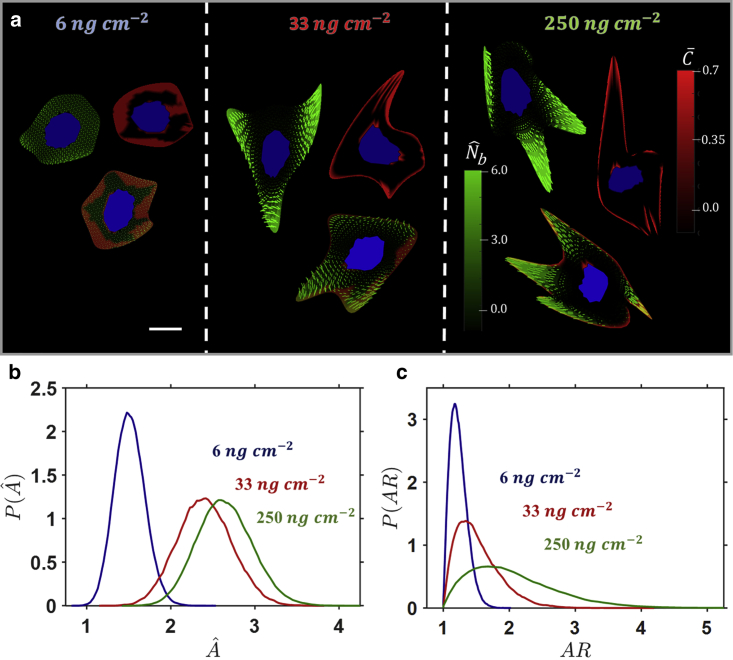
The influence of surface collagen density ${\rho }_{\text{col}}$ on cell spreading is shown in Fig. 1. Cells are spread on rigid substrates coated with three different values of ${\rho }_{\text{col}}$ (6, 33, and 250 ${\text{ng cm}}^{-2})$. A sample of cell spread states, with the same free energy for a given ${\rho }_{\text{col}}$, are shown in Fig. 1 a, including SF distributions (green), FA distributions (red), and nuclei (blue). In the case of a low ${\rho }_{\text{col}}$ (i.e., 6 ${\text{ng cm}}^{-2}$), cells are not highly spread, and they maintain regular rounded morphologies. A low-concentration smeared actin cytoskeleton is observed throughout the cell, with no regions of highly aligned SFs. For a higher ${\rho }_{\text{col}}$ of 33 ${\text{ng cm}}^{-2}$, cells become more highly spread. Additionally, the spread shapes become quite irregular in contrast to the rounded shapes observed on a lower ${\rho }_{\text{col}}$. Regions of aligned SFs are observed, and FAs cluster toward the cell periphery. In the case of the highest ${\rho }_{\text{col}}$ of 250 ${\text{ng cm}}^{-2}$, a further increase in spread area is observed, and the spread shape becomes highly irregular, with cells exhibiting elongated protrusions. High concentrations of aligned SFs are observed, and FAs are highly localized at the cell periphery and cell nucleus.

Figure 1.

(a) Contours of bound SF protein concentrations ${\hat{N}}_{\text{b}}$ (green) with dominant alignment, FA distributions $\hat{C}$ (red), and overlays in commonly observed cell shapes at a given surface collagen density ${\rho }_{\text{col}}$. The substrate is rigid, and the nucleus is highlighted in blue. The cell spread states for a given ${\rho }_{\text{col}}$ have the same free energy. The scale bar represents the undeformed cell radius $R_0$. Probability density functions (pdfs) for cells spread on a rigid substrate for three collagen densities of (b) cell spread area $\left(\hat{A}=A/\pi R_0^2\right)$ and (c) cell AR are shown. To see this figure in color, go online.

Probability density functions (pdfs) for cell spread area (Fig. 1 b) and for cell aspect ratio (AR) of a best-fit ellipse (Fig. 1 c) are constructed from the full population of spread states for each surface collagen density. With increasing ${\rho }_{\text{col}}$, the mean cell spread area increases, and the variance in spread area increases (i.e., in Fig. 1 a, as ${\rho }_{\text{col}}$ increases, the pdf moves to the right and becomes less peaked). A similar trend is observed for cell AR (Fig. 1 c), for which the mean is closer to 1, and the variance is very low (the pdf is more peaked) for the lowest ${\rho }_{\text{col}}$. In summary, the pdfs presented in Fig. 1, b and c show that a population of cells on a lower ${\rho }_{\text{col}}$ will have a lower mean spread area and a lower variance of spread area in addition to being rounded (AR close to 1) with a low variance of spread shape. As ${\rho }_{\text{col}}$ increases, a higher mean spread area is obtained for a population of cells, with a higher variance of spread area and spread shape. Additional spread shapes are presented in Figs. S1 and S2.

Influence of substrate stiffness on cell spreading

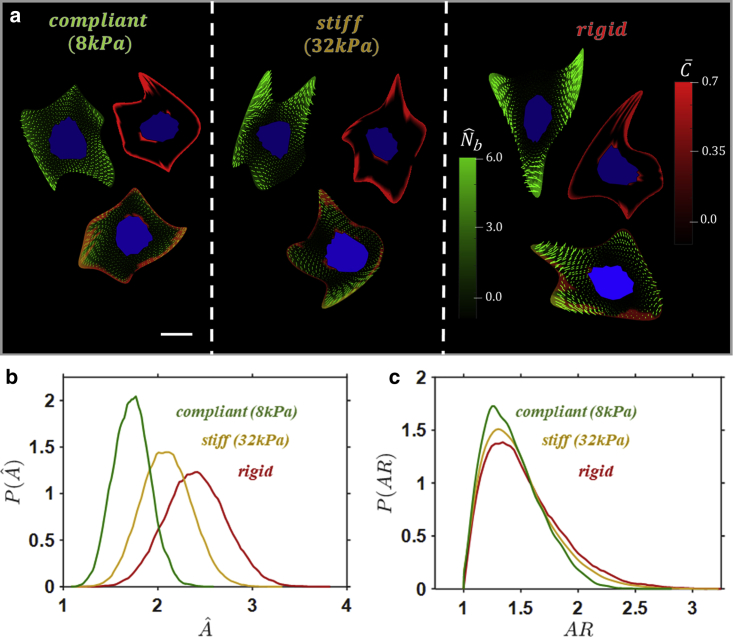
The influence of substrate stiffness $E_{\text{sub}}$ on cell spreading is shown in Fig. 2. Cells are spread on substrates of stiffness 8 and 32 kPa, in addition to a rigid substrate. All substrates have a ${\rho }_{\text{col}}$ of 33 ${\text{ng cm}}^{-2}$. A sample of cell spread states shown in Fig. 2 a suggests that cell spread area increases with $E_{\text{sub}}$. Cells on the compliant (8 kPa) substrate exhibit a low-concentration smeared actin cytoskeleton, compared to the highly aligned SFs on the stiff and rigid substrate. The irregularity of the spread shape increases with $E_{\text{sub}}$, with longest protrusions occurring on the rigid substrate.

Figure 2.

(a) Contours of bound SF protein concentrations ${\hat{N}}_{\text{b}}$ (green) with dominant alignment, FA distributions $\hat{C}$ (red), and overlays in commonly observed cell shapes at a given substrate stiffness $E_{\text{sub}}$. The surface collagen density ${\rho }_{\text{col}}$ is fixed at 33 ${\text{ng cm}}^{-2}$, and the nucleus is highlighted in blue. The cell spread states for a given $E_{sub}$ have the same free energy. The scale bar represents undeformed cell radius $R_0$. Probability density functions (pdfs) for cells spread on substrates of different stiffness at a surface collagen density ${\rho }_{\text{col}}$ of 33 ${\text{ng cm}}^{-2}$, of (b) cell spread area $\left(\hat{A}=A/\pi R_0^2\right)$, and (c) cell AR are shown. To see this figure in color, go online.

Pdfs for cell spread area (Fig. 2 b) and AR (Fig. 2 c) are constructed from the full population of spread states for each value of $E_{\text{sub}}$. Clearly, both the mean spread area and the variance in spread area increase with $E_{\text{sub}}$ (i.e., in Fig. 2 b, the pdf moves to the right and becomes less peaked as $E_{\text{sub}}$ is increased). The effect of $E_{\text{sub}}$ on cell shape is less pronounced for the value of ${\rho }_{\text{col}}$ considered here, with only a minor increase in the mean and variance of cell AR with increasing stiffness (Fig. 2 c).

Coupled dependence of collagen density and substrate stiffness

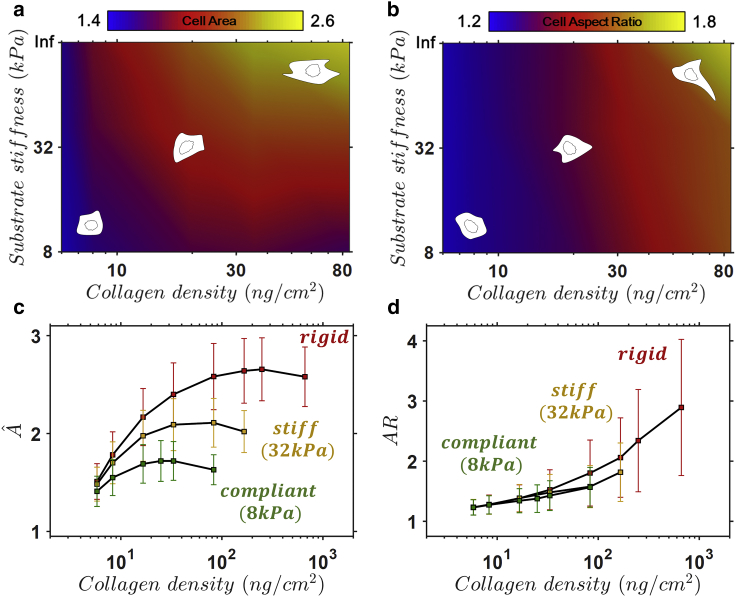
The coupled interplay between the influence of ${\rho }_{\text{col}}$ and $E_{\text{sub}}$ on cell spreading is next considered. Contour plots are constructed from mean spread areas (Fig. 3 a) and mean ARs (Fig. 3 b). Representative spread states are superimposed for illustrative purposes. As shown in Fig. 3 a, a very low ${\rho }_{\text{col}}$ results in a very weak dependence of mean spread area on $E_{\text{sub}}$. However, for moderate and high ${\rho }_{\text{col}}$, the mean spread area is highly dependent on $E_{\text{sub}}$. As shown in Fig. 3 b, the cell AR exhibits a very weak dependence on $E_{\text{sub}}$ (the contours in Fig. 4 b are almost uniform in the vertical direction), while exhibiting a very strong dependence on ${\rho }_{\text{col}}$.

Figure 3.

Contour plots for predicted mean spread area (a) and mean cell AR (b) in the ${\rho }_{\text{col}}-E_{\text{sub}}$ space. (c) The predicted cell area (mean$\pm$SD) and (d) cell AR (mean$\pm$SD) as a function of surface collagen density ${\rho }_{\text{col}}$ for cells spread on substrates of different stiffness (red: rigid; yellow: 32 kPa; green: 8 kPa). Sample cell spread states are shown for a given substrate in (a and b). To see this figure in color, go online.

Figure 4.

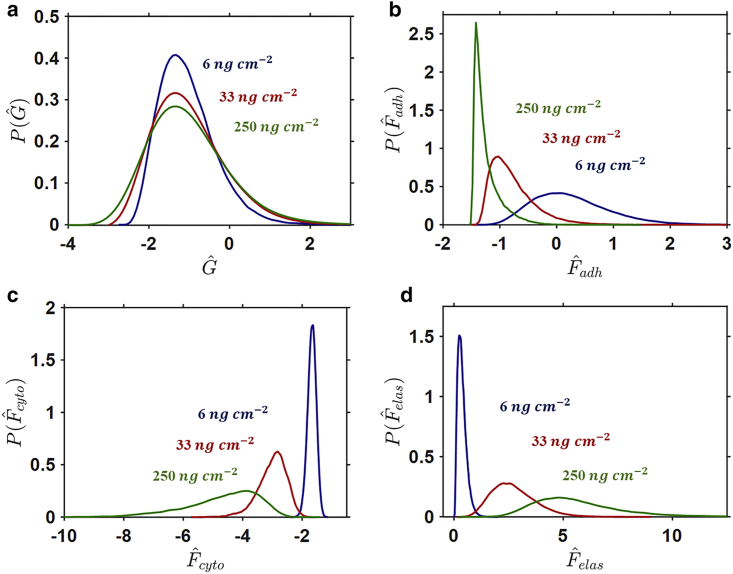
Probability density functions (pdfs) for cells spread on a rigid substrate for three surface collagen densities ${\rho }_{\text{col}}$ of (a) Gibbs free energy, (b) adhesion free energy, (c) cytoskeletal free energy, and (d) elastic free energy $\left({\hat{F}}_{elas}={\hat{F}}_{passive}+{\hat{F}}_{sub}\right)$. To see this figure in color, go online.

Both the mean and SD of cell spread area is shown in Fig. 3 c. A number of features should be noted: 1) as ${\rho }_{\text{col}}$ is increased, both the mean and SD increase up to a peak value ( this trend is observed for all values of $E_{\text{sub}}$); 2) if ${\rho }_{\text{col}}$ is increased beyond the peak value, a slight reduction in mean spread area (and its SD) is observed; again, this trend is observed for all values of $E_{\text{sub}}$; 3) the ${\rho }_{\text{col}}$ at which the mean spread area reaches a peak value increases with increasing $E_{\text{sub}}$; and 4) for a given ${\rho }_{\text{col}}$, both the mean and SD increase with increasing $E_{\text{sub}}$. Fig. 3 d shows that cell AR is highly dependent on ${\rho }_{\text{col}}$, with both the mean and SD increasing with increasing ${\rho }_{\text{col}}$. It is interesting to note that even though the cell mean spread area decreases when the ${\rho }_{\text{col}}$ is increased beyond the critical value, the mean AR continues to increase. However, the mean AR and its SD exhibit a weak dependence on $E_{\text{sub}}$.

Experimental support for predicted cell behavior

Remarkably, all the features described by Fig. 3 are directly supported by the experimental study of Engler et al. (3) in which the response of SMCs to $E_{\text{sub}}$ and ${\rho }_{\text{col}}$ was investigated. At a low ${\rho }_{\text{col}}$ on all substrates, SMCs that were detectably spread were found to be rounded with a low spread area. As the ${\rho }_{\text{col}}$ was increased, the spread area (mean and SD) was observed to increase up to a peak value. After this peak, any increase to the density of ${\rho }_{\text{col}}$ resulted in a reduction of mean spread area. This behavior is further supported by the experimental study of Gaudet et al. (24). Engler et al. (3) noted that the ${\rho }_{\text{col}}$ at which the peak mean spread area occurs is dependent on $E_{\text{sub}}$, that is, it increases with increasing $E_{\text{sub}}$, as predicted by our models). They also reported that an increase in $E_{\text{sub}}$ results in a higher mean cell spread area for a fixed ${\rho }_{\text{col}}$.

Although the AR is not directly measured in the experimental work of Engler et al. (3), with an increase in cell area (because of $E_{\text{sub}}$ or ${\rho }_{\text{col}}$), it was reported that cell shapes became less rounded and more irregular when cell spread area increases as a result of increased $E_{\text{sub}}$ and/or ${\rho }_{\text{col}}$. Such a reduction in cell roundness with increasing $E_{sub}$ has also been observed in the experimental study of Ren et al. (25) for skeletal muscle cells. Additionally, Prager-Khoutorsky et al. (26) reported that cells readily elongate (i.e., high AR) when plated on rigid substrates, with the behavior significantly less pronounced with decreasing $E_{\text{sub}}$. Similar to our predictions for SF distributions, Engler et al. (3) report that highly spread cells display a well-ordered SF network. Such ordered fibers were far less probable on rounded cells on low ${\rho }_{\text{col}}$ and on softer substrates. Similar observations are also reported in the experimental study by Deroanne et al. (27) in which a significant reduction in SF and FAs formation was observed in endothelial cells on soft gels compared to stiff substrates. Pelham and Wang (28) also showed such dependence of adhesion formation on substrate stiffness. The predicted trends of SF and FA organization in Figs. 1 and 2 of the current study are strongly supported by the aforementioned experimental studies. Additional samples of computed cell spread states are shown in Figs. S1 and S2.

Thermodynamically motivated insights and explanations for predicted cell behavior

We next provide a thermodynamically motivated explanation for the computed results in Figs. 1 and 3 and, by extension, for the experimental observations of Engler et al. (3). In Fig. 4 a, we plot the pdf of Gibbs free energy for the three values of ${\rho }_{\text{col}}$ on a rigid substrate. Recall that the system is subject to the homeostatic constraint such that the mean Gibbs free energy of all states is equal to the cellular homeostatic free energy $G_{\text{S}}$, which can be identified from the unique state of a freestanding cell. Therefore, the mean free energy is similar for all values of ${\rho }_{\text{col}}$ (Fig. 4 a). The pdf for adhesion free energy (Fig. 4 b) is highly peaked and negative for a high ${\rho }_{\text{col}}$ of 250 ${\text{ng cm}}^{-2}$. This indicates a high probability that adhesion complex forces are close to ${\mathcal{F}}_{\text{max}}$ so that a low adhesion energy is obtained. On the other hand, there is a low probability that adhesion complex forces exceed ${\mathcal{F}}_{\text{max}}$ and incur a positive adhesion energy penalty.

In the case of a high ${\rho }_{\text{col}}$ of 250 ${\text{ng cm}}^{-2}$, the cell-substrate tractions for a wide range of highly spread states can be supported without incurring an adhesion energy penalty (i.e., the adhesion free energy remains low). As a result, the entropy of spread states is very high for high values of ${\rho }_{\text{col}}$. Correspondingly, a high variance in the (negative) cytoskeletal and (positive) elastic free energies (Fig. 4, c and d) occurs. In effect, cell spreading on a rigid substrate coated with a high ${\rho }_{\text{col}}$ can be viewed as a competition between positive elastic free energy due to stretching of passive cell components and negative free energy due to the assembly of contractile SFs, with an additional negative free-energy contribution from the adhesion complexes.

When ${\rho }_{\text{col}}$ is reduced, higher forces occur in ligand complexes, resulting in a higher probability that ${\mathcal{F}}_{\text{max}}$ is exceeded and an adhesion energy penalty is incurred. Therefore, there is a low probability that highly spread states will occur, and the entropy of spread states decreases. In other words, a highly spread cell on a low ${\rho }_{\text{col}}$ will result in adhesion complex forces that exceed the maximal value, and the imposition of an energetic penalty results in a low probability that such highly spread states will occur. This explains the high probability of rounded cells with low spread areas on a ${\rho }_{\text{col}}$ of 6 ${\text{ng cm}}^{-2}$, as reported in Figs. 1 and 3. Correspondingly, as shown in Fig. 4, c and d, the cytoskeletal and elastic free-energy pdfs are highly peaked with mean values close to zero (as expected for the observed low spread areas and low variance in spread shapes (AR)).

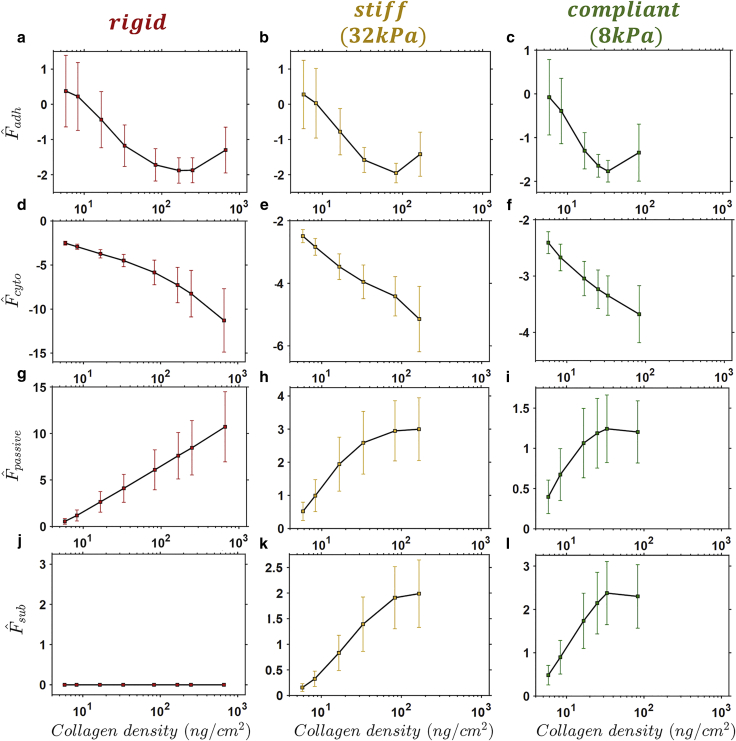
Recall from Fig. 3 that for all values of $E_{\text{sub}}$, cell spread area increases with increasing ${\rho }_{\text{col}}$ up to a peak value. In Fig. 5, we report the mean and SD of the free-energy densities across all ${\rho }_{\text{col}}$ and $E_{\text{sub}}$ (the SD is indicative of the variance observed in the corresponding pdfs). The peak spread areas shown in Fig. 3 b coincide with the lowest mean adhesion free energy for each substrate (Fig. 5, a–c). The ${\rho }_{\text{col}}$ associated with such a peak spread area on each substrate is hereafter referred to as “optimal.” At this optimal ${\rho }_{\text{col}}$, there is a high probability that the forces in adhesion complexes will result in a low adhesion free energy. For suboptimal ${\rho }_{\text{col}}$, highly spread states will result in an increased probability of adhesion complex forces higher than ${\mathcal{F}}_{\text{max}}$, resulting in an energetic penalty, as explained in Fig. 4 above. On the other hand, when the ${\rho }_{\text{col}}$ is increased beyond the “optimal” value, the cell must spread to a higher area to generate sufficient tractions to achieve sufficiently high adhesion complex forces (i.e., $\mathcal{F}\left(x_i\right)\cong {\mathcal{F}}_{\text{max}}$) and a low adhesion free energy. However, spreading to such a high area results in an increased elastic strain energy. There is a low probability that the adhesion (Fig. 5, a–c) and cytoskeletal (Fig. 5, d–f) free energy will overcome this “elastic penalty” and achieve the homeostatic state (i.e., ${\hat{G}}_{\text{S}}$). Therefore, on “postoptimal” ${\rho }_{\text{col}}$, there is a low probability that the cell area will increase beyond the peak spread area. In fact, a postoptimal ${\rho }_{\text{col}}$ leads to a reduction in mean spread area, as shown in Fig. 3 c (this has been also observed experimentally by Engler et al. (3) and Gaudet et al. (24), discussed in Experimental Support for Predicted Cell Behavior above). This occurs because cellular tractions are supported by a higher number of complexes so that individual bond forces are reduced. Therefore, the cell adhesion free energy moves toward zero (Fig. 5, a–c), providing a weaker competition to the elastic strain energy (Fig. 5, g–i) so that there is a lower probability that the cell will achieve the peak spread area. Although the mean spread area decreases for postoptimal ${\rho }_{\text{col}}$, the mean elastic free energy increases on rigid and stiff substrates (Fig. 5, g and h). This is because of a high variability in spread shape on stiffer substrates with high ${\rho }_{\text{col}}$ (see plots of cell AR in Fig. 3 d).

Figure 5.

Predicted adhesion (a–c), cytoskeletal (d–f), elastic (g–i), and substrate (j–l) free energy (mean$\pm$SD) as a function of surface collagen density ${\rho }_{\text{col}}$ for cells spread on rigid, stiff, and compliant substrates. To see this figure in color, go online.

A reduction in $E_{\text{sub}}$ lowers the probability of the cell achieving a high spread area, with rounded low-spread morphologies more frequently observed (Fig. 3 c). On a rigid substrate, there is no contribution from the elastic strain energy of the substrate (Fig. 5 j) because it is not deformed by the contractile activity of the cell. However, as the $E_{\text{sub}}$ is reduced (Fig. 5, k and l), it will be deformed by the cell. The associated substrate free energy causes the total system free energy to become increasingly positive. Thus, to achieve a homeostatic state, there is a high probability that the cell area will be lower on more compliant substrates. The highly coupled balance between the contributions to the system free energy causes the peak cell area to occur at a lower ${\rho }_{\text{col}}$ for a lower $E_{\text{sub}}$. As mentioned above, a low $E_{\text{sub}}$ results in lower spread areas, which leads to lower cell-substrate tractions. Therefore, a lower ${\rho }_{\text{col}}$ is required for an increased probability of optimal forces in adhesion complexes $\left(\mathcal{F}\left(x_i\right)\cong {\mathcal{F}}_{\text{max}}\right)$ and a correspondingly low adhesion free energy. Peak spreading occurs on lower ${\rho }_{\text{col}}$ for lower $E_{\text{sub}}$, as shown in Fig. 3 c (and as reported in the experiments of Engler et al. (3)).

Conclusions

The equilibrium statistical mechanics framework developed by Shishvan et al. (15) allows for the simulation of the homeostatic ensemble for cells on an elastic substrate in a nutrient bath. Cells assume a dynamic homeostatic equilibrium by means of a free-energy competition between the increasing elastic free energy due to stretching of passive cell components (and substrate deformation) and the decreasing cytoskeletal free energy as contractile proteins assemble to form SFs. In the current study, the framework is expanded to include the free energy associated with the formation of FAs between the cell and a collagen-coated substrate.

The expanded framework allows for the simulation of the coupled influence of surface collagen density ${\rho }_{\text{col}}$ and substrate stiffness $E_{\text{sub}}$ on cell spreading, as reported in the experimental study of Engler et al. (3). The key experimental observations predicted by our modeling framework are summarized as follows:

• 1)With increasing substrate ${\rho }_{\text{col}}$, cell spread area (mean and SD) increases up to a peak value.
• 2)A further increase in ${\rho }_{\text{col}}$ beyond this peak results in a reduction of the cell spread area (mean and SD).
• 3)The ${\rho }_{\text{col}}$ at which the mean cell area reaches a peak decreases with decreasing $E_{\text{sub}}$.
• 4)At a fixed ${\rho }_{\text{col}}$, the mean and SD of the spread area increase with increasing $E_{\text{sub}}$.

The ${\rho }_{\text{col}}$ directly influences the forces in adhesion complexes and, consequently, the adhesion free energy. This, in turn, influences the spread states that cells assume in achieving homeostasis. A low ${\rho }_{\text{col}}$ lowers the probability of a cell becoming highly spread, because sufficient complexes cannot form to support the tractions imposed by the substrate. Conversely, at a high ${\rho }_{\text{col}}$, the cell may form more adhesion complexes, lowering the associated free energy. Thus, the probability of cells having a high spread area increases. The influence of $E_{\text{sub}}$ and ${\rho }_{\text{col}}$ is highly coupled, as demonstrated in Figs. 3 and 5. A deformable substrate lowers the probability of a cell becoming highly spread, reducing the cell tractions and thereby causing the peak mean spread area to occur at a lower ${\rho }_{\text{col}}$.

In statistical thermodynamics, a closed system in a constant temperature and pressure environment attains equilibrium at minimal Gibbs free energy. However, metabolic systems such as cells cannot be viewed in this manner; in fact, cells never attain an equilibrium minimal free-energy state while alive. The approach developed by Shishvan et al. (15) (extended in the current study) acknowledges this and predicts the statistics of biological observables (e.g., cell area, AR, etc.) under the constraint that the cell maintains a homeostatic state. In previous studies, the importance of considering the system free energy in the interpretation of cell-spreading behavior has been recognized (13, 29). McEvoy et al. (13) identified low (or minimal) free-energy cell spread states within a limited phase space of axisymmetric configurations. This simplified approach provided a reasonable approximation of the detailed trends computed in the current study (as observed experimentally (3)), which can be explained by the fact that low free-energy states will of course be highly probable within the homeostatic ensemble; see Eq. 1. Although McEvoy et al. (13) correctly demonstrate that cell spreading is governed by a competition between decreasing cytoskeletal and adhesion free energy and increasing elastic energy, the identification of a low or minimal free-energy configuration is not physically appropriate for a fluctuating system. Therefore, the emergence of such an energetic competition within the statistical mechanics framework of the homeostatic ensemble provides a significant advance in current understanding of the influence of ligand density and substrate stiffness on cell spreading. Importantly, this framework correctly predicts the trends for observables such as the spread area and spread shape as a function of environmental cues, such as stiffness and ligand density, and quantifies inherent statistical variability in these observations. The homeostatic ensemble for cells, expanded to include the FA formation and an associated adhesion free-energy contribution, provides new insight into observed cell behavior on deformable collagen-coated substrates. The model may readily be used to simulate more complex extracellular environments, including the spreading of cells on ligand patterned ridges and ligand patterned micropillars. Furthermore, the computational framework will be extended in a future study to explore the influence of gradients of ligand density on cell motility.

Author Contributions

All authors contributed to the development and implementation of the computational model. E.M. performed all simulations and created all figures. E.M., J.P.M., and V.S.D. analyzed the results and wrote the article. J.P.M. and V.S.D. designed and coordinated the research.

Editor: Cynthia Reinhart-King.