Abstract
Single-pair Förster resonance energy transfer (spFRET) has become an important tool for investigating conformational dynamics in biological systems. To extract dynamic information from the spFRET traces measured with total internal reflection fluorescence microscopy, we extended the hidden Markov model (HMM) approach. In our extended HMM analysis, we incorporated the photon-shot noise from camera-based systems into the HMM. Thus, the variance in Förster resonance energy transfer (FRET) efficiency of the various states, which is typically a fitted parameter, is explicitly included in the analysis estimated from the number of detected photons. It is also possible to include an additional broadening of the FRET state, which would then only reflect the inherent flexibility of the dynamic biological systems. This approach is useful when comparing the dynamics of individual molecules for which the total intensities vary significantly. We used spFRET with the extended HMM analysis to investigate the dynamics of TATA-box-binding protein (TBP) on promoter DNA in the presence of negative cofactor 2 (NC2). We compared the dynamics of two promoters as well as DNAs of different length and labeling location. For the adenovirus major late promoter, four FRET states were observed; three states correspond to different conformations of the DNA in the TBP-DNA-NC2 complex and a four-state model in which the complex has shifted along the DNA. The HMM analysis revealed that the states are connected via a linear, four-well model. For the H2B promoter, more complex dynamics were observed. By clustering the FRET states detected with the HMM analysis, we could compare the general dynamics observed for the two promoter sequences. We observed that the dynamics from a stretched DNA conformation to a bent conformation for the two promoters were similar, whereas the bent conformation of the TBP-DNA-NC2 complex for the H2B promoter is approximately three times more stable than for the adenovirus major late promoter.
Introduction
Protein biosynthesis begins with DNA transcription and RNA translation. Many regulatory and accessory factors exist to control the early steps during DNA transcription (1). For genes with TATA-box promoter sites in eukaryotic cells, the first step in DNA transcription is binding of the TATA-box-binding protein (TBP) (2) to the core promoter TATA boxes. This step is accompanied by deformation of the DNA strand, resulting in an 80° bend (3, 4, 5, 6, 7, 8, 9). This conformation change is believed to lead to the recruitment of additional general transcription factors (TFs) that form the preinitiation complex (10, 11, 12). In eukaryotic cells, positive cofactors play the major role in regulation of the DNA transcription process (13, 14), whereas negative cofactors can sterically occlude association of other general TFs, which intermits the preinitiation complex formation and leads to repression of transcription. Some proteins, such as the evolutionarily conserved negative cofactor 2 (NC2) protein complex (15, 16, 17), have the capability to both suppress and enhance gene expression (18, 19, 20, 21, 22). Recent studies show that, in addition to steric interactions, dynamics also play an important role when investigating the interaction of TFs on DNA (23).
From x-ray crystallography experiments, it is known that NC2 forms a ringlike structure with TBP around the DNA (24), which can delocalize from TATA without leaving the DNA strand (23). Assuming that the formation of the TBP-NC2 subcomplex loosens the TBP-DNA interaction, the DNA is expected to relax into its original linear configuration. This stretched DNA conformation enables the TBP-NC2 subcomplex to move away from TATA and slide along the DNA strand. Using single-pair Förster resonance energy transfer (spFRET), we could directly visualize the conformational fluctuations of the TBP-NC2-DNA complex as well as movement of the TBP-NC2 complex along the DNA upon the binding of NC2 (23).
A wealth of information regarding the dynamics of the biomolecular system is buried within the spFRET traces. A detailed analysis can yield information regarding the number of states involved, which states can interconvert, and the transition rates between the individual states. One objective approach to extract this information from the spFRET data is the hidden Markov model (HMM) analysis. HMM was initially developed for speech-recognition algorithms but since then has been applied to many different fields and has become an important tool for analyzing spFRET data (25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37). A Markov model assumes discrete states with instantaneous transitions between the different states. In measurements with limited signal/noise ratio, the actual states become “hidden” because of the noise. The probability of measuring a particular value for a given state becomes distributed and, for the case of spFRET measurements, the distributions often overlap when multiple Förster resonance energy transfer (FRET) states are present. The power of the HMM analysis is that it can deal with overlapping probability distributions functions and, by optimizing a whole spFRET trace or family of traces, can reliably assign values to the hidden states. The HMM approach has been combined with maximal likelihood algorithms (25, 26, 29, 31, 37, 38, 39), variational Bayesian techniques (40), and empirical Bayesian methods (41).
One of the drawbacks of current HMM methods is that they assume a constant noise value for each state. However, the noise in spFRET traces is not necessarily constant. For example, the donor molecule can undergo partial quenching during the measurement. More importantly, a global HMM analysis is often desirable, but the total measured intensities of the donor and acceptor fluorophores and hence the signal/noise ratio will vary for different molecules. The signal/noise ratio for the individual molecules can be extracted from the raw data by estimating the total number of detected photons (37). With this approach, the shot noise does not need to be added as a parameter to the HMM analysis. To account for the diverse total intensities, particularly for a global analysis of hundreds of traces, we changed from the estimators commonly used in spFRET experiments, the donor and acceptor intensities, to the total intensity and proximity ratio (28).
In this work, we use the above-developed HMM analysis to investigate the number of conformations and the dynamics of the conformational changes induced by the formation of the TBP-NC2 subcomplex on DNA. SpFRET experiments were performed on immobilized molecules using total internal reflection fluorescence (TIRF) microscopy with a time resolution of 5 ms. Based on the new estimators, the HMM-assigned states could be determined and related to conformations of the TBP-NC2 subcomplex on the adenovirus major late (AdML) promoter sequence. Four states were observable. Three states corresponded to different conformations of the TBP-NC2-DNA complex with sharply bent DNA, partially bent DNA, and extended DNA. The fourth state is attributed to motion of the TBP-NC2 complex along the DNA. We also measured the dynamics of TBP-NC2 on the H2B promoter site, which revealed much richer dynamics. A comparison between the two promoter sites indicated that the dynamics were much more prevalent on the major late promoter site because of the lower stability of the bent conformation.
HMM
General introduction
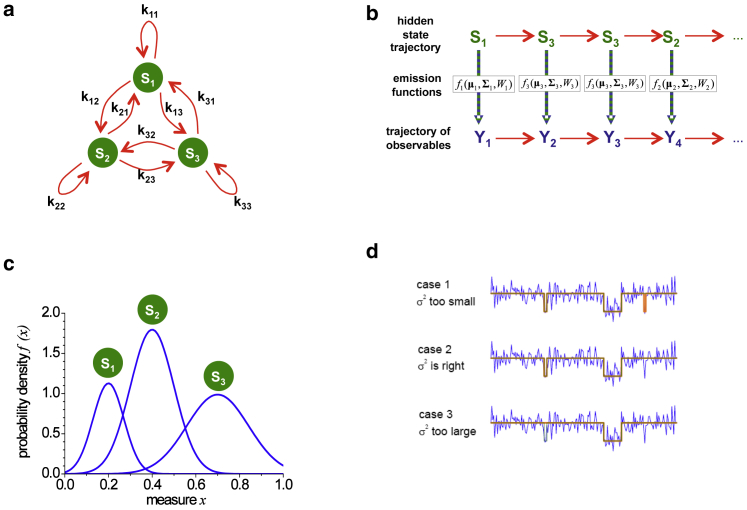
A Markov model is described by a discrete number of states, qi (where i = 1...Q), that the system can adopt. The system undergoes transitions between the different states, and the probability of a transition is constant, independent of the previous transitions. Hence, the dwell time in each state can be described by an exponential distribution. For a Q-state system, there are Q × (Q−1) independent transition probabilities kij of going from state i to state j, and together, they form the transition probability matrix K. A schematic of a three-state Markov model is shown in Fig. 1 a. Typically, one is interested in which state the system is in as a function of time as well as the transition probabilities between states (the upper sequence in Fig. 1 b). In a hidden Markov system, the states themselves are no longer directly observable but are hidden within the noise of the system (the lower sequence in Fig. 1 b). The measured observable, xt, depends on the state the system is in (i.e. qi) but its exact value will vary because of random noise. Thus, it is no longer possible to unequivocally back-assign the states q from xt.
Figure 1.
Principles of a hidden Markov model (HMM). (a) A scheme of a Markov model with three states (S1, S2, and S3) and their corresponding transition probabilities kij is shown. (b) A possible realization of a Markov chain is shown. For a series of states, the model emits an observable xi based upon the actual state Si and the probability density function fi. This yields a trajectory of observables. In an HMM, the states themselves are not directly determinable because of noise and are hence hidden. The HMM analysis finds the parameters of the emission functions that best describe the data. From the given parameters, the Viterbi path is determined, which gives the most likely trajectory of hidden states that describes the observed data. (c) Three Gaussian emission functions with different means, variances, and occurrences are shown (μq = {0.2, 0.4, 0.7}, σq = {0.05, 0.1, 0.2}, Wq = {0.20, 0.45, 0.35}). (d) The influence of the variance on the state assignments extracted during an HMM analysis of an spFRET trace is depicted. When the variance is too small, the HMM introduces too many transitions, which yields a reduction in the duration of the individual states (case 1). When the variance is too large, state transitions are missed, which yields exaggerated state durations (case 3). When the variance models the broadness of a state correctly, the state durations are consistent with the transition probabilities (case 2). To see this figure in color, go online.
The goal of an HMM analysis is to infer from the trajectory of observables (42) all system parameters of the underlying HMM. When the noise of the system in the different states is known, the probability density function for possible values of xt given that the system is in state qi can be calculated and is referred to as the emission function fi(x|qi). For example, the emission functions of a three-state HMM shown are given in Fig. 1 c. A measured value of 0.35 is possible from all three states, but the probability of it arising from state 2 is much higher than that of state 1 or 3. Using the emission functions, we can estimate the most likely HMM that describes the measured time series.
The log-likelihood function, log L
The key tool used to determine the most probable set of system parameter values from the observable data is the log-likelihood function, log L. The likelihood function, L, calculates the probability of measuring the measured data set from the given set of parameters and is given by the following:
| (1) |
where μq, , and wq,t, are the mean FRET value of state q, its covariance, and the probability of the data point xt corresponding to q, respectively. T denotes the number of data points in the measured trajectory. To avoid underflow errors during determination of the likelihood function, it is advantageous to calculate the logarithm of the likelihood function:
| (2) |
Because the logarithm is a monotonic increasing function, maximization of the log-likelihood function is equivalent to finding the maximum of the likelihood function. By defining the log-likelihood function, determination of the best parameter set of a given model for producing a given data set is reduced to an optimization problem. Because the log-likelihood function can depend on several parameters, a multidimensional optimization algorithm needs to be used (25, 43). An algorithm that has been shown to converge rapidly is the forward-backward algorithm (38, 44), which we have implemented in our approach.
Once the optimal model parameter values are obtained, the hidden-state trajectory itself can be reconstructed by the Viterbi algorithm (45), which assigns every time-binned data point to its most likely state. The main tasks in applying HMMs to spFRET data are now to choose the appropriate emission functions and derive the analytical estimators for the parameter determination (25, 26, 46).
Estimators for the emission functions
Often, Gaussian distributions are used as emission functions to model the probability density function of a state. The parameter estimators for the mean, the covariance, and the fraction of time spent in the q state is given by the following:
| (3) |
| (4) |
| (5) |
wq,t is called the “responsibility matrix” or the “posterior probabilities” and depends in turn on the model parameters:
| (6) |
Because Eq. 3, 4, 5, and 6 are interdependent, the parameters cannot be determined directly but have to be refined iteratively.
Incorporation of the transition matrix
With the estimators above, the likelihood is increased by optimizing the parameters of the emission functions. The assignments of the data points to the hidden states are optimized by tuning the posterior probabilities. These posterior probabilities are connected to the emission functions of their preceding and subsequent states by the transition probabilities. Briefly, we calculate the probability of being in state i at the time step t, αt(i), as the product of the transition probability of going from state j to state i, the probability of being in state j at time step t − 1, and the emission function of state i (forward estimate):
| (7) |
Hence, αt(j) can be iteratively determined. Likewise, we can calculate the probability of being in state j at the time step t, βt(j), by calculating backward from the end of the trace (backward estimate):
| (8) |
The total probability of being in state i at the time step t is then given by the following:
| (9) |
From the forward and backward estimates, we can also determine an estimate for the transition probability matrix:
| (10) |
To begin the analysis, initial estimates for the parameters (i.e., μq, σq, and K) are entered. From the initial values, a first likelihood value and posterior probabilities are estimated. The parameters are then adjusted to maximize the log likelihood. For optimization, we used the forward-backward algorithm, which is an implementation of an “expectation-maximization algorithm” (47, 48). More detailed introductions to HMMs can be found in (44, 49, 50).
Observables in single-molecule FRET data
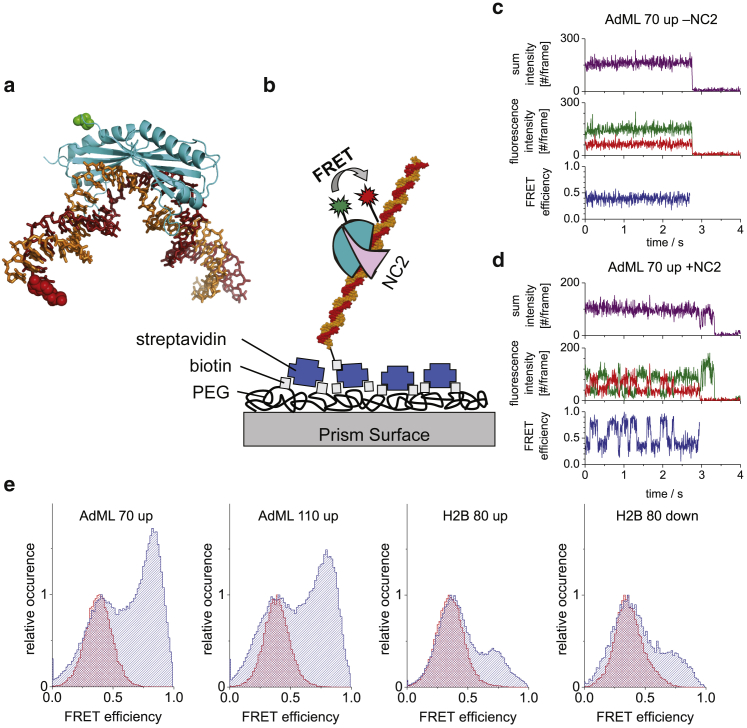
Everything discussed up to this point is independent of the type of data analyzed using HMM. In this work, we apply an HMM analysis to spFRET experiments on TBP (from Saccharomyces cerevisiae) interacting with DNA. TBP was labeled with the donor fluorophore, and DNA was labeled with the acceptor fluorophore (Fig. 2 a). A schematic of a single-molecule experiment with TBP bound to DNA immobilized on a PEGylated surface is shown in Fig. 2 b. In spFRET experiments, the fluorescence intensities of two fluorophores, the donor and acceptor molecules, are measured as a function of time (Fig. 2 c). The proximity ratio, EPR, which is related to the FRET efficiency, contains information regarding the separation of the two fluorophores and hence information about the conformation of the complex. It can be calculated directly from the experimentally accessible fluorescence intensity traces of the donor and acceptor molecules, ID and IA, respectively, using Eq. 11:
| (11) |
EPR provides information regarding the interfluorophore distance, and the total intensity
| (12) |
provides information on the accuracy of the measured proximity ratio. To convert the proximity ratio into FRET efficiency, differences in the detection efficiencies η of both detection channels as well as unequal fluorescence quantum yields ϕ of the fluorophores need to be accounted for. When the detection correction factor γ is known, the FRET efficiency EFRET is given by the following:
| (13) |
Figure 2.
SpFRET data of TBP-DNA in the absence and presence of NC2. (a) The crystal structure of TBP-DNA complex (Protein Data Bank: 1RM1) is shown. The labeling positions of the TBP (green) and DNA (red) are shown as spheres. For display purposes, the DNA has been extended downstream. (b) A scheme of the TBP-NC2-DNA complex immobilized to a functionalized, PEGylated glass surface over a streptavidin-biotin linkage is shown. TBP is specifically labeled with a donor fluorophore, and the DNA is specifically labeled with the acceptor fluorophore. The sample is excited by the evanescent wave generated at the prism/buffer interface by total internal reflection. (c and d) Single-molecule FRET trajectories from TBP bound to 70-bp DNA containing the AdML TATA box are plotted in the (c) absence and (d) presence of NC2 (purple: the scaled total intensity, , where γ is the detection correction factor; green: donor intensity; red: acceptor intensity; and blue: FRET efficiency). In the absence of NC2, a stable conformation of the TBP-DNA complex is observed, resulting in a constant FRET efficiency of ∼0.40. After the addition of NC2, the FRET efficiency fluctuates between different states. (e) Histograms of the frame-by-frame FRET efficiencies from the complete data set of the four different constructs measured are shown. Red histograms represent before the addition of NC2, whereas blue histograms represent after the addition of NC2.
In general, we transform the variables ID and IA into a new pair of variables, EPR and IT. When performing spFRET experiments using single-photon counting detection, a Poisson distribution will describe both ID and IA. For moderate count rates (greater than ∼50 photons per time bin), the Poisson distribution can be well approximated by a Gaussian distribution. The mean and variance of the Gaussian distribution are set equal to the mean (which is also the variance) of the Poisson distribution for the respective channel. The probability distribution function (pdf) for the total fluorescence intensity is then also approximated by a Gaussian distribution with a maximal value of IT, and the variance is given by the following:
| (14) |
The proximity ratio, EPR, can also be approximated by a Gaussian distribution (see Supporting Materials and Methods), yielding Eq. 15 for the mean and Eq. 16 for the variance:
| (15) |
| (16) |
The expectation value of the total intensity appears in the denominator of the variance, indicating that the total fluorescence intensity is a direct measure for the accuracy of the determined apparent FRET efficiency. The limited number of photons per time bin reduces the accuracy with which the FRET efficiency can be estimated. Hence, the corresponding emission function becomes broader because of shot noise, which can be quantified by Eq. 16. As long as the total fluorescence intensity is constant in time, the shot-noise broadening of the emission functions is also constant and can be included in the time-invariant covariance matrix σi provided by the classical HMM approach.
Often, single-molecule experiments are performed using wide-field illumination (typically with TIRF excitation) and a charged-coupled device (CCD) as a detector as we used in our studies of the dynamics of TBP-DNA complexes upon the binding of NC2 (23). Such an approach has the advantage that many molecules can be investigated simultaneously. However, CCD cameras are not photon-counting devices. With proper calibration, camera counts can be converted into an approximate number of detected photons (see Supporting Materials and Methods). However, the influence of additional noise sources needs to be considered. For the electron-multiplying CCD (EMCCD) in our setup, the variance in the fluorescence intensity is increased by a factor of two over the shot noise, as has been discussed in detail elsewhere (51, 52). This uncertainty can be included in the variance of the FRET efficiency, which can still be approximated, in this case, by a Gaussian distribution (see Supporting Materials and Methods).
When performing a global analysis on a collection of spFRET traces, the difference in the variances for the individual molecules as well as time-dependent changes in the total fluorescence intensity during a time trace needs to be accounted for. An incorrect variance for an HMM state will lead to errors in the recognition of transitions in the spFRET data. When the variance of the HMM is too small, noise fluctuations will also be incorrectly recognized as transitions (Fig. 1 d). Similarly, when the variance of the HMM is too large, rapid transitions between states will be ignored. Therefore, we have extended the standard HMM approach by introducing time-dependent weights to the classical parameter estimators, assuming that the degree of broadening is provided by the measured total fluorescence intensity IT.
Weighted HMMs
Incorporating photon-counting statistics as well as other known noise sources into the HMM analysis allows for a more accurate determination of the dynamics measured using spFRET. As the total intensity of an spFRET signal can drop because of partial, dynamic quenching of the donor, the variance of the data used in the emission functions needs to be variable on a frame-by-frame basis. Because this is not reasonable, we used the information available from photon statistics to estimate the broadening of FRET levels due to shot noise, and this can be done in a frame-wise manner.
Shot-noise broadening of FRET levels
A stable conformational state of a protein can be described well by a single pdf with two parameters: a mean and a variance. The variance includes the inherent amount of fluctuations within this conformation and should be independent of the measurement method. In addition, the pdf of spFRET values is broadened by the limited number of detected photons, which is often the dominating factor. Hence, it is necessary to combine the inherent uncertainty of the spFRET state with a second pdf that accounts for the uncertainty of the measurement. The pdfs for FRET efficiencies derived from shot-noise broadened fluorescence count rates follow a β-function (53, 54, 55). However, for count rates typically obtained in single-molecule experiments, the β-function can be well approximated by a Gaussian distribution (25, 53).
Weighted maximal likelihood estimators
When both factors contributing to the pdfs are Gaussian functions, the resulting emission function is again a Gaussian distribution with a mean and variance that are given by the sum of mean and variances of individual Gaussian distributions, respectively. Therefore, the classical HMM approach can be used by adding the variance of the broadened data point to the inherent variance of the FRET state, :
| (17) |
Accordingly, it is possible to account for the changes in the variances caused by the high diversity in the total fluorescence intensity of different molecules while maintaining a constant variance for the FRET efficiency of the state itself. The respective log-likelihood function log Lq for one state yields the following form and is the basis for obtaining the new estimator functions:
| (18) |
To derive initial expressions for the estimators of the HMM parameters, we set the derivate of the log-likelihood function, with respect to the desired parameters, equal to zero. Solving these equations for the parameters leads directly to the expressions for the estimators.
The newly introduced shot-noise variance leads to an additional weighting and hence to an expansion of the classical estimator. For the estimator of the mean value, the new parameter appears as an additional weighting factor for the observable x and cannot be eliminated:
| (19) |
As a consequence, solving the derivative of the likelihood function with respect to the variance for zero, given by:
| (20) |
is no longer solvable analytically. Fortunately, there are powerful methods that quickly find zeros for a one-dimensional function so that the computational time is only moderately increased (56).
Materials and Methods
Sample preparation and labeling
A recombinant mutant of TBP from S. cerevisiae with a single cysteine introduced at position 61 was covalently labeled with the donor fluorophore, Atto532 (57, 58). As shown previously, fluorescent labeling of the protein did not affect the functionality of the TBP (57, 58). The FRET acceptor Atto647 was attached to a DNA sequence containing a TATA box for TBP binding and a biotin anchor for the immobilization on a streptavidin-coated quartz-prism surface (Fig. 2, a and b). The FRET signal from individual TBP-DNA complexes is measured until one of the fluorophores photobleaches (typically ∼1 s, with a 5-ms time resolution). All samples were preincubated with the general initiation factor TFIIA recombinant homolog TOA to ensure the formation of stable TBP-DNA complexes forming the ∼80° DNA bend (59) and proper orientation (60). Fluorescence intensities of both the donor and acceptor fluorophores were recorded simultaneously by an EMCCD camera (DV887-BV iXon+; Andor Technology, Belfast, Northern Ireland) on our custom-build TIRF setup for single-molecule FRET. Details of the biochemical procedures and experimental conditions have been described previously (23).
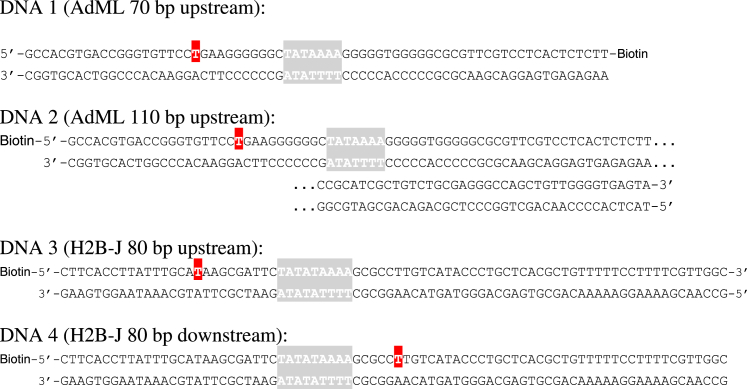
For the studies reported here, a total of four different DNAs (summarized in Fig. 3) were investigated. Two double-stranded DNAs contained the AdML promoter and were fluorescently labeled 11 basepairs (bp) upstream from the TATA box with the acceptor molecule (Atto647). They differed both in length (70 vs. 110 bps) and in the position of the attachment point to the surface. In addition, two double-stranded DNAs (80 bp in length) containing the TATA box from the H2B-J promoter were investigated. One of the H2B-J constructs was labeled 12 bp upstream from the TATA box, whereas the other DNA strand was labeled 13 bp downstream from the start of the TATA box.
Figure 3.
DNA sequences used in this study. DNA 1 and DNA 2 contain the adenovirus major later promoter sequence and DNA 3 and DNA 4 contain the H2B-J promoter sequence. The TATA box is highlighted in grey and the thymine base to which the acceptor fluorophore was attached is highlighted in red. The location of the biotin tag used to immobilize the DNA for the spFRET experiments is also shown. To see this figure in color, go online.
The Förster radius for the dye pair used is R0 = 6.0 nm (according to supplier), making it very sensitive to conformational fluctuations of the DNA and movement of the TBP-NC2 complex along the DNA. Between 103 and 431 TBP-DNA complexes were analyzed bound to the AdML promoters, and 55–279 complexes were measured bound to the H2B-J promoters.
EMCCD shot-noise corrections for HMM
To estimate the number of detected photons from the EMCCD measurements, the output of the camera has to be corrected for offset, gain, and the analog-to-digital conversion factor of the camera. In addition to the shot noise, which follows a Poisson distribution, other noise factors from the camera need to be incorporated. A detailed description of noise coming from EMCCD cameras can be found in (51, 52). The most important source of additional noise comes from the on-chip gain of the EMCCD, which broadens the variance of the intensity by a factor of two (or the SD by ). Further information is given in the Supporting Materials and Methods. Background correction will also increase the uncertainty of the measurement of the signal. However, because of the large number of pixels used to determine the level of the background signal in the vicinity of each individual complex, the additional uncertainty due to the background correction is negligible.
HMM analysis
Two variations of the HMM analysis were performed. In the first case, molecule-wise, each trace was fitted individually with up to 10 different states. In the second case, a global fit was performed in which the same FRET states and transition rates were used to fit the entire data set. For the global analysis, analyses were performed with different HMMs containing 1 to 10 hidden states. For the HMM analysis, we used the MATLAB toolbox of Murphy (61), which includes the forward-backward and Viterbi algorithm and supports HMM with mixtures of Gaussian outputs. Details of the analysis using different numbers of FRET states are given in the Supporting Materials and Methods.
Results
Monte Carlo test of the new estimators
Before analyzing the experimental spFRET data, we tested the reliability of our extended hidden Markov approach in handling additional shot-noise broadening by performing Monte Carlo simulations. Based on a normal distribution of FRET efficiencies representing a stable conformational state, a random trajectory with a length of 50,000 data points was created to mimic low inherent fluctuations of the FRET efficiency due to the flexibility of the observed protein. Mean total fluorescence intensities and average FRET efficiencies were introduced, and donor and acceptor fluorescence intensity trajectories were determined. Every point of this trajectory pair was finally replaced by a stretched Poissonian random number, taking the original value as its mean and a stretch factor of 2 to incorporate the additional noise component generated by the gain of an EMCCD camera (51, 52).
The results of the simulations are summarized in Fig. S1. The estimators extracted the time-dependent shot noise from the data and resolved the correct mean values and inherent variances even at very low photon count rates. The Gaussian approximation of the β-function was performed such that their mean values and therefore their maximal likelihood estimators were identical. Slight deviations were observed for the estimation of the variance at very low count rates and broad distributions. For comparison, the inherent amount of fluctuations of the experimental single-molecule FRET data had an SD of ∼0.1 with count rates of more than 50 counts per data point. The success of the new estimators, even at low signal/noise values, is notable because the shapes of the simulated distributions deviate strongly under those conditions.
Comparison to HMM without incorporation of photon counts
To compare our extended version of the HMM analysis with the standard approach (i.e., without explicit incorporation of the camera noise), we performed a simulation of a Markov model using four states. Details are given in the Supporting Materials and Methods and Table S1. An HMM analysis was performed, once with the width as a single free parameter and one in which the inherent noise of the FRET state due to shot noise and camera noise was calculated for each data point. After the learning algorithm determined the hidden Markov parameters, each frame of the simulated data was assigned with the best-fitting state by the Viterbi path, with the help of the learned parameters. A comparison of the two analyses is given in Table S1. Incorporation of the camera noise into the analysis slightly improves the already high accuracy, dropping the fraction of frames that are incorrectly assigned from 4 to 3%. Both approaches find the values of the four FRET states with high accuracy. The widths of the FRET states returned by the two HMM analyses are not comparable because the standard HMM is fitting the camera noise (the major contribution to the noise in this simulation), whereas the inherent noise of the FRET states is reliably returned with the new HMM model. Interestingly, there is a difference in the dwell times returned from the two different approaches. By incorporating the camera noise directly in the analysis, the probability of noise being misinterpreted as a transition decreases, yielding more accurate rates.
SpFRET measurements of TBP-DNA in the absence and presence of NC2
Having verified the reliability of our HMM analysis on simulated data, we now apply it to real data. Fig. 2 shows results from spFRET experiments on TBP-DNA complexes in the absence and presence of NC2. As observed in previous experiments (23), spFRET measurements typically showed a constant (“steady state”) FRET efficiency with EPR ∼0.4 of the TBP-DNA complex before addition of NC2, demonstrating the stable binding of TBP to the TATA box (Fig. 2 c) for the 70-bp AdML promoter DNA. After addition of NC2, the complex becomes dynamic, and fluctuations between distinct FRET states are observed. A typical FRET trace is shown in Fig. 2 d for the 70-bp AdML promoter DNA. A histogram of the FRET efficiency for the individual frames of the 70-bp AdML sample (frame-wise histogram) is shown in Fig. 2 e before (red) and after (blue) the addition of NC2.
One of the advantages of the modified HMM that we present here is its ability to account for the shot noise within the spFRET data. Fig. S2 shows histograms of the total intensity (in photons) per frame for the different measurements. The measured total intensities varied by more than a factor of four, from 50 photons per frame to more than 200 photons per frame. This broad distribution of intensities indicates the heterogeneities of single-molecule experiments and how important it is to correct for shot noise when performing a global analysis. This can be circumvented by using an intensity window for selection of traces to be analyzed further. However, variations in the total intensity can also happen within an spFRET trace, for example, when the donor molecule is partially quenched. Because the proximity ratio is calculated from the ratio of intensity in the acceptor channel to the total intensity within a frame, donor quenching will not strongly influence the calculated proximity ratio, but the uncertainty will be increased. Such an example is shown in Fig. S3. Because the uncertainty due to shot noise is determined frame by frame, the modified HMM is able to assign a constant low-FRET state during transient quenching of the donor, although the FRET signal strongly fluctuates. Whether photophysics of the acceptor is leading to apparent fluctuations in FRET efficiency can be monitored using millisecond alternating-laser excitation (62). Because acceptor blinking was not typically observed for these constructs (23), we forwent alternating-laser excitation measurements and opted for high data collection rates to improve the kinetics analysis.
To test how well the noise characterization of the camera explains our data, we have plotted the mean and variance of the donor and acceptor signals in Fig. S4 for TBP-DNA (AdML promoter 70-bp DNA) in the absence and presence of NC2. The theoretical expectations, assuming Poissonian statistics for photon counting corrected for the additional EMCCD noise, are plotted as lines. In the absence of NC2, the experimental data are well described by the theoretical expression, indicating that the conformation of the TBP-DNA complexes with respect to the given labeling positions is static, and the shot-noise calculations of the measurement uncertainty are appropriate. In contrast, the individual traces demonstrate higher variances than expected from the shot noise alone because of the dynamics in the presence of NC2.
Dynamics of the FRET-labeled TBP-NC2 complex, two-state model
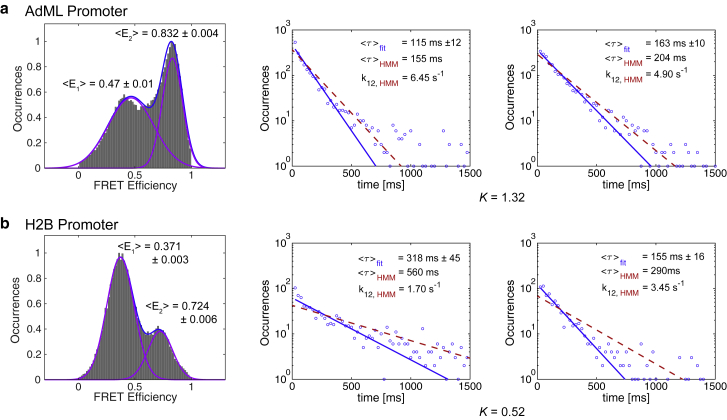
Histograms of the frame-wise spFRET efficiency for the measured complexes are shown in Fig. 2 e. In the presence of NC2 (shown in blue), two populations are observable with FRET efficiencies of ∼0.40 and ∼0.80. The subpopulation with a FRET efficiency of 0.40 is similar in conformation to TBP-DNA in the absence of NC2, whereas the higher FRET state is attributed to a conformational change of the DNA in the TBP-NC2-DNA complex (23). Fitting the data using a two-state HMM model, we obtained FRET values and equilibrium coefficients, K, of 0.39, 0.78, and K40/80 = 1.32 for the 70-bp DNA construct and 0.36, 0.75, and K40/80 = 1.21 for the 110-bp DNA construct. The results are in excellent agreement with each other, indicating that the dynamics are independent of the length of the DNA and do not depend on which end of the DNA is anchored to the surface.
The FRET histogram for the H2B-J promoter upstream-labeled construct after addition of NC2 shows clearly different dynamics. The same two dominant FRET subpopulations are observed, but the original TBP-DNA conformation is more stable and populated much more often. The results of the two-state HMM yielded FRET values and equilibrium coefficients of 0.36, 0.71, and K40/70 = 0.52 for the upstream- labeled H2B-J promoter. Interestingly, measurements with the downstream-labeled H2B-J promoter also show fluctuations in the FRET signal from ∼0.4 to higher FRET values. The HMM analysis yielded 0.33, 0.68, and K40/70 = 0.40. The fact that FRET increases upon addition of NC2 for both the upstream- and downstream-labeled constructs confirms that the observed dynamics are coming from conformational changes of the DNA and not from motion of the TBP-NC2 complex along the DNA.
For a traditional spFRET analysis, the two FRET states would be fitted with Gaussian distributions, the FRET values would be given by the peak values, and the equilibrium coefficient would be given by the respective areas. For the AdML promoter constructs, these lead to FRET values of 0.47, 0.83, and an equilibrium coefficient of K40/80 = 0.71 for the 70-bp DNA (Fig. 4 a) and 0.43, 0.80, and K40/80 = 0.71 for the 110-bp DNA. The Gaussian fits are consistent between the two AdML DNAs again verifying that the DNAs have similar dynamics and that the experiments are reproducible. The FRET values extracted from the peak of the Gaussian distributions approximately agree with the HMM data, but the equilibrium coefficients are significantly different. This is due to the width of the Gaussian distributions in which a significant population of the 0.40 FRET state overlaps with the 0.80 FRET state. Because the HMM uses not only the FRET values but also the time information in the spFRET traces, it is capable of distinguishing overlapping populations. The difficulty in this case is that the two-state model is an oversimplification of the actual dynamics. This leads to an increase in the width of the 0.40 FRET population and hence incorrect results when fitting with two Gaussians.
Figure 4.
Two-well analysis of the TBP-DNA-NC2 dynamics. The results of a two-well analysis of the TBP-DNA-NC2 data are shown for the (a) 70-bp upstream-labeled AdML promoter DNA (DNA 1) and (b) the 80-bp upstream-labeled H2B promoter DNA (DNA 3). Left panels: Frame-wise spFRET histograms are shown for the respective measurements. Two dominant populations are observed, and the equilibrium coefficient can be estimated by fitting to the two populations to Gaussian distributions. Middle and right panels: from the two-state HMM analysis, the duration of each state before undergoing a transition was calculated from the Viterbi path determined for each trace from the parameters of the global HMM. The survival probability was fit to an exponential function (solid line, red). In addition, the rates from the HMM are shown (dashed line, blue). The given equilibrium coefficients are determined from the ratio of the rates determined from the HMM analysis. To see this figure in color, go online.
Interestingly, for the H2B-J promoter DNAs in which the 0.40 FRET state is more prevalent, the results from Gaussian fits are more comparable with the HMM analysis. The FRET values and equilibrium coefficients are 0.39, 0.73, and K40/70 = 0.35 (Fig. 4 b) and 0.37, 0.73, and K40/70 = 0.37 for the upstream and downstream labels, respectively. However, the broader population is still overestimated by the Gaussian analysis. This indicates the advantages of using an HMM analysis even for a simple evaluation.
Determination of the number of states
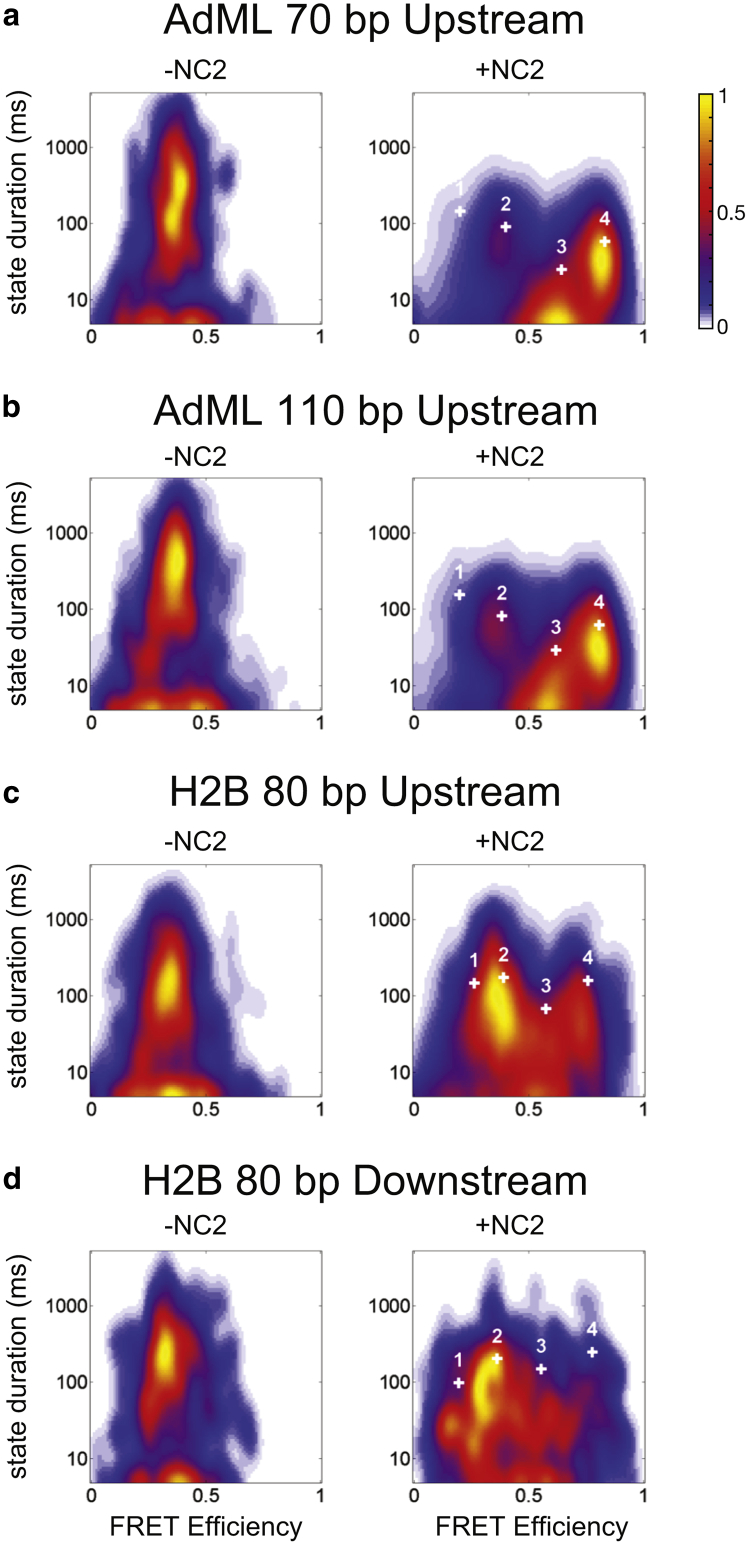
Depending on the quality of the data and in how much detail one wishes to analyze the data, HMM can be used to investigate how many FRET states are present. Ideally, it would be convenient when the HMM analysis would directly yield how many significantly different FRET populations are present in the data. Unfortunately, the log likelihood, the Bayesian information parameter, and reduced χ2 calculations of the Viterbi path were insufficient in unambiguously determining the optimal number of states necessary to describe the data (see Supporting Materials and Methods; Fig. S5). One approach we found that worked well was to perform a cluster analysis of the molecule-by-molecule HMM results of the data in which each trace was optimized independently with up to 10 available FRET states. The number of 10 states was sufficient to allocate all rarely appearing intermediate states in each molecule. The unassigned states were not occupied and did not disturb the analysis. Similar states extracted because of overfitting will merge into a single state when plotting the data in histograms. The results are summarized as two-dimensional (2D) histograms according to their mean FRET efficiencies and average duration within the conformation in Fig. 5 for all four DNA constructs in the absence and presence of NC2. Each transition is presented by a Gaussian with a width of ∼1% of the image size. Four states are clearly observable for the AdML promoter, whereas the presence of additional minor states is observable for the H2B promoter. In addition to the HMM analysis, we visually inspected the individual spFRET traces to verify that the results from the HMM correspond to distinctly observable FRET states in a single trace. The advantage of the molecule-wise HMM analysis approach is that the number of states does not have to be known in advance. However, when the number of states is known, a global analysis also worked well.
Figure 5.
Molecule-wise HMM analysis. Displayed are 2D histograms of the FRET efficiency of the states derived by the molecule-wise HMMs versus the length of time the complex resided in that state before transitioning to another state or photobleaching. The plots are shown for TBP bound to a (a) 70-bp upstream-labeled DNA containing the AdML TATA box (DNA 1), (b) 110-bp upstream-labeled DNA containing the AdML TATA box (DNA 2), (c) an 80-bp upstream-labeled DNA containing the H2B TATA box (DNA 3), and (d) an 80-bp downstream-labeled DNA containing the H2B TATA box (DNA 4). Results for TBP-DNA in the absence of NC2 are shown in the left panels, and results for TBP-DNA in the presence of NC2 are shown in the right panels. The white plus signs show the FRET efficiencies returned from the global four-well HMM analysis. The histograms are normalized to the maximal number of transitions. The color scale is shown in the upper right corner.
In the absence of NC2, one dominant population at EPR ∼0.40 is observed. The average duration of the molecule in this configuration is given by photobleaching. A small amount of dynamics is observed between FRET states at 20 and 40% FRET efficiency, indicating that a minority of complexes exhibits dynamics before the addition of NC2. Measurements with the H2B-J promoter DNA in the absence of NC2 revealed a higher fraction of dynamic complexes than for the AdML promoter containing DNA (Fig. 5).
Upon the addition of NC2, four subpopulations are observable for complexes containing the AdML promoter site, having FRET efficiencies of ∼0.20, ∼0.40, ∼0.60, and ∼0.80% (Fig. 5). Visual inspection of the FRET traces of individual complexes often showed transitions between all four of these FRET states. When performing a global HMM analysis with the AdML-promoter complexes, four states were sufficient to completely describe the dynamics we measured. The three-state model does not find the FRET state at EFRET = 0.2, which is clearly visible in the spFRET traces, and models containing a higher number of states always have the four major states at ∼0.20, 0.40, 0.64, and 0.83.
Analysis of the H2B-J promoter labeled upstream showed that the 0.40 FRET efficiency state is strongly populated, with fluctuations to a state with an efficiency value of 0.75 FRET. The 2D HMM histogram also shows transitions to other states with FRET values of 0.20, 0.50, 0.65, and 0.90. Hence, at least six FRET subpopulations are present for the H2B-J promoter. This is also confirmed by visual inspection of the individual traces. Analysis of the downstream-labeled H2B-J promoter DNA revealed at least seven states. As the number of states differs between the upstream and downstream label, FRET subpopulations are distinguishable with the downstream labeled that cannot be distinguished with the upstream label. Hence, an accurate mapping of the FRET states between the upstream and downstream label is currently not possible.
Dynamics of the FRET-labeled TBP-NC2 complex, four-state model
For a more detailed analysis of the dynamics of the TBP-DNA-NC2 complex, we analyzed the AdML promoter data using a four-state HMM. A four-state model is justified because all four states are directly observed in individual spFRET traces. Fig. 6 a shows a FRET trajectory and the corresponding optimized Viterbi path for a single TBP-NC2 complex on the 70-bp DNA promoter AdML. In the first second of this time trajectory, the FRET efficiency was high (EFRET = 0.83), with short excursions to EFRET = 0.64 and EFRET = 0.40. After 1.2 s, the TBP-NC2-DNA complex switched to a low FRET conformation (EFRET = 0.20) for ∼1 s before returning to the 0.40 FRET efficiency conformation. At the end of the trace, the complex oscillates between EFRET 0.40 and higher FRET states. From the HMM analysis, we do not only get the values of the different FRET states but also the intrinsic width of the FRET state beyond shot-noise broadening (Table S3). For the two AdML promoters, the widths determined for the different FRET states are very similar, validating the reproducibility of the analysis. An inherent broadening of the FRET distribution is always seen in single-molecule FRET experiments and most likely corresponds to slight heterogeneities in the structure and dynamics of the linkers used to attach the fluorophores to the protein. The FRET states of EFRET = 0.40, 0.64, and 0.83 have widths of 0.07, 0.07, and 0.04 FRET efficiency values corresponding to structural heterogeneities of 3, 3, and 2 Å, respectively. These widths are relatively small corresponding to well-defined conformations. The inherent width of the EFRET = 0.20 state, though similar in value (±0.08), indicates a larger conformational heterogeneity of ±5–8 Å because of the lower sensitivity of FRET at the extremities due to the R6 dependence of the FRET efficiency.
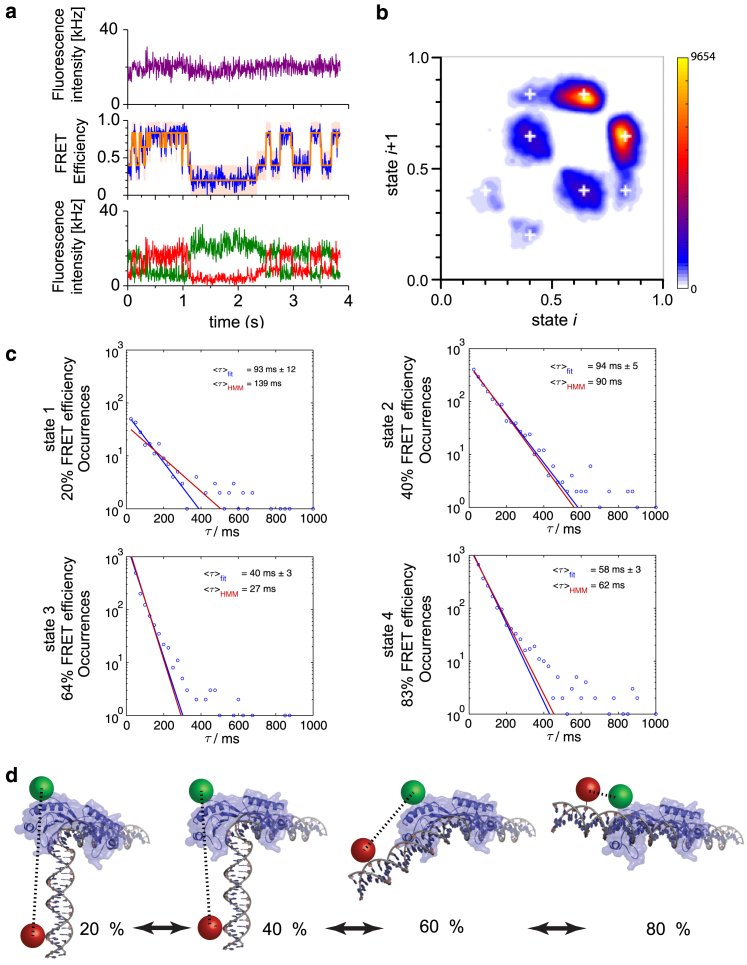
Figure 6.
Four-well analysis of the TBP-DNA-NC2 dynamics. (a) A single-molecule FRET trajectory from a TBP-DNA-NC2 complex in which the 70-bp upstream-labeled DNA contains the AdML TATA box is plotted showing four different conformations with FRET efficiencies of 0.20, 0.40, 0.64, and 0.83 (purple: total intensity; green: donor intensity; red: acceptor intensity; and blue: FRET efficiency). The optimized Viterbi path derived using parameters from the global four-state HMM is overlaid in orange. (b) The TDP from the HMM analysis of the 70-bp AdML DNA is shown. The number of observed transitions is represented via the color code, with rare transitions shown in blue and more frequent transitions shown in yellow. The color scale bar is shown on the right with a maximal number of transitions at 9654. The FRET states returned from a global four-well HMM analysis are shown as white plus signs. Fast fluctuations between the high FRET state at ∼0.83 and a short intermediate state at ∼0.64 are observed. Transitions from 0.40 to 0.64 also occur frequently, whereas transitions between 0.40 and 0.83 occur over the short-lived intermediate FRET state with an efficiency of 0.64. The FRET state at 0.20 is connected only with the 0.40 FRET state. (c) The survival probabilities (circles), results from the global HMM values (red line) from an exponential fit to the data (blue line) are shown for the four FRET conformations. The survival probabilities can be reasonably described by a single exponential. (d) A schematic of the connections between the different conformations observed in the spFRET experiments on the AdML promoter complexes is shown. From the TDP, it is clear that the four different conformations are connected by a linear four-well model. The 0.40 FRET state is the initial, bent structure of TBP-DNA. The 0.60 and 0.80 FRET states represent conformational changes in the DNA in the TBP-DNA-NC2 complex, whereas the 0.20 FRET state represents motion of TBP-NC2 along the DNA. NC2 is not displayed for clarity.
In addition to the average FRET values and intrinsic width of the FRET states, the HMM analysis also provides the transition rates between the different states. From the optimized Viterbi path for each spFRET trace, we can extract the lifetime distribution for each state (Fig. 6 c). The 0.83 and 0.64 FRET efficiency states have short average lifetimes of 82 and 34 ms, respectively, whereas the lower FRET efficiency states are more stable with lifetimes of 112 and 175 ms for EFRET = 0.40 and EFRET = 0.20, respectively. With the exception of the intermediate EFRET = 0.64 state, all conformations can be described reasonably well with a monoexponential lifetime. For the EFRET = 0.64 state, at least two components are visible. This may be due to a structural change in which a transition to the high FRET state becomes faster. This would explain the change in the dynamics observed between the beginning and end of the spFRET trace in Fig. 6 a. However, this is purely speculative. For the HMM analysis, exponential rates are assumed, but the model can explain the current data reasonably well even though the rates for the EFRET = 0.64 state are nonexponential.
To look into the details of the kinetics, we generate a FRET transition density plot (TDP). To do this, we took the results from the global HMM analysis and calculated the optimized Viterbi path for each spFRET trace. From the Viterbi path, we determined the average FRET value for each transition and the survival probability of the different states (Fig. 6, b and c). Each transition was plotted as a Gaussian with a width of ∼1% in FRET efficiency. In the TDP, only 8 of the theoretically possible 12 state transitions are populated. The most frequent transitions are between the 0.64 and 0.83 FRET states and between the 0.40 and 0.64 FRET states. Transitions to the 0.20 FRET efficiency state are rare and occur exclusively through the 0.40 FRET state. A few direct transitions are observed between the 0.40 and 0.83 FRET states. However, because of the fast fluctuations between the E = 0.64 and E = 0.83 FRET states, it is possible that a two-step transition between E = 0.40 and E = 0.64 and then on to the E = 0.83 FRET efficiency state occurs, which is detected as only a single step in the HMM analysis. From the rates, we can estimate how often such a transition would be missed. Assuming that a minimal dwell time of 5 ms (one frame from the data) is necessary for the HMM to detect the intermediate state, ∼18% of the transitions from E = 0.40 to 0.064 to 0.83 would be detected as a straight transition to E = 0.83 (Fig. S6). This corresponds well to the relative amplitude of what is observed in the TDP in Fig. 6 b. When we set the transition rates between E = 0.40 and E = 0.83 to zero and reanalyze the data, we did not detect a significant difference in the results of the HMM (Table S5). Hence, the HMM detects a direct transition between the 0.40 and 0.83 FRET states although the transition went through the 0.64 FRET state. Thus, the TDP indicates that the dynamics can be explained by a linear four-well model (Fig. 6 d). The dynamics observed with the 70-bp DNA and 110-bp DNA strands containing the AdML-promoter TATA box are identical within experimental error (Fig. S7). This again suggests that neither the length of the DNA nor the attachment point of the DNA to the surface influences the dynamics.
In contrast to the AdML promoter DNA, the H2B-J promoter DNAs showed more complex dynamics. For the H2B-J promoter labeled upstream, at least six states are observable, and at least seven states are observable for the downstream-labeled construct (Fig. 5). One beautiful aspect of the HMM approach is that one has a complete description of all the states and all the transitions. Hence, for comparison, more complex models can be reduced using either an HMM with fewer states or by clustering results together. To quantify the difference between the AdML and H2B-J promoters, we approximated the H2B-J promoter with a global four-state model. The optimized Vitrebi paths for the global HMM were calculated for the individual traces, and the TDP was generated by calculating the average FRET efficiency for each state and plotting it as a Gaussian with a width of ∼1%. The transition matrix for the HMM analysis is shown in Fig. S7. As for the AdML promoter, transitions to the low FRET state occur only through the 0.39 FRET subpopulation. From the 0.39 FRET state, transitions to all other states are observable.
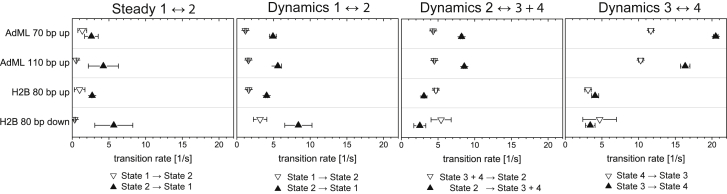
For analysis purposes, we consider the following transitions: the transition between the low FRET state and initial FRET conformation (k1 ↔ 2), the transition between the initial FRET conformation and the higher FRET states (k2 ↔ 3 + 4), and the transition between the intermediate and high FRET states (k3 ↔ 4). The forward and backward transition rates for the transitions defined above are summarized in Fig. 7 for all four complexes investigated. In the absence of NC2 (left panel), only very few transitions between the ∼0.40 and ∼0.20 FRET efficiency states (k1 ↔ 2) were observed. The rates were similar to what was observed in the presence of NC2. For the upstream labels, the transition rates k2 → 1 exhibited promoter-independent values of ∼1.6 s−1. The backward transition rates k1 → 2 were 5–7 s−1 for the constructs labeled upstream. The transition rate from the low FRET state to the 0.40 FRET state was somewhat faster in the downstream-labeled construct, which may indicate that we are sensitive to slightly different motions with this construct. The dynamics of the conformational changes in the DNA are given by the fluctuations between the initial FRET state (bent DNA conformation) and the higher FRET states (highly bent conformations), k2 ↔ 3 + 4. Interestingly, the rate of unbending was independent of the promoter site (∼4.5 s−1), whereas the bending rate was a factor of 2.7 faster for the AdML promoter as for the H2B-J promoter (∼8.4 vs. 3.1 s−1). Hence, the initial TBP-DNA conformation is more stable for the H2B-J promoter, and the AdML promoter exhibits more pronounced dynamics. Also, the transition rates between different highly bent conformations were faster for the AdML promoter DNA. k3 → 4 and k4 → 3 were ∼18.5 and 11 s−1, respectively, for the AdML promoter DNA and ∼4 and ∼4 s−1 for the H2B-J promoter DNA. The results of the six-state HMM model of upstream-labeled H2B-J promoter showed slower transition rates between the various states in comparison to the k3 ↔ 4 values for the AdML promoter DNA above. This indicates that the slower dynamics of the H2B-J promoter is an attribute of the promoter and not the analysis.
Figure 7.
Comparison of the kinetics for the different constructs. Resulting rate constants of the four different sample preparations are shown. (k1 ↔ 2) The rate constants for transitions to a possible alternative TBP-binding site (EFRET = 0.20) in the absence (left panel) and presence (middle left panel) of NC2 are shown. The transition rate from EFRET = 0.40 to 0.20 is between 2 and 8 s−1 (arrow up) and the return the rate lies between 0.5 and 3.5 s−1 (arrow down). The affinity to this binding site appears to be neither dependent on the promoter nor influenced by the addition of NC2. (k2 ↔ 3 + 4) The rate for transitions between the EFRET = 0.40 and higher FRET states are shown (middle right panel). The transition rate from the bent conformation to the higher FRET conformations (arrow up) is a factor of ~3 higher for the AdML promoter than for the H2B promoter, whereas the relaxation rate for returning to the bent 40% FRET conformation (arrow down) was similar for all four samples. (k3 ↔ 4) The transition rates between the intermediate and high FRET states are shown. The transition rates from the intermediate state to high FRET conformation (arrow up) and back (arrow down) were faster for the AdML promoter than for the H2B promoter. The error bars are the standard error of the mean (SEM) determined empirically by splitting the data set into four equal subsets (two subsets in the case of transitions in the absence of NC2 due to limited statistics) and calculating the mean and the standard error of the mean (SEM) of the different subsets.
Discussion
We have presented a modification of the HMM approach for the analysis of spFRET data. By incorporating the photon-counting statistics into the analysis, the noise factor in the HMM analysis is reduced to the actual noise of the biological system. Thus, a global analysis is possible even when the total intensity coming from the single-molecule traces and hence the shot-noise contribution to the spFRET traces differ by severalfold (Fig. S2). In many cases, the shot noise is the dominant component to the noise of the measurement, and an HMM can be used without an additional factor to account for the noise. The number of fitted parameters is then reduced, making the analysis more robust. In addition, the shot noise is calculated on a frame-by-frame basis, making it possible to account for frames in which partial quenching of the donor molecule is observed via the HMM analysis (Fig. S3). We verified the performance of the HMM analysis using simulations. The algorithm was found to be robust over a large range of count rates and noise contributions.
We utilized the newly adapted HMM approach to analyze the dynamics of eukaryotic TBP-DNA complexes in the presence and absence of the TF NC2. From the frame-wise spFRET histograms, at least two populations were clearly visible (Fig. 2 e). However, a Gaussian fit to the spFRET histograms gave results that deviated significantly from the HMM analysis, suggesting that additional states are present. By using a cluster analysis of the molecule-by-molecule HMM analysis along with visual inspection of the different FRET trajectories, we could distinguish up to four different FRET states for the AdML promoter at FRET efficiencies of {0.20, 0.40, 0.64, 0.83}, and more states were detectable for the H2B-J promoter. For the sake of comparison, we analyzed both promoters using a linear four-well model (Fig. 6 d).
The ∼0.40 FRET efficiency state is observed as a static state in the absence of NC2 and is also always observed in the dynamic traces after the addition of NC2 for all promoters. This suggests that the 0.40 FRET efficiency state corresponds to a conformation of the TBP-NC2-DNA complex similar to that of the TBP-DNA complex, which has a strongly bent DNA conformation (Fig. 2 a). The low FRET state (∼0.20) is observable for both upstream-labeled promoters in the absence and presence of NC2. According to the crystal structure of the TBP-NC2-DNA construct and the positions of the labels, it is not possible to explain the 0.20 FRET efficiency with only a conformational change in the DNA (23). Furthermore, this state is only accessible through the 0.40 FRET state. This would suggest that the TBP-NC2 complex may slide along the DNA. The 0.20 FRET efficiency state is also observed as a minor conformation for static traces measured in the absence of NC2 (23). Hence, the low FRET state most likely represents an alternative binding position of the TBP and TBP-NC2 complex on the DNA. Assuming that the conformation of the TBP-NC2-DNA complex is similar for the 0.40 and 0.20 FRET efficiency states, the 0.20 FRET efficiency state would correspond to a shift of the TBP-NC2 duplex by ∼4 bp. Transitions between the 0.20 and 0.40 FRET states are also observed in a small fraction of complexes in the absence of NC2 and were observed during the binding of TBP to the DNA (60). The higher FRET states (0.64 and 0.83 FRET values for the AdML promoter) are attributed to conformation changes in the DNA. This conclusion is supported by the experiments with the H2B-J promoter labeled in the upstream and downstream locations. Both constructs show transitions from the initial FRET conformation in the absence of NC2 (between 0.35 and 0.40) to higher FRET states. If the TBP-NC2 complex were to move along the DNA without a conformational change of the DNA, one would expect that when the signal of the upstream FRET pair increases, the downstream FRET signal must decrease and vice versa. Even when accounting for the three-dimensional motion of TBP along the minor groove of the DNA, it is not possible to explain an increase in FRET efficiency for both upstream and downstream labels by complex motion alone. Hence, we conclude that the DNA is changing conformation in the higher FRET states. Most likely, this is due to the interactions between NC2 and TBP decreasing the strength of the TBP-DNA interactions, allowing the highly kinked DNA to relax. As we see two intermediates for the AdML promoter, this could represent the removal of one or both of the “phenylalanine stirrups” that bind to the minor grove and kink the DNA. Theoretically, with a global analysis of both upstream- and downstream-labeled constructs, it should be possible to gain insight into the conformational changes occurring in the TBP-DNA complex. However, because of the complex nature of the dynamics of the H2B-J-promoter site and the different number of FRET states observed for the two constructs, a mapping of the FRET states between the two constructs was not possible.
The results for four-state HMM of the two AdML constructs were very similar, indicating that neither the length of the DNA nor the location of the biotin used to immobilize the complex on the surface influences the FRET values and dynamics. In addition, these experiments provide a measure of the reproducibility and accuracy of the HMM analysis. The TDP plots for the AdML promoter (Fig. S7) show that the four states are connected via a linear four-well model (Fig. 6 d). Hence, only adjacent states can interconvert. The low FRET state can only exchange with the initial bent conformation (0.40 FRET state). From the initial conformation, the complex can also fluctuate to the intermediate FRET state (0.64) in which the DNA is more stretched. From there, it can either return to the initial conformation or undergo quick fluctuations between the two high-FRET conformations (0.64 and 0.83). The kinetics of the fluctuations between the 0.64 and 0.83 FRET values in the AdML promoter determined from the Viterbi paths is ∼18 s−1 for k3 → 4 and k4 → 3 = ∼11 s−1 (Fig. 7), and a similar ratio is obtained directly from the HMM (Table S5). The TDP for the upstream-labeled H2B-J promoter is similar to what we determined for the AdML promoter, with the exception that transitions are directly observed from the initial FRET conformation (0.39) to the highest FRET state (0.76) (Fig. S7). That the TDP pattern depends on the DNA sequence used supports our interpretation of the higher FRET states as different DNA conformations.
A comparison of the dynamics for two different promoter sites yields interesting molecular insights into the TBP-NC2-DNA complex. The quantitative difference between the two promoter sites comes from the difference in transition rates from the bent conformation to the stretched conformation, k2 → 3 + 4. However, the transition rates from the stretched conformation to the bent conformation, k2 ← 3 + 4, are the same for both promoters. Hence, the promoter has a direct influence on the observed kinetics, with the bent conformation being more stable by a factor of three for the H2B-J promoter.
This HMM-based FRET analysis can be expanded further to freely diffusing proteins, when surface attachment is not suitable (28, 37, 63). For example, the membrane protein FoF1-ATP synthase was reconstituted into lipid vesicles of 100–150 nm diameter, and a pH gradient was established across the membrane for the catalytic synthesis of ATP (64). Monitoring the rotary subunit movement in single FoF1-ATP synthase was achieved in real time by single-molecule FRET using confocal excitation schemes (65, 66, 67). In this case, the overall fluorescence intensity varies strongly over millisecond time intervals within the time trajectory of each single protein because of the arbitrary diffusion pathways through the Gaussian-shaped excitation and detection volume. In addition, using fluorescent proteins as genetically fused labels to the enzyme results in lower photon count rates for FRET analyses of FoF1-ATP synthase (28, 68). Identifying conformations and dwell times in these FRET trajectories by manual assignment is a time-consuming process and remains questionable, especially for those parts of the photon bursts with low-fluorescence sum intensity. Hence, applying our weighted HMM approach using the counting statistics for each data point in the photon burst provides an unbiased and robust methodology for the analysis of conformational dynamics of freely diffusing biomolecules, even for systems in which little a priori information about the likely structures or conformations and the reaction pathways is known.
One additional possibility with our expanded HMM approach is to include an additional variance for each FRET state that represents the residual broadening of the FRET efficiency beyond the shot-noise limit. As shown in Fig. S4, dynamics lead to a higher variance in the FRET signal beyond what is expected from photon statistics. This is also true when dynamics occur within a FRET state. The expanded analysis we describe allows one to explicitly account for the photon statistics, and any additional broadening can then be assigned to heterogeneities within the different states, yielding how well defined or dynamic a particular conformation is. For TBP/NC2 bound to the AdML promoter containing DNA studied here, the FRET states of 0.40, 0.64, and 0.83 showed well-defined conformations, whereas the FRET state at 0.20 showed more intrinsic heterogeneity.
Conclusions
The number of states and the corresponding transition rate constants for TBP-DNA in the presence and absence of NC2 were analyzed with an extended HMM approach. For the HMM analysis, it was necessary to determine the appropriate accuracy of the fluorescence intensities measured using EMCCD cameras. The developed HMM method was capable of acting directly on the time trajectory of the FRET efficiency without being affected by the variations in total fluorescence intensities from complex to complex.
Experiments on DNA with the same promoter and labeled at different positions confirmed that the higher FRET states observed are due to conformational changes in the DNA and not the motion of the complex along the DNA. Experiments with the AdML promoter with DNA of different lengths and attachment points to the surface verified that the observed dynamics do not depend on the length of the DNA construct nor on which end is attached to the surface.
Using the extended HMM approach, we could determine that the AdML promoter has four distinct conformations and extract the transition matrix for the different states. Transitions to the low FRET state can only be reached through the bent FRET conformation. The dynamics of the H2B-J promoter are more complex but could be simplified into a four-state model for comparison with the AdML promoter. The difference in the dynamics between these two promoter sites is due to the higher stability of the bent conformation of the DNA for the H2B-J promoter. Hence, the dynamics are qualitatively similar for the different promoter sites, but the stronger promoter site, AdML, shows faster dynamics.
Author Contributions
N.Z. developed the analysis method and performed the simulations. P.S. performed the spFRET measurements. Both N.Z. and P.S. analyzed of the data. M.M. provided the protein. M.B. and D.C.L. oversaw the project. D.C.L. and N.Z. wrote the manuscript with contributions from all authors.
Acknowledgments
We thank Christine Goebel for excellent technical assistance and Dr. Sushi Madhira and Dr. Evelyn Plötz for helpful and critical discussions regarding HMM and TBP. We also thank Dr. Evelyn Plötz and Simon Wanninger for assistance with the figures and Dr. Richard Börner for constructive comments on the manuscript.
We gratefully acknowledge the financial support by the Deutsche Forschungsgemeinschaft to D.C.L. and M.M. (SFB646; projects A2 and B11) and the Ludwig-Maximilians-Universität through the Center for NanoScience and the BioImaging Network. N.Z. was supported by the Deutsche Forschungsgemeinschaft (grant BO1891/10-1 to M.B.).
Editor: Keir Neuman.
Footnotes
Supporting Materials and Methods, seven figures, and five tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)31279-7.
Supporting Material
References
- 1.Sims R.J., III, Mandal S.S., Reinberg D. Recent highlights of RNA-polymerase-II-mediated transcription. Curr. Opin. Cell Biol. 2004;16:263–271. doi: 10.1016/j.ceb.2004.04.004. [DOI] [PubMed] [Google Scholar]
- 2.Burley S.K. The TATA box binding protein. Curr. Opin. Struct. Biol. 1996;6:69–75. doi: 10.1016/s0959-440x(96)80097-2. [DOI] [PubMed] [Google Scholar]
- 3.Horikoshi M., Bertuccioli C., Roeder R.G. Transcription factor TFIID induces DNA bending upon binding to the TATA element. Proc. Natl. Acad. Sci. USA. 1992;89:1060–1064. doi: 10.1073/pnas.89.3.1060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nikolov D.B., Chen H., Burley S.K. Crystal structure of a human TATA box-binding protein/TATA element complex. Proc. Natl. Acad. Sci. USA. 1996;93:4862–4867. doi: 10.1073/pnas.93.10.4862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Werner M.H., Gronenborn A.M., Clore G.M. Intercalation, DNA kinking, and the control of transcription. Science. 1996;271:778–784. doi: 10.1126/science.271.5250.778. [DOI] [PubMed] [Google Scholar]
- 6.Pardo L., Campillo M., Weinstein H. Binding mechanisms of TATA box-binding proteins: DNA kinking is stabilized by specific hydrogen bonds. Biophys. J. 2000;78:1988–1996. doi: 10.1016/S0006-3495(00)76746-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kim J.L., Nikolov D.B., Burley S.K. Co-crystal structure of TBP recognizing the minor groove of a TATA element. Nature. 1993;365:520–527. doi: 10.1038/365520a0. [DOI] [PubMed] [Google Scholar]
- 8.Kim J.L., Burley S.K. 1.9 A resolution refined structure of TBP recognizing the minor groove of TATAAAAG. Nat. Struct. Biol. 1994;1:638–653. doi: 10.1038/nsb0994-638. [DOI] [PubMed] [Google Scholar]
- 9.Kim Y., Geiger J.H., Sigler P.B. Crystal structure of a yeast TBP/TATA-box complex. Nature. 1993;365:512–520. doi: 10.1038/365512a0. [DOI] [PubMed] [Google Scholar]
- 10.Alberts B.J.A., Lewis J., Walter P. Fourth Edition. Garland Pub.; New York: 2002. Molecular Biology of the Cell. [Google Scholar]
- 11.Nikolov D.B., Burley S.K. RNA polymerase II transcription initiation: a structural view. Proc. Natl. Acad. Sci. USA. 1997;94:15–22. doi: 10.1073/pnas.94.1.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Roeder R.G. The role of general initiation factors in transcription by RNA polymerase II. Trends Biochem. Sci. 1996;21:327–335. [PubMed] [Google Scholar]
- 13.Kaiser K., Meisterernst M. The human general co-factors. Trends Biochem. Sci. 1996;21:342–345. [PubMed] [Google Scholar]
- 14.Roeder R.G. Transcriptional regulation and the role of diverse coactivators in animal cells. FEBS Lett. 2005;579:909–915. doi: 10.1016/j.febslet.2004.12.007. [DOI] [PubMed] [Google Scholar]
- 15.Meisterernst M., Roeder R.G. Family of proteins that interact with TFIID and regulate promoter activity. Cell. 1991;67:557–567. doi: 10.1016/0092-8674(91)90530-c. [DOI] [PubMed] [Google Scholar]
- 16.Iratni R., Yan Y.T., Shen M.M. Inhibition of excess nodal signaling during mouse gastrulation by the transcriptional corepressor DRAP1. Science. 2002;298:1996–1999. doi: 10.1126/science.1073405. [DOI] [PubMed] [Google Scholar]
- 17.Prelich G., Winston F. Mutations that suppress the deletion of an upstream activating sequence in yeast: involvement of a protein kinase and histone H3 in repressing transcription in vivo. Genetics. 1993;135:665–676. doi: 10.1093/genetics/135.3.665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gadbois E.L., Chao D.M., Young R.A. Functional antagonism between RNA polymerase II holoenzyme and global negative regulator NC2 in vivo. Proc. Natl. Acad. Sci. USA. 1997;94:3145–3150. doi: 10.1073/pnas.94.7.3145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Xie J., Collart M., Meisterernst M. A single point mutation in TFIIA suppresses NC2 requirement in vivo. EMBO J. 2000;19:672–682. doi: 10.1093/emboj/19.4.672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chitikila C., Huisinga K.L., Pugh B.F. Interplay of TBP inhibitors in global transcriptional control. Mol. Cell. 2002;10:871–882. doi: 10.1016/s1097-2765(02)00683-4. [DOI] [PubMed] [Google Scholar]
- 21.Geisberg J.V., Holstege F.C., Struhl K. Yeast NC2 associates with the RNA polymerase II preinitiation complex and selectively affects transcription in vivo. Mol. Cell. Biol. 2001;21:2736–2742. doi: 10.1128/MCB.21.8.2736-2742.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Klejman M.P., Pereira L.A., Timmers H.T. NC2alpha interacts with BTAF1 and stimulates its ATP-dependent association with TATA-binding protein. Mol. Cell. Biol. 2004;24:10072–10082. doi: 10.1128/MCB.24.22.10072-10082.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Schluesche P., Stelzer G., Meisterernst M. NC2 mobilizes TBP on core promoter TATA boxes. Nat. Struct. Mol. Biol. 2007;14:1196–1201. doi: 10.1038/nsmb1328. [DOI] [PubMed] [Google Scholar]
- 24.Kamada K., Shu F., Burley S.K. Crystal structure of negative cofactor 2 recognizing the TBP-DNA transcription complex. Cell. 2001;106:71–81. doi: 10.1016/s0092-8674(01)00417-2. [DOI] [PubMed] [Google Scholar]
- 25.McKinney S.A., Joo C., Ha T. Analysis of single-molecule FRET trajectories using hidden Markov modeling. Biophys. J. 2006;91:1941–1951. doi: 10.1529/biophysj.106.082487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Messina T.C., Kim H., Talaga D.S. Hidden Markov model analysis of multichromophore photobleaching. J. Phys. Chem. B. 2006;110:16366–16376. doi: 10.1021/jp063367k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bronson J.E., Fei J., Wiggins C.H. Learning rates and states from biophysical time series: a Bayesian approach to model selection and single-molecule FRET data. Biophys. J. 2009;97:3196–3205. doi: 10.1016/j.bpj.2009.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Düser M.G., Zarrabi N., Börsch M. 36 degrees step size of proton-driven c-ring rotation in FoF1-ATP synthase. EMBO J. 2009;28:2689–2696. doi: 10.1038/emboj.2009.213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lee T.H. Extracting kinetics information from single-molecule fluorescence resonance energy transfer data using hidden markov models. J. Phys. Chem. B. 2009;113:11535–11542. doi: 10.1021/jp903831z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bronson J.E., Hofman J.M., Wiggins C.H. Graphical models for inferring single molecule dynamics. BMC Bioinformatics. 2010;11(Suppl 8):S2. doi: 10.1186/1471-2105-11-S8-S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Liu Y., Park J., Ha T. A comparative study of multivariate and univariate hidden Markov modelings in time-binned single-molecule FRET data analysis. J. Phys. Chem. B. 2010;114:5386–5403. doi: 10.1021/jp9057669. [DOI] [PubMed] [Google Scholar]
- 32.Taylor J.N., Makarov D.E., Landes C.F. Denoising single-molecule FRET trajectories with wavelets and Bayesian inference. Biophys. J. 2010;98:164–173. doi: 10.1016/j.bpj.2009.09.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pirchi M., Ziv G., Haran G. Single-molecule fluorescence spectroscopy maps the folding landscape of a large protein. Nat. Commun. 2011;2:493. doi: 10.1038/ncomms1504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Uphoff S., Gryte K., Kapanidis A.N. Improved temporal resolution and linked hidden Markov modeling for switchable single-molecule FRET. Chemphyschem. 2011;12:571–579. doi: 10.1002/cphc.201000834. [DOI] [PubMed] [Google Scholar]
- 35.Greenfeld M., Pavlichin D.S., Herschlag D. Single molecule analysis research tool (SMART): an integrated approach for analyzing single molecule data. PLoS One. 2012;7:e30024. doi: 10.1371/journal.pone.0030024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Okamoto K., Sako Y. Variational Bayes analysis of a photon-based hidden Markov model for single-molecule FRET trajectories. Biophys. J. 2012;103:1315–1324. doi: 10.1016/j.bpj.2012.07.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zarrabi N., Ernst S., Börsch M. Analyzing conformational dynamics of single P-glycoprotein transporters by Förster resonance energy transfer using hidden Markov models. Methods. 2014;66:168–179. doi: 10.1016/j.ymeth.2013.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Baum L.E., Petrie T., Weiss N. A maximization technique occurring in statistical analysis of probabilistic functions of Markov chains. Ann. Math. Stat. 1970;41:164–171. [Google Scholar]
- 39.Schmid S., Götz M., Hugel T. Single-molecule analysis beyond dwell times: demonstration and assessment in and out of equilibrium. Biophys. J. 2016;111:1375–1384. doi: 10.1016/j.bpj.2016.08.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Jordan M.I., Ghahramani Z., Saul L.K. An introduction to variational methods for graphical models. Mach. Learn. 1999;37:183–233. [Google Scholar]
- 41.van de Meent J.W., Bronson J.E., Gonzalez R.L., Jr. Empirical Bayes methods enable advanced population-level analyses of single-molecule FRET experiments. Biophys. J. 2014;106:1327–1337. doi: 10.1016/j.bpj.2013.12.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Auble D.T. The dynamic personality of TATA-binding protein. Trends Biochem. Sci. 2009;34:49–52. doi: 10.1016/j.tibs.2008.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Press W.H., Teukolsky S.A., Flannery B.P. Cambridge Univ. Press; New York: 1992. Numerical Recipes the Art of Scientific Computing. [Google Scholar]
- 44.Rabiner L.R. A tutorial on hidden markov-models and selected applications in speech recognition. Proc. IEEE. 1989;77:257–286. [Google Scholar]
- 45.Viterbi A.J. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans. Inf. Theory. 1967;13:260–269. [Google Scholar]
- 46.Andrec M., Levy R.M., Talaga D.S. Direct determination of kinetic rates from single-molecule photon arrival trajectories using hidden Markov models. J. Phys. Chem. A. 2003;107:7454–7464. doi: 10.1021/jp035514+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Press W.H., Teukolsky S.A., Flannery B.P. Third Edition. Cambridge Univ. Press; New York: 2007. Numerical Recipes the Art of Scientific Computing. [Google Scholar]
- 48.Davison A.C. Cambridge University Press; Cambridge, UK: 2003. Statistical Models. [Google Scholar]
- 49.Bilmes J.A. What HMMs can do. IEICE Trans. Inf. Syst. 2006;E89D:869–891. [Google Scholar]
- 50.Talaga D.S. COCIS: markov processes in single molecule fluorescence. Curr. Opin. Colloid Interface Sci. 2007;12:285–296. doi: 10.1016/j.cocis.2007.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hirsch M., Wareham R.J., Rolfe D.J. A stochastic model for electron multiplication charge-coupled devices--from theory to practice. PLoS One. 2013;8:e53671. doi: 10.1371/journal.pone.0053671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Börner R., Kowerko D., Sigel R.K.O. Simulations of camera-based single-molecule fluorescence experiments. PLoS One. 2018;13:e0195277. doi: 10.1371/journal.pone.0195277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Dahan M., Deniz A.A., Weiss S. Ratiometric measurement and identification of single diffusing molecules. Chem. Phys. 1999;247:85–106. [Google Scholar]
- 54.Gopich I., Szabo A. Theory of photon statistics in single-molecule Förster resonance energy transfer. J. Chem. Phys. 2005;122:14707. doi: 10.1063/1.1812746. [DOI] [PubMed] [Google Scholar]
- 55.Nir E., Michalet X., Weiss S. Shot-noise limited single-molecule FRET histograms: comparison between theory and experiments. J. Phys. Chem. B. 2006;110:22103–22124. doi: 10.1021/jp063483n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Forsythe G.E., Malcolm M.A., Moler C.B. Prentice-Hall; Englewook Cliffs, NJ: 1977. Computer Methods for Mathematical Computations. [Google Scholar]
- 57.Banik U., Beechem J.M., Weil P.A. Fluorescence-based analyses of the effects of full-length recombinant TAF130p on the interaction of TATA box-binding protein with TATA box DNA. J. Biol. Chem. 2001;276:49100–49109. doi: 10.1074/jbc.M109246200. [DOI] [PubMed] [Google Scholar]
- 58.Gumbs O.H., Campbell A.M., Weil P.A. High-affinity DNA binding by a Mot1p-TBP complex: implications for TAF-independent transcription. EMBO J. 2003;22:3131–3141. doi: 10.1093/emboj/cdg304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Bleichenbacher M., Tan S., Richmond T.J. Novel interactions between the components of human and yeast TFIIA/TBP/DNA complexes. J. Mol. Biol. 2003;332:783–793. doi: 10.1016/s0022-2836(03)00887-8. [DOI] [PubMed] [Google Scholar]
- 60.Schluesche P., Heiss G., Lamb D.C. Dynamics of TBP binding to the TATA box. In: Enderlein J., Gryczynski Z.K., Erdmann R., editors. Single Molecule Spectroscopy and Imaging. SPIE; 2008. 6862E-1–6862E-8. [Google Scholar]
- 61.Murphy, K. P. 1998. Hidden Markov Model (HMM) Toolbox for Matlab.
- 62.Kapanidis A.N., Laurence T.A., Weiss S. Alternating-laser excitation of single molecules. Acc. Chem. Res. 2005;38:523–533. doi: 10.1021/ar0401348. [DOI] [PubMed] [Google Scholar]
- 63.Zarrabi N., Düser M.G., Börsch M. Detecting substeps in the rotary motors of F0F1-ATP synthase by hidden Markov models. Proc. SPIE. 2007;6444:64440E. [Google Scholar]
- 64.Börsch M., Gräber P. Subunit movement in individual H+-ATP synthases during ATP synthesis and hydrolysis revealed by fluorescence resonance energy transfer. Biochem. Soc. Trans. 2005;33:878–882. doi: 10.1042/BST0330878. [DOI] [PubMed] [Google Scholar]
- 65.Börsch M., Diez M., Gräber P. Stepwise rotation of the gamma-subunit of EF(0)F(1)-ATP synthase observed by intramolecular single-molecule fluorescence resonance energy transfer. FEBS Lett. 2002;527:147–152. doi: 10.1016/s0014-5793(02)03198-8. [DOI] [PubMed] [Google Scholar]
- 66.Diez M., Zimmermann B., Gräber P. Proton-powered subunit rotation in single membrane-bound F0F1-ATP synthase. Nat. Struct. Mol. Biol. 2004;11:135–141. doi: 10.1038/nsmb718. [DOI] [PubMed] [Google Scholar]
- 67.Zimmermann B., Diez M., Börsch M. Movements of the epsilon-subunit during catalysis and activation in single membrane-bound H(+)-ATP synthase. EMBO J. 2005;24:2053–2063. doi: 10.1038/sj.emboj.7600682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Düser M.G., Bi Y., Börsch M. The proton-translocating a subunit of F0F1-ATP synthase is allocated asymmetrically to the peripheral stalk. J. Biol. Chem. 2008;283:33602–33610. doi: 10.1074/jbc.M805170200. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.