Summary
Actions are guided by a Bayesian-like interaction between priors based on experience and current sensory evidence. Here, we unveil a complete neural implementation of Bayesian-like behavior, including adaptation of a prior. We recorded the spiking of single neurons in the smooth eye movement region of the frontal eye fields (FEFSEM), a region that is causally involved in smooth pursuit eye movements. Monkeys tracked moving targets in contexts that set different priors for target speed. Before the onset of target motion, preparatory activity encodes and adapts in parallel with the behavioral adaptation of the prior. During the initiation of pursuit, FEFSEM output encodes a maximum a posteriori estimate of target speed based on a reliability-weighted combination of the prior and sensory evidence. FEFSEM responses during pursuit are sufficient both to adapt a prior that may be stored in FEFSEM and, through known downstream pathways, to cause Bayesian-like behavior in pursuit.
Introduction
Nearly all behaviors are guided by an interaction between past experience and current sensory information. When sensory evidence is weak, past experience dominates behavior; conversely reliable sensory evidence dominates past experience. This intuitive mode of operation has been formalized using Bayesian inference, where a prior based on past experience interacts with sensory evidence to create a posterior distribution that can be used to generate a stimulus estimate and guide behavior1,2,3. Many studies have revealed that sensory-motor behavior can be understood in relation to the features of Bayesian inference2,4,5,6,7,8,9,10,11. Here, we reveal how one particular neural circuit creates Bayesian-like behavior.
For many years, we have known that past experience and expectation have an influence on anticipatory smooth pursuit eye movements12,13,14. More recently, our lab showed that priors for target speed and direction also bias the visually-driven initiation of pursuit eye movements10 and that the priors themselves are rapidly adaptable based on the recent history of target motion11. The initiation of pursuit conforms to the expectations of Bayesian inference in that priors have a strong impact when the motion of unreliable, low-contrast targets drives pursuit, and a weaker influence for more-reliable, high-contrast targets10. Darlington et al.11 showed that the reliability-weighted interaction of sensory evidence and priors for pursuit is Bayes optimal according to the definitions of Stocker and Simoncelli15, even though optimality is not a requirement for Bayesian behavior16,17.
Pursuit provides a behavioral and anatomical framework to analyze the neural basis for the reliability-weighted combination of priors and sensory evidence: we know the basic neural circuit for pursuit and the general contribution of each node in the circuit to generation of the behavior18. Extrastriate area MT encodes the direction and speed of visual motion in its population spiking activity, provides the visual drive to the pursuit system19 and, importantly, encodes stimulus reliability in the amplitude of its population response20. The smooth eye movement region of the frontal eye fields (FEFSEM) is a vital node of the intact smooth pursuit circuit. Suprathreshold stimulation of FEFSEM elicits smooth eye movements21 and neurons in FEFSEM selectively modulate their activity during pursuit22,23. Subthreshold microstimulation demonstrates that the output of FEFSEM controls the strength of visual-motor transmission24,25,26. The effect of FEFSEM output on pursuit eye movements is mediated through known pathways to the pontine brainstem and pursuit-related regions of the cerebellum27,28,29. Inactivation of FEFSEM has drastic effects on pursuit30,31,32. Even though pursuit recovers somewhat over weeks after lesions of FEFSEM31, the weight of the evidence indicates that FEFSEM plays an important, causal role in pursuit by modulating the strength (or gain) of visual-motor transmission.
Our previous papers suggested a tight link between visual-motor gain control, FEFSEM, and Bayesian behavior in pursuit eye movements10,11,33. Therefore, the aim of the present experiments was to determine the role of the FEFSEM in generating Bayesian-like behavior in pursuit. We recorded single neuron activity in FEFSEM during pursuit eye movements in a behavioral paradigm that rapidly adapts a prior for target speed. Our results reveal a complete account of a neural computation that appears to mediate Bayesian inference in a sensory-motor system.
Results
Previous papers showed that experience-based priors for target speed and direction influence the speed and direction in the initiation of smooth pursuit eye movement10,11. The effect of the priors depends on the strength of visual motion inputs and can be explained in the framework provided by Bayesian inference. Here, we use recordings from FEFSEM to shed light on the neural mechanisms of three important components of Bayesian-like behavior. (1) We discover a neural representation of recent experience that adapts in parallel with a behavioral prior for target speed. (2) We reveal that FEFSEM uses a reliability-weighted combination of sensory evidence and the neural prior to compute an output that is qualitatively similar to a maximum a posteriori estimate of target speed; that estimate is used to guide pursuit behavior. (3) We demonstrate how the neural prior could be stored in the strength of recurrent synapses and adapted locally in FEFSEM based on experience.
A system for assessing and adapting priors for target speed in smooth pursuit eye movements
We start by introducing the behavioral paradigm we have been using to study the effect of recent experience on the initiation of pursuit eye movement. Most of the data were described in detail by Darlington et al.11, but we summarize it here to set the context for subsequent presentation of neural data.
In each trial, an initially-stationary target underwent ramp target motion (Figure 1c) and moved at a speed of 2, 10, or 20 deg/s. Monkeys initiated pursuit tracking by rapidly increasing eye speed in the direction of target motion and achieved accurate tracking within 200–300 ms after the onset of target motion. To alter recent experience, we used a blocked experimental design and manipulated the statistics of target speeds in different blocks of trials (Figure 1a). During 50-trial “fast-context” blocks, 80% of the trials presented target motion at 20 deg/s and 20% presented motion at 10 deg/s. During 50-trial “slow-context” blocks, 80% of the trials presented target motion at 2 deg/s and 20% presented motion at 10 deg/s. During interspersed 20-trial control-blocks, all of the trials presented target motion at 10 deg/s. To control the reliability of visual motion signals we used targets of high-contrast (reliable visual motion signals) and low-contrast (unreliable visual motion signals).
Figure 1. Effect of speed context on behavior.
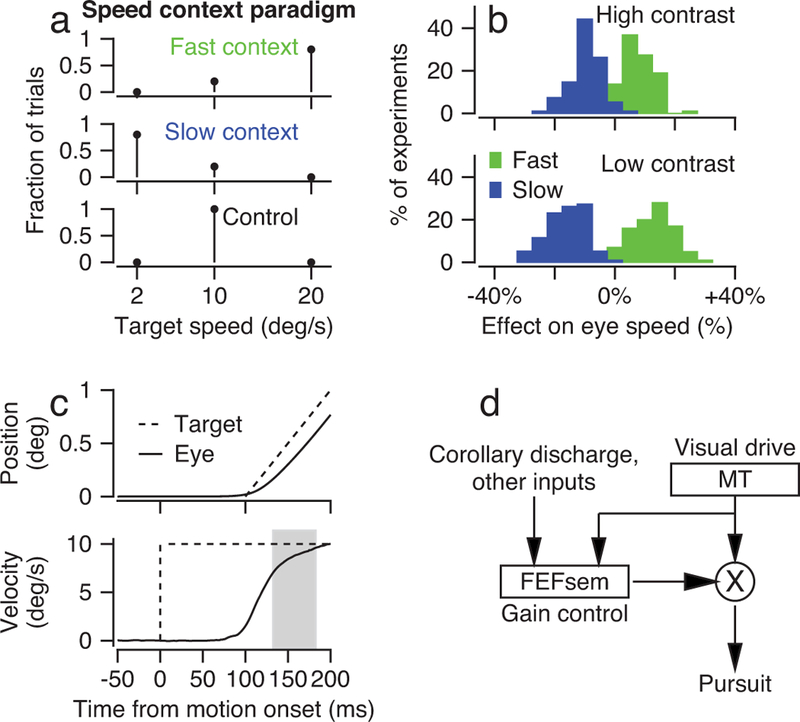
a: Schematic shows the fraction of speeds of target motion in each speed context. b: Histograms compare eye speed for high-contrast (top) versus low-contrast (bottom) targets for the 10 deg/s target motion during the fast (green) and slow (blue) context. The x-axis shows eye speed as a percentage change from eye speed measured in control blocks for the same stimulus speed and contrast. Data are for 95 speed-context experiments during which neural responses were recorded. c: Eye movements during the initiation of pursuit for target motion showing position in the top graph and speed in the bottom graph. Dashed and continuous traces show target and eye movement, and the gray rectangle shows the analysis interval for the initiation of pursuit. Note that the first 100 ms of target motion comprises local motion within a stationary aperture, and the target position starts to ramp 100 ms after the target velocity steps to 10 deg/s. d: A simplified circuit diagram based on previous knowledge of how signals emanating from FEFSEM control the gain of visual motion signals from area MT to the oculomotor machinery to drive pursuit eye movements.
As shown before11, target motion at the control speed of 10 deg/s evokes faster initial eye speeds during the fast-context versus the slow-context (Figure 1b, green versus blue bars). Because the target motion used to probe the behavioral prior is the same in both contexts, the effects on eye speed must be related to the expectations created by context rather than to any physical attribute of the visual stimulus. As expected for Bayesian-like behavior, the recent experience has a stronger behavioral effect when sensory evidence is weaker (low contrast) and therefore less reliable. In the slow-context (blue bars), eye speed averaged 16% versus 10% slower than control for low- versus high-contrast targets (paired t-test, t94 = −8.34, p = 6.18×10−13, n = 95, Cohen’s d = −0.86). In the fast-context (green bars), eye speed averaged 13% versus 8% faster than control for low- versus high-contrast targets (paired t-test, t94 = 7.03, p = 3.22×10−10, n = 95, Cohen’s d = 0.72). The behavioral data summarized in Figure 1b are approximated well by a Bayesian model that we derived using the general strategy outlined in Stocker and Simoncelli15 (Supplementary Figure 1). Because the speed estimated by the Bayesian model falls between the peak of the prior and the sensory likelihood, it is best characterized as a reliability-weighted average.
Representation of a prior in FEFSEM preparatory activity
Preparatory activity in FEFSEM represents the speed context before target motion onset. Modulation of activity during fixation has been observed before35,36, but we now show in Figure 2a that the ramp is larger during the fast-context (green trace) compared to the slow-context (blue trace). We obtained similar results across a population of 164 FEFSEM neurons in two monkeys. The modulation of preparatory activity, defined as the firing rate at the end of fixation minus that at the beginning of fixation (shaded intervals in Figure 2a), is 24% smaller during the slow-context compared to the fast-context (Figure 2b, linear regression slope 0.76). The magnitude and sign of the preparatory activity varies across neurons but is closely correlated with the amplitude of each neuron’s firing rate response during the initiation of pursuit eye movements (Figure 2c). The degree of preparatory activity was similar in neurons categorized as putative inhibitory and excitatory neurons using the multidimensional waveform analysis developed by Snyder et al.37 (data not shown), suggesting that preparatory activity is part of the output from FEFSEM. Importantly, the preparatory activity appears during the fixation interval, which offers no explicit cues about either the upcoming target speed or the contrast of the pursuit target. We conclude that before the onset of target motion, the preparatory activity in FEFSEM could be interpreted as a noisy estimate of anticipated target speed and could represent the “prior probability” of speed in the coming trial.
Figure 2. Effect of speed context on preparatory activity in FEFSEM.
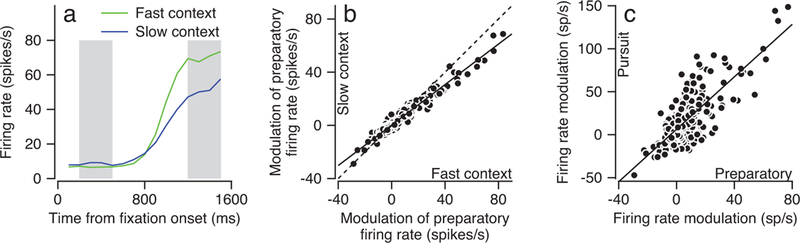
a: Green and blue curves plot average firing rate as a function of time from fixation onset for one example neuron during the fast and slow contexts. The fixation target appeared at time zero, and the pursuit target appeared and started to move 800–1600 ms later. Averages are synchronized on the onset of fixation and each trial contributed data only up to the time of appearance of the tracking target. The shading indicates the intervals used to calculate the modulation of preparatory activity from the averages. b: Scatter plot compares the average change in preparatory firing rate across fixation during the fast- versus slow-context. Each symbol shows data from a different experiment with a single direction of target motion: 321 data points, from 95 speed context experiments in 164 neurons. The solid and dashed lines are the regression fit and the unity line. c: Scatter plot compares the average change in preparatory firing rate during fixation versus the average pursuit-related modulation of firing rate. As in b, each symbol shows data for a different experiment: 321 data points, from 95 speed context experiments in 164 neurons. The solid line is a regression fit.
Parallel adaptation of neural priors and pursuit behavior
We show next that representation of pursuit’s prior for target speed in FEFSEM adapts gradually across tens of trials in parallel with the effect of context on eye speed in the initiation of pursuit (Figure 3). Agreement of the trial courses of behavioral and neural adaptation supports the conclusion that a neural prior in FEFSEM is tightly linked to the behavioral prior expressed in pursuit. Also, the slowness of both neural and behavioral adaptation implies that the behavior we are studying is the product of a probabilistic process as opposed to some higher-level switch. The monkeys did not learn that there were different contexts in a way that would allow them to instantaneously switch their behavior upon encountering a 20 (or 2) deg/s trial in the fast (or slow) context.
Figure 3. Agreement of time courses of contextual effects on eye speed and preparatory activity in FEFSEM.
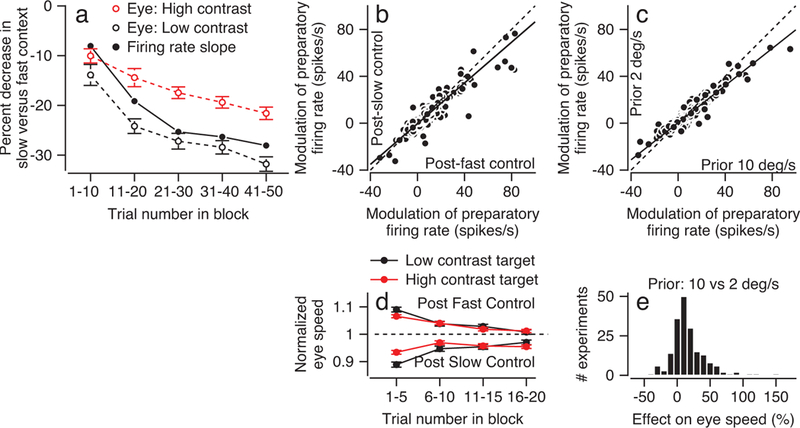
a: Red and black open symbols plot the time course of the average relative difference in eye speed between fast and slow context in response to the 10 deg/s target motion of high- and low-contrast targets. Filled symbols plot the time course of the average relative difference in FEFSEM preparatory firing rate between the fast and slow contexts. Data are averaged within successive bins of 10 trials. Error bars represent SEM (n = 95 speed context experiments). b: Scatter plot compares the average preparatory firing rate during control blocks that followed the fast-context versus control blocks that followed the slow context. c: Scatter plot compares the average preparatory firing rate when target speed on the previous trial was 10 deg/s versus 2 deg/s. Each symbol shows data for a different experiment: 321 data points, from 95 experiments in 164 neurons. In b and c, each symbol shows data for target motion in one direction for one neuron, and solid and dashed lines show regression fits and unity line. d: Symbols plot the time course of average normalized eye speed in response to the 10 deg/s target motion for the high- (red) and low-contrast (black) targets over the 20 trials in the control blocks. The symbols in the top portion of the plot represent normalized eye speeds in the post-fast control blocks and the symbols in the bottom portion of the plot represent normalized eye speeds in the post-slow control blocks. Error bars represent SEM (n = 95 speed context experiments). e: Distribution of single-trial effects on eye velocity when the target speed in the previous trial was 10 versus 2 deg/s. Each experiment contributes 2 entries: one each for the low- and high-contrast targets. Here and in all subsequent figures, “Trial number in block” takes all trials in the block into account.
Figure 3a quantifies the gradual adjustment of the representation of the prior in 10-trial bins according to the slope of the relationship between the modulations of preparatory activity in the slow- versus fast-context (same analysis as Figure 2b). The effect of context on preparatory activity evolves over approximately 30 trials before plateauing near a slope of 0.7, signifying a 30% decrease in the slow- versus fast-context (Figure 3a, solid black symbols). The effect of context on eye speed also evolves over 30 trials before plateauing around a 30% or 20% difference for low-contrast targets (Figure 3a, open black symbols) or high-contrast targets (Figure 3a, open red symbols). The smaller effect on behavior for high-contrast targets is expected because the prior has a smaller influence over behavior when sensory information is reliable. We observed similar agreement in measures of preparatory activity and eye speed for the slow- and fast-contexts, separately (Supplementary Figure 2).
The effects of the fast- and slow-contexts on both preparatory activity and eye speed linger with similar amplitude into the subsequent control blocks. Preparatory activity is 13% smaller in the control blocks that follow the slow- versus fast-context (Figure 3b). Eye speed showed similar effects (Figure 3d). Eye speed decays gradually across the 20-trial control blocks and reflects the previous context more strongly for low-contrast (black) versus high-contrast (red) targets.
We also found that a single trial adapts the preparatory activity in FEFSEM and the pursuit behavior. In Figure 3c, we measured the preparatory activity separately for trials in the slow-context that were preceded by target motion at 2 versus 10 deg/s. The average preparatory activity was 21% smaller in trials preceded by target motion at 2 deg/s (slope = 0.79). Eye speed in pursuit initiation was 16.9% smaller for target motion at 2 deg/s preceded by target motion at 2 versus 10 deg/s (Figure 3e, paired t-test, t189 = 6.53, p=5.95×10−10, n = 190, Cohen’s d = 0.64). We did not find a similar effect on preparatory activity in the fast-context for previous target speeds of 10 versus 20 deg/s, probably because previous target motion at 10 versus 20 deg/s creates effects that are too small to measure on the time scale of a single trial.
FEFSEM firing rates during pursuit initiation encode a Bayesian-like estimate of target speed
The same population of FEFSEM neurons responded strongly to the visual motion that drives pursuit during the first 100 ms of movement initiation. We call this “pursuit-related” activity.
Context has a larger effect on pursuit-related activity for less-reliable visual motion. For the motion of a high-contrast target at 10 deg/s, the example neuron in Figure 4a shows very similar trajectories of average firing rate during the initiation of pursuit in the fast- and slow-contexts (green versus blue traces). For the same neuron, the pattern was different for low-contrast targets (Figure 4b). The response was smaller and delayed in the slow-context (blue trace) compared to the fast-context (green trace), even though target contrast and speed were the same so that eye movement was not delayed (data not shown).
Figure 4. Effect of speed context on activity driven by target motion in FEFSEM during initiation of pursuit and successful decoding of FEFSEM activity to predict behavioral gain.
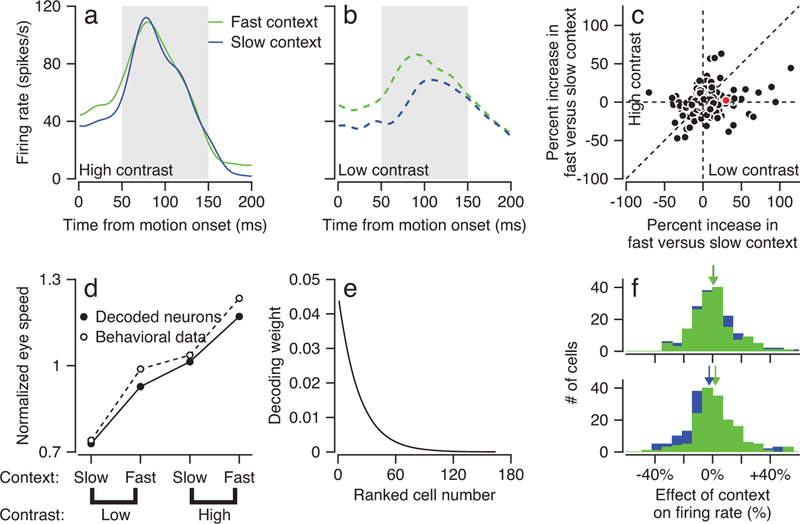
a, b: Curves plot average firing rate of an example FEFSEM neuron as a function of time from motion onset for target motion at 10 deg/s during the fast (green) and slow (blue) context for high- (a) and low-contrast (b) targets. Gray shading shows the interval used to analyze pursuit-related firing rate. c: Scatter plot compares the average percentage change in pursuit-related firing rate between the fast- and slow-contexts for the high- versus low-contrast targets at speeds of 10 deg/s. Each symbol represents data for target motion in one direction for one neuron: 164 data points collected from 118 neurons. Dashed lines indicate the unity line and x- and y-axes. The red symbol denotes the example cell in panel a. We averaged the firing rate across the interval from 50–150 ms after the onset of target motion (gray shading in a and b) because this represents the time period when the discharge in FEFSEM can affect the initiation of pursuit. d: Open symbols plot average eye speed for low- and high- contrast targets moving at 10 deg/s during the fast- and slow-contexts normalized to eye speed averaged across to all 10 deg/s conditions (n = 95 behavioral experiments). Filled symbols plot the normalized eye speed predicted by constrained linear decoding of pursuit-related FEFSEM firing rates. e: The curve plots the weight of each ranked neuron used in the decoder that generated the data in panel d. f: Histograms compare FEFSEM firing rates for high- (top) versus low-contrast (bottom) targets for the 10 deg/s target motion during the fast (green) and slow (blue) context. The x-axis shows firing rate as a percentage change from that measured in control blocks for the same stimulus speed and contrast. This way of plotting the data shows the result of using a uniform decoder to predict behavioral effects from the population response. There are 164 data points collected from 118 neurons. Green and blue arrows indicate the population average for the fast- and slow-contexts.
We quantified the effect of context on pursuit-related responses in FEFSEM by computing the percentage change in firing rate between the fast- and slow-context (100*(fast-slow)/slow) for a target of a given contrast moving at 10 deg/s. The effect of context on FEFSEM pursuit activity varies across neurons, but for the population the effect is significantly larger for low- versus high-contrast targets (Figure 4c, paired t-test, t163 = 3.09, p = 0.0024, n = 164, Cohen’s d = 0.24). Therefore, in good agreement with pursuit behavior, activity in FEFSEM during initiation of pursuit is affected more by context when sensory evidence is weak.
The effect of context on pursuit-related activity is quite variable across neurons, leading to the question of whether it is possible to decode the behavioral effects of context and stimulus contrast from the neural population. The answer is yes. Choice of a suitable linear decoder provided a close match of the decoded FEFSEM population response to the effects on smooth pursuit behavior for motion of high- and low-contrast targets at 10 deg/s in the slow- and fast-contexts (Figure 4d). We conclude that FEFSEM output during pursuit initiation combines prior and current sensory information in a way that is qualitatively similar to a maximum a posteriori (MAP) estimate of target speed, and that this estimate is appropriate to control the initiation of pursuit. Because pursuit’s prior for target speed is much slower than 10 deg/s (Supplementary Figure 1), preparatory activity is usually smaller than pursuit-related activity and the estimate of target speed provided by the pursuit-related activity is slower for low-contrast versus high-contrast targets.
To create the successful linear decoder, we first combined the pursuit-related firing rates for high- and low-contrast targets moving at 10 deg/s in the fast- and slow-context for each neuron. We then ranked the full sample of FEFSEM neurons according to the effect of context on pursuit-related firing rate and fitted an exponential distribution (a Gaussian distribution gave similar results) of weights (Figure 4e) for the firing rates of the ranked neurons. Thus, the decoder had only one free parameter. Also, it is important that neurons were ranked only according to overall effect of context; the effect of contrast emerges seamlessly, providing cross-validation of the decoder. When we used an alternative decoder that weighted the population response uniformly, the effects were in the right direction, but the magnitudes were small compared to the behavior (compare Figure 4f with Figure 1b).
Some of the data in Figures 1–4 were collected with high-contrast patches of dots and low-contrast gratings as stimuli, while others used high- and low-contrast dots. Supplementary Figure 3 verifies that the stimulus form did not have any effect on the results.
FEFSEM estimates target speed during pursuit initiation via a reliability-weighted average of the speed prior and sensory evidence
We show next that the relationship between preparatory activity and FEFSEM output during pursuit initiation has the two features we would expect in a Bayesian-like computation. First, preparatory activity contributes to the subsequent pursuit-related response. Higher preparatory activity pushes the absolute pursuit-related activity to higher levels, leading to a faster estimate of target speed and higher eye speeds in the initiation of pursuit. Second, preparatory activity interacts with visual motion input to control the sensory-driven increment in firing rate during the pursuit-related response, instantiating the reliability-weighted combination of prior and sensory evidence that occurs in pursuit behavior.
Our approach takes advantage of the fact that the firing rate at the end of the preparatory period varies from trial-to-trial even when the context and the stimulus are the same. First, we evaluated trial-by-trial correlation between (1) the preparatory firing rate in the last 100 ms before the moving target appeared (Figure 5a, “prep”), and (2) the absolute firing rate in the interval 50–150 ms after target motion onset (Figure 5a, “absolute”). For an example neuron (Figure 5b), the trial-by-trial correlation between the preparatory and absolute pursuit-related firing rate was 0.46. Strong positive correlations appeared for the entire population (Figure 5c), with statistically larger positive correlations for responses to low- versus high-contrast targets (mean Pearson’s r = 0.234 versus 0.187, paired t-test, t320 = 5.95, p = 6.87×10−9, n = 321, Cohen’s d = 0.33).
Figure 5. Trial-by-trial correlation between preparatory and pursuit firing rate.
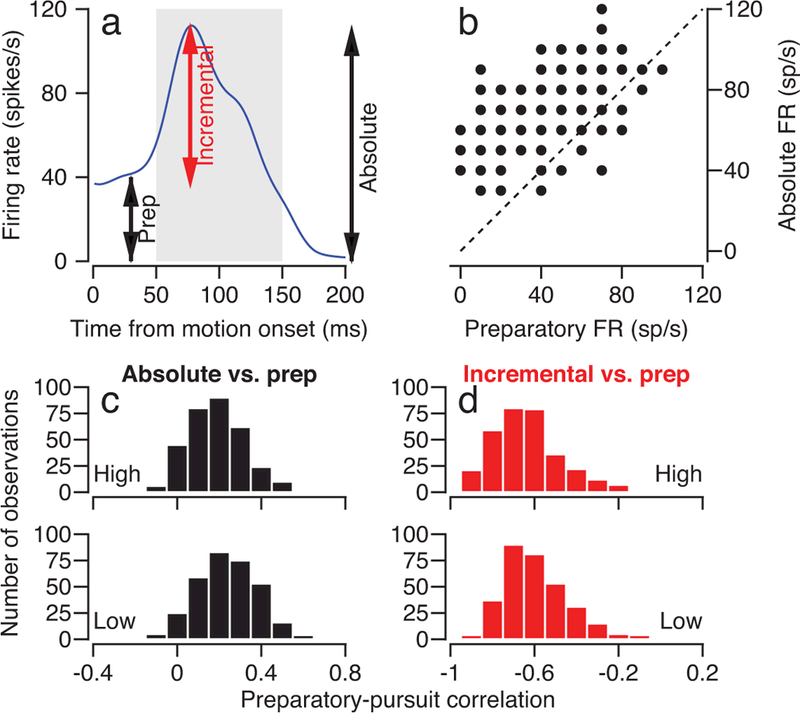
a: The curve replots (from Figure 4a) the average firing rate over time of one example neuron. Arrows indicate the three firing rate measurements used for the correlation analysis in b-d. b: Scatter plot showing trial-by-trial correlations between preparatory and absolute pursuit-related firing rate for an example neuron. Each symbol shows measurements for one trial. The dashed line represents the unity line. The Pearson correlation coefficient is 0.46. c: Histograms showing the distribution of trial-by-trial Pearson correlation coefficients between preparatory modulation of firing rate and absolute pursuit-related firing rate. Top and bottom histograms show data for the high- and low-contrast target motions, both at 10 deg/s. d: as in c, except that correlation is between preparatory modulation of firing rate and the incremental firing rate from the preparatory level during pursuit initiation. Each neuron could have contributed more than one “observation” for target motion in different directions. Data in c and d summarize results from 321 data points, from 95 speed context experiments in 164 neurons.
Next, we correlated the preparatory firing rate in the last 100 ms before the moving target appeared (Figure 5a, “prep”) with the change in firing rate during the initiation of pursuit (Figure 5a, “incremental” = absolute minus prep). We find strong negative trial-by-trial correlations between the firing rate in the preparatory period and the increment in firing rate between the preparatory and pursuit periods (Figure 5d). The negative correlations cannot represent a ceiling effect on FEFSEM firing because they were just as strong for the smaller pursuit-related responses evoked by target motion at 2 deg/s. Again, trial-by-trial preparatory-pursuit correlations were statistically more positive for low-contrast targets compared to high-contrast targets (mean Pearson’s r = -0.592 versus −0.631, paired t-test, t320 = 5.86, p = 1.17×10−8, n = 321, Cohen’s d = 0.33).
The strength and signs of the trial-by-trial correlations between Figures 5c and d suggests causal links from preparatory activity to pursuit-related activity, possibly within individual neurons. We suggest that the positive correlation between preparatory activity and absolute pursuit-related firing rate occurs because the preparatory firing pushes the eventual pursuit-related response toward a level that is commensurate with the prior represented by the preparatory activity. The negative correlation between incremental pursuit-related firing rate and preparatory activity means that the neural representation of the prior doesn’t simply provide a platform for the addition of sensory inputs. Instead, the preparatory activity modulates the increment in firing caused by the sensory input: higher preparatory activity leads to a smaller increment due to sensory input.
A theory-based explanation for trial-by-trial correlations
To make our interpretations more precise, we start from the principles of Bayesian inference and derive an equation that describes multiple features of our recordings from FEFSEM, including the positive and negative trial-by-trial correlations described in Figure 5. If the prior and likelihood are represented as Gaussians, then a MAP estimate is a precision-weighted combination of the mean of the prior for target speed () and the maximum likelihood (ML) estimate of target speed from sensory evidence () :
| (1) |
where is the precision of the likelihood and is assumed to be a function of contrast, and is the precision of the prior and is assumed to be constant across contexts. With the appropriate substitutions and some algebra:
| (2) |
where and always assumes a value between 0 and 1.
Equation (2) maps nicely onto the measurements we made in FEFSEM. The decoding analysis (Figure 4d and e) suggests that neural activity in FEFSEM during the initiation of pursuit (FRpurs) is qualitatively consistent with a MAP estimate of target speed that is used to drive pursuit behavior. The preparatory activity (FRprep) is related to the prior created by speed context. Therefore, we can rewrite Equation (2) as:
| (3) |
where represents visual motion input to FEFSEM related to the maximum likelihood estimate of target speed. Equation (3) accurately predicts the nature of trial-by-trial correlations between preparatory firing rate () and the firing rate of FEFSEM during pursuit initiation (). The second term on the right side of Equation (3) predicts the positive correlations between preparatory activity and the absolute pursuit-related firing rate (Figure 5c). Rearranging Equation (3) yields:
| (4) |
Equation (4) describes the relationship between preparatory activity and the increment in firing driven by sensory inputs during pursuit initiation (FRincremental), and qualitatively predicts the negative trial-by-trial correlations between preparatory activity and the increment in FEFSEM firing rate (Figure 5d).
Equations (1)–(4) explain how the data in Figures 4 and 5 would result from a Bayesian-like computation in FEFSEM. The preparatory activity (prior) pushes the output of FEFSEM towards the expectation it represents and combines with sensory evidence (likelihood) in a manner that depends on the reliability of visual motion. Also, Equation (3) can be generalized to explain the activity in FEFSEM as a MAP estimate of target speed across a pursuit trial, starting with activity driven entirely by expectation during fixation and ending with a reliability-weighted average between prior and likelihood during pursuit initiation.
Evidence for local updating in FEFSEM of the neural representation of the speed prior
Our final goal is to understand how a sensory-motor neural circuit could generate and store prior expectations based on experience.
Here, we use a model that maintains the prior as an explicit state variable, to ask whether adaptation of the neural representation of the prior could occur locally within FEFSEM. The prior is updated after each trial according to the pursuit-related responses of our population of neurons in FEFSEM (Figure 6a). We used two components of prior adaptation that we weighted separately to update the prior for the next trial.
Figure 6. Model for updating the representation of a Bayesian prior based on pursuit responses in FEFSEM.
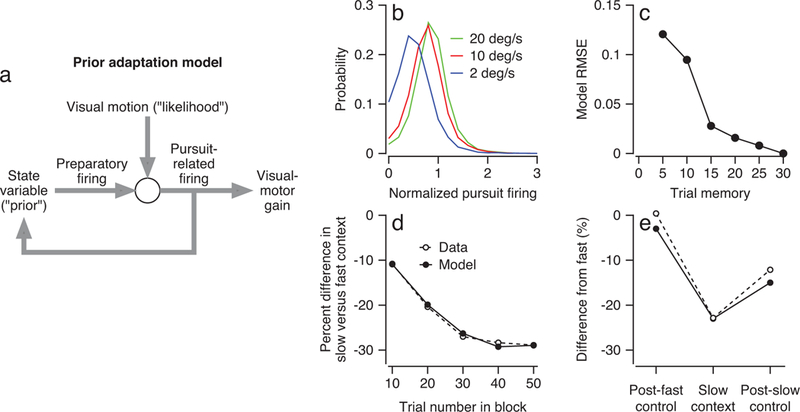
a: A conceptual model for how FEFSEM combines the prior on one trial with the likelihood from sensory input to set the gain of visual-motor transmission and to update the prior for the next trial. b: Blue, red, and green curves show distributions across trials of normalized pursuit-related firing rates across the population of FEFSEM neurons for target motion at 2, 10, and 20 deg/s. c: Symbols plot the root mean squared error between model and neural data as a function of the length of the trial history that influenced the model’s prior. d, e: Open and filled symbols plot the time course of the relative change in preparatory activity between fast and slow contexts for the data and the optimized model (d) and the relative change in preparatory activity between the fast-context and the post-fast, slow, and post-slow contexts (e).
| (5) |
FRprepn and FRpursn are the preparatory and pursuit-related firing rate on the nth trial. The “w1” term allows for single trial adaptation of the preparatory activity (Figures 3c and e); the “w2” term supports adaptation of the preparatory activity over a slower time course (Figures 3a, b, and d). Both components of adaptation compute prediction errors based on the difference between the actual level of pursuit activity in the most recent trial and predictions based on preparatory activity.
To test the model, we simulated blocks of trials with the same statistics of target speed used in the slow- and fast-contexts as well as the control blocks in our experiments (Figure 1a). We drew a pursuit-related response for each simulated trial from the distribution of normalized responses of real FEFSEM neurons for the target speed in that trial: 2, 10, or 20 deg/s (Figure 6b). To fit the model, we adjusted the two weights, w1 and w2, to account for: (1) the size of the single-trial effect on preparatory firing rate during the slow-context (Figure 3c) and (2) the magnitude of the difference between preparatory activity in the post-fast and post-slow control blocks (Figure 3b).
The choice of a history of 30 trials in Equation (3) optimizes the performance of the model (Figure 6c) and allows it to reproduce the time course of acquisition of preparatory activity (Figure 6d). A memory of 30 trials models the decay in preparatory activity in control blocks that follow fast- or slow-context blocks of trials (Figure 6e). Also, the model predicts an important feature of our data that was not explicitly built into it. The state variable in the model plateaus at the same slow-fast difference of −30% as the experimentally-observed preparatory activity in FEFSEM (Figure 6d). We explain this feature in Supplementary Figure 4.
We take the success of the model as evidence in favor of our suggestion that adaptation of the behavioral prior could occur locally in FEFSEM and be driven by the pursuit-related firing rate, which itself is an estimate of target speed that depends on the interaction between preparatory-related firing rate and sensory evidence.
Biologically-plausible recurrent neural network captures features of Bayesian-like computations in FEFSEM
Here, we demonstrate one kind of biologically-plausible model that can account for the qualitative pattern of results from our data. This is a “proof of concept” style of model and the actual implementation in the brain could look quite different. Our network model (Figure 7f) comprises a fully-recurrent network of excitatory and inhibitory rate model neurons, where the prior is stored in the weights of the recurrent excitatory connections. As inputs, the recurrent circuit receives a small step in activity during fixation in advance of impending target motion and a realistic population response from extrastriate area MT (Supplementary Figure 5).
Figure 7. Performance of a network model that reproduces the key features of recordings from FEFSEM.
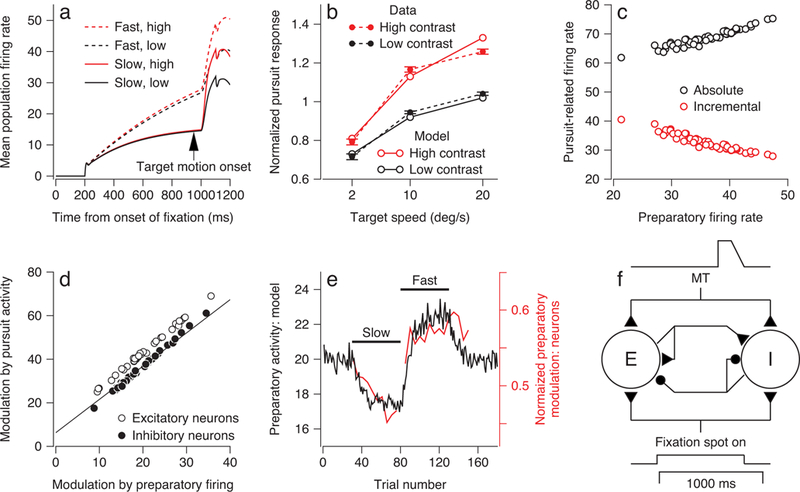
a: Average responses of full population of model neurons as a function of time. Dashed and continuous traces show results for fast- versus slow-context, red and black show high- versus low-contrast targets. b: Average pursuit response for full population of model neurons as a function of target speed. Red and black show results for high- and low-contrast targets. Filled and open symbols show results for real versus model FEFSEM neurons. Error bars on the filled symbols show the standard error of the mean across neurons (n = 164 data points collected from 118 neurons). c: Analysis of trial-by-trial variation showing competition between preparatory activity and sensory inputs (after Figure 5). Red and black symbols show analysis of incremental versus absolute pursuit-related firing rate. d: Plot of pursuit-related activity versus preparatory activity. Each symbol shows measurements from a different model neuron. Line is the same line used to fit the data in Figure 2c. e: Trial courses of mean preparatory activity across the population of model neurons (black) and averaged across our population (red) of recorded neurons during simulations with 30 control trials, 50 trials in the simulated fast-context, 50 trials in the simulated slow context, and 50 additional control trials. For both the neurons and the model, preparatory activity is about 30% larger in the fast- versus the slow-context. f: A cartoon showing the architecture of the recurrent neural network model.
The network model reproduces all of the main features of our recordings from FEFSEM. Model neurons show ramps of preparatory activity during fixation reaching a level that depends on whether the recurrent weights are set for the fast- or slow-context (Figure 7a). Pursuit-related activity depends on target speed, target contrast, and speed context in a way that closely follows the data (Figures 7a and b). For each model neuron in the network, the trial-by-trial variation in pursuit-related activity is positively correlated with preparatory activity (mean slope 0.54) and the incremental pursuit activity is negatively correlated with preparatory activity (mean slope −0.46) (Figure 7c), reproducing the data in Figures 5c and d. The pursuit-related activity of the 66 model neurons is tightly related to the modulation of the preparatory activity and falls close to the regression line for the actual data (Figure 7d). Under conditions that mimic the control-, slow-, and fast-contexts, the network adapts autonomously and produces changes in preparatory activity that have realistic amplitudes and time courses (Figure 7e).
The network model is detailed in the Methods. Briefly: (1) we used the recurrent excitatory-inhibitory network structure of Lim and Goldman38 to achieve a stable integrating circuit that was not overly sensitive to its internal weights; (2) we provided visual motion drive as the weighted sum of the activity of a realistic population of model MT neurons, each weighted by its preferred speed (Supplementary Figure 5); (3) we instantiated shunting inhibition to allow larger preparatory activity to modulate negatively the increment in firing caused by sensory evidence; and (4) we used a plasticity rule that increased or decreased the weight of excitatory inputs. Changes in the weights depended on a comparison of plasticity signals in the fixation interval before the onset of target motion versus during the initiation of pursuit. In effect, this comparison increases (or decreases) synaptic weights and increases (or decreases) future preparatory activity if the pursuit-related activity is larger (or smaller) than the expectation embedded in the preparatory activity. The plasticity signals were computed as by integrating the product of pre- and post-synaptic activity in each of the two intervals: the preparatory period and the initiation of pursuit.
In the network model, we used shunting inhibition to create the precision-weighted combination of preparatory and visual motion signals. Shunting inhibition is a form of divisive normalization and is predicted by a network that generates MAP estimates from sensory information encoded in the form of a linear probabilistic population code39. In a linear PPC, the natural parameters of the prior and likelihood are encoded linearly by neural activity. For a Gaussian-distributed posterior this means:
| (6) |
| (7) |
where is a vector of firing rates in area MT, is the ratio of prior mean and variance, is the precision of the prior, and and are constants determined from the first- and second-order statistics of MT activity. For example, if MT activity was associated with a population of independent Poisson neurons with Gaussian tuning curves with uniform width, then would be a vector of preferred speeds in MT neurons and would be a vector of ones. If FEFSEM activity linearly encodes the MAP estimate, then a divisive normalization is necessary to compute FEFSEM activity from MT activity:
| (8) |
A straightforward way to accomplish this would be for FEFSEM activity to evolve over time via the differential equation:
| (9) |
The second term on the right-hand side of Equation (9) implements the divisive normalization required to produce the MAP estimate via shunting inhibition. Equation (9) also has the property that the time constant of integration is related to the strength of the likelihood: more spikes coming from the sensory likelihood () cause faster dynamics. Thus, Equation (9) correctly predicts the faster dynamics for pursuit-related responses to high-contrast visual motion (see Figure 4a versus b). Moreover, Equation (9) models an increase in the prior mean by increasing bp, leading to higher preparatory activity during fixation before visual motion onset.
Discussion
Bayesian inference has been a useful metaphor for understanding a wide range of sensory-motor behaviors1,2,3,10,11,16 in terms of a reliability-weighted combination of sensory evidence and adaptable priors. Our recordings from FEFSEM use pursuit eye movements as a behavioral system to provide, to our knowledge, the first account of a complete set of neural components that implement Bayesian inference in a sensory-motor system. We supported the completeness of that account through a theoretical analysis that takes us from a normative description of Bayesian inference to an equation that maps onto the responses of neurons in FEFSEM.
Interaction of experience and sensory information to estimate target speed in FEFSEM
The activity of neurons in FEFSEM provides neural representations of the key elements of Bayesian inference to estimate target speed: the output of FEFSEM is qualitatively similar to a MAP estimate of target speed. During fixation, the estimate of target speed is based solely on the preparatory activity that represents the prior for target speed. During pursuit initiation, the estimate of target speed is based on a reliability-weighted average of the prior and the sensory evidence.
Preparatory activity in FEFSEM builds up during fixation before the onset of target motion35,36. It encodes the mean of a Bayesian-like prior based on speed context and influences subsequent visual motion processing in FEFSEM. Because our behavioral paradigm does not provide explicit cues about the upcoming visual motion during fixation, the preparatory activity must represent the pursuit system’s expectation, or prior. Importantly, it need not be the case that the prior was expressed in preparatory activity: it could have been entirely hidden away in synaptic weights or the activity of inputs from other areas, only to reveal its effects during pursuit-related responses.
FEFSEM output during pursuit initiation is the result of a Bayesian-like computation that estimates target speed through a reliability-weighted combination of sensory evidence (visual motion input from area MT) with expectation or a prior (preparatory activity). Target speed is represented in a “place code” in area MT, where cells have a wide range of preferred speeds40,41. In contrast, FEFSEM represents speed as a “rate code”: pursuit-related responses increase monotonically with visual motion speed in all neurons22,23. We take advantage of the fact that contrast (and therefore reliability) is reflected in the amplitude of area MT’s population response20. By using the sum of MT responses weighted by their preferred speed as its input, our model received a total sensory synaptic input that is larger for high-contrast versus low-contrast visual motion at any given target speed. This choice reproduced the measured responses of FEFSEM neurons, with faster estimates of visual motion for both higher target speeds and higher contrast targets. The model uses shunting inhibition, one potential neural implementation of the reliability-weighted combination of sensory evidence and priors. In effect, the ratio of the magnitudes of preparatory activity to visual motion input determines the weighting: as this ratio increases, preparatory activity (prior) is weighted higher and visual motion (sensory evidence) is weighted lower.
Our models show that a representation of the prior could be generated by a recurrently connected neural network and that synaptic plasticity could update the prior on the basis of the pursuit-related activity of FEFSEM neurons by altering the strength of recurrent excitatory connections. The state-variable model presented shows that the measured distributions of pursuit-related firing rates for target motion at 2, 10, and 20 deg/s can account fully for local adaptation of preparatory activity. Feedback of the posterior from a Bayesian computation to adapt the prior also is a feature of a hierarchical recurrent Bayesian model that accounts for some features of pursuit45. While the result from Figure 6 suggests that all of the information needed to update the prior is present in FEFSEM activity, it does not rule out the possibility that preparatory activity is adapted and originates upstream from FEFSEM.
Causal effect of FEFSEM on pursuit eye movement
We have shown that FEFSEM emits pursuit-related firing that is qualitatively similar to a MAP estimate of target speed, and we have revealed much about how the reliability-weighted combination of preparatory activity (the prior) and sensory evidence (the likelihood) sets the output during pursuit initiation. We have not quantitatively proven that FEFSEM output is exactly a MAP estimate. But, our ability to decode the behavior from FEFSEM output and the reliability-weighted nature of the interaction between prior and current evidence in FEFSEM support our conclusions and establish FEFSEM output as a reliability-weighted estimate of target speed that can be used to guide eye speed.
The output of FEFSEM provides an estimate of target speed that causally controls the strength, or gain, of visual-motor transmission. Subthreshold microstimulation demonstrates the role of FEFSEM in gain control by enhancing the strength of pursuit initiation for a given target motion25, as well as eye speed responses to visual motion perturbations24,26. Previous reports have highlighted the link between gain control, estimates of target speed, and Bayesian-like behavior in pursuit. Behavioral experiments showed that the setting of the gain of visual-motor transmission depends on target speed46, validating the use of a Bayesian-like estimate of target speed for gain control. Computational models suggest that Bayesian inference in pursuit is implemented by direction-selective visual-motor gain control10,11,33. The present paper links FEFSEM to gain control and its use to implement Bayesian inference.
Neural representations of Bayesian inference
We have identified all the components of Bayesian inference in FEFSEM, a part of the brain that plays a causal role in smooth pursuit eye movements. Bayes rule is based on a complete representation of prior and posterior distributions, but in FEFSEM we find neural representations of only the means of these components of Bayesian inference. We show that the neural representation of the posterior results from a non-linear combination of the prior and a complex population code representation of target speed and contrast in area MT. The non-linearity can be implemented with shunting inhibition. Computer simulations suggest that the entire Bayesian computation could reside in FEFSEM, with the prior represented by the adaptable weights of excitatory recurrent synaptic connections. We propose that the circuity in FEFSEM uses the principles of Bayesian inference to perform a reliability-weighted combination of previous experience and sensory evidence, yielding a statistically-optimal linear estimate of target speed that is in appropriate coordinates to guide motor output.
Methods
Please refer to our “Life Sciences Reporting Summary”.
Contact for reagent and resource sharing
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Stephen Lisberger (lisberger@neuro.duke.edu).
Experimental model and subject details
We conducted experiments on two male rhesus monkeys that weighed between 12 and 14 kg and were 8 and 10 years of age. Monkeys underwent several surgeries in preparation for the experiments. First, monkeys were surgically implanted with hardware onto the skull to restrain head movement and a scleral search coil to track eye movements47,48. Once the monkeys recovered from these surgeries, they were trained to fixate and smoothly track moving visual targets. The horizontal and vertical components of eye position were recorded through the analog signals produced by the scleral search system. These signals were passed through an analog circuit to obtain signals proportional to eye velocity. The circuit differentiated signals from DC to 25 Hz and rejected signals at higher frequencies (−20 dB/decade). Eye position and velocity signals were sampled at 1 kHz and stored for offline data analysis. Second, a craniotomy was performed in an area centered on the smooth eye movement region of the frontal eye fields (FEFSEM). A sealable, titanium recording cylinder was placed over this craniotomy to allow access to FEFSEM for electrophysiological recordings. All procedures received prior approval by Duke’s Institutional Animal Care and Use Committee and were in compliance with the National Institutes of Health’s Guide for the Care and Use of Laboratory Animals.
Method details
Our experimental paradigm had two key manipulations11.
First, we controlled the distribution of target speeds that the monkey experienced (Figure 1). During the fast-context, 80% of trials provided target motion at 20 deg/s and 20% of trials provided target motion at 10 deg/s. During the slow context, 80% of the trials provided target motion of 2 deg/s and 20% of the trials provided target motion of 10 deg/s. During a control block, all trials delivered target motion of 10 deg/s. The fast and slow contexts consisted of 50-trial blocks and the control blocks consisted of 20-trial blocks. These three types of blocks alternated during the experiment with control blocks falling between every fast and slow block.
Second, we controlled the strength of visual motion that the monkey experienced on each trial by using targets of different contrast and form. Targets comprised a 100% contrast patch of dots or Gabor for the “reliable visual motion target” and a 12% contrast patch of dots or a 6% contrast Gabor for the “unreliable visual motion target”. The patch of dots consisted of 72 dots within a 4-degree aperture. Half of the dots were bright and half were dark to render the average luminance the same as the background. The Gabor had a spatial frequency of 0.5 cycles/degree and was vignetted by a two-dimensional Gaussian function with a standard deviation of 1 degree. Visual targets were displayed on a 24-inch gamma-corrected CRT monitor with a refresh rate of 80 Hz placed 40 centimeters from the monkeys’ eyes, creating a field of view spanning 62 (horizontal) by 42 (vertical) degrees. It is important to note that contrast and motion adaptation are unlikely to have any effect in our paradigm given the short duration of our trials and the fact that high- and low-contrast trials were randomly interleaved.
Experiments were divided into discreet trials. Each trial started the same way, with the monkey fixating a small black dot at the center of the screen. After a period of 800–1600 ms, the black dot was replaced with a pursuit target that underwent 100 ms of coherent local pattern motion (of the patch of dots or Gabor) at a defined speed and direction within a stationary but invisible aperture. We used 100 ms of local motion to jump-start the pursuit system and avoid a large initial position error. The target and aperture subsequently moved en bloc with the parameters of the previous local motion. Monkeys were rewarded with juice for successfully tracking the position of the center of the target within a 4×4 degree window. This strategy allows us to study the visual-motor transformation occurring during the open-loop interval in the initiation of pursuit without confounding effects of saccades. It has the same advantages as the Rashbass “step-ramp” used in pursuit of spot-targets49. Previous publications have shown that pursuit to local followed by global motion is indistinguishable from that to targets that start with local and global motion simultaneously50.
Some of our data were obtained using a high-contrast patch of 100% correlated dots and a low-contrast Gabor (“mixed-form”), and some were obtained with matched forms of different contrasts. We started with targets that differed in both contrast and form, based on the strategy used in our first behavioral paper on Bayesian inference in pursuit10. However, we realized partway through data collection that the use of different stimulus forms was a potentially contaminating variable. Therefore, we switched to paradigms that held target form constant and varied only stimulus contrast. Form-matched neural data were collected in Monkey Xt and form-matched behavioral data were collected in both monkeys. Separating the data into form-matched and form-mixed versions of the experiment did not affect any of our conclusions (Supplementary Figure 3).
During a typical experiment, three Thomas Recording tetrodes were introduced into FEFSEM for isolation of single units. To allow us to customize the direction of target motion in a daily experiment, we first determined the direction of pursuit that elicited the maximal firing rate in the units that we isolated. The speed-context experiment was run in a fixed direction that represented a good compromise between the preferred directions of the neurons we were recording in a given session. When possible, we ran multiple speed-context experiments in different directions while recording from the same neurons. Our data set includes recordings from 164 FEFSEM neurons (83 in monkey Re and 81 in monkey Xt) with an average of two speed-context experiments (in different directions) per neuron.
Quantification
Data analysis.
We analyzed firing rate in two different time periods within our task: preparatory-related and pursuit-related epochs. For the analysis of preparatory-related activity, firing rate across the fixation period was computed in 100 ms bins and averaged across all trials in a specific context. Because the duration of the fixation interval varied from 800–1600 ms, each trial contributed data only from the onset of fixation to the onset of target motion, aligned on the onset of fixation. Thus, fewer trials contributed to the estimate of preparatory firing rate as fixation time grew closer to 1600 ms. We computed the average modulation of firing rate across the fixation period by subtracting the firing rate in the period 200–500 ms after fixation onset from the firing rate during the interval from 1200 to 1500 ms after fixation onset (Figure 1b, gray shading). To compare the modulation of preparatory activity in different conditions, we performed principal component regression. The slope of the regression gives an estimate for the relative difference in preparatory modulation between different conditions.
For pursuit-related activity, we analyzed the period 50–150 ms after target motion onset. We chose this window because it is centered on the time of pursuit onset and ends before the time when eye movement related visual feedback would be arriving at FEFSEM. To compare the effects of speed context on pursuit-related firing rate, we used the data for target motion at 10 deg/s and computed the percentage change in the average pursuit-related firing rate in the slow- versus the fast-context. The temporal profiles of the firing rate for our example neuron in Figure 3 were obtained by smoothing the trial-averaged firing rate with a Gaussian filter (standard deviation of 12 ms). Trials where the monkey made a saccade during the window 200 ms following the onset of target motion were excluded from analysis in Figure 3. Only neurons that had an increase in firing rate of at least 5 spikes/s during pursuit initiation in response to target motion at 10 deg/s were used in the analyses of Figure 4.
We used trial-averaged eye speed to analyze the behavioral effects of speed context. We determined the average onset of pursuit initiation for high- and low-contrast stimuli by eye. The analysis period for behavior was 50–100 ms after pursuit onset. This time period was chosen to avoid the effects of eye movement related visual feedback on behavior51. Trials with saccades in the first 200 ms following visual motion onset were excluded in Figure 1b. The splitting of data into 10-trial bins for the time course analysis greatly reduced the amount of data. Thus, we chose to detect saccades using acceleration and velocity thresholds and treat the times during saccades as missing data in the analysis of the time course of behavioral effects (Figure 3).
Decoding of FEFSEM pursuit-related firing rates analysis.
We used a linear decoder constrained by the effect of speed context to predict the effects of both context and target contrast on visual-motor gain, inferred by eye speed responses to the same speed of visual motion. Effect of context was calculated as the percent change of FEFSEM pursuit-related firing rate in response to 10 deg/s target motion during the slow- compared to the fast-context. Cells then were ranked by the effect of context. Importantly, data from high- and low-contrast trials were combined when calculating the effect of context. The weight of each neuron was determined by an exponential fit to rank within the population:
where μ is the sole free parameter, denotes the rank of each neuron within the population, and the weights were normalized so that they summed to a value of one. Visual-motor gain was decoded from the population:
Here, is the pursuit-related firing rate of the neuron with rank i normalized to its average response for all 10 deg/s conditions. The μ parameter was adjusted to minimize the root mean square error between the decoded gain of the fast- and slow-contexts and the visual-motor gain inferred by the relative eye speed responses to the 10 deg/s motions during the fast- and slow-contexts. We also were able to decode the population response successfully by optimizing a simple linear decoder that had the weights of all neurons as free parameters. However, the large number of free parameters allowed the decoder to simply choose a few neurons that had exactly the correct pursuit-related responses to match the behavior, and to assign zero weight to the activity of all other neurons. Finally, responses could be successfully decoded by weighting responses proportionally to their reliability of encoding context (data not shown).
State variable model of prior adaptation.
The model described by Equation 3 in the main text has three free parameters, the number of trials built into the memory term, w1, and w2. The parameters were optimized to minimize: (1) the root mean square error between the predicted and actual single trial effect on preparatory activity in the slow context; and (2) the root mean square error between the predicted and actual magnitude of the difference in preparatory activity in the post-fast versus post-slow controls blocks. The model was initialized with a random prior between 0 and 1 and run through 1000 iterations of the speed context paradigm. The prior then was averaged over these 1000 iterations for the results shown in Figure 6. We hypothesized that pursuit responses contained all of the information necessary to update preparatory activity. Therefore, only data from cells with meaningful pursuit responses were included in the population used for the state variable model, which we judged to be cells with modulations greater than 5 spikes/s. Because of the diversity of response magnitudes across neurons, we chose to normalize firing rates to the pursuit-related response to 20 deg/s target motions of high-contrast targets, responses that always were the largest in magnitude. This strategy allowed us to create clean distributions of firing rates for the different target speeds and provided a simple approach to keep the average value of the state-variable roughly between 0 and 1. The results are unchanged if we normalize in a different manner.
Recurrent network model.
After Lim and Goldman37, we created a recurrently-connected model of 33 excitatory and 33 inhibitory model rate neurons according to the following equations:
Here, sXYi,j and wXYi,j are the synaptic input variable and the weight for the connection from model neuron j to i, where X and Y indicate whether i and j refer to excitatory (Ei) or inhibitory (Ii) model neurons. F is a small “fixation” input that sets the network in motion and starts the preparatory activity by stepping from 0 to 5 spikes/s at t=200 ms. We set the value of k empirically so that pursuit-related activity would be twice preparatory activity for high-contrast target motion at 10 deg/s in the control-context. We created a set of simulated MT population responses (see Supplementary Figure 5) for high- and low-contrast target motion at 2, 10, and 20 deg/s based on data collected in our laboratory for patches of random dots of 100% or 12% contrast. MTj and PSj refer to the response and the preferred speed of the jth model MT neuron. We are happy to provide those population responses as text or matlab files. The effect of target contrast and speed on the pursuit related response (Figure 7b) is an emergent property of the model that is created entirely by the details of the population responses. We take the agreement between real and model FEFSEM neurons in Figure 7b as validation of the simulated MT population responses and the weighted summation decoding computation in the model.
All model synapses and neurons had time constants, so the state of the synaptic inputs from each neuron, si,j, were computed as:
where Xj denotes the firing rate of relevant pre-synaptic model neuron. The values of the shunting inhibition, SHi, for each model excitatory neuron was computed as:
The calculation was the same for inhibitory neurons, replacing sEI with sII. We applied the shunting inhibition only to the MT inputs to avoid disrupting the balance of excitatory and inhibitory neurons that makes the network operate as a stable integrator (Lim and Goldman, 2013). Indeed, because inhibition and excitation are balanced in the inputs to each neuron in the model network, application of shunting inhibition to the recurrent excitation would yield a constant firing rate and obviate the integrating properties of the network. If the actual circuit architecture is related to the structure of our model network, then the excitatory and inhibitory synapses would have to be positioned so that the MT input is subject to shunting inhibition but the recurrent excitation is not.
The input-output function of the model neurons was:
Time constants, drawn heavily from Lim and Goldman37, were: excitatory synapses from model FEFSEM neurons, 25 ms; excitatory synapses conveying MT activity, 30 ms; inhibitory synapses, 10 ms; excitatory neurons, 20 ms; inhibitory neurons, 10 ms. We created trial-by-trial variation in preparatory activity by varying the weight of the fixation input for each model neuron between 0.75 and 1.25 randomly. Initial synaptic weights were set randomly on a uniform distribution between 0.04 and 0.16.
We selected blends of target motions to simulate the slow-, control-, and fast-contexts in our experiments, and we ran simulated trials of duration 1200 ms, where the fixation input was applied from 200 to 1200 ms and the MT input consisted of a 100 ms pulse of input that started at time 1000 followed by a 100 ms ramp back to zero. We implemented the effect of the context on the activity of the model network using a plasticity rule based on calculation of a plasticity variable, Pi,j for each connection between model excitatory neurons:
Intuitively, the numerator and denominator compute the integrated product of pre- and post-synaptic activity at the synapse from model neurons j to i when the model input from MT is either greater than or equal to zero. The notation is the same as in the equations that describe the structure of the network model. Ei(t) is the postsynaptic activity of the ith excitatory model neuron, sEEi,j(t) is the synaptic input variable as a function of time (t) and wEEi,j is the synaptic weight so that their product (in parenthesis in both the numerator and denominator) is the presynaptic activity from the jth excitatory model neuron. Plasticity was applied at the end of each simulated trial, only to the excitatory inputs to excitatory neurons. The learning rate was 0.1% and each weight decayed back towards its initial condition by 9% after each trial. The strength of each model excitatory neuron’s excitatory inputs was increased or decreased if the value of Pi,j was >0.64 or <0.56, respectively.
Intuitively, the plasticity rule determines whether the actual pursuit-related firing rate is larger or smaller than the expectation defined by the preparatory activity. A comparison between pursuit and preparatory activity is necessary because any absolute rule based on overall pre- and post-synaptic activity would be unstable and would push the recurrent weights toward zero or infinity. That said, many other plasticity rules might work, as long as they are based on a comparison of pursuit-related and preparatory activity on a given trial.
We realize that some of the choices we have made for the structure and parameters of our model are less than 100% biologically realistic. Our goal was to show that the synaptic weights in a recurrent network could plausibly store the value of a prior, and that an autonomous plasticity rule could alter those weights in a way that simulated the results of our recordings. The next step of creating a model circuit with biologically realistic mechanisms and plasticity rules in conduction-based, spiking model neurons seems important, but would be a major next step that is beyond the scope defined by the goals of our study.
Statistics
No statistical methods were used to predetermine sample sizes, but our sample sizes are similar to those reported in previous studies. Data were collected from two Rhesus monkeys. A total of 164 single neurons were recorded across 95 speed context experiments: 83 neurons across 54 experiments in monkey Re and 81 neurons across 41 experiments in monkey Xt. Because the number of neurons was greater than the number of experiments, values of “n” are smaller for behavioral measures than for neural measures. On average, two speed context experiments (in two different directions) were run per neuron, yielding a total of 321 neural data points. An additional 16 behavioral speed context experiments were run in monkey Re with form-matched stimuli (Supplemental Figure 3). For the analysis of pursuit-related firing rate (Figure 4), we used only neurons with an increase in firing rate of at least 5 spikes/s for target motion at 10 deg/s: 164 data points from 118 neurons. Statistical comparisons of means were performed using 2-tailed t-tests. Paired t-tests were used for statistical analysis of contrast effects because high- and low- contrast targets were randomly interleaved throughout all experiments. Data distribution was assumed to be normal but this was not formally tested. Data collection and analysis were not performed blind to the conditions of the experiments.
Data availability
All data are available from the corresponding author upon reasonable request.
Software availability
All custom code is available from the corresponding author upon reasonable request.
Supplementary Material
Acknowledgements:
We thank Stefanie Tokiyama and Steven Happel for technical assistance, Greg Field for comments on an earlier version of the manuscript, and Mehrdad Jazayeri for encouragement. We are grateful to Nicolas Brunel for helpful guidance in the network modeling and constructive feedback on the paper, and to Andrew Rosko for pointing out a useful plasticity rule. NIH R01-EY027373 (SGL) and a gift from the Howard Hughes Medical Institute supported the research. TRD received support from the Wakeman Endowment Fund, the Duke University Medical Scientist Training Program (T32 GM007171), and from NIH award F30-EY027684 (TRD).
Footnotes
The authors declare no competing interests.
References
- 1.Körding KP & Wolpert DM Bayesian integration in sensorimotor learning. Nature 427, 244–7 (2004). [DOI] [PubMed] [Google Scholar]
- 2.Körding KP, Ku S & Wolpert DM Bayesian integration in force estimation. J. Neurophysiol 92, 3161–5 (2004). [DOI] [PubMed] [Google Scholar]
- 3.Körding KP Bayesian statistics: relevant for the brain? Curr. Opin. Neurobiol 25, 130–3 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Weiss Y, Simoncelli EP & Adelson EH Motion illusions as optimal percepts. Nat. Neurosci 5, 598–604 (2002). [DOI] [PubMed] [Google Scholar]
- 5.Alais D & Burr D The Ventriloquist Effect Results from Near-Optimal Bimodal Integration. Curr. Biol 14, 257–262 (2004). [DOI] [PubMed] [Google Scholar]
- 6.Battaglia PW, Jacobs RA & Aslin RN Bayesian integration of visual and auditory signals for spatial localization. J. Opt. Soc. Am. A 20, 1391 (2003). [DOI] [PubMed] [Google Scholar]
- 7.Knill DC & Saunders JA Do humans optimally integrate stereo and texture information for judgments of surface slant? Vision Res 43, 2539–2558 (2003). [DOI] [PubMed] [Google Scholar]
- 8.Knill DC Robust cue integration: a Bayesian model and evidence from cue-conflict studies with stereoscopic and figure cues to slant. J. Vis 7, 51–24 (2007). [DOI] [PubMed] [Google Scholar]
- 9.Verstynen T & Sabes PN How each movement changes the next: an experimental and theoretical study of fast adaptive priors in reaching. J. Neurosci 31, 10050–9 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yang J, Lee J & Lisberger SG The interaction of Bayesian priors and sensory data and its neural circuit implementation in visually guided movement. J. Neurosci 32, 17632–45 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Darlington TR, Tokiyama S, & Lisberger SG Control of the strength of visual-motor transmission as the mechanism of rapid adaptation of priors for Bayesian inference in smooth pursuit eye movements. J. Neurophysiol 118, 1173–89 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kowler E, Martins AJ, & Pavel M The effect of expectations on slow oculomotor control. II. Single target displacements. Vision Res 19, 633–646 (1979b). [DOI] [PubMed] [Google Scholar]
- 13.Kowler E, Martins AJ, & Pavel M The effects of expectations on slow oculomotor control. IV. Anticipatory smooth eye movements depend on prior target motions. Vision Res 24, 197–210 (1984). [DOI] [PubMed] [Google Scholar]
- 14.Kowler E & Steinman RM The effect of expectations on slow oculomotor control. I. Periodic target steps. Vision Res 19, 619–632 (1979a). [DOI] [PubMed] [Google Scholar]
- 15.Stocker AA & Simoncelli EP Noise characteristics and prior expectations in human visual speed perception. Nat. Neurosci 9(4), 578–85 (2006). [DOI] [PubMed] [Google Scholar]
- 16.Ma WJ Organizing probabilistic models of perception. Trends Cogn Sci 16, 511–518 (2012). [DOI] [PubMed] [Google Scholar]
- 17.Ma WJ, Beck JM, Latham PE, Pouget A. Bayesian inference with probabilistic population codes. Nature Neurosci 9, 1432–1438 (2006). [DOI] [PubMed] [Google Scholar]
- 18.Lisberger SG Visual guidance of smooth-pursuit eye movements: sensation, action, and what happens in between. Neuron 66, 477–91 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Newsome WT, Wurtz RH, Dursteler MR, Mikami A Deficits in visual motion processing following ibotenic acid lesions of the middle temporal visual area of the macaque monkey. J. Neurosci, 5(3), 825–40 (1985). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Krekelberg B, van Wezel RJA & Albright TD Interactions between speed and contrast tuning in the middle temporal area: implications for the neural code for speed. J. Neurosci 26, 8988–98 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gottlieb JP, Bruce CJ & MacAvoy MG Smooth eye movements elicited by microstimulation in the primate frontal eye field. J. Neurophysiol 69, 786–99 (1993). [DOI] [PubMed] [Google Scholar]
- 22.Gottlieb JP, MacAvoy MG & Bruce CJ Neural responses related to smooth-pursuit eye movements and their correspondence with electrically elicited smooth eye movements in the primate frontal eye field. J. Neurophysiol 72, 1634–53 (1994). [DOI] [PubMed] [Google Scholar]
- 23.Tanaka M & Lisberger SG Role of arcuate frontal cortex of monkeys in smooth pursuit eye movements. I. Basic response properties to retinal image motion and position. J. Neurophysiol 87, 2684–99 (2002a). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tanaka M & Lisberger SG Regulation of the gain of visually guided smooth-pursuit eye movements by frontal cortex. Nature 409, 191–4 (2001). [DOI] [PubMed] [Google Scholar]
- 25.Tanaka M & Lisberger SG Enhancement of multiple components of pursuit eye movement by microstimulation in the arcuate frontal pursuit area in monkeys. J. Neurophysiol 87, 802–18 (2002b). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nuding U, Kalla R, Muggleton NG, Büttner U, Walsh V, Glasauer S. TMS evidence for smooth pursuit gain control by the frontal eye fields. Cereb. Cortex 19, 1144–50 (2009). [DOI] [PubMed] [Google Scholar]
- 27.Ono S & Mustari MJ Smooth pursuit-related information processing in frontal eye field neurons that project to the NRTP. Cereb. Cortex 19, 1186–97 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Brodal P The cortical projection to the nucleus reticularis tegmenti pontis in the rhesus monkey. Exp. Brain Res 38, 19–27, 1980a. [DOI] [PubMed] [Google Scholar]
- 29.Brodal P The projection from the nucleus reticularis tegmenti pontis to the cerebellum in the rhesus monkey. Exp. Brain Res 38, 29–36, 1980b. [DOI] [PubMed] [Google Scholar]
- 30.Shi D, Friedman HR, & Bruce CJ Deficits in smooth-pursuit eye movements after muscimol inactivation within the primate’s frontal eye field. J. Neurophysiol 80, 458–64 (1998). [DOI] [PubMed] [Google Scholar]
- 31.Keating EG Frontal eye field lesions impair predictive and visually-guided pursuit eye movements. Exp. Brain Res 86, 311–23 (1991). [DOI] [PubMed] [Google Scholar]
- 32.MacAvoy MG, Gottlieb JP, & Bruce CJ Smooth-pursuit eye movement representation in the primate frontal eye field. Cereb. Cortex 1, 95–102 (1991). [DOI] [PubMed] [Google Scholar]
- 33.Lee J, Yang J & Lisberger SG Control of the gain of visual-motor transmission occurs in visual coordinates for smooth pursuit eye movements. J. Neurosci 33, 9420–30 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Laquitaine S and Gardner JL A switching observer for human perceptual estimation. Neuron 97: 1–13, 2018. [DOI] [PubMed] [Google Scholar]
- 35.Tanaka M & Fukushima K Neuronal responses related to smooth pursuit eye movements in the periarcuate cortical area of monkeys. J. Neurophysiol 80, 28–47 (1998). [DOI] [PubMed] [Google Scholar]
- 36.Mahaffy S & Krauzlis RJ Neural activity in the frontal pursuit area does not underlie pursuit target selection. Vision Res 51, 853–66 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Snyder AC, Morais MJ, & Smith MA Dynamics of excitatory and inhibitory networks are differentially altered by selective attention. J. Neurophysiol 116(4), 1807–20 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lim S & Goldman MS Balanced cortical microcircuitry for maintaining information in working memory. Nat. Neurosci 16(9), 1306–14 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Beck JM, Ma WJ, Kiani R, Hanks T, Churchland AK, Roitman J, Shadlen MN, Latham PE, & Pouget A Probabilistic population codes for Bayesian decision making. Neuron 60: 1142–1152 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Maunsell JH & Van Essen DC Functional properties of neurons in middle temporal visual area of the macaque monkey. I. Selectivity for stimulus direction, speed, and orientation. J. Neurophysiol 49(5), 1127–47 (1983). [DOI] [PubMed] [Google Scholar]
- 41.Mikami A, Newsome WT, Wurtz RH Motion selectivity in macaque visual cortex. I. Mechanisms of direction and speed selectivity in extrastriate area MT. J. Neurophysiol 55(6), 1308–27 (1986). [DOI] [PubMed] [Google Scholar]
- 42.Salinas E, Abbott LF Vector reconstruction from firing rates. J. Comput. Neurosci 1: 89–107 (1994). [DOI] [PubMed] [Google Scholar]
- 43.Groh JM Converting neural signals from place codes to rate codes. Biol. Cybern 85: 159–165 (2001). [DOI] [PubMed] [Google Scholar]
- 44.Churchland MM & Lisberger SG Shifts in the population response in the middle temporal visual area parallel perceptual and motor illusions produced by apparent motion. J. Neurosci 21: 9387–9403 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bogadhi AR, Montagnini A, & Masson GS Dynamic interaction between retinal and extraretinal signals in motion integration for smooth pursuit. J. Vis 13, 5, 1–26 (2013). [DOI] [PubMed] [Google Scholar]
- 46.Schwartz JD & Lisberger SG Initial tracking conditions modulate the gain of visuo-motor transmission for smooth pursuit eye movements in monkeys. Vis. Neurosci 11, 411–24 (1994). [DOI] [PubMed] [Google Scholar]
Methods References
- 47.Fuchs AF & Robinson DA A method for measuring horizontal and vertical eye movement chronically in the monkey. J. Appl. Physiol 21, 1068–70 (1966). [DOI] [PubMed] [Google Scholar]
- 48.Ramachandran R & Lisberger SG Normal performance and expression of learning in the vestibulo-ocular reflex (VOR) at high frequencies. J. Neurophysiol 93, 2028–2038 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Rashbass C The relationship between saccadic and smooth tracking eye movements. J. Physiol 159, 326–38 (1961). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Osborne LC, Hohl SS, Bialek W, & Lisberger SG Time course of precision in smooth-pursuit eye movements of monkeys. J. Neurosci 27(11), 2987–98 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lisberger SG & Westbrook LE Properties of visual inputs that initiate horizontal smooth pursuit eye movements in monkeys. J.Neurosci 5, 1662–73 (1985). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data are available from the corresponding author upon reasonable request.


