Electrostatic control of calcineurin’s intrinsically-disordered regulatory domain binding to calmodulin

Abstract

Calcineurin (CaN) is a serine/threonine phosphatase that regulates a variety of physiological and pathophysiological processes in mammalian tissue. The calcineurin (CaN) regulatory domain (RD) is responsible for regulating the enzyme’s phosphatase activity, and is believed to be highly-disordered when inhibiting CaN, but undergoes a disorder-to-order transition upon diffusion-limited binding with the regulatory protein calmodulin (CaM). The prevalence of polar and charged amino acids in the regulatory domain (RD) suggests electrostatic interactions are involved in mediating calmodulin (CaM) binding, yet the lack of atomistic-resolution data for the bound complex has stymied efforts to probe how the RD sequence controls its conformational ensemble and long-range attractions contribute to target protein binding. In the present study, we investigated via computational modeling the extent to which electrostatics and structural disorder co-facilitate or hinder CaM/CaN association kinetics. Specifically, we examined several RD constructs that contain the CaM binding region (CAMBR) to characterize the roles of electrostatics versus conformational diversity in controlling diffusion-limited association rates, via microsecond-scale molecular dynamics (MD) and Brownian dynamic (BD) simulations. Our results indicate that the RD amino acid composition and sequence length influence both the dynamic availability of conformations amenable to CaM binding, as well as long-range electrostatic interactions to steer association. These findings provide intriguing insight into the interplay between conformational diversity and electrostatically-driven protein-protein association involving CaN, which are likely to extend to wide-ranging diffusion-limited processes regulated by intrinsically-disordered proteins.

1. Introduction

Calcineurin (CaN) is a ubiquitously expressed protein that regulates myriad developmental and signaling processes (1; 2). It is chiefly regulated by calmodulin (CaM), one of the most prolific proteins in terms of its role in shaping intracellular signal transduction cascades. Despite the fundamental importance of CaM-regulated CaN phosphatase activity in organism physiology, the molecular mechanisms governing this process are incompletely understood. Given that CaM/CaN is a prototypical example of a protein/protein complex involving a globular protein (CaM) and an intrinsically disordered binding domain (CaN) (3; 4), structural details of the protein/protein complex are restricted to intact CaM bound to a small fragment of the CaN regulatory peptide. In this regard, the CaM/CaN complex is similar to the tens of CaM/protein target complexes (5) that have resisted structure determination methods beyond the binding of short peptides. Remarkably, despite the CaN regulatory domain presenting little stabilized secondary structure, the CaM/CaN complex binds with picomolar affinity (6), afforded in part by rapid, diffusion-limited binding.

CaN is heterodimeric protein consisting of two domains: chain A (57-61 kDa) and chain B (19 kDa) (2; 7), while CaM (17 kDa) is comprised of two alpha-helix rich domains capable of binding Ca²⁺. At Ca²⁺ concentrations typical of resting cells (50 to 100 nM) (8), CaN phosphatase activity is negligible, while CaM is believed to be in Ca²⁺-free state (9). Under these conditions, the CaN catalytic domain is autoinhibited by the protein’s auto-inhibitory domain (AID). At rising Ca²⁺ concentrations, the CaN AID is removed from the catalytic domain. CaM binding to the AID-containing CaN regulatory domain (RD) (Ser373 to Thr468) is a critical determinant of this process (4; 10). Interestingly, like many intrinsically disordered peptide (IDP)-containing complexes, well-defined secondary structure is observed only upon binding a protein target (11; 12; 13; 14).

In absence of hydrophobic residues (15) that would otherwise promote collapse of protein into a molten apolar core, many IDPs such as the CaN RD are polyampholytic (16). Metrics like the net charge per residue (NCPR) have been proposed to relate charge density in IDPs to ensemble properties including compactness and shape (17; 18). Formally, NCPR = ∣f₊ – f₋∣ where f₊ and f₋ are fractions of positively and negatively charged residues, respectively, and fraction of charged residues (FCR) is calculated as $\frac{N_c}{N_t}$ where N_c is the number of charged residues and N_t is the total number of residues. Generally, IDPs with large NCPR values (> 0.25) tend to adopt more extended conformations due to repulsive intra-molecular electrostatic interactions (17; 19). However, the distribution of charged residues in the CaN RD is heterogeneous, thus such sequence-dependent metrics have limited utility in determining localized properties, such as the availability of binding motifs to target proteins.

We hypothesized therefore that RD sequence charge composition (as measured by NCPR) and ionic strength influence the dynamic availability of conformations amenable to CaM binding, while long-range electrostatic interactions drive diffusion-limited association (see Fig. 1). To investigate this hypothesis, we utilize long-timescale MD simulations to probe the highly dynamic conformational ensembles comprising the RD constructs, toward delineating the extent to which conformational gating kinetics and long-range electrostatic interactions govern IDP/protein association. A chief outcome of this work is that charge-sensitive ’local’ and long range factors, namely IDP conformational dynamics and IDP/target electrostatic interactions, can jointly facilitate diffusion-limited target association.

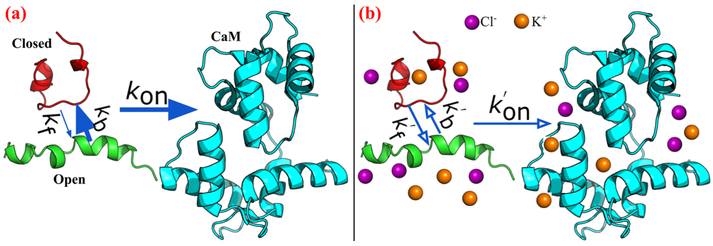
Figure 1.

Schematic of CaN peptide binding to CaM. The green and red peptides represent CaM conformations which are capable and incapable of binding to CaM (colored in cyan). The association rates between intrinsically-disordered CaN peptides and CaM are controlled by open/closed state gating kinetics (depicted by k_b and k_f) and the CaM/CaN diffusional encounter rate (depicted by k_on). Our study demonstrates that low (a) and high (b) ionic strengths influence both contributions to afford diffusion limited encounters

2. Methods

The initial structures of three CaN RD constructs predicted by Rosetta (20) (see Sect. 2.1) were followed by extensive microsecond scaled MD via Amber14 (21) (see Sect. 2.2). The 2D REUS potential of mean force (PMF) calculations of CaN RD constructs were performed by NAMD2.11 (22) (see Sect. 2.3). The MD trajectories were used to characterize the conformational dynamic of CaN RD constructs through Markov state model (MSM) via Aqualab (23) (see Sect. 2.4). The diffusional encounter rates of CaN RD constructs with CaM were simulated by BrownDye package (24) (see Sect. 2.5) and the effective association rates with conformational dynamics taken into account were given in Sect. 2.6.

2.1. Structure preparation

The N-domain (residue numbers 3 to 75) and C-domain (residue numbers 76 to 147) of CaN were extracted from the crystal structure (PDB ID: 4Q5U (25)). For CaN peptides, three different peptides with varying lengths and charge distributions were considered: 1) pCaN: native binding region for CaM. 2) lpCaN: elongated pCaN with five additional residues added to two ends of pCaN, respectively. 3) lpcCaN: charge mutated lpCaN having EESE to KKSK mutations at the C-terminal end. Since diffusion limited binding between CaM and CaN are suggested for both intact CaN and its regulatory domain (arXiv:1611.04080v1), we postulated that these comparatively shorter constructs could capture key factors governing diffusion limited association in a computationally-tractable manner. Rosetta (20) was used to model initial conformations for the CaN peptides.

The number of output conformations was set to ten. No pre-defined secondary structure file was specified. The rest parameters were not explicitly specified (namely using their default values, as that listed in (26)). According to the energy score, for each CaN peptide, the conformation with lowest energy was picked out for further extensive MD sampling. Although just one conformations was selected for each CaN peptide, it was expected that the following microsecond MD ensure adequate sampling.

2.2. Molecular dynamic simulation

We next performed MD simulations to extensively explore the conformational space of the CaN peptides. The Amber ff99SB-ILDN (27) force field was chosen, given its improved recapitulation of experimentally-observed IDP ensembles, in contrast to common forcefields that tend to predict overly collapsed states for IDPs (28). The MD was performed by using Amber14 (21). The implicit solvent model (igb = 2 with salt concentration = 0.15 M) was used. The reason for choosing implicit solvent model was as following: 1) According to a recent study (29), a combination of ff99SB-ILDN with implicit solvent model could achieve reasonably accurate sampling for IDPs; 2) Implicit solvent model would enable more sufficient sampling with affordable time cost. The cutoff value for non-bond interactions was set as 999 A. The starting structure was first subjected to 50000 steps of energy minimization. The minimized structure was slowly heated from 1 to 298.15 K by using the Berendsen Thermostat within 800 ps. During the MD process, the time interval was set to 2 fs and the SHAKE (30) constraints were applied on bonds involving hydrogen atoms. By setting the initial temperature in the heating stage equal to 1 instead of 0 and ig = −1 would generate different initial velocity distributions for the system, thus independent simulations can be achieved. For each peptide, three independent MDs were performed to ensure the reliability of the sampling (total 15 μs production run for each peptide). To study the effect of ionic strength on sampling, we ran analogous simulation with salt concentration = 1.5 M, resulting in a total 30 μs production run for each peptide (15 μs at 0.15 M and 15 μs at 1.5 M ionic strength). Although 1.5 M ionic strength is non-physiological, however, this high ionic strength would significantly increase the electrostatic-screening effect and facilitates more pronounced changes in CaN peptide conformational properties under a different electrostatic environment as compared to the physiological 0.15 M ionic strength. In RMSF calculations, for each peptide, we first performed rms-fitting of trajectory frames to the first frame of trajectory. The rms-fitting would eliminate the translational and rotational effect and ensure the RMSF reflect the fluctuation of atoms. Contact map data of heavy atoms was collected via CPPTRAJ in Amber with distance cutoff as 7 Å and only residue pairs which are at least 5 residues apart (i and i + 5) in sequence are considered.

2.3. Two-dimensional replica-exchange umbrella sampling (REUS) PMF calculation

Two-dimensional PMF calculations were performed to characterize the free energy profile associated with conformational space of each peptide. Two reaction coordinate (RC)s were defined: 1) α which describes the α-helical content of the peptide (ranging from 0.1 to 0.9) and 2) radius of gyration (R_g) of the peptide (ranging from 5 to 32 Å). Each RC range was divided into nine bins resulting in total 81 windows (with interval being 0.1 and 3 Å for α and R_g, respectively). The two force constants of the harmonic potentials imposed on these two RCs are 1.000 × 103 kcal mol⁻1 U⁻2 for α and 2.5 kcal mol⁻1

Å⁻2 for R_g. For each peptide, the representative structure from the most populated cluster was chosen as the starting structure. NAMD2.11 (22) was chosen to perform the 2D REUS calculations due to it’s colvar module which supports various user-defined collective variables. The CHARMM36 (31; 32) force field was used in the 2D REUS calculations. For each window, the simulation length was set to 20 ns and only the last 15 ns data was used to calculate free energy by WHAM (33).

2.4. Markov state model (MSM) analysis via Aqualab

For each peptide, a 1D kinetic trajectory was created from the 15 μs MD trajectory describing the state change along simulation time. Open states were defined based on examining Browndye-predicted association rates as a function of root mean squared deviations (RMSD); the RMSD value below which the association rate rapidly increased above negligible values was utilized as the open/closed state cutoff criterion. We note the ’closed states’ are not necessarily precluded from binding, but we assume that the timescale for assuming a conformation compatible with the complex via induced fit is slow. These criteria differed among the three peptides, based on our Fig. S10 and Fig. S9. For pCaN, the open state was defined as RMSD < 7 Å while for lpCaN and lpcCaN the open state are defined as RMSD < 5 Å. Using these cutoffs, Markovian networks were created based on the 1D trajectory (rates of open to closed and vice versa) via Aqualab (23), for which conditions such as detailed balance (34) were imposed to define P, the equilibrium probability matrix and T, the transition probability matrix.

2.5. Brownian dynamic (BD) simulations

The binding of CaN peptide and N/C terminal domains of CaM are treated as two independent events and simulated separately by using the BrownDye package (24). For each peptide, ten conformations for each RMSD cluster were randomly selected to perform BD simulations with N/C-domain of CaM. The PDB2PQR (35) was first used to generate the pqr files for CaM N/C domains and the selected conformations of CaN peptides from MD trajectory with radii and point charge parameters adapted from the AMBER99 (36) force field. The generated pqr files were then passed into APBS (37) to evaluate the electrostatic potential of these structures. APBS was used to numerically solve the linearized Poisson-Boltzmann equation assuming an ionic strength of 0.15 M and 1.5 M NaCl:

$$-ϵ{\nabla }^2\mathrm{\psi }=\sum {\rho }_i{q}_i-{\mathrm{\kappa }}^2\mathrm{\psi }$$ [1]

where ψ is the electrostatic potential, ρ_iq_i is the charge distribution of fixed charge i, and κ is the inverse of Debye length. The Debye length reflects the scale over which mobile charges could screen out electric potential fields.

In present BD simulation, the reaction criterion was chosen to be six pairs of contacts with distance of contact being less than 10 Å. The contact list was created via the make_rxn_pairs routine in Browndye package based on the pCaN-CaM complex crystal structure (PDB ID: 4Q5U (25)) with distance cutoff being 5 Å. 10000 single trajectory simulations for each system were conducted on 10 parallel processors using nam-simulation. Thus for each peptide, the total number of BD trajectories was about 1 million. The reaction rate constants were calculated using compute-rate-constant from the BrownDye package.

To estimate the association rate and its sensitivity to ionic strength, we computed association rates for the terminal domains separately, assuming that both components bind independently,

$$\frac{1}{k_{\text{on}}}=\frac{1}{k_{Cterm}}+\frac{1}{k_{Nterm}}$$ [2]

where the rates in the right hand side correspond to the association rates for the C and N terminal domains, respectively. We anticipate that this expression under-approximates the rate of complex formation, given that tethered binding partners generally exhibit higher efficiencies for forming intact complexes (38; 39).

2.6. Effective association rate combined with gating kinetics

The effective association rate constant after taking conformational dynamics into account was given by Szabo et al (40):

$$k_{\text{eff}}=\frac{K_D{K}_{eq}{k}_{b}Z\left[k_{\mathrm{f}}+k_{\mathrm{b}}\right]}{k_{\mathrm{f}}\left(K_{eq}+K_{D}Z\left[k_{\mathrm{f}}+k_{\mathrm{b}}\right]\right)+k_{\mathrm{b}}Z\left[k_{\mathrm{f}}+k_{\mathrm{b}}\right]\left(K_D+K_{eq}\right)}$$ [3]

where

$$Z[k_{\mathrm{f}}+k_{\mathrm{b}}]=1+\left(\right(k_{\mathrm{f}}+k_{\mathrm{b}})R^2∕D{)}^{0.5}$$ [4]

where K_D is the association rate when the peptide is always in open state and in present study, K_D is the BD simulated association rate constant of the open state CaN peptides with CaM (e.g., K_D = k_{on, open}). K_eq is characteristic constant indicating the extent to which the association is diffusion-controlled (see (40) for more details). In present study, we set K_eq = 1 × 10²⁰M⁻¹s⁻¹ and justified by showing in Fig. S8 the sensitivity of k_eff to K_eq, as we can see that k_eff values for all peptides become fixed after K_eq is larger than 1 × 10⁶ M⁻¹ s⁻1 (see also Sect. S.1). k_f and k_b are the conversion rate between the open and closed state determined from MSM. R is the contact distance at which the transient complex formed and in present study we set R equal to the average b-radius values from BD simulations. D is the relative translational diffusional constant and was calculated via (24; 41).

$$D=\frac{K_D}{4\pi R{f}_{\infty }}$$ [5]

where f_∞ is the reaction probability which was at the order of 1 × 10⁻4 given by BD simulations.

3. Results and Discussion

3.1. Molecular simulations confirm the intrinsically-disordered structure of the CaN regulatory domain

Several studies using circular dichroism spectroscopy, hydrogen-deuterium exchange mass spectrometry, Fourier transform infrared spectroscopy and X-ray crystallography indicate that the nearly one-hundred amino acids of the CaN RD domain (Ser373 to Thr468 (3; 4)) form an intrinsically disordered ensemble (42; 43; 44; 4). Of these, approximately twenty amino acids (Ala391-Arg414) comprising the CAMBR adopt an alpha-helix in the presence of CaM (25). Here we examine three RD constructs (pCaN, lpCaN and lpcCaN, see Fig. 2) that present diffusion-limited association with CaM (arXiv:1611.04080v1). pCaN spans residues A391 to R414 and has been co-crystallized with CaM (PDB ID: 4Q5U (25)). lpCaN includes three additional polar residues (Ser3, Ser32 and Ser34) and four additional charged residues (Asp1, Glu30, Glu31 and Glu33) while lpcCaN is a peptide of the same length with substitutions of three glutamic acids with lysines at the C-termini of lpCaN. The set of constructs considered here span a range of charge densities that we later demonstrate tune CaM/CaN association kinetics. pCaN and lpcCaN have similar NCPR values of 0.291 and 0.264, which are considerably larger than the value for lpCaN (0.088); previous works (17; 19), suggest NCPR scores above 0.25 reflect extended IDP conformations given the propensity for repulsive intramolecular interactions, whereas those below this threshold are comparatively compact. We expected therefore that 1) the CaN peptides lack well-resolved secondary structure characteristic of a folded protein and 2) the ensemble of lpCaN should be modestly more compact than that of lpcCaN, given that latter has higher charge density.

Figure 2:

Amino acid sequences of three CaN peptide constructs examined here, including their respective FCR and NCPR scores. pCaN: native CAMBR of CaN (Ala391- Arg414). lpCaN: five predominantly negatively charged residues affixed to the pCaN termini. lpcCaN: lpCaN construct with three positively-charged substitutions at the C-terminus. In present study, the residue numbers of lpCaN and lpcCaN are counted from 1 to 34 while pCaN has the residue numbers from 6 to 29.

To investigate the hypothesis, we performed 5 μs MD simulations in triplicate (total 15 μs) at 0.15 M and 1.5 M ionic strength, respectively. The choice of physiological (0.15 M) and high ionic strength was intended to probe the contribution of intra-peptide electrostatic interactions to ensemble properties, as such interactions would be screened at high ionic strength. While simulations of IDPs of up to 100 residues have been reported elsewhere (19), the breadth of simulations used in this study restricted our construct sizes to 24 to 34 a.a. Our MD simulations indicate that the heavy atom root mean squared fluctuations (RMSF) for each residue in Fig. S1(e-f) are shown to be larger than 5 Å for all three peptides at both ionic strengths, which is consistent with the high mobility loop scores reported in Fig. S1(b). These data suggest that the peptides do not form stable folded structures in solution regardless of ionic strength.

The MD-generated structures present a multitude of conformations, ranging from loosely-formed, hairpin-like configurations to extended structures. lpCaN presents perhaps the most hairpin character, as corroborated by intramolecular contacts reported through contact map analyses in Fig. S2. Among these contacts are prominent interactions between Arg12-Glu30, Arg23-Glu30 and Arg13-Glu32, which we attribute to transient salt-bridge formation. For lpcCaN, the mutation of negative residues (Glu30, Glu31 and Glu33) to the positively charged residues (Lys30, Lys31 and Lys33) appears to disrupt these intramolecular contacts, thereby yielding a more extended conformational ensemble relative to lpCaN. Given the similar NCPR values of pCaN and lpcCaN, we expected pCaN would similarly present fewer intramolecular contacts than lpCaN. Surprisingly, pCaN has similar contact map features as lpCaN, that is, both peptides have comparable intra-contacts. Later we will demonstrate that it is in fact the interconversion kinetics, not the average structural properties, of lpCaN and pCaN that dictate binding kinetics. Additionally, we found that increasing ionic strength to 1.5 M screens the electrostatic interactions between residues comprising the reported salt bridges. As a result, we observe for pCaN and lpcCaN that the structures become modestly more extended on average.

It is important to acknowledge that while implicit solvent simulations permit greater degrees of conformation sampling compared to their all-atom counterparts (45), the utilization of an implicit solvent comes with certain limitations. Among these include the propensity to overestimate alpha-helical character and to alter the interaction strengths of salt-bridging amino acid pairs (46). Similarly, in the event that charged amino acids might chelate counterions in solution, as exemplified by acidic EF-hands in diverse Ca²⁺ binding proteins (47), implicit solvent may underestimate the strength of such interactions. It would therefore be of interest in future studies to assess the significance of these limitations in IDPs using explicit all-atom simulations of comparable length to implicit solvent trajectories.

To support the formation of the CaN/CaM protein-protein interaction (PPI), the CaN CAMBR must be revealed to the solvent-exposed CaM surface. The exposure of the CAMBR could occur spontaneously, which would promote binding by presenting mutually compatible conformations independent of the complementary species, or via an induced-fit mechanism when the binding partner, CaM, is present. In the previous section, we indicated that the peptides have considerable structural variability, therefore here we determine whether this variability confers greater access to the CAMBR independent of CaM.

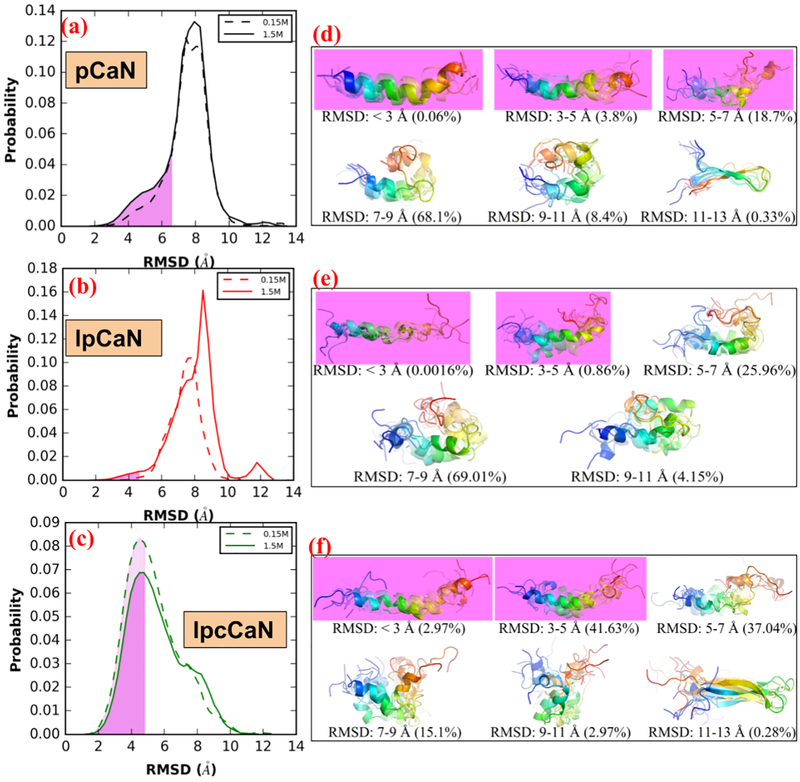
In Fig. 3(a-c), we report the RMSD of the CAMBR binding region for each configuration from the MD simulations, relative to the extended, alpha-helical pCaN conformation that is compatible with the CaM binding surface. From these simulations, we identify conformations that are amenable for CaM binding (”open” state) and those unsuitable for CaM binding (”closed” state), using a cutoff of pCaN: 7 Å, lpCaN and lpcCaN: 5 Å. We utilized a more restrictive criterion for the longer constructs, as the 7 Å cutoff assumed for pCaN yielded structures that were incompatible with CaM. RMSD values below the cutoff more closely resemble the fully-extended reference structure, whereas values above this cutoff are more compact. As shown in Fig. 3(a-c), all three peptides adopt a small percentage of CaM-compatible configurations as measured by RMSD and the percentages appear to be insensitive to ionic strength. These data additionally indicate that lpCaN (NCPR = 0.088) has the smallest percentage of CaM-campatible structures as assessed by RMSD compared with the bound CaN complex, relative to lpcCaN (NCPR = 0.264) and pCaN (NCPR = 0.291).

Figure 3:

Distribution of RMSD (with respect to bound-pCaN crystal structure in PDB 4Q5U) in the MD of each CaN peptide at 0.15 M ionic strength and 1.5M ionic strength, respectively(a-c). The shaded area colored in violet denotes the open state-like conformation. The representative structures (colored in rainbow with N-termini as blue and C-termini as red) for each RMSD range and percentage of conformations within this RMSD range were also shown(d-f).

In Fig. 3(d-f), we present the structures of the most probable conformations based on RMSD clustering analysis. Significantly, each peptide was observed to partially fold into an α-helix, indicating that bound-like ’residual’ structures can spontaneously form in the absence of the binding partner, as has been reported for other IDPs (48; 49; 50; 51). The open state probabilities we determined represented a small, but significant fraction (pCaN: ~20%; lpCaN: ~1%; lpcCaN: ~45%) of the conformations sampled. Importantly, these data indicate extended CaM-compatible conformations form spontaneously and in a charge density (NCPR)-dependent manner (see Fig. 3(a-c)). We speculate that the tendency for a percentage of the conformational ensemble to assume an extended pose relative to a hairpin fold suggests that intra-molecular repulsion may partially destabilize the formation of loose hairpins. This effect would be exacerbated with charge densities of increasing magnitude, such as those reflected in the NCPR values for pCaN and lpcCaN, and relatively diminished for low NCPR peptides like lpCaN.

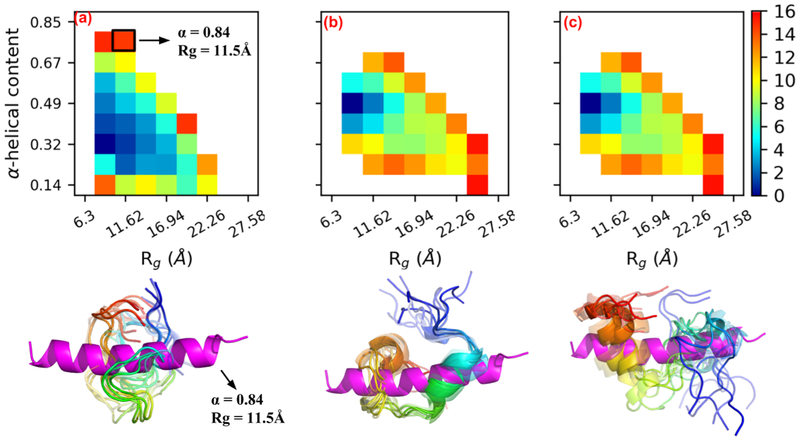
To establish a thermodynamic basis for the trends of greater conformational diversity for the high NCPR cases (pCaN and lpcCaN) relative to the low NCPR case (lpCaN), we report potential of mean force (PMF) calculations for these peptides as a function of α-helical character, a measure of secondary structure formation, and R_g, a measure of compactness (see Fig. 4). Such PMFs have been used to characterize the propensity for IDPs to assume specific ensemble characteristics, including IDP compactness (52; 53). Each construct preferentially adopted smaller α-helical character than the 84% reflected in pCaN when bound to CaM. Lacking CaM, unfolded CaN RD states dominate the conformational distribution, thus CaM is apparently necessary to shift the IDP ensemble toward the bound state via an induced-fit mechanism.

Figure 4:

Two dimensional PMFs for pCaN (a), lpCaN (b) and lpcCaN (c) at 0.15 M ionic strength. The x and y axis depict α-helical and R_g reaction coordinates, respectively. The x axis of (b) and (c) are hidden for clarity. For each peptide, ten randomly selected structures (colored in rainbow with N-termini as blue and C-termini as red) from lowest energy area are compared against bound state pCaN conformation (colored in magenta) from PDB 4Q5U (α = 0.844, R_g = 11.54 Å). The unit of color bar is k_bT where k_b is Boltzmann constant and T = 298 K is temperature.

Interestingly, we observe that the range of R_g and α-helical values within a few k_bT of the energy minima (0 k_bT) are larger for the high NCPR cases compared to lpCaN. These data mirror our findings for the histogram of RMSD distributions in Fig. 3, with the low NCPR case presenting a narrower distribution relative to the high NCPR cases. Further, the PMF data support the observation for the lpCaN and lpcCaN peptides that the former structure assumes a more compact, hairpin-like configuration relative to the latter, as we observed in Fig. 3(d-f). This indicates that the high NCPR cases access a larger range of conformations in their IDP ensembles that overlap with the CaM-bound structures, albeit in contrast to the more narrowly peaked distributions presented for the low NCPR (lpCaN) configuration. Our results are consistent with the work done by Mao et al (17) for protamine IDPs demonstrating that globule-to-coil transitions were more favored with increasing of NCPR values.

3.2. CaN regulatory domain ensemble conformational dynamics are rapid and have modest ionic-strength dependence

Our unconstrained MD and PMF calculations both indicate that the CaN RD peptides do not readily assume an open-state compatible with CaM, although there exist some infrequent, CaM-compatible configurations. In this regard, one can view the accessibility of the prefolded CAMBR domain to CaM as a ’gating’ event, which in principle could control the apparent binding rate for this process (54; 55). Given that our previous work (arXiv:1611.04080v1) in which CaN peptides are assumed to have fully CaM-compatible CAMBR conformations demonstrated that all three peptides are capable of binding CaM, albeit at substantially different rates. We hypothesized that the appearance of bound-like structures before binding serves to nucleate loosely-associated CaM-compatible transient encounter states with low alpha-helical character, which permits ’induced folding ‘ in the presence of CaM to access alpha-helix rich bound-states.

As a first step towards probing this hypothesis, we first estimated the transition kinetics between open and closed states identified in Sect. 3.1.2 using Markov state model (MSM) analysis. Intuitively, we would expect that higher rates of accessing CaM-compatible open states would maximize the CaM/CaN association rate. We note here that we defined the open state as consisting of conformations below the 7 Å (for pCaN) and 5 Å (for lpCaN and lpcCaN) RMSD cutoff used in Fig. S10 (the red dash lines depict the RMSD of open and closed state for each peptide), while all conformations with dissimilar RMSDs were lumped into a single closed state. We verify that the states are essentially Markovian as the correlation times become negligible beyond roughly tens of nanoseconds (see Fig. S4) which is faster than the diffusion encounter time. Overall, based on this partition of MD data, the transition rates between closed and open states are rapid (the slowest rate is at 1 × 10⁷ s⁻1 order, see Table S1) and lead to the short-lived open states shown in Fig. S5 (average life times of open state for all three peptides under both ionic strengths are around 0.2 ns).

Ionic strength was shown to have negligible impact on the RMSD of our predicted peptide structures relative to CaM-bound conformation. However, given the pronounced role of electrostatics in facilitating protein/protein association rates and protein folding (56; 57), we sought to determine whether transition kinetics between conformations were influenced by ionic strength. Hence, we compared MSM rate predictions for MD generated structures at low (0.15 M) and high (1.5 M) ionic strength. Here we found that for pCaN and lpcCaN, increasing ionic strength does not affect the gating rates between open and closed states. However, for lpCaN, increasing ionic strength increased k_f from 1 × 10⁷ s⁻1 to 1 × 10⁸ s⁻1 order. As a result the lifetime of its closed states decreased from 12.83 to 4.42 ns, as shown in Fig. S5. Hence, the open and closing kinetics of peptides with high NCPR are appear to be less sensitive to ionic strength, compared to structures with low NCPR. These results concur with findings from Liu et al (58), for which they demonstrated that the fast-phase structural fluctuations as measured by Fluorescence correlation spectroscopy (FCR) for the IDP Sic1 disappeared with decreasing ionic strength. At first glance, it is surprising that the ionic strength did not appreciably alter the average properties of the conformation ensemble. However, we anticipate that the change in ionic strength, while significant, was insufficient to strongly disfavor the desolvation of the charged groups in order to drive hydrophobic collapse. In contrast, a less hydrophilic solvent, e.g. one with a low dielectric constant, would strongly reduce the desolvation energy and thereby is expected to lead to a hydrophobic collapse.

3.3. Long-range interactions promote rapid CaM/CaN association

Our results thus far indicate that the CaN RD peptides adopt CaM-compatible conformations in the absence of CaM frequently, albeit transiently. Here we determine the compatibility of these transient states with the CaM/CaN binding interface using Brownian dynamic (BD) simulations. Specifically, we sought to evaluate two hypotheses: 1) that frequent presentation of CaN open states promote near diffusion-limited association rates and 2) that long-range electrostatic interactions are exploited in PPIs involving IDPs. Motivating our first hypothesis are recent indications that target-compatible residual structures of the isolated p53 up-regulated modulator of apoptosis (PUMA) IDP form spontaneously as a function of ionic strength and electrolyte composition (59). For the latter hypothesis, we adopt the paradigm of electrostatically-driven association of globular proteins (60; 61; 62; 41), which depends critically on the notion of a transient encounter complex (63; 64). The encounter complex serves as the rate determining step in PPI formation, whereby a protein loosely binds to its protein target, before adopting the fully-formed bound configuration. However, unlike PPIs involving globular partners that typically feature regions of complementarily-charged hydrophilic patches (65; 66), such patches may only be transiently presented in IDPs. Though these results offer specific insights into the ubiquitous Ca²⁺ signaling partners CaM and CaN, these trends may vary in importance depending on the IDP sequence, particularly those with vastly different amino acid charge densities and distributions.

We tested these hypotheses by assuming each peptide must achieve a minimal number of ’native contacts’ with the CaM N-terminal and C-terminal domains to constitute a transient encounter complex. The native contacts are obtained by analyzing the crystal structure of CaM-pCaN complex, in which key interactions between CaM and pCaN were extracted to guide the BD simulations. From this standpoint, the lenient conditions for association are tantamount to the notion of a transient encounter complex (67; 68), which is formed upon association of two binding partners prior to forming the fully-bound complex. Because we test the first hypothesis using conformations generated from the MD simulations without CaM, this test bears similarity to the conformational selection paradigm (69), though we emphasize CaM is likely required to completely form the bound complex from the transient encounter state. However, the abundance IDP-target protein complexes that exhibit diffusion-limited association suggest that the folding rate from the encounter state to the bound complex is rapid, as elaborated in Sect. S.1. In Fig. S10 and Fig. S9 we show that the MD-generated open states presented in each of the peptide configurations are compatible with both the N- and C-terminal CaM domains to varying degrees, as the open state of each peptide gives BD-simulated k_ons in the diffusion-limited regime (> 1 × 10⁷ M⁻1 s⁻1). Notably, all peptides considered here are capable of forming the transient encounter complex with CaM at rates that decrease with increasing ionic strength (see also Sect. S. 4.1). While not explored in this study, binding affinities via methods including Molecular Mechanics-Generalized Born Surface area (MM-GBSA) techniques (70; 71) could help rank configurations most compatible with the bound complex.

3.4. Rapid IDP conformational ensemble dynamics promote rapid association

Lastly, we investigated the role of conformational gating rates on the effective association rates based on the stochastic gating model postulated by Szabo et al (40). In this gating model, k_on is the expected ’ideal’ association rate between CaN peptide and CaM. By ’ideal’ it means that the CaN peptide is aways in CaM-compatible open state and the concentration of CaN peptide and CaM are sufficiently large, thus k_on here reflect the diffusion timescale of CaN peptide to CaM. By considering this, k_on can be compared with k_b/k_f which reflect the conversion time scale between open/closed states of CaN peptide. In the gating model, there are two limits that bound the effective rates: 1) given gating rates that are significantly faster than diffusional encounter rate (k_f + k_b ⪢ k_on), the effective association rate k_eff is equivalent to the rate associated with the open state, that is, k_eff = k_on. 2) given gating rates significantly smaller than the diffusional encounter rate (k_f + k_b ⪡ k_on), k_eff is given by the weighted average of the association rates for all accessed states, that is k_eff = ⟨k_on⟩.

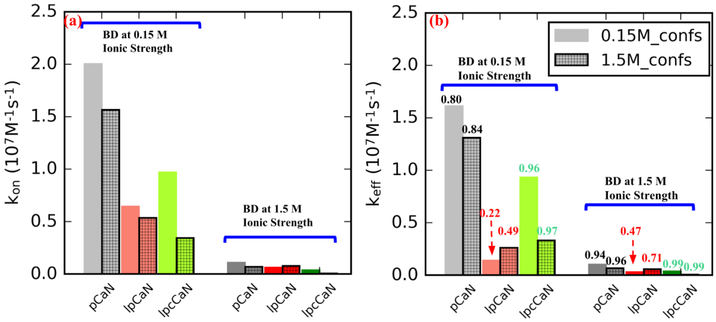
Rates associated with intermediate regimes are obtained by evaluating Eq. 3 using the MSM-estimated gating rates. Based on the data in Table S2 we show in Fig. 5 for pCaN and lpcCaN that k_eff and k_on are comparable (e.g. k_eff / k_on → 1), indicating a marginal effect of conformational gating on the association rate. This arises because the conformational transition rates are of the order 1 × 10⁹ s⁻1, roughly 100 times faster than diffusional encounter rate, based on our BD simulated k_ons of 1 × 10⁷ M−1 s−1 order (see Table S2). In contrast, the slower transition kinetics for lpCaN yield a k_eff that is about 50% of the maximal k_on, albeit it is still in a diffusion-limited regime. Moreover, the rates are strongly attenuated at 1.5 M relative to low ionic strength conditions of 0.15 M, which suggest the strong role of long-range electrostatic interactions in promoting association. These data indicate that diffusion-limited association kinetics are realized in the CaN IDP constructs, though the effective rate depends both on ensemble gating kinetics and long-range electrostatic interactions.

Figure 5:

Association rate constants between CaN peptide and CaM before (a) and after (b) taking CaN peptide’s conformational dynamic (from MSM modeling) into con-sideration using Eq. 3. The bars without grids and with grids depict results in which CaN peptide conformations were sampled at 0.15 M and 1.5 M ionic strength, respectively. In (a), kon was calculated via Eq. 2 where k_Cterm and K_Nterm are the average values of ten randomly selected conformations from each peptide’s open state. In (b) the numbers above each bar represent the ratios of k_eff to k_on.

An important factor to consider in this model is that the inability of the closed state to bind as rapid as the open state does not render the former ’unsuitable’ for binding. Rather, we anticipate its binding rate will be much slower relative to the open states, as the latter of which requires lesser structural reorganization to assume the correct binding pose. We support this speculation based on Go model predictions summarized in Sect. S4, for which we demonstrated a greater degree of frustration of transition from closed-like conformations to open-like. Namely, for closed state pCaN conformations, the BD-simulated complex presents an average fraction of native contact as Q_n = 0.24 and Q_c = 0.22, for the percent native contacts of the N and C terminal CaM domains, respectively while the open state pCaN conformations yield, Q_n = 0.56 and Q_c = 0.59 (see Fig. S12 and Fig. S11). Since lower native contact values will likely encounter greater frustration in folding landscapes compared to near native states, and reduced frustration results in increased rates of folding kinetics (72), we anticipate that induced-fit binding occurs more slowly than the binding of open-state conformations.

We acknowledge that experimental validation would have nicely complemented the model predictions. However, given the availability of experimental kinetics data from stopped-flow measurements of pCaN/CaN binding to CaM (arXiv: 1611.04080v1), a computational model consistent with these data offers experimentally-verifiable insights into molecular mechanisms governing their binding. Of these, the couplings between peptide charge distribution and ionic strength on the dynamics of an IDP conformational ensemble is one that could be examined through spectroscopic techniques including time-resolved Forster resonance energy transfer (25) or spin-relaxation times from nuclear magnetic resondance spectroscopy (73). As with many techniques used to resolve structural characteristics of IDP conformational ensembles, the measurements present ensemble-averaged information, therefore atomistic-scale, computational models will continue to be a strong complement to such probes for characterization of IDP behavior.

4. Conclusions

Our studies of CaN conformational dynamics and CaM/CaN association reveal several interesting features. While the role of charge distribution in IDPs has been shown to be a strong predictor of ensemble structure including compactness (17; 19), our simulations reveal that measures such as NCPR may offer predictive estimates for the ionic strength sensitivity of conformation transition kinetics. Namely, higher NCPR structures are more likely to adopt conformations that complement their binding target, and are less sensitive to changes in ionic strength that may influence gating kinetics. However, it is important to note that this trend may not generalize to necessarily all IDPs, given the wide range of protein/protein association rates (< 1 × 10³ to > 1 × 10⁹ M⁻1 s⁻1 (41)) reported in the literature, which hints at the possibility of different assembly mechanisms. Second, we demonstrate that long-range electrostatic interactions can play a paramount role in determining the kinetics of forming PPIs involving intrinsically-disordered partners, while protein-solvent and protein-protein electrostatic interactions govern the kinetics of presenting target-compatible binding motifs. Together, these factors suggest that IDPs can achieve diffusion-limited association by controlling conformational gating, so long as a conformation amenable to association is rapidly sampled. Overall our findings build upon the growing understanding of the roles of conformation selection and induced fit in dictating PPIs, both identifying how conformational selection can accelerate association, despite potential requirements for induced fitting in order to adopt the final binding pose.

Our study focused on CaN ‘s binding interaction with CaM, of which the latter regulates a staggering array of eukaryotic signaling cascades through forming PPIs with target protein (5). What sets CaM apart from other such hubs is the surprisingly diverse variety of targets it regulates, despite presenting a single isoform across all mammalian species (74). In part, its ability to regulate this diversity is attributed to the conformational heterogeneity of the CaM binding interface (75) it is capable of forming. These findings provide intriguing insight into the interplay between conformational diversity and electrostatically-driven protein-protein association involving CaN, which are likely to extend to wide-ranging processes regulated by intrinsically-disordered proteins. As such, exploiting IDP composition to tune PPI kinetics could offer new tools to probe and modulate important biochemical signal transduction pathways.