Abstract
The topological state of covalently closed, double-stranded DNA is defined by the knot type  and the linking-number difference
and the linking-number difference 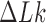 relative to unknotted relaxed DNA. DNA topoisomerases are essential enzymes that control the topology of DNA in all cells. In particular, type-II topoisomerases change both
relative to unknotted relaxed DNA. DNA topoisomerases are essential enzymes that control the topology of DNA in all cells. In particular, type-II topoisomerases change both 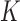 and
and 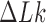 by a duplex-strand-passage mechanism and have been shown to simplify the topology of DNA to levels below thermal equilibrium at the expense of ATP hydrolysis. It remains a key question how small enzymes are able to preferentially select strand passages that result in topology simplification in much larger DNA molecules. Using numerical simulations, we consider the non-equilibrium dynamics of transitions between topological states
by a duplex-strand-passage mechanism and have been shown to simplify the topology of DNA to levels below thermal equilibrium at the expense of ATP hydrolysis. It remains a key question how small enzymes are able to preferentially select strand passages that result in topology simplification in much larger DNA molecules. Using numerical simulations, we consider the non-equilibrium dynamics of transitions between topological states 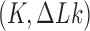 in DNA induced by type-II topoisomerases. For a biological process that delivers DNA molecules in a given topological state
in DNA induced by type-II topoisomerases. For a biological process that delivers DNA molecules in a given topological state 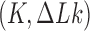 at a constant rate we fully characterize the pathways of topology simplification by type-II topoisomerases in terms of stationary probability distributions and probability currents on the network of topological states
at a constant rate we fully characterize the pathways of topology simplification by type-II topoisomerases in terms of stationary probability distributions and probability currents on the network of topological states 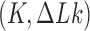 . In particular, we observe that type-II topoisomerase activity is significantly enhanced in DNA molecules that maintain a supercoiled state with constant torsional tension. This is relevant for bacterial cells in which torsional tension is maintained by enzyme-dependent homeostatic mechanisms such as DNA-gyrase activity.
. In particular, we observe that type-II topoisomerase activity is significantly enhanced in DNA molecules that maintain a supercoiled state with constant torsional tension. This is relevant for bacterial cells in which torsional tension is maintained by enzyme-dependent homeostatic mechanisms such as DNA-gyrase activity.
INTRODUCTION
The topological state of covalently closed, double-stranded DNA is defined by the knot type, 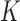 , and the linking number,
, and the linking number, 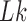 . DNA topoisomerases play a critical role in controlling the topology of double-stranded DNA through torsional relaxation and supercoiling, decatenation of interlocked DNA duplexes, and elimination of knotted DNA-recombination products, which cannot support transcription and replication (1–5). Supercoiling is quantitatively defined in terms of the linking-number difference relative to relaxed DNA,
. DNA topoisomerases play a critical role in controlling the topology of double-stranded DNA through torsional relaxation and supercoiling, decatenation of interlocked DNA duplexes, and elimination of knotted DNA-recombination products, which cannot support transcription and replication (1–5). Supercoiling is quantitatively defined in terms of the linking-number difference relative to relaxed DNA,  , rather than
, rather than 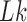 itself; here,
itself; here, 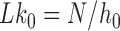 where
where 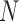 is the number of DNA base pairs in the DNA molecule and
is the number of DNA base pairs in the DNA molecule and 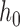 is the number of base pairs per helical turn in topologically relaxed DNA.
is the number of base pairs per helical turn in topologically relaxed DNA.
DNA topoisomerases are divided into two classes, type-I and type-II, corresponding to mechanisms that involve cleavage of one or both DNA strands, respectively (6). On fully double-helical DNA type-I enzymes regulate the torsional tension in double-stranded DNA by changing  exclusively whereas type-II enzymes can change both
exclusively whereas type-II enzymes can change both  and
and  by passing one duplex DNA segment through another (it is known, however, that topoisomerase I can perform strand passages, and therefore knot-type changes, by acting at the site of a DNA nick (7)). Torsional relaxation of DNA is energetically favorable and can be performed by ATP-independent enzymes, such as topoisomerase I. In contrast, type-II enzymes have a general cofactor requirement for ATP, in particular type-IIA enzymes such as bacterial topoisomerase IV and eukaryotic topoisomerase II (8), which hydrolyze ATP during supercoil relaxation and unknotting. Bacterial DNA gyrase is an exception in that this type-II enzyme introduces (–) supercoils at the expense of ATP hydrolysis and relaxes supercoils in the absence of ATP (9,10). The cofactor requirement was poorly understood until Rybenkov et al. showed in 1997 that type-II topoisomerases selectively perform strand passages that reduce the steady-state fraction of knotted or catenated, torsionally relaxed plasmid DNAs to levels 80 times below that at thermal equilibrium (11). In particular, the width of the
by passing one duplex DNA segment through another (it is known, however, that topoisomerase I can perform strand passages, and therefore knot-type changes, by acting at the site of a DNA nick (7)). Torsional relaxation of DNA is energetically favorable and can be performed by ATP-independent enzymes, such as topoisomerase I. In contrast, type-II enzymes have a general cofactor requirement for ATP, in particular type-IIA enzymes such as bacterial topoisomerase IV and eukaryotic topoisomerase II (8), which hydrolyze ATP during supercoil relaxation and unknotting. Bacterial DNA gyrase is an exception in that this type-II enzyme introduces (–) supercoils at the expense of ATP hydrolysis and relaxes supercoils in the absence of ATP (9,10). The cofactor requirement was poorly understood until Rybenkov et al. showed in 1997 that type-II topoisomerases selectively perform strand passages that reduce the steady-state fraction of knotted or catenated, torsionally relaxed plasmid DNAs to levels 80 times below that at thermal equilibrium (11). In particular, the width of the 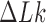 distribution for torsionally relaxed plasmid DNAs acted on by type-IIA topoisomerases was found to be narrower, i.e. less supercoiled, than that observed with ATP-independent enzymes (11). Thus, type-II topoisomerases use the free energy of ATP hydrolysis to drive the system away from thermal equilibrium. However, it remains a key question how a relatively small enzyme is able to preferentially select strand passages that lead to unknotting rather than to formation of knots in large DNA molecules because the topological state of DNA is a property of the entire molecule that cannot be determined by local DNA–enzyme interactions.
distribution for torsionally relaxed plasmid DNAs acted on by type-IIA topoisomerases was found to be narrower, i.e. less supercoiled, than that observed with ATP-independent enzymes (11). Thus, type-II topoisomerases use the free energy of ATP hydrolysis to drive the system away from thermal equilibrium. However, it remains a key question how a relatively small enzyme is able to preferentially select strand passages that lead to unknotting rather than to formation of knots in large DNA molecules because the topological state of DNA is a property of the entire molecule that cannot be determined by local DNA–enzyme interactions.
Since the seminal work by Rybenkov et al. several models have been suggested to explain how ATP-hydrolysis-driven type-II topoisomerases can selectively lower the frequency of DNA knotting (11–22), These models are generally based on geometric or kinetic mechanisms that increase the probability of strand-passage reactions and result in topology simplification from an initial state. A widely accepted model that has emerged from these studies is that of a hairpin-like gate (G) segment, where the type-II enzyme strongly bends the G-segment DNA and accepts for passage only a transfer (T) segment from the inside to the outside of the hairpin-formed G segment (Figure 1A) (12–14,21). For torsionally unconstrained (nicked) DNA, the model predicts a large decrease in the steady-state proportion of knots and catenanes relative to those at equilibrium, although it is insufficient to explain the magnitude of the effect observed with torsionally relaxed DNA plasmids (12,21). Indeed, strong (∼150°) protein-induced bending of the G segment, as required by the model, is observed in a co-crystal structure of yeast topoisomerase II with G-segment DNA (Figure 1B) (23). Experimental AFM measurements are consistent with bend angles between 94° and 100°, whereas FRET measurements suggest somewhat larger bend angles of 126° and 140° (24).
Figure 1.
(A) Mechanistic details of duplex-DNA passage in type-II topoisomerases. Step 1: enzyme binding to gate (G) segment in duplex DNA, followed by an encounter with transfer (T) segment; step 2: binding of two ATP molecules seals the gate; step 3: cleavage of the G segment duplex, catalyzed by the binding of 2 Mg2+ ions; step 4: passage of the T segment through the G segment; step 5: hydrolysis of the first ATP molecule releases a phosphate group and reseals the G segment strand; step 6: hydrolysis of the second ATP molecule dismantles the complex releasing both DNA strands; step 7: the enzyme resets to its original conformation. (B) Structure of yeast type-II topoisomerase dimer bound to a doubly nicked 34-mer duplex DNA (PDB 4GFH) and AMP-PNP. The DNA is bent 160° via interactions with an invariant isoleucine (64).
Type-II topoisomerases drive the system away from thermodynamic equilibrium and cause topology simplification due to a combination of two mechanisms, which are incorporated in the model of a hairpin-like G segment (12–14,21). First, type-II enzymes use the energy of ATP hydrolysis to promote passage of the T segment in one direction relative to the enzyme (unidirectional motion), whereas at thermodynamic equilibrium segment passages occur in both directions due to detailed balance. Secondly, the strongly bent hairpin G segment creates local asymmetry in the DNA, so that unidirectional segment passage from inside to outside of the hairpin can reduce the fraction of knotted DNA below thermodynamic-equilibrium values. Thus, type-II enzymes work like a Maxwell's demon that allows only selected segment passages subject to consumption of chemical energy (12–14,21). Conversely, for a straight G segment all axial orientations of the enzyme bound to the G segment have equal passage probabilities, and topology simplification below equilibrium values does not occur.
Another group of studies did not directly address mechanisms of topoisomerase action but considered the probability distribution  , and distributions derived therefrom, at thermal equilibrium (15,25–27). This distribution is directly related to the free-energy landscape
, and distributions derived therefrom, at thermal equilibrium (15,25–27). This distribution is directly related to the free-energy landscape 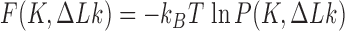 where
where 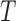 is the temperature and
is the temperature and 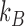 is Boltzmann's constant. The distribution
is Boltzmann's constant. The distribution  corresponds to a phantom-chain ensemble where the DNA molecules are free to explore all topological states
corresponds to a phantom-chain ensemble where the DNA molecules are free to explore all topological states 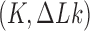 at thermal equilibrium, referred to here as the equilibrium segment-passage (ESP) ensemble (28). Characterization of
at thermal equilibrium, referred to here as the equilibrium segment-passage (ESP) ensemble (28). Characterization of  therefore yields important insight about the most likely relaxation path of a given DNA knot by a hypothetical topoisomerase that lacks any bias towards topology simplification and is driven only by the topological free-energy gradient. Indeed, the actual extent of bias for an ATP-driven type-II enzyme in favor of unknotting can only be quantified if we know the probability of acting in the absence of any bias, corresponding to topoisomerase action in absence of ATP hydrolysis. The system's behavior at thermal equilibrium thus provides a necessary reference state for investigating mechanisms of topoisomerase activity such as chirality bias (29–31).
therefore yields important insight about the most likely relaxation path of a given DNA knot by a hypothetical topoisomerase that lacks any bias towards topology simplification and is driven only by the topological free-energy gradient. Indeed, the actual extent of bias for an ATP-driven type-II enzyme in favor of unknotting can only be quantified if we know the probability of acting in the absence of any bias, corresponding to topoisomerase action in absence of ATP hydrolysis. The system's behavior at thermal equilibrium thus provides a necessary reference state for investigating mechanisms of topoisomerase activity such as chirality bias (29–31).
Motivated by the fact that type-II enzymes drive the system away from equilibrium, we investigate a model of topoisomerase activity based on a network of topological states  of circular DNAs with knot type
of circular DNAs with knot type  and linking number difference
and linking number difference 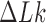 in which the dynamics of transitions between states
in which the dynamics of transitions between states 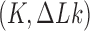 mediated by type-II enzymes is described by a chemical master equation. Previous studies showed the existence of unknotting/unlinking pathways followed by type-II topoisomerases that stepwise progressively reduce the topological complexity of knotted/catenated molecules (32,33). The main goal of our study is to identify significant pathways along which topology simplification by type-II enzymes occurs in terms of non-equilibrium steady states (NESSs) for the network
mediated by type-II enzymes is described by a chemical master equation. Previous studies showed the existence of unknotting/unlinking pathways followed by type-II topoisomerases that stepwise progressively reduce the topological complexity of knotted/catenated molecules (32,33). The main goal of our study is to identify significant pathways along which topology simplification by type-II enzymes occurs in terms of non-equilibrium steady states (NESSs) for the network 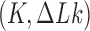 . We also quantify type-II topoisomerase activity for a hairpin-like G segment compared to a straight (unbent) G segment. To address these questions we generated a large set of equilibrium ensembles of knotted and supercoiled 6-kbp DNAs by Monte Carlo simulations to find transition rates and NESS parameters in the network of topological states
. We also quantify type-II topoisomerase activity for a hairpin-like G segment compared to a straight (unbent) G segment. To address these questions we generated a large set of equilibrium ensembles of knotted and supercoiled 6-kbp DNAs by Monte Carlo simulations to find transition rates and NESS parameters in the network of topological states 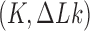 .
.
Our analytical approach can be thought of as a two-level model. At the macroscopic level, the model uses topological states as the variable, so it allows DNA-topology transitions between states 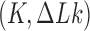 according to a chemical master equation. Transitions between topological states occur with rates that are determined, in turn, by microscopic interactions and geometric features of type-II enzyme action. The master-equation formulation allows one to compute the occupancies of the different macrostates, including their dynamics. In principle, other mesoscopic models for knotted supercoiled DNA can be used to capture the underlying microscopic behavior of the system, such as those obtained from Brownian or molecular dynamics (34).
according to a chemical master equation. Transitions between topological states occur with rates that are determined, in turn, by microscopic interactions and geometric features of type-II enzyme action. The master-equation formulation allows one to compute the occupancies of the different macrostates, including their dynamics. In principle, other mesoscopic models for knotted supercoiled DNA can be used to capture the underlying microscopic behavior of the system, such as those obtained from Brownian or molecular dynamics (34).
A novel feature of our model is the capability to dynamically account for processes that generate complex knots extrinsically, either in vitro or in vivo. For example, the process may describe the activity of an intracellular enzyme creating the knots, and is extrinsic in the sense that this enzyme is not explicitly included in our model; instead, the activity of the enzyme is described by the presence of a source rate creating the knots. The favorable unknotting pathways were determined in terms of universal NESS probabilities and probability currents, derived from transition rates. The idea of an induced probability current stems from the presence of an idealized source of complex knots. For example, type-II enzymes crucially maintain the integrity of genomic DNA during transcription and replication, requiring relaxation of (+) supercoils that build up ahead of RNA and DNA polymerases (35,36). Moreover, knotting occurs in site-specific recombination reactions, for example, creating torus knots with 5 and more nodes (32,37,38). In vitro, type-IIA enzymes efficiently generate not-trivial knots through processes that facilitate intramolecular interactions among duplex-DNA segments, such as DNA supercoiling, DNA looping, or segment-segment interactions promoted by polycations and other DNA-condensing agents (39–41). There is little information regarding endogenous knotting of DNA in vivo, although recent studies in yeast suggest that there can be low steady-state levels of knots in intracellular chromatin (42). If such knots exist in vivo, there must be mechanisms to efficiently resolve such topological entanglements, which are a potential death sentence for the cell (2,43–45).
COMPUTATIONAL METHODS
DNA model and simulation procedure
Following previous studies (25,26,28,46) circular duplex DNA is modeled as a discrete semi-flexible chain with  extensible segments of mean length
extensible segments of mean length  nm, corresponding to a total chain length of
nm, corresponding to a total chain length of 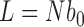 ; in this work we use
; in this work we use  corresponding to 6-kb DNA (each segment has approximately 30 bp). The potential energy of a chain conformation is given by
corresponding to 6-kb DNA (each segment has approximately 30 bp). The potential energy of a chain conformation is given by
 |
(1) |
where  K is the temperature and
K is the temperature and 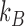 is Boltzmann's constant.
is Boltzmann's constant. 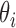 is the bending angle between successive segments
is the bending angle between successive segments  and
and 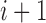 ,
, 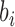 is the length of segment
is the length of segment 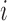 , and
, and 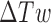 is the double-helical twist relative to relaxed DNA. During a Monte Carlo simulation, the value of
is the double-helical twist relative to relaxed DNA. During a Monte Carlo simulation, the value of  was calculated for each chain conformation using White's equation
was calculated for each chain conformation using White's equation 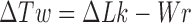 where
where  is the writhe of the chain conformation and
is the writhe of the chain conformation and  was fixed during the simulation. The bending energy constant
was fixed during the simulation. The bending energy constant  is chosen such that the persistence length
is chosen such that the persistence length 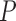 of the chain is equal to 5 segments, i.e.,
of the chain is equal to 5 segments, i.e.,  nm, resulting in
nm, resulting in 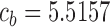 (28). The stretching energy constant is given by
(28). The stretching energy constant is given by  where
where 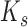 is the stretch modulus of DNA; using the approximate value
is the stretch modulus of DNA; using the approximate value 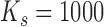 pN for B-form DNA under physiological conditions (47) results in
pN for B-form DNA under physiological conditions (47) results in  . The twisting energy constant is given by
. The twisting energy constant is given by 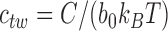 where
where 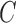 is the torsional rigidity constant of DNA; using
is the torsional rigidity constant of DNA; using  erg·cm for B-form DNA (46) results in
erg·cm for B-form DNA (46) results in 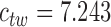 . Excluded-volume and electrostatic interactions between DNA segments are modeled by an effective hard-cylinder diameter
. Excluded-volume and electrostatic interactions between DNA segments are modeled by an effective hard-cylinder diameter 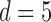 nm, corresponding to an ionic strength of 150 mM (48).
nm, corresponding to an ionic strength of 150 mM (48).
Equilibrium ensembles of chains with fixed knot type 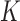 and linking number difference
and linking number difference 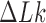 were generated by Monte Carlo (MC) simulation. In our procedure, chain conformations evolved by crankshaft rotations and stretching moves of sub-chains (28), and sub-chain translations, or reptations, along the local chain axis; the purpose of reptation moves was to increase the probability of extrusion and resorption of superhelix branches (see reference (46) for the definition and numerical implementation of reptation moves). Trial conformations were accepted with probability
were generated by Monte Carlo (MC) simulation. In our procedure, chain conformations evolved by crankshaft rotations and stretching moves of sub-chains (28), and sub-chain translations, or reptations, along the local chain axis; the purpose of reptation moves was to increase the probability of extrusion and resorption of superhelix branches (see reference (46) for the definition and numerical implementation of reptation moves). Trial conformations were accepted with probability 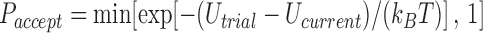 according to the Metropolis criterion, where
according to the Metropolis criterion, where  and
and 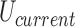 are the potential energies of trial and current conformations, respectively, according to Equation (1). Excluded-volume interactions and preservation of knot type
are the potential energies of trial and current conformations, respectively, according to Equation (1). Excluded-volume interactions and preservation of knot type 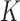 were implemented by rejecting any trial conformation in which chain segments overlapped or which resulted in a change of
were implemented by rejecting any trial conformation in which chain segments overlapped or which resulted in a change of 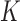 . Knot types
. Knot types 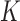 of current and trial conformations were determined by calculating the Alexander polynomial
of current and trial conformations were determined by calculating the Alexander polynomial  for
for  and the HOMFLY polynomial
and the HOMFLY polynomial  (49). Averages for given knot type
(49). Averages for given knot type  and linking number
and linking number 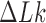 were calculated from ensembles containing
were calculated from ensembles containing 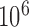 saved conformations for the unknot
saved conformations for the unknot 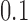 and the trefoil knot
and the trefoil knot 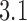 , and
, and 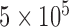 saved conformations for all other knot types
saved conformations for all other knot types 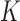 . The simulation period between saved conformations entering these ensembles was 1000 MC moves.
. The simulation period between saved conformations entering these ensembles was 1000 MC moves.
The calculation of  requires numerical calculation of the probability
requires numerical calculation of the probability  of a knot type
of a knot type  in an equilibrium segment-passage (ESP) ensemble of torsionally unconstrained (nicked) chains (see Supplementary Data, Section S1, Figure S1 and Table S1 for details regarding the calculation of
in an equilibrium segment-passage (ESP) ensemble of torsionally unconstrained (nicked) chains (see Supplementary Data, Section S1, Figure S1 and Table S1 for details regarding the calculation of  ). To obtain numerically accurate values of
). To obtain numerically accurate values of  for a complex knot
for a complex knot 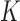 , which occurs with very low frequency in an unrestricted ESP ensemble due to its large free energy, we use the method of restricted ESP ensembles in which one or more dominating knot types are excluded so that less dominant knot types occur with higher frequency (Supplementary Figure S1) (28). If the knot
, which occurs with very low frequency in an unrestricted ESP ensemble due to its large free energy, we use the method of restricted ESP ensembles in which one or more dominating knot types are excluded so that less dominant knot types occur with higher frequency (Supplementary Figure S1) (28). If the knot 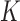 occurs with sufficient frequency in the restricted ensemble ESP’ its probability
occurs with sufficient frequency in the restricted ensemble ESP’ its probability 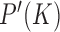 in ESP’ can be accurately determined, which, in turn, yields the probability
in ESP’ can be accurately determined, which, in turn, yields the probability 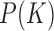 in the unrestricted ensemble ESP.
in the unrestricted ensemble ESP.
Model of type-II enzymes
DNA-bound type-II enzymes with hairpin and straight G segments were modeled by selecting four or two contiguous chain segments, respectively, whose local geometry during a trial move conformed to specific criteria (Figure 2). A hairpin G segment formed two sides of an equilateral triangle with side lengths  nm, corresponding to a 120° bend. A putative T segment was considered to be juxtaposed with the G segment if it passed through the triangle in such a way that none of the chain segments overlapped, i.e., excluded-volume interactions were preserved for the enzyme (Figure 2A). For a straight G segment, a potential T segment was considered to be juxtaposed if it passed through an equilateral triangle with one side formed by the straight G segment of length
nm, corresponding to a 120° bend. A putative T segment was considered to be juxtaposed with the G segment if it passed through the triangle in such a way that none of the chain segments overlapped, i.e., excluded-volume interactions were preserved for the enzyme (Figure 2A). For a straight G segment, a potential T segment was considered to be juxtaposed if it passed through an equilateral triangle with one side formed by the straight G segment of length  nm (Figure 2B). The orientation of this triangle about the center axis of the chain was chosen randomly for each trial conformation. Again, excluded-volume interactions of chain segments were preserved. The juxtaposition condition for a straight G segment using the same unilateral triangle as for a hairpin G segment was guided by computational convenience; however, we note that our results for a straight G segment do not depend on details of the juxtaposition condition such as the shape and size of the juxtaposition sector for T segments. This is because of the universality of the NESS probabilities and probability currents obtained by our model as discussed below.
nm (Figure 2B). The orientation of this triangle about the center axis of the chain was chosen randomly for each trial conformation. Again, excluded-volume interactions of chain segments were preserved. The juxtaposition condition for a straight G segment using the same unilateral triangle as for a hairpin G segment was guided by computational convenience; however, we note that our results for a straight G segment do not depend on details of the juxtaposition condition such as the shape and size of the juxtaposition sector for T segments. This is because of the universality of the NESS probabilities and probability currents obtained by our model as discussed below.
Figure 2.

Simulation snapshots of the left-handed trefoil knot  with (A) hairpin-like G segment and (B) straight G segment (74). The conformations shown correspond to states in which a T segment (green) is properly juxtaposed with the G segment (red) to initiate strand passage. Deformed chains used to determine knot type
with (A) hairpin-like G segment and (B) straight G segment (74). The conformations shown correspond to states in which a T segment (green) is properly juxtaposed with the G segment (red) to initiate strand passage. Deformed chains used to determine knot type  and linking number
and linking number 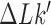 of the chain conformation after strand passage are indicated by grey lines. We use a modified Alexander-Briggs notation for knots, where the first number indicates the minimal crossing number, the subscript number indicates the tabular position among the knots with the same minimal crossing number (75) and the subscripts + or – indicate right- or left-handed form of the given knot.
of the chain conformation after strand passage are indicated by grey lines. We use a modified Alexander-Briggs notation for knots, where the first number indicates the minimal crossing number, the subscript number indicates the tabular position among the knots with the same minimal crossing number (75) and the subscripts + or – indicate right- or left-handed form of the given knot.
Juxtaposition probabilities and transition rates
Strand passages by type-II enzymes generate transitions from topological states 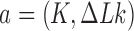 to states
to states  with
with  . The associated transition rates
. The associated transition rates 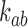 are assumed to be of the form
are assumed to be of the form
 |
(2) |
where 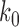 is a constant which depends on enzyme activity and concentration, but is independent of the topological states
is a constant which depends on enzyme activity and concentration, but is independent of the topological states  ,
, 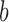 of the DNA (12,21).
of the DNA (12,21).  is the juxtaposition frequency of the enzyme in state
is the juxtaposition frequency of the enzyme in state  , corresponding to the fraction of DNA conformations in state
, corresponding to the fraction of DNA conformations in state 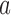 in which a potential T segment is properly juxtaposed with the G segment as described above.
in which a potential T segment is properly juxtaposed with the G segment as described above. 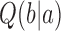 is the conditional probability that strand passage from a juxtaposed conformation in state
is the conditional probability that strand passage from a juxtaposed conformation in state 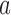 results in state
results in state  .
.
The state  of the chain that would result from the juxtaposed state
of the chain that would result from the juxtaposed state 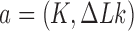 by passage of the T segment through the G segment was determined by considering local, virtual deformations of the chain obtained by replacing the red segments corresponding to the G segment by the gray segments shown in Figure 2. Note that the virtual, deformed conformations were solely used as a tool to identify knot type
by passage of the T segment through the G segment was determined by considering local, virtual deformations of the chain obtained by replacing the red segments corresponding to the G segment by the gray segments shown in Figure 2. Note that the virtual, deformed conformations were solely used as a tool to identify knot type  and
and 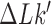 of a passed conformation; however, the virtual, deformed conformations were not part of the equilibrium ensembles, which implies that elastic energies of the deformed conformations did not enter the calculation. The knot type
of a passed conformation; however, the virtual, deformed conformations were not part of the equilibrium ensembles, which implies that elastic energies of the deformed conformations did not enter the calculation. The knot type  was determined by calculating the Alexander and HOMFLY polynomials of the deformed chain (49).
was determined by calculating the Alexander and HOMFLY polynomials of the deformed chain (49). 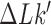 was determined by calculating the writhe
was determined by calculating the writhe  of the deformed chain and assuming that strand passage leaves the twist
of the deformed chain and assuming that strand passage leaves the twist  nearly unchanged; applying White’s equation
nearly unchanged; applying White’s equation 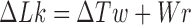 to original and deformed chain, and using
to original and deformed chain, and using  , then gives
, then gives  . Using the fact that the change of
. Using the fact that the change of 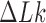 occurs strictly in steps of
occurs strictly in steps of 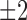 allowed us to determine the sign of the change of
allowed us to determine the sign of the change of 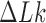 by the corresponding change of the writhe
by the corresponding change of the writhe  , which was always close to
, which was always close to 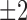 in our simulations. Thus, both
in our simulations. Thus, both 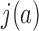 and
and 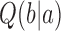 can be determined by MC simulations of equilibrium ensembles of chains in a fixed topological state
can be determined by MC simulations of equilibrium ensembles of chains in a fixed topological state  . The validity of this approach is based on the assumption that the reaction is not diffusion limited, which implies that the probability
. The validity of this approach is based on the assumption that the reaction is not diffusion limited, which implies that the probability  of finding a potential T segment properly juxtaposed with the G-segment is equal to the equilibrium probability of this juxtaposed conformation in the absence of strand passage (12).
of finding a potential T segment properly juxtaposed with the G-segment is equal to the equilibrium probability of this juxtaposed conformation in the absence of strand passage (12).
Master equation and non-equilibrium steady states
Consider an ensemble of circular duplex DNA molecules acted on by type-II enzymes in the presence of ATP. The rates  for transitions from topological states
for transitions from topological states 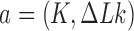 to states
to states 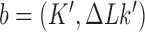 induced by the enzyme are given by Equation (2). The probability
induced by the enzyme are given by Equation (2). The probability 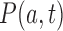 to find a given DNA molecule in topological state
to find a given DNA molecule in topological state 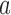 at time
at time  obeys the master equation
obeys the master equation
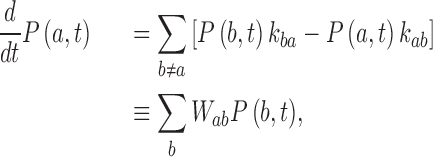 |
(3) |
where the transition matrix 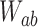 is given in terms of the rates
is given in terms of the rates  by
by 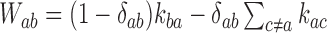 . We consider here the situation where the probabilities
. We consider here the situation where the probabilities 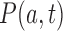 are stationary, i.e. time-independent, for all topological states
are stationary, i.e. time-independent, for all topological states  , corresponding to non-equilibrium steady states (NESS). Stationary NESS probabilities
, corresponding to non-equilibrium steady states (NESS). Stationary NESS probabilities 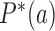 were calculated as follows (the star symbol for
were calculated as follows (the star symbol for  is used to distinguish NESS probabilities from the equilibrium probabilities
is used to distinguish NESS probabilities from the equilibrium probabilities  obtained in ESP ensembles). According to Equation (3), for stationary NESS probabilities
obtained in ESP ensembles). According to Equation (3), for stationary NESS probabilities 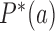 with
with 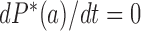 one obtains
one obtains 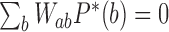 for all topological states
for all topological states  present in the system, which implies that the vector [P* (b); states[pxe]Tilde; b] is an eigenvector of the transition matrix
present in the system, which implies that the vector [P* (b); states[pxe]Tilde; b] is an eigenvector of the transition matrix  with eigenvalue 0. This eigenvector is uniquely determined by the normalization condition
with eigenvalue 0. This eigenvector is uniquely determined by the normalization condition  (50,51). Stationary NESS probability currents from topological states
(50,51). Stationary NESS probability currents from topological states 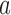 to states
to states 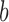 are found from
are found from 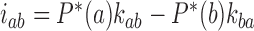 . Note that at thermal equilibrium the detailed balance condition implies
. Note that at thermal equilibrium the detailed balance condition implies 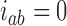 ; conversely, in our study, NESS with appreciable probability currents
; conversely, in our study, NESS with appreciable probability currents 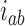 were generated by continuously delivering a complex topology, e.g., knot type
were generated by continuously delivering a complex topology, e.g., knot type  with
with  , to the ensemble by introducing a source rate
, to the ensemble by introducing a source rate  with origin
with origin 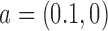 (the unknot with
(the unknot with  ) and source state
) and source state  .
.
Universal NESS probabilities and probability currents
For nonzero source rates 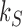 the NESS probabilities
the NESS probabilities 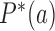 and probability currents
and probability currents  depend on enzyme properties such as intrinsic rate and concentration in terms of the constant
depend on enzyme properties such as intrinsic rate and concentration in terms of the constant 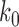 in Equation (2). In order to obtain results independent of such largely unknown details (in this sense ‘universal’) we define normalized transition rates as
in Equation (2). In order to obtain results independent of such largely unknown details (in this sense ‘universal’) we define normalized transition rates as
 |
(4) |
where 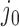 is the juxtaposition frequency in a reference state, which we choose as
is the juxtaposition frequency in a reference state, which we choose as 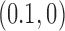 (the unknot with
(the unknot with 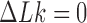 ). The normalization factor
). The normalization factor  in Equation (4), with
in Equation (4), with 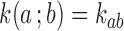 from Equation (4), corresponds to the total rate of enzyme reaction in the reference state
from Equation (4), corresponds to the total rate of enzyme reaction in the reference state 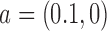 . The normalized juxtaposition frequency
. The normalized juxtaposition frequency  in Equation (4) is the ratio of the actual juxtaposition frequency
in Equation (4) is the ratio of the actual juxtaposition frequency 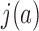 in state
in state 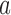 and the juxtaposition frequency
and the juxtaposition frequency  in the reference state, where the unknown constant
in the reference state, where the unknown constant  drops out. Universal NESS probabilities
drops out. Universal NESS probabilities  as a function of the parameter
as a function of the parameter  were calculated using the normalized rates
were calculated using the normalized rates  in Equation (4) as described above, and universal NESS probability currents are obtained as
in Equation (4) as described above, and universal NESS probability currents are obtained as 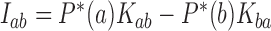 . The universal NESS probabilities
. The universal NESS probabilities 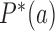 and probability currents
and probability currents 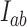 as functions of the parameter
as functions of the parameter 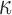 are expected to depend only on geometric properties of the enzyme, such as the bend angle of the G segment. Thus these quantities are expected to be independent of properties that do not involve the particular topological state of the DNA, for example the overall size of the enzyme (as long as it is much smaller than the DNA) and the precise form of the interaction potential between the G and T segments. We tested the hypothesis that
are expected to depend only on geometric properties of the enzyme, such as the bend angle of the G segment. Thus these quantities are expected to be independent of properties that do not involve the particular topological state of the DNA, for example the overall size of the enzyme (as long as it is much smaller than the DNA) and the precise form of the interaction potential between the G and T segments. We tested the hypothesis that 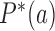 and
and 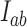 are universal functions of the parameter
are universal functions of the parameter 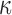 by showing that
by showing that 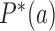 and
and 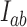 remained unchanged when altering the interaction between G and T segments (Supplementary Figure S6). This test also provided an internal control for the validity of our computational approach.
remained unchanged when altering the interaction between G and T segments (Supplementary Figure S6). This test also provided an internal control for the validity of our computational approach.
Summary of computational procedure
To summarize, the reaction pathways presented below were calculated as follows. For given knot type and linking number 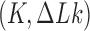 , equilibrium ensembles with
, equilibrium ensembles with 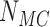 saved conformations were generated by Monte Carlo simulation (MC) for chains with straight G segment and chains with hairpin G segment, respectively (Figure 2). Juxtaposed conformations in these ensembles were identified as described above (Figure 2) resulting in
saved conformations were generated by Monte Carlo simulation (MC) for chains with straight G segment and chains with hairpin G segment, respectively (Figure 2). Juxtaposed conformations in these ensembles were identified as described above (Figure 2) resulting in  juxtaposed conformations. The juxtaposition frequency in Equation (2) was calculated as
juxtaposed conformations. The juxtaposition frequency in Equation (2) was calculated as 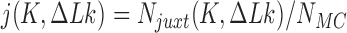 . For each juxtaposed conformation in the ensemble for given
. For each juxtaposed conformation in the ensemble for given  , virtual, deformed chain conformations were considered to identify the state
, virtual, deformed chain conformations were considered to identify the state  of the chain that would result from the juxtaposed state
of the chain that would result from the juxtaposed state 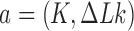 by passage of the T segment through the G segment (Figure 2). The knot type
by passage of the T segment through the G segment (Figure 2). The knot type  and linking number
and linking number 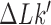 was determined by calculating the Alexander and HOMFLY polynomials and the writhe
was determined by calculating the Alexander and HOMFLY polynomials and the writhe  of the virtual, deformed chains as described above. For given juxtaposed conformation
of the virtual, deformed chains as described above. For given juxtaposed conformation 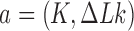 the number
the number  of passed conformations
of passed conformations  was determined, resulting in transition probabilities
was determined, resulting in transition probabilities 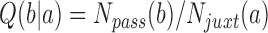 in Equation (2). This procedure was repeated for a sufficiently large set of states
in Equation (2). This procedure was repeated for a sufficiently large set of states 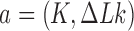 . Normalized transition rates
. Normalized transition rates  were then calculated using Equation (4); in our calculations, the parameter
were then calculated using Equation (4); in our calculations, the parameter  in Equation (2) was set to 1 because it drops out in the ratio of Equation (4). Normalized NESS probabilities
in Equation (2) was set to 1 because it drops out in the ratio of Equation (4). Normalized NESS probabilities 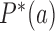 were calculated from the eigenvector of the transition matrix
were calculated from the eigenvector of the transition matrix  in Equation (3) with eigenvalue 0, and universal NESS probability currents were calculated as
in Equation (3) with eigenvalue 0, and universal NESS probability currents were calculated as 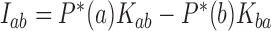 .
.
RESULTS
Equilibrium distribution and free-energy landscape
As outlined in the Introduction, the topological distribution at thermal equilibrium provides a reference state necessary to understand ATP-driven type-II enzyme action that results in topology simplification beyond equilibrium. The equilibrium ensemble is characterized by the joint probability distribution  , corresponding to an equilibrium segment-passage (ESP) ensemble of phantom chains, and distributions derived therefrom (25,26). In particular, Podtelezhnikov et al. found that
, corresponding to an equilibrium segment-passage (ESP) ensemble of phantom chains, and distributions derived therefrom (25,26). In particular, Podtelezhnikov et al. found that 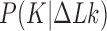 , the conditional distribution of
, the conditional distribution of  for given
for given  , is dominated by only a few knots
, is dominated by only a few knots 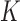 for any fixed value of
for any fixed value of  ; moreover, the dominating knots except for the unknot were all chiral (25). Later, Burnier et al. pointed out that for chiral knots
; moreover, the dominating knots except for the unknot were all chiral (25). Later, Burnier et al. pointed out that for chiral knots 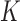 the level of supercoiling is characterized by the quantity
the level of supercoiling is characterized by the quantity 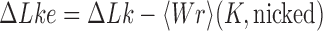 rather than
rather than 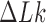 , where
, where  is the signed, nonzero mean value of the 3D writhe for a torsionally unconstrained (nicked) DNA molecule with chiral knot type
is the signed, nonzero mean value of the 3D writhe for a torsionally unconstrained (nicked) DNA molecule with chiral knot type  (Figure 3) (26). This result can be easily understood by taking the average of White’s equation for fixed
(Figure 3) (26). This result can be easily understood by taking the average of White’s equation for fixed  , i.e.
, i.e.  : for a torsionally relaxed, i.e., not supercoiled, chain one has
: for a torsionally relaxed, i.e., not supercoiled, chain one has  and
and 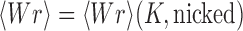 , thus
, thus 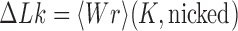 and
and  (Figure 3). Burnier et al. found that the conditional distribution
(Figure 3). Burnier et al. found that the conditional distribution  is dominated by the unknot for any fixed value of
is dominated by the unknot for any fixed value of  ; moreover,
; moreover, 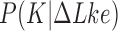 decreases with increasing
decreases with increasing  for any knot
for any knot  , implying that increasing levels of supercoiling favor unknotting (26).
, implying that increasing levels of supercoiling favor unknotting (26).
Figure 3.
Standard forms of (A) the unknot  and (B) the left-handed knot
and (B) the left-handed knot 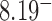 , and simulation snapshots of 6-kb DNAs of these knots with values of
, and simulation snapshots of 6-kb DNAs of these knots with values of 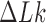 and
and 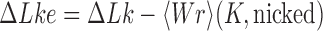 as shown (74). The mean writhe
as shown (74). The mean writhe  of torsionally relaxed (nicked) DNA is 0 for
of torsionally relaxed (nicked) DNA is 0 for  and
and 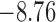 for
for 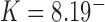 . The states with
. The states with 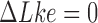 appear relaxed, whereas for
appear relaxed, whereas for 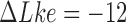 supercoiling is present.
supercoiling is present.
We first verified that our calculation reproduces the behavior of the equilibrium distribution 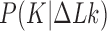 found earlier (see Figure 4 in reference (25) and Figure 2A in reference (26)). For our 6-kb DNAs we indeed find that for any fixed, small value of
found earlier (see Figure 4 in reference (25) and Figure 2A in reference (26)). For our 6-kb DNAs we indeed find that for any fixed, small value of  only a few knot types
only a few knot types 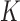 dominate the distribution. However, for
dominate the distribution. However, for 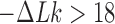 , corresponding to superhelix density
, corresponding to superhelix density  for 6-kb DNAs, the distribution rapidly becomes degenerate and many different knot types
for 6-kb DNAs, the distribution rapidly becomes degenerate and many different knot types  contribute to
contribute to  (Supplementary Figure S2). This value of
(Supplementary Figure S2). This value of  is closely similar to the experimentally measured average level of in-vivo plectonemic supercoiling in prokaryotes determined by site-specific recombination assays (52,53). Such levels account for only 40–50% of the plectonemic supercoiling present in bacterial plasmids in vitro, the remainder presumed to be constrained by the intracellular binding of specific and non-specific DNA-binding proteins. If conditions inside the cell increase the level of unconstrained supercoiling beyond this
is closely similar to the experimentally measured average level of in-vivo plectonemic supercoiling in prokaryotes determined by site-specific recombination assays (52,53). Such levels account for only 40–50% of the plectonemic supercoiling present in bacterial plasmids in vitro, the remainder presumed to be constrained by the intracellular binding of specific and non-specific DNA-binding proteins. If conditions inside the cell increase the level of unconstrained supercoiling beyond this 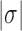 value, the resulting distribution of knot types would be expected to become highly degenerate.
value, the resulting distribution of knot types would be expected to become highly degenerate.
Figure 4.
Free energy landscape 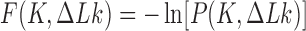 in units of
in units of 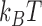 for 6-kb DNAs, where
for 6-kb DNAs, where  is the joint probability distribution of
is the joint probability distribution of  and
and 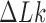 . Along sections with fixed
. Along sections with fixed  ,
, 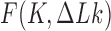 is minimum for nontrivial knots, i.e., knots different from the unknot 0.1. This is indicated for
is minimum for nontrivial knots, i.e., knots different from the unknot 0.1. This is indicated for  (
(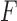 minimum for
minimum for  , orange line/dot) and
, orange line/dot) and 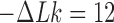 (
( minimum for
minimum for  , brown line/dot). The white curves are sections for fixed values 0,
, brown line/dot). The white curves are sections for fixed values 0,  of the degree of supercoiling
of the degree of supercoiling 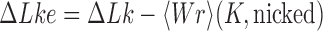 where
where 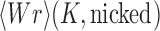 is the mean writhe for torsionally relaxed (nicked) DNA with knot type
is the mean writhe for torsionally relaxed (nicked) DNA with knot type  . Along these sections,
. Along these sections,  is always minimum for the unknot 0.1 and the corresponding free energy gradient towards 0.1 becomes steeper with increasing
is always minimum for the unknot 0.1 and the corresponding free energy gradient towards 0.1 becomes steeper with increasing 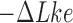 .
.
Next, in order to understand the most-probable relaxation path of a given DNA knot  with linking number
with linking number 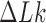 by a topoisomerase that is driven only by the topological free-energy gradient, we calculated the free energy landscape
by a topoisomerase that is driven only by the topological free-energy gradient, we calculated the free energy landscape  including all knot types
including all knot types  which dominate the distribution
which dominate the distribution 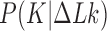 and have 12 or fewer crossings (Figure 4) (see Computational Methods). The free-energy landscape also explains the difference between results for
and have 12 or fewer crossings (Figure 4) (see Computational Methods). The free-energy landscape also explains the difference between results for  and
and 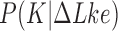 obtained in references (18) and (26), respectively, by noting that distributions for fixed
obtained in references (18) and (26), respectively, by noting that distributions for fixed 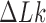 or
or  correspond to different sections of the free energy landscape
correspond to different sections of the free energy landscape  (Figure 4). Along sections with fixed
(Figure 4). Along sections with fixed  , the minimum value of
, the minimum value of 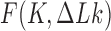 corresponds to the chiral knot
corresponds to the chiral knot 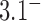 , whereas along sections with fixed
, whereas along sections with fixed  , the minimum in
, the minimum in 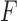 always coincides with the unknot
always coincides with the unknot 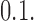 The corresponding free-energy gradient towards
The corresponding free-energy gradient towards  is steeper for increasing
is steeper for increasing  , in agreement with earlier results (25,26). The latter situation, namely involving sections of the free-energy landscape with fixed
, in agreement with earlier results (25,26). The latter situation, namely involving sections of the free-energy landscape with fixed  , is relevant in biological systems in which a finite amount of supercoiling is maintained for DNA undergoing transitions changing the knot type
, is relevant in biological systems in which a finite amount of supercoiling is maintained for DNA undergoing transitions changing the knot type  and therefore changing the equilibrium writhe
and therefore changing the equilibrium writhe 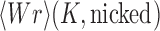 . This is the case, for example, for bacterial cells where the torsional tension is maintained by a homeostatic mechanism involving topoisomerase I and DNA gyrase (58,59).
. This is the case, for example, for bacterial cells where the torsional tension is maintained by a homeostatic mechanism involving topoisomerase I and DNA gyrase (58,59).
Steady-state knot distributions in supercoiled DNA and topology simplification
In addressing the influence of DNA supercoiling on the unknotting efficiency of type-II enzymes, we first consider an ensemble of supercoiled 6-kbp circular duplex DNAs in the presence of type-II topoisomerase and ATP without additional components. Each round of type-II enzyme action converts a DNA substrate in the state  to a product state
to a product state  where
where 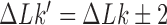 and
and  is a knot that can be obtained from
is a knot that can be obtained from  by one intersegmental passage (54). Figure 5 shows steady-state fractions
by one intersegmental passage (54). Figure 5 shows steady-state fractions 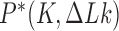 of the unknot
of the unknot  and stereoisomers
and stereoisomers  and
and  of the trefoil knot for type-II enzymes modeled in terms of hairpin-like and straight G segments, respectively. Knots with more than three crossings occurred with low frequency and were omitted from Figure 5 for simplicity. As a comparison we also show the equilibrium probabilities
of the trefoil knot for type-II enzymes modeled in terms of hairpin-like and straight G segments, respectively. Knots with more than three crossings occurred with low frequency and were omitted from Figure 5 for simplicity. As a comparison we also show the equilibrium probabilities  corresponding to ESP ensembles.
corresponding to ESP ensembles.
Figure 5.
Steady-state fractions 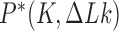 for the unknot
for the unknot  and isoforms
and isoforms  and
and 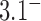 of the trefoil knot in the presence of type-II enzymes modeled with hairpin-like and straight G segments, respectively, in the state space spanned by knot type
of the trefoil knot in the presence of type-II enzymes modeled with hairpin-like and straight G segments, respectively, in the state space spanned by knot type 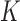 and linking number
and linking number  . Also shown are the corresponding equilibrium fractions
. Also shown are the corresponding equilibrium fractions  for comparison. The group of numbers shown for each knot
for comparison. The group of numbers shown for each knot  are steady-state fractions
are steady-state fractions 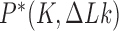 , in percent, for DNAs with hairpin-like G segments (upper entries, magenta), straight G segments (middle entries, green), and equilibrium fractions
, in percent, for DNAs with hairpin-like G segments (upper entries, magenta), straight G segments (middle entries, green), and equilibrium fractions  corresponding to ESP ensembles (lower entries, blue). The fractions for right-handed isoforms of a chiral knot are the same as for left-handed isoforms by symmetry. The upper panel displays sums of
corresponding to ESP ensembles (lower entries, blue). The fractions for right-handed isoforms of a chiral knot are the same as for left-handed isoforms by symmetry. The upper panel displays sums of 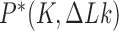 over the
over the 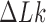 - values shown in the figure. The arrows and associated numbers indicate residual probability currents
- values shown in the figure. The arrows and associated numbers indicate residual probability currents 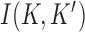 for enzymes with hairpin (magenta) and straight G segments (green).
for enzymes with hairpin (magenta) and straight G segments (green).
Figure 5 shows that the steady-state fraction of 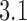 knots is reduced for enzymes with hairpin G segments compared to enzymes with straight G segments, consistent with results obtained earlier for torsionally unconstrained (nicked) chains (12). For the sums
knots is reduced for enzymes with hairpin G segments compared to enzymes with straight G segments, consistent with results obtained earlier for torsionally unconstrained (nicked) chains (12). For the sums  and
and  , corresponding to steady-state probabilities of knots
, corresponding to steady-state probabilities of knots 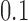 and
and 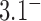 for nicked chains, we find
for nicked chains, we find 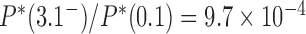 (hairpin G segment) and
(hairpin G segment) and  (straight G segment). This corresponds to a reduction by a factor of 8.5 (compare column
(straight G segment). This corresponds to a reduction by a factor of 8.5 (compare column  in Table 1 in reference (12), where both isoforms
in Table 1 in reference (12), where both isoforms  and
and 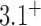 were included in the statistics of the trefoil knot
were included in the statistics of the trefoil knot 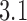 for nicked 7-kbp DNAs). The difference in reduction factors of 14 in reference (12) and 8.5 in our study may be explained by the fact that the hairpin-like G segment considered in (12) had an overall
for nicked 7-kbp DNAs). The difference in reduction factors of 14 in reference (12) and 8.5 in our study may be explained by the fact that the hairpin-like G segment considered in (12) had an overall 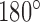 -bend compared to a smaller
-bend compared to a smaller  -bend in our model (see Computational Methods). However, for fixed values of
-bend in our model (see Computational Methods). However, for fixed values of 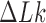 the reduction factor depends strongly on the value of
the reduction factor depends strongly on the value of  ; for example, for
; for example, for  the reduction factor is only
the reduction factor is only  whereas for
whereas for 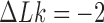 it is
it is  (Figure 5). The dependence of the reduction factor on
(Figure 5). The dependence of the reduction factor on 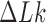 is related to the fact that the free-energy gradient depends on the relevant section of the free-energy landscape
is related to the fact that the free-energy gradient depends on the relevant section of the free-energy landscape 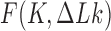 : the gradient toward
: the gradient toward  is steeper for fixed
is steeper for fixed 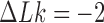 than for
than for 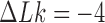 (Figure 4). Similarly, for fixed
(Figure 4). Similarly, for fixed 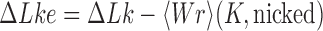 the reduction factor is expected to depend on the gradient along sections with fixed
the reduction factor is expected to depend on the gradient along sections with fixed 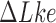 in the free-energy landscape (Figure 4). We also found that the steady-state fractions
in the free-energy landscape (Figure 4). We also found that the steady-state fractions  for knots
for knots  different from the unknot are slightly larger for type-II enzymes with straight G segment than the corresponding equilibrium probabilities
different from the unknot are slightly larger for type-II enzymes with straight G segment than the corresponding equilibrium probabilities  (Figure 5), again in agreement with results obtained previously for nicked chains (compare reference (12), Table 1).
(Figure 5), again in agreement with results obtained previously for nicked chains (compare reference (12), Table 1).
Interestingly, for supercoiled DNA, residual cycle (or closed-loop) probability currents appear. For example, consider the probability currents for hairpin G segment indicated by magenta arrows in Figure 5. For 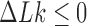 (right side in Figure 5), two cycles occur, namely
(right side in Figure 5), two cycles occur, namely 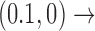
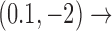
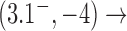
 and
and 
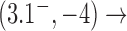

 . For
. For 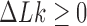 (left side in Figure 5) the corresponding cycles occur by symmetry. Closed-loop probability currents are typical for non-equilibrium steady states (NESS) and occur because type-II enzymes drive the reaction away from thermal equilibrium so that detailed balance between directed fluxes
(left side in Figure 5) the corresponding cycles occur by symmetry. Closed-loop probability currents are typical for non-equilibrium steady states (NESS) and occur because type-II enzymes drive the reaction away from thermal equilibrium so that detailed balance between directed fluxes 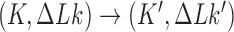 and
and 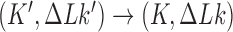 is violated in general (50,51). The numerical values for NESS probabilities and probability currents shown in Figure 5 are accurate within our numerical calculation; however, these values are expected to depend on finite-size effects and other approximations involved with our simple model for the enzyme (Figure 2). Moreover, it is not clear whether the residual cyclic probability currents have any significance regarding the unknotting efficiency of type-II enzymes.
is violated in general (50,51). The numerical values for NESS probabilities and probability currents shown in Figure 5 are accurate within our numerical calculation; however, these values are expected to depend on finite-size effects and other approximations involved with our simple model for the enzyme (Figure 2). Moreover, it is not clear whether the residual cyclic probability currents have any significance regarding the unknotting efficiency of type-II enzymes.
Apart from DNA unknotting, another aspect of DNA-topology simplification by type-II enzymes is a reduction of the degree of supercoiling, which translates into a narrower 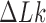 -distribution about its mean value
-distribution about its mean value  for a given knot type
for a given knot type 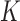 . A metric used to quantify this type of topology simplification is the topology simplification factor
. A metric used to quantify this type of topology simplification is the topology simplification factor  where
where  is the variance of
is the variance of  in the presence of type-II enzyme and ATP, and
in the presence of type-II enzyme and ATP, and 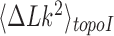 is the variance of
is the variance of 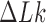 in the presence of type-I enzyme. The latter does not consume energy from ATP hydrolysis and thus generates the
in the presence of type-I enzyme. The latter does not consume energy from ATP hydrolysis and thus generates the 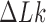 distribution corresponding to an ESP ensemble at thermal equilibrium. In reference (11) the variance of the
distribution corresponding to an ESP ensemble at thermal equilibrium. In reference (11) the variance of the 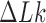 -distribution was measured for the nicked unknot form of 7-kbp pAB4 DNA in the presence of Escherichia coli topoisomerase IV and ATP and gave the result
-distribution was measured for the nicked unknot form of 7-kbp pAB4 DNA in the presence of Escherichia coli topoisomerase IV and ATP and gave the result 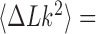 1.7 compared with the equilibrium value 3.1, which yields
1.7 compared with the equilibrium value 3.1, which yields 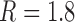 .
.
Three other studies found values of  in the range 1.3–1.7 (55–57). We studied the narrowing of the
in the range 1.3–1.7 (55–57). We studied the narrowing of the 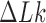 distribution for the unknot
distribution for the unknot 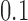 in the presence of type-II enzymes modeled with the hairpin-like G segment and compared the standard deviations of the steady-state distribution
in the presence of type-II enzymes modeled with the hairpin-like G segment and compared the standard deviations of the steady-state distribution 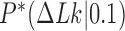 and the equilibrium distribution
and the equilibrium distribution 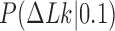 (Supplementary Data, Section S3 and Figure S3). Note that the distributions
(Supplementary Data, Section S3 and Figure S3). Note that the distributions 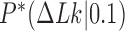 for even and odd values of
for even and odd values of  are disjunct because type-II enzymes change
are disjunct because type-II enzymes change 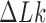 in steps of 2; conversely, type-I enzymes change
in steps of 2; conversely, type-I enzymes change  in steps of 1. We thus find
in steps of 1. We thus find 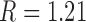 for
for  even and
even and  for
for 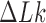 odd, in reasonable agreement with the experimental results (11,55–57) (Supplementary Data, Section S3).
odd, in reasonable agreement with the experimental results (11,55–57) (Supplementary Data, Section S3).
Pathways of topology simplification in knotted, supercoiled DNA
For DNAs in the size range considered here and in the absence of a process that actively delivers a complex knot type to the ensemble of DNAs, the equilibrium probabilities 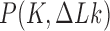 are very small for any knot
are very small for any knot 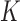 different from the unknot. Thus, for single, decatenated DNA molecules at thermal equilibrium practically no knotted DNAs appear. In the presence of type-II enzymes these probabilities are reduced even further. However, a typical situation in vivo is that some biological process is present that actively generates knotted DNAs, and type-II enzymes are essentially needed to remove these knots. To address this biologically relevant situation, we now assume the presence of an extrinsic process that continuously delivers DNA molecules in a complex source state
different from the unknot. Thus, for single, decatenated DNA molecules at thermal equilibrium practically no knotted DNAs appear. In the presence of type-II enzymes these probabilities are reduced even further. However, a typical situation in vivo is that some biological process is present that actively generates knotted DNAs, and type-II enzymes are essentially needed to remove these knots. To address this biologically relevant situation, we now assume the presence of an extrinsic process that continuously delivers DNA molecules in a complex source state 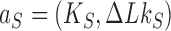 . Specifically, we assume that a process is present in the ensemble of 6-kbp duplex DNAs that continuously converts unknotted DNAs with
. Specifically, we assume that a process is present in the ensemble of 6-kbp duplex DNAs that continuously converts unknotted DNAs with  to DNAs forming the knot
to DNAs forming the knot  with linking number
with linking number 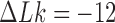 at constant rate
at constant rate 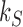 . The knot
. The knot  contributes notably to the distribution
contributes notably to the distribution 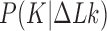 at
at 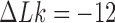 (Supplementary Figure S2) and is chosen here to illustrate the pathway of topology simplification by type-II topoisomerase given an initial complex topological state.
(Supplementary Figure S2) and is chosen here to illustrate the pathway of topology simplification by type-II topoisomerase given an initial complex topological state.
The DNA molecules delivered in the source state 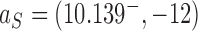 by the extrinsic process are converted by type-II enzyme strand passages to simpler topological forms in a stepwise manner, resulting in a pathway of intermediate topological states. As discussed in the previous section, each round of type-II enzyme action converts a DNA substrate in the state
by the extrinsic process are converted by type-II enzyme strand passages to simpler topological forms in a stepwise manner, resulting in a pathway of intermediate topological states. As discussed in the previous section, each round of type-II enzyme action converts a DNA substrate in the state 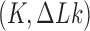 to a product state
to a product state 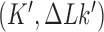 where
where 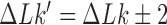 and
and  is a knot that can be obtained from the knot
is a knot that can be obtained from the knot 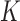 by one intersegmental passage (54). Eventually the DNAs are converted back to the originating state
by one intersegmental passage (54). Eventually the DNAs are converted back to the originating state 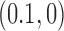 , i.e., the unknot with
, i.e., the unknot with  . The latter is then converted again to molecules in the source state
. The latter is then converted again to molecules in the source state 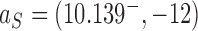 by the extrinsic process, resulting in a continuous cycle. The cyclic process is characterized by non-equilibrium steady state (NESS) probabilities
by the extrinsic process, resulting in a continuous cycle. The cyclic process is characterized by non-equilibrium steady state (NESS) probabilities  for DNAs in topological states
for DNAs in topological states 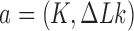 , and probability currents
, and probability currents 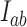 for transitions from states
for transitions from states  to
to  . The NESS probabilities
. The NESS probabilities  are appreciable for the source state
are appreciable for the source state 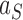 and all intermediate states
and all intermediate states 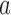 along the pathway of topology simplification by topoisomerase-II action. Note that for the case of a hairpin G segment, the system is out of equilibrium by two mechanisms, namely (i) the presence of a source rate creating the
along the pathway of topology simplification by topoisomerase-II action. Note that for the case of a hairpin G segment, the system is out of equilibrium by two mechanisms, namely (i) the presence of a source rate creating the 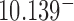 knots and resulting nonzero probability currents
knots and resulting nonzero probability currents  , and (ii) the action of the type-II enzyme modeled as hairpin G segment which drives the system away from equilibrium even in the absence of a source current (see Introduction).
, and (ii) the action of the type-II enzyme modeled as hairpin G segment which drives the system away from equilibrium even in the absence of a source current (see Introduction).
Figure 6 shows resulting pathways of topology simplification for type-II enzymes modeled by a hairpin-like (Figure 6A) and straight G segments (Figure 6B), respectively. Steady-state probabilities  , in percent, are shown next to each state
, in percent, are shown next to each state 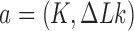 (filled circles), and probability currents
(filled circles), and probability currents 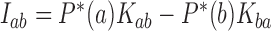 with normalized transition rates
with normalized transition rates 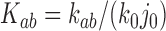 defined in Equation (4) are given by numbers next to the arrows (see Computational Methods). Accordingly, the source probability current associated with the external process that converts DNAs in the originating state
defined in Equation (4) are given by numbers next to the arrows (see Computational Methods). Accordingly, the source probability current associated with the external process that converts DNAs in the originating state  to the source state
to the source state 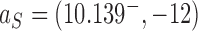 at constant rate
at constant rate 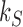 is given by
is given by 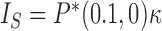 with
with  (see Computational Methods). Only probability currents
(see Computational Methods). Only probability currents  with
with 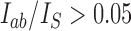 are shown, where dominant currents with
are shown, where dominant currents with 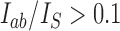 are shown as dark blue arrows and subdominant currents with
are shown as dark blue arrows and subdominant currents with 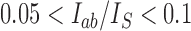 are shown as light blue arrows. Empty circles indicate states
are shown as light blue arrows. Empty circles indicate states  for which
for which 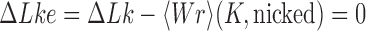 , corresponding to torsionally relaxed chains (cf. white curve on the left in Figure 4). It is apparent that the pathways shown on the left sides in Figure 6A, B closely follow the path
, corresponding to torsionally relaxed chains (cf. white curve on the left in Figure 4). It is apparent that the pathways shown on the left sides in Figure 6A, B closely follow the path  . Interestingly, only a small number of intermediates contribute to the pathways although there exist ∼250 different knot types with 10 or fewer crossings.
. Interestingly, only a small number of intermediates contribute to the pathways although there exist ∼250 different knot types with 10 or fewer crossings.
Figure 6.
Comparison of NESS probabilities and probability currents generated by type-II topoisomerase activity with (A) hairpin and (B) straight G segment (74) in the state space spanned by knot type  and linking number
and linking number  . In both cases, we imposed an external process that converts unknotted DNA with
. In both cases, we imposed an external process that converts unknotted DNA with 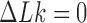 to DNA forming a (source) knot
to DNA forming a (source) knot  with
with 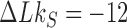 in the limit of large source rate
in the limit of large source rate  (pathways shown on the left in (A) and (B)). Dominant probability currents with
(pathways shown on the left in (A) and (B)). Dominant probability currents with  are shown as dark blue arrows and subdominant probability currents with
are shown as dark blue arrows and subdominant probability currents with 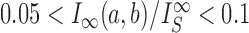 are shown as light blue arrows. Steady-state probabilities
are shown as light blue arrows. Steady-state probabilities 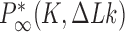 , in percent, are shown next to each knot
, in percent, are shown next to each knot  . Open circles indicate positions of
. Open circles indicate positions of  , i.e.,
, i.e., 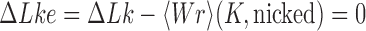 (cf. white curve on the left in Figure 4). The pathways shown on the right in (A) and (B) show cases in which a supercoiled state is maintained by introducing the constraint
(cf. white curve on the left in Figure 4). The pathways shown on the right in (A) and (B) show cases in which a supercoiled state is maintained by introducing the constraint  . In these cases, we assumed the presence of an external process that converts unknotted DNA with
. In these cases, we assumed the presence of an external process that converts unknotted DNA with  to DNA forming a source knot
to DNA forming a source knot  with
with 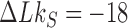 , and the source rate
, and the source rate 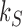 was adjusted to obtain the same source probability current
was adjusted to obtain the same source probability current  as for the pathway shown on the left to facilitate comparison.
as for the pathway shown on the left to facilitate comparison.
For the pathways shown on the left sides in Figure 6A, B we consider the limit of a large source rate  for the external process. In this limit, the originating state
for the external process. In this limit, the originating state 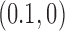 is depleted by the external process, which implies that the steady-state probability of the originating state vanishes as
is depleted by the external process, which implies that the steady-state probability of the originating state vanishes as 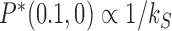 . For all other states
. For all other states 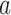 the steady-state probabilities approach finite values
the steady-state probabilities approach finite values 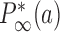 in the limit of a large source rate
in the limit of a large source rate 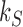 . Likewise, all probability currents
. Likewise, all probability currents  approach finite values
approach finite values 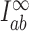 in the limit of large source rate
in the limit of large source rate 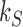 , including the source probability current
, including the source probability current  . Therefore, the values of the steady-state probabilities
. Therefore, the values of the steady-state probabilities 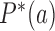 and probability currents
and probability currents  in Figure 6A, B are universal in the sense that they are independent of the precise value of the source rate
in Figure 6A, B are universal in the sense that they are independent of the precise value of the source rate 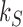 as long as
as long as  is large enough. The full dependence of
is large enough. The full dependence of  and
and 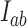 on the parameter
on the parameter 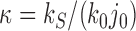 is shown in Supplementary Figures S4 and S5.
is shown in Supplementary Figures S4 and S5.
In many biological systems a finite amount of supercoiling is maintained. For example, for bacterial cells the torsional tension is maintained by a homeostatic mechanism involving topoisomerase I and DNA gyrase (58,59). To study this situation, on the right sides in Figure 6A, B we show pathways of topology simplification for the case that a state of finite DNA supercoiling is maintained by introducing the constraint  . For these pathways we assume that an external process is present that continuously converts DNAs in the originating state
. For these pathways we assume that an external process is present that continuously converts DNAs in the originating state 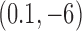 to the source state
to the source state 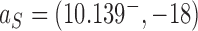 . The parameter
. The parameter  is adjusted so as to produce the same source probability current
is adjusted so as to produce the same source probability current  as for the pathways shown on the left sides in Figure 6A, B to facilitate comparison between cases in which a finite amount of supercoiling is maintained (right sides in Figure 6A, B) and those for which this is not the case (left sides in Figure 6A, B). However, the qualitative shape of the decay pathway is largely independent of the value of
as for the pathways shown on the left sides in Figure 6A, B to facilitate comparison between cases in which a finite amount of supercoiling is maintained (right sides in Figure 6A, B) and those for which this is not the case (left sides in Figure 6A, B). However, the qualitative shape of the decay pathway is largely independent of the value of  . Figure 6 reveals the dependence of the unknotting capability of a type-II enzyme on the degree of supercoiling. For the source state
. Figure 6 reveals the dependence of the unknotting capability of a type-II enzyme on the degree of supercoiling. For the source state 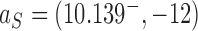 of the pathways shown on the left sides in Figure 6A, B we find
of the pathways shown on the left sides in Figure 6A, B we find  for hairpin G segment and
for hairpin G segment and  for straight G segment, corresponding to a reduction by a factor of 4.2 (see numbers to the right of the filled circles representing state
for straight G segment, corresponding to a reduction by a factor of 4.2 (see numbers to the right of the filled circles representing state 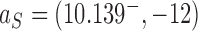 in Figure 6A, B, respectively). Conversely, for the source state
in Figure 6A, B, respectively). Conversely, for the source state 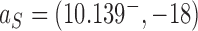 of the pathways shown on the right sides in Figure 6A, B, for which the DNAs are more supercoiled, we find
of the pathways shown on the right sides in Figure 6A, B, for which the DNAs are more supercoiled, we find 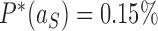 for the hairpin G segment and
for the hairpin G segment and 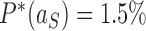 for the straight G segment, corresponding to a larger reduction factor of 10 (see numbers to the right of the filled circles representing state
for the straight G segment, corresponding to a larger reduction factor of 10 (see numbers to the right of the filled circles representing state  in Figure 6A, B, respectively). The larger reduction factor of 10 in the latter case compared to 4.2 in the former implies that supercoiling favors unknotting for the present non-equilibrium situation where a complex knot type is continuously delivered to the ensemble of DNA conformations.
in Figure 6A, B, respectively). The larger reduction factor of 10 in the latter case compared to 4.2 in the former implies that supercoiling favors unknotting for the present non-equilibrium situation where a complex knot type is continuously delivered to the ensemble of DNA conformations.
As discussed above, the knot 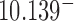 is chosen here to illustrate the pathway of topology simplification by type-II topoisomerase of a given initial complex topological state. However, it should be noted that Figure 6A, B also implicitly describe decay pathways of other knots located on the pathway for
is chosen here to illustrate the pathway of topology simplification by type-II topoisomerase of a given initial complex topological state. However, it should be noted that Figure 6A, B also implicitly describe decay pathways of other knots located on the pathway for 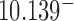 ; e.g., the torus knots
; e.g., the torus knots 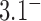 ,
, 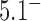 , and
, and 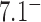 occurring in site-specific recombination reactions (32,37,38). For example, the decay pathway of
occurring in site-specific recombination reactions (32,37,38). For example, the decay pathway of 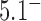 with
with  may be read off from Figure 6A, B by considering
may be read off from Figure 6A, B by considering 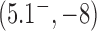 as a source state with emanating probability currents as shown in the figure.
as a source state with emanating probability currents as shown in the figure.
How do type-II enzymes with hairpin G segments suppress knotting below equilibrium?
Importantly, the pathways for hairpin and straight G segments are somewhat similar. This surprising result will now be explained further in terms of juxtaposition probabilities  and transition probabilities
and transition probabilities 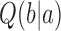 for enzymes with hairpin and straight G segments. As discussed in the previous section, a type-II topoisomerase with hairpin G segment reduces the steady-state fraction of complex knots below the equilibrium value relative to an enzyme with a straight G segment; moreover, the unknotting efficiency of the hairpin enzyme increases with DNA supercoiling. To better understand the origin of this effect, Figure 7 compares normalized juxtaposition probabilities
for enzymes with hairpin and straight G segments. As discussed in the previous section, a type-II topoisomerase with hairpin G segment reduces the steady-state fraction of complex knots below the equilibrium value relative to an enzyme with a straight G segment; moreover, the unknotting efficiency of the hairpin enzyme increases with DNA supercoiling. To better understand the origin of this effect, Figure 7 compares normalized juxtaposition probabilities  and transition probabilities
and transition probabilities 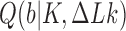 appearing in Equation (4) for type-II enzymes with straight (
appearing in Equation (4) for type-II enzymes with straight (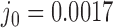 ) and hairpin G segments (
) and hairpin G segments ( ), respectively. The quantity
), respectively. The quantity  denotes the juxtaposition probability for the reference state
denotes the juxtaposition probability for the reference state  so that
so that  by definition (see Computational Methods). Figure 7 shows the dependence of
by definition (see Computational Methods). Figure 7 shows the dependence of 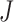 and
and 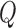 on states
on states  for the knots
for the knots 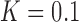 ,
, 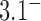 ,
, 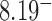 as a function of
as a function of 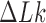 . In order to maximize the number of unknotted molecules, the type-II enzyme has to fulfill two tasks: 1. keep unknotted molecules unknotted, i.e., avoid creation of nontrivial knots from the unknot, and 2. simplify stepwise knotted molecules according to the decay pathway (Figure 6) in order eventually to generate unknotted products. Figure 7 focuses on these two aspects 1. and 2. in parts 7A and 7B, respectively, using
. In order to maximize the number of unknotted molecules, the type-II enzyme has to fulfill two tasks: 1. keep unknotted molecules unknotted, i.e., avoid creation of nontrivial knots from the unknot, and 2. simplify stepwise knotted molecules according to the decay pathway (Figure 6) in order eventually to generate unknotted products. Figure 7 focuses on these two aspects 1. and 2. in parts 7A and 7B, respectively, using 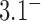 and
and 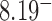 as examples for nontrivial knots. Accordingly, we define
as examples for nontrivial knots. Accordingly, we define 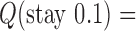
 as the probability that strand passage in an unknot with linking number
as the probability that strand passage in an unknot with linking number 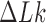 again results in an unknot (with
again results in an unknot (with 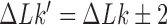 ), i.e. no knotting occurs. For
), i.e. no knotting occurs. For  and
and  ,
,
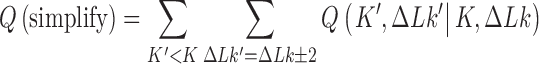 |
(5) |
Figure 7.
Normalized juxtaposition frequencies  and transition probabilities
and transition probabilities 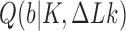 for type-II enzymes modeled in terms of a hairpin-like G segment (blue dots and lines) and straight G segment (green dots and lines) for knot types (A)
for type-II enzymes modeled in terms of a hairpin-like G segment (blue dots and lines) and straight G segment (green dots and lines) for knot types (A)  and (B)
and (B) 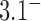 ,
,  (74). The dots correspond to calculated values and the lines were obtained by linear interpolation. The quantity
(74). The dots correspond to calculated values and the lines were obtained by linear interpolation. The quantity  denotes the juxtaposition probability for the reference state
denotes the juxtaposition probability for the reference state 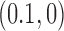 , with
, with 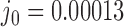 for hairpin G-segment and
for hairpin G-segment and 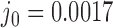 for straight G-segment. Note that
for straight G-segment. Note that 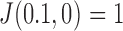 by definition.
by definition. 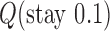 is the probability that strand passage in an unknot with linking number
is the probability that strand passage in an unknot with linking number 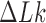 again results in an unknot (with
again results in an unknot (with  ), i.e. no knotting occurs. For
), i.e. no knotting occurs. For  ,
,  ,
, 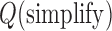 is the probability that strand passage results in unknotting, i.e., in a knot
is the probability that strand passage results in unknotting, i.e., in a knot  with a smaller number of crossings than
with a smaller number of crossings than  (see text). The vertical lines indicate values
(see text). The vertical lines indicate values  and
and 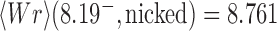 , respectively, corresponding to
, respectively, corresponding to 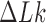 - values for which the degree of supercoiling vanishes, i.e.
- values for which the degree of supercoiling vanishes, i.e. 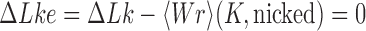 (cf. Figure 3). Supercoiled chains correspond to
(cf. Figure 3). Supercoiled chains correspond to 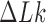 – values to the left and right from these vertical lines.
– values to the left and right from these vertical lines.
is the probability that strand passage results in unknotting, i.e., yields a knot  with a smaller number of crossings than
with a smaller number of crossings than 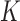 (denoted
(denoted 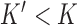 ).
).
As shown in Figure 7 (upper panels), the normalized juxtaposition probabilities  are larger for hairpin than for straight G segment, and this effect increases with the complexity of the knot
are larger for hairpin than for straight G segment, and this effect increases with the complexity of the knot 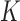 and with the degree of supercoiling
and with the degree of supercoiling 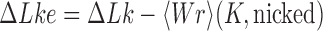 . The fact that
. The fact that  increases with knot complexity is expected because complex knots are more compact than less complex knots on average, so that more complex knots have higher probabilities of segment juxtaposition. This is consistent with the corresponding behavior of the unknot
increases with knot complexity is expected because complex knots are more compact than less complex knots on average, so that more complex knots have higher probabilities of segment juxtaposition. This is consistent with the corresponding behavior of the unknot 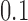 compared with the trefoil knot
compared with the trefoil knot 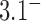 for nicked DNA (12). However, for supercoiled DNA,
for nicked DNA (12). However, for supercoiled DNA,  also increases with the degree of supercoiling
also increases with the degree of supercoiling  , and this effect is dramatically larger for type-II enzymes with hairpin versus straight G segments. This can be qualitatively explained in terms of correlated juxtaposition of chain segments. In juxtaposed conformations of type-II enzymes with hairpin G segments, typically two crossings of the chain are made by the juxtaposed T and hairpin G segments (Figure 8C); conversely, in juxtaposed conformations with straight G segment typically only one crossing is made by the juxtaposed T and straight G segments (Figure 8A) (12). This leaves, on average, one extra crossing that has to be absorbed by the rest of the chain for a straight G segment compared with the hairpin case. The free energy
, and this effect is dramatically larger for type-II enzymes with hairpin versus straight G segments. This can be qualitatively explained in terms of correlated juxtaposition of chain segments. In juxtaposed conformations of type-II enzymes with hairpin G segments, typically two crossings of the chain are made by the juxtaposed T and hairpin G segments (Figure 8C); conversely, in juxtaposed conformations with straight G segment typically only one crossing is made by the juxtaposed T and straight G segments (Figure 8A) (12). This leaves, on average, one extra crossing that has to be absorbed by the rest of the chain for a straight G segment compared with the hairpin case. The free energy 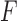 of unknotted supercoiled DNA increases quadratically with the superhelix density
of unknotted supercoiled DNA increases quadratically with the superhelix density 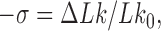 i.e.
i.e. 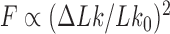 (see, e.g. equation (8) in (60)). Assuming that this relationship generalizes for knotted, supercoiled DNA to
(see, e.g. equation (8) in (60)). Assuming that this relationship generalizes for knotted, supercoiled DNA to 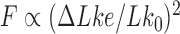 and that the extra crossing involved in the case of the straight G segment amounts to an increment
and that the extra crossing involved in the case of the straight G segment amounts to an increment 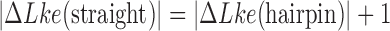 in linking number that has to be absorbed by the rest of the chain, we find
in linking number that has to be absorbed by the rest of the chain, we find 
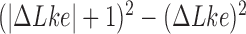
 (here
(here  ). This linear increase in free energy as a function of
). This linear increase in free energy as a function of 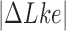 for a straight G segment compared to a hairpin G segment results in an exponential decrease in juxtaposition probability for a straight G segment; that is, conversely, to an exponential increase in juxtaposition probability for a hairpin G segment, i.e.
for a straight G segment compared to a hairpin G segment results in an exponential decrease in juxtaposition probability for a straight G segment; that is, conversely, to an exponential increase in juxtaposition probability for a hairpin G segment, i.e. 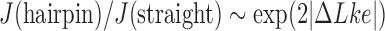 (Figure 7, upper panel).
(Figure 7, upper panel).
Figure 8.

Schematic depiction of juxtaposed and passed conformations of type-II enzymes modeled by straight and hairpin G segments, respectively. The G segment is indicated by the purple portion and the T segment by the green portion of the chain. (A) Juxtaposed and (B) passed conformations for straight G segment. (C) Juxtaposed and (D) passed conformations for hairpin G segment. Note the different number of crossings made by the T and G segments.
A similar argument also explains the behavior of 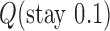 as a function of
as a function of  for hairpin compared to straight G segments (Figure 7, lower panel, left). In a conformation generated by the passage of a T segment through a hairpin G segment, corresponding to the juxtaposition of a straight segment to the outside of a hairpin, typically the passed T and hairpin G segments do not cross (Figure 8D). Thus, if the passed conformation is knotted, all of the crossings of the knot have to be absorbed by the rest of the chain. Conversely, in passed conformations with straight G segments typically one crossing is made by the passed T and straight G segments, leaving one crossing less that has to be absorbed by the rest of the chain if the passed conformation is knotted (Figure 8B) (12). Thus, a similar argument as above leads to
for hairpin compared to straight G segments (Figure 7, lower panel, left). In a conformation generated by the passage of a T segment through a hairpin G segment, corresponding to the juxtaposition of a straight segment to the outside of a hairpin, typically the passed T and hairpin G segments do not cross (Figure 8D). Thus, if the passed conformation is knotted, all of the crossings of the knot have to be absorbed by the rest of the chain. Conversely, in passed conformations with straight G segments typically one crossing is made by the passed T and straight G segments, leaving one crossing less that has to be absorbed by the rest of the chain if the passed conformation is knotted (Figure 8B) (12). Thus, a similar argument as above leads to 
 ; see Figure 7 (lower panel, left) where
; see Figure 7 (lower panel, left) where 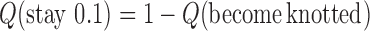 . Interestingly, and in opposition to the behavior of
. Interestingly, and in opposition to the behavior of 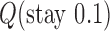 , the probability
, the probability  that strand passage in the nontrivial knots
that strand passage in the nontrivial knots 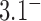 ,
, 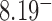 results in unknotting is similar for hairpin and straight G segments, albeit somewhat larger for the hairpin G segment (Figure 7, lower panel middle and right). This may be explained as follows. Consider, for example, a trefoil knot which is transformed to an unknot by strand passage. Both for hairpin and straight G-segments, there is no extra crossing that needs to be absorbed by the rest of the chain in the resulting unknot after strand passage. Thus the transition probabilities
results in unknotting is similar for hairpin and straight G segments, albeit somewhat larger for the hairpin G segment (Figure 7, lower panel middle and right). This may be explained as follows. Consider, for example, a trefoil knot which is transformed to an unknot by strand passage. Both for hairpin and straight G-segments, there is no extra crossing that needs to be absorbed by the rest of the chain in the resulting unknot after strand passage. Thus the transition probabilities 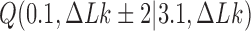 are expected to be similar for hairpin and straight G segments regardless of the value of
are expected to be similar for hairpin and straight G segments regardless of the value of 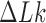 (Figure 7, lower panel, middle).
(Figure 7, lower panel, middle).
Thus, the unknotting capability of type-II enzymes for complex knots is enhanced for a type-II enzyme with hairpin G segment compared to a type-II enzyme with straight G segment mainly due to a combination of two effects: (i) enhanced juxtaposition probability 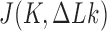 for complex knots and (ii) enhanced probability
for complex knots and (ii) enhanced probability 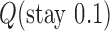 for an unknot to stay unknotted after strand passage. Both these effects increase exponentially with the degree of supercoiling
for an unknot to stay unknotted after strand passage. Both these effects increase exponentially with the degree of supercoiling 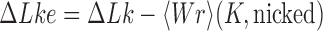 . Note that this effect cannot be explained alone by the free-energy landscape
. Note that this effect cannot be explained alone by the free-energy landscape 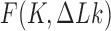 (Figure 4) but is a result of the non-equilibrium dynamics associated with type-II action. Conversely, the probability
(Figure 4) but is a result of the non-equilibrium dynamics associated with type-II action. Conversely, the probability  that strand passage in a complex knot results in unknotting is similar for hairpin and straight G segments, and thus does not contribute much to the unknotting capability of type-II enzymes with a hairpin versus a straight G segment. In this sense, type-II enzymes with hairpin G segments are not ‘smarter’ than type-II enzymes with straight G segments (the latter corresponding to the equilibrium situation) but are more efficient mainly due to enhanced frequencies of juxtaposition
that strand passage in a complex knot results in unknotting is similar for hairpin and straight G segments, and thus does not contribute much to the unknotting capability of type-II enzymes with a hairpin versus a straight G segment. In this sense, type-II enzymes with hairpin G segments are not ‘smarter’ than type-II enzymes with straight G segments (the latter corresponding to the equilibrium situation) but are more efficient mainly due to enhanced frequencies of juxtaposition 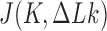 and probabilities
and probabilities  .
.
DISCUSSION
Although much attention, experimentally and theoretically, has been devoted to understanding the action of type-II topoisomerases on unknotted, supercoiled DNA and relaxed or nicked, knotted DNA, respectively, there has been little examination of type-II enzyme activity on DNAs that are both knotted and supercoiled. Whereas negative (–) supercoiling is acknowledged to be essential for normal transactions involving DNA in living systems, unresolved knotting of a genome is generally believed to be fatal to the cell (2,43–45). The question of how homeostatic mechanisms properly regulate supercoiling and, at the same time, completely eliminate knots hinges on detailed understanding of the respective rates for linking-number changes versus unknotting. Toward that end we have developed a model based on a network of topological states 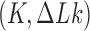 of circular DNAs with knot type
of circular DNAs with knot type  and linking-number difference
and linking-number difference 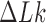 in which the dynamics of transitions between states
in which the dynamics of transitions between states  mediated by type-II enzymes is described by a chemical master equation. For the special case that the non-equilibrium fractions of states
mediated by type-II enzymes is described by a chemical master equation. For the special case that the non-equilibrium fractions of states  are time-independent, corresponding to non-equilibrium steady states (NESS), we fully characterize pathways of topology simplification mediated by type-II enzymes as network graphs having steady-state probabilities
are time-independent, corresponding to non-equilibrium steady states (NESS), we fully characterize pathways of topology simplification mediated by type-II enzymes as network graphs having steady-state probabilities 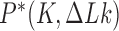 and probability currents
and probability currents  (Figures 5, 6). Our approach thus comprehensively and simultaneously addresses the kinetics of superhelix relaxation and knot resolution. One novel feature of our model is that we consider the biologically relevant case that complex knots are generated extrinsically, e.g. by an intracellular knotting activity independent of the topology-resolving activity inherent in the network (Figure 6). Our analysis complements the work of Shimokawa and colleagues, who considered stepwise unlinking of DNA-replication catenanes by the Xer site-specific recombinase (32). Indeed, our approach can be generalized to quantitatively analyze rates of linking/unlinking and other topological changes resulting from diverse processes including genetic recombination.
(Figures 5, 6). Our approach thus comprehensively and simultaneously addresses the kinetics of superhelix relaxation and knot resolution. One novel feature of our model is that we consider the biologically relevant case that complex knots are generated extrinsically, e.g. by an intracellular knotting activity independent of the topology-resolving activity inherent in the network (Figure 6). Our analysis complements the work of Shimokawa and colleagues, who considered stepwise unlinking of DNA-replication catenanes by the Xer site-specific recombinase (32). Indeed, our approach can be generalized to quantitatively analyze rates of linking/unlinking and other topological changes resulting from diverse processes including genetic recombination.
As a starting point for our non-equilibrium model, we first investigated the equilibrium probability distribution 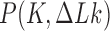 and free-energy landscape
and free-energy landscape 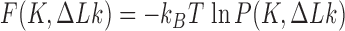 to obtain the most likely relaxation pathway of a given DNA knot by a hypothetical topoisomerase that lacks any bias towards topology simplification and is driven only by the topological free-energy gradient. In particular, we clarify two apparently contradictory results in the literature concerning how supercoiling and knotting affect the thermodynamically most-stable topology of a circular DNA molecule. A previous study used Monte Carlo simulations to address the dependence of the topological free energy of knotted circular DNA on supercoiling and showed that non-trivially knotted species were free-energy minima for even modest, fixed values of
to obtain the most likely relaxation pathway of a given DNA knot by a hypothetical topoisomerase that lacks any bias towards topology simplification and is driven only by the topological free-energy gradient. In particular, we clarify two apparently contradictory results in the literature concerning how supercoiling and knotting affect the thermodynamically most-stable topology of a circular DNA molecule. A previous study used Monte Carlo simulations to address the dependence of the topological free energy of knotted circular DNA on supercoiling and showed that non-trivially knotted species were free-energy minima for even modest, fixed values of  (25). Moreover, complexity of the knots corresponding to the free-energy minimum increases with increasing
(25). Moreover, complexity of the knots corresponding to the free-energy minimum increases with increasing  (Supplementary Figure S2); thus, supercoiling favors more complex knots according to this view (25). In a study published nine years later a different team argued that in type-II enzyme action an effective linking number difference,
(Supplementary Figure S2); thus, supercoiling favors more complex knots according to this view (25). In a study published nine years later a different team argued that in type-II enzyme action an effective linking number difference, 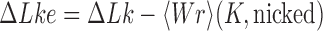 , is fixed instead of
, is fixed instead of 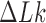 (cf. Figure 3), and concluded that the unknot is a universal free energy minimum, consistent with a picture in which supercoiling inhibits DNA knotting (26). The difference between these results can be understood by considering the full free-energy landscape
(cf. Figure 3), and concluded that the unknot is a universal free energy minimum, consistent with a picture in which supercoiling inhibits DNA knotting (26). The difference between these results can be understood by considering the full free-energy landscape  of knotted supercoiled DNA, in which distributions for fixed
of knotted supercoiled DNA, in which distributions for fixed  or
or 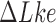 correspond to different paths along the contours of this landscape (Figure 4). However, for biological systems in which a finite amount of supercoiling is maintained by DNA gyrase (58,59), for example, the relevant sections of the free-energy landscape correspond to fixed values of
correspond to different paths along the contours of this landscape (Figure 4). However, for biological systems in which a finite amount of supercoiling is maintained by DNA gyrase (58,59), for example, the relevant sections of the free-energy landscape correspond to fixed values of 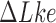 (26).
(26).
Our non-equilibrium model recapitulates the experimental observation that type-II topoisomerases remove crossings in trefoil knots in DNA below the level expected at thermal equilibrium (11) (Figure 5). As found previously, the efficiency of unknotting strongly depends on the presence or absence of a topoisomerase-induced bend in the gate (G) segment (12,21): a hairpin-like G segment having an induced bend of 120° gave more efficient unknotting than an unbent G segment, resulting in an 8-fold reduction of trefoil knots in the hairpin G segment case compared to a straight G segment. In addition, for our 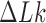 -resolved model we show that the efficiency of unknotting (the reduction factor for trefoil knots) depends strongly on the value of
-resolved model we show that the efficiency of unknotting (the reduction factor for trefoil knots) depends strongly on the value of 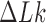 (Figure 5). We find that the
(Figure 5). We find that the  distribution in the unknot is narrower, i.e. the DNA is less supercoiled on average in the presence of type-II enzyme activity compared to the product
distribution in the unknot is narrower, i.e. the DNA is less supercoiled on average in the presence of type-II enzyme activity compared to the product  distribution for a type-I enzyme, in agreement with experimental results (11) (Supplementary Figure S3). The latter does not consume the energy of ATP hydrolysis and therefore generates the
distribution for a type-I enzyme, in agreement with experimental results (11) (Supplementary Figure S3). The latter does not consume the energy of ATP hydrolysis and therefore generates the 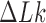 distribution expected at equilibrium.
distribution expected at equilibrium.
Introducing an extrinsic biological process that continuously converts unknotted DNAs with 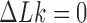 to a complex topological form
to a complex topological form 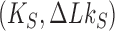 (chosen to be
(chosen to be  in our study) at a constant rate
in our study) at a constant rate 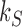 leads to the following main results for the pathways of topology simplification mediated by type-II enzymes (Figure 6):
leads to the following main results for the pathways of topology simplification mediated by type-II enzymes (Figure 6):
Only a small number of intermediate topological states contribute to the pathways, namely those that dominate the equilibrium distribution
 (Supplementary Figure S2);
(Supplementary Figure S2);Pathways of knots generated with
 closely follow the path
closely follow the path  (pathways shown on the left in Figure 6A, B) corresponding to the minimum in the free-energy landscape
(pathways shown on the left in Figure 6A, B) corresponding to the minimum in the free-energy landscape 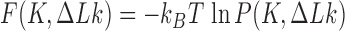 (white line on the left in Figure 4). Similarly, pathways of knots for which finite DNA supercoiling is maintained by imposing the constraint
(white line on the left in Figure 4). Similarly, pathways of knots for which finite DNA supercoiling is maintained by imposing the constraint  closely follow the path
closely follow the path  (pathways shown on the right in Figure 6A, B). Apparently, intersegment collisions that lead to torsional relaxation are more common than those for unknotting, so that the chain adopts the minimum value of
(pathways shown on the right in Figure 6A, B). Apparently, intersegment collisions that lead to torsional relaxation are more common than those for unknotting, so that the chain adopts the minimum value of  allowed by the conditions for a given knot type before the knot type changes, i.e., unknotting is the rate-limiting step;
allowed by the conditions for a given knot type before the knot type changes, i.e., unknotting is the rate-limiting step;The unknotting efficiency strongly depends on the geometry of the G segment and on the degree of DNA supercoiling, being largest for a hairpin-like G segment activity in DNA for which a finite degree of supercoiling is maintained (pathway shown on the right in Figure 6A). These results suggest that only the combined effects of type-II topoisomerase activity, driving the system away from equilibrium, and increased DNA supercoiling can generate the degree of topology simplification observed in experimental measurements;
The dominating pathways for hairpin and straight G segments are closely similar. This surprising result can be explained by the fact that the unknotting capability of a type-II enzyme with a hairpin G segment compared to a straight G segment is enhanced mainly due to an enhanced juxtaposition probability in complex knots and enhanced probability for an unknot to remain unknotted after strand passage, as opposed to a different selection of strand passages in knotted DNA (Figure 7). In this sense, the requirement for a bent G segment acts as a topological filter. Type-II enzymes that require a hairpin G segment are not ‘smarter’ than type-II enzymes that employ a straight G segment (the latter closely corresponding to the equilibrium situation), but rather are more active.
Other models apart from the hairpin-like G segment have considered the ramifications of ‘hooked’ juxtapositions on topology simplification (17). The main difference between the hooked-juxtaposition model and the hairpin-like G segment model is that the enzyme binds two juxtaposed DNA segments simultaneously rather than successively. Thus the principle of both models is essentially the same, apart from the fact that hooked juxtapositions occur much more rarely than juxtapositions with a hairpin-like G segment (12,21). Moreover, it is difficult to imagine how the enzyme could impose a geometric requirement for hooked juxtapositions on the transiently passed T segment. For this to be the case the enzyme would need to have preferential affinity for a pre-bent incoming T segment, implying also that there should be a preferred geometric orientation of this segment. We are not aware of any experimental evidence to support the latter requirement.
Results obtained in this study are based on the assumption that the affinity of type-II enzymes to bind to DNA and generate an appropriate G segment geometry is independent of the topological state 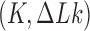 of the DNA, in particular, independent of the degree of supercoiling. This implies that the constant
of the DNA, in particular, independent of the degree of supercoiling. This implies that the constant  in Equation (2), describing the affinity and concentration of the enzyme, is assumed to be independent of the topological state
in Equation (2), describing the affinity and concentration of the enzyme, is assumed to be independent of the topological state  of the DNA. Thus the constant
of the DNA. Thus the constant  drops out in the ratio in Equation (4) so that our results are universal in the sense that they do not depend on the value of
drops out in the ratio in Equation (4) so that our results are universal in the sense that they do not depend on the value of 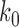 . However, recent experimental results suggest that type-II enzymes have a propensity to bind to DNA and form G segments in highly supercoiled DNA, presumably because the latter is strongly bent on average, thereby facilitating the formation of bent G segments (61). This effect can be implemented in our model by making
. However, recent experimental results suggest that type-II enzymes have a propensity to bind to DNA and form G segments in highly supercoiled DNA, presumably because the latter is strongly bent on average, thereby facilitating the formation of bent G segments (61). This effect can be implemented in our model by making  in Equation (2) a function of the degree of supercoiling
in Equation (2) a function of the degree of supercoiling 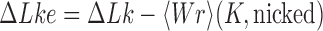 . Our results were obtained for 6-kbp DNA; however, the transition rates and resulting decay pathways are expected to depend on the total length of the DNA. Moreover, in many cases DNA in vivo is spatially confined (e.g. inside the nucleus in eukaryotes) or subject to molecular crowding. It would be of interest to study the dependence of transition rates on DNA length and confinement in future work.
. Our results were obtained for 6-kbp DNA; however, the transition rates and resulting decay pathways are expected to depend on the total length of the DNA. Moreover, in many cases DNA in vivo is spatially confined (e.g. inside the nucleus in eukaryotes) or subject to molecular crowding. It would be of interest to study the dependence of transition rates on DNA length and confinement in future work.
It has long been argued that, for thermodynamic reasons, type-II enzyme action requires the energy of ATP hydrolysis to move the system out of topological equilibrium. Bates et al. have argued that only a small portion of the free energy gained from ATP hydrolysis is needed to achieve topology simplification (62). However, recent reviews by Rybenkov (14) and Grosberg (63) point out that there is additional free-energy dissipation potentially required by various irreversible steps in the type-II mechanism. In a study of E. coli topoisomerase-IV mutants, Lee et al. found that the extent of topoisomerase II-induced DNA bending in the substrate DNA G segment, but not DNA binding, was correlated with ATP-hydrolysis activity (64). Type-II enzymes can vary widely in terms of topology-simplification efficiency and also optimum reaction conditions, so it is perhaps not surprising that a mechanism that dissipates excess free energy is both biochemically and evolutionarily advantageous. In summary, many questions remain pertaining to when, during the segment-passage reaction, energy gained from ATP hydrolysis is used by the enzyme and for what purpose. Even without ATP hydrolysis the enzyme can bind to DNA and perform strand passage (65,66); this implies that these steps are essentially driven by the free-energy gradient so that the enzyme–DNA complex after passage should be very stable. It has been proposed that ATP hydrolysis serves to release the energy necessary for dissociating the stable enzyme-DNA complex after segment passage, thereby resetting the original conformation of the protein (19,67) (Figure 1A). Other studies suggested that two ATP molecules are hydrolyzed sequentially before and after segment passage, respectively (68,69). It would be interesting to address these questions by modeling the enzymatic reaction in terms of graphs on networks formed by chemical and conformational states of the enzyme–DNA complex, similar as has been recently done for molecular motors and other nanomachines (70–73).
The work by Rybenkov et al. (11) remains to our knowledge the only paper that has comprehensively and quantitatively addressed topology simplification by type-II enzymes. We hope that our study will motivate new experimental work that addresses topology simplification of complex knots in supercoiled DNA.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Keir Neuman and Cristian Micheletti for communicating results to us in advance of publication and for helpful discussions. We also thank Eric Rawdon for helping to identify some of the complex knots that appeared in the simulations.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
National Institutes of Health and the Joint DMS/NIGMS Initiative to Support Research at the Interface of the Biological and Mathematical Sciences [NIH R01GM117595 to S.D.L.]. Funding for open access charge: National Institutes of Health.
Conflict of interest statement. None declared.
REFERENCES
- 1. Zechiedrich E.L., Cozzarelli N.R.. Roles of topoisomerase IV and DNA gyrase in DNA unlinking during replication in Escherichia coli. Genes Dev. 1995; 9:2859–2869. [DOI] [PubMed] [Google Scholar]
- 2. Mann J.K., Deibler R.W., Sumners D.W.L., Zechiedrich E.L.. Unknotting by type II topoisomerases. Abstracts of Papers Presented to the American Mathematical Society. 2004. [Google Scholar]
- 3. Massé E., Drolet M.. Escherichia coli DNA topoisomerase I inhibits R-loop formation by relaxing transcription-induced negative supercoiling. J. Biol. Chem. 1999; 274:16659–16664. [DOI] [PubMed] [Google Scholar]
- 4. Mondal N., Zhang Y., Jonsson Z., Dhar S.K., Kannapiran M., Parvin J.D.. Elongation by RNA polymerase II on chromatin templates requires topoisomerase activity. Nucleic Acids Res. 2003; 31:5016–5024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Mondal N., Parvin J.D.. DNA topoisomerase IIα is required for RNA polymerase II transcription on chromatin templates. Nature. 2001; 413:435–438. [DOI] [PubMed] [Google Scholar]
- 6. Champoux J.J. DNA topoisomerases: structure, function, and mechanism. Annu. Rev. Biochem. 2001; 70:369–413. [DOI] [PubMed] [Google Scholar]
- 7. Dean F.B., Stasiak A., Koller T., Cozzarelli N.R.. Duplex DNA knots produced by Escherichia coli Topoisomerase I. J. Biol. Chem. 1985; 260:4975–4983. [PubMed] [Google Scholar]
- 8. Wang J.C. Moving one DNA double helix through another by a type II DNA topoisomerase: The story of a simple molecular machine. Q. Rev. Biophys. 1998; 31:107–144. [DOI] [PubMed] [Google Scholar]
- 9. Gellert M., Mizuuchi K., O’Dea M.H., Itoh T., Tomizawa J.-I.. Nalidixic acid resistance: A second genetic character involved in DNA gyrase activity. Proc. Natl. Acad. Sci. U.S.A. 1977; 74:4772–4776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Sugino A, Peebles C.L., Kreuzer K.N., Cozzarelli N.R.. Mechanism of action of nalidixic acid: purification of Escherichia coli nalA gene product and its relationship to DNA gyrase and a novel nicking-closing enzyme. Proc. Natl. Acad. Sci. U.S.A. 1977; 74:4767–4771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Rybenkov V.V., Ullsperger C., Vologodskii A.V., Cozzarelli N.R.. Simplification of DNA topology below equilibrium values by type II topoisomerases. Science. 1997; 277:690–693. [DOI] [PubMed] [Google Scholar]
- 12. Vologodskii A.V., Zhang W., Rybenkov V.V., Podtelezhnikov A.A., Subramanian D., Griffith J.D., Cozzarelli N.R.. Mechanism of topology simplification by type II DNA topoisomerases. Proc. Natl. Acad. Sci. U.S.A. 2001; 98:3045–3049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Vologodskii A.V. Disentangling DNA molecules. Phys. Life Rev. 2016; 18:118–134. [DOI] [PubMed] [Google Scholar]
- 14. Rybenkov V.V. When Maxwellian demon meets action at a distance: Comment on “Disentangling DNA molecules” by Alexander Vologodskii. Phys. Life Rev. 2016; 18:150–153. [DOI] [PubMed] [Google Scholar]
- 15. Flammini A., Maritan A., Stasiak A.. Simulations of action of DNA topoisomerases to investigate boundaries and shapes of spaces of knots. Biophys. J. 2004; 87:2968–2975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Liu Z., Mann J.K., Zechiedrich E.L., Chan H.S.. Topological information embodied in local juxtaposition geometry provides a statistical mechanical basis for unknotting by Type-2 DNA topoisomerases. J. Mol. Biol. 2006; 361:268–285. [DOI] [PubMed] [Google Scholar]
- 17. Buck G.R., Zechiedrich E.L.. DNA disentangling by type-2 topoisomerases. J. Mol. Biol. 2004; 340:933–939. [DOI] [PubMed] [Google Scholar]
- 18. Yan J., Magnasco M.O., Marko J.F.. A kinetic proofreading mechanism for disentanglement of DNA by topoisomerases. Nature. 1999; 401:932–935. [DOI] [PubMed] [Google Scholar]
- 19. Burnier Y., Weber C., Flammini A., Stasiak A.. Local selection rules that can determine specific pathways of DNA unknotting by type II DNA topoisomerases. Nucleic Acids Res. 2007; 35:5223–5231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Witz G., Dietler G., Stasiak A.. Tightening of DNA knots by supercoiling facilitates their unknotting by type II DNA topoisomerases. Proc. Natl. Acad. Sci. U.S.A. 2011; 108:3608–3611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Vologodskii A.V. Theoretical models of DNA topology simplification by type IIA DNA topoisomerases. Nucleic Acids Res. 2009; 37:3125–3133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Yan J., Magnasco M.O., Marko J.F.. Kinetic proofreading can explain the suppression of supercoiling of circular DNA molecules by type-II topoisomerases. Phys. Rev. E. 2001; 63:031909. [DOI] [PubMed] [Google Scholar]
- 23. Schmidt B.H., Osheroff N., Berger J.M.. Structure of a topoisomerase II-DNA-nucleotide complex reveals a new control mechanism for ATPase activity. Nat. Struct. Mol. Biol. 2012; 19:1147–1154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Hardin A.H., Sarkar S.K., Seol Y., Liou G.F., Osheroff N., Neuman K.C.. Direct measurement of DNA bending by type IIA topoisomerases: Implications for non-equilibrium topology simplification. Nucleic Acids Res. 2011; 39:5729–5743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Podtelezhnikov A.A., Cozzarelli N.R., Vologodskii A.V.. Equilibrium distributions of topological states in circular DNA: interplay of supercoiling and knotting. Proc. Natl. Acad. Sci. U.S.A. 1999; 96:12974–12979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Burnier Y., Dorier J., Stasiak A.. DNA supercoiling inhibits DNA knotting. Nucleic Acids Res. 2008; 36:4956–4963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Rawdon E.J., Dorier J., Racko D., Millett K.C., Stasiak A.. How topoisomerase IV can efficiently unknot and decatenate negatively supercoiled DNA molecules without causing their torsional relaxation. Nucleic Acids Res. 2016; 44:4528–4538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Giovan S.M., Scharein R.G., Hanke A., Levene S.D.. Free-energy calculations for semi-flexible macromolecules: Applications to DNA knotting and looping. J. Chem. Phys. 2014; 141:174902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Roca J. Varying levels of positive and negative supercoiling differently affect the efficiency with which topoisomerase II catenates and decatenates DNA. J. Mol. Biol. 2001; 305:441–450. [DOI] [PubMed] [Google Scholar]
- 30. Charvin G., Bensimon D., Croquette V.. Single-molecule study of DNA unlinking by eukaryotic and prokaryotic type-II topoisomerases. Proc. Natl. Acad. Sci. U.S.A. 2003; 100:9820–9825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Seol Y., Gentry A.C., Osheroff N., Neuman K.C.. Chiral discrimination and writhe-dependent relaxation mechanism of human topoisomerase IIα. J. Biol. Chem. 2013; 288:13695–13703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Shimokawa K., Ishihara K., Grainge I., Sherratt D.J., Vazquez M.. FtsK-dependent XerCD-dif recombination unlinks replication catenanes in a stepwise manner. Proc. Natl. Acad. Sci. U.S.A. 2013; 110:20906–20911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Seol Y., Hardin A.H., Strub M.-P., Charvin G., Neuman K.C.. Comparison of DNA decatenation by Escherichia coli topoisomerase IV and topoisomerase III: Implications for non-equilibrium topology simplification. Nucleic Acids Res. 2013; 41:4640–4649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Coronel L., Suma A., Micheletti C.. Dynamics of supercoiled DNA with complex knots: Large-scale rearrangements and persistent multi-strand interlocking. Nucleic Acids Res. 2018; 46:7533–7541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Liu L.F., Wang J.C.. Supercoiling of the DNA template during transcription. Proc. Natl. Acad. Sci. U.S.A. 1987; 84:7024–7027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Wu H.-Y., Shyy S., Wang J.C., Liu L.F.. Transcription generates positively and negatively supercoiled domains in the template. Cell. 1988; 53:433–440. [DOI] [PubMed] [Google Scholar]
- 37. Grainge I., Bregu M., Vazquez M., Sivanathan V., Ip S.C.Y., Sherratt D.J.. Unlinking chromosome catenanes in vivo by site-specific recombination. EMBO J. 2007; 26:4228–4238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Grainge I., Lesterlin C., Sherratt D.J.. Activation of XerCD-dif recombination by the FtsK DNA translocase. Nucleic Acids Res. 2011; 39:5140–5148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Hsieh T. Knotting of the circular duplex DNA by type II DNA topoisomerase from Drosophila melanogaster. J. Biol. Chem. 1983; 258:8413–8420. [PubMed] [Google Scholar]
- 40. Wasserman S.A., Cozzarelli N.R.. Supercoiled DNA-directed knotting by T4 topoisomerase. J. Biol. Chem. 1991; 266:20567–20573. [PubMed] [Google Scholar]
- 41. Roca J., Berger J.M., Wang J.C.. On the simultaneous binding of eukaryotic DNA topoisomerase II to a pair of double-stranded DNA helices. J. Biol. Chem. 1993; 268:14250–14255. [PubMed] [Google Scholar]
- 42. Valdés A., Segura J., Dyson S., Martínez-García B., Roca J.. DNA knots occur in intracellular chromatin. Nucleic Acids Res. 2017; 46:650–660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Deibler R.W., Mann J.K., Sumners D.W.L., Zechiedrich E.L.. Hin-mediated DNA knotting and recombining promote replicon dysfunction and mutation. BMC Mol. Biol. 2007; 8:44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Portugal J., Rodríguez-Campos A.. T7 RNA polymerase cannot transcribe through a highly knotted DNA template. Nucleic Acids Res. 1996; 24:4890–4894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Olavarrieta L., Martínez-Robles M.L., Sogo J.M., Stasiak A., Hernández P., Krimer D.B., Schvartzman J.B.. Supercoiling, knotting and replication fork reversal in partially replicated plasmids. Nucleic Acids Res. 2002; 30:656–666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Vologodskii A.V., Levene S.D., Klenin K.V., Frank-Kamenetskii M., Cozzarelli N.R.. Conformational and thermodynamic properties of supercoiled DNA. J. Mol. Biol. 1992; 227:1224–1243. [DOI] [PubMed] [Google Scholar]
- 47. Bouchiat C., Wang M.D., Allemand J.F., Strick T., Block S.M., Croquette V.. Estimating the persistence length of a worm-like chain molecule from force-extension measurements. Biophys. J. 1999; 76:409–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Rybenkov V.V., Cozzarelli N.R., Vologodskii A.V.. Probability of DNA knotting and the effective diameter of the DNA double helix. Proc. Natl. Acad. Sci. U.S.A. 1993; 90:5307–5311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Gouesbet G., Meunier-Guttin-Cluzel S.. Computer evaluation of Kauffman polynomials by using Gauss codes, with a skein-template algorithm. Appl. Math. Comput. 2001; 122:229–252. [Google Scholar]
- 50. Zia R.K.P., Schmittmann B.. A possible classification of nonequilibrium steady states. J. Phys. A. Math. Gen. 2006; 39:L407. [Google Scholar]
- 51. Jiang D.-Q., Qian M.-P., Qian M.-P.. Mathematical Theory of Nonequilibrium Steady States: On the Frontier of Probability and Dynamical Systems. 2004; Berlin: Springer. [Google Scholar]
- 52. Pettijohn D.E., Pfenninger O.. Supercoils in prokaryotic DNA restrained in vivo. Proc. Natl. Acad. Sci. U.S.A. 1980; 77:1331–1335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Dorman C.J., Dorman M.J.. DNA supercoiling is a fundamental regulatory principle in the control of bacterial gene expression. Biophys. Rev. 2016; 8:209–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Darcy I.K., Scharein R.G., Stasiak A.. 3D visualization software to analyze topological outcomes of topoisomerase reactions. Nucleic Acids Res. 2008; 36:3515–3521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Trigueros S., Salceda J., Bermúdez I., Fernández X., Roca J.. Asymmetric removal of supercoils suggests how topoisomerase II simplifies DNA topology. J. Mol. Biol. 2004; 335:723–731. [DOI] [PubMed] [Google Scholar]
- 56. Stuchinskaya T., Mitchenall L.A., Schoeffler A.J., Corbett K.D., Berger J.M., Bates A.D., Maxwell A.. How do type II topoisomerases use ATP hydrolysis to simplify DNA topology beyond equilibrium? Investigating the relaxation reaction of nonsupercoiling type II topoisomerases. J. Mol. Biol. 2009; 385:1397–1408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Martínez-García B., Fernández X., Díaz-Ingelmo O., Rodríguez-Campos A., Manichanh C., Roca J.. Topoisomerase II minimizes DNA entanglements by proofreading DNA topology after DNA strand passage. Nucleic Acids Res. 2014; 42:1821–1830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Drlica K. Control of bacterial DNA supercoiling. Mol. Microbiol. 1992; 6:425–433. [DOI] [PubMed] [Google Scholar]
- 59. Zechiedrich E.L., Khodursky A.B., Bachellier S., Schneider R., Chen D., Lilley D.M.J., Cozzarelli N.R.. Roles of topoisomerases in maintaining steady-state DNA supercoiling in Escherichia coli. J. Biol. Chem. 2000; 275:8103–8113. [DOI] [PubMed] [Google Scholar]
- 60. Marko J.F. Torque and dynamics of linking number relaxation in stretched supercoiled DNA. Phys. Rev. E - Stat. Nonlinear Soft Matter Phys. 2007; 76:1–13. [DOI] [PubMed] [Google Scholar]
- 61. Litwin T.R., Solà M., Holt I.J., Neuman K.C.. A robust assay to measure DNA topology-dependent protein binding affinity. Nucleic Acids Res. 2015; 43:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Bates A.D., Berger J.M., Maxwell A.. The ancestral role of ATP hydrolysis in type II topoisomerases: prevention of DNA double-strand breaks. Nucleic Acids Res. 2011; 39:6327–6339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Grosberg A.Y. Vingt ans après (Twenty years after): Comment on “Disentangling DNA molecules” by Alexander Vologodskii. Phys. Life Rev. 2016; 18:139–143. [DOI] [PubMed] [Google Scholar]
- 64. Lee I., Dong K.C., Berger J.M.. The role of DNA bending in type IIA topoisomerase function. Nucleic Acids Res. 2013; 41:5444–5456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Williams N.L., Howells A.J., Maxwell A.. Locking the ATP-operated clamp of dna gyrase: Probing the mechanism of strand passage. J. Mol. Biol. 2001; 306:969–984. [DOI] [PubMed] [Google Scholar]
- 66. Roca J., Wang J.C.. DNA transport by a type II DNA topoisomerase: evidence in favor of a two-gate mechanism. Cell. 1994; 77:609–616. [DOI] [PubMed] [Google Scholar]
- 67. Rosselli W., Stasiak A.. Energetics of RecA-mediated recombination reactions. Without ATP hydrolysis RecA can mediate polar strand exchange but is unable to recycle. J. Mol. Biol. 1990; 216:335–352. [DOI] [PubMed] [Google Scholar]
- 68. Harkins T.T., Lewis T.J., Lindsley J.E.. Pre-steady-state analysis of ATP hydrolysis by Saccharomyces cerevisiae DNA topoisomerase II. 2. Kinetic mechanism for the sequential hydrolysis of two ATP. Biochemistry. 1998; 37:7299–7312. [DOI] [PubMed] [Google Scholar]
- 69. Baird C.L., Harkins T.T., Morris S.K., Lindsley J.E.. Topoisomerase II drives DNA transport by hydrolyzing one ATP. Proc. Natl. Acad. Sci. U.S.A. 1999; 96:13685–13690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Liepelt S., Lipowsky R.. Steady-state balance conditions for molecular motor cycles and stochastic nonequilibrium processes. Europhys. Lett. 2007; 77:50002. [Google Scholar]
- 71. Liepelt S., Lipowsky R.. Kinesin's network of chemomechanical motor cycles. Phys. Rev. Lett. 2007; 98:258102. [DOI] [PubMed] [Google Scholar]
- 72. Seifert U. Stochastic thermodynamics of single enzymes and molecular motors. Eur. Phys. J. E. 2011; 34:26. [DOI] [PubMed] [Google Scholar]
- 73. Seifert U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Reports Prog. Phys. 2012; 75:126001. [DOI] [PubMed] [Google Scholar]
- 74. Scharein R.G. Interactive Topological Drawing. 1998; University of British Columbia, Department of Computer Science; Ph.D. dissertation. [Google Scholar]
- 75. Adams C.C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. 1994; NY: W. H. Freeman and Company. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.








