STATISTICAL INFERENCE FOR THE MEAN OUTCOME UNDER A POSSIBLY NON-UNIQUE OPTIMAL TREATMENT STRATEGY

Abstract

We consider challenges that arise in the estimation of the mean outcome under an optimal individualized treatment strategy defined as the treatment rule that maximizes the population mean outcome, where the candidate treatment rules are restricted to depend on baseline covariates. We prove a necessary and sufficient condition for the pathwise differentiability of the optimal value, a key condition needed to develop a regular and asymptotically linear (RAL) estimator of the optimal value. The stated condition is slightly more general than the previous condition implied in the literature. We then describe an approach to obtain root-n rate confidence intervals for the optimal value even when the parameter is not pathwise differentiable. We provide conditions under which our estimator is RAL and asymptotically efficient when the mean outcome is pathwise differentiable. We also outline an extension of our approach to a multiple time point problem. All of our results are supported by simulations.

1. Introduction

There has been much recent work in estimating optimal treatment regimes (TRs) from a random sample. A TR is an individualized treatment strategy in which treatment decisions for a patient can be based on their measured covariates. Doctors generally make decisions this way, and thus it is natural to want to learn about the best strategy. The value of a TR is defined as the population counterfactual mean outcome if the TR were implemented in the population. The optimal TR is the TR with the maximal value, and the value at the optimal TR is the optimal value. In a single time point setting, the optimal TR can be defined as the sign of the “blip function,” defined as the additive effect of a blip in treatment on a counterfactual outcome, conditional on baseline covariates [Robins (2004)]. In a multiple time point setting, treatment strategies are called dynamic TRs (DTRs). For a general overview of recent work on optimal (D)TRs, see Chakraborty and Moodie (2013).

Suppose one wishes to know the impact of implementing an optimal TR in the population, that is, one wishes to know the optimal value. Before estimating the optimal value, one typically estimates the optimal rule. Recently, researchers have suggested applying machine learning algorithms to estimate the optimal rules from large classes which cannot be described by a finite dimensional parameter [see, e.g., Zhang et al. (2012b), Zhao et al. (2012), Luedtke and van der Laan (2014)].

Inference for the optimal value has been shown to be difficult at exceptional laws, that is, probability distributions where there exists a strata of the baseline covariates that occurs with positive probability and for which treatment is neither beneficial nor harmful [Robins (2004), Robins and Rotnitzky (2014)]. Zhang et al. (2012a) considered inference for the optimal value in restricted classes in which the TRs are indexed by a finite-dimensional vector. At non-exceptional laws, they outlined an argument showing that their estimator is (up to a negligible term) feequal to the estimator that estimates the value of the known optimal TR under regularity conditions. The implication is that one can estimate the optimal value and then use the usual sandwich technique to estimate the standard error and develop Wald-type confidence intervals (CIs). van der Laan and Luedtke (2014b) and van der Laan and Luedtke (2014a) developed inference for the optimal value when the DTR belongs to an unrestricted class. van der Laan and Luedtke (2014a) provide a proof that the efficient influence curve for the parameter which treats the optimal rule as known is equal to the efficient influence curve of the optimal value at non-exceptional laws. One of the contributions of the current paper is to present a slightly more precise statement of the condition for the pathwise differentiability of the mean outcome under the optimal rule. We will show that this condition is necessary and sufficient.

However, restricting inference to non-exceptional laws is limiting as there is often no treatment effect for people in some strata of baseline covariates. Chakraborty, Laber and Zhao (2014) propose using the m-out-of-n bootstrap to obtain inference for the value of an estimated DTR. With an inverse probability weighted (IPW) estimator this yields valid inference when the treatment mechanism is known or is estimated according to a correctly specified parametric model. They also discuss an extension to an double robust estimator. The m-out-of-n bootstrap draws samples of size m patients from the data set of size n. In non-regular problems, this method yields valid inference if m,n→∞ and m= o(n). The CIs for the value of an estimated regime shrink at a root-m (not root-n) rate. In addition to yielding wide CIs, this approach has the drawback of requiring a choice of the important tuning parameter m, which balances a trade-off between coverage and efficiency. Chakraborty, Laber and Zhao propose using a double bootstrap to select this tuning parameter.

Goldberg et al. (2014) instead consider truncating the criteria to be optimized, that is, the value under a given rule, so that only individuals with a clinically meaningful treatment effect contribute to the objective function. These authors then propose proceeding with inference for the truncated value at the optimal DTR. For a fixed truncation level, the estimated truncated optimal value minus the true truncated optimal value, multiplied by root-n, converges to a normal limiting distribution. Laber et al. (2014b) propose instead replacing the indicator used to define the value of a TR with a differentiable function. They discuss situations in which the estimator minus the smoothed value of the estimated TR, multiplied by root-n, would have a reasonable limit distribution.

In this work, we develop root-n rate inference for the optimal value under reasonable conditions. Our approach avoids any sort of truncation, and does not require that the estimate of the optimal rule converge to a fixed quantity as the sample size grows. We show that our estimator minus the truth, properly standardized, converges to a standard normal limiting distribution. This allows for the straightforward construction of asymptotically valid CIs for the optimal value. Neither the estimator nor the inference rely on a complicated tuning parameter. We give conditions under which our estimator is asymptotically efficient among all regular and asymptotically linear (RAL) estimators when the optimal value parameter is pathwise differentiable, similar to those we presented in van der Laan and Luedtke (2014b). However, they do not require that one knows that the optimal value parameter is pathwise differentiable from the outset. Implementing the procedure only requires a minor modification to a typical one-step estimator.

We believe the value of the unknown optimal rule is an interesting target of inference because the treatment strategy learned from the given data set is likely to be improved upon as clinicians gain more knowledge, with the treatment strategy given in the population eventually approximating the optimal rule. Additionally, the optimal rule represents an upper bound on what can be hoped for when a treatment is introduced. Nonetheless, as we and others have argued in the references above, the value of the estimated rule is also an interesting target of inference [Chakraborty, Laber and Zhao (2014), Laber et al. (2014b), van der Laan and Luedtke (2014a, 2014b)]. Thus, although our focus is on estimating the optimal value, we also give conditions under which our CI provides proper coverage for the data adaptive parameter which gives the value of the rule estimated from the entire data set.

Organization of article

Section 2 formulates the statistical problem of interest. Section 3 gives necessary and sufficient conditions for the pathwise differentiability of the optimal value. Section 4 outlines the challenge of obtaining inference at exceptional laws and gives a thought experiment that motivates our procedure for estimating the optimal value. Section 5 presents an estimator for the optimal value. This estimator represents a slight modification to a recently presented online one-step estimator for pathwise differentiable parameters. Section 6 discusses computationally efficient implementations of our proposed procedure. Section 7 discusses each condition of the key result presented in Section 5. Section 8 describes our simulations. Section 9 gives our simulation results. Section 10 closes with a summary and some directions for future work.

All proofs can be found in Supplementary Appendix A [Luedtke and van der Laan (2015)]. We outline an extension of our proposed procedure to the multiple time point setting in Supplementary Appendix B. Additional figures appear in Supplementary Appendix C.

2. Problem formulation

Let O = (W,A, Y) ~ P₀ ∈ ℳ, where W represents a vector of covariates, A a binary intervention, and Y a real-valued outcome. The model for P₀ is nonparametric. We observe an independent and identically distributed (i.i.d.) sample O₁, …, O_n from P₀. Let 𝒲 denote the range of W. For a distribution P, define the treatment mechanism g(P)(A|W) ≜ Pr_P (A|W). We will refer to g(P₀) as g₀ and g(P) as g. For a function f, we will use E_P [f(O)] to denote ∫ f(o)dP(o). We will also use E₀[f(O)] to denote E_P0[f(O)] and Pr₀ to denote the P₀ probability of an event. Let Ψ : ℳ→ℝ be defined by

$$\mathrm{\Psi }(P)\triangleq E_P{E}_P[Y\mid A=d(P)(W),W],$$

where d(P) ≜ argmax_dE_PE_P (Y |A = d(W),W) is an optimal treatment rule under P. We will resolve the ambiguity in the definition of d when the argmax is not unique later in this section. Throughout we assume that Pr₀(0 < g₀(1|W) < 1) so that Ψ(P₀) is well defined. Under causal assumptions, Ψ(P) is equal to the counterfactual mean outcome if, possibly contrary to fact, the rule d(P) were implemented in the population. We can also identify d(P) with a causally optimal rule under those same assumptions. We refer the reader to van der Laan and Luedtke (2014b) for a more precise formulation of such a treatment strategy. As the focus of this work is statistical, all of the results will hold when estimating the parameter Ψ(P₀) whether or not the causal assumptions needed for identifiability hold. Let

$$\begin{gathered} \overline{Q}(P)(A,W)\triangleq E_P[Y\mid A,W], \\ {\overline{Q}}_b(P)(W)\triangleq \overline{Q}(P)(1,W)-\overline{Q}(P)(0,W). \end{gathered}$$

We will refer to Q̄_b(P) the blip function for the distribution P. We will denote to the above quantities applied to P₀ as Q̄₀ and Q̄_b,0, respectively. We will often omit the reliance on P altogether when there is only one distribution P under consideration: Q̄(A,W) and Q̄_b(W). We also define Ψ_d(P) = E_PQ̄(d(P)(W),W). Consider the efficient influence curve of Ψ_d at P:

$$D(d,P)(O)=\frac{I(A=d(W))}{g(A\mid W)}(Y-\overline{Q}(A,W))+\overline{Q}(d(W),W)-{\mathrm{\Psi }}_d(P).$$

Let B(P) ≜ {w : Q̄_b(w) = 0}. We will refer to B(P₀) as B₀. An exceptional law is defined as a distribution P for which Pr_P (W ∈ B(P)) > 0 [Robins (2004)]. We note that the ambiguity in the definition of d(P) occurs precisely on the set B(P). In particular, d(P) must almost surely agree with some rule in the class

$$\{w\mapsto I({\overline{Q}}_b(w)>0)I(w\notin B(P))+b(w)I(w\in B(P)):b\},$$ (1)

where b :𝒲 → {0, 1} is some function. Consider now the following uniquely defined optimal rule:

$$d^{\ast }(P)(W)\triangleq I({\overline{Q}}_b(W)>0).$$

We will let $d_0^{\ast }=d^{\ast }(P_0)$. We have Ψ(P) = Ψ_d^*(P)(P), but now d^*(P) is uniquely defined for all W. More generally, d^*(P) represents a uniquely defined optimal rule. Other formulations of the optimal rule can be obtained by changing the behavior of the rule B₀. Our goal is to construct root-n rate CIs for Ψ(P₀) that maintain nominal coverage, even at exceptional laws. At non-exceptional laws, we would like these CIs to belong to and be asymptotically efficient among the class of regular asymptotially linear (RAL) estimators.

3. Necessary and sufficient conditions for pathwise differentiability of Ψ

In this section, we give a necessary and sufficient condition for the pathwise differentiability of the optimal value parameter Ψ. When it exists, the pathwise derivative in a nonparametric model can be written as an inner product between an almost surely unique mean zero, square integrable function known as the canonical gradient and a score function. The canonical gradient is a key object in nonparametric statistics. We remind the reader that an estimator Φ̂ is asymptotically linear for a parameter mapping Φ at P₀ with influence curve IC₀ if

$$\widehat{\mathrm{\Phi }}(P_n)-\mathrm{\Phi }(P_0)=\frac{1}{n}\sum _{i=1}^n{IC}_0(O_i)+o_{P_0}(n^{-1/2}),$$

where E₀[IC₀(O)] = 0. The pathwise derivative is important because, when Φ is pathwise differentiable in a nonparametric model, any regular estimator Φ̂ is asymptotically linear with influence curve IC₀(O_i) if and only if IC₀ is the canonical gradient [Bickel et al. (1993)]. We discuss negative results for non-pathwise differentiable parameters and formally define “regular estimator” later in this section.

The pathwise derivative of Ψ at P₀ can be defined as follows. Define paths {P_ε : ε ∈ ℝ} ⊂ ℳ that go through P₀ at ε = 0, that is, P_ε=0 = P₀. In particular, these paths are given by

$$\begin{gathered} d{Q}_{W,\epsilon }=(1+\epsilon S_W(W))d{Q}_{W,0}, \\ \text{where}{E}_0[S_W(W)]=0\text{and}\underset{w}{sup}\mid S_W(w)\mid <\infty ; \\ d{Q}_{Y,\epsilon }(Y\mid A,W)=(1+\epsilon S_Y(Y\mid A,W))d{Q}_{Y,0}(Y\mid A,W), \\ \text{where}{E}_0[S_Y\mid A,W]=0\text{and}\underset{w,a,y}{sup}\mid S_Y(y\mid a,w)\mid <\infty . \end{gathered}$$ (2)

Above Q_W,0 and Q_Y,0 are respectively the marginal distribution of W and the conditional distribution of Y given A,W under P₀. The parameter Ψ is not sensitive to fluctuations of g₀(a|w) = Pr₀(a|w), and thus we do not need to fluctuate this portion of the likelihood. The parameter Ψ is called pathwise differentiable at P₀ if

$${\frac{d}{d\epsilon }\mathrm{\Psi }(P_{\epsilon })|}_{\epsilon =0}=\int D^{\ast }(P_0)(o)(S_W(w)+S_{Y\mid A,W}(y\mid a,w))d{P}_0(o)$$

for some P₀ mean zero, square integrable function D^*(P₀) with E₀[D^* × (P₀)(O)|A,W] almost surely equal to E₀[D^*(P₀)(O)|W]. We refer the reader to Bickel et al. (1993) for a more general exposition of pathwise differentiability.

In van der Laan and Luedtke (2014a), we showed that Ψ is pathwise differentiable at P₀ with canonical gradient $D(d_0^{\ast },P_0)$ if P₀ is a non-exceptional law, that is, Pr₀(W ∉ B₀) = 1. Exceptional laws were shown to present problems for estimation of optimal rules indexed by a finite dimensional parameter by Robins (2004), and it was observed by Robins and Rotnitzky (2014) that these laws can also cause problems for unrestricted optimal rules. Here, we show that mean outcome under the optimal rule is pathwise differentiable under a slightly more general condition than requiring a non-exceptional law, namely that

$${Pr}_0\left\{w\in \mathcal{W}:w\notin B_0\text{or}\underset{a\in \{0,1\}}{max}{\sigma }_0^2(a,w)=0\right\}=1,$$ (3)

where ${\sigma }_0(a,w)\triangleq \sqrt{{\text{Var}}_{P_0}(Y\mid A=a,W=w)}$. The upcoming theorem also gives the converse result, that is, the mean outcome under the optimal rule is not pathwise differentiable if the above condition does not hold.

Theorem 1

Assume Pr₀(0 < g₀(1|W) < 1) = 1, Pr₀(|Y |< M) = 1 for some M < ∞, and ${\text{Var}}_{P_0}(D(d_0^{\ast },P_0)(O))<\infty$. The parameter Ψ(P₀) is pathwise differentiable if and only if (3) holds. If Ψ is pathwise differentiable at P₀, then Ψ has canonical gradient $D(d_0^{\ast },P_0)$ at P₀.

In the proof of the theorem, we construct fluctuations S_W and S_Y such that

$$\underset{\epsilon \uparrow 0}{lim}\frac{\mathrm{\Psi }(P_{\epsilon })-\mathrm{\Psi }(P_0)}{\epsilon }\ne \underset{\epsilon \downarrow 0}{lim}\frac{\mathrm{\Psi }(P_{\epsilon })-\mathrm{\Psi }(P_0)}{\epsilon }$$ (4)

when (3) does not hold. It then follows that Ψ(P₀) is not pathwise differentiable. The left- and right-hand sides above are referred to as one-sided directional derivatives by Hirano and Porter (2012).

This condition for the mean outcome differs slightly from that implied for unrestricted rules in Robins and Rotnitzky (2014) in that we still have pathwise differentiability when the Q̄_b,0 is zero in some strata but the conditional variance of the outcome given covariates and treatment is also zero in all of those strata. This makes sense, given that in this case the blip function could be estimated perfectly in those strata in any finite sample with treated and untreated individuals observed in that strata. Though we do not expect this difference to matter for most data generating distributions encountered in practice, there are cases where it may be relevant. For example, if no one in a certain strata is susceptible to a disease regardless of treatment status, and researchers are unaware of this a priori so that simply excluding this strata from the target population is not an option, then the treatment effect and conditional variance are both zero in this strata.

In general, however, we expect that the mean outcome under the optimal rule will not be pathwise differentiable under exceptional laws encountered in practice. For this reason, we often refer to “exceptional laws” rather than “laws which do not satisfy (3)” in this work. We do this because the term “exceptional law” is well established in the literature, and also because we believe that there is likely little distinction between “exceptional law” and “laws which do not satisfy (3)” for many problems of interest.

For the definitions of regularity and local unbiasedness, we let P_ε be as in (2), with g₀ also fluctuated. That is, we let dP_ε = dQ_Y,ε × g_ε × dQ_W,ε, where g_ε(A|W) = (1+εS_A(A|W))g₀(A|W) with E₀[S_A(A|W)|W] = 0 and sup_a,w |S_A(a|w)| < ∞. The estimator Φ̂ of Φ(P₀) is called regular if the asymptotic distribution of $\sqrt{n}(\widehat{\mathrm{\Phi }}(P_n)-\mathrm{\Phi }(P_0))$ is not sensitive to small fluctuations in P₀. That is, the limiting distribution of $\sqrt{n}(\widehat{\mathrm{\Phi }}(P_{n,\epsilon =1/\sqrt{n}})-\mathrm{\Phi }(P_{\epsilon =1/\sqrt{n}}))$ does not depend on S_W, S_A, or S_Y, where $P_{n,\epsilon =1/\sqrt{n}}$ is the empirical distribution O₁, …, O_n drawn i.i.d. from $P_{\epsilon =1/\sqrt{n}}$. The estimator Φ̂ is called locally unbiased if the limiting distribution of $\sqrt{n}(\widehat{\mathrm{\Phi }}(P_{n,\epsilon =1/\sqrt{n}})-\mathrm{\Phi }(P_{\epsilon =1/\sqrt{n}}))$ has mean zero for all fluctuations S_W, S_A and S_Y, and is called asymptotically unbiased (at P₀) if the bias of Φ̂(P_n) for the parameter Φ(P₀) is o_P0(n^−1/2) at P₀.

The non-regularity of a statistical inference problem does not typically imply the nonexistence of asymptotically unbiased estimators [see Example 4 of Liu and Brown (1993) and the discussion thereof in Chen (2004)], but rather the non-existence of locally asymptotically unbiased estimators whenever (4) holds for some fluctuation [Hirano and Porter (2012)]. It is thus not surprising that we are able to find an estimator that is asymptotically unbiased at a fixed (possibly exceptional) law under mild assumptions. Hirano and Porter also show that there does not exist a regular estimator of the optimal value at any law for which (4) holds for some fluctuation. That is, no regular estimators of Ψ(P₀) exist at laws which satisfy the conditions of Theorem 1 but do not satisfy (3), that is, one must accept the non-regularity of their estimator when the data is generated from such a law. Note that this does not rule out the development of locally consistent confidence bounds similar to those presented by Laber and Murphy (2011) and Laber et al. (2014a), though such approaches can be conservative when the estimation problem is non-regular.

In this work, we present an estimator Ψ̂ for which ${\mathrm{\Gamma }}_n\sqrt{n}(\widehat{\mathrm{\Psi }}(P_n)-\mathrm{\Psi }(P_0))$ converges in distribution to a standard normal distribution for a random standardization term Γ_n under reasonable conditions. Our estimator does not require any complicated tuning parameters, and thus allows one to easily develop root-n rate CIs for the optimal value. We show that our estimator is RAL and efficient at laws which satisfy (3) under conditions.

4. Inference at exceptional laws

4.1. The challenge

Before presenting our estimator, we discuss the challenge of estimating the optimal value at exceptional laws. Suppose d_n is an estimate of $d_0^{\ast }$ and Ψ̂_dn (P_n) is an estimate of Ψ(P₀) relying on the full data set. In van der Laan and Luedtke (2014b), we presented a targeted minimum loss-based estimator (TMLE) Ψ̂_dn (P_n) which satisfies

$${\widehat{\mathrm{\Psi }}}_{d_n}(P_n)=\mathrm{\Psi }(P_0)=(P_n-P_0)D(d_n,P_n^{\ast })+\underset{o_{P_0}(n^{-1/2})\text{under}\text{conditions}}{\underbrace{{\mathrm{\Psi }}_{d_n}(P_0)-\mathrm{\Psi }(P_0)}}+o_{P_0}(n^{-1/2}),$$

where we use the notation Pf = E_P [f(O)] for any distribution P and the second o_P0(n^−1/2) term is a remainder from a first-order expansion of Ψ. The term Ψ_dn(P₀)−Ψ(P₀) being o_P0(n^−1/2) relies on the optimal rule being estimated well in terms of value and will often prove to be a reasonable condition, even at exceptional laws (see Theorem 8 in Section 7.5). Here, $P_n^{\ast }$ is an estimate of the components of P₀ needed to estimate D(d_n, P₀). To show asymptotic linearity, one might try to replace $D(d_n,P_n^{\ast })$ with a term that does not rely on the sample:

$$(P_n-P_0)D(d_n,P_n^{\ast })=(P_n-P_0)D(d_0^{\ast },P_0)+\underset{\text{empirical}\text{process}}{\underbrace{(P_n-P_0)(D(d_n,P_n^{\ast })-D(d_0^{\ast },P_0))}}.$$

If $D(d_n,P_n^{\ast })$ belongs to a Donsker class and converges to $D(d_0^{\ast },P_0)$ in L²(P₀), then the empirical process term is o_P0(n^−1/2) and $\sqrt{n}({\widehat{\mathrm{\Psi }}}_{d_n}(P_n)-\mathrm{\Psi }(P_0))$ converges in distribution to a normal random variable with mean zero and variance ${\text{Var}}_{P_0}(D(d_0^{\ast },P_0))$ [van der Vaart and Wellner (1996)]. Note that $D(d_n,P_n^{\ast })$ being consistent for $D(d_0^{\ast },P_0)$ will typically rely on d_n being consistent for the fixed $d_0^{\ast }$ in L²(P₀), which we emphasize is not implied by Ψ_dn(P₀) − Ψ(P₀) = o_P0(n^−1/2). Zhang et al. (2012a) make this assumption in the regularity conditions in their Web Appendix A when they consider an analogous empirical process term in deriving the standard error of an estimate of the optimal value in a restricted class. More specifically, Zhang et al. assume a non-exceptional law and consistent estimation of a fixed optimal rule. van der Laan and Luedtke (2014b) also make such an assumption. If P₀ is an exceptional law, then we likely do not expect d_n to be consistent for any fixed (non-data dependent) function. Rather, we expect d_n to fluctuate randomly on the set B₀, even as the sample size grows to infinity. In this case, the empirical process term considered above is not expected to behave as o_P0(n^−1/2).

Accepting that our estimates of the optimal rule may not stabilize as sample size grows, we consider an estimation strategy that allows d_n to remain random even as n → ∞.

4.2. A thought experiment

First, we give an erroneous estimation strategy which contains the main idea of the approach but is not correct in its current form. A modification is given in the next section. For simplicity, we will assume that one knows v_n ≜ Var_P0(D(d_n, P₀)) given an estimate d_n and, for simplicity, that v_n is almost surely bounded away from zero. Under reasonable conditions,

$$v_n^{-1/2}({\widehat{\mathrm{\Psi }}}_{d_n}(P_n)-\mathrm{\Psi }(P_0))=(P_n-P_0)v_n^{-1/2}D(d_n,P_n^{\ast })+o_{P_0}(n^{-1/2}).$$

The empirical process on the right is difficult to handle because d_n and v_n are random quantities that likely will not stabilize to a fixed limit at exceptional laws.

As a thought experiment, suppose that we could treat { $v_n^{-1/2}D(d_n,P_n^{\ast }):n$} as a deterministic sequence, where this sequence does not necessarily stabilize as sample size grows. In this case, the Lindeberg–Feller central limit theorem (CLT) for triangular arrays [see, e.g., Athreya and Lahiri (2006)] would allow us to show that the leading term on the right-hand side converges to a standard normal random variable. This result relies on inverse weighting by $\sqrt{v_n}$ so the variance of the terms in the sequence stabilizes to one as sample size gets large.

Of course, we cannot treat these random quantities as deterministic. In the next section, we will use the general trick of inverse weighting by the standard deviation of the terms over which we are taking an empirical mean, but we will account for the dependence of the estimated rule d_n on the data by inducing a martingale structure that allows us to treat a sequence of estimates of the optimal rule as known (conditional on the past). We can then apply a martingale CLT for triangular arrays to obtain a limiting distribution for our estimator.

5. Estimation of and inference for the optimal value

In this section, we present a modified one-step estimator Ψ̂ of the optimal value. This estimator relies on estimates of the treatment mechanism g₀, the strata-specific outcome Q̄₀, and the optimal rule $d_0^{\ast }$. We first present our estimator, and then present an asymptotically valid two-sided CI for the optimal value under conditions. Next, we give conditions under which our estimator is RAL and efficient, and finally we present a (potentially conservative) asymptotically valid one-sided CI which lower bounds the mean outcome under the unknown optimal treatment rule. The one-sided CI uses the same lower bound from the two-sided CI, but does not require a condition about the rate at which the value of the optimal rule converges to the optimal value, or even that the value of the estimated rule is consistent for the optimal value.

The estimators in this section can be extended to a martingale-based TMLE for Ψ(P₀). Because the primary purpose of this paper is to deal with inference at exceptional laws, we will only present an online one-step estimator and leave the presentation of such a TMLE to future work.

5.1. Estimator of the optimal value

In this section, we present our estimator of the optimal value. Our procedure first estimates the needed features g₀, Q̄₀, and $d_0^{\ast }$ of the likelihood based on a small chunk of data, and then evaluates a one-step estimator with these nuisance function values on the next chunk of the data. It then estimates the features on the first two chunks of data, and evaluates the one-step estimator on the next chunk of data. This procedure iterates until we have a sequence of estimates of the optimal value. We then output a weighted average of these chunk-specific estimates as our final estimate of the optimal value. While the first chunk needs to be large enough to estimate the desired nuisance parameters, that is, large enough to estimate the features, all subsequent chunks can be of arbitrary size (as small as a single observation).

We now formally describe our procedure. Define

$$\stackrel{\sim }{D}(d,\overline{Q},g)(o)\triangleq \frac{I(a=d(w))}{g(a\mid w)}(Y-\overline{Q}(a,w))+\overline{Q}(d(w),w).$$

Let {ℓ_n} be some sequence of non-negative integers representing the smallest sample on which the optimal rule is learned. For each j = 1, …, n, let P_n,j represent the empirical distribution of the observations (O₁, O₂, …, O_j). Let g_n,j, Q̄_n,j, and d_n,j respectively represent estimates of the g₀, Q̄₀, and $d_0^{\ast }$ based on (some subset of) the observations (O₁, …, O_j−1) for all j > ℓ_n. We subscript each of these estimates by both n and j because the subsets on which these estimates are obtained may depend on sample size. We give an example of a situation where this would be desirable in Section 6.1.

Define

$${\stackrel{\sim }{\sigma }}_{0,n,j}^2\triangleq {\text{Var}}_{P_0}(\stackrel{\sim }{D}(d_{n,j},{\overline{Q}}_{n,j},g_{n,j})(O)\mid O_1,\dots ,O_{j-1}).$$

Let ${\stackrel{\sim }{\sigma }}_{n,j}^2$ represent an estimate of ${\stackrel{\sim }{\sigma }}_{0,n,j}^2$ based on (some subset of) the observations (O₁, …, O_j−1). Note that we omit the dependence of σ̃_n,j and σ̃_0,n,j on d_n,j, Q̄_n,j, and g_n,j in the notation. Our results apply to any sequence of estimates ${\stackrel{\sim }{\sigma }}_{n,j}^2$ which satisfies conditions (C1) through (C5), which are stated later in this section. Also define

$${\mathrm{\Gamma }}_n\triangleq \frac{1}{n-{\ell }_n}\sum _{j={\ell }_n+1}^n{\stackrel{\sim }{\sigma }}_{n,j}^{-1}.$$

Our estimate Ψ̂(P_n) of Ψ(P₀) is given by

$$\widehat{\mathrm{\Psi }}(P_n)\triangleq {\mathrm{\Gamma }}_n^{-1}\frac{1}{n-{\ell }_n}\sum _{j={\ell }_n+1}^n{\stackrel{\sim }{\sigma }}_{n,j}^{-1}{\stackrel{\sim }{D}}_{n,j}(O_j)=\frac{{\sum }_{j={\ell }_n+1}^n{\stackrel{\sim }{\sigma }}_{n,j}^{-1}{\stackrel{\sim }{D}}_{n,j}(O_j)}{{\sum }_{j={\ell }_n+1}^n{\stackrel{\sim }{\sigma }}_{n,j}^{-1}},$$ (5)

where D̃_n,j ≜ D̃(d_n,j, Q̄_n,j, g_n,j). We note that the ${\mathrm{\Gamma }}_n^{-1}$ standardization is used to account for the term-wise inverse weighting so that Ψ̂(P_n) estimates $\mathrm{\Psi }(P_0)=E_0[\stackrel{\sim }{D}(d_0^{\ast },{\overline{Q}}_0,g_0)]$. The above looks a lot like a standard augmented inverse probability weighted (AIPW) estimator, but with $d_0^{\ast }$ estimated on chunks of data increasing in size and with each term in the sum given weight proportional to an estimate of the conditional variance of that term. Our estimator constitutes a minor modification of the online one-step estimator presented in van der Laan and Lendle (2014). In particular, each term in the sum is inverse weighted by an estimate of the standard deviation of D̃_n,j. For ease of reference, we will refer to the estimator above as an online one-step estimator.

This estimation scheme differs from sample split estimation, where features are estimated on half of the data and then a one-step estimator is evaluated on the remaining half of the data. While one can show that such estimators achieve valid coverage using Wald-type CIs, these CIs will generally be approximately $\sqrt{2}$ times larger than the CIs of our proposed procedure (see the next section) because the one-step estimator is only applied to half of the data. Alternatively, one could try averaging two such estimators, where the training and the one-step sample are swapped between the two estimators. Such a procedure will fail to yield valid Wald-type CIs due to the non-regularity of the inference problem: one cannot replace the optimal rule estimates with their limits because such limits will not generally exist, and thus the estimator averages over terms with a complicated dependence structure.

5.2. Two-sided confidence interval for the optimal value

Define the remainder terms

$$\begin{gathered} R_{1n}\triangleq \frac{1}{n-{\ell }_n}\sum _{j={\ell }_n+1}^n{\stackrel{\sim }{\sigma }}_{n,j}^{-1}{E}_0\left[\left(1-\frac{g_0(d_{n,j}(W)\mid W)}{g_{n,j}(d_{n,j}(W)\mid W)}\right)\times ({\overline{Q}}_{n,j}(d_{n,j}(W),W)-{\overline{Q}}_0(d_{n,j}(W),W))\right], \\ {R}_{2n}\triangleq \frac{1}{n-{\ell }_n}\sum _{j={\ell }_n+1}^n\frac{{\mathrm{\Psi }}_{d_{n,j}}(P_0)-\mathrm{\Psi }(P_0)}{{\stackrel{\sim }{\sigma }}_{n,j}}. \end{gathered}$$

The upcoming theorem relies on the following assumptions:

• (C1)n − ℓ_n diverges to infinity as n diverges to infinity.
• (C2)
  Lindeberg-like condition: for all ε > 0,

  $$\frac{1}{n-{\ell }_n}\sum _{j={\ell }_n+1}^n{E}_0\left[{\left(\frac{{\stackrel{\sim }{D}}_{n,j}(O)}{{\stackrel{\sim }{\sigma }}_{n,j}}\right)}^2{T}_{n,j}(O)|O_1,\dots ,O_{j-1}\right]=o_{P_0}(1),$$

Where $T_{n,j}(O)\triangleq I(\frac{\mid {\stackrel{\sim }{D}}_{n,j}(O)\mid }{{\stackrel{\sim }{\sigma }}_{n,j}}>\epsilon \sqrt{n-{\ell }_n})$.

• (C3) $\frac{1}{n-{\ell }_n}{\sum }_{j={\ell }_n+1}^n\frac{{\stackrel{\sim }{\sigma }}_{0,n,j}^2}{{\stackrel{\sim }{\sigma }}_{n,j}^2}$ converges to 1 in probability.
• (C4)R_1n = o_P0(n^−1/2).
• (C5)R_2n = o_P0(n^−1/2).

The assumptions are discussed in Section 7. We note that all of our results also hold with R_1n and R_2n behaving as $o_{P_0}(1/\sqrt{n-{\ell }_n})$, though we do not expect this observation to be of use in practice as we recommend choosing ℓ_n so that n − ℓ_n increases at the same rate as n.

Theorem 2

Under conditions (C1) through (C5), we have that

$${\mathrm{\Gamma }}_n\sqrt{n-{\ell }_n}(\widehat{\mathrm{\Psi }}(P_n)-\mathrm{\Psi }(P_0))⇝N(0,1),$$

where we use “↝” to denote convergence in distribution as the sample size converges to infinity. It follows that an asymptotically valid 1 − α CI for Ψ(P₀) is given by

$$\widehat{\mathrm{\Psi }}(P_n)\pm z_{1-\alpha /2}\frac{{\mathrm{\Gamma }}_n^{-1}}{\sqrt{n-{\ell }_n}},$$

where z_1−α/2 denotes the 1 − α/2 quantile of a standard normal random variable.

We have shown that, under very general conditions, the above CI yields an asymptotically valid 1 − α CI for Ψ(P₀). We refer the reader to Section 7 for a detailed discussion of the conditions of the theorem. We note that our estimator is asymptotically unbiased, that is, has bias of the order o_P0(n^−1/2), provided that Γ_n = O_P0(1) and n − ℓ_n grows at the same rate as n.

Interested readers can consult the proof of Theorem 2 in the Appendix for a better understanding of why we proposed the particular estimator given in Section 5.1.

5.3. Conditions for asymptotic efficiency

We will now show that, if P₀ is a non-exceptional law and d_n,j has a fixed optimal rule limit d₀, then our online estimator is RAL for Ψ(P₀). The upcoming corollary makes use of the following consistency conditions for some fixed rule d₀ which falls in the class of optimal rules given in (1):

$$\frac{1}{n-{\ell }_n}\sum _{j={\ell }_n+1}^n{E}_0[{(d_{n,j}(W)-d_0(W))}^2\mid O_1,\dots ,O_{j-1}]=o_{P_0}(1),$$ (6)

$$\frac{1}{n-{\ell }_n}\sum _{j={\ell }_n+1}^n{E}_0[{({\overline{Q}}_{n,j}(d_0(W),W)-{\overline{Q}}_0(d_0(W),W))}^2\mid O_1,\dots ,O_{j-1}]=o_{P_0}(1),$$ (7)

$$\frac{1}{n-{\ell }_n}\sum _{j={\ell }_n+1}^n{E}_0[{(g_{n,j}(d_0(W)\mid W)-g_0(d_0(W)\mid W))}^2\mid O_1,\dots ,O_{j-1}]=o_{P_0}(1).$$ (8)

It also makes use of the following conditions, which are, respectively, slightly stronger than conditions (C1) and (C3):

• (C1′)ℓ_n = o(n).
• (C3′) $\frac{1}{n-{\ell }_n}{\sum }_{j={\ell }_n+1}^n\mid \frac{{\stackrel{\sim }{\sigma }}_{0,n,j}^2}{{\stackrel{\sim }{\sigma }}_{n,j}^2}-1\mid \to 0$ in probability.

Corollary 3

Suppose that conditions (C1′), (C2), (C3′), (C4) and (C5) hold. Also suppose that Pr₀(δ < g₀(1|W) < 1 − δ) = 1 for some δ > 0, the estimates g_n,j are bounded away from zero with probability 1, Y is bounded, the estimates Q̄_n,j are uniformly bounded, ℓ_n = o(n), and that, for some fixed optimal rule d₀, (6), (7) and (8) hold. Finally, assume that Var_P0(D̃(d₀, Q̄₀, g₀)) > 0 and that, for some δ₀ > 0, we have that

$${Pr}_0\left(\underset{j,n}{inf}{\stackrel{\sim }{\sigma }}_{n,j}^2>{\delta }_0\right)=1,$$

where the infimum is over natural number pairs (j, n) for which ℓ_n < j ≤ n. Then we have that

$${\mathrm{\Gamma }}_n^{-1}\to {\text{Var}}_{P_0}(\stackrel{\sim }{D}(d_0,{\overline{Q}}_0,g_0))in\mathit{probability}asn\to \infty .$$ (9)

Additionally,

$$\widehat{\mathrm{\Psi }}(P_n)-\mathrm{\Psi }(P_0)=\frac{1}{n}\sum _{i=1}^{n}D(d_0,P_0)+o_{P_0}(1/\sqrt{n}).$$ (10)

That is, Ψ̂(P_n) is asymptotically linear with influence curve D(d₀, P₀). Under the conditions of this corollary, it follows that P₀ satisfies (3) if and only if Ψ̂(P_n) is RAL and asymptotically efficient among all such RAL estimators.

We note that (9) combined with (C1′) implies that the CI given in Theorem 2 asymptotically has the same width [up to an o_P0(n^−1/2) term] as the CI which treats (10) and D(d₀, P₀) as known and establishes a typical Wald-type CI about Ψ̂(P_n).

The empirical averages over j in (6), (7) and (8) can easily be dealt with using Lemma 6, presented in Section 7.3. Essentially, we have required that d_n,j, Q̄_n,j and g_n,j are consistent for d₀, Q̄₀ and g₀ as n and j get large, where d₀ is some fixed optimal rule. One would expect such a fixed limiting rule d₀ to exist at a non-exceptional law for which the optimal rule is (almost surely) unique. If g₀ is known, then we do not need Q̄_n,j to be consistent for Q̄₀ to get asymptotic linearity, but rather that Q̄_n,j converges to some possibly misspecified fixed limit Q̄.

5.4. Lower bound for the optimal value

It would likely be useful to have a conservative lower bound on the optimal value in practice. If policymakers were to implement an optimal individualized treatment rule whenever the overall benefit is greater than some fixed threshold, that is, Ψ(P₀) > v for some fixed v, then a one-sided CI for Ψ(P₀) would help facilitate the decision to implement an individualized treatment strategy in the population.

The upcoming theorem shows that the lower bound from the 1 − 2α CI yields a (potentially conservative) asymptotic 1 − α CI for the optimal value. If $d_0^{\ast }$ is estimated well in the sense of condition (C5), then the asymptotic coverage is exact. Define

$$L{B}_n(\alpha )\triangleq \widehat{\mathrm{\Psi }}(P_n)-z_{1-\alpha }\frac{{\mathrm{\Gamma }}_n^{-1}}{\sqrt{n-{\ell }_n}}.$$

Theorem 4

Under conditions (C1) through (C4), we have that

$$\underset{n\to \infty }{liminf}{Pr}_0(\mathrm{\Psi }(P_0)>L{B}_n(\alpha ))\ge 1-\alpha .$$

If condition (C5) also holds, then

$$\underset{n\to \infty }{lim}{Pr}_0(\mathrm{\Psi }(P_0)>L{B}_n(\alpha ))=1-\alpha .$$

The above condition should not be surprising, as we base our CI for Ψ(P₀) on a weighted combination of estimates of Ψ_dn,j(P₀) for j < n. Because Ψ(P₀) ≥ Ψ_dn,j(P₀) for all such j, we would expect that the lower bound of the 1 − α CI given in the previous section provides a valid 1 − α/2 one-sided CI for Ψ(P₀). Indeed this is precisely what we see in the proof of the above theorem.

5.5. Coverage for the value of the rule estimated on the entire data set

Suppose one wishes to evaluate the coverage of our CI for the data dependent parameter Ψ_dn(P₀), where d_n is an estimate of the optimal rule based on the entire data set of size n. We make two key assumptions in this section, namely that there exists some real number ψ₁ such that:

• (C6)Γ_n(Ψ_dn (P₀) − ψ₁) = o_P0(n^−1/2).
• (C7) $\frac{1}{n-{\ell }_n}{\sum }_{j={\ell }_n+1}^n\frac{{\mathrm{\Psi }}_{d_{n,j}}(P_0)-{\psi }_1}{{\stackrel{\sim }{\sigma }}_{n,j}}=o_{P_0}(n^{-1/2})$.

Typically, Γ_n = O_P0(1) so that condition (C6) is the same as ${\mathrm{\Psi }}_{d_n}(P_0)={\psi }_1+o_{P_0}(1/\sqrt{n})$. As will become apparent after reading Section 7, condition (C6) will typically imply (C7) (see Lemma 6). Theorem 8 shows that condition (C6) is often reasonable with ψ₁ =Ψ(P₀), though we do not require that ψ₁ =Ψ(P₀).

Theorem 5

Suppose conditions (C1) through (C4) and conditions (C6) and (C7) hold. Then

$${\mathrm{\Gamma }}_n\sqrt{n-{\ell }_n}(\widehat{\mathrm{\Psi }}(P_n)-{\mathrm{\Psi }}_{d_n}(P_0))⇝N(0,1).$$

Thus, the same CI given in Theorem 2 is an asymptotically valid 1 − α CI for Ψ_dn(P₀).

6. Computationally efficient estimation schemes

Computing Ψ̂(P_n) may initially seem computationally demanding. In this section, we discuss two estimation schemes which yield computationally simple routines.

6.1. Computing the features on large chunks of the data

One can compute the estimates of Q̄₀, g₀ and $d_0^{\ast }$ far fewer than n − ℓ_n times. For each j, the estimates Q̄_n,j, g_n,j, and d_n,j may rely on any subset of the observations O₁, …, O_j−1. Thus, one can compute these estimators on S increasing subsets of the data, where the first subset consists of observations O₁, …, O_ℓn and each of the S − 1 remaining samples adds a 1/S proportion of the remaining n − ℓ_n observations. Note that this scheme makes use of the fact that, for fixed j, the feature estimates, indexed by n and j, for example, d_n,j, may rely on different subsets of observations O₁, …, O_j−1 for different sample sizes n.

6.2. Online learning of the optimal value

Our estimator was inspired by online estimators which can operate on large data sets that will not fit into memory. These estimators use online prediction and regression algorithms which update the initial fit based on previously observed estimates using new observations as they are read into memory. Online estimators of pathwise differentiable parameters were introduced in van der Laan and Lendle (2014). Such estimation procedures often require estimates of features of the likelihood, which can be obtained using modern online regression and classification approaches [see, e.g., Zhang (2004), Langford, Li and Zhang (2009), Luts, Broderick and Wand (2014)]. Our estimator constitutes a slight modification of the one-step online estimator presented by van der Laan and Lendle (2014), and thus all discussion of computational efficiency given in that paper applies to our case.

For our estimator, one could use online estimators of Q̄₀, g₀ and $d_0^{\ast }$, and then update these estimators as the index j in the sum in (5) increases. Calculating the standard error estimate σ̃_n,j will typically require access to an increasing subset of the past observations, that is, as sample size grows one may need to hold a growing number of observations in memory. If one uses a sample standard deviation to estimate σ̃_0,n,j based on subset of observations O₁, …,O_j−1, the results we present in Section 7.3 will indicate that one really only needs that the number of points on which σ̃_0,n,j is estimated grows with j rather than at the same rate as j. This suggest that, if computation time or system memory is a concern for calculating σ̃_n,j, then one could calculate σ̃_n,j based on some o(j) subset of observations O₁, …, O_j−1.

7. Discussion of the conditions of Theorem 2

For ease of notation, we will assume that, for all j >ℓ_n, we do not modify our feature estimates based on the first j−1 data points as the sample size grows. That is, for all sample sizes m,n and all j ≤ min{m,n}, d_n,j = d_m,j, Q̄_n,j = Q̄_m,j, g_n,j = g_m,j, and σ̃_n,j = σ̃_m,j. One can easily extend all of the discussion in this section to a more general case where, for example, d_n,j ≠ d_m,j for n ≠ m. This may be useful if the optimal rule is estimated in chunks of increasing size as was discussed in Section 6.1. To make these object’s lack of dependence on n clear, in this section we will denote d_n,j, Q̄_n,j, g_n,j, σ̃_n,j, and σ̃_0,n,j as d_j, Q̄_j, g_j, σ̃_j and σ̃_0,j. This will also help make it clear when o_P0 notation refers to behavior as j, rather than n, goes to infinity.

For our discussion, we assume there exists a (possibly unknown) δ₀ > 0 such that

$${Pr}_0\left(\underset{j>{\ell }_n}{inf}{\stackrel{\sim }{\sigma }}_{0,j}^2>{\delta }_0\right)=1,$$ (11)

where the probability statement is over the i.i.d. draws O₁,O₂, …. The above condition is not necessary, but will make our discussion of the conditions more straightforward.

7.1. Discussion of condition (C1)

We cannot apply the martingale CLT in the proof of Theorem 2 if n − ℓ_n does not grow with sample size. Essentially, this condition requires that a non-negligible proportion of the data is used to actually estimate the mean outcome under the optimal rule. One option is to have n − ℓ_n grow at the same rate as n grows, which holds if, for example, ℓ_n = pn for some fixed proportion p of the data. This allows our CIs to shrink at a root-n rate. One might prefer to have ℓ_n = o(n) so that $\frac{n-{\ell }_n}{n}$ converges to 1 as sample size grows. In this case, we can show that our estimator is asymptotically linear and efficient at non-exceptional laws under conditions, as we did in Corollary 3.

7.2. Discussion of condition (C2)

This is a standard condition that yields a martingale CLT for triangular arrays [Gaenssler, Strobel and Stute (1978)]. The condition ensures that the variables which are being averaged have sufficiently thin tails. While it is worth stating the condition in general, it is easy to verify that the condition is implied by the following three more straightforward conditions:

• (11) holds.

• Y is a bounded random variable.

• There exists some δ > 0 such that Pr₀(δ < g_j (1|W) < 1 − δ) = 1 with probability 1 for all j.

Indeed, under the latter two conditions |D̃_n,j(O)|<C is almost surely bounded for some C >0, and thus (11) yields that $\mid {\stackrel{\sim }{D}}_{n,j}(O){\stackrel{\sim }{\sigma }}_{n,j}^{-1}\mid <C{\delta }_0^{-1}<\infty$ with probability 1. For all ε > 0, $\epsilon \sqrt{n-{\ell }_n}>C{\delta }_0^{-1}$ for all n large enough under condition (C1). Thus, T_n,j from condition (C2) is equal to zero with probability 1 for all n large enough.

7.3. Discussion of condition (C3)

This is a rather weak condition given that σ̃_0,j still treats d_j as random. Thus, this condition does not require that d_j stabilizes as j gets large. Suppose that

$${\stackrel{\sim }{\sigma }}_j^2-{\stackrel{\sim }{\sigma }}_{0,j}^2=o_{P_0}(1).$$ (12)

By (11) and the continuous mapping theorem, it follows that

$$\frac{{\stackrel{\sim }{\sigma }}_{0,j}^2}{{\stackrel{\sim }{\sigma }}_j^2}-1=o_{P_0}(1).$$ (13)

The following general lemma will be useful in establishing conditions (C3), (C4) and (C5).

Lemma 6

Suppose that R_j is some sequence of (finite) real-valued random variables such that R_j = o_P0(j^−β) for some β ∈ [0, 1), where we assume that each R_j is measurable with respect to the sigma-algebra generated by (O₁, …, O_j). Then

$$\frac{1}{n}\sum _{j=1}^n{R}_j=o_{P_0}(n^{-\beta }).$$

Applying the above lemma with β =0 to (13) shows that condition (C3) holds provided that (11) and (12) hold. We will use the above lemma with β = 1/2 when discussing conditions (C4) and (C5).

It remains to show that we can construct a sequence of estimators such that (12) holds. Suppose we estimate ${\stackrel{\sim }{\sigma }}_{0,j}^2$ with

$${\stackrel{\sim }{\sigma }}_j^2\triangleq max\left\{{\delta }_j,\frac{1}{j-1}\sum _{i=1}^{j-1}{\stackrel{\sim }{D}}_j^2(O_i)-{\left(\frac{1}{j-1}\sum _{i=1}^{j-1}{\stackrel{\sim }{D}}_j(O_i)\right)}^2\right\},$$ (14)

where {δ_j} is a sequence that may rely on j and each D̃_n,j = D̃_j for all n ≥ j. We use δ_j to ensure that ${\stackrel{\sim }{\sigma }}_j^{-2}$ is well defined (and finite) for all j. If a lower bound δ₀ on ${\stackrel{\sim }{\sigma }}_{0,j}^2$ is known then one can take δ_j = δ₀ for all j. Otherwise, one can let {δ_j} be some sequence such that δ_j ↓0 as j→∞.

Note that ${\stackrel{\sim }{\sigma }}_j^2$ is an empirical process because it involves sums over observations O₁, …,O_j−1, and functions D̃_j which were estimated on those same observations. The following theorem gives sufficient conditions for (12), and thus condition (C3), to hold.

Theorem 7

Suppose (11) holds and that {D̃ (d, Q̄, g) : d, Q̄, g} is a P₀ Glivenko–Cantelli (GC) class with an integrable envelope function, where d, Q̄ and g are allowed to vary over the range of the estimators of $d_0^{\ast }$, Q̄₀, and g₀. Let ${\stackrel{\sim }{\sigma }}_j^2$ be defined as in (14). Then we have that ${\stackrel{\sim }{\sigma }}_j^2-{\stackrel{\sim }{\sigma }}_{0,j}^2=o_{P_0}(1)$. It follows that (13) and condition (C3) are satisfied.

We thus only make the very mild assumption that our estimators of $d_0^{\ast }$, Q̄₀ and g₀ belong to GC classes. Note that this assumption is much milder than the typical Donsker condition needed when attempting to establish the asymptotic normality of a (non-online) one-step estimator. An easy sufficient condition for a class to have a finite envelope function is that it is uniformly bounded, which occurs if the conditions discussed in Section 7.2 hold.

7.4. Discussion of condition (C4)

This condition is a weighted version of the typical double robust remainder appearing in the analysis of the AIPW estimator. Suppose that

$$E_0\left[\left(1-\frac{g_0(d_j(W)\mid W)}{g_j(d_j(W)\mid W)}\right)({\overline{Q}}_j(d_j(W),W)-{\overline{Q}}_0(d_j(W),W))\right]=o_{P_0}(j^{-1/2}).$$ (15)

If g₀ is known (as in an RCT without missingness) and one takes each g_j = g₀, then the above ceases to be a condition as the left-hand side is always zero. We note that the only condition on Q̄_j appears in condition (C4), so that if R_1n = 0 as in an RCT without missingness then we do not require that Q̄_j stabilizes as j grows. A typical AIPW estimator require the estimate of Q̄₀ to stabilize as sample size grows to get valid inference, but here we have avoided this condition in the case where g₀ is known by using the martingale structure and inverse weighting by the standard error of each term in the definition of Ψ̂(P_n).

More generally, Lemma 6 shows that condition (C4) holds if (13) and (15) hold and Pr₀(0 < g_j(1|W) < 1) = 1 with probability 1 for all j. One can apply the Cauchy–Schwarz inequality and take the maximum over treatment assignments to see that (15) holds if

$$max\left\{\frac{{\Vert g_j(a\mid W)-g_0(a\mid W)\Vert }_{2,P_0}{\Vert {\overline{Q}}_j(a,W)-{\overline{Q}}_0(a,W)\Vert }_{2,P_0}}{g_j(a\mid W)}:a=0,1\right\}$$

is o_P0 (j^−1/2). If g₀ is not known, the above shows that then (15) holds if g₀ and Q̄₀ are estimated well.

7.5. Discussion of condition (C5)

This condition requires that we can estimate $d_0^{\ast }$ well as sample size gets large. We now give a theorem which will help us to establish condition (C5) under reasonable conditions. The theorem assumes the following margin assumption: for some α>0,

$${Pr}_0(0<\mid {\overline{Q}}_{b,0}(W)\mid \le t)\lesssim t^{\alpha }\forall t>0,$$ (16)

where “≲” denotes less than or equal to up to a nonnegative constant. This assumption is a direct restatement of Assumption (MA) from Audibert and Tsybakov (2007) and was considered earlier by Tsybakov (2004). Note that this theorem is similar in spirit to Lemma 1 in van der Laan and Luedtke (2014b), but relies on weaker, and we believe more interpretable, assumptions.

Theorem 8

Suppose (16) holds for some α > 0 and that we have an estimate Q̄_b,n of Q̄_b,0 based on a sample of size n. If||Q̄_b,n − Q̄_b,0||_2,P0 = o_P0 (1), then

$$\mid {\mathrm{\Psi }}_{d_n}(P_0)-{\mathrm{\Psi }}_{d_0^{\ast }}(P_0)\mid \lesssim {\Vert {\overline{Q}}_{b,n}-{\overline{Q}}_{b,0}\Vert }_{2,P_0}^{2(1+\alpha )/(2+\alpha )},$$

where d_n is the function w ↦ I(Q̄_b,n(w) > 0). If||Q̄_b,n − Q̄_b,0||_∞,P0 = o_P0 (1), then

$$\begin{gathered} \mid {\mathrm{\Psi }}_{d_n}(P_0)-{\mathrm{\Psi }}_{d_0^{\ast }}(P_0)\mid \\ \le {\Vert {\overline{Q}}_{b,n}-{\overline{Q}}_{b,0}\Vert }_{\infty ,P_0}{Pr}_0(0<\mid {\overline{Q}}_{b,0}(W)\mid \le {\Vert {\overline{Q}}_{b,n}-{\overline{Q}}_{b,0}\Vert }_{\infty ,P_0}) \\ \lesssim {\Vert {\overline{Q}}_{b,n}-{\overline{Q}}_{b,0}\Vert }_{\infty ,P_0}^{1+\alpha }. \end{gathered}$$

The above theorem thus shows that ${\mathrm{\Psi }}_{d_j}(P_0)-{\mathrm{\Psi }}_{d_0^{\ast }}(P_0)=o_{P_0}(j^{-1/2})$ the distribution of |Q̄_b,0(W)| and our estimates of Q̄_b,0 satisfy reasonable conditions. If additionally σ̃_0,j is estimated well in the sense of (13), then an application of Lemma 6 shows that condition (C5) is satisfied.

The first part of the proof of Theorem 8 is essentially a restatement of Lemma 5.2 in Audibert and Tsybakov (2007). Figure A.1 in Supplementary Appendix C shows various densities which satisfy (16) at different values of α, and also the slowest rate of convergence for the blip function estimates for which Theorem 8 implies condition (C5). As illustrated in the figure, α>1 implies that p_b,0(t)→0 as t→0. Given that we are interested in laws where Pr₀(Q̄_b,0(W) = 0) > 0, it is unclear how likely we are to have that α > 1 when W contains only continuous covariates. One might, however, believe that the density is bounded near zero so that (16) is satisfied at α= 1.

If ||Q̄_b,n − Q̄_b,0||_∞,P0 = o_P0 (1), then the above theorem indicates an arbitrarily fast rate for ${\mathrm{\Psi }}_{d_n}(P_0)-{\mathrm{\Psi }}_{d_0^{\ast }}(P_0)$ when there is a margin around zero, that is, Pr₀(0 < |Q̄_b,0(W)| ≤ t) = 0 for some t > 0. In fact, ${\mathrm{\Psi }}_{d_n}(P_0)-{\mathrm{\Psi }}_{d_0^{\ast }}(P_0)=0$ with probability approaching 1 in this case. Such a margin will exist when W is discrete.

One does not have to use a plug-in estimator for the blip function to estimate the mean outcome under the optimal rule. One could also use one of the weighted classification approaches, often known as outcome weighted learning (OWL), recently discussed in the literature to estimate the optimal rule [Qian and Murphy (2011), Zhao et al. (2012), Zhang et al. (2012b), Rubin and van der Laan (2012)]. In some cases, we expect these approaches to give better estimates of the optimal rule than methods which estimate the conditional outcomes, so using them may make condition (C5) more plausible. In Luedtke and van der Laan (2014), we describe an ensemble learner that can combine estimators from both the Q-learning and weighted classification frameworks.

8. Simulation methods

We ran four simulations. Simulation D-E is a point treatment case, where the treatment may rely on a single categorical covariate W. Simulations C-NE and C-E are two different point treatment simulations where the treatment may rely on a single continuous covariate W. Simulation C-NE uses a non-exceptional law, while simulation C-E uses an exceptional law. Simulation TTP-E gives simulation results for a modification of the two time point treatment simulation presented by van der Laan and Luedtke (2014b), where the data generating distribution has been modified so the second time point treatment has no effect on the outcome. This simulation uses the extension to multiple time point treatments given in Supplementary Appendix B [Luedtke and van der Laan (2015)].

Each simulation setting was run over 2000 Monte Carlo draws to evaluate the performance of our new martingale-based method and a classical (and for exceptional laws incorrect) one-step estimator with Wald-type CIs. Table 1 shows the combinations of sample size (n) and initial chunk size (ℓ_n) considered for each estimator. All simulations were run in R [R Core Team (2014)].

Table 1.

Primary combinations of sample size (n) and initial chunk size (ℓ_n) considered in each simulation. Different choices of ℓ_n were considered for C-NE and C-E to explore the sensitivity of the estimator to the choice of ℓ_n

Simulation	(n, ℓn)
D-E	(1000, 100), (4000, 100)
C-NE, C-E, TTP-E	(250, 25), (1000, 25), (4000, 100)

8.1. Simulation D-E: Discrete W

Data

This simulation uses a discrete baseline covariate W with four levels, a dichotomous treatment A, and a binary outcome Y. The data is generated by drawing i.i.d. samples as follows:

$$\begin{gathered} W~\text{Uniform}\{0,1,2,3\}, \\ A\mid W~\text{Binomial}(0.5+0.1W), \\ Y\mid A,W~\text{Binomial}(0.4+0.2I(A=1,W=0)), \end{gathered}$$

where Uniform {0, 1, 2, 3} is the discrete distribution which returns each of 0, 1, 2 and 3 with probability 1/4. The above is an exceptional law because Q̄_b,0(w) = 0 for w ≠ 0. The optimal value is 0.45.

Estimation methods

For each j = ℓ_n + 1, …, n, we used the nonparametric maximum likelihood estimator generated by the first j – 1 samples to estimate P₀ and the corresponding plug-in estimators to estimate all of the needed features of the likelihood, including the optimal rule. We used the sample standard deviation of D̃_n,j(O₁), …, D̃_n,j(O_j–1) to estimate σ̃_0,j.

8.2. Simulations C-NE and C-E: Continuous univariate W

Data

This simulation uses a single continuous baseline covariate W and dichotomous treatment A which are sampled as follows:

$$\begin{gathered} W~\text{Uniform}(-1,1), \\ A\mid W~\text{Binomial}(0.5+0.1W). \end{gathered}$$

We consider two distributions for the binary outcome Y. The first distribution (C-NE) is a non-exceptional law with Y |A,W drawn from to a $\text{Binomial}({\overline{Q}}_0^{\text{n-e}}(A,W))$, where

$${\overline{Q}}_0^{\text{n-e}}(A,W)-\frac{3}{10}\triangleq \{\begin{array}{ll}-W^3+W^2-\frac{1}{3}W+\frac{1}{27},\hfill & \text{if}A=1\text{and}W\ge 0,\hfill \\ \frac{3}{4}{W}^3+W^2-\frac{1}{3}W+\frac{1}{27},\hfill & \text{if}A=1\text{and}W<0,\hfill \\ 0,\hfill & \text{if}A=0.\hfill \end{array}$$

The optimal value of approximately 0.388 was estimated using 10⁸ Monte Carlo draws. The second distribution (C-E) is an exceptional law with Y |A,W drawn from to a $\text{Binomial}({\overline{Q}}_0^{\mathrm{e}}(A,W))$, where for W̃ ≜W +5/6 we define

$${\overline{Q}}_0^{\mathrm{e}}(A,W)-\frac{3}{10}\triangleq \{\begin{array}{ll}-{\stackrel{\sim }{W}}^3+{\stackrel{\sim }{W}}^2-\frac{1}{3}\stackrel{\sim }{W}+\frac{1}{27},\hfill & \text{if}A=1\text{and}W<-1/2,\hfill \\ -W^3+W^2-\frac{1}{3}W+\frac{1}{27},\hfill & \text{if}A=1\text{and}W>1/3,\hfill \\ 0,\hfill & \text{otherwise.}\hfill \end{array}$$

The above distribution is an exceptional law because ${\overline{Q}}_0^{\mathrm{e}}(1,w)-{\overline{Q}}_0^{\mathrm{e}}(0,w)=0$ whenever $w\in [-\frac{1}{2},\frac{1}{3}]$. The optimal value of approximately 0.308 was estimated using 10⁸ Monte Carlo draws.

Estimation methods

To show the flexibility of our estimation procedure with respect to estimators of the optimal rule, we estimated the blip functions using a Nadaraya–Watson estimator, where we behave as though g₀ is unknown when computing the kernel estimate. For the next simulation setting, we use the ensemble learner from Luedtke and van der Laan (2014) that we suggest using in practice. Here, we estimated

$${\overline{Q}}_{b,n}^h(w)\triangleq \frac{{\sum }_{i=1}^n{y}_i{a}_{i}K((w-w_i)/h)}{{\sum }_{i=1}^n{a}_{i}K((w-w_i)/h)}-\frac{{\sum }_{i=1}^n{y}_i(1-a_i)K((w-w_i)/h)}{{\sum }_{i=1}^n(1-a_i)K((w-w_i)/h)},$$

where $K(u)\triangleq \frac{3}{4}(1-u^2)I(\mid u\mid \le 1)$ is the Epanechnikov kernel and h is the bandwidth. Computing ${\overline{Q}}_{b,n}^h$ for a given bandwidth is the only point in our simulations where we do not treat g₀ as known. For a candidate blip function estimate Q̄_b, define the loss

$$L_{{\overline{Q}}_0,g_0}({\overline{Q}}_b)(o)\triangleq {\left(\left[\frac{2a-1}{y_0(a\mid w)}(y-{\overline{Q}}_0(a,w))+{\overline{Q}}_0(1,w)-{\overline{Q}}_0(0,w)\right]-{\overline{Q}}_b(w)\right)}^2.$$

To save computation time, we behave as though Q̄₀ and g₀ are known when using the above loss. We selected the bandwidth H_n using 10-fold cross-validation with the above loss function to select from the candidates h = (0.01, 0.02, …, 0.20). We also behave as though Q̄₀ and g₀ are known when estimating each D̃_n,j, so that the function D̃_n,j only depends on O₁, …, O_j–1 through the estimate of the optimal rule. This is mostly for convenience, as it saves on computation time and our estimate of the optimal rule $d_0^{\ast }$ will still not stabilize, that is, our optimal value estimators will still encounter the irregularity at exceptional laws. Note that g₀ is known in an RCT, and subtracting and adding Q̄₀ in the definition of the loss function will only serve to stabilize the variance of our cross-validated risk estimate. In practice, one could substitute an estimate of Q̄₀ and expect similar results. We update our estimates d_n,j and σ̃_0,n,j using the method discussed in Section 6.1 with $S=\frac{n-{\ell }_n}{{\ell }_n}$.

To explore the sensitivity to the choice of ℓ_n, we also considered (n, ℓ_n) pairs (1000, 100) and (4000, 400), where these pairs are only considered where explicitly noted. To explore the sensitivity of our estimators to permutations of our data, we ran our estimator twice on each Monte Carlo draw, with the indices of the observations permuted so that the online estimator sees the data in a different order.

8.3. Simulation TTP-E: Two time point simulation

The simulation used in this section was described in Section 8.1.2 of van der Laan and Luedtke (2014b), though here we modify the distribution slightly so that the second time point treatment has no effect on the outcome.

Data

The data is generated as follows:

$$\begin{gathered} L_1(0),L_2(0)\stackrel{\text{i.i.d.}}{\sim }\text{Uniform}(-1,1), \\ A(0)\mid L(0)~\text{Bernoulli}(1/2), \\ {U}_1,U_2\mid A(0),L(0)\stackrel{\text{i.i.d.}}{\sim }\text{Uniform}(-1,1), \\ {L}_1(1)\mid A(0),L(0),U_1,U_2~U_1\times (1.25A(0)+0.25), \\ {L}_2(1)\mid A(0),L(0),L_1(1),U_1,U_2~U_2\times (1.25A(0)+0.25), \\ A(1)\mid A(0),\overline{L}(1)~\text{Bernoulli}(1/2), \\ Y\mid \overline{A}(1),\overline{L}(1)~\text{Bernoulli}(0.4+0.0345A(0)b(L(0))), \end{gathered}$$

where b(L(0)) ≜ −0.8 – 3(sgn(L₁(0)) + L₁(0)) − L₂(0)². The treatment decision at time point 0 may rely on L(0), and the treatment at time point 1 may rely on L(0), A(0) and L(1).

Estimation methods

As in the previous simulation, we assume that the treatment mechanism is known and supply the online estimator with correct estimates of the conditional mean outcome so that D̃_n,j is random only through the estimate of $d_0^{\ast }$ (see Supplementary Appendix B for a definition of D̃_n,j in the two time point case). Given a training sample O₁, …, O_j, our estimator of $d_0^{\ast }$ corresponds to using the full candidate library of weighted classification and blip-function based estimators listed in Table 2 of Luedtke and van der Laan (2014), with the weighted log loss used to determine the convex combination of candidates. We update our estimate d_n,j and σ̃_0,n,j using the method described in Section 6.1 with $S=\frac{n-{\ell }_n}{{\ell }_n}$.

8.4. Comparison with the m-out-of-n bootstrap

We compared our approach to the m-out-of-n bootstrap for the value of an estimated rule as presented by Chakraborty, Laber and Zhao (2014). By the theoretical results in Section 7.5, it is reasonable to expect that the optimal rule estimate will perform well and that one can obtain inference for the optimal value using these same CIs. We ran the m-out-of-n bootstrap on D-E, C-NE, and C-E, with the same sample sizes given in Table 1. We drew 500 bootstrap samples per Monte Carlo simulation, where we did 500 Monte Carlo simulations per setting due to the burdensome computation time.

The m-out-of-n bootstrap requires a choice of m, the size of each nonparametric bootstrap sample. Chakraborty, Laber and Zhao present a double bootstrap procedure for the two-time point case when the optimal value is restricted to belong to a class of linear decision functions. Because we do not restrict the set of possible regimes to have linear decision functions, we instead set m equal to 0.1n, 0.2n, …, n. When n = 1000 and m = 100, the NPMLE for D-E is occasionally ill-defined due to empty strata. For these bootstrap draws, we return the true optimal value, thereby (very slightly) improving the coverage of the m-out-of-n confidence intervals. We will compare our procedure to the oracle regime, that is, the m which yields the shortest average CI length which achieves valid type I error control. That is, we assume that one already knows the (on average) optimal choice of m from the outset.

9. Simulation results

9.1. Online one-step compared to classical one-step

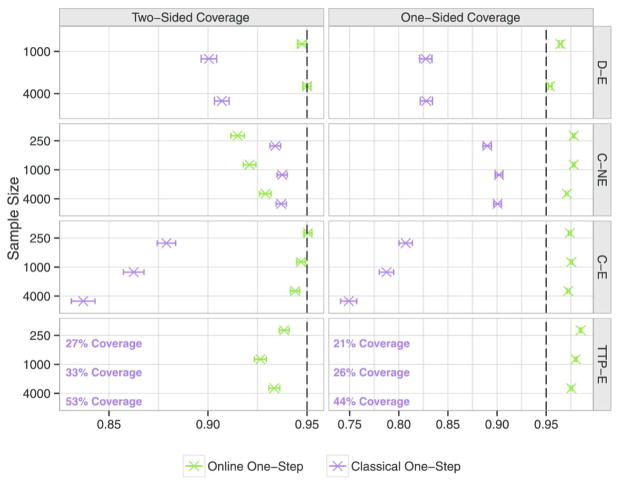
Figure 1 shows the coverage attained by the online and classical (non-online) one-step estimates of the optimal value. The two-sided CIs resulting from the online estimator (nearly) attains nominal coverage for all simulations considered, whereas the non-online estimator only (nearly) attains nominal coverage for the nonexceptional law in C-NE. The one-sided CIs from the online one-step estimator attain proper coverage for all simulation settings. The one-sided CIs from the non-online one-step estimates do not (nearly) achieve nominal coverage in any of the simulations considered because the rule is estimated on the same data as the optimal value. Thus, we expect to need a large sample size for the positive bias of the non-online one-step to be negligible. In van der Laan and Luedtke (2014b), we avoided this finite sample positive bias at non-exceptional laws by using a cross-validated TMLE for the optimal value.

Fig. 1.

Coverage of 95% two-sided and one-sided (lower) CIs. The online one-step estimator achieves near-nominal coverage for all of the two-sided CIs and attains better than nominal coverage for the one-sided CI. The classical one-step estimator only achieves near-nominal coverage for C-NE. Error bars indicate 95% CIs to account for Monte Carlo uncertainty.

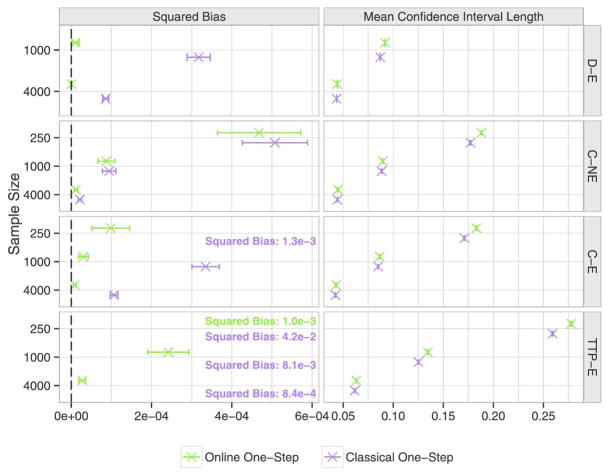
Figure 2 displays the squared bias and mean CI length across the 2000 Monte Carlo draws. The online estimator consistently has lower squared bias across all of our simulations. The online estimator was negatively biased in all of our simulations, whereas the non-online estimator was positively biased in all of our simulations. This is not surprising: Theorem 4 already implies that the online estimator will generally be negatively biased in finite samples, whereas the non-online estimator will generally be positively biased as we have discussed.

Fig. 2.

Squared bias and 95% two-sided CI lengths for the online and classical one-step estimators, where the mean is taken across 2000 Monte Carlo draws. The online estimator has lower squared bias than the non-online estimator, while its mean CI length is only slightly longer. Error bars indicate 95% CIs to account for Monte Carlo uncertainty.

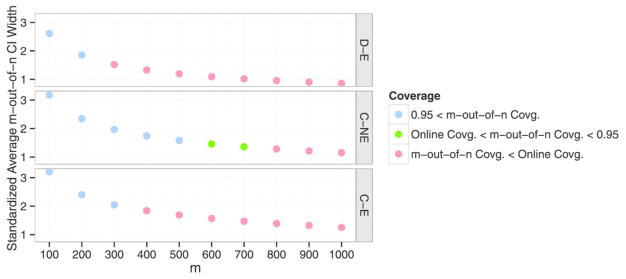
9.2. Online one-step compared to m-out-of-n bootstrap

Figure 3 shows that our estimator outperforms the m-out-of-n bootstrap D-E and C-E for all choices of m considered at sample size 1000. That is, our CI achieves near-nominal coverage and is essentially always narrower than the CI from the m-out-of-n, except when m is very nearly equal to the sample size. When m is nearly equal to the sample size, coverage is low for D-E and C-E: for m = n, the coverage is respectively 77% and 65%. When m does achieve near-nominal coverage, the average CI width is between 1.5 and 2 times larger than the average width of the online one-step CIs. For C-NE, the estimation problem is regular and the bootstrap performs (reasonably) well as expected by theory. Nonetheless, so does the online procedure, and the online procedure yields CIs of slightly shorter length for C-NE. The same general results hold at other sample sizes, which we show in Figure A.3 in Supplementary Appendix C.

Fig. 3.

Performance of the m-out-of-n bootstrap at sample size 1000. The vertical axis shows the average CI width divided by the average CI width of the online one-step CI. That is, any vertical axis value above 1 indicates the m-out-of-n bootstrap has on average wider CIs than the online one-step CI.

One might argue that our oracle procedure is not truly optimal, since in principle one could select a different choice of m for each Monte Carlo draw. While a valid criticism, we believe the overwhelming evidence in favor of the online estimator presented in Figure 3 should convince users that the online approach will typically outperform any selection of m at exceptional laws. As m is selected to be much less than n at exceptional laws, the m-out-of-n will typically yield wider CIs than our procedure. Given that our procedure has achieved near-nominal coverage at all simulation settings, it seems hard to justify such a loss in precision.

9.3. Sensitivity to permutations of the data and choice of ℓ_n

While we would hope that our estimator is not overly sensitive to the order of the data, the online estimator we have proposed necessarily relies on a data ordering. Figure A.2 in Supplementary Appendix C demonstrates how the optimal value estimates vary for C-E when the estimator is computed on two permutations of the same data set. Our point estimates are somewhat sensitive to the ordering of the data, but this sensitivity decreases as sample size grows. We computed two-sided CIs based on the two permuted data sets. We found that either both or neither CI covered the true optimal value in 94%, 94% and 93% of the Monte Carlo draws at sample sizes 250, 1000 and 4000, respectively. For C-NE, either both or neither CI covered the true optimal value in 91%, 93% and 95% of the Monte Carlo draws at sample sizes 250, 1000 and 4000, respectively.

Different choices of ℓ_n did not greatly affect the coverage in C-E and C-NE. Increasing ℓ_n for C-E decreased the coverage by less than 1% for sample sizes 1000 and 4000. Increasing ℓ_n for C-NE increased the coverage by less than 1% for sample sizes 1000 and 4000. Mean CI length increased predictably based on the increased value of $\sqrt{n-{\ell }_n}$: for n = 1000, increasing ℓ_n from 25 to 100 increased the CI length by a multiplicative factor of $\sqrt{\frac{1000-25}{1000-100}}\approx 1.04$. Similarly, increasing ℓ_n from 100 to 400 increased the CI length by a factor of 1.04 for n = 4000.

10. Discussion and future work

We have accomplished two tasks in this work. The first was to establish conditions under which we would expect that regular root-n rate inference is possible for the mean outcome under the optimal rule. In particular, we completely characterize the pathwise differentiability of the optimal value parameter. This characterization on the whole agrees with that implied by Robins and Rotnitzky (2014), but differs in a minor fringe case where the conditional variance of the outcome given covariates and treatment is zero. This fringe case may be relevant if everyone in a strata of baseline covariates is immune to a disease (regardless of treatment status) but are still included in the study because experts are unaware of this immunity a priori. In general, however, the two characterizations agree.

The remainder of our work shows that one can obtain an asymptotically unbiased estimate of and a CI for the optimal value under reasonable conditions. This estimator uses a slight modification of the online one-step estimator presented by van der Laan and Lendle (2014). Under reasonable conditions, this estimator will be asymptotically efficient among all RAL estimators of the optimal value at non-exceptional laws in the nonparametric model where the class of candidate treatment regimes is unrestricted. The main condition for the validity of our CI is that the value of one’s estimate of the optimal rule converges to the optimal value at a faster than root-n rate, which we show is often a reasonable assumption. The lower bound in our CI is valid even if this condition does not hold.

We confirmed the validity of our approach using simulations. Our two-sided CIs attained near-nominal coverage for all simulation settings considered, while our lower CIs attained better than nominal coverage (they were conservative) for all simulation settings considered. Our CIs were of a comparable length to those attained by the non-online one-step estimator. The non-online one-step estimator only attained near-nominal coverage for the simulation which used a non-exceptional data generating distribution, as would be predicted by theory.

In future work, we hope to mitigate the sensitivity of our estimator to the order of the data. While we showed in our simulations that the effect of permutations was minor, this property may be unappealing to some. Such problems occur for many sample-split estimators; however, one often has the option of estimating the parameter on several permutations of the data and then averaging these estimates together. The typical argument for averaging sample split estimates together is that the estimator is asymptotically linear, that is, approximately an average of a deterministic function applied to each of the n i.i.d. observations. Under mild conditions, we have an estimator which, properly scaled, is equivalent to a sum of random functions applied to the n observations, where these functions rely only on past observations, making it impossible to apply this typical argument. Further study is needed to determine if one can remove finite sample noise from this estimator without affecting its asymptotic behavior.

Unsurprisingly, there is still more work to be done in estimating CIs for the optimal rule. While we have shown that the lower bound from our CI maintains nominal coverage under mild conditions, the upper bound requires the additional assumption that the optimal rule is estimated at a sufficiently fast rate. We observed in our simulations that the non-online estimate of the optimal value had positive bias for all settings. This is to be expected if the optimal rule is chosen to maximize the estimated value, and can easily be explained analytically under mild assumptions. It may be worth replacing the upper bound UB_n in our CI by something like max{UB_n,ψ_n(d_n)}, where ψ_n(d_n) is a non-online one-step estimate or TMLE of the optimal value. One might expect that the upper bound ψ_n(d_n) will dominate the maximum precisely when the optimal rule is estimated poorly.

Finally, we note that our estimation strategy is not limited to unrestricted classes of optimal rules. One could replace our unrestricted class with, for example, a parametric working model for the blip function and expect similar results. This is because the pathwise derivative of P ↦ E_P0[Y_d(P)], which treats the P₀ in the expectation subscript as known, will typically be zero when d(P) is an optimal rule in some class and does not fall on the boundary of that class (with respect to some metric). Such a result does not rely on d(P) being a unique optimal rule. When the pathwise derivative of P ↦ E_P0[Y_d(P)] is zero, one can often prove something like Theorem 8, which shows that the value of the estimated rule converges to the optimal value at a faster than root-n rate under conditions.

Here, we considered the problem of developing a confidence interval for the value of an unknown optimal treatment rule in a non-parametric model. Under reasonable conditions, our proposed optimal value estimator provides an interpretable and statistically valid approach to gauging the effect of implementing the optimal individualized treatment regime in the population.