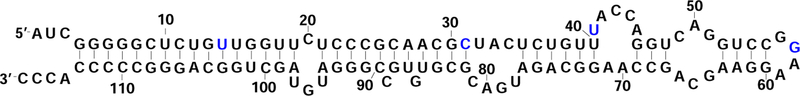Predicting Cotranscriptional Folding Kinetics For Riboswitch

Abstract

Based on a helix-based transition rate model, we developed a new method for sampling cotranscriptional RNA conformational ensemble and the prediction of cotranscriptional folding kinetics. Applications to E. Coli. SRP RNA and pbuE riboswitch indicate that the model may provide reliable predictions for the cotranscriptional folding pathways and population kinetics. For E. Coli. SRP RNA, the predicted population kinetics and the folding pathway are consistent with the SHAPE profiles in the recent cotranscriptional SHAPE-seq experiments. For the pbuE riboswitch, the model predicts the transcriptional termination efficiency as a function of the force. The theoretical results show (a) a force-induced transition from the aptamer (antiterminator) to the terminator structure and (b) the different folding pathways for the riboswitch with and without the ligand (adenine). More specifically, without adenine, the aptamer structure emerges as a short-lived kinetic transient state instead of a thermodynamically stable intermediate state. Furthermore, from the predicted extension-time curves, the model identifies a series of conformational switches in the pulling process, where the predicted relative residence times for the different structures are in accordance with the experimental data. The model may provide a new tool for quantitative predictions of cotranscriptional folding kinetics and results can offer useful insights into cotranscriptional folding-related RNA functions such as regulation of gene expression with riboswitches.

Graphical Abstract

Introduction

RNA molecules fold as they are transcribed.^{1, 2} During the cotranscriptional folding of RNA, the transcribed sequence is prone to quick folding of local structures rather than the slow formation of long-range contacts, whose formation often requires synthesis of the entire RNA chain. Therefore, nascent intermediate states formed during transcription may differ from the thermodynamically most stable structure formed in the refolding of the full-length RNA sequence. Due to the competition between the different rate processes (folding, unfolding, and chain elongation), cotranscriptional folding pathway can be sensitive to the transcription speed and transcriptional pausing (often related to RNA-protein interactions).^3–6 For example, lowing the nucleoside triphosphate concentration leads to an increase in the population of the metastable folding intermediates during the transcription of potato spindle tuber viroid RNA.⁷ Rapid elongation by phage polymerase leads to inactive transcripts of col E1 RNA II and ribosomal RNA.^{8, 9} These kinetic intermediate structures are not static and interactions formed in the early stage of transcription can be replaced by thermodynamically more stable interactions in the later stage of the transcription.

Various theories and simulations have been developed to model cotranscriptional folding. For example, kinetic Monte Carlo approach¹⁰ has successfully predicted the formation of misfolded helices as kinetic traps in cotranscriptional RNA folding process.^{11, 12} Simulations using genetic algorithms have been applied to investigate the cotranscriptional folding of various RNA structures, including pseudoknots.^{13, 14} These studies have provided deep insights into the kinetic mechanism for the folding kinetics such as the disruption of transiently formed nascent structures during cotranscriptional process. Based on a map for the complete energy landscape, map-based Monte Carlo simulations can give successful predictions for folding intermediates and population kinetics for RNAs of lengths over 200 nucleotides.¹⁵ Through sequential addition and combination of secondary structure elements, the Kin-walker model can predict the cotranscriptional kinetics for large RNAs of sequence length up to 1500 nucleotide.¹⁶ Moreover, based on a series of kinetic simulations for the elongation steps and coarse-grained energy landscape, the BarMap method allows computation of folding kinetics through numerical integration for the growing chain.^{17, 18} Kinetic cluster model, an RNA folding kinetics model based on the complete conformational ensemble and the pre-equilibrated conformational macrostates, enables deterministic predictions for the population kinetics, rate constants, and pathways for RNA folding, including ligand dependent cotranscriptional folding of riboswitches.^19–23 However, due to the large conformational ensemble for long sequences, the method is limited to short RNA sequences. In the present study, we develop a new cotranscriptional folding kinetics model based on helix-based kinetic moves to investigate the cotranscriptional folding kinetics for longer sequences. Furthermore, in addition to the computational studies at the 2D structural level, all-atom and coarse-grained simulations can provide further novel insights into the detailed pathways at the 3D structure level.^24–26

Recently, using SHAPE-seq (selective 2’-hydroxyl acylation analyzed by primer extension sequencing) Watters et al.²⁷ studied the cotranscriptional folding of E. Coli. SRP RNA. In the experiment, single nucleotide SHAPE reactivity during the transcription process was monitored. reactivity is correlated to the flexibility of each nucleotide.^28–30 High reactivity corresponds to nucleotides in a flexible (unpaired) state and low reactivity corresponds to rigid nucleotides, whose dynamics may be restricted by canonical base pairs or noncanonical interactions. The SHAPE reactivity data shows distinct signature for nascent RNA structures and major conformational rearrangements during transcription.

A quantitative model would complement SHAPE-seq kinetics experiment to interpret the data and to uncover the structure-based kinetic mechanism. With the fast transcription speed around 10∼20 ms/nt for E. Coli. RNAP³¹ and most fast-acting SHAPE probe reacting at half-life of 250 ms, cotranscriptional SHAPE-seq timescale is longer (slower) than the rate of transcription. As a result, the temporal resolution of cotranscriptional SHAPE-seq may be limited. Second, SHAPE reactivity gives information about nucleotide flexibility, not the structure. Considering the above limitations, a quantitative model would be a useful complement to the SHAPE experiment in order to gain insights into the kinetic mechanism such as folding pathways and the intermediate states.

Riboswitches regulate gene expression through ligand-induced conformational changes.^{32, 33} Riboswitches can form alternative folds in the presence and absence of small ligands such as metabolites or coenzymes. A riboswitch consists of two domains: an aptamer domain that binds the ligand, and an expression platform that controls gene expression. Ligand binding to the aptamer domain results in conformational change in the expression platform, causing on-off switch for the transcription^{34, 35} or translation.^{36, 37}

Riboswitches fold cotranscriptionally as they are synthesized during transcription. Frieda et al. developed an optical-trapping assay to measure the cotranscriptional folding of pbuE adenine riboswitch.³⁸ An adenine riboswitch can form two different structures, the terminator and the antiterminator structures, resulting in transcriptional termination and read-through (Fig. 1),^39–41 respectively. Without adenine binding, the aptamer structure transforms to a terminator structure that halts the transcription. As the aptamer structure binds to adenine, the riboswitch folds into an antiterminator structure which leads to run-through of the transcription. The aptamer and the terminator domains act in concert in real time. The experiment observes the termination efficiency as a function of the adenine concentration and the pulling force. Experimental results show that under the saturating level of adenine, the termination efficiency is lower than that in the absence of adenine. However, with higher tension force the termination efficiency decreases.

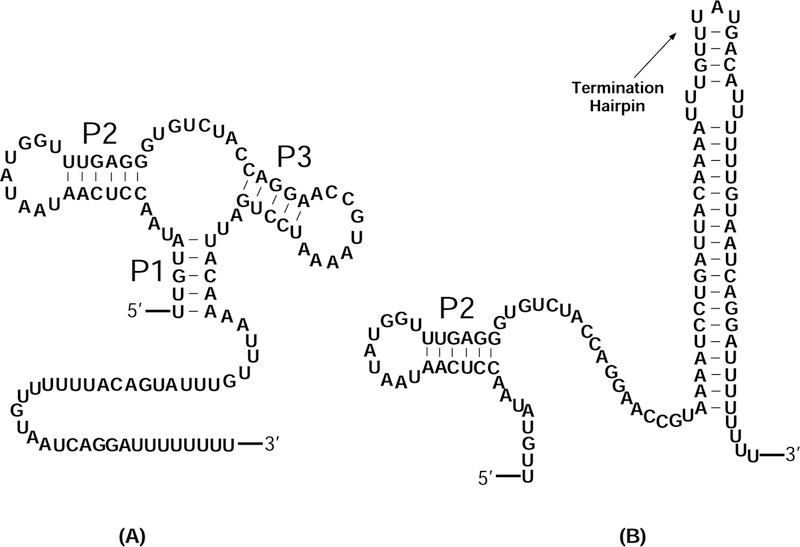
Figure 1:

The secondary structures of (A) aptamer and (B) terminator of pbuE riboswitch.^39–41 The aptamer structure contains 3 helices (P1, P2 and P3) and 2 hairpin loops. The terminator and the aptamer structures share the same P2 helix. However, the terminator structure contains a termination hairpin that halts transcription.

Riboswitch conformational changes and functions can be thermodynamically or kinetically controlled. pbuE riboswitch may involve both mechanisms.⁴² When transcription is slow due to transcription pausing or slow RNAP speed, the riboswitch can reach conformational equilibrium in the presence/absence of the ligand. However, when transcription is fast, the system is off-equilibrium and pubE is kinetically controlled.⁴³ One of the key questions for riboswitch is about the time point for the ligand to bind to the aptamer. Because riboswitch is synthesized during transcription, the predicted cotranscriptional folding kinetic pathways will offer much needed insights into the mechanism about when and how ligand-aptamer binding occurs.

In this paper, using an improved helix-based method in combination with a reduced conformation approach, we investigate the cotranscriptional folding of pbuE riboswitch and E. Coli. SRP RNA and compare the theoretical predictions with experiment results.

Theory and Model

The master equation method for predicting folding kinetics

For a given sequence, we consider the full conformational ensemble of all the secondary structures. The populational kinetics p_i(t) for the i-th conformation at time t can be determined from the master equation $\frac{d{p}_i\left(t\right)}{dt}={\sum }_j\left[k_{j\to i}{p}_j\left(t\right)-k_{i\to j}{p}_j\left(t\right)\right]$, where k_i→j and k_j→i are the transition rates from i to j and j to i respectively. The rate constants constitute an Ω × Ω rate matrix M. Ω is the total number of conformations. So the rate equation can be written as the matrix form: $\frac{d\overrightarrow{p}\left(t\right)}{dt}=\text{M}\cdot \overrightarrow{p}\left(t\right)$. Here $\overrightarrow{p}\left(t\right)$ is the fractional populational vector. The matrix elements are defined as M_i→j = k_j→i for i ≠ j and $M_{i\to i}=-{\sum }_{j\ne i}{k}_{i\to j}$.

By diagonalizing the rate matrix M, the population kinetics for any given initial conformational distribution can be obtained from the eigenvalues −λ_m (m = 1, 2, ..., Ω) and eigenvectors ${\overrightarrow{n}}_m\left(m=1,2,\cdots ,\Omega \right)$, $\overrightarrow{p}\left(t\right)={\sum }_{m=1}^{\Omega }{C}_m{\overrightarrow{n}}_m{e}^{-{\text{λ}}_{m}t}$, where C_m is the coefficient dependent on the initial condition. For any time t, we can determine the population of each structure in the form as a populational vector $\overrightarrow{p}\left(t\right)=\left[p_1\left(t\right),p_2\left(t\right),\cdots ,p_{\Omega }\left(t\right)\right]$.

Helix-based rate model

Since a lone base pair is not stable in RNA secondary structure, we use stack-based instead of base pair-based structure model for the kinetics calculation.¹⁹ Specifically, each kinetic move is for the formation or disruption of a stacked base pair. The rate constants for the formation (k₊) and disruption (k₋) of a base stack are given by $k_{+}=k_0{e}^{-\Delta S_{stack}/k_B}$ and $k_{-}=k_0{e}^{-\Delta H_{stack}/k_{B}T}$, respectively. Here, prefactor k₀ is a rate constant derived from the kinetic experimental data for short RNAs,⁴⁴ k_B is Boltzmann constant, T is the temperature, ΔS and ΔH are the entropy and enthalpy changes for the formation of the base stack. In the calculation of the rate constants, we assume that for the formation of a base stack, the participating bases are juxtaposed near the base pairing positions while the stabilizing interactions, such as hydrogen-bonding and base stacking, have not occurred yet between the two nucleotides. In the above rate model, the free energy barrier for the formation of a base stack is primarily entropic. In contrast, for the disruption of a base stack, we assume that in the transition state, the hydrogen-bonding and base stacking interactions between the base pair have been interrupted, while the torsional angles of the chain are not liberated from the restricted base pairing configuration. Therefore, the free energy barrier for the disruption of a base pair is assumed to be primarily enthalpic, equal to the enthalpy change for the disruption of a base pair.^{19, 20, 45} Similarly, the rate for a loop-closing/opening reaction is given by $k_{+}^{loop}=k_0{e}^{-\Delta S/k_B}$, and $k_{-}^{loop}=k_0{e}^{-\Delta H/k_{B}T}$, where the entropy change upon loop closure (and the formation of the loop-closing base stack) is ∆S = ∆S_loop + ∆S_stack, and ∆H = ∆H_stack is the enthalpy change for the formation of the loop-closing base stack.

The large number of the conformations prohibits kinetic calculations for long RNA sequences. Therefore, we use a helix-based kinetics model, where the elementary kinetic steps are defined as the addition/deletion/replacement of a helix instead of a base pair in base stack. The approach leads to a drastic reduction in the conformational space for the kinetics calculation. The basic assumption for the helix-based model is that the zipping of a helix is fast (10–100 µs) compared to the rearrangement of the different secondary structures, thus, we can treat helices as elementary kinetic building blocks. The transcription speed ranges from 200 nt/s in phages, to 20–80 nt/s in the bacteria, and 10–20 nt/s for human polymerase.⁴⁶ A hairpin with short stem and 4–10 bases in the loop can form on the timescale of tens of microseconds, which is much faster than the transcription speed.^47–50 Therefore, as an approximation, we here ignore the time difference between hairpin folding and helix seeding. In the helix-based kinetics model, partially formed helical intermediates will quickly slip into the fully folded helix through fast-folding pathways such as branch migration or helix-helix exchange.^{21, 22, 51} For a kinetic step in the helix-based kinetic model, depending on whether the formation of the new structure requires the disruption/rearrangement of existing helices, the conformational transition may involve different pathways. Below is a brief summary of the helix-base rate model.^{21, 22, 51}

1. The rate for the formation of a new helix without disrupting the existing helices. We assume a downhill helix zipping process after the formation of the first three loop-closing base stacks. Then the rate of helix formation is given by the following formula:^{21, 22, 51} $k_f=k_{+}^{loop}K$, where K is net fractional population for the forward reaction: $K\simeq K_1\left(1-{K^{\prime }}_2{K^{\prime }}_1\frac{1}{1-{K^{\prime }}_2{K}_1}\right)$ Here K_n and ${K^{\prime }}_n$ for the structure with n base stacks formed loop side) are the probabilities for (forward zipping), i.e., formation of the (n + 1)-th stack, and (backward) unzipping, i.e., disruption of the n-th stack, respectively.^{21, 22, 51, 52} Previous experimental data suggested that this simple rate model can give reliable estimation for the rate of helix formation.^{21, 22} The rate k_u of helix disruption can be estimated from the equilibrium constant $k_f/k_u=e^{-\Delta G/k_{B}T}$ where ∆G is the folding free energy of the helix, k_B is the Boltzmann constant, T is the temperature.

   Because any base stack in the helix may serve as the initial base stack for the subsequent helix zipping process, there exist multiple branching-out pathways, a more rigorous rate estimation can be given by the sum over all the different pathways.

2. The rate for the formation of a new helix B that requires disruption (or partial disruption) of an existing helix A. The lowest-barrier pathway is to convert an existing helix (base pairs) through step-wise exchange between base pairs in the original helix A and the new helix B.^{21, 51} The rates for the exchange between helices A and B can be estimated as^21,52, $k_{A\to B}=\frac{{\prod }_i^n{K}_i}{{\sum }_{j=0}^{n-1}\left({\prod }_{i=1}^j{K^{\prime }}_i{\prod }_{m=j+2}^n{K}_m\right)}$, $k_{B\to A}=k_{A\to B}{e}^{-\frac{\Delta G_{AB}}{K_{B}T}}$ where ∆G_AB is the free energy difference between helices A and B, k_n and $k_n^{\prime }$, as shown in Fig. 2, are the rate constants for the formation and disruption of a base stack in B and A respectively.

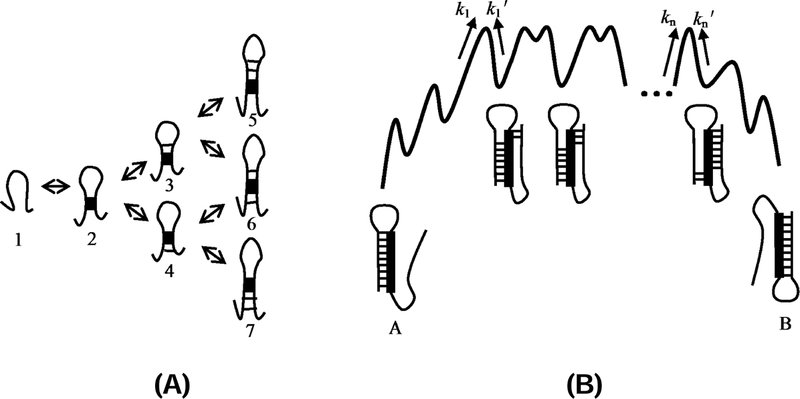
Figure 2:

(A) Multiple pathways for the formation of a helix after the first nucleation stack is formed. For example, after stage 2, there are two folding pathways: 1→2→3 and 1→2→4. (B) The free energy landscape of the tunneling pathway between two overlapping helices A and B. k₁ denotes the transition rate of the unfolding of helix A to form the first stack of helix B. ${k^{\prime }}_1,k_2,{k^{\prime }}_2,\cdots ,k_n$ denote the transition rates between the neighboring intermediates along the tunneling pathways.²²

Cotranscriptional folding model

To characterize the process of cotranscriptional folding, we treat the transcription of a single nucleotide as an elementary time step. For example, if the transcription speed is $\upsilon$ nt/sec, the real time step is $\frac{1}{\upsilon }\text{s}/\text{nt}$ , which means it costs $\frac{1}{\upsilon }$ seconds for the polymerase to synthesis a nucleotide.

After the nth nucleotide is newly transcribed, from the master equation, we compute the time evolution of the population distribution from [p₁(n)_begin, p₂(n)_begin · · · , p_Ω(n)_begin] at time t to [p₁(n)_end, p₂(n)_end · · · , p_Ω(n)_end] at time $t+\frac{1}{\upsilon }$ . Here Ω is the total number of conformations for an n-nt chain. We call the above process as the nth step.

At time $t+\frac{1}{\upsilon }$, as the (n + 1)-th nucleotide is synthesized, the beginning population of the (n + 1)th step is inherited from the ending population of the nth step.¹⁷ The initial populations for the additional conformations formed due to the newly added (n + 1)-th nucleotide are set to be zero. Using the master equation, we can compute the population distribution from the beginning of the (n + 1)-th step [p₁(n + 1)_begin, p₂(n + 1)_begin · · · , p_Ω(n + 1)_begin]. The population will be relaxed to [p₁(n + 1)_end, p₂(n + 1)_end · · · , p_Ω′ (n + 1)_end] at the end of the (n + 1)-th step, where Ω^′ denotes the number of conformations for a (n + 1)-nt chain.

Conformational resampling through kinetic relaxation (CRKR)

Although the helix-based kinetics model has a much smaller ensemble of structures than the original base pair/stack-based model, the number of helix-based conformations can quickly grows with the increase of the sequence length. For example, the number of helix-based structures quickly increases from 69 to 107 as RNA chain length increases from 46 to 50 nucleotides (by adding only four nucleotides) for the SRP RNA. To treat long RNA sequences, we need a new approach. We here develop an algorithm to further effectively reduce the conformational ensemble for modeling cotranscriptional kinetics.

Computations on the large number of low population conformations cost a substantial amount of computational time. However, in general, low-populated conformations are usually make less important contributions to the overall kinetics than the high-populated conformations. Therefore, we may reduce the structural ensemble for the step-wise cotranscriptional kinetics calculation by keeping only potentially important conformations. For helix-based conformations, as shown below, such conformations can be constructed through the assembly of kinetically important helices.

The algorithm is applied to long RNA sequences, of which the conformational ensemble is large. For RNA with (nascent) chain length of N larger than N₀, the minimum chain length for which the conformational resampling algorithm is “turned on”, we use the following conformational resampling algorithm, Conformational Resampling Through Kinetic Relaxation (CRKR), to generate the conformational ensemble for the next cotranscriptional step with chain length equal to N + 1 nucleotides.

Specifically, for an RNA with (nascent) chain length N longer than a (short) sequence length N₀ (the minimum chain length for which the conformational resampling algorithm is turned on), we run the master equation to let the N -nt chain kinetically evolve for a time duration equal to the transcription time for all the remaining nucleotides to be transcribed. We identify all the conformations that emerge (transiently) with populations higher than a threshold level P₀ during the relaxation process. We then extract the helices contained in the identified conformations. Such extracted helices may be potentially important for the subsequent kinetics. Combinations of the above extracted “important” helices gives a new, much smaller ensemble of conformations. Such a reduced conformational ensemble is transferred to the kinetic calculation of the next (N + 1)-th transcriptional step.

The advantage of the CRKR resampling algorithm is that the new ensemble, although significantly smaller than the complete conformational ensemble, keeps the potentially important structural elements for the subsequent kinetics.

Test of the CRKR conformational resampling approach

To test the validity of the CRKR conformational resampling approach, we calculate the population kinetics of a 73-nt “reverse” RNA and first 90-nt of SRP RNA. We find that the CRKR algorithm can indeed give much reduced conformational ensembles. For example, the number of conformation states of “reverse” RNA at the final transcription step is 288 in the original (helix-based) conformation ensemble. In the reduced conformation ensemble with the CRKR resampling, the number of conformations is reduced to 17 with N₀ = 30 and P₀ = 0.5%. In order to further examine the sensitivity of predicted kinetics to the N₀ and P₀ parameters, we performed tests with N₀=30, 40, 50 and 60 for the “reverse” RNA, N₀=20, 30, 40, 50, 60 and 70 for the 90-nt SRP RNA. For each N₀, we tested the results for the different P₀s (Figs. S2 & S4). By monitoring the population kinetics of the kinetically important states, we are able to determine the reliable range of P₀ for each given N₀.

By comparing the population kinetics predicted based on the CRKR and that based on the (original) complete conformation ensemble, we test the accuracy of the CRKR-based predictions. We use the fractional population values for the kinetically populated states as the measure for the accuracy. Specifically, for an L-nucleotide RNA chain, if the predicted population of a state is in the range of $\left[1\pm {\left(\frac{N_0}{L}\right)}^4\right]P_{\text{exact}}$, where P_exact is the predicted population based on the complete conformational ensemble, we consider the result as a successful prediction.

From the population of each state, we can estimate the optimal values of the N₀ and P₀ parameters. For example, for the “reverse” RNA, we find that parameter P₀ = 2.4%, 4.4%, and 5% can lead to reliable predictions for the fractional population for N₀ = 30, 40, and 60, respectively. A smaller N₀ means that the conformational resampling algorithm is applied in an earlier step and thus requires a lower P₀ in order to keep the potentially important conformations for subsequent steps.

From our extensive tests for the different values of the parameters, we fit the following analytical formula for a given RNA sequence:

$$P_0=6.12698{[\text{Log}\left(\frac{L-N_0}{L}\right)]}^2+0.220353[\text{Log}\left(\frac{L-N_0}{L}\right)]$$

Here L (nt) is the RNA sequence length, N₀ is the minimum length of the nascent chain for which the population resampling is applied, and P₀ is the lowest fractional population for the structures whose helices are used for the conformational resampling (Fig. S3).

Force-dependent kinetics

In single molecule studies such as optical trapping experiments,³⁸ RNA folds cotranscriptionally under a pulling force. In these experiments, by monitoring the transcript extension as a function of time, the folding transitions are observed. Here to gain direct structure-based insights into the kinetics, we develop a force-dependent kinetic model. Specifically, we model the effect of the tension on the rate constants for the formation (k₊) and disruption (k₋) of a base stack using a simplified rate model:⁵³ $k_{\left(+\right)}\left(f\right)=k_0{e}^{\left(-T\text{Δ}S+2g_s\left(f\right)\right)/k_{B}T}$, $k_{\left(-\right)}\left(f\right)=k_0{e}^{-\Delta H/k_{B}T}$ Here g_s(f) is the force-induced free energy per nucleotide under external force f : $g_s\left(f\right)=l_{ss}{\int }_0^f\left(\coth \frac{f^{\prime }b}{k_{B}T}-\frac{k_{B}T}{f^{\prime }b}\right)d{f}^{\prime }$, where l_ss = 5.6 Ǻ is nucleotide length, b = 15Ǻ is the Kuhn length. With the above force-dependent rate model, we can simulate the folding kinetics under the different tensions applied to the RNA.

Results and Discussion

E. Coli. SRP RNA cotranscriptional folding kinetics: SHAPE reactivity and base pairing probability

We apply the new model to the 117-nt E. Coli. SRP RNA, whose cotranscriptional kinetics has been experimentally studied.²⁷ In the experiment, the folding pathway is probed using nucleotide SHAPE reactivity. In the theoretical calculation, we compute the time-dependent population of each structure in each transcription step. From the population distribution, we can compute the base pairing $P_{\text{bp}}^i\left(k\right)$ and unpairing $P_{\text{nbp}}^i\left(k\right)$ probabilities for nucleotide i in the k-th transcription step:

$$P_{\text{bp}}^i\left(k\right)=\frac{\sum _j{P}_j\left(k\right)\cdot {\delta }_{ij}\left(k\right)}{\sum _j{P}_j\left(k\right)},P_{\text{nbp}}^i\left(k\right)=1-P_{\text{bp}}^i\left(k\right)$$

$${\delta }_{ij}\left(k\right)={\{}_{0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{otherwise}}^{1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{if}i\text{is involved in a base pair in conformation}j}$$

Here P_j (k) is the probability of finding conformation j in step k. The base pairing and unpairing probabilities can be related to the SHAPE profile. In general, a larger P_nbp corresponds to a higher reactivity. Therefore, the comparison between the theoretical prediction and the experimental SHAPE data may provide a useful test for the model. Following the experimental condition, we assume the transcription speed to be 0.01–0.02 s/nt. To test the dependence of the folding kinetics on the transcription speed, we set 3 different transcription speeds (0.01 s/nt, 0.015 s/nt and 0.02 s/nt) in our model. Although without the detailed information about the noncanonical interactions in the loop regions, the prediction of the SHAPE reactivity from 2D structure alone remains a challenge, Therefore, an exact comparison with the experimental SHAPE profile is not viable. Nevertheless, as shown below, our model pro-vides a low-resolution scheme for the folding pathway that may be consistent with the experiment. In the experiment, SHAPE reactivity values for positions U14, C31, U41, and G57 were measured over the course of transcription. Therefore, we use these nucleotides for the comparison between the theoretically predicted cotranscriptional kinetic pathways and the experimental results.

1. For nucleotide U14 (Fig. 3), the experimental result shows a decrease in SHAPE reactivity as the RNA chain is transcribed to 100th nucleotide.²⁷ Similarly, our predicted P_nbp for U14 shows an abrupt drop in the same transcription step. Specifically, we find that as the nascent RNA chain is transcribed to the 100th nucleotide, the originally unpaired (hence SHAPE-reactive) U14, with the formation of a new helix, becomes base-paired and hence significantly less SHAPE-reactive.

2. For nucleotide C31 (Fig. 3), its SHAPE reactivity reaches the maximum value when the transcript length is 83 nucleotide before undergoing a rapid decrease as transcription proceeds.²⁷ Our theoretical calculation suggests that the maximum P_nbp for C31 occurs when RNA transcribes to the 80th nucleotide, which is close to the experimental result. As transcription further proceeds, the SHAPE reactivity of C31 decreases and reaches a plateau. The predicted profile is consistent with the experimental result. Our predicted population analysis indicates C31 undergoes a loop-to-helix transition at the sequence length of 80 nucleotide.

3. Nucleotide U41 is a loop closing nucleotide in the native structure (Fig. 3). Experimental SHAPE data indicates that the SHAPE reactivity of U41 increases during the transcription process.²⁷ Our prediction shows that U41 becomes base-paired when the transcribed chain reaches 100-nucleotide long. We note that U41 is a loop closing nucleotide, which is less stable than nucleotides in the middle of a helix, therefore, we expect the SHAPE reactivity for U41 is higher than other base-paired nucleotides.

4. Similar to U41 (Fig. 3), nucleotide G54 is inside a hairpin loop. The experiment data shows an increasing SHAPE reactivity in the transcription process.²⁷ Our predicted population curve shows that for most of the transcription process, G54 is not paired with other nucleotides and maintains the unpaired state throughout the transcription. This result is consistent with the experimental finding.

Figure 3:

Secondary structure of E. Coli. SRP RNA.⁶¹ The E. Coli. SRP RNA has 6 helices (H2, H3, H4, H5, H6 and H7), 4 internal loops, 2 bulge loops and a hairpin loop. Nucleotides whose SHAPE reactivity were measured in experiment are marked in blue.

E. Coli. SRP RNA cotranscriptional folding kinetics: Structure transitions

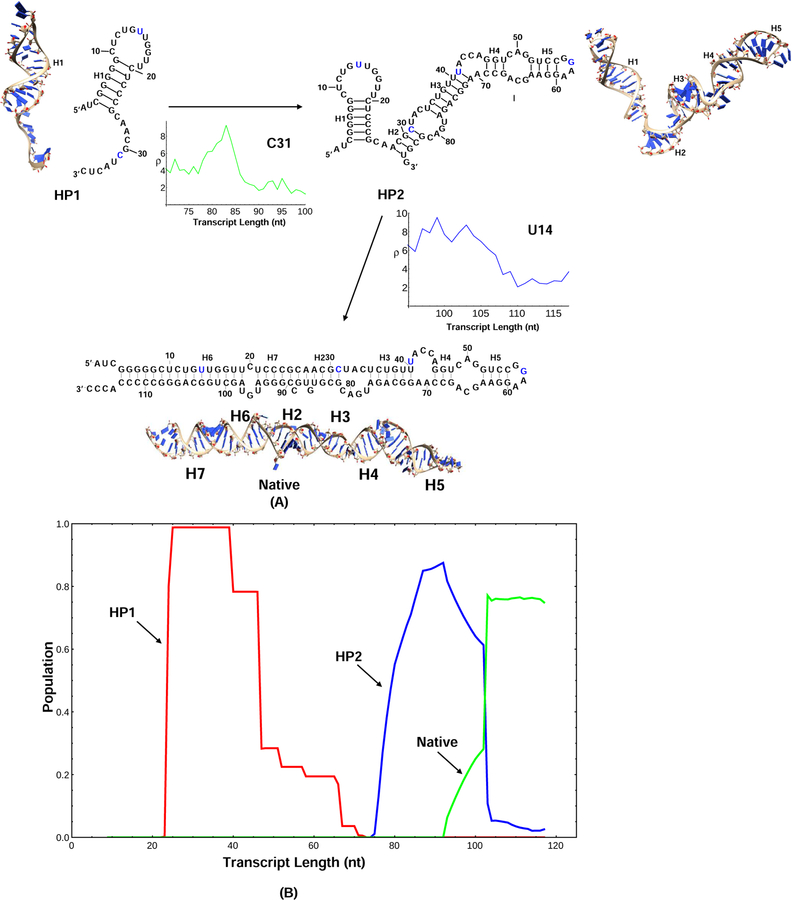
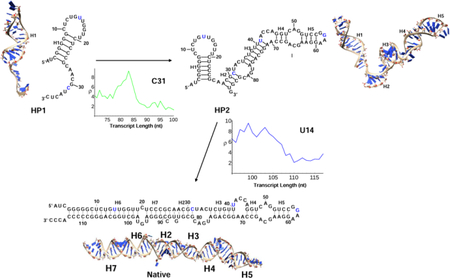
The cotranscriptional SHAPE-seq experiment suggested the following folding pathway for SRP RNA. As shown in Fig. 4A, when the first 50 nucleotides are transcribed, hairpin structure HP1 is formed with a 12-nt long hairpin loop, 6-bp (base pair) helix, and a long 3^′ tail. U14 in the structure is in the loop region and C31 is in the tail region, therefore, both U14 and C31 show high SHAPE reactivity. As the nascent chain extends to 86 nt, a new structure HP2 with a new 4-nt hairpin loop and a new 4-bp helix is formed, and the structure contains two stem-loop structures connected in series. Nucleotides U14, C31, U41 and G57 are unpaired and thus show high SHAPE reactivity. When the transcription length reaches 100 nucleotides, the long-range base pairs begin to form between the 5^′− and the 3^′−end nucleotides. The RNA has a high probability to form the native base pairs, resulting in the native structure that contains 4 helices, 2 internal loops and 2 hairpin loops. In the native fold, nucleotide C31 is in helical region hence has low reactivity, and U14, U41, G57 remain in the loop region thus show high SHAPE reactivity. As the transcription length grows to 125 nt, the RNA finally folds to the full native structure.

Figure 4:

(A) The figure shows that major SHAPE reactivity change for each transition, where the horizontal axis shows the elongating chain length during transcription and the vertical axis shows the SHAPE reactivity.²⁷ During the transition from HP1 to HP2, C31 is paired with G82, the SHAPE reactivity of C31 begins to decrease after the chain is transcribed to the 83th nucleotide. From HP2 to the native structure, U14 become paired with G103 and the SHAPE profile also indicates the transition. The 3D structures for the kinetically important structures are predicted using the Vfold3D software^55–58 and the Coarse-Grained MD simulations.⁵⁹ (B) The population kinetics of 3 kinetically important conformations during the cotranscriptional folding process. The major transitions during the folding process are extracted from the predicted population kinetics for the different conformations. HP1 is first formed in the early transcription stage, followed by the formation of HP2, and additional helices and loops are added to HP1. In the late stage of the folding process, the first hairpin (H1) in HP2 is disrupted and the native structure is formed. From the population kinetics, the major folding pathway of E.Coli. SRP RNA is HP1→HP2→Native.

Our model can predict the population kinetics during the transcription for the different states. Here we focus on the results of the three kinetically important structures shown in Fig. 4A. As shown in Fig. 4B, the population of the HP1 grows fast and dominates the early folding process. As more nucleotides are transcribed, the HP1 population decreases and the population of the HP2 structure begins to increase. The HP2 population reaches its peak value when the nascent chain is transcribed to the 95th nucleotide. After the 95th nucleotide is transcribed, with the formation of the long-range base pairs in helix H6, the native structure begins to emerge as the population of the HP2 decreases. The main transformation during this time window is the breaking of the H1 helix in structure HP2 and the formation of the native H6 helix. As shown in Fig. 4B, the predicted population kinetics is consistent with the model derived from the SHAPE data. Furthermore, from Fig. 4B, we find that the slowest step in this cotranscriptional folding process is the transition from HP1 to HP2. This result is different from refolding scenario, where the slowest step is often the detrapping of the misfolded helix (H1 in HP2 as in our case).

The pbuE adenine riboswitch: force and ligand-dependent folding stability

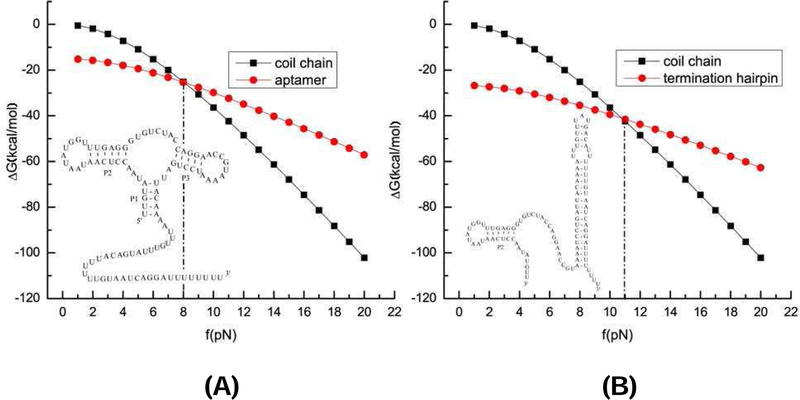
To model the cotranscriptional folding kinetics for the pbuE adenine riboswitch, we need to model the energetic gain in ligand binding. Previous experiment suggested that the tertiary contacts and the ligand binding can contribute an additional stabilizing free energy 6±2 kcal/mol to the aptamer structure.⁵⁴ Therefore, we apply a free energy G_bind in the range of 5∼7 kcal/mol once the aptamer structure is formed in the presence of ligand. We found that a smaller G_bind would give a lower population of the aptamer structure and a higher population of the terminator conformation. Fig. 5 shows the free energies of the folded state (either the aptamer structure or the terminator structure) and the unfolded state under the different pulling forces. For the folding/unfolding two-state equilibrium system, we estimate the unfolding force from the equal free energy condition for the folded and the unfolded states. Our result shows that the unfolding force of the adenine-bound aptamer is about 8 pN, which is close to the experimental value 7.65 pN.³⁸ The unfolding force for the terminator is predicted to be 11 pN, which is lower than the experimental value 13.58 pN.³⁸ The difference between the theoretical prediction and the experiment results for the unfolding forces may be caused by the noncanonical interactions in the structures and Mg²⁺-induced stabilization (as compared to the 1M NaCl condition assumed in the theoretical calculations). Experimental data³⁸ suggests that in the presence of adenine, the population of the terminator structure without the force is about 50%. As shown in Fig. S6, our calculation with G_bind = −5.3 kcal/mol gives the terminator and the aptamer populations equal to 45% and 53%, respectively, and the unfolding forces for the aptamer and the terminator are equal to 8 pN and 11 pN, respectively.

Figure 5:

Free energy ∆G as a function of the force for the coil state, the terminator, and the aptamer structure. The free energy profiles give the equilibrium unfolding forces 11 pN and 8 pN for the terminator hairpin and the adenine-bound aptamer, respectively. In the free energy calculations, we use G_BIND = 5.3 kcal/mol for the ligand-induced additional stability of the aptamer.

The pbuE adenine riboswitch: transcriptional termination efficiency

We estimate the termination efficiency T E from the relative population of the terminator structure at the end of the transcription:

$$TE\approx \frac{\left[T\right]}{\left[T\right]+\left[A\right]+\left[U\right]}$$

where [T ], [A] and [U ] denote the populations of the terminator, the aptamer, and the unfolded states, respectively.

As shown in Fig. 5, the aptamer structure A, which is disrupted at 8 pN, is mechanically less stable than the terminator structure T , which has an unfolding force at 11 pN. The difference in the mechanical stability between A and T leads to the different behavior of the termination efficiency T E as a function of the force.

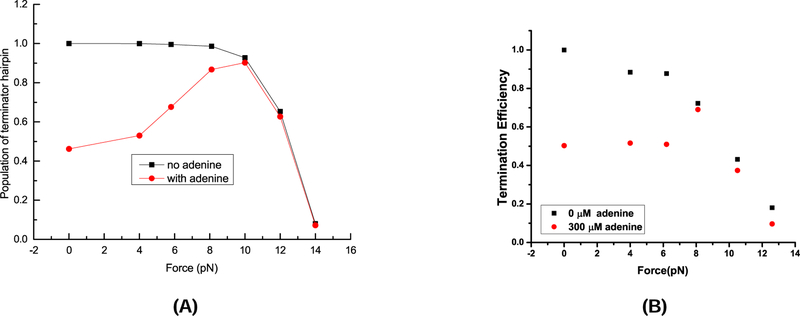
In the absence of (aptamer-stabilizing) adenine, the terminator population [T] would would dominate over the aptamer population [A], thus, T E is predominantly determined by the stability of T . As shown in Fig. 5B, an increasing force would destabilize T , causing a monotonic decrease in [T ] and T E; See Figs. 6A (theory) and B (experiment).

Figure 6:

The theoretical and experimental results for the Termination Efficiency (TE). (A) The predicted TE under 20 nt/s transcription speed. The TE is shown as the fractional population of the terminator at the end of cotranscriptional folding as a function of force with and without adenine. (B) Experimentally determined termination efficiency as a function of force with and without adenine.³⁸ It is important to note that for both cases (with and without the presence of adenine), the theoretical predictions in (A) and the experimental results in (B) for the termination efficiency show similar force-dependence.

In the presence of adenine, without the force, the free energy calculation predicts that A and T occupy about 46% and 54% of the total population, respectively. For an increasing force under 8 pN, [A] shows a significant decrease with an increasing force. With the disruption of A would lead to an increased probability for the riboswitch to fold to T , resulting in an increase in [T ] and the termination efficiency T E. The maximum T E (90%) occurs at the force equal to 9 pN. At this force, which is higher than the unfolding force (8 pN) of the aptamer, the aptamer structure is nearly fully disrupted while the terminator hairpin, which has a much higher unfolding force (11 pN), remains nearly intact. For the further increase in the force beyond 9 pN, the terminator structure begins to unfold and the TE drops. As shown in Fig. 6, the above theoretically predicted nonmonotonic behavior of T E agrees with the experimental result.

The pbuE adenine riboswitch: population kinetics during transcription.

The solution of the master equation gives the population of each structure at any given time point. During the different stages of the transcription, different structures may fold and unfold. We may infer the pathway from the time series of the emerged structures.

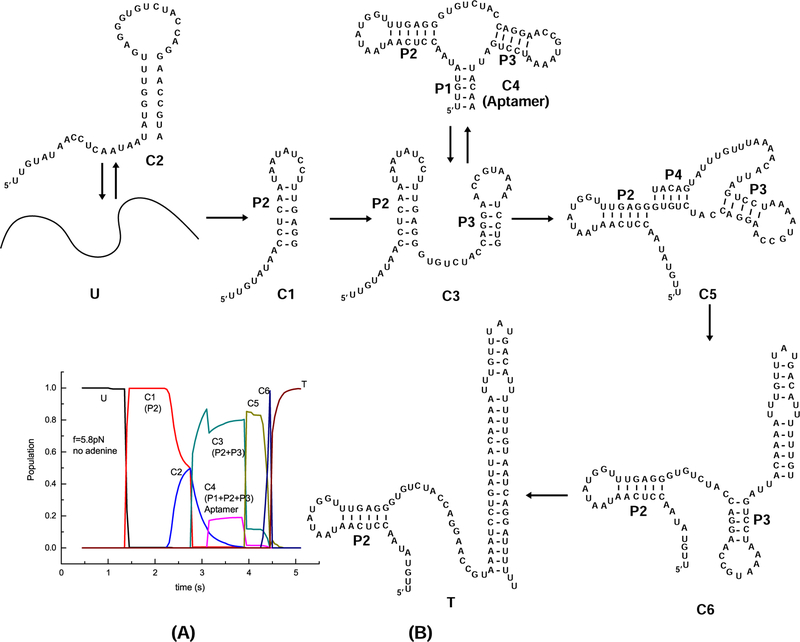
In the absence of adenine, as shown in Fig. 7, the P2 stem-loop (transient state C1) is formed first. Before P3 is folded, an intermediate state C2 emerges transiently. After C3, which contains P2 stem and P3 stem, is formed, P1 and hence the aptamer structure A (C4 in the figure) are folded at 3.1s and unfolded at 3.9s. C4 is switched to to C3 followed by the formation of helix P4 and structure C5 that contains P4. However, the newly formed helix is quickly disrupted and the terminator hairpin is partially folded. Finally, stem P3 is unfolded and the full terminator conformation T is formed.

Figure 7:

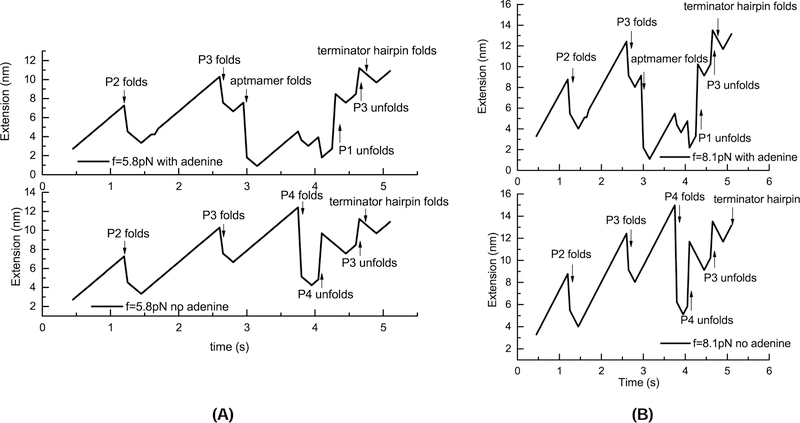
(A) The population kinetics for the cotranscriptional folding of the pbuE riboswitch under 5.8 pN pulling force and transcription speed 20 nt/s without adenine. There are 8 kinetically important states identified during the folding process, U (Black), C1 (Red), C2 (Blue), C3 (Dark Cyan), C4 (Magenta), C5 (Dark Yellow), C6 (Navy), and T (Wine). (B) The folding pathway inferred from the populational kinetics. The major folding pathway for the pbuE riboswitch under 5.8 pN pulling force and transcription speed 20 nt/s without adenine is U→C1→C3→C5 →C6→T with C2 and C4 as off-pathway kinetic intermediates (traps) connected to U and C3, respectively.

From the predicted pathway, the ligand needs to bind to the aptamer during the time window between 3.1s to 4.0s in order to stabilize the aptamer. If the ligand cannot bind in time, helix P1 of the aptamer will unfold and the termination hairpin will form. In the calculation, the aptamer free energy without adenine is −9.2 kcal/mol, and the terminator hairpin free energy −26.57 kcal/mol is much lower. The aptamer is stabilized only with ligand binding. Our results indicate that the ligand binding in pubE riboswitch is kinetically controlled.

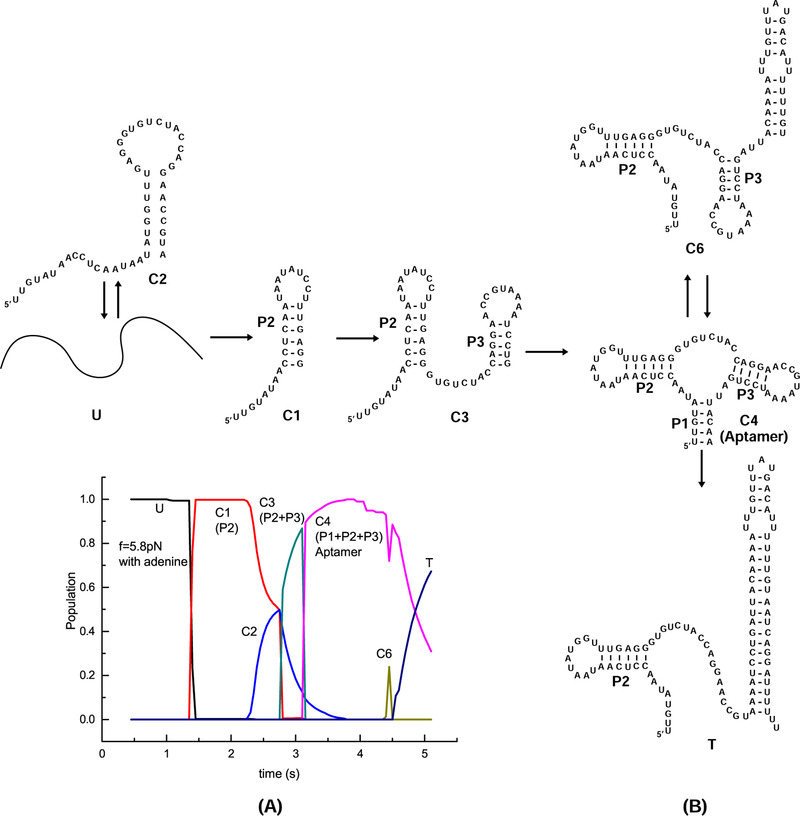
With the presence of adenine, we assume that the adenine binding to the aptamer can stabilize the aptamer by −5.3 kcal/mol. This adenine binding-induced stabilization is in accordance with the experiment value of 6±2 kcal/mol.⁵⁴ As shown in Fig. 8A, compared with the adenine-free kinetics, under the pulling force of 5.8 pN, the population of the aptamer A (C4) is significantly increased and is stabilized for a long time duration from 0.9 sec to 1.5 sec. Moreover, C5 disappears from the kinetics and C6 emerges only as a brief low-population transient state. The population of the termination hairpin drops significantly as the aptamer structure remains at the end of transcription. This is because the formation of the terminator requires the disruption of the aptamer, which is stable with the ligand binding. The folding pathway is U→C1→C3→C4 (Aptamer)→T (Terminator). The result is in accordance with the experimental observation.³⁸

Figure 8:

(A) The population kinetics for the cotranscriptional folding of the pbuE riboswitch under 5.8 pN pulling force and transcription speed 20 nt/s with adenine. There are also 8 kinetically important states identified during the folding process, U (Black), C1 (Red), C2 (Blue), C3 (Dark Cyan), C4 (Magenta), C6 (Dark Yellow), and T (Navy). (B) The folding pathway inferred from the populational kinetics. The major folding pathway for the pbuE riboswitch under 5.8 pN pulling force and transcription speed 20 nt/s with adenine is U→C1→C3 →C4→T with C2 and C6 as off-pathway kinetic intermediates (traps) connected to U and C4, respectively.

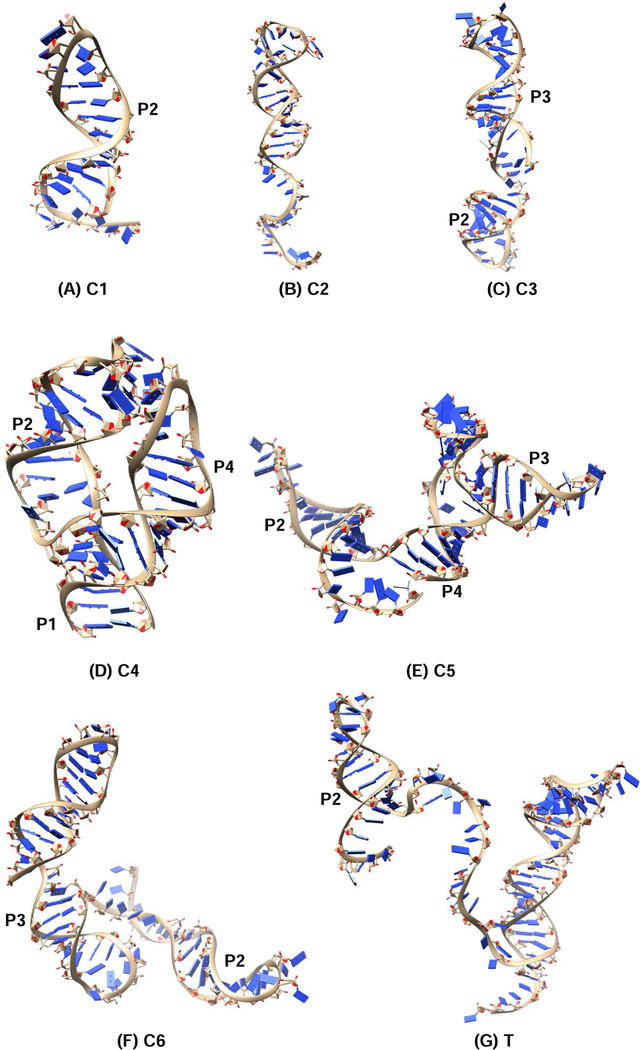
We also calculate the kinetics under a larger force f = 8.1 pN. As shown in Fig. S7A, without adenine, in contrast to the case with a lower force f = 5.8 pN, the aptamer structure A (C4) is not formed in the process while the rest intermediates are the same as those with 5.8 pN in Fig. 7A. With adenine, except for the disappearance of the intermediate state C6 in the 8.1 pN case, the other intermediate states are the same as the states in the 5.8 pN case (Fig. 8B). The absence of the C4 and C6 structures are due to the destabilization caused by the larger force. Using the Vfold3D software^55–58 combined with the IsRNA coarse-grained molecular dynamics simulation,⁵⁹ we can predict the 3D structures of these kinetically important conformations (see Fig. 9).

Figure 9:

The predicted 3D structure for the kinetically important states during the cotranscription process of pbuE riboswitch. The 3D structures are predicted using the Vfold3D software^55–58 and Coarse-Grained MD simulations.⁵⁹

The pbuE adenine riboswitch: extension-time curve

For an N -nt single-stranded RNA, the force (fʹ) - extension (X_{RN A}) relation can be given by the equation⁶⁰ $X_{RN\hspace{0.17em}A}=N{l}_{ss}\left(\text{coth}\frac{f^{\prime }b}{k_{B}T}-\frac{k_{B}T}{f^{\prime }b}\right)$ where l_ss = 5.6Ǻ is nucleotide length, b = 15Ǻ is Kuhn length. For conformations with local stem-loop structures, we use three nucleotides to replace the extension of a stem-loop (i.e., end-end distance of a base pair) in the chain for the force-extension calculation. Fig. 10 shows the kinetics for the end-end extension for the riboswitch under 5.8 pN and 8.1 pN pulling force.

Figure 10:

The extension as a function of time for the cotranscriptional folding under force (A) f = 5.8 pN and (B) f = 8.1 pN.

In the presence of adenine, helix P3 (see Fig. 8A) is predicted to form in 1.4s after P2 is formed, which is close to the experimental result of 1.28s, and the aptamer folds in 0.36s after P3 folds, which is also close to the experimental result of 0.3s. In addition, P1 is predicted to unfold at t ≈ 4.3 s and P3 unfolds at t ≈ 4.65 s. With P3 unfolding, the terminator hairpin is formed at t ≈ 4.9 s as the U-tract sequence is synthesized. As shown in the experiment,³⁸ the time interval between aptamer folding and U-tract synthesis is around 1.96 s, which is close to the experimental result of 1.43 s. Helix formation can lead to decrease in the extension. For example, the formation of P2 and P3 are predicted to cause extension reduction of 3.85 nm and 3.51 nm, respectively, which are close to the experimental result of 3.47 nm for both. The reduction for P2 is greater than P3, which is one stack shorter than P2. The reduction in extension for the aptamer formation is predicted to be 6.55 nm, which is close to 6.03 nm determined in experiment.

Without adenine, the time interval between P2 folding and the synthesis of the U-tract is predicted to be 3.72 s, which is close to the experimental results of 3.54 s. In our prediction, P3 is formed 1.28 s after P2 folding. The P3 folding causes an 3.51 nm reduction in the extension in the time-extension kinetics. The time interval between P2 and P4 folding is predicted be around 1.67 s, which is close to the experimental result 1.8 s. The theory-experiment difference may be attribute to the approximation used in the model: the conformational states in our kinetics model are based on fully zipped helices while in experiment the partially folded helices may also contribute to the kinetics.

Conclusions

We have developed a new approach (“conformational resampling through kinetic relaxation”) to the prediction of cotranscriptional RNA folding kinetics. The kinetic steps are based on helix creation/annihilation and helix-exchange. Furthermore, the model enhances the efficiency of conformational sampling by keeping only the kinetically important states. Application of the model to the cotranscriptional folding of E Coli. SRP RNA and the pbuE riboswitch lead to several conclusions:

1. For E. Coli. SRP RNA, the predicted population kinetics is consistent with the experimental SHAPE reactivity results. Specifically, the major conformational transitions during the transcription is for the formation of helices H2, H3, H4 and H5 (in structure HP2) as the 86th nucleotide is transcribed in the nascent chain.

2. For pbuE riboswitch, our predicted population of the terminator conformations at the end of the cotranscriptional folding as a function of force is in agreement with the experimental result. In the absence of ligand (adenine), under 5.8 pN pulling force, the kinetic process from the formation of the helix P2 to the folding of the terminator involves multiple intermediate states. The aptamer structure emerges as an off-pathway low-population (< 20%) kinetic transient state (lifetime < 1 s). The results of the kinetic modeling suggest a possible time window for ligand binding to the aptamer.

3. For pbuE adenine riboswitch, with the presence of the ligand, the aptamer structure emerges as an on-pathway intermediate. Ligand binding can stabilize the aptamer structure, causing a higher aptamer population (peak value > 90%) and a longer dwell time (> 1s) than the ligand-free case. Furthermore, the ligand-stabilized aptamer results in an effective suppression of the terminator population and consequently a decrease in termination efficiency. Further modeling of the cotranscriptional folding kinetics under a large force (8.1 pN) shows that the folding pathways are sensitive to the pulling force. For example, in the absence of the ligand, due to the destabilization by the larger force, the aptamer structure disappears from the kinetic intermediates under the larger force.

Putting the above results together, we find an overall consistency between the theoretical predictions and the experimental results for the population kinetics, time-extension curves, the kinetic pathways and various timescales. Furthermore, the model provides new insights. For example, the model uncovers the detailed structural information for intermediate states under the different forces and the time intervals for the different kinetic events. The new method developed here may also be useful for future investigation of the kinetic effects from transcriptional pausing, cotranscription speed, ligand concentration, and RNA sequence for large RNAs.