Transferable Machine-Learning Model of the Electron Density

Abstract

The electronic charge density plays a central role in determining the behavior of matter at the atomic scale, but its computational evaluation requires demanding electronic-structure calculations. We introduce an atom-centered, symmetry-adapted framework to machine-learn the valence charge density based on a small number of reference calculations. The model is highly transferable, meaning it can be trained on electronic-structure data of small molecules and used to predict the charge density of larger compounds with low, linear-scaling cost. Applications are shown for various hydrocarbon molecules of increasing complexity and flexibility, and demonstrate the accuracy of the model when predicting the density on octane and octatetraene after training exclusively on butane and butadiene. This transferable, data-driven model can be used to interpret experiments, accelerate electronic structure calculations, and compute electrostatic interactions in molecules and condensed-phase systems.

Short abstract

A machine-learning scheme that incorporates seamlessly locality and atom-scale symmetries can predict the electron charge density of large, flexible molecules based on training on smaller compounds.

Introduction

The electron density ρ(r) is a fundamental property of atoms, molecules, and condensed phases of matter. ρ(r) can be measured directly by high-resolution electron diffraction^1,2 and transmission electron microscopy,³ and can be analyzed to identify covalent and noncovalent patterns.⁴⁻⁸ On the basis of density-functional theory (DFT), in the framework of the first Hohenberg–Kohn theorem,⁹ knowledge of ρ(r) gives access, in principle, to any ground-state property. Especially for large systems, however, the computation of ρ(r) requires considerable effort, involving the solution of an electronic structure problem with a more or less approximate level of theory. Sidestepping these calculations and directly accessing the ground-state electron density for a given configuration of atoms would have broad implications, including real-time visualization of chemical fingerprints based on the electron density,⁷ acceleration of DFT calculations by providing an estimate of the self-consistent charge density, and an exact treatment of the electrostatic interactions within an atomistic simulation. Another field of application involves the analysis and interpretation of experimental techniques that probe the electron density, such as transmission electron microscopy³ and X-ray crystallography.^1,2 In the latter, the decomposition of the density in pseudoatomic contributions that is often performed to resolve the structure^10,11 foreshadows some of the ideas we will use here.

Following a number of successful applications of machine-learning methods to predict materials properties,¹²⁻⁷¹ a recent landmark paper by Brockherde et al. showed that it is also possible to predict the ground-state electron density in a way that mimics the Hohenberg–Kohn mapping between the nuclear potential and the density.¹⁶ A smoothed representation of the nuclear potential was used as a fingerprint to describe molecular configurations and to carry out individual predictions of the expansion coefficients of ρ(r) represented in a plane-wave basis. Though in principle it is very effective, the structure of the model imposes significant constraints on its transferability to large and flexible systems. Indeed, the use of a global representation of the structure, and of an orthogonal basis to expand the density, means that the model is limited to interpolation between conformers of relatively rigid, small molecules.

In this paper, we show how to overcome these limitations by constructing a machine-learning model of the valence electron density that can be used on both large and flexible systems by predicting the density of large molecules based on training on smaller compounds. This is possible, in a nutshell, thanks to the combination of a local basis set to represent ρ(r), which is reminiscent of local expansions of the wave function¹⁷ and of the atom density multipole analysis of X-ray diffraction,¹⁸⁻²² and thanks to a recently introduced regression model which allows us to predict the local components of ρ(r) in a symmetry-adapted fashion without the need to make simplifying assumptions on the description of molecular environments.

The method is tested on the carbon series C₂, C₄, and C₈ of both fully saturated and unsaturated hydrocarbons, having increasing complexity because of the exponentially growing number of conformers. In particular, interpolation of the electron density is first shown for ethene (C₂H₄), ethane (C₂H₆), butadiene (C₄H₆), and butane (C₄H₁₀). As a major result, the electron density of the corresponding C₈ molecules, namely, octa-tetraene (C₈H₁₀) and octane (C₈H₁₈), is instead predicted by extrapolating the information learned on the local environments of the corresponding C₄ molecules.

Symmetry-Adapted Gaussian Process Regression for the Charge Density

Several widely adopted machine-learning schemes applied to materials rely on an additive decomposition of the target property in atom-centered contributions.²³⁻²⁸ These approaches are very effective in achieving transferability across systems of different composition and size. An additive ansatz is justified by the exponential decay of the electronic density matrix (the so-called nearsightedness principle²⁹) for insulators and metals at finite temperature, which underlies a plethora of linear-scaling, embedding, and fragment decomposition electronic structure methods.^17,30−37 Many methods exist to decompose the density in atom-centered contributions,^38,39 which however cannot be defined uniquely.⁴⁰ Rather than imposing that the machine-learning model should be consistent with a specific choice of density decomposition, we introduce locality only by expanding the density as a sum of atom-centered basis functions (for further details see section Basis set optimization in Supporting Information),

1

where k runs over the basis functions centered on each atom, and atoms of different species can have different kinds of functions. We then write a regression model for the combination coefficients c_kⁱ based exclusively on the knowledge of the positions of the nuclei, but we only use as the target property the total electron density ρ(r). In this way, the model determines simultaneously the regression coefficients and the most convenient (and otherwise arbitrary) decomposition of ρ(r) into atom-centered contributions.

From an atom-centered description, it is natural to factorize each basis function ϕ_k(r – r_i) into a product of radial functions R_n(r_i) and spherical harmonics Y_m^l(r̂_i) (with r_i = |r – r_i| and r̂_i = (r – r_i)/r_i). The subscript k refers to the combination nlm, and we will use the compact or the extended notation based on convenience. For every atom-centered environment 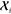, which defines the structure of a neighborhood of atom i, and for each radial function R_n, the coefficients can be grouped according to their value of angular momentum l in a set of spherical multipoles c_nlⁱ of dimension 2l + 1, which transform as vector spherical harmonics Y_l under a rigid rotation of the environment. This choice has the advantage of highlighting the tensorial nature of the density components, meaning that a significant portion of the variability of c_nlⁱ can be attributed to the orientation of the local environments 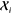, rather than to an actual structural distortion of the molecule.

Dealing with the regression of tensorial properties raises nontrivial issues in terms of setting up an effective machine-learning model that takes into account the proper covariances in three dimensions. For rigid molecules, one could eliminate this geometric variability by expressing the coefficients in a fixed molecular reference frame, analogously to what has already been done in the context of electric multipoles and response functions.^41,42

This problem has long been known in the context of the determination of electron densities from experimental X-ray diffraction data.¹⁸⁻²² One of the most widely used methods is the multipole model proposed by Stewart^10,43 and by Hansen and Coppens,¹¹ which models the valence charge density with both a spherical and multipolar component;⁴⁴ this is essentially equivalent to the expansion (1). In practice, existing pseudoatom methods are constructed from tabulated multipolar parameters (e.g., the libraries ELMAM,⁴⁵⁻⁴⁸ ELMAM2,^49,50 UBDB,^51,52 Invarioms,⁵³ and SBFA⁵⁴), that are based on the determination of molecular fragments, that also provide a local reference frame to describe the anisotropy of the density. In most cases, these fragment decompositions are used as an initial guess for the density. The nuclear coordinates and the local multipoles are both optimized to match the experimental diffraction pattern during structural refinement.⁵⁵

Our goal here is more ambitious, as we aim to predict the charge density based exclusively on nuclear coordinates. Furthermore, we aim at a scheme that does not rely on the definition of discrete molecular fragments and captures the density modulation by structural distortions and nonbonded interactions in arbitrarily complex and flexible molecules. As shown recently, Gaussian process regression can be modified to naturally endow the machine-learning model of vectors⁵⁶ and tensors of arbitrary order⁵⁷ with the symmetries of the three-dimensional (3D) rotation group SO(3). Within this method, called symmetry adapted Gaussian process regression (SA-GPR), the machine-learning prediction of the tensorial density components is

2

In this expression, 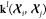is a rank-2 kernel matrix of dimension (2l + 1) × (2l + 1) that expresses, at the same time, both the structural similarity and the geometric relationship between the atom-centered environment 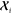of the target molecule and a set M of reference environments 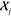. The (tensorial) regression weights x_nlm′^j are determined from a set of N training configurations and their associated electron densities.

According to eq 2, the prediction of the density expansion coefficients c_nlmⁱ(x) is performed independently for each radial channel n, angular momentum value l and atomic species α. However, working with a nonorthogonal basis implies that the density components belonging to different atoms of the molecule are not independent of each other. One can indeed evaluate the projections of the density on the basis functions

3

but these differ from the expansion coefficients c_kⁱ. In fact, w and c are related by Sc = w, where S_kk′^ii′ = ⟨ϕ_kⁱ | ϕ_k′⟩ is the overlap between basis functions. For a given density, the coefficients could therefore be determined by inverting S, so that each individual nlα component could be machine-learned separately. We observed, however, that doing so led to poor regression performance and unstable predictions. Applying S^–1 on w corresponds to a partitioning of the charge which is, most of the time, affected by numerical noise. This is connected to the fact that S is often ill-conditioned, and so small numerical errors in the determination of w translate into large instabilities in the coefficients c, making it hard for the machine-learning algorithm to find a unique relationship between the nuclear coordinates of the molecule and the density components. To avoid this issue and improve the accuracy of the physically relevant total density, the basis set decomposition and the construction of the machine-learning model need to be combined into a single step. This essentially consists of building a regression model that, of the many nearly equivalent decompositions of ρ, is able to determine the one which best fits the target density associated with a given structure.

The problem can be cast into a single least-squares optimization of a loss function that measures the discrepancy between the reference and the model densities,

4

Here the index 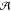 runs over the training set 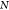, while i runs over the environments of a given training structure. The second term in the loss is a regularization, which avoids overfitting. In this context, η represents an adjustable parameter that is related to the intrinsic noise of the training data set. The coefficients c depend parametrically on the regression weights x via eq 2; by differentiating the loss with respect to x_nlm^j one obtains a set of linear equations that makes it possible to evaluate the weights in practice. In compact notation, the solution of this problem reads

5

where x and w are vectors containing the regression weights and the density projections on the basis functions, while K and S are sparse matrix representations containing the symmetry-adapted tensorial kernels and the spatial overlaps between the basis functions. The details of this derivation and the resulting expressions are given in the Supporting Information. It should, however, be stressed that the final regression problem is highly nontrivial. The kernels that involve environments within the same training configuration are coupled by the overlap matrix, so that all the regression weights x for different elements, radial and angular momentum values must be determined simultaneously. An efficient implementation of a ML model based on eq 5 requires the optimization of a basis set for the expansion, the evaluation of ρ(r) on dense atom-centered grids, the sparsification of the descriptors that are used to evaluate the kernels, and the determination of a diverse, minimal set of reference environments 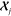. All of these technical aspects are discussed extensively in the Supporting Information.

Results and Discussion

Charge Decomposition Analysis

It is instructive to inspect the decomposition of the charge density in terms of the optimized basis, obtained from density projections on the basis functions w and the overlap matrix S as c = S^–1w, which corresponds to the best accuracy that can be obtained with a given basis. With a basis set of four contracted radial functions, and angular momentum components up to l = 3, the typical error in the density decomposition can be brought down to about 1%. In Table 1 we compare, for the case of a butane molecule, the residual in the expansion with the typical error that can be expected by taking a superimposition of free-atom densities, between 16 and 20%.

Table 1. Mean Absolute Errors in the Representation of the Electron Density Using a Superimposition of Free Atoms (Proatomic Density) and the Optimized Basis Set Used in This Work (Basis Set Decomposition), Averaged over the Whole Training Set for the C₂ and C₄ Molecules^a.

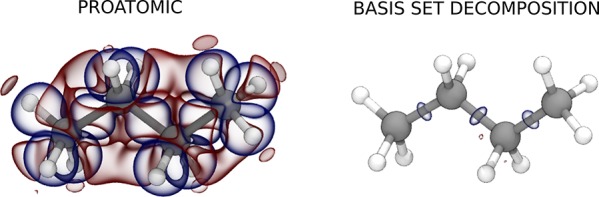
	⟨ερ⟩ (%)
	C2H4	C2H6	C4H6	C4H10
proatomic	18.06	19.23	16.79	18.13
basis set	1.04	1.14	0.98	1.19

^aThe graphic shows isosurfaces for the error in the electron density for proatomic (left) and basis set (right) representation, for a typical configuration of butane (red and blue isosurfaces correspond to an error of ±0.005 electrons Bohr⁻³, respectively).

It is also possible to compute separately the contributions to the charge carried by each angular momentum channel l, e.g., ρ_l(r) = ∑_inmc_nlmⁱϕ_nlm(r – r_i). As exemplified in Figure 1, while the isotropic l = 0 functions determine the general shape of the density, the l = 1 functions primarily describe the gradient of electronegativity in the region close to C–H bonds. Furthermore, the l = 2 functions describe the charge modulation associated with the C–C bonds along the main chain as well as the π-cloud along the conjugated backbone, while the l = 3 functions act as a further modulation that captures the nontrivial anisotropy. The figure also shows the collective contribution to the charge variability carried by each angular momentum channel l and atomic type α, i.e., 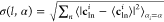, with the average ⟨·⟩ involving all the atoms of the same type included in the data set.

Figure 1.

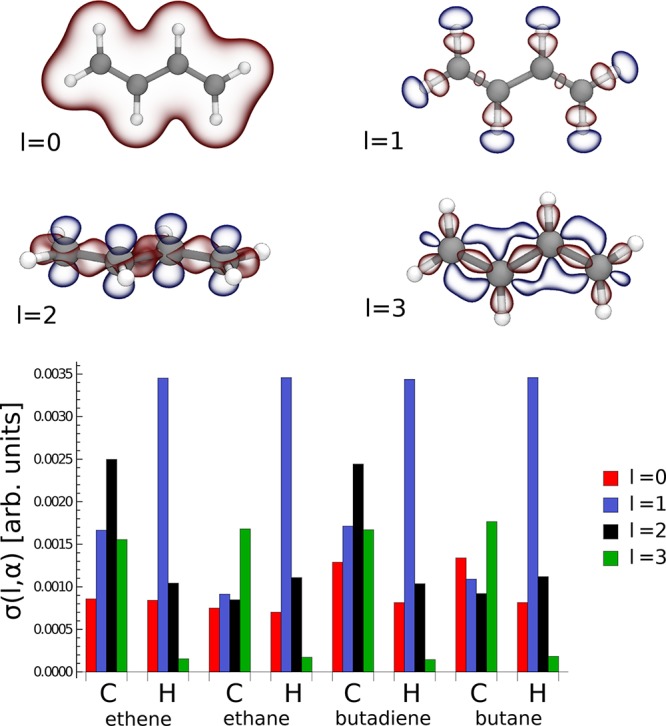
(Top) representation of the angular momentum decomposition of the electron density. Red and blue isosurfaces refer to ±0.01 electrons Bohr^–3 respectively. (Bottom) angular momentum spectrum of the valence electron density of C₂ and C₄ data sets. The isotropic contributions l = 0 express the collective variations with respect to the data set’s mean value, while the mean is statistically zero for l > 0.

After having subtracted the mean atomic density of pure l = 0 character, the l = 1 components largely dominate the charge density variability associated with hydrogen atoms. As previously demonstrated,⁴⁵ functions with l = 2 symmetry also carry a substantial contribution, particularly for the carbon atoms of alkenes, while l = 3 functions appear to be dominant for carbon atoms of alkanes and almost irrelevant for hydrogen atoms in all the four molecules. In comparison to an atom-centered expansion of the wave function ψ, the choice of using a larger basis set is justified by the greater complexity in describing an electron density field rather than the N_e/2 occupied orbitals being the solution of an effective single particle Hamiltonian. The need for high angular momentum components can be also justified by the fact that—even neglecting the overlap between adjacent atoms—the squaring of ψ that yields ρ(r) would introduce nonzero components with up to twice the maximum l used to expand the wave function.

Density Learning with SA-GPR

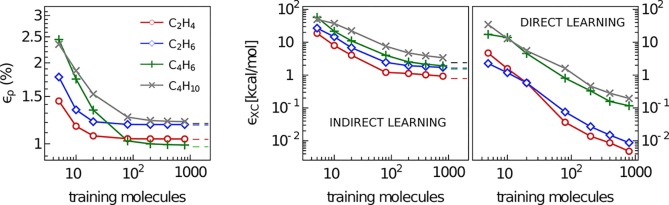
Having optimized the basis set and analyzed the variability of the electron density when expanded in this optimized basis, we now proceed to test the SA-GPR regression scheme. The difficulty of the learning exercise largely depends on the structural flexibility of the molecules. Small, rigid systems such as ethene and ethane require little training, and could be equivalently learned through a machine-learning framework based on a pairwise comparison of aligned molecules. Butadiene data, containing both cis and trans conformers, as well as distorted configurations approaching the isomerization transition state, poses a more significant challenge, due to an extended conjugated system that makes the electronic structure very sensitive to small molecular deformations. The case of butane is also particularly challenging because of the broad spectrum of intramolecular noncovalent interactions spanned by the many different conformers contained in the data set. Being fully flexible, this kind of system is expected to benefit most from a ML scheme that can adapt its kernel similarity measure to different orientations of molecular subunits. Figure 2 shows the performance of the method in terms of prediction accuracy of the electron density as a function of the number of training molecules. The number M of reference environments has been fixed to the 1500 most diverse, FPS-selected, environments contained in each data set. The convergence with respect to M is discussed in the Supporting Information. The symmetry adapted similarity measure which enters in the regression formula of eq 5 is given by the tensorial λ-SOAP kernels of ref (57). This generalizes the scalar (λ = 0) smooth overlap of atomic positions framework⁵⁸ that has been used successfully for constructing interatomic potentials^24,59 and predicting molecular properties.^60,61 In constructing these kernel functions, we chose a radial cutoff of 4.5 Å for the definition of atomic environments (further details are in the Supporting Information). Learning curves are then obtained by varying the number of training molecules up to 800 randomly selected configurations out of the total of 1000. The remaining 200 molecules for each of these random selections are used to estimate the error in the density prediction.

Figure 2.

Learning curves for C₂ and C₄ molecules. (Left) % mean absolute error of the predicted SA-GPR densities as a function of the number of training molecules. The error normalization is provided by the total number of valence electrons. (Right) root-mean-square errors of the exchange-correlation energies indirectly predicted from the SA-GPR densities and directly predicted via a scalar SOAP kernel, as a function of the number of training molecules. Dashed lines refer to the error carried by the basis set representation.

We express the error in terms of the mean absolute difference between the predicted and quantum mechanical densities, i.e., ε_ρ(%) = 100 × ⟨ ∫ dr|ρ_QM(r) – ρ_ML(r)|⟩/N_e. The prediction errors of ethene and ethane saturate to the limit imposed by the basis set representation, which is around 1% for all molecules, with as few as 10 training points. As expected, given the greater flexibility, learning the charge density of butadiene and butane is more challenging, requiring the inclusion of more than 100 training structures in order to approach the basis set limit. This level of accuracy (an error which is almost 20 times smaller than that obtained with a superposition of rigid atomic densities, as discussed above) was demonstrated to be sufficient⁴⁵ for most applications that rely on the accuracy of the density representation, such as the modeling of X-ray and transmission electron microscopy,¹⁻³ or the evaluation of density-based fingerprints of chemical interactions.⁴⁻⁸

Using the predicted ρ(r) as the basis for a density-functional calculation is more challenging. As a benchmark for this application, we use the SA-GPR predictions for ρ(r) to evaluate the PBE exchange-correlation functional E_XC[ρ] used for the reference quantum-mechanical calculations. Depending on the gradient of the density, this quantity is very sensitive to small density variations, especially localized around the atomic nuclei. Figure 2 shows the root-mean-square error for the exchange-correlation energies ε_XC. Using the full set of 800 training molecules, we reach a, RMSE of 0.9 and 1.7 kcal/mol for ethene and ethane, 1.9 kcal/mol for butadiene, and 3.5 kcal/mol for butane, basically matching the basis set limit. It is clear that the ML scheme has the potential to reach higher accuracy with a small number of reference configurations, but a significant reduction of the basis set error is necessary to reach chemical accuracy (roughly 1 kcal/mol RMSE) in the prediction of E_XC. At the same time, it is not obvious that computing E_XC indirectly, by first predicting the electron charge density, is the most effective strategy to obtain an ML model of DFT energetics. As shown in the figure, applying a direct, scalar regression based on conventional SOAP kernels to learn the relationship between the molecular structure and E_XC leads to vastly superior performance while requiring a much simpler machine-learning model.

Size-Extensive Extrapolation

While incremental improvements of the underlying density representation framework are desirable to use the predicted density as the basis of DFT calculations, we can already demonstrate the potential of our SA-GPR scheme in terms of transferability of the model. From the prediction formula of eq 2, it is clear that no assumption is made about the identity of the molecule for which the electron density is predicted. Practically speaking, the regression weights x_nlm^j are associated with representative environments that could be taken from any kind of compound, not necessarily the same as that for which the density is being predicted. As long as the training set is capable of describing different chemical environments, and contains local configurations similar to the ones of our prediction target, accurate densities can be obtained simply by computing the kernels 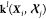between the envi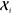ronments of an arbitrarily large molecule and the reference environments 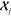. The cost of this prediction is proportional to the number of environments, making this method of evaluating the electron charge density strictly linear scaling in the size of the target molecule.

As a proof of concept of this extrapolation procedure, we use environments and training information from the butadiene and butane configurations already discussed to construct the electron density of octatetraene (C₈H₁₀) and octane (C₈H₁₈), respectively. It is important to stress that the transferability is because on a local scale the larger molecules are similar to those used for training, and so the prediction is effectively an interpolation in the space of local environments. This is emphasized by the observation that the optimal extrapolation accuracy is obtained using a machine learning cutoff of r_cut = 3 Å, versus a value of r_cut = 4.5 Å that was optimal for same-molecule predictions. On a scale larger than 3 Å, the environments present in C8 molecules differ substantially from those in the corresponding C4 compound, which negatively affects the transferability of the model. Ideally, as the training data set is extended to include larger and larger molecules, this locality constraint can be relaxed until no substantial difference can be appreciated between the prediction accuracy of the interpolated and extrapolated density.

For both octane and octatetraene, the extrapolation is carried out on a challenging data set made of the 100 most diverse structures extracted by farthest point sampling from the 300 K replica of a long replica exchange molecular dynamics (REMD) run. When learning on the full data set of butadiene and butane, we obtain a low density mean absolute error of 1.8% for octatetraene and of 1.4% for octane. As shown in Figure 3 for two representative configurations, the size-extensive SA-GPR prediction accurately reproduces the structure of the electron density for both octane and octatetraene. Because of the high sensitivity of the electronic π-cloud to the molecular identity and configuration, major difficulties arise in predicting the electron density of octatetraene, particularly in the middle regions, for which no analogous examples are contained in the butadiene training data set.

Figure 3.

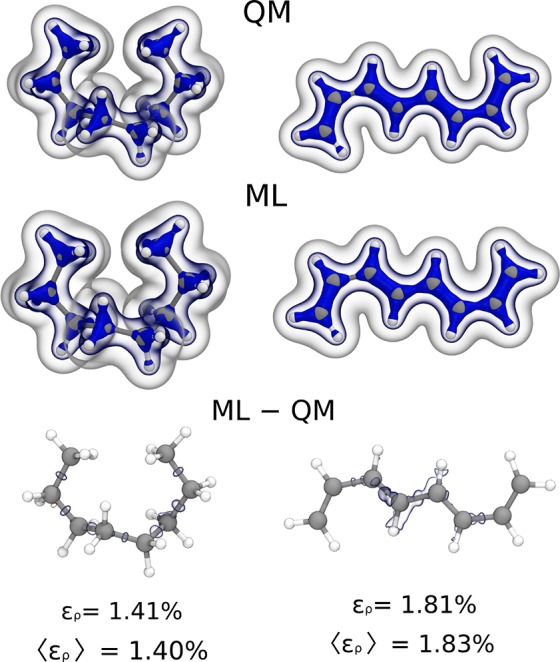
Extrapolation results for the valence electron density of one octane (left) and one octatetraene (right) conformer. (Top) DFT/PBE density isosurface at 0.25, 0.1, 0.01 electrons Bohr^–3, (middle) machine-learning prediction isosurface at 0.25, 0.1, 0.01 electrons Bohr^–3, (bottom) machine-learning error, red and blue isosurfaces refer to ±0.005 electrons Bohr^–3 respectively. Relative mean absolute errors averaged over 100 conformers are also reported for both cases.

The SOAP representation can be easily extended to more complex molecules and condensed phases,⁶² and has been shown to be remarkably effective in making predictions on larger molecules based on training on very simple compounds.⁶³ Achieving similar results for the charge density involves some technical challenges, connected with the presence of correlations between coefficients due to the nonorthogonal basis expansion, that makes the cost of training (but not of predicting) the density scale unfavorably with the system size. In the presence of large electric fields, or long-range charge transfer, it will be necessary to extend the scheme to be compatible with a description of the underlying physical process. One can look for inspiration to existing self-consistent equilibration schemes for atomic charges,⁶⁴ or to the use of local electric fields as part of the input representation.⁴²

Conclusions

Machine-learning the electronic charge density of molecular systems as a function of nuclear coordinates poses great technical and conceptual challenges. Transferability across molecules of different size and stoichiometry calls for a scheme based on a local decomposition, which should be performed without relying on arbitrary charge partitioning or discarding the fundamental physical symmetries of the problem. The framework we present here overcomes these hurdles by decomposing the density in optimized atom-centered basis functions, exploiting a symmetry-adapted regression scheme to incorporate geometric covariances, and by designing a loss function that relies only on the total charge density as a physically meaningful constraint. The atom-centered decomposition means the ML model can predict the density of large molecules or condensed phases with a cost that scales linearly with the number of atoms. For instance, learning the chemical environment of all the functional units of the 20 natural amino acids in all their protonation states and forms (N-terminal, nonterminal, C-terminal), one possible perspective for our method will be the prediction of the charge density of proteins.

We have demonstrated the viability and accuracy of this scheme by learning the ground-state valence electron density of saturated and unsaturated hydrocarbons with two and four carbon atoms, achieving in all cases an error of the order of 1% on the reconstructed density. Given that this estimate is based exclusively on the nuclear position, it could be used for structural determination, e.g., in the analysis of X-ray⁴⁵ and transmission electron microscopy experiments. What is more, models trained on C4 compounds can be used to predict the electronic charge of their larger, C8 counterparts, providing a first example of the transferability that is afforded by a symmetry-adapted local decomposition scheme.

Further improvements of the accuracy are likely to be possible, by better optimization of the basis set, by simultaneously fine-tuning the representation of environments by λ-SOAP kernels and the representation of the density in terms of projections on a local basis set, and also by using inexpensive semiempirical methods to provide a baseline for the electron density prediction. In fact, this work can be seen as a first, successful attempt to apply machine learning in a transferable way to molecular properties that cannot be simply decomposed as the sum of atom-centered values, but exhibit a richer, more complex geometric structure. The Hamiltonian, the density matrix, vector fields, and density response functions are other examples that will require careful consideration of both the representation of the input structure, and of the property one wants to predict, and that can benefit from the framework we have introduced in the present work.

Methods

As a demonstration of our framework, we consider hydrocarbons, using a data set of 1000 independent structures of ethene, ethane, butadiene, and butane. Atomic configurations are generated by running REMD simulations at the density functional tight binding level,⁶⁵ using a combination of the DFTB+⁶⁶ and i-PI⁶⁷ simulation software.⁶⁸ In order to construct a realistic and challenging test of the ML scheme, we chose the replica at T = 300 K and selected a diverse set of 1000 configurations, by a farthest point sampling (FPS) algorithm based on the SOAP metric.^60,69 For each selected configuration we computed the valence electron pseudo density at the DFT/PBE level with SBKJC effective core potentials. Further details of the data set construction are given in the Supporting Information.

The problem of representing a charge density in terms of a nonorthogonal localized basis set shares many similarities with that of expanding the wave function. For this reason, we resort to many of the tricks used in quantum chemistry codes, including the use of Gaussian type orbitals (GTOs) to compute the basis set overlap analytically, and the contraction of 12 regularly spaced radial GTOs down to four optimized functions. We find that angular momentum channels up to l = 3 functions are needed to obtain a decomposition error around 1% for the density. The coefficients of the contraction are optimized to minimize the mean charge decomposition error and the condition number of the overlap matrix for the four molecules,⁷⁰ as discussed in the Supporting Information. A systematic analysis of the interplay between the details of the basis set and the performance of the ML model goes beyond the scope of this work. It is likely however that substantial improvements of this approach could be achieved by further optimization of the basis.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.8b00551.

• Supporting Information of the manuscript contains further details about the derivation, implementation and benchmarks of the method, including: a summary of the symmetry-adapted Gaussian process regression (SA-GPR) method; a detailed derivation of the regression formula for the learning of the charge density; the definition of the primitive basis set together with the recipe to compute the overlap matrix analytically; the details about the numerical evaluation of density projections over the basis functions; the definition of the grid used to estimate the error associated with the predicted densities; the procedure adopted to optimize the primitive basis set; a detailed description of how the molecular configurations are selected; details about the quantum-mechanical calculations used to produce the training densities; the machine-learning parameters used to compute λ-SOAP kernels; the details about the selection of the reference environments used for the density learning; a comparison between the prediction accuracy obtained with our data set of ethane (C₂H₆) and the data set of ethane generated in ref (16); a summary of regression performances (PDF)

The authors declare no competing financial interest.