Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Nov 30;122(51):12396–12402. doi: 10.1021/acs.jpcb.8b07901

Weak Shape Anisotropy Leads to a Nonmonotonic Contribution to Crowding, Impacting Protein Dynamics under Physiologically Relevant Conditions

Jin Suk Myung †,*, Felix Roosen-Runge †,*, Roland G Winkler ‡, Gerhard Gompper ‡, Peter Schurtenberger †, Anna Stradner †,*
PMCID: PMC6349356  PMID: 30499666

Abstract

graphic file with name jp-2018-07901f_0006.jpg

The effect of a nonspherical particle shape on the dynamics in crowded solutions presents a significant challenge for a comprehensive understanding of interaction and structural relaxation in biological and soft matter. We report that small deviations from a spherical shape induce a nonmonotonic contribution to the crowding effect on the short-time cage diffusion compared with spherical systems, using molecular dynamics simulations with mesoscale hydrodynamics of a multiparticle collision dynamics fluid in semidilute systems with volume fractions smaller than 0.35. We show that the nonmonotonic effect due to anisotropy is caused by the combination of a reduced relative mobility over the entire concentration range and a looser and less homogeneous cage packing of nonspherical particles. Our finding stresses that nonsphericity induces new complexity, which cannot be accounted for in effective sphere models, and is of great interest in applications such as formulations as well as for the fundamental understanding of soft matter in general and crowding effects in living cells in particular.

Introduction

Diffusion of proteins in cells is an essential aspect, as it strongly influences the cellular machinery through numerous processes such as signal transmission or reactions between proteins.1−3 In a dense and crowded environment such as the interior of a living cell, individual proteins strongly feel the presence of surrounding proteins through direct and hydrodynamic interactions.4−7 These interactions cause a severe slowing down of diffusional transport in crowded solutions,1,8 with a strong dependence on the nature of the crowder and tracer.9−13 Concentrated protein solutions present promising systems for the investigation of generic crowding effects, since systematic experimental studies have been successfully linked to colloid-inspired descriptions,14−19 as for example for the critical slowing down and dynamical arrest in crystallin solutions mimicking the eye lens fluid.20−23 On the basis of this overall success of colloidal concepts, previous studies1,14−18,21,23 argued that a weak shape anisotropy as found for many globular proteins can be successfully modeled using effective spherical particles,24 thereby neglecting the specific shape of the particle.

Here, using mesoscale hydrodynamic simulations, we critically examine this approach in the appropriate short-time limit, in which the single-particle hydrodynamic mobility governs the motions without being obstructed by other particles. We stress that an accurate characterization of the short-time limit is essential for a quantitative understanding of dynamic processes at longer times, as short-time processes always enter the description, e.g., owing to mobility as well as collision or escape times. We show that slightly nonspherical particles experience a nonmonotonic contribution to the slowing down of the short-time cage diffusion, i.e., the short-time collective diffusion on a length scale comparable to the particle size, which cannot be understood based on colloidal models of effective spheres, and is not caused by interparticle attraction. We remark that this effect is not caused by jamming close to dynamical arrest, but is an intrinsic property of colloidal and protein diffusion in semidilute systems with volume fractions smaller than 0.35. We rationalize the finding based on the mobility, i.e., the short-time self-diffusion, and structural properties of the system. We discuss the broad implications for the understanding of biological and soft matter given the prevalence of particles with anisotropic interactions and a nonspherical shape.

Methods

Mesoscale Hybrid Simulation

We investigate the effect of shape anisotropy on the dynamical behavior of colloids by a mesoscale hybrid simulation approach combining the multiparticle collision dynamics (MPC) method for the fluid with molecular dynamics simulations (MD) for ellipsoids.25−28 Importantly, this simulation approach allows for a reliable account of hydrodynamic interactions of nonspherical particles, and is thus ideally suited to address crowding effects in such systems. We recently used this approach to show that short-time dynamics of weakly attractive colloids is strongly affected by anisotropic interactions,23 and the clustering dynamics of proteins has been investigated.29 Furthermore, the MPC method has successfully been used in complex systems such as polymers,25,26 colloids,28,30 vesicles, and blood cells,31,32 as well as active systems.33

Model Ellipsoid

An ellipsoid is represented by a set of Nm beads of mass M distributed over the ellipsoid surface and one in the center (cf. Figure 1 inset). This structure allows for a computationally efficient coupling of the solvent and ellipsoid.28 Neighboring beads and the center of the ellipsoid are connected by a harmonic bond potential

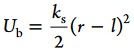graphic file with name jp-2018-07901f_m001.jpg 1

to maintain a nearly rigid ellipsoid. Here, r is the center-to-center distance of the two beads, l is the preferred bond length, and ks is the spring constant. The interactions between ellipsoids are assumed to be short ranged, and are represented by a Yukawa attraction with hard core-like repulsion for all interellipsoid bead pairs

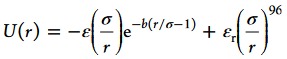graphic file with name jp-2018-07901f_m002.jpg 2

with the bead diameter σ. ε and εr are the interaction strengths of interellipsoid attraction and repulsion, respectively. b is the parameter characterizing the interaction range.

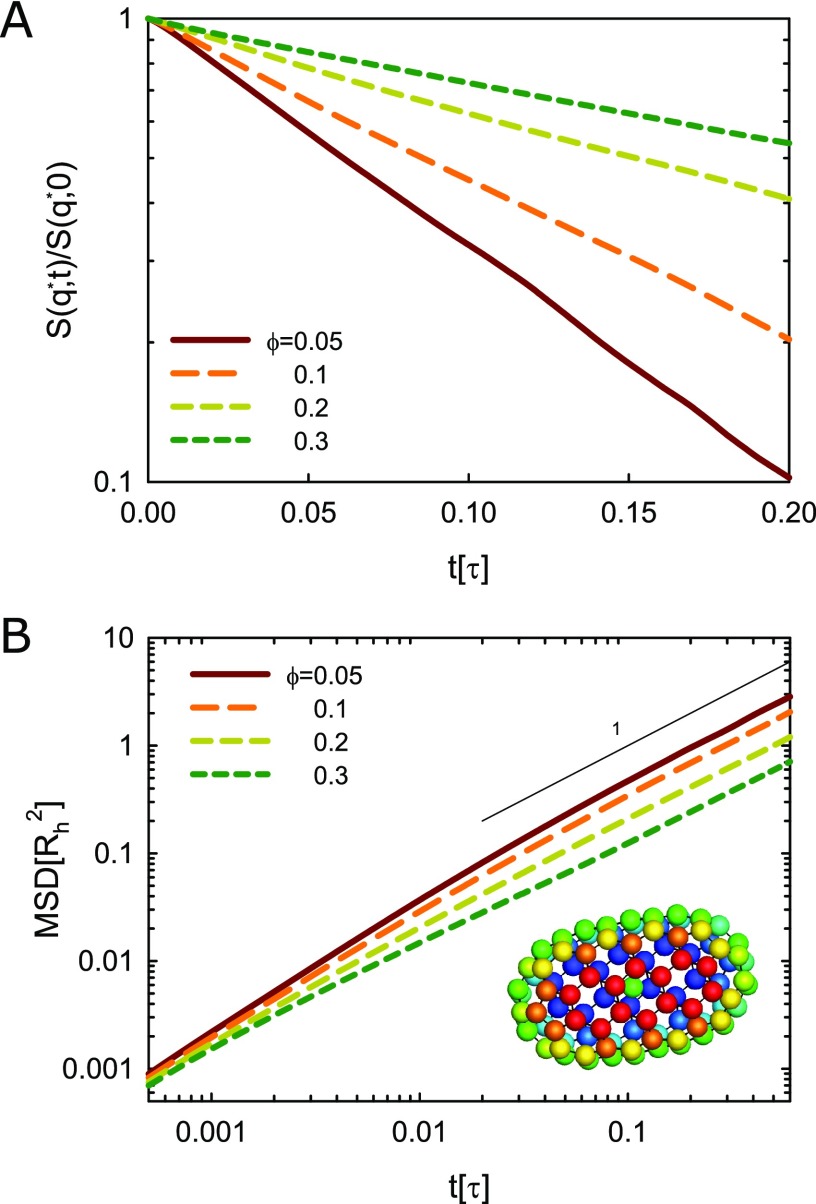
Figure 1.

Figure 1

Open in a new tab

(A) Intermediate scattering function (ISF) for different volume fractions of attractive ellipsoids. The ISF of 0.02τ ≤ t ≤ 0.2τ is used for the fit to obtain the short-time collective diffusion coefficient Ds(q), where τ = Rh2/D0 is the characteristic time of colloids. (B) Mean-square-displacement (MSD) for different volume fractions of attractive ellipsoids. The MSD of 0.02τ ≤ t ≤ 0.6τ is used for the fit to obtain the short-time self-diffusion coefficient Dss. Inset: bead configuration for the model ellipsoid.

Multiparticle Collision Dynamics Fluid

The MPC approach is a particle-based simulation technique, which incorporates thermal fluctuations and hydrodynamic correlations,25−27 and, thus, provides a solution for fluctuating hydrodynamic equations (Landau–Lifshitz Navier–Stokes equations).27,34 In addition, it is easily coupled with other simulation techniques, such as molecular dynamics simulations for embedded particles.25,26,35,36 In MPC, the fluid is represented by point particles, Ns in the current study, of mass m, which interact with each other by a stochastic process.25−27 The algorithm consists of two steps: streaming and collision. In the streaming step, the particles move ballistically and their positions are updated according to

graphic file with name jp-2018-07901f_m003.jpg 3

where ri and vi are the position and velocity of particle i, and h is the time between collisions. In the collision step, a coarse-grained interaction between the fluid particles is imposed by a stochastic process. Thereby, particles are sorted into cells of a cubic lattice, defining the collision environment, with lattice constant a. Various collision schemes have been introduced.25,26,30,37 Here, we apply the stochastic rotation version of MPC,38 where for all particles in a cell, their relative velocity with respect to the center-of-mass velocity vcm of the cell is rotated by the fixed angle α. This yields the new velocities

graphic file with name jp-2018-07901f_m004.jpg 4

with the rotation matrix R(α) around a randomly oriented axis chosen independently for every collision cell and collision step. These steps conserve the linear momentum on the collision cell level and thereby yield proper hydrodynamic correlations.34 The MPC procedure can be considered as a coarse-grained description of pairwise elastic collisions of hard-sphere fluid particles. In the center-of-mass reference frame, such a two-particle collision leads to particle scattering by a certain angle defined by their energy and momenta. The MPC rotation of relative velocities can be considered as the net effect of various collisions averaged over time and space.

The colloid–solvent coupling is implemented by including the beads in the collision step. Hence, the particle center-of-mass velocity vcm(t) of a cell containing beads is

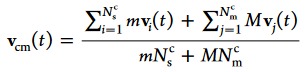graphic file with name jp-2018-07901f_m005.jpg 5

where Nsc and Nm are the number of solvent particles and beads in the cell, respectively.25 In the MPC collision step, the velocity of colloid beads is updated via eq 4, in the same way as for the solvent particles, leading to a local exchange of momentum between the fluid particles and the colloid beads, while conserving the overall momentum in the collision cell. During the MPC streaming step, the beads are propagated using standard molecular dynamics (with the velocity Verlet algorithm), taking into account only the direct interactions with neighboring beads of the same colloid and any nearby beads of other colloids, to ensure conformational colloid integrity and accurate colloid–colloid interactions.

The applied MPC approach results in a translational and rotational diffusive motion of a colloid, with, in dilute solution, diffusion coefficients agreeing quantitatively with those predicted by the solution of Stokes equation for a colloid of nonslip boundary conditions.28 Moreover, colloid center-of-mass and rotational velocity autocorrelation functions exhibit a long-time tail consistent with a solution of the linear fluctuating hydrodynamics equations (Landau–Lifshitz Navier–Stokes).28,34

To control and maintain a constant temperature, we apply a local Maxwellian thermostat by scaling velocities.39 For this purpose, the kinetic energy is taken from the Γ distribution, which describes the distribution of kinetic energy, accounting for the number of degrees of freedom of the particles in a collision cell. A scaling factor is determined as the ratio between the actual kinetic energy of the particles in the respective cell and the value from the distribution function. Then, the relative velocities vi – vcm of all of the particles in a cell are multiplied by the scaling factor. This algorithm ensures conservation of momentum in a collision cell and a Maxwell–Boltzmann distribution of the particle velocities.

Simulation Setup and Parameters

An ellipsoid is comprised of Nm = 101 beads, and the semiprincipal axes are ra = 5σ, rb = 2.95σ, and rc = 2.5σ. The shape of the ellipsoid is chosen to mimic the model protein γB-crystallin, for which short-time diffusion and phase behavior are experimentally well-characterized.22,23 The direct interactions are characterized by ks = 2000kBT/σ2, b = 15, and εr = kBT, where kB is the Boltzmann constant and T the absolute temperature. Note that the deformation of ellipsoids during simulations is less than 0.1% (cf. Figure S1). The attraction strength ε = 2.9kBT for attractive ellipsoids is chosen such that the system is in the one-phase region above the coexistence curve for metastable liquid–liquid phase separation,22,2322,23 which is typically observed for colloids and proteins with short-range attraction.40,41 We employed a cubic simulation box of side length Ls = 100a, corresponding to a total number of ellipsoids ranging from N = 245 (ϕ = 0.05) to 1485 (ϕ = 0.3). The volume fraction is defined as ϕ = (4/3)π(ra + rh)(rb + rh)(rc + rh)N/Ls3, where rh = 0.3σ is the hydrodynamic radius of the surface bead.28 The parameters for the MPC fluid are a = σ, M = 10m, α = 130°, 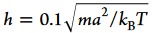Inline graphic, and the mean number of fluid particles in a collision cell ⟨Ns⟩ = 10. This choice of MPC fluid parameters leads to a sufficiently large Schmidt number (Sc ≈ 20), such that the momentum diffusion exceeds mass diffusion and transport properties are dominated by the hydrodynamics.36 By setting M = ⟨Nsc⟩m = 10m, we ensure an adequate hydrodynamic coupling between a colloidal bead and the MPC particles in a collision cell, because of their comparable momenta. Newton’s equations of motion for the beads were solved by the velocity Verlet algorithm with time step hp = h/10.42

The hydrodynamic radius of the ellipsoid is Rh = 3.9σ calculated from the free diffusion coefficient D0 = kBT/(6πηRh) with the solvent viscosity η, where D0 was obtained from the extrapolation of the short-time self-diffusion coefficient Dss(ϕ) toward ϕ = 0. Here, the short-time self-diffusion coefficient Ds was calculated from the mean-square-displacement (MSD) ⟨Δr2⟩ = 6Dsst of the colloids at short times (t < 0.6τ), where τ = Rh2/D0 is the characteristic time of colloids.

As a remark on the MPC method, for the first few MPC steps, the hydrodynamics are not fully developed and almost the same MSD is found for any concentration. As apparent in Figures 1B and S2B, the curves for the various concentrations approach each other at short times. After a sufficient number of steps, hydrodynamic interactions are established and cause a diffusive regime with a MSD linear in time. The crossover between the initial nonhydrodynamic regime and the diffusive regime shifts to shorter times with increasing concentration,28 resulting in the diffusive regime extending down to 0.001τ for ϕ = 0.3.

The dynamic properties are investigated in the short-time regime, i.e., on a time scale shorter than the characteristic time of the colloids. Correspondingly, we denote the observed self- and collective diffusion as short-time diffusion. We remark that our notion might differ from the formal definition of short-time diffusion based on the instantaneous mobility tensor, as the latter is not necessarily observable from trajectories in dense, attractive, and anisotropic systems. The basic reason is that a clear separation of the Brownian time scale (on which particles become diffusive) and interaction time scale (on which interaction potentials become effective) may not be ensured for all conditions.

Results and Discussion

In a crowded solution such as the cytoplasm, numerous factors affect the phase behavior and diffusion of proteins. An increasing volume fraction as the control parameter directly linked to crowding enhances hydrodynamic and direct interactions, resulting in a slowing down of diffusion and the eventual arrest of macroscopic dynamics at the glass line.1,16,17,21,45 A second commonly considered factor is attractive interactions that cause, e.g., molecular docking, cluster formation, gelation, and liquid–liquid phase separation, which in turn affect the diffusion in complex and crucial ways.1,18,22,23

Interestingly, much less is known about crowding effects on diffusion in the presence of interaction and shape anisotropy, although these are ubiquitous in proteins, and patchy particle models have been shown to successfully reproduce the phase behavior of such protein solutions quantitatively.46−49 Very recent studies outlined coupled rotational–translational protein diffusion due to anisotropic attraction,45 and a drastic slowing down of short-time diffusion due to attractive patches on spheres.23 These findings on anisotropic attraction emphasize that the statistical–mechanistic understanding of crowding is hampered by the lack of information on the effects of anisotropy. Moreover, systematic studies on the influence of a nonspherical shape are missing so far, because of the challenge of including hydrodynamic interactions for nonspherical particles.

To address the mechanism of how a nonspherical shape affects crowding, we focus on the initial step of structural relaxation on the nearest-neighbor distance, i.e., the short-time cage diffusion.23,43 Short-time cage diffusion as a collective effect characterizes the dynamical relaxation of structural correlations between neighbor particles (cf. Figure 2 inset), and is thus qualitatively different from self-diffusion rattling in and out of a cage (cf. Figure 3 inset). Short-time cage diffusion is interesting not only from a colloidal point of view, where it has been studied in detail,43 but also in physiology because of its crucial role for cellular processes such as enzymatic reactions and recognition.1−3,23

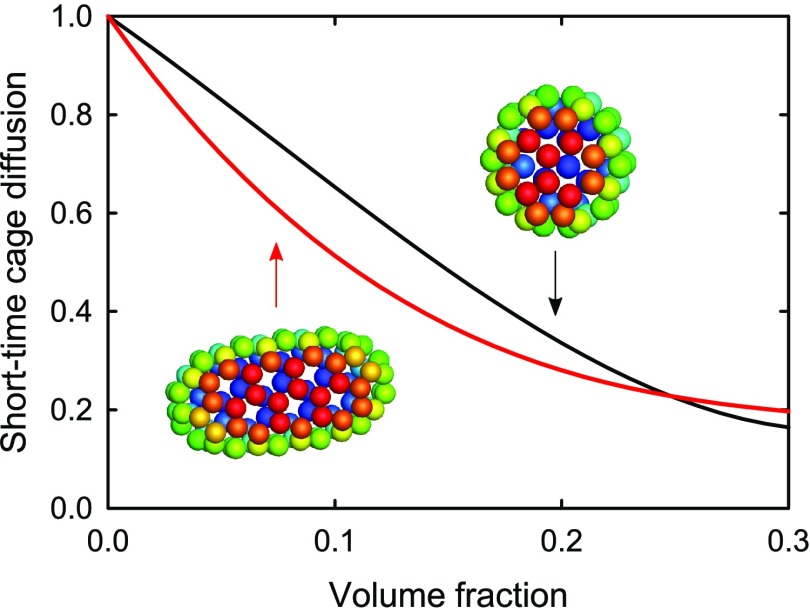
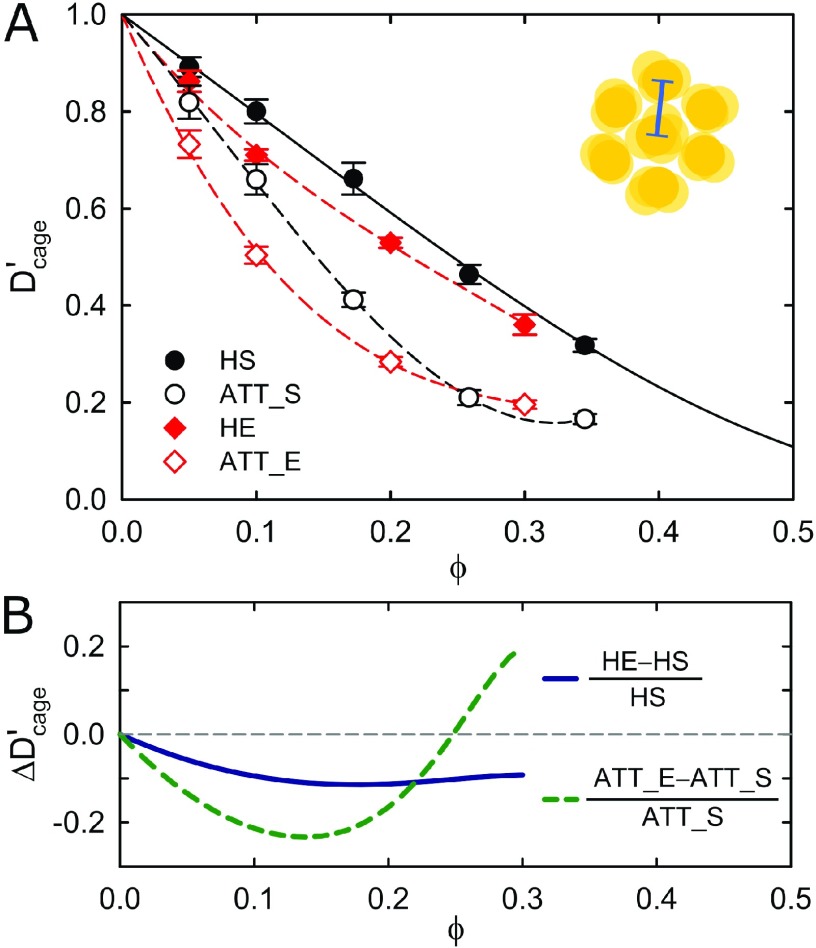
Figure 2.

Figure 2

Open in a new tab

(A) Normalized short-time cage diffusion Dcage′ = Ds(q*)/D0 as a function of the volume fraction ϕ. Results for the hard (HE) and attractive (ATT_E) ellipsoids are displayed, together with results for the hard (HS) and attractive (ATT_S) spheres.23 Inset: short-time cage diffusion as a collective effect characterizes the dynamical relaxation of structural correlations between neighboring particles. (B) The nonmonotonic contribution to the crowding effect due to a nonspherical shape can be clearly seen from the normalized difference between short-time cage diffusion of ellipsoids and spheres, as obtained from theoretical predictions for hard spheres43 (solid black line in panel A) and polynomial guide-to-the-eyes (dashed lines in panel A).

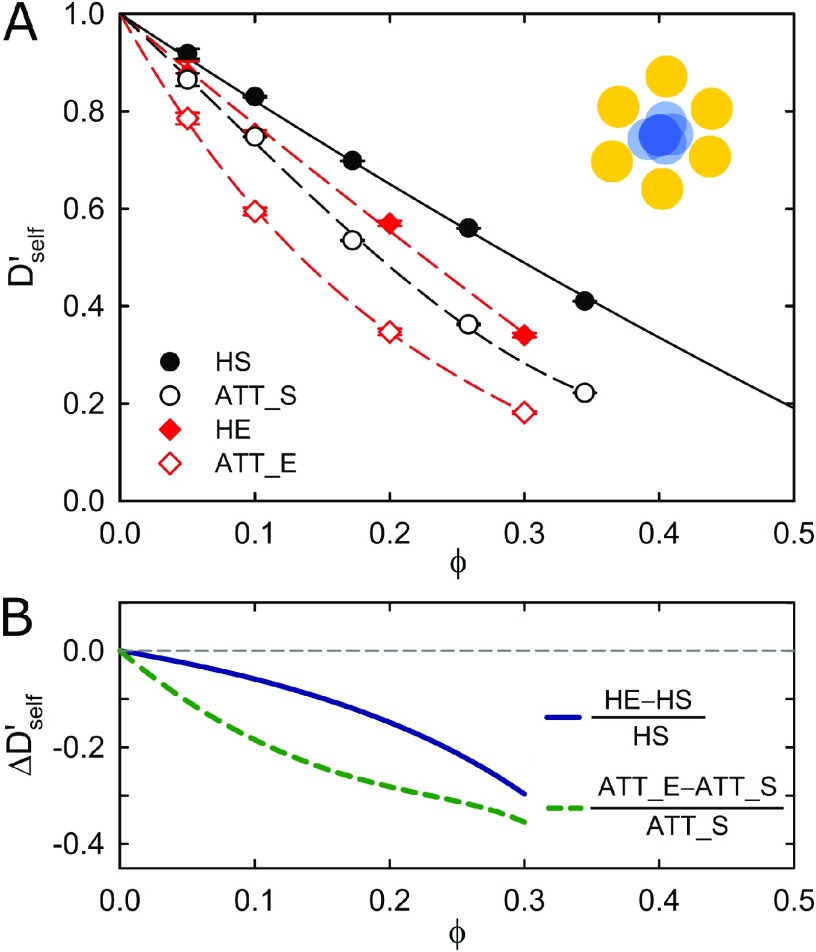
Figure 3.

Figure 3

Open in a new tab

(A) Normalized short-time self-diffusion coefficient, Dself′ = Ds/D0, as a function of the volume fraction ϕ. Results for the hard (HE) and attractive (ATT_E) ellipsoids are displayed, together with results for the hard (HS) and attractive (ATT_S) spheres. Ellipsoids show a lower mobility than spheres because of the larger effective hydrodynamic size. Inset: short-time self-diffusion describes the Brownian motion within the cage of neighboring particles. (B) The normalized difference between self-diffusion of ellipsoids and spheres, as obtained from theoretical predictions for hard spheres43,44 (solid black line in panel A) and polynomial guide-to-the-eyes (dashed lines in panel A).

In experiment, short-time cage diffusion can be studied using dynamic scattering techniques, where the nearest-neighbor distance d* is defined by the position q* = 2π/d* of the principal peak in the structure factor S(q) with the scattering wavenumber q. In our simulation approach, we calculated the intermediate scattering function S(q,t) from the positions of all particles and subsequently obtained the short-time cage diffusion coefficient Ds(q*) from a single exponential fit of S(q*,t) ≈ S(q*,0)e–q*2Ds(q*)t at short times (t < 0.2τ) (cf. Figures 1A and S2A).

Normalized by the respective free diffusion coefficients D0 observed in the limit of infinite dilution, the short-time cage diffusion coefficients Dcage′ = Ds(q*)/D0 of hard and attractive ellipsoids are displayed in Figure 2A as a function of the volume fraction ϕ, together with published results for hard and attractive spheres23 for a comparison. Figure 2A evidences two factors affecting the short-time cage diffusion. First, already a weak nonspherical shape, as found for many globular proteins, causes a slowing down at intermediate volume fractions 0.05 ≤ ϕ ≤ 0.2, whereas no significant effect of anisotropy is observed at higher volume fractions. The nonmonotonic characteristic of the additional crowding effect due to the nonspherical shape is clearly seen from the difference between cage diffusion of ellipsoids and spheres (Figure 2B). Second, attraction causes an overall slowing down of cage diffusion independent of the shape. The effect of a nonspherical shape appears more pronounced at a lower volume fraction. The difference for attractive particles initially exhibits a decay similar to that of hard particles, but passes for larger concentrations (ϕ ≥ 0.15) through a minimum and even becomes positive for ϕ ≥ 0.25.

To understand these two effects, it is important to recall the fundamental factors affecting short-time cage diffusion. The collective diffusion coefficient Ds(q) is linked to the structure factor S(q) and the hydrodynamic function H(q) via43

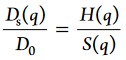graphic file with name jp-2018-07901f_m007.jpg 6

First, the structure factor S(q) represents the dependence of the collective diffusion on the volume-fraction-dependent time-averaged structural correlations between particles (i.e., the configuration of the nearest-neighbor cage). Second, hydrodynamic interactions modulate the collective diffusion, expressed in the hydrodynamic function H(q). H(q) follows roughly the functional form of S(q) in a dampened way, and has a high-q limit H(q → ∞) = Dss/D0. Given that S(q → ∞) = 1, the collective diffusion D(q) thus approaches self-diffusion Ds at high q. We remark that the appearance of S(q) in eq 6 expresses the insight that the relaxation of correlated features—e.g., cage diffusion—is slowed down compared with individual mobilities—i.e., self-diffusion. Thus, both self-diffusion (i.e., mobility) and structure (i.e., the cage configuration and formation of transient clusters) need to be characterized for a comprehensive explanation of the slowing down of cage diffusion.

Starting with the mobility effect, Figure 3A shows the normalized short-time self-diffusion coefficient Dself′ = Ds/D0 as a function of the volume fraction ϕ, as calculated from the mean-square-displacement ⟨Δr2⟩ = 6Dsst of the colloids at short times (t < 0.6τ) (cf. Figures 1B and S2B). The short-time self-diffusion of ellipsoids is clearly slowed down compared with that of spheres, as expected from the increased hydrodynamic friction of ellipsoids compared with spheres of a similar volume.50 Importantly, the slowing down due to a nonspherical shape also occurs for volume fractions around 0.2–0.35, where the monotonic effect is clearly seen from the difference between self-diffusion of ellipsoids and spheres (Figure 3B). Thus, the nonmonotonic effect due to a nonspherical shape on the short-time cage diffusion is not caused by mobility alone, but is tightly linked to the structure of the cage.

Indeed, significant differences between structural properties of spheres and ellipsoids are evident when comparing the particle configurations. The representative snapshots of attractive spheres and ellipsoids at ϕ = 0.1 shown in Figure 4 illustrate the formation of transient clusters, as previously discussed in ref (23). The clusters are only transient and the size of the clusters fluctuates in time. Importantly, attractive ellipsoids show a pronounced network structure, where many ellipsoids (∼50%) form a single large and extended cluster. Attractive spheres also exhibit clusters, but these are more compact and comprise only about 20% of the spheres. The average number of connected neighbors (cf. Figure S3) of the ellipsoids is also higher than that of spheres for low and intermediate volume fractions (ϕ ≤ 0.15), which correspond to pronounced clusters of ellipsoids, whereas the largest cluster comprises most of the colloids for both systems for higher volume fractions (ϕ ≳ 0.2), and presents a similar local environment for ellipsoids and spheres. Note that only a weak orientational ordering of ellipsoids is observed even for the attractive ellipsoids (cf. Figure S4).

Figure 4.

Figure 4

Open in a new tab

Configuration of (A) attractive spheres and (B) ellipsoids for ϕ = 0.1. The color code of the colloids corresponds to the size of the cluster, Nc/N, to which the colloid belongs.

To understand the reason behind the nonmonotonic contribution to the crowding effect due to a nonspherical shape at volume fractions up to 0.35, we examined a short-range structural property. Figure 5A displays the average coordination number Nb, which is the number of nearest neighbors, of attractive spheres and ellipsoids as a function of the volume fraction. We define neighboring colloids as those having a bead–bead distance r ≤ 1.4σ, to account for all colloids with attractive interaction. For low and intermediate volume fractions (ϕ ≤ 0.1), both spheres and ellipsoids show a similar average number of neighbors ⟨Nb⟩, and thus both colloids are surrounded by a comparable number of neighbors. However, for higher volume fractions (ϕ ≥ 0.15), ellipsoids show a lower ⟨Nb⟩, indicating less homogeneous and less compact cage configurations. These loose packings allow for a faster cage relaxation of ellipsoids compared with spheres at larger volume fractions.

Figure 5.

Figure 5

Open in a new tab

(A) Average coordination number ⟨Nb⟩ of attractive spheres (ATT_S) and ellipsoids (ATT_E) as a function of the volume fraction ϕ. Although similar at a low volume fraction, attractive spheres have a higher coordination number, implying a more homogeneous and compact cage configuration. Inset: the structure factor S(q*) supports this notion, and the larger values at a high volume fraction cause a stronger slowing down for spheres compared with ellipsoids, which compensates the mobility difference. (B, C) The structure factor S(q) for different volume fractions of (B) attractive sphere and (C) ellipsoid. rs = 3σ is the radius of the sphere,23 and ra = 5σ, rb = 2.95σ, and rc = 2.5σ are the semiprincipal axes of the ellipsoid.

The essential structural influence on short-time cage diffusion Ds(q*) as expressed by eq 6 is encoded in the structure factor peak S(q*), which has been calculated from the simulations as a second measure independent of a cluster analysis. S(q*) is clearly lower for ellipsoids compared with spheres, in particular at a larger ϕ (cf. Figure 5 inset), where the corresponding structure factor S(q) is shown in Figure 5B,C. This difference in cage configurations at large volume fractions combined with eq 6 causes a weaker slowing down for the Ds(q*) of ellipsoids compared with spheres (cf. Figure 2). Thus, comparing ellipsoids with spheres, the effects of structural nearest-neighbor correlation and mobility effectively compensate each other for cage diffusion at volume fractions around 0.3–0.35.

Interestingly, the compensation is observed for both attractive and hard colloids, suggesting a steric origin, and not an origin from special cage configurations induced by anisotropic attraction. We stress that attraction should, however, not be seen as an irrelevant aspect for the nonmonotonic additional contribution to crowding, since attraction actually enhances the effect, in particular at a lower ϕ as shown in Figure 2B. This behavior supports the interpretation in terms of a steric origin, since attraction simply induces a denser neighborhood already at a lower ϕ because of cluster formation.

We remark that the reported nonmonotonic effect on short-time cage diffusion due to the shape at volume fractions lower than 0.35 is fundamentally different from the expected nonmonotonic effect on mobility due to jamming at a higher volume fraction. In the latter case, the higher volume fraction for random closed packing for ellipsoids compared with spheres also suggests a higher volume fraction for dynamical arrest of the short-time self-diffusion. Given the stronger decay at low volume fractions (cf. Figure 3), the self-diffusion of ellipsoids and spheres have to cross somewhere, implying a nonmonotonic effect of the shape on self-diffusion. In our case, we report a nonmonotonic contribution to the slowing-down of cage diffusion at volume fractions below 0.35 where the systems are still clearly dynamic. Under these conditions, the short-time self-diffusion shows no sign of nonmonotonic behavior (Figure 3), and thus the observed nonmonotonic signature is an intrinsic property of the short-time cage diffusion.

Conclusions

We have presented a nonmonotonic contribution to the crowding effect on short-time cage diffusion due to a nonspherical shape. Using mesoscale MPC-MD simulations accounting for hydrodynamic interactions in semidilute solutions with volume fractions up to 0.35, we can conclusively link this effect to the interplay of two factors: first, the normalized mobility of ellipsoids is reduced compared with that of spheres for the full volume fraction range. Second, the cage configuration in suspensions of ellipsoids is less homogeneous and less compact than for spheres, enabling a faster cage relaxation of ellipsoids compared with spheres. The compensation of these two factors at larger volume fractions causes the nonmonotonic characteristic of the additional crowding effect due to a nonspherical shape.

Our findings show that the shape plays an important role in dense suspensions already in the initial short-time regime. This finding on the initial step of structural relaxation challenges the prevailing concept of effective sphere models often used to study and describe dense systems of weakly nonspherical particles in various areas such as cell biophysics, formulation of pharmaceuticals, nanotechnological applications, or fundamental colloid science. Moreover, it also provides interesting perspectives for the statistical–mechanistic understanding of dynamical arrest in anisotropic systems prevalent in soft and biological matter.

Acknowledgments

We gratefully acknowledge the financial support from the Swedish Research Council (VR; grants 2009-6794 and 2016-03301), the Faculty of Science at Lund University, the European Research Council (ERC-339678-COMPASS), and the Knut and Alice Wallenberg Foundation (project grant KAW 2014.0052). The simulations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at LUNARC.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.8b07901.

  • Deformation of ellipsoids; intermediate scattering function (ISF); mean-square-displacement (MSD); number of connected neighbors; orientational angle distribution (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp8b07901_si_001.pdf (389.6KB, pdf)

References

  1. Ando T.; Skolnick J. Crowding and Hydrodynamic Interactions Likely Dominate in Vivo Macromolecular Motion. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 18457–18462. 10.1073/pnas.1011354107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. McGuffee S. R.; Elcock A. H. Diffusion, Crowding & Protein Stability in a Dynamic Molecular Model of the Bacterial Cytoplasm. PLoS Comput. Biol. 2010, 6, e1000694 10.1371/journal.pcbi.1000694. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Miermont A.; Waharte F.; Hu S.; McClean M. N.; Bottani S.; Léon S.; Hersen P. Severe Osmotic Compression Triggers a Slowdown of Intracellular Signaling, Which Can Be Explained by Molecular Crowding. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 5725–5730. 10.1073/pnas.1215367110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Ellis R. J. Macromolecular Crowding: an Important but Neglected Aspect of the Intracellular Environment. Curr. Opin. Struct. Biol. 2001, 11, 114–119. 10.1016/S0959-440X(00)00172-X. [DOI] [PubMed] [Google Scholar]
  5. Ralston G. Effects of “Crowding” in Protein Solutions. J. Chem. Educ. 1990, 67, 857–860. 10.1021/ed067p857. [DOI] [Google Scholar]
  6. Zhou H.-X.; Rivas G.; Minton A. P. Macromolecular Crowding and Confinement: Biochemical, Biophysical, and Potential Physiological Consequences. Annu. Rev. Biophys. 2008, 37, 375–397. 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Zimmerman S. B.; Minton A. P. Macromolecular Crowding: Biochemical, Biophysical, and Physiological Consequences. Annu. Rev. Biophys. Biomol. Struct. 1993, 22, 27–65. 10.1146/annurev.bb.22.060193.000331. [DOI] [PubMed] [Google Scholar]
  8. Konopka M. C.; Shkel I. A.; Cayley S.; Record M. T.; Weisshaar J. C. Crowding and Confinement Effects on Protein Diffusion In Vivo. J. Bacteriol. 2006, 188, 6115–6123. 10.1128/JB.01982-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dix J. A.; Verkman A. Crowding Effects on Diffusion in Solutions and Cells. Annu. Rev. Biophys. 2008, 37, 247–263. 10.1146/annurev.biophys.37.032807.125824. [DOI] [PubMed] [Google Scholar]
  10. Wang Y.; Li C.; Pielak G. J. Effects of Proteins on Protein Diffusion. J. Am. Chem. Soc. 2010, 132, 9392–9397. 10.1021/ja102296k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Balbo J.; Mereghetti P.; Herten D.-P.; Wade R. C. The Shape of Protein Crowders is a Major Determinant of Protein Diffusion. Biophys. J. 2013, 104, 1576–1584. 10.1016/j.bpj.2013.02.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. di Rienzo C.; Piazza V.; Gratton E.; Beltram F.; Cardarelli F. Probing Short-range Protein Brownian Motion in the Cytoplasm of Living Cells. Nat. Commun. 2014, 5, 5891 10.1038/ncomms6891. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Höfling F.; Franosch T. Anomalous Transport in the Crowded World of Biological Cells. Rep. Prog. Phys. 2013, 76, 046602 10.1088/0034-4885/76/4/046602. [DOI] [PubMed] [Google Scholar]
  14. Doster W.; Longeville S. Microscopic Diffusion and Hydrodynamic Interactions of Hemoglobin in Red Blood Cells. Biophys. J. 2007, 93, 1360–1368. 10.1529/biophysj.106.097956. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Cardinaux F.; Zaccarelli E.; Stradner A.; Bucciarelli S.; Farago B.; Egelhaaf S. U.; Sciortino F.; Schurtenberger P. Cluster-Driven Dynamical Arrest in Concentrated Lysozyme Solutions. J. Phys. Chem. B 2011, 115, 7227–7237. 10.1021/jp112180p. [DOI] [PubMed] [Google Scholar]
  16. Heinen M.; Zanini F.; Roosen-Runge F.; Fedunova D.; Zhang F.; Hennig M.; Seydel T.; Schweins R.; Sztucki M.; Antalik M.; et al. Viscosity and Diffusion: Crowding and Salt Effects in Protein Solutions. Soft Matter 2012, 8, 1404–1419. 10.1039/C1SM06242E. [DOI] [Google Scholar]
  17. Roosen-Runge F.; Hennig M.; Zhang F.; Jacobs R. M. J.; Sztucki M.; Schober H.; Seydel T.; Schreiber F. Protein Self-diffusion in Crowded Solutions. Proc. Natl. Acad. Sci. U.S.A. 2011, 108, 11815–11820. 10.1073/pnas.1107287108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Grimaldo M.; Roosen-Runge F.; Hennig M.; Zanini F.; Zhang F.; Zamponi M.; Jalarvo N.; Schreiber F.; Seydel T. Salt-Induced Universal Slowing Down of the Short-Time Self-Diffusion of a Globular Protein in Aqueous Solution. J. Phys. Chem. Lett. 2015, 6, 2577–2582. 10.1021/acs.jpclett.5b01073. [DOI] [PubMed] [Google Scholar]
  19. Anunciado D. B.; Nyugen V. P.; Hurst G. B.; Doktycz M. J.; Urban V.; Langan P.; Mamontov E.; O’Neill H. In Vivo Protein Dynamics on the Nanometer Length Scale and Nanosecond Time Scale. J. Phys. Chem. Lett. 2017, 8, 1899–1904. 10.1021/acs.jpclett.7b00399. [DOI] [PubMed] [Google Scholar]
  20. Fine B. M.; Pande J.; Lomakin A.; Ogun O. O.; Benedek G. B. Dynamic Critical Phenomena in Aqueous Protein Solutions. Phys. Rev. Lett. 1995, 74, 198–201. 10.1103/PhysRevLett.74.198. [DOI] [PubMed] [Google Scholar]
  21. Foffi G.; Savin G.; Bucciarelli S.; Dorsaz N.; Thurston G. M.; Stradner A.; Schurtenberger P. Hard Sphere-like Glass Transition in Eye Lens α-crystallin Solutions. Proc. Natl. Acad. Sci. U.S.A. 2014, 111, 16748–16753. 10.1073/pnas.1406990111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Bucciarelli S.; Casal-Dujat L.; de Michele C.; Sciortino F.; Dhont J.; Bergenholtz J.; Farago B.; Schurtenberger P.; Stradner A. Unusual Dynamics of Concentration Fluctuations in Solutions of Weakly Attractive Globular Proteins. J. Phys. Chem. Lett. 2015, 6, 4470–4474. 10.1021/acs.jpclett.5b02092. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Bucciarelli S.; Myung J. S.; Farago B.; Das S.; Vliegenthart G. A.; Holderer O.; Winkler R. G.; Schurtenberger P.; Gompper G.; Stradner A. Dramatic Influence of Patchy Attractions on Short-time Protein Diffusion under Crowded Conditions. Sci. Adv. 2016, 2, e1601432 10.1126/sciadv.1601432. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Jennings B. R.; Parslow K. Particle Size Measurement: The Equivalent Spherical Diameter. Proc. R. Soc. London, Ser. A 1988, 419, 137–149. 10.1098/rspa.1988.0100. [DOI] [Google Scholar]
  25. Gompper G.; Ihle T.; Kroll D.; Winkler R. G. Multi-Particle Collision Dynamics: A Particle-Based Mesoscale Simulation Approach to the Hydrodynamics of Complex Fluids. Adv. Polym. Sci. 2009, 221, 1–87. 10.1007/978-3-540-87706-6_1. [DOI] [Google Scholar]
  26. Kapral R. Multiparticle Collision Dynamics: Simulation of Complex Systems on Mesoscales. Adv. Chem. Phys. 2008, 140, 20080718 10.1002/9780470371572.ch2. [DOI] [Google Scholar]
  27. Malevanets A.; Kapral R. Solute Molecular Dynamics in a Mesoscale Solvent. J. Chem. Phys. 2000, 112, 7260–7269. 10.1063/1.481289. [DOI] [Google Scholar]
  28. Poblete S.; Wysocki A.; Gompper G.; Winkler R. G. Hydrodynamics of Discrete-particle Models of Spherical Colloids: A Multiparticle Collision Dynamics Simulation Study. Phys. Rev. E 2014, 90, 033314 10.1103/PhysRevE.90.033314. [DOI] [PubMed] [Google Scholar]
  29. Das S.; Riest J.; Winkler R. G.; Gompper G.; Dhont J. K. G.; Nägele G. Clustering and Dynamics of Particles in Dispersions with Competing Interactions: Theory and Simulation. Soft Matter 2018, 14, 92–103. 10.1039/C7SM02019H. [DOI] [PubMed] [Google Scholar]
  30. Padding J. T.; Louis A. A. Hydrodynamic Interactions and Brownian Forces in Colloidal Suspensions: Coarse-graining over Time and Length Scales. Phys. Rev. E 2006, 74, 031402 10.1103/PhysRevE.74.031402. [DOI] [PubMed] [Google Scholar]
  31. Noguchi H.; Gompper G. Shape Transitions of Fluid Vesicles and Red Blood Cells in Capillary Flows. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 14159–14164. 10.1073/pnas.0504243102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. McWhirter J. L.; Noguchi H.; Gompper G. Flow-induced Clustering and Alignment of Vesicles and Red Blood Cells in Microcapillaries. Proc. Natl. Acad. Sci. U.S.A. 2009, 106, 6039–6043. 10.1073/pnas.0811484106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Elgeti J.; Winkler R. G.; Gompper G. Physics of Microswimmers–Single Particle Motion and Collective Behavior: a Review. Rep. Prog. Phys. 2015, 78, 056601 10.1088/0034-4885/78/5/056601. [DOI] [PubMed] [Google Scholar]
  34. Huang C.-C.; Gompper G.; Winkler R. G. Hydrodynamic Correlations in Multiparticle Collision Dynamics Fluids. Phys. Rev. E 2012, 86, 056711 10.1103/PhysRevE.86.056711. [DOI] [PubMed] [Google Scholar]
  35. Malevanets A.; Yeomans J. M. Dynamics of Short Polymer Chains in Solution. Europhys. Lett. 2000, 52, 231–237. 10.1209/epl/i2000-00428-0. [DOI] [Google Scholar]
  36. Ripoll M.; Mussawisade K.; Winkler R. G.; Gompper G. Dynamic Regimes of Fluids Simulated by Multi-Particle-Collision Dynamics. Phys. Rev. E 2005, 72, 016701 10.1103/PhysRevE.72.016701. [DOI] [PubMed] [Google Scholar]
  37. Noguchi H.; Kikuchi N.; Gompper G. Particle-based Mesoscale Hydrodynamic Techniques. Europhys. Lett. 2007, 78, 10005 10.1209/0295-5075/78/10005. [DOI] [Google Scholar]
  38. Ihle T.; Kroll D. M. Stochastic Rotation Dynamics I: Formalism, Galilean Invariance, Green-Kubo Relations. Phys. Rev. E 2003, 67, 066705 10.1103/PhysRevE.67.066705. [DOI] [PubMed] [Google Scholar]
  39. Huang C. C.; Varghese A.; Gompper G.; Winkler R. G. Thermostat for Nonequilibrium Multiparticle-Collision-Dynamics Simulations. Phys. Rev. E 2015, 91, 013310 10.1103/PhysRevE.91.013310. [DOI] [PubMed] [Google Scholar]
  40. Noro M. G.; Frenkel D. Extended Corresponding-states Behavior for Particles with Variable Range Attractions. J. Chem. Phys. 2000, 113, 2941–2944. 10.1063/1.1288684. [DOI] [Google Scholar]
  41. Platten F.; Valadez-Pérez N. E.; Castañeda-Priego R.; Egelhaaf S. U. Extended Law of Corresponding States for Protein Solutions. J. Chem. Phys. 2015, 142, 174905 10.1063/1.4919127. [DOI] [PubMed] [Google Scholar]
  42. Allen M. P.; Tildesley D. J.. Computer Simulation of Liquids; Oxford University Press: Oxford, 1987. [Google Scholar]
  43. Banchio A. J.; Nägele G. Short-time Transport Properties in Dense Suspensions: From Neutral to Charge-stabilized Colloidal Spheres. J. Chem. Phys. 2008, 128, 104903 10.1063/1.2868773. [DOI] [PubMed] [Google Scholar]
  44. Lionberger R. A.; Russel W. B. High Frequency Modulus of Hard Sphere Colloids. J. Rheol. 1994, 38, 1885–1908. 10.1122/1.550530. [DOI] [Google Scholar]
  45. Roos M.; Ott M.; Hofmann M.; Link S.; Rössler E.; Balbach J.; Krushelnitsky A.; Saalwächter K. Coupling and Decoupling of Rotational and Translational Diffusion of Proteins under Crowding Conditions. J. Am. Chem. Soc. 2016, 138, 10365–10372. 10.1021/jacs.6b06615. [DOI] [PubMed] [Google Scholar]
  46. Lomakin A.; Asherie N.; Benedek G. B. Aeolotopic Interactions of Globular Proteins. Proc. Natl. Acad. Sci. U.S.A. 1999, 96, 9465–9468. 10.1073/pnas.96.17.9465. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Gögelein C.; Nägele G.; Tuinier R.; Gibaud T.; Stradner A.; Schurtenberger P. A Simple Patchy Colloid Model for the Phase Behavior of Lysozyme Dispersions. J. Chem. Phys. 2008, 129, 085102 10.1063/1.2951987. [DOI] [PubMed] [Google Scholar]
  48. Bianchi E.; Blaak R.; Likos C. N. Patchy Colloids: State of the Art and Perspectives. Phys. Chem. Chem. Phys. 2011, 13, 6397–6410. 10.1039/c0cp02296a. [DOI] [PubMed] [Google Scholar]
  49. Roosen-Runge F.; Zhang F.; Schreiber F.; Roth R. Ion-activated Attractive Patches as a Mechanism for Controlled Protein Interactions. Sci. Rep. 2014, 4, 7016 10.1038/srep07016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Perrin F. Mouvement Brownien d’un Ellipsoide (I). Dispersion Dielectrique pour des Molecules Ellipsoidales. J. Phys. Radium 1934, 5, 497–511. 10.1051/jphysrad:01934005010049700. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp8b07901_si_001.pdf (389.6KB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES