Abstract
The size of a cell is central to many functions, including cellular communication and exchange of materials with the environment. This modeling and experimental study focused on understanding how the size of a cell determines its ability to uptake nanometer-scale extracellular materials from the environment. Several mechanisms in the cell plasma membrane mediate cellular uptake of nutrients, biomolecules, and particles. These mechanisms involve recognition and internalization of the extracellular molecules via endocytic components, such as clathrin-coated pits, vacuoles, and micropinocytic vesicles. Because the demand for an external resource could be different for cells of different sizes, the collective actions of these various endocytic routes should also vary based on the cell size. Here, using a reaction-diffusion model, we analyze single-cell data to interrogate the one/one mapping between the size of the MDA-MB 231 breast cancer cells and their ability to uptake nanoparticles. Our analysis indicates that under both reaction- and diffusion-controlled regimes, cellular uptake follows a linear relationship with the cell radius. Furthermore, this linear dependency is insensitive to particle size variation within 20–200 nm range. This result is counterintuitive because the general perception is that cellular uptake is proportional to the cell volume (mass) or surface area and hence follow a cubic or square relationship with the cell radius. A further analysis using our model reveals a potential mechanism underlying this linear relationship.
Introduction
Cell size is a critical attribute central to many cellular functions. The plasma membrane is the sole interface between a cell and the extracellular medium. It mediates the exchange of nutrients, particles, proteins, biomolecules, and metabolites between the cell and its environment. Therefore, the size of a cell or the surface area of its plasma membrane may play a central role in determining the rate of cellular uptake of materials. The general perception is that cellular uptake is proportional to the volume of a cell because the demand for the external resources might be determined by the cell mass. However, it is also argued that uptake is proportional to the surface area of a cell because the extracellular materials are internalized by a variety of transporter proteins and endocytic structures in the cell plasma membrane (1, 2). A larger surface area of a cell perhaps implies a more abundance of these plasma-membrane-associated components involved in the recognition, transport, and trafficking of the extracellular molecules and particles.
Nevertheless, in addition to the cell volume or surface area, several other factors may also contribute to the uptake characteristics of a cell. For example, the extracellular transport of a molecule or particle could influence its uptake in a diffusion-controlled environment (3). Examples of such environments include porous media or biological tissues, in which a variety of barriers may hinder the motion of the molecules and particles (4, 5). On the contrary, transport could play a minor role in a cell-culture medium, in which the limiting factor could be a cell’s intrinsic ability to process materials via different endocytic pathways (6). Therefore, the uptake behavior of a cell may be influenced by the relative rate of diffusion and reaction (cell-surface recognition and intracellular trafficking). However, the ultimate uptake characteristics could be more complicated given the possibility that the size or growth of a cell may be dictated by its rate of uptake of the extracellular resources and vice versa (7, 8, 9). Under such circumstances, a feedback-like relationship between cellular uptake and cell size is expected.
Several works in the past investigated cell-size-dependent nutrient uptake by the phytoplanktonic organisms (2, 3, 10, 11, 12, 13). These earlier works focused on understanding how the size of these organisms define their uptake behavior under a limiting nutrient environment. However, for the mammalian cells, relevant literature seems surprisingly limited. As noted earlier, the reason might be that the correlation between cell size and uptake seems too intuitive to deserve a systematic investigation. In a recent work, Wang et al. (14) investigated cell-size-dependent uptake of nanoparticles in human mesenchymal stem cells (hMSCs). In this study, a micropatterned surface was used to grow cells of different sizes. Their experiments revealed a linear increase in particle uptake with cell size. Furthermore, the larger cells displayed a reduced uptake per unit area of the cell membrane compared to their smaller counterparts. The authors attributed these observed uptake behaviors to the higher plasma membrane tension in the larger micropatterened hMSCs.
In recent years, remarkable efforts have been made to understand endocytic recognition and internalization of biomolecules and nanoparticles (15, 16). However, many of these studies, inspired primarily by the drug delivery or cancer research, have paid little attention to the cell size or other cellular attributes at the single-cell level. Instead, attention has been mostly directed to investigating how the physiochemical attributes of the nanoparticles determine the mean (cell population average) uptake (17, 18, 19, 20, 21, 22, 23, 24, 25, 26). The size of a nanoparticle (or a cargo molecule) perhaps remains to be the most extensively studied particle attribute in this context (15, 24, 25, 26, 27). It has been demonstrated that phagocytosis and micropinocytosis mediate trafficking of relatively larger cargoes in the micrometer range. In contrast, clathrin-coated pits primarily mediate uptake of smaller particles in the nanometer range. An earlier work by Rejman et al. (24) demonstrated that particles larger than 500 nm are internalized predominantly by the caveolae-mediated pathway, whereas particles smaller than 200 nm size are internalized primarily by the clathrin-mediated endocytosis. More recently, Zhang et al. (25) demonstrated that 25–30 nm particles represent the optimal size range for internalization via the endocytic pathways. The review article by Shang et al. (26) provides a detailed overview of particle-size-dependent uptake of nanoparticles in various cell types. Nevertheless, despite these advancements, it remains poorly understood how the physical attributes of a single cell govern its ability to uptake particles because the measurements and analysis have mostly focused on the cell population average uptake with an interest in the attributes of the particles rather than cells.
Here, using a reaction-diffusion model, we analyze single-cell data to investigate the one/one correspondence between cell size and particle uptake. Our model incorporates cellular heterogeneity in cell size and cell-to-cell variability in endocytic capacities. The model couples these cell-specific attributes to nanoparticle diffusion in the extracellular medium. Using the model, we investigate cell-size-dependent nanoparticle uptake in the reaction- and diffusion-limited conditions. By analyzing flow cytometry data and microscopy image analysis, we map the MDA-MB 231 cell size to nanoparticle uptake in a typical cell-culture condition. By model fitting to the experimental, we identify parameters governing the particle uptake behavior of MDA-MB 231 cells. For a range of nanoparticle sizes, we show that cellular uptake of particles may vary linearly with cell radius under both diffusion- and reaction-controlled conditions. From diffusion theory, such linear relationship is expected only in the diffusion-limited regime. Nevertheless, our single-cell experimental data reveal similar behavior in a regular cell-culture medium, in which the diffusion effect is expected to be minimal. Based on our analysis, we propose a potential mechanism that can explain the linear correlation between cell size and uptake in a reaction-limited regime.
Materials and Methods
Cell culture
MDA-MB 231 cells were grown in Roswell Park Memorial Institute (RPMI) 1640 medium (Corning Cellgro Mediatech, Manassas, VA) supplemented with 10% fetal bovine serum (Gibco Life Technologies, Grand Island, NY), and 1% penicillin/streptomycin (Gibco). Cells were kept in a humidified incubator at 37°C and 5% CO2 and split at 70–80% confluence, using 0.25% trypsin-EDTA solution (Gibco).
For flow cytometry and fluorescence microscopy experiments, cells were seeded in 24-well plates. Each well was added with 1 mL media (100,000 cells per mL of RPMI 1640) and incubated for 24 h to allow cell attachment. After the incubation, the media in each well was replaced with a solution of nanoparticles in RPMI 1640. The cells were incubated with the nanoparticle solution for 5 h before conducting flow cytometry.
Nanoparticle preparation
Green fluorescent polystyrene nanoparticles (Thermo Scientific Fluoro-Max, Fremont, CA) were used without further modification and purification. The particles had a mean size (diameter) of 100 nm. Particle stock solutions were stored in accordance with the manufacturer’s instructions. Dynamic light scattering was used to confirm particle size. Before the uptake experiment, the particle solutions were vortexed and sonicated in accordance with the manufacturer’s recommendations. For use in the dynamic light scattering measurements (Zetasizer Nano ZS; Malvern Panalytical, Westborough, MA), the sample stock solutions were diluted with deionized water to maintain the specific concentrations recommended in the Zetasizer protocol.
Working particle solution was prepared by diluting the stock solution with deionized water at room temperature. The solution was then further diluted in RPMI 1640 media and vortexed to ensure uniform mixing. The RPMI 1640 media was prewarmed to 37°C for better particle dispersion.
Flow cytometry
After 5 h of incubation with the nanoparticle-RPMI solution, cells were washed three times with phosphate-buffered saline and detached with 0.25% trypsin-EDTA (Gibco). The cell suspension was mixed with 500 μL of fresh RPMI 1640 media solution for flow cytometric measurement. Measurements were performed using a BD Accuri C6 plus (Becton Dickinson, Franklin Lakes, NJ) with a 488 nm argon-ion laser. Fluorescence data were collected through a 533/30 nm bandpass filter. At least 20,000 events per sample were taken for analysis. A forward scatter (FSC) versus 90° side scatter (SSC) log-log plot revealed two distinct populations, one with low SSC and FSC and the other with high SSC and FSC. The former was understood to be dust or debris and discarded, whereas the latter, which accounted for over 80% of the data, was used for analysis.
Cell-size estimation from FSC
The BD Accuri C6 plus was used to collect forward-scatter (FSC-A) data for a mixture of standard fluorescent particles of mean diameter 2 and 3 μm. The data revealed two distinct peaks corresponding to the two particle sizes. The size of individual MDA-MB 231 cells was then estimated from linear extrapolation: cell size (μm) = 3 + (Fc − F3)/(F3 − F2), where Fc, F2, and F3 represent the FSC peak intensities of the MDA-MB 231 cells, 2 μm bead, and 3 μm bead, respectively.
Fluorescence microscopy
MDA-MB 231 cell suspension on a cover glass was imaged using a Zeiss Apotome 2 microscope with a 63× objective lens. Images were analyzed using the ImageJ software to quantify the size of individual MDA-MB 231 cells.
Model implementation
A detailed derivation of the reaction-diffusion model is provided in the Supporting Materials and Methods. The model was implemented in Python. The Python code is also provided in the Supporting Materials and Methods.
Results
Correlation between MDA-MB 231 cell size and nanoparticle uptake
We carried out flow cytometer measurement to identify the correlation between MDA-MB 231 cell size and nanoparticle uptake. Measurements were done to acquire the FSC-A and the fluorescence intensity of the cell-internalized nanoparticles in single cells. The FSC-A was converted into the cell size, which was then mapped to the particle uptake (fluorescence intensity of the internalized particles).
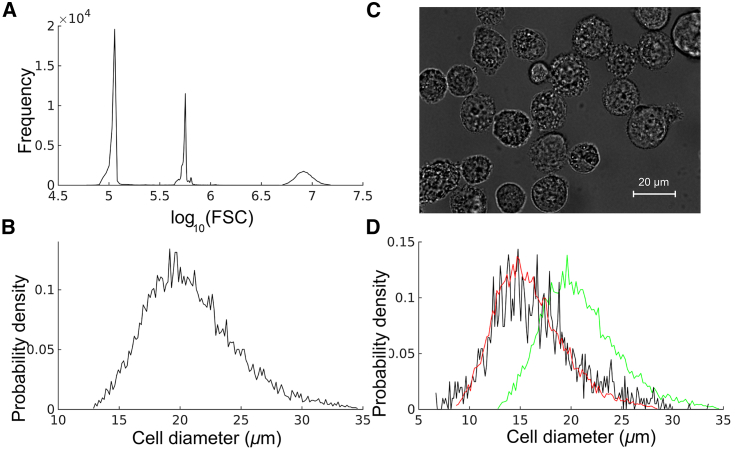
Fig. 1 shows the conversion of the FSC signal into cell size. In Fig. 1 A, FSC-A peaks of two standard fluorescent beads and the MDA-MB 231 cells are shown. The relative positions of these three peaks were used to estimate the cell sizes, as described in Materials and Methods. The cell-size distribution is shown in Fig. 1 B. The data suggests that MDA-MB 231 cell-size distribution can be approximated to a lognormal distribution with mean cell size 11 μm and SD σc = 0.20.
Figure 1.
Size distribution of MDA-MB 231 cells. (A) From left to right: flow cytometer forward scatter (FSC-A) peaks corresponding to 2 μm beads, 3 μm beads, and MDA-MB 231 cells. (B) MDA-MB 231 cell-size distribution estimated from flow cytometer FSC-A. The distribution represents calculation based on 10,000 cells. (C) An image showing a few representative MDA-MB 231 cells. (D) MDA-MB 231 cell-size distribution obtained from microscopy images (black) and FSC-A-based calculation (green). The shifted (corrected) FSC-A-based distribution is shown in red. To see this figure in color, go online.
To check the reliability of the FSC-based estimate, we also calculated cell size directly from microscopy images (Fig. 1 D). The comparison between the FSC-based estimate and the actual cell size (microscopy-image-based calculation) indicates that the FSC provides a slight overestimate. Nevertheless, it provides a pretty accurate estimate for the peak width (distribution variance). After shifting, the FSC-based distribution showed good agreement with the actual cell-size distribution (Fig. 1 D). Because the microscopy data corresponds to a relatively small sample (1500 cells), we used the shifted distribution as the correct measure of cell-size distribution. The mean and standard deviation (SD) of the shifted distribution are μm and σc = 0.20, respectively.
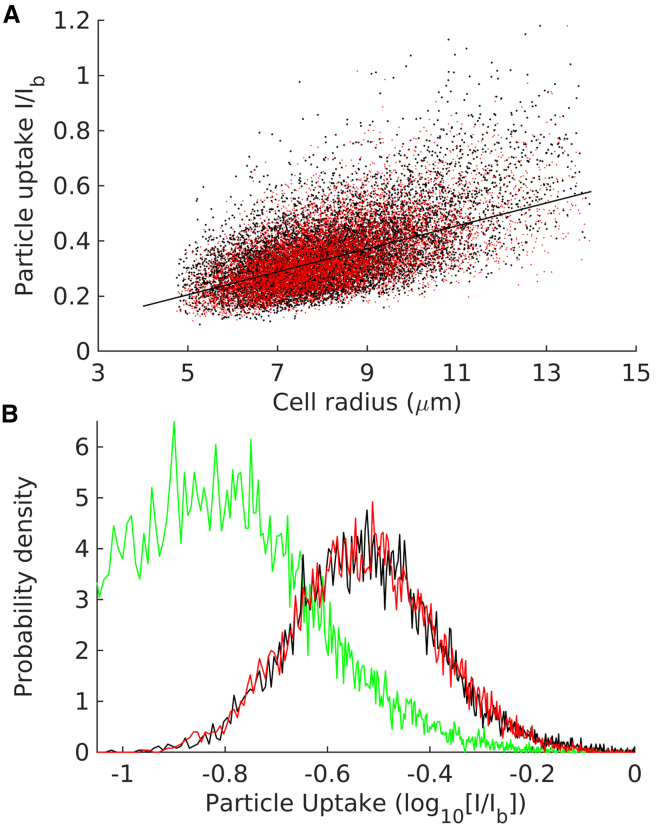
The cell sizes calculated above were mapped to the corresponding fluorescence of internalized nanoparticles, as shown in Fig. 2 A. The figure indicates almost a perfect linear increase in the uptake of 100 nm nanoparticles with cell size. A linear equation with a lognormally distributed noise shows an excellent agreement with the experimental data.
Figure 2.
Flow cytometer analysis reveals a linear correlation between cell size and nanoparticle uptake. The experiment was carried out with 100 nm (diameter) nanoparticles. (A) Each black point represents flow-cytometer-measured single-cell nanoparticle uptake plotted against corresponding cell size. The uptake is expressed as a normalized quantity, which is the ratio of the fluorescence intensity of a cell’s internalized nanoparticle (I) to the median fluorescence of a 3 μm fluorescent bead (Ib). The red points represent the following linear relationship with lognormally distributed noise: , where K = 0.046, σt = 0.263, and is a normally distributed random variable. (B) Green represents distribution of the cell autofluorescence (normalized with Ib). Black represents cellular distribution of particle uptake (measured , black points in A). Red represents distribution of uptake based on the above linear relationship (red points in A). To see this figure in color, go online.
A recent experimental study has reported similar linear correlation between cell size and uptake of nanoparticles in micropatterned hMSCs (14). This observed behavior is, however, unexpected because cell size is expressed in cell radius (r0), not in cell surface area or cell mass. It defies the intuition that particle uptake rate is proportional to the cell surface area or cell mass. Both cases define a nonlinear relationship between the particle uptake rate and r0. If uptake is directly proportional to the surface area, it can be defined as
| (1) |
where is the rate of uptake, ks is a constant, Cb is the concentration of nanoparticles in the extracellular solution, and is a normal distribution with mean 0 and SD σt. accounts for the possibility of noise in particle uptake among cells of identical sizes. On the other hand, if uptake rate is proportional to cell mass, it can be described as
| (2) |
where kv is a constant and ρ is the mass per unit cell volume. However, these simple models, which appear to be physically meaningful, are inconsistent with the linear trend observed in Fig. 2 A because uptake rate in these two models is proportional to and , respectively.
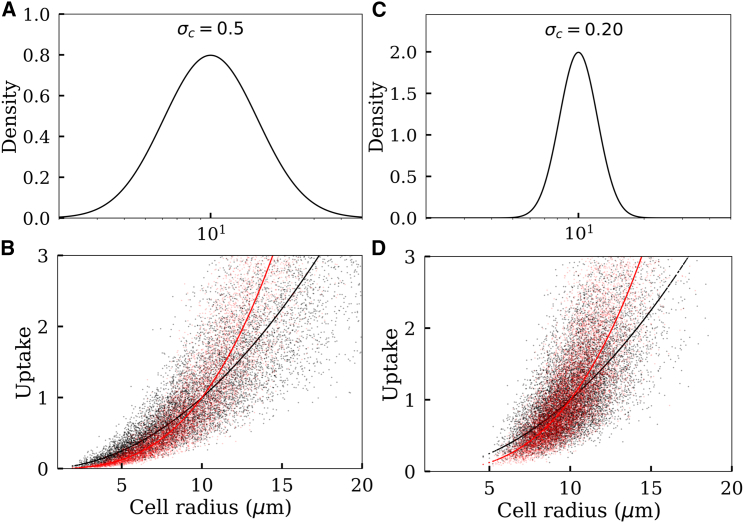
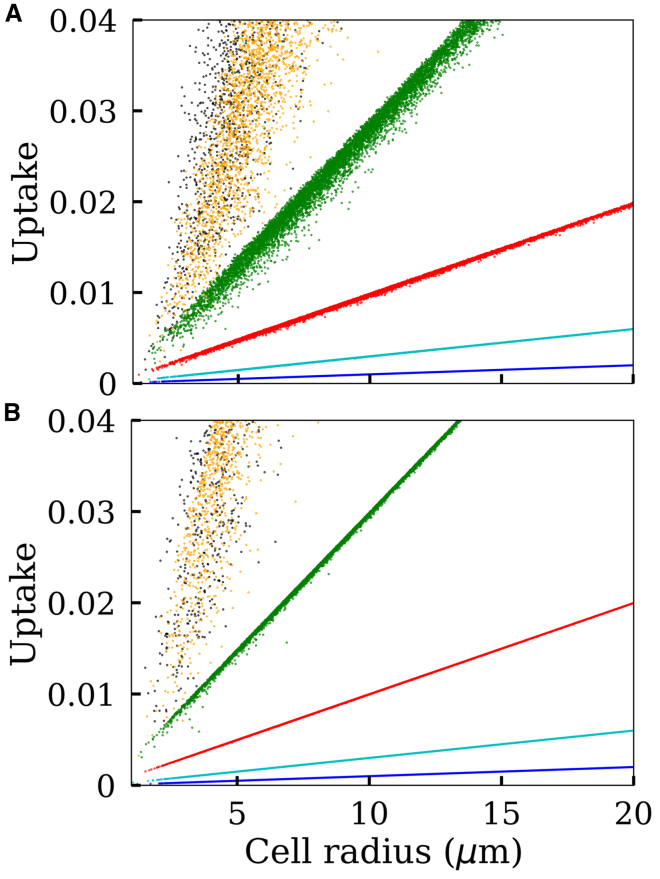
In Fig. 3, we present two hypothetical cases showing how particle uptake should vary against cell size according to the above simple intuitive models (Eqs. 1 and 2). In one case, we consider a widely distributed cell size (Fig. 3, A and B), whereas in another case, we consider a relatively narrowly distributed cell size (Fig. 3, C and D). In both cases, the nonlinearities of the noisy curves are evident even though it is more apparent for the wider cell-size distribution (Fig. 3 B). However, because our measurements (Fig. 2) indicate quite narrowly distributed MDA-MB 231 cell sizes, we also provide a direct comparison between these nonlinear models and the experimental data. As seen in Fig. 4, the nonlinear models poorly describe the data compared to the linear fit in Fig. 2. Note that the theoretical points in the scatter plots (Fig. 4 A) appear to be more condensed compared to the experimental data. However, an attempt to reduce this discrepancy by increasing noise (σt) led to greater disagreements between the experimental and the theoretical peaks in Fig. 4 B.
Figure 3.
Cell-size-dependent particle uptake described by two simple nonlinear models. (A) An assumed distribution for cell size , where μm represents the mean cell size and σc = 0.5 represents the SD. (B) Black: uptake is proportional to cell surface area . Red: uptake is proportional to the cell mass . The solid lines and points correspond to σt = 0 and σt = 0.4, respectively. The cell sizes (X axis values) are sampled from the distribution in (A). (C) The same as in (A) for a narrower cell-size distribution (σc = 0.20). (D) The same as (B) for a narrower cell-size distribution (σc = 0.20). To see this figure in color, go online.
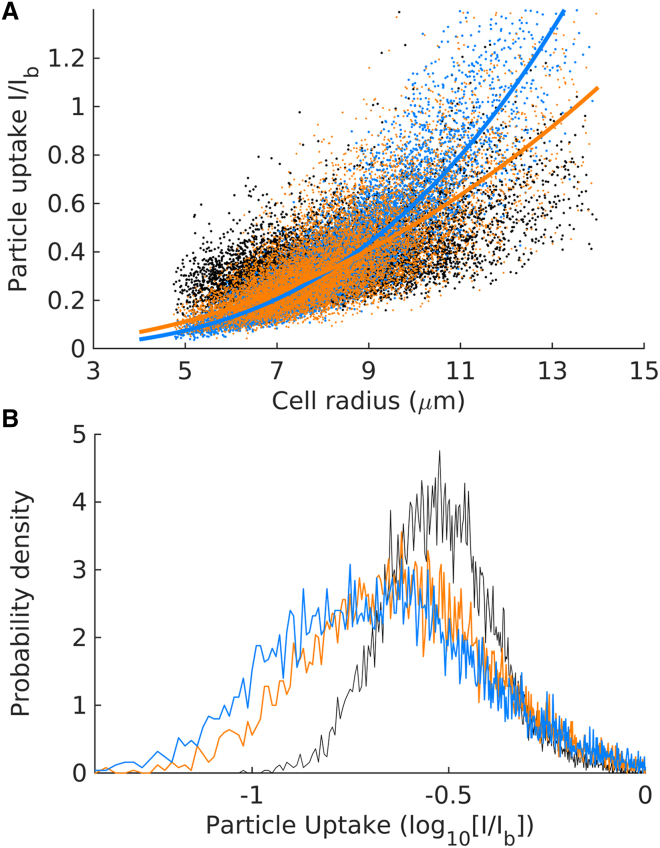
Figure 4.
Comparison between the experimental data and the two simple nonlinear cases in Eqs. 1 and 2. (A) The black dots represent the flow cytometer data presented in Fig. 2A. The orange and blue dots, respectively, are generated using Eqs. 1 and 2, in which particle uptake is assumed proportional to the cell surface area and cell mass, respectively. (B) Probability distributions corresponding to the points in (A). To see this figure in color, go online.
Reaction-diffusion model
The scatter plot in Fig. 2 A revealed two distinct types of heterogeneities in particle uptake by cells. One type of heterogeneity reflects the differences in the cell size, as revealed by the linear increase in particle uptake with cell radius r0. The other type of heterogeneity is the noise, which probably originates from cell-to-cell variation in the endocytic capacities. Because the two simple models above were inadequate to describe these variations, we sought for a more complex model, as detailed below.
In an earlier work, Pasciak et al. (3) developed a reaction-diffusion model to study nutrient absorption by the phytoplanktonic organisms. By adopting a similar approach, we develop a model in which we consider a spherical cell and freely diffusing nanoparticles in the extracellular space. The diffusing particles are captured and internalized at the cell boundary. Unlike the model of Pasciak et al. (3), we explicitly consider nanoparticle uptake by a finite number of endocytic components in the cell plasma membrane. Transmembrane nanoparticle uptake is mediated by a variety of endocytic components (clathrin-coated pits, vacuoles, or phagosomes) in the cell plasma membrane (28). We lump together all these different components into one single (average) component. We assume that there are ne such components per unit area of the plasma membrane of a cell. Each such component, on average, can handle maximal nt particles at a time. Based on this consideration, we assume that unit area of the cell membrane contains n = ne × nt number of hypothetical particle processing units, each of which can handle at most one nanoparticle at a time. We call each of these hypothetical units a “transporter.”
We consider a reversible interaction between a transporter and a nanoparticle. A particle captured by a transporter may dissociate and return to the solution, or it may be taken inside the cell through endocytosis. These steps are described by the following Michaelis-Menten reaction scheme:
In the above scheme, the three reactions are associated with the following three rate constants (Table 1): kf is associated with the forward reaction that leads to the formation of the particle-transporter complex, kr is associated with the reverse reaction that leads to dissociation of the complex, and k1 is associated with the reaction that leads to particle endocytosis and regeneration of the transporter.
Table 1.
Nominal Values for the Model Parameters
| Parameter | Value | Comment |
|---|---|---|
| (μm) | 10 | Cell-population-averaged cell size (radius). |
| 0.0225–0.25 | Cell size (r0) distribution variance: . | |
| (μm−2) | 0.119 | Cell-population-averaged transporter density. |
| 0.16 | Variance describing the noise in transporter density n: . | |
| α | 0 | Parameter correlating cell size (r0) and mean cell-surface transporter density : . |
| kf (μm3 s−1) | 0.1 | Forward rate constant for particle recruitment by a transporter. |
| kr (s−1) | 0.1 | Reverse rate constant for particle detachment from a transporter. |
| k1 (s−1) | 0.02 | Rate constant for particle internalization. |
| D (μm2/s) | 4.29 | Nanoparticle diffusivity, D = kBT/(6πμrp), where temperature, T = 298.15 K, kB is Boltzmann constant, particle radius, rp = 50 nm, and dynamic viscosity of the extracellular solution, μ = 1 cP. |
At steady-state condition, the flux of nanoparticles across the cell membrane can be described by the Michaelis-Menten rate law:
| (3) |
Here, C0 represents nanoparticle concentration at the solution-cell membrane interface, and Jm = k1n represents maximal flux when there are n transporter molecules per unit area of the cell membrane. The constant Km is the Michaelis-Menten constant and is given by Eq. 4:
| (4) |
A function similar to Eq. 3 describes nutrient flux in the model of Pasciak et al. (3). However, in the Pasciak model, it was a phenomenological function and no mechanism of uptake was described at the molecule level. In our model, it appears naturally from the interaction between a finite number of endocytic components and their interaction with particles.
For convenience, we rewrite Eq. 3 in dimensionless form:
| (5) |
where and J∗ = J/Jm. We consider a spherical cell of radius r0 and define dimensionless distance r∗ = r/r0. Now, steady-state mass balance leads to the following differential equation:
| (6) |
where C∗ = C/Km is the dimensionless nanoparticle concentration at r∗ > 1, and D is the particle diffusion constant. D is estimated using the Einstein-Stokes equation:
| (7) |
where kB is the Boltzmann constant, T is temperature, μ is the dynamic viscosity of the extracellular fluid, and a is the particle radius. Because of the symmetry of the spherical geometry, we assume no gradient in C∗ in the θ and ϕ directions. The two boundary conditions for the system are at and at r∗ = 1, where Cb represents the bulk nanoparticle concentration. The solution to Eq. 6 is
| (8) |
Therefore, particle flux
| (9) |
where . The net rate of particle uptake by the entire cell
| (10) |
where k = 4πr0DKm. From Eqs. 5 and 9, the following quadratic equation is obtained:
| (11) |
The solution to this quadratic equation yields nanoparticle concentration at the cell boundary:
| (12) |
Again, from Eq. 10, the total particle uptake rate by the entire cell
| (13) |
The model above is deterministic and describes an average (or ideal) single-cell behavior, as in the nutrient uptake model of Pasciak et al. (3). It does not account for the heterogeneity arising from the difference in the cell size or cell-to-cell variability in the endocytic capacities. We consider a lognormal size distribution for cells: , where represents the mean cell size and σc represents the SD of the distribution. With this consideration, a larger cell can have more cell-surface transporter molecules compared to a smaller cell given the two cells have identical transporter density (n) in the cell membrane.
However, the above consideration is inadequate to fully describe cellular heterogeneity in particle uptake. Two cells of identical size may still differ in their ability to uptake particles because of the intrinsic transcriptional noise associated with the endocytic pathways. To incorporate this additional source of noise, we consider a nominal case in which we assume cell-surface transporter density n varies from cell to cell following a lognormal distribution: . Here, is the mean transporter density and σt is the SD describing the noise in n.
Nonetheless, the nominal case above ignores a possibility that could be dependent on cell size. Therefore, we consider , where represents the ensemble average over all cells. The exponent α takes a positive or negative value (α = 0 represents the nominal case discussed above). The rationale behind this relation is explained later when the relevant analysis is provided.
With the above considerations, both k and ψ become random numbers, and Eq. 13 takes the following form:
| (14) |
where and .
Predicted correlation between cell size and nanoparticle uptake
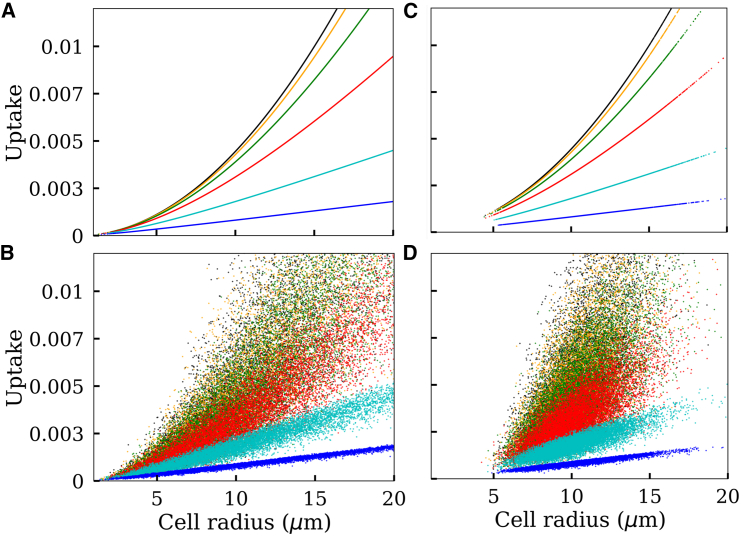
We first investigated how particle uptake varies with cell size when different levels of diffusion barriers are imposed on nanoparticle transport in the extracellular medium. As shown in Fig. 5, two different cell-size distributions were studied. Fig. 5, A and B correspond to a wider cell-size distribution, whereas Fig. 5, C and D correspond to a narrower cell-size distribution. All parameters were assigned with their nominal values (Table 1) unless mentioned explicitly in the figure caption.
Figure 5.
Model-predicted correlation between cell size and nanoparticle uptake. The X axis represents cell size, and the Y axis represents nanoparticle uptake. The uptake is expressed as a dimensionless quantity , where Dm = 4.29 μm2/s represents diffusivity of a 100 nm particle in water at 25°C (Table 1) and Cb is the particle concentration in the bulk solution. (A) Each curve represents a different particle diffusivity in the extracellular medium. Black represents diffusivity in a cell-culture medium, in which viscosity is assumed to be 1 cP. Orange, green, red, cyan, and blue, respectively, represent a 0.1, 0.03, 0.01, 0.003, and 0.001-fold reduced diffusivity relative to the cell-culture medium. Cell sizes are sampled from a lognormal distribution ( μm, σc = 0.5), and cell-surface transporter density is assumed to be constant (, σt = 0, α = 0). (B) All conditions are identical to (A), but a noise is incorporated by sampling n from a lognormal distribution (, σt = 0.4, α = 0). (C and D) All conditions are identical to (A) and (B), respectively, but a narrower cell-size distribution is assumed (, σc = 0.2). To see this figure in color, go online.
All black lines and points in the figure represent particle uptake in a cell-culture medium. We assumed a viscosity of 1 cP and estimated particle diffusion constant using the Einstein-Stokes equation. As expected, the result indicates that particle uptake in a cell-culture medium occurs in a reaction-limited regime. A decrease or increase in the diffusivity by 10-fold does not make any noticeable difference. For the diffusion effect to be visible, it requires at least 30-fold reduced diffusivity (green lines and points).
Fig. 5 indicates a nonlinear relationship between the cell size and nanoparticle uptake rate in the reaction-limited condition. However, this relationship tends to be linear as the system approaches the diffusion-controlled regime. This could be explained by interpreting the model equations. Based on Eq. 12, the reaction-limited condition prevails when
| (15) |
Under this condition, particle concentration at the cell boundary tends to be similar to the bulk concentration , and we recover the Michaelis-Menten rate law in Eq. 5 by replacing with . The resulting cellular uptake rate can be given as
| (16) |
Moreover, if , this equation reduces to , leading to the simple model in Fig. 3, where uptake is proportional to the cell membrane area. On the other hand, the diffusion effect becomes apparent when 1/ψ takes a value comparable to . In particular, the diffusion effect becomes more apparent for cells larger than 5 μm. In contrast when , the system falls into the diffusion-controlled regime, and . From Eq. 11, the uptake rate becomes
| (17) |
thus leading to a linear correlation between particle uptake and cell size.
In summary, the result in Fig. 5 suggests a linear correlation between cellular uptake in the diffusion-controlled regime. However, the linearity observed in Fig. 2 still remains unexplained because a significant transport barrier is not expected in an in vitro cell-culture medium. Note that the result in Fig. 5 represents the nominal case where we assume there is no correlation between the cell size and the density of transporter molecule in the cell membrane (α = 0). As we will show later, anticorrelation between these two (i.e., a negative value of α) can explain a linear dependency between cell size and uptake rate in the reaction-limited region as well.
Noise in particle uptake
An interesting thing to note in Fig. 5 is that there is a high degree of cellular noise in particle uptake in the reaction-limited regime. The noise diminishes gradually with increasing diffusion effect. To investigate the noise further, we raised the intrinsic forward rate constant (kf) in an attempt to drive the system into the diffusion-limited regime. This change in kf led to a reduced noise, as seen in Fig. 6. This suppression of the noise indicates a reduced influence of n on particle uptake in the transport-limited regime. In a purely diffusion-controlled regime, uptake becomes independent of n: (Eq. 17). Therefore, the relationship appears deterministic. On the other hand, based on Eq. 16, the noise in the reaction-controlled regime should vary in proportion to the cellular heterogeneity in n when . This result suggests that the cellular noise in particle uptake may provide insights into the diffusion barrier of the extracellular medium. From such noise, it may be possible to infer whether particle uptake occurred in a reaction- or diffusion-controlled condition.
Figure 6.
Noise characteristics in the diffusion limit. The curves (and their colors) in each panel correspond to those in Fig. 5B, except that the value of the parameter kf is (A) 10 times and (B) 100 times higher than the nominal value (Table 1). To see this figure in color, go online.
Correlating cell-surface transporter density with cell size
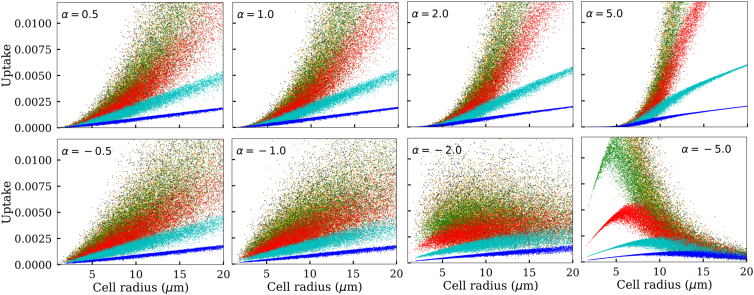
In the previous analyses, we assumed that the cell-surface transporter density is uncorrelated to cell size. As a result, the mean number of transporters per cell was directly proportional to the cell surface area . Here, refers to the mean transporter density excluding the stochastic noise . However, it is possible that varies with r0 because of the following reasons. A growing cell may try to maintain the same rate of uptake per unit of mass (volume). Therefore, the uptake rate per unit area of the plasma membrane of a growing cell may increase in proportion to . Thus, for two cells of radius r0,1 and r0,2, , i.e., ∼ r0. On the other hand, a counterargument may be that decreases with cell size, i.e., the two are anticorrelated. The rationale is that the transcriptional output of a growing cell may not be able to cope up with the growing mass of the cell. Thus, such anticorrelation may actually contain a cell from an abnormally high growth. A third possibility may be that the amount of transporter per cell has nothing to do with cell size and all cells on average express the same number of transporter molecules (except for the stochastic variations). This leads to , i.e., .
To study the above possibilities, we consider , as noted in the model description. Here, α = 0 refers to the nominal case (Figs. 5 and 6). In Fig. 7, we show several hypothetical cases in which α takes different positive and negative values. In these figures, particle uptake rate in the reaction-limited condition is
| (18) |
whereas particle uptake rate in the diffusion-limited condition is
| (19) |
Figure 7.
Predicted correlation between cell size and particle uptake when cell-surface transporter density is a function of cell size. The mean transporter density () varies with cell size according to . The top and bottom panels correspond to positive and negative values of α, respectively, as indicated. Each color represents a distinct particle diffusivity, as in Fig. 5. To see this figure in color, go online.
As seen in the figure, in the positive range of α, the effect of this parameter becomes apparent at α > 1, where uptake increases sharply with cell size under reaction control. In contrast, in the negative range of α, its effect becomes apparent at α < −1.
Notice that, our earlier analysis with α = 0 (Fig. 5) indicated a nonlinear correlation between cell size and particle uptake rate in the reaction-limited regime. However, Fig. 7 suggests that a linear correlation in this regime is possible as well if α is negative and close to −1. The model predicts that the correlation between cell size and uptake is lost when α ≈ −2. Again, at α = −5, the model predicts an optimal cell size for which particle uptake is maximal.
Experiment versus model predictions
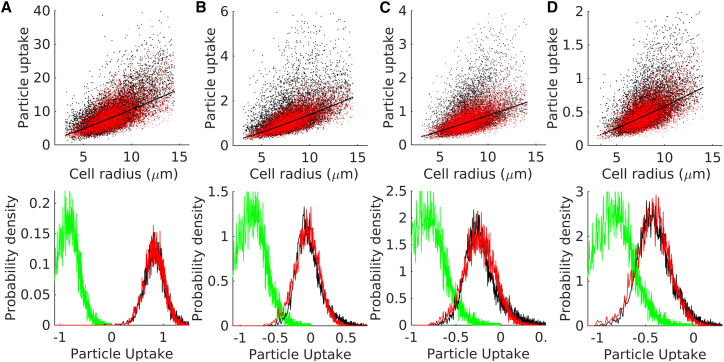
We took four sets of fluorescent nanoparticles of mean diameter 26, 47, 100, and 200 nm, respectively, and analyzed their uptake in MDA-MB 231 cells using the model considering nonzero α. Fig. 8 shows fitting between the experimental data and model predictions for the four different nanoparticle sizes. The model was used to make predictions on particle uptake against each of the measured cell sizes. The predicted particle uptake values were scaled and fitted to the observed (normalized) fluorescence. Fitting was done to capture the following observations: 1) cell-size-dependent particle uptake and associated noise (upper panels in Fig. 8) and 2) cellular distribution of particle uptake (lower panels in Fig. 8). The figure shows good agreements between the experiments and the model. The model parameter values obtained from these fittings are listed in Table 2.
Figure 8.
Nanoparticle uptake by MDA-MB 231 cells. The top panels (scatter plots) show single-cell fluorescence of internalized nanoparticles (black) for four different nanoparticle sizes (diameters): (A) 26 nm, (B) 47 nm, (C) 100 nm, and (D) 200 nm. In the panels, black and red points represent experimental data and model prediction (after fitting), respectively. The solid lines represent the deterministic predictions (σt = 0). The experimental data (fluorescence of cell-internalized particles) are presented after normalizing with a bead fluorescence. The model predictions are scaled with a constant value (free parameter) to fit the normalized fluorescence data. The lower panels (histograms) show the cellular distribution of particle uptake for the four particle sizes. In each panel, black, red, and green refer to the internalized particle fluorescence, the model predicted uptake, and control cell fluorescence, respectively. To see this figure in color, go online.
Table 2.
Parameter Values Estimated by Fitting the Model to the MDA-MB 231 Cell Data
| Particle Size (Diameter) | ||||
|---|---|---|---|---|
| Parameter | 26 nm | 47 nm | 100 nm | 200 nm |
| 0.946a | 0.946a | 0.946a | 0.946a | |
| 0.099a | 0.071a | 0.077a | 0.116a | |
| α | −0.878a | −0.792a | −0.896a | −0.811a |
| kf (μm3 s−1) | 0.495a | 0.079a | 0.160a | 0.269a |
| kr (s−1) | 0.1 | 0.1 | 0.1 | 0.1 |
| k1 (s−1) | 0.02 | 0.02 | 0.02 | 0.02 |
| D (μm2/s) | 16.80 | 9.29 | 4.29 | 2.18 |
The diffusion constants for different particle sizes were estimated from Einstein-Stokes equation. Parameters n, kr, and k1 were constrained to have the same values for all particle sizes.
Values obtained from the fitting. Other values were held fixed.
The data for all four particle types reveals significant noise, indicating uptake occurs in the reaction-limited regime in the cell-culture medium. However, a linear dependency between cell size and the internalized number of nanoparticles is seen for all four particles, thus contradicting the expectation that uptake in the reaction-limited regime should vary in proportion to (Fig. 5). Note that, in Fig. 7, the model predicted that a linear relationship between cell size and particle uptake is possible in the reaction-limited regime if α is negative and falls within a certain range. Our fitting led to α between −0.8 and −0.9 (Table 2). This negative value indicates that the cell-surface density of the trafficking components (clathrin pits or other structures) may decrease with the increasing size of an MDA-MB 231 cell.
From the fitting, we estimated transporter density, μm−2 and its lognormal variance (Table 2). Therefore, a typical MDA-MB 231 cell of radius 8 μm is expected to have 760 transporter molecules in the plasma membrane. As explained before, in our model, a transporter molecule is a hypothetical unit that processes only one particle at a time. Reportedly, clathrin-coated pits play the key role in the uptake of nanoparticles smaller than a few hundred nanometers in size (27). Thus, ignoring other endocytic pathways and assuming 50–150 coated pits per cell (29), an average pit may represent 4–15 transporter molecules. This implies each pit, on average, may handle maximal 4–15 nanoparticles at a time. However, this could be an overestimate given other endocytic pathways may contribute as well. Regardless, our analysis indicates that the endocytic components of an MDA-MB 231 cell can easily be saturated at high enough nanoparticle concentration in the solution, thus leading to a reaction-limited condition.
In the fitting, for all particle sizes, we held k1 and kr fixed at their nominal values (Table 2) because these two parameters are supposed to be cellular properties and hence independent of the size of a particle. The fitting led to different values for the parameter kf depending on the particle size (Table 2). This parameter defines the intrinsic rate of particle capture at the cell plasma membrane. As seen in Table 2, for the two intermediate particle sizes (47 and 100 nm), kf is relatively small. Because different endocytic pathways preferentially mediate uptake for different cargo sizes, it is not surprising that this parameter varies with particle size. However, a definite conclusion in this regard will require an investigation of particle-size-specific involvement of different endocytic pathways.
Note that a slight difference could be seen between our model and the flow cytometer data in Fig. 8. The data reveals considerably larger uptake in a small fraction of cells that fall outside the range of the theoretical values, as evident in the scatter plots. This little discrepancy could also be seen in the lower panels, in which the experimental peaks are little more stretched to the right compared to the theoretical peaks. It is possible that some unknown factors make a small subpopulation significantly more capable. Nevertheless, the model does not incorporate a mechanism to account for these outliers and has limited ability to explain this small discrepancy.
Discussion
In this work, we provided a detailed analysis of nanoparticle uptake at the single-cell level. In our analysis, we mainly focused on two cellular attributes that may jointly determine particle uptake: 1) cell size (r0), and 2) membrane expression (density) of transporter molecules (n). We have shown that a simple scatter plot (Fig. 2) can dissect cellular heterogeneity in particle uptake arising from the joint contributions of these two attributes of a cell. The plot itself reveals how uptake varies with cell size. On the other hand, the noise in the plot reveals cell-to-cell variability in n. Importantly, the noise, even though it originates from n, is tightly coupled to the diffusion barrier of the extracellular medium (Fig. 6). We postulate that such noise in a flow cytometer data may provide information about the level of the transport barrier in the extracellular medium.
Our study shows no noticeable transport effect on particle uptake in a cell-culture medium with water-like viscosity. However, in a in vivo tissue or tumor, the transport effect may be significant. The uptake of nanoparticles by a target (cancer) cell in the tumor interstitial matrix may be governed by the poor effective diffusion in the presence of the nonspecific cells, the dense network of collagen fibers, and other biological barriers (30, 31, 32). In addition, the physiological concentration of nanoparticles in a tissue or tumor could be very small (33), which may also lead to transport-controlled uptake.
Using flow cytometer FSC, we have characterized MDA-MB 231 cell-size distribution, which was further confirmed by analyzing microscopy images. The general notion is that FSC-A may provide an unreliable estimate of cell sizes because the measurement can be influenced by the refractive index of the fluid, intracellular light-absorbing structures, and the design of the FSC-measurement device itself (34, 35). Our analysis shows that FSC provides a slight overestimate of cell size, but it can be pretty accurate in estimating the cell size distribution. A slight shift of the FSC-based cell-size distribution to the left showed an excellent agreement with the actual cell-size distribution obtained from microscopy image analysis (Fig. 1).
By fitting our model to flow cytometer data, we obtained an accurate agreement between the model predictions and the measured particle uptake in MDA-MB 231 cells. Our measurement revealed significant noise in uptake (Fig. 8). The data indicated almost a linear increase in the uptake rate with increase in the cell size (radius). Our model-based analysis of the experimental data suggests that the number of transporter molecules per unit cell membrane may decrease with an increase in the cell size. This phenomenon may be a defining characteristic of cell growth. Cells above a certain size may struggle to maintain uptake through the plasma membrane in proportion to their mass , and this might manifest itself in a reduction in transporter density (7, 8, 9).
In a recent work, Wang et al. (14) reported several findings that are consistent with our experimental data and analysis. The authors reported an approximately liner correlation between nanoparticle uptake and cell radius (Fig. 7, B and C in (14)). In the study, hMSCs were cultured on micropatterened surfaces. The growth (size) of the cells were controlled by the patterns of the surfaces. Consistent with our work, the study also reported that larger cells displayed a reduced level of particle uptake per unit area of the plasma membrane. This observation was attributed to the difference in the stiffness of the cells. The study showed that the larger cells were stiffer compared to their smaller counterparts. Nevertheless, a direct evidence was not established that the stiffness was indeed the reason behind the cell-size-dependent difference in the particle flux across the cell membrane. Our work provides a new perspective to explain these observations. A larger micropatterned cell with an increased surface area may imply a reduced number of transporter molecules per unit area of the plasma membrane. Therefore, the decrease in particle flux may reflect a reduced endocytic activity per unit area of a larger cell. It should be noted that, in our experiments, all cells were grown in a common identical environment (cell-culture medium) unlike in (14), in which micropatterened surfaces were used to direct the cell growth. Our cell sizes reflect the natural heterogeneity in cell growth under a common growth medium. Therefore, although our observations are similar, the uptake behaviors of our cells may not be attributable to their differential stiffness. It would be, however, interesting to investigate whether the naturally grown cells also display similar size-dependent stiffness like the micropatterned cells reported in (14).
Although it was not our focus to study the physicochemical attributes of nanoparticles, our experiments with MDA-MB 231 cells involved nanoparticles of four different sizes (Fig. 8). Our interest in this case was to see if the uptake characteristics could vary based on the size of the particles. Our data revealed no significant qualitative differences among the particles. For all four particle sizes, our experimental data revealed nearly linear correlation between cell size and the amount of particle uptake. The model was also able to accurately describe the uptake data associated with all four particles. However, from the fitting, the intrinsic rate of particle capture (kf) appeared to be different depending on the particle size. This could be due to the fact that particles of different sizes are differentially handled by the endocytic pathways.
Particle uptake at the cellular level is governed by many factors associated with the highly complex endocytic and intracellular trafficking pathways as reviewed in (26). In addition, the diffusion of the transporter molecule or particle-specific receptor proteins in the plasma membrane can influence particle uptake (36). However, in the absence of cell type-specific quantitative information, incorporation of such details entails more parameters and associated uncertainties in a model. Therefore, the net contributions from these individual factors are often homogenized into an effective rate of uptake and the entire uptake process can be simplified into a reaction-diffusion problem (33, 37, 38, 39, 40, 41). In our study, we also ignored the individual factors that are associated with distinct pathways. Instead, we divided the uptake process into two steps. The first step is associated with the diffusion of particles through the external medium, and the second step is particle uptake by a generic transporter molecule in the cell membrane. Incorporation of the detailed molecular mechanisms and individual factors associated with various endocytic mechanisms is beyond the scope of this study.
It should be noted that our model ignores convective transport of nanoparticles. We consider pure diffusion in our system, which is typical for a cell-culture medium. Also, in the dense interstitial matrix of a tumor, convection is usually poor, whereas diffusion serves as the dominant transport mechanism (32). The single-cell nanoparticle uptake characteristics can be more complex in the presence of an advective transport in a biological tissue. A more complex model and experimental investigation are necessary to determine how reaction, diffusion, and advection together may determine cell-size-dependent nanoparticle uptake in in vivo tissue conditions.
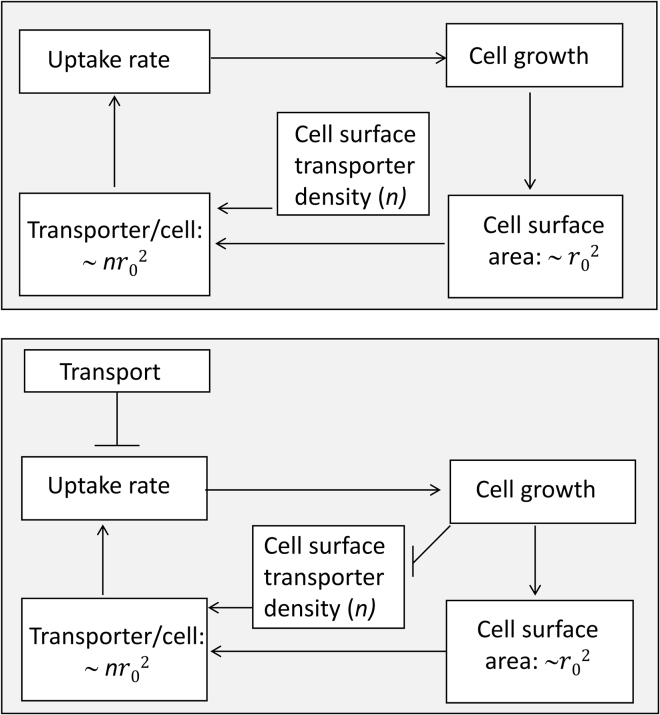
An interesting extension of our study might be to investigate whether the uptake of other external resources, including various nutrients, follows similar behavior described in this study. One of the core findings of this work, that the particle flux (uptake per unit cell surface area) might decrease in a growing cell, provides an interesting possibility. If such behavior applies to some other molecules necessary for cell growth, it may work as a feedback mechanism for limiting cell sizes in different growth environments, as depicted in Fig. 9.
Figure 9.
A possible relationship between cellular uptake of external resources and cell growth. Top: common perception about how cellular uptake might be related to cell size. Bottom: a potential regulation of cell size based on a growing cell’s ability to avail the external resources. An arrow represents a positive influence, and a blunt arrow indicates a negative influence.
Conclusions
Our study emphasizes understanding cellular uptake processes at the single-cell level. The analysis shows that the rate of nanoparticle uptake by single cells is tightly coupled to the cell size as well as the transport barrier of the extracellular medium. Using model predictions and quantitative single-cell analysis, we have shown how the extracellular diffusion and cellular heterogeneities in cell size and endocytic capacities shape the overall nanoparticle uptake behavior of single cells. Although the predictions and analyses provided are in the context of nanoparticle uptake, it may be possible to extend the findings to the cellular uptake of different nutrients and biomolecules as well. However, further investigations are necessary to confirm such a hypothesis.
Author Contributions
J.K. carried out modeling, data analysis, and part of the experiments. M.S. carried out experiments and part of the data analysis. D.B. and S.B. conceptualized and supervised the work. All authors contributed to manuscript preparation and revision.
Acknowledgments
The authors are grateful to Dr. Christopher V. Rao (Professor, Chemical and Biomolecular Engineering, University of Illinois Urbana-Champaign) for his critical and insightful suggestions about this work.
Research presented in this work was supported by the National Science Foundation CBET-CDS&E grant No. 1609642 and the University of Missouri Research Board (UMRB) seed grant.
Editor: James Sneyd.
Footnotes
Jawahar Khetan and Md Shahinuzzaman contributed equally to this work.
Supporting Materials and Methods are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)34456-4.
Supporting Material
References
- 1.Amodeo A.A., Skotheim J.M. Cell-size control. Cold Spring Harb. Perspect. Biol. 2016;8:a019083. doi: 10.1101/cshperspect.a019083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lindemann C., Fiksen Ø., Aksnes D.L. Scaling laws in phytoplankton nutrient uptake affinity. Front. Mar. Sci. 2016;3:26. [Google Scholar]
- 3.Pasciak W.J., Gavis J. Transport limitation of nutrient uptake in phytoplankton1. Limnol. Oceanogr. 1974;19:881–888. [Google Scholar]
- 4.Syková E., Nicholson C. Diffusion in brain extracellular space. Physiol. Rev. 2008;88:1277–1340. doi: 10.1152/physrev.00027.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Florence A.T. “Targeting” nanoparticles: the constraints of physical laws and physical barriers. J. Control. Release. 2012;164:115–124. doi: 10.1016/j.jconrel.2012.03.022. [DOI] [PubMed] [Google Scholar]
- 6.Zhao F., Zhao Y., Zhao Y. Cellular uptake, intracellular trafficking, and cytotoxicity of nanomaterials. Small. 2011;7:1322–1337. doi: 10.1002/smll.201100001. [DOI] [PubMed] [Google Scholar]
- 7.Marshall W.F., Young K.D., Roeder A.H. What determines cell size? BMC Biol. 2012;10:101. doi: 10.1186/1741-7007-10-101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mader S., Windelspecht M. McGraw Hill Education; New York: 2016. Biology. [Google Scholar]
- 9.Biggs A., Rillero P., Zike D. McGraw Hill Education; New York: 2017. Biology: Dynamics of Life. [Google Scholar]
- 10.Marañón E., Cermeño P., Rodríguez J. Unimodal size scaling of phytoplankton growth and the size dependence of nutrient uptake and use. Ecol. Lett. 2013;16:371–379. doi: 10.1111/ele.12052. [DOI] [PubMed] [Google Scholar]
- 11.Aksnes D., Egge J. A theoretical model for nutrient uptake in phytoplankton. Mar. Ecol. Prog. Ser. 1991;70:65–72. [Google Scholar]
- 12.Friebele E., Correll D.L., Faust M.A. Relationship between phytoplankton cell size and the rate of orthophosphate uptake: in situ observations of an estuarine population. Mar. Biol. 1978;45:39–52. [Google Scholar]
- 13.Stolte W., Riegman R. Effect of phytoplankton cell size on transient-state nitrate and ammonium uptake kinetics. Microbiology. 1995;141:1221–1229. doi: 10.1099/13500872-141-5-1221. [DOI] [PubMed] [Google Scholar]
- 14.Wang X., Hu X., Chen G. Influence of cell size on cellular uptake of gold nanoparticles. Biomater. Sci. 2016;4:970–978. doi: 10.1039/c6bm00171h. [DOI] [PubMed] [Google Scholar]
- 15.Verma A., Stellacci F. Effect of surface properties on nanoparticle-cell interactions. Small. 2010;6:12–21. doi: 10.1002/smll.200901158. [DOI] [PubMed] [Google Scholar]
- 16.Nel A.E., Mädler L., Thompson M. Understanding biophysicochemical interactions at the nano-bio interface. Nat. Mater. 2009;8:543–557. doi: 10.1038/nmat2442. [DOI] [PubMed] [Google Scholar]
- 17.Chithrani B.D., Ghazani A.A., Chan W.C. Determining the size and shape dependence of gold nanoparticle uptake into mammalian cells. Nano Lett. 2006;6:662–668. doi: 10.1021/nl052396o. [DOI] [PubMed] [Google Scholar]
- 18.Davda J., Labhasetwar V. Characterization of nanoparticle uptake by endothelial cells. Int. J. Pharm. 2002;233:51–59. doi: 10.1016/s0378-5173(01)00923-1. [DOI] [PubMed] [Google Scholar]
- 19.He C., Hu Y., Yin C. Effects of particle size and surface charge on cellular uptake and biodistribution of polymeric nanoparticles. Biomaterials. 2010;31:3657–3666. doi: 10.1016/j.biomaterials.2010.01.065. [DOI] [PubMed] [Google Scholar]
- 20.Huang X., Teng X., He J. The effect of the shape of mesoporous silica nanoparticles on cellular uptake and cell function. Biomaterials. 2010;31:438–448. doi: 10.1016/j.biomaterials.2009.09.060. [DOI] [PubMed] [Google Scholar]
- 21.Fröhlich E. The role of surface charge in cellular uptake and cytotoxicity of medical nanoparticles. Int. J. Nanomedicine. 2012;7:5577–5591. doi: 10.2147/IJN.S36111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pelaz B., del Pino P., Parak W.J. Surface functionalization of nanoparticles with polyethylene glycol: effects on protein adsorption and cellular uptake. ACS Nano. 2015;9:6996–7008. doi: 10.1021/acsnano.5b01326. [DOI] [PubMed] [Google Scholar]
- 23.Gratton S.E., Ropp P.A., DeSimone J.M. The effect of particle design on cellular internalization pathways. Proc. Natl. Acad. Sci. USA. 2008;105:11613–11618. doi: 10.1073/pnas.0801763105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rejman J., Oberle V., Hoekstra D. Size-dependent internalization of particles via the pathways of clathrin- and caveolae-mediated endocytosis. Biochem. J. 2004;377:159–169. doi: 10.1042/BJ20031253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang S., Li J., Suresh S. Size-dependent endocytosis of nanoparticles. Adv. Mater. 2009;21:419–424. doi: 10.1002/adma.200801393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shang L., Nienhaus K., Nienhaus G.U. Engineered nanoparticles interacting with cells: size matters. J. Nanobiotechnology. 2014;12:5. doi: 10.1186/1477-3155-12-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Harush-Frenkel O., Debotton N., Altschuler Y. Targeting of nanoparticles to the clathrin-mediated endocytic pathway. Biochem. Biophys. Res. Commun. 2007;353:26–32. doi: 10.1016/j.bbrc.2006.11.135. [DOI] [PubMed] [Google Scholar]
- 28.Kafshgari M.H., Harding F.J., Voelcker N.H. Insights into cellular uptake of nanoparticles. Curr. Drug Deliv. 2015;12:63–77. doi: 10.2174/1567201811666140821110631. [DOI] [PubMed] [Google Scholar]
- 29.Ehrlich M., Boll W., Kirchhausen T. Endocytosis by random initiation and stabilization of clathrin-coated pits. Cell. 2004;118:591–605. doi: 10.1016/j.cell.2004.08.017. [DOI] [PubMed] [Google Scholar]
- 30.Netti P.A., Berk D.A., Jain R.K. Role of extracellular matrix assembly in interstitial transport in solid tumors. Cancer Res. 2000;60:2497–2503. [PubMed] [Google Scholar]
- 31.Jain R.K., Stylianopoulos T. Delivering nanomedicine to solid tumors. Nat. Rev. Clin. Oncol. 2010;7:653–664. doi: 10.1038/nrclinonc.2010.139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ramanujan S., Pluen A., Jain R.K. Diffusion and convection in collagen gels: implications for transport in the tumor interstitium. Biophys. J. 2002;83:1650–1660. doi: 10.1016/S0006-3495(02)73933-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Islam M.A., Barua S., Barua D. A multiscale modeling study of particle size effects on the tissue penetration efficacy of drug-delivery nanoparticles. BMC Syst. Biol. 2017;11:113. doi: 10.1186/s12918-017-0491-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Shapiro H.M. John Wiley & Sons, Inc.; Hoboken, NJ: 2005. Practical Flow Cytometry. [Google Scholar]
- 35.Tzur A., Moore J.K., Kirschner M.W. Optimizing optical flow cytometry for cell volume-based sorting and analysis. PLoS One. 2011;6:e16053. doi: 10.1371/journal.pone.0016053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Li L., Zhang Y., Wang J. Effects of ligand distribution on receptor-diffusion-mediated cellular uptake of nanoparticles. R. Soc. Open Sci. 2017;4:170063. doi: 10.1098/rsos.170063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Batsilas L., Berezhkovskii A.M., Shvartsman S.Y. Stochastic model of autocrine and paracrine signals in cell culture assays. Biophys. J. 2003;85:3659–3665. doi: 10.1016/S0006-3495(03)74783-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Berezhkovskii A.M., Makhnovskii Y.A., Shvartsman S.Y. Boundary homogenization for trapping by patchy surfaces. J. Chem. Phys. 2004;121:11390–11394. doi: 10.1063/1.1814351. [DOI] [PubMed] [Google Scholar]
- 39.Monine M.I., Berezhkovskii A.M., Shvartsman S.Y. Ligand accumulation in autocrine cell cultures. Biophys. J. 2005;88:2384–2390. doi: 10.1529/biophysj.104.051425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.King C.C., Brown A.A., Beckman S.P. Modeling of reaction-diffusion transport into a core-shell geometry. J. Theor. Biol. 2018;460:204–208. doi: 10.1016/j.jtbi.2018.09.026. [DOI] [PubMed] [Google Scholar]
- 41.Barua D. A model-based analysis of tissue targeting efficacy of nanoparticles. J. R. Soc. Interface. 2018;15:20170787. doi: 10.1098/rsif.2017.0787. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.