Statistical Mechanics of an Elastically Pinned Membrane: Static Profile and Correlations

Abstract

The relation between thermal fluctuations and the mechanical response of a free membrane has been explored in great detail, both theoretically and experimentally. However, understanding this relationship for membranes locally pinned by proteins is significantly more challenging. Given that the coupling of the membrane to the cell cytoskeleton, to the extracellular matrix, and to other internal structures is crucial for the regulation of a number of cellular processes, understanding the role of the pinning is of great interest. In this manuscript, we consider a single protein (elastic spring of a finite rest length) pinning a membrane modeled in the Monge gauge. First, we determine the Green’s function for the system and complement this approach by the calculation of the mode-coupling coefficients for the plane wave expansion and the orthonormal fluctuation modes, in turn building a set of tools for numerical and analytic studies of a pinned membrane. Furthermore, we explore static correlations of the free and the pinned membrane, as well as the membrane shape, showing that all three are mutually interdependent and have an identical long-range behavior characterized by the correlation length. Interestingly, the latter displays a nonmonotonic behavior as a function of membrane tension. Importantly, exploiting these relations allows for the experimental determination of the elastic parameters of the pinning. Last but not least, we calculate the interaction potential between two pinning sites and show that even in the absence of the membrane deformation, the pinnings will be subject to an attractive force because of changes in membrane fluctuations.

Introduction

Most living cells and a number of their internal organelles are bounded by membranes, which are composed primarily of phospholipids and proteins. The latter, in selected cases, are designed to interact with neighboring structures, thereby pinning the membrane. As such, protein complexes become spatially coordinated, which has important consequences for the structural integrity of cells. A typical instance of such pinning is found in red blood cells, in which the plasma membrane couples to the underlying spectrin network (1), although in this case, additional forces associated with the soft scaffold will play a role. Another example is the pinning of the membrane to stiffer scaffolds such as actin. This affects a number of cellular functions (2) because it allows for the transmission of force (3), for example, during cell adhesion. In this case, proteins such as integrins or cadherins on the plasma membrane associate into supramolecular ensembles, binding the membrane to the cytoskeleton in the cell interior and, simultaneously, to the extracellular matrix or another cell (4). Similarly, inside the cell—for example, on the nuclear envelope—the cytoskeleton again couples to the external nuclear membrane by nesprins, whereas toward the interior, protein p58 serves as a membrane attachment site for the nuclear lamina by acting as a specific receptor for lamin B (5). All these couplings regulate the mechanical state of the cell, which in turn affects the cell motility, division rate, proliferation, mechanosensitivity, and a number of other processes (4). Hence, understanding the principles of protein-mediated interactions between membranes and the surrounding scaffolds is one of the key problems in mechanobiology.

Modeling pinned membranes—be it the adhesion process (6, 7, 8), in the context of the interactions with the cytoskeleton (9), or the nuclear envelope (10)—requires defining the force response at the single pinning site. Although different models have been used in the literature (11, 12, 13), the linear relation, in which the protein attachment is described by a harmonic spring of a finite rest length, seems to capture a number of biological situations (14, 15, 16). In particular, such models have been used for more than two decades to study the interplay between the pinning sites and the forces induced by the cytoskeleton, with the assumption that the role of the membrane is merely to provide spatial coordination to the proteins. However, it is becoming more obvious that the membrane itself is not a simple spectator but can act as a regulatory component (17, 18) because it also produces forces (19). Nonetheless, because the membrane is in principle very soft, the pinning will have appreciable effects on the membrane itself.

Already, in the early theoretical works, it was demonstrated that protein-mediated attachments of the membrane affect its shape and fluctuations (11, 20, 21), a fact that was used to identify binding sites in cells and vesicles (22, 23, 24). Subsequent simulations and analytical modeling showed that the mean membrane shape and roughness depend nontrivially on the instantaneous bond density (15, 25, 26, 27, 28, 29, 30, 31). Alternative approaches showed, furthermore, that pinnings that experience strong frictional coupling in the membrane introduce corrections to the membrane tension (32). Polymeric anchors, on the other hand, were found to be responsible for the rescaling of the bending stiffness of the composite membrane in a mode-dependent fashion (33). Another useful strategy relied on finding appropriate approximations to homogenize the pinning sites. As a result, a family of effective potentials that predict static properties of fluctuations were suggested in different regimes of fluctuation strength (34, 35, 36, 37).

Many studies showed that membrane fluctuations depend on the properties of the pinning itself, such as the pinning’s length and mechanical stiffness (18, 21, 38, 39, 40, 41, 42, 43). However, efforts to understand this coupling theoretically are scarce (13, 15, 36, 37, 44, 45). The difficulty lies in the pinning-induced coupling of plane wave modes or spherical harmonics (46, 47), which are otherwise independent in free membranes. The need to circumvent these technical problems led to the development of several computational approaches, which used the conveniences of Fourier transforms and plane-wave-basis sets (8, 28, 48) and allowed for the numerical evaluation of mode-coupling effects (31) or alternative basis sets (12). Ultimately, these extensive simulations pointed to interesting many-body effects, which, however, could be distinguished from two-body interactions only in very limited regimes.

In this manuscript, we provide a full analysis of static properties of a membrane pinned by an elastic spring (Fig. 1). We first calculate the static Green’s function for the pinned membrane (Green’s Function Approach), which is the working horse of analytic calculations. Given that they were not previously reported in the literature, we also provide explicit expressions for the orthonormal modes (Appendix A) and the mode-coupling amplitudes for the plane wave expansion (Appendix B), both of which may be particularly useful for numerical calculations and the development of simulations and show that they yield equivalent description as the Green’s function approach. We use the Green’s function to provide a comprehensive description of static properties of a pinned membrane in the full parameter range (Properties of the Mean Shape and the Correlation Function), focusing on the membrane’s mean shape, the fluctuation amplitude, and the two-point spatial correlation function. Besides recovering the limits known in the literature for tensionless membranes and rigid pinning, our analysis of the correlation length (Effect of the Membrane Tension on the Long-Range Behavior of the Shape and Correlation Function) elucidates the interplay between the membrane rigidity and tension, the strength of the nonspecific potential, and the pinning elasticity. In the final Membrane-Mediated Interactions Between Two Pinnings, we calculate explicitly and then analyze in detail the interaction potential and the force between two pinning sites.

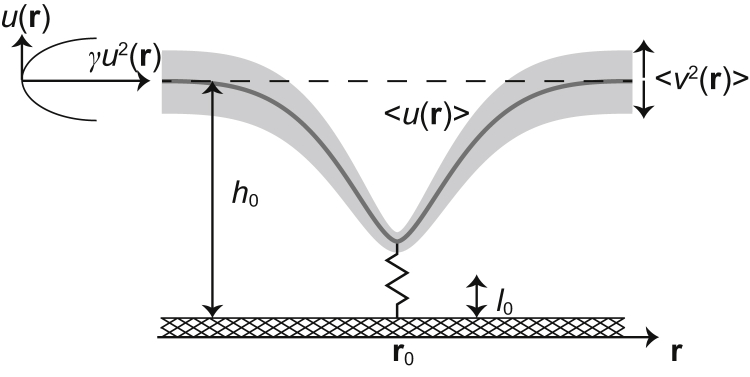
Figure 1.

Mean shape $\langle u\left(\mathbf{r}\right)\rangle$ (gray line) and the spatially dependent fluctuation amplitude $\langle v^2\left(\mathbf{r}\right)\rangle$ (gray shaded area) of a membrane residing in a harmonic potential of strength γ at h₀ separation from a flat substrate and pinned by an elastic spring of rest length l₀.

Methods

Theoretical setup

The system (Fig. 1) consists of one flexible pinning site (harmonic spring of an elastic constant λ and rest length l₀, placed at the lateral position r₀) that confines fluctuations of a tensed membrane (bending rigidity κ, tension σ). The membrane resides in the minimum of a harmonic nonspecific potential (strength γ) at a height h₀ above the substrate, except near r₀, where it could be displaced by the pinning.

The membrane shape is parametrized in the linearized Monge gauge (49) such that u(r) denotes deviations from the shape of a flat membrane positioned in the minimum of the nonspecific potential along the lateral position r. Because pinnings typically introduce membrane displacements from the minimum (order of magnitude of 1–10 nm) (18, 50) that are small in comparison with the correlation length of the membrane (order of 100 nm), we use the linearized Hamiltonian

$$\mathcal{H}=\underset{A}{\int }\text{d}\mathbf{r}\left[\frac{\kappa }{2}{\left({\mathit{\nabla }}^{2}u\left(\mathbf{r}\right)\right)}^2+\frac{\sigma }{2}{\left(\mathit{\nabla }u\left(\mathbf{r}\right)\right)}^2+\frac{\gamma }{2}{\left(u\left(\mathbf{r}\right)\right)}^2+\frac{1}{2}\lambda {\left(u\left(\mathbf{r}\right)-\left(l_0-h_0\right)\right)}^2\delta \left(\mathbf{r}-{\mathbf{r}}_0\right)\right]$$ (1)

to describe the system. The first two terms in the integral on the right-hand side comprise the Helfrich Hamiltonian (51) for a bendable, pretensed membrane that resides in a nonspecific potential (third term). The energetic contribution of a harmonic spring for the pinning is represented by the fourth term, which includes a δ function δ(r) positioning the pinning, as further discussed in Supporting Methods, Section SI. The integration goes over the projected membrane surface A. Here and throughout the study, the energy scale k_BT (with Boltzmann constant k_B and absolute temperature T) is set to unity. The validity of this Hamiltonian has been recently discussed in detail in (52), in which a reasonable agreement between numerically calculated and experimentally measured correlations and shapes has been obtained.

With $u\left(\mathbf{r}\right)=\langle u\left(\mathbf{r}\right)\rangle +v\left(\mathbf{r}\right)$, minimization of the Hamiltonian (Eq. 1) provides the equation for the mean shape $\langle u\left(\mathbf{r}\right)\rangle$

$$\left[\kappa {\mathit{\nabla }}^4-\sigma {\mathit{\nabla }}^2+\gamma +\lambda \delta \left(\mathbf{r}-{\mathbf{r}}_0\right)\right]\langle u\left(\mathbf{r}\right)\rangle =\lambda \left(l_0-h_0\right)\delta \left(\mathbf{r}-{\mathbf{r}}_0\right).$$ (2)

The fluctuations v(r) can be obtained from diagonalizing the second variation of the Hamiltonian, which leads to the eigenequation

$$\left[\kappa {\mathit{\nabla }}^4-\sigma {\mathit{\nabla }}^2+\gamma +\lambda \delta \left(\mathbf{r}-{\mathbf{r}}_0\right)\right]{\psi }_i\left(\mathbf{r}\right)=E_i{\psi }_i\left(\mathbf{r}\right),$$ (3)

the latter containing the same operator as the shape Eq. 2. By expanding the fluctuations in these eigenmodes (see Appendix A),

$$v\left(\mathbf{r}\right)=\sum _i{a}_i{\psi }_i\left(\mathbf{r}\right),$$ (4)

and using the equipartition theorem

$$\langle a_i{a}_j\rangle =\frac{k_{\text{B}}T}{E_i}{\delta }_{ij},$$ (5)

we find the spatial two-point correlation function

$$\langle v\left(\mathbf{r}\right)v\left(\mathbf{r}\text{'}\right)\rangle =\sum _i\frac{{\psi }_i\left(\mathbf{r}\right){\psi }_i^{\ast }\left(\mathbf{r}\text{'}\right)}{E_i}.$$ (6)

We assume that the probability for membrane fluctuations with an amplitude larger than h₀ is small such that these configurations will not contribute significantly to the average properties of the membrane profile. With this assumption, the details of these configurations, which would involve a nonpermeable boundary at the substrate, are not important, and we can instead deal with a simpler problem in which the substrate is completely permeable to the membrane. This approximation is satisfied if the protein that pins the membrane has a finite size (larger than the fluctuation amplitude of the membrane but smaller than h₀), which is, in experimental systems, satisfied by the self-adjustment of the effective nonspecific potential. Namely, if the proteins or the fluctuation amplitude of the membrane were larger than h₀, this would renormalize the nonspecific potential and move the minimum away from the substrate (hence, h₀ would be increased, and the curvature of the minimum, in our model captured by γ, would be changed) such that the required condition is recovered before the pinning. Practically, in the calculations, this assumption is implied by having no boundary conditions on the amplitude of the membrane fluctuations.

Green’s function approach

Green’s function for the free membrane

Before addressing the problem of a pinned membrane, it is instructive to notice that the Green’s function g_f(r|r′) for the free membrane (λ = 0) is defined by

$$\left[\kappa {\mathit{\nabla }}^4-\sigma {\mathit{\nabla }}^2+\gamma \right]g_f\left(\mathbf{r}|{\mathbf{r}}^{\prime }\right)=\delta \left(\mathbf{r}-{\mathbf{r}}^{\prime }\right).$$ (7)

It is translationally invariant (g_f(r|r′) = g_f(r − r′)) and can be expressed as

$$g_f\left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)=\frac{1}{{\left(2\pi \right)}^2}\underset{{\mathbb{R}}^2}{\int }d\mathbf{k}\frac{e^{i\mathbf{k}\left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)}}{\kappa k^4+\sigma k^2+\gamma }.$$ (8)

The solution of the integral on the right-hand side of Eq. 8 is given in (53) and is a combination of modified Bessel functions of the second kind K₀

$$g_f\left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)=\frac{K_0\left(a_{-}|\mathbf{r}-{\mathbf{r}}^{\prime }|\right)-K_0\left(a_{+}|\mathbf{r}-{\mathbf{r}}^{\prime }|\right)}{2\pi \sigma \sqrt{1-{\left(\frac{{\lambda }_{\text{m}}^0}{4\sigma }\right)}^2}}.$$ (9)

Here,

$${\lambda }_{\text{m}}^0=8\sqrt{\kappa \gamma }$$ (10)

and the coefficients a_± are given in the form

$$a_{\pm }=\frac{1}{{\xi }_0}{\left[\frac{4\sigma }{{\lambda }_{\text{m}}^0}\left(1\pm \sqrt{1-{\left(\frac{{\lambda }_{\text{m}}^0}{4\sigma }\right)}^2}\right)\right]}^{1/2},$$ (11)

with

$${\xi }_0=\sqrt[4]{\kappa /\gamma }.$$ (12)

We note that the Green’s function Eq. 9 is real even if a_± are complex numbers.

As for any quadratic integral kernel, the Green’s functions g_f(r − r′) and, respectively, g_f(0) are associated with the spatial correlation function $\langle v_f\left(\mathbf{r}\right)v_f\left({\mathbf{r}}^{\prime }\right)\rangle$ and the mean-square fluctuation amplitude $\langle v_f^2\left(\mathbf{r}\right)\rangle$ of the free membrane, initially calculated by several groups (38, 54, 55, 56). The later is commonly denoted by 1/λ_m (8, 18, 44). Hence,

$$g_f\left(0\right)=\frac{1}{{\lambda }_m}=\frac{\text{arctan}\left(\sqrt{{\left(\frac{{\lambda }_{\text{m}}^0}{4\sigma }\right)}^2-1}\right)}{2\pi \sigma \sqrt{{\left(\frac{{\lambda }_{\text{m}}^0}{4\sigma }\right)}^2-1}},$$ (13)

which, for a tensionless case (57), simplifies to

$$g_f{\left(0\right)}_{|\sigma =0}=\frac{1}{{\lambda }_{\text{m}}^0}.$$ (14)

Under this condition, Eq. 9 adopts the well-known form (21, 56)

$$g_f{\left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)}_{|\sigma =0}=-\frac{4}{\pi {\lambda }_{\text{m}}^0}{\text{kei}}_0\left(\frac{|\mathbf{r}-{\mathbf{r}}^{\prime }|}{{\xi }_0}\right),$$ (15)

with kei₀ being the Kelvin function and ξ₀ being the lateral correlation length of the free tensionless membrane given by Eq. 12.

Green’s function for the pinned membrane

The Green’s function g(r|r′) providing the response of a membrane at the position r because of a disturbance at the position r′ is defined as

$$\left[\kappa {\mathit{\nabla }}^4-\sigma {\mathit{\nabla }}^2+\gamma +\lambda \delta \left(\mathbf{r}-{\mathbf{r}}_0\right)\right]g\left(\mathbf{r}|{\mathbf{r}}^{\prime }\right)=\delta \left(\mathbf{r}-{\mathbf{r}}^{\prime }\right).$$ (16)

With the use of Eq. 7, Eq. 16 can be recast as

$$\left[\kappa {\mathit{\nabla }}^4-\sigma {\mathit{\nabla }}^2+\gamma \right]\left[g\left(\mathbf{r}|{\mathbf{r}}^{\prime }\right)+\lambda g_f\left(\mathbf{r}|{\mathbf{r}}_0\right)g\left({\mathbf{r}}_0|{\mathbf{r}}^{\prime }\right)-g_f\left(\mathbf{r}|{\mathbf{r}}^{\prime }\right)\right]=0,$$ (17)

which can be generally valid only if the second bracket identically vanishes. Consequently,

$$g\left(\mathbf{r}|{\mathbf{r}}^{\prime }\right)=g_f\left(\mathbf{r}|{\mathbf{r}}^{\prime }\right)-\lambda g_f\left(\mathbf{r}|{\mathbf{r}}_0\right)g\left({\mathbf{r}}_0|{\mathbf{r}}^{\prime }\right).$$ (18)

Setting r = r₀ in Eq. 18 provides

$$g\left({\mathbf{r}}_0|{\mathbf{r}}^{\prime }\right)=\frac{g_f\left({\mathbf{r}}_0|{\mathbf{r}}^{\prime }\right)}{1+\lambda g_f\left({\mathbf{r}}_0|{\mathbf{r}}_0\right)}=\frac{{\lambda }_{\text{m}}}{\lambda +{\lambda }_{\text{m}}}{g}_f\left({\mathbf{r}}_0|{\mathbf{r}}^{\prime }\right),$$ (19)

which, upon reinsertion into Eq. 18, gives rise to the Green’s function for the pinned membrane

$$g\left(\mathbf{r}|{\mathbf{r}}^{\prime }\right)=g_f\left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)-\frac{\lambda {\lambda }_{\text{m}}}{\lambda +{\lambda }_{\text{m}}}{g}_f\left(\mathbf{r}-{\mathbf{r}}_0\right)g_f\left({\mathbf{r}}_0-{\mathbf{r}}^{\prime }\right).$$ (20)

Although g(r|r′) is comprised of the translationally invariant g_f(r − r′), it itself is not generally translationally invariant.

Representing shape and fluctuations

By construction, g(r|r₀) differs only by a prefactor from the solution of the shape Eq. 2

$$\langle u\left(\mathbf{r}\right)\rangle =\lambda \left(l_0-h_0\right)g\left(\mathbf{r}|{\mathbf{r}}_0\right).$$ (21)

Combining Eqs. 19 and 21 gives the mean shape

$$\langle u\left(\mathbf{r}\right)\rangle =\frac{\lambda {\lambda }_{\text{m}}}{\lambda +{\lambda }_{\text{m}}}\left(l_0-h_0\right)g_f\left(\mathbf{r}-{\mathbf{r}}_0\right).$$ (22)

As shown previously (15, 44), in the tensionless case, combining Eqs. 15 and 22 yields

$${\langle u\left(\mathbf{r}\right)\rangle }_{|\sigma =0}=-\frac{4}{\pi }\frac{\lambda }{\lambda +{\lambda }_m^0}\left(l_0-h_0\right){\text{kei}}_0\left(\frac{|\mathbf{r}-{\mathbf{r}}_0|}{{\xi }_0}\right),$$ (23)

which is a function of the kei function, as expected for the differential operator of the shape equation that is bilaplacian plus a constant (58, 59). In the limit of an infinitely stiff pinning λ → ∞, Eq. 23 reproduces the result obtained in (21).

By comparing the bilinear expansion of the Green’s function in the eigenfunctions ψ_j (Eq. 3)

$$g\left(\mathbf{r}|{\mathbf{r}}^{\prime }\right)=\sum _j\frac{{\psi }_j\left(\mathbf{r}\right){\psi }_j^{\ast }\left({\mathbf{r}}^{\prime }\right)}{E_j}$$ (24)

and Eq. 6, we find

$$\langle v\left(\mathbf{r}\right)v\left({\mathbf{r}}^{\prime }\right)\rangle =g\left(\mathbf{r}|{\mathbf{r}}^{\prime }\right),$$ (25)

where the factor k_BT = 1 on the right-hand side is implicit. Hence,

$$\langle v\left(\mathbf{r}\right)v\left({\mathbf{r}}^{\prime }\right)\rangle =g_f\left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)-\frac{\lambda {\lambda }_{\text{m}}}{\lambda +{\lambda }_{\text{m}}}{g}_f\left(\mathbf{r}-{\mathbf{r}}_0\right)g_f\left({\mathbf{r}}_0-{\mathbf{r}}^{\prime }\right).$$ (26)

Naturally, by setting r′ = r in Eq. 26, we obtain the fluctuation amplitude

$$\langle v^2\left(\mathbf{r}\right)\rangle =\frac{1}{{\lambda }_{\text{m}}}-\frac{\lambda {\lambda }_{\text{m}}}{\lambda +{\lambda }_{\text{m}}}{g}_f^2\left(\mathbf{r}-{\mathbf{r}}_0\right),$$ (27)

with

$$\langle v^2\left({\mathbf{r}}_0\right)\rangle =\frac{1}{\lambda +{\lambda }_{\text{m}}}.$$ (28)

The same result can be obtained by calculating the eigenfunctions ψ_j(r) for a system with a single pinning (see Appendix A.1)

$${\psi }_m\left(\mathbf{r},q\right)=\frac{i^m{e}^{im\varphi }}{\sqrt{\left(1+{\delta }_{m0}{\left(\text{Π}\left(q\right)\right)}^2\right)}}\left[J_m\left(qr\right)+{\delta }_{m0}\text{Π}\left(q\right)\left(Y_m\left(qr\right)+\frac{2}{\pi }{K}_m\left(\sqrt{q^2+\frac{\sigma }{\kappa }}r\right)\right)\right]$$ (29)

and using Eq. 24 to obtain the Green’s function (see Appendix A.2).

Results

Properties of the mean shape and the correlation function

Although the previous sections reveal the formal framework describing the effect of the pinning on the fluctuations of the membrane, several results warrant further discussion. Specifically, inserting the solution for the mean shape Eq. 22 into the Hamiltonian Eq. 1 determines the total elastic energy of the average configuration of the system (pinning and membrane):

$$\mathcal{H}\left[\langle u\left(\mathbf{r}\right)\rangle \right]=\frac{1}{2}\frac{\lambda {\lambda }_{\text{m}}}{\lambda +{\lambda }_{\text{m}}}{\left(h_0-l_0\right)}^2\equiv \frac{1}{2}\mathcal{K}{\left(h_0-l_0\right)}^2.$$ (30)

Equation 30 shows that the deformation energy increases quadratically with the height separation between the free membrane and the pinning, whereas it vanishes for h₀ = l₀ as described previously (15, 60). The prefactor $\mathcal{K}$ is an effective spring constant made up of two “springs” (the membrane and the pinning) connected in series, with λ_m being the membrane spring constant. From this point of view, $\mathcal{K}$ can be seen as the effective elastic constant of the system (8, 18, 44).

The quadratic nature of Eq. 30 is consistent with the quadratic form of the Hamiltonian Eq. 1 and the “local” nature of the pinning. A further consequence is the linear relation between the mean shape and the correlation function from the pinning site

$$\langle u\left(\mathbf{r}\right)\rangle =-\lambda \left(h_0-l_0\right)\langle v\left(\mathbf{r}\right)v\left({\mathbf{r}}_0\right)\rangle ,$$ (31)

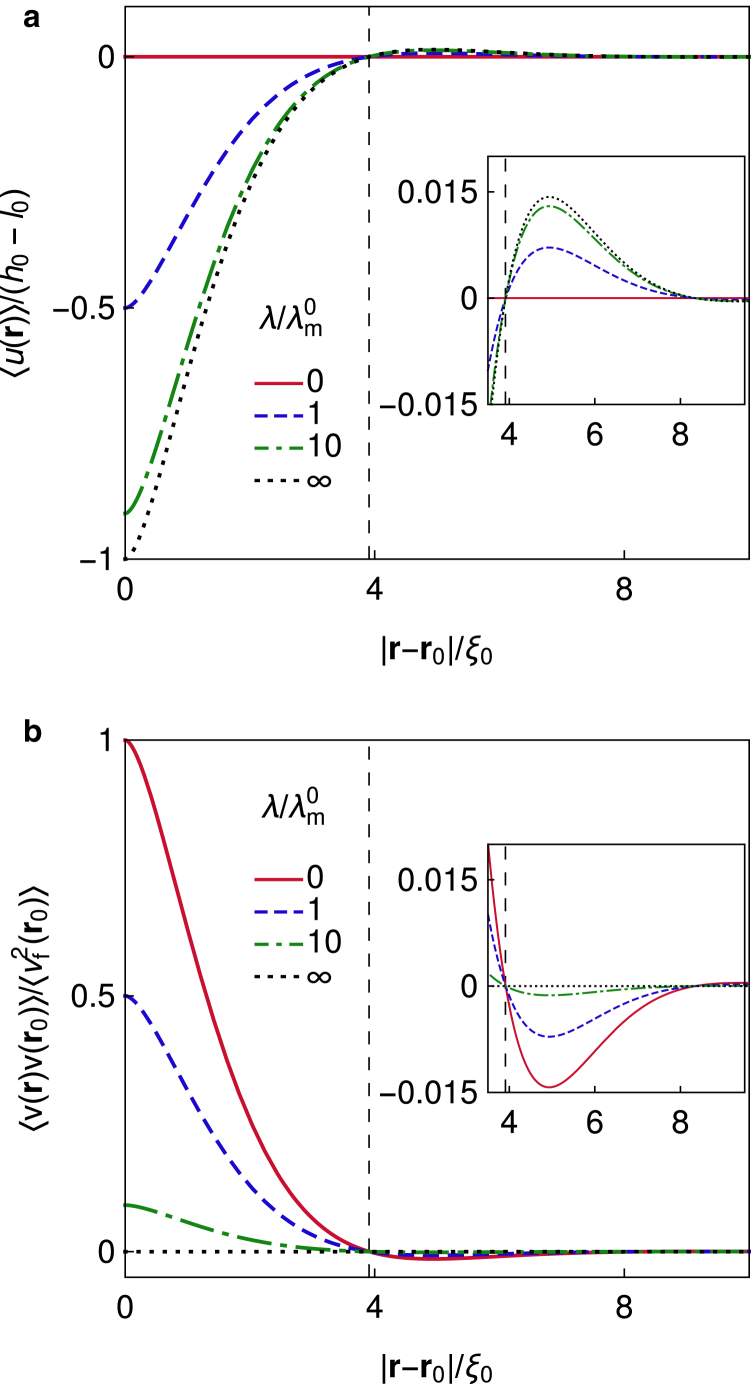
which emerges by inspection of Eqs. 21 and 25. Here, the spatially independent prefactor has a form of a force on a harmonic spring. As a result, both the shape and the correlation function have the same features, but because of a minus sign on the left-hand side of Eq. 31, the trends are opposite. For instance, the well-documented overshoot of the membrane shape (15, 21, 59) at distances of a couple of correlation lengths from the pinning is reflected in the anticorrelations in the same range (Fig. 2). Likewise, the displacement of the mean shape from the minimum of the nonspecific potential increases with the increased pinning stiffness λ (Fig. 2 a), whereas the amplitude of the pinning site correlation $\langle v\left(\mathbf{r}\right)v\left({\mathbf{r}}_0\right)\rangle$ decreases (Fig. 2 b).

Figure 2.

Spatial dependence of the static characteristics of the membrane for varying pinning stiffness λ. (a) The mean shape given by Eq. 22 and (b) the correlation function extracted from Eq. 33 show the same properties. The overshoots in the shape coincide with anticorrelations presented in the insets. Note that a more conventional parametrization of the mean shape in terms of height above the substrate is trivially obtained with $\langle h\left(\mathbf{r}\right)\rangle =h_0+\langle u\left(\mathbf{r}\right)\rangle$. Parameters: κ = 20 k_BT, σ = 10⁻²⁰k_BT/nm², γ = 3 × 10⁻⁷k_BT/nm⁴, and h₀ − l₀ = 1 nm. To see this figure in color, go online.

Interestingly, following Eqs. 19 and 22, the correlation function and the mean shape can also be expressed in terms of the correlation function for the free membrane

$$\langle u\left(\mathbf{r}\right)\rangle =-\mathcal{K}\left(h_0-l_0\right)\langle v_f\left(\mathbf{r}\right)v_f\left({\mathbf{r}}_0\right)\rangle ,$$ (32)

which emerges from the proportionality between the pinned- and the free-membrane correlation functions

$$\frac{\langle v\left(\mathbf{r}\right)v\left({\mathbf{r}}_0\right)\rangle }{\langle v_f\left(\mathbf{r}\right)v_f\left({\mathbf{r}}_0\right)\rangle }=\frac{\langle v^2\left({\mathbf{r}}_0\right)\rangle }{\langle v_f^2\left({\mathbf{r}}_0\right)\rangle }=\frac{{\lambda }_{\text{m}}}{\lambda +{\lambda }_{\text{m}}}.$$ (33)

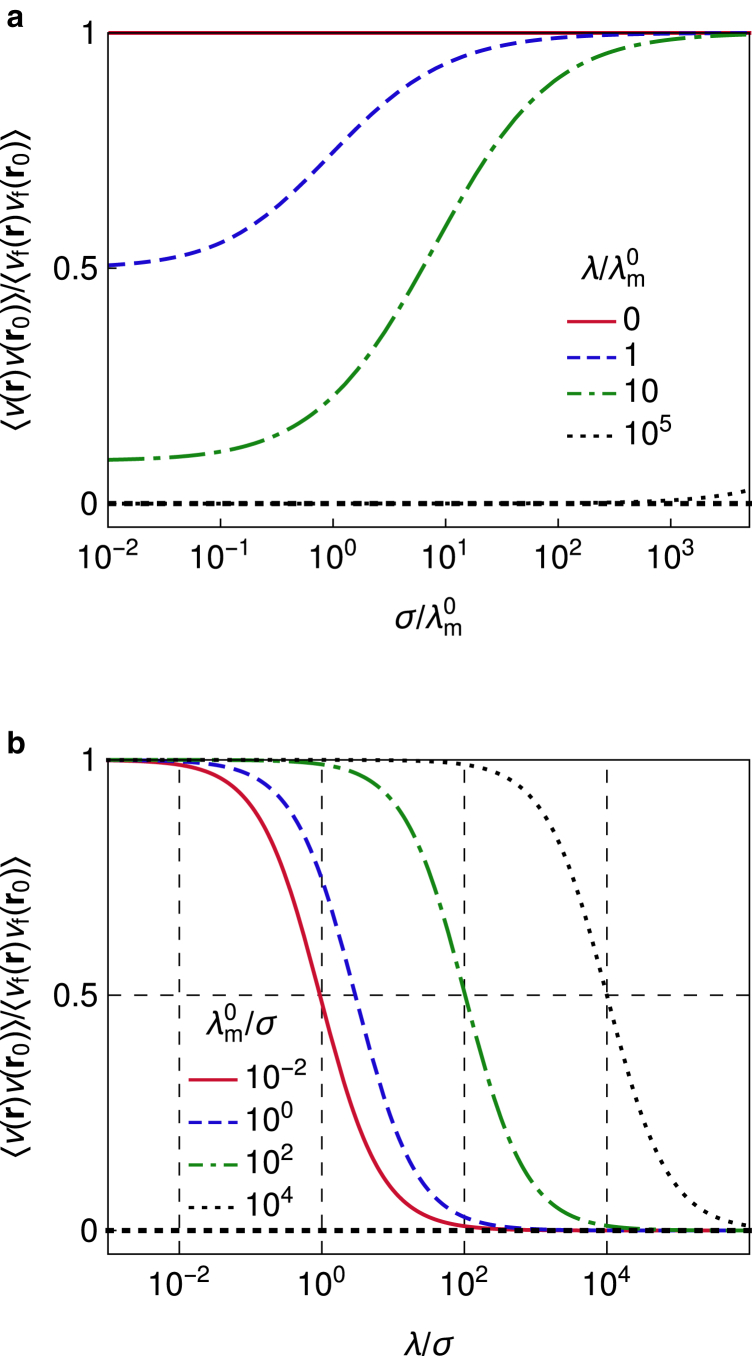
This result clearly captures the interplay between the pinning stiffness λ and the parameters of the membrane (σ and ${\lambda }_{\text{m}}^0$) which are combined in λ_m. If $\lambda \ll {\lambda }_{\text{m}}$, the pinning does not affect membrane fluctuations, whereas if $\lambda \gg {\lambda }_{\text{m}}$, fluctuations at the pinning are completely suppressed, and small changes in λ do not affect the system behavior. However, in the regime λ ≈ λ_m, fluctuations can change noticeably, even for small changes in the pinning stiffness (Fig. 3). Low-tensed membranes will show such sensitivity if $\lambda \approx {\lambda }_{\text{m}}^0$ (large λ/σ in Fig. 3 b), whereas highly tensed membranes do so if $\lambda \gg {\lambda }_{\text{m}}^0$ (small λ/σ in Fig. 3 b). Moreover, because the decay of correlations from the pinning site is independent of h₀ and l₀ (i.e., from the mean deformation), elastic properties of the pinning can be extracted directly from the change in the fluctuation amplitude between the pinned and the free states of the membrane.

Figure 3.

Effect of the pinning on the membrane fluctuations (Eq. 33) (a) varying σ and λ and (b) varying λ and ${\lambda }_{\text{m}}^0$. To see this figure in color, go online.

Another interesting relation is the one between the spatially dependent mean-square fluctuation amplitude and the square of the membrane shape

$$\langle v{\left(\mathbf{r}\right)}^2\rangle =\frac{1}{{\lambda }_{\text{m}}}-\frac{{\langle u\left(\mathbf{r}\right)\rangle }^2}{\mathcal{K}{\left(h_0-l_0\right)}^2}.$$ (34)

Both of these features can be measured using reflection interference contrast microscopy with very high accuracy (61). Using very sparsely distributed pinnings and allowing for independent measurements of λ_m and h₀ − l₀, stiffness of the pinning becomes the only unknown parameter, which can thus be extracted by comparing the shape and fluctuation profiles. So far, the stiffness of the proteins was typically measured using atomic force microscopy but outside of the membrane environment, so this relation opens a possibility to extract mechanical properties of the pinning protein in its native environment.

Actually, the existence of such a relation has been inferred in imaging of pinning sites using reflection interference contrast microscopy (22, 24). In these studies, the suppression of membrane fluctuations was used to identify pinning sites that are of a lateral dimension smaller than the optical resolution of the microscope, which was possible because the correlation length of the membrane was similar or larger than the diffraction limit of the setup. Further development of this approach relies, however, on the understanding of the dependence of the correlation length of the pinned membrane on system parameters, as provided herein.

Effect of the membrane tension on the long-range behavior of the shape and correlation function

Both the mean shape and the correlations from the pinning site are proportional to the free-membrane correlations. Hence, the decay length of the correlation function will be that of the free-membrane correlation function, implying the insensitivity of the correlation length and the deformation range to the length and stiffness of the pinning. Accordingly, dependent on various regimes (see Supporting Methods, Section SV for details), a power law and an oscillatory behavior are dominated by an exponential decay of a length $\xi \left(\kappa ,\sigma ,\gamma \right)=\xi \left({\xi }_0,\sigma /{\lambda }_m^0\right)$ identified through

$$\langle v_f\left(r\right)v_f\left(0\right)\rangle =g_f\left(r\right)\stackrel{r\to \infty }{\sim }{e}^{-r/\xi \left({\xi }_0,\sigma /{\lambda }_m^0\right)},$$ (35)

where

$$\frac{\xi }{{\xi }_0}=\{\begin{array}{cc}\sqrt{2}& \text{if }\sigma =0,\\ {\left(\text{cos}\left(\frac{1}{2}\text{arctan}\left(\sqrt{{\left(\frac{{\lambda }_{\text{m}}^0}{4\sigma }\right)}^2-1}\right)\right)\right)}^{-1}& \text{if }0<\sigma <\frac{{\lambda }_{\text{m}}^0}{4},\\ 1& \text{if }\sigma =\frac{{\lambda }_{\text{m}}^0}{4},\\ {\left[\frac{4\sigma }{{\lambda }_m^0}\left(1-\sqrt{1-{\left(\frac{{\lambda }_{\text{m}}^0}{4\sigma }\right)}^2}\right)\right]}^{-1/2}& \text{if }\sigma >\frac{{\lambda }_{\text{m}}^0}{4}.\end{array}$$ (36)

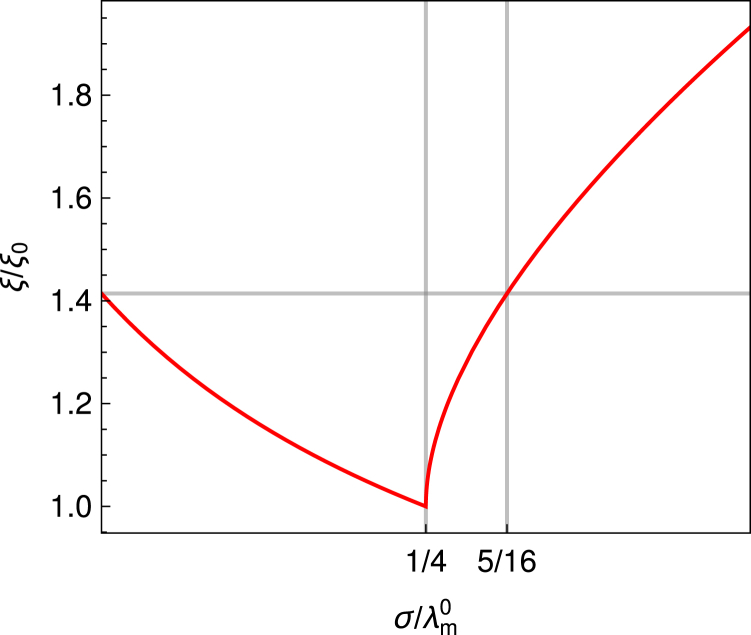
Remarkably, increasing tension does not necessarily increase the range of height correlations. Instead, when bending dominates, small amounts of tension $\left(\sigma <\left(1/4\right){\lambda }_{\text{m}}^0\right)$ actually reduce the decay length of correlations (Fig. 4). In this regime, the membrane shape and correlation function exhibit an overshoot/anticorrelations of the long-range limit immediately after the pinning (Fig. 2), followed by an oscillatory behavior within an exponentially decaying envelope (Eq. SI-V.8). Similarly to systems that are governed only by bending and tension (no nonspecific potential), the tension here flattens the membrane so that the spatial correlations decrease because of changes in curvature that decay faster as the distance from the inclusion increases. Specifically, as the tension increases toward the critical value of ${\sigma }_c={\lambda }_{\text{m}}^0/4$, the amplitude of the oscillations decreases. When the tension reaches σ_c, the oscillations are completely flattened, and the system enters a tension-dominated regime. Now, coupling to the nonspecific potential induces a slow, purely exponential decay of the shape and the correlations (Eq. SI-V.7). In this case, the larger the tension, the longer the range of the deformation and the correlation function simply because of the increase in the energy penalty for large curvatures in a nonspecific potential. However, only when the tension reaches $\sigma =5{\lambda }_{\text{m}}^0/16$ does the correlation length become longer than that of a tensionless free membrane.

Figure 4.

Correlation decay length $\xi \left({\xi }_0,\sigma /{\lambda }_m^0\right)$ in the asymptotic limit (r → ∞) (Eq. 36). The dark gray lines mark the value $\sigma =\left(5/16\right){\lambda }_{\text{m}}^0$, beyond which an increase in tension results in longer range correlations than in the tensionless case. To see this figure in color, go online.

Notably, the mean shape and correlations (and their derivatives with respect to the spatial coordinate r) are continuous functions of σ, even at σ_c, and no actual singularity appears in the system at the crossover between the bending- and tension-dominated regimes.

Membrane-mediated interactions between two pinnings

Equations 35 and 36 are significant in the context of interactions between pinnings on the membrane separated by a relative distance x. Following previous work (15), the interaction energy between two pinnings is

$${\mathcal{V}}_2\left(x\right)=\frac{\mathcal{K}{\left(l_0-h_0\right)}^2}{1+\mathcal{K}{g}_f\left(x\right)}+\frac{1}{2}\text{ln}\left(1-{\left[\mathcal{K}{g}_f\left(x\right)\right]}^2\right),$$ (37)

where the first term is the deformation energy stored in the system with two bonds and the second term is the entropic cost associated with the suppression of fluctuations (see Supporting Methods, Section SIV for details of the calculation). Terms that are independent of the relative distance between the two pinnings are omitted because they drop out in the calculation of the force between two pinnings ${\mathcal{F}}_2\left(x\right)=-\partial {\mathcal{V}}_2\left(x\right)/\partial x$, which becomes

$${\mathcal{F}}_2\left(x\right)=\frac{{\mathcal{K}}^2{\left(l_0-h_0\right)}^2{g^{\prime }}_f\left(x\right)}{{[1+\mathcal{K}{g}_f\left(x\right)]}^2}+\frac{{\mathcal{K}}^2{g}_f\left(x\right){g^{\prime }}_f\left(x\right)}{1-{\mathcal{K}}^2{g}_f{\left(x\right)}^2}.$$ (38)

Thus, the spatial dependence of the force is given by the correlation function of a free membrane at the relative distance x. The first term on the right-hand side of Eq. 38 can be associated with the force that emerges because of the membrane deformation, whereas the second term is the force arising from the suppression of membrane fluctuations in a spatially dependent manner. If the pinning deforms the membrane $\left(h_0\ne l_0\right)$, the deformation term determines the long-range behavior of the force because it decays two times slower than the fluctuation term (Fig. 5). Namely, the deformation term is proportional to g′_f(x), which decays exponentially, and independent of the amount of the deformation in the system, whereas the fluctuation term, being proportional to g_f(x)g′_f(x), decays exponentially but twice as fast (Fig. 5 a). The deformation term typically dominates closer to the pinning as well (Fig. 5). However, if $h_0\simeq l_0$, fluctuation forces dominate, in which case the decay length of the force is halved in comparison to the case of a deformed membrane. This means that even if the protein does not affect the membrane shape (h₀ = l₀), a significant force may emerge and potentially lead to the agglomeration of pinning sites, as suggested by simulations of a membrane containing many pinnings, described by the same Hamiltonian (8, 31, 37, 48). Although only limited understanding of the conditions necessary for the formation of domains is available at the moment, access to Eq. 38 sets the foundation of the calculation of critical parameters that are necessary for the process of agglomeration.

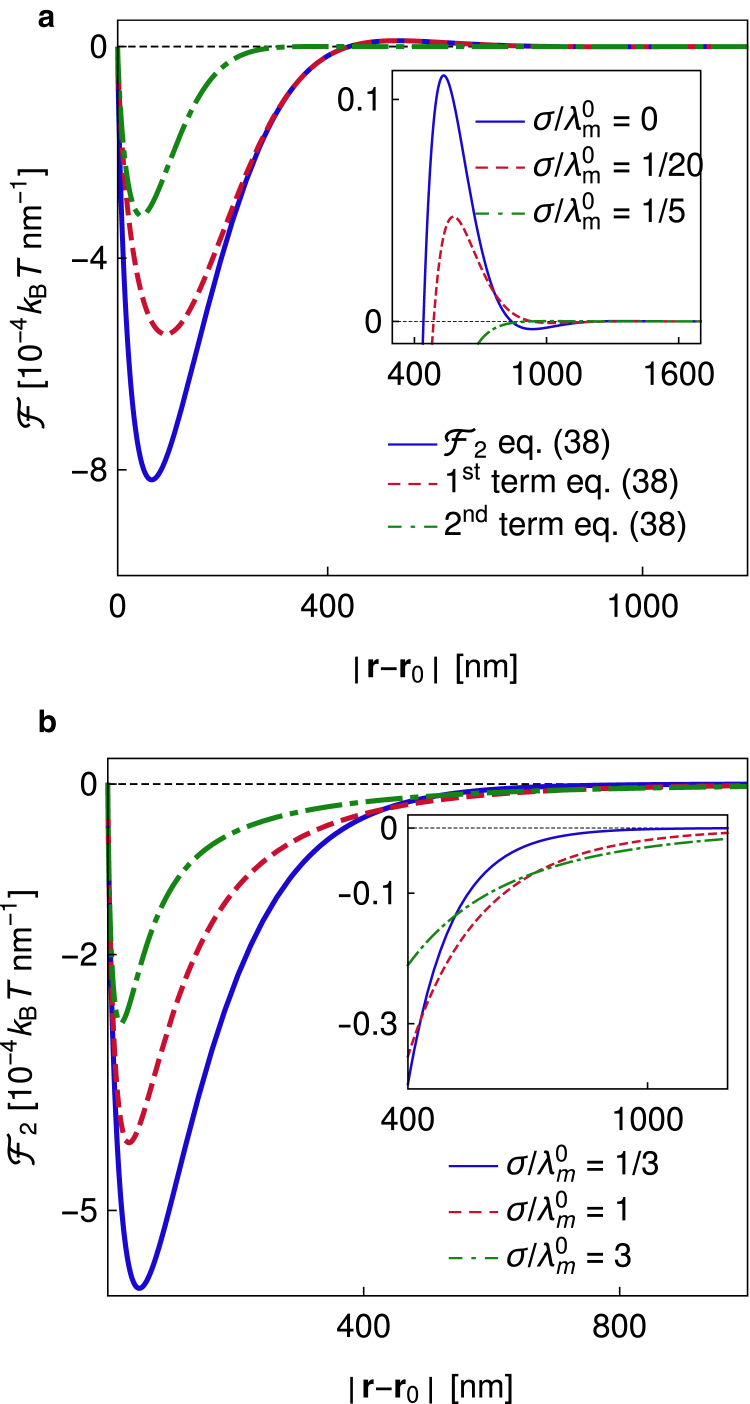
Figure 5.

Force between two pinnings. (a) The bending-dominated regime $\left(\sigma /{\lambda }_{\text{m}}^0<1/4\right)$ is shown. For this specific set of parameters, the deformation and the fluctuation contributions to the force are comparable. Both contributions oscillate around zero (inset), but the fluctuation part decays two times faster. (b) The tension-dominated regime $\left(\sigma /{\lambda }_{\text{m}}^0>1/4\right)$ is shown. As we increase the tension, the range of the force increases. Parameters: λ = 0.75 × 10⁻²k_BT/nm², κ = 20 k_BT, γ = 3.125 × 10⁻⁷k_BT/nm⁴, h₀ − l₀ = 10 nm. To see this figure in color, go online.

Based on the qualitative behavior of the forces, we can recognize two regimes, namely, the bending-dominated (σ < σ_c) and the tension-dominated regimes (σ > σ_c). These regimes correspond to different regimes of the correlation function (see Supporting Methods, Section SV). In the bending-dominated regime, a repulsive barrier appears in the force at distances of a few membrane correlation lengths (Fig. 5 a). Increasing tension but staying under σ_c flattens the barrier and the oscillating tail of the force (Fig. 5 a, inset). This is contrasted by the tension-dominated regime, in which the repulsive barrier and the oscillating tail disappear, and the long-range forces are attractive (Fig. 5 b). Moreover, the range of the force increases with tension (Fig. 5 b, inset). In all cases, the range of these weak interactions is of the order of 100 nm, which is nearly two orders of magnitude more than the direct protein-protein interactions. They are therefore considered long range despite their universally exponential nature.

This exponential decay is contrasted by a body of work performed on forces between membrane inclusions in “bending-only” or “tension-only” systems, for which the differential operator exhibits no scale. In the former case, the Green’s function behaves as g_f(r) ∼ r²logr² (62, 63, 64), and switching tension affects the power-law nature of the decay (40, 65, 66). Because the nonspecific potential introduces a length scale, the pinned membrane clearly delineates from these models for inclusions. However, it was recently proposed that a Hamiltonian that is mathematically identical to that in Eq. 1 can be used to model the inclusion of a protein with hydrophobic mismatch into a membrane (67). Although the parameter range in which the linearized theory is valid could be narrower than in the case of pinnings, the analogy of formalisms between the two problems, in principle, allows for the exploitation of the current results. Consequently, exponential decays should also appear in forces acting between membrane inclusions. However, these forces will have very different magnitudes and overall range.

It is worth mentioning that so far, we have neglected the finite size of proteins. This is appropriate for sparse or immobile protein attachments (the size of the attachment is still smaller than the correlation length of the membrane). When proteins approach within a few nanometers’ separation between their surfaces, direct protein interactions will compete with the typically attractive membrane-mediated interactions. The result of this competition at short range is nonuniversal and is most likely dominated by the direct contributions. Our hope is that the current approaches can be expanded to account for this case—either using the GF approach in analytic calculations or using the expansions into relevant basis set for numerical simulations.

Discussion

In this work, we studied the effect of a pinning on the statics of a membrane fluctuating in a harmonic nonspecific potential. We showed that the membrane and the pinning can be seen as two springs in series in the context of the energetics, as discussed previously (18). Hence, in the case in which the length of the pinning does not coincide with the position of the undisturbed membrane in an effective potential, the deformation in the system depends on the effective spring constants of the pinning and the membrane (the later characterized by the inverse of the fluctuation amplitude in the absence of pinning). For stiff membranes, the pinning will extend its shape, whereas for stiff pinnings, membrane deformation will be considerable. However, because the lateral correlation length of the membrane is not affected by the pinning properties, the range of the deformation is independent of the pinning. This is very different from the effect of tension, which directly affects the correlation length in a nonhomogeneous fashion.

The pinning, on the other hand, has a major effect on the membrane fluctuation amplitude, which is an inverse function of the pinning stiffness. The correlation length and the long-range exponential behavior are, however, fully given by the correlation length of the free membrane. For small tensions, a pinning may induce short-range anticorrelations of fluctuations and an overshoot of the membrane shape. In this regime, the correlation length decreases with increasing tension. At high tensions, the correlation length increases, whereas the shape and the correlations continuously decay to their long-range limits. These correlations translate into long-range interactions between pinnings, which also decay exponentially. The forces associated with this interaction potential are stronger if the pinning displaced the membrane; however, even in the absence of the deformation, the pinnings interact because of the suppression of fluctuations, analogous to Casimir forces.

The results presented here open the possibility for differentiating between actively and passively pinned membranes in experiments just by measuring the shape and fluctuations around a binding site, which can be either a single protein or a nanodomain, when the line tension remains small. Violation of the relationship (Eqs. 31, 32, 33, and 34) between the correlation functions and the shape provided in Properties of the Mean Shape and the Correlation Function could be taken as a notion of activity. Moreover, in passive systems with small nonlinear effects, exploiting the same relations could provide the foundation for the measurement of the stiffness of proteins in their natural membrane environment. The models proposed here should be suitable for analysis of data obtained using interferometric methods or in conjunction with atomic force microscopy of membrane-protein interactions, in which vesicles are used as soft probes.

Given that membranes, locally pinned by proteins or macromolecular assemblies, are indeed ubiquitous in nature, a toolbox developed herein consisting of mode-coupling coefficients, orthonormal modes, and the Green’s function of the system is highly useful for future theoretical studies of membranes that aim to elucidate the interplay between the membrane elasticity and the forces transmitted by the proteins in the biological context. We may anticipate that the Green’s function approach may be the method of choice for analytic modeling; however, normal modes and the mode-coupling coefficients for the plane waves may be particularly useful in the context of numerical calculations. Of course, the equivalence of all three approaches can be stated by construction. Nevertheless, in terms of results presented herein, GF and plane wave approaches give exactly the same representation of the mean shape (Eqs. 22 versus 70) and the correlations (Eqs. 26 versus 71), whereas the normal modes give an alternative but numerically identical representation (Eqs. 58 and 60 for the mean shape and correlations, respectively).

Besides studies in which membranes are used as probes for proteins binding during cell-cell and cell-substrate adhesion or in the analysis of the interaction of the cytoskeleton with the plasma or nuclear membranes, which were in some cases based on the same Hamiltonian, other systems may benefit from the tools and relations developed here. In particular, as pointed out in the recent work of (67), the same Hamiltonian could be used in studies of the interactions between membrane inclusions (49, 68, 69). However, because the energetics and the length scales of characteristic interactions are very different, nonlinear corrections may become important. Because there is a wealth of systems in which protein-mediated pinning is important in the biological and biotechnological context, further developing a theory to account for the fluctuation dynamics of a permanently but also stochastically pinned membrane appears as a natural and necessary extension of this study, a task that we plan to undertake in our future work.

All data and computer code for this study are available on request from the authors.

Author Contributions

A.-S.S. and U.S conceived the study. A.-S.S. was in charge of overall direction and supervision. U.S. provided critical feedback and helped shape the research. D.S. obtained the mode-coupling coefficients. J.A.J. and D.S calculated the orthonormal modes. J.A.J. developed the Green’s function approach. H.S. performed the asymptotic analysis. The force between two pinnings was calculated by H.S. and J.A.J. A.-S.S., J.A.J., and H.S. wrote the manuscript with contributions from all authors. All data needed to evaluate the conclusions in the article are present in the article and/or the Supporting Methods.

Editor: Markus Deserno.

Appendix A: Normal Modes Expansion

Appendix A.1: Solution of the Eigenmode Equation

It remains to determine the normal modes ψ_j given by Eq. 3. By placing the pinning at the origin (r₀ = 0), the solution of Eq. 3 obeys radial symmetry with respect to the pinning site. Hence, the eigenmodes are a product of axial and radial functions, characterized by relevant mode numbers m and n, respectively

$${\psi }_{nm}\left(\mathbf{r}\right)=R_{nm}\left(r\right){\text{e}}^{im\varphi },$$ (39)

where (r, ϕ) are polar coordinates of the position r. In this case, Eq. 3 takes the form

$$\left[\kappa {\mathit{\nabla }}^4-\sigma {\mathit{\nabla }}^2+\gamma +\lambda \delta \left(\mathbf{r}\right)\right]{\psi }_{nm}\left(\mathbf{r}\right)=E_{nm}{\psi }_{nm}\left(\mathbf{r}\right),$$ (40)

where E_nm are the eigenvalues corresponding to modes {n, m}. The square brackets on the left-hand side enclose the energy operator, which must be Hermitian (Supporting Methods, Section SII).

The general solution of Eq. 40 emerges as a sum of Bessel functions (Supporting Methods, Section SII)

$$R_{nm}\left(r\right)=a_{nm}{J}_m\left(q_{nm}r\right)+b_{nm}{Y}_m\left(q_{nm}r\right)+c_{nm}{K}_m\left(Q_{nm}r\right)+d_{nm}{I}_m\left(Q_{nm}r\right)$$ (41)

with

$$Q_{nm}=\sqrt{q_{nm}^2+\frac{\sigma }{\kappa }}.$$ (42)

Here, J_m and Y_m are Bessel functions of the first and second kind, K_m and I_m are the modified Bessel functions of the first and second kind, respectively, and a_nm, b_nm, c_nm, and d_nm are coefficients associated with the n and m mode numbers.

The corresponding eigenvalues in Eq. 40 are given by

$$E_{nm}=\kappa q_{nm}^4+\sigma q_{nm}^2+\gamma ,$$ (43)

and the general solution R_nm(r) is specified by appropriate boundary conditions.

Boundary condition 1

R_nm(r) stays finite when r → 0: the Bessel functions of the first kind, J_m and I_m, inherently fulfill this boundary condition (J₀(0) = I₀(0) = 1 and J_m(0) = I_m(0) = 0 for m > 0). The remaining Bessel functions Y_m and K_m diverge for r → 0. However, for m = 0, both Bessel functions diverge logarithmically such that the sum b₀Y₀(q_nmr) + c₀K₀(Q_nmr) stays finite with c₀ = 2b₀/π, whereas for m > 0, such cancellation is not possible. Consequently,

$$R_{nm}\left(r\right)=a_{nm}{J}_m\left(q_{nm}r\right)+d_{nm}{I}_m\left(Q_{nm}r\right)+{\delta }_{m0}{b}_{nm}\left(Y_m\left(q_{nm}r\right)+\frac{2}{\pi }{K}_m\left(Q_{nm}r\right)\right),$$ (44)

where δ_m0 is the Kronecker δ. The term multiplied by δ_m0 is contributing only for m = 0.

Boundary condition 2

The integral of the eigenvalue Eq. 40 over an infinitesimally small disk D(ϵ) centered at the pinning has to vanish,

$$\underset{D\left(\mathit{\epsilon }\right)}{\int }\text{d}\mathbf{r}\left[\kappa {\mathit{\nabla }}^4-\sigma {\mathit{\nabla }}^2+\gamma +\lambda \delta \left(\mathbf{r}\right)\right]{\psi }_{nm}\left(\mathbf{r}\right)=0.$$ (45)

This boundary condition, often introduced around a δ function, is necessary to ensure the finiteness of the membrane profile at the origin. With this imposed, the integration of the right-hand side of the eigen Eq. 5 vanishes in the relevant limit, and the limit is well defined. By extension, the integral of the left-hand side of the eigen Eq. 5 vanishes, too (see Supporting Methods, Section SII for details).

By solving the integral for each mode, one obtains

$$b_{n0}=\text{Π}\left(q_{n0}\right)\left(a_{n0}+d_{n0}\right),$$ (46)

where

$$\text{Π}\left(q_{n0}\right)=\frac{\lambda }{8\kappa \left(q_{n0}^2+\frac{\sigma }{2\kappa }\right)+\frac{\lambda }{\pi }\text{ln}\left(1+\frac{\sigma }{\kappa q_{n0}^2}\right)}.$$ (47)

Boundary conditions 3 and 4

At the membrane edge, r = P, we have

$$R_{nm}\left(P\right)=0,$$ (48)

$$\mathit{\Delta }{R}_{nm}\left(P\right)=0,$$ (49)

where Δ denotes the Laplacian operator. These boundary conditions arise in pairs after imposing hermiticity of the operator in the eigenvalue Eq. 40, as shown in Supporting Methods, Section SII.

From Eqs. 46, 47, 48, and 49, we obtain the asymptotic form of R_nm(r) for a large membrane radius P (Supporting Methods, Section SII)

$$R_{nm}\left(r\right)\sim a_{nm}\left\{J_m\left(q_{nm}r\right)+{\delta }_{m0}\left[\text{Π}\left(q_{n0}\right)\left(Y_m\left(q_{nm}r\right)+\frac{2}{\pi }{K}_m\left(Q_{nm}r\right)\right)\right]\right\},$$ (50)

with

$$q_{nm}\sim n\frac{\pi }{P}.$$ (51)

This asymptotic form of q_nm emerges when n → ∞ and membrane radius P → ∞ as shown in Supporting Methods, Section SII.

Normalization of the solution of the eigenvalue problem (Supporting Methods, Section SII), requires setting

$$a_{nm}=\frac{i^m}{\sqrt{\left(1+{\delta }_{m0}{\left(\text{Π}\left(n\mathit{\Delta }q\right)\right)}^2\right)}}.$$ (52)

Finally, by letting P → ∞, $q_{nm}\to q\in \mathbb{R}$, the basis functions become ψ_m(r, q), and are given by (Supporting Methods, Section SIII)

$${\psi }_m\left(\mathbf{r},q\right)=\frac{i^m{e}^{im\varphi }}{\sqrt{\left(1+{\delta }_{m0}{\left(\mathit{\Pi }\left(q\right)\right)}^2\right)}}\left[J_m\left(qr\right)+{\delta }_{m0}\mathit{\Pi }\left(q\right)\left(Y_m\left(qr\right)+\frac{2}{\pi }{K}_m\left(\sqrt{q^2+\frac{\sigma }{\kappa }}r\right)\right)\right].$$ (53)

Naturally, the orthogonality condition

$$\underset{{\mathbb{R}}^2}{\int }\text{d}\mathbf{r}{\psi }_m\left(\mathbf{r},q\right){\psi }_{m^{\prime }}^{\ast }\left(\mathbf{r},q^{\prime }\right)=\frac{\delta \left(q-q^{\prime }\right)}{q}2\pi {\delta }_{m,m^{\prime }}$$ (54)

is satisfied, and the profile of an infinite pinned membrane can be expanded in the basis functions ψ_m(r, q) as (Supporting Methods, Section SII)

$$u\left(\mathbf{r}\right)=\frac{1}{2\pi }\underset{m=-\infty }{\sum ^{\infty }}{\int }_0^{\infty }dqq{U}_m\left(q\right){\psi }_m\left(\mathbf{r},q\right),$$ (55)

with

$$U_m\left(q\right)=2\pi {\int }_0^{\infty }\text{d}rr{u}_m\left(r\right)R_m^{\ast }\left(r,q\right),$$ (56)

where

$$u_m\left(r\right)=\frac{1}{2\pi }{\int }_0^{2\pi }\text{d}\varphi u\left(\mathbf{r}\right)e^{-im\varphi }.$$ (57)

For vanishing λ (Supporting Methods, Section SII), the eigenmodes are given by the Bessel functions J_m(qr) for all m, which is equivalent to a basis set constructed from plane waves in radial geometry, as demonstrated for a free membrane. For a nonvanishing λ, on the other hand, the pinning properties affect explicitly only the eigenmode with $m=0$.

Appendix A.2: Representing Shape and Fluctuations

Expansion of the mean shape of the membrane pinned at r₀ = 0 is given only by m = 0 modes (Supporting Methods, Section SII):

$$\langle u\left(\mathbf{r}\right)\rangle =\lambda \left(l_0-h_0\right)\frac{1}{2\pi }{\int }_0^{\infty }dqq\frac{R_0\left(r,q\right)R_0^{\ast }\left(0,q\right)}{E_q}.$$ (58)

At the pinning site r = 0,

$$\langle u\left(0\right)\rangle =\lambda \left(l_0-h_0\right)\frac{1}{2\pi }{\int }_0^{\infty }dqq\frac{{\left|{\psi }_0\left(0,q\right)\right|}^2}{E_q}=\frac{\lambda }{\lambda +{\lambda }_{\text{m}}}\left(l_0-h_0\right).$$ (59)

The correlation function is given by

$$\langle v\left({\mathbf{r}}_1\right)v^{\ast }\left({\mathbf{r}}_2\right)\rangle =g\left({\mathbf{r}}_1|{\mathbf{r}}_2\right)=\frac{1}{2\pi }\stackrel{\infty }{\sum _{m=-\infty }}{\int }_0^{\infty }dqq\frac{{\psi }_m\left({\mathbf{r}}_1,q\right){\psi }_m^{\ast }\left({\mathbf{r}}_2,q\right)}{E_q}$$ (60)

and the fluctuation amplitude by

$$\langle v^2\left(\mathbf{r}\right)\rangle =\frac{1}{2\pi }\underset{m=-\infty }{\sum ^{\infty }}{\int }_0^{\infty }dqq\frac{{\left|{\psi }_m\left(\mathbf{r},q\right)\right|}^2}{E_q}.$$ (61)

At the position of the pinning site,

$$\langle v^2\left(0\right)\rangle =\frac{1}{2\pi }\stackrel{\infty }{\underset{0}{\int }}\text{d}q\frac{q}{\kappa q^4+\sigma q^2+\gamma }\frac{{\left(8\kappa q^2+4\sigma \right)}^2}{{\lambda }^2+{\left[8\kappa q^2+4\sigma +\frac{\lambda }{\pi }\text{ln}\left(1+\sigma /\left(\kappa q^2\right)\right)\right]}^2}=\frac{1}{\lambda +{\lambda }_{\text{m}}},$$ (62)

The last equality, which coincides with Eq. 27, was checked numerically to the machine precision for an arbitrary tension and analytically for σ = 0.

Appendix B: Plane Wave Expansion

Appendix B.1: Mode Coupling

Relating the shape and the fluctuation amplitude to the properties of the free membrane should be also possible in the most commonly used plane wave expansion

$$u\left(\mathbf{r}\right)=\frac{1}{{\left(2\pi \right)}^2}\underset{{\mathbb{R}}^2}{\int }d\mathbf{k}u\left(\mathbf{k}\right){\text{e}}^{i\mathbf{k}\mathbf{r}},$$ (63)

where for the mean shape, we find

$$\langle u\left(\mathbf{r}\right)\rangle =\frac{1}{{\left(2\pi \right)}^2}\underset{{\mathbb{R}}^2}{\int }d\mathbf{k}\langle u\left(\mathbf{k}\right)\rangle {\text{e}}^{i\mathbf{k}\mathbf{r}}$$ (64)

and for the correlation function,

$$\langle v\left(\mathbf{r}\right)v\left({\mathbf{r}}^{\prime }\right)\rangle =\frac{1}{{\left(2\pi \right)}^4}\underset{{\mathbb{R}}^2}{\int }d\mathbf{k}\underset{{\mathbb{R}}^2}{\int }d{\mathbf{k}}^{\prime }\langle u\left(\mathbf{k}\right)u\left({\mathbf{k}}^{\prime }\right)\rangle {\text{e}}^{i\mathbf{k}\mathbf{r}}{\text{e}}^{i{\mathbf{k}}^{\prime }{\mathbf{r}}^{\prime }}-\frac{1}{{\left(2\pi \right)}^4}\underset{{\mathbb{R}}^2}{\int }d\mathbf{k}\underset{{\mathbb{R}}^2}{\int }d{\mathbf{k}}^{\prime }\langle u\left(\mathbf{k}\right)\rangle \langle u\left({\mathbf{k}}^{\prime }\right)\rangle {\text{e}}^{i\mathbf{k}\mathbf{r}}{\text{e}}^{i{\mathbf{k}}^{\prime }{r}^{\prime }}.$$ (65)

The disadvantage of this approach is the coupling of the modes, giving rise to expansion coefficients $\langle u\left(\mathbf{k}\right)u\left({\mathbf{k}}^{\prime }\right)\rangle$ that have so far not been calculated explicitly.

As previously discussed (15), the amplitudes $\langle u\left(\mathbf{k}\right)\rangle$ and the mode-coupling coefficients $\langle u\left(\mathbf{k}\right)u\left({\mathbf{k}}^{\prime }\right)\rangle$ are defined as

$$\begin{array}{l}\langle u\left(\mathbf{k}\right)\rangle \equiv \frac{1}{\mathrm{Z}}\int \mathcal{D}\left[u\right]u\left(\mathbf{k}\right)\text{exp}\left[-\mathcal{H}\right],\\ \langle u\left(\mathbf{k}\right)u\left({\mathbf{k}}^{\prime }\right)\rangle \equiv \frac{1}{\mathrm{Z}}\int \mathcal{D}\left[u\right]u\left(\mathbf{k}\right)u\left({\mathbf{k}}^{\prime }\right)\text{exp}\left[-\mathcal{H}\right],\end{array}$$ (66)

with $\mathrm{Z}$ being the partition function

$$\mathrm{Z}=\int \mathcal{D}\left[u\right]\text{exp}\left[-\mathcal{H}\right].$$ (67)

Treating identities in Eq. 66 as Gaussian integrals (Supporting Methods, Section SIII) gives

$$\langle u\left(\mathbf{k}\right)\rangle =-\frac{\lambda {\lambda }_{\text{m}}}{\lambda +{\lambda }_{\text{m}}}\left(h_0-l_0\right)\frac{e^{-i\mathbf{k}{\mathbf{r}}_0}}{\kappa k^4+\sigma k^2+\gamma },$$ (68)

$$\langle u\left(\mathbf{k}\right)u\left({\mathbf{k}}^{\prime }\right)\rangle =\frac{\delta \left(\mathbf{k}+{\mathbf{k}}^{\prime }\right)}{\kappa k^4+\sigma k^2+\gamma }+\langle u\left(\mathbf{k}\right)\rangle \langle u\left({\mathbf{k}}^{\prime }\right)\rangle -\frac{\lambda {\lambda }_{\text{m}}}{\lambda +{\lambda }_{\text{m}}}\frac{e^{-i\mathbf{k}{\mathbf{r}}_0}}{\kappa k^4+\sigma k^2+\gamma }\frac{e^{-i{\mathbf{k}}^{\prime }{\mathbf{r}}_0}}{\kappa k^{\text{'}4}+\sigma k^{\text{'}2}+\gamma }.$$ (69)

Appendix B.2: Representing Shape and Fluctuations

Combining Eqs. 64 and 68, we obtain the mean shape for a pinned membrane

$$\langle u\left(\mathbf{r}\right)\rangle =\frac{\lambda {\lambda }_{\text{m}}}{\lambda +{\lambda }_{\text{m}}}\left(l_0-h_0\right)g_f\left(\mathbf{r}-{\mathbf{r}}_0\right).$$ (70)

By combining Eqs. 65, 68, and 69, we obtain for the spatial correlations

$$\langle v\left(\mathbf{r}\right)v\left({\mathbf{r}}^{\prime }\right)\rangle =g_f\left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)-\frac{\lambda {\lambda }_{\text{m}}}{\lambda +{\lambda }_{\text{m}}}{g}_f\left(\mathbf{r}-{\mathbf{r}}_0\right)g_f\left({\mathbf{r}}_0-{\mathbf{r}}^{\prime }\right)$$ (71)

and for the fluctuation amplitude (r = r′)

$$\langle v^2\left(\mathbf{r}\right)\rangle =\frac{1}{{\lambda }_{\text{m}}}-\frac{\lambda {\lambda }_{\text{m}}}{\lambda +{\lambda }_{\text{m}}}{g}_f^2\left(\mathbf{r}-{\mathbf{r}}_0\right).$$ (72)

We have therefore independently derived the same result as with the Green’s function approach (Eqs. 22 and 26).

Supporting Citations

References (70, 71, 72) appear in the Supporting Material.