β-Branched Amino Acids Stabilize Specific Conformations of Cyclic Hexapeptides

Abstract

Cyclic peptides (CPs) are a promising class of molecules for drug development, particularly as inhibitors of protein-protein interactions. Predicting low-energy structures and global structural ensembles of individual CPs is critical for the design of bioactive molecules, but these are challenging to predict and difficult to verify experimentally. In our previous work, we used explicit-solvent molecular dynamics simulations with enhanced sampling methods to predict the global structural ensembles of cyclic hexapeptides containing different permutations of glycine, alanine, and valine. One peptide, cyclo-(VVGGVG) or P7, was predicted to be unusually well structured. In this work, we synthesized P7, along with a less well-structured control peptide, cyclo-(VVGVGG) or P6, and characterized their global structural ensembles in water using NMR spectroscopy. The NMR data revealed a structural ensemble similar to the prediction for P7 and showed that P6 was indeed much less well-structured than P7. We then simulated and experimentally characterized the global structural ensembles of several P7 analogs and discovered that β-branching at one critical position within P7 is important for overall structural stability. The simulations allowed deconvolution of thermodynamic factors that underlie this structural stabilization. Overall, the excellent correlation between simulation and experimental data indicates that our simulation platform will be a promising approach for designing well-structured CPs and also for understanding the complex interactions that control the conformations of constrained peptides and other macrocycles.

Introduction

Small molecules are versatile for targeting many enzymes and receptors, and protein therapeutics can be used to target many extracellular proteins. However, when targeting protein-protein interactions, these two classes of inhibitors can be limited by an inability to present a large enough surface area (for small molecules) or difficulties in development, production, and delivery (for antibodies and other protein therapeutics) (1). For developing inhibitors of intracellular protein-protein interactions, macrocyclic molecules have been proposed as an ideal “middle ground” (2, 3).

Cyclic peptides (CPs) are among the most well-studied macrocycles, and yet the sequence-structure relationships of CPs remain poorly understood. Various strategies can be utilized for designing CPs with specific conformations, including the use of β-amino acids (4, 5, 6, 7, 8) and D-amino acids (9, 10, 11). N-methylated or N-substituted amino acids can also be used to control CP conformations, and these modifications mask backbone amides to increase membrane permeability (12, 13, 14, 15). Also, proline affords an exceptional conformational rigidity owing to the cyclic structure of its side chain. Incorporation of proline into a CP enhances the formation of specific turn or kink structures and thus restricts conformational freedom (16, 17, 18). Recently, Hosseinzadeh et al. used generalized kinematic closure, Monte Carlo simulations, and energy calculations to enumerate the stable structures that can be adopted by 7–14-residue CPs (19). More than 200 designs were predicted to fold into single stable structures, and several were experimentally verified. L- and D-proline residues were shown to play important roles in stabilizing the structures. Because these residues dominated the design and preferred structures of the designed CPs, it was unclear what other factors might contribute to promoting a single low-energy structure for designed CPs. In addition, although design algorithms can produce examples of well-structured CPs and predict a single low-energy structure, they do not typically provide information on the peptides’ global structural ensembles. Herein, we analyze a series of designed, well-structured cyclic hexapeptides and use simulations and experimental techniques to understand their global structural ensembles. By doing so, we discovered a previously unappreciated role for β-branched residues in stabilizing specific conformations of cyclic hexapeptides.

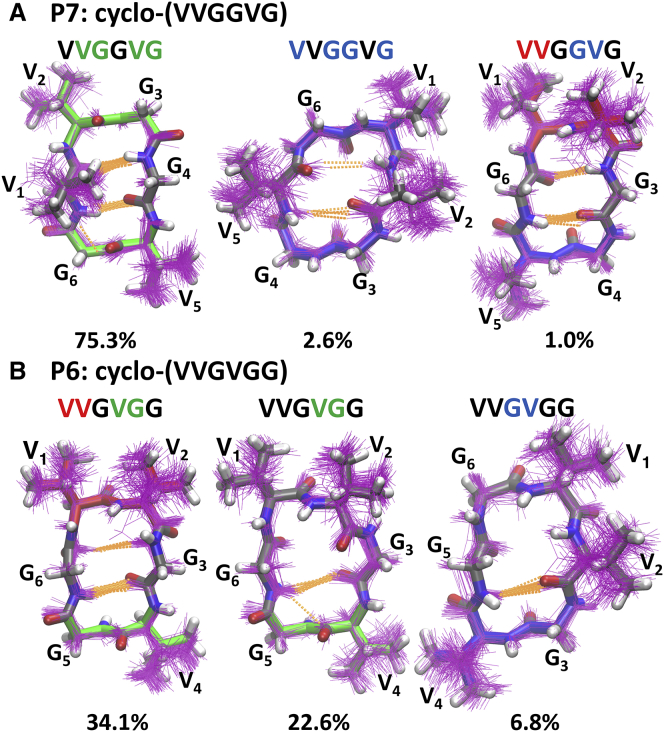
Recently, our lab developed an efficient enhanced sampling method tailored for CP simulation (20, 21). We found that for small CPs, two dihedral angles, either the ϕ and ψ angles of the same residue (ϕ_i and ψ_i) or the ψ angle of one residue and the ϕ angle of the next residue (ψ_i and ϕ_i+1), need to change coherently to enable conformational switches. By targeting these essential transitional motions using bias-exchange metadynamics (BE-META) simulations, we can efficiently sample the conformational space of a CP (22, 23, 24). Using this method, we started examining CP sequence-structure relationships with explicit-water molecular dynamics (MD) simulations by gradually substituting Gly residues in cyclo-(GGGGGG) with Val. This systematic study consisted of 14 G_nV_6-n cyclic hexapeptides (i.e., cyclo-(GGGGGG), cyclo-(VGGGGG), cyclo-(VVGGGG), cyclo-(VGVGGG), cyclo-(VGGVGG),…, cyclo-(VVVVVV)) and allowed us to identify one CP predicted to have a single highly populated conformation in aqueous solution. Specifically, for the peptide cyclo-(VVGGVG), ∼80% of the population formed two type II β turns at residues 2–3 and 5–6 in the simulation (Fig. 1 A) (22). This prediction was unique among the 14 G_nV_6-n CPs because all the others adopted multiple conformations with small populations in solution (Fig. 1 B). This included cyclo-(VVGVGG), which has the same amino acid composition but different ordering of residues compared to cyclo-(VVGGVG). Herein, we report experimental verification of these structure predictions for cyclo-(VVGGVG), here called P7 (peptide #7 in the series of the 14 G_nV_6-n cyclic hexapeptides), and cyclo-(VVGVGG), here called P6, using NMR spectroscopy of synthetic peptides. These results validate our simulation protocol and demonstrate how efficient MD methods can be used to systematically characterize CP structural ensembles and identify well-structured sequences.

Figure 1.

Simulated structural ensembles for (A) P7 and (B) P6. One hundred randomly selected structures of the top three clusters are shown in purple lines, with a representative structure shown in sticks. Types I, II, and II′ β turns are colored red, green, and blue, respectively. Hydrogen bonds are shown in orange dashed lines. The population of each cluster is given below the structures. To see this figure in color, go online.

In this work, we sought to better understand the sequence determinants that result in P7 having a high degree of structure but its isomer P6 being more poorly structured. To understand the importance of each valine residue for stabilizing the β_II+β_II structural motif adopted by P7, we performed, to our knowledge, new simulations on analogs which altered the degree of β-branching within P7. These results suggested a critical role for β-branching at position 1, which was supported by experimental data from NMR spectroscopy. Finally, thermodynamics analysis of the simulation results provided a molecular-level understanding of this effect.

Materials and Methods

BE-META simulations

BE-META simulations (25, 26) were performed for P7 cyclo-(VVGGVG), P6 cyclo-(VVGVGG), P7-V1A cyclo-(AVGGVG), P7-V2A cyclo-(VAGGVG), P7-V5A cyclo-(VVGGAG), P7-V1I cyclo-(IVGGVG), P7-V1L cyclo-(LVGGVG), P7-V1T cyclo-(TVGGVG), and P7-V1S cyclo-(SVGGVG) to computationally characterize the structural ensembles adopted by these CPs. The residue-specific force field 2 (RSFF2) (27) plus TIP3P water (28) was used throughout this work.

Two initial structures of each CP were prepared from scratch using the Chimera molecular modeling package (29). The initial CP structure was solvated, and the dimensions of the water box were chosen such that the minimal distance between any atom of the peptide and the walls of the box was 1.0 nm. The solvated system was energy minimized using the steepest descent algorithm to remove bad contacts. The solvated CP then underwent two stages of equilibrations. During the first stage of equilibration, the peptide’s heavy atoms were restrained by a harmonic potential with a force constant of 1000 kJ⋅mol⁻¹⋅nm⁻² to equilibrate the solvent molecules and adjust the density. The first stage of equilibration consisted of a 50 ps NVT simulation at 300 K and a subsequent 50 ps NPT simulation at 300 K and one bar. The second stage of equilibration consisted of an additional 100 ps NVT simulation at 300 K followed by a 100 ps NPT simulation at 300 K and one bar without restraints to equilibrate the whole system. All production simulations were performed using an NPT ensemble at 300 K and one bar. The leapfrog algorithm with a time step of 2 fs was used for dynamics evolution. All bonds involving hydrogen were constrained using the LINCS algorithm. Cutoff of 1.0 nm was used for neighbor searching, Lennard-Jones interactions, and short-range electrostatics. Long-range electrostatics were treated using the particle mesh Ewald (PME) summation with a Fourier spacing of 0.12 nm and a PME order of 4. A long-range dispersion correction for energy and pressure was applied to account for the 1.0 nm cutoff of Lennard-Jones interactions.

All BE-META simulations were performed using the PLUMED 2 plugin (30) in Gromacs 4.6.7 (31). In each BE-META simulation, two types of two-dimensional (2D) biases, (ϕ_i, ψ_i) and (ψ_i, ϕ_i+1), were used. These coordinates were found to effectively enhance conformation sampling of CPs by targeting the coupled two-dihedral changes (21). Therefore, in each simulation, there are a total of twelve CVs: six 2D biases for (ϕ_i, ψ_i), and six 2D biases for (ψ_i, ϕ_i+1). To obtain the unbiased structural ensemble for analysis, five neutral replicas (i.e., with no bias) were added. The length of the BE-META simulations was 100 ns for all CP except V1L, which was extended to 300 ns to reach convergence between the two parallel runs.

Structural ensemble analysis

To characterize the structural ensemble of each CP, the last 50 ns of the neutral replicas from the BE-META simulations were analyzed. We performed dihedral angle principal component analysis (dPCA) (32, 33) utilizing the ϕ and ψ angles of all residues, followed by a grid density peak-based clustering (34) to quantify the population of each cluster. Principal component analysis is a popular technique for dimensionality reduction while preserving as much information (variance) as possible. In our dPCA, the first three principal components (PC1, PC2, and PC3) accounted for >60% of the total variances for all the CPs simulated in this study (Table S1). During the clustering, the three-dimensional principal subspace along PC1, PC2, and PC3 was first divided into 50 × 50 × 50 grids, and the data population within each grid was then calculated. Cluster analysis was only performed on the grids with probability density larger than 0.1. The local density of a specific grid i was evaluated by a Gaussian kernel:

$${\rho }_i=\sum _{j\mathit{\in \Omega }}{w}_j{e}^{-\frac{d_{ij}}{d_{\text{c}}}},$$ (1)

where w_j is the data population of grid j, d_ij is the distance between grids i and j, and d_c is the cutoff distance, which was chosen such that the average number of neighboring grids is 2% of the total grids. The sum over j is over all the grids (including i). The population for each state was determined by summarizing the data populations of the grids that the state contained.

To verify that the BE-META simulations were long enough to provide converged structural description for the CPs studied, two sets of simulations were performed for all CPs, starting from two different initial configurations. The normalized integrated product (35) of the population densities in the three-dimensional principal subspace was calculated to monitor the similarity between the results from the two sets of simulations and verify their convergence (Fig. S1). The length of the BE-META simulations performed was 100–300 ns. All the final normalized integrated products were larger than 0.93 (with a value of 1.0 showing full convergence).

Thermodynamics analysis

We performed thermodynamics decomposition analysis to identify the origins of structural preferences of each CP (36). ΔG between clusters was calculated via the Boltzmann equation using the ratios of their populations, and the most-populated cluster was used as the reference state. ΔG was further separated into ΔH and ΔS, in which ΔH was estimated using the difference in potential energies between clusters and ΔS was estimated using ΔS = (ΔH − ΔG)/T. ΔH was further decomposed based on 1) whether the interaction was within just peptide (ΔH_P^vac) or the rest of the system (ΔH_rest) and 2) whether the interaction was for bonds (ΔH^bond), angles (ΔH^angle), dihedrals (ΔH^dih. and ΔH^imp. for proper and improper dihedrals), Lennard-Jones (ΔH^LJ), or Coulombic interactions (ΔH^EE, short-range ΔH^EE(SR), long-range ΔH^EE(LR), 1–4 ΔH^EE(1,4)). For 1), we note that periodic boundary conditions and PME were used in the simulations, and we excluded the interaction of the peptide and its images by excluding the long-range Coulombic potential when calculating peptide enthalpy, yielding ΔH_P^vac; the excluded long-range Coulombic potential was assigned to ΔH_rest. ΔS was further decomposed into peptide configurational entropy (ΔS_P^conf) and solvation entropy (ΔS_W). ΔS_P^conf was evaluated using the maximum information spanning tree approach (37, 38, 39), which provides a tight estimation of the upper bound of the entropy, and the solvation entropy was calculated by ΔS_W = ΔS − ΔS_P^conf.

A large sample size is critical for the accurate estimation of both enthalpy and entropy. According to our evaluation, with the trajectories saved every 1 ps, 60,000 frames of data were needed for each conformation, which amounted to 60 ns of accumulated simulation time. For clusters that had small populations, there were not enough frames from the BE-META simulations for the thermodynamics analysis. To obtain enough data, we performed additional MD simulations using randomly selected structures from each cluster as starting points. The simulation parameters used in the additional MD simulations were the same as those used in the BE-META simulations described above. We performed dPCA and cluster analysis on these trajectories to exclude frames that did not belong to the target cluster, and we ran these MD simulations until at least 60,000 frames were available for each cluster. Thus, all the thermodynamics analysis comparing different structural clusters was based on the same number of frames (60,000) from the MD simulations. To ensure that the frames used for thermodynamics analysis for each cluster accurately represent the equilibrium structural ensembles, we also ensured that the rotamer distribution along the χ₁ angles (g⁺, t, g⁻) of the first residue calculated using the 60,000 frames was the same as the rotamer distribution observed for each cluster in the BE-META simulations.

Peptide synthesis, cyclization, and purification

The linear peptide was synthesized at 0.05 mmol scale on Wang resin preloaded with Fmoc-glycine (0.7 mmol/g; Novabiochem, San Diego, CA). Solid-phase peptide synthesis was carried out on an automated synthesizer (Tribute; Gyros Protein Technologies, Uppsala, Sweden) using ultraviolet deprotection monitoring and infrared heating on all couplings, resulting in the linear peptide with a deprotected N-terminus. The peptide was cleaved from the resin using 4% H₂O (v/v) in a solution of trifluoroacetic acid for 3 h at room temperature. The peptide solution was filtered from the resin and dried using a rotary evaporator. The resulting film was dissolved in 50% H₂O: 50% acetonitrile and lyophilized. The lyophilized crude peptide was directly used for cyclization. Cyclizations were carried out at room temperature for 1 h with 0.5 mM peptide, 1.5 mM 1-[bis(dimethylamino)methylene]-1H-1,2,3-triazolo [4,5-b]pyridinium 3-oxid hexafluorophosphate and 3 mM N, N-diisopropylethylamine in dimethylformamide. The cyclization reaction was quenched by adding trifluoroacetic acid. After removing solvents by rotary evaporator, the reaction mixture was redissolved in 50:50 H₂O:acetonitrile and purified via high-performance liquid chromatography with a preparative reverse-phase C8 column. CP purity of >95% was confirmed by analytical high-performance liquid chromatography, and identity was confirmed by liquid chromatography-mass spectrometry (Agilent 6530 Accurate Mass Q-TOF with an Agilent 1290 UHPLC; Agilent, Santa Clara, CA).

NMR characterization

Peptides were dissolved in 90:10 H₂O:D₂O at a concentration of roughly 3.0 mM. One-dimensional and 2D ¹H NMR spectra were recorded on a Bruker cryo-600 MHz spectrometer at 288 K (Bruker, Billerica, MA). Complete resonance assignments were made using data from homonuclear ¹H–¹H total correlation spectroscopy (TOCSY) and rotating-frame Overhauser spectroscopy (ROESY) experiments. Standard pulse programs available from the Bruker library were used, with mixing times of 60 ms for the TOCSY and 250 ms for the ROESY. ¹H chemical shifts were referenced to 4,4-dimethyl-4-silapentane-1-sulfonic acid (δ 0.00 ppm) in water. ³J_NH,CHα coupling constants were measured from ¹H NMR.

Results and Discussion

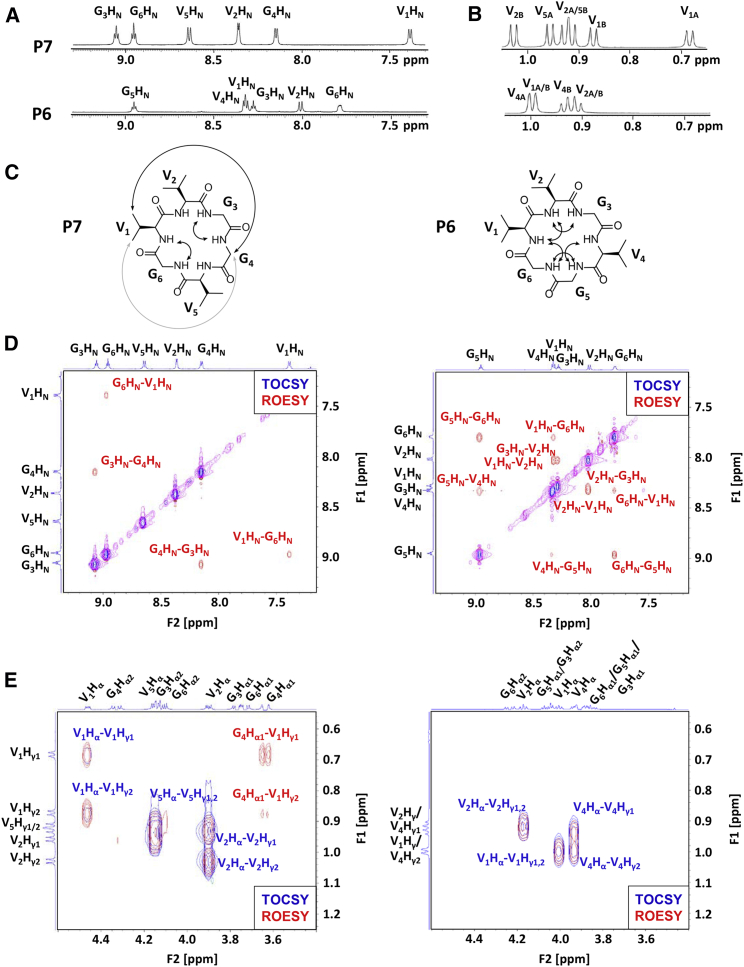
To follow up on our previous structure predictions of peptides P7 and P6, (Fig. 1; (22)) we prepared these CPs and obtained ¹H NMR spectra and TOCSY and ROESY spectra in aqueous solution. These results allowed complete, unambiguous assignment for each peptide. Although the two peptides have the same residue composition, the proton chemical shifts revealed large structural differences between P7 and P6 (Fig. 2 A). The P7 amide protons spanned widely from 9.07 to 7.39 ppm, whereas P6 amide protons spanned a much narrower range from 8.96 to 7.80 ppm. Overlap among amide protons from residues of the same type is common in less-structured peptides. For example, overlap between the amide protons of V₁ and V₄ was observed in P6. However, no such overlap was observed for P7. The greater range and lack of overlap for P7 amide protons indicated a greater degree of structure.

Figure 2.

2D-NMR data for peptides P7 (cyclo-VVGGVG) and P6 (cyclo-VVGVGG) in water. (A) Amide proton region of ¹H NMR for P7 and P6. (B) Methyl proton region of ¹H NMR for P7 and P6. (C) Double-headed arrows show strong (black) and weak (gray) NOEs from the ROESY spectra for P7 and P6. (D) Amide-to-amide proton region of the TOCSY and ROESY spectra for P7 and P6. NOE crosspeaks are expected for positions at which β turns predominate in the solution ensemble. (E) α-to-methyl proton region of the TOCSY and ROESY spectra for P7 and P6. NOE crosspeaks show medium-range interactions between methyl protons and α protons. To see this figure in color, go online.

We found similar results when examining the chemical shifts of the methyl protons (Fig. 2 B). P6 methyl protons showed significant overlap and their chemical shifts spanned from 1.00 to 0.91 ppm, whereas the P7 methyl protons all had distinct chemical shifts and spanned from 1.03 to 0.69 ppm. For P7 methyl protons, six separate doublets were observed, corresponding to six methyl groups with different chemical shifts among the three valines. Side-chain flexibility typically results in averaged peaks for valine methyl protons, so the separation of all six of P7’s valine methyl resonances implied a high degree of structure. In particular, the methyl resonances within valine 1 of P7 (P7-V₁) were at 0.88 and 0.69 ppm, a difference of 0.19 ppm. This was an unusually large difference between methyl resonances within a single valine. The dramatic upfield shift of the P7-V₁ methyl at 0.69 ppm, along with the upfield chemical shift of the P7-V₁ amide proton, suggested that this residue is unusually well structured. This was our first indication that V₁ might be critical for the overall structural organization of P7.

ROESY data were used to further investigate the structures of P7 and P6. Strong nuclear Overhauser effects (NOEs) occur when a large proportion of the peptide ensemble keeps two protons near each other in space (within roughly 3.5 Å), whereas weak NOEs occur either when two protons are further away (up to 5.5 Å) or when the protons are near each other only in a smaller proportion of the structural ensemble (40). For large proteins, the broad range of NOE peak volumes is typically used to calibrate NOEs to specific distances between protons. However, because of the relatively small number of protons and NOEs in a cyclic hexapeptide, in the following analysis, we simply binned NOEs into “strong” and “weak” groups to avoid overinterpretation. Several strong interresidue NOEs and one weak interresidue NOE were observed for P7 and P6 (Fig. 2 C). Two sets of simulated annealing simulations incorporating the NOE restraints were performed for each compound. The results demonstrate that the experimentally derived NOE constraints are consistent with the predicted structural ensembles for P7 and P6 (Fig. S2). To avoid overinterpretation, we focused further analysis on the primary NMR data rather than these NMR-derived structural simulations.

The presence of (i, i+1) amide-to-amide NOEs can address the existence and location of β turns within the peptide backbone. For P7, two strong amide-to-amide NOEs were observed (V₁H_N–G₆H_N and G₃H_N–V₄H_N), and no other strong or weak amide-to-amide NOEs were observed (Fig. 2 D). These NOEs are consistent with types II and II′ β turn structures at positions 5–6 and 2–3 (24), and these positions match the predicted positions for two type II β turns for P7 (residues 2–3 and 5–6, Fig. 1 A). For P6, five of the six possible sequential amide-to-amide NOEs were observed, with varying intensities. These data suggested that P6 populates an ensemble of backbone conformations with β turns at various positions.

Interresidue, nonsequential NOEs (often called “medium-range” or “long-range” NOEs for larger proteins) add important constraints and are particularly indicative of a high degree of structure. Notably, we observed NOEs for each of the P7-V₁ methyl protons with an α-proton of the G₄ residue (G₄H_α1–V₁H_γ, Fig. 2 E). The upfield-shifted P7-V₁ methyl group had a stronger NOE to G₄H_α1 compared to the other P7-V₁ methyl group. These NOEs are consistent with the predicted structure for P7, which positions the V₁ methyl groups at median distances of 3.4 and 5.8 Å from the nearest G₄H_α1 proton (Fig. 1 A). No such interactions were observed for P6, for which no nonsequential NOEs were detected.

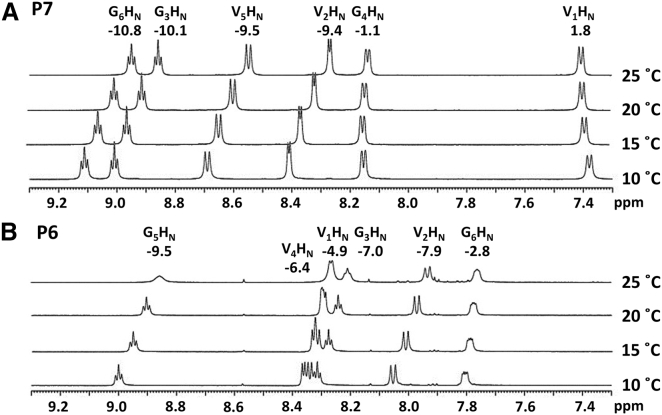
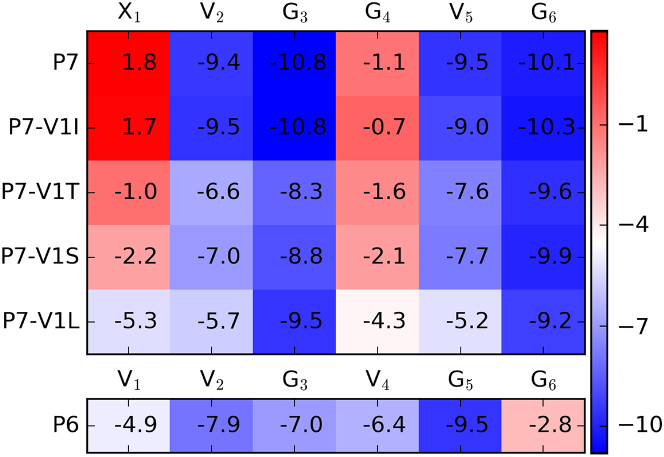
We next used variable-temperature NMR to identify backbone amides that are engaged in intramolecular hydrogen bonding. The chemical shifts of solvent-exposed backbone amide protons will change with temperature, shifting upfield between 16 and 4.5 ppb per degree K (−16 to −4.5 ppb/K). The chemical shifts of amide protons that are protected from solvent, such as those engaged in intramolecular hydrogen bonds, will change to a lesser extent with temperature (−4.5 to 2 ppb/K) (41, 42). For P6, only one amide proton, that of G₆ (−2.8 ppb/K), had a temperature dependence consistent with hydrogen bonding (Fig. 3 B). This observation is consistent with the simulation results that a hydrogen bond was formed between G₆’s NH and G₃’s CO in 71.4% of the most-populated cluster and 31.7% of the second most-populated cluster of P6’s predicted structural ensemble (Fig. 1 B). For P7, four of the six amide protons had temperature dependences between −9.4 and −10.8 ppb/K (Fig. 3 A). Strikingly, the amide protons of P7-V₁ and P7-G₄ had temperature dependences of 1.8 and −1.1 ppb/K, respectively, indicating a large degree of protection from solvent. In fact, these temperature coefficients match values typically observed in the folded core of globular proteins (41, 42). These solvent-protected amide protons match the positions of predicted hydrogen bonds in the most-populated cluster of P7’s predicted structural ensemble (Fig. 1 A). The variable-temperature NMR data are consistent with the conclusion that the solution ensemble of P6 has several interconverting, internally hydrogen-bonded structures, but that the ensemble of P7 is predominated by a single structure with the predicted hydrogen bond pattern.

Figure 3.

Temperature dependence of amide proton chemical shifts for (A) P7 and (B) P6. Stacked spectra show the amide regions of ¹H NMR experiments at the indicated temperature. Temperature coefficients are shown in ppb/K for each amide proton. Solvent-exposed amide protons typically have chemical shifts that shift upfield with temperature by more than 4.5 ppb/K (temperature coefficient between −4.5 and −16 ppb/K). Temperature coefficients between 2.0 and −4.5 ppb/K indicate protection from solvent as occurs when an amide proton is involved in a hydrogen bond.

To understand the importance of each valine residue in stabilizing the β_II+β_II structure of P7 (Fig. 1), we performed simulations in which each of the three valine residues was replaced with alanine. Compared to P7, for which the β_II+β_II conformation had a population of 75.3%, the V2A analog, cyclo-(VAGGVG), and the V5A analog, cyclo-(VVGGAG), had slightly lower populations (70.6% and 61.7%, respectively). The V1A analog, cyclo-(AVGGVG), still had the original β_II+β_II conformation as its most-populated structure but this was only 47.2% of the total population (Fig. 4). These data led us to hypothesize that β-branching at position 1 is essential for stabilizing the β_II+β_II structure of P7. To further test this hypothesis, we simulated the V1I, V1L, V1T, and V1S analogs of P7. For the β-branched analogs V1I and V1T, the population of the β_II+β_II conformation was 77.8% and 63.8%, respectively. For the non-β-branched analogs V1L and V1S, β_II+β_II was still the most-populated conformation, but its population was only 32.4% and 44.2%, respectively. Overall, these simulations suggested that β-branching at position 1 is critical for stabilizing the overall β_II+β_II structure of P7 (Fig. 4).

Figure 4.

Simulated structural ensembles for the V1A, V2A, V5A, V1I, V1L, V1T, and V1S analogs of P7. Top three clusters are shown with their populations given in parentheses. One hundred randomly selected structures of each cluster are shown in purple lines, with a representative structure shown in sticks. Types I, I′, II, and II′ β turns are colored red, yellow, green, and blue, respectively. Hydrogen bonds are shown in orange dashed lines. To see this figure in color, go online.

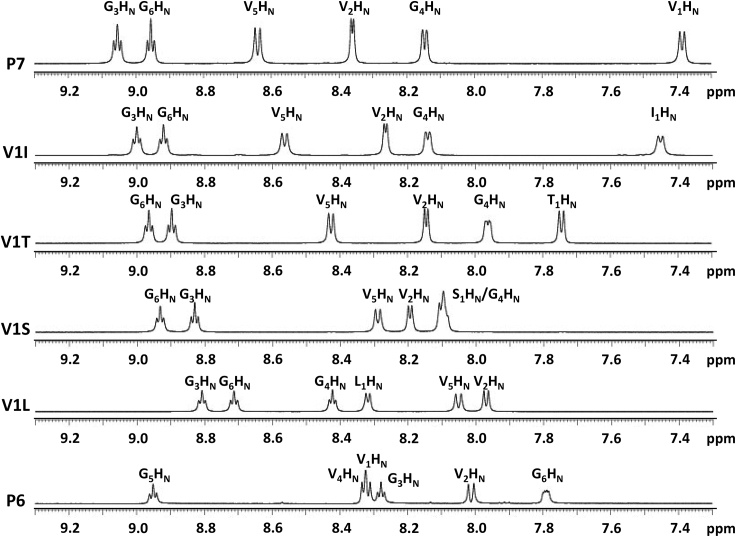
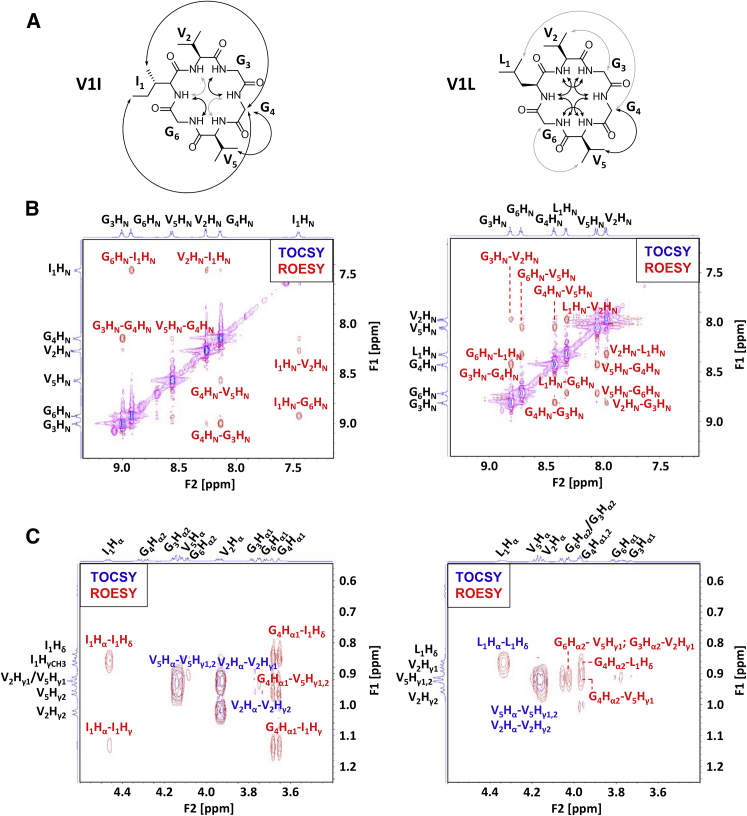
Because the simulations predicted such a strong effect for β-branching at position 1, we sought to confirm these predictions experimentally. The same NMR experiments used to compare P7 and P6 were first performed for P7 analogs V1I and V1L. As discussed above, amide proton chemical shifts provided insight into the overall degree of structure (Fig. 5). For V1I, amide chemical shifts spanned from 9.00 to 7.45 ppm, whereas its non-β-branched isomer V1L had a smaller range (from 8.81 to 7.97 ppm). The individual resonances of V1I were very similar to that of P7 as might be expected for a valine-to-isoleucine substitution. The predominant locations of β turns were investigated by examining amide-to-amide NOEs. For V1I, two strong amide-to-amide NOEs were observed, I₁H_N–G₆H_N and G₃H_N–G₄H_N (Fig. 6, A and B). These NOEs occurred at the same positions observed for P7 (Fig. 2 D), and these are also consistent with the β turn positions predicted by simulations of V1I (at residues 5–6 and 2–3) (Fig. 4). We also observed two weaker NOEs at I₁H_N–V₂H_N and G₄H_N–V₅H_N, indicating a minor contribution of other β turn structures to the overall solution ensemble of V1I. For V1L, all six possible amide-to-amide NOEs were observed at strong intensities (Fig. 6, A and B). These data indicate V1L populates an ensemble with varied β turn positions and no predominant β turn location. In contrast, the NMR data indicate that V1I has a predominant structure that is highly similar to that of P7 but with a somewhat lower degree of overall structure than P7.

Figure 5.

¹H NMR spectra for P7, P6, and P7 analogs V1I, V1T, V1S, and V1L. The more well-structured peptides (P7, V1I, and V1T) have a wider span of amide chemical shifts, whereas the less well-structured peptides (V1S, V1L, and P6) have a narrower span of amide chemical shifts.

Figure 6.

2D-NMR data for peptides V1I (cyclo-IVGGVG) and V1L (cyclo-LVGGVG) in water. (A) Double-headed arrows show strong (black) and weak (gray) NOEs from the ROESY spectra for V1I and V1L. (B) Amide-to-amide proton region of the TOCSY and ROESY spectra. NOE crosspeaks are expected for positions at which β turns predominate in the solution ensemble. (C) α-to-methyl proton region of the TOCSY and ROESY spectra. NOE crosspeaks show medium-range interactions between methyl protons and α protons. To see this figure in color, go online.

NOEs between protons on nonadjacent residues provided further indications of structure and relative side-chain flexibility. Strong NOEs were observed in the V1I spectrum between G₄ and the side chain of I₁ (I₁H_γ–G₄H_α and I₁H_δ–G₄H_α), whereas only one weak interaction was observed for V1L (L₁H_δ–G₄H_α, Fig. 6 C). Variable-temperature NMR experiments for V1I showed that two amide protons, I₁H_N and G₄H_N, had temperature coefficients in the range of −4.5 to 2 ppb/K (1.7 and −0.7 ppb/K, respectively). This observation suggests that these amide protons are extremely well-protected from solvent, similar to the corresponding protons of P7 (Fig. 8). V1L, in contrast, had only one amide proton (G₄H_N) falling barely above the threshold of −4.5 ppb/K (−4.3 ppb/K). The rest of the amide protons had temperature coefficients ranging from −5.2 to −9.5 ppb/K, indicating that these are, on average, unprotected from solvent.

Figure 8.

Variable-temperature NMR data. The temperature coefficients (change in chemical shift over temperature, in ppb/K) for the amide protons of peptides P7, V1I, V1T, V1S, V1L, and P6 are shown. Temperature coefficients between −4.5 and −16 ppb/K are typical for solvent-exposed amide protons. Temperature coefficients between 2.0 and −4.5 ppb/K indicate protection from solvent, as occurs when an amide proton is involved in intramolecular hydrogen bonding. To see this figure in color, go online.

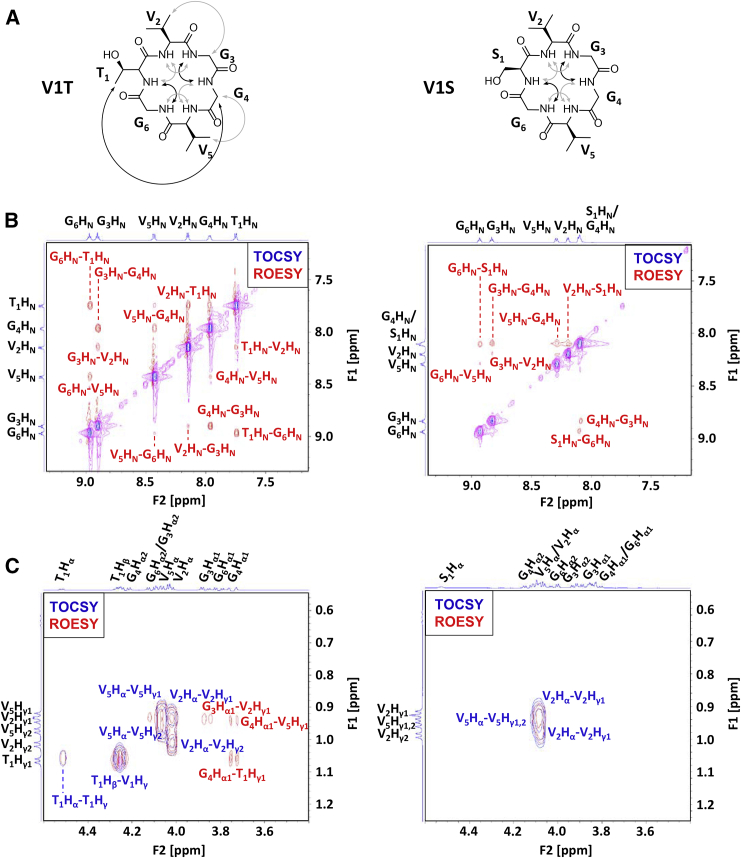
To examine the effects of β-branching using a second set of P7 analogs, we prepared V1T and V1S and analyzed them using NMR. V1T had a wider overall span of amide chemical shifts than V1S, indicating a higher degree of structure (Fig. 5). Both peptides had strong amide-to-amide NOEs at the predicted turn locations and weak amide-to-amide NOEs at the other four possible turn locations (Fig. 7 B). These data indicated that both peptides have a dominant conformation that corresponds to the top cluster from the simulations, with minor contributions of other β turn structures to the overall ensemble. For V1T, a strong medium-range NOE was observed for T₁H_γ–G₄H_α (Fig. 7 C). In variable-temperature experiments, the T₁H_N and G₄H_N protons of V1T had temperature coefficients of −1.0 and −1.6 ppb/K, respectively. Interestingly, the analogous S₁H_N and G₄H_N protons of V1S also showed substantial protection from solvent, with temperature coefficients of −2.2 and −2.1 ppb/K, respectively. Overall, the NMR data indicated that V1T and V1S are both relatively well structured, with V1T slightly more so, but neither are as well structured as P7 or V1I.

Figure 7.

2D-NMR data for peptides V1T (cyclo-TVGGVG) and V1S (cyclo-SVGVGG) in water. (A) Double-headed arrows show strong (black) and weak (gray) NOEs from the ROESY spectra for V1T and V1S. (B) Amide-to-amide proton region of the TOCSY and ROESY spectra for V1T and V1S. NOE crosspeaks are expected for positions at which β turns predominate in the solution ensemble. (C) α-to-methyl proton region of the TOCSY and ROESY spectra for V1T and V1S. NOE crosspeaks show medium-range interactions between methyl protons and α protons. To see this figure in color, go online.

Using the variable-temperature data to compare overall degree of structure (Fig. 8), the peptides rank as follows from most structured to least structured: P7, V1I, V1T, V1S, P6, and V1L. This order matches the trends observed for chemical shift data (Figs. 2 and 5) and NOE data (Figs. 2, 6, and 7). Importantly, this ranking is consistent with the predictions from the simulations based on the percentage population of the most-populated cluster for each peptide: P7 75.3%, V1I 77.8%, V1T 63.8%, V1S 44.2%, P6 34.1%, and V1L 32.4% (Figs. 1 and 4). Thus, the NMR data suggest that our simulations not only identified the predominant structure for each peptide in solution, but also successfully predicted the overall population of that structure compared to similar peptides.

We performed thermodynamics analysis of our simulation results to provide some molecular-level understanding of the effects of β-branching at position 1 on the structural ensemble of P7. Table S2 shows the ΔG, ΔH, ΔS, and further decomposition of ΔH and ΔS of the β_II′+β_II′ conformation relative to the β_II+β_II conformation for each of the peptides P7, V1A, V1I, V1L, V1T, and V1S. The β_II+β_II conformation refers to the most-populated cluster for all of these peptides, which had type II β turns at residues 2–3 and 5–6 (Figs. 1 and 4). The β_II′+β_II′ conformation refers to a conformation which had type II′ β turns at residues 6–1 and 3–4; this was the second most-populated cluster for P7, V1A, V1I, and V1L and the third most-populated cluster for V1T and V1S (Fig. 4). The ΔH’s between the two conformations were almost equal to ΔG’s for all CPs except V1S (Table S2), which indicates that the most-populated β_II+β_II conformation was favored over the β_II′+β_II′ mostly because of enthalpy. On the other hand, the −TΔS_P^conf between the β_II′+β_II′ and β_II+β_II conformations shows that the β_II′+β_II′ conformation was relatively favorable in configurational entropy. Peptide entropy plays an important role in protein folding, peptoid helix formation, and dimerization (43, 44, 45). In protein folding, the peptide entropy typically decreases as the protein goes from the unfolded to the folded state. Because of the crowdedness near the backbone, β-branched amino acids have less conformational freedom in the unfolded state, and β-branching can make the folding process more favorable (46). In our case here, β-branching made the top cluster (the β_II+β_II conformation) even more unfavorable in configurational entropy, as shown in Table S2. To understand this phenomenon, Fig. S3 A shows the decomposition of TS_P^conf into the self-entropy term, which had contributions from bonds, angles, and dihedrals, and the mutual information term (39) for cluster 1 (β_II+β_II) and cluster 2 (β_II′+β_II′) of V1L. It was found that the major contribution to the difference in configurational entropy between the two clusters came from the dihedral component of the self-entropy term. The same conclusion was found for the other five CPs: V7, V1A, V1I, V1T, and V1S. To get an idea of which dihedrals contributed the most to the change in TΔS_P^conf, when the first residue was changed from a non-β-branched amino acid to a β-branched amino acid, we plotted the contribution to TS_P^conf_self from each dihedral degree of freedom for clusters 1 and 2 of V1L (Fig. S3 B) and V1I (Fig. S3 C). We found that the largest difference in the two CPs lay in the self-entropy of the dihedral N-C_α-C_β-C_γ (χ₁) of residue 1 in V1L versus N-C_α-C_β-C_γ2 (which was related to the χ₁ angle) of residue 1 in V1I. Although the self-entropy of N-C_α-C_β-C_γ of residue 1 was similar between clusters 1 and 2 in V1L, the self-entropy of N-C_α-C_β-C_γ2 of residue 1 was much smaller in cluster 1 than cluster 2 in V1I. Document S1. Figs. S1–S32 and Tables S1–S24, Document S2. Article plus Supporting Material shows that the distribution of the dihedrals was much more confined in cluster 1 relative to cluster 2 in V1I but not in V1L, which explains in part why CPs with a β-branched amino acid at position 1 had an even more unfavorable configurational entropy for cluster 1 than cluster 2 than CPs with a non-β-branched amino acid at position 1.

ΔH between the β_II′+β_II′ and β_II+β_II conformations shows that the β_II′+β_II′ conformation was relatively unfavorable in enthalpy, and having a β-branched residue at position 1 increased this gap. Further breaking down ΔH into its components, we found that ΔH_P^dih. was larger for the CPs with β-branched residue 1 (P7, V1I, and V1T) than for the CPs with non-β-branched residue 1 (V1A, V1L, and V1S). To isolate the origin of this difference, we decomposed ΔH_P^dih. into contributions from each dihedral. Fig. S3 E plots the potential energy difference for each dihedral angle between the β_II′+β_II′ and the β_II+β_II conformation for V1I and V1L. This analysis showed that the difference of ΔH_P^dih. in V1I compared to V1L was mainly due to the energy differences in ϕ, ϕ′, ψ, ψ′, and χ₁′ of residue 1.

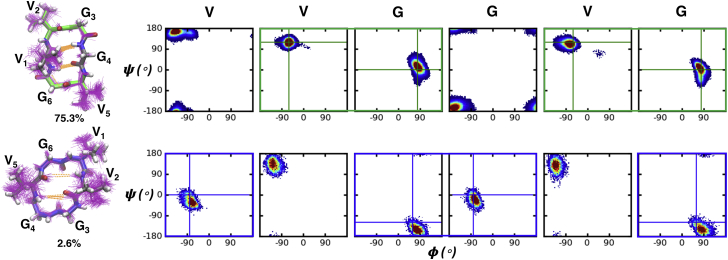
Fig. 9 shows the Ramachandran plot for the most-populated cluster (the β_II+β_II conformation) and the second most-populated cluster (the β_II′+β_II′ conformation) of P7. In the β_II+β_II conformation, the ϕ and ψ dihedrals of residue 1 reside in the β conformer region, whereas in the β_II′+β_II′ conformation, these dihedrals populate the right-handed α helix (α_R) conformer region. In general, β-branched residues, such as V, I, and T, tend to have a higher propensity to form a β sheet than non-β-branched residues, such as A, L, and S. Analysis of the coil library shows that β-branched residues have higher intrinsic propensity for the β conformer than the non-β-branched residues (47, 48, 49). This stronger preference for the β conformer of β-branched residues could explain their importance in stabilizing the β_II+β_II conformation in cyclo-(XVGGVG).

Figure 9.

Ramachandran plots for the top two clusters of P7. Boxes around residues are colored by β turn type (types II and II′ β turns are colored green and blue, respectively) and solid lines indicate the ideal dihedral angles for each type of β turn. To see this figure in color, go online.

In this study, we used the RSFF2 force field (27, 50), which was based on amber99sb but modified to capture the intrinsic ϕ/ψ propensities observed in the protein coil library for each amino acid. Because our thermodynamic analysis of simulations with RSFF2 attributed a large overall effect to β-branching, we were curious whether modifications to backbone dihedral propensities were critical for obtaining the correct structures. To test this, we performed BE-META simulations of these CPs using the amber99sb force field. Table S3 shows that the β_II + β_II conformation was no longer the most-populated structure for any of the CPs when the amber99sb force field was used. Instead, the top clusters formed a type I β turn at residues 1–2 and a type II′ β turn at residues 4–5, and these clusters had populations <40%. These observations and the agreement between our simulations and experimental results support the improvement and value of the RSFF2 force field.

Conclusions

In this work, we used explicit-solvent MD simulations with enhanced sampling to predict the global structural ensembles of several cyclic hexapeptides. As synthesizing and structurally characterizing CPs was rather labor and resource intensive, we chose six CPs for synthesis and structural characterization to assess the predictions. The structural data was acquired by solution-phase NMR in aqueous solution with no organic solvent. Commonly, constraints from NMR data are used to calculate an ensemble of lowest-energy structures (19). Although we performed this analysis (Fig. S2), it can lead to overinterpretation for molecules of small size. It also ignores the potential for a molecule to populate multiple conformations in solution, which is common for CPs (51). Thus, we used NMR data to verify the predicted lowest-energy structure, and we also analyzed chemical shifts, NOEs, and variable-temperature data directly. This allowed us to analyze the degree of structure of the global conformational ensemble, rather than limiting our analysis to one lowest-energy cluster. Notably, the MD simulations were used to make predictions that were subsequently validated by experiment, rather than using MD simulations to rationalize previous experimental observations.

We observed that small modifications to peptide sequence can lead to large changes in the CP solution ensemble. This phenomenon is well known in the medicinal chemistry literature, in which structure-activity relationships (SAR) for macrocyclic molecules are notoriously noncooperative and hard to predict. Although there is currently little understanding of the SAR of CPs, using MD simulations, we were able to identify for cyclo-(VVGGVG) a critical position at which β-branching was important for structure. We confirmed the validity of the simulations by comparing simulation data to solution-phase structural information, successfully predicting degree of structure for a series of analogs differing only by one side chain.

Fully predictive computational SAR models for CPs and other macrocycles will be impossible without the ability to simulate accurately the global ensemble of populated structures. With additional simulations of CPs of different sizes and compositions, we anticipate that our MD simulations, coupled with careful comparisons to experimental data, will produce fully predictive computational SAR models for CPs. Such models would be enormously helpful in drug development for CPs and other macrocycles.

Author Contributions

J.A.K. and Y.-S.L. designed the research. A.E.C. performed the peptide synthesis and NMR spectroscopy. J.M., D.P.S., and S.M.M. performed the simulations and analysis. A.E.C., J.M., J.A.K., and Y.-S.L. interpreted the data and wrote the manuscript. All authors read and approved the final version.

Editor: Margaret Cheung.