Efficient Variant Set Mixed Model Association Tests for Continuous and Binary Traits in Large-Scale Whole-Genome Sequencing Studies

Abstract

With advances in whole-genome sequencing (WGS) technology, more advanced statistical methods for testing genetic association with rare variants are being developed. Methods in which variants are grouped for analysis are also known as variant-set, gene-based, and aggregate unit tests. The burden test and sequence kernel association test (SKAT) are two widely used variant-set tests, which were originally developed for samples of unrelated individuals and later have been extended to family data with known pedigree structures. However, computationally efficient and powerful variant-set tests are needed to make analyses tractable in large-scale WGS studies with complex study samples. In this paper, we propose the variant-set mixed model association tests (SMMAT) for continuous and binary traits using the generalized linear mixed model framework. These tests can be applied to large-scale WGS studies involving samples with population structure and relatedness, such as in the National Heart, Lung, and Blood Institute’s Trans-Omics for Precision Medicine (TOPMed) program. SMMATs share the same null model for different variant sets, and a virtue of this null model, which includes covariates only, is that it needs to be fit only once for all tests in each genome-wide analysis. Simulation studies show that all the proposed SMMATs correctly control type I error rates for both continuous and binary traits in the presence of population structure and relatedness. We also illustrate our tests in a real data example of analysis of plasma fibrinogen levels in the TOPMed program (n = 23,763), using the Analysis Commons, a cloud-based computing platform.

Introduction

In recent years, massive DNA sequence data have been generated. Large-scale whole-genome sequencing projects, such as the National Heart, Lung, and Blood Institute’s (NHLBI) Trans-Omics for Precision Medicine (TOPMed) program and the National Human Genome Research Institute’s (NHGRI) Genome Sequencing Project (GSP), have produced whole-genome sequences from more than 120,000 samples. The designs of the studies from which participants are drawn need not be uniform or simple; for example, TOPMed includes population-based cohorts, family studies, and case-control studies, some of which are conducted in recently admixed populations, and some of which involve large pedigrees of closely related participants.

In population-based cohorts and case-control studies, population stratification and cryptic relatedness are major sources of confounding that need to be accounted for in association tests. For common single-variant analysis, linear mixed models that use an estimated genetic relationship matrix (GRM) to account for both population stratification and cryptic relatedness have been widely applied in genome-wide association studies (GWASs) to analyze structured and related samples.^{1, 2, 3, 4, 5, 6} For binary traits, however, we previously showed that linear mixed models may not be appropriate in the presence of population stratification due to misspecified mean-variance relationships. Therefore, we instead proposed a computationally efficient method GMMAT⁷ to perform common single-variant tests in GWASs by fitting generalized linear mixed models (GLMMs),⁸ which simultaneously account for population structure, cryptic relatedness, and shared environmental effects, using multiple variance components and/or random effects.

Hundreds of millions of genetic variants, mostly with a low and extremely rare minor allele frequency (MAF), are being analyzed in large-scale sequencing projects such as TOPMed and GSP. Yet, single-variant tests that have been widely used in GWASs are generally underpowered for analyzing rare genetic variants from sequencing studies. To circumvent this problem, statistical tests such as the burden test,^{9, 10, 11, 12} sequence kernel association test (SKAT),¹³ and their various combinations^{14, 15, 16} have been proposed. These tests analyze multiple genetic variants in sets, grouped by genes, genomic regions, or other bioinformatic aggregation units. Most of these tests were originally developed to analyze samples from unrelated individuals, as well as extensions to analyze family data with known pedigree structures in the parametric mixed model and semiparametric generalized estimating equation frameworks.^{17, 18, 19, 20, 21, 22, 23}

Linear mixed models using a single random effect with the GRM covariance matrix to account for population structure have been developed and implemented in software programs for sequencing data analysis, such as EPACTS and Rvtests.²⁴ Meta-analysis methods for family data have been developed and implemented in seqMeta and RAREMETAL,^{25, 26} but only for continuous traits in the linear mixed model framework. Moreover, these existing methods do not account for cryptic relatedness and between-subject relatedness from multiple sources and have not been applied to large-scale whole-genome sequencing studies with complex study samples, due to statistical and computational challenges.

One challenge is that among traditional variant set tests such as burden tests and SKAT, no single approach is uniformly most powerful. Another challenge is that existing hybrid tests that combine burden tests and SKAT, such as SKAT-O,¹⁴ MiST,¹⁵ and aSPU,¹⁶ are powerful but are subject to much greater computational loads than either the burden test or SKAT alone in the GLMM framework. Of note, SKAT-O is slower than SKAT because it searches on a grid for the optimal linear combination of the burden test and SKAT statistics. MiST requires adjusting for the genetic burden as a covariate in the SKAT model and hence needs to fit a burden model for each variant set. In large samples of possibly related individuals, extension of MiST is not as practical as in unrelated samples, since fitting a mixed effects model using the burden score for each variant set (or each test unit) is computationally intensive across the genome. Finally, aSPU uses a permutation or Monte Carlo simulation procedure to compute the p values, which can also be challenging in the context of large-scale whole-genome sequencing studies with both population structure and relatedness. Therefore, there is a pressing need to develop powerful and computationally efficient statistical methods for large-scale whole-genome sequencing studies.

To address these statistical and computational challenges, we develop the variant set mixed model association tests (SMMATs), computationally efficient variant set tests for both continuous and binary traits, which are applicable to structured and related samples with potential multiple sources of correlations, from large-scale whole-genome sequencing studies. We include four tests in the SMMAT framework: the burden test (SMMAT-B), SKAT (SMMAT-S), SKAT-O (SMMAT-O), and an efficient hybrid test to combine the burden test and SKAT (SMMAT-E), with power improvements over mixed model-based burden test, SKAT and SKAT-O. All four SMMATs share the same reduced model under the null hypothesis, i.e., the GLMM with only covariates, which needs to be fit only once for all genetic variant sets in an analysis. We show that all of these tests can be constructed using shared single-variant scores and their covariance matrices, thus further improving the computational efficiency in practice compared to performing these tests separately. Moreover, it has been shown that single-variant scores and their covariance matrices can also be used in the meta-analysis of variant set tests,^{25, 27} and thus SMMAT has been implemented to be directly applicable to combining multi-cohort studies ranging from unstructured independent samples to structured and related samples. Finally, we develop a unified analysis pipeline in our software package GMMAT that implements SMMAT variant set tests in both single study (pooled analysis) and meta-analysis contexts to facilitate research on rare genetic variants from large-scale sequencing studies. We demonstrate the application of our method to the analysis of fibrinogen levels in the TOPMed study.

Material and Methods

Generalized Linear Mixed Models (GLMMs)

We formulate the SMMATs (SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E) from the same GLMM

$$g\left({\mu }_i\right)={\mathit{X}}_i\mathit{\alpha }+{\mathit{G}}_i\mathit{\beta }+b_i,$$ (Equation 1)

where $g(\cdot )$ is a monotonic “link” function that connects the mean of phenotype y_i, denoted by ${\mu }_i=E\left(y_i|{\mathit{X}}_i,{\mathit{G}}_i,b_i\right)$, for subject i of n samples, to the covariate row vector ${\mathit{X}}_i$, the genotype row vector ${\mathit{G}}_i$ for q genetic variants in a set, and the random effects b_i that accounts for population structure and relatedness. The phenotypes y_i follow a distribution in the exponential family. For continuous traits, we usually assume that y_i follow a normal distribution and use an identity link function; for binary traits, we assume y_i follow a Bernoulli distribution and use a logit link function. In Equation 1, $\mathit{\alpha }$ is a p × 1 vector of fixed covariate effects including an intercept, and the genotype effects $\mathit{\beta }$ are assumed to be a q × 1 vector whose distribution has mean$\mathit{W}{\mathbf{1}}_q{\beta }_0$ and covariance $\theta {\mathit{W}}^2$, where $\mathit{W}=diag\left\{w_j\right\}$ is a pre-specified q × q matrix assigning weights to each variant, $\theta$ is a variance component parameter, and ${\mathbf{1}}_q$ is a column vector of length q with all elements 1. We assume that $\mathit{b}\sim N\left(0,{\sum }_{k=1}^K{\nu }_k{\mathbf{\Phi }}_k\right)$ is an n × 1 vector of random effects with each entry b_i, K variance component parameters v_k, and known n × n relatedness matrices ${\mathbf{\Phi }}_k$ $\left(1\le k\le K\right)$. We allow for multiple random effects to account for complex sampling designs such as hierarchical designs, shared environmental effects, and repeated-measures from longitudinal studies.

SMMAT-B, SMMAT-S, and SMMAT-O

In Equation 1, testing the genotype effects of q variants $H_0:\mathit{\beta }=0$ is equivalent to testing the null hypothesis that $H_0:{\beta }_0=0$ and $\theta =0$. The reduced GLMM under this null hypothesis specifies that

$$g\left({\mu }_{0_i}\right)={\mathit{X}}_i\mathit{\alpha }+b_i,$$ (Equation 2)

where ${\mu }_{0_i}=E\left(y_i|{\mathit{X}}_i,b_i\right)$. If we test $H_0:{\beta }_0=0$ under the assumption that $\theta =0$, a burden score test SMMAT-B can be constructed as

$$T_B=\frac{{\left(\mathit{y}-{\hat{\mathit{\mu }}}_0\right)}^T\mathit{GW}{\mathbf{1}}_q{\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\left(\mathit{y}-{\hat{\mathit{\mu }}}_0\right)}{{\hat{\varphi }}^2},$$

where $\mathit{y}={\left(\begin{array}{cc}\begin{array}{cc}{y}_1& y_2\end{array}& \begin{array}{cc}\cdots & y_n\end{array}\end{array}\right)}^T$ is an n × 1 vector of phenotypes y_i, ${\hat{\mathit{\mu }}}_0$ is a vector of fitted mean values under the model in Equation 2, $\mathit{G}={\left(\begin{array}{cc}\begin{array}{cc}{\mathit{G}}_1^T& {\mathit{G}}_2^T\end{array}& \begin{array}{cc}\cdots & {\mathit{G}}_n^T\end{array}\end{array}\right)}^T$ is an n × q genotype matrix of the variant set in the test, and $\hat{\varphi }$ is an estimate of the dispersion parameter (or the residual variance) $\varphi$. Under $H_0:{\beta }_0=0$, the statistic T_B asymptotically follows ${\xi }_B{\chi }_1^2$, where the scalar ${\xi }_B={\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q$, ${\chi }_1^2$ is a chi-square distribution with 1 df, and $\hat{\mathit{P}}={\hat{\mathbf{\Sigma }}}^{-1}-{\hat{\mathbf{\Sigma }}}^{-1}\mathit{X}{\left({\mathit{X}}^T{\hat{\mathbf{\Sigma }}}^{-1}\mathit{X}\right)}^{-1}{\mathit{X}}^T{\hat{\mathbf{\Sigma }}}^{-1}$ is the n × n projection matrix of the null GLMM (Equation 2), $\mathit{X}={\left(\begin{array}{cc}\begin{array}{cc}{\mathit{X}}_1^T& {\mathit{X}}_2^T\end{array}& \begin{array}{cc}\cdots & {\mathit{X}}_n^T\end{array}\end{array}\right)}^T$ is an n × p covariate matrix, $\hat{\mathbf{\Sigma }}=\hat{\mathit{V}}+{\sum }_{k=1}^K{\hat{\nu }}_k{\mathbf{\Phi }}_k$ with $\hat{\mathit{V}}=\hat{\varphi }{\mathit{I}}_n$ for continuous traits in linear mixed models, and $\hat{\mathit{V}}=diag\left\{1/\left({\hat{\mu }}_{0_i}\left(1-{\hat{\mu }}_{0_i}\right)\right)\right\}$ for binary traits in logistic mixed models (where the dispersion parameter $\varphi$is known to be 1).

On the other hand, if we test $H_0:\theta =0$ under the assumption ${\beta }_0=0$, a variance component score-type test SMMAT-S can be constructed as

$$T_S=\frac{{\left(\mathit{y}-{\hat{\mathit{\mu }}}_0\right)}^T\mathit{GWW}{\mathit{G}}^T\left(\mathit{y}-{\hat{\mathit{\mu }}}_0\right)}{{\hat{\varphi }}^2}.$$

Under $H_0:\theta =0$, T_S asymptotically follows ${\sum }_{j=1}^q{\xi }_{S_j}{\chi }_{1,j}^2$, where ${\chi }_{1,j}^2$ are independent chi-square distributions with 1 df, and ${\xi }_{S_j}$ are the eigenvalues of ${\mathbf{\Xi }}_S=\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}$.

If one assumes ${\beta }_0$has mean 0 and variance $\gamma$, $\mathit{\beta }$ then follows a distribution 0 and covariance $\tau \mathit{W}\left\{\left(1-\rho \right){\mathit{I}}_q+\rho {\mathbf{1}}_q{\mathbf{1}}_q^T\right\}\mathit{W}$, where$\tau =\gamma +\theta$ and $\rho =\gamma /\left(\gamma +\theta \right)$, which takes values between 0 and 1. The joint null hypothesis $H_0:{\beta }_0=0$ and $\theta =0$ is equivalent to $H_0:\tau =0.$Given $\rho$, a variance component score-type test can be constructed as

$$T_{\rho }=\rho T_B+\left(1-\rho \right)T_S.$$

If $\rho =1$, $T_{\rho }$ becomes the SMMAT-B burden statistic T_B, which assumes $\mathit{\beta }$ are the same for all q variants after weighting. If $\rho =0,{\text{T}}_{\text{ρ}}$ becomes the SMMAT-S SKAT statistic T_S. If an optimal $\rho$ is obtained by minimizing the p value of $T_{\rho }$, then SMMAT-O can be constructed, with its p value calculated using a one-dimensional numerical integration, following SKAT-O.¹⁴ A key advantage of SMMAT-O is that it maximizes the power by using the optimal linear combination of the mixed model burden test SMMAT-B and the mixed model SKAT SMMAT-S. As it requires a grid search over $\rho ,$ it is computationally considerably more expensive than SMMAT-B and SMMAT-S. We propose in the next section a computationally much more efficient method to combine SMMAT-B and SMMAT-S.

SMMAT-E

An alternative joint test to SMMAT-O for $H_0:{\beta }_0=0$ and $\theta =0$ can be constructed using two asymptotically independent tests: a test for $H_0:{\beta }_0=0$ versus $H_1:{\beta }_0\ne 0$ under the constraint $\theta =0$ and a test for $H_0:\theta =0$ versus $H_1:\theta >0$ with ${\beta }_0$ as a nuisance parameter that is estimated under$H_0:\theta =0$. In unrelated samples, this testing strategy is a special case of MiST adjusting for the genotype burden score as a single fixed-effects covariate,¹⁵ which requires the burden model to be fit for each SNP set. We note that the first test is SMMAT-B T_B in the SMMAT framework, and the second test $T_{\theta }$ can be constructed from the null burden GLMM

$$g\left({\mu }_{B_i}\right)={\mathit{X}}_i\mathit{\alpha }+{\mathit{G}}_i\mathit{W}{\mathbf{1}}_q{\beta }_0+b_i,$$ (Equation 3)

where ${\mu }_{B_i}=E\left(y_i|{\mathit{X}}_i,{\mathit{G}}_i\mathit{W}{\mathbf{1}}_q,b_i\right)$ is the mean of y_i in the burden GLMM. We can construct a SKAT-type statistic adjusting for the genetic burden

$$T_{\theta }=\frac{{\left(\mathit{y}-{\tilde{\mathit{\mu }}}_B\right)}^T\mathit{GWW}{\mathit{G}}^T\left(\mathit{y}-{\tilde{\mathit{\mu }}}_B\right)}{{\tilde{\varphi }}^2},$$

where${\tilde{\mathit{\mu }}}_B$ is a vector of fitted values ${\tilde{\mu }}_{B_i}$ using the burden GLMM in Equation 3 for a given variant set. However, fitting this burden GLMM separately for each variant set is computationally expensive in large-scale whole-genome association studies.

Therefore, we propose a different computationally efficient strategy by assuming that the mean of genetic effects ${\beta }_0$ is not large, a reasonable assumption for most genomic regions and most complex human diseases. Then we can construct $T_{\theta }$ efficiently without refitting the burden GLMMs in Equation 3 for each variant set across the genome. We show in Appendix A that $T_{\theta }$ can be approximated by

$$T_{\theta }\approx {\hat{\varphi }}^{-2}{\left(\mathit{y}-{\hat{\mathit{\mu }}}_0\right)}^T\mathit{GW}\left\{{\mathit{I}}_q-{\mathbf{1}}_q{\left({\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q\right)}^{-1}{\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}\right\}\left\{{\mathit{I}}_q-\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q{\left({\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q\right)}^{-1}{\mathbf{1}}_q^T\right\}\mathit{W}{\mathit{G}}^T\left(\mathit{y}-{\hat{\mathit{\mu }}}_0\right).$$

Therefore, under $H_0:\theta =0$, $T_{\theta }$ asymptotically approximately follows ${\sum }_{j=1}^q{\xi }_{{\theta }_j}{\chi }_{1,j}^2$, where ${\chi }_{1,j}^2$ are independent chi-square distributions with 1 df, and ${\xi }_{{\theta }_j}$ are the eigenvalues of ${\mathbf{\Xi }}_{\theta }=\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}-\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q{\left({\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q\right)}^{-1}{\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}$. By the central limit theorem, both $\mathit{W}{\mathit{G}}^T\left(\mathit{y}-{\tilde{\mathit{\mu }}}_B\right)/\tilde{\varphi }$ and ${\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\left(\mathit{y}-{\hat{\mathit{\mu }}}_0\right)/\hat{\varphi }$ are asymptotically normal, and their covariance matrix is

$$Cov\left(\frac{\mathit{W}{\mathit{G}}^T\left(\mathit{y}-{\tilde{\mathit{\mu }}}_B\right)}{\tilde{\varphi }},\frac{{\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\left(\mathit{y}-{\hat{\mathit{\mu }}}_0\right)}{\hat{\varphi }}\right)$$

$$\approx \left\{{\mathit{I}}_q-\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q{\left({\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q\right)}^{-1}{\mathbf{1}}_q^T\right\}\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q=\mathbf{0.}$$

Therefore, $T_{\theta }$ and T_B are approximately asymptotically independent. Let $p_{\theta }$ and $p_B$ be the p value of the two tests, respectively, then SMMAT-E p value $p_E$ is computed using Fisher’s method with a chi-square distribution with 4 df as $p_E=P\left({\chi }_4^2>-2\log \left(p_{\theta }{p}_B\right)\right)$.

Meta-analysis

SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E can all be conducted in the meta-analysis context. Assuming the single-variant scores $\mathit{S}={\mathit{G}}^T\left(\mathit{y}-{\hat{\mathit{\mu }}}_0\right)/\hat{\varphi }$ and their covariance matrix $\mathbf{\Psi }={\mathit{G}}^T\hat{\mathit{P}}\mathit{G}$ are computed for each variant set in each study, we can reconstruct $T_B={\mathit{S}}^T\mathit{W}{\mathbf{1}}_q{\mathbf{1}}_q^T\mathit{WS}$ with ${\xi }_B={\mathbf{1}}_q^T\mathit{W}\mathbf{\Psi }\mathit{W}{\mathbf{1}}_q$; $T_S={\mathit{S}}^T\mathit{WWS}$ with ${\mathbf{\Xi }}_S=\mathit{W}\mathbf{\Psi }\mathit{W}$; $T_{\rho }=\rho T_B+\left(1-\rho \right)T_S$ and $T_{\theta }={\mathit{S}}^T\mathit{W}\left\{{\mathit{I}}_q-{\mathbf{1}}_q{\left({\mathbf{1}}_q^T\mathit{W}\mathbf{\Psi }\mathit{W}{\mathbf{1}}_q\right)}^{-1}{\mathbf{1}}_q^T\mathit{W}\mathbf{\Psi }\mathit{W}\right\}\left\{{\mathit{I}}_q-\mathit{W}\mathbf{\Psi }\mathit{W}{\mathbf{1}}_q{\left({\mathbf{1}}_q^T\mathit{W}\mathbf{\Psi }\mathit{W}{\mathbf{1}}_q\right)}^{-1}{\mathbf{1}}_q^T\right\}\mathit{WS}$ with ${\mathbf{\Xi }}_{\theta }=\mathit{W}\mathbf{\Psi }\mathit{W}-\mathit{W}\mathbf{\Psi }\mathit{W}{\mathbf{1}}_q{\left({\mathbf{1}}_q^T\mathit{W}\mathbf{\Psi }\mathit{W}{\mathbf{1}}_q\right)}^{-1}{\mathbf{1}}_q^T\mathit{W}\mathbf{\Psi }\mathit{W}$.

For each variant set, let $m=\mathrm{1,2},\cdots ,M$ be the index of studies and ${\mathit{S}}_m$ and ${\mathbf{\Psi }}_m$ be the single-variant scores and covariance matrix from study m. In testing the “weak” null hypothesis²⁸ of summary genetic effects $H_0:\mathit{\beta }=0$,^{25, 27} we can compute meta summary statistics $\mathit{S}={\sum }_{m=1}^M{\mathit{S}}_m$ and $\mathbf{\Psi }={\sum }_{m=1}^M{\mathbf{\Psi }}_m$ and use them in SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E. If a genetic variant is monomorphic in a study, its single-variant score statistic and the corresponding row and column in the covariance matrix will be set to 0 for that study. When combining studies with very different sample characteristics, testing the “strong” null hypothesis²⁸ that genetic effects in all studies are 0 is sometimes desired. In the general case, we may choose to group studies that are similar and test whether the summary genetic effects in all groups are 0, for example, in the meta-analysis of multi-ethnic samples. Let $c=\mathrm{1,2},\cdots ,C$ be a partition of M studies $\left(C\le M\right)$, where C is the number of ethnicities, ${\mathit{S}}_{c_m}$ and ${\mathbf{\Psi }}_{c_m}$ be the single-variant scores and covariance matrix from study m in partition c ($m=\mathrm{1,2},\cdots ,M_c$ in partition c, and ${\sum }_{c=1}^C{M}_c=M$), such that genetic effects for the same variant are summarized within each partition c but heterogeneous across partitions,²⁷ we can also compute summary statistics$\mathit{S}={\left(\begin{array}{cc}\begin{array}{cc}{\sum }_{m=1}^{M_1}{\mathit{S}}_{1_m}^T& {\sum }_{m=1}^{M_2}{\mathit{S}}_{2_m}^T\end{array}& \begin{array}{cc}\cdots & {\sum }_{m=1}^{M_C}{\mathit{S}}_{C_m}^T\end{array}\end{array}\right)}^T$ and $\mathbf{\Psi }=diag\left\{{\sum }_{m=1}^{M_c}{\mathbf{\Psi }}_{c_m}\right\}$. Note that $\mathit{S}$ is now a vector of length Cq and $\mathbf{\Psi }$ is a block-diagonal matrix with C blocks of q × q matrices, one for each partition of studies (with total dimension Cq × Cq), so we should replace $\mathit{W}$, ${\mathbf{1}}_q$, and ${\mathit{I}}_q$ by ${\mathit{I}}_C\otimes \mathit{W}$ (where $\otimes$ denotes the Kronecker product), ${\mathbf{1}}_{Cq}$, and ${\mathit{I}}_{Cq}$, respectively, in the above expressions for T_B, $T_{\rho }$, T_S, and $T_{\theta }$ for meta-analysis.

Simulation Studies

Type I Error in Single-Cohort Studies

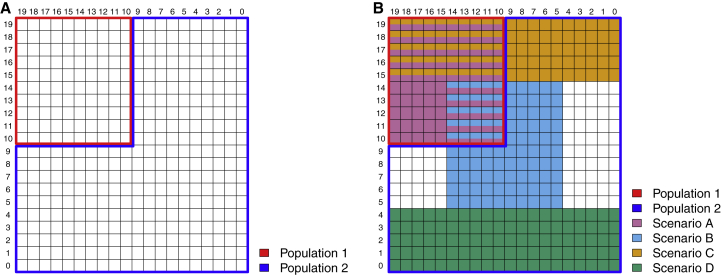
We performed coalescent simulations to generate sequence data with 100 genetic variants in each set, and 10,000 independent sets for 8,000 individuals from a 20 × 20 grid of spatially continuous populations with migration rate between adjacent cells M = 10 (Figure 1A). Within each cell, we paired 20 individuals into 10 families and simulated 2 children for each family using gene dropping,²⁹ and in total we had 4,000 families and 16,000 individuals. For continuous traits, in each simulation replicate, we simulated the phenotype y_ij for individual j in family i under the null hypothesis of no genetic association from

$$y_{ij}={\alpha }_1{Z}_i+b_{ij}+{\mathit{\varepsilon }}_{ij},$$ (Equation 4)

where the “population effect” ${\alpha }_1=1$ and the population indicator Z_i = 1 if family i was from a 10 × 10 grid in the top left of the map (population 1) and Z_i = 0 otherwise (population 2). The familial random effects were simulated as

$${\mathit{b}}_i=\left(\begin{array}{c}\begin{array}{c}{b}_{i1}\\ b_{i2}\end{array}\\ \begin{array}{c}{b}_{i3}\\ b_{i4}\end{array}\end{array}\right)\sim N\left(\left(\begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right),\left(\begin{array}{cc}\begin{array}{cc}0.5& 0\\ 0& 0.5\end{array}& \begin{array}{cc}0.25& 0.25\\ 0.25& 0.25\end{array}\\ \begin{array}{cc}0.25& 0.25\\ 0.25& 0.25\end{array}& \begin{array}{cc}0.5& 0.25\\ 0.25& 0.5\end{array}\end{array}\right)\right),$$ (Equation 5)

and the random error ${\mathit{\epsilon }}_{ij}\sim N\left(0,1\right)$ for each individual j in family i. Then we randomly sampled 3,500 individuals from the 10 × 10 grid in the top left and 6,500 individuals from the rest of the map. The family identifier was removed for all individuals in the analysis, so that there were both population structure and cryptic relatedness in the sample. We compared SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E in analyzing 10,000 independent variant sets based on a linear mixed model using our GMMAT package, including random effects with their covariance matrix proportional to the GRM, and adjusted for the first ten principal components (PCs) of ancestry. We repeated this 4,000 times to get p values combined from 40 million independent genetic variant sets for each test.

Figure 1.

Map of Spatially Continuous Populations from Which Genotypes Were Simulated Based on the Coalescent Model

(A) Map for a single-cohort simulation study: the top left 10 × 10 grid formed population 1, and the rest formed population 2.

(B) Map for a meta-analysis simulation study: scenario A studies were unrelated individuals sampled from population 1 only; scenario B studies were related individuals sampled from specific regions in population 1 and population 2; scenario C studies were unrelated individuals sampled from specific regions in population 1 and population 2; and scenario D studies were related individuals sampled from specific regions in population 2 only.

For binary traits, in each simulation replicate, we simulated the phenotype y_ij for individual j in family i under the null hypothesis of no genetic association from

$$\log \left(\frac{P\left(y_{ij}=1\right)}{1-P\left(y_{ij}=1\right)}\right)={\alpha }_0+b_{ij},$$ (Equation 6)

where ${\alpha }_0$ was chosen such that the disease prevalence was 0.01 in all populations, and the familial random effects b_ij were simulated in the same way as for continuous traits. Then we randomly sampled 2,500 case subjects and 1,000 control subjects from the 10 × 10 grid in the top left (population 1), and 2,500 case subjects and 4,000 control subjects from the rest of the map (population 2) to form a hypothetical study with balanced case and control subjects in combined populations. Therefore, there was confounding by population structure resulting from unequal sampling, even though the disease prevalence was the same. We removed the family identifier, compared SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E in analyzing 10,000 independent variant sets based on a logistic mixed model using our GMMAT package, similarly as described above, and repeated this 4,000 times to get p values combined from 40 million independent genetic variant sets for each test.

Type I Error in Meta-analysis

We also conducted simulation studies in the meta-analysis context to evaluate the type I error rates. We considered four scenarios: unrelated individuals, without confounding by population structure (scenario A studies); related individuals, with confounding by population structure (scenario B studies); unrelated individuals, with confounding by population structure (scenario C studies); and related individuals, without confounding by population structure (scenario D studies).

For scenario A studies, we simulated 16 unrelated individuals in each cell from the 10 × 10 grid in the top left of the map (Figure 1B). For continuous traits, we simulated the phenotype y_ij from Equation 4, with ${\alpha }_1=0$ and b_ij = 0 and randomly sampled 1,000 individuals. For binary traits, we simulated y_ij from Equation 6, with b_ij = 0, and randomly sampled 500 case subjects and 500 control subjects.

For scenario B studies, we simulated eight unrelated individuals, paired them into four families, and simulated two children for each family in each cell from the 10 × 10 grid in the center of the map (Figure 1B). For continuous traits, we simulated the phenotype y_ij from Equation 4, with ${\alpha }_1=1$ and the population indicator Z_i = 1 if family i was from population 1, and Z_i = 0 if from population 2. Familial random effects b_ij were simulated using Equation 5, and we randomly sampled 350 individuals from population 1 and 650 individuals from population 2. For binary traits, we simulated y_ij from Equation 6, with b_ij from Equation 5, and randomly sampled 250 case subjects and 100 control subjects from population 1, and 250 case subjects and 400 control subjects from population 2.

For scenario C studies, we simulated 16 unrelated individuals in each cell from the 20 × 5 grid in the top of the map (Figure 1B). For continuous traits, we simulated the phenotype y_ij from Equation 4, with ${\alpha }_1=1$, the population indicator Z_i = 1 if family i was from population 1 and Z_i = 0 if from population 2, and b_ij = 0, and we randomly sampled 350 individuals from population 1 and 650 individuals from population 2. For binary traits, we simulated y_ij from Equation 6, with b_ij = 0, and randomly sampled 250 case subjects and 100 control subjects from population 1 and 250 case subjects and 400 control subjects from population 2.

For scenario D studies, we simulated 8 unrelated individuals, paired them into 4 families and simulated 2 children for each family in each cell from the 20 × 5 grid in the bottom of the map (Figure 1B). For continuous traits, we simulated the phenotype y_ij from Equation 4, with ${\alpha }_1=0$, familial random effects b_ij simulated using Equation 5, and we randomly sampled 1,000 individuals. For binary traits, we simulated y_ij from Equation 6, with b_ij from Equation 5, and randomly sampled 500 case subjects and 500 control subjects.

In each simulation replicate, we simulated 3 studies from each scenario, totaling 12 studies with a combined sample size of 12,000 (6,000 case subjects and 6,000 control subjects for binary traits). We compared SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E using two meta-analysis strategies: all studies in the same group, and scenario A, B, C, and D studies in four separate groups. In the latter case, three studies from the same scenario were grouped in the same partition with shared genetic effects, while studies from different scenarios were allowed to have heterogeneous genetic effects. Variants are included in the meta-analysis as long as they are polymorphic in at least one of the 12 studies. We repeated 4,000 simulation replicates to get p values from 40 million independent genetic variant sets.

Power

We used the same genotype data as in the single-cohort type I error simulations and evaluated the empirical power of SMMAT-B, SMMAT-S, SMMAT-O, SMMAT-E, and the GLMM extension of MiST (GLMM-MiST) that combines the p value of SMMAT-B (Equation 2) and the p value of SMMAT-S (Equation 3) using Fisher’s method. All tests were performed using weights equal to a beta distribution density function with parameters 1 and 25 on the MAF of each variant.¹³ We considered 9 scenarios, with the proportion of causal variants in a test unit changing from 10% to 20% to 50%, and the proportion of variants with negative effects out of causal variants changing from 100% to 80% to 50%. For continuous traits, we simulated the phenotype y_ij for individual j in family i from

$$y_{ij}={\alpha }_1{Z}_i+\sum _l{G}_{ijl}{\beta }_l+b_{ij}+{\mathit{\epsilon }}_{ij},$$

where ${\alpha }_1=1$, the population indicator Z_i = 1 if family i was from population 1 and Z_i = 0 if from population 2, g_ijl was the centered genotype for causal variant l of individual j in family i, the causal effect size was $\left|{\beta }_l\right|=c\left|{\log }_{10}MA{F}_l\right|$ for variant l with MAF_l, where the constant c was set to 0.2, 0.1, and 0.05 when the proportion of causal variants was 10%, 20%, and 50%, the familial random effects b_ij were simulated using Equation 5, and the random error ${\mathit{\varepsilon }}_{ij}\sim N\left(\mathrm{0,1}\right)$. We randomly sampled 35% individuals from population 1 and 65% individuals from population 2.

For binary traits, we simulated the phenotype y_ij for individual j in family i from

$$\log \left(\frac{P\left(y_{ij}=1\right)}{1-P\left(y_{ij}=1\right)}\right)={\alpha }_0+\sum _l{G}_{ijl}{\beta }_l+b_{ij},$$

where ${\alpha }_0$ was chosen such that the disease prevalence was 0.01 in all populations, G_ijl was the centered genotype for causal variant l of individual j in family i, the causal effect size was $\left|{\beta }_l\right|=c\left|{\log }_{10}MA{F}_l\right|$ for variant l with MAF_l, where the constant c was set to 0.3, 0.2, and 0.1 when the proportion of causal variants was 10%, 20%, and 50%, the familial random effects b_ij were simulated using Equation 5. We randomly sampled 35% individuals (with 25% case subjects and 10% control subjects out of the total sample size) from population 1, and 65% individuals (with 25% case subjects and 40% control subjects out of the total sample size) from population 2 to form a hypothetical study with balanced case and control subjects in combined populations.

For both continuous and binary traits, we varied the total sample size from 2,000 to 5,000 to 10,000, repeated 1,000 simulation replicates for each scenario under the alternative hypothesis, and compared the empirical power at the significance level of 2.5 × 10⁻⁶.

TOPMed Example Involving Fibrinogen Levels

Samples with both plasma fibrinogen measures and whole-genome sequence data (Freeze 5b) from the following 11 TOPMed studies were included in the analysis: the Old Order Amish Study (Amish), Cleveland Family Study (CFS), Genetic Epidemiology of COPD Study (COPDGene), Framingham Heart Study (FHS), Jackson Heart Study (JHS), San Antonio Family Study (SAFS), the Atherosclerosis Risk in Communities (ARIC) Study, Genetic Studies of Atherosclerosis Risk (GeneSTAR), Genetic Epidemiology Network of Arteriopathy (GENOA), the Multi-Ethnic Study of Atherosclerosis (MESA), and Women’s Health Initiative (WHI). The TOPMed studies were approved by institutional review boards at participating institutions, and informed consent was obtained from all study participants. Amish, CFS, FHS, JHS, and SAFS are family-based studies with differing degrees of relatedness. The total sample size was 23,763. Within each study and each ethnicity, measured fibrinogen levels were adjusted for age, sex, and study-specific covariates, and the residuals were rank normalized and rescaled by multiplying by the original standard deviation, so that the transformed phenotype data have the same variances as on the original scale. The transformed phenotype data were pooled together in the analysis, using a heteroscedastic linear mixed model³⁰ allowing for different residual variances in each study/ethnicity, adjusting for study, ethnicity, sequence center, and top ten ancestry PCs³¹ as fixed-effects covariates, and including a GRM calculated by mixed model analysis for pedigrees and populations (MMAP) to model the random effects for relatedness. Rare and low-frequency genetic variants on chromosome 4 with MAF less than 5%, including all singletons and extremely rare variants, were included in our rare variant association analysis of fibrinogen levels using the sliding window method³² with 4 kb non-overlapping windows, using SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E with weights equal to a beta distribution density function with parameters 1 and 25 on the MAF of each variant.¹³ As sensitivity analyses, we also included 1 kb, 10 kb, and 40 kb non-overlapping sliding windows, as well as an analysis using 4 kb windows with no ancestry PC adjustment. The analyses were performed using the GMMAT App (v.0.9.3), which includes the implementation of the SMMAT method, with 32 parallel threads on a single computing node with 240 GB total memory in the Analysis Commons.³³ To benchmark the computational speed in running SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E, we also ran re-analyses to perform each test separately, using summary statistics from the sliding window analysis and a single thread on a computing node with 15 GB total memory in the Analysis Commons.

Results

Simulation Studies

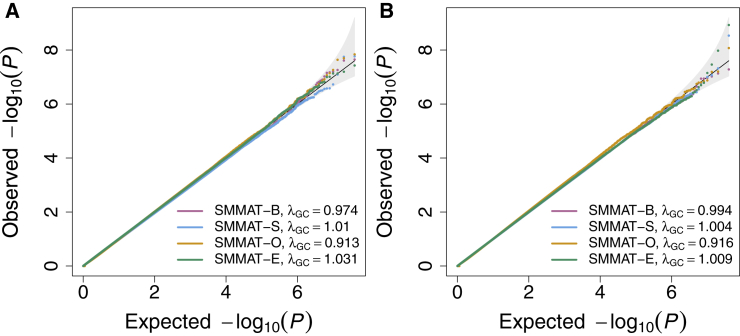
Table 1 shows the empirical type I error rates of SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E at significance levels of 0.05, 0.0001, and 2.5 × 10⁻⁶ in the variant set analyses of continuous and binary traits in single-cohort simulation studies. All four tests have well-controlled type I error rates at these significance levels, suggesting that GLMMs can be effective in adjusting for population structure and cryptic relatedness in complex study samples. This is also consistent with the quantile-quantile (QQ) plots in Figure 2, which show neither inflation nor deflation in the tail.

Table 1.

Empirical Type I Error Rates of SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E in Single-Cohort Simulation Studies at Significance Levels of 0.05, 0.0001, and 2.5 × 10⁻⁶

	Continuous Traits			Binary Traits
Level	0.05	0.0001	2.5 × 10−6	0.05	0.0001	2.5 × 10−6
SMMAT-B	0.047	8.7 × 10−5	2.0 × 10−6	0.049	9.6 × 10−5	2.0 × 10−6
SMMAT-S	0.048	8.7 × 10−5	2.0 × 10−6	0.049	9.5 × 10−5	2.3 × 10−6
SMMAT-O	0.050	1.1 × 10−4	3.0 × 10−6	0.052	1.2 × 10−4	3.0 × 10−6
SMMAT-E	0.050	1.0 × 10−4	3.0 × 10−6	0.050	9.9 × 10−5	2.0 × 10−6

The total sample size was 10,000, and results from 4,000 simulation replicates were combined to get 40 million genetic variant sets.

Figure 2.

Quantile-Quantile Plots of SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E in the Analysis of 10,000 Samples in Single-Cohort Studies with Both Population Structure and Cryptic Relatedness, under the Null Hypothesis of No Genetic Association

(A) Continuous traits in linear mixed models.

(B) Binary traits in logistic mixed models.

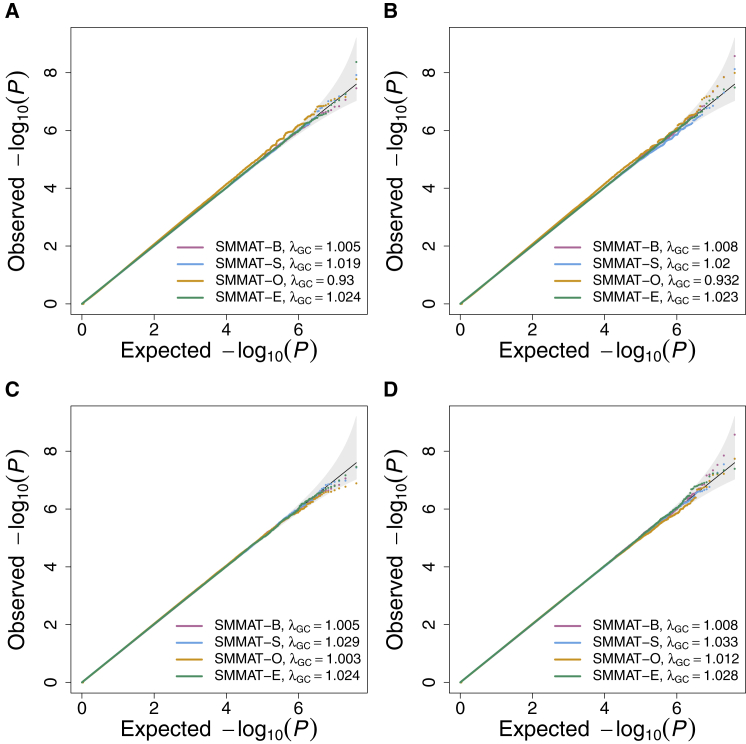
Table 2 and Figure 3 show simulation results of SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E assuming all studies in the same group (hom) or in four separate groups (het) in meta-analyses for combining four types of studies: with and without confounding by population structure, with and without cryptic relatedness. We note that SMMAT-B statistic T_B has the same form in these two meta-analysis strategies,²⁷ so we included seven tests in the simulation studies. In het SMMAT-S, SMMAT-O, and SMMAT-E, studies from the same scenario were grouped together to assume shared genetic effects. Under the null hypothesis of no genetic associations, hom SMMAT-O shows very mild inflation in our simulation settings, but all other six tests in the SMMAT framework control type I error rates well at significance levels of 0.05, 0.0001, and 2.5 × 10⁻⁶ and have well-calibrated tail probabilities, for both continuous and binary traits.

Table 2.

Empirical Type I Error Rates of SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E Assuming All Studies in the Same Group (hom) and Scenario A, B, C, and D Studies in Four Separate Groups (het), in Meta-analysis Simulation Studies at Significance Levels of 0.05, 0.0001, and 2.5 × 10⁻⁶

	Continuous Traits			Binary Traits
Level	0.05	0.0001	2.5 × 10−6	0.05	0.0001	2.5 × 10−6
SMMAT-B	0.051	1.0 × 10−4	2.6 × 10−6	0.051	1.1 × 10−4	2.5 × 10−6
Hom SMMAT-S	0.051	1.0 × 10−4	2.6 × 10−6	0.051	1.1 × 10−4	2.1 × 10−6
Het SMMAT-S	0.051	1.0 × 10−4	2.8 × 10−6	0.052	1.0 × 10−4	2.4 × 10−6
Hom SMMAT-O	0.053	1.3 × 10−4	4.0 × 10−6	0.053	1.4 × 10−4	3.4 × 10−6
Het SMMAT-O	0.052	1.1 × 10−4	2.6 × 10−6	0.052	1.1 × 10−4	2.2 × 10−6
Hom SMMAT-E	0.051	1.0 × 10−4	2.5 × 10−6	0.051	1.1 × 10−4	2.6 × 10−6
Het SMMAT-E	0.051	1.0 × 10−4	2.8 × 10−6	0.052	1.1 × 10−4	3.0 × 10−6

The total sample size was 12,000 from 12 studies, and results from 4,000 simulation replicates were combined to get 40 million genetic variant sets.

Figure 3.

Quantile-Quantile Plots of SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E in the Meta-analysis of 12 Studies with a Total Sample Size of 12,000, under the Null Hypothesis of No Genetic Association

(A) Continuous traits in linear mixed models, all studies in the same group.

(B) Binary traits in logistic mixed models, all studies in the same group.

(C) Continuous traits in linear mixed models, scenario A, B, C, and D studies in four separate groups.

(D) Binary traits in logistic mixed models, scenario A, B, C, and D studies in four separate groups.

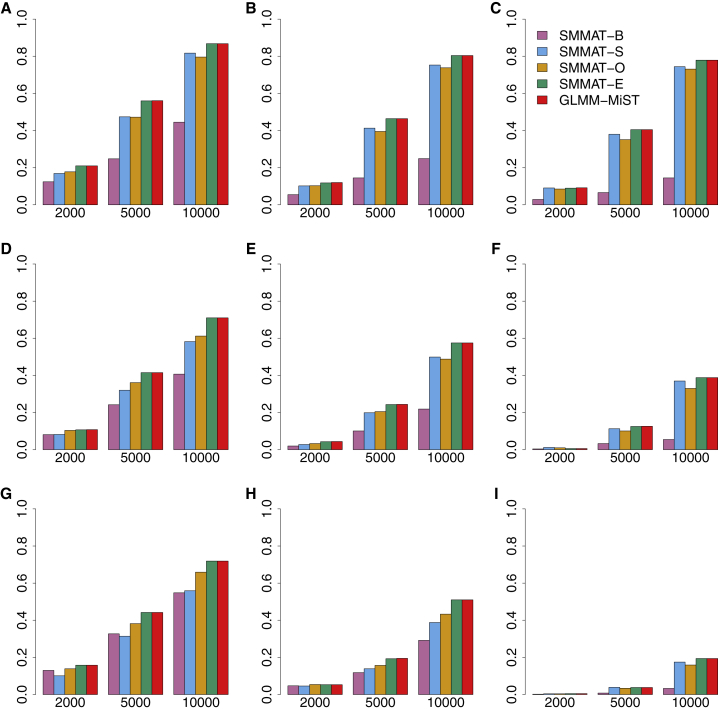
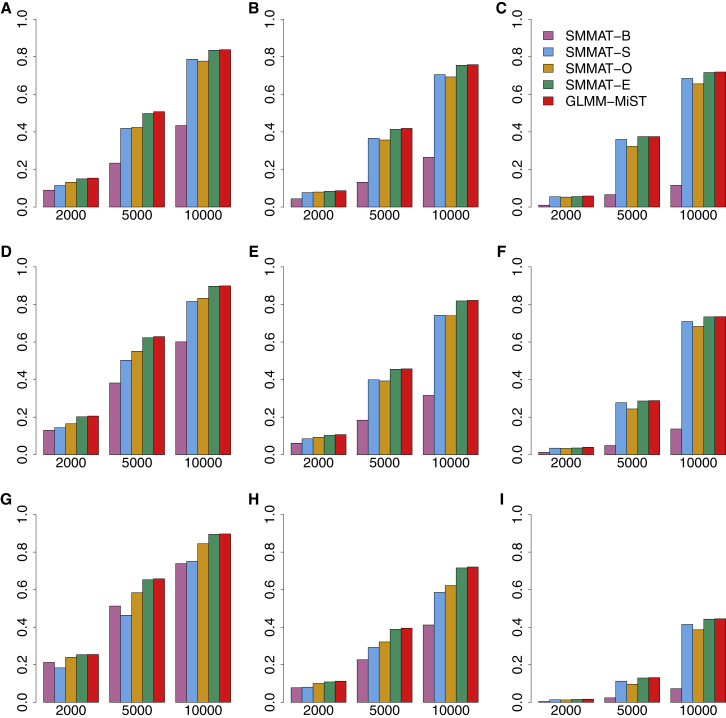
Figures 4 and 5 present the empirical power for causal variant sets at the significance level of 2.5 × 10⁻⁶ for continuous and binary traits, respectively. The power increases with the sample size. As the proportion of causal variants with effects in the same direction drops from 100% to 80% to 50% in each row, the power drops for all tests, but most substantially for the burden test SMMAT-B. When the sample size is large (i.e., 10,000 samples), SMMAT-E and GLMM-MiST have the highest power, for both continuous and binary traits in all nine simulation scenarios. SMMAT-E and GLMM-MiST have almost the same power in all these settings, while GLMM-MiST requires fitting a separate GLMM for each variant set. When all genetic variants in a test unit are causal with large effects in the same direction (a simulation scenario in favor of SMMAT-B, see Supplemental Material and Methods for details), SMMAT-B has the highest power, followed by SMMAT-O and SMMAT-E or GLMM-MiST (Figures S1A and S1B). On the log scale, SMMAT-E and GLMM-MiST p values are very close (Figures S1C and S1D).

Figure 4.

Empirical Power of Linear Mixed Model-Based SMMAT-B, SMMAT-S, SMMAT-O, SMMAT-E, and GLMM-MiST in Continuous Trait Analysis of 2,000, 5,000, and 10,000 Samples

(A–C) 10% causal variants with 100% (A), 80% (B), or 50% (C) negative effects.

(D–F) 20% causal variants with 100% (D), 80% (E), or 50% (F) negative effects.

(G–I) 50% causal variants with 100% (G), 80% (H), or 50% (I) negative effects.

Effect sizes were simulated using the same parameter in each row, but different across rows.

Figure 5.

Empirical Power of Logistic Mixed Model-Based SMMAT-B, SMMAT-S, SMMAT-O, SMMAT-E, and GLMM-MiST in Binary Trait Analysis of 2,000, 5,000, and 10,000 Samples

(A–C) 10% causal variants with 100% (A), 80% (B), or 50% (C) negative effects.

(D–F) 20% causal variants with 100% (D), 80% (E), or 50% (F) negative effects.

(G–I) 50% causal variants with 100% (G), 80% (H), or 50% (I) negative effects.

Effect sizes were simulated using the same parameter in each row, but different across rows.

In the presence of genetic relatedness from multiple sources (see Supplemental Material and Methods for details), linear and logistic mixed models with single GRM random effects and multiple random effects all control type I errors for continuous and binary traits (Figure S2). The multiple random effects model is more powerful than the single GRM random effects models for continuous traits in our simulation settings, although the single GRM random effects models with and without ancestry PC adjustment almost have the same power (Figure S3). For binary traits, compared to the single GRM random effects model adjusting for ten ancestry PCs as fixed effects, the multiple random effects model is slightly more powerful and the single GRM random effects model with no ancestry PC adjustment is generally slightly less powerful, in our simulation settings (Figure S4).

TOPMed Example Involving Fibrinogen Levels

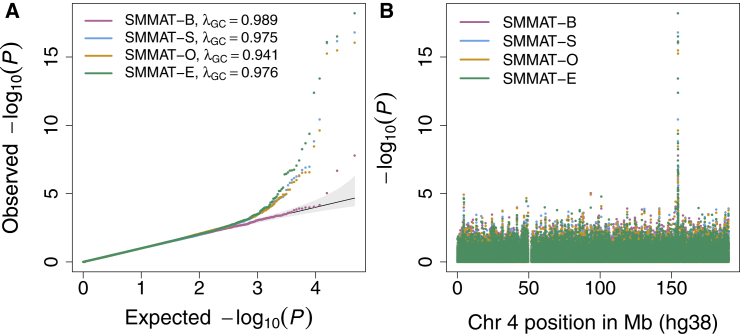
We compared the results from SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E in an analysis of fibrinogen levels, using chromosome 4 (including the genomic region that encodes the fibrinogen protein, FGB) whole-genome sequence data from 11 TOPMed studies. Previous studies have reported two rare variants within FGB on chromosome 4, rs6054 (hg38 position 154,568,456) and rs201909029 (hg38 position 154,567,636) associated with lower fibrinogen levels, with similar effect sizes in all ancestry groups.³⁴ In the sliding window analysis, we grouped low-frequency and rare genetic variants with MAF less than 5% into 46,859 non-overlapping 4 kb windows containing at least one variant. The number of variants in each window passing the MAF filter ranged from 1 to 1,290, with a median of 351 (25% quartile 326 and 75% quartile 380). The QQ plot (Figure 6A) shows that all four tests have well-calibrated tail probabilities. Table 3 summarizes heteroscedastic linear mixed model-based SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E p values in FGB and flanking regions. SMMAT-S, SMMAT-O, and SMMAT-E give the most significant results in the 4 kb window 154,554–154,558 kb, with p values 1.6 × 10⁻¹⁷, 8.9 × 10⁻¹⁷, and 6.2 × 10⁻¹⁹, respectively, while SMMAT-B p value is much larger (6.9 × 10⁻⁵). In the 4 kb window that covers both known association rare variants rs6054 and rs201909029 (window 154,566–154,570 kb), SMMAT-E gives the smallest p value (3.1 × 10⁻¹⁷), followed by SMMAT-S (p value 9.7 × 10⁻¹⁷), SMMAT-O (p value 3.3 × 10⁻¹⁶), and SMMAT-B (p value 1.6 × 10⁻⁸).

Figure 6.

TOPMed Fibrinogen Level SMMAT Analysis Results via a Heteroscedastic Linear Mixed Model on Rare Variants with MAF < 5% in Non-overlapping 4 kb Sliding Windows on Chromosome 4 (n = 23,763)

(A) Quantile-quantile plot.

(B) p values on the log scale versus physical positions of the windows on chromosome 4 (build hg38).

Table 3.

TOPMed Fibrinogen-Level SMMAT p Values in Known Association Gene FGB and Flanking Regions on Chromosome 4, using a Heteroscedastic Linear Mixed Model on Rare Variants with MAF < 5% (n = 23,763)

Start (kb)	End (kb)	No. of Variants	SMMAT-B	SMMAT-S	SMMAT-O	SMMAT-E
154,554	154,558	348	6.9 × 10−5	1.6 × 10−17	8.9 × 10−17	6.2 × 10−19
154,558	154,562	370	0.078	3.7 × 10−11	2.4 × 10−10	3.7 × 10−14
154,562	154,566	326	0.76	1.5 × 10−9	3.5 × 10−9	4.2 × 10−10
154,566	154,570	309	1.6 × 10−8	9.7 × 10−17	3.3 × 10−16	3.1 × 10−17
154,570	154,574	332	0.030	1.9 × 10−7	5.2 × 10−7	8.9 × 10−8
154,574	154,578	349	2.1 × 10−7	7.3 × 10−7	2.8 × 10−7	4.1 × 10−13
154,578	154,582	342	1.7 × 10−4	2.7 × 10−5	2.8 × 10−5	2.1 × 10−9

Physical positions of each window are on build hg38.

In this TOPMed data example, linear mixed models with and without adjusting for ten ancestry PCs as fixed-effects covariates gave very close p values (Figure S5). When we changed the window size from 4 kb to 1 kb (Figure S6), 10 kb (Figure S7), and 40 kb (Figure S8), the QQ plots showed that the analyses were well calibrated and the same association was identified. Regardless of the window size, SMMAT-E almost always gave the smallest p values, except for the 1 kb window 154,567–154,568 kb, which covers rs201909029. For this 1 kb window, none of the tests gave significant p values after adjusting for multiple testing, indicating potential lack of power, since rs201909029 has only 33 minor allele counts in our TOPMed samples (Table S1).

Computation Time

Table 4 shows the CPU time for running the sliding window analysis for 23,763 individuals with TOPMed whole-genome sequence data and fibrinogen levels, using summary statistics from 46,859 non-overlapping 4 kb windows on chromosome 4. The GMMAT App (v.0.9.3) in the Analysis Commons cloud computing platform has implemented SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E, with the option of running one or more tests in an analysis. SMMAT-B results are automatically included when running SMMAT-O or SMMAT-E, and SMMAT-S p values will also be output when running SMMAT-O. Of the four tests in Table 4, SMMAT-B takes shortest time as the p value calculation does not involve any eigen-decomposition of covariance matrices. SMMAT-S takes only about 10 min longer than SMMAT-B for the eigen-decomposition of 46,859 covariance matrices. SMMAT-E takes about 12 min longer than SMMAT-S and gives both SMMAT-B and SMMAT-E p values. SMMAT-O takes 175 min longer than SMMAT-S, as more eigen-decompositions are performed in SMMAT-O when it searches for the optimal combination of SMMAT-B and SMMAT-S on a grid of $\rho$ values. We did not include GLMM-MiST in the analysis, because it took 159 min CPU time to fit a GLMM for this TOPMed sample. By extrapolation, it would take more than 14 years CPU time for analyzing 23,763 related individuals with 46,859 windows using GLMM-MiST.

Table 4.

CPU Time in the TOPMed Fibrinogen Level SMMAT using Summary Statistics from a Sliding Window Analysis using Non-overlapping 4 kb Windows on Chromosome 4 (n = 23,763)

Test	Time (min)
SMMAT-B	81
SMMAT-S	91
SMMAT-O	266
SMMAT-E	103

Tests were performed using the GMMAT App (v.0.9.3) with one single thread on a computing node with 15 GB total memory in the Analysis Commons.

Discussion

We have developed and implemented SMMAT, a family of computationally efficient variant set mixed model association tests for continuous and binary traits in large-scale whole-genome sequencing studies. This framework includes extensions of three widely used variant set tests for unrelated individuals to complex study samples with population structure and cryptic relatedness: the burden test (SMMAT-B), SKAT (SMMAT-S), and SKAT-O (SMMAT-O), as well as a new efficient hybrid test that combines the mixed model burden and SKAT tests (SMMAT-E). Specifically, SMMAT-E is constructed by combining the burden test and an adjusted mixed model SKAT statistic that is approximately asymptotically independent from the mixed model burden test statistic, in a similar spirit to MiST in non-mixed model setting,¹⁵ but that differs from MiST in that it does not require fitting separate mixed effect burden models for each variant set with the set genetic burden as a fixed-effects covariate. Instead, we use matrix projections to approximate the adjusted SKAT statistic from a global null model without any fixed effects for the variant set-specific genetic burden. Of note, this global null model needs to be fit only once in a whole-genome analysis, which greatly reduces the computational cost. The approximation is highly accurate, even in the presence of large genetic effects. We show in simulation studies and the TOPMed fibrinogen example that SMMAT-E is more powerful than the other three tests in large samples, at the computational cost almost on the same scale of SMMAT-B and SMMAT-S. Therefore, SMMAT-E is recommended in the analysis of large-scale whole-genome sequencing studies.

In the SMMAT framework, different weighting strategies can be used. One can use a function of the MAF,^{11, 13} or external measures based on functional annotation such as CADD,³⁵ Eigen,³⁶ FATHMM-XF,³⁷ or tissue-specific annotations, such as GENOSKYLINE,³⁸ as the weight for each variant in a set. In the analysis of fibrinogen levels in TOPMed, we used MAF-based weights. Recently, unified variant set tests allowing for multiple functional annotations have been developed,³⁹ and the SMMAT framework can possibly be extended to accommodate multiple weights. Nevertheless, the optimal weighting strategy in rare variant analysis remains an open question and an active field of research.

As SMMAT-E combines the burden test p value p_B with an asymptotically independent adjusted SKAT p value $p_{\theta }$ using Fisher’s method in our SMMAT implementation in the GMMAT App, we note that other forms of combinations may also be applied.⁴⁰ For example, previous studies have shown that Tippett’s procedure based on the minimum of $p_{\theta }$ and p_B might be more powerful than Fisher’s method in MiST when only one of the p values is small.¹⁵ Alternatively, instead of combining the p values, weighted linear combinations of chi-square statistics have been proposed^{41, 42, 43} and they can also be applied to combine the burden test statistic T_B and the asymptotically independent SKAT statistic $T_{\theta }$ in the SMMAT framework.

SMMAT also has some limitations. SMMAT p values are computed based on asymptotic distributions, which may be not be accurate in small samples, especially for binary traits and heavily skewed continuous traits. For continuous traits, small-sample inference procedures have been proposed for SKAT,^{44, 45} and the same methodology can be applied to SMMAT. For ultra-rare genetic variants with very low minor allele counts, the single-variant scores used to construct SMMAT-B, SMMAT-S, SMMAT-O, and SMMAT-E may not be close to a normal distribution, even if the total sample size is large. If there are only ultra-rare variants (e.g., singletons, doubletons) in a test region and the number of variants is small, SMMAT-B might be the best analysis strategy as its asymptotic property depends on the cumulative minor allele counts. Moreover, the asymptotic issue of single-variant scores also exists for binary traits with highly unbalanced case-control ratios, and a saddlepoint approximation approach has been proposed to match the cumulant generating function of the single-variant scores,⁴⁶ and it has recently been extended to GLMMs.⁴⁷

Fitting GLMMs with a GRM has $O\left(n^3\right)$ complexity in general, where n is the sample size. We have overcome this computational challenge by fitting only one GLMM in a whole-genome analysis and using matrix multiplications with $O\left(n^2\right)$ complexity for each variant set in SMMAT. In large-scale whole-genome sequencing studies, solutions to other computational challenges are being proposed. For example, when the number of variants q in SKAT is very large, eigendecomposition of the covariance matrix, which has $O\left(\min {\left(n,q\right)}^3\right)$ complexity, could be computationally expensive. Recently, the fastSKAT approach has been proposed to efficiently approximate the null distribution of SKAT when q is very large,⁴⁸ and the same strategy can be applied to speed up SMMAT p value calculation for very large q. On the other hand, as the sample size in ongoing large-scale sequencing projects such as TOPMed eventually expands to hundreds of thousands, using a full n × n GRM would not be computationally practical in pooled analyses, as it may take several weeks to fit even only one GLMM with $O\left(n^3\right)$ complexity and $O\left(n^2\right)$ memory footprint. Meta-analyses may be a more appealing analysis strategy in that situation by combining summary statistics from study-specific or ancestry-specific analyses. Essentially equivalently, in pooled analyses, using a sparse and/or block-diagonal GRM with each block corresponding to an individual study in meta-analyses, will help reduce the computational cost in fitting GLMMs, providing one uses specialized routines for manipulation of sparse matrices.⁴⁹ Although whole-genome sequencing studies have not yet been conducted in large biobanks with sample sizes on the scale of millions of individuals, it is expected that calculating the GRM itself would become a major computational bottleneck. Recently, GRM-free mixed effects models such as BOLT-LMM^{6, 50} and SAIGE⁴⁷ have been developed for single variant tests, and we note that extension of these methods to the SMMAT framework will further reduce the computational cost in biobank-scale whole-genome sequencing studies in the future.

In summary, SMMAT provides a flexible and practical statistical framework for large-scale whole-genome sequencing studies with complex study samples, with balanced power and computational performance. With continuing advances in technology, lowering cost and development of new analytical methods, large-scale whole-genome sequencing studies will facilitate human genetic research and enhance our understandings of complex diseases and traits.

Declaration of Interests

In the past three years, E.K.S. received honoraria from Novartis for Continuing Medical Education Seminars and grant and travel support from GlaxoSmithKline. M.H.C. has received grant support from GlaxoSmithKline.

Published: January 10, 2019

Appendix A: Approximations in SMMAT-E

Here we derive the approximations used in SMMAT-E to construct the SKAT-type statistic adjusting for the genetic burden

$$T_{\theta }=\frac{{\left(\mathit{y}-{\tilde{\mathit{\mu }}}_B\right)}^T\mathit{GWW}{\mathit{G}}^T\left(\mathit{y}-{\tilde{\mathit{\mu }}}_B\right)}{{\tilde{\varphi }}^2}.$$

Let $\tilde{\varphi }$, $\tilde{\mathit{\alpha }}$, ${\tilde{\beta }}_0$, ${\tilde{b}}_i$, $\tilde{\mathit{V}}$, and $\tilde{\mathbf{\Sigma }}$ be estimates for $\varphi$, $\mathit{\alpha }$, ${\beta }_0$, $b_i$, $\mathit{V}$, and $\mathbf{\Sigma }$, respectively, from the burden GLMM (Equation 3). We define $\tilde{\mathit{Y}}=\mathit{y}$ as the phenotype vector for continuous traits, and the “working vector” with components ${\tilde{Y}}_i={\mathit{X}}_i\tilde{\mathit{\alpha }}+{\mathit{G}}_i\mathit{W}{\mathbf{1}}_q{\tilde{\beta }}_0+{\tilde{b}}_i+{\left\{{\tilde{\mu }}_{B_i}\left(1-{\tilde{\mu }}_{B_i}\right)\right\}}^{-1}\left(y_i-{\tilde{\mu }}_{B_i}\right)$ at convergence of the logistic burden mixed model for binary traits (Equation 3), where $\tilde{\mathit{\alpha }}$, ${\tilde{\beta }}_0$, ${\tilde{b}}_i$ are fixed-effects and random-effects estimates from the burden GLMM. We have

$$\frac{\mathit{y}-{\tilde{\mathit{\mu }}}_B}{\tilde{\varphi }}={\tilde{\mathit{V}}}^{-1}\left(\tilde{\mathit{Y}}-\mathit{X}\tilde{\mathit{\alpha }}-\mathit{GW}{\mathbf{1}}_q{\tilde{\beta }}_0-\tilde{\mathit{b}}\right)$$

$$={\tilde{\mathbf{\Sigma }}}^{-1}\left(\tilde{\mathit{Y}}-\mathit{X}\tilde{\mathit{\alpha }}-\mathit{GW}{\mathbf{1}}_q{\tilde{\beta }}_0\right)$$

$$={\tilde{\mathbf{\Sigma }}}^{-1}\left\{\tilde{\mathit{Y}}-\left(\begin{array}{cc}\mathit{X}& \mathit{GW}{\mathbf{1}}_q\end{array}\right){\left(\begin{array}{cc}{\mathit{X}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\mathit{X}& {\mathit{X}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\mathit{GW}{\mathbf{1}}_q\\ {\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\mathit{X}& {\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\mathit{GW}{\mathbf{1}}_q\end{array}\right)}^{-1}\left(\begin{array}{c}{\mathit{X}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\\ {\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\end{array}\right)\tilde{\mathit{Y}}\right\}$$

$$=\left\{{\tilde{\mathbf{\Sigma }}}^{-1}-{\tilde{\mathbf{\Sigma }}}^{-1}\mathit{X}{\left({\mathit{X}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\mathit{X}\right)}^{-1}{\mathit{X}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\right\}\tilde{\mathit{Y}}-\left\{{\tilde{\mathbf{\Sigma }}}^{-1}-{\tilde{\mathbf{\Sigma }}}^{-1}\mathit{X}{\left({\mathit{X}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\mathit{X}\right)}^{-1}{\mathit{X}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\right\}\mathit{GW}{\mathbf{1}}_q$$

$${\left[{\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\left\{{\tilde{\mathbf{\Sigma }}}^{-1}-{\tilde{\mathbf{\Sigma }}}^{-1}\mathit{X}{\left({\mathit{X}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\mathit{X}\right)}^{-1}{\mathit{X}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\right\}\mathit{GW}{\mathbf{1}}_q\right]}^{-1}{\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\left\{{\tilde{\mathbf{\Sigma }}}^{-1}-{\tilde{\mathbf{\Sigma }}}^{-1}\mathit{X}{\left({\mathit{X}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\mathit{X}\right)}^{-1}{\mathit{X}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\right\}\tilde{\mathit{Y}}\mathit{.}$$

Note that $\tilde{\varphi }=1$ for binary traits. Moreover, since the true value of ${\beta }_0$ is small, assuming including the genetic burden ${\mathit{G}}_i\mathit{W}{\mathbf{1}}_q$ in the second term in Equation 3 does not dramatically change the variance component estimates for ${\nu }_k$ and $\varphi$ (and for binary traits, also the “working vector” $\tilde{\mathit{Y}}$ at convergence of the model from Equation 2), we have the approximation ${\tilde{\mathbf{\Sigma }}}^{-1}-{\tilde{\mathbf{\Sigma }}}^{-1}\mathit{X}{\left({\mathit{X}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\mathit{X}\right)}^{-1}{\mathit{X}}^T{\tilde{\mathbf{\Sigma }}}^{-1}\approx \hat{\mathit{P}}$ and $\left(\mathit{y}-{\hat{\mathit{\mu }}}_0\right)/\hat{\varphi }\approx \hat{\mathit{P}}\tilde{\mathit{Y}}$, then

$$\frac{\mathit{W}{\mathit{G}}^T\left(\mathit{y}-{\tilde{\mathit{\mu }}}_B\right)}{\tilde{\varphi }}\approx \mathit{W}{\mathit{G}}^T\left\{\hat{\mathit{P}}\tilde{\mathit{Y}}-\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q{\left({\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q\right)}^{-1}{\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\tilde{\mathit{Y}}\right\}$$

$$\approx \left\{{\mathit{I}}_q-\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q{\left({\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q\right)}^{-1}{\mathbf{1}}_q^T\right\}\frac{\mathit{W}{\mathit{G}}^T\left(\mathit{y}-{\hat{\mathit{\mu }}}_0\right)}{\hat{\varphi }}.$$

Therefore,

$$T_{\theta }=\frac{{\left(\mathit{y}-{\tilde{\mathit{\mu }}}_B\right)}^T\mathit{GWW}{\mathit{G}}^T\left(\mathit{y}-{\tilde{\mathit{\mu }}}_B\right)}{{\tilde{\varphi }}^2}$$

$$\approx {\hat{\varphi }}^{-2}{\left(\mathit{y}-{\hat{\mathit{\mu }}}_0\right)}^T\mathit{GW}\left\{{\mathit{I}}_q-{\mathbf{1}}_q{\left({\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q\right)}^{-1}{\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}\right\}\left\{{\mathit{I}}_q-\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q{\left({\mathbf{1}}_q^T\mathit{W}{\mathit{G}}^T\hat{\mathit{P}}\mathit{GW}{\mathbf{1}}_q\right)}^{-1}{\mathbf{1}}_q^T\right\}\mathit{W}{\mathit{G}}^T\left(\mathit{y}-{\hat{\mathit{\mu }}}_0\right).$$

Web Resources

• Analysis Commons, http://analysiscommons.com/

• DNAnexus, https://www.dnanexus.com/

• EPACTS, https://github.com/statgen/EPACTS

• GMMAT (including implementation of SMMAT), https://github.com/hanchenphd/GMMAT

• MMAP, https://github.com/MMAP

• RAREMETAL, https://genome.sph.umich.edu/wiki/RAREMETAL_Documentation

• Rvtests, http://zhanxw.github.io/rvtests/

• seqMeta, https://cran.r-project.org/packages/seqMeta/index.html

• Xihong Lin’s group (including GMMAT), https://content.sph.harvard.edu/xlin/software.html