Asymptotic performance of PCA for high-dimensional heteroscedastic data

Abstract

Principal Component Analysis (PCA) is a classical method for reducing the dimensionality of data by projecting them onto a subspace that captures most of their variation. Effective use of PCA in modern applications requires understanding its performance for data that are both high-dimensional and heteroscedastic. This paper analyzes the statistical performance of PCA in this setting, i.e., for high-dimensional data drawn from a low-dimensional subspace and degraded by heteroscedastic noise. We provide simplified expressions for the asymptotic PCA recovery of the underlying subspace, subspace amplitudes and subspace coefficients; the expressions enable both easy and efficient calculation and reasoning about the performance of PCA. We exploit the structure of these expressions to show that, for a fixed average noise variance, the asymptotic recovery of PCA for heteroscedastic data is always worse than that for homoscedastic data (i.e., for noise variances that are equal across samples). Hence, while average noise variance is often a practically convenient measure for the overall quality of data, it gives an overly optimistic estimate of the performance of PCA for heteroscedastic data.

1. Introduction

Principal Component Analysis (PCA) is a classical method for reducing the dimensionality of data by representing them in terms of a new set of variables, called principal components, where variation in the data is largely captured by the first few principal components [23]. This paper analyzes the asymptotic performance of PCA for data with heteroscedastic noise. In particular, we consider the classical and commonly employed unweighted form of PCA that treats all samples equally and remains a natural choice in applications where estimates of the noise variances are unavailable or one hopes the noise is “close enough” to being homoscedastic. Our analysis uncovers several practical new insights for this setting; the findings both broaden our understanding of PCA and also precisely characterize the impact of heteroscedasticity.

Given zero-mean sample vectors $y_1,\dots ,y_n\in {\mathbb{C}}^d$, the first k principal components ${\widehat{u}}_1,\dots ,{\widehat{u}}_k\in {\mathbb{C}}^d$ and corresponding squared PCA amplitudes ${\widehat{\theta }}_1^2,\dots ,{\widehat{\theta }}_k^2\in {\mathbb{R}}_{+}$ are the first k eigenvectors and eigenvalues, respectively, of the sample covariance matrix $(y_1{y}_1^{\mathrm{H}}+\cdots +y_n{y}_n^{\mathrm{H}})∕n$. The associated score vectors ${\widehat{z}}^{\left(1\right)},\dots ,{\widehat{z}}^{\left(k\right)}\in {\mathbb{C}}^n$ are standardized projections given, for each i ∈ {1,…,k}, by ${\widehat{z}}^{\left(i\right)}=(1∕{\widehat{\theta }}_i){\left\{{\widehat{u}}_i^{\mathrm{H}}\right(y_1,\dots ,y_n\left)\right\}}^{\mathrm{H}}$. The principal components ${\widehat{u}}_1,\dots ,{\widehat{u}}_k$, PCA amplitudes ${\widehat{\theta }}_1,\dots ,{\widehat{\theta }}_k$ and score vectors ${\widehat{z}}^{\left(1\right)},\dots ,{\widehat{z}}^{\left(k\right)}$ are efficiently obtained from the data matrix $(y_1,\dots ,y_n)\in {\mathbb{C}}^{d\times n}$ as its left singular vectors, (scaled) singular values and (scaled) right singular vectors, respectively.

A natural setting for PCA is when data are noisy measurements of points drawn from a subspace. In this case, the first few principal components ${\widehat{u}}_1,\dots ,{\widehat{u}}_k$ form an estimated basis for the underlying subspace; if they recover the underlying subspace accurately then the low-dimensional scores ${\widehat{z}}^{\left(1\right)},\dots ,{\widehat{z}}^{\left(k\right)}$ will largely capture the meaningful variation in the data. This paper analyzes how well the first k principal components ${\widehat{u}}_1,\dots ,{\widehat{u}}_k$, PCA amplitudes ${\widehat{\theta }}_1,\dots ,{\widehat{\theta }}_k$ and score vectors ${\widehat{z}}^{\left(1\right)},\dots ,{\widehat{z}}^{\left(k\right)}$ recover their underlying counterparts when the data are heteroscedastic, that is, when the noise in the data has non-uniform variance across samples.

1.1. High-dimensional, heteroscedastic data

Dimensionality reduction is a fundamental task, so PCA has been applied in a broad variety of both traditional and modern settings. See [23] for a thorough review of PCA and some of its important traditional applications. A sample of modern application areas include medical imaging [2, 33], classification for cancer data 35], anomaly detection on computer networks [24], environmental monitoring [31, 39] and genetics [25], to name just a few.

It is common in modern applications in particular for the data to be high-dimensional (i.e., the number of variables measured is comparable with or larger than the number of samples), which has motivated the development of new techniques and theory for this regime [22]. It is also common for modern data sets to have heteroscedastic noise. For example, Cochran and Horne [11] apply a PCA variant to spectrophotometric data from the study of chemical reaction kinetics. The spectrophotometric data are absorptions at various wavelengths over time, and measurements are averaged over increasing windows of time causing the amount of noise to vary across time. Another example is given in [36], where data are astronomical measurements of stars taken at various times; here changing atmospheric effects cause the amount of noise to vary across time. More generally, in the era of big data where inference is made using numerous data samples drawn from a myriad of different sources, one can expect that both high-dimensionality and heteroscedasticity will be the norm. It is important to understand the performance of PCA in such settings.

1.2. Contributions of this paper

This paper provides simplified expressions for the performance of PCA from heteroscedastic data in the limit as both the number of samples and dimension tend to infinity. The expressions quantify the asymptotic recovery of an underlying subspace, subspace amplitudes and coefficients by the principal components, PCA amplitudes and scores, respectively. The asymptotic recoveries are functions of the samples per ambient dimension, the underlying subspace amplitudes and the distribution of noise variances. Forming the expressions involves first connecting several results from random matrix theory [3, 5] to obtain initial expressions for asymptotic recovery that are difficult to evaluate and analyze, and then exploiting a nontrivial structure in the expressions to obtain much simpler algebraic descriptions. These descriptions enable both easy and efficient calculation and reasoning about the asymptotic performance of PCA.

The impact of heteroscedastic noise, in particular, is not immediately obvious given results of prior literature. How much do a few noisy samples degrade the performance of PCA? Is heteroscedasticity ever beneficial for PCA? Our simplified expressions enable such questions to be answered. In particular, we use these expressions to show that, for a fixed average noise variance, the asymptotic subspace recovery, amplitude recovery and coefficient recovery are all worse for heteroscedastic data than for homoscedastic data (i.e., for noise variances that are equal across samples), confirming a conjecture in [18]. Hence, while average noise variance is often a practically convenient measure for the overall quality of data, it gives an overly optimistic estimate of PCA performance. This analysis provides a deeper understanding of how PCA performs in the presence of heteroscedastic noise.

1.3. Relationship to previous works

Homoscedastic noise has been well-studied, and there are many nice results characterizing PCA in this setting. Benaych-Georges and Nadakuditi [5] give an expression for asymptotic subspace recovery, also found in [21, 29, 32], in the limit as both the number of samples and ambient dimension tend to infinity. As argued in [21], the expression in [5] reveals that asymptotic subspace recovery is perfect only when the number of samples per ambient dimension tends to infinity, so PCA is not (asymptotically) consistent for high-dimensional data. Various alternatives [6, 15, 21] can regain consistency by exploiting sparsity in the covariance matrix or in the principal components. As discussed in [5, 29], the expression in [5] also exhibits a phase transition: the number of samples per ambient dimension must be sufficiently high to obtain non-zero subspace recovery (i.e., for any subspace recovery to occur). This paper generalizes the expression in [5] to heteroscedastic noise; homoscedastic noise is a special case and is discussed in Section 2.3. Once again, (asymptotic) consistency is obtained when the number of samples per ambient dimension tends to infinity, and there is a phase transition between zero recovery and non-zero recovery.

PCA is known to generally perform well in the presence of low to moderate homoscedastic noise and in the presence of missing data [10]. When the noise is standard normal, PCA gives the maximum likelihood (ML) estimate of the subspace [37]. In general, [37] proposes finding the ML estimate via expectation maximization. Conventional PCA is not an ML estimate of the subspace for heteroscedastic data, but it remains a natural choice in applications where we might expect noise to be heteroscedastic but hope it is “close enough” to being homoscedastic. Even for mostly homoscedastic data, however, PCA performs poorly when the heteroscedasticity is due to gross errors (i.e., outliers) [13, 19, 23], which has motivated the development and analysis of robust variants; see [8, 9, 12, 16, 17,26, 34, 40, 42] and their corresponding bibliographies. This paper provides expressions for asymptotic recovery that enable rigorous understanding of the impact of heteroscedasticity.

The generalized spiked covariance model, proposed and analyzed in [4] and [41], generalizes homoscedastic noise in an alternate way. It extends the Johnstone spiked covariance model [20, 21] (a particular homoscedastic setting) by using a population covariance that allows, among other things, non-uniform noise variances within each sample. Non-uniform noise variances within each sample may arise, for example, in applications where sample vectors are formed by concatenating the measurements of intrinsically different quantities. This paper considers data with non-uniform noise variances across samples instead; we model noise variances within each sample as uniform. Data with nonuniform noise variances across samples arise, for example, in applications where samples come from heterogeneous sources, some of which are better quality (i.e., lower noise) than others. See Section S1 of the Online Supplement for a more detailed discussion of connections to spiked covariance models.

Our previous work [18] analyzed the subspace recovery of PCA for heteroscedastic noise but was limited to real-valued data coming from a random one-dimensional subspace where the number of samples exceeded the data dimension. This paper extends that analysis to the more general setting of real- or complex-valued data coming from a deterministic low-dimensional subspace where the number of samples no longer needs to exceed the data dimension. This paper also extends the analysis of [18] to include the recovery of the underlying subspace amplitudes and coefficients. In both works, we use the main results of [5] to obtain initial expressions relating asymptotic recovery to the limiting noise singular value distribution.

The main results of [29] provide non-asymptotic results (i.e., probabilistic approximation results for finite samples in finite dimension) for homoscedastic noise limited to the special case of one-dimensional subspaces. Signal-dependent noise was recently considered in [38], where they analyze the performance of PCA and propose a new generalization of PCA that performs better in certain regimes. A recent extension of [5] to linearly reduced data is presented in [14] and may be useful for analyzing weighted variants of PCA. Such analyses are beyond the scope of this paper, but are interesting avenues for further study.

1.4. Organization of the paper

Section 2 describes the model we consider and states the main results: simplified expressions for asymptotic PCA recovery and the fact that PCA performance is best (for a fixed average noise variance) when the noise is homoscedastic. Section 3 uses the main results to provide a qualitative analysis of how the model parameters (e.g., samples per ambient dimension and the distribution of noise variances) affect PCA performance under heteroscedastic noise. Section 4 compares the asymptotic recovery with non-asymptotic (i.e., finite) numerical simulations. The simulations demonstrate good agreement as the ambient dimension and number of samples grow large; when these values are small the asymptotic recovery and simulation differ but have the same general behavior. Sections 5 and 6 prove the main results. Finally, Section 7 discusses the findings and describes avenues for future work.

2. Main results

2.1. Model for heteroscedastic data

We model n heteroscedastic sample vectors $y_1,\dots ,y_n\in {\mathbb{C}}^d$ from a k-dimensional subspace as

$$y_i=\mathrm{U}{ϴ}_{z_i}+{\eta }_i{\epsilon }_i=\sum _{j=1}^k{\theta }_j{u}_j{\left(z_i^{\left(j\right)}\right)}^{\ast }+{\eta }_i{\epsilon }_i.$$ (1)

The following are deterministic: $\mathbf{U}=(u_1,\dots ,u_k)\in {\mathbb{C}}^{d\times k}$ forms an orthonormal basis for the subspace, $ϴ=\text{diag}({\theta }_1,\dots ,{\theta }_k)\in {\mathbb{R}}_{+}^{k\times k}$ is a diagonal matrix of amplitudes, η_i ∈ {σ₁,…,σ_L} are each one of L noise standard deviations σ₁,…,σ_L, and we define n₁ to be the number of samples with η_i = σ₁, n₂ to be the number of samples with η_i = σ₂ and so on, where n₁ + … + n_L = n.

The following are random and independent: $z_i\in {\mathbb{C}}^k$ are iid sample coefficient vectors that have iid entries with mean E(z_ij) = 0, variance E∣z_ij∣² = 1, and a distribution satisfying the log-Sobolev inequality [1], ${\epsilon }_i\in {\mathbb{C}}^d$ are unitarily invariant iid noise vectors that have iid entries with mean E(ε_ij) = 0, variance E∣ε_ij∣² = 1 and bounded fourth moment E∣ε_ij∣⁴ < ∞, and we define the k (component) coefficient vectors ${\widehat{z}}^{\left(1\right)},\dots ,{\widehat{z}}^{\left(k\right)}\in {\mathbb{C}}^n$ such that the ith entry of z^(j) is $z_i^{\left(j\right)}={\left(z_{ij}\right)}^{\ast }$, the complex conjugate of the jth entry of z_i. Defining the coefficient vectors in this way is convenient for stating and proving the results that follow, as they more naturally correspond to right singular vectors of the data matrix formed by concatenating y₁,…,y_n as columns.

The model extends the Johnstone spiked covariance model [20, 21] by incorporating heteroscedasticity (see Section S1 of the Online Supplement for a detailed discussion). We also allow complex-valued data, as it is of interest in important signal processing applications such as medical imaging; for example, data obtained in magnetic resonance imaging are complex-valued.

Remark 1. By unitarily invariant, we mean that left multiplication of ε_i by any unitary matrix does not change the joint distribution of its entries. As in our previous work [18], this assumption can be dropped if instead the subspace U is randomly drawn according to either the “orthonormalized model” or “iid model” of [5]. Under these models, the subspace U is randomly chosen in an isotropic manner.

Remark 2. The above conditions are satisfied, for example, when the entries z_ij and ε_ij are circularly symmetric complex normal $\mathcal{CN}(0,1)$ or real-valued normal $\mathcal{N}(0,1)$. Rademacher random variables (i.e., ±1 with equal probability) are another choice for coefficient entries z_ij; see Section 2.3.2 of [1] for discussion of the log-Sobolev inequality. We are unaware of non-Gaussian distributions satisfying all conditions for noise entries ε_ij, but as noted in Remark 1, unitary invariance can be dropped if we assume the subspace is randomly drawn as in [5].

Remark 3. The assumption that noise entries ε_ij are identically distributed with bounded fourth moment can be relaxed when they are real-valued as long as an aggregate of their tails still decays sufficiently quickly, i.e., as long as they satisfy Condition 1.3 from [30]. In this setting, the results of [30] replace those of [3] in the proof.

2.2. Simplified expressions for asymptotic recovery

The following theorem describes how well the PCA estimates ${\widehat{u}}_1,\dots ,{\widehat{u}}_k$, ${\widehat{\theta }}_1,\dots ,{\widehat{\theta }}_k$ and ${\widehat{z}}^{\left(1\right)},\dots ,{\widehat{z}}^{\left(k\right)}$ recover the underlying subspace basis u₁,…, u_k, subspace amplitudes θ₁,…, θ_k and coefficient vectors z⁽¹⁾,…, z^(k), as a function of the sample-to-dimension ratio n/d → c > 0, the subspace amplitudes θ₁,…, θ_k, the noise variances ${\sigma }_1^2,\dots ,{\sigma }_L^2$ and corresponding proportions n_ℓ/n → p_ℓ for each ℓ ∈ {1,…, L}. One may generally expect performance to improve with increasing sample-to-dimension ratio and subspace amplitudes; Theorem 1 provides the precise dependence on these parameters as well as on the noise variances and their proportions.

Theorem 1 (Recovery of individual components). Suppose that the sample-to-dimension ratio n/d → c > 0 and the noise variance proportions n_ℓ/n → p_ℓ for ℓ ∈ {1,…, L} as n, d → ∞. Then the ith PCA amplitude ${\widehat{\theta }}_i$ is such that

$${\widehat{\theta }}_i^2\stackrel{a.s.}{\to }\frac{1}{c}\max (\alpha ,{\beta }_i)\left\{1+c\sum _{\ell =1}^L\frac{p_{\ell }{\sigma }_{\ell }^2}{\max (\alpha ,{\beta }_i)-{\sigma }_{\ell }^2}\right\},$$ (2)

where α and β_i are, respectively, the largest real roots of

$$A\left(x\right)=1-c\sum _{\ell =1}^L\frac{p_{\ell }{\sigma }_{\ell }^4}{{(x-{\sigma }_{\ell }^2)}^2},B_i\left(x\right)=1-c{\theta }_i^2\sum _{\ell =1}^L\frac{p_{\ell }}{x-{\sigma }_{\ell }^2}.$$ (3)

Furthermore, if A(β_i) > 0, then the ith principal component ${\widehat{u}}_i$ is such that

$${\mid \langle {\widehat{u}}_i,\text{Span}\{u_j:{\theta }_j={\theta }_i\}\rangle \mid }^2\stackrel{a.s.}{\to }\frac{A\left({\beta }_i\right)}{{\beta }_i{B}_i^{\prime }\left({\beta }_i\right)},{\mid \langle {\widehat{u}}_i,\text{Span}\{u_j:{\theta }_j\ne {\theta }_i\}\rangle \mid }^2\stackrel{a.s.}{\to }0,$$ (4)

the normalized score vector ${\widehat{z}}^{\left(i\right)}∕\sqrt{n}$ is such that

$$\begin{array}{cc}\hfill & {\mid \langle \frac{{\widehat{z}}^i}{\sqrt{n}},\text{Span}\{z^{\left(j\right)}:{\theta }_j={\theta }_i\}\rangle \mid }^2\stackrel{a.s.}{\to }\frac{A\left({\beta }_i\right)}{c\{{\beta }_i+(1-c\left){\theta }_i^2\right\}{B}_i^{\prime }\left({\beta }_i\right)},\hfill \\ \hfill & {\mid \langle \frac{{\widehat{z}}^{\left(i\right)}}{\sqrt{n}},\text{Span}\{z^{\left(j\right)}:{\theta }_j\ne {\theta }_i\}\rangle \mid }^2\stackrel{a.s.}{\to }0,\hfill \end{array}$$ (5)

and

$$\sum _{j:{\theta }_j={\theta }_i}\langle {\widehat{u}}_i,u_j\rangle {\langle \frac{{\widehat{z}}^{\left(i\right)}}{\sqrt{n}},\frac{z^{\left(j\right)}}{\mid \mid z^{\left(j\right)}\mid \mid }\rangle }^{\ast }\stackrel{a.s.}{\to }\frac{A\left({\beta }_i\right)}{\sqrt{c{\beta }_i\{{\beta }_i+(1-c\left){\theta }_i^2\right\}}{B}_i^{\prime }\left({\beta }_i\right)}.$$ (6)

Section 5 presents the proof of Theorem 1. The expressions can be easily and efficiently computed. The hardest part is finding the largest roots of the univariate rational functions A(x) and B_i(x), but off-the-shelf solvers can do this efficiently. See [18] for an example of similar calculations.

The projection ${\mid \langle {\widehat{u}}_i,\text{Span}\{u_j:{\theta }_j={\theta }_i\}\rangle \mid }^2$ in Theorem 1 is the square cosine principal angle between the ith principal component ${\widehat{u}}_i$ and the span of the basis elements with subspace amplitudes equal to θ_i. When the subspace amplitudes are distinct, ${\mid \langle {\widehat{u}}_i,\text{Span}\{u_j:{\theta }_j={\theta }_i\}\rangle \mid }^2={\mid \langle {\widehat{u}}_i,u_i\rangle \mid }^2$ is the square cosine angle between ${\widehat{u}}_i$ and u_i. This value is related by a constant to the squared error between the two (unit norm) vectors and is one among several natural performance metrics for subspace estimation. Similar observations hold for ${\mid \langle {\widehat{z}}^{\left(i\right)}∕\sqrt{n},\text{Span}\{z^{\left(j\right)}:{\theta }_j={\theta }_i\}\mid }^2$. Note that ${\widehat{z}}^{\left(i\right)}∕\sqrt{n}$ has unit norm.

The expressions (4), (5) and (6) apply only if A(β_i) > 0. The following conjecture predicts a phase transition at A(β_i) = 0 so that asymptotic recovery is zero for A(β_i) ≤ 0.

Conjecture 1 (Phase transition). Suppose (as in Theorem 1) that the sample-to-dimension ratio n/d → c > 0 and the noise variance proportions n_ℓ/n → p_ℓ for ℓ ∈ {1,…, L} as n, d → ∞. If A(β_i) ≤ 0, then the ith principal component ${\widehat{u}}_i$ and the normalized score vector ${\widehat{z}}^{\left(i\right)}∕\sqrt{n}$ are such that

$${\mid \langle {\widehat{u}}_i,\text{Span}\{u_1,\dots ,u_k\}\rangle \mid }^2\stackrel{a.s.}{\to }0,{\mid \langle \frac{{\widehat{z}}^{\left(i\right)}}{\sqrt{n}},\text{Span}\{z^{\left(1\right)},\dots ,z^{\left(k\right)}\}\rangle \mid }^2\stackrel{a.s.}{\to }0.$$

This conjecture is true for a data model having Gaussian coefficients and homoscedastic Gaussian noise as shown in [32]. It is also true for a one-dimensional subspace (i.e., k = 1) as we showed in [18]. Proving it in general would involve showing that the singular values of the matrix whose columns are the noise vectors exhibit repulsion behavior; see Remark 2.13 of [5].

2.3. Homoscedastic noise as a special case

For homoscedastic noise with variance σ², A(x) = 1 – cσ⁴/(x – σ²)² and $B_i\left(x\right)=1-c{\theta }_i^2∕(x-{\sigma }^2)$. The largest real roots of these functions are, respectively, $\alpha =(1+\sqrt{c}){\sigma }^2$ and ${\beta }_i={\sigma }^2+c{\theta }_i^2$. Thus the asymptotic PCA amplitude (2) becomes

$${\widehat{\theta }}_i^2\stackrel{a.s.}{\to }\{\begin{array}{cc}{\theta }_i^2\{1+{\sigma }^2∕(c{\theta }_i^2\left)\right\}(1+{\sigma }^2∕{\theta }_i^2)\hfill & \text{if}c{\theta }_i^4>{\sigma }^4,\hfill \\ {\sigma }^2{(1+1∕\sqrt{c})}^2\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (7)

Further, if $c{\theta }_i^4>{\sigma }^4$, then the non-zero portions of asymptotic subspace recovery (4) and coefficient recovery (5) simplify to

$$\begin{array}{cc}\hfill {\mid \langle {\widehat{u}}_i,\text{Span}\{u_j:{\theta }_j={\theta }_i\}\rangle \mid }^2& \stackrel{a.s.}{\to }\frac{c-{\sigma }^4∕{\theta }_i^4}{c+{\sigma }^2∕{\theta }_i^2},\hfill \\ \hfill {\mid \langle \frac{{\widehat{z}}^{\left(i\right)}}{\sqrt{n}},\text{Span}\{z^{\left(j\right)}:{\theta }_j={\theta }_i\}\rangle \mid }^2& \stackrel{a.s.}{\to }\frac{c-{\sigma }^4∕{\theta }_i^4}{c(1+{\sigma }^2∕{\theta }_i^2)},\hfill \end{array}$$ (8)

These limits agree with the homoscedastic results in [5, 7, 21, 29, 32]. As noted in Section 2.2, Conjecture 1 is known to be true when the coefficients are Gaussian and the noise is both homoscedastic and Gaussian, in which case (8) becomes

$$\begin{array}{cc}\hfill {\mid \langle {\widehat{u}}_i,\text{Span}\{u_j:{\theta }_j={\theta }_i\}\rangle \mid }^2& \stackrel{a.s.}{\to }\max \left(0,\frac{c-{\sigma }^4∕{\theta }_i^4}{c+{\sigma }^2∕{\theta }_i^2}\right),\hfill \\ \hfill {\mid \langle \frac{{\widehat{z}}^{\left(i\right)}}{\sqrt{n}},\text{Span}\{z^{\left(j\right)}:{\theta }_j={\theta }_i\}\rangle \mid }^2& \stackrel{a.s.}{\to }\max \left\{0,\frac{c-{\sigma }^4∕{\theta }_i^4}{c(1+{\sigma }^2∕{\theta }_i^2)}\right\}.\hfill \end{array}$$

See Section 2 of [21] Section and 2.3 of [32] for a discussion of this result.

2.4. Bias of the PCA amplitudes

The simplified expression in (2) enables us to immediately make two observations about the recovery of the subspace amplitudes θ₁,…,θ_k by the PCA amplitudes ${\widehat{\theta }}_1,\dots ,{\widehat{\theta }}_k$

Remark 4 (Positive bias in PCA amplitudes). The largest real root β_i of B_i(x) is greater than ${\max }_{\ell }\left({\sigma }_{\ell }^2\right)$. Thus $1∕({\beta }_i-{\sigma }_{\ell }^2)>1∕{\beta }_i$ for ℓ ∈ {1,…, L} and so evaluating (3) at β_i yields

$$0=B_i\left({\beta }_i\right)=1-c{\theta }_i^2\sum _{\ell =1}^L\frac{p_{\ell }}{{\beta }_i-{\sigma }_{\ell }^2}<1-c{\theta }_i^2\frac{1}{{\beta }_i}.$$

As a result, ${\beta }_i>c{\theta }_i^2$, so the asymptotic PCA amplitude (2) exceeds the subspace amplitude, i.e., ${\widehat{\theta }}_i$ is positively biased and is thus an inconsistent estimate of θ_i. This is a general phenomenon for noisy data and motivates asymptotically optimal shrinkage in [27].

Remark 5 (Alternate formula for amplitude bias). If A(β_i) ≥ 0, then β_i ≥ α because A(x) and B_i(x) are both increasing functions for $x>{\max }_{\ell }\left({\sigma }_{\ell }^2\right)$. Thus, the asymptotic amplitude bias is

$$\begin{array}{cc}\hfill \frac{{\widehat{\theta }}_i^2}{{\theta }_i^2}\stackrel{a.s.}{\to }\frac{{\beta }_i}{c{\theta }_i^2}\left(1+c\sum _{\ell =1}^L\frac{p_{\ell }{\sigma }_{\ell }^2}{{\beta }_i-{\sigma }_{\ell }^2}\right)& =\frac{{\beta }_i}{c{\theta }_i^2}\left\{1+c\sum _{\ell =1}^L{p}_{\ell }\left(-1+\frac{{\beta }_i}{{\beta }_i-{\sigma }_{\ell }^2}\right)\right\}\hfill \\ \hfill & =\frac{{\beta }_i}{c{\theta }_i^2}\left(1+{\beta }_{i}c\sum _{\ell =1}^L\frac{p_{\ell }}{{\beta }_i-{\sigma }_{\ell }^2}-c\right)=\frac{{\beta }_i}{c{\theta }_i^2}\left[1+\frac{{\beta }_i}{{\theta }_i^2}\{1-B_i({\beta }_i\left)\right\}-c\right]\hfill \\ \hfill & =\frac{{\beta }_i}{c{\theta }_i^2}\left(1+\frac{{\beta }_i}{{\theta }_i^2}-c\right)=1+\left(\frac{{\beta }_i}{c{\theta }_i^2}-1\right)\left(\frac{{\beta }_i}{{\theta }_i^2}+1\right),\hfill \end{array}$$ (9)

where we have applied (2), divided the summand with respect to ${\sigma }_{\ell }^2$, used the facts that p₁ +…+ p_L = 1 and B_i(β_i) = 0, and finally factored. The expression (9) shows that the positive bias is an increasing function of β_i when A(β_i) ≥ 0.

2.5. Overall subspace and signal recovery

Overall subspace recovery is more useful than individual component recovery when subspace amplitudes are equal and so individual basis elements are not identifiable. It is also more relevant when we are most interested in recovering or denoising low-dimensional signals in a subspace. Overall recovery of the low-dimensional signal, quantified here by mean square error, is useful for understanding how well PCA “denoises” the data taken as a whole.

Corollary 1 (Overall recovery). Suppose (as in Theorem 1) that the sample-to-dimension ratio n/d → c > 0 and the noise variance proportions n_ℓ/n → p_ℓ for ℓ ∈ {1,…, L} as n, d → ∞. If A(β₁),…, A(β_k) > 0, then the subspace estimate $\widehat{\mathrm{U}}=({\widehat{u}}_1,\dots ,{\widehat{u}}_k)\in {\mathbb{C}}^{d\times k}$ from PCA is such that

$$\frac{1}{k}{\mid \mid {\widehat{\mathrm{U}}}^{\mathrm{H}}\mathrm{U}\mid \mid }_F^2\stackrel{a.s.}{\to }\frac{1}{k}\sum _{i=1}^k\frac{A\left({\beta }_i\right)}{{\beta }_i{B}_i^{\prime }\left({\beta }_i\right)},$$ (10)

and the mean square error is

$$\frac{1}{n}\sum _{i=1}^n{\Vert \mathrm{U}{ϴ}_{z_i}-\widehat{\mathrm{U}}{\widehat{ϴ}}_{{\widehat{z}}_i}\Vert }_2^2\stackrel{a.s.}{\to }\sum _{i=1}^{k}2\left\{{\theta }_i^2-\frac{A\left({\beta }_i\right)}{c{B}^{\prime }\left({\beta }_i\right)}\right\}+\left(\frac{{\beta }_i}{c{\theta }_i^2}-1\right)({\beta }_i+{\theta }_i^2),$$ (11)

where A(x), B_i(x) and β_i are as in Theorem 1, and ${\widehat{z}}_i$ is the vector of score entries for the ith sample. Proof of Corollary 1. The subspace recovery can be decomposed as

$$\frac{1}{k}{\mid \mid {\widehat{\mathrm{U}}}^{\mathrm{H}}\mathrm{U}\mid \mid }_F^2=\frac{1}{k}\sum _{i=1}^k{\Vert {\widehat{u}}_i^{\mathrm{H}}{\mathrm{U}}_{j:{\theta }_j={\theta }_i}\Vert }_2^2+{\Vert {\widehat{u}}_i^{\mathrm{H}}{\mathrm{U}}_{j:{\theta }_j\ne {\theta }_i}\Vert }_2^2,$$

where the columns of U_j:θj=θi are the basis elements u_j with subspace amplitude θ_j equal to θ_i, and the remaining basis elements are the columns of U_j:θj≠θi. Asymptotic overall subspace recovery (10) follows by noting that these terms are exactly the square cosine principal angles in (4) of Theorem 1.

The mean square error can also be decomposed as

$$\begin{array}{cc}\hfill \frac{1}{n}\sum _{i=1}^n{\Vert \mathrm{U}{ϴ}_{Z_i}-\widehat{\mathrm{U}}{\widehat{ϴ}}_{{\widehat{z}}_i}\Vert }_2^2& ={\Vert \mathrm{U}ϴ{\left(\frac{1}{\sqrt{n}}\mathrm{Z}\right)}^{\mathrm{H}}-\widehat{\mathrm{U}}\widehat{ϴ}{\left(\frac{1}{\sqrt{n}}\widehat{Z}\right)}^{\mathrm{H}}\Vert }_F^2\hfill \\ \hfill & =\sum _{i=1}^k{\theta }_i^2\left[{\Vert \frac{z^{\left(i\right)}}{\sqrt{n}}\Vert }_2^2+\frac{{\widehat{\theta }}_i^2}{{\theta }_i^2}-2\Re \left\{\frac{{\widehat{\theta }}_i}{{\theta }_i}\sum _{j=1}^k\frac{{\theta }_j}{{\theta }_i}\langle {\widehat{u}}_i,u_j\rangle {\langle \frac{{\widehat{z}}^{\left(i\right)}}{\sqrt{n}},\frac{z^{\left(j\right)}}{\sqrt{n}}\rangle }^{\ast }\right\}\right],\hfill \end{array}$$ (12)

where $\mathbf{Z}=(z^{\left(1\right)},\dots ,z^{\left(k\right)})\in {\mathbb{C}}^{n\times k}$, $\widehat{\mathbf{Z}}=({\widehat{z}}^{\left(1\right)},\dots ,{\widehat{z}}^{\left(k\right)})\in {\mathbb{C}}^{n\times k}$ and $\Re$ denotes the real part of its argument. The first term of (1212) has almost sure limit 1 by the law of large numbers. The almost sure limit of the second term is obtained from (9). We can disregard the summands in the inner sum for which θ_j ≠ θ_i; by (4) and (5) these terms have an almost sure limit of zero (the inner products both vanish). The rest of the inner sum

$$\sum _{j:{\theta }_j={\theta }_i}\frac{{\theta }_j}{{\theta }_i}\langle {\widehat{u}}_i,u_j\rangle {\langle \frac{{\widehat{z}}^{\left(i\right)}}{\sqrt{n}},\frac{z^{\left(j\right)}}{\sqrt{n}}\rangle }^{\ast }=\sum _{j:{\theta }_j={\theta }_i}\left(1\right)\langle {\widehat{u}}_i,u_j\rangle {\langle \frac{{\widehat{z}}^{\left(i\right)}}{\sqrt{n}},\frac{z^{\left(j\right)}}{\sqrt{n}}\rangle }^{\ast }$$

has the same almost sure limit as in (6) because ${\Vert z^{\left(i\right)}∕\sqrt{n}\Vert }^2\to 1\text{as}n\to \infty$. Combining these almost sure limits and simplifying yields (11).

2.6. Importance of homoscedasticity

How important is homoscedasticity for PCA? Does having some low noise data outweigh the cost of introducing heteroscedasticity? Consider the following three settings:

1. - All samples have noise variance 1 (i.e., data are homoscedastic).

2. - 99% of samples have noise variance 1.01 but 1% have noise variance 0.01.

3. - 99% of samples have noise variance 0.01 but 1% have noise variance 99.01.

In all three settings, the average noise variance is 1. We might expect PCA to perform well in Setting 1 because it has the smallest maximum noise variance. However, Setting 2 may seem favorable because we obtain samples with very small noise, and suffer only a slight increase in noise for the rest. Setting 3 may seem favorable because most of the samples have very small noise. However, we might also expect PCA to perform poorly because 1% of samples have very large noise and will likely produce gross errors (i.e., outliers). Between all three, it is not initially obvious what setting PCA will perform best in. The following theorem shows that PCA performs best when the noise is homoscedastic, as in Setting 1.

Theorem 2. Homoscedastic noise produces the best asymptotic PCA amplitude (2), subspace recovery (4) and coefficient recovery (5) in Theorem 1 for a given average noise variance ${\stackrel{‒}{\sigma }}^2=p_1{\sigma }_1^2+\cdots +p_L{\sigma }_L^2$ over all distributions of noise variances for which A(β_i) > 0. Namely, homoscedastic noise minimizes (2) (and hence the positive bias) and it maximizes (4) and (5).

Concretely, suppose we had c = 10 samples per dimension and a subspace amplitude of θ_i = 1. Then the asymptotic subspace recoveries (4) given in Theorem 1 evaluate to 0.818 in Setting 1, 0.817 in Setting 2 and 0 in Setting 3; asymptotic recovery is best in Setting 1 as predicted by Theorem 2. Recovery is entirely lost in Setting 3, consistent with the observation that PCA is not robust to gross errors. In Setting 2, only using the 1% of samples with noise variance 0.01 (resulting in 0.1 samples per dimension) yields an asymptotic subspace recovery of 0.908 and so we may hope that recovery with all data could be better. Theorem 2 rigorously shows that PCA does not fully exploit these high quality samples and instead performs worse in Setting 2 than in Setting 1, if only slightly.

Section 6 presents the proof of Theorem 2. It is notable that Theorem 2 holds for all proportions p, sample-to-dimension ratios c and subspace amplitudes θ_i; there are no settings where PCA benefits from heteroscedastic noise over homoscedastic noise with the same average variance. The following corollary is equivalent and provides an alternate way of viewing the result.

Corollary 2 (Bounds on asymptotic recovery). If A(β_i) ≥ 0 then the asymptotic PCA amplitude (2) is bounded as

$${\widehat{\theta }}_i^2\stackrel{a.s.}{\to }{\theta }_i^2+{\theta }_i^2\left(\frac{{\beta }_i}{c{\theta }_i^2}-1\right)\left(\frac{{\beta }_i}{{\theta }_i^2}+1\right)\ge {\theta }_i^2\left(1+\frac{{\stackrel{‒}{\sigma }}^2}{c{\theta }_i^2}\right)\left(1+\frac{{\stackrel{‒}{\sigma }}^2}{{\theta }_i^2}\right),$$ (13)

the asymptotic subspace recovery (4) is bounded as

$${\mid \langle {\widehat{u}}_i,\text{Span}\{u_j:{\theta }_j={\theta }_i\}\rangle \mid }^2\stackrel{a.s.}{\to }\frac{A\left({\beta }_i\right)}{{\beta }_i{B}_i^{\prime }\left({\beta }_i\right)}\le \frac{c-{\stackrel{‒}{\sigma }}^4∕{\theta }_i^4}{c+{\stackrel{‒}{\sigma }}^2∕{\theta }_i^2},$$ (14)

and the asymptotic coefficient recovery (5) is bounded as

$${\mid \langle \frac{{\widehat{z}}^{\left(i\right)}}{\sqrt{n}},\text{Span}\{z^{\left(j\right)}:{\theta }_j={\theta }_i\}\rangle \mid }^2\stackrel{a.s.}{\to }\frac{A\left({\beta }_i\right)}{c\{{\beta }_i+(1-c\left){\theta }_i^2\right\}{B}_i^{\prime }\left({\beta }_i\right)}\le \frac{c-{\stackrel{‒}{\sigma }}^4∕{\theta }_i^4}{c(1+{\stackrel{‒}{\sigma }}^2∕{\theta }_i^2)},$$ (15)

where ${\stackrel{‒}{\sigma }}^2=p_1{\sigma }_1^2+\cdots +p_L{\sigma }_L^2$ is the average noise variance and the bounds are met with equality if and only if ${\sigma }_1^2=\cdots ={\sigma }_L^2$. Proof of Corollary 2. The bounds (13), (14) and (15) follow immediately from Theorem 2 and the expressions for homoscedastic noise (7) and (8) in Section 2.3.

Corollary 2 highlights that while average noise variance may be a practically convenient measure for the overall quality of data, it can lead to an overly optimistic estimate of the performance of PCA for heteroscedastic data. The expressions (2), (4) and (5) in Theorem 1 are more accurate.

Remark 6 (Average inverse noise variance). Average inverse noise variance $\mathcal{I}=p_1\times 1∕{\sigma }_1^2+\cdots +p_L\times 1∕{\sigma }_L^2$ is another natural measure for the overall quality of data. In particular, it is the (scaled) Fisher information for heteroscedastic Gaussian measurements of a fixed scalar. Theorem 2 implies that homoscedastic noise also produces the best asymptotic PCA performance for a given average inverse noise variance; note that homoscedastic noise minimizes the average noise variance in this case. Thus, average inverse noise variance can also lead to an overly optimistic estimate of the performance of PCA for heteroscedastic data.

3. Impact of parameters

The simplified expressions in Theorem 1 for the asymptotic performance of PCA provide insight into the impact of the model parameters: sample-to-dimension ratio c, subspace amplitudes θ₁,…, θ_k, proportions p₁,…, p_L and noise variances ${\sigma }_1^2,\dots ,{\sigma }_L^2$. For brevity, we focus on the asymptotic subspace recovery (4) of the ith component; similar phenomena occur for the asymptotic PCA amplitudes (2) and coefficient recovery (5) as we show in Section S3 of the Online Supplement.

3.1. Impact of sample-to-dimension ratio c and subspace amplitude θ_i

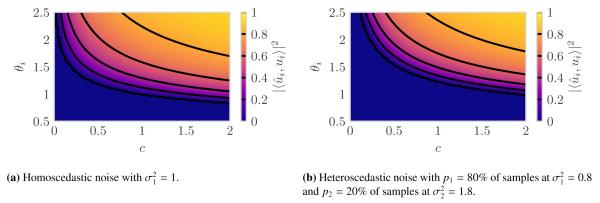
Suppose first that there is only one noise variance fixed at ${\sigma }_1^2$ while we vary the sample-to-dimension ratio c and subspace amplitude θ_i. This is the homoscedastic setting described in Section 2.3. Figure 1a illustrates the expected behavior: decreasing the subspace amplitude θ_i degrades asymptotic subspace recovery (4) but the lost performance could be regained by increasing the number of samples. Figure 1a also illustrates a phase transition: a sufficient number of samples with a sufficiently large subspace amplitude is necessary to have an asymptotic recovery greater than zero. Note that in all such figures, we label the axis ${\mid \langle {\widehat{u}}_i,u_i\rangle \mid }^2$ to indicate the asymptotic recovery on the right hand side of (4).

Figure 1:

Asymptotic subspace recovery (4) of the ith component as a function of sample-to-dimension ratio c and subspace amplitude θ_i with average noise variance equal to one. Contours are overlaid in black and the region where A(β_i) ≤ 0 is shown as zero (the prediction of Conjecture 1). The phase transition in (b) is further right than in (a); more samples are needed to recover the same strength signal.

Now suppose that there are two noise variances ${\sigma }_1^2=0.8$ and ${\sigma }_2^2=1.8$ occurring in proportions p₁ = 80% and p₂ = 20%. The average noise variance is still 1, and Figure 1b illustrates similar overall features to the homoscedastic case. Decreasing subspace amplitude θ_i once again degrades asymptotic subspace recovery (4) and the lost performance could be regained by increasing the number of samples. However, the phase transition is further up and to the right compared to the homoscedastic case. This is consistent with Theorem 2; PCA performs worse on heteroscedastic data than it does on homoscedastic data of the same average noise variance, and thus more samples or a larger subspace amplitude are needed to recover the subspace basis element.

3.2. Impact of proportions p₁,…, p_L

Suppose that there are two noise variances ${\sigma }_1^2=0.1$ and ${\sigma }_2^2=3.25$ occurring in proportions p₁ = 1 – p₂ and p₂, where the sample-to-dimension ratio is c = 10 and the subspace amplitude is θ_i = 1. Figure 2 shows the−asymptotic subspace recovery (4) as a function of the proportion p₂. Since ${\sigma }_2^2$ is significantly larger, it is natural to think of p₂ as a fraction of contaminated samples. As expected, performance generally degrades as p₂ increases and low noise samples with noise variance ${\sigma }_1^2$ are traded for high noise samples with noise variance ${\sigma }_2^2$. The performance is best when p₂ = 0 and all the samples have the smaller noise variance ${\sigma }_1^2$ (i.e., there is no contamination).

Figure 2:

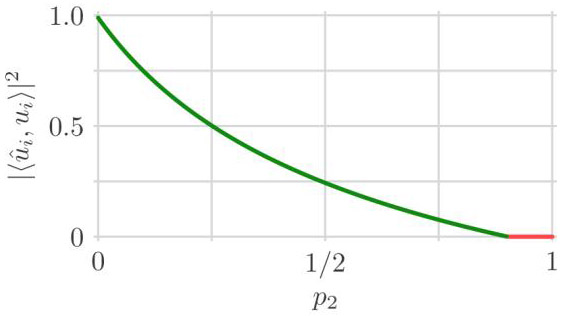
Asymptotic subspace recovery (4) of the ith component as a function of the contamination fraction p₂, the proportion of samples with noise variance ${\sigma }_2^2=3.25$, where the other noise variance ${\sigma }_1^2=0.1$ occurs in proportion p₁ = 1 – p₂. The sample-to-dimension ratio is c = 10 and the subspace amplitude is θ_i = 1. The region where A(β_i) ≤ 0 is the red horizontal segment with value zero (the prediction of Conjecture 1).

It is interesting that the asymptotic subspace recovery in Figure 2 has a steeper slope initially for p₂ close to zero and then a shallower slope for p₂ close to one. Thus the benefit of reducing the contamination fraction varies across the range.

3.3. Impact of noise variances ${\sigma }_1^2,\dots ,{\sigma }_L^2$

Suppose that there are two noise variances ${\sigma }_1^2$ and ${\sigma }_2^2$ occurring in proportions p₁ = 70% and p₂ = 30%, where the sample-to-dimension ratio is c = 10 and the subspace amplitude is θ_i = 1. Figure 3 shows the asymptotic subspace recovery (4) as a function of the noise variances ${\sigma }_1^2$ and ${\sigma }_2^2$. As expected, performance typically degrades with increasing noise variances. However, there is a curious regime around ${\sigma }_1^2=0$ and ${\sigma }_2^2=4$ where increasing ${\sigma }_1^2$ slightly from zero improves asymptotic performance; the contour lines point slightly up and to the right. We have also observed this phenomenon in finite-dimensional simulations, so this effect is not simply an asymptotic artifact. This surprising phenomenon is an interesting avenue for future exploration.

Figure 3:

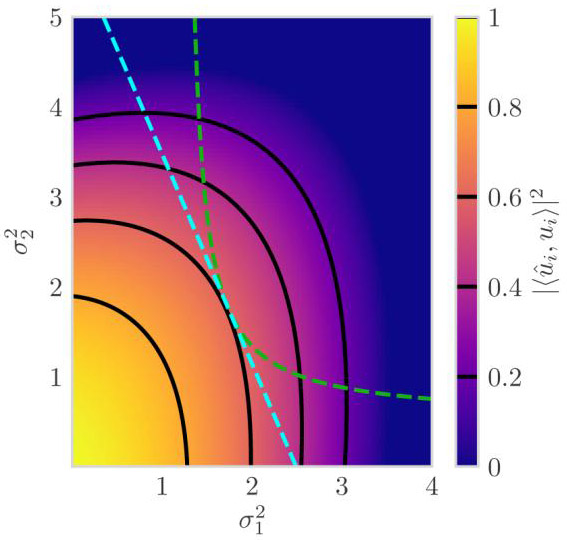
Asymptotic subspace recovery (4) of the ith component as a function of noise variances ${\sigma }_1^2$ and ${\sigma }_2^2$ occurring in proportions p₁ = 70% and p₂ = 30%, where the sample-to-dimension ratio is c = 10 and the subspace amplitude is θ_i = 1. Contours are overlaid in black and the region where A(β_i) ≤ 0 is shown as zero (the prediction of Conjecture 1). Along the dashed cyan line, the average noise variance is ${\stackrel{‒}{\sigma }}^2\approx 1.74$ and the best performance occurs when ${\sigma }_1^2={\sigma }_2^2={\stackrel{‒}{\sigma }}^2$. Along the dashed green curve, the average inverse noise variance is $\mathcal{I}\approx 0.575$ and the best performance again occurs when ${\sigma }_1^2={\sigma }_2^2$.

The contours in Figure 3 are generally horizontal for small ${\sigma }_1^2$ and vertical for small ${\sigma }_2^2$. This indicates that when the gap between the two largest noise variances is “sufficiently” wide, the asymptotic subspace recovery (4) is roughly determined by the largest noise variance. While initially unexpected, this property can be intuitively understood by recalling that β_i is the largest value of x satisfying

$$\frac{1}{c{\theta }_i^2}=\sum _{\ell =1}^L\frac{p_{\ell }}{x-{\sigma }_{\ell }^2}.$$ (16)

When the gap between the two largest noise variances is wide, the largest noise variance is significantly larger than the rest and it dominates the sum in (16) for $x>{\max }_{\ell }\left({\sigma }_{\ell }^2\right)$, i.e., where β_i occurs. Thus β_i, and similarly, A(β_i) and $B_i^{\prime }\left({\beta }_i\right)$ are roughly determined by the largest noise variance.

The precise relative impact of each noise variance ${\sigma }_2^{\ell }$ depends on its corresponding proportion p_ℓ, as shown by the asymmetry of Figure 3 around the line ${\sigma }_1^2={\sigma }_2^2$. Nevertheless, very large noise variances can drown out the impact of small noise variances, regardless of their relative proportions. This behavior provides a rough explanation for the sensitivity of PCA to even a few gross errors (i.e., outliers); even in small proportions, sufficiently large errors dominate the performance of PCA.

Along the dashed cyan line in Figure 3, the average noise variance is ${\stackrel{‒}{\sigma }}^2\approx 1.74$ and the best performance occurs when ${\sigma }_1^2={\sigma }_2^2={\stackrel{‒}{\sigma }}^2$, as predicted by Theorem 2. Along the dashed green curve, the average inverse noise variance is $\mathcal{I}\approx 0.575$ and the best performance again occurs when ${\sigma }_1^2={\sigma }_2^2$, as predicted in Remark 6. Note, in particular, that the dashed line and curve are both tangent to the contour at exactly ${\sigma }_1^2={\sigma }_2^2$. The observation that larger noise variances have “more impact” provides a rough explanation for this phenomenon; homoscedasticity minimizes the largest noise variance for both the line and the curve. In some sense, as discussed in Section 2.6, the degradation from samples with larger noise is greater than the benefit of having samples with correspondingly smaller noise.

3.4. Impact of adding data

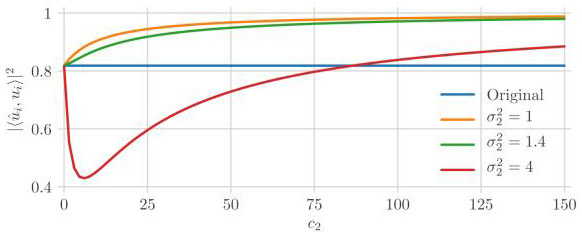
Consider adding data with noise variance ${\sigma }_2^2$ and sample-to-dimension ratio c₂ to an existing dataset that has noise variance ${\sigma }_1^2=1$, sample-to-dimension ratio c₁ = 10 and subspace amplitude θ_i = 1 for the ith component. The combined dataset has a sample-to-dimension ratio of c = c₁+c₂ and is potentially heteroscedastic with noise variances ${\sigma }_1^2$ and ${\sigma }_2^2$ appearing in proportions p₁ = c₁/c and p₂ = c₂/c. Figure 4 shows the asymptotic subspace recovery (4) of the ith component for this combined dataset as a function of the sample-to-dimension ratio c₂ of the added data for a variety of noise variances ${\sigma }_2^2$. The orange curve, showing the recovery when ${\sigma }_2^2=1={\sigma }_1^2$, illustrates the benefit we would expect for homoscedastic data: increasing the samples per dimension improves recovery. The red curve shows the recovery when ${\sigma }_2^2=4>{\sigma }_1^2$. For a small number of added samples, the harm of introducing noisier data outweighs the benefit of having more samples. For sufficiently many samples, however, the tradeoff reverses and recovery for the combined dataset exceeds that for the original dataset; the break even point can be calculated using expression (4). Finally, the green curve shows the performance when ${\sigma }_2^2=1.4>{\sigma }_1^2$. As before, the added samples are noisier than the original samples and so we might expect performance to initially decline again. In this case, however, the performance improves for any number of added samples. In all three cases, the added samples dominate in the limit c₂ → ∞ and PCA approaches perfect subspace recovery as one may expect. However, perfect recovery in the limit does not typically happen for PCA amplitudes (2) and coefficient recovery (5); see Section S3.4 of the Online Supplement for more details.

Figure 4:

Asymptotic subspace recovery (4) of the ith component for samples added with noise variance ${\sigma }_2^2$ and samples-per-dimension c₂ to an existing dataset with noise variance ${\sigma }_1^2=1$, sample-to-dimension ratio c₁ = 10 and subspace amplitude θ_i = 1.

Note that it is equivalent to think about removing noisy samples from a dataset by thinking of the combined dataset as the original full dataset. The green curve in Figure 4 then suggests that slightly noisier samples should not be removed; it would be best if the full data was homoscedastic but removing slightly noisier data (and reducing the dataset size) does more harm than good. The red curve in Figure 4 suggests that much noisier samples should be removed unless they are numerous enough to outweigh the cost of adding them. Once again, expression (4) can be used to calculate the break even point.

4. Numerical simulation

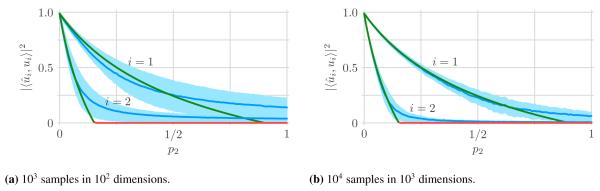
This section simulates data generated by the model described in Section 2.1 to illustrate the main result, Theorem 1, and to demonstrate that the asymptotic results provided are meaningful for practical settings with finitely many samples in a finite-dimensional space. As in Section 3, we show results only for the asymptotic subspace recovery (4) for brevity; the same phenomena occur for the asymptotic PCA amplitudes (2) and coefficient recovery (5) as we show in Section S4 of the Online Supplement. Consider data from a two-dimensional subspace with subspace amplitudes θ₁ = 1 and θ₂ = 0.8, two noise variances ${\sigma }_1^2=0.1$ and ${\sigma }_2^2=3.25$, and a sample-to-dimension ratio of c = 10. We sweep the proportion of high noise samples p₂ from zero to one, setting p₁ = 1 – p₂ as in Section 3.2. The first simulation considers n = 10³ samples in a d = 10² dimensional ambient space (10⁴ trials). The second increases these to n = 10⁴ samples in a d = 10³ dimensional ambient space (10³ trials). Both simulations generate data from the standard normal distribution, i.e., $z_{ij},{\epsilon }_{ij}~\mathcal{N}(0,1)$. Note that sweeping over p₂ covers homoscedastic settings at the extremes (p₂ = 0, 1) and evenly split heteroscedastic data in the middle (p₂ = 1/2).

Figure 5 plots the recovery of subspace components ${\mid \langle {\widehat{u}}_i,u_i\rangle \mid }^2$ for both simulations with the mean (blue curve) and interquartile interval (light blue ribbon) shown with the asymptotic recovery (4) of Theorem 1 (green curve). The region where A(β_i) ≤ 0 is the red horizontal segment with value zero (the prediction of Conjecture 1). Figure 5a illustrates general agreement between the mean and the asymptotic recovery, especially far away from the non-differentiable points where the recovery becomes zero and Conjecture 1 predicts a phase transition. This is a general phenomenon we observed: near the phase transition the smooth simulation mean deviates from the non-smooth asymptotic recovery. Intuitively, an asymptotic recovery of zero corresponds to PCA components that are like isotropically random vectors and so have vanishing square inner product with the true components as the dimension grows. In finite dimension, however, there is a chance of alignment that results in a positive square inner product.

Figure 5:

Simulated subspace recovery (4) as a function of the contamination fraction p₂, the proportion of samples with noise variance ${\sigma }_2^2=3.25$, where the other noise variance ${\sigma }_1^2=0.1$ occurs in proportion p₁ = 1 – p₂. The sample-to-dimension ratio is c = 10 and the subspace amplitudes are θ₁ = 1 and θ₂ = 0.8. Simulation mean (blue curve) and interquartile interval (light blue ribbon) are shown with the asymptotic recovery (4) of Theorem 1 (green curve). The region where A(β_i) ≤ 0 is the red horizontal segment with value zero (the prediction of Conjecture 1). Increasing data size from (a) to (b) results in smaller interquartile intervals, indicating concentration to the mean, which is itself converging to the asymptotic recovery.

Figure 5b shows what happens when the number of samples and ambient dimension are increased to n = 10⁴ and d = 10³. The interquartile intervals are roughly half the size of those in Figure 5a, indicating concentration of the recovery of each component (a random quantity) around its mean. Furthermore, there is better agreement between the mean and the asymptotic recovery, with the maximum deviation between simulation and asymptotic prediction still occurring nearby the phase transition. In particular for p₂ < 0.75 the largest deviation for ${\mid \langle {\widehat{u}}_1,u_1\rangle \mid }^2$ is around 0.03. For p₂ ∉ (0.1, 0.35), the largest deviation for ${\mid \langle {\widehat{u}}_2,u_2\rangle \mid }^2$ is around 0.02. To summarize, the numerical simulations indicate that the subspace recovery concentrates to its mean and that the mean approaches the asymptotic recovery. Furthermore, good agreement with Conjecture 1 provides further evidence that there is indeed a phase transition below which the subspace is not recovered. These findings are similar to those in [18] for a one-dimensional subspace with two noise variances.

5. Proof of Theorem 1

The proof has six main parts. Section 5.1 connects several results from random matrix theory to obtain an initial expression for asymptotic recovery. This expression is difficult to evaluate and analyze because it involves an integral transform of the (nontrivial) limiting singular value distribution for a random (noise) matrix as well as the corresponding limiting largest singular value. However, we have discovered a nontrivial structure in this expression that enables us to derive a much simpler form in Sections 5.2-5.6.

5.1. Obtain an initial expression

Rewriting the model in (1) in matrix form yields

$$\mathbf{Y}=(y_1,\dots ,y_n)=UϴZ^{\mathrm{H}}+\mathbf{EH}\in {\mathbb{C}}^{d\times n},$$ (17)

where $\mathbf{Z}=(z^{\left(1\right)},\dots ,z^{\left(k\right)})\in {\mathbb{C}}^{n\times k}$ is the coefficient matrix, $\mathbf{E}=({\epsilon }_1,\dots ,{\epsilon }_n)\in {\mathbb{C}}^{d\times n}$ is the (unscaled) noise matrix, $\mathbf{H}=\text{diag}({\eta }_1,\dots ,{\eta }_n)\in {\mathbb{R}}_{+}^{n\times n}$ is a diagonal matrix of noise standard deviations.

The first k principal components ${\widehat{u}}_1,\dots ,{\widehat{u}}_k$, PCA amplitudes ${\widehat{\theta }}_1,\dots ,{\widehat{\theta }}_k$ and (normalized) scores ${\widehat{z}}^{\left(1\right)}∕\sqrt{n},\dots ,{\widehat{z}}^{\left(k\right)}∕\sqrt{n}$ defined in Section 1 are exactly the first k left singular vectors, singular values and right singular vectors, respectively, of the scaled data matrix $\mathbf{Y}∕\sqrt{n}$.

To match the model of [5], we introduce the random unitary matrix

$$\mathbf{R}=\left[\tilde{\mathrm{U}}{\tilde{\mathrm{U}}}^{\perp }\right]{\left[\mathrm{U}{\mathrm{U}}^{\perp }\right]}^{\mathrm{H}}=\tilde{\mathrm{U}}{\mathrm{U}}^{\mathrm{H}}+{\tilde{\mathrm{U}}}^{\perp }{\left({\mathrm{U}}^{\perp }\right)}^{\mathrm{H}},$$

where the random matrix $\tilde{\mathrm{U}}\in {\mathbb{C}}^{d\times k}$ is the Gram-Schmidt orthonormalization of a d × k random matrix that has iid (mean zero, variance one) circularly symmetric complex normal $\mathcal{CN}(0,1)$ entries. We use the superscript ⊥ to denote a matrix of orthonormal basis elements for the orthogonal complement; the columns of U^⊥ form an orthonormal basis for the orthogonal complement of the column span of U.

Left multiplying (17) by $\mathbf{R}∕\sqrt{n}$ yields that $\mathbf{R}{\widehat{u}}_1,\dots ,\mathbf{R}{\widehat{u}}_k$, ${\widehat{\theta }}_1,\dots ,{\widehat{\theta }}_k$ and ${\widehat{z}}^{\left(1\right)}∕\sqrt{n},\dots ,{\widehat{z}}^{\left(k\right)}∕\sqrt{n}$ are the first k left singular vectors, singular values and right singular vectors, respectively, of the scaled and rotated data matrix

$$\tilde{\mathrm{Y}}=\frac{1}{\sqrt{n}}\mathbf{RY}.$$

The matrix $\tilde{\mathbf{Y}}$ matches the low rank (i.e., rank k) perturbation of a random matrix model considered in [5] because

$$\tilde{\mathrm{Y}}=\mathbf{P}+\mathbf{X},$$

where

$$\mathbf{P}=\frac{1}{\sqrt{n}}\mathbf{R}\left(\mathrm{U}ϴ{\mathrm{Z}}^{\mathrm{H}}\right)=\frac{1}{\sqrt{n}}\tilde{\mathrm{U}}ϴ{\mathrm{Z}}^{\mathrm{H}}=\sum _{i=1}^k{\theta }_i{\tilde{u}}_i{\left(\frac{1}{\sqrt{n}}{z}^{\left(i\right)}\right)}^{\mathrm{H}},\mathrm{X}=\frac{1}{\sqrt{n}}\mathbf{R}\left(\mathbf{EH}\right)=\left(\frac{1}{\sqrt{n}}\mathbf{RE}\right)\mathbf{H}.$$

Here P is generated according to the “orthonormalized model” in [5] for the vectors ${\tilde{u}}_i$ and the “iid model” for the vectors z⁽ⁱ⁾ and P satisfies Assumption 2.4 of [5]; the latter considers ${\tilde{u}}_i$ and z⁽ⁱ⁾ to be generated according to the same model, but its proof extends to this case. Furthermore RE has iid entries with zero mean, unit variance and bounded fourth moment (by the assumption that ε_i are unitarily invariant), and H is a non-random diagonal positive definite matrix with bounded spectral norm and limiting eigenvalue distribution $p_1{\delta }_{{\sigma }_1^2}+\cdots +p_L{\delta }_{{\sigma }_L^2}$, where ${\delta }_{{\sigma }_{\ell }^2}$ is the Dirac delta distribution centered at ${\sigma }_{\ell }^2$. Under these conditions, Theorem 4.3 and Corollary 6.6 of [3] state that X has a non-random compactly supported limiting singular value distribution μ_X and the largest singular value of X converges almost surely to the supremum of the support of μ_X. Thus Assumptions 2.1 and 2.3 of [5] are also satisfied.

Furthermore, ${\widehat{u}}_i^{\mathrm{H}}{u}_j={\widehat{u}}_i^{\mathrm{H}}{\mathbf{R}}^{\mathrm{H}}\mathbf{R}{u}_j={\left(\mathbf{R}{\widehat{u}}_i\right)}^{\mathrm{H}}{\tilde{u}}_j$ for all i, j ∈ {1,…, k} so

$$\begin{array}{cc}\hfill {\mid \langle \mathbf{R}{\widehat{u}}_i,\text{Span}\{{\tilde{u}}_j:{\theta }_j={\theta }_i\}\rangle \mid }^2& ={\mid \langle {\widehat{u}}_i,\text{Span}\{u_j:{\theta }_j={\theta }_i\}\rangle \mid }^2,\hfill \\ \hfill {\mid \langle \mathbf{R}{\widehat{u}}_i,\text{Span}\{{\tilde{u}}_j:{\theta }_j\ne {\theta }_i\}\rangle \mid }^2& ={\mid \langle {\widehat{u}}_i,\text{Span}\{u_j:{\theta }_j\ne {\theta }_i\}\rangle \mid }^2,\hfill \end{array}$$

and hence Theorem 2.10 from [5] implies that, for each i ∈ {1,…, k},

$${\widehat{\theta }}_i^2\stackrel{a.s.}{\to }\{\begin{array}{cc}{\rho }_i^2\hfill & \text{if}{\theta }_i^2>{\stackrel{‒}{\theta }}^2,\hfill \\ b^2\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$ (18)

and that if ${\theta }_i^2>{\stackrel{‒}{\theta }}^2$, then

$$\begin{array}{cc}\hfill {\mid \langle {\widehat{u}}_i,\text{Span}\{u_j:{\theta }_j={\theta }_i\}\rangle \mid }^2& \stackrel{a.s.}{\to }\frac{-2\phi \left({\rho }_i\right)}{{\theta }_i^2{D}^{\prime }\left({\rho }_i\right)},\hfill \\ \hfill {\mid \langle \frac{{\widehat{z}}^{\left(i\right)}}{\sqrt{n}},\text{Span}\{z^{\left(j\right)}:{\theta }_j={\theta }_i\}\rangle \mid }^2& \stackrel{a.s.}{\to }\frac{-2\left\{c^{-1}\phi \right({\rho }_i)+(1-c^{-1})∕{\rho }_i\}}{{\theta }_i^2{D}^{\prime }\left({\rho }_i\right)},\hfill \end{array}$$ (19)

and

$$\begin{array}{cc}\hfill {\mid \langle {\widehat{u}}_i,\text{Span}\{u_j:{\theta }_j\ne {\theta }_i\}\rangle \mid }^2& \stackrel{a.s.}{\to }0,\hfill \\ \hfill {\mid \langle \frac{{\widehat{z}}^{\left(i\right)}}{\sqrt{n}},\text{Span}\{z^{\left(j\right)}:{\theta }_j\ne {\theta }_i\}\rangle \mid }^2& \stackrel{a.s.}{\to }0,\hfill \end{array}$$ (20)

where ${\rho }_i=D^{-1}(1∕{\theta }_i^2)$, ${\stackrel{‒}{\theta }}^2=1∕D\left(b^{+}\right)$, for z > b, φ(z) = ∫ z/z² – t²) d_μx (t), b is the supremum of the support of μ_X and μ_X is the limiting singular value distribution of X (compactly supported by Assumption 2.1 of [5]). We use the notation f (b⁺) = lim_z→b⁺ f (z) as convenient shorthand for the limit from above of a function f (z).

Theorem 2.10 from [5] is presented therein for d ≤ n (i.e., c ≥ 1) to simplify their proofs. However, it also holds without modification for d > n if the limiting singular value distribution μ_X is always taken to be the limit of the empirical distribution of the d largest singular values (d – n of which will be zero). Thus we proceed without the condition that c > 1.

Furthermore, even though it is not explicitly stated as a main result in [5], the proof of Theorem 2.10 in [5] implies that

$$\sum _{j:{\theta }_j={\theta }_i}\langle {\widehat{u}}_i,u_j\rangle {\langle \frac{{\widehat{Z}}^{\left(i\right)}}{\sqrt{n}},\frac{z^{\left(j\right)}}{\Vert z^{\left(j\right)}\Vert }\rangle }^{\ast }\stackrel{a.s.}{\to }\sqrt{\frac{-2\phi \left({\rho }_i\right)}{{\theta }_i^2{D}^{\prime }\left({\rho }_i\right)}\times \frac{-2\left\{c^{-1}\phi \right({\rho }_i)+(1-c^{-1})∕{\rho }_i\}}{{\theta }_i^2{D}^{\prime }\left({\rho }_i\right)}},$$ (21)

as was also noted in [27] for the special case of distinct subspace amplitudes.

Evaluating the expressions (18), (19) and (21) would consist of evaluating the intermediates listed above from last to first. These steps are challenging because they involve an integral transform of the limiting singular value distribution μ_X for the random (noise) matrix X as well as the corresponding limiting largest singular value b, both of which depend nontrivially on the model parameters. Our analysis uncovers a nontrivial structure that we exploit to derive simpler expressions.

Before proceeding, observe that the almost sure limit in (21) is just the geometric mean of the two almost sure limits in (19). Hence, we proceed to derive simplified expressions for (18) and (19); (6) follows as the geometric mean of the simplified expressions obtained for the almost sure limits in (19).

5.2. Perform a change of variables

We introduce the function defined, for z > b, by

$$\psi \left(z\right)=\frac{cz}{\phi \left(z\right)}={\left\{\frac{1}{c}\int \frac{1}{z^2-t^2}d{\mu }_{\mathrm{X}}\left(t\right)\right\}}^{-1},$$ (22)

because it turns out to have several nice properties that simplify all of the following analysis. Rewriting (19) using ψ(z) instead of φ(z) and factoring appropriately yields that if ${\theta }_i^2>{\stackrel{‒}{\theta }}^2$ then

$$\begin{array}{cc}\hfill {\mid \langle {\widehat{u}}_i,\text{Span}\{u_j:{\theta }_j={\theta }_i\}\rangle \mid }^2& \stackrel{a.s.}{\to }\frac{1}{\psi \left({\rho }_i\right)}\frac{-2c}{{\theta }_i^2{D}^{\prime }\left({\rho }_i\right)∕{\rho }_i},\hfill \\ \hfill {\mid \langle \frac{{\widehat{z}}^{\left(i\right)}}{\sqrt{n}},\text{Span}\{z^{\left(j\right)}:{\theta }_j={\theta }_i\}\rangle \mid }^2& \stackrel{a.s.}{\to }\frac{1}{c\left\{\psi \right({\rho }_i)+(1-c\left){\theta }_i^2\right\}}\frac{-2c}{{\theta }_i^2{D}^{\prime }\left({\rho }_i\right)∕{\rho }_i},\hfill \end{array}$$ (23)

where now

$$D\left(z\right)=\frac{c{z}^2}{{\psi }^2\left(z\right)}+\frac{c-1}{\psi \left(z\right)}$$ (24)

for z > b and we have used the fact that

$$\frac{1}{c}\left\{\frac{1}{\psi \left({\rho }_i\right)}+\frac{1-c^{-1}}{{\rho }_i^2}\right\}=\frac{1}{c}{\left\{\psi \left({\rho }_i\right)+\frac{1-c}{D\left({\rho }_i\right)}\right\}}^{-1}=\frac{1}{c\left\{\psi \right({\rho }_i)+(1-c\left){\theta }_i^2\right\}}.$$

5.3. Find useful properties of ψ(z)

Establishing some properties of ψ(z) aids simplification significantly.

Property 1. We show that ψ(z) satisfies a certain rational equation for all z > b and derive its inverse function ψ⁻¹(x). Observe that the square singular values of the noise matrix X are exactly the eigenvalues of cXX^H, divided by c. Thus we first consider the limiting eigenvalue distribution μ_cXX^H of cXX^H and then relate its Stieltjes transform μ to ψ(z).

Theorem 4.3 in [3] establishes that the random matrix cXX^H = (1/d)EH²E^H has a limiting eigenvalue distribution μ_cXX^H whose Stieltjes transform is given, for μ, by

$$m\left(\zeta \right)=\int \frac{1}{t-\zeta }d{\mu }_{c{\mathrm{XX}}^{\mathrm{H}}}\left(t\right),$$ (25)

and satisfies the condition

$${\forall }_{\zeta \in {\mathbb{C}}^{+}}m\left(\zeta \right)=-{\left\{\zeta -c\sum _{\ell =1}^L\frac{p_{\ell }{\sigma }_{\ell }^2}{1+{\sigma }_{\ell }^{2}m\left(\zeta \right)}\right\}}^{-1},$$ (26)

where μ is the set of all complex numbers with positive imaginary part.

Since the d square singular values of X are exactly the d eigenvalues of cXX^H divided by c, we have for all z > b

$$\psi \left(z\right)={\left\{\frac{1}{c}\int \frac{1}{z^2-t^2}d{\mu }_{\mathrm{X}}\left(t\right)\right\}}^{-1}=-{\left\{\int \frac{1}{t-z^{2}c}d{\mu }_{c{\mathrm{XX}}^{\mathrm{H}}}\left(t\right)\right\}}^{-1}.$$ (27)

For all z and μ and so combining (25)–(27) yields that for all z > b

$$\psi \left(z\right)=-{\left\{\underset{\xi \to 0^{+}}{\lim }m(z^{2}c+i\xi )\right\}}^{-1}=z^{2}c-c\sum _{\ell =1}^L\frac{p_{\ell }{\sigma }_{\ell }^2}{1-{\sigma }_{\ell }^2∕\psi \left(z\right)}.$$

Rearranging yields

$$0=\frac{c{z}^2}{{\psi }^2\left(z\right)}-\frac{1}{\psi \left(z\right)}-\frac{c}{\psi \left(z\right)}\sum _{\ell =1}^L\frac{p_{\ell }{\sigma }_{\ell }^2}{\psi \left(z\right)-{\sigma }_{\ell }^2},$$ (28)

for all z > b, where the last term is

$$-\frac{c}{\psi \left(z\right)}\sum _{\ell =1}^L\frac{p_{\ell }{\sigma }_{\ell }^2}{\psi \left(z\right)-{\sigma }_{\ell }^2}=\frac{c}{\psi \left(z\right)}-c\sum _{\ell =1}^L\frac{P_{\ell }}{\psi \left(z\right)-{\sigma }_{\ell }^2},$$

because p₁ + … + p_L = 1. Substituting back into (28) yields 0 = Q{ψ (z), z} for all z > b, where

$$Q(s,z)=\frac{c{z}^2}{s^2}+\frac{c-1}{s}-c\sum _{\ell =1}^L\frac{p_{\ell }}{s-{\sigma }_{\ell }^2}.$$ (29)

Thus ψ(z) is an algebraic function (the associated polynomial can be formed by clearing the denominator of Q). Solving (29) for z > b yields the inverse

$${\psi }^{-1}\left(x\right)=\sqrt{\frac{1-c}{c}x+x^2\sum _{\ell =1}^L\frac{p_{\ell }}{x-{\sigma }_{\ell }^2}}=\sqrt{\frac{x}{c}\left(1+c\sum _{\ell =1}^L\frac{p_{\ell }{\sigma }_{\ell }^2}{x-{\sigma }_{\ell }^2}\right)}.$$ (30)

Property 2. We show that ${\max }_{\ell }\left({\sigma }_{\ell }^2\right)<\psi \left(z\right)<c{z}^2$ for z > b. For z > b, one can show from (22) that ψ(y) increases continuously and monotonically from ψ(z) to infinity as y increases from z to infinity, and hence ψ⁻¹(x) must increase continuously and monotonically from z to infinity as x increases from ψ(z) to infinity. However, ψ⁻¹(x) is discontinuous at $x={\max }_{\ell }\left({\sigma }_{\ell }^2\right)$ because ψ⁻¹(x) → ∞ as $x\to {\max }_{\ell }\left({\sigma }_{\ell }^2\right)$ from the right, and so it follows that $\psi \left(z\right)>{\max }_{\ell }\left({\sigma }_{\ell }^2\right)$. Thus $1∕\left\{\psi \right(z)-{\sigma }_{\ell }^2\}>0$ for all ℓ ∈ {1,…,L} and so

$$c{z}^2=c{\left[{\psi }^{-1}\right\{\psi \left(z\right)\left\}\right]}^2=\psi \left(z\right)\left\{1+c\sum _{\psi \left(z\right)}^L\frac{p_{\ell }{\sigma }_{\ell }^2}{\psi \left(z\right)-{\sigma }_{\ell }^2}\right\}>\psi \left(z\right).$$

Property 3. We show that 0 < ψ(b⁺) < ∞ and ψ′ (b⁺) = ∞. Property 2 in the limit z = b⁺ implies that

$$0<\underset{\ell }{\max }\left({\sigma }_{\ell }^2\right)\le \psi \left(b^{+}\right)\le c{b}^2<\infty .$$

Taking the total derivative of 0 = Q{ψ(z), z} with respect to z and solving for ψ′ (z) yields

$${\psi }^{\prime }\left(z\right)=-\frac{\partial Q}{\partial z}\left\{\psi \right(z),z\}/\frac{\partial Q}{\partial s}\left\{\psi \right(z),z\}.$$ (31)

As observed in [28], the non-pole boundary points of compactly supported distributions like μ_cXX^H occur where the polynomial defining their Stieltjes transform has multiple roots. Thus ψ(b⁺) is a multiple root of Q(·, b) and so

$$\frac{\partial Q}{\partial s}\left\{\psi \right(b^{+}),b\}=0,\frac{\partial Q}{\partial z}\left\{\psi \right(b^{+}),b\}=\frac{2cb}{{\psi }^2\left(b^{+}\right)}>0.$$

Thus ψ′ (b⁺) = ∞, where the sign is positive because ψ(z) is an increasing function on z > b.

Summarizing, we have shown that

1. 0 = Q{ψ (z), z} for all z > b where Q is defined in (29), and the inverse function ψ⁻¹(x) is given in (30),

2. ${\max }_{\ell }\left({\sigma }_{\ell }^2\right)<\psi \left(z\right)<c{z}^2$,

3. 0 < ψ(b⁺) < ∞ and ψ′ (b⁺) = ∞.

We now use these properties to aid simplification.

5.4. Express D(z) and D′(z)/z in terms of only ψ(z)

We can rewrite (24) as

$$D\left(z\right)=Q\left\{\psi \right(z),z\}+c\sum _{\ell =1}^L\frac{p_{\ell }}{\psi \left(z\right)-{\sigma }_{\ell }^2}=c\sum _{\ell =1}^L\frac{p_{\ell }}{\psi \left(z\right)-{\sigma }_{\ell }^2}.$$ (32)

because 0 = Q{ψ (z), z} by Property 1 of Section 5.3. differentiating (32) with respect to z yields

$$D^{\prime }\left(z\right)=-c{\psi }^{\prime }\left(z\right)\sum _{\ell =1}^L\frac{p_{\ell }}{{\left\{\psi \right(z)-{\sigma }_{\ell }^2\}}^2},$$

and so we need to find ψ′ (z) in terms of ψ(z). Substituting the expressions for the partial derivatives ∂Q{ψ (z), z}/∂z and ∂Q{ψ (z), z}/∂s into (31) and simplifying we obtain ψ′ (z) = 2cz/γ(z), where the denominator is

$$\gamma \left(z\right)=c-1+\frac{2c{z}^2}{\psi \left(z\right)}-c\sum _{\ell =1}^L\frac{p_{\ell }{\psi }^2\left(z\right)}{{\left\{\psi \right(z)-{\sigma }_{\ell }^2\}}^2}.$$

Note that

$$\frac{2c{z}^2}{\psi \left(z\right)}=-2(c-1)+c\sum _{\ell =1}^L\frac{2p_{\ell }\psi \left(z\right)}{\psi \left(z\right)-{\sigma }_{\ell }^2},$$

because 0 = Q{ψ (z), z} for z > b. Substituting into γ(z) and forming a common denominator, then dividing with respect to ψ(z) yields

$$\gamma \left(z\right)=1-c+c\sum _{\ell =1}^L{p}_{\ell }\frac{{\psi }^2\left(z\right)-2\psi \left(z\right){\sigma }_{\ell }^2}{{\left\{\psi \right(z)-{\sigma }_{\ell }^2\}}^2}=1-c\sum _{\ell =1}^L\frac{p_{\ell }{\sigma }_{\ell }^4}{{\left\{\psi \right(z)-{\sigma }_{\ell }^2\}}^2}=A\left\{\psi \right(z\left)\right\},$$

where A(x) was defined in (3). Thus

$${\psi }^{\prime }\left(z\right)=\frac{2cz}{A\left\{\psi \right(z\left)\right\}},$$ (33)

and

$$\frac{D^{\prime }\left(z\right)}{z}=-\frac{2c^2}{A\left\{\psi \right(z\left)\right\}}\sum _{\ell =1}^L\frac{p_{\ell }}{{\left\{\psi \right(z)-{\sigma }_{\ell }^2\}}^2}=-\frac{2c}{{\theta }_i^2}\frac{B_i^{\prime }\left\{\psi \right(z\left)\right\}}{A\left\{\psi \right(z\left)\right\}},$$ (34)

where $B_i^{\prime }$ is the derivative of B_i(x) defined in (3).

5.5. Express the asymptotic recoveries in terms of only ψ(b⁺) and ψ(ρ_i)

Evaluating (32) in the limit z = b⁺ and recalling that $D\left(b^{+}\right)=1∕{\stackrel{‒}{\sigma }}^2$ yields

$${\theta }_i^2>{\stackrel{‒}{\theta }}^2\iff 0>1-\frac{{\theta }_i^2}{{\stackrel{‒}{\theta }}^2}=1-c{\theta }_i^2\sum _{\ell =1}^L\frac{p_{\ell }}{\psi \left(b^{+}\right)-{\sigma }_{\ell }^2}=B_i\left\{\psi \right(b^{+}\left)\right\},$$ (35)

where B_i(x) was defined in (3). Evaluating the inverse function (30) both for ψ(ρ_i) and in the limit ψ(b⁺) then substituting into (18) yields

$${\widehat{\theta }}_i^2\stackrel{a.s.}{\to }\{\begin{array}{cc}\frac{\psi \left({\rho }_i\right)}{c}\left\{1+c\sum _{\ell =1}^L\frac{p_{\ell }{\sigma }_{\ell }^2}{\psi \left({\rho }_i\right)-{\sigma }_{\ell }^2}\right\}\hfill & \text{if}{B}_i\left\{\psi \right(b^{+}\left)\right\}<0,\hfill \\ \frac{\psi \left(b^{+}\right)}{c}\left\{1+c\sum _{\ell =1}^L\frac{p\ell {\sigma }_{\ell }^2}{\psi \left(b^{+}\right)-{\sigma }_{\ell }^2}\right\}\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (36)

Evaluating (34) for z = ρ_i and substituting into (23) yields

$$\begin{array}{cc}\hfill {\mid \langle {\widehat{u}}_i,\text{Span}\{u_j:{\theta }_j={\theta }_i\}\rangle \mid }^2& \stackrel{a.s.}{\to }\frac{1}{\psi \left({\rho }_i\right)}\frac{A\left\{\psi \right({\rho }_i\left)\right\}}{B_i^{\prime }\left\{\psi \right({\rho }_i)},\hfill \\ \hfill {\mid \langle \frac{{\widehat{z}}^{\left(i\right)}}{\sqrt{n}},\text{Span}\{z^{\left(j\right)}:{\theta }_j={\theta }_i\}\rangle \mid }^2& \stackrel{a.s.}{\to }\frac{1}{c\left\{\psi \right({\rho }_i)+(1-c\left){\theta }_i^2\right\}}\frac{A\left\{\psi \right({\rho }_i\left)\right\}}{B_i^{\prime }\left\{\psi \right({\rho }_i\left)\right\}},\hfill \end{array}$$ (37)

if B_i{ψ (b⁺)} < 0.

5.6. Obtain algebraic descriptions

This subsection obtains algebraic descriptions of (35), (36) and (37) by showing that ψ(b⁺) is the largest real root of A(x) and that ψ(ρ_i) is the largest real root of B_i(x) when ${\theta }_i^2>{\stackrel{‒}{\theta }}^2$. Evaluating (33) in the limit z = b⁺ yields

$$A\left\{\psi \right(b^{+}\left)\right\}=\frac{2cb}{{\psi }^{\prime }\left(b^{+}\right)}=0,$$ (38)

because ψ′ (b⁺) = ∞ by Property 3 of Section 5.3. If ${\theta }_i^2>{\stackrel{‒}{\theta }}^2$ then ${\rho }_i=D^{-1}(1∕{\theta }_i^2)$ and so

$$0=1-{\theta }_i^{2}D\left({\rho }_i\right)=1-c{\theta }_i^2\sum _{\ell =1}^L\frac{p_{\ell }}{\psi \left({\rho }_i\right)-{\sigma }_{\ell }^2}=B_i\left\{\psi \right({\rho }_i\left)\right\}.$$ (39)

(38) shows that ψ(b⁺) is a real root of A(x), and (39) shows that ψ(ρ_i) is a real root of B_i(x).

Recall that ψ(b⁺), $\psi \left({\rho }_i\right)\ge {\max }_{\ell }\left({\sigma }_{\ell }^2\right)$ by Property 2 of Section 5.3, and note that both A(x) and B_i(x) monotonically increase for $x>{\max }_{\ell }\left({\sigma }_{\ell }^2\right)$. Thus each has exactly one real root larger than ${\max }_{\ell }\left({\sigma }_{\ell }^2\right)$, i.e., its largest real root, and so ψ(b⁺) = α and ψ(ρ_i) = β_i when ${\theta }_i^2>{\stackrel{‒}{\theta }}^2$, where α and β_i are the largest real roots of A(x) and B_i(x), respectively.

A subtle point is that A(x) and B_i(x) always have largest real roots α and β even though ψ(ρ_i) is defined only when ${\theta }_i^2>{\stackrel{‒}{\theta }}^2$. Furthermore, α and β are always larger than ${\max }_{\ell }\left({\sigma }_{\ell }^2\right)$ and both A(x) and B_i(x) are monotonically increasing in this regime and so we have the equivalence

$$B_i\left(\alpha \right)<0\iff \alpha <{\beta }_i\iff 0<A\left({\beta }_i\right).$$ (40)

Writing (35), (36) and (37) in terms of α and β, then applying the equivalence (40) and combining with (20) yields the main results (2), (4) and (5).

6. Proof of Theorem 2

If A(β_i) ≥ 0 then (4) and (5) increase with A(β_i) and decrease with β_i and B′(β_i). Similarly, (2) increases with β_i, as illustrated by (9). As a result, Theorem 2 follows immediately from the following bounds, all of which are met with equality if and only if ${\sigma }_1^2=\cdots ={\sigma }_L^2$:

$${\beta }_i\ge c{\theta }_i^2+{\stackrel{‒}{\sigma }}^2,B_i^{\prime }\left({\beta }_i\right)\ge \frac{1}{c{\theta }_i^2},A\left({\beta }_i\right)\le 1-\frac{1}{c}{\left(\frac{\stackrel{‒}{\sigma }}{{\theta }_i}\right)}^4.$$ (41)

The bounds (41) are shown by exploiting convexity to appropriately bound the rational functions B_i(x), $B_i^{\prime }\left(x\right)$ and A(x). We bound β_i by noting that

$$0=B_i\left({\beta }_i\right)=1-c{\theta }_i^2\sum _{\ell =1}^L\frac{p_{\ell }}{{\beta }_i-{\sigma }_{\ell }^2}\le 1-\frac{c{\theta }_i^2}{{\beta }_i-{\stackrel{‒}{\sigma }}^2},$$

because ${\sigma }_{\ell }^2<{\beta }_i$ and f(v) = 1/(β_i – v) is a strictly convex function over v < β_i. Thus ${\beta }_i\ge c{\theta }_i^2+{\stackrel{‒}{\sigma }}^2$. We bound $B_i^{\prime }\left({\beta }_i\right)$ by noting that

$$B_i^{\prime }\left({\beta }_i\right)=c{\theta }_i^2\sum _{\ell =1}^L\frac{p_{\ell }}{{({\beta }_i-{\sigma }_{\ell }^2)}^2}\ge c{\theta }_i^2{\left(\sum _{\ell =1}^L\frac{p_{\ell }}{{\beta }_i-{\sigma }_{\ell }^2}\right)}^2=c{\theta }_i^2{\left(\frac{1}{c{\theta }_i^2}\right)}^2=\frac{1}{c{\theta }_i^2},$$

because the quadratic function z² is strictly convex. Similarly

$$A\left({\beta }_i\right)=1-c\sum _{\ell =1}^L\frac{p_{\ell }{\sigma }_{\ell }^4}{{({\beta }_i-{\sigma }_{\ell }^2)}^2}\le 1-c{\left(\sum _{\ell =1}^L\frac{p_{\ell }{\sigma }_{\ell }^2}{{\beta }_i-{\sigma }_{\ell }^2}\right)}^2\le 1-\frac{1}{c}{\left(\frac{\stackrel{‒}{\sigma }}{{\theta }_i}\right)}^4,$$

because the quadratic function z² is strictly convex and

$$\sum _{\ell =1}^L\frac{p_{\ell }{\sigma }_{\ell }^2}{{\beta }_i-{\sigma }_{\ell }^2}={\beta }_i\sum _{\ell =1}^L\frac{p_{\ell }}{{\beta }_i-{\sigma }_{\ell }^2}-1=\frac{{\beta }_i}{c{\theta }_i^2}-1\ge \frac{c{\theta }_i^2+{\stackrel{‒}{\sigma }}^2}{c{\theta }_i^2}-1=\frac{{\stackrel{‒}{\sigma }}^2}{c{\theta }_i^2}.$$

All of the above bounds are met with equality if and only if ${\sigma }_1^2=\cdots ={\sigma }_L^2$ because the convexity in all cases is strict. As a result, homoscedastic noise minimizes (2), and it maximizes (4) and (5). See Section S2 of the Online Supplement for some interesting additional properties in this context.

7. Discussion and extensions

This paper provided simplified expressions (Theorem 1) for the asymptotic recovery of a low-dimensional subspace, the corresponding subspace amplitudes and the corresponding coefficients by the principal components, PCA amplitudes and scores, respectively, obtained from applying PCA to noisy high-dimensional heteroscedastic data. The simplified expressions provide generalizations of previous results for the special case of homoscedastic data. They were derived by first connecting several recent results from random matrix theory [3, 5] to obtain initial expressions for asymptotic recovery that are difficult to evaluate and analyze, and then exploiting a nontrivial structure in the expressions to find the much simpler algebraic descriptions of Theorem 1.

These descriptions enable both easy and efficient calculation as well as reasoning about the asymptotic performance of PCA. In particular, we use the simplified expressions to show that, for a fixed average noise variance, asymptotic subspace recovery, amplitude recovery and coefficient recovery are all worse when the noise is heteroscedastic as opposed to homoscedastic (Theorem 2). Hence, while average noise variance is often a practically convenient measure for the overall quality of data, it gives an overly optimistic estimate of PCA performance. Our expressions (2), (4) and (5) in Theorem 1 are more accurate.

We also investigated examples to gain insight into how the asymptotic performance of PCA depends on the model parameters: sample-to-dimension ratio c, subspace amplitudes θ₁,…, θ_k, proportions p₁,…, p_L and noise variances ${\sigma }_1^2=\cdots ={\sigma }_L^2$. We found that performance depends in expected ways on

1. sample-to-dimension ratio: performance improves with more samples;

2. subspace amplitudes: performance improves with larger amplitudes;

3. proportions: performance improves when more samples have low noise.

We also learned that when the gap between the two largest noise variances is “sufficiently wide”, the performance is dominated by the largest noise variance. This result provides insight into why PCA performs poorly in the presence of gross errors and why heteroscedasticity degrades performance in the sense of Theorem 2. Nevertheless, adding “slightly” noisier samples to an existing dataset can still improve PCA performance; even adding significantly noisier samples can be beneficial if they are sufficiently numerous.

Finally, we presented numerical simulations that demonstrated concentration of subspace recovery to the asymptotic prediction (4) with good agreement for practical problem sizes. The same agreement occurs for the PCA amplitudes and coefficient recovery. The simulations also showed good agreement with the conjectured phase transition (Conjecture 1).

There are many exciting avenues for extensions and further work. An area of ongoing work is the extension of our analysis to a weighted version of PCA, where the samples are first weighted to reduce the impact of noisier points. Such a method may be natural when the noise variances are known or can be estimated well. Data formed in this way do not match the model of [5], and so the analysis involves first extending the results of [5] to handle this more general case. Preliminary findings suggest that whitening the noise with inverse noise variance weights $1∕{\sigma }_{\ell }^2$ is not optimal.

Another natural direction is to consider a general distribution of noise variances v, where we suppose that the empirical noise distribution $({\delta }_{{\eta }_1^2}+\cdots +{\delta }_{{\eta }_n^2})∕n\stackrel{a.s.}{\to }v\text{as}n\to \infty$. We conjecture that if η₁,…, η_n are bounded for all n and $\int dv\left(\tau \right)∕(x-\tau )\to \infty \text{as}x\to {\tau }_{\max }^{+}$, then the almost sure limits in this paper hold but with

$$A\left(x\right)=1-c\int \frac{{\tau }^{2}dv\left(\tau \right)}{{(x-\tau )}^2},B_i\left(x\right)=1-c{\theta }_i^2\int \frac{dv\left(\tau \right)}{x-\tau }.$$

where τ_max is the supremum of the support of v. The proofs of Theorem 1 and Theorem 2 both generalize straight-forwardly for the most part; the main trickiness comes in carefully arguing that limits pass through integrals in Section 5.3.

Proving that there is indeed a phase transition in the asymptotic subspace recovery and coefficient recovery, as conjectured in Conjecture 1, is another area of future work. That proof may be of greater interest in the context of a weighted PCA method. Another area of future work is explaining the puzzling phenomenon described in Section 3.3, where, in some regimes, performance improves by increasing the noise variance. More detailed analysis of the general impacts of the model parameters could also be interesting. A final direction of future work is deriving finite sample results for heteroscedastic noise as was done for homoscedastic noise in [29].