Modeling Neural Behavior and Pain During Bladder Distention using an Agent-based Model of the Central Nucleus of the Amygdala

Abstract

Chronic bladder pain evokes asymmetric behavior in neurons across the left and right hemispheres of the amygdala. An agent-based computational model was created to simulate the firing of neurons over time and in response to painful bladder stimulation. Each agent represents one neuron and is characterized by its location in the amygdala and response type (excited or inhibited). At each time step, the firing rates (Hz) of all neurons are stochastically updated from probability distributions estimated from data collected in laboratory experiments. A damage accumulation model tracks the damage accrued by neurons during long-term, painful bladder stimulation. Emergent model output uses neural activity to measure temporal changes in pain attributed to bladder stimulation. Simulations demonstrate the model’s ability to capture acute and chronic pain and its potential to predict changes in pain similar to those observed in the lab. Asymmetric neural activity during the progression of chronic pain is examined using model output and a sensitivity analysis.

1. Introduction

Chronic visceral pain syndromes affect millions of people in the US with crippling and debilitating chronic pain. Urologic chronic pelvic pain, commonly diagnosed as interstitial bladder pain syndrome or chronic pelvic pain syndrome, is one of the most common chronic visceral pain syndromes [17, 48, 50]. Many of the most common symptoms of chronic pain syndromes such as persistent pain and depression [31, 51] suggest the limbic nervous system is a strong mediator of these conditions. The peripheral nervous system plays a large role in urologic pain processing [1, 9]; however, during the transition from acute to chronic bladder pain a network including the prefrontal cortex, anterior cingulate, hippocampus, and amygdala is likely recruited to sustain pain and modulate its affects despite a lack of constant peripheral input [35, 49].

Recent data has indicated stable, significant changes in the central nervous system of men and women with visceral pain syndromes [5, 7, 21, 27, 28, 32, 34, 54]. One brain region in particular, the central nucleus of the amygdala (CeA), is altered in urologic chronic pelvic pain and has been implicated in both experiencing pain and modulating pain [5, 7, 20, 29, 34, 38, 39, 47]. Notably, the CeA is one area where visceral pain is regulated differently than somatic pain. Somatic pain is pain arising from stimulation or perceived stimulation of soft tissue, skin, and muscle while visceral pain is that arising from stimulation or perceived stimulation of internal organs. Pharmacological inhibition of the right CeA in mice decreases visceral [19] but not somatic [30] pain-like responses. Although it is difficult to truly distinguish visceral and somatic pain in the brain due to the convergence of neurons in the spinal cord, this observation positions the CeA as a novel target for the treatment of chronic bladder pain. Identifying new differences and similarities between somatic and visceral pain is critical to understanding the susceptibility, symptomology, and treatment of different pain disorders [6, 16]. Bladder-specific changes in CeAmediated behavior or gene expression could be targeted to manage pain in patients who often show other comorbidities (e.g., fibromyalgia, irritable bowel syndrome, anxiety, etc) [35].

Differences in the functions of left and right CeA in both processing and experiencing pain has been a recent focus of research [29, 34, 38]. Results from our work and the work of others have described a dominance by the right CeA in controlling somatic pain [15, 26, 30]. Recent data from our lab also suggest that neuronal activity is sensitized after bladder injury and differs between the left and right CeA. The right CeA has a pro-nociceptive function, meaning that pain increases during excitation of the right CeA. The left CeA has an anti-nociceptive function, meaning that pain decreases during excitation of the left CeA [45]. These differences may be driven in part by differences in the excitability of neurons in CeA in response to bladder stimulation. Lateralization of brain function has long been appreciated and exists across nearly all biological taxa [44]. Interestingly, right hemisphere lateralization of the limbic system, including the amygdala, has been observed in birds and mammals (rodents, primates, etc) especially in the context of stress and injury [44]. Nonetheless, the status quo in pain research is that functional lateralization remains relatively unexamined and unused from a clinical perspective.

In the current manuscript, we describe a computational agent-based modeling approach to understand the differences in excitability observed in preliminary electrophysiological recordings from naive and sensitized mice. During painful stimulation of the bladder, neurons in the CeA can either be excited or inhibited by the stimulation, determined by the changes in their firing rates. Inhibited neurons have a higher baseline firing rate and exhibit a decrease in firing rate during painful bladder stimulation. Excited neurons have a lower baseline firing rate and exhibit an increase in firing rate during painful bladder stimulation. Neurons in the CeA also show different physiological responses under normal conditions (noninjury) versus after bladder injury [22, 23, 25, 26]. In the present manuscript, this phenomenon of injury-induced changes was investigated in the context of bladder injury and sensitization. In laboratory experiments, mice were treated with cyclophosphamide (CYP), a chemotherapeutic drug that causes human patients to develop hemorrhagic cystitis, thus harming the bladder and inducing pain [18, 52]. Mice that were sensitized with CYP developed some symptoms (e.g., overactivity, bladder and pelvic nociception) similar to those of human patients with chronic bladder pain [11, 33]. The goal of these laboratory experiments was to provide preliminary data measuring changes in neural activity due to sensitization to support the development of the agent-based model.

Computational and mathematical models provide a non-invasive and humane method for studying pain and assessing different pain management strategies [2]. In 1986, Britton and Skevington constructed a system of differential equations describing the gate control theory of pain [14, 13]. Gate control theory asserts pain is modulated through the sending of signals from the spinal cord to the brain via “nerve gates” that open or close depending on conditions [36]. The differential equation model reproduced observations of acute pain and provided a framework for testing the theory’s applicability to chronic pain. Researchers have since developed computational and mathematical models that extend the basic assumptions of gate control theory to include, for example, functional properties of sub-categories of neurons [3, 4], interactions between neurons and increasing quantities of T-cells [41], and cortical reorganization attributed to amputation [10]. Other recent advances in pain modeling utilize artificial neural networks to explain the nonlinear processing of signals between the spinal cord and the brain [37, 24].

In this paper, we use an agent-based computational model to describe the behavior of individual neurons in response to painful bladder stimulation caused by distention. Agent-based models are used increasingly in all disciplines to study emergent features of complex systems governed by the actions and interactions of individual agents [43, 53]. In our model, each agent represents one neuron and the behavior (e.g., firing rate) of all neurons are stochastically updated at each time step. The primary emergent feature of the model is a measure of bladder pain and our objective is to investigate the role of specific neurons in pain modulation. Moreover, because each agent in the model is assigned a location within the amygdala, we use the model to assess asymmetric neural behavior observed across the left and right hemispheres of the CeA.

A complete description of our agent-based model is provided in Section 2. Model parameters were estimated using preliminary data from our laboratory experiments. Section 3 provides a description of these experiments and a summary of the statistical algorithm used to estimate model parameters from the experimental data. Results of model simulations and a sensitivity analysis are displayed in Section 4. Simulations demonstrate the model’s ability to capture acute and chronic pain and the model’s potential to predict changes in pain similar to those observed in the lab. A discussion of these results is provided in Section 5 and concluding remarks follow in Section 6.

2. Model Description

2.1. Purpose

The purpose of the agent-based model (ABM) is to observe system-level properties of excited and inhibited neurons in the central nucleus of the amygdala (CeA) during short and long-term bladder pain caused by bladder distention. System-level output measures pain attributed to bladder distention. Results are useful in understanding the role of excited and inhibited neurons in pain regulation and the lateralization of these neurons in the left and right hemispheres of the CeA.

2.2. Agents and Scale

Agents represent individual neurons in the CeA that are responsive to bladder pain. The model’s spatial domain includes 324 patches, each of which marks the location of one neuron. The space is partitioned into halves representing the left and right hemispheres of the CeA. Each model tick represents one time step.

Each neuron (i.e., agent) possesses five variables (Table 1) defining its properties and behavior. First, each neuron is assigned a location (loc) equal to either L or R, signifying the neuron’s placement in the left or right hemispheres of the CeA, respectively. Second, each neuron is assigned a response (res) equal to either Ex (excited) or In (inhibited). The classification of a neuron as either excited or inhibited refers to its behavior in response to painful bladder distention. A neuron’s location and response are both assigned during initialization and do not change during a simulation. Therefore, throughout a simulation each neuron can be categorized as one of four different types based on location and response. These types are Left Inhibited, Left Excited, Right Inhibited, and Right Excited.

Table 1:

Overview of variables assigned to each neuron.

Variable	Description	Value	Frequency of updates
loc	Neuron location in CeA	Left (L) or Right (R)	Assigned at initialization
res	Type of response exhibited by neuron	Excited (Ex) or Inhibited (In)	Assigned at initialization
tL	Length of damage latency period	integer in [20, 80]	Assigned at initialization
tS	Length of sensitizing period	integer in [50, 150]	Assigned at initialization
d	Damage (percent of total damage)	real number in [0, 100]	Updated each time step
fr	Firing rate	non-negative real number	Updated each time step

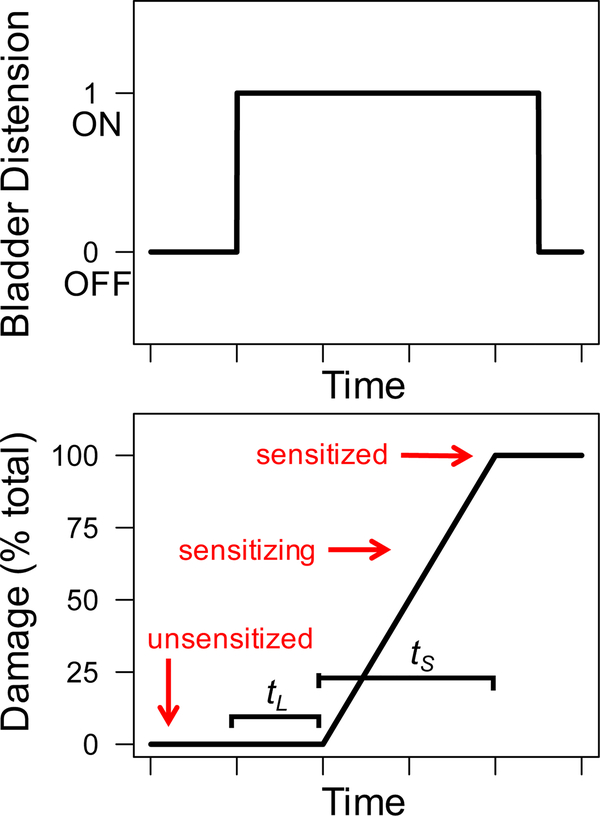
Additionally, each neuron possesses three variables related to neural ‘damage’. A damage accumulation model is used to track a neuron’s progress towards sensitization caused by long-term bladder distention. A neuron’s damage level (d) is a value with range [0,100] indicating the percent of total damage accumulated by the neuron and is updated each time step. A damage level of 0 indicates that the neuron has accumulated no damage. A damage level of 100 indicates that the neuron has reached its maximum damage level and is sensitized. Damage levels between 0 and 100 indicate the neuron is partially-damaged and is sensitizing (i.e, in the process of becoming sensitized). A neuron’s damage level starts at zero and increases only when the bladder has been distended for a number of time steps exceeding t_L, the length of the neuron’s damage latency period. A neuron accrues damage at a rate of $\frac{100}{t_S}$ units per time step, where t_S is the length of the neuron’s sensitizing period. Thus, when the bladder is distended, a sensitizing neuron will become sensitized after t_S time steps. Both t_L and t_S are positive integers assigned to each neuron during initialization and do not change during a simulation. In all simulations presented here, each neuron was assigned a value of t_L between 20 and 80 and a value of t_S between 50 and 150.

Lastly, each neuron has a firing rate (fr) describing the frequency in hertz (spikes per second) of the neuron’s action potential. A neuron’s firing rate is stochastically updated at each time step based on the bladder’s current state (distended or not distended) and the neuron’s location, response, and current damage level.

2.3. Global Variables

The model includes three global variables (Table 2). Variables p₁ and p₂ control the quantity of excited and inhibited neurons within the left and right hemispheres of the amygdala. Specifically, p₁ denotes the proportion of neurons in the left amygdala that are excited. Therefore, 1−p₁ denotes the proportion of neurons in the left amygdala that are inhibited. Similarly, p₂ denotes the proportion of neurons in the right amygdala that are excited and 1−p₂ denotes the proportion of neurons in the right amygdala that are inhibited. Both p₁ and p₂ are specified at the initialization of the model and do not change during a simulation.

Table 2:

Overview of global variables.

Variable	Description	Value	Frequency of updates
p1	Proportion of neurons in center hemisphere that are excited	real number in [0,1]	Assigned at initialization
p2	Proportion of neurons in right hemisphere that are excited	real number in [0,1]	Assigned at initialization
CBD	Cumulative number of time steps during which the bladder is distended	non-negative integer	Updated each time step

The third global variable, CBD, tracks the cumulative number of time steps during which the bladder is distended. Variable CBD is initially set to zero and incremented by 1 during appropriate time steps.

2.4. Model Input

The timing and duration of bladder distention during a simulation is specified by the user as a file consisting of zeros and ones. During the initialization, the model reads this file and creates a vector BD, where the i^th element of BD (denoted by BD_i) is equal to the i^th value from the file. A value BD_i = 0 indicates that the bladder is not distended during the i^th time step, while a value BD_i = 1 indicates that the bladder is distended during the i^th time step.

2.5. Model Processes

2.5.1. Overview

The model simulates neural behavior across the left and right hemispheres of the amygdala over time and in response to the bladder distention history provided by the user. The quantity of excited and inhibited neurons in the left and right hemispheres is determined at the model’s initialization and does not change during a simulation. During each time step, neural firing rates are stochastically updated in response to the current state of the bladder (distended or not distended). Individual neuron firing rates are determined using the neuron’s location, response, and current damage level. Damage is accrued by neurons during long-term bladder distentions. When damage reaches a threshold value, neurons become sensitized. Parameters defining the firing rates of neurons in the sensitized and unsensitized states were estimated from laboratory experiments. Emergent measures of pain are calculated as the difference in cumulative firing rates of excited and inhibited neurons in the left and right hemispheres.

2.5.2. Initialization

During the model’s initialization, the vector BD is established from the input file and 324 neurons are created on the agent space. Half of the neurons are assigned to the left hemisphere of the amygdala (loc = L) and the other half are assigned to the right hemisphere of the amygdala (loc = R). Each neuron on the left hemisphere is randomly assigned a response (res = Ex or In) based on the value of p₁. In particular, for each neuron in the left hemisphere, a random number in [0,1] is drawn using a uniform probability distribution. If the random number is less than or equal to p₁, then the response of the neuron is set to excited. If the random number is greater than p₁, then the response of the neuron is set to inhibited. Similarly, each neuron on the right hemisphere is randomly assigned a response type based on the value of p₂. Additionally, all neurons are randomly assigned individual values of t_L and t_S using a uniform probability distribution over the ranges specified in Table 1. The damage (d) of each neuron is set to 0. Lastly, global variable CBD is set to 0.

2.5.3. Neural behavior though time

The following procedures occur each time step to simulate neural behavior. First, at each time step i, global variable CBD is updated according to

$$CB{D}_i=\{\begin{array}{ll}CB{D}_{i-1}+1\hfill & \text{if}B{D}_i=1,\hfill \\ CB{D}_{i-1}\hfill & \text{if}B{D}_i=0,\hfill \end{array}$$ (1)

where CBD_i is the value of CBD at time step i, BD_i = 1 indicates the bladder is distended at time step i, and BD_i = 0 indicates the bladder is not distended at time step i. Therefore, CBD tracks the cumulative number of time steps during which the bladder is distended.

Second, the damage of each neuron is updated. For each neuron, damage (d) at time step i is updated using the damage accumulation model

$$d_i=\{\begin{array}{ll}\min \left(d_{i-1}+\frac{100}{t_S},100\right)& \text{if}CB{D}_i>t_L\\ & \text{and}B{D}_i=1,\\ d_{i-1}& \text{if}CB{D}_i\le t_L\\ & \text{or}B{D}_i=0,\end{array}$$ (2)

where d_i is the damage accrued by the neuron at time step i, t_S is the length of the neuron’s sensitization period, CBD_i is the cumulative bladder distention value at time step i, t_L is the length of the neuron’s latency period, and BD_i indicates whether the bladder is distended (BD_i = 1) or not distended (BD_i = 0) at time i. Therefore, a neuron’s damage increases only during time steps in which the bladder is distended (BD_i = 1) and the cumulative distention period has exceeded the neuron’s damage latency (CBD_i > t_L). The maximum value of damage is 100 and indicates the neuron is sensitized. If the bladder is not distended (BD_i = 0) or the cumulative distention period has not exceeded the neuron’s damage latency (CBD_i <= t_L), the neuron’s damage level does not change. Figure 1 displays an example bladder distention history and the corresponding accumulation of damage for a single neuron using equation (2).

Figure 1:

Example bladder distention history (Top) and corresponding damage level of a single neuron with latency period t_L and sensitization period t_S (Bottom). A neuron is unsensitized when damage is zero, sensitizing when damage is between zero and 100, and sensitized when damage reaches a max value of 100.

Lastly, during time step i, each neuron’s firing rate is stochastically updated using the equation

$$f{r}_i=\frac{100-d_i}{100}\cdot X+\frac{d_i}{100}\cdot Y$$ (3)

where fr_i is the firing rate at time i, X is a random variable describing the firing rate of the neuron in an unsensitized state, and Y is a random variable describing the firing rate of the neuron in a sensitized state. Both random variables X and Y are defined by truncated normal distributions and estimated using data collected in laboratory experiments (Section 3). Each random variable is defined by a mean (μ), standard deviation (σ), minimum value (min) and maximum value (max). These parameters depend on the neuron’s location (Left or Right), the neuron’s response (Excited or Inhibited) and whether or not the bladder is distended at time i (BD_i = 0 or BD_i = 1).

The model updates global variable CBD (equation (1)) and the damage (equation (2)) and firing rates (equation (3)) of all neurons each time step until the end of the simulation. The length of a simulation (i.e., number of time steps) is equal to the length of vector BD.

2.5.4. Emergence

The primary emergent feature of the model is the measure of pain attributed to bladder distention. In the model, pain is measured as the difference between the cumulative firing rates of all excited neurons and the cumulative firing rates of all inhibited neurons across the left and right hemispheres of the CeA. At time step i, pain is computed as

$$P_i=\sum _{loc=L,R}\sum _{res=Ex}f{r}_i-\sum _{loc=L,R}\sum _{res=In}f{r}_i$$ (4)

where fr_i denotes the firing rate of a neuron at time i.

2.6. Implementation

The model was coded in NetLogo (Version 6.0) [53]. This software has a unique programming language and customizable interface that is designed specifically for ABM development and implementation. For access to the NetLogo code, please contact the corresponding author. In Net-Logo, BehaviorSpace was used to automate the simulations. Statistical and graphical analyses of model output were completed using R statistical software [42].

3. Parameter Estimation

3.1. Overview

Random variables X and Y describe the firing rates of a neuron in the unsensitized and sensitized states, respectively. Each random variable is assumed to have a truncated normal distribution with mean (μ), standard deviation (σ), minimum value (min) and maximum value (max). Values of μ, σ, max and min depend on the current state of the bladder (distended or not distended) as well as the neuron’s location (Left or Right) and response (Excited or Inhibited). Thus, there are eight possible parameter sets defining X and eight possible parameter sets defining Y. These parameters were estimated using data from laboratory experiments in which the firing rates of neurons in the CeA of naive and chemically-sensitized mice were measured before and during painful bladder distention.

3.2. Laboratory Experiments

A brief description of the laboratory experiments is provided here. All laboratory experiments were approved by the Duquesne University Institutional Animal Care and Use Committee. Prior to experimental recording, female mice were treated three times over five days with either saline (control treatment) or cyclophosphamide (CYP) (sensitizing treatment). All animal experiments were completed blinded to animal treatment. On the sixth day, mice were prepared for bladder distention recording experiments. Animals were anesthetized at 37°C and a catheter was inserted into the bladder via the urethra [46]. The skull overlying the CeA was removed and a carbonfiber electrode was lowered into brain in 5μm bursts until single-unit spikes (action potentials) were identified for a neuron [45]. Neuronal activity was relayed in real time to a computer using Spike2 data acquisition software (Version 7, Cambridge Electronic Design).

Action potentials were recorded immediately before, during, and after a bladder distention. Each distention lasted 20 seconds and action potentials were measured for 20 seconds before and after the distention. This 60 second sequence is considered one distention trial. Between 3 and 5 distentions trials were performed for one neuron. Bladder distention was completed through a custom mechanical air controller connected to the urethral catheter. Pressures of 30mmHg (innocuous) and 60mmHg (noxious) were delivered in sequence with at least 2 minutes between trials. For the building of the agent based model, only 60mmHg data was used and is reported here. Action potentials were counted by a custom script in Spike2 software (Cambridge Electronic Design) using the WaveMark feature.

The location within the CeA of each neuron was established in the laboratory. After recording neural activity, electric current was used to mark the recording position of a neuron and the brain was sectioned to verify the neuron’s location in the left or right hemisphere of the CeA.

3.3. Classification of Neurons Observed in Laboratory Experiments

In the computational model, neurons are classified as one of four types based on location (Left or Right) and response (Excited or Inhibited). As described above, a neuron’s location was established in the laboratory.

The response (Excited or Inhibited) of each neuron was determined by applying the following statistical algorithm. For each of the 171 distention trials performed in the laboratory experiment described above, 20 measurements of the neuron’s firing rate before distention and 20 measurements of the same neuron’s firing rate during distention were recorded. A two sample t-test was applied to each set of measurements (40 values total) to determine if there was significant difference (p < 0.05) in the average firing rates observed before distention and during distention. The 171 distention trials were ranked in ascending order according the their corresponding p-value. A Benjamini-Hochberg controlling procedure [8] was then performed to decrease the likelihood of a false positive. Specifically, a critical value was calculated for each distention trial using the following formula.

$$\text{Critical}\text{value}=\frac{\text{rank}}{171}\cdot 0.05$$ (5)

If the measurements from one distention trial resulted in a p-value greater than its critical value, then that distention trial was disregarded from further analysis. The remaining 52 distention trials were grouped according to the corresponding neuron ID and inspected for either an increase or decrease in the average firing rate before and during bladder distention. If all distention trials corresponding to the same neuron showed an increase in average firing rates, then the neuron was classified as Excited. If all distention trials corresponding to the same neuron showed a decrease in average firing rates, then the neuron was classified as Inhibited. If any neuron exhibited an increase in its average firing rate during one distention trial and a decrease in average firing rate during a different distention trial, then the neuron was not classified and it was excluded from our analyses.

3.4. Determining X and Y

The procedure above yielded the classification of 18 neurons, 6 of which were CYP-sensitized and 12 of which were not. Firing rates from the 12 unsensitized neurons were used to estimate parameters defining random variable X. Of these 12 unsensitized neurons, 3 were Left Inhibited, 2 were Left Excited, 2 were Right Inhibited, and 5 were Right Excited. The mean, standard deviation, minimum and maximum of all firing rates observed before bladder distention and during bladder distention for each of the four types was calculated and used to define random variable X (Table 3). Firing rates from the 6 CYP-sensitized neurons were used to determine random variable Y. Of these 6 CYP-sensitized neurons, 1 was Left Inhibited, 3 were Left Excited, 1 was Right Inhibited, and 1 was Right Excited. The mean, standard deviation, minimum and maximum of all firing rates observed before bladder distention and during bladder distention for each of the four types was calculated and used to define random variable Y (Table 4)

Table 3:

Parameters defining random variable X. Random variable X describes the firing rate of an unsensitized neuron and is defined by a truncated normal distribution with mean, standard deviation, minimum, and maximum values. Each of the parameter values depend on the neuron’s type and the current bladder state.

Neuron Type	Bladder State	Mean μ	Standard Deviation σ	Minimum min	Maximum max
Left Inhibited	Not Distended	44.37	14.91	9	81
Left Inhibited	Distended	24.87	15.97	2	64
Left Excited	Not Distended	14.58	4.87	2	24
Left Excited	Distended	20.73	6.11	7	33
Right Inhibited	Not Distended	27.68	11.03	10	43
Right Inhibited	Distended	10.65	7.66	1	36
Right Excited	Not Distended	12.62	9.62	0	41
Right Excited	Distended	16.43	10.36	1	42

Table 4:

Parameters defining random variable Y. Random variable Y describes the firing rate of a sensitized neuron and is defined by a truncated normal distribution with mean, standard deviation, minimum, and maximum values. Each of the parameter values depend on the neuron’s type and the current bladder state.

Neuron Type	Bladder State	Meanμ	Standard Deviationσ	Minimum min	Maximum max
Left Inhibited	Not Distended	26.8	7.11	15	44
Left Inhibited	Distended	19.75	6.31	9	29
Left Excited	Not Distended	9.47	8.16	0	30
Left Excited	Distended	20.25	10.13	0	41
Right Inhibited	Not Distended	18.60	6.79	6	31
Right Inhibited	Distended	12.58	6.06	4	29
Right Excited	Not Distended	23.08	9.73	8	43
Right Excited	Distended	29.2	11.44	10	51

4. Model Simulations and Results

4.1. Simulation of Acute and Chronic Bladder Pain

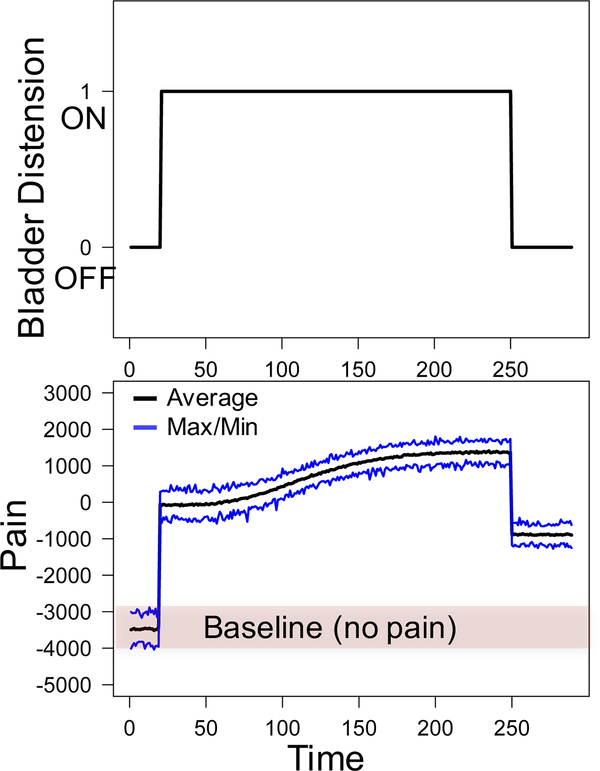
We provide an example of model output generated using a bladder distention history with no distention for the first 20 time steps (BD_i = 0 for 1 ≤ i ≤ 20), bladder distention for the subsequent 230 time steps (BD_i = 1 for 21 ≤ i ≤ 250), and no bladder distention for the remaining 40 time steps (BD_i = 0 for 251 ≤ i ≤ 290). The model was simulated 100 times with this distention history. In each simulation, we assumed an equal proportion of excited and inhibited neurons in both the left and right hemispheres (i.e., p₁ = p₂ = 0.5). Figure 2A displays the distention history and Figure 2B displays the corresponding measures of pain outputted by the model. Blue lines show the maximum and minimum values of pain over each of the 100 simulations while the black line indicates the average value of bladder pain obtained from the 100 simulations.

Figure 2:

Top: Bladder distention history inputted into the model. Bottom: Corresponding pain values outputted by model. Maximum, minimum, and average values were obtained from 100 model simulations.

As seen in Figure 2, pain values range from −4000 to −3000 with an average value of −3475 during the first 20 time steps when no bladder distention has occurred. These values are considered baseline values because they measure neural activity in the absence of pain. When the bladder is distended at time step 20, pain values immediately increase to an average of −83. This large increase in pain from the baseline value is interpreted as acute pain attributed to bladder distention. During the distention, all neurons accrue damage and become sensitized. Pain values increase to an average value of 1368 at time step 245. Finally, when the bladder is not distended at the end of the simulation, the average value of pain decreases to −867. This value is still substantially higher than the average baseline value of pain observed at beginning of the simulation and is therefore interpreted as chronic pain that exists when the bladder is not distended.

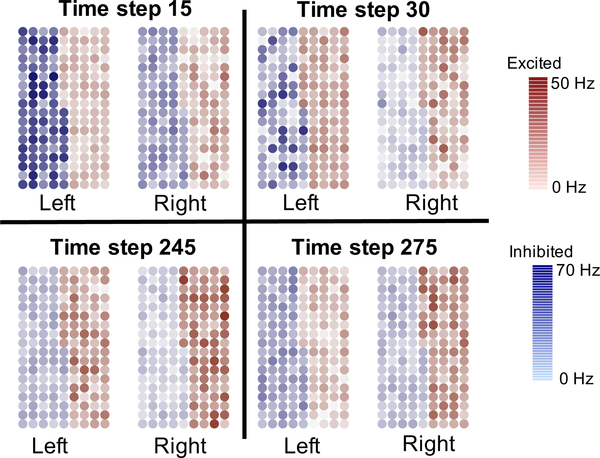
Figure 3 displays individual firing rates of inhibited neurons (blue circles) and excited neurons (red circles) in the left and right hemispheres at time steps 15, 30, 245, and 275 from one of the 100 simulations. These images aid in understanding the asymmetric neural behavior in the CeA during different pain states. At all times displayed in Figure 3, the inhibited neurons in the left hemisphere are on average firing at a higher rate than inhibited neurons in the right hemisphere. This asymmetric behavior of inhibited neurons is most apparent during the pain-free state (time step 15). On the other hand, during long-term and chronic pain (time steps 245 and 275), the excited neurons in the right hemisphere are on average firing at a higher rate than excited neurons in the left hemisphere.

Figure 3:

Firing rates of individual neurons in the left and right hemispheres of the CeA.

4.2. Sensitivity Analysis

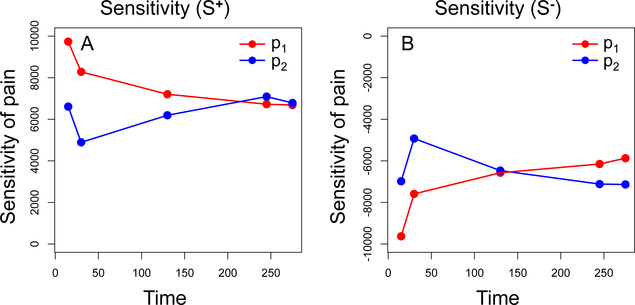
Using the steps outlined in [43], a local sensitivity analysis was performed to quantify the impact of global variables p₁ and p₂ on pain values outputted by the model at critical time steps. Recall that variable p₁ represents the proportion of neurons in the left hemisphere that are excited and p₂ represents the proportion of neurons in the right hemisphere that are excited. In the sensitivity analysis, both variables were assumed to have a range of [0.4,0.6] with a baseline value of 0.5. To generate sensitivity values for p₁, the model was simulated 100 times for p₁ valued at each the lower endpoint (R⁻ = 0.4), baseline (R = 0.5), and upper endpoint (R⁺ = 0.6) while p₂ remained at baseline value. Likewise, sensitivity values for p₂ were generated by simulating the model 100 times for p₂ valued at each the lower endpoint (R⁻ = 0.4), baseline (R = 0.5), and upper endpoint (R⁺ = 0.6) while p₁ remained at baseline value. The sensitivity of pain with respect to each parameter was then calculated as $S^{+}=\frac{P^{+}-P}{R^{+}-R}$ and $S^{-}=\frac{P^{-}-P}{R-R^{-}}$ where P⁻, P, P⁺ are the average values of pain when the parameter is valued at R⁻, R, R⁺, respectively. Each simulation used the bladder distention history displayed in Figure 2A and pain was outputted at time steps 15, 30, 130, 245, and 275.

Table 5 displays the sensitivity values for variables p₁ and p₂ at time steps 15, 30, 130, 245, and 275. Graphs displaying sensitivity values S⁺ and S⁻ over time are presented in Figure 4. The positive values of S⁺ indicate an increase in pain when each variable is increased by 0.1 and negative values of S⁻ indicate a decrease in pain when each variable is decreased by 0.1. At time steps 15, 30, and 130, pain output is more sensitive to p₁ than p₂. This indicates that the distribution of excited and inhibited neurons in the left hemisphere is most influential in pain modulation during the absence of pain and during short-term pain events. On the other hand, at times steps 245 and 275, pain output is more sensitive p₂ than p₁. This indicates that the distribution of excited and inhibited neurons in the right hemisphere is most influential in pain modulation during long-term pain events.

Table 5:

Sensitivity of pain with respect to global variables p₁ and p₂. Sensitivities S⁺ and S⁻ were calculated using measurements of pain at time steps 15, 30, 130, 245, and 275.

Variable	Time t = 15	Time t = 30	Time t = 130	Time t = 245	Time t = 275
p1	S+ = 9735.15	S+ = 8283.22	S+ = 7205.54	S+ = 6724.45	S+ = 6685.70
	S− = −9627.66	S− = −7589.11	S− = −6571.78	S− = −6150.93	S− = −5871.26
p2	S+ = 6609.61	S+ = 4891.26	S+ = 6193.34	S+ = 7091.35	S+ = 6786.03
	S− = −6979.88	S− = −4925.62	S− = −6468.30	S− = −7116.24	S− = −7134.70

Figure 4:

Sensitivity of pain with respect to global variables p₁ and p₂. Panel A illustrates changes in sensitivity value S⁺ over time. Panel B illustrates changes in sensitivity value S⁻ over time.

4.3. Model Predictions of Pain During Inhibition of the Left and Right CeA

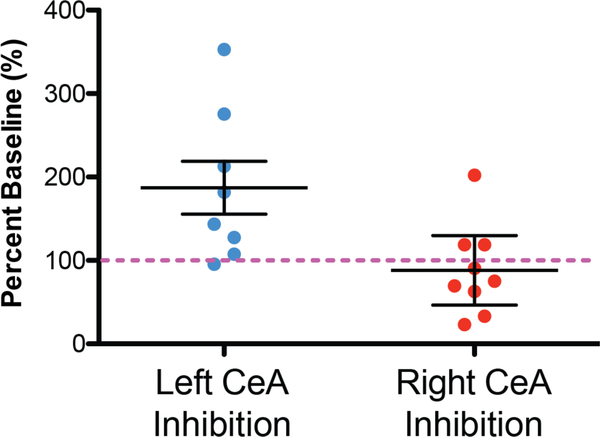
In this section, we assess the model’s predictive capability by comparing pain values outputted by the model with the behavioral responses of mice during painful bladder distention. In previously published laboratory experiments, optogenetic inhibition of neural activity in one hemisphere only was achieved by applying light stimulation to neurons in either the left or right CeA to decrease neural activity [45]. Figure 5 displays the percent change in pain-like responses compared to the average baseline value obtained when no inhibition occured. These experiments showed that optogenetic inhibition of the left CeA caused an increased in pain-like responses to bladder distention in unsensitized female mice. In contrast, optogenetic inhibition of the right CeA did not change pain-like responses in unsensitized mice. Overall, these data suggest the left CeA has an anti-nociceptive output at baseline. When this anti-nociceptive output is inhibited (using optogenetics), bladder pain increases. On the other hand, the right CeA is likely inactive at baseline so inhibition does not change the spontaneous output of these neurons and the overall output is likely similar to what would be seen with no optogenetic manipulation.

Figure 5:

Measurements of pain recorded in mice during optogenetic inhibition of the left or right CeA. Optogenetic inhibition (with halorhodopsin) of the left CeA caused an increase in bladder pain suggesting an on-going anti-nociceptive output from the left CeA in naive mice. Left CeA effects are statistically significantly different from right CeA optogenetic inhibition (t-test P = 0.013; n = 8 − 9) and significantly different from baseline (onesample t-test compared to hypothetical value of 100% (pink dotted line); P = 0.029). In contrast, optogenetic inhibition of the right CeA did not significantly change bladder pain-like effects compared to baseline (one sample t-test compared to hypothetical value of 100%; P = 0.53). Error bars represent mean ±1 standard error. Data adapted from Sadler et al. [45].

In the model, these optogenetic experiments were replicated by inputting the bladder distention history seen in Figure 2 and outputting pain at time step 30. Time step 30 was chosen because it corresponds to the a time at which all neurons are unsensitized. To simulate the inhibition of neurons in one of the hemispheres, pain was calculated as the difference in the cumulative firing rates of all excited and all inhibited neurons in the other hemisphere only. During inhibition of the left hemisphere, pain was calculated as

$$P_i^R=\sum _{loc=R}\sum _{res=Ex}f{r}_i-\sum _{loc=R}\sum _{res=In}f{r}_i$$ (6)

where i = 30. Similarly, during inhibition of the right hemisphere, pain was calculated as

$$P_i^L=\sum _{loc=L}\sum _{res=Ex}f{r}_i-\sum _{loc=L}\sum _{res=In}f{r}_i$$ (7)

where i = 30.

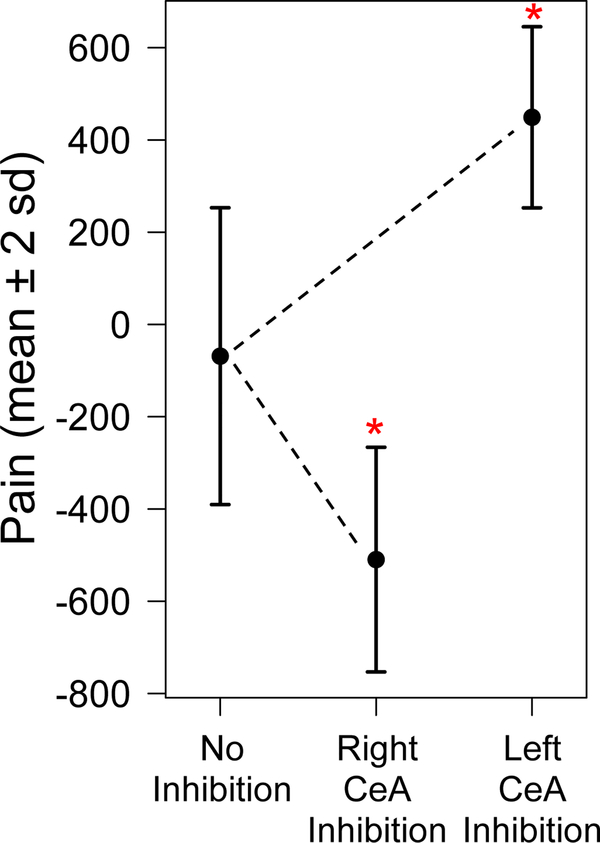
The model reproduced results similar to those observed in the lab. Figure 6 displays measures of pain at time step 30 from 100 simulations of the model in which pain was calculated using both hemispheres (equation (4)), left hemisphere only (equation (7)), and right hemisphere only (equation (6)). Solid dots represent average values of pain with error bars indicating ±2 standard deviations. Inhibition of the left hemisphere resulted in a statistically significantly higher pain output (449.1 ± 98.2) compared to pain values generated using both hemispheres (−68.7 ± 160.9), P < 0.001. On the other hand, pain values generated by the model during inhibition of the right hemisphere were significantly lower (−509.7 ± 121.8) than pain values generated using both hemispheres (−68.7 ± 160.9), P < 0.001. The decrease in pain during inhibition of the right hemisphere suggests pain is reduced but still present. Pain elimination would be expected only when pain values are within baseline range of −4000 to −3000.

Figure 6:

Measurements of pain predicted by the model during inhibition of the left or right CeA. Pain values at time step 30 generated by 100 model simulations using neural activity during no inhibition of the CeA, inhibition of the right CeA, and inhibition of the left CeA. Circles represent average values and bars indicate ±2 standard deviations. Asterisks denote a significant change in average pain output during inhibition (P < 0.001).

5. Discussion

Our agent-based model incorporates several important biological features including stochasticity and neural sensitization, but it does not yet include interaction between neurons. The central nucleus of the amygdala (CeA) is comprised of interconnected neurons that send and receive information with one another as well as other parts of the amygdala. In our current model, neurons act independently in response to painful bladder stimuli. This simplifying assumption is not biologically plausible, but it allowed us to focus on the function of each neuron and its role in pain, rather than focusing on the connectivity and interdependence of neurons. Enhancing the model by including more complex features, such as connectivity and the ability of neurons to transmit signals to one another, is feasible within the framework of our agent-based model and will be explored in future work.

Despite its simplicity, the model has the ability to simulate acute and chronic pain attributed to prolonged painful stimuli (Figure 2). The majority of mathematical and computational models of pain focus on acute pain and do not include features necessary for explaining chronic pain [2, 40]. In our model, chronic pain emerges from the sensitization of neurons. This is accomplished by assigning a damage variable to each neuron and using a damage accumulation model to track the neuron’s progress towards sensitization caused by long-term bladder distention. As far as we know, our use of a damage accumulation model to account for neural sensitization is new. The model is formulated such that neural damage accrues during periods of bladder distention; however, damage is never repaired in the absence of distention. Accounting for damage repair is a simple modification to the model (for example see [12]), but requires additional biological assumptions. Further laboratory experiments are needed to determine if sensitization can wane over time and, if so, under what conditions.

Our agent-based model serves as a theoretical framework for assessing asymmetric neural activity in the left and right hemispheres of the CeA. Figure 3 illustrates the differences in firing rates of excited and inhibited neurons across left and right hemispheres at critical times during pain progression. A main advantage of using an agent-based model to describe neural behavior in the CeA is the ability to utilize mathematical tools, such as a sensitivity analysis, to quantify the importance of select parameters on model output. Our sensitivity analysis revealed that measures of pain are more sensitive to neural behavior in left hemisphere (as controlled by p₁) during the absence or onset of pain whereas measures of pain were more sensitive to neural behavior in the right hemisphere (as controlled by p₂) during long-term and chronic pain (Figure 4). Both the graphical displays of model output and the sensitivity analysis provide a means of assessing asymmetric neural behavior related to pain that could not be inferred from the laboratory data alone.

The model’s ability to generate changes in pain similar to those observed in the laboratory during optogenetic inhibition experiments (described in Sadler et al. [45]) is encouraging and demonstrates potential for the model to aid future laboratory studies. Both the laboratory experiments (Figure 5) and model predictions (Figure 6) showed that inhibition of the left hemisphere in unsensitized mice leads to a significant increase in pain during bladder distention. This increase in pain suggests the left hemisphere of the CeA is responsible for anti-nociceptive output during painful bladder distention. On the other hand, the model predicted that inhibition of the right hemisphere in unsensitized mice would reduce, but not eliminate pain during bladder distention, suggesting that the right hemisphere of the CeA is responsible for pro-nociceptive output. The corresponding lab experiments showed no significant change in pain during optogenetic inhibition of the right hemisphere. While the model predictions and laboratory outcomes were not identical, both showed the persistence of pain during inhibition of the right CeA. Overall, the similarities in results from the lab experiments and corresponding model simulations support the continued use and refinement of the model.

6. Conclusions

We used preliminary laboratory data to develop and parameterize an agent-based model of neural activity in the central nucleus of the amygdala as it evolves in response to painful bladder stimuli. Given an individual’s history of bladder distention, the model simulates the firing of individual neurons and uses system-level output to measure bladder pain. The model is simple in design, but has the ability to simulate neural sensitization and the development of chronic pain over time. Model predictions of bladder pain were shown to be similar to those observed in independent laboratory experiments, thus validating the model’s potential for future use in pain prediction. The model and analyses presented in this paper complement ongoing laboratory studies to assess differences in neural behavior across the left and right hemispheres. Future work will aim to enhance the model with more complex and biologically plausible features, including connectivity of neurons.