Inferring the model and onset of natural selection under varying population size from the site frequency spectrum and haplotype structure

Abstract

A fundamental question about adaptation in a population is the time of onset of the selective pressure acting on beneficial alleles. Inferring this time, in turn, depends on the selection model. We develop a framework of approximate Bayesian computation (ABC) that enables the use of the full site frequency spectrum and haplotype structure to test the goodness-of-fit of selection models and estimate the timing of selection under varying population size scenarios. We show that our method has sufficient power to distinguish natural selection from neutrality even if relatively old selection increased the frequency of a pre-existing allele from 20% to 50% or from 40% to 80%. Our ABC can accurately estimate the time of onset of selection on a new mutation. However, estimates are prone to bias under the standing variation model, possibly due to the uncertainty in the allele frequency at the onset of selection. We further extend our approach to take advantage of ancient DNA data that provides information on the allele frequency path of the beneficial allele. Applying our ABC, including both modern and ancient human DNA data, to four pigmentation alleles in Europeans, we detected selection on standing variants that occurred after the dispersal from Africa even though models of selection on a new mutation were initially supported for two of these alleles without the ancient data.

1. Introduction

Adaptations to local selective pressures in natural populations have been broadly attributed to two main models of natural selection: selection on new mutations, also referred to as selective sweeps, and selection on pre-existing (i.e. standing) genetic variation [1–5]. An important difference between these models, in the context of exposure to new environmental pressures, is that under the selective sweep model the adaptive process must wait for the emergence of new beneficial mutations, while standing variants are immediately available as the source of beneficial alleles in the new environment. Therefore, these two models of natural selection result in different population dynamics of beneficial alleles [6]. Understanding the tempo and mode of natural selection can provide insights into the process of adaptation to new selective pressures.

Natural selection may leave distinctive footprints on patterns of neutral sequence variation linked to the advantageous allele [7], which are strongly shaped by the joint effects of allele frequency at the selected site (f₀) at present (i.e. t = 0) and of three additional parameters: the time of onset of selection (T), the frequency of the beneficial allele at the onset of selection (f_T) and the strength of selection acting on the selected site (s). Selective sweeps are expected to reduce levels of genetic variation at linked neutral sites due to the rapid increase of the beneficial allele frequency, and to generate a skew in the site frequency spectrum (SFS) [8–11]. By contrast, a standing adaptive variant may have existed in a population long enough to break up the association between the adaptive allele and nearby neutral alleles. Depending on the values of T, f_T and s, natural selection will leave a signature that ranges between the patterns expected from selective sweeps and those for neutral models [2–4]. Therefore, f₀ and intra-allelic variability at linked neutral sites are informative for identifying the model of natural selection and for estimating the onset of selection [12–15].

Many scans for selection signals have been performed in humans and in other species [16–18], and, especially in humans, they have been connected with specific traits by using either functional annotations or catalogues of variants identified in genome-wide association studies [19]. In this paper, our goal is to develop a framework to estimate the timing of the selective pressures acting on the selection signals identified in the studies above and ultimately to help distinguish among hypotheses of selective pressures shaping different traits. To this end, we developed an approximate Bayesian computation (ABC) approach for inference of the mode and tempo of natural selection with a particular focus on the history of selective pressures during human evolution. Handling efficiently high-dimensional summary statistics, which are necessary to capture the subtle differences in patterns of genetic variation expected for selection on standing variation versus neutral models or for selection on standing variation versus selective sweep models [2–4], is a well-known challenge in ABC approaches [20]. To address this challenge, we employ kernel ABC that enables the use of full genetic variation information to attain a better approximation [21,22]. Our approach is built on simulations of variation data under varying population size models that more closely approximate the true population history [23]. We also simulate a constant size model for comparison. A key innovation is that we condition the parameter space on the allele frequency in the past by using available ancient DNA data [24,25]. We first evaluate the performance of our ABC framework without using ancient DNA data to test the goodness-of-fit of selection models and estimate the onset of selection. Then, we condition on an allele frequency at a past time point estimated from ancient DNA data and compare the results to the inferences based only on contemporary allele frequency. Finally, applying our ABC to light skin pigmentation alleles, well-known examples of natural selection in humans, we find that our approaches provide greater support for selection on standing variation than for selective sweep and neutral models, allowing estimation of the onset of selection on pigmentation alleles.

2. Material and methods

Our goal is to infer the age of an advantageous allele. However, this inference is dependent on the mode of selection acting on the allele because different models are defined by different sets of parameters. Therefore, our ABC framework consists of three main steps: (i) specifying selection models, (ii) choosing the best fitting model and (iii) estimating the parameters of interest. This framework is developed by default to make use of DNA sequence variation from contemporary populations. We also provide an extended approach by incorporating ancient DNA data into our ABC as an additional observation.

(a). Defining and simulating evolutionary models

We simulated two different models of selection: on a new mutation (SNM) or on a standing variant (SSV), using four different parameters: f₀ is allele frequency at present, T is onset of natural selection, s is selection coefficient and f_T is allele frequency at T. The difference between SNM and SSV is whether f_T is equal to or larger than 1/2N_e, where N_e is the effective population size. We also simulated a neutral model with parameters N_e and f₀. The neutral simulations were used to confirm that the data for the alleles chosen for age estimation are consistent with the reported selection signals. Conversely, the SNM and SSV simulations were used to select the best-fit selection model to be used for allele age estimation in the ABC.

These three models were simulated using mssel (http://genapps.uchicago.edu/newlabweb/software.html), a modified version of ms [26], which allows incorporation of the change of allele frequency at a target site into the standard coalescent process with random mutation and recombination under a varying population size model. First, frequency trajectories of a focal allele were generated by Wright–Fisher forward and backward simulation for the selection and the neutral phases, respectively (see examples in electronic supplementary material, figure S1; codes are available from https://github.com/shigekinakagome/sim_trajectory). To incorporate information from ancient DNA data into this step, we conditioned the trajectories with an allele frequency $f_{T_{\mathrm{past}}}$ at an additional time point T_past, as well as with f₀ at the present. Second, neutral variation surrounding the selected site was generated by coalescent simulations conditional on the trajectory; coalescent events are confined to lineages descended from the same class of alleles (i.e. derived or ancestral allele) and their rate depends on the population size. Third, the simulated data were summarized into the full SFS and the decay of extended haplotype homozygosity, both calculated separately for sequences carrying derived (i.e. beneficial) and ancestral alleles at the focal site (electronic supplementary material, figure S2). Details about prior probability distributions and demographic settings, simulation scheme and summary statistics are provided in the electronic supplementary material, text. Furthermore, our simulations took account of genomic contexts by using estimates of local mutation and recombination rates from genomic data (see also electronic supplementary material, text).

(b). Model selection by kernel density estimation

This step aims to evaluate the goodness-of-fit of the evolutionary models to an observation and to identify the best-fit scenario. We applied the method developed in [27] that measures the similarity of high-dimensional summaries between the observed and simulated data based on a kernel density estimate, instead of an acceptance rate as commonly used in ABC [28], and that calculates an approximated marginal likelihood (aML) of a given model. To avoid over-smoothing or over-fitting to simulation data, we chose a bandwidth in a normalized Gaussian kernel function using the 10-fold cross validation [27]. One million datasets were generated for each model with the simulation scheme described above to compute kernel density estimates of aMLs. These estimates, in turn, were used to choose a model for the parameter estimation by calculating approximate Bayes factors (aBFs) between selection models, as well as between neutral and selection models.

(c). Parameter estimation by kernel approximate Bayesian computation

Once the best-fitting model is chosen, the final step is to estimate the parameters of interest under the model. To take advantage of the high-dimensional summaries, we employed kernel ABC that transforms the summary data into high-dimensional space to measure the similarity between the observed and simulated data and re-weights the prior samples with the similarity to estimate posterior means [21,22]. These weights were further used to define credible intervals of the posterior estimates with a smoothing kernel [29].

(d). Simulation study

We tested the performance of kernel ABC in model selection and parameter estimation by simulating selection events given f₀ = 50% or 80% at five time points of 200, 400, 600, 800 and 1200 generations ago with different values of f_T = 1/2N_e, 1%, 5%, 10%, 20%, 30% and 40%.

(i). Model selection

For each combination of f₀, T and f_T, 1000 pseudo-observations were simulated by sampling a total of 100 chromosomes with f₀ = 50% or 80%. The mutation and recombination rates were assumed to be 2.5 × 10⁻⁸ and 1.0 × 10⁻⁸ per site per generation, respectively. Next, one million simulation datasets were generated for each model under the prior and demographic conditions (electronic supplementary material, text). These datasets were used to estimate aMLs for each pseudo-observation and to evaluate the accuracy in distinguishing between (i) the SNM models versus the neutral or the SSV models (figure 1), and (ii) the SSV models versus the neutral or the SNM models (electronic supplementary material, figure S3). We define the power for model selection as the probability that our method can correctly identify a true model with aBF > 100 and was calculated as the ratio of the number of pseudo-observations classified into the true model to the total 1000. This threshold is based on the Kass and Raftery (1995) guidelines [30]. If the probability is larger than 80%, we consider our method has enough power to identify true models.

Figure 1.

Accuracy of kernel ABC in (a) choosing the SNM models against the neutral or the SSV models and (b) estimating T under the SNM models. Boxplots at the top panels show log₁₀-scaled aBFs that take ratios of approximate marginal likelihoods (aMLs) between a true model (i.e. SNM) and an alternative model (i.e. neutral or SSV). The percentage with the parentheses above each boxplot shows the probability that the method can correctly identify the true model with log₁₀(aBF) > 2. The plots at the bottom represent posterior means of T given the observed summary data, $E(T|S(\mathcal{D}))$. The total 1000 pseudo-observations are used at each time point for (a), of which 100 observations are randomly chosen for (b). The dashed line shows a diagonal plot with slope = 1. (Online version in colour.)

(ii). Parameter estimation

We estimated posterior means of T for 100 pseudo-observations using 12 000 simulated datasets under the SNM (figure 1) or the SSV model (electronic supplementary material, figure S4). A similar comparison was also made for the data simulated under a constant size model to evaluate the robustness of our approaches to the demographic assumptions (electronic supplementary material, figures S5 and S6).

(iii). The use of ancient DNA data

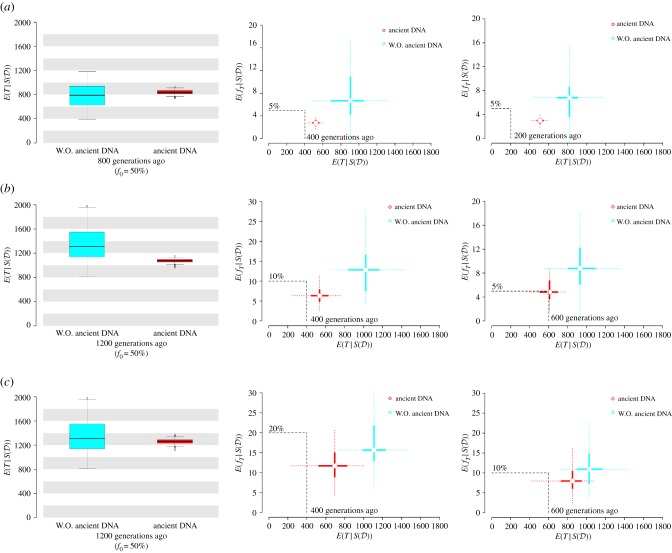
We generated an additional one million simulated datasets by conditioning the trajectory with $f_{T_{\mathrm{past}}}=5\text{\%}$, 10% or 20% at T_past = 400 under the SNM or SSV models (examples are shown in electronic supplementary material, figure S7). Then, we tested if the use of ancient DNA data can improve our ability to distinguish between selection models (electronic supplementary material, figure S8) and the accuracy in estimating the parameters under each model (figure 2).

Figure 2.

Comparisons of posterior estimates between kernel ABC with and without (W.O.) ancient DNA data. T_past is fixed as 400, and (a) $f_{T_{\mathrm{past}}}=5\text{\%}$, (b) 10% and (c) 20% are tested for different scenarios of the pseudo-observations under the SNM and SSV models (examples of trajectory under the true models are shown in electronic supplementary material, figure S7). Total 100 posterior means are estimated with (red) or without ancient DNA data (light blue). Boxplots represent posterior means of T given $S(\mathcal{D})$ under the SNM models with or without ancient DNA data. For the bar plots, points indicate posterior means of T and f_T given $S(\mathcal{D})$ under the SSV models with (red) or without ancient DNA data (light blue) and thick or dotted lines represent ranges between 25th and 75th quantiles or between 2.5th and 97.5th quantiles of the posterior estimates. The black dashed lines show the values of true parameters. (Online version in colour.)

(e). Application to human population data

As an application of our ABC approaches for a real dataset, we focused on four SNP sites that have been reported to be associated with signatures of natural selection in humans, as well as light skin pigmentation (electronic supplementary material, table S1). We used the complete genomics data for 64 unrelated individuals of European ancestry and calculated the set of summary statistics from DNA sequence variation in the genomic regions including the target SNP sites (see electronic supplementary material, figure S9 and text). A total of 1 million simulated datasets were generated under the three evolutionary models (i.e. SNM, SSV and neutrality) and under the same demographic model used in our simulation study; this is a varying population size model inferred in samples of European ancestry [23] (see electronic supplementary material, text). Parameters were sampled from the prior distributions taking account of the local mutation and recombination rates (electronic supplementary material, table S2). To incorporate ancient DNA data into our ABC framework, we estimated $f_{T_{\mathrm{past}}}$ from ancient European samples, dated within 10 − 7 thousand years ago (ka) [31–34], using the method described in [15] (see also electronic supplementary material, text). We conditioned trajectories on $f_{T_{\mathrm{past}}}$ under the SNM and SSV models by accepting them if allele frequency at 10 ka is $f_{T_{\mathrm{past}}}\pm 5\text{\%}$. We chose the models by testing the deviation from neutrality with the data only from the modern samples and distinguishing the models of natural selection with the data conditional on the ancient DNA data (table 1). We then estimated the parameters under the best fitting model using 30 000 simulations (figure 3).

Table 1.

Results from model selection for four pigmentation SNPs.

SNPs (genes)			rs16891982 (SLC45A2)	rs1426654 (SLC24A5)	rs642742 (KITLG)	rs1042602 (TYR)
allele frequency at 10–7 ka ($f_{T_{\mathrm{past}}}$)			33.74%	90.42%	59.61%	6.44%
allele frequency at present (f0)			96.88%	100.00%	81.25%	44.53%
without ancient DNA	log(aML) values	neutral	−222.450	−602.147	ln(0.0)	−251.018
		SNM	−275.158	−177.428	−222.769	−197.094
		SSV	−213.928	−170.599	−263.702	−201.849
	best model; log10(aBF) against neutral		SSV; 3.701	SSV; 187.419	SNM; 17.777	SNM; 23.419
with ancient DNA	log(aML) values	SNM	−260.592	−181.289	−503.696	−208.123
		SSV	−224.021	−179.457	−461.691	−204.835
	best model; log10(aBF) against SNM or SSV		SSV; 15.883	SSV; 0.796	SSV; 18.242	SSV; 1.428

Figure 3.

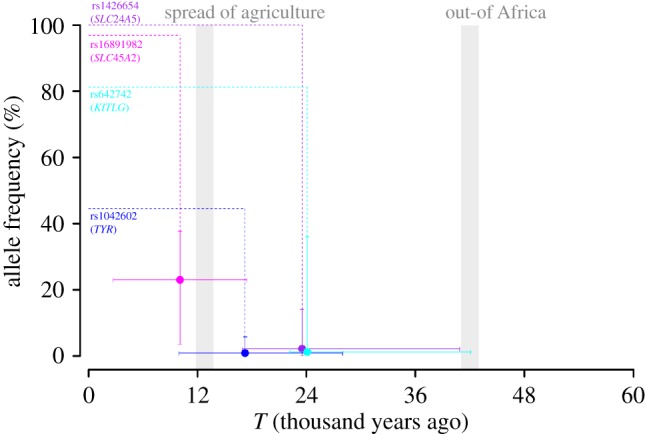
Posterior estimates of T and f_T for four pigmentation SNPs. The parameters are estimated under the best-fitting model shown from the model selection with ancient DNA (table 1). The x-axis represents time, while the y-axis represents allele frequency. The plots show posterior means of T and f_T with 95% credible intervals. Dotted lines describe the difference in allele frequency between 0 (i.e. the present) and T. Two major environmental transitions are highlighted with grey shades at 12.8 and 42 ka. (Online version in colour.)

3. Results

(a). Inferring onsets of natural selection on a new mutation

We first assessed the ability of our ABC approaches to distinguish the SNM from other models (figure 1; ‘Model selection' in Material and methods). Since s was sampled to simulate pseudo-observations from the exponential distribution until the trajectory that satisfied the fixed conditions of T, f_T and f₀ was accepted, combinations of younger T and higher f₀ tend to need stronger s to generate the trajectory, as expected (electronic supplementary material, table S3). For f₀ = 50%, our method can correctly infer SNM if T is within 200 to 600 generations ago (figure 1a). Even for an older time, such as 800 or 1200 generations ago, most of the observations show higher aMLs in the SNM models than those in the neutral models. The accuracy of the model selection further improved if f₀ = 80%; our method can accurately distinguish the SNM models from neutrality at any time points from 200 to 1200 generations ago. By contrast, the distinction between the SNM and SSV models is more difficult compared with that for selection versus neutral models. This is because SNM can be considered as an extreme case of SSV in terms of f_T. If f_T is as low as 1/2N_e and f₀ is high, selection from a rare mutation results in a selective sweep and the reduction in linked neutral diversity associated with SSV is expected to resemble that from SNM where a beneficial allele on a single haplotype is driven to f₀. Still, the majority of aMLs is higher in the SNM models than in the SSV models if T is younger than 800 generations ago under f₀ = 50% or 400 generations ago under f₀ = 80%.

We then tested the accuracy of our method in estimating the onset of selection under the SNM models by comparing posterior probability estimates to known ages (figure 1b; ‘Parameter estimation' in Material and methods). Even though we assumed incomplete sweeps of f₀ = 50% or 80%, which is expected to reduce the power in the inference compared with complete sweeps, the estimates are mostly close to the true ages. Therefore, the use of high-dimensional summary statistics can give sufficient information to capture differences in patterns of genetic variation among these time points.

(b). Inferring onsets of natural selection on a standing variant

The allele frequency path under the SSV models is expected to become similar to the trajectory under the SNM or the neutral models if f_T is close to 1/2N_e or f₀. Therefore, the aim of this analysis is to find a lower or an upper limit of f_T at different time points for distinguishing between SSV and neutral models or between SSV and SNM (electronic supplementary material, figure S3). The means of s under each combination of T, f_T and f₀ are listed in electronic supplementary material, table S3. The power to distinguish between the SSV and neutral models depends on f_T; the SSV models mostly have higher aMLs than those for neutral models if f_T is low relative to f₀, such as 1%, 5%, 10% or 20%. By contrast, the ability to distinguish SSV from SNM increases with f_T. We mostly make correct inferences on the SSV models, except when f_T is very low (i.e. 1%). The overall accuracy of the model selection improves if f₀ = 80%, and our method is likely to correctly classify the true models even if f_T = 1%. These results suggest that our method can accurately infer the SSV models if 5% ≤ f_T ≤ 40% and T ≤ 1200 under f₀ ≥ 50%.

We further explored the accuracy in the parameter estimation under the SSV models (electronic supplementary material, figure S4). In the case of f_T = 1%, the posterior means are close to the true ages, depending on the observations generated from different T. However, we found that the accuracy is poor if f_T = 5%, 10%, 20%. Different sets of T and f_T generate similar s estimates under a given f₀ (electronic supplementary material, table S3), which may result in similar patterns of linked neutral diversity in the samples at the present. If this is the case, the posterior estimates are likely to be biased towards the prior distributions. Indeed, the posterior estimates tend to be overestimated and get closer to the prior mean (i.e. 1600 generations ago; electronic supplementary material, figure S4).

(c). Extending the approximate Bayesian computation framework to include ancient DNA information

Given the challenges of parameter estimation under the SSV model, we investigated the improvement in accuracy by including information on the allele frequency in the past, defined as $f_{T_{\mathrm{past}}}$ at T_past (‘Defining and simulating evolutionary models' in Material and methods). Here, we assumed models where a beneficial allele is present at f₀ = 50%, but existed at $f_{T_{\mathrm{past}}}=5\text{\%}$, 10% or 20% at T_past = 400 (electronic supplementary material, figure S7; ‘The use of ancient DNA data'). Since f_T is fixed as 1/2N_e under the SNM models, T is expected to be older than T_past if $f_{T_{\mathrm{past}}}>1/2N_{\mathrm{e}}$. We used the observed data from T = 800 or 1200 to test the accuracy in the age estimation under the SNM models. With regard to the model selection between SNM and SSV, the inclusion of $f_{T_{\mathrm{past}}}$ makes only a small difference in distinguishing between selection models (electronic supplementary material, figure S8), even though adding the information on $f_{T_{\mathrm{past}}}$ can reduce variance of the estimates and increases the accuracy (figure 2).

By contrast, selection on standing variation could have happened at any time relative to T_past. We can still use the information to narrow down the time of onset of natural selection. If T is older than T_past, f_T is expected to be lower than $f_{T_{\mathrm{past}}}$ whereas f_T could take the frequency close to $f_{T_{\mathrm{past}}}$ if T is younger than T_past. We compared the accuracy of our method with and without ancient DNA data ($f_{T_{\mathrm{past}}}=5\text{\%}$, 10% or 20%) using the observations of f_T = 5%, 10% or 20% at T = 400, respectively. Additional cases that we considered in this comparison are f_T = 5% at T = 200, f_T = 5% at T = 600 or f_T = 10% at T = 600 (electronic supplementary material, figure S7). The accuracy in choosing the SSV models is similar with and without ancient DNA data (electronic supplementary material, figure S8). However, adding the condition of $f_{T_{\mathrm{past}}}$ to the estimation reduces the bias in the posterior means of T and f_T and the estimates get closer to the true values (figure 2). These results suggest that the use of ancient DNA data can help to restrict the parameter space and to improve the estimation under both SNM and SSV models.

(d). Application for modern and ancient data from humans

We applied our method to modern and ancient European data [31–34] for four SNPs associated with light skin pigmentation and recent positive selection in Europeans (electronic supplementary material, table S1; ‘Application to human population data' in Material and methods). Generating a sufficiently large number of simulated trajectories under a neutral model may take a long time if the difference between $f_{T_{\mathrm{past}}}$ and f₀ is large; few trajectories can achieve the change of allele frequency within T_past generations only by genetic drift. This implies that such observations on $f_{T_{\mathrm{past}}}$ and f₀ are unlikely to be explained by the neutral model. However, the allele frequency path captured only by two time points (i.e. T_past and T₀) may not be sufficient to confidently distinguish natural selection from neutral. Here, we built a framework to choose an evolutionary model through two-steps of the model selection; the first step aims to test the deviation from neutrality without ancient DNA data and the second step incorporates the condition of $f_{T_{\mathrm{past}}}$ into the simulation to evaluate which of SNM and SSV models provides a better fit to an observation.

The selection scenarios were significantly favoured with log₁₀-scaled aBFs >3.7 against neutral (table 1), which confirmed the previous evidence of natural selection. Two of the light pigmentation SNPs, rs16891982 at SLC45A2 and rs1426654 at SLC24A5, were found to better fit the SSV models, while the data for the other SNPs supported the SNM models. Then, we evaluated the goodness-of-fit of the selection models using simulation data with $f_{T_{\mathrm{past}}}$. Two out of the four SNPs fit better the SSV models even though SNM was inferred to be the best model in our test without ancient DNA data. This is likely to be because when f_T is low the two models are almost indistinguishable, as shown in our simulation study (figure 1; electronic supplementary material, figure S3).

We estimated the parameters under the best fitting models that were chosen from the model selection with ancient DNA data (figure 3). As we expected, f_T was estimated to be low for the SNPs where SNM was chosen without using ancient DNA and SSV was chosen when ancient DNA data was included in the inference (1.2% at rs642742; 0.8% at rs1042602). The estimates from the four SNPs show that selection on the pigmentation alleles occurred after the dispersal out of Africa. Two out of four SNPs (rs1426654 and rs6427442) have the posterior means of 23 527 years ago (16 920 − 40 896; s = 0.024 with 0.005−0.052) and 24 093 years ago (22 176 − 42 096; s = 0.006 with 0.001−0.021). This relatively old selection of rs1426654 supports a scenario that this allele may have slowly increased its frequency and fixed in Europeans during last 10 000 years. On the other hand, rs16891982 shows a relatively recent selection on the standing variant (10 089 years ago, 2736−17,472; s = 0.026 with 0.007−0.063). Another SNP (rs1042602) has the mean at 17 253 years ago (9984−27 984; s = 0.013 with 0.002−0.029), but the credible interval overlaps with the spread of agriculture.

4. Discussion

We present an ABC framework to make inferences about the timing of natural selection using high-dimensional data. Taking advantage of the strength in kernel ABC, we demonstrate our ABC approaches give reasonably accurate estimates of T under the SNM models (figure 1), which in turn suggests that the set of full SFS and decay of haplotype homozygosity contains more information than summary statistics used in previous ABC analyses [35]. One key limitation of our method is that the parameter estimation under the SSV models is prone to be biased by the priors (electronic supplementary material, figure S4). This reflects the difficulty in narrowing down the parameter space consistent with the SSV models only by using observations from a contemporary population. Recent advances of sequencing technologies have transformed our ability to generate population-scale data from ancient specimens. Making use of the new data on ancient specimens, we were able to reduce the bias and improve the accuracy by confining the parameter space (figure 2).

Choosing the appropriate model of selection for the beneficial allele being examined is a necessary step for its age estimation. To this end, we performed model selection aiming to distinguish between SNM and SSV. When f_T ≈ 1/2N_e, it is more challenging to distinguish between these models because both generate a similar reduction in linked neutral diversity levels [1,3,5,36]. However, if SNM occurred at a relatively recent time, such as 200 or 400 generations ago, we can distinguish the SNM from SSV models (figure 1). Moreover, as long as f_T ≥ 5%, our method is more likely to choose the SSV model than the SNM model (electronic supplementary material, figure S3). Although there is a parameter space where the two selection models are misclassified (if T ≥ 600 under SNM or if f_T ≤ 1% under SSV with f₀ = 50%), our method correctly identifies the SSV models if 5% ≤ f_T ≤ 20% or 1% ≤ f_T ≤ 40% under f₀ = 50% or 80%.

Our analysis of ancient and modern human data significantly supported natural selection on the pigmentation alleles that already existed as standing variants at the time of selection (table 1 and figure 3). The posterior estimates have no overlap with the dispersal out of Africa, suggesting that light skin pigmentation became advantageous during a move to higher latitude within Europe, as proposed in previous studies [37,38]. Growing evidence from ancient DNA studies shows that contemporary Europeans are a mixture of three different ancestries; ancestral hunter–gathers admixed with Anatolian farmers around 9 ka, followed by further migration from Pontic-Caspian Steppe around 5 ka [31–33]. We used ancient DNA data only from 10 to 7 ka as a reference of allele frequency in the ancestral lineage and assumed a panmictic population with bottleneck and expansion to avoid increasing the complexity of the model. However, this may lead to a violation of our assumption on the demographic history, and further studies taking account of realistic scenarios are necessary to reconstruct the history of human adaptation.

Our ABC framework was tested under the specific demographic condition inferred for Europeans with the aim of understanding the history of selective pressures in these populations. It can be applicable to other scenarios and/or other species; its applicability solely depends on the machinery for simulating data. The mssel software provides flexible options to simulate a variety of demographic scenarios. Our method works better with the constant size model (electronic supplementary material, figures S5 and S6) than the varying population size (figure 1; electronic supplementary material, figures S3 and S4); however, it still has sufficient power to correctly identify evolutionary models and accurately estimate the timing of natural selection as we demonstrate throughout this study (figures 1 and 2; electronic supplementary material, figures S3 and S4). A practical way of using our approach is, for example, to select an SNP site associated with selection signals or with phenotypic variation, identify the best selection model by incorporating demography inferred from existing methods (e.g. [23,39]), and estimate the age of the potentially beneficial variants. A further caveat to this application is additional assumptions on local genomic contexts including mutation and recombination rates, which need to be carefully taken into account for simulating realistic scenarios. Given a rapid growth of genomic-scale data from a variety of organisms, our framework of simulation and data usage lends itself to be extended to incorporating more complex demography (e.g. multi-ancestral lineages [40] or admixture with varying population size) into simulation and to integrating more ancient DNA data with modern samples.

Ethics

This study uses publicly available data from Complete Genomics.

Data accessibility

Data available at: http://ftp.1000genomes.ebi.ac.uk/vol1/ftp/release/20130502/supporting/cgi_variant_calls/filtered_calls/.

Authors' contributions

S.N., R.R.H. and A.D.R. conceived and designed the project; S.N. analysed data; S.N., R.R.H. and A.D.R. wrote the paper. All authors read and approved the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by Japan Society for the Promotion of Science Overseas Research Fellowships (to S.N.) and in part by NIH grant no. R01GM101682 (to A.D.R.).