The genetic architecture of teosinte catalyzed and constrained maize domestication

Significance

Crop domestication is a well-established system for understanding evolution. We interrogated the genetic architecture of maize domestication from a quantitative genetics perspective. We analyzed domestication-related traits in a maize landrace and a population of its ancestor, teosinte. We observed strong divergence in the underlying genetic architecture including change in the genetic correlations among traits. Despite striking divergence, selection intensities were low for all traits, indicating that selection under domestication can be weaker than natural selection. Analyses suggest total grain weight per plant was not improved and that genetic correlations placed considerable constraint on selection. We hope our results will motivate crop evolutionists to perform similar work in other crops.

Abstract

The process of evolution under domestication has been studied using phylogenetics, population genetics–genomics, quantitative trait locus (QTL) mapping, gene expression assays, and archaeology. Here, we apply an evolutionary quantitative genetic approach to understand the constraints imposed by the genetic architecture of trait variation in teosinte, the wild ancestor of maize, and the consequences of domestication on genetic architecture. Using modern teosinte and maize landrace populations as proxies for the ancestor and domesticate, respectively, we estimated heritabilities, additive and dominance genetic variances, genetic-by-environment variances, genetic correlations, and genetic covariances for 18 domestication-related traits using realized genomic relationships estimated from genome-wide markers. We found a reduction in heritabilities across most traits, and the reduction is stronger in reproductive traits (size and numbers of grains and ears) than vegetative traits. We observed larger depletion in additive genetic variance than dominance genetic variance. Selection intensities during domestication were weak for all traits, with reproductive traits showing the highest values. For 17 of 18 traits, neutral divergence is rejected, suggesting they were targets of selection during domestication. Yield (total grain weight) per plant is the sole trait that selection does not appear to have improved in maize relative to teosinte. From a multivariate evolution perspective, we identified a strong, nonneutral divergence between teosinte and maize landrace genetic variance–covariance matrices ($\mathit{G}$-matrices). While the structure of $\mathit{G}$-matrix in teosinte posed considerable genetic constraint on early domestication, the maize landrace $\mathit{G}$-matrix indicates that the degree of constraint is more unfavorable for further evolution along the same trajectory.

Crop domestication was central to Charles Darwin’s formulation of his theory of evolution by natural selection (1), and it continues to inspire modern evolutionists to investigate a broad range of questions in evolutionary biology. The power of domestication as a model for evolution draws from several of its features compared with cases of natural evolution. All crops were domesticated within the last 12,000 y, providing definitive and restricted timeline for events (2). Many crops have well-documented archaeological records (3, 4). Unlike evolution in nature where the ancestral species is often unknown, the wild ancestors for crops are mostly known and available for comparative analyses. Given the recent origin of crops, they typically remain cross-compatible with their nearest wild relatives, allowing genetic analysis using crosses of domesticated by wild species. As a result, there is a substantial body of research on evolution under domestication for many crops including maize, rice, wheat, sorghum, barley, cotton, common beans, and sunflower (5–7).

The origin and evolutionary history of maize has been intensely studied (8). Phylogenetic analysis and archaeological data revealed that maize originated from a single domestication event in southern Mexico about 9,000 y ago (9, 10). The direct ancestor of maize is a lowland wild grass known as teosinte (Zea mays ssp. parviglumis). Population genetics comparison of maize and teosinte revealed evidence for recent selection in multiple genomic regions, a moderate bottleneck causing loss in genetic diversity during domestication, and postdomestication gene flow from teosinte into maize that enhanced maize adaptation to diverse environments (11–14). Despite the loss of genetic diversity by selection and bottleneck, modern maize remains rich in genetic variation, facilitating its pre-Columbian adaptation to diverse habitats from Canada to Chile (15, 16).

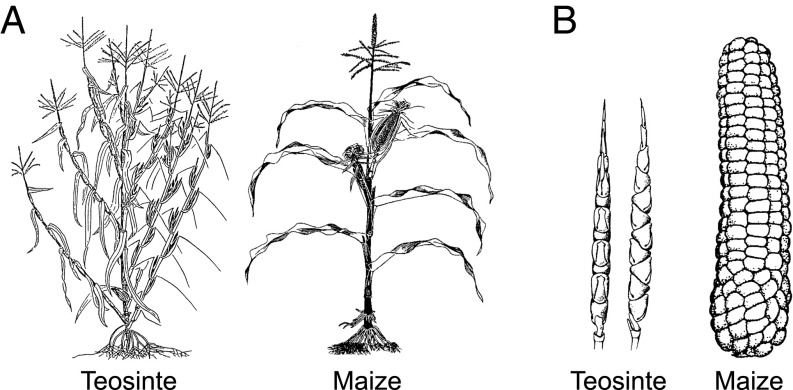
Teosinte and maize differ profoundly in plant and inflorescence architecture (Fig. 1) (17, 18). Teosinte plants typically have many long branches, each bearing multiple small ears along their length and tassels at their tip. In contrast, maize plants typically have one or two short branches, each with a single ear at its tip. A teosinte plant can have several hundred ears, each with only 10 grains, whereas maize typically has only two ears, each with several hundred grains. These differences in growth form and ear size are related to the different reproductive strategies. Teosinte has a plastic growth form, allowing the plant to branch prolifically in good environments to produce hundreds of ears or remain small and weakly branched with just a few ears in poor environments. Maize has a more fixed growth form, producing one or two large ears over a wide range of environments, which represents an adaptation for easy harvest of the grain by its human cultivators.

Fig. 1.

Morphology of teosinte and maize. Differences in plant morphology between teosinte and maize are highlighted in A, while differences in ear morphology are shown in B. Teosinte plant has many branches with multiple ears on each branch and tassel at the tip of the branch; maize plant has few branches with a single ear on each branch and ear at the tip of the branch. Teosinte ear has few grains enclosed in fruit cases, while maize ear has many grains with exposed fruit cases. Adapted from ref. 19.

The genetic basis of the morphological differences between maize and teosinte has been intensely investigated. Quantitative trait locus mapping defined the genetic architecture underlying trait differences as complex and involving many loci, a few of which have been mapped to the underlying genes (19–28). Still, many questions regarding the genetics of maize domestication have never been addressed. Does teosinte possess heritable variation for domestication traits? To what extent was that genetic variation depleted by domestication? How did the genetic architecture of domestication traits within teosinte constrain or direct domestication? Given the genetic architecture in teosinte, how strong would selection need to be to complete domestication within the known time frame?

Here, we seek to add to the understanding of maize domestication using a quantitative genetic approach based on the genomic similarities among relatives to infer the genetic architecture of domestication traits within teosinte and maize landrace. We selected parent plants from a modern teosinte and a modern maize landrace population sampled from nearby locations. We mated the teosinte parents with one another to produce a cohort of 4,455 offspring with variable degrees of kinship, and similarly, we mated the maize landrace parents with one another to produce a parallel cohort of 4,398 maize offspring. We scored the offspring for multiple domestication traits and estimated the genetic relationships among the offspring with molecular marker data. We fitted a statistical model to the data that allowed us to estimate a variety of genetic parameters that define genetic architecture. This approach provides a first glimpse into a previously uninvestigated aspect of the story of maize domestication.

In this article, we report that the narrow-sense heritabilities ($h^2$) for domestication traits are generally depleted in maize landrace compared with teosinte. In contrast, the proportion of genetic variance attributable to dominance and the proportion of phenotypic variance attributable to genetic-by-environment interaction increased in maize landrace compared with teosinte. Our estimates of the strength of selection during domestication indicate that reproductive (ear and grain) traits were under stronger selection than vegetative traits. The matrices of genetic variance–covariance among traits ($\mathit{G}$-matrices) within maize and teosinte are strongly differentiated, especially with respect to reproductive traits and this divergence was driven by selection. The teosinte $\mathit{G}$-matrix indicates that there was considerable constraint on domestication early on, and the maize $\mathit{G}$-matrix indicates that constraints increased over time. Overall, genetic architecture diverged strongly over the domestication process, especially in regard to reproductive traits.

Results

To infer the quantitative genetics of the maize ancestor, teosinte, and how this architecture was altered through domestication, we assayed the correlations among relatives for a set of 18 domestication traits (Table 1) in a large sample of teosinte plants of known pedigree derived from 49 founder teosinte parents chosen to serve a proxy for the ancestral teosinte population from which maize was domesticated. For comparison, we also assayed the correlations among relatives for the same domestication traits in a large sample of maize landrace plants of known pedigree derived from 40 founder parents chosen to serve as a proxy for maize postdomestication but before the era of modern scientific breeding. For simplicity, we refer to each of the 18 traits by their acronyms as defined in Table 1. Both our teosinte and maize landrace parents were collected near the town of Palmar Chico in the State of Mexico in the region identified as the likely cradle of maize domestication (9, 10). Trait evaluations of the two subspecies were conducted in adjacent field blocks of a daylength-neutral environment over 2 y. Genome-wide DNA markers were used to estimate the additive and dominance-realized genomic relationships among all pairs of individuals in each population.

Table 1.

Trait abbreviations

Trait	Acronym	Units	Trait group
Days to anthesis	DTA	days	Veg/FT
Days to silking	DTS	days	Veg/FT
Plant height	PLHT	cm	Veg/FT
Leaf length	LFLN	cm	Veg/FT
Leaf width	LFWD	cm	Veg/FT
Tiller number	TILN	count	EnvRes
Prolificacy	PROL	count	EnvRes
Lateral branch node number	LBNN	count	EnvRes
Lateral branch length	LBLN	mm	EnvRes
Lateral branch internode length	LBIL	mm	EnvRes
Ear length	EL	mm	Rep
Cupules per row	CUPR	count	Rep
Ear diameter	ED	mm	Rep
Grains per ear	GE	count	Rep
Ear internode length	EILN	mm	Rep
Total grain per plant	TGPP	count	Rep
Total grain weight per plant	TGWP	g	Rep
Grain weight	GW	mg	Rep

List of 18 teosinte–maize landrace comparable traits and the corresponding acronyms, units, and trait groups. The trait groups are abbreviated as Veg/FT for Vegetative/Flowering Time, EnvRes for Environmental Response, and Rep for Reproductive.

Univariate Genetic Analyses.

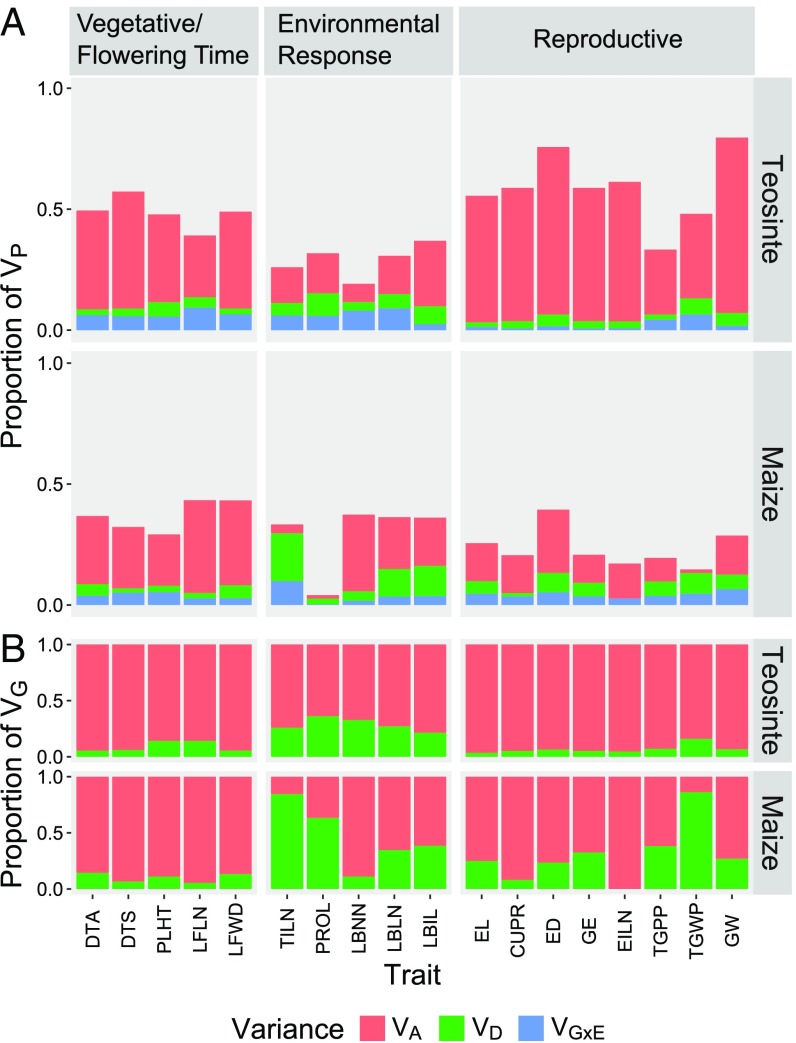
Our teosinte population generally possesses higher levels of heritable variation than our maize landrace population for domestication traits, suggesting that domestication partially depleted genetic variance for traits that were the targets of human selection (Fig. 2A and SI Appendix, Tables S1 and S2). Using a variance component approach, we partitioned the phenotypic variance $\left(V_P\right)$ into additive genetic variance $\left(V_A\right)$, dominance genetic variance $\left(V_D\right)$, genetic-by-environment variance $\left(V_{G\times E}\right)$, and environmental variance $\left(V_E\right)$. To compare the $V_A$ between teosinte and the maize landrace, we used the narrow-sense heritabilities $\left(h^2=V_A/V_P\right)$, which is a $V_P$-standardized measure of the $V_A$. We observed higher $h^2$ in teosinte ($h^2=0.39\pm 0.19$, ranging from 0.07 to 0.73) than in maize landrace ($h^2=0.19\pm 0.11$, ranging from 0.01 to 0.38) for 15 of 18 traits (Fig. 2A). Among the three predefined trait groups, Reproductive traits showed the strongest depletion in $h^2$ from teosinte to maize landrace while $h^2$ in the Vegetative/Flowering Time group showed little difference between teosinte and maize landrace (Fig. 2A). There is not a consistent pattern for $h^2$ within the Environmental Response trait group, since $h^2$ for PROL and TILN were depleted in the maize landrace, while $h^2$ for LBNN was increased in the maize landrace and $h^2$ for LBLN and LBIL remained similar (Fig. 2A). Despite the overall depletion of $h^2$ in maize, our maize landrace still possesses considerable amount of $h^2$ for most traits (Fig. 2A).

Fig. 2.

Variances for 18 teosinte and maize landrace comparable traits. Proportions of phenotypic variance (V_P) attributed to additive genetic variance (V_A), dominance genetic variance (V_D), and genetic-by-environment variance (V_G×E) are shown in A. Proportions of genetic variance (V_G) attributed to additive genetic variance (V_A) and dominance genetic variance (V_D) are shown in B.

While additive genetic variation is reduced in maize landrace relative to teosinte, the proportion of the genetic variance attributable to dominance effects is generally increased, suggesting that dominance genetic variance depletes more slowly than additive genetic variance during domestication (Fig. 2B and SI Appendix, Tables S1 and S2). We observed lower $V_D/V_G$ in teosinte ($V_D/V_G=0.14\pm 0.11$, ranging from 0.04 to 0.36) than maize landrace ($V_D/V_G=0.29\pm 0.26$, ranging from 0.00 to 0.86). Among the trait groups, Reproductive showed the most increase in $V_D/V_G$ from teosinte to maize landrace, while Vegetative/Flowering Time showed the least difference in $V_D/V_G$ between teosinte and maize landrace. Within Environmental Response, large increases in $V_D/V_G$ can be seen with TILN and PROL. Of all 18 traits, only four traits (PLHT, LFLN, LBNN, and EILN) showed a slight decrease in $V_D/V_G$ from teosinte to maize landrace.

Maize landrace displayed a smaller proportion of the phenotypic variance attributable to genetic-by-environment interaction $\left(V_{G\times E}/V_P\right)$ in Vegetative/Flowering Time and Environmental Response traits but larger $V_{G\times E}/V_P$ in Reproductive traits than teosinte, suggesting that genetic-by-environment interaction is also altered during domestication. Overall, $V_{G\times E}/V_P$, which is a $V_P$-standardized measure of the $V_{G\times E}$, is similar between teosinte ($V_{G\times E}/V_P=0.05\pm 0.03$, ranging from 0.01 to 0.09) and the maize landrace ($V_{G\times E}/V_P=0.04\pm 0.02$, ranging from 0.00 to 0.10). However, there are differences in $V_{G\times E}/V_P$ between teosinte and the maize landrace among the trait groups. Teosinte has about 69% more $V_{G\times E}/V_P$ for Vegetative/Flowering Time group and 65% more $V_{G\times E}/V_P$ for Environmental Response group compared with the maize landrace. In contrast, teosinte exhibits about 49% less $V_{G\times E}/V_P$ for Reproductive group compared with the maize landrace. Given that $V_{G\times E}/V_P$ provides the necessary phenotypic plasticity for survival in diverse wild settings compared with more uniform farmland, $V_{G\times E}/V_P$ is likely to be reduced during domestication. This expectation contradicts the greater $V_{G\times E}/V_P$ for Reproductive traits in maize, an observation we explore further in Discussion.

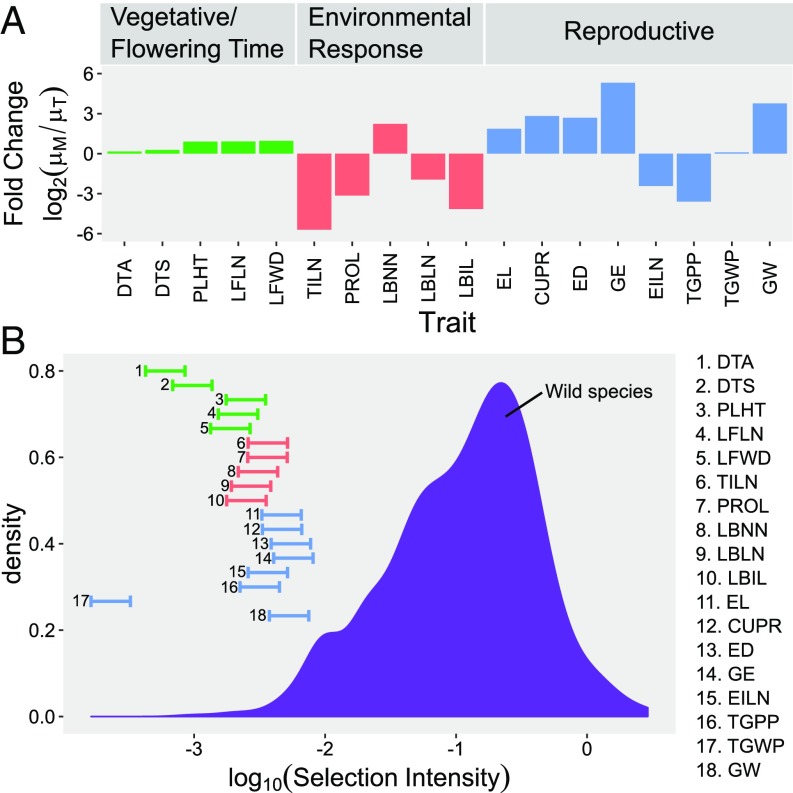
Our estimates of the selection intensity ($i$) during domestication are small, although highest among Reproductive traits except for TGWP. We computed the selection intensity for each trait and observed weak $i$ across all traits (Fig. 3 and SI Appendix, Table S3). The magnitude of $i$ ranges from 0.0002 to 0.0040, which equates to a selection differential of one phenotypic SD in about 250–6,000 generations. The difference in $i$ among the traits suggests that some traits underwent stronger selection than others. Generally, the traits with high magnitude of $i$ fall within the Reproductive group ($\left|i\right|$ = 0.0022–0.0040) except for TGWP. Moderate magnitude of $i$ are observed for the Environmental Response group ($\left|i\right|$ = 0.0018–0.0026). The lowest magnitude of $i$ is found for DTA, DTS, and TGWP ($\left|i\right|$ = 0.0002–0.0007). These three traits were probably either indirectly selected or weakly selected at most. Overall, $i$ correlates well with changes in $h^2$, suggesting that PROL, TILN, and all Reproductive traits (except TGWP) were key targets of the selection process.

Fig. 3.

Changes in trait means and selection intensities. In A, changes in trait mean $\left(\mu \right)$ are measured as $\mathrm{lo}{\mathrm{g}}_2\left({\mu }_M/{\mu }_T\right)$ or fold change of maize landrace outcross mean $\left({\mu }_M\right)$ over teosinte outcross mean $\left({\mu }_T\right)$. In B, absolute selection intensities $\left(\left|i\right|\right)$ for 741 traits in wild species under natural selection are shown in a density plot [data from Kingsolver et al. (54)] and $\left|i\right|$ for 18 traits in maize under domestication are shown in horizontal bars. Left end of the bars represents selection intensities estimated from 9,000 generations of selection, and right end represents selection intensities estimated from 4,500 generations of selection.

Multivariate Genetic Analyses.

Genetic correlations $\left(r_g\right)$ among traits indicate that the 18 traits fit the three predefined trait groups of Vegetative/Flowering Time, Environmental Response, and Reproductive such that genetic control of traits within the groups is due in part to shared sets of underlying genes in both teosinte and maize landrace. We constructed distance matrices as $\left(1-\left|r_g\right|\right)$ for teosinte and maize landrace and visualized the genetic relationships among traits using principal-coordinate analysis (PCoA) and neighbor-joining (NJ) trees (SI Appendix, Fig. S1). This analysis verified three groups of genetically related traits: Vegetative/Flowering Time, Environmental Response, and Reproductive. Traits within each group have shorter genetic distance (or higher absolute genetic correlation) than traits across groups. Each trait group is named after a common biological theme shared among the group members. For example, traits within the Vegetative/Flowering Time group are generally positively correlated, which translates to late flowering plants being taller and having bigger leaves. The Environmental Response group is composed of traits that are highly affected by environmental factors. For example, teosinte plants have many ears along long lateral branches under favorable conditions, but few ears on short branches in poor conditions.

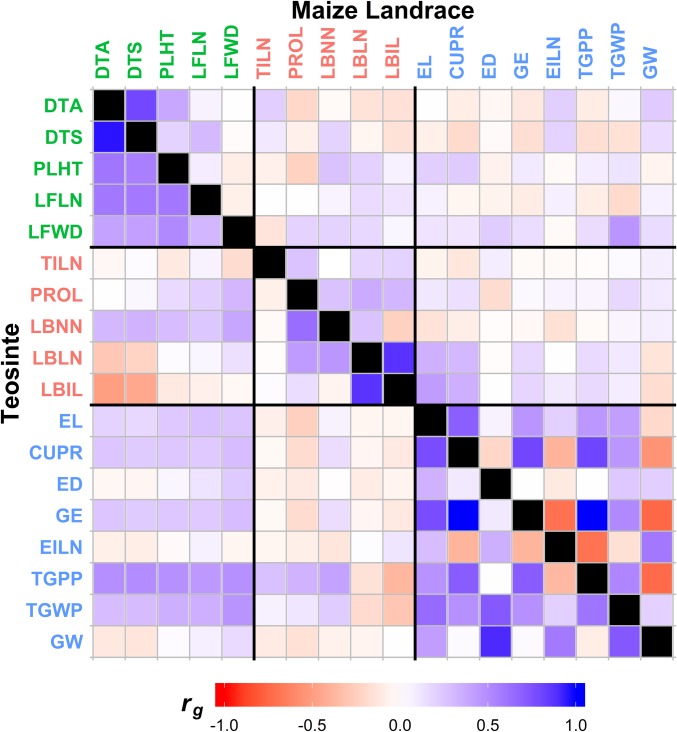
Most genetic correlations among traits are conserved between teosinte and maize landrace with the exception for Reproductive traits, indicating that the underlying genetic network for Reproductive traits changed through domestication. Through an element-wise comparison of the genetic correlation matrices using the Mantel test (29), we showed that the genetic correlations $\left(r_g\right)$ for teosinte are overall correlated with those for maize landrace (r = 0.51; P < 1 × 10⁻⁴) (Fig. 4). The genetic correlations are even better preserved within the submatrices of each trait group. Strongest preservation of genetic correlations is observed within the Vegetative/Flowering Time group (r = 0.90; P < 0.05), followed by the Reproductive group (r = 0.79; P < 0.01) and the Environmental Response group (r = 0.77; P < 0.05). On the other hand, eigenstructure comparison of the teosinte and maize landrace genetic correlation matrices yielded slightly different results. The first two leading eigenvectors of the full genetic correlation matrices are 89.6° and 88.4° apart, respectively. Similar comparisons of the submatrices resulted in 28.1° and 50.6° for the Vegetative/Flowering Time submatrices, 27.4° and 27.7° for the Environmental Response submatrices, and 87.8° and 86.7° for the Reproductive submatrices. While some elements of genetic correlation matrices remained similar during domestication, the overall structure of the genetic correlation matrices did not, especially in the submatrix involving Reproductive traits.

Fig. 4.

Genetic correlations for 18 teosinte and maize landrace comparable traits. Genetic correlations for traits in teosinte are shown in the Bottom Left triangle of the matrix, and maize landrace is shown in the Top Right triangle of the matrix. Genetic correlations are colored according to the scale as shown in the Bottom. Values of the genetic correlations can be found in SI Appendix, Tables S4 and S5.

An in-depth examination on the genetic correlation matrices revealed strong differences between teosinte and the maize landrace including change in sign of the correlations for some Reproductive traits, suggesting domestication modified the genetic networks underlying Reproductive trait variation. Out of the 153 genetic correlations, only 33 are significant and of the same sign in both teosinte and maize landrace. An additional 44 are nonsignificant in both maize and teosinte. There are 55 trait pairs significantly correlated in teosinte but not in maize landrace, and 17 are significant in maize landrace but not teosinte. Overall, teosinte shows more significant and stronger genetic correlations among traits than maize. Interestingly, there are four trait–pair correlations that are significant in both teosinte and maize landrace but with opposite signs, indicating a reversal during maize domestication. Two of the trait–pair correlations with opposite signs in teosinte and maize landrace are found within Reproductive traits, and the other two are between Reproductive and Vegetative/Flowering Time traits. Also, the genetic correlation between Reproductive and two other groups are stronger in teosinte but depleted in maize landrace.

The genetic variance–covariance $\left(\mathit{G}\right)$ matrices of teosinte and maize landrace are radically different, indicating that response to selection in modern maize would be very different to that in teosinte. Although genetic correlations can influence evolution of multiple traits through indirect response to selection, it is the genetic variances and covariances that define the magnitude of the influence. We asked whether the $\mathit{G}$-matrices are conserved between teosinte and maize landrace. First, we tested for correlation between teosinte and the maize landrace $\mathit{G}$-matrices (SI Appendix, Tables S4 and S5) using the Mantel test (29) and found that the $\mathit{G}$-matrices are not significantly correlated (r = 0.03; P = 0.21). We tested for the structural similarity in teosinte and the maize landrace $\mathit{G}$-matrices using Flury hierarchy (SI Appendix, Materials and Methods) (30, 31) and found no similarity in structure, which suggests that teosinte and maize landrace $\mathit{G}$-matrices are completely unrelated and the structure of $\mathit{G}$-matrix diverged during domestication (SI Appendix, Table S6). We also tested for similarity in the predicted evolutionary responses from teosinte and maize landrace $\mathit{G}$-matrices using random skewers (SI Appendix, Materials and Methods) (32). We found that the overall predicted evolutionary responses are not significantly more correlated than random (r = 0.19; P = 1.00), again suggesting that teosinte and maize landrace $\mathit{G}$-matrices are quite different. Comparison of the teosinte and maize landrace $\mathit{G}$-matrices with a Bayesian approach (33) showed that the matrices are completely distinct (q = 0.00 ± 0.00).

The dissimilarity of $\mathit{G}$-matrices of teosinte and maize landrace is primarily due to changes in the submatrix for Reproductive traits, while the submatrix for Vegetative/Flowering Time traits is conserved. The random skewers analysis indicated there would be highly correlated predicted evolutionary responses for Vegetative/Flowering Time traits (r = 0.89; P = 0.001), but uncorrelated responses for Reproductive traits (r = 0.09; P = 1.00). Environmental Response traits are intermediate in this regard (r = 0.80; P = 0.01). Bayesian comparison analysis showed high similarity in the Vegetative/Flowering Time submatrices (q = 0.31 ± 0.01) but no similarity in the Environmental Response (q = 0.00 ± 0.00) or Reproductive submatrices (q = 0.00 ± 0.00). These results again highlight that domestication has strongly modified the underlying genetic network for Reproductive traits such as GW and GE, but not that for time to flowering and plant size.

Change in the $\mathit{G}$-matrices of teosinte and maize landrace appears to be due to selection and not merely drift. We asked whether the difference in $\mathit{G}$-matrices can be solely attributed to neutral drift using the multivariate Q_ST–F_ST test (34). The multivariate Q_ST–F_ST test compares the proportionality of the between-population $\mathit{G}$-matrix $\left({\mathit{G}}_{\mathit{B}}\right)$ to within-population $\mathit{G}$-matrix $\left({\mathit{G}}_{\mathit{W}}\right)$. Under neutral trait evolution, the coefficient ρ_ST in ${\mathit{G}}_{\mathit{B}}={\rho }_{ST}{\mathit{G}}_{\mathit{W}}$ should be equal to $2{\mathrm{F}}_{\mathrm{ST}}/\left(1-{\mathrm{F}}_{\mathrm{ST}}\right)$, where ${\mathrm{F}}_{\mathrm{ST}}$ is estimated from neutral loci (common SNP markers in this case); however, the coefficient calculated from the traits (${\rho }_{ST,G}$ = 314; 95% CI, 190–908) is significantly higher than the expected coefficient calculated from neutral loci (${\rho }_{ST,N}$ = 0.372; 95% CI, 0.363–0.381). Overall, we see that the teosinte and maize landrace $\mathit{G}$-matrices have very different structures and predicted evolutionary responses, and these differences cannot be explained by neutral drift alone.

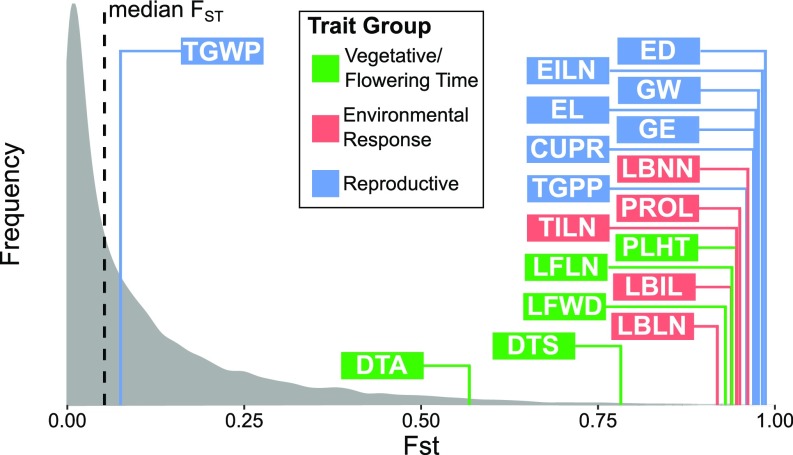
Individual trait divergence between teosinte and maize landrace appears to have been driven primarily by selection with the exception of a single trait, total grain weight per plant (TGWP). We performed univariate Q_ST–F_ST tests on the individual traits to ask whether neutral evolution can also be rejected at the individual trait level. In the univariate Q_ST–F_ST test, the observed difference between Q_ST and F_ST is compared with a null distribution of Q_ST–F_ST generated by parametric bootstrapping (SI Appendix, Materials and Methods) (35). The results of this analysis reject the neutral drift model for the differences in trait means between teosinte and maize landrace for all traits except TGWP, for which the population means were nearly equal (Fig. 5 and SI Appendix, Table S7).

Fig. 5.

Univariate Q_ST–F_ST comparison for all 18 traits. The distribution of F_ST was estimated from 21,157 markers that are in common between teosinte and maize landrace. The Q_ST for each trait is shown as individual line along the horizontal axis and is colored according to trait group.

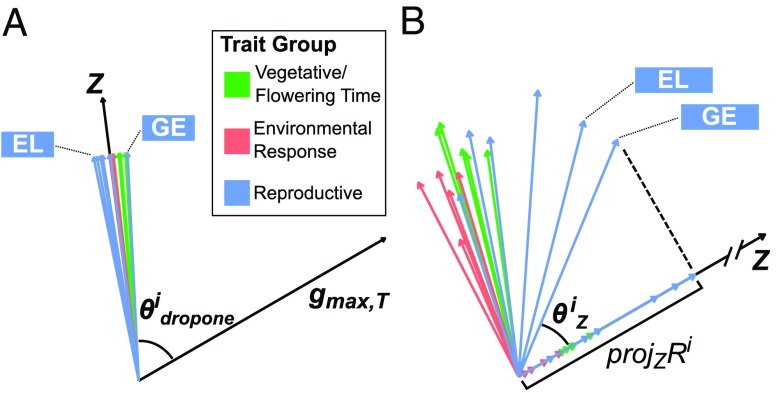
Comparison between the trajectory of phenotypic change during domestication $\left(\mathit{Z}\right)$ and the teosinte genetic line of least resistance $\left({\mathit{g}}_{\mathit{max},\mathit{T}}\right)$ suggests that genetic correlations in teosinte posed considerable constraint during the early domestication process. $\mathit{Z}$ defines the vector from the teosinte to the landrace centroids (trait means) through phenotypic space of 16 traits, while ${\mathit{g}}_{\mathit{max},\mathit{T}}$ is the first eigenvector of the teosinte genetic correlation matrix and explains the largest portion of the variance (27.2%) (SI Appendix, Fig. S2). While ${\mathit{g}}_{\mathit{max}}$ is commonly calculated from $\mathit{G}$-matrix (36), we opted to calculate it from the scaled $\mathit{G}$-matrix such that each trait has a genetic variance of 1, which is essentially the genetic correlation matrix. Doing so allows us to calculate unbiased ${\mathit{g}}_{\mathit{max}}$ since the first eigenvector can be skewed toward traits with highest magnitude. The $\mathit{Z}$ vector is also scaled similarly by standardizing the trait mean differences by their genetic SDs. The degree of evolutionary constraint is measured by ${\theta }_T$, the angle between $\mathit{Z}$ and ${\mathit{g}}_{\mathit{max},\mathit{T}}$, where ${\theta }_T$ ranges from 0° to 90°. Evolution is least constrained (small ${\theta }_T$) when the multitrait selection response is closest to the direction of the maximum genetic variation, and the opposite is true (large ${\theta }_T$) when the response is farthest to direction of the maximum genetic variation. Evolutionary constraint slows trait evolution since selection for improvement of one trait can be offset by decline in another due to a genetic correlation. Our estimate of ${\theta }_T$ is 67.3°, which suggests that maize domestication proceeded despite strong constraint imposed by the $\mathit{G}$-matrix. Such constraint would slow progress toward the optimal phenotype and require a circuitous evolutionary path over the generations.

Because the genetic line of least resistance (${\mathit{g}}_{\mathit{max},\mathit{T}}$) is informative only for the first eigenvector of the $\mathit{G}$-matrix, we also estimated the angles between observed trait responses to domestication $\left(\mathit{Z}\right)$ and each of the first five principal components of $\mathit{G}$, which accounted for 27.2, 18.8, 15.3, 9.7, and 7.3% of the variation (78.2% in total) (SI Appendix, Fig. S2). These angles were ${\theta }_{\mathrm{Ti}}=$ 67.3°, 79.4°, 88.1°, 54.1°, and 81.0°, indicating moderate to strong constraint to the trajectory of domestication in the five most important directions of multivariate genetic variation.

In addition to the overall constraint seen between $\mathit{Z}$ and ${\mathit{g}}_{\mathit{max},\mathit{T}}$, there is variation in the degree to which different traits contribute to genetic constraint (Fig. 6A and SI Appendix, Table S8). By dropping one trait at a time and calculating the angle ${\theta }_{dropone}^i$ between ${\mathit{Z}}_{\mathit{i}}$ and ${\mathit{g}}_{\mathit{max},\mathit{T},\mathit{i}}$, we can estimate the genetic constraint from the remaining 15 traits after dropping trait $i$. If the genetic constraint decreases $\left({\theta }_{dropone}^i<{\theta }_T\right)$ after dropping trait $i$, then it is said that trait $i$ constrained evolution. However, if ${\theta }_{dropone}^i>{\theta }_T$, then it is said that trait $i$ assisted evolution. Our results (Fig. 6A and SI Appendix, Table S8) showed that the response to selection was largely hindered by genetic correlations involving Vegetative/Flowering Time traits but assisted by the genetic correlations involving Reproductive traits.

Fig. 6.

Constraints and consequences of multivariate selection. Various possibilities due to multivariate selection in maize domestication are explored here. In A, individual trait contribution toward genetic constraint is identified by dropping ith trait from $\mathit{Z}$ (actual domestication trajectory) and ${\mathit{g}}_{\mathit{max},\mathit{T}}$ (genetic lines of least resistance) and measuring the angle ${\theta }_{dropone}^i$ between the two vectors. If ${\theta }_{dropone}^i$ is smaller than ${\theta }_T=67.3°$ (angle between $\mathit{Z}$ and ${\mathit{g}}_{\mathit{max},\mathit{T}}$), then the ith trait is said to constrain evolution. If ${\theta }_{dropone}^i$ is larger than ${\theta }_T$, then the ith trait is said to assist evolution. In B, multivariate response $\left({\mathit{R}}_{\mathit{i}}\right)$ from hypothetical selection on a single ith trait is explored. ${\mathit{R}}_{\mathit{i}}$ is compared with $\mathit{Z}$ through the angle $\left({\theta }_Z\right)$ and scalar projection $\left(\left|pro{j}_Z{R}^i\right|\right)$ of ${\mathit{R}}_{\mathit{i}}$ on $\mathit{Z}$ (B). ${\theta }_Z$ measures the deviation from $\mathit{Z}$ by selecting on ith trait. $\left|pro{j}_Z{R}^i\right|$ measures the evolutionary gain along $\mathit{Z}$ by selecting on ith trait.

The amount of constraint imposed by the $\mathit{G}$-matrix increased during the domestication process. To explore how evolutionary constraint changed during domestication, we also estimated ${\theta }_M$, the angle between the domestication trajectory $\left(\mathit{Z}\right)$ and the direction of maximum genetic variation in maize $\left({\mathit{g}}_{\mathit{max},\mathit{M}}\right)$, as a comparison with ${\theta }_T$. ${\mathit{g}}_{\mathit{max},\mathit{M}}$ explains 19.1% of the variance (SI Appendix, Fig. S2). Like teosinte, we also standardized the $\mathit{Z}$ vector and $\mathit{G}$-matrix here for calculating ${\theta }_M$. We observed that ${\theta }_M$ is 74.3°. The comparison of ${\theta }_M$ and ${\theta }_T$ indicates while there was substantial constraint early in domestication, it increased over time. It is not surprising to find ${\theta }_M>{\theta }_T$ since the domestication process likely depleted variants that contributed beneficially to the structure of the $\mathit{G}$-matrix. Given that the $\mathit{G}$-matrix toward the end of domestication likely resembled the $\mathit{G}$-matrix of our maize landrace, trait evolution toward the optimum defined by the trait centroid for our maize landrace is likely to have slowed.

Selection on some individual traits would engender more rapid evolution in the direction of the domestication trajectory than others due to the structure of the $\mathit{G}$-matrix. Using the multivariate breeders’ equation of $\mathit{G\beta }=\mathit{R}$ (37), we can estimate the multivariate response $\left(\mathit{R}\right)$ based on teosinte $\mathit{G}$-matrix and hypothetical selection differentials $\left(\mathit{\beta }\right)$. We took a “what-if” approach to ask whether the individual traits differ in the extent that selection on any one trait would maximize gain along the evolutionary trajectory for all traits. We used 16 different $\mathit{\beta }$ values, each ${\mathit{\beta }}^{\mathit{i}}$ having one element of a value of 1 and 15 elements of a value of zero. The ith trait with a value of 1 in ${\mathit{\beta }}^{\mathit{i}}$ would be directly selected while traits with a value of zero in ${\mathit{\beta }}^{\mathit{i}}$ are only indirectly selected. If the traits are selected for lower value in maize, the corresponding elements in ${\mathit{\beta }}^{\mathit{i}}$ would have a negative sign. Using the multivariate breeder’s equation, we obtained ${\mathit{R}}^{\mathit{i}}$ for each ${\mathit{\beta }}^{\mathit{i}}$. We then compared each ${\mathit{R}}^{\mathit{i}}$ to the actual domestication trajectory ($\mathit{Z}$) by measuring the angle (${\theta }_Z^i$) between ${\mathit{R}}^{\mathit{i}}$ and $\mathit{Z}$ and the scalar projection of ${\mathit{R}}^{\mathit{i}}$ on $\mathit{Z}$ $\left(\left|pro{j}_Z{R}^i\right|\right)$ (Fig. 6B and SI Appendix, Table S9). While ${\theta }_Z^i$ measures the deviation between ${\mathit{R}}^{\mathit{i}}$ and $\mathit{Z}$, $\left|pro{j}_Z{R}^i\right|$ measures the gain along $\mathit{Z}$ for each ${\mathit{R}}^{\mathit{i}}.$ $\mathit{Z}$ is also scaled similarly to the $\mathit{G}$-matrix, so that values of $\left|pro{j}_Z{R}^i\right|$ for different traits can be compared directly. Of all 16 traits, GE has the smallest ${\theta }_Z^i$ and largest $\left|pro{j}_Z{R}^i\right|$, indicating that direct selection for more GE would give an overall response most closely aligned with the evolutionary trajectory as well as maximum gain along the trajectory. However, GE has the smallest ${\theta }_{dropone}^i$, which makes it unfavorable since selection for higher GE contributed to more genetic constraint (Fig. 6A and SI Appendix, Table S8). Of all traits, EL comes closest to GE in terms of ${\theta }_Z^i$ and $\left|pro{j}_Z{R}^i\right|$ with only one rank behind GE, and EL also has the largest ${\theta }_{dropone}^i$, which suggests that selection for higher EL contributed less than others to genetic constraint. Our results here suggest that if the ancient farmers were to domesticate teosinte by selecting for only a single trait, EL would be the ideal candidate as EL produced the maximum desired multivariate gains with the least genetic constraint.

Discussion

Change in Genetic Variances.

Our results demonstrate that maize landrace experienced a substantial loss in additive genetic variance, as measured by narrow-sense heritabilities $\left(h^2\right)$, during domestication compared with teosinte. The loss in $h^2$ can be attributed to population bottleneck and selection during maize domestication (11, 38). Previous reports suggest that maize retained only ∼80% of genomic nucleotide diversity and cis regulatory variation present in teosinte (13, 39). Given that selection likely brought beneficial alleles to fixation, it is not surprising to find an overall reduction in $h^2$ in any domesticated relative of its wild progenitor.

Our estimates for the loss of $h^2$ on individual traits are consistent with the morphological changes during maize domestication and how these morphological changes relate to the maize population’s fitness as a crop. Modern maize typically possesses only a single stalk with few lateral branches that each carries a single large ear. This morphology was derived from that of teosinte, which is more branched and possesses many smaller ears. Given a strong reconfiguration of morphology during domestication, it is not surprising that the maize landrace is mostly depleted in $h^2$ for traits such as PROL and TILN. Similarly, maize landrace has very low $h^2$ for Reproductive traits, suggesting that many beneficial alleles for Reproductive traits were brought to fixation during domestication. Being a wild plant, teosinte may maintain higher $h^2$ than maize as the natural environment is apt to vary more across time and space than the cultivated field (40).

The observed high level of $h^2$ in teosinte means that selection during domestication could have acted largely on standing variation in teosinte populations rather than depending on the occurrence of new mutation. Among the trait groups, Reproductive traits have the highest level of $h^2$, ranging from 0.27 to 0.73 (Fig. 2). Consequently, ancient farmers would have been able to capitalize on the abundance of standing variation to select a productive crop from a wild plant. Previous studies have also suggested that standing variation can lead to a faster evolution than new mutations (41, 42), thus highlighting the importance of standing variation in domestication.

Previously, Ladizinsky (43) and Lester (44) argued that a major force in domestication is the fixation of recessive loss-of-function alleles. There are several known genes that fit this model as exemplified by nud in barley (45), Sh1 in sorghum (28), Black hull4 (BH4) in rice (46), and ZmYAB2.1 in maize (47). However, there are also counterexamples in which the domestication alleles act additively and encode/express a functional protein, as seen for three genes in maize: tga1 (24), tb1 (23), and gt1 (26). Intuitively, fixation of recessive loss-of-function alleles should deplete $V_D/V_P$ because of reduction of $V_D$ due to allele fixation. We observed no apparent depletion of $V_D/V_P$ in maize landrace relative to teosinte (Fig. 2A); however, $V_D/V_G$, or the proportion of genetic variance due to dominance, increased for PROL, TILN, and Reproductive traits while remaining similar for others (Fig. 2B). The increase in $V_D/V_G$ for those traits suggests that the additive genetic variance was depleted at a faster rate than the dominance genetic variance during domestication, congruent with the expected changes in $V_D/V_G$ due to increase in frequency of recessive alleles (SI Appendix, Fig. S3) and as commonly observed in populations under selection (37). Overall, our data suggest that domestication was not biased toward fixation of recessive loss-of-function alleles.

Despite having a general depletion in additive genetic variance, the maize landrace still possesses some additive genetic variance that could potentially be useful for future crop improvement. Such variation may be preserved by multiple forces including mutation–selection balance (48), variable selection (49), and negative interactions between two alleles of different genes (2). As a result, maize landraces serve as a rich source of genetic diversity for breeding modern maize (12).

Additive genetic variation is important for long term adaptation, but it is genetic-by-environment (G×E) variation that is crucial for short-term adaptation to changing environments through phenotypic plasticity. Phenotypic plasticity is the ability of an individual genotype to express phenotypes differently as a response to environmental fluctuation (50, 51). Gage et al. (52) demonstrated that selection for increased yield in maize reduced G×E in favor of stability. This finding can be extended to selection during domestication. Unlike maize that is adapted to growth in relatively uniform agricultural fields, teosinte likely requires more G×E for adaptation to a broader range of environments in the wild. Our results showed higher G×E in teosinte than maize landrace, specifically in traits belonging to the Vegetative/Flowering Time and Environmental Response group.

However, there is an exception: teosinte possesses less G×E than maize landrace for traits that relate to ear and grain size. This observation could be explained as follows. Teosinte and maize may have evolved different strategies to cope with environmental fluctuations as related to reproductive traits. Teosinte adapts by varying the number of ears per plant while maintaining constant ear and grain size across environments. Teosinte may need to maintain an optimal grain size for seedling establishment. In contrast, maize produces a small and fixed number of large ears for easy harvest. Aborting an entire ear in poor environments when there are only two ears per plant places a heavy cost on reproduction. Thus, maize evolved to modulate grains per ear or grain weight instead of ear number.

Strength of Selection During Domestication.

Crop domestication has been described as a process of slow evolution, where the selection force is similar or lower than selection force seen in natural selection (53), and maize domestication is no exception to that. Selection intensities for maize phenotypes during domestication are low $\left(0.0001<\left|i\right|<0.0040\right)$ and comparable to selection intensities in other domesticated crop species $\left(\left|i\right|<0.0040\right)$ (53) as well as wild species under natural selection $\left(0.001<\left|i\right|<2.911\right)$ (54). In fact, selection intensities for all 18 traits fall on the lower end of the distribution compared with selection intensities for traits in wild species under natural selection (Fig. 3). This is true whether one calculates the average selection intensity over 9,000 or 4,500 generations of selection (Fig. 3 and SI Appendix, Table S3). Fugère and Hendry (55) recently showed that human intervention on trait evolution tends to result in weaker selection forces, which further strengthens the hypothesis that domestication is a process of slow evolution.

Our observation of weak selection intensities is consistent with the mild domestication bottleneck for maize and weak selection on known domestication genes. Evidence for weak selection on major domestication loci is suggested by the observation that some domestication alleles were not at fixation 5,000 y ago, 4,000 y after the domestication process started at 9000 BP (56). The archaeological record also shows slow and continuous change in ear traits over a 5,000-y period, suggesting a gradual rather than abrupt process by which maize became a productive food source (57, 58). Overall, a slow process by weak selection rather than abrupt changes by strong selection as previously suggested seems more likely (17, 59).

While selection intensities appear to have been weak overall during maize domestication, they vary among trait groups. We observed strongest selection intensities within the Reproductive group, followed by Environmental Response, and last, Vegetative/Flowering Time. Average selection intensity within the Reproductive group is more than twice that within the Vegetative/Flowering Time group. This result is consistent with the expectation that maize domestication focused on restructuring the architecture of the ear more than other aspects of the plant.

While selection intensity is highest in Reproductive traits, there is one exception—TGWP—which has the lowest selection intensity among all traits. Ancient farmers were successful in selecting for larger grains and ears (making harvesting seeds much easier), but not overall edible biomass as measured by TGWP, which remained the same between teosinte and maize landrace (Fig. 3 and SI Appendix, Table S3). TGWP may be constrained by the ability of the plant to convert solar energy into chemical energy. While domestication led to repartition of the solar energy captured from many small grains to fewer larger grains, TGWP itself was not modified. Considering that 9,000 y of selection may not have increased yield per plant, it is not too surprising to find that modern maize breeding has only been successful in increasing yield per area but not yield per plant (60).

Conservation and Change in Genetic Correlations.

Moderate conservation between the teosinte and maize landrace genetic correlation matrices can be seen on a broad scale, with stronger conservation within Vegetative/Flowering Time and Environmental Response trait groups to little conservation within Reproductive trait group. Conservation of genetic correlations, in particular within the trait groups of Vegetative/Flowering Time and Environmental Response, suggests that genetic correlations can be resilient under selection. However, as seen within Reproductive trait group, it is possible to shift the genetic correlations under a sufficiently strong selection force. Change in allele frequency is expected whenever selection is present and may eventually lead to allele fixation. Naturally, genetic correlations diminish when alleles are fixed, as genetic correlations are measured from variation between a pair of traits. Consistent with Reproductive traits experiencing stronger selection than other domestication traits, we observe the largest change in genetic correlations within the Reproductive trait group.

While we observed both conservation and change in genetic correlations between teosinte and maize landrace, can we draw some inferences regarding the nature of the conservation and change? First, there is a general reduction in the magnitude of favorable correlations from teosinte to maize landrace (Fig. 4). This observation is consistent with the expectation that selection on correlated traits can drive favorable correlations to be less favorable (61–63). Second, the reduction in the magnitude of genetic correlations from teosinte to maize landrace is much stronger between trait groups than within them (Fig. 4). This difference suggests that domestication may have favored greater independence of trait groups, for example, disassociating correlations between reproductive traits and flowering time. Third, of many individual elements of the genetic correlation matrix, only four had a sign reversal between teosinte and maize landrace, and these correlations strictly involve Reproductive traits like ED, EL, CUPR, and GW (Fig. 4). When selection is strong, it is possible to reverse the sign of genetic correlations by increasing the contribution of unfavorable pleiotropy toward overall correlations through fixation of favorable pleiotropic alleles.

From a qualitative perspective, the genetic correlations in teosinte are largely in a favorable direction for domestication. Within the Reproductive group, we observed favorable genetic correlations among EL, CUPR, ED, GE, and GW that led to easier selection for larger ears. Favorable genetic correlations can also be seen among PLHT, LFLN, and LFWD, all of which led to easier selection for larger plants. In addition, PLHT, LFLN, and LFWD also displayed favorable genetic correlations with many Reproductive traits, which would have facilitated simultaneous selection for larger ears and plants, or in a broader sense, gigantism, a common feature of domestication (64).

The G-Matrix and Genetic Constraint.

While there is some conservation in the genetic correlations, the differences between teosinte and maize landrace $\mathit{G}$-matrices are pronounced. We found no similarities in elements and structures of the teosinte and maize landrace $\mathit{G}$-matrices via Mantel test, Flury hierarchy, random skewers, and Bayesian estimation. Within the submatrices for each trait group, both random skewers and Bayesian estimation reaffirmed that the submatrices for Vegetative/Flowering Time and Environmental Response are conserved while the submatrix for Reproductive is not. These observations again suggest that Reproductive traits were the focus of selection during domestication. Overall, our findings corroborate the hypothesis that the $\mathit{G}$-matrix is not conserved over long-term evolution (65), which limit us in making further predictions on the evolution of maize from teosinte.

What do the structures of the teosinte and landrace $\mathit{G}$-matrices and the differences between them tell us about early and subsequent evolutionary potential and constraint during domestication? First, there appears to have been substantial evolutionary constraint imposed by the structure of the $\mathit{G}$-matrix at the initial phase of domestication as measured by the angle of 67.3° between the genetic lines of least resistance in teosinte $\left({\mathit{g}}_{\mathit{max}}\right)$ and the axis along which teosinte evolved into maize. Unlike evolutionary stasis that brings evolution to a halt (66), evolutionary constraint still allows evolution to proceed, although at a slower rate (67). When an underlying genetic constraint (i.e., unfavorable genetic covariance) is present, evolution can proceed by changes in the frequencies of nonpleiotropic alleles (68) as has been previously shown by Marchini et al. (69). Furthermore, genetic constraint can be ameliorated over time by the decay of linkage disequilibrium between linked causative factors (68).

A comparison of the teosinte and maize landrace $\mathit{G}$-matrices also informs us that the degree of constraint increased over time. While the angle between the genetic lines of least resistance in teosinte $\left({\mathit{g}}_{\mathit{max}}\right)$ and the axis along which teosinte evolved into maize is large (67.3°), indicating substantial constraint, the similar angle in maize landrace is 74.3°, indicating higher constraint. An increase in constraint is not unexpected in the case of maize domestication. Arnold (70) described the change in genetic constraint as a function of changes in selection and mutation/recombination, which is essentially equivalent to mutation–selection balance. Increase in constraint from teosinte to maize suggests that domestication reduced advantageous genetic variances and covariances more rapidly than mutation could restore them.

Another way to think about the relationship between the $\mathit{G}$-matrix and the tempo of evolution comes from the multivariate breeder’s equation of $\mathit{R}=\mathit{G\beta }$. Here, the evolution of maize $\left(\mathit{R}\right)$ during domestication is a compromise between genetic constraints $\left(\mathit{G}\right)$ and humans’ needs $\left(\mathit{\beta }\right)$. Even though evolution along the genetic lines of least resistance $\left({\mathit{g}}_{\mathit{max}}\right)$ provides the maximum evolutionary gain for multiple traits, if ${\mathit{g}}_{\mathit{max}}$ does not align with human desires $\left(\mathit{\beta }\right)$, then the response $\left(\mathit{R}\right)$ will be attenuated. We have shown that slow trait evolution during the domestication of maize is likely due to the strong genetic constraint that increased over time from teosinte to maize landrace.

Causes and Consequences.

Results from both univariate and multivariate Q_ST–F_ST tests suggested that selection drove the change in trait values between teosinte and maize landrace. Q_ST measures genetic differentiation at trait level, while F_ST measures genetic differentiation at neutral loci. Under neutral evolution, traits are expected to evolve at the same pace as neutral loci, which is essentially Q_ST = F_ST (71). The multivariate Q_ST–F_ST test indicates that the 18 traits as a whole underwent nonneutral evolution; however, further dissection of individual traits using the univariate Q_ST–F_ST test reveals that one trait, TGWP, conforms to neutral expectations. This result implies that selection was not effective at increasing total yield. Maize domestication can be seen as having mostly improved harvestability by creating a plant with few ears with more and larger grains.

Our “what-if” analysis on the multivariate selection response revealed potential initial targets that would maximize evolutionary gain along the domestication trajectory for all traits. We compared the multivariate responses $\left({\mathit{R}}^{\mathit{i}}\right)$ from selecting $\left({\mathit{\beta }}^{\mathit{i}}\right)$ for a single trait to the actual evolutionary trajectory $\left(\mathit{Z}\right)$ by measuring the angle $\left({\theta }_Z^i\right)$ between ${\mathit{R}}^{\mathit{i}}$ and $\mathit{Z}$ and the scalar projection of ${\mathit{R}}^{\mathit{i}}$ on $\mathit{Z}$ $\left(\left|pro{j}_Z{R}^i\right|\right)$ (Fig. 6 and SI Appendix, Table S9). ${\theta }_Z^i$ measures how close is ${\mathit{R}}^{\mathit{i}}$ to $\mathit{Z}$, while $\left|pro{j}_Z{R}^i\right|$ measures the contribution of ${\mathit{R}}^{\mathit{i}}$ toward evolving along $\mathit{Z}$. Of all traits tested, EL is likely the most ideal option with small ${\theta }_Z^i$, large $\left|pro{j}_Z{R}^i\right|$, and large ${\theta }_{dropone}^i$. This result suggests that directional selection on EL alone would yield the most gain and be closest to the evolutionary trajectory with minimal constraint.

Caveats.

Caution is essential when interpreting our results and generalizing from them based on many limitations of our data and analyses. (i) Our single teosinte and maize landrace populations are not apt to be adequate proxies for the ancestral teosinte and resulting maize domesticate. (ii) Our field trials were performed in Florida, which is a different environment from the Balsas river drainage in Mexico where maize was domesticated. (iii) All of our parameter estimates are based on the start (teosinte) and end (maize landrace) without knowing the exact changes in each generation, so our estimates only represent an average over many generations, and it is likely that selection, genetic and residual covariances, and response to selection were not consistent among all generations. (iv) Inferences drawn from the genetic correlation and $\mathit{G}$-matrices are sensitive to the traits included. While we strived to be comprehensive in analyzing all possible domestication traits, there are several obvious domestication traits like kernel row number, ear shattering, and glume architecture that could not be studied here due to the lack of variation in either teosinte or maize landrace. Despite these limitations, we hope our approach will at least promote further thinking and study about domestication and how it was constrained by the genetic architecture of the ancestor and how the genetic architecture of crop species evolved over time.

Conclusions

Based on our overall results, we propose the following inferences about maize domestication. First, selection was clearly focused on ear architecture since most of the traits that define ear architecture suffered a loss of heritable variation and ear morphology changed dramatically. Second, the difference in plant architecture is likely a consequence or correlated response to selection on ear architecture to create a less branched plant with fewer, larger ears. Third, because of favorable genetic correlations among most selection targets, ancient farmers had multiple options to select for what a maize ear would become. For instance, EL is positively correlated to GE in teosinte, so selection could have been applied to either trait or even both traits concurrently to speed up the process. Fortunately, the relative differences among plants for these traits are easily observable by eye and do not require modern tools for selection. Last, evolution can proceed despite substantial genetic constraint since selection can be applied on traits that pose the least constraint.

Materials and Methods

Sample Population and Crossing Strategy.

We sampled a single population of teosinte (Zea mays ssp. parviglumis) and a single population of maize landrace Tuxpeño (Zea mays ssp. mays) from the Balsas region of Mexico as proxies for the founding teosinte population and first domesticated maize population, respectively. The teosinte population is chosen from individuals in the “Mound” population near Palmar Chico, Mexico (latitude, 18.6403°; longitude, −100.3570°; altitude, 1,008 m) that were previously sampled by van Heerwaarden et al. (72). The maize landrace population was chosen from individuals in a site less than 1 km away from the teosinte population (University of Guadalajara collection JSG-RMM-LCL-529; latitude, 18.6483°; longitude, −100.3542°; altitude, 983 m). We constructed our study populations by selfing and intermating 70 teosinte parent plants to obtain progeny with various allelic combinations from different parents. We also applied similar crossing scheme to 55 maize landrace parent plants. We obtained 49 selfed and 377 outcross families for teosinte (SI Appendix, Table S10), and 34 selfed and 89 outcross families for maize landrace (SI Appendix, Table S11).

Field Design.

We conducted field evaluations for the teosinte and maize landrace progeny over two winter seasons (2013 and 2014) under short daylength (<12 h) in Homestead, Florida (latitude, 25.5044°; longitude, −80.5045°; altitude, 3 m). Within each season, we planted the seeds in a randomized design and grid of 100 plants by 30 rows along with borders surrounding the experimental section. Each plant was separated by 30 cm within rows and 76 cm between rows. As an exception due to poor germination of teosinte seeds, we sampled some of the border plants in the first season and increased the grid to 112 plants by 54 rows in the second season.

Tissue Collection, DNA Isolation, and Genotyping.

DNAs from the parents were isolated using either DNeasy Plant Mini Kit (Qiagen) or modified CTAB protocol (73). DNAs from the progeny were isolated using DNeasy 96 Plant Kit (Qiagen). All DNA samples from the parents and progeny were genotyped using genotype-by-sequencing (GBS) (74). As per GBS protocol, all DNA samples were digested using ApeKI restriction enzyme and sequenced in 96-plex on Illumina HiSeq 2000, SE 1 × 100 bp (Illumina). Following that, genotypes were called from GBS raw sequencing reads using the TASSEL5-GBS Production Pipeline based on 955,690 SNPs in the ZeaGBSv2.7 Production TagsOnPhysicalMap (TOPM) file (75). The overall genotyping process from raw sequencing reads to final, clean, and imputed GBS dataset is highlighted in a flowchart (SI Appendix, Fig. S4). Final GBS dataset has been deposited in the figshare database (76).

Phenotyping.

We collected phenotypic trait data for a total of 18 traits from 4,455 teosinte plants and 4,398 maize landrace plants. Descriptions and methods of measurement for each trait are summarized in Table 1 and SI Appendix, Table S12.

Parentage Inference.

We inferred the parentage of each progeny for both teosinte and maize landrace by first estimating the realized additive genomic relationship matrix ($\mathit{A}$-matrix) (77, 78) in TASSEL5 (79) from the unfiltered raw SNP calls (including many missing calls) based on GBS data. We then identified the parents of each progeny from the $\mathit{A}$-matrix using a custom R script. A progeny is considered a self-fertilized offspring of a parent if there is only one unambiguous progeny–parent pair with a high additive relationship coefficient; a progeny is considered an outcross of two parents if there are two unambiguous progeny–parent pairs with high and similar additive relationship coefficients.

GBS Data Imputation.

Before imputation, we used the CrossMap (80) software to convert the GBS SNP positions from maize B73 reference AGPv2 coordinates to AGPv4 coordinates. Then, we applied the following filter on the raw GBS data: (i) no sites with minor allele frequency (maf) below 0.001, (ii) no sites with more than 20% missing data, (iii) no sites that are nonbiallelic, and (iv) no sites with insertion–deletion (indel) polymorphism. We imputed the GBS data for teosinte and maize landrace using the ParentPhasingPlugin and ImputeProgenyStatesPlugin as implemented in TASSEL5 (79). Briefly, the imputation is a two-part process with first identifying the parent phase using a heuristic approach, followed by inferring the parent state at each site using a hidden Markov model. Additional details on imputation and quality check are described in SI Appendix, Materials and Methods and Fig. S5.

Univariate Analysis.

We fitted a common univariate linear mixed model for each trait using ASReml, version 4 (81), which implements restricted maximum-likelihood (REML) estimation of model parameters. Briefly, among the fixed effects in the model are year, inbreeding coefficient, shading (SI Appendix, Fig. S6), and field positions; among the random effects in the model are polygenic additive, dominance, and genetic-by-environment effects. The covariances of additive and dominance effects of each individual were modeled to be proportional to the realized additive and dominance relationship matrices, respectively. The covariances of genotype-by-environment effects were modeled to be proportional to the additive relationships of individuals tested in a common year and zero for pairs of individuals tested in different years. The full model is shown in SI Appendix, Materials and Methods. Based on the model’s variance component estimates, we were able to estimate the proportions of phenotypic variance due to additive genetic variance (heritabilities), dominance genetic variance, and genetic-by-environment variance.

We estimated the selection intensity $\left(i\right)$ for each trait using results from the univariate analysis. We derived the following formula from the univariate breeder’s equation (82) to estimate $i$:

$$i=\frac{z_N-z_0}{{{\displaystyle \sum }}_{n=0}^{N-1}\frac{V_{A,0}+n\mathrm{\Delta }{V}_A}{\sqrt{V_{P,0}+n\mathrm{\Delta }{V}_P}}}.$$

The full derivation and notation for this formula can be found in SI Appendix, Materials and Methods. There are several assumptions in our estimate: (i) constant selection intensity; (ii) constant change in additive genetic variance $\left(V_A\right)$ and phenotypic variance $\left(V_P\right)$; and (iii) teosinte $V_A$ and $V_P$ as initial variances and maize landrace $V_A$ and $V_P$ as final variances. While these assumptions can be naive, they represent our best model for estimating $i$, unlike models proposed in the literature that assume constant environmental variance over generations (83–86).

Multivariate Analysis.

We fitted a common bivariate linear mixed model for each pair of traits using ASReml, version 4 (81). All of the fixed and random effects were the same as its univariate counterpart, except that polygenic dominance and genetic-by-environment effects are removed as a compromise to computational speed. The full model is shown in SI Appendix, Materials and Methods. Based on the model’s variance and covariance component estimates, we were able to estimate additive genetic correlation.

We confirmed the genetic relationship among the 18 traits based on the distance matrix of these traits. We calculated the distance matrices for teosinte and maize landrace as $1-\left|r_g\right|$, where $r_g$ is the genetic correlation. We performed PCoA and constructed NJ trees (SI Appendix, Fig. S1) to visualize the distance matrices.

We tested for similarity between teosinte and maize landrace genetic correlation matrices $\left({\mathit{r}}_{\mathit{g}}\right)$ using Mantel’s test (29). Mantel’s test tests the null hypothesis that two matrices are not correlated. Similarly, we also applied Mantel’s test to each trait group to see how each trait group similarity compares to overall similarity. The Mantel’s test is performed using mantel.test function with 10,000 permutations implemented in the package “ape” (87) in R (88). We also checked for the similarity in genetic correlation matrices by comparing the angle between the first two leading eigenvectors of the matrices, as well as the three submatrices defined by the trait groups.

We also tested for similarity between teosinte and maize landrace $\mathit{G}$-matrices (SI Appendix, Tables S4 and S5) using Mantel’s test (29), Flury hierarchy (30), random skewers (32), Bayesian estimation (33), and multivariate Q_ST–F_ST test (34). Flury hierarchy tests for structural similarity between two matrices by comparing their eigenvectors and eigenvalues in a hierarchical way (30). Flury hierarchy is implemented in the common principal component (CPC) software (31). Random skewers utilizes the multivariate breeder’s equation of $\mathit{R}=\mathit{G\beta }$ by comparing $\mathit{R}$ values calculated from two $\mathit{G}$-matrices and simulated $\mathit{\beta }$, where two $\mathit{G}$-matrices are considered similar if their $\mathrm{\Delta }\mathit{z}$ values are significantly correlated. This test is performed using skewers function with 1,000 simulations implemented in the “phytools” package (89) in R (88). The Bayesian estimation compares the probabilities of two matrices being derived from the samples of multivariate normal distribution that is specified by one of the matrices (33). Multivariate Q_ST–F_ST test compares the genetic differentiation of two or more populations at multiple-trait level (Q_ST) to genetic differentiation at neutral loci (F_ST) where Q_ST = F_ST under the null hypothesis (34, 90). This test is performed using R scripts provided by Martin et al. (34). Similarly, the univariate Q_ST–F_ST test is also performed for each trait using R scripts provided by Whitlock and Guillaume (35).

We quantified the genetic constraint from the $\mathit{G}$-matrix using the angle ($\theta$) between genetic lines of least resistance $\left({\mathit{g}}_{\mathit{max}}\right)$ (36) and actual domestication trajectory $\left(\mathit{Z}\right)$. To calculate $\theta$, we used the following formula: $\theta =\mathrm{co}{s}^{-1}\left(\widehat{\mathit{Z}}\cdot {\widehat{\mathit{g}}}_{\mathit{max}}\right)$, where $\theta$ ranges from 0° to 90°. $\mathit{Z}$ is a vector of differences in outcross trait means between teosinte and maize landrace. ${\mathit{g}}_{\mathit{max}}$ is the first eigenvector of the $\mathit{G}$-matrix, which is taken from eigendecomposition of the $\mathit{G}$-matrix using eigen function in R (88). Since the eigenvectors are sensitive to the magnitude of each trait, we opted to standardize the $\mathit{G}$-matrix and $\mathit{Z}$ such that each trait has a genetic SD or variance of 1. We computed $\theta$ for both ${\mathit{g}}_{\mathit{max}}$ values from teosinte and maize landrace $\mathit{G}$-matrices to identify the genetic constraints at the beginning and ending points of domestication. To compare individual trait contribution to genetic constraint, we calculated the angle ${\theta }_{dropone}^i$ between $\mathit{Z}$ and ${\mathit{g}}_{\mathit{max}}$ for every ith trait that is dropped from $\mathit{Z}$ and ${\mathit{g}}_{\mathit{max}}$.

Using the multivariate breeder’s equation again, we took a “what-if” approach to identify potential selection targets during domestication. For this approach, we simulated 18 unique $\mathit{\beta }$, where each ${\mathit{\beta }}^{\mathit{i}}$ had only a single element with a value of 1 and the remaining elements with a value of zero. We multiplied $\mathit{G}$ by each ${\mathit{\beta }}^{\mathit{i}}$ to obtain ${\mathit{R}}^{\mathit{i}}$, and we compared each ${\mathit{R}}^{\mathit{i}}$ to $\mathit{Z}$ by calculating the angle ${\theta }_Z$ between ${\mathit{R}}^{\mathit{i}}$ and $\mathit{Z}$ and the scalar projection of $\mathit{R}$ on $\mathit{Z}$ $\left(\left|\mathrm{pro}{j}_Z{R}^i\right|\right)$. ${\theta }_Z$ measures the deviation in direction from $\mathit{Z}$, while $\left|\mathrm{pro}{j}_Z{R}^i\right|$ measures the amount of evolutionary gain along $\mathit{Z}$.

Data and Code Availability.

Additional details on the materials and methods and all R scripts used in this project can be found in SI Appendix, Materials and Methods. Genotype files are available in Figshare, and phenotype files are available in Datasets S1 and S2.