Abstract
The enzyme nitrogenase catalyzes the reduction of N2 to ammonia but also that of protons to H2. These reactions compete at the mechanistically central ‘Janus’ intermediate, denoted E4(4H), which has accumulated 4e−/4H+ as two bridging Fe-H—Fe hydrides on the active-site cofactor. This state can lose e−/H+ by hydride protonolysis (HP) or become activated by reductive elimination (re) of the two hydrides and bind N2 with H2 loss, yielding an E4(2N2H) state that goes on to generate two NH3 molecules. Thus, E4(4H) represents the key branch point for these competing reactions. Here, we present a steady-state kinetic analysis that precisely describes this competition. The analysis demonstrates that steady-state, high-electron flux turnover overwhelmingly populates the E4 states at the expense of less reduced states, quenching HP at those states. The ratio of rate constants for E4(4H) hydride protonolysis (kHP) versus reductive elimination (kre) provides a sensitive measure of competition between these two processes and thus is a central parameter of nitrogenase catalysis. Analysis of measurements with the three nitrogenase variants (Mo-nitrogenase, V-nitrogenase, and Fe-nitrogenase) reveals that at a fixed N2 pressure their tendency to productively react with N2 to produce two NH3 molecules and an accompanying H2, rather than diverting electrons to the side reaction, HP production of H2, decreases with their ratio of rate constants, kre/kHP: Mo-nitrogenase, 5.1 atm−1; V-nitrogenase, 2 atm−1; and Fe-nitrogenase, 0.77 atm−1 (namely, in a 1:0.39:0.15 ratio). Moreover, the lower catalytic effectiveness of the alternative nitrogenases, with more H2 production side reaction, is not caused by a higher kHP but by a significantly lower kre.
Graphical Abstract
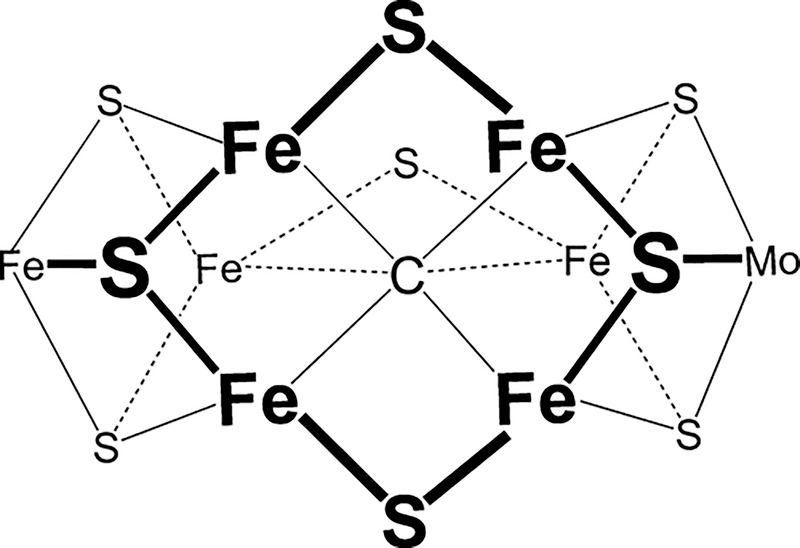
Nitrogenase is the bacterial enzyme responsible for biological nitrogen fixation, the reduction of N2 to two NH3 molecules.1–3 There are three known forms of nitrogenase, designated as the molybdenum-dependent Mo-nitrogenase, the vanadium-dependent V-nitrogenase, and the iron-only Fe-nitrogenase, each encoded by a unique gene cluster.4–8 Each nitrogenase comprises an electron-delivery Fe protein and a catalytic protein, the latter being denoted MoFe protein (MoFe), VFe protein (VFe), and FeFe protein (FeFe), respectively. Each catalytic protein contains a complex metal cluster called the FeMo-cofactor (FeMo-co), FeV-cofactor (FeV-co), and FeFe-cofactor (FeFe-co), as the active site for substrate reduction.4,5,9–12 A structural representation of the FeMo-co in the resting state is shown in Figure 1. A recent structure of the VFe protein shows that the FeV-co has a structure similar to that of the FeMo-co but has V replacing Mo and one bridging S replaced by a carbonate.13 No structure is available for the FeFe-co, but available spectroscopic signatures indicate that the overall structure is similar to those of the FeMo-co and FeV-co.11
Figure 1.
Structure of the core of the FeMo-cofactor, looking down on the Fe2,3,6,7 face.
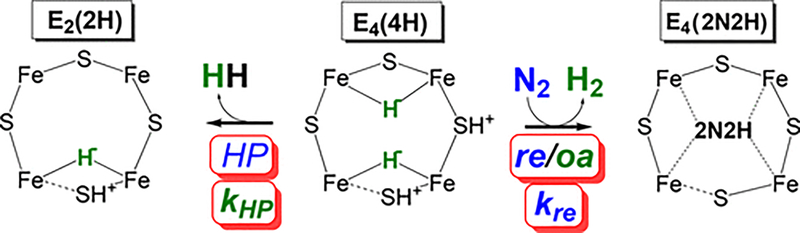
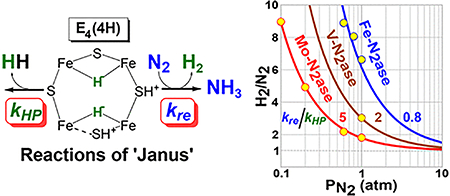
Mo-nitrogenase is the best characterized of the three nitrogenase forms. During catalysis, the Fe protein transiently associates with the MoFe protein, donating a single electron to the FeMo-co during association, mediated by an [8Fe-7S] cluster (P-cluster).9,14–16 Each electron delivery is coupled to the hydrolysis of two molecules of ATP by the Fe protein, the Pi release of which is known to be the overall rate-limiting step of catalysis.17 Studies of the enzyme trapped during catalysis have shown how electrons and protons accumulate on the FeMo-co and how the enzyme is activated for N2 binding and reduction.9,18–20 In short, before N2 can be reduced, four electrons and protons must accumulate on the FeMo-co to create a state denoted E4(4H), which stores these reducing equivalents as two Fe–H–Fe bridging hydrides. Recent structural and theoretical studies reveal that accumulation of electrons and protons on the FeMo-co can break one or both of the Fe–S–Fe bonds for a “belt” sulfide, thus opening coordination sites for binding of the hydrides to Fe atoms.13,21–24 These hydrides can produce H2 through two different reactions (Figure 2). Protonolysis of one hydride (HP) results in the formation of H2 and the “relaxation” of the E4(4H) state back to the E2(2H) state; HP of the second hydride then generates E0. In competition with HP at E4(4H) is the reductive elimination (re) of both hydrides to make H2, which is released upon N2 binding, in a process that leads to a diazene-level complex [E4(2N2H)]. Two molecules of NH3 are then generated through addition of four additional electrons/protons. As shown in Figure 2, the activation for catalysis by re of H2 is reversible, with the oxidative addition (oa) of H2 by E4(2N2H) leading to N2 release.9,18–21,25 As a result of the mechanistically required release of H2 for enzyme activation, the re/oa equilibrium incorporates an “eight-electron” limiting stoichiometry (eq 1) for N2 reduction19
| (1) |
as proposed by Lowe and Thorneley.26,27 This limiting stoichiometry is, in fact, approached under high N2 pressures.28
Figure 2.
Reactions of the E4 state. The E4(4H) state (center) is shown relaxing to the left by hydride protonolysis (HP) to generate E2(2H) with rate constant kHP or reacting with N2 to the right through the reductive elimination/oxidative addition (re/oa) equilibrium that activates nitrogenase to break the N≡N bond. Although this process is an equilibrium, the oa of H2 is not significant in our experiments (see the Supporting Information), so only the “forward”, re rate constant, kre, is shown. Note that the positioning of hydrides and protons is a matter of current interest, with plausible alternative possibilities; for the sake of concreteness, our own current best guess is shown, also noting the possible lability of an Fe–S bond with a dotted line. “2N2H” denotes a diazene-level intermediate.9
Recent studies indicate that all three nitrogenases follow a similar re/oa mechanism of nitrogen fixation.29 However, compared to the Mo-nitrogenase, the V- and Fe-nitrogenases exhibit significant differences in the relative rates of the two reaction pathways, H2 formation and N2 reduction. For example, under a 1 atm partial pressure of N2 [P(N2)], the observed ratio of H2 formed per N2 reduced for Fe-nitrogenase is ~7, whereas it is ~3 for V-nitrogenase and ~2 for Mo-nitrogenase.4,21,29–31
The stoichiometry of eq 1 was incorporated into a detailed kinetic scheme for the Mo-nitrogenase from the bacterium Klebsiella pneumoniae painstakingly developed by Lowe, Thorneley, and others (here termed the LT scheme).27 Although this scheme provides a framework for mechanistic studies of nitrogenase, the inclusion of all the steps in the complete catalytic cycle of nitrogen fixation came at the cost of significant uncertainties in key rate constants, in particular those associated with reactions of the critical E4(4H) inter- mediate.32 As a consequence, it is not feasible to obtain the large number of variables associated with this model with sufficient precision to use the model to compare the alternative nitrogenases.
To gain a precise description of the reactions at the E4(4H) state of the three nitrogenases, we have developed a kinetic description of steady-state turnover that optimally provides an analysis of the competing reactions of this ‘Janus’ intermediate.9 It focuses on the competition between progress toward NH3 formation through N2 binding/H2 re to generate E4(2N2H) and the relaxation toward the resting state by H2 formation through HP (Figure 2). Application of this kinetic model to measurements of turnover of catalysis by the three nitrogenases provides quantitative comparisons of the catalytic behavior of their Janus intermediates and critical insights into the differences in their reactivity.
MATERIALS AND METHODS
Reagents and General Procedures.
All reagents were obtained from Sigma-Aldrich (St. Louis, MO), Fisher Scientific (Fair Lawn, NJ), or Bio-Rad (Hercules, CA) unless specified otherwise and used without further purification. Argon and dinitrogen gases were purchased from Air Liquide America Specialty Gases LLC (Plumsteadville, PA). Proteins and buffers were manipulated anaerobically in septum-sealed serum vials and flasks using a vacuum Schlenk line, an argon or dinitrogen atmosphere, and gastight syringes. Gas transfers were made using gastight syringes.
Bacterial Growth and Protein Purification.
Fe-nitro- genase proteins (FeFe and Fe protein) were expressed and purified from Azotobacter vinelandii strain DJ1255 as previously described.29 Mo-nitrogenase proteins (MoFe and Fe proteins) were expressed and purified from A. vinelandii strains DJ995 (His-MoFe protein) and DJ884 (Fe protein) as previously described.33–35 Protein concentrations were determined using the Bio-Rad DC Protein Assay Kit.
Proton and Dinitrogen Reduction Assays.
Substrate reduction assays were performed in 9.4 mL serum vials containing a MgATP regeneration buffer (6.7 mM MgCl2, 30 mM phosphocreatine, 5 mM ATP, 0.2 mg/mL creatine phosphokinase, and 1.2 mg/mL BSA) and 10 mM sodium dithionite in 100 mM MOPS buffer at pH 7.0. Reaction vials were made anaerobic, and their headspaces adjusted to the partial pressure of N2 desired with the remaining headspace consisting of argon. The FeFe or MoFe protein was then added to the vials; the vials were vented to atmospheric pressure, and the reactions were initiated by the addition of the appropriate Fe protein. FeFe and MoFe concentrations in reactions were 0.1 mg/mL, corresponding to ~0.42 and ~0.4 nmol, respectively, per reaction vial. All data reported here were collected at a 1:30 FeFe:Fe protein molar ratio and a 1:20 MoFe:Fe protein molar ratio, except in a series of measurements designed to test the specific activity as a function of the electron flux, which is controlled by this ratio. Reactions were conducted at 30 °C for 8 min and then stopped by the addition of 300 μL of 400 mM EDTA (pH 8.0). To minimize the effects of slow re-reduction of Fe protein by sodium dithionite under low-flux conditions (high ratio of MoFe protein to Fe protein), The flux dependence of N2 reduction by Mo-nitrogenase employed a buffer containing a MgATP regeneration system (5 mM MgCl2, 22 mM phosphocreatine, 3.8 mM ATP, 0.15 mg/mL creatine phosphokinase, and 0.8 mg/mL BSA) with 0.125 mM 1,4-dithiothreitol, 0.6 mM flavodoxin in the hydroquinone state (FldHQ), and 12 mM sodium dithionite in 100 mM MOPS at pH 7.3. The Fe protein concentration was fixed at 0.1 mg/mL, and the MoFe protein concentration was varied from 0.2 to 6.4 mg/mL to give a [MoFe]:[Fe] ratio from 0.5 to 16. The reaction mixtures were incubated at 30 °C for 30 s under 1 atm of N2, and then the reactions were stopped by the addition of 500 μL of 400 mM EDTA at pH 8.0. H2 and NH3 were quantitated according to published methods.36,37
Kinetic Analysis.
Kinetic equations were modeled in Mathcad 15 or Sigmaplot version 12.5 and fit to experimental data using the latter.
RESULTS AND DISCUSSION
Developing a Kinetic Scheme for Reactions at E4(4H).
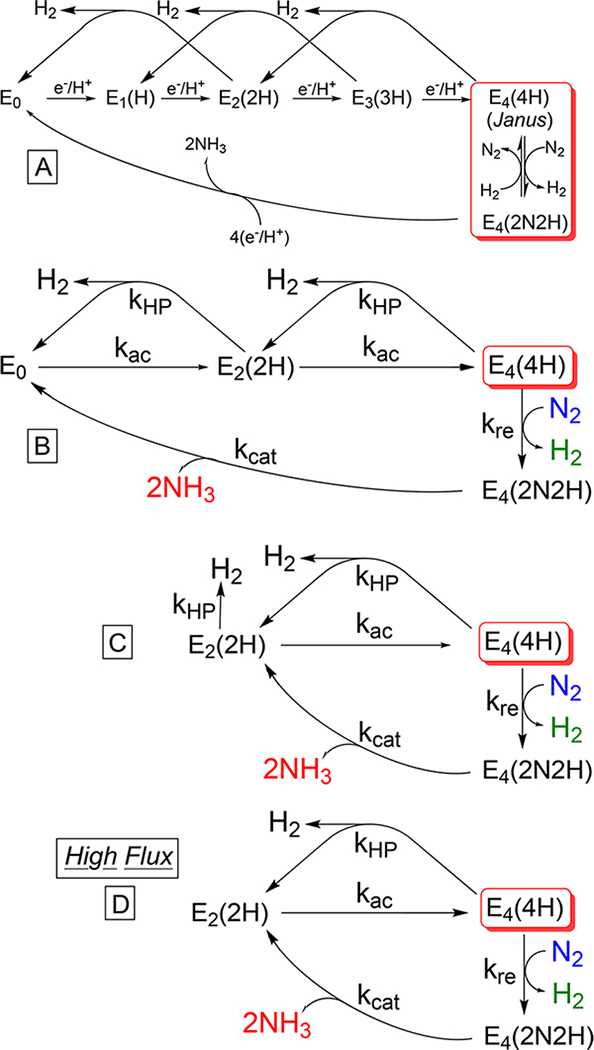
A simplified version of the LT kinetic scheme for N2 fixation that focuses on electron accumulation and centrally important re/oa equilibrium is shown in scheme A of Figure 3. It includes delivery of four e−/H+ to form E4(4H), with the hydrogenase-like side reaction, formation of H2 through HP, in states En (n = 2–4), and the catalytic re of H2 with N2 binding by E4(4H) to generate the diazene-level intermediate, E4(2N2H) (Figure 2). The subsequent formation of two NH3 molecules through accumulation of an additional 4 equiv by E4(2N2H) is represented as a single overall process with a composite rate constant (kcat). Following the strategy we developed in studying electrochemical H2 production,38 depicted in scheme B of Figure 3, we capture the essence of kinetic scheme A, the competition between nitrogenase on one hand acting “simply” as a hydrogenase through electron accumulation starting at E0 with H2 production by HP at E2(2H) and E4(4H) and on the other performing its function of N2 fixation through “capture” of E4(4H) by N2 binding/H2 re and release, to generate E4(2N2H), which irreversibly proceeds to generate two NH3 molecules. Scheme B omits the reaction in which E4(4H) is regenerated through oa of H2 by E4(2N2H) with N2 liberation (Figure 2), as being negligible in our measurements, because the partial pressures of H2 generated are so small. This approach is confirmed by a detailed analysis presented in the Supporting Information.
Figure 3.
As described in the text, scheme A is a simplified LT kinetic scheme for N2 fixation; its essence is captured by scheme B. This scheme in turn is further simplified under high-flux, steady-state turnover conditions to scheme C, which evolves into truncated kinetic scheme D.
Scheme B in turn can be mapped onto scheme C under steady-state turnover conditions. When E0 is formed either by HP at E2(2H) or by NH3 formation, it is promptly rereduced to E2(2H), so the E0-forming processes are instead treated as “directly” generating E2(2H). In this mapping, the rate constant for electron accumulation (kac) is a composite representative of the processes of electron delivery by Fe protein to MoFe protein, while the NH3-producing catalytic rate constant (kcat) in the final step of the cycle is to be understood as a composite corresponding to addition of six e−/H+ per N2 reduced, four involved in NH3 formation by reduction of diazene-level intermediate E4(2N2H) and two more associated with the prompt reduction to E2(2H) of resting state E0 formed upon release of the second of two NH3 molecules (compare scheme C with schemes A and B). Finally, liberation of H2 by E2(2H) without a change in state reflects HP at E2(2H) and rapid return of E0 thus formed to E2(2H).
Considering the behavior of E2(2H) more closely, every time it is generated, it is reduced to E4(4H) with rate constant kac, with a probability fac = kac/(kac + kHP), or liberates H2 with a rate constant kHP, with a probability fHP = kHP/(kac + kHp). High-flux conditions may then be defined as occurring when the rate of electron delivery during electron accumulation (rate constant kac) is much greater than that for the competing H2 production by HP (rate constant kHP) at states En (n = 2 or 3) in scheme A, namely fHP → 0 in schemes B and C, leading to catalytic behavior according to scheme D, in which all reaction occurs at E4(4H).
Such a high-flux condition is achievable, despite the fact that the overall electron-delivery process is well-known to be slow,17 because of a peculiarity in nitrogenase function. As reported by Lowe and Thorneley, after delivery of an electron from the Fe protein, H2 can only be released from free MoFe protein, namely after the oxidized Fe protein dissociates and before another reduced Fe protein binds.27 As a result, the competition between the release of H2 from free MoFe protein and conversion to the next higher En state is governed by the rate of binding of a reduced Fe protein to the MoFe protein. With high concentrations of reduced Fe protein relative to MoFe protein (high flux), this rate is increased to the point that reduced Fe protein binds to MoFe protein rapidly compared to the rate of release of H2 by MoFe protein. As a consequence, states En (n = 2 and 3) do not release H2 by the HP process, and instead, the states “before” E4(4H) En (n < 4) progressively accept (e−/H+) until they are converted to E4(4H). This state then reacts, either by HP or by the re process. As a result, the enzyme under high flux, as described by scheme D, behaves in a fashion not, to the best of our knowledge, noted previously: H2 production at electron-accumulation stages, En (n ≤ 3) is suppressed during turnover as these states become depopulated in favor of an E4-level state, either E4(4H) or E4(2N2H) depending on the partial pressure of N2; although E0 is regenerated by N2 fixation, under high flux it is promptly returned to E2(2H). In short, during catalysis, the enzyme effectively cycles between the two E4 states and the little-populated E2(2H), and thus, kinetic scheme C evolves into truncated scheme D. In this report, we validate scheme C and confirm that high-flux conditions convert it into scheme D.
It is centrally important that, although in steady-state experiments described by schemes C and D, kac and kcat are composite rate constants, rate constants kHP and kre correspond precisely to the rate constants for reaction of E4(4H) in scheme A and, indeed, in the full LT scheme. Moreover, the beauty of high-flux, steady-state experiments (scheme D) is that they emphasize the role of E4(4H) as the ‘Janus’ intermediate, which acts as a catalytic “branch point” that reacts through one of two channels. It can “fall back” in a “hydrogenase- like” catalytic cycle, releasing H2 by the first-order HP process (rate constant kHP) without further electron accumulation, regenerating E2(2H), or it can be “captured” by second-order reaction with N2 (rate constant kre) with accompanying release of H2 formed by re, to produce E4(2N2H), which irreversibly proceeds to generate two NH3 molecules with composite rate constant kcat. High-flux experiments thus provide precision measurements of the centrally important mechanistic rate constants that define the E4(4H) branch point: kHP and kre.
Kinetic Analysis.
As shown in the Supporting Information, according to schemes C and D, during steady-state turnover the differential equations for the rates of formation of H2 and NH3 and loss of N2 are zero-order in time, and the rates of NH3 formation/N2 loss and of H2 formation can be written as shown in eq 2
| (2) |
where is the total enzyme concentration. As a result, the total formation of NH3/loss of N2 and the formation of H2 during a turnover experiment are simply proportional to their respective rate constants. The rate constants for the production of the NH3 product and loss of N2 for schemes C and D are given by eq 3 where the numerical factor () converts eq 2 to the rate of NH3 formation per electron, according to the stoichiometry of eq 1. The maximum velocity for NH3 production is set by the equation , whose form causes it to equal the smaller of the two rate constants, kac and kcat. The bracketed term in eq 3 has the form
| (3) |
of a binding isotherm, with the apparent binding constant equaling the ratio . We allow for variations in flux, namely the rate constant ratio, z = kHP/kac > 0 and thus variations in HP at the E2(2H) state, but have simplified the appearance of the equation by defining the apparent rate constant, krez, in terms of the true kre and z, as indicated. For the sake of completeness, we note this equation can be rewritten in the form of a hyperbola or Michaelis-Menten equation (eq 4). The corresponding rate constant for H2 production for scheme C is presented in eq 5.
| (4) |
| (5) |
When , H2 is produced solely by HP with a rate constant kHP (per electron). At a high , H2 is produced solely by the re process, at a rate equaling the rate of consumption of N2; HP at E2(2H) is associated with the terms involving the kHP/kac ratio in the numerator of the first form of eq 5.
Schemes B and C and the resultant steady-state turnover rate constants provide a clear mathematical formulation of the competition at the E4(4H) branch point between the first- order process of H2 formation by HP without N2 binding and the second-order re process in which the binding and reduction of one N2 accompanies the re of one H2. This ability of a second-order process to outcompete a first-order one is most clearly captured by taking the ratio of the rate constants for production of H2 (eq 3) and N2 consumption (eq 4), denoted r, which can be written as shown in eq 6. According to eq 6, at
| (6) |
low values of , the rate of H2 production by HP from E4(4H) becomes independent of as , while the rate of N2 consumption, through reductive elimination and production of H2 and two NH3 molecules, falls in proportion to . Hence, as , the ratio r approaches infinity. At the other extreme, as increases so that re of H2 with N2 consumption becomes much faster than HP at E4(4H), , the ratio r tends toward a limiting value that depends on the extent of H2 formation at the E2(2H) stage of scheme C, which increases with the value of kHP/kac (eqs 5 and 6). If turnover is in the high-flux limit, kHP/kac → 0, there is no HP at the E2(2H) state, scheme C evolves into scheme D, and these equations predict that the limiting value at high is r = 1. HP at E2(2H) is abolished, and HP at E4(4H) is totally outcompeted by N2 binding with re and release of H2. One H2 is liberated as one N2 binds and is reduced to two NH3 molecules.
Turnover of Nitrogenases.
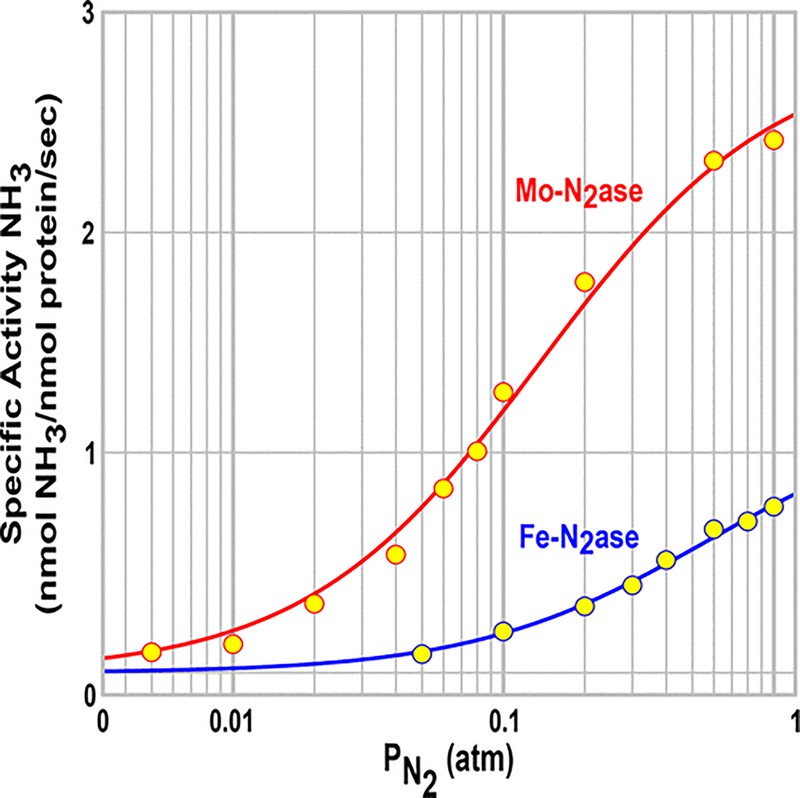
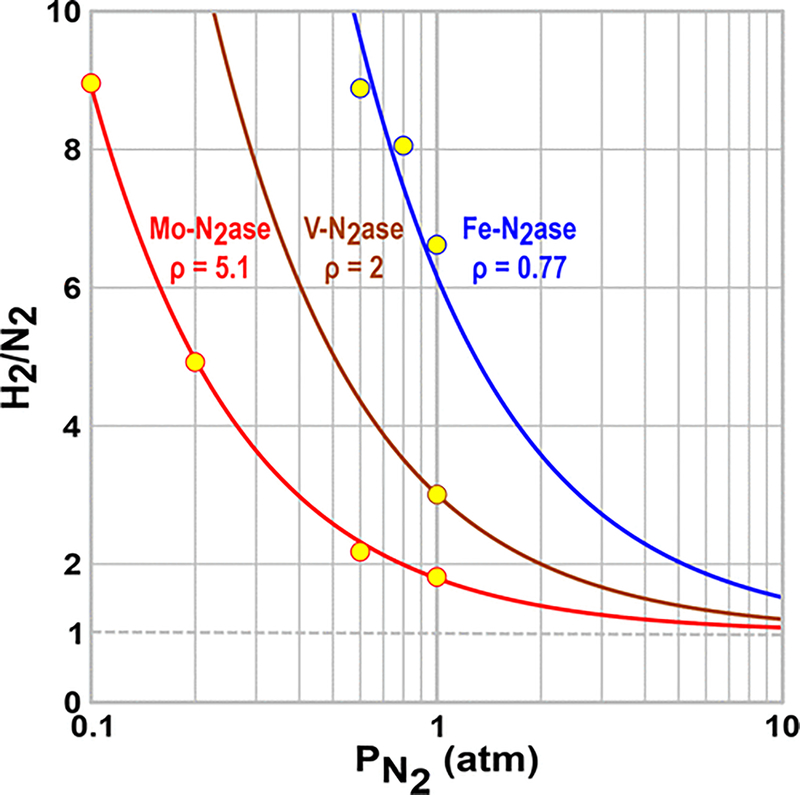
Figure 4 presents a plot of the specific activities for NH3 production at equal concentrations of Mo-nitrogenase and Fe-nitrogenase as a function of the partial pressure of N2 overlaid by the fits of these two data sets to eq 3. It is noteworthy that the apparent binding affinity constant, , and the maximum velocity obtained in the fits to the specific activities for Fe-nitrogenase (Table 1) are 4- and 10-fold smaller, respectively, than for Mo-nitrogenase. Figure 5 overlays the measurements of r as a function of for all three nitrogenases with the fits to eq 6. Table 1 lists the parameters derived from the fits for both Mo- and Fe-nitrogenases, including kre, kHP, , and the value for the central parameter of catalysis, the ratio of reaction rate constants at the E4 level, ρ = kre/kHP.
Figure 4.
Specific activities for NH3 formation by Mo- and Fe-nitrogenases as a function of the partial pressure of N2. Overlaid are fits to eq 3 obtained with SigmaPlot; values of kre and Ka for MoFe (red trace) and FeFe (blue) are listed in Table 1. Assays were performed as described in Materials and Methods.
Table 1.
Kinetic Parameters Obtained from High-Flux Turnover
Figure 5.
Ratio of H2 formed to N2 consumed as a function of the partial pressure of N2 for Mo-nitrogenase (red) and Fe-nitrogenase (blue). Overlaid are fits to eq 6 using SigmaPlot. Values of ρ = kre/kHP are listed in Table 1. Assays were performed as described in Materials and Methods.
With a focus on the behavior of Mo-nitrogenase, consider the ratio r (Figure 5). The fit to eq 6 yields as the ratio of the rate constants for HP and for electron accumulation z = kHP/kac = 0, which implies that the experiments are indeed performed under high-flux conditions, with HP fully suppressed at early stages of electron accumulation, En (n < 4), and that scheme D applies: both the reaction with N2 with correlated H2 production and the HP of H2 are described by the intrinsic rate constants associated with reactions of E4(4H), kre and kHP, respectively.
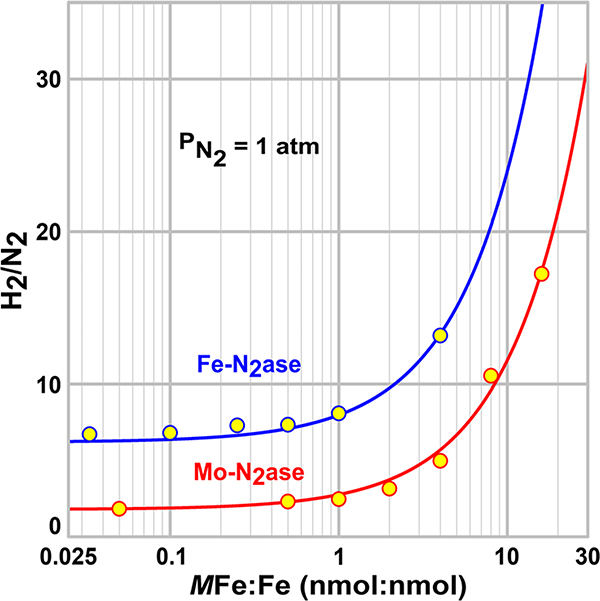
To test this analysis and conclusion, we performed a suite of experiments in which the electron flux is varied at a fixed . As noted above, the competition between formation of H2 through HP at E2 or E3 and conversion to the next higher En state is expressed in the ratio z = kHP/kac and is governed by the rate of binding of a reduced Fe protein to the MoFe protein. This influence may be incorporated into the description of r through a decrease in z with increasing flux, z = a[MoFe]/[Fe], where the parameter, a, is a scale-factor that relates the two ratios. Equation 6, the ratio of product-formation rate constants, r, can then be rewritten in terms of this relationship (also see, SI), (eq 7).
| (7) |
The plots of eq 7 in Figure 6 illustrate how, in the high-flux regime, where z ≪ 1, the ratio r is invariant with flux as expected, while as z increases and the system falls out of this regime, r increases. This measured ratio of H2/N2 as a function of the MoFe protein/Fe protein ratio shown in Figure 6 is consistent with an earlier study.39
Figure 6.
Ratio of H2 formed to N2 consumed as a function of flux ([MFe:Fe], where M = Mo or Fe) for Mo-nitrogenase (red) and Fe-nitrogenase (blue). Traces were determined by fixing ρ to the value in Table 1 and fitting parameter a in eq 7 using SigmaPlot (Table 1). Assays were performed as described in Materials and Methods.
For Mo-nitrogenase, the measured dependence of r on [MoFe]/[Fe] at atm is captured with precision by eq 7 using the corresponding values of ρ and a (Table 1). The data show that Mo-nitrogenase reaches the high-flux regime when [MoFe]/[Fe] ≳ 1, while our experiments in Figures 4 and 5 were performed at [MoFe]/[Fe] = 1/20! This finding shows that scheme D indeed is appropriate for analysis of our experiments, with z → 0, that the apparent rate constant for re obtained by combining the parameters from the fits to the titration (Figure 4) with rate ratio r (Figure 5) (krez, eq 3) is precisely the intrinsic value, kre, that describes the re process of E4(4H), and, finally, that rate constant kHP is precisely the value for E4(4H).
With this foundation, the plots in Figure 5, the “H2/N2” ratio, r, are shown to be a remarkable demonstration of the power of the present approach to reveal the kinetic basis for the different catalytic efficiencies of the alternative nitrogenases. The key difference is expressed in the ratio of reaction rate-constants at the E4 level, ρ = kre/kHP, which captures the tendency for the E4(4H) intermediate to undergo the re process with H2 release upon N2 binding and, ultimately, NH3 formation (second-order rate constant, kre), instead of producing H2 by HP (first-order rate constant, kHP). Equation 6 shows that ρ alone controls this branching at E4(4H), and the plots of r as a function of for the two nitrogenases, which so beautifully overlay the data, are generated through the use of eq 6 merely by adjusting this single parameter (Table 1).
Viewed from a different perspective, these measurements and their description by eq 6 clearly demonstrate that activation of E4(4H) for N2 binding indeed occurs through re and release of H2. This coupling between N2 binding and the release of H2, which was first incorporated in the LT kinetic scheme, is highlighted in scheme D and, as visualized through the plot of r versus in Figure 5, both predicts and provides an explanation for the experimental finding that an extremely high does not entirely suppress H2 formation by Mo-nitrogenase but instead leads asymptotically to the formation of one H2 per formation of two NH3 molecules per reduction of one N2.28 For atm, eq 6 yields an r value of 1.02 for Mo-nitrogenase, essentially reproducing the Burris value of r (1.13 ± 0.13).
With this analysis and the resulting parameters in hand, we can quantify the remark made above that under high flux all the electron accumulation stages, En (n ≤ 3), become depopulated in favor of an E4-level state. According to this analysis, in these high-flux experiments, [MoFe]/[Fe] = 1/20, one calculates that ~99% of the cofactor is present in the E4 state, as either E4(4H) or E4(2N2H), with the relative amounts depending on . Moreover, direct calculation with the full scheme A gives an equivalent result.
Focusing next on Fe-nitrogenase, we find the measured flux dependence of the ratio r at plotted in Figure 6 shows that this enzyme also operates in the high-flux regime in our measurements. Fe-nitrogenase reaches the high-flux regime when [FeFe]/[Fe] ≳ 1, whereas our experiments in Figures 4 and 5 were performed at a far smaller ratio ([FeFe]/[Fe] = 1/30). Thus, here too, all catalytic reactions occur at the E4(4H) state, and its catalytic properties captured in the reaction rate constants can be straightforwardly compared to those of Mo-nitrogenase through the kinetic analysis of the turnover experiments.
Comparison of the parameters derived from the N2 consumption titration for Fe-nitrogenase (Figure 4) and the H2/N2 titration (Figure 5) with those of Mo-nitrogenase (Table 1) reveals that the major functional difference between the Mo- and Fe-nitrogenases is associated with rate constant kre for H2 re/N2 binding by E4(4H). The kre for Mo-nitrogenase is 10-fold greater than that of Fe-nitrogenase, while the asymptotic maximum rate constant for N2 reduction, proportional to , is twice as big. As a result, the apparent affinity constant for N2, , is 4-fold greater for Mo-nitrogenase than for Fe-nitrogenase.
The higher H2 production by the Fe-nitrogenase is best considered in terms of the N2/H2 ratio. The fits to the data in Figure 5 show that the kre/kHP ratio, which captures the tendency of E4(4H) to undergo re rather than HP, is 7-fold larger for Mo-nitrogenase than for Fe-nitrogenase. Even though the value of kHP determined for MoFe is indeed slightly higher than that for Fe-nitrogenase, because the Mo-nitrogenase value of kre is 10-fold higher, there is a 7-fold greater preference for re instead of HP (rate ratio, ρ) for Mo-nitrogenase than for Fe-nitrogenase. Finally, even though Fe-nitrogenase is thus a considerably poorer N2 fixation catalyst, because it follows the same mechanism as Mo-nitrogenase, in the high-flux limit that applies here, eq 6 nonetheless predicts that r → 1 at sufficiently high ; extrapolation of the Fe-nitrogenase curve in Figure 5 to 50 atm predicts an r value of 1.11.
Finally, the V-nitrogenase is widely understood to have catalytic efficacy midway between those of Mo- and Fe-nitrogenases, and the kinetic model developed here can quantify this point using only the single value of the H2/N2 ratio at available in the literature.4,6,12,30,31 Given the intermediate behavior of V-nitrogenase and the finding that both more and less effective enzymes are in the high-flux regime during in vitro turnover, we may assume the same for V-nitrogenase, in which case the predicted curve of r versus for this enzyme is completely determined by the single parameter ρ, which is fixed by the single value of r at ; the resulting curve is plotted on Figure 5. The value of ρ and the curve it specifies indeed lie between those for Mo- and Fe-nitrogenase, which quantifies the relative tendency of E4(4H) to follow its two alternative reaction channels. The ratio for V-nitrogenase relates to those of the other two nitrogenases as kre/kHP (Mo) = 5.1, kre/kHP (V) = 2, and kre/kHP (Fe) = 0.77. In other words, at a given pressure of N2, V-nitrogenase is ~40% as likely to undergo reaction with N2 as Mo-nitrogenase and Fe-nitrogenase is only 15% as likely to thus react.
As a final comment about kinetic approaches to nitrogenase function, note that the kre/kHP ratio = 5.1 atm−1 derived in this fashion for A. vinelandii Mo-nitrogenase is of far higher precision but is satisfyingly similar to the ratio of rate constants measured by LT as refined by Wilson and Watt32 for a different Mo-nitrogenase, kre/kHP = 3.4 atm−1 (conversion of their kre in units of M−1 s−1 used a Henry’s law constant K of 6.1 × 10−4 M/atm).40 However, the benefits of the approach presented here are highlighted by the remark by Wilson and Watt that the value they report for kHP is “subject to error of a factor of approximately 2” whereas the key kinetic constants in Table 1 have errors of <10%. And, of course, the focused ability to compare the catalytically important rate constants associated with E4(4H) among the three nitrogenases that is introduced by the current approach is entirely new.
CONCLUSIONS
The work reported here provides a kinetic analysis of nitrogenase reactivity that focuses on reaction at the catalytically central E4 state and precisely describes observed H2 production and N2 consumption/NH3 production under steady-state turnover conditions. The measurements as analyzed with the new kinetic model provide unprecedented insight into the catalytic behavior of the E4(4H) ‘Janus’ intermediate, whose differing properties in the three nitrogenases give rise to their differing catalytic efficacy. Although electron transfer to the catalytic MFe proteins from the Fe protein is rate-limited by Pi release,17 analysis of the measurements shows that across a wide range of electron fluxes introduced by varying the protein concentration ratio, [MFe]/[Fe], the nitrogenase behaves in a fashion that had not been recognized previously: H2 production is suppressed at the electron accumulation stages, En (n < 3), and during catalysis, the enzyme effectively cycles between the two states at the E4 level and the little populated E2(2H), as is captured by the truncated cycle of scheme D. We note that the ratio of MoFe protein to Fe protein measured inside the cell ([MoFe]/[Fe] = 1/2) corresponds to “high-flux” conditions (Figure 6), which means that the present measurements reproduce the enzyme’s behavior in vivo.41 It is significant that the ratio of nitrogenase component proteins inside the cell is small enough to minimize the wasteful H2 formation by HP that would occur at concentration ratios greater than unity, yet at the same time, the ratio is not made even smaller, to no appreciable functional benefit, by the presence of excess Fe protein; the cell does not make more Fe protein than is necessary. This is of considerable physiological benefit, as protein production is a significant energy demand on the cell. It should be noted that Fe protein is also involved in the assembly of both of the metalloclusters contained with the MoFe protein, P-cluster, and FeMo-cofactor.42 However, the amount of Fe protein required to sustain these functions under steady-state growth conditions is likely to be minimal, indicating that the elevated level of Fe protein relative to MoFe protein within cells represents a physiologically relevant mechanism for maximizing catalytic efficiency.
The results further support the earlier findings that suggested that unlimited high pressures of N2 could not completely suppress H2 production and that the ratio of H2 production to N2 consumption in fact approaches unity at high pressures,,28 behavior explained by the re/oa mechanism we have developed recently.9,18–20 The kinetic analysis shows how this behavior arises: the second-order process of enzyme activation by H2 re with liberation through N2 binding outcompetes the first-order “decay” of E4(4H) through the HP process.
Two striking differences in the function of Mo-, V-, and Fe-nitrogenases are revealed here. Most importantly, the observation that Fe-nitrogenase produces far more H2 per N2 reduced at atm than the Mo-enzyme arises not, as might have been expected, because Fe-nitrogenase exhibits a correspondingly greater rate constant for HP. Indeed, the rate constant for HP by E4(4H) of Fe-nitrogenase is only 70% of that for Mo-nitrogenase! Instead, Mo-nitrogenase is a more efficient catalyst for N2 reduction because of the roughly 10-fold greater second-order rate constant for the N2-fixing pathway of E4(4H) reactivity, resulting in a kre/kHP rate constant ratio of ~7 (Table 1): Mo-nitrogenase is simply a better N2 reduction catalyst. Second, the maximum velocity for NH3 formation, , for Mo-nitrogenase is 2 times that of Fe-nitrogenase, a finding reinforced by previous data demonstrating that electron flux through Mo-nitrogenase is roughly twice that of Fe-nitrogenase. These two differences account for the poorer catalytic efficiency of Fe-nitrogenase and can be extrapolated to the intermediate reactivity observed for V-nitrogenase.
An experimental and theoretical study of the differences among the nitrogenases will provide a fruitful avenue for improving our understanding of how the differences in the metal clusters and their surrounding protein environments tune the reactivity to favor N2 reduction over H2 evolution in the different forms of nitrogenase, as quantified by the kinetic analysis presented here.
Supplementary Material
Acknowledgments
Funding
Support was provided by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, via Grants DE-SC0010687 and DE-SC0010834 to L.C.S. and D.R.D., and the National Science Foundation, via Grant MCB 1515981to B.M.H.
ABBREVIATIONS
- BSA
bovine serum albumin
- FeFe-co
active-site cofactor of iron-only nitrogenase
- FeMo-co
active-site cofactor of molybdenum-dependent nitrogenase
- Fe-N2ase
iron-only nitrogenase
- FeV-co
active-site cofactor of vanadium-dependent nitrogenase
- HP
hydride protonolysis
- ,
turnover number (kcat)
- K
binding constant for N2 (kre/)
- kac
rate constant for accumulation of electrons on a cofactor
- kcat
turnover number
- kHP
rate constant for hydride protonolysis
- kre
rate constant for reductive elimination
- LT
Lowe and Thorneley kinetic scheme
- Mo-N2ase
molybdenum-dependent nitrogenase
- oa
oxidative addition
- ,
partial pressure of dinitrogen
- r
- re
reductive elimination
- V-N2ase
vanadium-dependent nitrogenase
- z
kHP/kac
Footnotes
The authors declare no competing financial interest.
ASSOCIATED CONTENT
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.biochem.8b00784.
Rate equations for steady-state kinetic analysis of scheme D, H2 oa and the steady-state kinetics, and data for Figures 4–6 and Table 1 (PDF)
REFERENCES
- (1).Raymond J, Siefert JL, Staples CR, and Blankenship RE (2004) The natural history of nitrogen fixation. Mol. Biol. Evol 21, 541–554. [DOI] [PubMed] [Google Scholar]
- (2).Burris RH, and Roberts GP (1993) Biological nitrogen fixation. Annu. Rev. Nutr 13, 317–35. [DOI] [PubMed] [Google Scholar]
- (3).Gruber N, and Galloway JN (2008) An Earth-system perspective of the global nitrogen cycle. Nature 451, 293–296. [DOI] [PubMed] [Google Scholar]
- (4).Eady RR (1996) Structure-function relationships of alternative nitrogenases. Chem. Rev 96, 3013–3030. [DOI] [PubMed] [Google Scholar]
- (5).Burgess BK, and Lowe DJ (1996) Mechanism of molybdenum nitrogenase. Chem. Rev 96, 2983–3012. [DOI] [PubMed] [Google Scholar]
- (6).Hu Y, Lee CC, and Ribbe MW (2012) Vanadium nitrogenase: A two-hit wonder? Dalton Trans. 41, 1118–1127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Robson R, Woodley P, and Jones R (1986) Second gene (nifH) coding for a nitrogenase iron protein in Azotobacter chroococcum is adjacent to a gene coding for a ferredoxin-like protein. EMBO J. 5, 1159–1163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Joerger RD, Jacobson MR, Premakumar R, Wolfinger ED, and Bishop PE (1989) Nucleotide sequence and mutational analysis of the structural genes (anfHDGK) for the second alternative nitrogenase from Azotobacter vinelandii. J. Bacteriol 171, 1075–1086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Hoffman BM, Lukoyanov D, Yang Z-Y, Dean DR, and Seefeldt LC (2014) Mechanism of nitrogen fixation by nitrogenase: The next stage. Chem. Rev 114, 4041–4062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Fay AW, Blank MA, Lee CC, Hu Y, Hodgson KO, Hedman B, and Ribbe MW (2010) Characterization of isolated nitrogenase FeVco. J. Am. Chem. Soc 132, 12612–12618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Krahn E, Weiss B, Krockel M, Groppe J, Henkel G, Cramer S, Trautwein A, Schneider K, and Muller A (2002) The Fe-only nitrogenase from Rhodobacter capsulatus: identification of the cofactor, an unusual, high-nuclearity iron-sulfur cluster, by Fe K-edge EXAFS and 57Fe Mossbauer spectroscopy. JBIC, J. Biol. Inorg. Chem 7, 37–45. [DOI] [PubMed] [Google Scholar]
- (12).Hales BJ (1990) Alternative nitrogenase. Adv. Inorg. Biochem 8, 165–198. [PubMed] [Google Scholar]
- (13).Sippel D, and Einsle O (2017) The structure of vanadium nitrogenase reveals an unusual bridging ligand. Nat. Chem. Biol 13, 956–960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Peters JW, Fisher K, Newton WE, and Dean DR (1995) Involvement of the P-cluster in intramolecular electron transfer within the nitrogenase MoFe protein. J. Biol. Chem 270, 27007–27013. [DOI] [PubMed] [Google Scholar]
- (15).Chan JM, Christiansen J, Dean DR, and Seefeldt LC (1999) Spectroscopic evidence for changes in the redox state of the nitrogenase P-cluster during turnover. Biochemistry 38, 5779–5785. [DOI] [PubMed] [Google Scholar]
- (16).Danyal K, Dean DR, Hoffman BM, and Seefeldt LC (2011) Electron transfer within nitrogenase: evidence for a deficitspending mechanism. Biochemistry 50, 9255–9263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Yang Z-Y, Ledbetter R, Shaw S, Pence N, Tokmina-Lukaszewska M, Eilers B, Guo Q, Pokhrel N, Cash VL, Dean DR, Antony E, Bothner B, Peters JW, and Seefeldt LC (2016) Evidence that the Pi release event is the rate-limiting step in the nitrogenase catalytic cycle. Biochemistry 55, 3625–3635. [DOI] [PubMed] [Google Scholar]
- (18).Lukoyanov D, Khadka N, Yang Z-Y, Dean DR, Seefeldt LC, and Hoffman BM (2016) Reversible photoinduced reductive elimination of H2 from the nitrogenase dihydride state, the E4(4H) Janus intermediate. J. Am. Chem. Soc 138, 1320–1327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Lukoyanov D, Khadka N, Yang Z-Y, Dean DR, Seefeldt LC, and Hoffman BM (2016) Reductive elimination of H2 activates nitrogenase to reduce the N≡N triple bond: characterization of the E4(4H) Janus intermediate in wild-type enzyme. J. Am. Chem. Soc 138, 10674–10683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Lukoyanov D, Yang Z-Y, Khadka N, Dean DR, Seefeldt LC, and Hoffman BM (2015) Identification of a key catalytic intermediate demonstrates that nitrogenase is activated by the reversible exchange of N2 for H2. J. Am. Chem. Soc 137, 3610–3615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Rohde M, Sippel D, Trncik C, Andrade SLA, and Einsle O (2018) The critical E4 state of nitrogenase catalysis. Biochemistry, DOI: 10.1021/acs.biochem.8b00509. [DOI] [PubMed] [Google Scholar]
- (22).Spatzal T, Perez KA, Einsle O, Howard JB, and Rees DC (2014) Ligand binding to the FeMo-cofactor: structures of CO-bound and reactivated nitrogenase. Science 345, 1620–1623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Sippel D, Rohde M, Netzer J, Trncik C, Gies J, Grunau K, Djurdjevic I, Decamps L, Andrade SLA, and Einsle O (2018) A bound reaction intermediate sheds light on the mechanism of nitrogenase. Science 359, 1484–1489. [DOI] [PubMed] [Google Scholar]
- (24).Raugei S, Seefeldt LC, and Hoffman BM (2018) A critical computational analysis illuminates the reductive-elimination mechanism that activates nitrogenase for N2 reduction. Proc. Natl. Acad. Sci. U. S. A,. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Lukoyanov D, Yang Z-Y, Barney BM, Dean DR, Seefeldt LC, and Hoffman BM (2012) Unification of reaction pathway and kinetic scheme for N2 reduction catalyzed by nitrogenase. Proc. Natl. Acad. Sci. U. S. A 109, 5583–5587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Thorneley RN, and Lowe DJ (1983) Nitrogenase of Klebsiella pneumoniae. Kinetics of the dissociation of oxidized iron protein from molybdenum-iron protein: identification of the rate-limiting step for substrate reduction. Biochem. J 215, 393–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Thorneley RNF, and Lowe DJ (1985) Kinetics and mechanism of the nitrogenase enzyme In Molybdenum Enzymes (Spiro TG, Ed.) pp 221–284, Wiley-Interscience Publications, New York. [Google Scholar]
- (28).Simpson FB, and Burris RH (1984) A nitrogen pressure of 50 atm does not prevent evolution of hydrogen by nitrogenase. Science 224, 1095–1097. [DOI] [PubMed] [Google Scholar]
- (29).Harris DF, Lukoyanov DA, Shaw S, Compton P, Tokmina-Lukaszewska M, Bothner B, Kelleher N, Dean DR, Hoffman BM, and Seefeldt LC (2018) Mechanism of N2 reduction catalyzed by Fe-nitrogenase involves reductive elimination of H2. Biochemistry 57, 701–710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Eady RR, Robson RL, Richardson TH, Miller RW, and Hawkins M (1987) The vanadium nitrogenase of Azotobacter chroococcum. Purification and properties of the VFe protein. Biochem. J 244, 197–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Schneider K, and Muller A (2004) Iron-only nitrogenase: Exceptional catalytic, structural and spectroscopic features In Catalysts for Nitrogen Fixation, pp 281–307, Springer, Dordrecht, The Netherlands. [Google Scholar]
- (32).Wilson PE, Nyborg AC, and Watt GD (2001) Duplication and extension of the Thorneley and Lowe kinetic model for Klebsiella pneumoniae nitrogenase catalysis using a MATHEMATICA software platform. Biophys. Chem 91, 281–304. [DOI] [PubMed] [Google Scholar]
- (33).Christiansen J, Goodwin PJ, Lanzilotta WN, Seefeldt LC, and Dean DR (1998) Catalytic and biophysical properties of a nitrogenase apo-MoFe protein produced by an nifB-deletion mutant of Azotobacter vinelandii. Biochemistry 37, 12611–12623. [DOI] [PubMed] [Google Scholar]
- (34).Burgess BK, Jacobs DB, and Stiefel EI (1980) Large- scale purification of high activity Azotobacter vinelandii nitrogenase. Biochim. Biophys. Acta 614, 196–209. [DOI] [PubMed] [Google Scholar]
- (35).Peters JW, Fisher K, and Dean DR (1994) Identification of a nitrogenase protein-protein interaction site defined by residues 59 through 67 within the Azotobacter vinelandii Fe protein. J. Biol. Chem 269, 28076–28083. [PubMed] [Google Scholar]
- (36).Corbin JL (1984) Liquid chromatographic-fluorescence determination of ammonia from nitrogenase reactions: A 2-min assay. Appl. Environ. Microbiol 47, 1027–1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Barney BM, Igarashi RY, Dos Santos PC, Dean DR, and Seefeldt LC (2004) Substrate interaction at an iron-sulfur face of the FeMo-cofactor during nitrogenase catalysis. J. Biol. Chem 279, 53621–53624. [DOI] [PubMed] [Google Scholar]
- (38).Khadka N, Milton R, Shaw S, Lukoyanov D, Dean DR, Minteer SD, Raugei S, Hoffman BM, and Seefeldt LC (2017) Mechanism of nitrogenase H2 formation by metal-hydride protonation probed by mediated electrocatalysis and H/D isotope effects. J. Am. Chem. Soc 139, 13518–13524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Wherland S, Burgess BK, Stiefel EI, and Newton WE (1981) Nitrogenase reactivity: effects of component ratio on electron flow and distribution during nitrogen fixation. Biochemistry 20, 5132–5140. [DOI] [PubMed] [Google Scholar]
- (40).Sander R (2015) Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys 15, 4399–4981. [Google Scholar]
- (41).Poza-Carrion C, Jimenez-Vicente E, Navarro-Rodriguez M, Echavarri-Erasun C, and Rubio LM (2014) Kinetics of nif gene expression in a nitrogen-fixing bacterium. J. Bacteriol 196, 595–603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Jimenez-Vicente E, Yang Z-Y, Ray WK, Echavarri-Erasun C, Cash VL, Rubio LM, Seefeldt LC, and Dean DR (2018) Sequential and differential interaction of assembly factors during nitrogenase MoFe protein maturation. J. Biol. Chem 293, 9812–9823. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.