An omnibus non-parametric test of equality in distribution for unknown functions

Abstract

We present a novel family of nonparametric omnibus tests of the hypothesis that two unknown but estimable functions are equal in distribution when applied to the observed data structure. We developed these tests, which represent a generalization of the maximum mean discrepancy tests described in Gretton et al. [2006], using recent developments from the higher-order pathwise differentiability literature. Despite their complex derivation, the associated test statistics can be expressed rather simply as U-statistics. We study the asymptotic behavior of the proposed tests under the null hypothesis and under both fixed and local alternatives. We provide examples to which our tests can be applied and show that they perform well in a simulation study. As an important special case, our proposed tests can be used to determine whether an unknown function, such as the conditional average treatment effect, is equal to zero almost surely.

1. Introduction

In many scientific problems, it is of interest to determine whether two particular functions are equal to each other. In many settings these functions are unknown and may be viewed as features of a data-generating mechanism from which observations can be collected. As such, these functions can be learned from available data, and estimates of these respective functions can then be compared. To reduce the risk of deriving misleading conclusions due to model misspecification, it is appealing to employ flexible statistical learning tools to estimate the unknown functions. Unfortunately, inference is usually extremely difficult when such techniques are used, because the resulting estimators tend to be highly irregular. In such cases, conventional techniques for constructing confidence intervals or computing p-values are generally invalid, and a more careful construction, as exemplified by the work presented in this article, is required.

To formulate the problem statistically, suppose that n independent observations O₁, O₂, …, O_n are drawn from a distribution P₀ known only to lie in the nonparametric statistical model, denoted by $\mathcal{M}$. Let $\mathcal{O}$ denote the support of P₀, and suppose that P ↦ R_P and P ↦ S_P are parameters mapping from $\mathcal{M}$ onto the space of univariate bounded real-valued measurable functions defined on $\mathcal{O}$, i.e. R_P and S_P are elements of the space of univariate bounded real-valued measurable functions defined on $\mathcal{O}$. For brevity, we will write $R_0\triangleq R_{P_0}$ and $S_0\triangleq S_{P_0}$. Our objective is to test the null hypothesis

$${\mathcal{H}}_0:R_0\left(O\right)\stackrel{d}{=}{S}_0\left(O\right)$$

versus the complementary alternative ${\mathcal{H}}_1$ : not ${\mathcal{H}}_0$, where O follows the distribution P₀ and the symbol $\stackrel{d}{=}$ denotes equality in distribution. We note that $R_0(O)\stackrel{d}{=}{S}_0(O)$ if R₀ ≡ S₀, i.e. R₀(O) = S₀ (O) almost surely, but not conversely. The case where S₀ ≡ 0 is of particular interest since then the null simplifies to ${\mathcal{H}}_0:R_0\equiv 0$. Because P₀ is unknown, R₀ and S₀ are not readily available. Nevertheless, the observed data can be used to estimate P₀ and hence each of R₀ and S₀. The approach we propose will apply to functionals within a specified class described later.

Before presenting our general approach, we describe some motivating examples. Consider the data structure O = (W, A, Y) ~ P, where W is a collection of covariates, A is binary treatment indicator, and Y is a bounded outcome, i.e., there exists a universal c such that, for all $P\in \mathcal{M}$, P(|Y| ≤ c) = 1. Note that, in our examples, the condition that Y is bounded cannot easily be relaxed, as the parameter from Gretton et al. [2006] on which we will base our testing procedure requires that the quantities under consideration have compact support.

• Example 1: Random sample size variant of the two-sample test from Gretton et al. [2006].

  • If $R_P(o)\triangleq ay$ and $S_P(o)\triangleq (1-a)y$, the null hypothesis corresponds to Y|A = 1 and Y|A = 0 sharing the same distribution. This will differ from the setting considered in Gretton et al. [2006] in that, in our setting, the number of subjects with A = 0 and A = 1 will be treated as random, while the total number of observed subjects is fixed. This is in contrast to Gretton et al. [2006], who studied the case where the number of subjects with A = 0 and A = 1 were both fixed. This is the simplest example that we will give in this work. In particular, it is our only example in which the functions R_P and S_P do not rely on the (unknown) data generating distribution P.
• Example 2: Testing a null conditional average treatment effect.

  • If $R_P(o)\triangleq E_P(Y|A=1,W=w)-E_P(Y|A=0,W=w)$ and S_P ≡ 0, the null hypothesis corresponds to the absence of a conditional average treatment effect. This definition of R_P corresponds to the so-called blip function introduced by Robins [2004], which plays a critical role in defining optimal personalized treatment strategies [Chakraborty and Moodie, 2013].
• Example 3: Testing for equality in distribution of regression functions in two populations.

  • Suppose the setting of the previous example, but where A represents membership to population 0 or 1. If $R_P(o)\triangleq E_P(Y|A=1,W=w)$ and $S_P(o)\triangleq E_P(Y|A=0,W=w)$, the null hypothesis corresponds to the outcome having the conditional mean functions, applied to a random draw of the covariate, having the same distribution in these two populations. We note here that our formulation considers selection of individuals from either population as random rather than fixed so that population-specific sample sizes (as opposed to the total sample size) are themselves random. The same interpretation could also be used for the previous example, now testing if the two regression functions are equivalent.
• Example 4: Testing a null covariate effect on average response.

  • Suppose now that the data unit only consists of $O\triangleq (W,Y)$. If $R_P(o)\triangleq E_P(Y|W=w)$ and S_P ≡ 0, the null hypothesis corresponds to the outcome Y having conditional mean zero in all strata of covariates. This may be interesting when zero has a special importance for the outcome, such as when the outcome is the profit over some period.
• Example 5: Testing a null variable importance.

  • Suppose again that $O\triangleq (W,Y)$ and $W\triangleq (W(1),W(2),\dots ,W(K))$. Denote by W(−k) the vector (W(i) : 1 ≤ i ≤ K,i ≠ k). Setting $R_P(o)\triangleq E_P(Y|W=w)$ and $S_P(o)\triangleq E_P(Y|W(-k)=w(-k))$, the null hypothesis corresponds to W(k) having null variable importance in the presence of W(−k) with respect to the conditional mean of Y given W in the sense that E_P (Y | W) = E_P (Y | W(−k)) almost surely. This is true because if $R_0(W)\stackrel{d}{=}{S}_0(W(-k))$, the latter random variables have equal variance and so

    $$\begin{array}{lll}{E}_{P_0}\left\{Va{r}_{P_0}\left[R_0\left(W\right)|W\left(-k\right)\right]\right\}\hfill & =\hfill & Va{r}_{P_0}\left[R_0\left(W\right)\right]-Va{r}_{P_0}\left\{E_{P_0}\left[R_0\left(W\right)|W\left(-k\right)\right]\right\}\hfill \\ \hfill & =\hfill & Va{r}_{P_0}\left[R_0\left(W\right)\right]-Va{r}_{P_0}\left[S_0\left(W\left(-k\right)\right)\right]=0,\hfill \end{array}$$

    implying that $Va{r}_{P_0}[R_0(W)|W(-k)]=0$ almost surely. Thus, a test of $R_P(O)\stackrel{d}{=}{S}_P(O)$ is equivalent to a test of almost sure equality between R_P and S_P in this example. We will show in Section 5 that our approach cannot be directly applied to this example, but that a simple extension yields a valid test.

Gretton et al. [2006] investigated the related problem of testing equality between two distributions in a two-sample problem. They proposed estimating the maximum mean discrepancy (hereafter referred to as MMD), a non-negative quantitative summary of the relationship between the two distributions. In particular, the MMD between distributions P₁ and P₂ for observations X is defined as

$$\underset{f\in \mathcal{F}}{\text{sup}}\left(E_{P_1}\left[f\left(X\right)\right]-E_{P_2}\left[f\left(X\right)\right]\right).$$ (1)

Defining the MMD relies on selecting a function class $\mathcal{F}$. Gretton et al. [2006] propose selecting $\mathcal{F}$ to be the unit ball in a reproducing kernel Hilbert space. If the kernel defining this space is a so-called universal kernel and the support of X under P₁ and P₂ is compact, then they showed that the MMD is zero if and only if the two distributions are equal. They also observe that the Gaussian kernel is a universal kernel. Gretton et al. also investigated related problems using this technique [see, e.g., Gretton et al., 2009, 2012a, Sejdinovic et al., 2013]. In this work, we also utilize the MMD as a parsimonious summary of equality but consider the more general problem wherein the null hypothesis relies on unknown functions R₀ and S₀ indexed by the data-generating distribution P₀.

Other investigators have proposed omnibus tests of hypotheses of the form ${\mathcal{H}}_0$ versus ${\mathcal{H}}_1$ in the literature. In the setting of Example 2 above, the work presented in Racine et al. [2006] and Lavergne et al. [2015] is particularly relevant. The null hypothesis of interest in these papers consists of the equality $E_{P_0}(Y|A,W)=E_{P_0}(Y|W)$ holding almost surely. If individuals have a nontrivial probability of receiving treatment in all strata of covariates, this null hypothesis is equivalent to ${\mathcal{H}}_0$. In both these papers, kernel smoothing is used to estimate the required regression functions. Therefore, key smoothness assumptions are needed for their methods to yield valid conclusions. The method we present does not hinge on any particular class of estimators and therefore does not rely on this condition.

To develop our approach, we use techniques from the higher-order pathwise differentiability literature [see, e.g., Pfanzagl, 1985, Robins et al., 2008, van der Vaart, 2014, Carone et al., 2014]. Despite the elegance of the theory presented by these various authors, it has been unclear whether these higher-order methods are truly useful in infinite-dimensional models since most functionals of interest fail to be even second-order pathwise differentiable in such models. This is especially troublesome in problems in which under the null the first-order derivative of the parameter of interest (in an appropriately defined sense) vanishes, since then there seems to be no theoretical basis for adjusting parameter estimates to recover parametric rate asymptotic behavior. At first glance, the MMD parameter seems to provide one such disappointing example, since its first-order derivative indeed vanishes under the null. The latter fact is a common feature of problems wherein the null value of the parameter is on the boundary of the parameter space. It is also not an entirely surprising phenomenon, at least heuristically, since the MMD achieves its minimum of zero under the null hypothesis. Nevertheless, we are able to show that this parameter is indeed second-order pathwise differentiable under the null hypothesis – this is a rare finding in infinite-dimensional models. As such, we can employ techniques from the recent higher-order pathwise differentiability literature to tackle the problem at hand.

This paper is organized as follows. In Section 2, we formally present our parameter of interest, the squared MMD between two unknown functions, and establish asymptotic representations for this parameter based on its higher-order differentiability, which, as we formally establish, holds even when the MMD involves estimation of unknown nuisance parameters. In Section 3, we discuss estimation of this parameter, discuss the corresponding hypothesis test and study its asymptotic behavior under the null. We study the consistency of our proposed test under fixed and local alternatives in Section 4. We revisit our examples in Section 5 and provide an additional example in which we can still make progress using our techniques even though our regularity conditions fails. In Section 6, we present results from a simulation study to illustrate the finite-sample performance of our test, and we end with concluding remark in Section 7.

Supplementary Appendix A reviews higher-order pathwise differentiability. Supplementary Appendix B gives a summary of the empirical U−process results from Nolan and Pollard [1988] that we build upon. All proofs can be found in Supplementary Appendix C.

2. Properties of maximum mean discrepancy

2.1. Definition

For a distribution P and mappings T and U, we define

$${\Phi }^{TU}\left(P\right)\triangleq {\displaystyle \int {\displaystyle \int e^{-{\left[T_P\left(o_1\right)-U_P\left(o_2\right)\right]}^2}}}dP\left(o_1\right)dP\left(o_2\right)$$ (2)

and set $\Psi (P)\triangleq {\Phi }^{RR}(P)-2{\Phi }^{RS}(P)+{\Phi }^{SS}(P)$. The MMD between the distributions of R_P(O) and S_P(O) when O ~ P, defined in Eq. 1 using $\mathcal{F}$ to be the unit ball in the RKHS generated by the Gaussian kernel with unit bandwidth, is given by $\sqrt{\Psi (P)}$ and is always well-defined because Ψ(P) is non-negative. Indeed, denoting by ψ₀ the true parameter value Ψ(P₀), Theorem 3 of Gretton et al. [2006] establishes that ψ₀ equals zero if ${\mathcal{H}}_0$ holds and is otherwise strictly positive. Though the study in Gretton et al. [2006] is restricted to two-sample problems, their proof of this result is only based upon properties of Ψ and therefore holds regardless of the sample collected. Their proof relies on the fact that two random variables X and Y with compact support are equal in distribution if and only if E[f(Y)] = E[f(X)] for every continuous function f, and uses techniques from the theory of Reproducing Kernel Hilbert Spaces [see, e.g., Berlinet and Thomas-Agnan, 2011, for a general exposition]. We invite interested readers to consult Gretton et al. [2006] – and, in particular, Theorem 3 therein – for additional details. The definition of the MMD we utilize is based on the univariate Gaussian kernel with unit bandwidth, which is appropriate in view of Steinwart [2002]. The results we present in this paper can be generalized to the MMD based on a Gaussian kernel of arbitrary bandwidth h by simply rescaling the mappings R and S to R/h and S/h.

2.2. First-order differentiability

To develop a test of ${\mathcal{H}}_0$, we will first construct an estimator ψ_n of ψ₀. In order to avoid restrictive model assumptions, we wish to use flexible estimation techniques in estimating P₀ and therefore ψ₀. To control the operating characteristics of our test, it will be crucial to understand how to generate a parametric-rate estimator of ψ₀. For this purpose, it is informative to first investigate the pathwise differentiability of Ψ as a parameter from $\mathcal{M}$ to $ℝ$.

So far, we have not specified restrictions on the mappings P ↦ R_P and P ↦ S_P. However, in our developments, we will require these mappings to satisfy certain regularity conditions. Specifically, we will restrict our attention to elements of the class $\mathcal{S}$ of all mappings T for which there exists some measurable function X^T defined on $\mathcal{O}$, e.g. X^T(o) = X^T(w, a, y) = w, such that

• (S1)T_P is a measurable mapping with domain $\{X^T(o):o\in \mathcal{O}\}$ and range contained in [− b, b] for some 0 ≤ b < ∞ independent of P;
• (S2)for all submodels dP_t/dP = 1 + th with bounded h with Ph = 0, there exists some δ > 0 and a set ${\mathcal{O}}_1\subseteq \mathcal{O}$ with $P_0({\mathcal{O}}_1)=1$ such that, for all $(o,t_1)\in {\mathcal{O}}_1\times (-\delta ,\delta )$, $t\mapsto T_{P_t}(x^T)$ is twice differentiable at t₁ with uniformly bounded (in x^T) first and second derivatives;
• (S3)
  for any $P\in \mathcal{M}$ and submodel dP_t/dP = 1 + th for bounded h with Ph = 0, there exists a function $D_P^T:\mathcal{O}\to ℝ$ uniformly bounded (in P and o) such that ${\displaystyle \int D_P^T(o)dP(o|x^T)}=0$ for almost all $o\in \mathcal{O}$ and

  $${\frac{d}{dt}{T}_{P_t}\left(x^T\right)|}_{t=0}={\displaystyle \int D_P^T\left(o\right)h\left(o\right)dP\left(o|x^T\right)}.$$

Condition (S1) ensures that T is bounded and only relies on a summary measure of an observation O. Condition (S2) ensures that we will be able to interchange differentiation and integration when needed. Condition (S3) is a conditional (and weaker) version of pathwise differentiability in that the typical inner product representation only needs to hold for the conditional distribution of O given X^T under P₀. We will verify in Section 5 that these conditions hold in the context of the motivating examples presented earlier.

Remark 1. As a caution to the reader, we warn that simultaneously satisfying (S1) and (S3) may at times be restrictive. For example, if the observed data unit is $O\triangleq (W(1),W(2),Y)$, the parameter

$$T_P\left(o\right)\triangleq E_P\left[Y|W\left(1\right)=w\left(1\right),W\left(2\right)=w\left(2\right)\right]-E_P\left[Y|W\left(1\right)=w\left(1\right)\right]$$

cannot generally satisfy both conditions. In Section 5, we discuss this example further and provide a means to tackle this problem using the techniques we have developed. In concluding remarks, we discuss a weakening of our conditions, notably by replacing $\mathcal{S}$ by the linear span of elements in $\mathcal{S}$. Consideration of this larger class significantly complicates the form of the estimator we propose in Section 3. □

We are now in a position to discuss the pathwise differentiability of Ψ. For any elements $T,U\in \mathcal{S}$, we define

$${\Gamma }_P^{TU}\left(o_1,o_2\right)\triangleq \left[2\left[T_P\left(o_1\right)-U_P\left(o_2\right)\right]\left[D_P^U\left(o_2\right)-D_P^T\left(o_1\right)\right]+1-\left\{4{\left[T_P\left(o_1\right)-U_P\left(o_2\right)\right]}^2-2\right\}{D}_P^T\left(o_1\right)D_P^U\left(o_2\right)\right]e^{-{\left[T_P\left(o_1\right)-U_P\left(o_2\right)\right]}^2}.$$

and set ${\Gamma }_P\triangleq {\Gamma }_P^{RR}-{\Gamma }_P^{RS}-{\Gamma }_P^{SR}+{\Gamma }_P^{SS}$. Note that Γ_P is symmetric for any $P\in \mathcal{M}$. For brevity, we will write ${\Gamma }_0^{TU}$ and Γ₀ to denote ${\Gamma }_{P_0}^{TU}$ and ${\Gamma }_{P_0}$, respectively. The following theorem characterizes the first-order behavior of Ψ at an arbitrary $P\in \mathcal{M}$.

Theorem 1 (First-order pathwise differentiability of Ψ over $\mathcal{M}$). If $R,S\in \mathcal{S}$, the parameter $\Psi :\mathcal{M}\to ℝ$ is pathwise differentiable at $P\in \mathcal{M}$ with first-order canonical gradient given by $D_1^{\Psi }(P)(o)\triangleq 2\left[{\displaystyle \int {\Gamma }_P(o,o_2)dP(o_2)-\Psi (P)}\right]$.

Under some conditions, it is straightforward to construct an asymptotically linear estimator of ψ₀ with influence function $D_1^{\Psi }(P_0)$, that is, an estimator ψ_n of ψ₀ such that

$${\psi }_n-{\psi }_0=\frac{1}{n}{\displaystyle \sum _{i=1}^n{D}_1^{\Psi }}\left(P_0\right)\left(O_i\right)+o_{P_0}\left(n^{-1/2}\right).$$

For example, the one-step Newton-Raphson bias correction procedure [see, e.g., Pfanzagl, 1982] or targeted minimum loss-based estimation [see, e.g., van der Laan and Rose, 2011] can be used for this purpose. If the above representation holds and the variance of $D_1^{\Psi }(P_0)(O)$ is positive, then $\sqrt{n}({\psi }_n-{\psi }_0)⇝N(0,{\sigma }_0^2)$, where the symbol $⇝$ denotes convergence in distribution and we write ${\sigma }_0^2\triangleq P_0[D_1^{\Psi }{(P_0)}^2]$. If σ₀ is strictly positive and can be consistently estimated, Wald-type confidence intervals for ψ₀ with appropriate asymptotic coverage can be constructed.

The situation is more challenging if σ₀ = 0. In this case, $\sqrt{n}({\psi }_n-{\psi }_0)\to 0$ in probability and typical Wald-type confidence intervals will not be appropriate. Because $D_1^{\Psi }(P_0)(O)$ has mean zero under P₀, this happens if and only if $D_1^{\Psi }(P_0)\equiv 0$. The following lemma provides necessary and sufficient conditions under which σ₀ = 0.

Corollary 1 (First-order degeneracy under ${\mathcal{H}}_0$). If $R,S\in \mathcal{S}$, it will be the case that σ₀ = 0 if and only if either (i) ${\mathcal{H}}_0$ holds, or (ii) R₀(O) and S₀(O) are degenerate, i.e. almost surely constant but not necessarily equal, with $D_0^R\equiv D_0^S$.

The above results rely in part on knowledge of $D_0^R$ and $D_0^S$. It is useful to note that, in some situations, the computation of $D_P^T(o)$ for a given $T\in \mathcal{S}$ and $P\in \mathcal{M}$ can be streamlined. This is the case, for example, if P ↦ T_P is invariant to fluctuations of the marginal distribution of X^T, as it seems (S3) may suggest. Consider obtaining iid samples of increasing size from the conditional distribution of O given X^T = x^T under P, so that all individuals have observed X^T = x^T. Consider the fluctuation submodel $d{P}_t(o|x^T)\triangleq [1+th(o)]dP(o|x^T)$ for the conditional distribution, where h is uniformly bounded and ∫ h(o)dP(o|x^T) = 0. Suppose that (i) P ↦ T_P(x^T) is differentiable at t = 0 with respect to the above submodel and (ii) this derivative satisfies the inner product representation

$${\frac{d}{dt}{T}_{P_t}\left(x^T\right)|}_{t=0}={\displaystyle \int {\tilde{D}}_P^T}\left(o|x^T\right)h\left(o\right)dP\left(o|x^T\right)$$

for some uniformly bounded function $o\mapsto {\tilde{D}}_P^T(o|x^T)$ with ${\displaystyle \int {\tilde{D}}_P^T(o|x^T)dP(o|x^T)=0}$. If the above holds for all x^T, we may take $D_P^T(o)={\tilde{D}}_P^T(o|x^T)$ for all o with X^T(o) = x^T. If $D_P^T$ is uniformly bounded in P, (S3) then holds.

In summary, the above discussion suggests that, if T is invariant to fluctuations of the marginal distribution of X^T, (S3) can be expected to hold if there exists a regular, asymptotically linear estimator of each T_P(x^T) under iid sampling from the conditional distribution of O given X^T = x^T implied by P.

Remark 2. If T is invariant to fluctuations of the marginal distribution of X^T, one can also expect (S3) to hold if P ↦ ∫ T_P(X^T(o))dP(o) is pathwise differentiable with canonical gradient uniformly bounded in P and o in the model in which the marginal distribution of X is known. The canonical gradient in this model is equal to $D_P^T$. □

2.3. Second-order differentiability and asymptotic representation

As indicated above, if σ₀ = 0, the behavior of Ψ around P₀ cannot be adequately characterized by a first-order analysis. For this reason, we must investigate whether Ψ is second-order differentiable. As we discuss below, under ${\mathcal{H}}_0$, Ψ is indeed second-order pathwise differentiable at P₀ and admits a useful second-order asymptotic representation.

Theorem 2 (Second-order pathwise differentiability under ${\mathcal{H}}_0$). If $R,S\in \mathcal{S}$ and ${\mathcal{H}}_0$ holds, the parameter $\Psi :\mathcal{M}\to ℝ$ is second-order pathwise differentiable at P₀ with second-order canonical gradient $D_2^{\Psi }(P_0)\triangleq 2{\Gamma }_0$.

It is easy to confirm that Γ₀, and thus $D_2^{\Psi }$, is one-degenerate under ${\mathcal{H}}_0$ in the sense that ∫ Γ₀(o,o₂)dP₀(o₂) = ∫ Γ₀(o₁, o)dP₀(o₁) = 0 for all o. This is shown as follows. For any $T,U\in \mathcal{S}$, the law of total expectation conditional on X^U and fact that ${\displaystyle \int D_0^U(o)d{P}_0(o|x^U)}=0$ yields that

$${\displaystyle \int {\Gamma }_0^{TU}}\left(o,o_2\right)d{P}_0\left(o_2\right)={\displaystyle \int \left\{1-2\left[T_0\left(o\right)-U_0\left(o_2\right)\right]D_0^T\left(o\right)\right\}}{e}^{-{\left[T_0\left(o\right)-U_0\left(o_2\right)\right]}^2}d{P}_0\left(o_2\right),$$

where we have written ${\Gamma }_0^{TU}$ to denote ${\Gamma }_{P_0}^{TU}$. Since ∫ f(R₀(o))dP₀(o) = ∫ f(S₀(o))dP₀(o) for each measurable function f when $S_0(O)\stackrel{d}{=}{T}_0(O)$, this then implies that ${\displaystyle \int {\Gamma }_0^{RS}(o,o_2)d{P}_0(o_2)}={\displaystyle \int {\Gamma }_0^{RR}(o,o_2)dP(o_2)}$ and ${\displaystyle \int {\Gamma }_0^{SR}(o,o_2)d{P}_0(o_2)}={\displaystyle \int {\Gamma }_0^{SS}(o,o_2)d{P}_0(o_2)}$ under ${\mathcal{H}}_0$. Hence, it follows that ∫ Γ₀(o, o₂)dP₀(o₂) = 0 under ${\mathcal{H}}_0$ for any o.

If second-order pathwise differentiability held in a sufficiently uniform sense over $\mathcal{M}$, we would expect

$${\text{Rem}}_P^{\Psi }\triangleq \Psi \left(P\right)-\Psi \left(P_0\right)-\left(P-P_0\right)D_1^{\Psi }\left(P\right)+\frac{1}{2}{\left(P-P_0\right)}^2{D}_2^{\Psi }\left(P\right)$$ (3)

to be a third-order remainder term. However, second-order pathwise differentiability has only been established under the null, and in fact, it appears that Ψ may not generally be second-order pathwise differentiable under the alternative. As such, $D_2^{\Psi }$ may not even be defined under the alternative. In writing (3), we either naively set $D_2^{\Psi }(P)\triangleq 2{\Gamma }_P$, which is not appropriately centered to be a candidate second-order gradient, or instead take $D_2^{\Psi }$ to be the centered extension

$$\left(o_1,o_2\right)\mapsto 2\left[{\Gamma }_P\left(o_1,o_2\right)-{\displaystyle \int {\Gamma }_P\left(o_1,o\right)dP\left(o\right)}-{\displaystyle \int {\Gamma }_P\left(o,o_2\right)dP\left(o\right)}+P^2{\Gamma }_P\right].$$

Both of these choices yield the same expression above because the product measure (P − P₀)² is self-centering. The need for an extension renders it a priori unclear whether as P tends to P₀ the behavior of ${\text{Rem}}_P^{\Psi }$ is similar to what is expected under more global second-order pathwise differentiability. Using the fact that Ψ(P) = P²Γ_P, we can simplify the expression in (3) to

$${\text{Rem}}_P^{\Psi }=P_0^2{\Gamma }_P-{\psi }_0.$$ (4)

As we discuss below, this remainder term can be bounded in a useful manner, which allows us to determine that it is indeed third-order.

For all $T\in \mathcal{S}$, $P\in \mathcal{M}$ and $o\in \mathcal{O}$, we define

$${\text{Rem}}_P^T\left(o\right)\triangleq T_P\left(o\right)-T_0\left(o\right)+{\displaystyle \int D_P^T\left(o_1\right)}\left[dP\left(o_1|x^T\right)-d{P}_0\left(o_1|x^T\right)\right]$$

as the remainder from the linearization of T based on the conditional gradient $D_P^T$. Typically, ${\text{Rem}}_P^T(o)$ is a second-order term. Further consideration of this term in the context of our motivating examples is described in Section 5. Furthermore, we define

$$\begin{array}{lll}{L}_P^{RS}\left(o\right)\hfill & \triangleq \hfill & \text{max}\left\{\left|{\text{Rem}}_P^R\left(o\right)\right|,\left|{\text{Rem}}_P^S\left(o\right)\right|\right\}\hfill \\ M_P^{RS}\left(o\right)\hfill & \triangleq \hfill & \text{max}\left\{\left|R_P\left(o\right)-R_0\left(o\right)\right|,\left|S_P\left(o\right)-S_0\left(o\right)\right|\right\}.\hfill \end{array}$$

For any given function $f:\mathcal{O}\to ℝ$, we denote by ${\Vert f\Vert }_{p,P_0}\triangleq {\left[{\displaystyle \int |f(o){|}^{p}d{P}_0(o)}\right]}^{1/p}$ the L^p(P₀)-norm and use the symbol ≲ to denote ‘less than or equal to up to a positive multiplicative constant’. The following theorem provides an upper bound for the remainder term of interest.

Theorem 3 (Upper bounds on remainder term). For each $P\in \mathcal{M}$, the remainder term, admits the following upper bounds:

$$\begin{array}{l}Under{\mathcal{H}}_0:\left|{\text{Rem}}_P^{\Psi }\right|\lesssim K_{0P}\triangleq {\Vert L_P^{RS}\Vert }_{2,P_0}{\Vert M_P^{RS}\Vert }_{2,P_0}+{\Vert L_P^{RS}\Vert }_{1,P_0}^2+{\Vert M_P^{RS}\Vert }_{4,P_0}^4\\ Under{\mathcal{H}}_1:\left|{\text{Rem}}_P^{\Psi }\right|\lesssim K_{1P}\triangleq {\Vert L_P^{RS}\Vert }_{1,P_0}{\Vert M_P^{RS}\Vert }_{2,P_0}^2.\end{array}$$

To develop a test procedure, we will require an estimator of P₀, which will play the role of P in the above expressions. It is helpful to think of parametric model theory when interpreting the above result, with the understanding that certain smoothing methods, such as higher-order kernel smoothing, can achieve near-parametric rates in certain settings. In a parametric model where P₀ is estimated with ${\widehat{P}}_n$ (e.g., a maximum likelihood estimator), we could often expect $\parallel L_{{\widehat{P}}_n}^{RS}{\parallel }_{p,P_0}$ and $\parallel M_{{\widehat{P}}_n}^{RS}{\parallel }_{p,P_0}$ to be $O_{P_0}\left(n^{-1}\right)$ and $O_{P_0}\left(n^{-1/2}\right)$, respectively, for p ≥ 1. Thus, the above theorem suggests that the approximation error may be $O_{P_0}(n^{-3/2})$ in a parametric model under ${\mathcal{H}}_0$. In some examples, it is reasonable to expect that $L_{{\widehat{P}}_n}^{RS}\equiv 0$ for a large class of distributions P. In such cases, the upper bound on ${\text{Rem}}_{{\widehat{P}}_n}^{\Psi }$ simplifies to $\parallel M_{{\widehat{P}}_n}^{RS}{\parallel }_{4,P_0}^4$ under ${\mathcal{H}}_0$, which under a parametric model is often $O_{P_0}(n^{-2})$.

To make these results more concrete, we consider the special case where R_P, S_P, $D_P^R$, and $D_P^S$ are smooth mappings of regression functions under P conditional on the d−dimensional covariate W (e.g., as in Example 3 – see Section 5). Suppose that all of these regression functions under P₀ are at least ℓ−times differentiable. In this case, rates of convergence for the remainder terms are well understood for kernel smoothers using kernels of sufficiently high order. In particular, each regression function converges at rate $n^{-\frac{\ell }{2\ell +d}}$ in L²(P₀). Under ${\mathcal{H}}_0$, one could rely on $\parallel M_{{\widehat{P}}_n}^{RS}{\parallel }_{2,P_0}$ being $o_{P_0}(n^{-1/3})$ and $\parallel L_{{\widehat{P}}_n}^{RS}{\parallel }_{2,P_0}$ being $o_{P_0}(n^{-2/3})$. If $L_{{\widehat{P}}_n}^{RS}$ is second-order, this would generally require ℓ > d, which is more stringent than the usual ℓ > d/2 requirement for standard first-order estimators. If, on the other hand, $L_{{\widehat{P}}_n}^{RS}\equiv 0$, then we require that $\parallel M_{{\widehat{P}}_n}^{RS}{\parallel }_{4,P_0}^4$ is $o_{P_0}(n^{-1})$ under ${\mathcal{H}}_0$, which corresponds to requiring ℓ slightly greater than d/2.

3. Proposed test: formulation and inference under the null

3.1. Formulation of test

We begin by constructing an estimator of ψ₀ from which a test can then be devised. Using the fact that Ψ(P) = P²Γ_P, as implied by (4), we note that if Γ₀ were known, the U-statistic ${\mathbb{U}}_n{\Gamma }_0$ would be a natural estimator of ψ₀, where ${\mathbb{U}}_n$ denotes the empirical measure that places equal probability mass on each of the n(n − 1) points (O_i, O_j) with i ≠ j. In practice, Γ₀ is unknown and must be estimated. This leads to the estimator ${\psi }_n\triangleq {\mathbb{U}}_n{\Gamma }_n$, where we write ${\Gamma }_n\triangleq {\Gamma }_{{\widehat{P}}_n}$ for some estimator ${\widehat{P}}_n$ of P₀ based on the available data. Since a large value of ψ_n is inconsistent with ${\mathcal{H}}_0$, we will reject ${\mathcal{H}}_0$ if and only if ψ_n > c_n for some appropriately chosen cutoff c_n.

In the nonparametric model considered, it may be necessary, or at the very least desirable, to utilize a data-adaptive estimator ${\widehat{P}}_n$ of P₀ when constructing Γ_n. Studying the large-sample properties of ψ_n may then seem particularly daunting since at first glance we may be led to believe that the behavior of ψ_n – ψ₀ is dominated by $P_0^2({\Gamma }_n-{\Gamma }_0)$. However, this is not the case. As we will see, under some conditions, ψ_n – ψ₀ will approximately behave like $({\mathbb{U}}_n-P_0^2){\Gamma }_0$. Thus, there will be no contribution of ${\widehat{P}}_n$ to the asymptotic behavior of ψ_n – ψ₀. Though this result may seem counterintuitive, it arises because Ψ(P) can be expressed as P²Γ_P with Γ_P a second-order gradient (or rather an extension thereof) up to a proportionality constant. More concretely, this surprising finding is a direct consequence of (4).

As further support that ψ_n is a natural test statistic, even when a data-adaptive estimator ${\widehat{P}}_n$ of P₀ has been used, we note that ψ_n could also have been derived using a second-order one-step Newton-Raphson construction, as described in Robins et al. [2008]. The latter is given by

$${\psi }_{n,NR}\triangleq \Psi \left({\widehat{P}}_n\right)+P_n{D}_1^{\Psi }\left({\widehat{P}}_n\right)+\frac{1}{2}{\mathbb{U}}_n{D}_2^{\Psi }\left({\widehat{P}}_n\right),$$

where we use the centered extension of $D_2^{\Psi }$ as discussed in Section 2.3. Here and throughout, P_n denotes the empirical distribution. It is straightforward to verify that indeed ψ_n = ψ_n,NR.

3.2. Inference under the null

3.2.1. Asymptotic behavior

For each $P\in \mathcal{M}$, we let ${\tilde{\Gamma }}_P$ be the P₀−centered modification of Γ_P given by

$${\tilde{\Gamma }}_P\left(o_1,o_2\right)\triangleq {\Gamma }_P\left(o_1,o_2\right)-{\displaystyle \int {\Gamma }_P\left(o_1,o\right)d{P}_0\left(o\right)}-{\displaystyle \int {\Gamma }_P\left(o,o_2\right)d{P}_0\left(o\right)}+P_0^2{\Gamma }_P$$

and denote ${\tilde{\Gamma }}_{P_0}$ by ${\tilde{\Gamma }}_0$. While ${\tilde{\Gamma }}_0={\Gamma }_0$ under ${\mathcal{H}}_0$, this is not true more generally. Below, we use ${\text{Rem}}_n^{\Psi }$ and ${\tilde{\Gamma }}_n$ to respectively denote ${\text{Rem}}_P^{\Psi }$ and ${\tilde{\Gamma }}_P$ evaluated at $P={\widehat{P}}_n$. Straightforward algebraic manipulations allows us to write

$$\begin{array}{lll}{\psi }_n-{\psi }_0\hfill & =\hfill & {\mathbb{U}}_n{\Gamma }_n-{\psi }_0={\mathbb{U}}_n{\Gamma }_n-P_0^2{\Gamma }_n+P_0^2{\Gamma }_n-{\psi }_0\hfill \\ \hfill & =\hfill & \left({\mathbb{U}}_n-P_0^2\right){\Gamma }_n+{\text{Rem}}_n^{\Psi }\hfill \\ \hfill & =\hfill & {\mathbb{U}}_n{\Gamma }_0+2\left(P_n-P_0\right)P_0{\Gamma }_n+{\mathbb{U}}_n\left({\tilde{\Gamma }}_n-{\Gamma }_0\right)+{\text{Rem}}_n^{\Psi }.\hfill \end{array}$$ (5)

Our objective is to show that n (ψ_n – ψ₀) behaves like $n{\mathbb{U}}_n{\Gamma }_0$ as n gets large under ${\mathcal{H}}_0$. In view of (5), this will be true, for example, under conditions ensuring that

• C1)$n(P_n-P_0)P_0{\Gamma }_n=o_{P_0}(1)$ (empirical process and consistency conditions);
• C2)$n{\mathbb{U}}_n\left({\tilde{\Gamma }}_n-{\Gamma }_0\right)=o_{P_0}(1)$ (U−process and consistency conditions);
• C3)$n{\text{Rem}}_n^{\Psi }=o_{P_0}(1)$ (consistency and rate conditions).

We have already argued that C3) is reasonable in many examples of interest, including those presented in this paper. Nolan and Pollard [1987, 1988] developed a formal theory that controls terms of the type appearing in C2). In Supplementary Appendix B.1 we restate specific results from these authors which are useful to study C2). Finally, the following lemma gives sufficient conditions under which C1) holds. We first set $K_{1n}\triangleq \parallel L_{{\widehat{P}}_n}^{RS}{\parallel }_{1,P_0}+\parallel M_{{\widehat{P}}_n}^{RS}{\parallel }_{2,P_0}^2$.

Lemma 1 (Sufficient conditions for C1)). Suppose that o₁ ↦ ∫ Γ_n(o₁, o)dP₀(o)/K_1n, defined to be zero if K_1n = 0, belongs to a P₀−Donsker class [van der Vaart and Wellner, 1996] with probability tending to 1. Then, under ${\mathcal{H}}_0$,

$$\left(P_n-P_0\right)P_0{\Gamma }_n=O_{P_0}\left(\frac{K_{1n}}{\sqrt{n}}\right)$$

and thus C1) holds whenever $K_{1n}=o_{P_0}(n^{-1/2})$.

The following theorem describes the asymptotic distribution of nψ_n under the null hypothesis whenever conditions C1), C2) and C3) are satisfied.

Theorem 4 (Asymptotic distribution under ${\mathcal{H}}_0$). Suppose that C1), C2) and C3) hold. Then, under ${\mathcal{H}}_0$,

$$n{\psi }_n=n{\mathbb{U}}_n{\Gamma }_0+o_{P_0}\left(1\right)⇝{\displaystyle \sum _{k=1}^{\infty }{\lambda }_k\left(Z_k^2-1\right)},$$

where ${\left\{{\lambda }_k\right\}}_{k=1}^{\infty }$ are the eigenvalues of the integral operator h(o) ↦ ∫ Γ₀ (o₁, o)h(o₁)dP₀(o₁) repeated according to their multiplicity, and ${\left\{Z_k\right\}}_{k=1}^{\infty }$ is a sequence of independent standard normal random variables. Furthermore, all of these eigenvalues are nonnegative under ${\mathcal{H}}_0$.

We note that by employing a sample splitting procedure – namely, estimating Γ₀ on one portion of the sample and constructing the U−statistic based on the remainder of the sample – it is possible to eliminate the U−process conditions required for C2). In such a case, satisfaction of C2) only requires convergence of ${\tilde{\Gamma }}_n$ to Γ₀ with respect to the $L^2(P_0^2)$-norm. This sample splitting procedure would also allow one to avoid the empirical process conditions in C1): in particular, o ↦ P₀Γ_n(o, ·) would need to converge to zero, but no further requirements would then be needed on Γ_n for C1) to be satisfied. We also note that the L²(P₀) consistency of o ↦ P₀Γ_n(o, ·) and the $L^2(P_0^2)$ consistency of ${\tilde{\Gamma }}_n$ are implied by the $L^2(P_0^2)$ consistency of Γ_n for Γ₀, and so when sample splitting is used one could replace C1) and C2) by this single consistency condition.

We note also that, if sample splitting is not used, then one could replace C1) and C2) by this single consistency condition and the added assumption that Γ_n belongs to a class with a finite uniform entropy integral. See Supplementary Appendix B.2 for a proof that this suffices to imply the needed empirical process conditions for C1). It is also straightforward to show that controlling the entropy of the class to which Γ_n may belong also controls the entropy of the class to which the linear transformation ${\tilde{\Gamma }}_n$ of Γ_n may belong.

Remark 3. In Example 4, sample splitting may prove particularly important when the estimator of $E_{P_0}(Y|W=w)$ is chosen as the minimizer of an empirical risk since in finite samples the bias induced by using the same residuals $y-E_{{\widehat{P}}_n}(Y|W=w)$ as those in the definition of $D_{{\widehat{P}}_n}^R(o)$ may be significant. Thus, without some form of sample splitting, the finite sample performance of ψ_n may be poor even under the conditions stated in Supplementary Appendix B.1. □

3.2.2. Estimation of the test cutoff

As indicated above, our test consists of rejecting ${\mathcal{H}}_0$ if and only if ψ_n is larger than some cutoff c_n. We wish to select c_n to yield a non-conservative test at level α ∈ (0,1). In view of Theorem 4, denoting by q_1−α the 1 – α quantile of the described limit distribution, the cutoff c_n should be chosen to be q_1−α/n. We thus reject ${\mathcal{H}}_0$ if and only if nψ_n > q_1−α. As described in the following corollary, q_1−α admits a very simple form when S_P ≡ 0 for all P.

Corollary 2 (Asymptotic distribution under ${\mathcal{H}}_0$, S degenerate). Suppose that C1), C2) and C3) hold, that S_P ≡ 0 for all $P\in \mathcal{M}$, and that ${\sigma }_R^2\triangleq Va{r}_{P_0}[D_0^R(O)]>0$. Then, under ${\mathcal{H}}_0$,

$$\frac{n{\psi }_n}{2{\sigma }_R^2}⇝Z^2-1,$$

where Z is a standard normal random variable. It follows then that $q_{1-\alpha }=2{\sigma }_R^2(z_{1-\alpha /2}^2-1)$, where z_1−α/2 is the (1 − α/2) quantile of the standard normal distribution.

The above corollary gives an expression for q_1−α that can easily be consistently estimated from the data. In particular, one can use ${\widehat{q}}_{1-\alpha }\triangleq 2(z_{1-\alpha /2}^2-1)P_n{D}^R{({\widehat{P}}_n)}^2$ as an estimator of q_1−α, whose consistency can be established under a Glivenko-Cantelli and consistency condition on the estimator of $D_0^R$. However, in general, such a simple expression will not exist. Gretton et al. [2009] proposed estimating the eigenvalues ν_k of the centered Gram matrix and then computing ${\widehat{\lambda }}_k\triangleq {\nu }_k/n$. In our context, the eigenvalues ν_k are those of the n × n matrix $G\triangleq {\left\{G_{ij}\right\}}_{1\le i,j\le n}$ with entries defined as

$$G_{ij}\triangleq {\Gamma }_n\left(O_i,O_j\right)-\frac{1}{n}{\displaystyle \sum _{k=1}^n{\Gamma }_n\left(O_k,O_j\right)}-\frac{1}{n}{\displaystyle \sum _{\ell =1}^n{\Gamma }_n\left(O_i,O_{\ell }\right)}+\frac{1}{n^2}{\displaystyle \sum _{k=1}^n{\displaystyle \sum _{\ell =1}^n{\Gamma }_n\left(O_k,O_{\ell }\right)}}.$$ (6)

Given these n eigenvalue estimates ${\widehat{\lambda }}_1,\dots ,{\widehat{\lambda }}_n$, one could then simulate from ${\displaystyle {\sum }_{k=1}^n{\widehat{\lambda }}_k(Z_k^2-1)}$ to approximate ${\displaystyle {\sum }_{k=1}^{\infty }{\lambda }_k(Z_k^2-1)}$. While this seems to be a plausible approach, a formal study establishing regularity conditions under which this procedure is valid is beyond the scope of this paper. We note that it also does not fall within the scope of results in Gretton et al. [2009] since their kernel does not depend on estimated nuisance parameters. We refer the reader to Franz [2006] for possible sufficient conditions under which this approach may be valid. Though we do not have formal regularity conditions under which this procedure is guaranteed to maintain the type I error level, our simulation results do seem to suggest appropriate control in practice (Section 6).

In practice, it suffices to give a data-dependent asymptotic upper bound on q_1−α. We will refer to ${\widehat{q}}_{1-\alpha }^{ub}$, which depends on P_n, as an asymptotic upper bound of q_1−α if

$$\underset{n\to \infty }{\text{lim}\text{sup}}{P}_0^n\left(n{\psi }_n>{\widehat{q}}_{1-\alpha }^{ub}\right)\le 1-\alpha .$$ (7)

If q_1−α is consistently estimated, one possible choice of ${\widehat{q}}_{1-\alpha }^{ub}$ is this estimate of q_1−α – the inequality above would also become an equality provided the conclusion of Theorem 4 holds. It is easy to derive a data-dependent upper bound with this property using Chebyshev’s inequality. To do so, we first note that

$$Va{r}_{P_0}\left[{\displaystyle \sum _{k=1}^{\infty }{\lambda }_k\left(Z_k^2-1\right)}\right]={\displaystyle \sum _{k=1}^{\infty }{\lambda }_k^{2}Va{r}_{P_0}}\left(Z_k^2\right)=2{\displaystyle \sum _{k=1}^{\infty }{\lambda }_k^2}=2P_0^2{\Gamma }_0^2,$$

where we have interchanged the variance operation and the limit using the L² martingale convergence theorem and the last equality holds because λ_k, k = 1, 2,…, are the eigenvalues of the Hilbert-Schmidt integral operator with kernel ${\tilde{\Gamma }}_0$. Under mild regularity conditions, $P_0^2{\Gamma }_0^2$ can be consistently estimated using ${\mathbb{U}}_n{\Gamma }_n^2$. Provided $P_0^2{\Gamma }_0^2>0$, we find that

$${\left(2{\mathbb{U}}_n{\Gamma }_n^2\right)}^{-1/2}n{\psi }_n⇝{\left(2P_0^2{\Gamma }_0^2\right)}^{-1/2}{\displaystyle \sum _{k=1}^{\infty }{\lambda }_k\left(Z_k^2-1\right)},$$ (8)

where the limit variate has mean zero and unit variance. The following theorem gives a valid choice of ${\widehat{q}}_{1-\alpha }^{ub}$.

Theorem 5. Fix α ∈ (0, 1) and suppose that C1), C2) and C3) hold. Then, under ${\mathcal{H}}_0$ and provided ${\mathbb{U}}_n{\Gamma }_n^2\to P_0^2{\Gamma }_0^2>0$ in probability, ${\widehat{q}}_{1-\alpha }^{ub}\triangleq {(2[1-\alpha ]{\mathbb{U}}_n{\Gamma }_n^2/\alpha )}^{1/2}\ge q_{1-\alpha }$ is a valid upper bound in the sense of (7).

The proof of the result follows immediately by noting that P(X > t) ≤ (1 + t²)⁻¹ for any random variable X with mean zero and unit variance in view of the one-sided Chebyshev’s inequality. For α = 0.05, the above demonstrates that a conservative cutoff is $6.2\cdot {({\mathbb{U}}_n{\Gamma }_n^2)}^{1/2}$. This theorem illustrates concretely that we can obtain a consistent test that controls type I error. In practice, we recommend either using the result of Corollary 2 whenever possible or estimating the eigenvalues of the matrix in (6).

We note that the condition ${\sigma }_R^2>0$ holds in many but not all examples of interest. Fortunately, the plausibility of this assumption can be evaluated analytically. In Section 5, we show that this condition does not hold in Example 5 and provide a way forward despite this.

4. Asymptotic behavior under the alternative

4.1. Consistency under a fixed alternative

We present two analyses of the asymptotic behavior of our test under a fixed alternative. The first relies on ${\widehat{P}}_n$ providing a good estimate of P₀. Under this condition, we give an interpretable limit distribution that provides insight into the behavior of our estimator under the alternative. As we show, surprisingly, ${\widehat{P}}_n$ need not be close to P₀ to obtain an asymptotically consistent test, even if the resulting estimate of ψ₀ is nowhere near the truth. In the second analysis, we give more general conditions under which our test will be consistent if ${\mathcal{H}}_1$ holds.

4.1.1. Nuisance functions have been estimated well

As we now establish, our test has power against all alternatives P₀ except for the fringe cases discussed in Corollary 1 with Γ₀ one-degenerate. We first note that

$${\psi }_n-{\psi }_0={\mathbb{U}}_n{\Gamma }_n-{\psi }_0=2\left(P_n-P_0\right)P_0{\Gamma }_n+{\mathbb{U}}_n{\tilde{\Gamma }}_n+{\text{Rem}}_P^{\Psi }.$$

When scaled by $\sqrt{n}$, the leading term on the right-hand side follows a mean zero normal distribution under regularity conditions. The second summand is typically $O_{P_0}(n^{-1})$ under certain conditions, for example, on the entropy of the class of plausible realizations of the random function (o₁, o₂) ↦ Γ_n(o₁, o₂) [Nolan and Pollard, 1987, 1988]. In view of the second statement in Theorem 3, the third summand is a second-order term that will often be negligible, even after scaling by $\sqrt{n}$. As such, under certain regularity conditions, the leading term in the representation above determines the asymptotic behavior of ψ_n, as described in the following theorem.

Theorem 6 (Asymptotic distribution under ${\mathcal{H}}_1$). Suppose that $K_{1n}=o_{P_0}(n^{-1/2})$, that ${\mathbb{U}}_n{\tilde{\Gamma }}_n=o_{P_0}(n^{-1/2})$, and furthermore, that o ↦ ∫ Γ_n(o₁, o)dP₀(o) belongs to a fixed P₀−Donsker class with probability tending to 1 while $\parallel P_0({\Gamma }_n-{\Gamma }_0){\parallel }_{2,P_0}=o_{P_0}(1)$. If ${\mathcal{H}}_1$ holds, we have that $\sqrt{n}({\psi }_n-{\psi }_0)⇝N(0,{\tau }^2)$, where ${\tau }^2\triangleq 4Va{r}_{P_0}\left[{\displaystyle \int {\Gamma }_0(O,o)d{P}_0(o)}\right]$.

In view of the results of Section 2, τ² coincides with ${\sigma }_0^2$, the efficiency bound for regular, asymptotically linear estimators in a nonparametric model. Hence, ψ_n is an asymptotically efficient estimator of ψ₀ under ${\mathcal{H}}_1$. Sufficient conditions for ∫ Γ_n(o₁, o)dP₀(o) to belong to a fixed P₀−Donsker class with probability approaching one are given in Supplementary Appendix B.2.

The following corollary is trivial in light of Theorem 6. It establishes that the test $n{\psi }_n>{\widehat{q}}_{1-\alpha }^{ub}$ is consistent against (essentially) all alternatives provided the needed components of the likelihood are estimated sufficiently well.

Corollary 3 (Consistency under a fixed alternative). Suppose the conditions of Theorem 6. Furthermore, suppose that τ² > 0 and ${\widehat{q}}_{1-\alpha }^{ub}=o_{P_0}(n)$. Then, under ${\mathcal{H}}_1$, the test $n{\psi }_n>{\widehat{q}}_{1-\alpha }^{ub}$ is consistent in the sense that

$$\underset{n\to \infty }{\text{lim}}{P}_0^n\left(n{\psi }_n>{\widehat{q}}_{1-\alpha }^{ub}\right)=1.$$

The requirement that ${\widehat{q}}_{1-\alpha }^{ub}=o_{P_0}(n)$ is very mild given that q_1−α will be finite whenever $R,S\in \mathcal{S}$. As such, we would not expect ${\widehat{q}}_{1-\alpha }^{ub}$ to get arbitrarily large as sample size grows, at least beyond the extent allowed by our corollary. This suggests that most non-trivial upper bounds satisfying (7) will yield a consistent test.

4.1.2. Nuisance functions have not been estimated well

We now consider the case where the nuisance functions are not estimated well, in the sense that the consistency conditions of Theorem 6 do not hold. In particular, we argue that failure of these conditions does not necessarily undermine the consistency of our test. Let ${\widehat{q}}_{1-\alpha }^{ub}$ be the estimated cutoff for our test, and suppose that ${\widehat{q}}_{1-\alpha }^{ub}=o_{P_0}(n)$. Suppose also that $P_0^2{\Gamma }_n$ is asymptotically bounded away from zero in the sense that, for some δ > 0, $P_0^n\left(P_0^2{\Gamma }_n>\delta \right)$ tends to one. This condition is reasonable given that $P_0^2{\Gamma }_0>0$ if ${\mathcal{H}}_1$ holds and ${\widehat{P}}_n$ is nevertheless a (possibly inconsistent) estimator of P₀. Assuming that $({\mathbb{U}}_n-P_0^2){\Gamma }_n=O_{P_0}(n^{-1/2})$, which is true under entropy conditions on Γ_n [Nolan and Pollard, 1987, 1988], we have that

$$P_0^n\left(n{\psi }_n>{\widehat{q}}_{1-\alpha }^{ub}\right)=P_0^n\left(\sqrt{n}[{\mathbb{U}}_n-P_0^2]{\Gamma }_n>\frac{{\widehat{q}}_{1-\alpha }^{ub}}{\sqrt{n}}-\sqrt{n}{P}_0^2{\Gamma }_n\right)\to 1.$$

We have accounted for the random $n^{-1/2}{\widehat{q}}_{1-\alpha }^{ub}$ term as in the proof of Corollary 3. Of course, this result is less satisfying than Theorem 6, which provides a concrete limit distribution.

4.2. Consistency under a local alternative

We consider local alternatives of the form

$$d{Q}_n(o)=\left[1+n^{-1/2}{h}_n(o)\right]d{P}_0(o),$$

where h_n → h in ${\Gamma }_0^2(P_0)$ for some non-degenerate h and P₀ satisfies the null hypothesis ${\mathcal{H}}_0$. Suppose that the conditions of Theorem 4 hold. By Theorem 2.1 of Gregory [1977], we have that

$$n{\mathbb{U}}_n{\Gamma }_0\stackrel{Q_n}{⇝}{\displaystyle \sum _{k=1}^{\infty }{\lambda }_k\left[{(Z_k+\langle f_k,h\rangle )}^2-1\right]},$$

where ${\mathbb{U}}_n$ is the U−statistic empirical measure from a sample of size n drawn from Q_n, 〈·, ·〉 is the inner product in L²(P₀), Z_k and λ_k are as in Theorem 4, and f_k is a normalized eigenfunction corresponding to eigenvalue λ_k described in Theorem 4. By the contiguity of Q_n, the conditions of Theorem 4 yield that the result above also holds with ${\mathbb{U}}_n{\Gamma }_0$ replaced by ${\mathbb{U}}_n{\Gamma }_n$, our estimator applied to a sample of size n drawn from Q_n.

If each λ_k is non-negative, the limiting distribution under Q_n stochastically dominates the asymptotic distribution under P₀, and furthermore, if 〈f_k, h〉 ≠ 0 for some k with λ_k > 0, this dominance is strict. It is straightforward to show that, under the conditions of Theorem 4, the above holds if and only if $\text{lim}{\text{inf}}_n\sqrt{n}\Psi (Q_n)>0$, that is, if the sequence of alternatives is not too hard. Suppose that ${\widehat{q}}_{1-\alpha }$, is a consistent estimate of q_1−α. By Le Cam’s third lemma, ${\widehat{q}}_{1-\alpha }$, is consistent for q_1−α even when the estimator is computed on samples of size n drawn from Q_n rather than P₀. This proves the following theorem.

Theorem 7 (Consistency under a local alternative). Suppose that the conditions of Theorem 4 hold. Then, under ${\mathcal{H}}_0$ and provided lim $\text{lim}{\text{inf}}_{n\to \infty }\sqrt{n}\Psi (Q_n)>0$, the proposed test is locally consistent in the sense that ${\text{lim}}_{n\to \infty }{Q}_n(n{\psi }_n>{\widehat{q}}_{1-\alpha })>\alpha$, where ${\widehat{q}}_{1-\alpha }$ is a consistent estimator of q_1−a.

5. Illustrations

We now return to Examples 2, 3, 4, and 5. We do not return to Example 1 because it has already been well-studied, e.g. the fixed sample size variant was studied in detail in Gretton et al. [2006]. We first show that Examples 2, 3 and 4 satisfy the regularity conditions described in Section 2. Specifically, we show that all involved parameters R and S belong to $\mathcal{S}$ under reasonable conditions. Furthermore, we determine explicit remainder terms for the asymptotic representation used in each example and describe conditions under which these remainder terms are negligible. For any $T\in \mathcal{S}$, we will use the shorthand notation ${\dot{T}}_{\tilde{t}}(x^T)\triangleq \frac{d}{dt}{T}_{P_t}(x^T){|}_{t=\tilde{t}}$ for $\tilde{t}$ in a neighborhood of zero.

Example 2 (Continued).

The parameter S with S_P ≡ 0 belongs to $\mathcal{S}$ trivially, with $D_P^S\equiv 0$. Condition (S1) holds with x^R(o) = w. Condition (S2) holds using that R_t(w) equals

$${\displaystyle \sum _{a=0}^1{(-1)}^{a+1}}{\displaystyle \int y\left\{\frac{1+t{h}_1(w,a,y)+t^2{h}_2(w,a,y)}{1+t{E}_{P_0}[h_1(w,A,Y)]+t^2{E}_{P_0}[h_2(w,A,Y)]}\right\}}d{P}_0(y|a,w).$$ (9)

Since we must only consider h₁ and h₂ uniformly bounded, for t sufficiently small, we see that R_t(w) is twice continuously differentiable with uniformly bounded derivatives. Condition (S3) is satisfied by

$$D_P^R(o)\triangleq \frac{2a-1}{P(A=a|W=w)}\{y-E_P[Y|A=a,W=w]\}$$

and $D_P^S\equiv 0$. If min_a P (A = a | W) is bounded away from zero with probability 1 uniformly in P, it follows that $(P,o)\mapsto D_P^R(o)$ is uniformly bounded.

Clearly, we have that ${\text{Rem}}_P^S\equiv 0$. We can also verify that ${\text{Rem}}_P^R(o)$ equals

$${\displaystyle \sum _{\tilde{a}=0}^1{(-1)}^{\tilde{a}}{E}_{P_0}\left\{\left[1-\frac{P_0(A=\tilde{a}|W)}{P(A=\tilde{a}|W)}\right]\times [E_P(Y|A,W)-E_{P_0}(Y|A,W)]|A=\tilde{a},W=w\right\}}.$$

The above remainder is double robust in the sense that it is zero if either the treatment mechanism (i.e., the probability of A given W) or the outcome regression (i.e., the expected value of Y given A and W) is correctly specified under P. In a randomized trial where the treatment mechanism is known and specified correctly in P, we have that ${\text{Rem}}_P^R\equiv 0$ and thus $L_P^{RS}\equiv 0$. More generally, an upper bound for ${\text{Rem}}_P^R$ can be found using the Cauchy-Schwarz inequality to relate the rate of $\parallel {\text{Rem}}_P^R{\parallel }_{2,P_0}$ to the product of the L²(P₀)-norm for the difference between each of the treatment mechanism and the outcome regression under P and P₀.

Example 3 (Continued).

For (S1) we take x^R = x^S = w. Condition (S2) can be verified using an expression similar to that in (9). Condition (S3) is satisfied by

$$\begin{array}{lll}{D}_P^R(o)\hfill & \triangleq \hfill & \frac{a}{P(A=a|W=w)}[y-E_P(Y|A=a,W=w)]\hfill \\ D_P^S(o)\hfill & \triangleq \hfill & \frac{1-a}{P(A=a|W=w)}[y-E_P(Y|A=a,W=w)].\hfill \end{array}$$

If min_a P (A = a | W) is bounded away from zero with probability 1 uniformly in P, both $(P,o)\mapsto D_P^R(o)$ and $(P,o)\mapsto D_P^S(o)$ are uniformly bounded.

Similarly to Example 2, we have that ${\text{Rem}}_P^R(o)$ is equal to

$$E_{P_0}\left\{\left[1-\frac{P_0(A=1|W)}{P(A=1|W)}\right][E_P(Y|A,W)-E_{P_0}(Y|A,W)]|A=1,W=w\right\}.$$

The remainder ${\text{Rem}}_P^S(o)$ is equal to the above display but with A = 1 replaced by A = 0. The discussion about the double robust remainder term from Example 2 applies to these remainders as well.

Example 4 (Continued).

The parameter S is the same as in Example 2. The parameter R satisfies (S1) with x^R(o) = w and (S2) by an identity analogous to that used in Example 2. Condition (S3) is satisfied by $D_P^R(o)\triangleq y-E_P(Y|W=w)$. By the bounds on Y, $(P,o)\mapsto D_P^R(o)$ is uniformly bounded. Here, the remainder terms are both exactly zero: ${\text{Rem}}_P^R\equiv {\text{Rem}}_P^S\equiv 0$. Thus, we have that $L_P^{RS}\equiv 0$ in this example.

The requirement that $Va{r}_{P_0}\left[D_0^R(O)\right]>0$ in Corollary 2, and more generally that there exist a nonzero eigenvalue λ_j for the limit distribution in Theorem 4 to be non­degenerate, may at times present an obstacle to our goal of obtaining asymptotic control of the type I error. This is the case for Example 5, which we now discuss further. Nevertheless, we show that with a little finesse the type I error can still be controlled at the desired level for the given test. In fact, the test we discuss has type I error converging to zero, suggesting it may be noticeably conservative in small to moderate samples.

Example 5 (Continued).

In this example, one can take x^R = w and x^S = w(−k). Furthermore, it is easy to show that

$$\begin{array}{lll}{D}_P^R(o)\hfill & =\hfill & Y-E_P[Y|W=w]\hfill \\ D_P^S(o)\hfill & =\hfill & Y-E_P[Y|W(-k)=w(-k)].\hfill \end{array}$$

The first-order approximations for R and S are exact in this example as the remainder terms ${\text{Rem}}_P^R$ and ${\text{Rem}}_P^S$ are both zero. However, we note that if E_P (Y | W) = E_P (Y | W (−k)) almost surely, it follows that $D_P^R\equiv D_P^S$. This implies that Γ₀ ≡ 0 almost surely under ${\mathcal{H}}_0$. As such, under the conditions of Theorem 4, all of the eigenvalues in the limit distribution of nψ_n in Theorem 4 are zero and nψ_n → 0 in probability. We are then no longer able to control the type I error at level α, rendering our proposed test invalid.

Nevertheless, there is a simple albeit unconventional way to repair this example. Let A be a Bernoulli random variable, independent of all other variables, with fixed probability of success p ∈ (0,1). Replace S_P with o ↦ E_P (Y | A = 1, W(−k) = w(−k)) from Example 3, yielding then

$$D_P^S(o)=\frac{a}{p}[y-E_P(Y|A,W(-k)=w(-k))].$$

It then follows that $D_0^R\cancel{\equiv }{D}_0^S$ and in particular Γ₀ is no longer constant. In this case, the limit distribution given in Theorem 4 is non-degenerate. Consistent estimation of q_1−α thus yields a test that asymptotically controls type I error. Given that the proposed estimator ψ_n converges to zero faster than n⁻¹, the probability of rejecting the null approaches zero as sample size grows. In principle, we could have chosen any positive cutoff given that nψ_n → 0 in probability, but choosing a more principled cutoff seems judicious.

Because p is known, the remainder term ${\text{Rem}}_P^S$ is equal to zero. Furthermore, in view of the independence between A and all other variables, one can estimate $E_{P_0}(Y|A=0,W(-k))$ by regressing Y on W(−k) using all of the data without including the covariate A.

In future work, it may also be worth checking to see if the parameter is third-order differentiable under the null, and if so whether or not this allows us to construct an α−level test without resorting to an artificial source of randomness.

6. Simulation studies

In simulation studies, we have explored the performance of our proposed test in the context of Examples 2, 3 and 4, and have also compared our method to the approach of Racine et al. [2006] for which software is readily available – see, e.g., the R package np [Hayfield and Racine, 2008]. We evaluate the performance of computing the eigenvalues of the Gram matrix defined in (6) for Example 3 in two different scenarios. We report the results of our simulation studies in this section.

In all simulation settings, we consider an adaptive bandwidth selection procedure that is a variant of the median heuristic that has been employed in the classical MMD setting where P ↦ R_P and P ↦ S_P do not depend on P [Gretton et al., 2012a]. In that case, the median heuristic selects the bandwidth to be equal to the median of the 2n × 2n Euclidean distance matrix of {R(O_i) : i = 1, …, n} ⋃ {S(O_i) : i = 1, …, n}, where the subscript of R and S on a distribution P has been omitted to emphasize the lack of this dependence in the classical MMD setting. In our case, we choose the bandwidth to be equal to the median of the Euclidean distance matrix between scalar or vector-valued observations (see Concluding Remark b in Section 7 for the extension to vector-valued unknown functions) in

$$\{R_{{\widehat{P}}_n}(O_i)+D_{{\widehat{P}}_n}^R(O_i):i=1,\dots ,n\}\cup \{S_{{\widehat{P}}_n}(O_i)+D_{{\widehat{P}}_n}^S(O_i):i=1,\dots ,n\}.$$

This extension is natural in that $R_{{\widehat{P}}_n}+D_{{\widehat{P}}_n}^R$ and $S_{{\widehat{P}}_n}+D_{{\widehat{P}}_n}^S$ are reminiscent of one-step estimators [Pfanzagl, 1982] of the unknown R₀ and S₀, which should help this procedure account for the uncertainty in $R_{{\widehat{P}}_n}$ and $S_{{\widehat{P}}_n}$. Except where specified, every MMD result presented in this section uses thins mediann heuristic to select the bandwidth. We also compare this procedure to a fixed choice of bandwidth in two of our settings.

6.1. Simulation scenario 1

We use an observed data structure (W, A, Y), where W ≜ (W₁, W₂, …, W₅) is drawn from a standard 5-dimensional normal distribution, A is drawn according to a Bernoulli(0.5) distribution, and Y = μ(A, W) + 5ξ(A, W), where the different forms of the conditional mean function μ(a, w) are given in Table 1, and ξ(a, w) is a random variate following a Beta distribution with shape parameters α = 3expit(aw₂) and β= 2expit[(1 − a)w₁] shifted to have mean zero, where expit(x) = 1/(1 + exp(−x)).

Table 1.

Conditional mean function in each of three simulation settings within simulation scenario 1. Here, $m(a,w)\triangleq 0.2(w_1^2+w_2-2w_3{w}_4)$, and the third and fourth columns indicate, respectively, whether μ(1, W) and μ(0, W) are equal in distribution or almost surely.

	μ(a, w)	$\stackrel{d}{=}$	$\stackrel{a.s.}{=}$
Simulation 1a	m(a, w)	×	×
Simulation 1b	m(a, w) + 0.4[aw3 + (1 − a)w4]	×
Simulation 1c	m(a, w) + 0.8aw3

We performed tests of the null in which μ(1, W) is equal to μ(0, W) almost surely and in distribution, as presented in Examples 2 and 3, respectively. Our estimate ${\widehat{P}}_n$ of P₀ was constructed using the knowledge that P₀ (A = 1 | W) = 1/2, as would be available, for example, in the context of a randomized trial. The conditional mean function μ(a, w) was estimated using the ensemble learning algorithm Super Learner [van der Laan et al., 2007], as implemented in the SuperLearner package [Polley and van der Laan, 2013]. This algorithm was implemented using 10-fold cross-validation to determine the best convex combination of regression function candidates minimizing mean-squared error using a candidate library consisting of SL.rpart, SL.glm.interaction, SL.glm, SL.earth, and SL.nnet. We used the results of Corollary 2 to evaluate significance for Example 2, and the eigenvalue approach presented in Section 3.2.2 to evaluate significance for Example 3, where we used all of the positive eigenvalues for n = 125 and the largest 200 positive eigenvalues for n > 125 using the rARPACK package [Qiu et al., 2014].

To evaluate the performance of the adaptive bandwidth selection procedure in the context of a test of the equality in distribution of two unknown functions applied to w, namely μ(1, ·) and μ(0, ·), we also ran our procedure at fixed bandwidths with values 2^k, k = −2, 1, 0, 1, 2. In the context of a test of the almost sure equality of μ(1,W) and μ(0, W), we compare our adaptive bandwidth selection procedure to fixing the bandwidth at one. The performance of the adaptive bandwidth selection procedure is evaluated in more detail for a null hypothesis of the almost sure equality of two unknown functions in our third simulation setting.

We ran 1,000 Monte Carlo simulations with samples of size 125, 250, 500, 1000, and 2000, except for the np package, which we only ran for 500 Monte Carlo simulations. For Example 2 we compared our approach with that of Racine et al. [2006] using the npsigtest function from the np package. This requires first selecting a bandwidth, which we did using the npregbw function, specifying that we wanted a local linear estimator and the bandwidth to be selected using the cv.aic method [Hayfield and Racine, 2008].

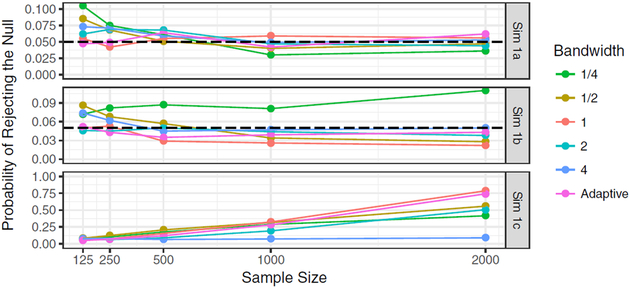
Figure 1 displays the empirical null rejection probability of our test of equality in distribution of μ(1, W) and μ(0, W) for simulation scenarios 1a, 1b and 1c. In particular, we observe that our method is able to properly control type I error for Simulation 1a when testing the hypothesis that μ(1, W) is equal in distribution to μ(0, W). Type I error is also properly controlled in Simulation 1b, though the control of the fixed bandwidth procedures appears to be conservative at the larger sample sizes. We also note that the adaptive bandwidth yielded similar performance to the best considered fixed bandwidth of 1. Our selection procedure generally picked values with an average of around 1.5 – at large sample sizes, there was little variability around this average bandwidth, while at smaller sample sizes the selected bandwidths generally fell between 1.25 and 1.75. The adaptive procedure always controlled type I error at or near the nominal level and had power increasing with sample size and comparable to that of a fixed bandwidth of 1. Choosing the largest fixed bandwidth, namely 4, yielded no power at the alternative in Simulation 1c. Choosing the smallest fixed bandwidth, namely 1/4, yielded inflated type I error levels at one of the null distributions, namely Simulation 1b.

Fig. 1.

Empirical probability of rejecting the null when testing the null hypothesis that μ(1, W) is equal in distribution to μ(0, W) (Example 3) in Simulation 1. Table 1 indicates that the null is true in Simulations 1a and 1b, and the alternative is true in Simulation 1c.

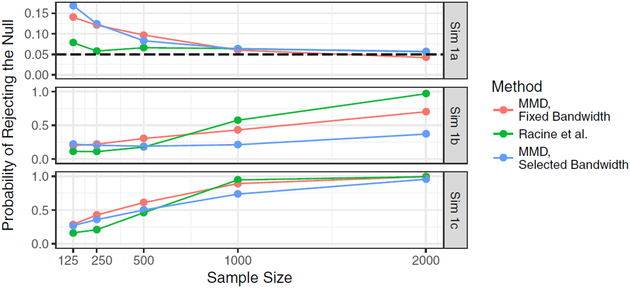
Figure 2 displays the empirical coverage of our approach as well as that resulting from use of the np package. At smaller sample sizes, our method does not appear to control type I error near the nominal level. This is likely because we use an asymptotic result to compute the cutoff, even when the sample size is small. Nevertheless, as sample size grows, the type I error of our test approaches the nominal level. We note that choosing the fixed unit bandwidth outperforms the median heuristic bandwidth selection procedure in this setting, especially in terms of power Simulation 1b. We note that in Racine et al. [2006], unlike in our proposal, the bootstrap was used to evaluate the significance of the proposed test. It will be interesting to see if applying a bootstrap procedure at smaller sample sizes improves our small-sample results. At larger sample sizes, it appears that the method of Racine et al. outperforms our approach in terms of power in simulation scenarios 1b and 1c. At smaller sample sizes (125, 250, 500), our method achieves higher power than that of Racine et al., but at the expense of double the type I error of that of Racine et al.: therefore, it appears that the method of Racine et al. outperforms our approach in Simulations 1a, 1b, and 1c when testing the null hypothesis that μ(1, W) – μ(0, W) is almost surely equal to zero. Nonetheless, we note that the generality of our approach allows us to apply our test in more settings than a test using the method of Racine et al.. For example, we are not aware of any other test devised to test the equality in distribution of μ(1, W) and μ(0, W) (Figure 1).

Fig. 2.

Empirical probability of rejecting the null when testing the null hypothesis that μ(1, W) – μ(0, W) is almost surely equal to zero (Example 2) in Simulation 1. Table 1 indicates that the null is true in Simulation 1a, and the alternative is true in Simulations 1b and 1c.

6.2. Simulation scenario 2: comparison with Racine et al. [2006]

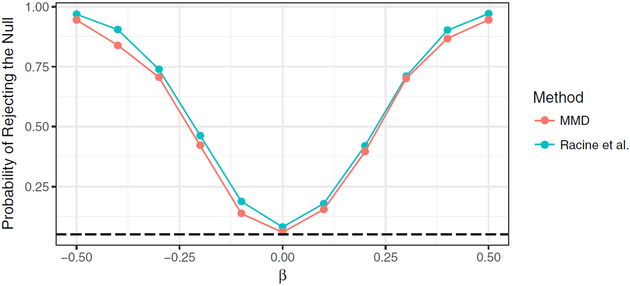
We reproduced a simulation study from Section 4.1 of Racine et al. [2006] at sample size n = 100. In particular, we let $Y=1+\beta A(1+W_2^2)+W_1+W_2+ϵ$, where A, W₁, and W₂ are drawn independently from Bernoulli(0.5), Bernoulli(0.5), and N(0,1) distributions, respectively. The error term ϵ is unobserved and drawn from a N(0,1) distribution independently of all observed variables. The parameter β was varied over values −0.5, −0.4,…, 0.4, 0.5 to achieve a range of distributions. The goal is to test whether E₀ (Y | A, W) = E₀ (Y | W) almost surely, or equivalently, that μ(1, W) – μ(0, W) = 0 almost surely.

Due to computational constraints, we only ran the ‘Bootstrap I test’ to evaluate significance of the method of Racine et al. [2006]. As the authors report, this method is anticonservative relative to their ‘Bootstrap II test’ and indeed achieves lower power (but proper type I error control) in their simulations.

Except for two minor modifications, our implementation of the method in Example 2 is similar to that as for Simulation 1. For a fair comparison with Racine et al. [2006], in this simulation study, we estimated P₀ (A = 1 | W) rather than treating it as known. We did this using the same Super Learner library and the ‘family=binomial’ setting to account for the fact that A is binary. We also scaled the function μ(1, w) – μ(0, w) by a factor of 5 to ensure most of the probability mass of R₀ falls between −1 and 1 (around 99% when β = 0). We note that even with scaling the variable Y is not bounded as our regularity conditions require. Nonetheless, an evaluation of our method under violations of our assumptions can itself be informative.

Figure 3 displays the empirical null rejection probability of our test as well as that of Racine et al. [2006]. In this setup, used by the authors themselves to showcase their test procedure, our method performs comparably to their proposal, with slightly lower type I error (closer to nominal) and slightly lower power.

Fig. 3.

Empirical probability of rejecting the null when testing the null hypothesis that μ(1, W) – μ(0, W) is almost surely equal to zero in Simulation 2.

6.3. Simulation scenario 3: higher dimensions

We also explored the performance of our method as extended to tackle higher-dimensional hypotheses, as discussed in Section 7. To do this, we used the same distribution as for Simulation 1 but with Y now a 20-dimensional random variable. Our objective here was to test μ(1,W) – μ (0, W) is equal to (0,0, …, 0) in probability, where $\mu (a,w)\triangleq ({\mu }_1(a,w),{\mu }_2(a,w),\dots ,{\mu }_{20}(a,w))$ with ${\mu }_j(a,w)\triangleq E_0(Y_j|A=a,W=w)$. Conditional on A and W, the coordinates of Y are independent. We varied the number of coordinates that represent signal and noise. For signal coordinate j, given A and W, 20Y_j was drawn from the same conditional distribution as Y give A and W in Simulation 1c. For noise coordinate j, given A and W, 20Y_j was drawn from the same conditional distribution as Y given A and W in Simulation 1a.

Relative to Simulation 1, we have scaled each coordinate of the outcome to be one twentieth the size of the outcome in Simulation 1. Apart from the adaptive bandwidth selection procedure discussed at the beginning of this section, we considered defining the MMD with a Gaussian kernel with bandwidths of 1/4, 1/2, 1, and 2. Alternatively, this could be viewed as considering bandwidths 5, 10, 20, and 40 if the outcome had not been scaled by 1/20.

We ran the same Super Learner to estimate μ(1,w) as in Simulation 1, and we again treated the probability of treatment given covariates as known. We evaluated significance by estimating all of the positive eigenvalues of the centered Gram matrix for n = 125 and the largest 200 positive eigenvalues of the centered Gram matrix for n > 125.

In Figure 4, the empirical null rejection probability is displayed for our proposed MMD method. We did not include the results for sample size 125 in the figure because type I error control was too poor. For example, for zero signal coordinates, the probability of rejection was 0.24 for bandwidth 1 and 0.33 for bandwidth 1/2. The adaptive bandwidth method performs comparably to the procedure that a priori fixes the bandwidth at 1/2. This observation is consistent with the fact that, across all signal levels and sample sizes, the selected bandwidth was closely concentrated about 1/2 for all Monte Carlo repetitions: the minimal selected bandwidth was 0.49 and the maximal selected bandwidth was 0.59. Among the considered fixed bandwidths, 1/2 or 1/4 seem to be the best at the largest sample sizes (1000, 2000), with the tradeoff between the two being that a bandwidth of 1/4 increases power (substantially for a signal of 5) at the cost of inflating type I error. At smaller sample sizes, the bandwidth of 1/4 yields unacceptably inflated type I error (0.4 at n = 250 and 0.15 at n = 500). Our adaptive bandwidth procedure appears to control type I error well at moderate to large sample sizes (i.e., n ≥ 500). This simulation shows that, overall, our method indeed has increasing power as sample size grows or as the number of coordinates j for which μ_j(1, W) – μ_j(0, W) not equal to zero in probability increases. The only sample size and signal number at which our adaptive bandwidth procedure appears to be outperformed by a fixed bandwidth is at 2000: a fixed bandwidth of 1/4 attains nominal coverage at this sample size but dramatically outperforms the adaptive bandwidth when the signal is 5. This discrepancy disappears when the signal is 10.

Fig. 4.

Probability of rejecting the null when testing the null hypothesis that μ(1, W) – μ(0, W) is almost surely equal to zero in Simulation 3.

7. Concluding remarks

We have presented a novel approach to test whether two unknown functions are equal in distribution. Our proposal explicitly allows, and indeed encourages, the use of flexible, data-adaptive techniques for estimating these unknown functions as an intermediate step. Our approach is centered upon the notion of maximum mean discrepancy, as introduced in Gretton et al. [2006], since the MMD provides an elegant means of contrasting the distributions of these two unknown quantities. In their original paper, these authors showed that the MMD, which in their context tests whether two probability distributions are equal using n random draws from each distribution, can be estimated using a U− or V−statistic. Under the null hypothesis, this U- or V−statistic is degenerate and converges to the true parameter value quickly. Under the alternative, it converges at the standard n^−1/2 rate. Because this parameter is a mean over a product distribution from which the data were observed, it is not surprising that a U− or V−statistic yields a good estimate of the MMD. What is surprising is that we were able to construct an estimator with these same rates even when the null hypothesis involves unknown functions that can only be estimated at slower rates. To accomplish this, we used recent developments from the higher-order pathwise differentiability literature. Our simulation studies indicate that our asymptotic results are meaningful in finite samples, and that in specific examples for which other methods exist, our methods generally perform at least as well as these established, tailor-made methods. Of course, the great appeal of our proposal is that it applies to a much wider class of problems.

In our simulation study, we adapted the median heuristic for selecting the Gaussian kernel bandwidth to our setting in which R₀ and S₀ are unknown. In some settings, this bandwidth selection procedure performed well in our simulation compared to specifying a fixed bandwidth in our simulation, though we did note settings where the adaptive procedure underperformed relative to using a fixed bandwidth. An advantage of this adaptive bandwidth selection procedure compared to selecting a fixed bandwidth (e.g., the unit bandwidth) is that it yields a procedure that is invariant to a rescaling of the unknown functions R₀ and S₀. For the classical MMD setting in which R₀ and S₀ are known functions, Gretton et al. [2012b] showed that other bandwidth selection procedures can outperform the median heuristic. One such procedure involves selecting the bandwidth to maximize an estimate of the power of the test of the null hypothesis of equality in distribution of R₀(O) and S₀ (O), subject to a constraint on the estimated type I error. Extending these procedures to our setting where R₀ and S₀ are unknown is an important area for future research.

We conclude with several possible extensions of our method that may increase further its applicability and appeal.

• (a)
  Although this condition is satisfied in all but one of our examples, requiring R and S to be in $\mathcal{S}$ can be somewhat restrictive. Nevertheless, it appears that this condition may be weakened by instead requiring membership to ${\mathcal{S}}^{*}$, the class of all parameters T for which there exist some M < ∞ and elements T¹, T², …, T^M in $\mathcal{S}$ such that $T={\displaystyle {\sum }_{m=1}^M{T}^m}$. While the results in our paper can be established in a similar manner for functions in this generalized class, the expressions for the involved gradients are quite a bit more complicated. Specifically, we find that, for $T,U\in {\mathcal{S}}^{*}$ with $T={\displaystyle {\sum }_{m=1}^M{T}^m}$ and $U={\displaystyle {\sum }_{\mathcal{l}=1}^L{U}^{\mathcal{l}}}$, the quantity ${\Gamma }_P^{TU}(o_1,o_2)$ equals

  $$e^{-{[T_P(o_1)-U_P(o_2)]}^2}+{\displaystyle \sum _{\ell =1}^L{E}_P\left\{2[T_P(o_1)-U_P(O)]e^{-{[T_P(o_1)-U_P(O)]}^2}|X^{U^{\ell }}=x_2^{U^{\ell }}\right\}}{D}_P^{U^{\ell }}(o_2)-{\displaystyle \sum _{m=1}^M{E}_P\left\{2[T_P(O)-U_P(o_2)]e^{-{[T_P(O)-U_P(o_2)]}^2}|X^{T^m}=x_1^{T^m}\right\}}{D}_P^{T^m}(o_1)-{\displaystyle \sum _{\ell =1}^L{\displaystyle \sum _{m=1}^M{E}_{P^2}\left[\left\{4{[T_P(O_1)-U_P(O_2)]}^2-2\right\}{e}^{-{[T_P(O_1)-U_P(O_2)]}^2}|X_1^{T^{\ell }}=x_1^{T^{\ell }},X_2^{U^m}=x_2^{U^m}\right]D_P^{T^{\ell }}(o_1)D_P^{U^m}(o_2).}}$$

  In particular, we note the need for conditional expectations with respect to $X^{R^m}$ and $X^{S^m}$ in the definition of Γ, which could render the implementation of our method more difficult. While we believe this extension is promising, its practicality remains to be investigated.
• (b)
  While our paper focuses on univariate hypotheses, our results can be generalized to higher dimensions. Suppose that P ↦ R_P and P ↦ S_P are ${ℝ}^d$-valued functions on $\mathcal{O}$. The class ${\mathcal{S}}_d$ of allowed such parameters can be defined similarly as $\mathcal{S}$, with all original conditions applying componentwise. The MMD for the vector-valued parameters R and S using the Gaussian kernel is given by ${\Psi }_d(P)\triangleq {\Phi }_d^{RR}(P)-2{\Phi }_d^{RS}(P)+{\Phi }_d^{SS}(P)$, where for any $T,U\in {\mathcal{S}}_d$ we set

  $${\Phi }_d^{TU}(P)\triangleq {\displaystyle \int {\displaystyle \int e^{-{\Vert T_P(o_1)-U_P(o_2)\Vert }^2}}}dP(o_1)dP(o_2).$$

  It is not difficult to show then that, for any $T,U\in {\mathcal{S}}_d(P_0)$, ${\Gamma }_{d,P}^{TU}(o_1,o_2)$ is given by

  $$\left[2[T_P(o_1)-U_P(o_2){]}^{\prime }[D_P^U(o_2)-D_P^T(o_1)]+1-2D_P^T(o_1{)}^{\prime }\{2[T_P(o_1)-U_P(o_2)][T_P(o_1)-U_P(o_2){]}^{\prime }-\text{Id}\}{D}_P^U(o_2)\right]\times e^{-{\Vert T_P(o_1)-U_P(o_2)\Vert }^2},$$

  where Id denotes the d−dimensional identity matrix and A′ denotes the transpose of a given vector A. Using these objects, the method and results presented in this paper can be replicated in higher dimensions rather easily.
• (c)Our results can be used to develop confidence sets for infinite dimensional parameters by test inversion. Consider a parameter T satisfying our conditions. Then one can test if $R_0\triangleq T_0-f$ is equal in distribution to zero for any fixed function f that does not rely on P. Under the conditions given in this paper, a 1 – α confidence set for T₀ is given by all functions f for which we do not reject ${\mathcal{H}}_0$ at level α. The blip function from Example 2 is a particularly interesting example, since a confidence set for this parameter can be mapped into a confidence set for the sign of the blip function, i.e. the optimal individualized treatment strategy [Robins, 2004]. We would hope that the omnibus nature of the test implies that the confidence set does not contain functions f that are “far away” from T₀, contrary to a test which has no power against certain alternatives. Formalization of this claim is an area of future research.
• (d)To improve upon our proposal for nonparametrically testing variable importance via the conditional mean function, as discussed in Section 5, it may be fruitful to consider the related Hilbert Schmidt independence criterion [Gretton et al., 2005]. Higher-order pathwise differentiability may prove useful to estimate and infer about this discrepancy measure.