Prediction of protein group function by iterative classification on functional relevance network

Abstract

Motivation

Biological experiments including proteomics and transcriptomics approaches often reveal sets of proteins that are most likely to be involved in a disease/disorder. To understand the functional nature of a set of proteins, it is important to capture the function of the proteins as a group, even in cases where function of individual proteins is not known. In this work, we propose a model that takes groups of proteins found to work together in a certain biological context, integrates them into functional relevance networks, and subsequently employs an iterative inference on graphical models to identify group functions of the proteins, which are then extended to predict function of individual proteins.

Results

The proposed algorithm, iterative group function prediction (iGFP), depicts proteins as a graph that represents functional relevance of proteins considering their known functional, proteomics and transcriptional features. Proteins in the graph will be clustered into groups by their mutual functional relevance, which is iteratively updated using a probabilistic graphical model, the conditional random field. iGFP showed robust accuracy even when substantial amount of GO annotations were missing. The perspective of ‘group’ function annotation opens up novel approaches for understanding functional nature of proteins in biological systems.

Availability and implementation: http://kiharalab.org/iGFP/

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

With the rapid development of genomic and proteomic technologies, massive amount of omics data has become available. Consequently, computational methods for annotating protein’s function and explaining the mechanisms through which multiple proteins work together in a cell becomes ever more important. To meet the pressing need for protein function annotation, many function prediction methods have been developed in the past (Hawkins and Kihara, 2007). Based on the classical homology search (Altschul et al., 1990; Pearson and Lipman, 1988) and motif/domain search tools (Finn et al., 2017), various methods have been developed recently that extract function information thoroughly and more accurately from sequence database search results often in combination with other sources (Hawkins et al., 2009; Wass and Sternberg, 2008). There are also categories of function prediction that consider co-expression patterns of genes (van Noort et al., 2003), the tertiary structures of proteins (Laskowski et al., 2005; Zhu et al., 2015), protein–protein interaction (PPI) networks (Chua et al., 2006; Sharan et al., 2007), natural language processing (Cao et al., 2017) and various features (Cao and Cheng, 2016). It is notable that there is a community effort in this field, the Critical Assessment of Function Annotation (Radivojac et al., 2013), which assesses performance of automatic function prediction methods on a large set of protein sequences which are not annotated at the time of the assessment.

Although these methods differ in features of proteins and algorithms used for predicting protein function, they all have the same logical flow: a method takes a protein as an input and predicts function [typically Gene Ontology (GO) terms] of the protein as output. However, real-life scenarios in an experimental lab often do not always fit into this single-protein-single-function framework: typical in a proteomics and transcriptomic study, an experiment will identify dozens of proteins that are in some way involved in the biological phenomenon (e.g. disease) under study. To understand why these proteins are involved, one can perform a conventional function prediction, e.g. using BLAST, to predict function for each protein separately, but such an approach does not consider the critical information that these proteins are involved in the same or related pathways that lead to the biological phenomenon. Rather than making predictions separately, it is desired to consider the set of all proteins as input, and assign a function to the group as a whole as well as to individual proteins. The concept of group function prediction we propose in this work thus has two main aims and advantages: (i) to predict function of a group of proteins even when function of some of the individual proteins in the group cannot be predicted. (ii) To better predict function of individual proteins by considering the identified function of the group.

The problem of building a computational model to predict protein group functions is unique and significant. The present bioinformatics approach that comes closest to the notion of group function is the functional (GO) enrichment analyses (Subramanian et al., 2005), which identifies statistically enriched GO terms in annotations of the proteins relative to the background distribution. Drawbacks of such an approach are that it relies on identified protein functions/GO terms, which is often sparse knowledge for a group of novel proteins. Later in this work, we highlight that our approach performs substantially better than the GO enrichment analysis in particular when annotations are sparse in proteins.

In this study, we propose a novel computational method termed iterative Group Function Prediction (iGFP), which takes a set of proteins as input and predicts the function of the protein groups as well as function of individual proteins by iteratively updating grouping of proteins and functional assignments. Taking into account that the function of individual proteins may not be fully available, proteins are clustered on a functional relevance network and are related in the context of functional and physical interaction relationships. Several features were incorporated, including physical PPI (Calderone et al., 2013; Szklarczyk et al., 2017), gene co-expression network (GE), phylogenetic profile similarity network (Phyl), GO similarity network and KEGG pathway similarity (Kanehisa et al., 2017). Figure 1 shows a schematic diagram of the iGFP model workflow. Briefly, it takes a group of target proteins pre-identified to be involved in a biological context such as disease/disorder as input; (i) and builds the functional relevance network including the target proteins and other proteins in the same organism. A network integration method, similarity network fusion (SNF) (Wang et al., 2014), was used to combine multiple functional network. (ii) Proteins are clustered based on the similarity of integrated features. The target proteins are grouped in a cluster with some other proteins, whose function will be predicted iteratively in the subsequent steps. Each protein group will be assigned GO terms, which have P-value ≤0.01 in the group relative to the annotations of the organism. Some groups remain un-annotated if they do not contain enough annotated proteins. (iii) iGFP predicts function of the un-annotated clusters using a conditional random field (CRF) framework (Tang et al., 2013). The essence of the CRF module is to predict cluster functions in the network based on the functional properties of the cluster neighborhood and existing annotations of the cluster. (iv) iGFP propagates the new CRF cluster GO labels to the unknown proteins in each cluster so that it reflects the cluster function predicted by the CRF module in the previous step. (i’) Now that the GO term annotations of proteins are updated, protein networks are integrated again with the updated GO similarity network and computation (i)–(iv) is iterated until the process converges or sufficient number of iterations have been reached.

Fig. 1.

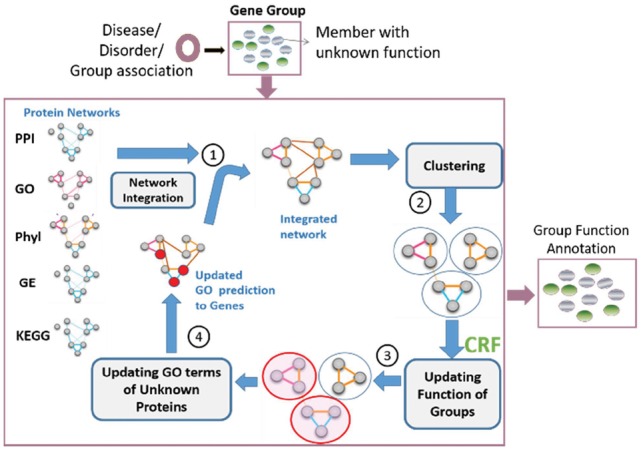
Schematic diagram of the group function prediction (iGFP) model. Iterative procedure of group function prediction. In (3) and (4), clusters/proteins in red are updated with their predicted GO annotations. PPI, protein–protein interaction; Phyl, phylogenetic profile; GE, gene expression; KEGG, pathway similarity

iGFP was validated at two phases of the algorithm. First, we validated the CRF module in a task of assigning function to individual proteins in protein groups. Subsequently, the whole iGFP pipeline was validated on datasets of gene groups found to be involved in Rheumatoid Arthritis (RA). In comparison with the GO enrichment analysis, which is used as the baseline, iGFP showed robust accuracy even when substantial amount of GO annotations were missing.

2 Materials and methods

2.1 Functional features of proteins

Input proteins are represented as a graph, which connect proteins with functional relevance. Expecting that function annotation of proteins is not fully available, we combine following features of human proteins.

1. PPI network. The PPI network was constructed using the high confidence physical interactions (>0.7 confidence score) of the STRING database (Szklarczyk et al., 2017). From Human proteins (NCBI taxID: 9606), a total of 15 036 proteins had high confidence interactions.

2. Phyl. Phyl characterizes relevance of proteins by the location of coding regions of the proteins in genomes. Protein pairs were considered as relevant if they have a medium confidence score or higher (>0.4) in any of the following genomic features in STRING: ‘gene neighborhood’, ‘fusion’ or ‘co-occurrence’. A total of 1197 human proteins had phylogenetically relevant proteins.

3. GO similarity network. GO annotation for proteins was taken from UniProt. Since the size of GO is very large and includes rare terms, we slimmed the GO space by mapping GO terms to their parental terms that have an information content of 0.3 (the author-recommended cutoff) or higher using a GO slim creation pipeline (Davis et al., 2010). The space was reduced from 13 709 to 303 terms. The use of the slimmed GO space was needed because CRF cannot be trained for rare GO terms, and also training CRF for each of the all GO terms are not practically feasible. GO similarity is quantified with the funSim score using Biological Process (BP) and Molecular Function (MF) terms (Schlicker et al., 2006). Two proteins were defined to have functional similarity if they have a funSim score of over 0.7.

4. GE network. GE profiles were taken from the COXPRESdb database (Okamura et al., 2015). Two protein genes were considered as co-expressed if the absolute value of the Pearson’s correlation coefficient of expression levels was ranked within the top 2% among all the protein pairs. The correlation values were downloaded from the database. After this filtering, 17 341 proteins had at least one correlated proteins.

5. Pathway association. There were 287 unique pathways found in the 23 658 human proteins in the KEGG database. We constructed a binary vector of length 287 indicating if a protein exists or does not exist in each KEGG pathway. Then two proteins were considered as related if the cosine similarity between their vectors is 0.2 or larger. The cutoff of 0.2 was determined based on the score distribution (Supplementary Fig. S1).

2.2 Network integration

Similarity networks for each of the five protein features were generated, where proteins are represented by nodes and functional relevance between two proteins by edges. The five networks were then integrated by the SNF method, which performs a non-linear message passing algorithm. SNF iteratively integrates individual networks and converges them into one composite network within few iterations.

2.3 Affinity propagation-based clustering method

Proteins on the functional relevance network were clustered using the affinity propagation-based clustering method in Step 2 of iGFP (Fig. 1). We used this method because it was shown to have a low error rate and is as fast as other common clustering methods (Frey and Dueck, 2007). The inter-node distance was defined as the mean of the integrated functional relevance network’s edge weights and the funSim score of protein pairs.

2.4 Function prediction model using conditional random field (CRF)

In the third step of iGFP (Fig. 1) we used CRF to predict GO terms to protein groups in the functional relevance network. CRF is a discriminative probabilistic undirected graphical model, which can model posterior probability of labels (in this work GO terms) of nodes (protein groups) that are dependent on neighboring node labels given observed variables (functional features of nodes).

More formally, a CRF computes the probability of having binary labels Y (here whether proteins have a particular GO term annotation) given parameters θ and input variables X (the protein features provided in the integrated network):

$$p\left(Y||\theta ,X\right)=\frac{1}{Z}\prod _{c\in C}{\Psi }_c\left(Y_c,X\right)= \frac{1}{Z}\prod _{c\in C}\left\{{\Psi }_{c,s}\left(y_i;\theta ,X\right)+{\Psi }_{c,p}\left(y_i,y_j;\theta ,X\right)\right\}\}$$ (Eq. 1)

where Z(X) is a normalization factor, c is a clique and C is the set of all cliques in the graph. The rightmost part of Equation (1) shows that the probability is computed from two terms, a single term Ψ_c,s, which considers the GO term label y_i of one node, and a pairwise term Ψ_c,p, which takes into account neighboring nodes’ GO term labels, y_i and y_j. The two terms are defined concretely by potential functions as:

$${\Psi }_{c,s}\left(y_i;\theta ,X\right)+{\Psi }_{c,p}\left(y_i,y_j;\theta ,X\right)=exp\left\{U_s\left(y_i;\theta ,X\right)\right\}+exp\left\{U_s\left(y_{i,}{y}_j;\theta ,X\right)\right\}$$ (Eq. 2)

The first term on the right-hand side represents a single term where the probability of a label (GO term) y_j, depends only on features X of each node (and the parameter set θ). As feature X of a node, we considered other GO annotations of the node. Thus,

$$U_s\left(y_i;\theta ,X\right)=\sum _{j\in N_i}{w}_{1}P\left({GO}_i|{GO}_j\right)+\sum _{k\in N_0}{w}_{2}P\left({GO}_i|{GO}_k\right)$$ (Eq. 3)

where y_i = GO_i, N₁ and N₀ are the number of GO terms that annotate/do not annotate the node (protein or protein group) (i.e. 1s and 0s in the GO annotation vector for the node, and P(GO_i|GO_j) is the function association score developed previously in our group (Hawkins et al., 2009), which expresses the conditional probability that y_i is assigned simultaneously with y_j, to each sequence in UniProt. Thus, annotation y_i for a protein depends on existing GO annotation of the node.

The second term of the right-hand side in Equation (2) is a pairwise term where dependency of neighboring labels is expressed:

$$U_p\left(y_i,y_j;\theta ,X\right)=w_3{y}_{j}e\left(i,j\right)+w_4(1-y_j)e\left(i,j\right)+w_5{y}_{j}funSim\left(i,j\right){+w}_6(1-y_j)funSim\left(i,j\right)$$ (Eq. 4)

In the pairwise term that considers two proteins (or protein clusters; we call it node in the rest of the method) i and j, e(i, j) is the edge weight of the two nodes in the functional relevance network and funSim(i, j) is the funSim score between i and j. Weights w₃–w₆ control the influence of the neighboring nodes when the node has the GO term (y_j = 1) and when it does not (y_j = 0). The terms with funSim(i, j) is to consider influence of neighboring nodes with overall similar function in assigning a particular GO term, which would be biologically intuitive and reasonable. Weights w₁–w₆ were trained on the training set.

There is a previous work which uses CRF for function prediction from a PPI network (Gehrmann et al., 2013). Differences of iGFP over their work are that iGFP uses the single term that considers the coherence of the GO term’s annotation or lack thereof relative to the existing GO terms for the protein (or protein group). More fundamentally, CRF is used as a component for performing protein group function prediction in iGFP, a new and important problem setting that reflects real-life biology research, whereas the existing work was for predicting single-protein function in a network.

Using the equations above, the conditional probability of a node annotated with a GO term, $p(y_i=1|Y_{-i},\theta ,X)$ can be expressed in terms of the logistic function. Parameters of the GFP model (w₁–w₆) were trained using a Metropolis–Hastings algorithm and inference was performed using Gibbs sampling.

2.5 Assignment of individual proteins’ function derived from the group function

At the last step of iGFP (Step 4 of Fig. 1), GO annotations of the individual proteins in each group are updated reflecting the group function predicted by the CRF module. The procedure of this step is illustrated in Figure 2. F_gⁱ denotes a list of GO terms for the group after iteration i and F_m denotes the same for an individual member protein. If the protein is an unknown protein with no GO annotations, we directly assign the group function F_g as its member protein function F_m. Otherwise (if the protein has some GO annotations), a new GO term g_j will be checked with the group function F_gⁱ to see if it is compatible with the existing GO annotations of the protein. More precisely, functional similarity score SS between g_j and any existing GO term annotation of the protein, F_m, is computed in terms of the relevance semantic similarity score (Schlicker et al., 2006) for within-domain (BP, MF and Cellular Component domains) GO pairs, and the function association score, i.e. P(GO_i|GO_j) in Equation (3), for cross-domain GO pairs. If the SS score is above a pre-defined cutoff, we add the group function g_j to F_m. The SS score cut-off values used was 0.3 for the GO removal test (see Results) and 0.7 for the protein removal test. As shown in Supplementary Figure S2, the values were determined on the MAPK pathway data in Table 1. After this step, the GO annotations of all the individual protein nodes in the graph are updated according to their respective group functions, i.e. group annotations predicted by the CRF module. Note that at each iteration, F_m is taken from the original known annotation of the member protein, i.e. F_m⁰, so that successive updates of the group functions would not dilute too far away from the original annotation.

Fig. 2.

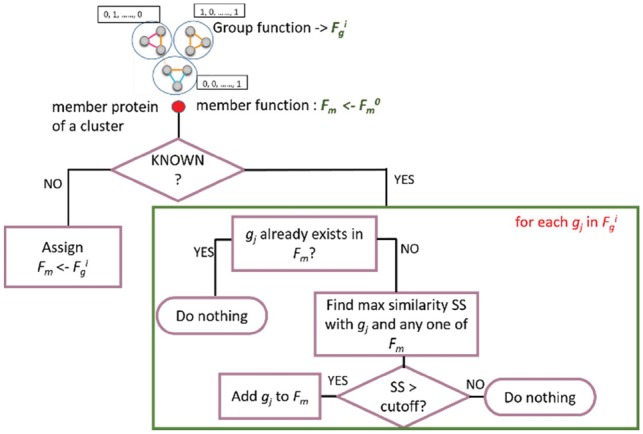
Assignment of protein’s function derived from the group function. Step 4 of the iGFP pipeline shown in Figure 1

Table 1.

Dataset of 10 protein groups involved in RA

KEGG pathway	# Proteins	# Nodes	# Edges
Allograft rejection	8	37	220
Apoptosis	11	155	2074
Pathways in cancer	32	1159	23 907
Chemokine signaling	26	1013	33 914
Jak-STAT	15	403	5817
Leukocyte migration	17	757	13 715
MAPK signaling	20	715	12 019
Neurotrophin signaling	20	779	14 950
T cell receptor signaling	16	595	11 240
Toll-like rec. signaling	13	611	10 405

Note: This dataset is comprised of experimentally verified protein groups taken from Table 3 of the paper by Bakir-Gungor and Sezerman.

3 Results

iGFP was validated in two ways. First, we benchmarked the CRF module by itself because it is the key part of the pipeline and the operation is more complex than other parts. To ensure the correctness of the CRF module, we tested it on tasks of individual protein function prediction in groups. In the second test, the entire iGFP pipeline was tested in terms of function assignment to target proteins.

3.1 Validation of the CRF module

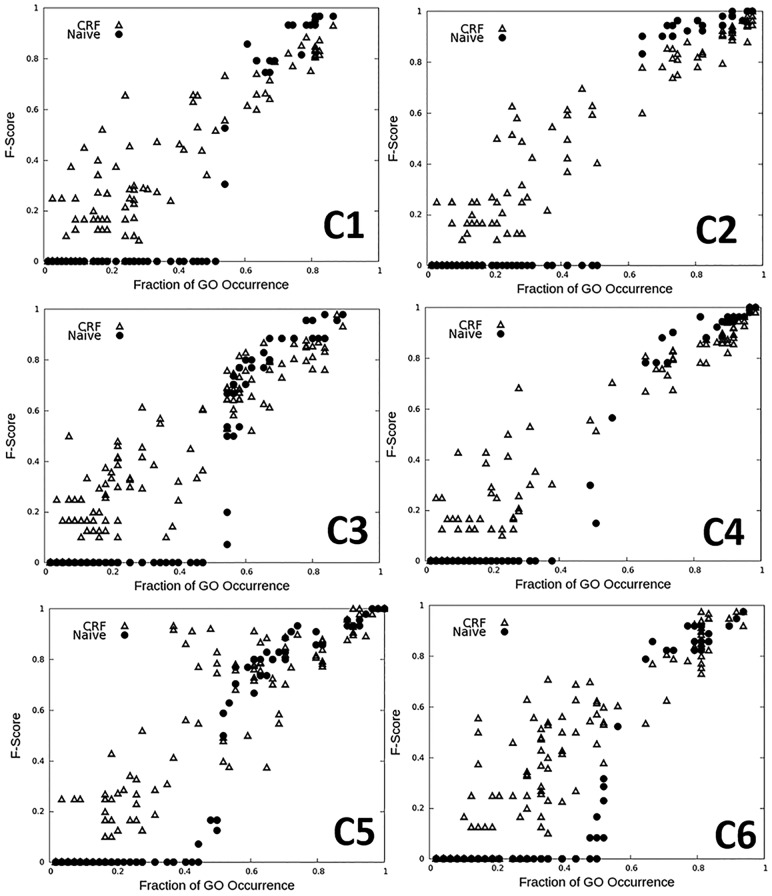
First, we validated the CRF module on function prediction of individual proteins in a PPI network. The dataset for this benchmark was constructed by clustering proteins in the human PPI network (see Materials and methods). The PPI network from the interactions consists of 6124 human proteins that are involved in 112 895 interactions. The network was then clustered by apcluster, from which six clusters that contains only annotated proteins and have at least 50 members were selected as benchmark datasets. Each cluster has dominant GO term annotations in its member proteins that characterized function of the cluster. An exemplary GO term of Cluster 1 was protein modification process (GO: 0043412); Cluster 2 had terms of protein folding, chaperon activity, GTPase activity and transcription activity; Cluster 3 had a GO term of hydrolase activity as a dominant term; Cluster 4 included proteins of mRNA metabolic process, transcription factor activity; Cluster 5 had general (i.e. shallow depth) terms as dominant ones and Cluster 6 had proteins of aromatic compound metabolic process.

For each of these six selected clusters we tested whether the CRF with different feature combinations [used in Equations (3)–(4)] can correctly predict the GO terms of proteins using the GO term annotation of neighboring proteins in the network. For all validation results shown in this section, a slimmed GO vocabulary of 303 GO terms was used (see Materials and methods). In the PPI network clusters, 10% of the proteins were randomly chosen as prediction targets and their annotations were removed. The rest of the proteins were used for training.

We tested three different levels of feature combinations (Fig. 3). A 4-fold cross-validation was performed. The first combination is with two network edge terms in Equation (2) (black bars in Fig. 3). The second combination is all four terms in Equation (4), i.e. the edge features and the other protein similarity (funSim) terms (red bars). The next combination used all six features in Equations (3) and (4) (green). For these three feature combinations, the GO term label (1 or 0 for each GO term) of an unknown target protein was initialized based on neighboring protein's GO labels. For each GO term among the vocabulary of 303 terms, the fraction of neighboring proteins that have the GO term in their annotations was computed; with which a random uniform number between 0 and 1 was generated and compared. Next, the GO term was assigned to the target protein if the random number was smaller than the fraction from the neighbors. For the six feature combinations, two more different settings were compared: The first variation (yellow) used score cutoffs for considering the funSim (cutoff: 0.4) [Equation (4)] and the GO association scores in Equation (3) (cutoff: 0.25), which means the funSim terms were considered only for neighboring proteins that are sufficiently similar and the GO term association was considered only GO pairs with a conditional probability of 0.25 or higher. The second variation used a different prior on top of the first variation, a naïve prior distribution of GO annotations in UniProt, for initializing GO assignments (blue bars). Average F-scores (the harmonic mean of precision and recall) of GO predictions are used as the performance measure (Fig. 3).

Fig. 3.

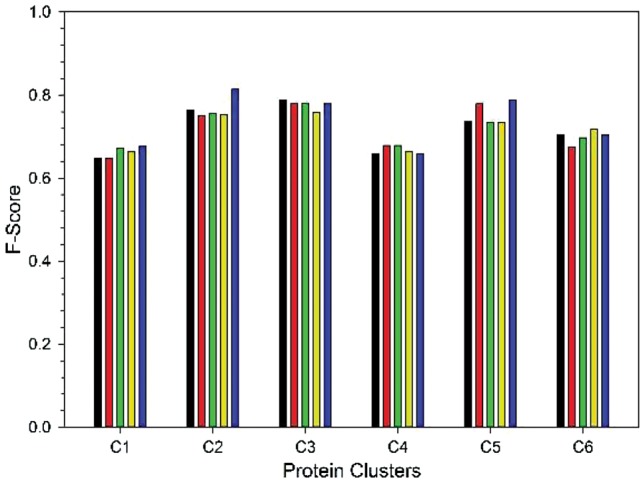
Average F-score of GO prediction using the CRF module for the six protein clusters. For the six protein clusters (C1–C6), GO term prediction was performed using five different feature combinations: black, two features, the first two network edge-based features in Equation (4); red, four features, all four features (two edge-based features and two protein similarity, the funSim score-based features) in Equation (4); green, six features from Equations (3) and (4); yellow, the same six features but used score cutoffs for considering the funSim (cutoff: 0.4) [Equation (4)] and the GO association scores in Equation (3) (cutoff: 0.25); blue, same as yellow except that the known GO term distribution was used as prior of function annotation. See text for more details. The average values from a 4-fold cross-validation are reported

Comparing the five distinct feature combinations, the second variation of the six-feature combination (blue) showed the highest average F-score, 0.737, considering all six clusters, while the other feature combinations showed values between 0.716 and 0.720. Thus, the subsequent results in this paper used this best feature combination for the CRF module.

Next, we evaluated prediction accuracy for individual GO terms. Figure 4 reports the result with CRF (Δ) for the six clusters as in Figure 3 in comparison with a naïve prediction based simply on the frequency of GO terms in the group (● in the plot). The x-axis in the plots is the fraction of proteins in the cluster that have the GO annotation (more precisely, proteins in the training data set of the cluster) and y-axis is the average cross-validation F-score for that GO term. For all six selected clusters in Figure 4, CRF showed a strong ability to make a correct GO assignment when GO terms are not common in the group (left half of the plots), where the frequency-based prediction breaks down. When GO terms are rare and only occur in 35% or less proteins (i.e. x = 0.0–0.35), on average 27.1% of GO terms had positive F-score, while the naïve assignment cannot predict any of such GO terms. The CRF was still effective when the GO occurrence is from 0.35 to 0.7 as shown in the plots. The average F-score of CRF and the naïve prior for this range of GO occurrence were 0.588 and 0.352, respectively. When a GO term is abundant in the cluster, it is trivial for both CRF and the naïve prior to assign the term, showing comparable high F-score in the all six clusters (the right upper corner of plots).

Fig. 4.

GO term prediction accuracy of the CRF module. Prediction results of CRF with six features with the funSim and GO association score cutoff using naïve prior (triangles), which corresponds to the blue bars in Figure 3, was compared with GO assignment based on the background GO distribution (black dots). A 4-fold cross-validation was performed for the six protein clusters, C1–C6

3.2 Performance of the iGFP pipeline

Now we investigated how well the entire iGFP pipeline (Fig. 1) predicts functions of proteins in groups. We used a dataset of 10 experimentally verified protein groups involved in RA. These groups of proteins were identified by a genome-wide association study to be involved in the disease (Bakir-Gungor and Sezerman, 2011), where disease-related genes were identified by considering statistical significance of single nucleotide polymorphisms of genes and the functional groups of the genes were found by mapping onto a human PPI network and annotated with KEGG pathways. Table 1 shows the pathway and the size of the 10 groups.

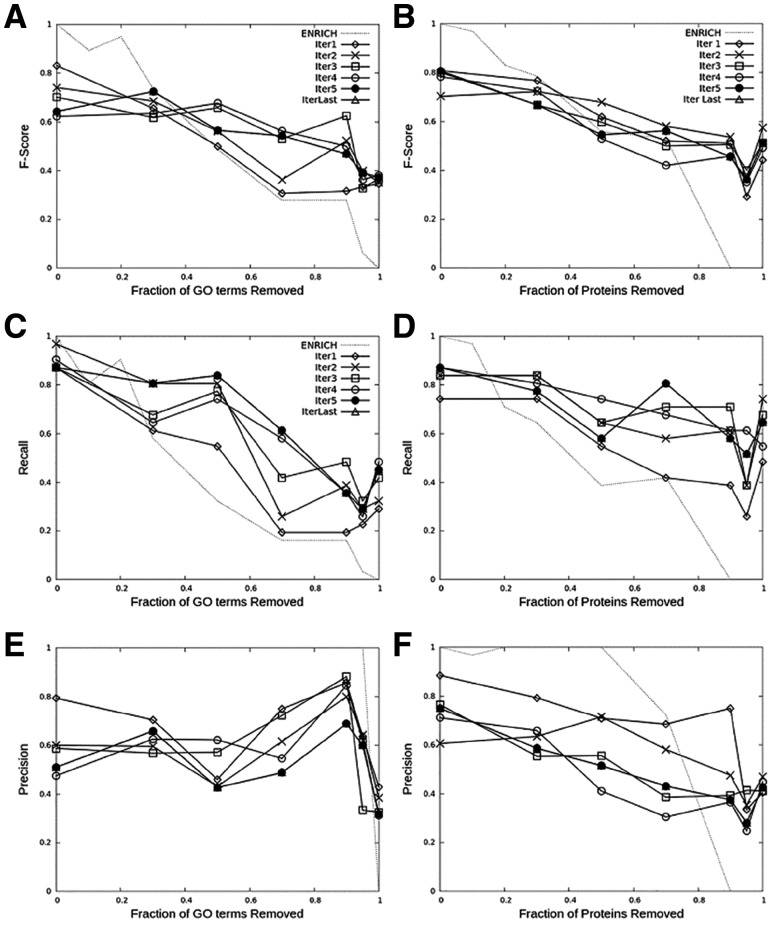
For a group in Table 1, proteins in the group were first mapped onto the five functional feature networks, which were then integrated into the functional relevance network. iGFP was run as shown in Figure 1 on these network until convergence. For this test, the training of CRF was performed on clusters that have <10% of target proteins as members while their GO term annotations were kept empty. As an example, the results of iGFP pipeline for the MAP Kinase pathway are shown in Figure 5. iGFP was run on 715 proteins including the 20 target proteins with 12 019 interactions in the integrated functional relevance network. iGFP was run until either the predicted GO terms of protein groups converged or the number of iterations reached 10. In the benchmark, to examine the robustness of the iGFP pipeline’s prediction, an increasing fraction (shown in x-axis) of the GO terms annotating the 20 target proteins (there were 475 terms in total) were removed from the 20 target proteins and the F-score of the prediction for the removed terms was computed (Fig. 5A, C and E). The last iteration is shown separately (Δ in the plots). For the GO removal experiment of the 20 proteins from the MAPK pathway, there were six iterations of the CRF run. The sixth iteration output had 34 clusters. Out of the 34 clusters, 16 had at least one gene from MAPK.

Fig. 5.

GO term prediction for 20 proteins in the Map Kinase signaling pathway. iGFP was run six iterations and the F-score was reported at each iteration (Iter1–Iter 5 and IterLast). iGFP results were compared with GO assignment with a GO enrichment analysis (ENRICH). Two tests were performed: prediction after removing a fraction of GO terms (panel A, C, E) and after removing all GO annotations from a fraction of target proteins (panel B, D, F). A, F-score of the GO term removal test; B, F-score of the protein removal test; C, recall of the GO term removal test; D, recall of the protein removal test; E, precision of the GO term removal test; F, precision of the protein removal test

Figure 5A, C and E shows F-score, recall and precision for GO annotations to the 20 MAPK target proteins after removal of a fraction of the GO terms. When compared with the baseline, assignment of enriched GO terms in a cluster to target proteins (dotted line, enrichment), iGFP showed robust accuracy (F-score) even after more than 50% of GO terms were removed (Fig. 5A). In contrast, the reference GO enrichment quickly lost correct annotations as GO terms were removed from proteins. Notably, recall (Fig. 5C) grew significantly better with successive iterations. iGFP showed significant improvement over the enrichment for all x-axis points after 50% or more of the annotations were removed with a high recall of 0.839 at 50% removal (x = 0.5) where the enrichment showed a recall of 0.323. On the other hand, precision went lower as the iteration progressed (Fig. 5C), which is intuitive as iGFP tends to add more GO terms in successive iterations. As for precision (Fig. 5E), the enrichment has naturally a very high value until 100% of the annotations were removed because at each removal of GO terms from the target proteins, remaining terms are still all correct existing annotations.

In Figure 5B, D and F, instead of removing an increasing fraction of GO terms we removed entire GO annotations for an increasing fraction of target proteins. This test simulates the situation that we have proteins of unknown functions in the dataset.

Overall, the conclusion remains the same as the results in the previous GO term removal test. While GO annotation by naïve enrichment naturally deteriorates as GO annotations of more proteins were removed, iGFP showed more stable annotations even when annotations were removed from over 50% of target proteins (recall and F-score, Fig. 5B and D). In particular, for recall (Fig. 5D), we observe that iterations improve the annotations. A difference between the previous GO term removal (Fig. 5A, C and E) and the protein full annotation removal (Fig. 5B, D and F) is that the baseline model (enrichment) has a slightly higher accuracy in the latter than the former. This is because in the latter even after removal of a protein’s annotation, the same GO annotations still remain in the other proteins, which contribute to retain accuracy for the baseline enrichment analysis. Nevertheless, iGFP achieved recall as high as 0.806 at 70% protein’s annotation removal, compared to baseline recall of 0.419.

Table 2 summarizes GO term prediction performance, F-score and recall of iGFP on all the 10 protein groups (Table 1) in comparison with the baseline enrichment analysis. Results of the GO term removal and the protein removal tests are shown. The fraction of the GO terms and proteins removed was 0.9 (i.e. corresponds to x = 0.9 in Fig. 5). It is apparent that iGFP’s performance was substantially superior to the baseline enrichment analysis for all the ten protein groups. In the situation where the majority of annotations was not available (90% of GO terms and annotations of 90% of proteins were removed for these results in Table 2), the conventional enrichment analysis failed to provide any useful function annotation most of the time. In contrast, iGFP was still able to provide a notable amount of correct GO annotations. Regarding recall (Table 2B), iGFP identified on average 41.5% (recall: 0.415) of correct GO terms after 90% of GO term removal and 79.3% (recall: 0.793) of correct GO terms after annotations of 90% of target proteins for the 10 protein groups. These results demonstrate strong superiority of iGFP over the conventional enrichment analysis in identifying functions of proteins by considering the functional relevance groups they belong to.

B. Recall
KEGG Pathway	GO removal		Protein removal
	iGFPa	Enrich	iGFP	Enrich
Allograft rejection	0.667	0.000	0.667	0.000
Apoptosis	0.438	0.125	0.938	0.000
Pathways in cancer	0.453	0.075	0.925	0.000
Chemokine signaling	0.281	0.031	0.778	0.000
Jak-STAT	0.273	0.000	0.545	0.000
Leukocyte migration	0.333	0.000	0.958	0.000
MAPK signaling	0.354	0.000	0.581	0.161
Neurotrophin signaling	0.259	0.037	0.889	0.000
T cell receptor signaling	0.565	0.261	0.782	0.000
Toll-like rec. signaling	0.522	0.217	0.870	0.000
Average	0.415	0.075	0.793	0.016

^aResults from the last iteration were shown.

Table 2.

Prediction performance of iGFP on the 10 protein groups

A. F-score
KEGG pathway	GO removal		Protein removal
	iGFPa	Enrichb	iGFP	Enrich
Allograft rejection	0.200	0.000	0.600	0.000
Apoptosis	0.233	0.211	0.667	0.000
Pathways in cancer	0.527	0.140	0.778	0.000
Chemokine signaling	0.429	0.061	0.938	0.000
Jak-STAT	0.182	0.000	0.154	0.000
Leukocyte migration	0.348	0.000	0.676	0.000
MAPK signaling	0.468	0.000	0.456	0.278
Neurotrophin signaling	0.359	0.071	0.828	0.000
T cell receptor signaling	0.456	0.414	0.581	0.000
Toll-like rec. signaling	0.522	0.357	0.714	0.000
Average	0.372	0.125	0.584	0.028

Note: Results of the GO term removal test (the MAPK signaling pathway results corresponds to Fig. 5A, C and E) and the protein removal test (corresponds to Fig. 5B, D and F) are shown. The fraction of the GO terms and proteins removed was 0.9.

^aResults from the last iteration were shown.

^bGO assignment by enrichment analysis where GO terms with P-value ≤0.01 in a cluster are assigned to member proteins.

4 Discussion

In this work, we proposed a new concept of protein group function as opposed to the conventional single-protein-single-function framework. The developed method, iGFP, is aimed at identifying function of groups of proteins even in cases that proteins are sparsely annotated. As shown in Supplementary Table S1, iGFP performed even better than sequence-based function prediction methods, PFP (Hawkins et al., 2009) and ESG (Chitale et al., 2009), for a fraction of proteins when the accuracy of single-protein function prediction was concerned. The results suggest that the group function prediction may further improve by combining with single-protein function prediction by PFP and ESG. The accuracy of iGFP will improve as more protein function association information becomes available by the advancement of omics experiments and phylogenetic analysis of the increasing number of genomes.

Funding

This work was partially supported by the National Institutes of Health [R01GM123055] and National Science Foundation [DBI1262189, DMS1614777].

Conflict of Interest: none declared.