Abstract
Brain tumor growth and tumor-induced edema result in increased intracranial pressure (ICP), which, in turn, is responsible for conditions as benign as headaches and vomiting or as severe as seizures, neurological damage, or even death. Therefore, it has been hypothesized that tracking ICP dynamics may offer improved prognostic potential in terms of early detection of brain cancer and better delimitation of the tumor boundary. However, translating such theory into clinical practice remains a challenge, in part because of an incomplete understanding of how ICP correlates with tumor grade. Here, we propose a multiphase mixture model that describes the biomechanical response of healthy brain tissue—in terms of changes in ICP and edema—to a growing tumor. The model captures ICP dynamics within the diseased brain and accounts for the ability/inability of healthy tissue to compensate for this pressure. We propose parameter regimes that distinguish brain tumors by grade, thereby providing critical insight into how ICP dynamics vary by severity of disease. In particular, we offer an explanation for clinically observed phenomena, such as a lack of symptoms in low-grade glioma patients versus a rapid onset of symptoms in those with malignant tumors. Our model also takes into account the effects tumor-derived proteases may have on ICP levels and the extent of tumor invasion. This work represents an important first step toward understanding the mechanisms that underlie the onset of edema and ICP in cancer-afflicted brains. Continued modeling effort in this direction has the potential to make an impact in the field of brain cancer diagnostics.
Introduction
Gliomas arise from non-neuronal brain cells such as neuroglia or glial cells and are the most common type of primary brain tumors diagnosed in the United States each year (1). Per World Health Organization guidelines (2), gliomas are classified by grade, which is based on histological and molecular assessments of tumor biopsy samples. In particular, grade I gliomas are slow-growing, nonmalignant, and associated with a better prognosis than grade IV gliomas, which are highly malignant and invasive with a mean overall survival of 15 months postdiagnosis (1, 3). Each year, 23,000 new cases of glioma are diagnosed in the U.S., and it is responsible for over 16,000 deaths (4, 5). This high mortality rate is, in part, due to relatively modest advances in therapies over the last 25 years (6, 7). The standard course of treatment involves a combination of surgery, radiotherapy, and chemotherapy. This treatment remains palliative rather than curative because of multiple factors, such as late detection of high-grade tumors and an inability of current imaging techniques to accurately capture the tumor boundary, especially when the cancer has infiltrated healthy tissue (6).
As brain cancers grow, tumor cells displace adjacent healthy tissue, which, together with tumor-induced vascular abnormalities, causes a disruption of the blood-brain barrier. As a result, a large volume of blood plasma leaks into the tumor tissue, causing cerebral edema, that is, abnormal swelling in the brain parenchyma (8). Because the cranial vault is an enclosed and environmentally controlled space, a growing tumor—and any associated cerebral edema—may lead to an increase in intracranial pressure (ICP), thereby disrupting the homeostatic environment within the brain. It is this increase in ICP that is responsible for many adverse symptoms associated with brain cancers, such as headaches, nausea, and seizures. Left unchecked, ICP may ultimately cause patient death (9). For these reasons, it has been hypothesized that tracking the degree of edema or changes in ICP may offer improved prognostic potential in terms of early detection of disease and better delimitation of the tumor boundary (6). This has motivated the recent development of new ultrasound techniques, such as shear-wave elastography (SWE), which can detect changes in ICP that may be caused by a growing tumor (10).
Our goal in this article is to explicate how edema and elevated ICP develop in brains afflicted with cancer. To realize this aim, we propose a mathematical model of the biomechanical effects of cancer on adjacent, healthy brain tissue. Specifically, a multiphase framework is employed to describe the physical forces and interactions that are involved in the response of brain tissue to a growing tumor. Using analytical and numerical techniques, we explore parameter regimes that correspond to different tumor grades and establish how these may correlate with ICP time courses. Our model, if validated with experimental data, has the potential to accelerate the clinical applicability of new diagnostic modalities such as SWE. Indeed, mathematical models have been employed extensively to describe the growth and response to treatment of gliomas (for instance, see (11, 12, 13, 14, 15, 16); we refer the reader to (17) for a recent review). However, the focus of these previous models has been to predict either the extent to which the tumor has invaded brain tissue or the outcome of different treatment strategies. To the best of our knowledge, ours is the first model to explicitly consider tumor-induced changes in ICP.
The remainder of this manuscript is organized as follows. In Mathematical Model, we present our mathematical model and describe the numerical scheme employed to simulate our model. We also provide a discussion on parameter values and constitutive assumptions. In Astrocytomas by Grade: Scaling Regimes and Simulations, we employ singular perturbation techniques to study parameter regimes that correspond to brain cancer by grade and present numerical validation of our analysis (details of the numerical methods and model analysis are provided in the Supporting Materials and Methods). In Application: Modeling Peritumoral Edema with Proteases, we extend our model to investigate the effect of proteases released by the tumor on the emergence of peritumoral edema. Finally, we conclude with a discussion on the significance of our findings in Discussion.
Mathematical Model
Model derivation
A multiphase framework is used to describe the response of healthy brain tissue to a growing tumor. Indeed, multiphase models have been used extensively to simulate various aspects of cancer biology, such as tumor growth, tumor-extracellular matrix interactions (18), cancer infiltration (19, 20, 21, 22), and tumor encapsulation (23). We refer the reader to (24) for a review of such models. We remark that although we follow the general framework provided in (20, 23), our model differs significantly from those preceding it in that we are focused on the biomechanical response of healthy tissue to a growing (brain) tumor rather than the tumor itself or the tumor’s response to therapeutic intervention.
In our modeling framework, healthy brain tissue is viewed as a mixture of two distinct phases: a cellular phase comprising brain cells, such as neurons and glial cells, and an aqueous phase consisting of interstitial fluid, blood, and any dissolved components. Mass and momentum balances are applied to both phases. The resulting equations are closed by imposing suitable constitutive relations for mass exchange between the different phases, the partial stress tensors, and momentum transfer between the phases. The mass exchange terms are chosen to encourage the maintenance of healthy homeostasis, whereas the choice of stress tensors and momentum transfer terms are based on the assumed mechanical properties of each phase. Note that, because our focus is on describing the development of edema and ICP in the healthy tissue surrounding the tumor, we do not explicitly model the tumor itself.
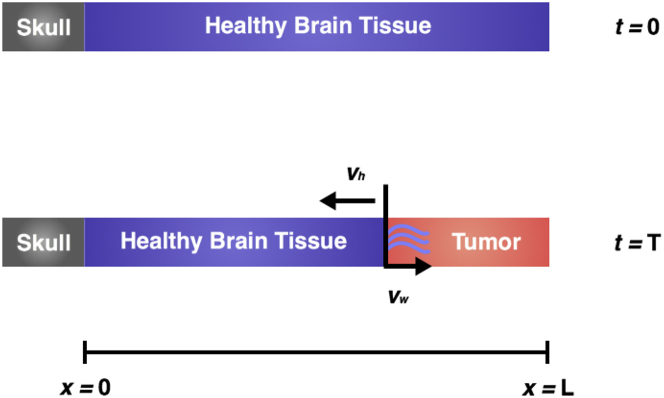
For simplicity, we formulate our model in one-dimensional Cartesian geometry with x = 0 representing the skull and x = G(t) representing the boundary of an implicit growing tumor. Specifically, the tumor is assumed to occupy the region G(t) < x < L, and the tumor-healthy tissue boundary moves with a fixed velocity v, which is assumed to correlate with tumor growth rate. That is, G(t) = G(t = 0) − vt, where G(t = 0) = L. Of course, high-grade cancers may not have well-defined boundaries, and individual cells shed from the primary tumor mass may infiltrate surrounding tissue. However, these cells occupy a negligible volume and will not contribute to changes in ICP and may, therefore, be ignored in our formulation. In such cases, G(t) may be viewed as representing the boundary of the bulk of the tumor mass. A model schematic is shown in Fig. 1.
Figure 1.
Schematic showing the geometry of the model domain. The skull is located at x = 0, and x = G(t) represents the boundary of a growing tumor, which is assumed to occupy the region G(t) < x < L, shown in red. The tumor-tissue interface is assumed to move into healthy tissue with a fixed velocity v that is representative of tumor growth. This boundary is permeable to fluid but impermeable to healthy tissue, and the skull is impermeable to both tissue and fluid. To see this figure in color, go online.
We denote the volume fraction of healthy tissue by h(x,t) and that of the aqueous phase by w(x,t). Their corresponding velocities and stress tensors are denoted vh, vw, σh, and σw, respectively, these quantities being scalars for the one-dimensional geometry considered here. Both phases are assumed to be incompressible fluids whose densities are, to leading order, equal. In consequence, mass balances for each phase may be expressed as:
| (1) |
| (2) |
where [⋅]t and [⋅]x denote partial derivatives with respect to time and space, and Sh and Sw denote the net rates of the production of healthy cells and water, respectively. We assume that the system is closed, and hence, there is no net volume change; the volume is simply transformed from one phase to another. Assuming further that there are no voids within the region, we obtain:
| (3) |
Following (23), healthy cells are assumed to proliferate by absorbing water at a rate which is proportional to h and w, and they undergo apoptosis at a rate that is proportional to h. Taken together, these assumptions yield:
| (4) |
where ρ = rh − δh is the net growth rate of healthy cells, and h∞ = (1 − δh/rh) represents their steady-state volume fraction in the absence of external stimuli.
Next, neglecting inertial effects and assuming that no external forces act on the system, the momentum conservation laws may be written as follows:
| (5) |
| (6) |
where Fhw is the force exerted on healthy tissue by the aqueous phase, an equal and opposite force being exerted by healthy tissue on the aqueous phase. We view the cells and aqueous fluid as inviscid fluids and, following (23, 25), we prescribe the stress tensors σh and σw to be the following:
| (7) |
| (8) |
where p is the assumed pressure common to both phases, and Γ(h) represents an additional isotropic pressure that distinguishes healthy tissue from water and may account for cell-cell adhesion and membrane stress. Following (23), the interaction or drag term Fhw is taken to be proportional to both the product of the volume fractions, wh, and the relative velocities of the phases, so that:
| (9) |
This choice of Fhw ensures that that there is no drag if one of the phases is not present. The equations governing the dependent variables h(x,t), w(x,t), vh, vw, and p are closed by prescribing Γ(h) and appropriate boundary and initial conditions. Specifically, brain tissue is taken to be at its spatially homogeneous equilibrium state initially, that is, h(x, 0) = h∞ < 1. The skull is assumed to be impermeable to both tissue and water so that vh = 0 = vw at x = 0. The tumor is also assumed to be impermeable to the solid tissue phase. That is, vh = −v at x = G(t), where G(t) = L − vt. Further, brain cancer growth is known to disrupt the blood-brain barrier, inducing vessel permeability that allows fluid to leak into the tumor tissue (8); therefore, we assume that the tumor is permeable to fluid. In practice, water may flow from the tumor into the healthy tissue or vice versa. Here, we assume that once fluid enters the tumor it cannot escape.
Model simplification
We now reduce the two-phase model developed above to a single nonlinear parabolic equation for the volume fraction of the cellular phase. We eliminate w = 1 − h from the model equations via the “no voids” assumption in Eq. 3. Then, adding Eqs. 1 and 2:
| (10) |
Integrating the above with respect to x and recalling that the skull (at x = 0) is impermeable to fluid and tissue, we obtain:
| (11) |
Adding Eqs. 5 and 6, and using Eqs. 3, 7, and 8, the momentum balance for the system reduces to:
| (12) |
that is, p(x,t) = −hΓ (h) + p0(t). We now substitute from Eqs. 4, 8, 9, 11, and 12 into Eq. 6 to obtain the following expression for the velocity of the tissue phase:
| (13) |
We note that the positive constant khw may be absorbed into Γ(h), and therefore, we neglect it in what follows. Finally, we substitute from Eq. 13 into Eq. 1 to arrive at the following partial differential equation (PDE) describing the biomechanical response of healthy tissue to a growing tumor:
| (14) |
Model parameters
The following parameters have been introduced in Eq. 14: h∞, a dimensionless constant representing the volume fraction of healthy brain tissue at homeostasis; L, the characteristic distance in micrometers from tumor origin to the skull; ρ, the rate, per unit time, of brain remodeling; and v, the velocity, in micrometers per unit time (26), of the detectable tumor margin. Parameters arising from the choice of Γ(h) are discussed in Parameter Values and Functional Forms. Because we are interested in the response of healthy tissue to a growing tumor, the unit of time should correspond to the timescale of tumor growth, for instance, days.
Numerical methods
Our challenge now is to numerically solve the nonlinear reaction-diffusion system (14) with a moving boundary. We first transform the moving domain [0, L − vt] to a fixed one [0, L] via:
| (15) |
Consequently, Eq. 14 transforms to:
| (16) |
Note that the coordinate transformation introduces an advection term on the left-hand side of the PDE. Thus, (16) is an advection-reaction-diffusion PDE with variable-coefficient advection and nonlinear diffusion. To integrate this system forward in time, we employ operator splitting, which has the advantage of superior stability (27). In particular, we integrate the reaction-diffusion term over one time step using Crank-Nicolson, with the nonlinearities lagged. This provisional solution is then advected using upwinding to obtain u at the next time step. Note that the advection term vanishes at the left boundary, which allows the associated boundary condition to be safely omitted from the advection step. The overall accuracy of this scheme is second order in space and first order in time. Further details on the numerical scheme and its validation with a test problem can be found in the Supporting Materials and Methods.
Parameter values and functional forms
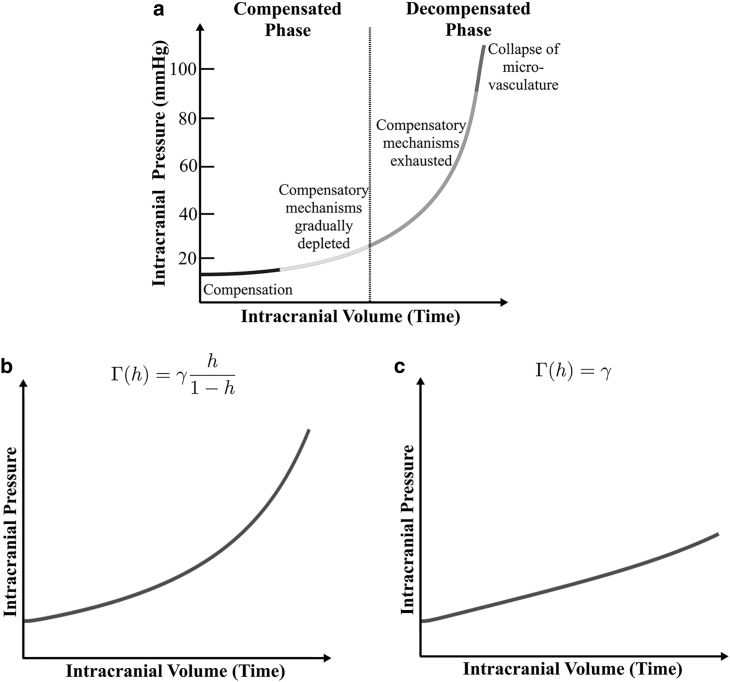
Eq. 14 are completely determined by the appropriate choices of the additional isotropic pressure Γ(h) in the tissue fraction, the volume fraction h∞ of healthy brain at homeostasis, the speed v at which the tumor-healthy tissue boundary moves, and the rate ρ of healthy brain tissue remodeling. We first discuss our choice for Γ(h). Patients with slow-growing tumors are initially asymptomatic because of minimal changes in their ICP. If the tumor continues to grow in size, eventually different compensatory mechanisms of the brain will be exhausted, resulting in a sharp increase in ICP (28). Langfitt et al. (29) proposed a qualitative relation between ICP and intracranial volume, shown in Fig. 2 a, which represents this sequence of disease progression and which remains widely used in the biomedical literature (30, 31, 32). We therefore choose a functional form for Γ(h) that reproduces the Langfitt curve. Specifically, we take:
| (17) |
for some constant of proportionality, γ, with units μm2/day.
Figure 2.
(a) Reproduction of the qualitative Langfitt Curve following (45), Fig. 2 in (46), and Fig. 2 in (47). As intracranial volume increases with time, the compensatory mechanisms that prevent an initial rise in ICP are exhausted. (b) Shown is a model output of average ICP versus time for simulations of Eq. 14 with v = 0.01 and ρ = 0.1. (c) Shown is a model output of average ICP versus time when there is constant isotropic pressure with v = 0.01 and ρ = 0.1.
Model parametrization
We now discuss our choice of model parameter values. Without loss of generality, we set h∞ = 0.5. The choice of v and, to a certain extent, ρ will determine the type of brain cancer being simulated and are expected to vary with cancer by grade. γ may be regarded as representative of the mechanical properties of brain tissue. In the absence of biological data with which to estimate these parameters, we begin by nondimensionalizing (16) by introducing the rescaled variables x∗ = x/L and t∗ = (γ/L2)t. With this rescaling, model parameters in dimensionless terms are v∗ = (L/γ)v, ρ∗ = (L2/γ)ρ, γ∗ = 1, and L∗ = 1. We then illustrate the various responses of brain tissue to a growing tumor by numerically integrating the model for a range of values of v and ρ (see below). In Astrocytomas by Grade: Scaling Regimes and Simulations, we analytically investigate how the system dynamics change as the timescales of tumor growth and brain remodeling are varied with respect to γ. In Clinical Data Required for Model Parametrization and Validation, we present a short discussion on the type of clinical data required to estimate these parameters and to validate model results. Note that, in what follows, the asterisks are dropped for convenience. A list of parameter values used to simulate the model is provided in Table 1.
Table 1.
Nondimensional Parameters and Their Values
| Parameter | Value or Range |
|---|---|
| h∞ | 0.5 |
| ρ | 0–1 |
| v | 0.01–1 |
Fig. 2 b shows model predictions of the average ICP versus time for a specified set of model parameters (v = 0.01, ρ = 0.1), which is observed to qualitatively agree with the behavior of ICP expected from the Langfitt curve. We calculated average ICP by integrating Eq. 12 and averaging the resulting pressure p(x,t) over space. We remark that other functional forms of Γ(h) are also possible; our choice was governed by reasons of simplicity and to keep the number of unknown parameters at a minimal.
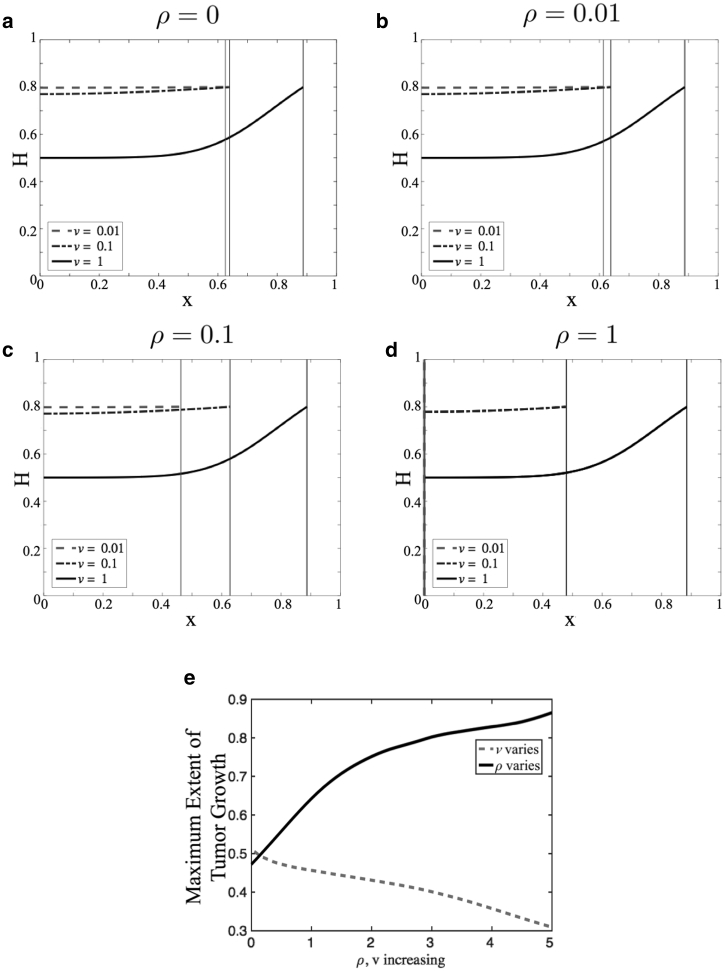
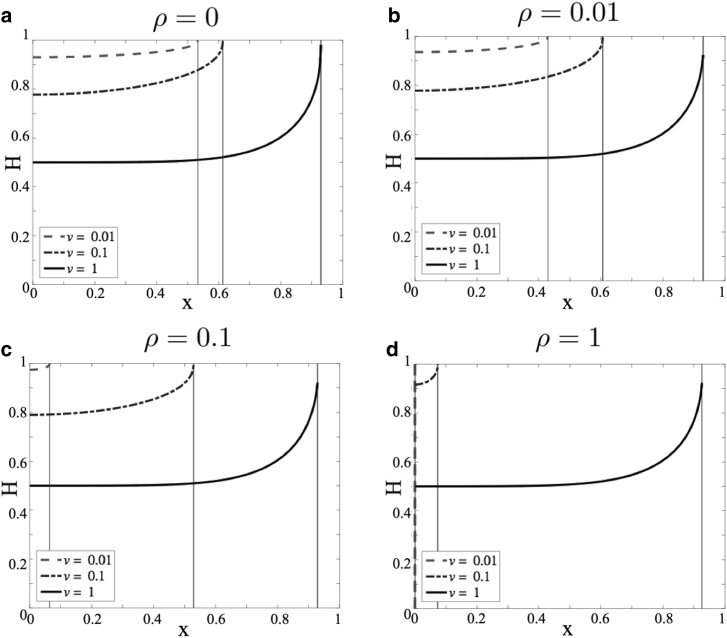
To illustrate model dynamics for this choice of Γ(h), we present numerical simulations because model parameters are varied. Specifically, we vary v and ρ. Fig. 3, a–d show plots of h(x,t) versus x as the rate ρ of tissue remodeling is increased. For each value of ρ, different rates v of tumor growth are considered, as indicated. The simulations are run until t = tf, where tf is the time when either h(x,t) = 0.8 or the tumor boundary G(t) reaches x = 0, whichever happens first. The plots are snapshots of the volume fraction of healthy tissue at this final time. As the tumor grows, water leaks into the tumor space, and consequently, the volume fraction of healthy tissue increases across the simulation domain. Because we do not model tumor growth explicitly, we cannot quantify fluid accumulation or edema in the tumoral space. Rather, any increase in h above its equilibrium value h∞ is taken to represent tumoral edema because the motion of the tumor boundary into healthy tissue causes fluid to leak into the tumor space. In all cases considered, when v is small compared to γ (dashed and dash-dotted curves), the healthy tissue fraction appears to increase uniformly across the domain as the tumor grows. This is because the diffusion of healthy tissue over space overcomes the pushing effect of the tumor boundary. As a consequence, the tumor can invade far into the healthy tissue. Moreover, when ρ is large and v is small (Fig. 3 d, dashed and dash-dotted curves), remodeling ensures that the healthy tissue fractions stay below one longer so that the tumor invades the farthest. This observation is summarized in Fig. 3 e, which shows the maximal degree of tumor invasion into healthy tissue as v and ρ are varied. On the other hand, when v is comparable to γ, h(x,t) → 1 rapidly at the tumor boundary, and the tumor is predicted to cease growth because of a lack of space. Biologically, this could mean that the primary tumor mass has reached a critical size. At this point, individual tumor cells may be shed from the primary tumor and invade into healthy tissue as is known to happen in GBM (33).
Figure 3.
(a)–(d) Plots of h(x,t) versus x as ρ, in which the rate of tissue remodeling varies ((a) ρ = 0, (b) ρ = 0.01, (c) ρ = 0.1, and (d) ρ = 1). In each case, different values of v, the tumor growth rate, are considered (dashed curve, v = 0.01; dash-dotted curve, v = 0.1; and solid black curve, v = 1). Simulations of Eq. 14 were run until either h(x,t) = 0.8 or the tumor boundary reaches x = 0. The vertical lines denote the position of the tumor. (e) Distance invaded by the tumor into healthy tissue as v and ρ are varied.
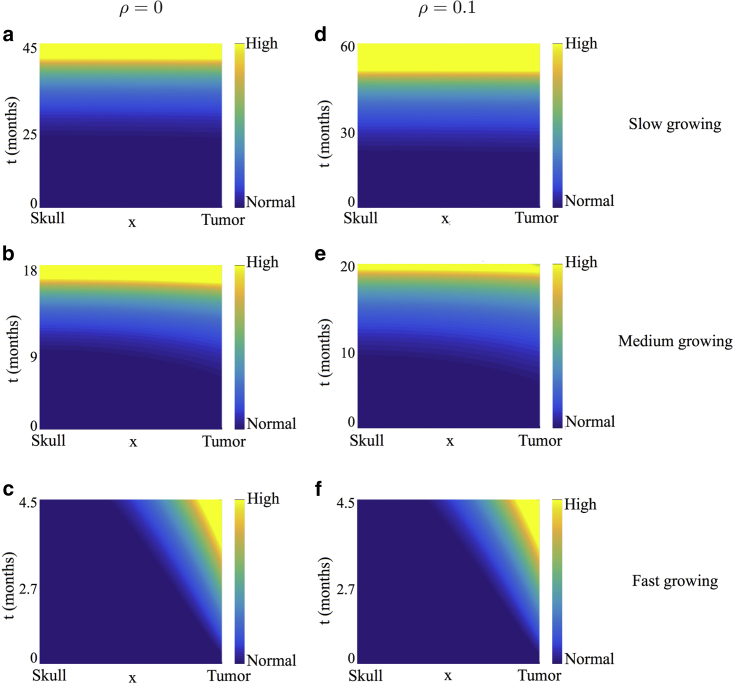
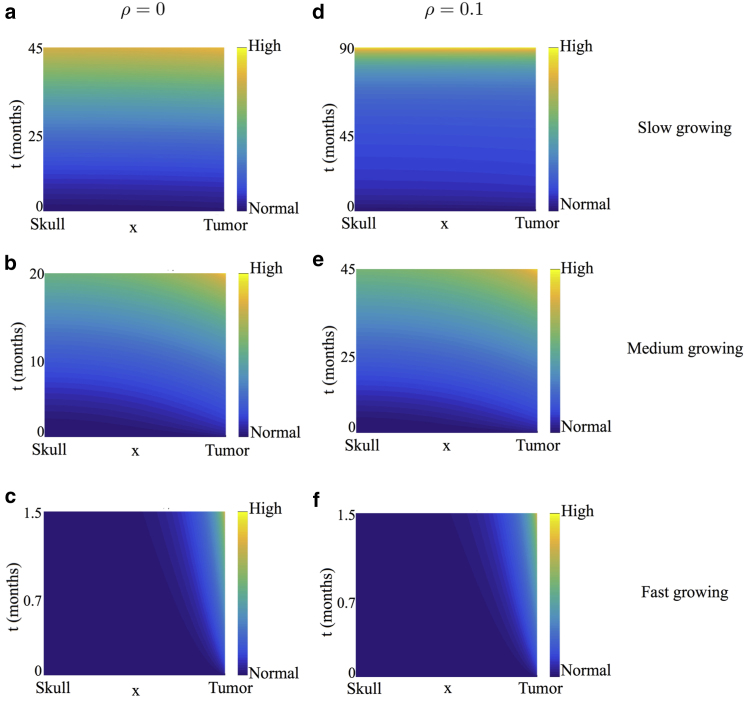
We also present a heat map of pressure corresponding to some of the cases discussed above. Specifically, we choose ρ = 0 (Fig. 4, first column) and ρ = 0.1 (Fig. 4, second column) for illustrative purposes. For each value of ρ, we consider a slow-, medium-, and fast-growing tumor as before. These pressure plots correspond to the profiles in Fig. 3, a and c, respectively. Time is plotted on the y axis, and space is plotted on the x axis. For ease of visualization, the pressure plots are shown in the transformed stationary domain, with the skull at x = 0 and the tumor boundary at x = 1. In all cases, when v is small compared to γ (Fig. 4, a, b, d, and e), ICP is predicted to increase almost uniformly across the domain with minimal increase initially when the tumor is small. Such a patient may remain asymptomatic during the initial stages of tumor growth with symptoms manifesting only when ICP changes appreciably. For a faster growing tumor (Fig. 4, c and f), pressure throughout the domain barely changes except near the tumor. These predictions reflect what is observed clinically, that is, sharp increases in ICP when compensatory mechanisms are exhausted (28, 34, 35), lending credibility to our model.
Figure 4.
Heat map of pressure corresponding to the healthy tissue profiles shown in Fig. 3, a and c. Time, measured in months, is plotted on the y axis, and space is measured on the x axis. For ease of visualization, the pressure plots are shown in the stationary domain with the skull located at the minimal of the x axis and the tumor boundary at the maximal of the x axis. (a)–(c) correspond to ρ = 0, and (d)–(f) correspond to ρ = 0.1. For each value of ρ, different values of v, the tumor growth rate, are considered ((a and d) v = 0.01, (b and e) v = 0.1, and (c and f) v = 1). To see this figure in color, go online.
Finally, for illustrative purposes, we also present numerical simulations of the case when Γ(h) is a constant rather than an increasing function of h(x,t). Fig. 5 presents plots of h(x,t) versus x as ρ is increased, with different tumor growth rates v considered for each value of ρ as before. The corresponding pressure plots are shown in Fig. 6. Qualitatively, Figs. 3 and 5 are similar; they both predict that slow-growing tumors can invade farther into the brain, but for faster growing tumors, the primary tumor mass ceases growth sooner. Thus, these graphs are not by themselves indicative of whether Γ(h) = γ or Γ(h) = γh/(1 − h) is a more biologically appropriate functional form for the additional isotropic pressure in the tissue phase. However, when we look at the predicted changes in ICP shown in Fig. 6—which are quantified in Fig. 2 c—we observe that when Γ(h) is constant, ICP increases linearly and does not match the Langfitt curve.
Figure 5.
(a)–(d) Plots of h(x,t) versus x when the additional isotropic pressure in the tissue phase is constant, that is, Γ(h) = γ, and ρ, the rate of tissue remodeling, is varied ((a) ρ = 0, (b) ρ = 0.01, (c) ρ = 0.1, and (d) ρ = 1). In each case, different values of v, the tumor growth rate, are considered (dashed curve, v = 0.01; dash-dotted curve, v = 0.1; and solid black curve, v = 1). Simulations of Eq. 14 were run until either h(x,t) approaches 1 or the tumor boundary reaches x = 0. The vertical lines denote the position of the tumor.
Figure 6.
Heat map of pressure corresponding to the healthy tissue profiles shown in Fig. 5, a and c when the additional isotropic pressure in the tissue phase is constant, that is, Γ(h) = γ. For ease of visualization, the pressure plots are shown in the stationary domain with the skull and the tumor boundary located at the minimal and maximal of the x axis, respectively. Time, measured in months, is plotted on the y axis. (a)–(c) correspond to ρ = 0, and (d)–(f) correspond to ρ = 0.1. For each value of ρ, different values of v, the tumor growth rate, are considered ((a and d) v = 0.01, (b and e) v = 0.1, and (c and f) v = 1. To see this figure in color, go online.
Clinical data required for model parametrization and validation
Normal ICP ranges from 5 to 15 mmHg in healthy adults and is significantly affected by changes in intracranial volume (36). As mentioned in the Introduction, SWE is a noninvasive technique capable of measuring increases in ICP. It is routinely used to diagnose breast or liver disease but not brain diseases (10). It can generate real-time, two-dimensional maps of shear-wave velocity and shear modulus within the tumor, at its border, and within normal brain tissue. Generally, images are 38.4 × 40.0 mm, and data are presented in kilopascals. Such measurements can be used to calculate the Young’s modulus, in kilopascals, which correlates linearly with ICP, in mmHg (10). For our purposes, multiple images of the same brain region per patient would be needed to generate averaged time course data comparable to the model output presented in Fig. 2 b. Once available, these time courses can be used to infer an appropriate functional form for Γ(h) and to estimate the rate of brain remodeling, even at an individual patient level. Because such data would be spatially resolved, the SWE technique is a natural choice for model parametrization.
Results
Astrocytomas by grade: scaling regimes and simulations
As mentioned in the Introduction, brain tumors are classified by grade I–IV, in which grade I is a benign tumor and grade IV the most malignant (2). In our model, γ (additional isotropic pressure), ρ (healthy tissue remodeling), and v (tumor growth rate) are critical determinants of the response of healthy tissue to a growing tumor in terms of the following: changes in ICP; how far the tumor can invade into healthy tissue; and peritumoral edema, the change in tissue volume fraction above a normal state. We now propose regimes of parameter space that correspond to each grade, focusing on astrocytomas, the most common and malignant type of gliomas (1, 37). However, similar analyses may be conducted for other types of brain cancer.
Specifically, we identify and analyze distinguished limits of the parameters γ, v, and ρ that yield distinct profiles for ICP, the degree of tumor invasion, and the deviation of tissue volume fraction from its healthy steady state. These profiles are then compared qualitatively to clinical observations and are supported by numerical simulations for typical cases. For simplicity, and without loss of generality, we set L = 1 in Eq. 14. This is equivalent to rescaling the spatial variable x by 1/L, leading to a rescaling of v by 1/L and γ by 1/L2. We restrict our attention to and . Note that is biologically unrealistic because in such a regime, there will be no increase in ICP as the tumor grows. In particular, we focus on ; yields qualitatively similar results. Time is rescaled, if necessary, so that significant tumor growth can be observed. A summary of how parameter regimes correspond to astrocytomas by grade is provided in Table 2.
Table 2.
Parameter Regimes for Astrocytomas by Grade
| Grade | γ | v | ρ | t | Results | |
|---|---|---|---|---|---|---|
| Pilocytic astrocytoma | I | minimal uniform increase in ICP | ||||
| Diffusive astrocytoma | II | slow uniform increase in ICP | ||||
| Anaplastic astrocytoma | III | fast uniform increase in ICP | ||||
| Glioblastoma | IV | fast nonuniform increase in ICP |
Pilocytic astrocytoma (grade I)
Pilocytic astrocytomas are benign, slow-growing tumors of moderate cellularity. Patients with grade I astrocytomas have a good prognosis in general because gross total resection is typically curative (38). Despite this, these tumors can become very large and remain asymptomatic for prolonged periods of time because of minimal changes in ICP (35, 39).
In our model, taking and corresponds to a pilocytic astrocytoma. This can be seen by performing the transformation , and in Eq. 14. Additionally, we rescale time to be on a long timescale , so that we can observe significant tumor growth, that is, we define τ = ϵt. Then, Eq. 14 reduces to:
| (18) |
We seek solutions of Eq. 18 in the form of a regular power series expansion, with . At leading order, we obtain:
| (19) |
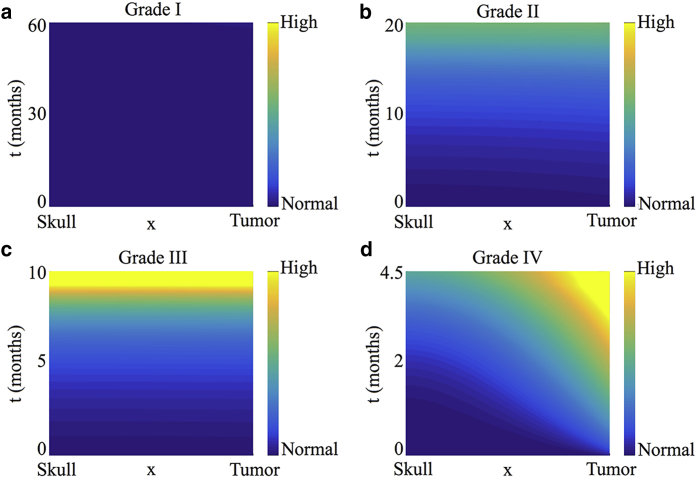
Thus, we predict that the volume fraction of the healthy tissue will increase uniformly across the simulation domain as the tumor boundary moves. Higher-order correction terms may be determined in a similar manner (details of this analysis are presented in Supporting Materials and Methods, Section S4.1, together with figures showing a comparison of h(x,t) time courses for the full model and the asymptotic solution). Fig. 7 a shows a heat map of the predicted pressure under this parameter regime. As expected, the slowly growing tumor invades the healthy tissue without a significant buildup of ICP. Our results are therefore consistent with clinical observations because grade I astrocytomas are benign and remain asymptomatic for a long time (35, 39).
Figure 7.
Pressure heat maps for parameter regimes corresponding to tumors by grade: (a) grade I, pilocytic astrocytoma, , ; (b) grade II, diffusive astrocytoma, , ; (c) grade III, anaplastic astrocytoma, , ; and (d) grade IV, glioblastoma, , . In all cases, . Specific parameter values for the simulations shown are given in Table S4.1. To see this figure in color, go online.
Diffusive astrocytoma (grade II)
Diffusive astrocytomas grow faster than pilocytic astrocytomas but slower than tumors of grades III and IV and have ill-defined boundaries. Consequently, they cannot easily be cured by surgical resection alone. Patients with diffusive astrocytomas typically survive for 5–8 years and display symptoms related to increased ICP (35, 38, 39).
We show below that taking and corresponds to a diffusive astrocytoma. In this case, remodeling and tumor growth occur on the same timescale, and this is shorter than that for the grade I pilocytic astrocytoma considered in Pilocytic Astrocytoma (Grade I). Additionally, with (as before), Eq. 14 supplies:
| (20) |
As before, we look for regular power series expansions of the form . It is straightforward to show that the leading order term is given by:
| (21) |
Higher-order correction terms may be determined in a similar manner. Figures comparing time courses of h(x,t) for the full model and the asymptotic solutions can be found in Supporting Materials and Methods, Section S4.2 (Fig. S4.6). Fig. 7 b shows a heat map of the pressure for this parameter regime. As expected, there is a slow but noticeable buildup of ICP, and the distribution of h(x,t) across the spatial domain is no longer uniform. Our results are consistent with clinical observations of diffusive astrocytomas, which are relatively slow growing but cause ICP to increase.
Anaplastic astrocytoma (grade III)
Anaplastic astrocytomas are malignant tumors with a mean survival of three years (38). They are more aggressive than grade I and II astrocytomas and tend to have tentacle-like projections (39). In contrast to the previous cases, in which the brain can adapt, to some extent, to the growing tumor, now the increase in ICP is more rapid. Consequently, symptoms for grade III (and also grade IV) astrocytomas appear more rapidly (35).
For anaplastic astrocytomas we assume that the tumor grows at a comparable speed as in the previous case, so that . Because the brain does not adapt as quickly to volume changes induced by tumor growth, we fix . In particular, we take ρ = 0 for analytical tractability. Additionally, with (as before), Eq. 14 reduces to:
| (22) |
with initial and boundary conditions remaining unchanged from the previous case (grade II). By seeking solutions of the form , it is straightforward to show that:
| (23) |
Thus, at leading order, anaplastic astrocytomas behave like pilocytic astrocytomas. However, the first correction term for anaplastic astrocytomas reveals spatial inhomogeneity. That is:
| (24) |
This is in contrast to the case of pilocytic astrocytomas, in which the first correction term is also independent of space. Details of this analysis are presented in Supporting Materials and Methods, Section S4.3, together with figures comparing time courses for the full model and the asymptotic approximation (Fig. S4.7). Fig. 7 c shows a heat map of the predicted pressure under this parameter regime. Our results are consistent with clinical observations in that the buildup of ICP is more rapid as compared to that in astrocytomas of grades I and II.
Glioblastoma multiforme (grade IV)
Glioblastomas (GBM) are the most rapidly growing and malignant of astrocytomas (1). GBM are extremely aggressive, and patients have an average survival period of 12–18 months postdiagnosis (38).
We show below that taking , so that , corresponds to GBM. As in the case of anaplastic astrocytoma, we assume , that is, , because the brain does not adapt quickly to volume changes induced by tumor growth. When modeling GBM, we rescale time by setting τ = t/ϵ so that we can capture effects that act on the short growth timescale. Additionally, we consider . Under these assumptions, Eq. 14 reduces to:
| (25) |
In this case, if we seek a regular power series expansion for h(x,τ), then we recover Eq. 14 at leading order. Therefore, this case needs to be considered numerically. However, the asymptotic approximation for grade III cancer as given by Eqs. 23 and 24 can be rescaled to approximate the initial stage of GBM. That is, introducing the transformation and t = ϵτ in Eqs. 23 and 24 supplies:
| (26) |
Figures comparing h(x,t) time courses for numerical solutions of the full model and approximation (26) are included in Supporting Materials and Methods, Section S4.4 (see Fig. S4.8). Fig. 7 d shows a heat map of the pressure under this parameter regime. In agreement with clinical observations, our model simulations predict a rapid increase in ICP due to GBM growth. In contrast to the case for anaplastic astrocytomas, the increase in ICP is no longer spatially uniform, with the tumor-healthy tissue interface corresponding to the region of highest pressure.
Application: modeling peritumoral edema with proteases
The results presented in the previous sections reveal that our model captures key aspects of the mechanical response of brain tissue to tumor growth and that it can be used to identify parameter regimes that correspond to tumor grades. One limitation of the model is that if the tumor growth rate v is large, then all the fluid adjacent to the tumor leaks into it, causing the volume fraction of healthy tissue rapidly to approach one near the tumor boundary, which is biologically unrealistic. In practice, the mechanisms of tumor invasion are complex and depend, in part, on the secretion of several proteases that degrade healthy tissue and create space locally for tumor cells to invade and migrate (40). In this section, we explain how we can extend our model to investigate the effect that tumor-derived proteases may have on ICP levels and tumor invasion.
Existing models (23, 41) typically view proteases as diffusible species. However, others argue that proteases act locally in the immediate vicinity of the tumor source (42). This point of view has been validated in recent experiments wherein protease expression was evaluated in vivo in a rat brain gliosarcoma xenograft model using magnetic resonance imaging. The experiments showed that proteases were localized in the peritumoral region (43). Consequently, we assume that tumor-derived proteases will degrade healthy tissue adjacent to the moving tumor boundary, within a small region of width ∼δ. To account for this effect, Eq. 14 is amended as follows:
| (27) |
where the rate of tissue degradation λ(x,t) is assumed to be of the form:
| (28) |
The initial and boundary conditions used to close Eq. 27 remain unchanged. In Eq. 28, the constant α represents the maximal rate at which proteases degrade healthy tissue, and the constant ω determines the sharpness of the boundary of the region within which proteases are active.
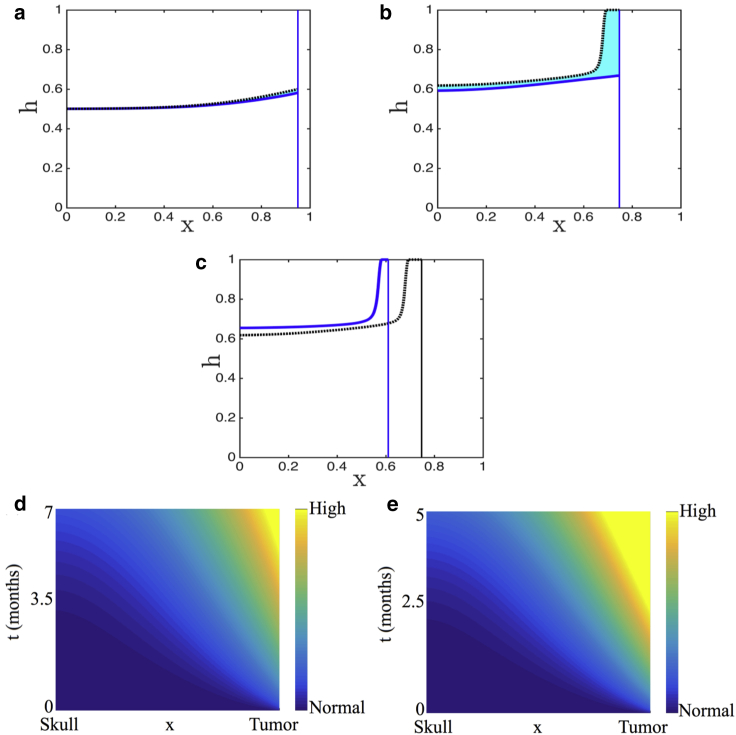
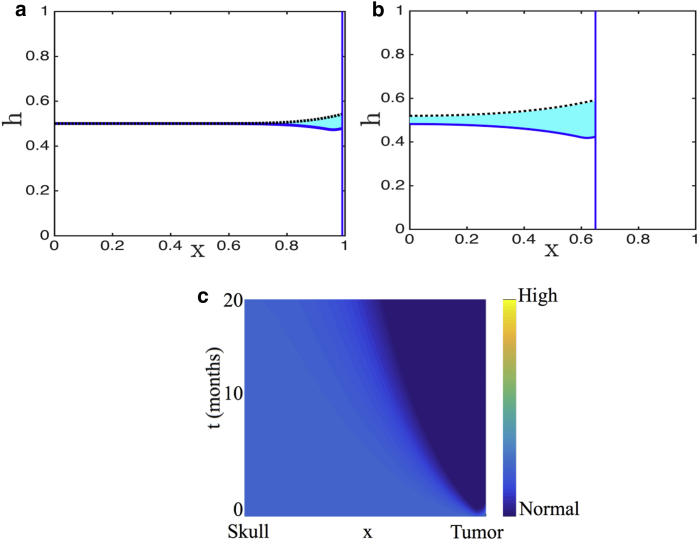
For illustrative purposes, we simulate the response of brain tissue to a fast-growing tumor, such as GBM, and a slow-growing tumor. Results for other malignancies can be similarly simulated. Fig. 8, a–c show time snapshots of GBM growth, with and without active proteases. Specifically, Fig. 8 a shows an early stage of tumor growth, Fig. 8 b shows a snapshot at the time when the tumor not secreting proteases has invaded its farthest, and Fig. 8 c shows the simulations at the time when the tumor-secreting proteases has invaded its farthest. As can be seen, secreting proteases allows the tumor to keep growing for longer, with greater invasiveness. Fig. 8, d and e graph the heat maps of corresponding changes in ICP with and without the effect of proteases, respectively. In both cases, a nonuniform increase in ICP is predicted as in the case of GBM earlier. However, ICP onset is slightly delayed with active proteases because the degradation of healthy tissue relieves the initial increase in ICP. Clinically, this could explain why symptoms manifest late.
Figure 8.
Numerical solution of the model including proteases (solid blue line) is contrasted with the solution of the model without proteases (dashed black line). The area in between is shaded in cyan to highlight the difference. Parameter values are representative of GBM (γ = 10, ρ = 0.01, v = 10, and α = 20). We present snapshots at (a) an early time, (b) the time when the tumor in the absence of proteases has ceased to invade, and (c) the time when the tumor-secreting proteases have ceased to invade. (d and e) show the corresponding heat maps of pressure in GBM with (d) and without (e) protease secretion. To see this figure in color, go online.
On the other hand, in Fig. 9, a and b, we present h(x,t) time snapshots for a slow-growing tumor, with and without the effect of proteases. In this case, the tumor invades the simulation domain regardless of whether active proteases are present. However, the release of proteases results in an elevated fluid fraction near the tumor, which may be interpreted as peritumoral edema. As for pilocytic astrocytomas, there is minimal change in ICP regardless of whether tumor-derived proteases are present (Fig. 9 c). These minimal changes in ICP are insignificant compared to the changes in ICP in the case of GBM.
Figure 9.
Numerical solution of the model including proteases (solid blue line) is contrasted with the solution of the model without proteases (dashed black line). The area in between is shaded in cyan to highlight the difference. Parameters values are representative of a slow-growing tumor (γ = 0.01, ρ = 0.2, v = 0.01, and α = 0.4). We present snapshots at (a) an early time and (b) an intermediate time. (c) Shown is the corresponding heat map of pressure in a slow-growing tumor that is secreting proteases. To see this figure in color, go online.
Discussion
Brain tumor growth disrupts the blood-brain barrier, thereby causing cerebral edema (8, 9, 35, 38). Because the brain is enclosed in the cranial vault, tumor growth and/or edema results in an increase in ICP that is initially offset by compensatory mechanisms, such as cerebrospinal fluid displacement, cerebral blood flow decrease, and changes in the parenchyma shape. Over time, as the tumor progresses, such compensatory mechanisms are exhausted, and ICP increases sharply (28). Currently, there is no clearly defined ICP threshold signaling the need for therapeutic intervention (44). Understanding the relationship between ICP and tumor volume is crucial for determining such a threshold and could be used as a new prognostic indicator.
Here, we proposed a biomechanical model of the response of brain tissue to a growing tumor to understand how factors, such as tumor growth rate, healthy tissue remodeling rate, and the mechanical properties of brain tissue, affect ICP. We viewed the brain as a two-phase mixture: a healthy tissue phase and a watery phase. The model was derived using principles of mass and momentum balances and numerically integrated using an operator splitting scheme. Tumor growth was simulated by shrinking the right boundary of the domain. Model simulations and analysis provided critical insight into how edema and ICP depend on brain tumor by grade. In particular, we proposed parameter regimes that capture the differences in ICP dynamics associated with different grades of astrocytomas and used perturbation methods to derive analytical approximations to model solutions in these cases.
Slow-growing astrocytomas were predicted to grow further into healthy tissue than faster, more malignant tumors, resulting in more edema over time. At the same time, changes in ICP were minimal in such tumors. This could explain why clinically, patients with grade I and II astrocytomas often exhibit symptoms only once their tumors have grown to a large extent. In contrast to those with astrocytomas of lower grade, patients with grade III and IV cancers typically present with acute symptoms. Model simulations revealed that for such faster growing tumors, the compensatory mechanisms of the brain are exhausted, inducing a sharp rise in ICP, especially near the tumor boundary. We remark that, as a first step toward a better understanding of tumor-induced edema and elevated ICP, we made the simplifying assumption of prescribing tumor growth rather than explicitly modeling the tumor itself. In future work, we plan to relax this assumption. Model validation—and extension to higher spatial dimensions—will be possible once increased clinical data in the form of SWE-derived real-time estimates of brain and cancer tissue stiffness become available.
One limitation of our model was that faster growing tumors such as GBM could not invade far into the brain because of the volume fraction of healthy tissue rapidly approaching one near the tumor boundary. We therefore extended the scope of our model to include the effect that tumor-derived proteases may have on ICP levels and tumor invasion. Model simulations predicted that accounting for protease secretion by the tumor increased its invasiveness and may also be a potential mechanism underlying peritumoral edema onset.
Although simple, our model captures the biomechanical response of healthy brain tissue, in terms of changes in ICP and edema, to a growing tumor. Key differences in edema and pressure profiles were predicted that corresponded to tumors by grade. Thus, this model represents an important first step toward understanding the mechanisms that underlie ICP onset caused by brain cancer. We look forward to validating our model with clinical data as and when it becomes available. Once validated, such a model has the potential to improve brain cancer diagnostics via quantification of the (currently theoretical) notion of the Langfitt curve.
Author Contributions
I.C.S. performed research, analyzed data, and wrote the manuscript. M.N.J.M. contributed analytic tools and wrote the manuscript. H.M.B. designed research, contributed analytic tools, and wrote the manuscript. H.V.J. designed research, contributed analytic tools, and wrote the manuscript.
Acknowledgments
This work was supported by the Simons Foundation Collaboration Grant for Mathematicians 280544 to H.V.J.
Editor: Jeffrey Fredberg.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2019.02.030.
Supporting Material
References
- 1.Bleeker F.E., Molenaar R.J., Leenstra S. Recent advances in the molecular understanding of glioblastoma. J. Neurooncol. 2012;108:11–27. doi: 10.1007/s11060-011-0793-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Louis D.N., Perry A., Ellison D.W. The 2016 world health organization classification of tumors of the central nervous system: a summary. Acta Neuropathol. 2016;131:803–820. doi: 10.1007/s00401-016-1545-1. [DOI] [PubMed] [Google Scholar]
- 3.Gupta A., Dwivedi T. A simplified overview of world health organization classification update of central nervous system tumors 2016. J. Neurosci. Rural Pract. 2017;8:629–641. doi: 10.4103/jnrp.jnrp_168_17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Noone, A. M., N. Howlader, …, K. A. Cronin. 2018. Seer Cancer Statistics Review (CSR) 1975–2015. Released April 16, 2018. https://seer.cancer.gov/csr/.
- 5.Pokhrel K.P., Vovoras D., Tsokos C.P. Histological and demographic characteristics of the distribution of brain and central nervous system tumors’ sizes: results from SEER registries using statistical methods. Int. J. Biomed. Sci. 2012;8:152–162. [PMC free article] [PubMed] [Google Scholar]
- 6.Lin Z.X. Glioma-related edema: new insight into molecular mechanisms and their clinical implications. Chin. J. Cancer. 2013;32:49–52. doi: 10.5732/cjc.012.10242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Preusser M., de Ribaupierre S., Stupp R. Current concepts and management of glioblastoma. Ann. Neurol. 2011;70:9–21. doi: 10.1002/ana.22425. [DOI] [PubMed] [Google Scholar]
- 8.Hambardzumyan D., Bergers G. Glioblastoma: defining tumor niches. Trends Cancer. 2015;1:252–265. doi: 10.1016/j.trecan.2015.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Esquenazi Y., Lo V.P., Lee K. Critical care management of cerebral edema in brain tumors. J. Intensive Care Med. 2017;32:15–24. doi: 10.1177/0885066615619618. [DOI] [PubMed] [Google Scholar]
- 10.Imbault M., Déméné C., Boch A. 2014 IEEE International Ultrasonics Symposium (IUS) IEEE; 2014. Intraoperative quantitative measurement of brain tumor stiffness and intracranial pressure assessment using ultrasound shear wave elastography; pp. 201–204. [Google Scholar]
- 11.Cruywagen G.C., Woodward D.E., Alvord E.C. The modelling of diffusive tumours. J. Biol. Syst. 1995;3:937–945. [Google Scholar]
- 12.Murray J.D. Mathematical Biology II: Spatial Models and Biomedical Applications. Volume 18. Springer; 2003. Growth and control of brain tumors; pp. 536–605. [Google Scholar]
- 13.Swanson K.R., Alvord E.C., Jr., Murray J.D. A quantitative model for differential motility of gliomas in grey and white matter. Cell Prolif. 2000;33:317–329. doi: 10.1046/j.1365-2184.2000.00177.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Swanson K.R., Bridge C., Alvord E.C., Jr. Virtual and real brain tumors: using mathematical modeling to quantify glioma growth and invasion. J. Neurol. Sci. 2003;216:1–10. doi: 10.1016/j.jns.2003.06.001. [DOI] [PubMed] [Google Scholar]
- 15.Tracqui P., Cruywagen G.C., Alvord E.C., Jr. A mathematical model of glioma growth: the effect of chemotherapy on spatio-temporal growth. Cell Prolif. 1995;28:17–31. doi: 10.1111/j.1365-2184.1995.tb00036.x. [DOI] [PubMed] [Google Scholar]
- 16.Stein A.M., Demuth T., Sander L.M. A mathematical model of glioblastoma tumor spheroid invasion in a three-dimensional in vitro experiment. Biophys. J. 2007;92:356–365. doi: 10.1529/biophysj.106.093468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Alfonso J.C.L., Talkenberger K., Deutsch A. The biology and mathematical modelling of glioma invasion: a review. J. R. Soc. Interface. 2017;14:20170490. doi: 10.1098/rsif.2017.0490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Preziosi L., Tosin A. Multiphase modelling of tumour growth and extracellular matrix interaction: mathematical tools and applications. J. Math. Biol. 2009;58:625–656. doi: 10.1007/s00285-008-0218-7. [DOI] [PubMed] [Google Scholar]
- 19.Araujo R.P., McElwain D.S. A mixture theory for the genesis of residual stresses in growing tissues I: a general formulation. SIAM J. Appl. Math. 2005;65:1261–1284. [Google Scholar]
- 20.Byrne H., Drasdo D. Individual-based and continuum models of growing cell populations: a comparison. J. Math. Biol. 2009;58:657–687. doi: 10.1007/s00285-008-0212-0. [DOI] [PubMed] [Google Scholar]
- 21.Cristini V., Li X., Wise S.M. Nonlinear simulations of solid tumor growth using a mixture model: invasion and branching. J. Math. Biol. 2009;58:723–763. doi: 10.1007/s00285-008-0215-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ward J.P., King J.R. Mathematical modelling of avascular-tumour growth. IMA J. Math. Appl. Med. Biol. 1997;14:39–69. [PubMed] [Google Scholar]
- 23.Jackson T.L., Byrne H.M. A mechanical model of tumor encapsulation and transcapsular spread. Math. Biosci. 2002;180:307–328. doi: 10.1016/s0025-5564(02)00118-9. [DOI] [PubMed] [Google Scholar]
- 24.Lowengrub J.S., Frieboes H.B., Cristini V. Nonlinear modelling of cancer: bridging the gap between cells and tumours. Nonlinearity. 2010;23:R1–R9. doi: 10.1088/0951-7715/23/1/r01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Byrne H.M., Owen M.R. A new interpretation of the Keller-Segel model based on multiphase modelling. J. Math. Biol. 2004;49:604–626. doi: 10.1007/s00285-004-0276-4. [DOI] [PubMed] [Google Scholar]
- 26.Swanson K.R., Rostomily R.C., Alvord E.C., Jr. A mathematical modelling tool for predicting survival of individual patients following resection of glioblastoma: a proof of principle. Br. J. Cancer. 2008;98:113–119. doi: 10.1038/sj.bjc.6604125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lanser D., Verwer J.G. Analysis of operator splitting for advection–diffusion–reaction problems from air pollution modelling. J. Comput. Appl. Math. 1999;111:201–216. [Google Scholar]
- 28.Tameem A., Krovvidi H. Cerebral physiology. Contin. Educ. Anaesth. Crit. Care Pain. 2013;13:113–118. [Google Scholar]
- 29.Langfitt T.W., Kassell N.F., Weinstein J.D. Cerebral blood flow with intracranial hypertension. Neurology. 1965;15:761–773. doi: 10.1212/wnl.15.8.761. [DOI] [PubMed] [Google Scholar]
- 30.Hoz S.S., Pinilla-Monsalve G.D., Moscote-Salazar L.R. Langfitt curve: importance in the management of patients with neurotrauma. J. Neuroanaesth. Crit. Care. 2018;5:121–122. [Google Scholar]
- 31.Prabhakar H., Mahajan C., Kapoor I. CRC Press; Boca Raton, FL: 2018. Essentials of Anesthesia for Neurotrauma. [Google Scholar]
- 32.Ropper A.H. Hyperosmolar therapy for raised intracranial pressure. N. Engl. J. Med. 2012;367:746–752. doi: 10.1056/NEJMct1206321. [DOI] [PubMed] [Google Scholar]
- 33.Molina J.R., Hayashi Y., Georgescu M.M. Invasive glioblastoma cells acquire stemness and increased Akt activation. Neoplasia. 2010;12:453–463. doi: 10.1593/neo.10126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Haskell C.M., Berek J.S., Haskell C.M. Saunders; New York: 1985. Cancer Treatment. [Google Scholar]
- 35.Huang H., Hara A., Ohgaki H. Altered expression of immune defense genes in pilocytic astrocytomas. J. Neuropathol. Exp. Neurol. 2005;64:891–901. doi: 10.1097/01.jnen.0000183345.19447.8e. [DOI] [PubMed] [Google Scholar]
- 36.Zhang X., Medow J.E., Webster J.G. Invasive and noninvasive means of measuring intracranial pressure: a review. Physiol. Meas. 2017;38:R143–R182. doi: 10.1088/1361-6579/aa7256. [DOI] [PubMed] [Google Scholar]
- 37.Furnari F.B., Fenton T., Cavenee W.K. Malignant astrocytic glioma: genetics, biology, and paths to treatment. Genes Dev. 2007;21:2683–2710. doi: 10.1101/gad.1596707. [DOI] [PubMed] [Google Scholar]
- 38.Dong X., Noorbakhsh A., Chen C.C. Survival trends of grade i, ii, and iii astrocytoma patients and associated clinical practice patterns between 1999 and 2010: a seer-based analysis. Neurooncol. Pract. 2016;3:29–38. doi: 10.1093/nop/npv016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Buckner J.C., Brown P.D., Uhm J.H. Central nervous system tumors. Mayo Clin. Proc. 2007;82:1271–1286. doi: 10.4065/82.10.1271. [DOI] [PubMed] [Google Scholar]
- 40.Levicar N., Nuttall R.K., Lah T.T. Proteases in brain tumour progression. Acta Neurochir. (Wien) 2003;145:825–838. doi: 10.1007/s00701-003-0097-z. [DOI] [PubMed] [Google Scholar]
- 41.Levine H.A., Sleeman B.D., Nilsen-Hamilton M. A mathematical model for the roles of pericytes and macrophages in the initiation of angiogenesis. I. The role of protease inhibitors in preventing angiogenesis. Math. Biosci. 2000;168:77–115. doi: 10.1016/s0025-5564(00)00034-1. [DOI] [PubMed] [Google Scholar]
- 42.Perumpanani A.J., Sherratt J.A., Byrne H.M. Biological inferences from a mathematical model for malignant invasion. Invasion Metastasis. 1996;16:209–221. [PubMed] [Google Scholar]
- 43.Haris M., Singh A., Reddy R. In vivo magnetic resonance imaging of tumor protease activity. Sci. Rep. 2014;4:6081. doi: 10.1038/srep06081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kawoos U., McCarron R.M., Chavko M. Advances in intracranial pressure monitoring and its significance in managing traumatic brain injury. Int. J. Mol. Sci. 2015;16:28979–28997. doi: 10.3390/ijms161226146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lindsay K.W., Bone I., Fuller G. Elsevier Health Sciences; New York: 2010. Neurology and Neurosurgery Illustrated. [Google Scholar]
- 46.Hawthorne C., Piper I. Monitoring of intracranial pressure in patients with traumatic brain injury. Front. Neurol. 2014;5:121. doi: 10.3389/fneur.2014.00121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Harary M., Dolmans R.G.F., Gormley W.B. Intracranial pressure monitoring-review and avenues for development. Sensors (Basel) 2018;18:E465. doi: 10.3390/s18020465. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.