Integrated Powered Density: Screening Ultrahigh Dimensional Covariates with Survival Outcomes

Summary:

Modern biomedical studies have yielded abundant survival data with high-throughput predictors. Variable screening is a crucial first step in analyzing such data, for the purpose of identifying predictive biomarkers, understanding biological mechanisms and making accurate predictions. To nonparametrically quantify the relevance of each candidate variable to the survival outcome, we propose integrated powered density (IPOD), which compares the differences in the covariate-stratified distribution functions. The proposed new class of statistics, with a flexible weighting scheme, is general and includes the Kolmogorov statistic as a special case. Moreover, the method does not rely on rigid regression model assumptions and can be easily implemented. We show that our method possesses sure screening properties, and confirm the utility of the proposal with extensive simulation studies. We apply the method to analyze a multiple myeloma study on detecting gene signatures for cancer patients’ survival.

1. Introduction

As a key aspect of scientific discovery is to identify low-dimensional presentations of predictive features in a high-dimensional space, there is an urgent need to develop a fast but crude method to screen relevant variables, and ensure that the unselected variables are indeed irrelevant (Fan and Lv, 2008). In the context of integrative analysis, screening steps are crucial in simultaneously reducing dimensionality and ensuring estimation accuracy (Fan and Lv, 2010). More broadly, screening has found wide applications, ranging from quality control in the data processing step for genome/genetic studies (Beyene et al., 2009), to identifying predictive biomarkers for understanding biological mechanisms (Heinzel et al., 2014). This paper is motivated by a clinical study (Shaughnessy et al., 2007) on multiple myeloma, the second-most common hematological cancer, which often results in bone lesions, immunological disorders, and renal failure. A deeper understanding of the molecular etiology of this disease, such as through detecting the gene signatures that are relevant to cancer patients’ survival, would lead to novel therapeutic targets and more accurate risk classification systems (Mulligan et al., 2007). However, with expression level measurements on more than 50,000 probe sets, this dataset presents substantial challenges that defy the existing statistical tools for dimension reduction.

While screening approaches, including sure independence screening (Fan and Lv, 2008), have been actively pursued for fully observed outcomes, the development of high dimensional screening tools with survival outcomes has been less fruitful. Limited works include a sure screening procedure for Cox’s proportional hazards model (Fan et al., 2010), a Cox univariate shrinkage estimator (Tibshirani, 2009), a marginal maximum partial likelihood estimator (Zhao and Li, 2012), a general class of single-index hazard rate models (Gorst-Rasmussen and Scheike, 2013), and a conditional screening with prior information (Hong et al., 2016). As successful as these methods have been, their validity often hinges upon modeling assumptions between outcomes and predictors (Lin and Halabi, 2013), violations of which can lead to inflated false discoveries or non-discoveries.

There has been a surge of effort in developing model-free screening procedures that achieve sure screening properties under weak conditions; see Zhu et al. (2011), Li et al. (2012), Liu et al. (2014), Mai and Zou (2015), Li et al. (2012) and Shao and Zhang (2014). However, the extension of these nonparametric works to accommodate censored outcome data is elusive and nontrivial. Limited works include a quantile adaptive method (He et al., 2013) and a censored rank independence screening method (Song et al., 2014), and a survival impact index procedure (Li et al., 2016).

In a survival setting, nonparametric variable screeners have focused on discerning how each candidate variable influences overall survival functions. Studying the variability of survival functions for strata defined by each variable is one possible way. We note that such survival differences may occur either during the early or late period in the follow-up due to disease-related characteristics. Therefore, screening approaches that rely on a single screening criterion may not be able to capture the complex difference patterns and may lead to false non-discovery.

Our paper proposes a model-free method for screening ultrahigh dimensional predictors when the outcome is randomly right censored. We propose an integrated powered density (IPOD) criterion to screen predictors that are relevant to the survival outcome. With an embedded weighting scheme, IPOD flexibly compares the differences in covariate-stratified distribution functions that occur at various time points. The proposed framework is general, including the Kolmogorov filter (Mai and Zou, 2015) as a special case.

Compared to the other screening methods, our work presents several novel contributions. First, we have introduced a general nonparametric screening framework to accommodate survival outcomes and provided a convenient means to select ultrahigh dimensional predictors of mixed types, discrete or continuous. Second, by embedding our screening criteria in a new class of statistics, our method provides more flexibility and power in efficiently selecting signals out of ultrahigh dimenionsal predictors. We have established sure screening properties, and conducted simulations to validate the method.

The remainder is organized as follows. In Section 2, we introduce the concept of integrated powered density and propose a model-free screening procedure to screen covariates of different types (e.g. discrete or continuous). We present in Section 3 the sure screening property. In Section 4, we evaluate the finite-sample performance via simulation studies. In Section 5, we apply the method to analyze a multiple myeloma study and identify gene signatures that are relevant to patients’ survival. We conclude with some final remarks in Section 6. Technical details are deferred to the Supplementary Web Materials.

2. Integrated Powered Density (IPOD) for Survival Outcomes

Suppose we have n observations with p covariates, where p ≫ n. Denote by X_ij the jth covariate for subject i, and write X_i = (X_i1, …,X_ip)^T. Let T_i be the underlying survival time and C_i be the potential censoring time. We observe Y_i = min{T_i, C_i} and δ_i = I (T_i ⩽ C_i), where I(·) is the indicator function. We assume that T_i and C_i are independent given X_i, and (Y_i, δ_i, X_i) are independently and identically distributed (i.i.d). In particular, we assume (T_i, X_ij), i = 1, …,n, are i.i.d copies of (T, X_j), the random variables that underlie the survival time and covariates. To ensure the estimability of the survival function, we assume that there exists a τ > 0 such that P(Y_i > τ|X_i)> 0 and restrict our analysis to [0, τ], a common practice in survival analysis (Zeng and Lin, 2007). In practice, τ is often chosen to be the study duration.

Denote by S(·) the marginal survival function of T and by S(t|X) the conditional survival function of T given X. To facilitate the selection of covariates that are relevant to T, we define the set of active covariates as

$$\mathcal{M}=\left\{j:S(t|X)\text{ functionally depends on }{X}_j\text{ for some }t\in (0,\infty )\right\}.$$

In biomedical studies, it is not unreasonable to stipulate a sparsity condition that only a small number of biomarkers are relevant to the disease-specific survival. That is, the cardinality of $\mathcal{M}$ is small relative to p. Our goal is to identify $\mathcal{M}$. As the candidate variables can be of mixed types, we start by considering a categorical variable, say, X_j, with R_j categories such that X_j ∈ {1, 2, …,R_j}. Later we will extend the method to cover continuous covariates.

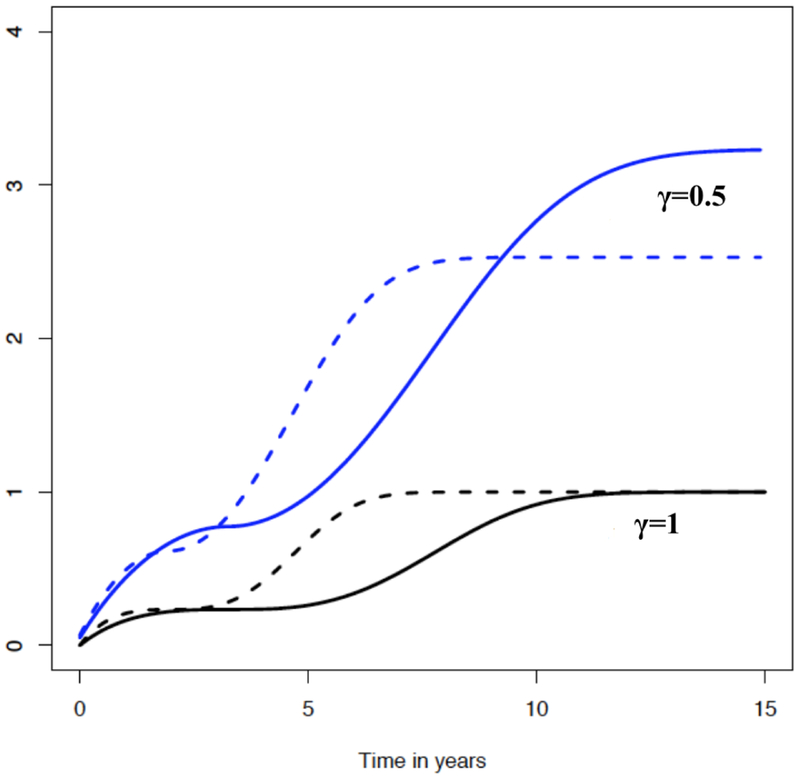
For a generic density function corresponding to a (continuous) survival time, denoted by f(·), and for t ∈ (0, ∞), we define the integrated powered density (IPOD) as ${\int }_0^t{f}^{\gamma }(s)ds$, for γ > 0. IPOD resembles the cumulative density function (CDF) and satisfies the basic properties of CDFs, except that it does not necessarily approach to one when t → ∞. This unique property is advantageous for using IPOD to detect distributional differences, as exemplified in Figure 1.

Figure 1.

Integrated Powered Density: ${\int }_0^t{f}^{\gamma }(s|x)ds$ is shown for x = 1 (solid line) and x = 0 (dashed line) with γ = 1 and γ = 0.5, respectively. Here, f(s|x) is the density function corresponding to the crossing hazard function of λ(s|x) = 0.1 exp(−0.5x){s exp(−0.5x)−2}², which is adapted from Zhang and Peng (2009). This figure appears in color in the electronic version of this article.

When γ = 1, IPOD is a CDF. When γ ≠ 1, IPOD is closely related to the Renyi entropy with a power index γ (Cover and Thomas, 2012). To study the relevance of covariate X_j to the survival time T, we propose to characterize the variability of IPOD across different categories of X_j. Specifically, for each pair of categories, say, X_j = r₁ and X_j = r₂ (r₁, r₂ ∈ {1, …,R_j}), we compute the absolute difference of IPOD, take the maximum over all pairs of r₁, r₂ and use it as the screening criterion:

$${\mathcal{I}}_j^{(\gamma )}=\underset{{}_{r_1,r_2\in \left\{1,\dots ,R_j\right\}}}{\text{max}}\underset{t\in \left[0,\tau \right]}{\text{sup}}\left|{\int }_0^t{f}_{T|X_j}^{\gamma }\left(s|X_j=r_1\right)ds-{\int }_0^t{f}_{T|X_j}^{\gamma }\left(s|X_j=r_2\right)ds\right|,$$ (1)

where f_T|X_j(s|X_j = r) denotes the conditional density function of T given X_j = r. The rationale is that ${\mathcal{I}}_j^{(\gamma )}=0$ implies T and X_j are independent and so does the converse. Hence, an estimated ${\mathcal{I}}_j^{(\gamma )}$ empirically gauges the relevance of X_j to T. When γ = 1, (1) is simply the classical Kolmogorov difference, ${\text{max}}_{r_1,r_2\in \left\{1,\dots ,R_j\right\}}{\text{sup}}_{t\in [0,\tau ]}\left|F_{T|X_j}\left(t|X_j=r_1\right)-F_{T|X_j}\left(t|X_j=r_2\right)\right|$. However, the added power index γ in (1) may inflate early (γ > 1) or late differences (γ < 1) and thus gives more flexibility to detect the distributional differences. For example, Figure 1 illustrates that IPOD with γ = 0.5 amplifies the late differences in CDF (corresponding to γ = 1), which exemplifies the possible role of γ in differentiating distributions.

This leads to a natural question of which γ should be chosen in analysis. For unbiased analysis, it is not reasonable to look at the survival curves first, and then choose weights. However, prior medical knowledge might guide the choice of γ. For example, late differences are more likely to occur in childhood cancers (National Cancer Policy Board, 2003), while early treatment differences are more prominent in late stage lung cancer remission (Fossella et al., 2000).

2.1. Estimation of IPOD

To estimate (1) for a given γ > 0, we need to first reliably estimate the density of the survival time. We adopt a kernel type density estimation. We illustrate the idea by estimating the marginal density of T.

Denote by 0 ≡ t₀ < t₁ < t₂ < ⋯ < t_M the ordered observed failure times in the data, and by ${\widehat{S}}_T(t)$ the Kaplan-Meier estimate of S_T(t), the marginal survival function of T at time t. Then the estimated kernel density function for T is

$${\widehat{f}}_T(t)=-\int K\left(\frac{t-s}{h_n}\right)d{\widehat{S}}_T(s)=\sum _{i=1}^{M}K\left(\frac{t-t_i}{h_n}\right)\left({\widehat{S}}_T\left(t_{i-1}\right)-{\widehat{S}}_T\left(t_i\right)\right),$$

where h_n > 0 is the bandwidth and K(·) is a kernel function.

Similarly, restricting samples to X_j = r, we can compute ${\widehat{f}}_{T|X_j}\left(t|X_j=r\right)$, the estimate of the conditional density function given X_j = r. Thus, (1) can be estimated by

$${\widehat{\mathcal{I}}}_j^{(\gamma )}=\underset{{}_{r_1,r_2}}{\text{max}}\underset{t\in [0,\tau ]}{\text{sup}}\left|{\int }_0^t{\widehat{f}}_{T|X_j}^{\gamma }\left(s|X_j=r_1\right)ds-{\int }_0^t{\widehat{f}}_{T|X_j}^{\gamma }\left(s|X_j=r_2\right)ds\right|.$$ (2)

When X_j is continuous, without loss of generality, we assume the support of X_j is the real line $ℝ$. We can discretize X_j into R_j slices by using the percentiles of the empirical distribution of X_j. That is, ${\tilde{X}}_j=r$ if $X_j\in \left[{\widehat{q}}_{j(r-1)},{\widehat{q}}_{j(r)}\right)$, where ${\widehat{q}}_{j(r)}$ is the r/R_jth percentile of the empirical distribution of X_j. For notational convenience, we set ${\widehat{q}}_{j(0)}=-\infty$ and ${\widehat{q}}_{j\left(R_j\right)}=\infty$. We then replace X_j by its discretized version ${\tilde{X}}_j$ in (2) and compute the corresponding IPOD statistic, which sheds light on the dependence between T and X_j, even when the latter is continuous. As Mai and Zou (2015) noted, discretization could be more preferable than using the continuous version, not only for computational convenience but also for added discriminative power. Moreover, without discretization, the criterion (2) requires the calculation of the pairwise-difference of the conditional density functions for all distinct X_j values, which is computationally intensive even for low-dimensional covariates, let alone for the ultrahigh dimensional settings.

Finally, we use the following criterion to select active variables

$${\widehat{\mathcal{M}}}_1=\left\{j:{\widehat{\mathcal{I}}}_j^{(\gamma )}>c{n}^{-v},j=1,\dots ,p\right\},$$

where c > 0 is a pre-specified constant, and term the procedure as the IPOD screening.

When X_j is continuous with infinitely many possible values, the slicing scheme may be driven by the consideration of retaining enough samples within each slice to control the estimation variance. Mai and Zou (2015) noted that the choice of slices does not affect variable screening results much, but fusion can achieve significant improvement. We consider a fusion-based IPOD screening as follows. Suppose there are N different ways of slicing X_j, denoted by Λ_ju, u = 1, …,N, with each slicing Λ_ju containing R_jU intervals. Specifically, ${\Lambda }_{ju}=\left\{\left[{\widehat{q}}_{ju(r-1)},{\widehat{q}}_{ju(r)}\right):r=1,\dots R_{ju},\text{ and }{\cup }_{r=1}^{R_{ju}}\left[{\widehat{q}}_{ju(r-1)},{\widehat{q}}_{ju(r)}\right)=ℝ\right\}$, where the slicing point ${\widehat{q}}_{ju(r)}$ is the r/R_juth percentile of the empirical distribution of X_j under partition Λ_ju. We then replace X_j by its discretized version ${\tilde{X}}_{ju}$ under Λ_ju. That is, ${\tilde{X}}_{ju}=r$ if $X_j\in \left[{\widehat{q}}_{ju(r-1)},{\widehat{q}}_{ju(r)}\right)$. For example, we can take N = [log(n)] − 2, and R_ju = u + 2,u = 1, …,N to ensure there are enough samples within each slice for all slicing schemes. Our numerical experiments suggest that at least 30 samples are needed within each slice for a reasonable estimate.

Let ${\widehat{\mathcal{I}}}_{j,{\Lambda }_{ju}}^{(\gamma )}$ be the IPOD screening statistic corresponding to the slicing scheme of Λ_ju for covariate X_j such that ${\widehat{\mathcal{I}}}_{j,{\Lambda }_{ju}}^{(\gamma )}={\text{max}}_{r_1,r_2}{\text{sup}}_{t\in [0,\tau ]}\left|{\int }_0^t{\widehat{f}}_{T|{\tilde{X}}_j}^{\gamma }\left(s|{\tilde{X}}_{ju}=r_1\right)ds-{\int }_0^t{\widehat{f}}_{T|{\tilde{X}}_j}^{\gamma }\left(s|{\tilde{X}}_{ju}=r_2\right)ds\right|$. Then, the fused IPOD screening statistic ${\tilde{\mathcal{I}}}_j^{(\gamma )}$ is

$${\tilde{\mathcal{I}}}_j^{(\gamma )}=\sum _{u=1}^N{\widehat{\mathcal{I}}}_{j,{\Lambda }_{ju}}^{(\gamma )},$$

leading to the following screening criterion:

$${\widehat{\mathcal{M}}}_2=\left\{j:{\tilde{\mathcal{I}}}_j^{(\gamma )}>c{n}^{-v},j=1,\dots ,p\right\},$$ (3)

where c > 0 is a constant. As our numerical experiment suggests that the fused method performs better than the single slicing-based, we opt to use (3) as the screening criterion in practice.

3. Sure Screening Properties

To establish the sure screening property, we need to set regularity conditions. First, we stipulate the conditions for when all the variables are categorical.

(C1) P(T > τ|X_j) > θ₁ > 0 for 1 ⩽ j ⩽ p, where θ₁ is a positive constant.

(C2) For any t ∈ [0, τ], f_T|X_j (t|r) is greater than a positive constant ${\tilde{c}}_0$, and has a bounded second order derivative for $r\in \left\{1,\dots ,R_j\right\},j\in \mathcal{M}$.

(C3) There exist c > 0 and 0 < v < 1/2 such that ${\text{min}}_{j\in \mathcal{M}}{\mathcal{I}}_j^{(\gamma )}⩾2c{n}^{-v}$ for a specific γ.

(C4) K(·) is a symmetric probability density function defined on a bounded support with bounded variation V_K < ∞ and bandwidth h_n = O(n^−μ), where μ > 0 is a constant.

(C5) $R={\text{max}}_{1⩽j⩽p}{R}_j=O\left(n^{\kappa }\right)$, where R_j is the number of categories for X_j (j = 1, …,p), κ ⩾ 0, and 2v + 3κ + 2μ < 1.

Condition (C1) is imposed to avoid problems with estimating the tail of the conditional survival functions, which is common in survival analysis; see Dabrowska (1989). Conditions (C2) and (C4) are assumed for the kernel function involved in conditional density estimation of censored data, which are common in the nonparametric literature; see Lo et al. (1989) and Chen et al. (2015). Condition (C3) is typical in the feature screening literature; see Condition 3 in Fan and Lv (2008) and Ni and Fang (2016). Condition (C5) allows the number of the classes for covariates diverge with a specific order. A similar assumption was also made in Ni and Fang (2016).

Theorem 1: If all the covariates are categorical, under conditions (C1)–(C5), we have

$$P\left(\mathcal{M}\subset {\widehat{\mathcal{M}}}_1\right)⩾1-O\left(p\text{exp}\left(-b_0{n}^{1-3\kappa -2v-2\mu }+\kappa \text{log}n\right)\right),$$

where b₀ is a positive constant. Hence, if log p = O(n^α) where 0 < α < 1 − 3κ − 2v − 2μ, IPOD has the sure screening property.

Corollary 1: Under the conditions of Theorem 1, and assuming ${\sum }_{j=1}^p{\mathcal{I}}_j^{(\gamma )}=O\left(n^{\zeta }\right)$ for some ζ > 0, we have

$$P\left\{\left|{\widehat{\mathcal{M}}}_1\right|⩽O\left(n^{\zeta +v}\right)\right\}⩾1-O\left(p\text{exp}\left(-b_0{n}^{1-3\kappa -2v-2\mu }+\kappa \text{log}n\right)\right).$$

If X_j is continuous, we replace condition (C5) by the following:

(C6) $R={\text{max}}_{1⩽j⩽p}{R}_j=O\left(n^{\kappa }\right)$, where R_j is the number of slices for X_j. Moreover, there exist a positive constant c₁ and 0 ⩽ ρ < 1/2 such that 2v + 3κ + 2μ + 2ρ < 1 and $f_{X_j}(x)⩾c_1{n}^{-\rho }$ for any 1 ⩽ j ⩽ p, where $f_{X_j}(x)$ is continuous and bounded from above on the support of X_j.

Theorem 2: When the covariates include both continuous and categorical types, under conditions (C1)–(C4) and (C6), we have

$$P\left(\mathcal{M}\subset {\widehat{\mathcal{M}}}_1\right)⩾1-O\left(p\text{exp}\left(-b_1{n}^{1-3\kappa -2v-2\mu -2\rho }+\kappa \text{log}n\right)\right),$$

where b₁ is a positive constant. Hence, if log p = O(n^α) and 0 < α < 1 − 3κ − 2v − 2μ − 2ρ, IPOD has the sure screening property.

Corollary 2: Under the conditions of Theorem 2 and assuming ${\sum }_{j=1}^p{\mathcal{I}}_j^{(\gamma )}=O\left(n^{\zeta }\right)$ for some ζ > 0, we have

$$P\left(\left|{\widehat{\mathcal{M}}}_1\right|⩽O\left(n^{\zeta +v}\right)\right)⩾1-O\left(p\text{exp}\left(-b_1{n}^{1-3\kappa -2v-2\mu -2\rho }+\kappa \text{log}n\right)\right).$$

Let Λ_juo be the partition using the theoretical quantiles q_ju(r), r = 0, …,R_ju of X_j as the slicing points. Denote the true value of IPOD for the specific partition Λ_juo by ${\mathcal{I}}_{j,{\Lambda }_{juo}}^{(\gamma )}$ and let ${\mathcal{I}}_{jo}^{(\gamma )}={\sum }_{u=1}^N{\mathcal{I}}_{j,{\Lambda }_{juo}}^{(\gamma )}$. The fused IPOD screening method needs some different regularity conditions:

(C7) There exist a c > 0 and 0 < v < 1/2 such that ${\text{min}}_{j\in \mathcal{M}}{\mathcal{I}}_{jo}^{(\gamma )}⩾2c{n}^{-v}$ for a specific γ.

(C8) Let $R={\text{max}}_{1⩽j⩽p,1⩽u⩽N}{R}_{ju}$ R_ju and assume R = O(n^κ). There exist a positive constant c₃ and 0 ⩽ ρ < 1/2 such that 2v + 3κ + 2μ + 2ρ < 1, and $f_{X_j}(x)⩾c_3{n}^{-\rho }$ for any 1 ⩽ j ⩽ p and $f_{X_j}(x)$ is bounded from above and continuous with respect to x.

Theorem 3: When the covariates include both continuous and categorical types, under conditions (C1)–(C2), (C4) and (C7)-(C8), we have

$$P\left(\mathcal{M}\subset {\widehat{\mathcal{M}}}_2\right)⩾1-O\left(Np\text{exp}\left(-b_2{n}^{1-3\kappa -2v-2\mu -2\rho }+\kappa \text{log}n\right)\right),$$

where b₂ is a positive constant. If N = O(log n) and log p = O(n^α) where 0 < α < 1 − 3_κ − 2_v − 2_μ − 2_ρ, then the fused IPOD has the sure screening property.

Corollary 3: Under the conditions of Theorem 3 and assuming ${\sum }_{j=1}^p{\mathcal{I}}_{jo}^{(\gamma )}=O\left(n^{\zeta }\right)$ for some ζ > 0, we have

$$P\left\{\left|{\widehat{\mathcal{M}}}_2\right|⩽O\left(n^{\zeta +v}\right)\right\}⩾1-O\left(Np\text{exp}\left(-b_2{n}^{1-3\kappa -2v-2\mu -2\rho }+\kappa \text{log}n\right)\right).$$

4. Simulation Studies

The finite sample performance of the proposed method was assessed by comparing it with the following methods that are often used for screening survival data.

• PSIS: the principled sure independence screening for Cox models by Zhao and Li (2012).

• CRIS: the censored rank independence screening proposed by Song et al. (2014).

• CS: the conditional screening for survival outcome by Hong et al. (2016).

• SII: the survival impact index by Li et al. (2016) with the uniform weight W(t, x) = 1.

• IPOD (γ): the proposed screening with power index γ. Note that γ = 1 corresponds to the Kolmogorov statistic.

Example 1. The survival time was generated from the proportional hazards model,

$$h(t|X)=0.1\text{exp}\left\{\sum _{j=1}^p{\beta }_{j}I\left(X_j\in \{2,3\}\right)\right\},$$

where $\beta ={\left(0.5_5,0_{p-5}^{\text{T}}\right)}^{\text{T}}$. The covariates x* underlying these discrete variables were generated from a multivariate normal distribution with mean 0 and a covariance matrix Σ = (σ_jj′)_p×p, where σ_jj = 1 and σ_jj′ = 0.5 for j ≠ j′. For each j, $x_j^{*}$ was further quarterized by its quartile values: the obtained quarterly variable $x_j^{*}$ is less than the lower quartile, 2 if between the lower quartile and the median, 3 if between the median and the upper quartile, and 4 otherwise.

Example 2. The survival time was generated from the Cox model λ(t|X) = 2t(|X₁| + |X₂|), where all the covariates X_j ,j = 1, …,p, were generated from an independent standard normal distribution. In this case, the marginal correlation between each of the active variables, X₁ and X₂, and the survival time is 0.

Example 3. The survival time was generated from log(t) = g₁(X₁)+g₂(X₂)+g₃(X₃)+g₄(X₄) + ϵ, where g₁(x) = 5x, g₂(x) = −4x(1−x), g₃(x) = 10[exp{−3(x−1)²}+exp{−4(x−3)²}]−1.5, and g₄(x) = 4sin(2πx). The vector of covariates X was generated from the multivariate normal distribution with mean 0 and a covariance matrix Σ = (σ_jj′)_p×p, with σ_jj = 1 and σ_jj′ = ρ^|j−j′| for j ≠ j′ and ϵ ~ N(0, 1) is independent of X. The censoring time C was generated from a 3-component normal mixture distribution N(0, 4) − N(5, 1) + 0.5N(25, 1).

Example 4. The survival time was generated from log(t) = g₁(X₁) + g₂(X₂) + g₃(X₃) + g₄(X₄) + 0.3(X₅ + X₆ + X₇ + X₈ + X₉ + X₁₀) + ϵ, where all other conditions are the same as in Example 3.

In all examples, we used p = 1000 and n = 300 and 500. In Examples 1–2, the censoring times C_i were independently generated from a uniform distribution U[0, c], with c chosen to give approximately 20% and 50% of censoring proportions. Example 3 was adopted from Li et al. (2016). The censoring proportions of Examples 3–4 were set around 35%. In addition, we explored the simulation studies when the censoring times C_i were dependent on covariates; see Table S1 in the Supplementary Web Materials.

The bandwidth h_n was chosen to be h₀n^−1/5 with h₀ = 2 based on the exploratory analysis reported in Figure S1 in the Supplementary Web Materials; when covariate X_j was continuous, we took various slicings (3, …,⌈log(n)⌉) and reported the fused results.

As the conditional screening (Hong et al., 2016) requires prior information, we chose X₁ as the conditioning variable for Examples 1–4. For each configuration, a total of 500 simulated datasets were generated. We considered the minimum model size (MMS) to ensure inclusion of the true model, the true positive rate (TPR), and the probability of including all active variables (PIT) as metrics to compare the performance between different methods. To compute the TPR and PIT, we selected the first [n/log n] variables in relation to selection criteria. In general, smaller MMS and larger TPR and PIT indicate better performance of a method in efficiently discovering true signals.

Table 1 demonstrates that the proposed IPOD method worked well in a variety of set tings, with improving performance as the sample size increased. This is an appealing feature not necessarily shared by the competing methods. For IPOD, we investigated γ = 0.8, 1, 1.2, 1.5, 1.7, but we only presented here the results of γ = 0.8, 1, 1.2 as they well represented the overall results. More results can be found in Figure S1 of the Supplementary Web Materials.

Table 1.

Comparisons of competing methods with (n, p) = (300, 1000) and (n, p) = (500, 1000) in terms of the minimum model size to ensure inclusion of the true model (MMS) with interquartile range in parentheses, the true positive rate (TPR), and the probability of including all active variables (PIT)

Method	MMS	TPR	PIT	MMS	TPR	PIT	MMS	TPR	PIT	MMS	TPR	PIT
	(n, p) = (300, 1000)			(n, p) = (500, 1000)			(n, p) = (300, 1000)			(n, p) = (500, 1000)
Example 1	CR=20%						CR=50%
IPOD (γ = .8)	201 (254)	0.63	0.11	59 (92)	0.91	0.60	298 (279)	0.50	0.02	115 (165)	0.82	0.38
IPOD (γ = 1)	161 (218)	0.70	0.16	41 (71)	0.94	0.71	254 (277)	0.57	0.06	182 (135)	0.87	0.49
IPOD (γ = 1.2)	159 (217)	0.71	0.17	38 (65)	0.94	0.73	234 (273)	0.59	0.08	72 (112)	0.89	0.56
PSIS	855 (211)	0.06	0.00	858 (217)	0.09	0.00	874 (91)	0.05	0.00	849 (198)	0.08	0.00
CRIS	919 (133)	0.03	0.00	921 (128)	0.04	0.00	913 (155)	0.03	0.00	914 (135)	0.04	0.00
CS	834 (245)	0.24	0.00	830 (230)	0.25	0.00	842 (218)	0.24	0.00	837 (219)	0.26	0.00
SII	258 (274)	0.51	0.02	82 (110)	0.86	0.49	327 (277)	0.41	0.01	136 (181)	0.75	0.28
Example 2	CR=20%						CR=50%
IPOD (γ = .8)	2 (2)	0.99	0.99	2 (0)	1.00	1.00	5 (10)	0.94	0.89	2 (0)	1.00	1.00
IPOD (γ = 1)	2 (3)	0.99	0.99	2 (0)	1.00	1.00	4 (11)	0.94	0.89	2 (0)	1.00	1.00
IPOD (γ = 1.2)	2 (4)	0.99	0.99	2 (0)	1.00	1.00	5 (15)	0.95	0.90	2 (1)	1.00	1.00
PSIS	721 (330)	0.03	0.00	727 (349)	0.06	0.01	700 (392)	0.07	0.01	714 (371)	0.08	0.01
CRIS	738 (339)	0.04	0.00	707 (325)	0.07	0.01	732 (324)	0.06	0.00	706 (324)	0.06	0.00
CS	461 (532)	0.54	0.09	426 (502)	0.55	0.11	457 (571)	0.56	0.12	459 (557)	0.56	0.12
SII	19 (27)	0.90	0.84	3 (4)	1.00	1.00	67 (119)	0.63	0.43	11 (32)	0.95	0.92
Example 3	ρ = 0						ρ = 0.8
IPOD (γ = 0.8)	84 (173)	0.85	0.39	22 (51)	0.96	0.83	6 (10)	0.98	0.93	4 (0)	1.00	1.00
IPOD (γ = 1)	114 (226)	0.82	0.30	35 (84)	0.92	0.69	8 (19)	0.97	0.90	4 (1)	1.00	1.00
IPOD (γ = 1.2)	158 (280)	0.81	0.24	61 (132)	0.89	0.57	14 (36)	0.95	0.80	4 (3)	0.99	0.98
PSIS	560 (466)	0.61	0.03	539 (429)	0.67	0.03	330 (624)	0.50	0.17	206 (454)	0.66	0.36
CRIS	619 (415)	0.57	0.02	579 (505)	0.62	0.03	314 (591)	0.53	0.16	183 (384)	0.73	0.37
CS	703 (505)	0.55	0.03	659 (518)	0.62	0.04	886 (993)	0.74	0.38	27 (109)	0.92	0.69
SII	376 (405)	0.69	0.04	296 (330)	0.77	0.12	24 (82)	0.90	0.64	8 (14)	0.99	0.98
Example 4	ρ = 0						ρ = 0.8
IPOD (γ = 0.8)	867 (166)	0.38	0.00	863 (178)	0.47	0.00	57 (166)	0.89	0.49	13 (19)	0.99	0.90
IPOD (γ = 1)	876 (171)	0.37	0.00	872 (156)	0.45	0.00	96 (253)	0.84	0.36	22 (47)	0.97	0.81
IPOD (γ = 1.2)	881 (171)	0.36	0.00	868 (178)	0.43	0.00	155 (347)	0.78	0.23	44 (110)	0.94	0.64
PSIS	895 (162)	0.29	0.00	882 (182)	0.36	0.00	102 (267)	0.84	0.37	31 (80)	0.96	0.73
CRIS	925 (121)	0.25	0.00	926 (112)	0.28	0.00	111 (277)	0.82	0.32	24 (51)	0.97	0.80
CS	892 (150)	0.31	0.00	877 (167)	0.38	0.00	774 (305)	0.51	0.00	689 (366)	0.68	0.01
SII	870 (163)	0.31	0.00	874 (192)	0.38	0.00	33 (95)	0.92	0.58	12 (11)	0.99	0.93

With active variables all being categorical as in Example 1, the results for all competing methods were poor since these methods were not originally developed for screening categorical variables. When the marginal correlations between the active variables and the survival time were 0 as in Examples 2, all the competing methods, including CS that even assumed one active variable was known, had difficulty recruiting active variables. In Example 3, where the active covariates have nonlinear relationships with the response variable, IPOD worked better than the other methods, especially when ρ was high. When the size of active variables was moderate as in Example 4, the performance was poor for all methods when the covariates were independent of each other, but was better with higher correlations among the covariates.

Finally, it is of interest to note that the “optimal” γ varied across examples. However, this optimal γ is rarely known in reality. Illustrated by a real example in the next section, we briefly discuss how to combine results from the IPOD with different γ’s.

5. An Application

We applied the proposed methods to analyze a multiple myeloma (MM) study (Shaughnessy et al., 2007), concerning the development and evaluation of a gene-based prognostic tool among 554 newly diagnosed MM patients treated on 2 separate but similar protocols, namely, total treatment 2 (TT2) and total treatment 3 (TT3). The former served as the training set (n₁ = 340 patients), while the latter served as the validation set (n₂= 2 1 4 patients). The outcome for our investigation is event-free survival. Gene expressions on 54,675 probe sets were measured for each subject using Affymetrix U133Plus2.0 microarrays. Prior to analysis, we standardized the gene expressions.

For comparisons, we also applied the other competing methods, including PSIS, CRIS, SII and CS to screen genes that may be relevant to event-free survival. Based on our investigation in the simulation setup, we chose γ = 0.7, 1.0, 1.3, 1.5, 1.7 for our IPOD method. In addition, we also considered the overlapping genes selected by all these γ’s and termed the way of obtaining these genes as composite IPOD. We took the bandwidth to be $2n_1^{-1/5}$. Since the gene expressions were continuous, we chose the combination of Λ = 3, …,⌈log(340)⌉ = 6 for slicing in the proposed IPOD. Moreover, as CS requires a pre-specified conditioning set, we identified the candidates as the overlapping genes selected by composite IPOD, PSIS, SII, and CRIS. These were Probes 225834, 218595, 206332, 208965, and 208966. In our analysis, we used various subsets of these genes as the conditioning sets. We found that CS was sensitive to the choice, leading to quite variable predictive performance; see Table 3.

Table 3.

Comparisons of the C-index (standard errors) in the multiple myeloma validation set based on 100 bootstraps

IPOD
γ = .7	γ = 1	γ = 1.3	γ = 1.5	γ = 1.7	Composite
0.639 (0.003)	0.638 (0.003)	0.655 (0.003)	0.651 (0.003)	0.657 (0.003)	0.652 (0.003)
PSIS	CRIS	CS	STT
0.620 (0.003)	0.602 (0.004)	0.641 (0.004)	0.638 (0.003)

In a finite sample setting, there are no established ways to select v in (3). Instead, practitioners commonly use the screening statistic to rank variables and select the top variables. We used [n/ log(n)] as suggested by Fan and Lv (2008), which may have become a convention in the follow-up screening works; see Li et al. (2016), He et al. (2013), Gorst-Rasmussen and Scheike (2013), and Zhao and Li (2012). To proceed, we first applied each screening method to the training data to reduce the dimension from p = 54, 675 to d = [n₁/log(n₁)] = 58.

Table 2 shows the numbers of overlapping genes selected by different methods and reveals that IPOD with different γ’s ended up with various genes.

Table 2.

Numbers of overlapping genes selected by different screening methods on the multiple myeloma training set

	IPOD						PSIS	CRIS	CS	SII
	γ = 0.7	γ = 1	γ = 1.3	γ = 1.5	γ = 1.7	Composite
IPOD
γ = 0.7	58
γ = 1	40	58
γ = 1.3	29	46	58
γ = 1.5	24	39	51	58
γ = 1.7	20	34	46	53	58
Composite	20	20	20	20	20	20
PSIS	18	23	20	17	16	10	58
CRIS	0	0	1	1	1	0	1	58
CS	1 1	10	10	8	7	6	18	5	58
SII	6	5	5	5	5	5	7	5	15	58

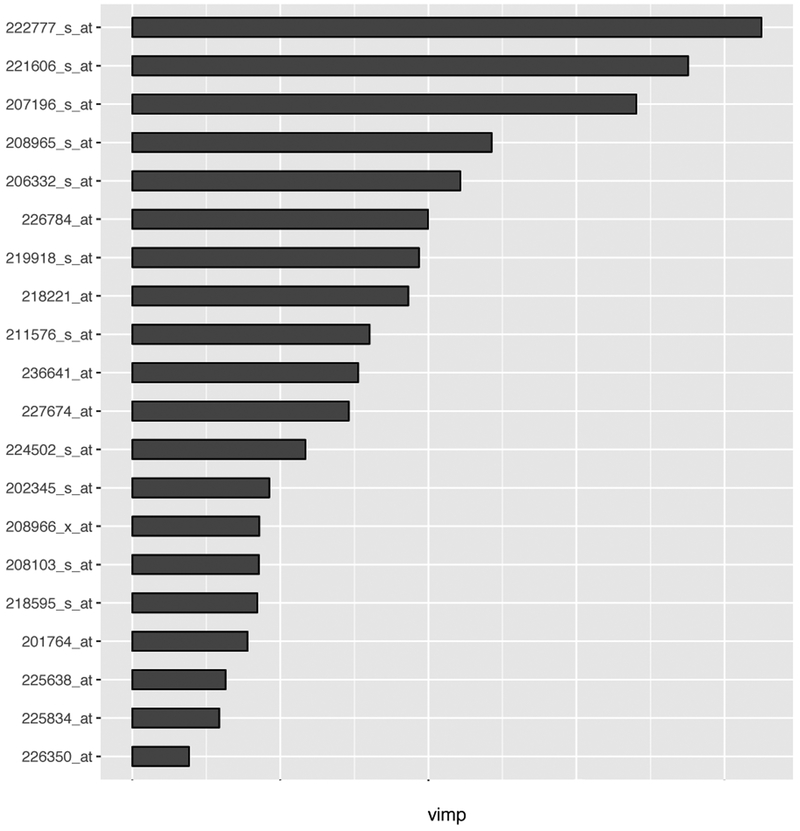
We next examined how variable screening helps predict the response variable by using random survival forest (Ishwaran et al., 2008), a nonparametric machine learning strategy for building a predictive survival model. We fitted a random survival forest model, based on a total of 1000 replicate trees by using the R package, namely, randomSurvivalForest (Ishwaran and Kogalur, 2007). In the interest of space, we reported the results of the composite IPOD method, for which the importance of each selected variable in the “forest” was shown in Figure 2.

Figure 2.

The ranking of variable importance (vimp) among those selected by the composite IPOD method for the multiple myeloma training set.

To measure the prediction accuracy, we reported the C-index, which gauges the agreement between the observed and predicted responses. The average C-index based on 100 bootstrap replicates of the validation data is listed in Table 3.

Overall, IPOD performed better than or at least on par with the other competing methods, and the IPOD with a larger γ tends give better predictions for this particular dataset.

Finally, we highlight some biological insight offered by our method. Probe 222777 (WHSC1), the most important gene as identified in Figure 2, has been found involved in the chromosomal translocation in multiple myeloma (Xie et al., 2013). Over-expression of Probe 221606 (HMGN5), the second on the list, has been linked to bladder cancer (Gan et al., 2015), prostate cancer (Guo et al., 2015) and breast cancer (Weng et al., 2015). On the other hand, neoplastic B-cell growth is regulated by gene TNIP1 (Probe 207196, the third gene of importance), whose dysfunction may cause multiple myeloma (Naji et al., 2012). Moreover, reduction or loss of IFI16 expression (Probe 208965, the fourth gene in the list) in cells is associated with the development of certain cancers, such as breast and prostate cancer (Choubey et al., 2008). Finally, CHML (Probe 226350, the last gene shown in Figure 2) is able to induce apoptosis or programmed cancer cell death and suppress tumor cell growth in multiple tumor lines (Zhan et al., 2001).

6. Discussion

Motivated by a multiple myeloma genomic study, we introduced a new framework for variable screening based on IPOD. As the method is model-free, it can be applicable in a variety of parametric, semiparametric, and nonparametric settings. In addition, it is theoretically justifiable, and computationally efficient. Using the proposed method, we identified a predictive gene signature model which was more accurate than the models obtained by using other screening methods.

Our work enlightens a few future directions. As our simulations revealed, the optimal γ may vary by the particular simulation configuration. Without knowing the true model in reality, it is challenging, conceptually and computationally, to identify an optimal γ, even in a data-driven way. However, the established framework may lead to some systematic ways of combining the results from IPOD with various γ’s. For example, we are currently investigating the means of combining the results of L possible values of γ’s using the following composite screening statistics:

$${\mathcal{I}}_{1j}={\text{max}}_{1⩽l⩽L}{\tilde{\mathcal{I}}}_j^{\left({\gamma }_l\right)},{\mathcal{I}}_{2j}=\underset{1⩽l\le L}{\text{min}}{\tilde{\mathcal{I}}}_j^{\left({\gamma }_l\right)},{\mathcal{I}}_{3j}=\frac{{\tilde{\mathcal{I}}}_j^{(\gamma )}-{\mathcal{I}}_{2j}}{{\mathcal{I}}_{1j}-{\mathcal{I}}_{2j}},$$

where γ_l, l = 1, …,L. Each option has pros and cons. In ${\mathcal{I}}_{1j}$, covariates selected by any γ_l, l = 1, …,L are to be included in the final selected set. This method could guarantee recovery of the true active set to the greatest extent in theory, though at the cost of inflating false discoveries. In ${\mathcal{I}}_{2j}$, only the covariates which are selected by all γ_l, l = 1, …,L could be included in the final selected set. This method could guarantee exclusion of the unimportant covariates to the greatest extent. However, the rather restrictive criterion may lead to many false negatives, which may not be ideal for knowledge discovery at the exploratory phase. The third option ${\mathcal{I}}_{3j}$ may be a compromise between these two extreme cases. Through rescaling to be a number between 0 and 1, it makes screening statistics across γ comparable. Comprehensively evaluating and studying all these proposals are currently undergoing and may be out of scope of this current paper. We expect to report the results elsewhere.