Receptor-Ligand Rebinding Kinetics in Confinement

Abstract

Rebinding kinetics of molecular ligands plays a key role in the operation of biomachinery, from regulatory networks to protein transcription, and is also a key factor in design of drugs and high-precision biosensors. In this study, we investigate initial release and rebinding of ligands to their binding sites grafted on a planar surface, a situation commonly observed in single-molecule experiments and that occurs in vivo, e.g., during exocytosis. Via scaling arguments and molecular dynamic simulations, we analyze the dependence of nonequilibrium rebinding kinetics on two intrinsic length scales: the average separation distance between the binding sites and the total diffusible volume (i.e., height of the experimental reservoir in which diffusion takes place or average distance between receptor-bearing surfaces). We obtain time-dependent scaling laws for on rates and for the cumulative number of rebinding events. For diffusion-limited binding, the (rebinding) on rate decreases with time via multiple power-law regimes before the terminal steady-state (constant on-rate) regime. At intermediate times, when particle density has not yet become uniform throughout the diffusible volume, the cumulative number of rebindings exhibits a novel, to our knowledge, plateau behavior because of the three-dimensional escape process of ligands from binding sites. The duration of the plateau regime depends on the average separation distance between binding sites. After the three-dimensional diffusive escape process, a one-dimensional diffusive regime describes on rates. In the reaction-limited scenario, ligands with higher affinity to their binding sites (e.g., longer residence times) delay entry to the power-law regimes. Our results will be useful for extracting hidden timescales in experiments such as kinetic rate measurements for ligand-receptor interactions in microchannels, as well as for cell signaling via diffusing molecules.

Introduction

The process of diffusion is a simple way of transporting ligand particles (e.g., proteins, drugs, neurotransmitters, etc.) throughout biological and synthetic media (1, 2). Even though each ligand undergoes simple diffusive motion to target-specific or nonspecific binding sites, ensemble kinetics of diffusing particles can exhibit complex behaviors. These behaviors can be traced back to physiochemical conditions, such as distribution of binding sites, concentration of ligands in solution, or heterogeneities in the environment. For instance, biomolecular ligands, such as DNA-binding proteins, can self-regulate their unbinding kinetics via facilitated dissociation mechanisms dictated by the bulk concentration of competing proteins (3, 4, 5, 6, 7, 8, 9). Similarly, spatial distribution of binding sites, such as the fractal dimensions of a long DNA molecule (10) or surface density of receptors on cell membranes (11, 12, 13, 14) and in flow chambers (15, 16, 17), can influence the association and dissociation rates of the ligands.

One way of probing these molecular reaction rates is to observe the relaxation of a concentration quench, in which dissociation of ligands from their binding sites into a ligand-free solution is monitored to explore the kinetic rates of corresponding analytes (4, 5, 18, 19, 20). The complete time evolution of this relaxation process depends on factors such as chemical affinity between the binding sites and the ligands, dimensions of the diffusion volume, and average distance between the binding sites. Although the affinity determines the residence time of the ligand on the binding site (21), the volume available for diffusion can control onset of the steady-state regime at which bulk density of the ligands becomes uniform throughout the entire diffusion volume and when binding and unbinding rates become constants. The spatial distribution of the binding sites can decide how often dissociated ligands revisit the reactive surface on which binding sites are located (22). Particularly during the nonsteady state at which ligand concentration is not homogeneous inside the confined diffusion volume, these factors can significantly influence the time dependence of the rebinding kinetics in a nontrivial way.

This concentration-quench scenario mentioned above is indeed common both in vivo and in vitro (Fig. 1). In single-molecule (SM) studies of protein-DNA interactions, short-DNA binding sites are sparsely grafted (∼1 μm spacings) inside a finite-height flow cell (4, 6, 23). The bound proteins may be observed to dissociate into a protein-free solution from their DNA binding sites, allowing measurement of unbinding kinetics. Similarly, in surface plasmon resonance (SPR) experiments, ligands initially located on their receptors dissociate into a ligand-free solution. Usually, SPR experiments involve more tightly spaced receptor sites (∼100 nm spacings) relative to SM experiments (24, 25). On the other hand, in vivo processes such as exocytosis and paracrine signaling, in which small molecules are discharged into intercellular space to provide chemical communication between cells, can be examples for the relaxation of (effective) concentration-quench scenario (26). Indeed, because of systemic circulation of ligands in vivo (e.g., time-dependent synthesis and digestion or phosphorylation-dephosphorylation of ligands in cells), a non-steady-state scenario is the dominant situation in biology.

Figure 1.

(a) Schematics of cell communication via secretion of small ligands into intercellular space of characteristic size of h. (b) In single-molecule (SM) experiments, binding sites (orange) saturated by ligands (purple spheres) are more sparsely distributed compared to SPR experiments. The binding sites are separated by a distance s. (c) An illustration of diffusion of ligand particles of size a initially located at their binding sites is shown. The diffusion volume is confined by two identical surfaces separated by a distance h. The particles can diffuse to neighboring binding sites within a diffusion time τ_s and to the confining upper surface within a diffusion time of τ_z. Representative trajectories are shown by dashed curves. To see this figure in color, go online.

Whether it is a biological or lab-on-chip system, before the steady state is achieved, the separation distance between the binding sites (i.e., grafting density of receptors) influences the rebinding rates (22, 27, 28); upon the initial dissociation of a ligand from its binding site into solution, the ligand can return the same binding site (self-binding) or diffuse to neighboring binding sites (cross-binding) (Fig. 1 c). In the latter case, the frequency of rebinding events (i.e., on rate for diffusion-limited reactions) depends on the average distance traveled by the ligand from one binding site to another. At timescales comparable to the intersite diffusion time, the average separation between binding sites becomes a key kinetic parameter.

Experimental studies on ligand-receptor kinetics (22, 29) and signal transduction pathways (13, 30, 31) have highlighted the importance of the spatial distribution of binding sites. In the context of SPR experiments, the effect of correlated rebinding events on the interpretation of dissociation curves has been brought to attention by using a self-consistent mean-field approximation (22, 32). These previous studies have highlighted the erroneous usage of exponential-fit functions to obtain association rates and instead suggested a stretched exponential-fit function for the case when the fraction of initially bound ligands is small (22, 27). Lattice MC simulations (22, 27, 32) and experiments on insulin-like growth factors interacting with their binding proteins (22) showed a nonexponential decay of binding-site association rate, followed by a −1/2 power-law regime associated with one-dimensional diffusion perpendicular to the binding-site surface. Other power-law regimes can arise because of the diffusion of ligands between neighboring binding sites, and a −3/2 power law has been derived to be associated with this (27). In addition, the reservoir height can be expected to affect the kinetics (22, 27, 32).

Motivated by experiments as well as the generality of rebinding kinetics in biological systems, we focus on understanding the different kinetic regimes of time evolution of spontaneous dissociation of an ensemble of Brownian particles from their binding sites into a confined reservoir (Fig. 1 c). Using scaling arguments and molecular dynamics (MD) simulations, we show that the on rate exhibits two distinct power laws at times longer than the initial positional relaxation of the particles but shorter than the time-independent steady-state regime in diffusion-limited reactions. We also derive scaling expressions for the total number of rebinding events experienced by each binding site as a function of time. This quantity can be related to the time-integrated fraction of bound and unbound ligands in experiments (4, 15). Our results indicate that the total number of rebinding events exhibits an unexpected plateau behavior at times much earlier than the onset of the steady state. This plateau regime is terminated by a threshold timescale, which increases with the fourth power of the separation distance. Interestingly, this threshold timescale cannot be detected easily in the on-rate measurements.

This work is organized as follows. Scaling Analysis for Ligands Diffusing in Vertical Confinement presents the scaling theory, providing an overview of how the various kinetic regimes fit together and how they are controlled by experimental parameters. Comparison with MD Simulations compares our scaling results to coarse-grained MD simulations of ligands, modeled as Brownian particles interacting with their binding sites. In the Discussion, we examine how our results relate to existing experiments, as well as to future SM studies and experiments in biological systems.

Materials and Methods

In our coarse-grained MD simulations, n₀ = 400–6400 binding sites separated by a distance s are placed on a planar surface composed of beads of size a arranged in a square lattice configuration. To model ligands, n₀ beads of size 1σ ≈ a are placed at contact with binding sites, where σ is the unit distance in the simulations. The simulations were performed in implicit background solvent, in which each bead experiences a viscous force proportional to its instantaneous thermal velocity; thus, a constant average temperature can be maintained throughout the simulation boxes without considering solvent molecules explicitly (33).

The ligands interact with each other and the surfaces via a short-range truncated and shifted Lennard-Jones (LJ) potential, also known as Weeks-Chandler-Anderson (WCA),

$$V^{\text{LJ}}\left(r\right)=\{\begin{array}{c}4\epsilon \left[{\left(\sigma /r\right)}^{12}-{\left(\sigma /r\right)}^6+v_s\right]r\le r_c\\ 0r>r_c\end{array},$$ (1)

where r_c is the cutoff distance. Cutoff distances of r_c/σ = 2^1/6, 2.5 are used with a shift factor v_s = 1/4 for the interactions between all beads unless otherwise noted. The interaction strength is set to ε = 1k_BT for all beads, where k_B is the Boltzmann constant and T is the absolute room temperature. For attractive cases, the cutoff distance is set to r_c/σ = 2.5, and the strength of the potential is varied between ε = 0.5–3k_BT.

All MD simulations were run with LAMMPS MD package (34) at constant volume V and reduced temperature T_r = 1.0. Each system is simulated for 10⁶ to 2 × 10⁹ MD steps. The simulations were run with a time step of Δt = 0.005τ, where the unit timescale in the simulations is τ ≈ τ₀. The data sampling is performed by recording each 1, 10, 10², 10³, and 10⁴ steps for MD intervals 0–10², 10²–10³, 10³–10⁴, 10⁴–10⁵, and 10⁵–10⁸, respectively. The monomeric LJ mass is m = 1 for all beads. The temperature is kept constant by a Langevin thermostat with a thermostat coefficient γ = 1.0τ⁻¹.

The volume of the total simulation box is set to n₀(s²h)σ³, where the vertical height is h/σ = 12.5–2000. Periodic boundary conditions are used in the lateral ($\hat{x}$ and $\hat{y}$) directions, and at z = h, the simulation box is confined by a surface identical to that at z = 0. VMD is used for the visualizations (35).

In the fitting procedures, a weight function inversely proportional to the square of the data point is used. Error bars are not shown if they are smaller than the size of the corresponding data point.

Results

Scaling analysis for ligands diffusing in vertical confinement

Consider n₀ identical particles of size a initially (i.e., at t = 0) residing on n₀ identical binding sites located on a planar surface at z = 0 (Fig. 1 c). A second surface at z = h confines the reservoir in the vertical (i.e., $\hat{z}$) direction. The size of a binding site is a, and the average separation distance between two binding sites is s. At t = 0, all particles are released and begin to diffuse away from their binding sites into a particle-free reservoir (Fig. 1 c). The assumption of instant relaxation ignores the finite residence times of ligands on their binding sites and will be discussed further in the following sections.

After the initial release of the ligand particles from their binding sites, each particle revisits its own binding site as well as other binding sites multiple times. The on rate, k_on (proportional to the local concentration of ligands in diffusion-limited reactions), and the total number of revisits experienced by each binding site, ${\mathcal{N}}_{\text{coll}}$, reach their equilibrium values once rebinding events become independent of time (i.e., when the ligand concentration in the reservoir becomes uniform). At intermediate times, during which particle concentration in the reservoir is not uniform, various regimes can arise depending on the separation distance s or the height of the reservoir h.

The time-dependent expressions for k_on and ${\mathcal{N}}_{\text{coll}}$ before the steady state can be related to the length scales of the system on a scaling level after making a set of simplifying assumptions. First, we assume that each particle diffuses with a position independent diffusion coefficient, D. The calculation we present here is for vanishing flow rates. For nonvanishing flows, no-slip boundary conditions can provide a weaker flow profile near the surface than bulk (36), and thus, a zone through which diffusion is not affected by the flow can be assumed (22). We also neglect hydrodynamic interactions between the particles and the surface because of the separation of the length scale at which hydrodynamics is relevant (comparable to the few-nanometer size of the particle and the inter-receptor and system size length scales of many nanometers to microns). We do note that short-ranged hydrodynamic effects can be accounted for in our coarse-grained description through the precise values of a, D, and τ₀. More detailed description of hydrodynamic effects is essential when considering details of motion at length and timescales comparable to a and τ₀, respectively. However, to establish large-length and long-time scaling descriptions, the local hydrodynamic-drag model that we use here is sufficient.

We also assume that the particles interact with each other, the binding sites, and surfaces via short-ranged interactions (i.e., interaction range is comparable to the particle size). This approximation is appropriate for physiological salt concentrations, for which electrostatic interactions are short-ranged. We also ignore all prefactors on the order of unity.

After the initial dissociation of a ligand particle from its binding site, it can explore a volume of V(t) before revisiting any binding site at time t. If there are ω binding sites in V(t), the particle can return any of ω possible binding sites (i.e., ω is the degeneracy of the binding sites). Thus, a general scaling ansatz for the on rate can then be written as

$$k_{\text{on}}\left(t\right)\approx \frac{Da}{V\left(t\right)}\omega .$$ (2)

Alternatively, Eq. 2 can also be interpreted as the inverse of the time that is required for a particle to diffuse through V(t)/a³ discrete lattice sites if the diffusion time per lattice site is D/a². Note that for diffusion-limited reactions, k_on(t) ∼ c(t), where c(t) ∼ V(t)⁻¹ is the time-dependent concentration of ligands within the pervaded volume of the particle cloud. Also note that for simplicity, we assume that ω has no explicit time dependence, although this could be added to the ansatz in Eq. 2, for instance, for binding sites along a fluctuating chain or for diffusing protein rafts on cell membranes.

The cumulative number of rebinding events detected by each binding site at time t is related to the on rate as

$${\mathcal{N}}_{\text{coll}}\left(t\right)\approx {\int }_{t_0}^t{k}_{\text{on}}\left(t^{\prime }\right)d{t}^{\prime },$$ (3)

where t₀ is the initial time for counting the collisions between the binding sites and ligands.

At the initial times of the diffusion of n₀ ligand particles (i.e., t ≈ τ₀ ≈ a²/D), each particle can undergo a three-dimensional diffusion process to a distance roughly equivalent to its own size (i.e., self-diffusion distance). Because, at 0 < t < τ₀, particles can only collide with their own original binding sites, we have ω ≈ 1, and the interaction volume is V ≈ a³ ≈ (τ₀D)^3/2. Thus, according to Eq. 2, the on rate is k_on = 1/τ₀ and can be considered to be time independent during t < τ₀ on the scaling level. From Eq. 3, a constant on rate leads to a linearly increasing total number of rebinding events as ${\mathcal{N}}_{\text{coll}}\sim t$ (Fig. 2 b).

Figure 2.

Results of scaling arguments for (a) the on rates k_on and (b) the total number of rebinding events ${\mathcal{N}}_{\text{coll}}$ as a function of time in a log-log scale. Arrows indicate the directions of decreasing separation distance between two binding sites (i.e., s → a). SM and SPR indicate the regimes related to SM and SPR experiments, respectively. The threshold timescales refer to onset for darker lines. See also Table 1 for the definition of the threshold times. To see this figure in color, go online.

For t > τ₀, each particle can diffuse to a distance r > a. If the separation distance between the binding sites is s ≈ a, particles can visit any of the nearest binding sites at t ≈ τ₀. If the separation distance is large (i.e., $s\gg a$), particles can travel to neighboring sites only after a time τ_s ≈ s²/D, at which the average distance traveled by any particle is s. At τ₀ < t < τ_s, individual particles perform three-dimensional diffusion, and thus, the interaction volume is given by V(t) ≈ (Dt)^3/2. Because the volume experienced by particles is V(t) < s³ at t < τ_s, on average, one binding site is available per particle in the interaction volume (i.e., ω ≈ 1). Thus, using Eq. 2, we obtain k_on ∼ t^−3/2.

Interestingly, at τ₀ < t < τ_s, the number of revisits per binding site, ${\mathcal{N}}_{\text{coll}}$, does not increase because most particles are on average far away from their own and other binding sites. On the scaling level, this results in a plateau behavior for the cumulative collision number (i.e., ${\mathcal{N}}_{\text{coll}}\approx 1$), as illustrated in Fig. 2 b. Note that plugging k_on ∼ t^−3/2 into Eq. 3 leads to a weak explicit time dependence for the ${\mathcal{N}}_{\text{coll}}$ at 0 < t < τ_s (i.e., ${\mathcal{N}}_{\text{coll}}\sim 1+t^{-1/2}$). The t^−1/2 dependence indicates that ${\mathcal{N}}_{\text{coll}}$ stays almost constant during this regime.

At t > τ_s ≈ s²/D, the particles can encounter other neighboring binding sites apart from their own, thus, ω > 1. At this time window, the particle density near the bottom surface of the reservoir is nearly uniform, but the overall density is still nonuniform throughout the reservoir. This can be seen in the simulation snapshots shown in Fig. 3 (we will discuss our simulation results further in the next section). Only at a threshold time dictated by the height of the reservoir, τ_z ≈ h²/D, does each particle on average reach the physical limits of the reservoir and the on rate reach its steady-state limit (i.e., k_on ≈ Da/hs²), as shown in Fig. 2. At earlier times, t < τ_z, because there are ligand-free regions in the reservoir (Fig. 3), V(t) and thus the on rate still must exhibit a time dependence.

Figure 3.

Simulation snapshots at various time windows showing the time evolution of the particle concentration throughout a simulation box of height h/a = 50. The separation distance between the binding sites is s/a = 2.5. The blue lines indicate the borders of the original simulation box. Periodic boundary conditions are applied only in the $\hat{x}$ and $\hat{y}$ directions, whereas the reservoir is confined in the $\hat{z}$ direction by two identical surfaces. To see this figure in color, go online.

One way of obtaining a scaling expression for the time-dependent on rate at τ_s < t < τ_z is to consider the diffusion of a single-particle in a volume of V(t) ≈ (Dt)^3/2 and use ω ≈ (Dt/s²) for the number of binding sites per area of A ≈ (Dt). Consequently, Eq. 2 leads to k_on ≈ D^1/2a/s²t^1/2 ∼ t^−1/2. Alternatively, to obtain the same scaling form for the on rate, one can consider the overall diffusion of the entire particle cloud at t > τ_s (Fig. 3): the explored volume scales as V(t) ∼ (Dt)^1/2, and the total number of binding sites in this volume is ω ∼ 1/s². Thus, Eq. 2 also leads to k_on ∼ t^−1/2. This scaling is due to quasi-one-dimensional propagation of the particle cloud across the reservoir, although each particle undergoes a three-dimensional diffusion process (Fig. 3).

The rapid drop of the on rate at t > τ₀ with multiple negative exponents affects ${\mathcal{N}}_{\text{coll}}$ as well. According to Eq. 3, the scaling form for ${\mathcal{N}}_{\text{coll}}$ at t > τ_s can be obtained from the partial integration of the corresponding on-rate expressions at the appropriate intervals (i.e., 0 < τ₀ < τ_s < t) as

$${\mathcal{N}}_{\text{coll}}\left(t\right)\approx 1+\frac{D^{1/2}a}{s^2}{t}^{1/2}.$$ (4)

We note that inserting t = τ_s into Eq. 4 leads to ${\mathcal{N}}_{\text{coll}}\approx 1$ for any value of s/a > 1 because the second term on the right-hand side of Eq. 4 is smaller than unity. This indicates that the plateau regime predicted for ${\mathcal{N}}_{\text{coll}}$ at t < τ_s persists even at t > τ_s (Fig. 2 b). Only at a later threshold time, τ_c > τ_s, does the second term of Eq. 4 become considerably larger than unity, and so does the number of revisits, ${\mathcal{N}}_{\text{coll}}$. The threshold time, τ_c, can be obtained by applying this result on the second term of Eq. 4 (i.e., $D^{1/2}a{\tau }_{\text{c}}^2/s^2\approx 1$), which provides an expression for the terminal time of the plateau regime as

$${\tau }_{\text{c}}\approx \frac{s^4}{D{a}^2}.$$ (5)

At t > τ_c, the total number of revisits per binding site begins to increase above unity. The functional form of this increase at τ_c < t < τ_z can be obtained by integrating the on rate (i.e., k_on ∼ t^−1/2) as ${\mathcal{N}}_{\text{coll}}\sim t^{1/2}$. This sublinear increase of ${\mathcal{N}}_{\text{coll}}$ continues until the particle density becomes uniform throughout the entire reservoir at t = τ_z. At later times t > τ_z, diffusion process obeys Einstein-Smoluchowski kinetics, in which the on rate reaches its time-independent steady-state value and ${\mathcal{N}}_{\text{coll}}$ increases linearly (Fig. 2).

To summarize, according to our scaling analysis, at t < τ₀, the on rate is constant because of self-collisions with the original binding site, as also schematically illustrated in Fig. 2. At the later times, the on rate decreases as k_on ∼ t^−3/2 until t < τ_s because of the three-dimensional escape process of particles away from their binding sites (Fig. 2 a). Once particles diffuse to distances on the order of s, the particle cloud diffuses in a one-dimensional manner, and the on rate decays with a slower exponent, k_on ∼ t^−1/2. When the particles fill the reservoir uniformly, a steady-state value of k_on ∼ a/(hs²) takes over. Interestingly, at the threshold time τ_c, at which we predict a crossover for ${\mathcal{N}}_{\text{coll}}$, the on rate does not exhibit any alterations and continues to scale as k_on ∼ t^−1/2.

The regime during which ${\mathcal{N}}_{\text{coll}}$ is independent of time on the scaling level is smeared out in the limit of s → a as shown in Fig. 2 b. If s = a, the plateau in ${\mathcal{N}}_{\text{coll}}$ completely disappears, and a scaling ${\mathcal{N}}_{\text{coll}}\sim t^{1/2}$ determines the cumulative rebinding events at τ₀ < t < τ_z. This indicates that the three-dimensional escape process disappears and a one-dimensional diffusion-like behavior prevails after the initial dissociation of ligands. This behavior is common in SPR experiments, in which receptors are often densely grafted.

In the equations below, the scaling expressions for the on rates rescaled by 1/τ₀ ≈ (D/a²)⁻¹ and the total number of revisits are given together with their respective prefactors for corresponding time intervals (see Table 1) as

$$k_{\text{on}}{\tau }_0\approx \{\begin{array}{c}10<t<{\tau }_0\\ {\left({\tau }_0/t\right)}^{3/2}{\tau }_0<t<{\tau }_{\text{s}}\\ \left(a^2/s^2\right){\left({\tau }_0/t\right)}^{1/2}{\tau }_{\text{s}}<t<{\tau }_z\\ a^3/\left(h{s}^2\right)t>{\tau }_z.\end{array}$$ (6)

Table 1.

The Threshold Times and their Scaling Expressions with Numerical Estimates for Various Systems

	Scaling	SPRa (s)	SMb (s)	Exocytosisc (s)	Exocytosisd (s)
τ0	a2/D	10−9	10−9	10−9	10−9
τs	s2/D	10−6	10−2	10−6	10−4
τc	s4/a2D	10−4	104	10−4	100
τz	h2/D	102	106	10−5	102

In the estimates, a ligand of size a = 1 nm and a diffusion coefficient of D = 100 μm²/s are assumed. The estimates are for the parameters in the following footnotes.s

^as = 10 nm and h = 10²μm (e.g., SPR case).

^bs = 1 μm and h = 10⁴μm (e.g., SM case (4)).

^cDiffusion of insulin secreted from isolated vesicles into intercellular space of height h = 30 nm and s = 10 nm (determined from the average insulin concentration of ∼40 mM in the vesicle (58)).

^dRelease of ∼10 μM of GTPγS (i.e., s = 100 nm) from an eosinophils-cell vesicle (59) with an average cell-to-cell distance of h = 100 μm (i.e., ∼500 cells per microliter).

Similarly, for the total number of revisits,

$${\mathcal{N}}_{\text{coll}}\approx \{\begin{array}{c}t/{\tau }_{0}0<t<{\tau }_0\\ 1{\tau }_0<t<{\tau }_{\text{c}}\\ \left(a^2/s^2\right){\left(t/{\tau }_0\right)}^{1/2}{\tau }_{\text{c}}<t<{\tau }_z\\ \left(a^3/\left[h{s}^2\right]\right)\left(t/{\tau }_0\right)t>{\tau }_z.\end{array}$$ (7)

In Table 1, we provide some numerical examples for the above timescales approximately corresponding to SPR and SM experiments and exocytosis. Note that the scaling expression given in Eqs. 6 and 7 can also be obtained by considering the relaxation of a Gaussian particle distribution in corresponding dimensions (see Appendix). In fact, the solution of the master equation for the corresponding system also leads to k_on ∼ t^−1/2 as a limiting behavior, as we will discuss further in the next sections (22, 27).

In the next section, we will compare our scaling arguments with the coarse-grained MD simulations and investigate the relation between threshold timescales and the two length scales, namely the separation distance between the binding sites s and the height of the diffusion volume h.

Comparison with MD simulations

As described in the Materials and Methods above, a prescribed number of ligands initially located at the bottom surface are allowed to diffuse into the confined volume at t > 0 (Fig. 3). The rescaled height of the simulation box h/a and the rescaled separation distance between the binding sites s/a were separately varied, and their effects on time dependencies of k_on(t) and ${\mathcal{N}}_{\text{coll}}\left(t\right)$ were monitored. In the extraction of k_on values, the binding sites are defined as the initial positions of ligands at t = 0. Any particle that is found within the collision range of any binding site (i.e., r_c/a = 2^1/6) at a given time t is counted as a bound particle. In our computational analyses, τ₀k_on(t) is defined as the normalized fraction of binding sites occupied by ligands for diffusion-limited reactions. For the reaction-limited case, τ₀k_on(t) corresponds to raw dissociation data. The values of ${\mathcal{N}}_{\text{coll}}\left(t\right)$ were calculated via Eq. 3; the collisions of ligands with the binding sites were counted starting from t₀ = 0. All simulations were carried out until the calculated on rates reached their respective steady states (see Appendix for further simulation details).

Diffusion-limited kinetics

We first consider the scenario for which the reactions between the binding sites and ligands are diffusion limited. Thus, the average residence time of the ligand on the binding site is on the order of τ₀, which is the self-diffusion time of a particle in the simulations. We achieved this by using a purely repulsive WCA potential (37) with a cutoff distance of r_c/a = 2^1/6 (Eq. 8 in the Appendix). This setup, as we will see, allows us to observe the regimes predicted in Scaling Analysis for Ligands Diffusing in Vertical Confinement more clearly. We will further discuss the longer residence times in conjunction with other timescales in the following sections.

In Fig. 3, we present a series of simulation snapshots to demonstrate the diffusion process of n₀ = 400 particles over the time course of the simulations for a setup with h/a = 50 and s/a = 2.5. These numbers lead to characteristic times ranging from τ_s ≈ τ₀ to beyond τ_z ≈ 10⁴τ₀ for the system shown in Fig. 3. At short times, t ≈ τ₀, the particles are mostly near the reactive (bottom) surface, as can be seen in Fig. 3. As the time progresses, the particle cloud diffuses vertically to fill the empty sections of the box. At t < τ_z, the particle density near the surface changes with time, and visually, the concentration is not uniform in the simulation box. Only for t > τ_z does the particle density become uniform and the initial concentration quench completely relaxed, as illustrated in Fig. 3.

Densely placed binding sites in finite-height reservoirs. To systematically compare our scaling predictions with the simulations, we fixed the separation distance to s/a = 2.5 and varied the height of the reservoir between h/a = 13 and h/a = 200. Fig. 4 shows the calculated on rates rescaled by the unit time, k_onτ₀, and the total number of revisits, ${\mathcal{N}}_{\text{coll}}$, as a function of the rescaled simulation time t/τ₀. At short times (i.e., t < τ₀), during which particles can diffuse only to a distance of their own size, ${\mathcal{N}}_{\text{coll}}$ increases linearly, whereas on rates k_on have no or weak time dependence, in accord with our scaling calculations (Fig. 4 a). In the same figure, at approximately t ≈ τ₀, we observe a rapid drop in k_on, which is described nominally by an exponential function (exp(−t/τ₀)) (dashed curve in Fig. 4 a). However, we should also note that, in the system presented in Fig. 4 a, s/a = 2.5, and thus, τ_s ≈ 6τ₀. Hence, the decay in the on rate is arguably the beginning of a power law with an exponent approximately −3/2 (Fig. 2 a).

Figure 4.

(a) Rescaled on rates as a function of the rescaled simulation time for various reservoir heights. The distance between two binding sites is s/a = 2.5. A running average over 20 data points is shown for all cases for clarity. (b) Total number of revisits per binding site obtained via Eq. 3 is shown by using nonaveraged data series of (a). For all cases, the number of ligand particles is n₀ = 400. The vertical lines indicate the threshold times calculated via τ_z = 2h²/D (i.e., for the one-dimensional case). To see this figure in color, go online.

According to our scaling analysis, for small enough separation distances (i.e., s ≈ a), the on rate obeys a power law (i.e., k_on ∼ t^−1/2) at the intermediate times, τ_s < t < τ_z (see Fig. 2 a). In Fig. 4 a, a slope of −0.56 ± 0.04 describes the decay of the on rates, in agreement with our scaling result to within statistical errors. We have also tested larger systems with n₀ = 1600 and n₀ = 6400 particles and obtained similar exponents (Supporting Materials and Methods). At longer times (i.e., t > τ_z ≈ h²/D), the on rates in Fig. 4 a reach their respective steady-state values, which depend on the equilibrium concentrations of the ligands in each system (i.e., k_on ∼ 1/hs²). That is, for a fixed number of ligands, increasing the height h/a decreases the concentration. Thus, the steady-state values of the on rates go down, as seen in Fig. 4 a.

As for the total number of revisits, ${\mathcal{N}}_{\text{coll}}$, in Fig. 4 b, the simulation results for densely packed binding sites show a power-law dependence on time as ${\mathcal{N}}_{\text{coll}}\sim t^{0.44\pm 0.05}$ at the intermediate times, statistically consistent with the prediction (Fig. 2 b). Once this regime ends, a subsequent terminal linear regime, in which ${\mathcal{N}}_{\text{coll}}\sim t^{1.0}$, manifests itself in Fig. 4 b. According to our scaling analysis (Eq. 7), the onset of this long-time linear regime is set by τ_z. Thus, increasing the height of the reservoir h only shifts the onset to later times (Fig. 4 b). Note that in Fig. 4 b, for small values of h/a, the exponent is closer to unity because it takes less time to reach a uniform ligand density in smaller simulation boxes.

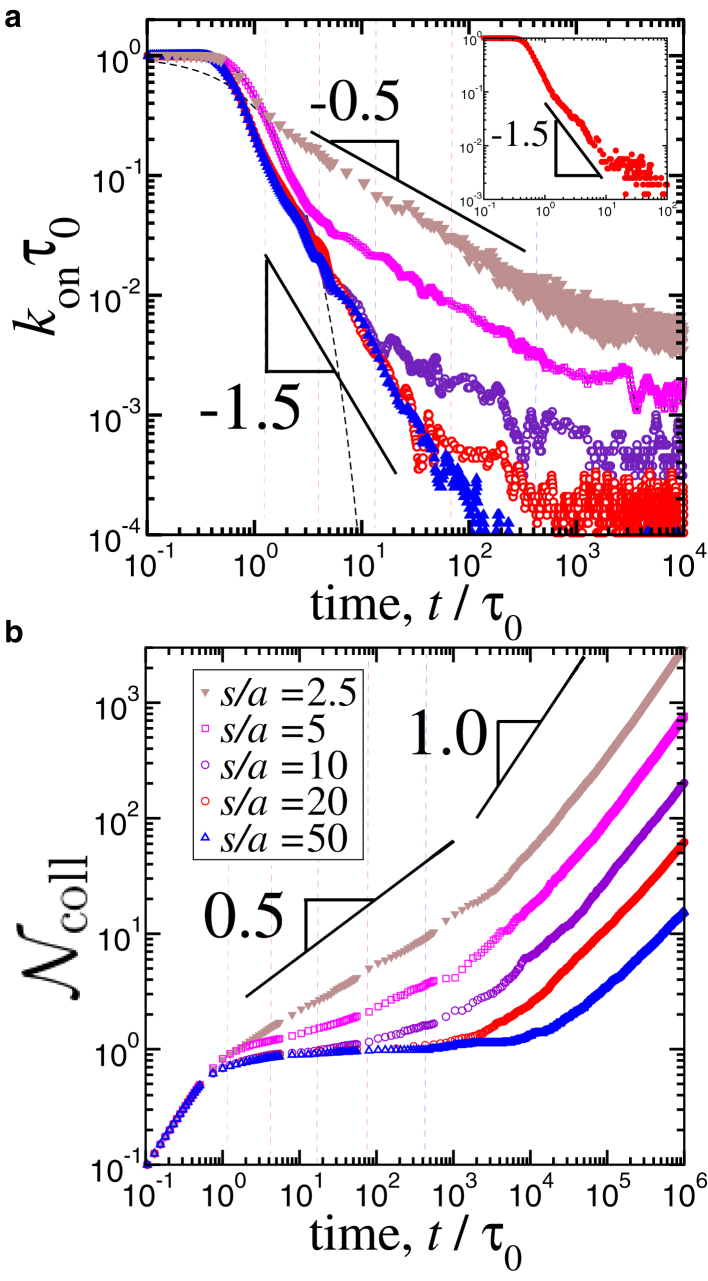
Effect of separation distance on rebinding kinetics. As discussed in Scaling Analysis for Ligands Diffusing in Vertical Confinement, before the steady state, diffusion time between binding sites significantly affects the apparent dissociation kinetics of ligands. To study this phenomenon, we ran simulations with various values of the separation distance ranging from s/a = 2.5 to s/a = 50 for a fixed height of h/a = 50 (Fig. 5). Although the short-time kinetic behaviors in Fig. 5 are similar to those in Fig. 4 regardless of the surface separation, the long-time behavior exhibits various regimes depending on the separation distance s/a in the simulations.

Figure 5.

(a) On rates rescaled by the unit diffusion time τ₀ as a function of rescaled time for various separation distances between binding sites for a fixed box height of h/a = 50. Each data set is averaged over 3–5 separate simulations of the systems containing n₀ = 400–6400 particles. For clarity, running averages over 10 points are shown. Inset shows the on rate for a system composed of n₀ = 1600 particles for s/a = 10 and h/a = 1000. (b) The total number of rebinding events obtain via Eq. 3 for n₀ = 400 particle systems by using nonaveraged data sets is shown. The vertical lines indicate the threshold times calculated via τ_s = 6s²/D (i.e., for the three-dimensional case). To see this figure in color, go online.

In our scaling analysis, for large separation distances, the exponent −3/2 controls the decay of the on rate until the threshold time τ_s, above which the decay of the on rate is described by a weaker exponent of −1/2 (Fig. 2 a). Our simulation results are also in agreement with this scaling prediction within statistical errors: in Fig. 5 a, for s/a ≈ 1, a slope close to −1/2 can describe the decay of the on rates before the time-independent steady state, as discussed earlier. As s/a is increased, this slope is gradually replaced by a stronger decay as k_on ∼ t^{−1.46 ± 0.13} at t > τ₀ (Fig. 5 a). For the intermediate values of s/a (i.e., s/a = 5, 10, 20, 50 in Fig. 5 a), this transition is demonstrated in Fig. 5 a. Additionally, in the inset of Fig. 5 a, we also show a system with s/a = 10 and h/a = 1000 for a larger system of n₀ = 1600 particles: the −3/2 exponent is more apparent because the two threshold times, τ_z and τ_s, are well separated because of the large ratio of $h/s\gg 1$.

Emergence of plateau behavior in total rebinding events for sparsely placed binding sites. The data in Fig. 5 b show the distinct behavior of ${\mathcal{N}}_{\text{coll}}$ for $s/a\gg 1$ as compared to the cases in which binding sites are closer to each other (Figs. 4 b and S1). As discussed earlier in Fig. 4 b, for s/a ≈ 1, a slope around ${\mathcal{N}}_{\text{coll}}\sim t^{0.44}$ is dominant at t < τ_z. However, for $s/a\gg 1$, a plateau regime replaces this behavior at the intermediate times in the simulations (Fig. 5 b). As the separation between the binding sites s/a is increased, the plateau regime becomes broader by expanding to longer times. This trend is also in accord with our scaling analyses (Fig. 2 b).

The plateau regime in ${\mathcal{N}}_{\text{coll}}$ that we observe in the simulations is followed by an incremental behavior, as seen in Fig. 5 b. The predicted power law after the plateau is ${\mathcal{N}}_{\text{coll}}\sim t^{1/2}$ for τ_s < t < τ_z (Fig. 2 b). Within the duration of our simulations, we observe a mixture of slopes instead of a single exponent of 1/2. For instance, for h/a = 50, the slope that we can extract at the long times is smaller than unity but larger than 1/2 because the two threshold times, τ_s and τ_z, are close to each other (blue triangles in Fig. 5 b). This is due to the small ratio of the two threshold timescales, τ_z/τ_c = (ha/s²)² ≈ 10, for the data shown in Fig. 5 b.

To further separate these two timescales, we performed simulations for various values of h/a = 50–2000 with a fixed value of s/a = 10. The results are shown in Fig. 6 for t > τ_s ≈ 100τ₀. For all the data sets in Fig. 6, τ_s and τ_c are identical (i.e., equal s/a). Thus, the only difference in their kinetic behaviors arises because of the variations in h/a, which in turn determines the duration of the τ_z–τ_c interval. In Fig. 6, ideally, the regime with ${\mathcal{N}}_{\text{coll}}\sim t^{1/2}$ should be observable at τ_s < t < τ_z. However, we rather observe a weaker increase before a slope of around 1/2 emerges. We attribute this behavior to the inherent weakness of scaling analyses because even at t > τ_s, ligands can collide with multiple binding sites frequently enough, particularly for small separation distances. These collisions, in turn, can result in a slight increase in ${\mathcal{N}}_{\text{coll}}$ similar to that observed in Fig. 6.

Figure 6.

The total number of rebinding events as a function of rescaled simulation time for various rescaled heights at a fixed separation distance s/a = 10. For clarity, only the data for t > τ_s ≈ 100τ₀ are shown. For all cases, number of ligands is n₀ = 400. To see this figure in color, go online.

Simulations also confirm that at long times t > τ_z, ${\mathcal{N}}_{\text{coll}}$ increases with an exponent around unity (Figs. 5 b and 6) in accord with a time-independent k_on prediction. Note that, for simulations longer than performed here, which are not feasible for computational reasons, we anticipate a convergence to a slope of unity for all of our configurations.

Threshold time for ${\mathcal{N}}_{\text{coll}}$ plateau. We also performed a separate set of simulations to specifically identify the scaling dependence of τ_c on the separation distance (Eq. 5). We fixed the ratio h/s = 10 and varied the separation distance between s/a = 10–100 and the height between h/a = 100–1000. We fitted the data encompassing the time interval τ₀ < t < τ_z to a function in the form of f(t) = 1 + (t/τ_s)^1/2 to extract the threshold times τ_c at which plateau regimes end. The results shown in Fig. 7 are in close agreement with our scaling prediction; the data are fitted by τ_c ∼ s^{3.5 ± 0.5}. The finding that the exponent extracted from the simulations is smaller than 4 but larger than 2 in Fig. 7 indicates that the terminal threshold time for the plateau, τ_c, is distinct and well separated from τ_s.

Figure 7.

Log-log plot of τ_c extracted from simulations by fitting the respective intervals to a function in the form of f(t) = 1 + (t/τ_c)^1/2 for h/s = 10 as a function of the rescaled separation distance. The thin lines show slopes of 3.0 and 3.5. For the data sets, h/a = 100, 200, 500, 1000, and s/a = 10, 20, 50, 100. For all cases, the number of ligands is n₀ = 400. To see this figure in color, go online.

Reaction-limited kinetics

In Diffusion-Limited Kinetics, we consider the diffusion-limited case, in which being within the collision range of a binding site is enough to be counted as bound for any ligand, that is, τ_off ≈ τ₀. However, most molecular ligands, including DNA-binding proteins, can have finite lifetimes on the order of minutes to hours (4, 5). Long residence times can indeed intervene with the threshold times and regimes predicted by our scaling arguments.

To test how the finite residence times can affect the rebinding rates, we ran a separate set of simulations, in which a net attraction was introduced between the binding sites and the ligands for two different separation distances, s/a = 2.5 and s/a = 20, with h/a = 50 (Fig. 8). The attraction was provided by increasing the cutoff distance and varying the strength of the interaction potential in the simulations (see Appendix for details). As a result of this net attraction, the ligands stay on their binding sites for longer times (i.e., τ_off > τ₀). Importantly, the data presented in Fig. 8 correspond to the fractions of occupied binding sites because the on rate is no more proportional to the concentration in the reaction-limited case.

Figure 8.

Time dependence of the fraction of binding sites that are initially occupied by ligands. In the simulations, net attraction between the binding sites and ligand particles leads to finite residence times prior to dissociation. The strength of attractions is e (in the units of k_BT) (see Appendix for the pair potential). The brown and red data sets are the same as those in Figs. 4 and 5 with no net attraction. (a) s/a = 2.5 and (b) s/a = 20 for h/a = 50. (c) and (d) show log-linear plots of the data sets in (a) and (b). The dashed curves are exponential fits (≈ exp(−t/τ_off)), whereas the solid curves are stretched exponential fits (22) to the data sets for $t\mathrm{\gtrsim }3{\tau }_0$. (e) The log-log plot of residence times obtained from plots (a–d) is shown as a function of the attraction strength of the interaction potential for the s/a = 2.5 and s/a = 20 cases. The dotted curve is f(ε) = exp(ε/k_BT).The error bars were obtained by varying the intervals of the fitting procedures. To see this figure in color, go online.

In Fig. 8, at the short times, we observe a rapid drop regardless of the strength of the attraction. We attribute this common initial behavior to the escape process of the ligands from the attractive potential. After the rapid decay, for high affinities (longer lifetimes), the power-law regimes with either −1/2 or −3/2 exponents disappear. This can also be seen in the log-linear plots in Fig. 8, c and d: as the attraction strength is decreased, the power laws become dominant again, as expected from the diffusion-limited cases (Fig. 8, a–d). In general, for much longer simulations, we anticipate that the power laws should be attainable for all values of s and h. This can be seen in Fig. 8 a; after the exponential decay at around t = 100τ₀, a slope of −1/2 begins to emerge. We will further discuss the criterion for observing an exponential decay in the Discussion (Fig. 9)

Figure 9.

Summary of on-rate scaling behaviors predicted for various systems. Along the dashed lines, the on rate follows a $-\left(1/2\right)$ exponent. The residence time of a ligand on its binding site is defined as the inverse off rate, ${\tau }_{\text{off}}\equiv 1/k_{\text{off}}$. To see this figure in color, go online.

In Fig. 8 e, the residence times, τ_off, extracted by fitting dissociation data to exponential functions in the form of exp(−t/τ_off) (dashed curves in Fig. 8, a–d) are shown for two separation distances, s/a = 2.5 and s/a = 20. Even though the attraction strengths between the ligands and binding sites are identical for two cases (i.e., ε = 3, 2, 1, 0.5k_BT), the extracted lifetimes are longer for the smaller separation distance (Fig. 8). This difference highlights that the rebinding of ligands from neighboring binding sites can influence measurements of intrinsic rates. Particularly for weakly binding ligands, the lifetimes, and thus the off rates, are overestimated for the systems in which binding sites are closer.

We also fitted the dissociation data in Fig. 8, a–b with a fit function in the form of a stretched exponential, $f\left(t\right)\approx \text{exp}\left[{\tau }_{\text{s}}t/{\tau }_{\text{off}}^2\right]erfc\left[\sqrt{{\tau }_{\text{s}}t/{\tau }_{\text{off}}^2}\right]$ (22). Although the data for the small separation case, s/a = 2.5, are better described by the stretched exponential fit, the s/a = 20 case exhibits an exponential decay, possibly due to weaker rebinding events occurring between sparsely placed binding sites. The off rates (i.e., 1/τ_off) obtained via fitting the data to the stretched exponential functions are also shown in Fig. 8 e: for s/a = 2.5, these off rates are higher than those given by the exponential fits but lower than those obtained from the sparsely grafted case (i.e., s/a = 20), particularly for weakly binding ligands. This confirms that, depending on the surface coverage levels, the rebinding events can significantly influence the dissociation kinetics (22, 27, 32).

Overall, our MD simulations statistically and consistently agree with the scaling analyses suggested in Scaling Analysis for Ligands Diffusing in Vertical Confinement for rebinding rates as well as total rebinding statistics. All regimes and their dependencies on two parameters, h and s, are in good agreement with the data extracted from our constant temperature simulations. Below, we will discuss some implications of our results for various in vivo and in vitro situations.

Discussion

Overview of results

The collective kinetic behavior of diffusing ligands can exhibit novel properties compared to that of a single ligand. In this study, we focus on the nonequilibrium rebinding kinetics of an ensemble of ligands modeled as Brownian particles in a confined volume that is initially free of ligands. This scenario is highly related to SPR and SM experiments, as well as the exocytosis process in vivo. Our study shows that non-steady-state on rates k_on(t) and total number of revisits detected by each binding site ${\mathcal{N}}_{\text{coll}}\left(t\right)$ depend on the two timescales imposed by the two intrinsic length scales of the corresponding system.

The first length scale is the largest spatial dimension of the diffusion volume. A steady-state kinetic behavior is reached only when the bulk density of diffusers becomes uniform in the corresponding volume. In experimentally typical flow cells, this length scale corresponds to the height of the microchannel. For in vivo diffusion of signaling molecules throughout intercellular void or in suspensions of cells or vesicles, this length scale can be related to average distance between receptor-bearing structures (i.e., $h\sim c_{\text{cell}}^{-1/3}$, where the concentration of cells is c_cell). Once the steady state is reached, the on rate exhibits a time-independent behavior as k_on ∼ 1/hs². In the steady state, the rebinding frequency is characterized by an Einstein-Smoluchowski limit, which leads to a linearly increasing ${\mathcal{N}}_{\text{coll}}$ (Fig. 2).

The second length scale that we discuss in this work is the average separation distance between two binding sites, s, which is inversely proportional to the square root of grafting density of binding sites. At intermediate times (i.e., before the steady state is established), depending on s, the on rate shows one or two power-law behaviors. For large values of s, because of the three-dimensional escape process of ligands from their binding sites, the on rate exhibits a k_on ∼ t^−3/2 type of decay after the initial release of the ligand. Once the ligands diffuse to a distance larger than the separation distance s, above a threshold time of τ_s, a quasi-one-dimensional diffusion process takes over with a smaller decay exponent of −1/2. For densely grafted binding sites (i.e., small s), the exponent −3/2 is completely smeared out, and the time dependence of the diffusion process is defined by a single exponent of −1/2 at intermediate times (Fig. 2 a).

We also defined a time-dependent parameter ${\mathcal{N}}_{\text{coll}}\left(t\right)$ as the time integral of the on rate k_on(t) (more generally, the integral of raw dissociation data) to characterize rebinding kinetics. The parameter ${\mathcal{N}}_{\text{coll}}$ exhibits a novel, to our knowledge, plateau behavior on the scaling level at intermediate times for sparsely grafted binding sites (Fig. 2 b). The plateau is a result of decreasing probability of finding any ligand near the binding sites during the three-dimensional escape process. This behavior leads to a plateau behavior during which binding sites experience minimal number of collisions with the unbound ligands. Moreover, because of the integral form of Eq. 3, ${\mathcal{N}}_{\text{coll}}$ does not suffer from the fluctuations in the time traces of dissociation data (i.e., k_on) and can be used to invoke the regimes otherwise difficult to observe because of relatively noisy statistics (see Figs. 4 b and 5 b).

The ${\mathcal{N}}_{\text{coll}}\left(t\right)$ plateau expands to longer times if the binding sites are sparsely distributed because the terminal time for the plateau scales as τ_c ∼ s⁴ (Eq. 5). The termination of the plateau regime is at τ_c ∼ s⁴ instead of at τ_s ∼ s². We attribute this behavior to the nonuniform particle distribution near the surface at t < τ_c: only after the particle density becomes uniform near the reactive surface can binding sites experience the incremental collision signals. The threshold time τ_c does not manifest itself in the dissociation data (Figs. 4 a and 5 a) and can be detected only from the cumulative consideration of the dissociation events (e.g., Figs. 4 b and 5 b). In the steady state, at which the rebinding frequency is characterized by a time-independent Einstein-Smoluchowski limit, the plateau ends, and a linearly increasing ${\mathcal{N}}_{\text{coll}}$ takes over (Fig. 2).

Our scaling model compares well to the results of highly coarse-grained MD simulations, in which each ligand is modeled as a structureless spherical Brownian particle diffusing in a continuum solvent. Despite its simplicity, the model captures the long-time behavior of ligand-release kinetics and validates our scaling predictions, particularly for weakly interacting particles. By adding an attractive potential (Eq. 1) between the ligands and binding sites, we also model the reaction-limited scenario. Even though this attraction is a simplistic description of more complex interactions between ligand molecules and receptor sites in real systems (i.e., atomic-structure-specific electrostatic, hydrogen bonding and hydrophobic interactions), it provides finite residence times and thus allows us to probe the effects of separation distance between binding sites on the kinetic rates (Fig. 8).

The MD results demonstrate the −1/2 and −3/2 power laws for the on rates (to within statistical errors of the MD simulations) and the distinct plateau behavior for the cumulative collision number of a range that extends with increasing separation distance between the binding sites (e.g., Figs. 4 b and 5 b). Although our simulations revealed those phenomena for diffusion-limited reactions, in which ligand residence time on binding sites is short (i.e., τ_off ≈ τ₀), for large enough separation distances, these phenomena would emerge for longer residence times (Fig. 8).

Limitations of this model

This study has presented a scaling theory developed from a coarse-grained and single-particle kinetics point of view, which neglects biochemical details, as well as many-body and hydrodynamic effects. The MD simulations indicate that many-body effects do not strongly modify the scaling behavior, as might be expected given the relatively low concentrations of diffusing particles that we consider. Hydrodynamic interactions are likely not of importance to the situations we are considering, although position-dependent diffusion constants may play a role in controlling transfer between closely spaced binding sites. For long distances and long times, however, we do not expect modifications of our basic scaling picture.

The theory of this work neglects all chemical details and assumes single-step binding-unbinding kinetics. Ligands are essentially “bound” or “unbound,” without intermediate states. The possibility of multivalent binding with intermediate states between fully bound and fully dissociated states could give rise to effects such as “facilitated dissociation” (competitive binding), which could well modify the kinetics outlined in this study (see below).

Connection of results to prior theory, simulation, and SPR experiments

Our results are connected closely to theory, simulations and SPR experiments on ligand rebinding of (22). The −1/2 exponent predicted by our scaling analysis coincides with the long-time limit for the exact solution of the self-consistent mean-field theory for rebinding kinetics of that work; Monte Carlo (MC) simulations in the same study observed the long-time −1/2 power law for dissociation kinetics for two cases of binding-site separation. Notably, the more sparse-coverage MC case displays a rapid decay before the onset of the −1/2 regime (Fig. 9; (22)). This rapid drop is likely the onset of the −3/2 scaling regime, which becomes stronger at lower binding-site densities (Fig. 5 a).

Turning to experimental SPR data of (22), we note that although those data do not clearly show the −1/2 law, this is most likely due to the choice of binding-site separation and a short time window. A replot of those experimental data (Fig. S4) suggests that for the higher coverage case (“12 pixels”), the data are tending toward the −1/2 behavior at long times. Although the binding-site coverages in (22) are not quantified in terms of molecules per unit area, from the data in the study, we estimate that the intersite spacing is approximately s = 100 nm in the “4 pixel” case and 60 nm for the “12 pixel” case (the “pixel” unit is stated to be similar to the “refractive index unit,” which in most SPR experiments is associated with a protein surface density of ∼100 pg/mm²). It appears quite practical that similar experiments over longer time windows, at varied inter-binding-site distances and flow cell heights and with weakly binding ligands, could test the scaling theory for the interplay between −3/2 and −1/2 kinetic regimes. Use of SM fluorescence rather than SPR would allow surface binding-site densities as well as site-binding histories to be precisely quantified.

Relevance to experiments performed in microfluidic channels

Experimental studies exploring the kinetics of ligand-receptor interactions or SM-based biosensors are commonly performed in microfluidic channels with well-defined dimensions. We will now discuss the general relationship between our results and such experiments.

Low grafting density of receptors is essential to extract intrinsic kinetic rates in experiments

The measurable quantity in kinetic experiments such as SPR and fluorescence imaging is the population of intact receptor-ligand complexes as a function of time, from which kinetic rates can be obtained. These apparatuses cannot distinguish dissociation and subsequent association of ligands because of their finite-resolution windows. This means that, within the sampling time, a ligand-receptor pair can be broken and reform, possibly with new partners, and thus contribute to the statistics as an intact complex. This can lead to artificially longer or shorter rates. Our study shows that if receptors are separated by small distances, the three-dimensional escape process is rapid. Thus, rebinding of ligands desorbing from nearby receptors can alter intrinsic rates. We demonstrate this in our simulations (Fig. 8): densely placed binding sites lead to longer lifetimes for ligands compared to the case in which binding sites are farther apart.

Association rates can have strong time dependence for weakly binding ligands

In the kinetic studies of receptor-ligand interactions (29) or in modeling signaling pathways (38), time- and concentration-independent rates in master equations are common practices. Our study suggests that on rates can have nontrivial time dependence before the steady state is reached for diffusion-limited reactions in the case of weakly binding ligands (e.g., a binding energy on the order of thermal energy). The time window within which this dependence continues is determined by the dimensions of experimental reservoirs or average distance between ligand-emitting and absorbing surfaces. As an example, a range of values around h = 10²–10⁴ μm (4, 39, 40) leads to τ_z ≈ h²/D ≈ 10²–10⁶ s if we assume a diffusion coefficient of D = 100 μm²/s for a ligand of size a = 1 nm (Table 1). These estimated values for τ_z are comparable to the residence times of molecular ligands (4), and the measurement taken earlier may not reflect true on rates but rather quantify an unrelaxed concentration quench. Note that according to our results, in the cases for which τ_s > τ_z, the regime with a $\left(1/2\right)$ exponent in ${\mathcal{N}}_{\text{coll}}$ cannot be observed, and a direct transition to the long-time linear regime will be observed (Figs. 2 and 4 b).

Separation distance brings about its own characteristic timescale

In SM fluorescence imaging experiments of protein-DNA interactions, DNA binding sites are separated by distances on the order of s ≈ 1 μm (4, 6, 40). In SPR experiments, the distance between the surface-grafted receptors is often smaller and can be on the order of s ≈ 10 nm (25, 39). Using the same values for D and a as above, we can obtain some estimates as τ_s = 10⁻⁶–10⁻² s and τ_c = 10⁻⁴–10⁴ s, respectively. Although τ_s, which characterizes the onset of the one-dimensional diffusion regime for on rate, is on the order of tens of milliseconds, τ_c can extend to hours because τ_c ∼ s⁴ (Eq. 5). This wide spectrum of timescales suggests that with adequate design, receptor separations can be used to identify intermingled timescales in a heterogeneous system. For instance, biosensors can be prepared with multiple types of receptors (e.g., various nucleic acid sequences), each of which can have a distinct and tractable surface coverage level. Identification of signals coming from different sets of receptors can allow us to interpret the kinetic behavior of certain receptor-ligand pairs if each separation distance distinctly manifests itself in dissociation kinetics.

Threshold timescales can be used to probe complex systems

The regimes that we discuss for experimentally measurable on rates and collision numbers can be used to extract the average distance between receptors or receptor-bearing surfaces. For instance, the threshold value τ_s in Eq. 6 can be utilized to obtain or confirm surface coverage levels of receptors without any prior knowledge if the decay of the dissociation data is not purely exponential. That is, as we discuss later, τ_s should be larger than the τ_off.

Possible experiments to study the different kinetic scaling regimes

Recently, novel electrochemical-sensor applications based on the hybridization of a single-stranded DNA binding site have been reported (15, 16). In these experiments, the voltage difference due to hybridization events of the grafted DNA by complementary strands in solution can be measured. Possibly, in these systems, extremely dilute binding-site schemes can be constructed, and thus, the timescales we discuss above can be validated experimentally. Indeed, as mentioned above, different nucleic acid strands can be grafted with varying separation distances, and in principle, the resulting signals can be separated because our analysis suggests that each unique separation distance imposes its own terminal threshold times τ_s and τ_c.

Another experiment setup that would be interesting could incorporate two SPR surfaces separated by a distance h. While one SPR surface can accommodate receptors saturated by ligands, the opposing surface can have empty receptor sites and hence create a “sink” for the ligands. In this way, both rebinding rates and arrival frequencies can be measured simultaneously. Signals on both surfaces could be compared by systematically varying the density of binding sites, surface separations, etc. Indeed, this or similar scenarios can be used to model diffusion of neurotransmitters or growth factors in vivo (26, 41) because rebinding events on the secreting cells can become slower or faster depending on the number of receptors or their spatial distribution on target cell surfaces (13, 27, 42).

Signaling and communication via chemical gradients

The intercellular void formed by loosely packed cells can percolate to distances on the order of microns (43, 44), which can lead to diffusion times on the order of minutes. On the other hand, average (closest) distance between two neighboring cells can be on the order of 10 nm (e.g., for synaptic cleft). Small molecules, such as cytokines, secreted from one cell can diffuse throughout these intercellular spaces and provide a chemical signaling system between surrounding cells. This type of communication is controlled by both secretion and transport rates (45). Indeed, recent studies suggest that spatiotemporal organizations of receptors and ligands can provide diverse signaling responses (46, 47). In this regard, our result can be used to shed light on some aspects of chemical signaling processes in vivo, as we will discuss next.

Time-dependent concentration near receptors can provide a feedback mechanism

Our results suggest that both on rates and total number of rebinding events are sensitive to time-dependent concentration fluctuations of ligands near secreting surfaces. According to our analyses, this time dependence ends when the ligands secreted from a cell arrive at their target receptors located on the surface of an opposing cell (e.g., when neurotransmitters diffuse to the receptors of postsynaptic neuron). This suggests a feedback mechanism in which the secreting cells can determine the arrival of the released molecules to the target cells. This would be possible if the secreting cell bears receptors that are sensitive to the local concentration of the secreted molecules, possibly via time-dependent conformational (48, 49) or organizational (50, 51, 52) changes of membrane components. In this way, once the signal molecules reach their target surface, the secreting cell can alter the outgoing molecular signals depending on the rebinding regime experienced.

Exocytosis can be altered by concentrated vesicles or small openings

Our analysis shows that time-dependent on rates can reach their time-independent regimes faster, and the ligands return to their initial position more often, if the ligands are closer to each other at the time of the initial release (see Figs. 2 and 5). In the process of exocytosis of small molecules, vesicles fuse with the plasma membrane and create an opening to release the molecules into intercellular space. One can imagine a scenario in which, given the concentrations of the contents of two vesicles are similar, a ligand released from the vesicle with a larger opening would return less often to the original position (Fig. 2). If the vesicle opening is small, this would effectively lead to a smaller separation distance, and thus, more return would occur. In fact, the amount of opening can also determine the efficiency of endocystosis (e.g., the process of intake of ligand back to vesicle). Further, in exocytosis, secreting vesicles can control the release rates by changing modes of fusion (53). In accord with this concept, our calculations show that one order of magnitude decrease in the separation distance can increase the return rates by two orders of magnitude (Fig. 5 a). Similarly, given the sizes of openings are roughly equivalent for two vesicles, more concentrated vesicles can lead to more collisions per unit time with the opposing cell surface because the number of ligands per unit area is higher during the initial release for the concentrated vesicle (i.e., k_on ∼ 1/s²). Similar arguments could be made to explain the observed differences in exocytosis rates induced by the fusion of multiple vesicles (54).

Finite residence time of ligands on binding sites

In the traditional view of molecular kinetics, the equilibrium constant of a bimolecular reaction (e.g., for a protein binding and unbinding its binding site along a DNA molecule or a drug targeting its receptor) is defined as the ratio of off rate $k_{\text{off}}\equiv 1/{\tau }_{\text{off}}$ and the corresponding on rate. As we discuss in Reaction-Limited Kinetics, molecular ligands can have slow off rates (long residence times) that can intervene with the threshold times and regimes predicted by our scaling arguments. Moreover, these off rates can have strong concentration dependence (4, 5). Below, based on recent experimental findings (55), we will briefly discuss some implications of the finite residence times on our results.

Slow off rates can delay power laws

Because of various energetic and entropic components (7, 56), disassociation process of a ligand from its binding site can be considered a barrier-crossing problem. This rare event manifests itself as a slower decay (compared to a diffusion-limited case) in dissociation curves, which is usually fitted by either exponential or nonexponential curves (32) to extract dissociation rates. For ligands with strong affinity toward their binding sites (i.e., ${\tau }_{\text{off}}/{\tau }_{\text{s}}\gg 1$), this slow decay can occlude the power laws that we discuss here. Hence, in Fig. 9, we demonstrate the possible effects of the residence times on our calculations with an illustrative diagram in the dimensions of s/h and τ_off/τ_s.

In Fig. 9, if the residence time of a ligand is short compared to the intersite diffusion time (i.e., τ_off/τ_s < 1), the ratio of s/h determines which power law or laws can be dominant at intermediate times. For instance, for s/h < 1, which is the common scenario in SPR experiments, both of the decay exponents can be apparent. In other SM experiments, for which s/h > 1, only the −3/2 type of exponent can be observable if there are enough empty sites for rebinding ligands (i.e., τ_s > τ_off). If the residence and intersite diffusion times are comparable (i.e., τ_off/τ_s ≈ 1), the regime of k_on ∼ t^−3/2 is not observable, and the on rate decays by −1/2 exponent until the steady-state regime. For a dense array of binding sites and for strong affinities, unbinding events can be correlated, and a nonexponential decay can emerge as a result of correlated rebinding events (22) as also schematically illustrated in Fig. 9.

Time-dependent concentration can induce time-dependent facilitated dissociation

Recent studies of protein-DNA interactions have shown that off rates, k_off, have a strong dependence on concentration of unbound (free) proteins in solution (4, 6, 8). According to this picture, free ligands in solution can accelerate dissociation of bound proteins by destabilizing the protein-DNA complex (4, 57). Our study shows that, for a concentration quench, concentration of ligands near the binding site changes with time before steady state. The time-dependent concentration can lead to time-dependent facilitated dissociation and shorten the lifetimes of ligands on their binding sites in a time-dependent manner, particularly in the reaction-limited scenario. This can be more important when binding sites are closer to each other because rebinding events can induce more facilitated dissociation and further shorten residence times. This effect is not present in either the scaling theory or simulations of this work because strong facilitated dissociation effects require ligands with multivalent interactions that can exhibit partially bound states (57). Taking multivalent binding and facilitated dissociation into account, inclusion of hydrodynamic effects, and addressing other limitations of this model are topics for future work.

Author Contributions

All authors contributed equally to this work.

Editor: Andrew Spakowitz.

Appendix A: Derivation of on Rates via Gaussian Distribution

Here, we derive expressions for k_on and ${\mathcal{N}}_{\text{coll}}$ by using a Gaussian spatial distribution for ligands. Consider at time t > 0, the probability distribution for a set of identical particles in d dimensions evolves from a Dirac δ distribution at the origin as

$$P\left(\overrightarrow{r},t\right)={\left(\frac{1}{2dDt}\right)}^{d/2}\text{exp}\left(-\frac{|\overrightarrow{r}{|}^2}{2\pi dDt}\right),$$ (8)

where $\overrightarrow{r}=x_1{\hat{x}}_1+x_2{\hat{x}}_2\dots +x_d{\hat{x}}_d$ is the position vector in d dimensions. The weight of the distributions in Eq. 8 at position $\overrightarrow{r}=0$ provides the probability for diffusing particles to revisit the origin

$$P\left(0,t\right)={\left(2dDt\right)}^{-d/2}.$$ (9)

After dimensional adjustment, at time t the total number of the revisits can be obtained by integrating Eq. 9:

$${\mathcal{N}}_{\text{coll}}\left(t\right)\approx \frac{a^d}{t_0}{\int }_{t_0}^{t}P\left(\overrightarrow{0},t^{\prime }\right)d{t}^{\prime }={\tau }_0^{d/2-1}{\int }_{t_0}^t\frac{d{t}^{\prime }}{t{\text{'}}^{d/2}}.$$ (10)

Note that to obtain the above equation, we use the exact form a² = 2dDτ₀ rather than its scaling form a² ≈ Dτ₀. According to Eq. 10, the returning probability, $P\left(\overrightarrow{0},t\right)$, can also be considered as the rate of revisits, k_on, at the origin $\overrightarrow{r}=0$ at a given period T.

$$k_{\text{on}}\equiv \frac{d{\mathcal{N}}_{\text{coll}}\left(t\right)}{dt}.$$ (11)

Eq. 11 can also be written as

$$k_{\text{on}}\approx a^d/{\tau }_{0}P\left(\overrightarrow{0},t\right).$$ (12)

From Eq. 12, the on rates are

$$k_{\text{on}}\approx {\tau }_0^{-1}\{\begin{array}{cc}{\left({\tau }_0/t\right)}^{1/2}& \text{for }d=1\\ \left({\tau }_0/t\right)& \text{for }d=2\\ {\left({\tau }_0/t\right)}^{3/2}& \text{for }d=3.\end{array}$$ (13)

If the integral in Eq. 10 can be performed with t₀ = τ₀ to obtain the expressions for ${\mathcal{N}}_{\text{coll}}\left(t\right)$, then

$${\mathcal{N}}_{\text{coll}}\left(t\right)\approx \{\begin{array}{cc}{\left(t/{\tau }_0\right)}^{1/2}-1,& \text{for }d=1\\ \text{log}\left(t/{\tau }_0\right),& \text{for }d=2\\ 1-{\left({\tau }_0/t\right)}^{1/2}& \text{for }d=3.\end{array}$$ (14)

Using Eqs. 13 and 14, the scaling arguments presented in the main text can be obtained for each step of the diffusion process. Note that even though a two-dimensional scenario has been realized for this problem, it has been shown before that the diffusion profile of protein particles that are initially positioned along a one-dimensional chain obeys a logarithmic revisit rate (10).