Modelling and measuring intracellular competition for finite resources during gene expression

Abstract

Dissecting the competition between genes for shared expressional resources is of fundamental importance for understanding the interplay between cellular components. Owing to the relationship between gene expression and cellular fitness, genomes are shaped by evolution to improve resource allocation. Whereas experimental approaches to investigate intracellular competition require technical resources and human expertise, computational models and in silico simulations allow vast numbers of experiments to be carried out and controlled easily, and with significantly reduced costs. Thus, modelling competition has a pivotal role in understanding the effects of competition on the biophysics of the cell. In this article, we review various computational models proposed to describe the different types of competition during gene expression. We also present relevant synthetic biology experiments and their biotechnological implications, and discuss the open questions in the field.

1. Introduction

Gene expression is a central biological process by which information encoded in the genetic material (DNA and RNA) is used by various intracellular factors to produce proteins and other gene products such as ribosomal RNA [1]. This multistage process includes various steps and substeps such as transcription, RNA processing and splicing, translation, mRNA degradation and protein degradation. These steps involve the action of multiple cellular factors including, among others, transcription factors (TFs), RNA polymerase (RNAP) enzymes, spliceosomes, translation factors and ribosomes [1].

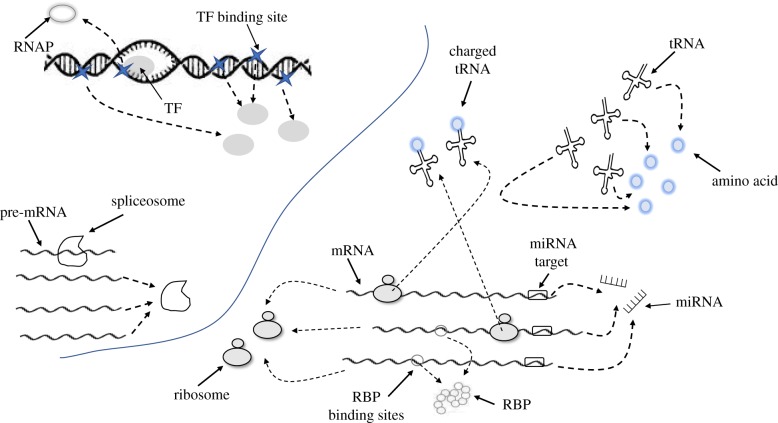
Naturally, as cellular resources are finite, each of these expression factors is available only in a limited amount (see table 1 for a few estimations). This implies that cellular components must compete for shared resources. The idea of competition for common resources has already been raised decades ago, when protein synthesis in Escherichia coli turned out to be limited by the number of free ribosomes [14]. However, competition for shared resources is a common biophysical aspect related to all stages of gene expression. The competing components change dynamically along the progression of gene expression, from DNA binding sites competing for TFs at the stage of transcription to mRNA molecules competing for ribosomes, or codons competing for tRNAs, at the stage of translation (figure 1).

Table 1.

Estimated numbers of some intracellular gene expression factors.

S. cerevisiae	number of protein coding genes	6.2 × 104 [2]
	number of ribosomes	2 × 105 [3]
	number of mRNAs	6 × 104 [2]
	number of proteins per mRNA	5.6 × 103 [4]
	number of tRNAs	3 × 106 [5,6]
	the average number of tRNAs per ribosome	12.2 [5]
	the average number of codons per mRNA	420 [7]
human	number of protein coding genes	2 × 104 [8]
	number of miRNA genes	8 × 102–103 [9]a
	TF copy number in a mammalian cell	4 × 103–1.5 × 108 [10]a
	number of RNA polymerases-II	8 × 104 [11]
E. coli	number of protein coding genes	4.3 × 103 [12]
	number of RNA polymerases	4.6 × 103–104 [13]a

^aPapers that contain a range of estimations.

Figure 1.

Illustration of various types of competition during eukaryotic gene expression. Competition in the nucleus (to the left): multiple promoters along the DNA compete for TFs; TFs bounded to promoters compete for RNAPs and splicing sites along pre-mRNAs compete for spliceosomes. Competition in the cytoplasm (to the right): mRNAs compete for ribosomes, tRNAs compete for free amino acids, charged tRNAs compete for codons at the ribosomal A-site, binding sites along the mRNA compete for RNA binding proteins (RBP) and miRNA binding sites compete for miRNAs. A dashed arrow links the binding site to the resource it demands. (Online version in colour.)

The interplay between the multiple elements participating in gene expression imposes substantial challenges for controlling experimental approaches due to effects arising from coupling of the individual elements. Computational models, however, can be easily controlled, allowing the prediction of the unique effect of each individual element on the process. Moreover, since competition aspects are critical for the understanding of cellular biophysics and genome evolution, it is impossible to study these topics without directly modelling competition. Nevertheless, due to the complexity of gene expression and the numerous intracellular factors required for the process, modelling competition remains challenging.

Several important reviews related to computational and mathematical modelling of gene expression have been previously published (e.g. [15–19]). However, these reviews were usually focused on modelling the dynamics of single molecules, whereas further complex aspects of competition at different stages of gene expression have only received little attention. Nevertheless, the rapid development of relevant experimental approaches has elucidated important concepts of competition, leading to an increased number of mathematical/computational models for competition in the recent years.

In this review, we thus aim to describe and discuss the competition aspects related to gene expression and its modelling. Specifically, we will review recent models for competition at different stages of gene expression, relevant experimental procedures for studying the effect of competition on the biophysics of the cell and the important practical implications of considering competitional aspects in the design of synthetic biology solutions. Finally, we will discuss the current gaps between the existing computational/mathematical models and the relevant biological/biophysical data and phenomena.

2. Unifying principles in competition models

Various approaches have been suggested to model competition for shared resources, including the usage of computational simulations, mathematical equations and statistics. Despite non-negligible differences in the specific parameters defined by each model and the assumptions made by it (more details in the next sections), all competition models rely fundamentally on unifying concepts. The most pivotal principle of such models is the ratio between the number of competing entities (‘binding sites’) and the corresponding number of available resources (‘binders’). The simplest type of competition is presented when each type of binding site is competing for only one type of binder, and each type of binder can bind only to one type of binding site. In practice, however, intracellular competition is further complicated and whereas different binding sites can compete for the same binder, a binder can bind to various types of binding sites with different affinities. Moreover, as gene expression stages are stochastic processes, binders are randomly distributed in the cell. Therefore, the arrival time of a binder at its binding site is roughly affected by two main factors: the intracellular concentration of the binder and the number of competing binding sites. Thus, the components of an intracellular competition model usually comprise the number of binding sites, the concentration of the binders and the binding affinities.

Another common factor in these models is the transport mechanism by which intracellular binders arrive at their targets. Although it is often assumed that diffusion is, in principle, the means whereby molecules are transported through the cell, the actual intracellular flow does not genuinely reflect a simple passive diffusion in a homogeneous medium. Additionally, the fact that in certain cases, cells need to invest energy to actively transport molecules to their targets, further complicates the ability to model intracellular competition.

Additional aspects that should be considered by these models include the geometry of the binder and the binding site, the various thermodynamic factors related to the binding interaction and complex events such as recycling resources.

Taken together, modelling competition of cellular processes in general, and gene expression in particular, is a challenging task. In the next sections, we provide specific examples related to the general principles mentioned above.

3. Different modelling aspects of competition for shared resources between eukaryotic and prokaryotic cells

Intrinsic differences between prokaryotic and eukaryotic cells constitute fundamentally different strategies of transcriptional and translational regulation by resource sharing in the two kingdoms. Although gene expression is similar in all domains of life, its regulation in eukaryotes is more complex than in prokaryotes [1]. For example: (i) in prokaryotes, transcription and translation occur simultaneously in the cytoplasm, (ii) prokaryotic cells are smaller, and their DNA is usually much shorter, (iii) all prokaryotes are unicellular (i.e. there is no tissue-specific regulation of gene expression), and (iv) some regulatory aspects, such as splicing, alternative splicing and regulation by small RNA genes such as miRNAs, are very common in eukaryotes, but relatively rare in prokaryotes.

Indeed, since prokaryotic genomes are usually easier to manipulate, the first competition models were developed for prokaryotes and were mainly focused on aspects such as competition for shared transcriptional resources [20]. On the other hand, models related to the competition of miRNA binding sites on shared miRNAs were tailored for eukaryotes [21].

A meaningful difference between prokaryotic and eukaryotic transcriptional models is related to TFs. First, the compactification of DNA into chromosomes in eukaryotes constitutes a complex consideration in competition models. Specifically, since part of the DNA is organized into compact nucleosomes with the assistance of histones, certain TF-binding sites within nucleosomes are inaccessible to most of the TFs (reviewed in [22]). In these cases, unwinding of the relevant nucleosomes is required. Thus, competition models for transcription in eukaryotes should consider the fact that TFs compete for binding to their binding sites not only with other TFs, but also with histones and other chromatin proteins. Second, whereas TF-mediated gene regulation in eukaryotes requires the coordinated interactions of multiple proteins, in prokaryotes, only a single protein is usually required. In addition, whereas in prokaryotes, TFs mainly bind to promoters, in eukaryotes, TFs can bind to many additional binding sites [1]. Finally, the larger size of the eukaryotic genome and the fact that genes comprise only a small percentage of it [1] should also be considered in eukaryotic transcription models.

Prokaryotic genomes in general and bacterial genomes in particular are usually under a strong evolutionary pressure to optimize their growth rate. Thus, it is believed that bacterial gene expression depends, among others, on global parameters that affect bacterial growth [23,24]. Specifically, the abundance of ribosomes and RNAPs depends on the amount of nutrients available in the growth medium, which can thus induce global changes in gene expression [25]. Therefore, models for competition in bacterial cells are expected to assume optimal growth conditions, or alternatively, take potential changes in the medium into consideration.

4. Stage-specific competition types during gene expression

4.1. Ribosomes and mRNAs

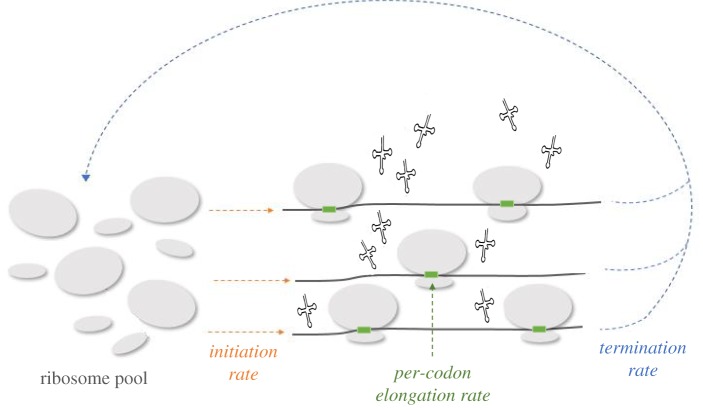
A finite reservoir of ribosomes in the cell has been suggested to limit protein synthesis in bacteria [14]. However, the idea that the limited pool of ribosomes leads to a competition between mRNAs for free ribosomes and thereby, affects the rate of mRNA translation stands also for eukaryotic organisms. In S. cerevisiae, for example, a pool of 2 × 10⁵ ribosomes [3] is expected to be used for the translation of approximately 60 000 mRNAs [2] for which the average production rate is 5600 proteins per mRNA [4]. Accurate modelling of mRNA translation should thus consider the competition between all mRNAs in the cell for the pool of available ribosomes. The basic components of such a model include the total number of mRNAs and ribosomes and the initiation and termination rates of each mRNA (figure 2). The initiation rate of an mRNA is locally affected by features of the mRNA molecule such as the strength of the ribosomal binding site. However, it can also be globally affected by the number of ribosomes in the free pool. Specifically, a higher number of free ribosomes increases the probability that a ribosome will diffuse into the mRNA, leading to a higher initiation rate. In addition, the number of ribosomes in the free pool is inevitably affected by the time ribosomes spend on each mRNA during translation elongation. Particularly, slowly decoded mRNAs are associated with higher ribosome density and ribosome ‘traffic jams’, thus reducing the number of free ribosomes in the pool.

Figure 2.

A general schematic plot of the competition model of mRNA and ribosomes: the model includes all mRNAs in the cell such that each mRNA (in black) has a specific initiation rate (in orange). Each codon on the mRNA has a specific elongation rate (in green). In addition, the model in the illustration includes all ribosomes in the cell (in grey) which are divided into two groups: the free ribosomes and the occupied ribosomes (i.e. ribosomes that are actively translating the mRNAs). Ribosomes move along the mRNA based on the TASEP rules (described in the main text) and the pool status is dynamically changed accordingly. Specifically, ribosomes that complete the translation of an mRNA are added to the free pool of ribosomes (termination rates are in blue), and ribosomes that begin translating an mRNA are subtracted from the free pool of ribosomes (initiation rates are in orange). (Online version in colour.)

Modelling competition between mRNAs for ribosomes has been extensively studied in recent years. The first models were mathematical [26,27], usually based on a set of totally asymmetric simple exclusion processes (TASEP), or a set of mean field approximations of TASEP (such as ribosomal flow models (RFM), see [28]). A standard TASEP is a stochastic process describing the movement of particles along a one-dimensional lattice. For modelling translation, each mRNA of a certain length is modelled as a TASEP in which the number of sites corresponds to the length of the mRNA in codons, and the moving particles are the ribosomes. Due to the size of the ribosomal footprint, a particle (ribosome) covers a few sites (codons). On the lattice (the mRNA), the ribosome hops stochastically from its current site to the next site, if the latter is empty. The rates by which ribosomes enter and leave an mRNA are the initiation and termination rates, respectively. These rates are intimately related to the size of the free ribosomal pool. The initiation rates monotonically increase with the number of ribosomes in the pool [26,29,30], whereas the size of the pool is positively affected by an increase in the termination rates. Trivially, each terminating ribosome increases the pool of free ribosomes by one.

Greulich et al. [27] describe two possible major phases for the TASEP model of translation, based on two possible states of translation. The first phase is a low-density phase which describes a scenario in which initiation is the rate limiting stage of translation, and the number of ribosomes on the mRNAs is low. The second phase is a high-density phase that describes a scenario in which the rate limiting stage of translation is elongation (the flow rate from one site to another), and the number of ribosomes on the mRNAs is high. Importantly, it was suggested that when a subset of TASEP undergoes a phase transition from low (i.e. when the initiation is rate limiting) to high density (i.e. when the elongation is rate limiting), the currents along the entire set of TASEP become independent of the total number of particles (ribosomes).

The effect of a finite pool of ribosomes has been further investigated by Raveh et al. [26] using a set of mean field TASEP approximation (the RFM [28]) connected to a common pool of ribosomes. Implementing this model revealed that increasing the elongation rate of any codon along a specific mRNA yields a local effect on the mRNA and a global effect on all other mRNAs. Specifically, whereas the translation rate of the specific mRNA is always increased, the translation rates of all other mRNA molecules can either increase or decrease. These results suggest that the effect of codon decoding rates on protein production is more complicated than previously thought.

In all the models above, it is not only the pool of ribosomes that affects the rate of translation, but rather the ratio between the number of ribosomes and the number of mRNAs. This ratio has been specifically studied by Mather et al. [31] using a stochastic computational/mathematical model for the competition between mRNAs for ribosomes. Interestingly, the correlations of their analytical solution of the stochastic model with steady-state protein counts turned out to be affected by this ratio. Specifically, the correlation was weakly positive when the total transcript count only slightly exceeded the ribosome count, whereas when the total transcript count significantly exceeded the ribosome count, the correlation was strongly negative. This may suggest that the former is a more physiological relevant regime.

Later computational models have included parameters that have been directly inferred from experimental data such as ribosome profiling [32]. The usage of actual measurements of translation enables tailoring of models to the intracellular translation status. In [33], for example, the elongation and initiation rates used for the RFM-based model that included all the mRNAs and ribosomes in the cell were inferred based on ribosome profiling data. The model has suggested that competition for finite resources may induce non-trivial correlations between different gene expression steps. Specifically, oscillations in the mRNA levels of either a single gene or a group of genes can induce significant periodic behaviour in translational parameters, such as oscillations in the ribosomal densities and the translation rates of the mRNAs. In S. cerevisiae, for example, oscillations in the mRNA levels of a set of endogenous genes caused oscillations of up to 50% in the steady-state translation rates of the rest of the genes [33]. The reported estimation of the actual magnitude of the effect in a physiological condition provides a possible mechanism for the regulation and induction of intracellular oscillations.

However, models of translation dynamics have been shown to not only be capable of inducing interesting behaviour such as oscillations, but also of capturing translation rates without characterizing the decoding rates of individual codons. Gorochowski et al. [34], for example, have developed a minimal model of ribosome allocation dynamics that was able to make precise predictions of transcript levels and translation elongation times, from solely the rate of protein production. Since this model is focused on translation initiation and does not explicitly include ribosome dynamics along the mRNA during elongation, it is expected to have a faster running time compared to the TASEP-based models. Using their model to investigate the effect of introducing a synthetic burden of heterologous genes to the cell revealed that the heterologous protein production rate did not linearly increase with the initiation rate and the number of heterologous mRNAs. This response arose from competition for the shared ribosome pool and a trade-off in allocating the ribosomes to the endogenous and heterologous mRNAs.

4.2. tRNAs and codons

The interplay between codons and tRNAs was shown early on to control translation elongation kinetics [35]. In S. cerevisiae, for example, the expected number of codons and tRNAs can be estimated in the following way: there is an average of approximately 420 codons per mRNA [7], and the number of mRNAs is estimated to be 60 000 [2]. Thus, in this organism, we expect to see an order of 2.5 × 10⁷ codons. In addition, since the number of tRNAs per ribosome was estimated to be up to 12.2 [5] and the number of ribosomes is of the order of 2 × 10⁵, we expect to see an order of 2.4 × 10⁶ tRNA in S. cerevisiae cells.

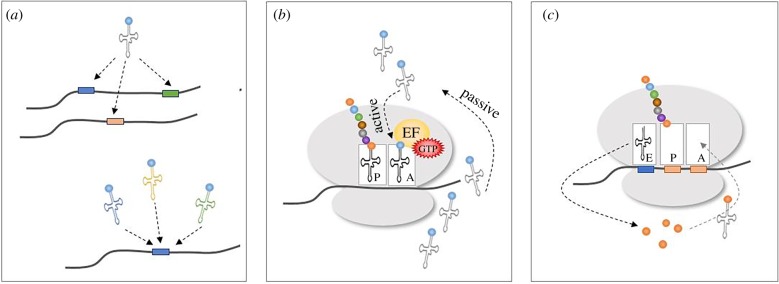
Modelling the competition between codons for charged tRNAs is challenging due to the following reasons: (i) there is a large but finite pool of codons and tRNAs; (ii) there are up to 61 types of codons and tRNAs; (iii) allowed by the redundancy of the genetic code, one amino acid can be encoded by several codons. Specifically, one type of tRNA can bind to several codons with different affinities via wobble interactions in the third nucleotide of the codon [36]. Similarly, one codon can be recognized by several tRNAs with different affinities; (iv) the ribosome GTPase (elongation factor G in bacteria and elongation factor 2 in eukaryotes), which induces ribosome translocation along the mRNA, also induces conformational changes in the ribosome that facilitate the diffusion of tRNAs through the ribosome [37]; (v) codon order can have an effect on tRNA diffusion [38]. Specifically, successive codons, which are encoded by the same cognate-tRNA species, can improve the efficiency of local tRNA diffusion and thus, the translation rate. These aspects are illustrated in figure 3.

Figure 3.

Different aspects of the competition between codons for tRNAs. (a) One tRNA can recognize different codons with different affinities (top); similarly, several tRNAs can recognize the same codon with different affinities (bottom). The different affinities are emphasized by different colours. (b) tRNAs can be passively transported to the ribosomal A-site by diffusion or actively, by conformational changes of the ribosome induced by GTPase. (c) Successive usage of codons encoded by the same cognate-tRNA can improve the efficiency of local tRNA diffusion, as the ribosome can benefit from the vicinity of the tRNA that has just been used to translate the upstream codon. (Online version in colour.)

Currently, there are no models that consider all these aspects; however, various works have aimed at dealing with different aspects of tRNA–codons competition. A simple measure was proposed by Pechmann & Frydman [39], based on the ratio between the tRNA supply that can translate the codon and the demand for this codon. Specifically, the relative demand of a codon was estimated based on the relative frequency of the codon among all the transcripts expressed at a certain time point. The supply of a codon was estimated based on a computational measure [40,41] that considers an estimation of the intracellular tRNAs, and the interaction affinities of all the different tRNAs with the codon. Although this is an efficient measure, it ignores various aspects such as points, (i), (iv) and (v) above.

Brackley et al. [42] developed and analysed a computational simulative model of translation elongation which includes the dynamics of the use of tRNAs and their recharging with amino acids. Their approach describes a TASEP model in which ribosomes move from site to site with rates that are dependent on the size of the pool of charged tRNAs (aa-tRNAs). Every time a ribosome leaves a site of type x, an x type aa-tRNA is removed from the pool and an x type tRNA is added to the corresponding pool of bare/uncharged tRNAs. Bare x type tRNAs are recharged with a rate Rx. Using this simulation, the authors showed that increasing the initiation rate of translation can lead to a depletion of some species of aa-tRNA, which can thereby lead to slow codons and queueing. This can induce striking ‘competition’ effects when considering multiple species of mRNAs that share the same pool of tRNA resources. This model includes various important aspects of the competitions of codons for tRNAs; however, the analysis has not been tailored to fit experimental data and did not consider all the transcripts presented in the cell. In addition, points (iii), (iv) and (v) that were mentioned above were not addressed by this model.

It is important to mention that although many of these models consider all codons of a certain tRNA as relevant competitors, in practice, only codons occupied by the A-site of the ribosome are actually competing for tRNAs. In S. cerevisiae, for example, it was roughly estimated that 85% of the ribosomes are engaged in translation [2,43]. Thus, the demand for tRNAs is expected to be 0.85 multiplied by 2 × 10⁵, which equals 170 000.

This distinction has been made, for example, by Fluitt et al. [44], in their mathematical model for codon competition on tRNAs. Based on their approach, translation elongation was modelled as a stochastic process in which the transport of aa-tRNAs throughout the cytoplasm was modelled as a random walk that may lead to the ribosomal A-site. Elongation rates were thus determined by the competition between cognate, near-cognate and non-cognate aa-tRNAs on the ribosomal A-site. Specifically, the model divided the cytoplasm volume, into discrete occupation sites, each of a length d_i which corresponds to the size of the aa-tRNA of type i. The transition time required for a random walker to move from one site to the other defined as τ_i was estimated to be $d_i^2/6D_i$, where D_i is the diffusion coefficient of the random walker (as measured by Elowitz et al. [45]). The probability p_i that a walker of type i arrives at an open A-site in time interval τ_i was estimated by the ratio between the number of walkers of this type and the total number of sites. Finally, the average arrival time of a specific aa-tRNA was set to be the ratio between τ_i and p_i. Despite the additional parameters this model includes, such as the volume of the cytoplasm and the size of the sites, points (iii), (iv) and (v) were not taken into consideration.

4.3. miRNAs and RNA binding sites

miRNAs are small non-coding RNAs that play a role in post-transcriptional regulation via sequence-specific binding to target RNAs. Specifically, their binding sites can include mRNAs as well as non-coding RNAs [46–48]. The idea that competition between binding sites to bind common miRNAs can regulate the rate of protein synthesis of individual genes has been substantiated by a wide variety of studies (e.g. [48–50]). One of the main challenges in modelling such competition is related to the huge amount of different miRNA species. In the human genome, for example, there are 800–1000 different miRNAs [9], and one miRNA gene can be presented in the cell in more than 50 000 copies [51]. Moreover, the fact that 30–90% of the human genes can be regulated by miRNAs [9,52] elucidates the importance of understanding the competition effect of miRNAs on human health.

We believe that all aspects mentioned above for the case of competition between codons for charged tRNAs should apply also for the case of competition of miRNA binding sites on miRNAs. Equivalently, the following aspects should be considered: (i) there is a large but finite pool of miRNAs and their binding sites; (ii) there are different types of miRNAs and binding sites; (iii) each miRNA has the potential to target a huge number of mRNAs, and one mRNA species can be regulated by multiple miRNAs [53,54]. Moreover, the miRNA–mRNA interaction can occur at different hybridization affinities; (iv) ribosome movement, as well as the movement of other RNA binding proteins, can mask the recognition of miRNA motifs inside the coding regions; and (v) the order and the distance between competing binding sites can affect miRNA binding efficiency [55,56].

However, there are additional aspects related specifically to miRNA competition modelling which are more challenging than for the case of tRNAs and codons [57]. For example, the total number of parameters used for predicting miRNA–mRNA interactions is much larger and typically includes dozens of sequence variables surrounding the miRNA–mRNA interaction site [52]. In addition, it was shown that functional target sites for one miRNA tend to be preferentially conserved in a subset of species. Thus, the conservation of the sequence is another meaningful parameter in modelling competition between miRNA binding sites on miRNAs [58]. Moreover, the expression of individual miRNAs can vary drastically; in mammalian cells, for instance, the abundance of individual miRNAs can vary by orders of magnitude [59]; on the other hand, it is currently believed that the changes in tRNA levels across tissues and conditions are less drastic [60].

It is thus important to emphasize that due to the complex nature of miRNA competition, developing a complete model of miRNA competition is considered a notably challenging task. Particularly, as some of the points mentioned above have not yet been studied. Nevertheless, various initial attempts to model miRNA competition have been suggested in recent years.

A simple model of competition between target sites on miRNAs considers only one type of miRNA with multiple binding sites of the same strength. For example, Jens & Rajewsky [21] proposed a model of the transcriptome of white blood cells to study competition for the human miRNA, miR-20a. Assuming M binding sites, each having a binding strength K_i and a concentration c_i; at equilibrium, all sites of a given K_i have the same occupancy (Θ_i). According to the binding equation, Θ equals the number of free miRNAs (F) divided by the sum of F and K_i. Thus, Θ is expected to monotonically increase with F until saturation. The total number of all miRNAs (miR-20a, in the specific instance) can be represented by the sum of F and the aggregate number of bound miRNAs (the sum over c_i · Θ_i). Based on these parameters, their simple steady-state model of binding site occupancies comprised a set of binding equations that can be solved numerically for any combination of binding sites with the constraint that the total number of regulator molecules (miRNAs or RBP) is not changed by binding or unbinding.

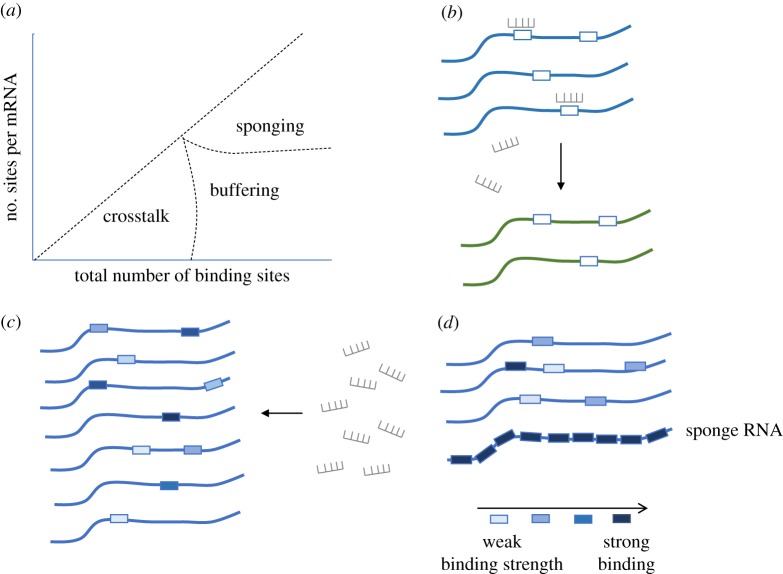
Jens & Rajewsky [21] further described the competition effect between all miRNA or RBP-binding sites using three regimes, reflecting three possible changes in the number of competing binding sites and their effect on the binding site occupancies. Specifically, the three described regimes are: (i) crosstalk, (ii) buffering and (iii) sponging (figure 4). The crosstalk scenario requires that both the total number of competing binding sites and the number of binding sites per transcript would be small enough for an individual mRNA to influence the binding site occupancies. Furthermore, for crosstalk to hold, the binding sites need to undergo specific interactions with miRNAs/RBP and thus, to be sensitive to changes in the concentration of free miRNAs/RBP. Mathematically, this is modelled by setting F to be close to the dissociation constant, K_d. In practice, however, sequence specificity is usually low and thus, the effect of a single mRNA becomes negligible. In the buffering scenario, the total number of potential binding sites is significantly larger than the number of binding sites per transcript. Buffering thus prevents saturation and allows changes in the cellular concentration of a miRNA to regulate binding sites with different affinities. In the model, buffering leads to an increased occupancy threshold. Finally, sponging describes the insertion of RNAs that adds a large number of strong binding sites for a single type of miRNA, allowing a maximum sequestration of this miRNA [48]. Specifically, in the sponging regime, the number of binding sites contributed by a single mRNA becomes comparable to the total number of binding sites in the transcriptome, substantially reducing site occupancies. The term ‘sponges’ refers to the unique RNA species that include many strong binding sites and are presented in the cell in high-copy numbers that vastly exceed the thresholds of physiological mRNAs.

Figure 4.

Types of competition effects between miRNA binding sites. (a) The three regimes based on the relation between the total number of binding sites and the number of miRNA binding sites per mRNA. (b) Low total number of binding sites and a low number of sites per transcripts lead to a regulatory crosstalk between transcripts. In this scenario, certain RNA molecules (blue) can regulate the levels of target transcript (green) by competing for binding to the same miRNA. (c) The buffering effect of miRNAs describes a situation in which the large number of potential binding sites prevents saturation, and thus, allows changes in the concentration of a miRNA to sensitively regulate binding sites with different affinities. (d) The ‘sponge’ effect describes the expression of RNAs with many strong binding sites that can reduce site occupancies by sequestration of miRNAs. (Online version in colour.)

In the model, sponging is represented by increasing the parameter related to the concentration of strong binding sites which reduces the concentration of free miRNAs. Consequently, the binding site occupancies are also reduced.

Using a stochastic modelling of binding sites competition for miRNA binding validated by single-cell experiments, Bosia et al. have further investigated the crosstalk scenario, showing that the optimal cross-regulation regime is compatible with low numbers of mRNA molecules. Their model relied on two types of target mRNAs that contain binding sites for the same miRNA. The parameters of the model included the transcription and degradation rates of the two mRNAs, the effective binding rates of each binding site to the miRNA, the expression levels and the degradation rates of the proteins that can be produced by these mRNAs and finally, the probability of miRNA recycling. Analysis of the model and its experimental validation revealed that crosstalk between binding sites is quantitatively relevant only when the number of target mRNA molecules is relatively small and the binding rates of the miRNA molecules to the competing sites are similar [61].

It is important to mention that although many models are focused on miRNA binding sites that are located on mRNAs, additional binding sites located on non-coding RNAs such as long non-coding RNA (lncRNAs) and pseudogenes can critically affect competitional aspects. For example, sponging by lncRNAs can significantly reduce the number of miRNAs that are available for binding to their target mRNAs. Martirosyan et al. [62] reviewed several mathematical and in silico models employed in the recent years to shed light on this topic.

4.4. Transcription factors, RNA polymerases and DNA binding sites

Modelling transcription usually relies on the interplay between available TFs and RNAPs, and the number of competing promoters and other non-specific binding sites along the DNA. In E. coli cells, the typical number of RNAPs is between 4.6 × 10³ and 10⁴ [13], while the number of protein coding genes is 4.3 × 10³ [12]. In mammalian cells, it was estimated that there are 8 × 10⁴ RNAP-II [11] and approximately 2 × 10⁴ protein coding genes [8]; the number of copies of a certain TF can vary between 4 × 10³ and 1.5 × 10⁸ [63]. Moreover, there are various types of TFs that can act on the same promoter. In addition, a gene that is found in the DNA in multiple copies directly increases the demand for the corresponding TF. Furthermore, most of the TFs have many target genes (reviewed in [64]). Thus, eventually due to the complex relation between RNAPs, TFs and promoters, modelling competition during transcription remains challenging.

Mathematically, modelling competition of TFs and RNAPs on their binding sites is expected to resemble other gene expression competitions in certain aspects. Specifically, there are several similarities between competition on resources during transcription and translation; for example, between genes competing for RNAPs and mRNAs competing for ribosomes. Similarly, competition of promoters on TFs can be equivalent, in some manners, to the competition of codons on tRNAs, or the competition of miRNA binding sites on miRNAs. However, the specific parameters and other factors involved in each competition are of course different.

In 2006, an equilibrium-based model has been proposed to study transcriptional regulation in E. coli in vivo [20]. In bacteria, transcription initiation requires RNAP to form a complex with transcription initiation factor σ [65]. The recruitment of the complex to promoters depends on the binding affinity and is modulated by several repressors and activators. In their mathematical model, Grigorova et al. [20] aimed to quantify the partitioning of RNAPs, and complexes of RNAPs and σ factors, between promoters, non-specific DNA binding sites and the free pool of RNAPs in the cytoplasm. The two major parameters of the model are the dissociation constants for specific and non-specific binding of RNAP. The model includes a fixed total concentration of sigma factors that are split into the two following fractions: (i) the house keeping sigma factors and (ii) alternative sigma factors, designated σ⁷⁰ and σ^A, respectively. Both types were assumed to have the same binding affinity for free RNAPs. In addition, it was assumed that σ⁷⁰ promoters can be occupied only by complexes of RNAPs and σ⁷⁰, whereas σ^A promoters can be occupied only by complexes of RNAPs and σ^A. The model examined how competition between σ⁷⁰ and σ^A is affected by several factors, including: the total number of σ factors, promoter saturation by RNAP attached to σ⁷⁰ (in the absence of σ^A) and the amount of free RNAPs (either with or without a σ factor). Accordingly, it describes three potential equilibrium binding states between: (i) free RNAPs and σ factors, (ii) complexes of RNAPs with σ and promoters, and (iii) RNAPs and RNAPs with σ binding to non-specific DNA sites. The model assumes strong specificity of the promoters such that complexes of RNAP and σ⁷⁰ can bind only to σ⁷⁰ promoters (similarly, σ^A promoters can be occupied only by RNAP and σ^A); all promoters of the same type are assumed to have equal binding affinity. Mathematically, the model equations composed of a set of conservation equations describing the constant and finite pools of RNAPs, σ factors and promoters, and a set of mass-action equations describing the dissociation constants.

In 2014, the work of Grigorova et al. [20] was extended by Mauri & Klumpp [66] in a theoretical model developed for the competition of sigma factors for RNAPs. The model aimed at studying the effect of competition between canonical and alternative sigma factors on the bacterial response to changes in the environmental conditions. Whereas the model of Grigorova et al. was focused on transcription initiation, the model of Mauri & Klumpp [66] included an explicit description of transcript elongation. In addition, cases of promoters that can be recognized by two types of sigma factors were also examined. The model revealed that sigma factor competition provides a mechanism for a passive upregulation of the stress-specific sigma-driven genes. Specifically, the increased number of RNAPs in stress leads to an increase in the number of alternative sigma factors that bind the RNAP and direct it towards the appropriate stress response genes. The model was validated by comparison with in vitro competition experiments [67,68], with which a good agreement was found.

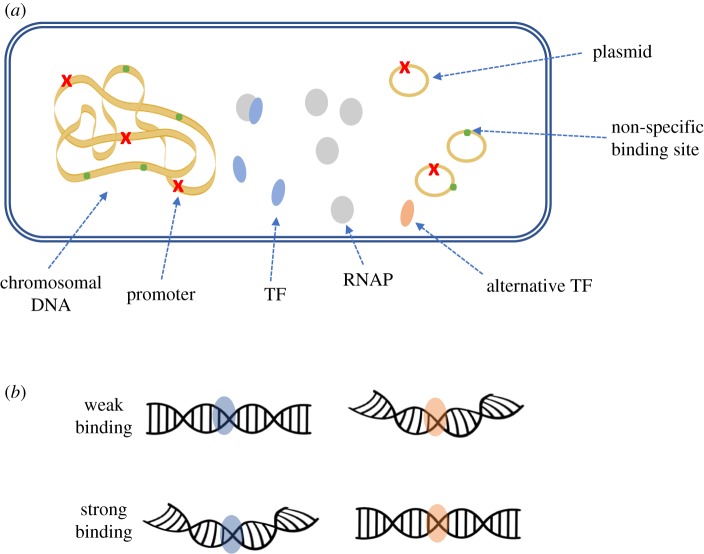
The interplay between TF copy number and the number of its target binding sites in E. coli was further characterized by Brewster et al. [69] using a thermodynamic model. The main idea of the model was to enumerate the possible configurations of RNAP and TF among the available specific and non-specific binding sites, in order to infer the probability of finding RNAP bound at a specific promoter. Using a simple repression architecture [70,71] which consists of a promoter with a single repressor binding site such that when repressor is bound no transcription ensues, different scenarios of competition were examined. For example, competition from multiple, identical genes with promoters that are either placed on a high-copy number plasmid or integrated in multiple chromosomal locations (figure 5a). The model estimated the fold-change in gene expression based on the ratio between the expression level in the presence of a TF to the level in its absence, taking into account the number of repressors present in the cell, the size of the non-specific binding sites (which was set to be the whole E. coli chromosome, specifically, 5 × 10⁶), the binding energy of a repressor to its operator and finally, the copy number of the gene.

Figure 5.

Competition during transcription. (a) Competition aspects during bacterial transcription. Promoters (red multi symbol) and non-specific binding sites (green dots) can be located either on the chromosomal DNA or on plasmids. These sites can be bound by a strong TF (blue ellipse), alternative TF with lower affinity (orange ellipse), RNAP or a complex of TF with RNAP. (b) Flanking sequences around the promoters can differentially affect binding of TF with identical DNA binding motifs through DNA shape. (Online version in colour.)

Another important and challenging aspect that needs to be considered when modelling competition between binding sites on TFs is the fact that DNA folding has a global effect on the binding of TFs (reviewed in [72]). Specifically, chromosomes are organized into chromosome territories such that genes from different territories can co-localize in the nucleus together with TFs [73], inducing local competition between TFs binding sites in each territory. This presents an additional layer of complexity to the target-search problem of TFs and thus, further challenges the attempts to genuinely model their competition.

Although the competition between TFs for available RNAPs has been extensively studied in bacteria, initial evidence for target selection mechanisms in eukaryotic genomes was provided by a quantification of the DNA binding affinities for different TFs in Xenopus oocytes [74].

5. Experimental studies related to competition for finite resources during gene expression

While various experiments that were mentioned above (table 1) measured parameters related indirectly to competition, there are currently only a few studies that have performed measurements related directly to the dynamics induced by competition and their effect on organism fitness. In this section, we will briefly review a few of them.

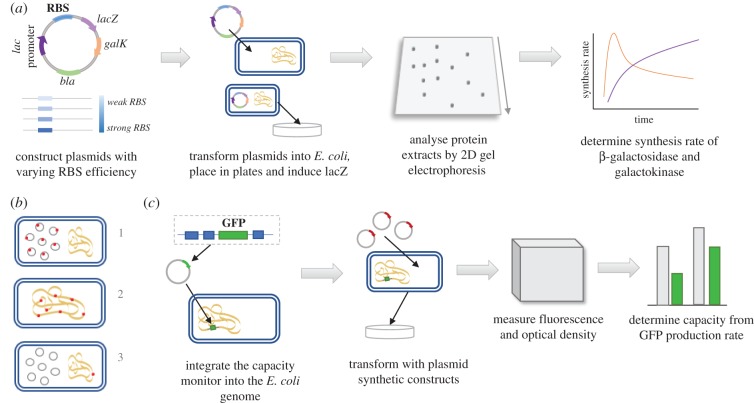
Early in 1993, Vind et al. [14] showed that competition between ribosomal binding sites (RBSs) on ribosomes limits protein synthesis in E. coli. A construction of an operon containing a lacZ gene and a galK reporter gene, encoding for the proteins β-galactosidase and galactokinase, respectively, were used. The only difference between the constructs was a mutation in the RBS that changes the binding efficiency to the ribosome and thereby, the expected translation initiation rates. Specifically, four types of RBSs were tested: RBS from the wild-type original lacZ, two ‘improved’ RBSs from the tufA gene and the rspA which are highly expressed in E. coli, and a rspA mutant, selected as having increased expression in vivo (figure 6a). Analysing protein synthesis rates using two-dimensional gel electrophoresis revealed differences between the different variants. Specifically, in the variant that included the most expectedly efficient RBS, the rate of galactokinase synthesis reached a maximum level after 3 min of induction of the lacZ gene and then decreased by 40%. However, in the other variants, the rate of both β-galactosidase and galactokinase continued to increase. Additionally, despite a significant decrease in the rate of synthesis of the individual galactokinase proteins, the rate of total protein synthesis seemed to be unaffected. Together with the fact that the full lacZ gene is much larger than the average protein in E. coli, and can thus occupy more ribosomes, this suggests that utilization of translation initiation factor was reduced after the induction. Since the rate of total protein synthesis was unaffected by induction and translation initiation factor utilization was reduced after the induction, the reduction in the synthesis rate of individual proteins could not be explained by the limited availability of initiation factors or charged tRNAs, but rather, by the reduction in the number of free ribosomal subunits which increased the competition among RBSs for available ribosomes.

Figure 6.

(a) Illustration of the experiment performed by Vind et al. [14] to measure the effect of competition on free ribosomes. A series of plasmids containing the lacZ–galK operon with different RBSs were constructed, each included a lac promoter, a specific RBS, the lacZ and galK genes and a gene for antibiotic resistance (bla). After transformation into E. coli hosts and lacZ induction, proteins were extracted and analysed by two-dimensional gel electrophoresis. (b) Three constructs for measuring competition on TFs as used by Brewster et al. [69]. Promoters are designated by red dots. (i) Competition from multiple promoters located on high-copy number plasmids, (ii) competition from multiple promoters located on the chromosome and (iii) competition from multiple non-specific binding sites on plasmids and a single chromosomal promoter. (c) Illustration of the experiment performed by Ceroni et al. [75] to measure the effect of synthetic burden on competition for resources. A capacity monitor was constructed and integrated into a specified genomic location; synthetic plasmid constructs were transformed into the cells and the capacity was calculated from the GFP production rate. (Online version in colour.)

Competition between multiple specific and non-specific DNA binding sites is commonly dissected experimentally using simple repression regulatory architecture. Simple repression occurs when a repressor is bound to a binding site that is located upstream from the promoter of a reporter gene (such as a fluorescent gene, [70,71]). The bound repressor blocks the possibility of RNAP to bind the promoter and thus, prevents the transcription of the gene [76,77]. This approach has been used in E. coli to analyse the interplay between TF copy number and the number of its target binding sites which were placed in multiple locations on chromosomal DNA or plasmids [69], using the Lac repressor [78]. Specifically, three types of competition were examined (figure 6b), each represents a different distribution of the multiple locations of the TF-binding sites: first, competition from multiple, identical genes in the simple repression architecture when the promoters are placed only on a high-copy number plasmid (and not on the chromosome); second, competition from multiple, identical genes when the promoters are integrated in multiple chromosomal locations (and not on plasmids); and third, a single copy of the gene of interest and its promoter is located on the chromosome, but multiple plasmids which have binding sites for the repressor (but not for the promoter) are presented. These architectures allowed the identification of the source of transcription and thus, measuring the fluorescence from the reporter gene can be related to binding of TFs to the promoter. In the third case, for example, an observed fluorescence must be due to binding to the single chromosomal copy of the promoter. When all competing binding sites had the same strength, the change in the gene expression was observed once the repressor copy number exceeded the number of competitors. However, when the competitors were weaker, the transition was shifted towards lower repressor numbers.

Ceroni et al. [75] proposed an experiment to study direct competition effects induced by heterologous gene expression. Instead of estimating the burden that heterologous expression represents indirectly from changes in the growth rates, Ceroni et al. suggested a fluorescence-based method for in vivo quantification of the load. A synthetic green fluorescent protein (GFP) was inserted into the E. coli genome, functioning as a monitor for the capacity of gene expression based on the GFP production rate per cell. After integrating the capacity monitor into the bacterial genome, synthetic constructs from a high-copy plasmid were transformed into the cell and subjected to induction, acting as the ‘burden’ on the cell. Finally, the reduction in the GFP production rate was measured, enabling estimation of the cellular capacity (figure 6c). Substantial reduction in the GFP fluorescence, compared to uninduced cells, was observed rapidly before a change in growth rate was detected. In addition, the expression of constructs on high-copy plasmids gave approximately fivefold greater output compared to equivalents on medium-copy plasmids. As GFP are known to lack regulation [79], it could be concluded that changes in GFP expression due to global expression changes indeed reflect changes in the availability of resources, such as RNAPs or ribosomes.

6. The effect of competition for finite resources during gene expression on synthetic biology

Competition models constitute an important aspect of synthetic biology circuits. Commonly, genetic circuits are designed to include genes that can control the expression of other genes in the circuit. However, this approach is challenged by the fact that expression of each gene can also be affected by competition between different genes for various transcription/translation factors. Recently, a model that examines the resource competition effects on the behaviour of the circuit was proposed by Qian et al. [80]. By explicitly accounting for the limited concentrations of RNAPs and ribosomes and for their competition by the different nodes in the circuit, their model predicted non-regulatory interactions that could later be rationally minimized. Furthermore, Shopera et al. [81] demonstrated both computationally and experimentally that competition for resources can induce indirect coupling between unconnected genetic circuits. Their work suggested using negative feedback loops to reduce resource-coupled interference in such independent regulatory circuits. Negative feedback loops prevent the accumulation of the product of the circuit by inhibiting the gene that drives its production, thus, they can prevent one circuit from continually consuming expression resources. Another example for taking into account competition effects in genetic circuit engineering is described by Carbonell-Ballestero et al. [82]. In their study, they proposed a mathematical model for predicting the reduction in the expression of a given gene within a synthetic circuit when competition for resources is presented. Each gene in the circuit imposed a ‘genetic load’ to the cell which was estimated by the strength of its promoter, the strength of its RBS and the efficiency of its codon sequence. Considering an organism with M endogenous genes and N synthetic genes, the model described the expression level of a gene of interest (g_i) as the ratio between its genetic load and the sum of the genetic loads of the M endogenous genes and the N foreign synthetic, including g_i. This ratio was multiplied by a constant corresponding to the limited transcriptional and translational resources.

7. Discussion and open questions

In this review, we have described some intracellular competition phenomena related to gene expression, and the initial attempts for their modelling and analysis. We show that competition for shared finite resources is fundamental for many research topics, including the biophysics of gene expression, genome evolution and synthetic biology. However, the modelling approaches described here are only initial steps towards an accurate understanding of cellular competition. Particularly, these models are only partial, among others due to missing measurements of the analysed parameters, various computational challenges, the complexity of the analysed systems and the fact we lack knowledge about the regulation of many important processes related to gene expression. For example, the numbers reported by experimental studies as the measured abundance of intracellular molecules comprise only partial information and a wider (possibly much wider) range is very likely to exist. In addition, it is not clear how well certain experiments designed for quantitatively estimating competition effects resemble real physiological conditions. For instance, the introduction of many copies of identical plasmids into a bacterial cell may contribute to the understanding of competition mainly in synthetic systems, but not in physiological conditions. Some additional general challenges and directions are depicted below.

First, while there are attempts for developing whole cell simulations (e.g. [83]), there is currently no comprehensive model that includes all different the aspects of competition that were described in this review. Although simpler simulations can also be very useful for studying many cellular aspects, the investigation of complex aspects of interactions between multiple components is only enabled by whole cell models. This can be done, however, only if the parameters of the complex models can be accurately estimated. As mentioned above, competition affecting one aspect of gene expression may also have indirect effects on other aspects of gene expression. For example, competition of promoters on RNAPs and TFs is expected to affect mRNA levels; due to the finite number of ribosomes and tRNAs, the changes in mRNA levels can thus also affect translation. Similarly, competition of miRNA binding sites on miRNAs affects mRNA levels which can thereby affect translation. It will be important to develop computational/mathematical models that combine competition in all gene expression steps such as transcription, translation and mRNA degradation. Among others, such models will enable the study of correlation between different gene expression steps due to finite resources.

Second, the computational analysis of realistic models that include all relevant aspects of gene expression often comes with a substantial demand for computational resources. Since complex interactions exist between many intracellular components, it is entirely not trivial to use parallel computing to accelerate such simulations. Thus, the current whole cell simulations related to competition (e.g. [15,33,34,83]) include many approximations, omitting central gene expression aspects. Similarly, while mathematical analyses related to competition (e.g. [26,27,31]) are important for studying fundamental phenomena in the field, it is impossible to employ mathematical tools that will consider all the biological details related to competition during gene expression. One possible direction to overcome these limitations may include the development of hardware tailored for such simulations.

Third, it will be important to study (from the biophysical and evolutionary points of view) the ‘competition’ among subpopulations of intracellular entities such as mRNAs and ribosomes. For example, it was suggested that viral coding regions undergo adaptation to the host codons [84] and specifically a condition-specific adaptation [85]; it will be interesting to understand and model how competition between the host codons and the viral codons on the host resources (such as tRNA molecules) shapes the viral coding regions. In addition, it was also suggested that in various conditions, the set of ribosomes is not homogeneous [86] and the cell includes various subpopulations of ribosomes with different biophysical parameters. Thus, computational and mathematical modelling of the competition among mRNAs on different types of ribosomes is clearly an important research topic for the coming years.

Fourth, it has been previously shown that the structure of different molecules can contribute to accelerating target site finding. For example, an unusual enrichment of TFs in dimers and tetramers suggests that they have been shaped by evolution to enable efficient intersegmental transfer [87]. Incorporating the effect of the three-dimensional structure of the different factors required for gene expression can introduce additional improvement to the current models. In addition to basepair recognition which has usually been assumed to be a major determinant of the binding specificity of molecules to their targets, the local shape of the binding sites has also been proven to have a regulatory effect. It was suggested, among others, that nucleotides outside the binding site can influence its three-dimensional structure. Consequently, binding sites of identical sequences can achieve different specificities in vivo, due to different sequence contexts. While this topic has gained much attention in the case of TF-binding sites interactions modelling (e.g. [88–92]), similar structural aspects are relevant to additional types of competition. For example, the elongation speed of the ribosome is affected by local secondary structures downstream from the codon [93,94], and the efficiency of miRNA hybridization is affected by the mRNA folding surrounding the binding site [95].

However, not only local structures should be considered in modelling competition, but also the local density of the binder molecules. Moreover, the local density of the binders is expected to affect the expression of a gene more critically than the global density. For example, it was suggested that efficiently translated mRNAs are associated with higher local density of both ribosomes [96] and tRNAs [38]. Although this idea has been mainly used in TASEP-based models of mRNAs on ribosomes [97], local densities should be an important parameter that should be included in any competition model during gene expression.

Finally, the concentrations of gene expression factors are not constant among different cellular conditions (see, for example [98]). Thus, it will be interesting to perform a comparative study of competition models in different conditions and tissues. Such an analysis can reveal novel layers of regulation related to the biophysics and evolution of competition. To the best of our knowledge, these types of studies have yet to be performed.

Data accessibility

This article does not contain any additional data.

Authors' contributions

R.S. and T.T. wrote the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This study was supported in part by a fellowship from the Israeli Ministry of Science, Space and Technology and by the Ela Kodesz Institute for Medical Physics and Engineering.