Efficient integration of heterogeneous single-cell transcriptomes using Scanorama

Abstract

Integration of single-cell RNA sequencing (scRNA-seq) data from multiple experiments, laboratories, and technologies can uncover biological insights, but current methods for scRNA-seq data integration are limited by a requirement for datasets to derive from functionally similar cells. We present Scanorama, an algorithm that identifies and merges the shared cell types among all pairs of datasets and accurately integrates heterogeneous collections of scRNA-seq data. We apply Scanorama to integrate and remove batch effects across 105,476 cells from 26 diverse scRNA-seq experiments representing 9 different technologies. Scanorama is sensitive to subtle temporal changes within the same cell lineage, successfully integrating functionally similar cells across time series data of CD14+ monocytes at different stages of differentiation into macrophages. Finally, we show that Scanorama is orders of magnitude faster than existing techniques and can integrate a collection of 1,095,538 cells in just ~9 hours.

Introduction

Individual single-cell RNA sequencing (scRNA-seq) experiments have already been used to discover novel cell states and reconstruct cellular differentiation trajectories^1–7. Through global efforts like the Human Cell Atlas⁸, researchers are now generating large, comprehensive collections of scRNA-seq datasets that profile a diverse range of cellular functions, which promises to enable high resolution insight into processes underlying fundamental biology and disease. Assembling large, unified reference datasets, however, may be compromised by differences due to experimental batch, sample donor, or experimental technology. While recent approaches have shown that it is possible to integrate scRNA-seq studies across multiple experiments^9,10, these approaches automatically assume that all datasets share at least one cell type in common⁹ or that the gene expression profiles share largely the same correlation structure across all datasets¹⁰. These methods are therefore prone to overcorrection, especially when integrating collections of datasets with considerable differences in cellular composition.

Here we present Scanorama, a strategy for efficiently integrating multiple scRNA-seq datasets, even when they are composed of heterogeneous transcriptional phenotypes. Our approach is based on computer vision algorithms for panorama stitching that identify images with overlapping content and merge these into a larger panorama (Fig. 1a)¹¹. Analogously, Scanorama automatically identifies scRNA-seq datasets containing cells with similar transcriptional profiles and can leverage those matches for batch-correction and integration (Fig. 1b), without also merging datasets that do not overlap (Methods). Scanorama is robust to different dataset sizes and sources, preserves dataset-specific populations, and does not require that all datasets share at least one cell population⁹.

Figure 1.

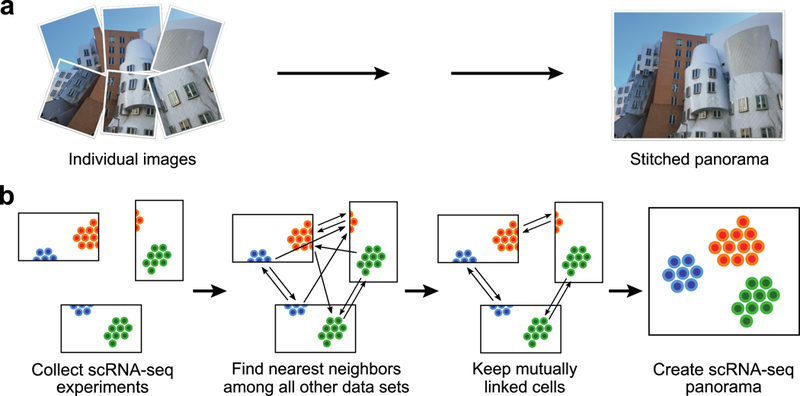
Illustration of “panoramic” dataset integration. (a) A panorama stitching algorithm finds and merges overlapping images to create a larger, combined image. (b) A similar strategy can also be used to merge heterogeneous scRNA-seq datasets. Scanorama searches nearest neighbors to identify shared cell types among all pairs of datasets. Dimensionality reduction techniques and an approximate nearest neighbors algorithm based on hyperplane locality sensitive hashing and random projection trees greatly accelerate the search step. Mutually linked cells form matches that can be leveraged to correct for batch effects and merge experiments together (Methods), where the datasets forming connected components based on these matches become a scRNA-seq “panorama.”

Our approach generalizes mutual nearest neighbors matching, a technique which finds similar elements between two datasets, to instead find similar elements among many datasets. Originally developed for pattern matching in images¹², finding mutual nearest neighbors has also been used to identify common cell types between two scRNA-seq datasets at a time⁹. However, to align more than two datasets, existing methods^9,10 select one dataset as a reference and successively integrate all other datasets into the reference, one at a time, which may lead to suboptimal results depending on the order in which the datasets are considered (Supplementary Fig. 1). Although Scanorama takes a similar approach when aligning a collection of two datasets, on larger collections of data, it is insensitive to order and less vulnerable to overcorrection, because it finds matches between all pairs of datasets.

To optimize the process of searching for matching cells among all datasets, we introduce two key procedures. Instead of performing the nearest neighbor search in the high-dimensional gene space, we compress the gene expression profiles of each cell into a low-dimensional embedding using an efficient, randomized singular value decomposition (SVD)¹³ of the cell-by- gene expression matrix, which also helps improve the method’s robustness to noise. Additionally, we use an approximate nearest neighbor search based on hyperplane locality sensitive hashing¹⁴ and random projection trees¹⁵ to greatly reduce the nearest neighbor query time both asymptotically and in practice (Methods).

Notably, Scanorama can perform both scRNA-seq dataset integration and (optionally) batch correction. Integration methods (e.g., Seurat CCA¹⁰) find lower dimensional representations of high dimensional gene expression vectors such that the representations minimize confounding variation (e.g., batch effects) with respect to some variation of interest (e.g., biological differences among cell types). Batch correction methods (e.g., scran MNN⁹) also remove confounding variation in the original high dimensional space. Scanorama always performs integration of low dimensional embeddings but can also perform batch correction if required. Though incurring a greater computational cost, batch correction enables a wider array of downstream analyses. For example, differential expression analysis can be performed on batch corrected gene expression data but not on integrated low dimensional representations.

Results

Dataset alignment using Scanorama

Scanorama integrates data from heterogeneous scRNA-seq experiments by finding common cell types among all pairs of datasets. Conceptually, given four cell types A, B, C, and D that make up three data sets (A, B), (C, D), and (B, C), Scanorama automatically finds the correct set of alignments (A, B) to (B, C) to (C, D) by finding mutual nearest neighbors across all three possible pairs of these datasets, whereas other methods are sensitive to the order of the datasets and are prone to finding spurious alignments between disparate cell types, e.g., first aligning (A, B) to (C, D). Once cell type alignments have been determined, they can then be used to merge datasets together to create scRNA-seq “panoramas,” e.g., a combined reference dataset (A, B, C, D) (Fig. 1; Methods).

Improved integration of simulated and toy heterogeneous scRNA-seq datasets

To verify the merit of our approach, we first tested Scanorama on simulated data and a small collection of scRNA-seq datasets. We simulated¹⁶ three datasets with four cell types in total but where the first and third datasets had no cell types in common (Supplementary Fig. 2a,e). We also obtained three previously-generated¹⁷ real datasets: one of 293T cells, one of Jurkat cells, and one with a 50:50 mixture of 293T and Jurkat cells (Fig. 2a). In both cases, we were able to merge common cell types across datasets (Fig. 2b; Supplementary Fig. 2b,f) without also merging disparate cell types together. In contrast, existing integration methods are either sensitive to the order in which datasets are considered or are highly prone to overcorrection (Fig. 2c,d; Supplementary Fig. 2c,d,g,h). Scanorama’s improved performance on the simulated datasets and the real 293T/Jurkat collection, while relatively idealized or simple cases, led us to consider if we could also achieve improved performance on larger and more complex collections of scRNA-seq datasets.

Figure 2.

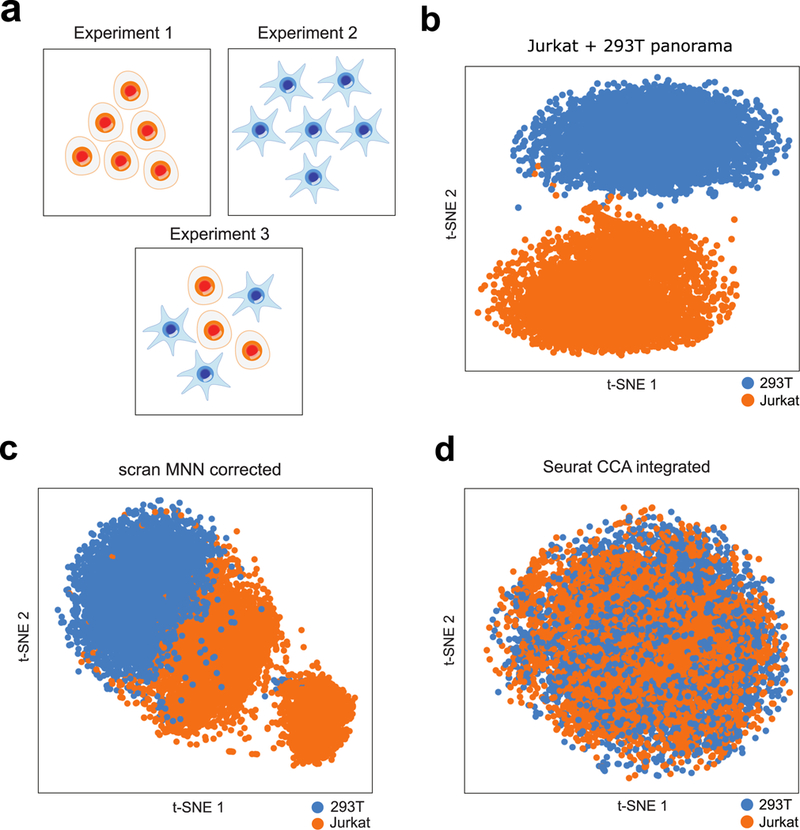
Scanorama correctly integrates a simple collection of datasets where other methods fail. (a) We apply Scanorama to a collection of three datasets¹⁷: one entirely of Jurkat cells (n = 3257 cells) (Experiment 1), one entirely of 293T cells (n = 2885 cells) (Experiment 2), and a 50:50 mixture of Jurkat and 293T cells (n = 3388 cells) (Experiment 3). (b) Our method correctly identifies Jurkat cells (orange) and 293T cells (blue) as two separate clusters. (c,d) Existing methods for scRNA-seq dataset integration are sensitive to the order in which they consider datasets (see Supplementary Fig. 1) and can incorrectly merge a Jurkat dataset and a 293T dataset together first before subsequently incorporating a 293T/Jurkat mixture, forming clusters that do not correspond to actual cell types.

Scanorama enables integration of105,476 cells across 26 diverse datasets

We then sought to demonstrate the ability of Scanorama to assemble a larger and more diverse set of cell types. In total, we ran our pipeline on 26 scRNA-seq datasets representing nine different technologies and containing a total of 105,476 cells (Fig. 3a; Supplementary Table 1), each dataset coming from a different scRNA-seq experiment from a total of 11 different studies. Scanorama identifies datasets with the same cell types and merges them together such that they cluster by cell type instead of by experimental batch (Fig. 3a-c; Supplementary Fig. 3). In contrast with existing methods, our algorithm does not merge disparate cell types together (Fig. 3b,c) and identifies a “negative control” dataset of mouse neurons as distinct from the cell types of all other datasets (Fig. 3a). One of the panoramas identified by Scanorama consists of two datasets of hematopoietic stem cells (HSCs)^18,19 which, once corrected for batch effects and plotted along the first two principal components, reconstruct the expected HSC differentiation hierarchy (Supplementary Fig. 4). We also observe cell type-specific clusters within panoramas of pancreatic islet cells (Supplementary Fig. 5–7) and peripheral blood mononuclear cells (Supplementary Fig. 8–9) but now have greater power to detect rare cell populations. For example, in the pancreatic islet panorama, we observe a cluster of cells consistent with a previously-reported rare subpopulation of pancreatic beta cells marked by increased expression of endoplasmic reticulum (ER) stress genes GADD45A and HERPUD1 (Supplementary Fig. 6g,h)¹⁰. We also note that datasets are aligned according to biological similarity instead of confounding differences in transcriptional quiescence such as dataset-specific dropouts (Supplementary Fig. 10a). Scanorama also aligns biologically similar datasets across experiments that use absolute transcript counts or relative expression values; e.g., the pancreatic islet panorama consists of UMI experiments^20–22 and datasets with TPM²³ and RPKM²⁴ values.

Figure 3.

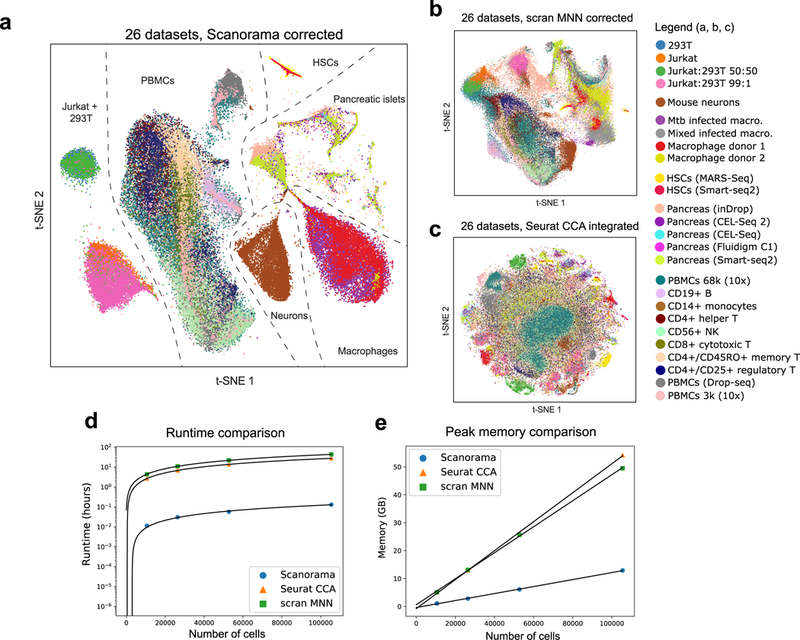
Panoramic integration of 26 single cell datasets across 9 different technologies. (a) t-SNE visualization of 105,476 cells after batch-correction by our method, with cells clustering by cell type instead of by batch (median Silhouette Coefficient of 0.17). (b, c) Other methods for scRNA-seq dataset integration (scran MNN⁹ and Seurat CCA¹⁰) are not designed for heterogeneous dataset integration and therefore naively merge all datasets into a single large cluster (median Silhouette Coefficient of −0.03 for scran MNN and −0.18 for Seurat CCA; Supplementary Fig. 10). (d, e) Scanorama integrates 105,476 cells across 26 datasets in less than 6 minutes and in under 12 GB of RAM, which is substantially more efficient than current methods for scRNA-seq integration.

Improved integration and batch correction performance on heterogenous datasets

We sought to quantify the integration performance of our algorithm on the collection of 26 datasets by calculating a Silhouette Coefficient²⁵ for each cell (Methods), where higher values indicate that a cell is near cells of the same type and far from cells of a different type in the integrated low dimensional space. On the above collection of 26 datasets, the distribution of Silhouette Coefficients is significantly higher (two-sided, independent t-test P < 4e-6; n = 105,476 cells) after Scanorama integration (median of 0.17) compared to scran MNN (median of −0.03), Seurat CCA (median of −0.18), and no integration (median of 0.14) (Supplementary Fig. 11). We note that this improvement in performance is also robust to changes in the algorithm’s parameters (Supplementary Fig. 12) and a more detailed discussion on parameter choice and sensitivity is provided in the Supplementary Materials. Clustering analyses of Scanorama-integrated data find structure related to cell type and orthogonal to dataset-specific batch (Supplementary Fig. 7a-c), with comparable integration performance to existing methods when all datasets have similar cell type compositions (Supplementary Fig. 4, 5) and significantly better integration performance than existing methods on collections of datasets with cell type heterogeneity (Fig. 3; Supplementary Fig. 1, 2).

In addition to integration performance, we can also quantify the batch correction performance of our algorithm by looking at the similarity of the gene expression distributions across datasets before and after batch correction. On five pancreatic islet datasets^20–24, for each gene, we calculate the one-way ANOVA F-value testing the null hypothesis that there are equal gene expression means among all five datasets, where lower F-values indicate more similar means (Methods). We compute F-values for each gene in the uncorrected data and after batch correction by Scanorama and scran MNN (we note that this analysis is not applicable to the output of Seurat CCA since it only does integration, not batch correction, and therefore does not modify gene expression values). We find that 89% of the genes have lower F-values after Scanorama correction (Supplementary Fig. 7d) compared to only 76% of the genes after scran MNN correction (Supplementary Fig. 7e), while the variances across genes after Scanorama or scran MNN correction are still very similar to those of the uncorrected data (Scanorama Pearson ρ = 0.97; scran MNN Pearson ρ = 0.99; P < 5e-324 for both methods; n = 15,369 genes), indicating that either method is not achieving lower F-values by trivially homogenizing gene expression.

Scanorama’s improved scalability enables integration of 1 million cells

Due to our algorithmic optimizations, our tool is also substantially more efficient than existing methods for scRNA-seq dataset integration or batch correction. In particular, to integrate our collection of 26 datasets containing 105,476 cells, Scanorama can integrate datasets in roughly five minutes and performs batch-correction of all panoramas in under 20 minutes. In contrast, existing methods require more than 27 hours to integrate the same collection of datasets (Fig. 3d) using more than three times the amount of memory (Fig. 3e) yet perform poorly at preserving real biological heterogeneity in the integrated result (Fig. 3b,c).

We further demonstrate the scalability of our method by applying Scanorama to integrate 1,095,538 cells from two large-scale single-cell transcriptomic studies of the central nervous system (CNS) in mouse,^26,27 including samples taken from the mouse spinal cord and from different regions of the mouse brain. Scanorama aligns functionally similar cells across different regions of the brain, where we can identify cell types using known marker genes^26,27 (Figure 4, Supplementary Fig. 13). Scanorama integrates this collection of 1,095,538 cells in 9.1 hours with a peak memory usage of 95 GB, though additional optimizations may improve the efficiency of our method further. In contrast, other methods exceed the maximum memory capacity of our benchmarking hardware when run on this data, illustrating the advantage of our algorithm’s computational efficiency when integrating large-scale datasets containing millions of cells.

Figure 4.

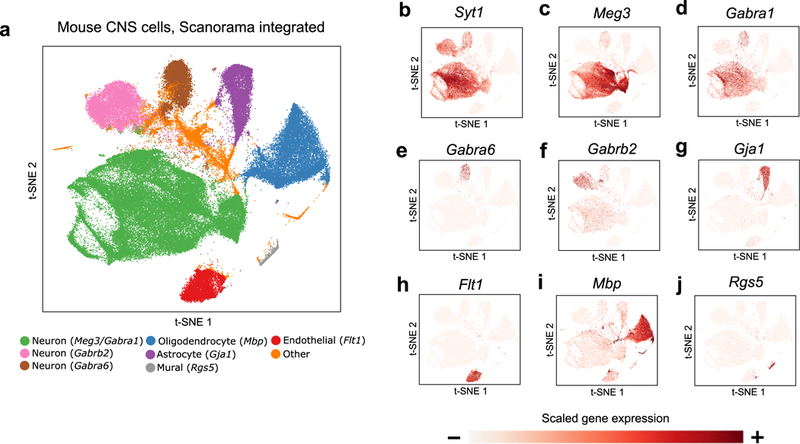
Scanorama scales to collections of data sets with more than a million cells. (a) Scanorama integrates a collection of 1,095,538 cells from the mouse brain and spinal cord. (b-j) Marker gene expression reveals cell type-specific clusters including (b-f) Syt1, Meg3, Gabra1, Gabra6, and Gabrb2 in neurons, (g) Gja1 in astrocytes, (h) Flt1 in endothelial cells, (i) Mbp in oligodendrocytes, and (j) Rgs5 in mural cells.

Scanorama improves robustness to overcorrection

Theoretically, Scanorama relaxes the requirement that all datasets share at least one cell type in common, instead only requiring that each dataset shares at least one cell type with at least one other dataset. However, in practice, we find that even this assumption is often too strict and that Scanorama can avoid overcorrection when a dataset has no overlapping cell types with any other dataset (e.g., mouse neurons among the collection of 26 diverse datasets; Fig. 3a).Although Scanorama essentially reduces to the algorithm used in scran MNN when aligning a single pair of datasets together (although with much greater computational efficiency), we observe that Scanorama can be robust to overcorrection when integrating a larger collection of datasets even when none of the datasets being integrated have overlapping cell types (Supplementary Fig. 14). In principle, forming spurious mutual links between biologically disparate cell types becomes less likely as the number of cells or the number of datasets being integrated increases, so that Scanorama’s approach becomes more robust to overcorrection with more data. Some amount of supervision, however, is still recommended when integrating heterogeneous datasets, and further minimizing the likelihood of overcorrection is an important concern for future integrative approaches.

Scanorama alignment scores reflect subtle temporal changes

Since Scanorama can differentiate between disparate cell types, we were interested in determining if Scanorama would be sensitive to subtler transcriptional changes such as, for example, a cell population responding to a biological stimulus over time. To test this hypothesis, we obtained three different scRNA-seq time series studies: a collection of seven public datasets involving mouse dendritic cells stimulated with LPS at 0, 1, 2, 4, and 6 hours²⁸; 11 public datasets of aging Drosophila melanogaster brain cells at 0, 1, 3, 6, 9, 15, 30, and 50 days²⁹; and five newly generated scRNA-seq datasets of human CD14+ monocytes that are stimulated with M-CSF (to be differentiated into macrophages) at 0, 3, and 6 days along with a public dataset of CD14+ monocytes¹⁷. Within each time series, Scanorama computes an alignment score for all pairs of datasets by computing the percentage of the cells in each dataset involved in a mutual nearest neighbors matching and taking the maximum of the two percentages for that pair; a high alignment score suggests a high amount of overlapping transcriptional activity involving at least one of the datasets.

Without exception, the Scanorama alignment scores are significantly inversely correlated with the amount of time separating the pairs of datasets (Spearman ρ < –0.49, P < 0.0043 for each of the three studies; Figure 5; Supplementary Table 2), where the negative sign on the correlation is consistent with transcriptional similarity, reflected in a higher alignment score, increasing with proximity in age or stimulation time. The temporal correlation of Scanorama alignment scores is also stronger than that of other heuristic measures of the similarity between two datasets (Supplementary Table 3). Furthermore, the pairs of datasets with the highest alignment scores are those between datasets from the same timepoint or from temporally adjacent timepoints (Figure 5, Supplementary Table 2). In both the dendritic and monocyte time series, the maximum spanning tree of the graph with datasets as nodes and alignment scores as edge weights perfectly reconstructs the temporal structure underlying the data (Supplementary Figure 15). While the dendritic and brain datasets are from the same study, Scanorama successfully aligned a public CD14+ monocyte dataset to our newly generated unstimulated CD14+ monocyte dataset despite different laboratories and technologies (10X and SeqWell, respectively).

Figure 5.

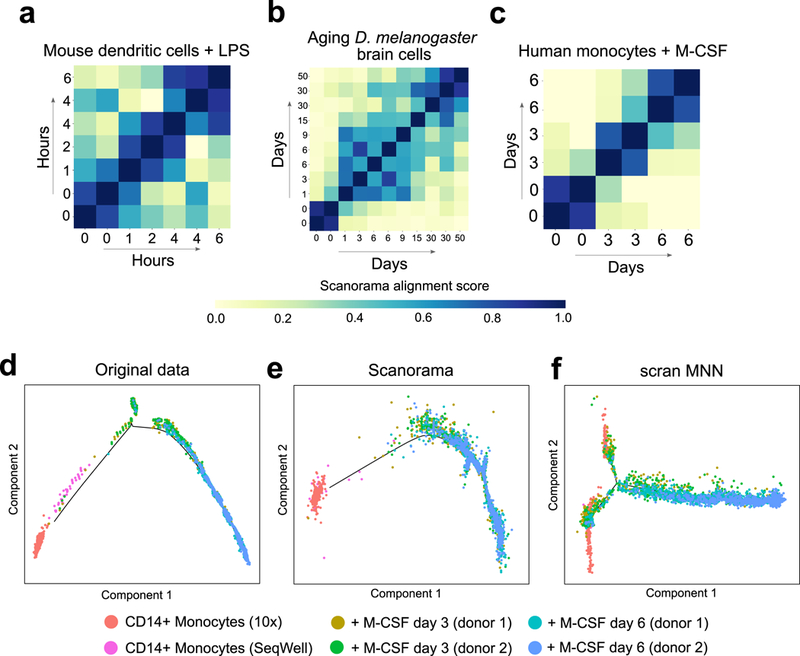
Scanorama is sensitive to subtle transcriptional changes in cellular state over time. (a-c) Heatmap rows and columns correspond to different datasets within the time course study (including replicate datasets at the same timepoint) and diagonal entries are set to 1. Higher alignment scores (darker blue) tend to be close to the diagonal, indicating greater transcriptional similarity between datasets from closer time points. The temporal differences and the alignment scores are significantly correlated in each time series experiment: Spearman correlation of (a) −0.60 (P = 0.0043, n = 42 pairs of time points) for mouse dendritic cells with LPS, (b) −0.49 (P = 1.3e-4, n = 110 pairs of time points) for aging D. melanogaster brain cells, and (c) −0.88 (P = 1.8e-5, n = 30 pairs of timepoints) for monocytes with M-CSF stimulation. (d-f) Scanorama removes batch effects separating CD14+ monocytes obtained by different technologies when visualized according to pseudo-time assigned by the Monocle 2 algorithm. Due to overcorrection, Monocle 2 can no longer identify the main differentiation trajectory after batch correction with scran MNN.

Scanorama enables integration of macrophage differentiation datasets

We were further interested in seeing if Scanorama correction of time series datasets would substantially dampen the dynamic processes as profiled by scRNA-seq, since batch correction of these datasets may also remove some amount of real biological variation. We therefore applied the Monocle 2 method for ordering cells in pseudotime⁶ to the above monocyte- to-macrophage time series datasets, repeating the analysis on data with no batch correction and after correction by Scanorama and scran MNN, noting that Seurat CCA does not correct gene expression values and thus does not naturally interface with Monocle 2. In the uncorrected case, Monocle 2 learns a trajectory that separates CD14+ monocytes generated by different technologies (Figure 5d). On Scanorama-corrected data, Monocle 2 still orders cells along a single pseudo-temporal trajectory consistent with real time while also removing batch effects separating the monocyte datasets (Figure 5e), indicating that Scanorama correction removes batch effects and largely preserves pseudo-temporal patterns. On data corrected by scran MNN, Monocle 2 has a more difficult time reconstructing the main differentiation trajectory (Figure 5f) most likely because scran MNN forces all datasets to accumulatively merge into a single reference that removes most of the pseudo-temporal signal, whereas Scanorama alignments are sensitive to the temporal relationships among the datasets (Figure 5c).

Monocle 2 assigns greater pseudo-temporal similarity to cells between day 3 and 6 than to those between day 0 and day 6 in both the uncorrected and Scanorama-corrected data (Figure 5d,e). Moreover, differential expression analysis between days 0 and 3 reveals genes that are significantly enriched for the IL-12 pathway and immunity-related myeloid activation (Supplementary Table 4) whereas there are no significant enrichments between days 3 and 6. These findings suggest that most of the transcriptional changes involved in macrophage differentiation are rapid and occurred within the first three days of our experiments, thus providing single cell insight into the transition dynamics of a widely used model of human macrophages. Scanorama is therefore not only able to differentiate between completely disparate cell types but is also sensitive to subtler transcriptional changes within a cell type due to processes like stimulation or aging.

Discussion

Scanorama provides a powerful and efficient integrative framework that is robust to differences in cell type and sensitive to subtle functional changes across a diversity of tissues, organisms, biological conditions, technologies, dataset sizes, and different levels of data quality and noise. We note that when the cell type composition among datasets is similar, Scanorama does not necessarily lead to improved accuracy over existing approaches, but will still attain comparable performance along with increased computational efficiency and robustness to overcorrection. However, Scanorama outperforms existing approaches for heterogeneous dataset integration and scales to millions of cells, potentially enabling the detection of rare or new cell states across multiple diseases and other biological processes. Scanorama is designed to be used in scRNA-seq pipelines downstream of noise-reduction methods, including those for imputation and highly- variable gene filtering^30–32. Although Scanorama still aligns functionally similar cells across datasets even with relatively light amounts of preprocessing, more advanced methods for noise reduction may improve the results even further^33,34. The results from Scanorama integration and batch correction can be used as input to other tools; for example, to assemble the reference dataset required for projective methods³⁵ or it can be used in combination with different methods for scRNA-seq clustering, visualization, and analysis^{5–7,31,36–40}. The batch-corrected output from Scanorama can be used in differential expression analysis to identify cluster-specific marker genes, which can be accomplished using a variety of existing tools^41–43.

One decision made when implementing our method was to only align datasets based on the intersection of all genes, a conservative strategy meant to minimize differences due to expression quantification methods. Given the high information redundancy of gene expression data⁴⁴, we are still able to identify biologically similar cells on the intersected gene set, but analyses wishing to preserve more genes could apply a union-based strategy (Supplementary Fig. 10d) or re-quantify expression values using a standard pipeline. While the current algorithm is fully unsupervised, adding some amount of supervision may lead to even more confident dataset alignments⁴⁵. Although we currently align all cells that meet a cutoff for unique genes, random or diversity-preserving sampling of the data⁴⁶ could further improve computational efficiency.

As researchers work to assemble a more complete picture of diverse biological function at a single-cell resolution, the need to integrate heterogeneous experiments also increases. Our algorithm provides a robust and efficient solution to this problem with an implementation that includes simple integration with scanpy⁴², a popular Python-based framework for scRNA-seq analysis, and with R-based pipelines through the reticulate library⁴⁷. We make Scanorama version 1 publicly available at http://scanorama.csail.mit.edu.

Online Methods

Dataset processing for panoramic integration

We obtained 26 scRNA-seq datasets from 11 different studies (see Data Availability). In each dataset, we removed low-quality cells by including only those with at least 600 identified genes to avoid artefacts such as cells with high levels of dropout aligning to transcriptionally quiescent cells (see Supplementary Fig. 10a,b). When searching for scRNA-seq panoramas, we only consider the genes that are present in all datasets and l₂-normalize the expression values for each cell for scale-invariant comparison. Normalization ensures that cells are not matched simply due to dataset-specific differences in the magnitude of the gene expression vectors, enabling alignment of relative expression values (e.g., TPM or RPKM) or absolute transcript counts (e.g., DGE from UMI experiments). We use the l₂-norm since we use the Euclidean distance in our analyses. In our study, there were 5,216 genes present across all 26 datasets, each dataset containing between 90 and 18,018 cells, and which in total contained 105,476 cells after filtering (Supplementary Table 1). An important implementation detail for greatly reducing memory usage is representing the data as sparse matrices, for which we use the sparse matrix implementation in scipy.⁴⁸ For additional details, see Supplementary Note 1.

Dimensionality reduction using randomized SVD

We compute a compressed, low-dimensional embedding of the gene expression values for each cell by taking the SVD of the combined cell-by-gene expression matrix, taking inspiration from different compressive techniques for other biological problems⁴⁹. The SVD is normally very expensive to compute on large matrices, so we leverage an efficient, randomized approach to find an approximate SVD¹³, which is implemented in the fbpca Python package (http://fbpca.readthedocs.io/en/latest/). We use a reduced dimension of 100 in all of our experiments, determined by inspecting the top 300 singular values of the SVD of the combined 26 datasets and using the “elbow method” to choose a cutoff that conservatively preserves most of the variation in the data (Supplementary Fig. 10c). Learning a low dimensional embedding via the SVD not only improves efficiency but enables the method to better tolerate noise (e.g., random dropouts of individual genes), since each component consists of a combination of potentially many individual genes. For additional details, see Supplementary Note 1.

All-to-all dataset matching

For each dataset, we query for its cells’ nearest neighbors among the cells of all remaining datasets in the low-dimensional embedding space. In all of our experiments we search the 20 nearest neighbors to identify a robust set of matches without also being overly permissive (Supplementary Fig. 12a). After repeating this for all datasets, we find all instances where a cell in one dataset is the nearest neighbor of a cell in another dataset, and vice versa. For additional details, see Supplementary Note 2.

Approximate nearest neighbors using locality sensitive hashing

To greatly accelerate our nearest neighbor queries, our algorithm conducts an approximate search based on locality sensitive hashing, where multiple trees of random hyperplanes, used as hash functions, divide the search space of the points in the query set.^14,15 We use the Annoy C++/Python package (https://github.com/spotify/annoy), a memory efficient implementation of this algorithm. For additional details, see Supplementary Note 2.

Nonlinear dataset merging and panorama stitching

After we identify mutual nearest neighbor matches between datasets, we merge connected components of datasets together into larger panoramas. We build upon the nonlinear batch-correction strategy of Haghverdi et al.⁹ that maps one scRNA-seq dataset onto another by computing translation vectors in the full gene expression space for all cells in a dataset. Translation vectors for each cell are obtained as a weighted average of the matching vectors (defined by the pairs of matched cells), where a Gaussian kernel function upweights matching vectors belonging to nearby points. We order pairs of datasets based on the percentages of cells in the datasets that are involved in a matching and use this ordering to build panoramas of datasets by successively merging a dataset into a panorama or using the pair of datasets to merge two panoramas together using the nonlinear correction procedure described above. When correcting large matrices, we divide the correction into multiple batches to substantially lower memory usage, while incurring a small increase in runtime and no change in performance. For additional details, see Supplementary Note 3.

t-SNE visualization

We modified the implementation of t-Distributed Stochastic Neighbor Embedding (t-SNE)⁵⁰ in scikit-learn⁵¹ by replacing the exact nearest neighbors search phase with an approximate nearest neighbors search using the same locality sensitive hashing algorithm and implementation as in our dataset matching procedure. This modification was done to improve the runtime of the default scikit-learn t-SNE when visualizing our results and is included in the code package for our algorithm. We generally increase the perplexity parameter when learning t-SNE embeddings for a larger number of cells or on datasets with greater biological diversity (see Supplementary Fig. 12e).

Clustering performance

Previous scRNA-seq analyses^9,52 have used the Silhouette Coefficient²⁵ as a quantitative measure of clustering performance that does not assume all datasets share the same cell types, unlike other methods for assessing the quality of scRNA-seq batch correction based on dataset mixing⁵². The Silhouette Coefficient is calculated using the mean of the distances from cell i to all other cells of the same type (a_i) and the mean of the distances from cell i to all other cells that belong to the cell type that is nearest to the cell type of i (b_i). The Silhouette Coefficient for a cell is $\frac{b_i-a_i}{\max \left\{a_i,b_i\right\}},$ taking values between 1 and −1, inclusive, where higher values indicating better clustering performance. Intuitively, the Silhouette Coefficient improves if a cell is close to other cells of the same type and far from cells of a different type. For Scanorama, we computed Silhouette Coefficients using the Euclidean distance in the low dimensional embedding space learned by randomized SVD and then integrated using our panorama stitching strategy. For Seurat CCA, we computed Silhouette Coefficients in the integrated low dimensional embedding space using 15 canonical correlation vectors. For the uncorrected and scran MNN-corrected data, we used randomized SVD to learn 100-dimensional embeddings, which we used to compute the Silhouette Coefficients. We use the Silhouette Coefficient implementation provided by scikit-learn.

Parameter sensitivity analysis

The integrative performance of Scanorama was assessed by varying each parameter across a range of possible values in the case of continuous parameters or all values in the case of binary parameters, while holding all other parameters constant at their default values. For Scanorama alignment parameters, Silhouette Coefficients were computed on the resulting integrated low dimensional embeddings as described above. For t-SNE visualization parameters, Silhouette Coefficients were computed on the 2-dimensional t-SNE embeddings. Distributions of Silhouette Coefficients were compared for statistical significance using a two-sided, independent t-test.

Simulation of non-overlapping datasets

We simulated datasets using the Splatter package¹⁶ that generates scRNA-seq gene expression data based on a gamma-Poisson distribution using default parameters. We simulated three datasets each containing two of four cell types, and where two of the datasets had no cell types in common. The datasets were also separated by simulated batch effects by generating a different Gaussian noise vector for each dataset and adding the noise vector to all cells in a given dataset. Each dataset contained 1,000 cells and 10,000 genes with a 50/50 probability of assignment into one of the two cell types per dataset; we used the default simulation parameters.

Panorama of 293Tand Jurkat cells

We obtained three separate datasets consisting of 293T cells, Jurkat cells, and a 50:50 mixture of 293T and Jurkat cells from 10x Genomics¹⁷. These datasets were processed, aligned, and merged using the procedure described previously to give a total of 9,530 cells. We defined cell types using labels from the original study.

Panorama of hematopoietic stem cells (HSCs)

Two publicly available datasets^18,19 of HSCs were processed, aligned, and merged using the procedure described previously to give a total of 3,175 cells. We used the cell types that were reported by both studies, and we examined the expression of marker genes indicating erythropoiesis provided by a previous study⁹ for additional validation (Supplementary Fig. 4). We quantified the quality of our batch correction by computing the likelihood-ratio using the likelihood that the corrected MARS-Seq dataset came from the same distribution as the uncorrected MARS-Seq dataset (H₀) or from the same distribution as the corrected Smart-seq 2 dataset (H₁), where we can more confidently reject the null hypothesis H₀ if the likelihood-ratio $\frac{\mathcal{L}\left(H_0\right)}{\sup \left\{\mathcal{L}\left(H_0\right),\mathcal{L}\left(H_1\right)\right\}}$ is very small. We modeled each distribution with a three-component Gaussian mixture model on the whole gene expression space.

Panorama of pancreatic islets

Five publicly-available pancreatic islet datasets^20–24 were processed, aligned, and merged using the procedure described previously to give a total of 15,921 cells (Supplementary Fig. 5). We k- means clustered the cells in the corrected gene expression space, obtaining 40 clusters, and assigned cell types to each cluster based on previously provided cell type labels and the relative expression levels of cell type-specific marker genes from previous analyses^10,21,23 (Supplementary Fig. 6). This allowed us to identify a cluster corresponding to a rare subpopulation of beta cells with upregulated ER stress genes identified by a previous analysis of the data¹⁰, which we identified using previously inferred labels and by confirming upregulation of the marker genes HERPUD1 and GADD45A in cells from all datasets within that cluster (Supplementary Fig. 6g,h). We quantified batch correction performance by using the one-way analysis of variance (ANOVA) test to compute F-values for each gene across the five datasets before and after batch correction by either Scanorama or scran MNN (Supplementary Fig. 7d,e).

Panorama of peripheral blood mononuclear cells (PBMCs)

Ten publicly-available datasets^17,53 involving PBMCs, or cell types found in PBMCs, were processed, aligned, and merged using the procedure described previously to give a total of 47,994 cells. Cell types were either experimentally determined¹⁷ using fluorescence activated cell sorting (FACS) or inferred by previous clustering analyses^9,10 (Supplementary Fig. 8), and we examined the expression levels of cell type-specific marker genes given by the previous studies for additional validation (Supplementary Fig. 9).

Large-scale panorama of the mouse CNS

We obtained a scRNA-seq dataset from different regions of the mouse brain²⁶ and a singlenucleus RNA-seq dataset from the mouse brain and spinal cord²⁷ to give a total of 1,095,538 cells. To increase the cell count for this analysis so that we could benchmark Scanorama on a very large collection of cells, we applied a less stringent minimum unique gene cutoff of 100. We k-means clustered the cells in the integrated embedding space, obtaining 40 clusters, and assigned cell types to each cluster based on consistency with cell type labels provided by previous clustering analyses and the relative expression levels of cell type-specific marker genes also provided by the previous studies^26,27. We use a memory efficient implementation of the matching vector computation with a batch size of 10,000 (Supplementary Note 3). For visualization purposes only, we subsampled cells uniformly at random by a factor of 10 to allow for tractable embedding computation with our particular t-SNE implementation.

Runtime and memory profiling

We used Python’s time module to obtain runtime measurements for the alignment and merging portions of our algorithm and used the top program in Linux (Ubuntu 17.04) to make periodic memory measurements. We also randomly subsampled sets of 10,547 (10%), 26,369 (25%), and 52,738 (50%) cells from our total of 105,476 cells and measured the runtime and memory of our algorithm on the subsampled data. We compared computational resource usage to two methods, Seurat CCA¹⁰ (with 15 canonical correlation vectors) and scran MNN⁹, using their default parameters. For a fair comparison, we used the same preprocessed data and only measured the resources required for the portions of the methods responsible for alignment and dataset integration. We used R’s proc.time function and Linux’s top to measure runtime and memory usage, respectively, of these programs. All methods were limited to 10 cores and run on a 2.30 GHz Intel Xeon E5–2650v3 CPU with 384 GB of RAM.

Monocyte to macrophage differentiation protocol

Human monocytes were isolated from human buffy coats purchased from the Massachusetts General Hospital blood bank using a standard Ficoll gradient and subsequent CD14+ cell positive selection (Stemcell Technologies). Selected monocytes were cultured in ultra low- adherence flasks (Corning) for 0, 3, or 6 days with RPMI media (Invitrogen) supplemented with 10% FBS (Invitrogen) and 50 ng/mL human M-CSF (Biolegend). SeqWell analysis was performed as previously described⁵⁴. Briefly, at the respective timepoint, cells were detached using trypsin, spun down, and counted. Approximately 12,000 cells were loaded on each array for each timepoint and condition to minimize doublet-loading. The arrays were sealed with a semi-permeable membrane prior to cell lysis and hybridization to single-cell beads. Beads were subsequently pooled for reverse transcription and whole transcriptome amplification.

Read alignment and transcript quantification

Read alignment and transcript quantification were performed as in Macosko et al.⁵⁵. Briefly, raw sequencing data was converted to demultiplexed FASTQ files using bcl2fastq2 based on Nextera N700 indices corresponding to individual samples/arrays. Reads were then aligned to the hg19 genome using the Galaxy portal maintained by the Broad Institute for Drop-Seq alignment using standard settings. Individual reads were tagged according to the 12-bp barcode sequence and the 8-bp UMI contained in Read 1 of each fragment. Following alignment, reads were binned onto 12-bp cell barcodes and collapsed by their 8-bp UMI. Digital gene expression matrices for each sample were obtained from quality filtered and mapped reads, with an automatically determined threshold for cell count.

Time series integration data integration and analysis

We obtained publicly available scRNA-seq time series datasets from Shalek et al. (2014)²⁸, Davie et al. (2018)²⁹, and a newly generated monocyte time series data as described above. We removed low-quality cells by including only those with at least 600 identified genes and l₂-normalized the gene expression values for scale-invariant comparison. Within each time series, we computed an alignment score for each pair as the maximum percentage of cells in either of the datasets that are involved in a mutual nearest neighbors matching. Alignment scores were Spearman correlated with the time differences between dataset pairs across all possible pairs of datasets, where for each time series we obtained a two-sided P-value for the null hypothesis that the two datasets are uncorrelated. The maximum spanning tree on alignment scores was computed using Python’s networkx package (https ://networkx .github.io/).⁵⁶

Temporal correlation benchmarking

We computed the Euclidean distances in the l₂-normalized space (for scale invariant comparison) between all pairs of cells across two datasets and we took the mean distance as the summary measure of the similarity between the two datasets. We performed the above analysis on the first 100 PCs of the uncorrected and scran MNN-corrected datasets and on the low dimensional embedding (with 15 canonical correlation vectors) learned by Seurat CCA. This similarity measure was computed for all pairs of datasets within each time series study and correlated with the time differences between the pairs of datasets as was described for the Scanorama alignment scores above.

Monocyte-to-macrophage gene ontology enrichment analysis

Differential expression analysis between days 0 and 3 and between days 3 and 6 was performed with and without Scanorama correction using a two-sided, Mann-Whitney U test at a Bonferroni-corrected P-value cutoff of less than 0.01 across all hypotheses (with and without Scanorama correction, between days 0 and 3 and between days 3 and 6). On the set of differentially expressed genes, using a background set of the genes present in all datasets in the time series, we looked for gene ontology (GO) process enrichment using the GOrilla web tool (http://cbl-gorilla.cs.technion.ac.il/)⁵⁷.

Monocyte-to-macrophage pseudo-temporal analysis

We ran the Monocle 2 method⁶ for ordering cells within a dataset in pseudo-time on the monocyte-to-macrophage differentiation data. The analysis was done on the differentially expressed genes between day 0 and day 6 using a two-sided, Mann-Whitney U-test at a Bonferroni-corrected P-value cutoff of 0.01. The data was visualized in two dimensions using Monocle 2’s DDRTree method. The analysis was applied to the concatenation of the uncorrected datasets and to the datasets after either Scanorama or scran MNN correction.

Statistical analysis

We use the scipy.stats Python package⁴⁸ implementation of the two-sided independent t-test, two-sided Welch’s t-test, one-way ANOVA, Mann-Whitney U test, Pearson correlation, and Spearman correlation statistics and associated P-values used in this study. P-values given as less than 5e-324 indicate P-values below the floating-point precision of the computer system used for our analysis. We use the statsmodels Python package⁵⁸ to implement Bonferroni multiple hypothesis correction. GO process enrichment was performed using the default hypergeometric test and false discovery rate procedure in the GOrilla web tool⁵⁷. Box plots were generated using the matplotlib Python package⁵⁹.