Abstract
Accumulating evidence indicates that resting-state functional magnetic resonance imaging (rsfMRI) signals correspond to propagating electrophysiological infra-slow activity (<0.1 Hz). Thus, pairwise correlations (zero-lag functional connectivity (FC)) and temporal delays among regional rsfMRI signals provide useful, complementary descriptions of spatiotemporal structure in infra-slow activity. However, the slow nature of fMRI signals implies that practical scan durations cannot provide sufficient independent temporal samples to stabilize either of these measures. Here, we examine factors affecting sampling variability in both time delay estimation (TDE) and FC. Although both TDE and FC accuracy are highly sensitive to data quantity, we use surrogate fMRI time series to study how the former is additionally related to the magnitude of a given pairwise correlation and, to a lesser extent, the temporal sampling rate. These contingencies are further explored in real data comprising 30-minute rsfMRI scans, where sampling error (i.e., limited accuracy owing to insufficient data quantity) emerges as a significant but underappreciated challenge to FC and, even more so, to TDE. Exclusion of high-motion epochs exacerbates sampling error; thus, both sides of the bias-variance (or data quality-quantity) tradeoff associated with data exclusion should be considered when analyzing rsfMRI data. Finally, we present strategies for TDE in motion-corrupted data, for characterizing sampling error in TDE and FC, and for mitigating the influence of sampling error on lag-based analyses.
Keywords: time delay estimation, functional connectivity, lag, sampling error, head motion, reliability
1. INTRODUCTION
Since the seminal observations of Biswal and colleagues (Biswal et al., 1995), interest in resting-state functional magnetic resonance imaging (rsfMRI) for the study of spontaneous brain activity has increased exponentially (Snyder and Raichle, 2012). Studying the zero-lag temporal correlation structure of spontaneous fluctuations in the blood oxygen level-dependent (BOLD) signal (i.e., “functional connectivity (FC)” analysis) provides an efficient means for mapping the large-scale spatial organization of brain function (Fox et al., 2005; Damoiseaux et al., 2006; Fox and Raichle, 2007; Power et al., 2011; Yeo et al., 2011). Although FC is the standard mode of rsfMRI analysis, spontaneous BOLD fluctuations additionally exhibit spatiotemporal dynamics not captured by zero-lag FC (i.e., processes whose measurement is contingent upon the temporal ordering of BOLD time points) (Liegeois et al., 2017). In particular, rsfMRI signals reflect infra-slow (<0.1 Hz) electrophysiological activity (Hiltunen et al., 2014; Palva and Palva, 2012; Pan et al., 2013), which exhibits stereotyped propagation patterns across the brain; this widespread propagation leads to reliable interregional time delays on the order of one second between BOLD signals (Matsui, Murakami and Ohki, 2016; Mitra et al., 2018). The resultant temporal latency structure comprises multiple reproducible propagation sequences (Mitra et al., 2015a), is dramatically rearranged across arousal states (Mitra et al., 2015b; Mitra et al., 2016; Mitra et al., 2018), and is sensitive to behavior (Mitra et al., 2014) and pathology (Mitra et al., 2017) even in the absence of significant changes in FC. Thus, time delay estimation (TDE) provides a useful complement to zero-lag FC for characterizing spatiotemporal structure in rsfMRI.
Importantly, the predominance of very low frequencies (<0.1 Hz) in infra-slow activity and BOLD signals means that practical scan durations do not provide sufficient independent temporal samples to stabilize second-order statistical measures (Laumann et al., 2015). These include cross-correlation among pairs of regional BOLD signals, from which both FC and time delays can be derived (Fig. 1). There is growing appreciation for the consequences of such sampling variability on FC (Hlinka and Hadrava, 2015; Laumann et al., 2015; Laumann et al., 2016; Hindriks et al., 2016), although the effects of rsfMRI artifacts such as those arising from head motion have received more attention. Crucially, procedures such as temporal censoring (i.e., the exclusion of high-motion time points) are effective for mitigating artifact (Power et al., 2012) but at the cost of increased sampling error. Thus, it is important to consider both sides of the tradeoff between data quality and quantity, or between bias associated with specific artifacts and variance arising from reduced data quantity. Although the “correct” balance depends on the question of interest, in general, the latter becomes increasingly problematic the less stable a statistical measure is. Hence, sampling variability is a significant concern for correlations, and even more so for lag-based measures (Smith et al., 2011). Further, temporal censoring complicates TDE, which generally requires contiguous data.
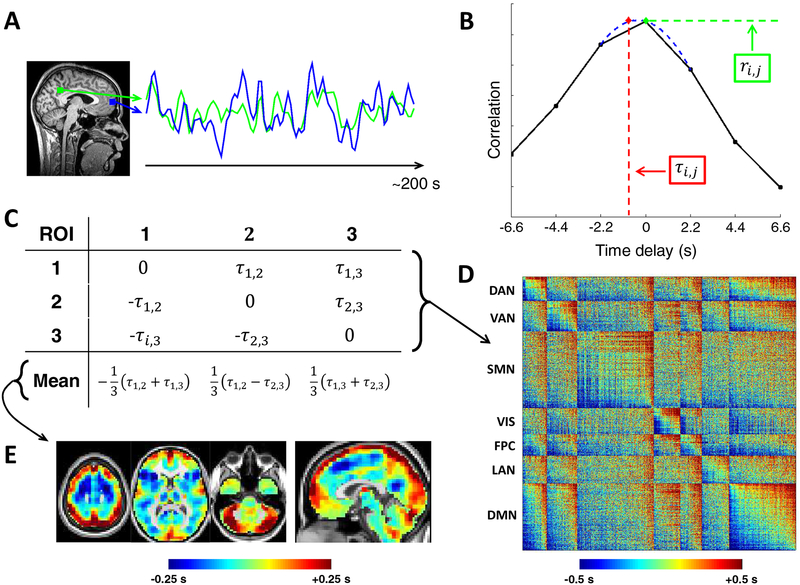
Figure 1. Computation and visualization of time delays from cross-covariance functions.
(A) Two exemplar ROI time series from the default mode network over ~200 s. (B) The corresponding CCF (Eq. (4)) is computed here over ± 6.6 s, which is equivalent to ± 3 frames as the repetition time was 2.2 s. The time delay (TD; τi,j) between these time series is the value at which the absolute value of the CCF is maximal. TD can be determined at a resolution finer than the temporal sampling density by parabolic interpolation (red) through the empirical extremum and the points on either side of it (blue) (Eq. (7)). Zero-lag correlation (FC; ri,j) is computed from the normalized CCF at zero-lag. (C) Toy case illustration of a TD matrix (Eq. (8)) comprising 3 voxels. TD matrices contain time delays between every pair of analyzed ROls and are anti symmetric by definition. Computing the mean over each column of a TD matrix generates a lag projection map (Eq. (9)), a one-dimensional projection of lag structure (D) TD matrix from real rsfMRI data (MSC group average). The rows and columns of this matrix have been sorted from early-to-late and by functional network affiliation. Doing so reveals a range of delays on the order of 1 s both within (on-diagonal) and between (off-diagonal) networks. See text for description of ROls. (E) Example lag projection map computed from the full MSC average TD matrix. The projection identifies regions whose spontaneous activity on average tends to be early (blue) or late (red) with respect to ongoing activity in the rest of the brain (Mitra et al., 2014). DAN, dorsal attention network; VAN, ventral attention network; SMN, sensorimotor network; VIS, visual network; FPC, frontoparietal control network; LAN, language network; DMN, default mode network.
The primary goals of this work are to examine factors impacting TDE (and FC) sampling variability in fMRI, to address the integration of motion censoring with TDE, and to examine bias-variance tradeoffs in both TDE and FC. We begin with analyses of surrogate fMRI time series pairs with modeled time delays; these allow us to quantify, as a function of multiple factors, TDE and FC error with respect to “true” delays and correlations, respectively. Next, we use insights from these simulations to demonstrate how the effects of sampling variability in both TDE and FC can be easily observed in real data. Finally, we conclude with strategies to reduce the influence of sampling error on inferences drawn from TDE. Importantly, although interregional TDE is perhaps the most straightforward approach for quantifying BOLD propagation (Fig. 1), results are pertinent to the variety of approaches that have been used to detect or exploit temporal offsets among fMRI signals (Goebel et al., 2003; Sun, Miller and D’Esposito, 2005; Garg, Cecchi and Rao, 2011; Majeed et al., 2011; Friston et al., 2014; Mitra et al., 2014; Amemiya et al., 2016; Gilson et al., 2016; Raatikainen et al., 2017) (see Friston et al. (Friston, Moran and Seth, 2013; Friston et al., 2014) for taxonomy of these approaches).
2. TIME DELAY ESTIMATION
2.1. Theory
The Pearson correlation coefficient, r, for zero-lag correlation (i.e., FC) between continuous signals, x1(t) and x2(t), is given by:
| #(1) |
where and are the temporal standard deviations of the zero-mean signals x1 and x2 and T is the interval of integration. By generalizing this equation to accommodate temporal delays, τ, between the signals, correlation (or covariance, for simplicity, where is not normalized by the signal standard deviations) can be computed as a function of delay in seconds. Thus,
| #(2) |
defines the cross-covariance function (CCF). The lag between x1and x2, τ1,2, is then determined to be the value of τ at which exhibits an extremum. Thus,
| #(4) |
While the CCF of periodic time series is likely to feature multiple extrema, BOLD signals are aperiodic (He et al., 2010; Zarahn, Aguirre and D’Esposito, 1997) and almost always produces a single, well-defined cross-covariance extremum for a given pair of time series, typically in the range of ±1 s.
2.2. Implementation
In practice, we first construct the CCF in the time domain at discrete multiples of the TR (i.e., at the sampling interval). A single CCF for each session is obtained by summing unnormalized cross-covariance over blocks (b) of contiguous frames, and subsequently normalizing based on the entire time series. (Variations of this approach are discussed in the next section). Thus,
| #(5) |
| #(6) |
where Δ is the temporal shift in units of TRs, t indexes frames, Nb is the total number of frames within the block, NΔ=0 is the total number of frames contributing to the zero-lag CCF estimate, and B is the total number of blocks. Because BOLD signals are best understood as stationary random processes (Liegeois et al., 2017), we set time series to zero-mean prior to Equation (5) by subtracting the mean computed over the maximum number of realizations (i.e., all non-censored frames from the time series), rather than de-meaning each block separately, which would also increase the bias associated with CCF estimation (Marriott and Pope, 1954; Kendall, 1954).
We subsequently use three-point parabolic interpolation among the empirical peak of and the values immediately preceding (cpeak-1) and succeeding (cpeak+1) it in order to approximate the extremum and its associated abscissa, , at a temporal resolution finer than the sampling rate (Fig. 1A–B) (Mitra et al., 2014):
| #(7) |
We currently discount delays longer than four seconds as, in our experience, such results appear to reflect sampling error or artifact. Because a given time delay will typically result in a peak in the empirical CCF at the nearest multiple of the TR, a true time delay at the maximum allowable can be resolved by allowing at least that number of time shifts, plus an additional time shift for parabolic interpolation , where round() evaluates to the nearest integer. In the present case (TR = 2.2 s), three time shifts (Δmax = 3) were needed in each direction to estimate . Hence, was computed over Δ ∈ [−3, 3].
The above approach can be generalized to a set of n time series [x1(t),x2(t), …,xn(t)]. Thus, will be an n × n × Δ cross-covariance matrix from which can be obtained for every pair of time series, xixj (i,j ∈ 1,2, …, n), yielding an n × n time delay matrix:
| #(8) |
The diagonal entries of TD are 0 by definition, given that a time series is perfectly correlated with itself at zero-lag. Moreover, TD is anti-symmetric : if the time series xi is determined to precede xj by a certain magnitude, then xj can equivalently be said to succeed xi by the same magnitude, yielding the opposite sign.
Here we compute as the temporal delay of xj relative to xi, such that a negative value implies that xj precedes xi. Thus, in accord with Nikolić et al. (Schneider, Havenith and Nikolić, 2006; Nikolić, 2007), a column-wise mean will yield a one-dimensional projection of TD, which we refer to as a “lag projection” (TDP), reflecting the mean latency of each region of interest (ROI), n, with respect to all other ROIs. Hence,
| #(9) |
Further, for a given “seed” region comprising one or multiple ROIs, the entire rows of TD corresponding to these ROIs can be averaged to give a seed-based lag map - a one-dimensional map of each voxel’s temporal delay with respect to the seed. The majority of real data presented here utilize a widely used set of 264 ROIs (Power et al., 2011) for simplicity. Exceptions are Figures 1E, 5, and 10, which utilize 6 mm cubic gray matter voxels (Mitra et al., 2014) to provide uniform spatial coverage.
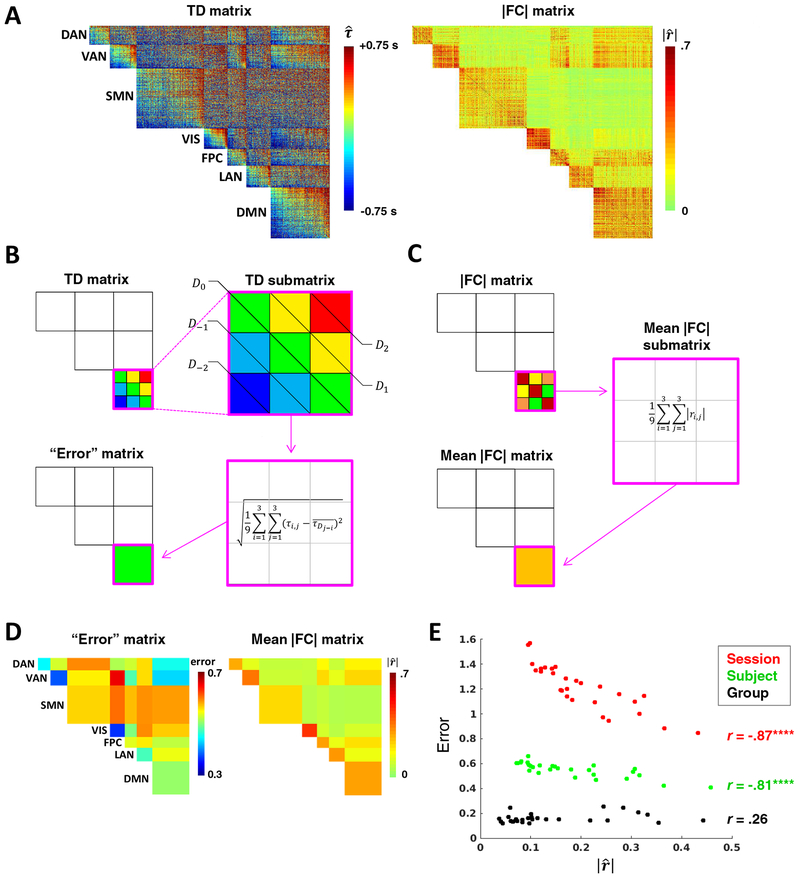
Figure 5. Temporal structure in intra- and inter-network relationships is obscured by sampling error.
(A) Subject-level (MSC01) TD (left) and |FC| (right) matrices comprising 6 mm gray matter cube ROIs grouped by functional network (as in Fig. 1D). (B) Toy case illustrating computation of blockwise diagonal “error” (non-square blocks are first interpolated to yield square blocks). TD matrix blocks in (A) that appear more organized seem to comprise (roughly) iso-latent diagonals. Thus, temporal structure of a given block (submatrix) can be estimated as the RMSE of all time delays in the block relative to the mean delay of their respective diagonals. Error of the perfectly structured toy submatrix amounts to 0. Repeating this process for each unique block yields an error matrix. (C) Toy case illustrating computation of the mean |FC| matrix. (D) MSC01 error and mean |fC| matrices computed from the TD and |FC| matrices shown in (a). Submatrices were interpolated to be square before computing diagonals. (The main diagonal is all zeroes by definition and therefore excluded in error computations). (E) Error in temporal structure as a function of mean |FC|, computed for the 28 unique network blocks at the session (MSC01 session 1), subject (MSC01) and group (MSC average) levels. Error is strongly inversely correlated with FC magnitude at the session and subject levels. At the group level (3,000 minutes of data), this correlation is not significant. Note overall decrease in error and leftward shift of values associated with increasing data. (****p <.0001; N = 28 blocks). DAN, dorsal attention network; VAN, ventral attention network; SMN, sensorimotor network; VIS, visual network; FPC, frontoparietal control network; LAN, language network; DMN, default mode network.
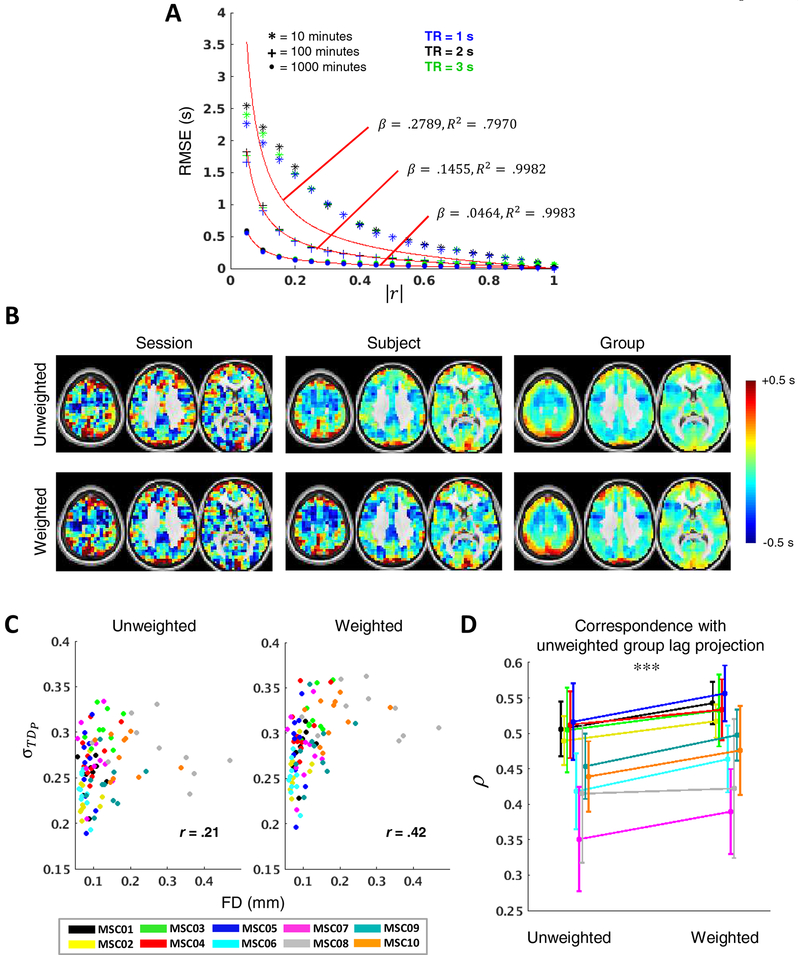
Figure 10. |FC|-weighted lag projections improve reliability.
(A) Modeling the relationship between TDE error and zero-lag correlation magnitude. By adjusting a single parameter, β, Eq.(15) (red) captures this relationship well for a range of data quantities and TRs. For each data quantity, β and R2 values are based on fit to 2 s TR. (B) Example unweighted (top) and weighted (bottom) lag projections for MSC01 session 1 (left), MSC01 (middle; TD averaged over all 10 sessions prior to lag projection computation), and MSC01–10 (right; TD first averaged over all 100 sessions). (C) σ:FD plots depicting the width of the distributions of lag projection values for each MSC session as a function of mean FD. Weighting increases distribution widths as well as the relationship between distribution width and data loss. (D) Correspondence of session-level unweighted and weighted lag projections with group unweighted lag projection. Weighting strongly improves reliability. (***p < .001).
2.3. TDE and motion censoring
Unlike surrogate data, real fMRI data are contaminated by artifact generated by head motion, cardio-pulmonary pulsations and fluctuating arterial pCO2, which poses challenges to accurately estimating time delays of interest. Rather than individually examining each of these artifact sources, we reason that existing denoising strategies (Power, Schlaggar and Petersen, 2015; Liu, 2016; Caballero-Gaudes and Reynolds, 2017; Satterthwaite et al., 2017) should improve TDE. However, one such technique, motion censoring (Power et al., 2012), is worth revisiting in detail in the context of TDE.
Removal of high-motion time points (censoring or scrubbing) from rsfMRI data reduces motion artifact (Power et al., 2012) but integration of censoring into TDE is not straightforward. Zero-lag correlation is invariant to re-ordering of data points within a time series, provided that the new ordering is common to both time series (Liegeois et al., 2017). This means that, within each time series, time points on either side of flagged high-motion frames can be directly concatenated. However, when computing pairwise correlation or covariance as a function of time delay (i.e., ci,j (Δ) where Δ ≠ 0), the flagged frames of the shifted time series will be misaligned with those of the first time series (Fig. 2a). In this case, concatenation would lead to erroneous results (Scargle, 1989). Instead, at each time shift, Δ, a proper “temporal mask” of flagged frames will be the intersection of the temporal mask at zero-lag and the shifted temporal mask. This implies that, for each time shift, the number of frames excluded from the covariance computation exceeds the number of high-motion frames. Theoretically, this temporal masking strategy can lead to data loss by as much as a factor of two; however, in practice, the loss is less because high-motion frames tend to cluster together (Power, Schlaggar and Petersen, 2015).
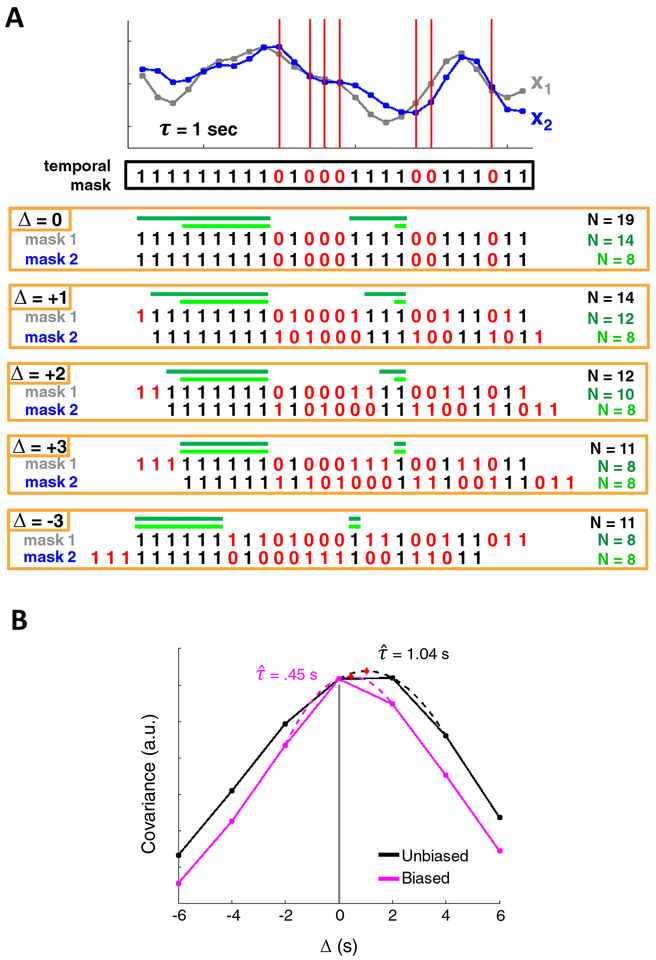
Figure 2. Cross-covariance among discontinuous time series.
(A) x1 and x2 are two surrogate time series. An example temporal mask shows censored time points in red (zeros). Although x1 and x2 share a temporal mask at zero-lag, computing cross-covariance requires that the time series be shifted with respect to one another, and with them, their associated temporal masks. Several shifts of the temporal masks are shown. To compute covariance at a given CCF lag, Δ, one could use all pairs of valid frames that align at that lag (all frames in black). This approach maximizes data usage but results in a substantially different number of samples (N) at each shift. Alternatively, one could restrict the minimum size of a block of non-censored data at zero-lag such that each block contributes at least one sample to every CCF lag (dark green). The minimum allowable block duration satisfying this requirement, is equal to the total number of lags (i.e.,Δmax + 1 = 4 frames). This approach would limit (but not eliminate) uneven samples, at the cost of using less data. Note the symmetry of positive and negative CCF lags. Finally, a restriction may be imposed such that an equal number of samples contribute to each CCF lag, although this leads to still further data loss (light green). (B) CCFs for two surrogate time series, modeled at r = 0.9 and τ = 1 s, following censoring with a real temporal mask from a moderate-motion scan (MSC10 session 1). The black and pink CCFs represent the unbiased and biased CCF estimators, respectively. Note the triangular bias in the pink CCF, resulting in a τ value much lower than the true delay. Although the black CCF is quite accurate in this case, the unbiased estimator leads to values that have comparatively higher variance and may often exceed the true delay.
There are several ways to incorporate censoring into TDE (Fig. 2). One straightforward approach is simply to include, for each lag, all valid pairs of temporal samples as defined by the intersection temporal mask. Although this strategy makes use of all non-flagged frames, it can produce large differences in the number of frames contributing to each Δ of the CCF (Fig. 2a, black). Consequently, the variance of each CCF point can differ substantially. Another concern is that motion artifacts may have temporally extended effects. Thus, while a pair of frames separated by a single high-motion time point may be valid, including them may corrupt the CCF at that Δ.
An alternative strategy is to compute CCFs only over blocks of contiguous data (Fig. 2A, dark and light green), which avoids both above discussed limitations. We refer to this strategy as the “block approach.” Summing (unnormalized) cross-covariance estimates across such blocks yields a single CCF for the time series (Eq. (6)). In prior analyses, we have used a conservative version of this approach, retaining only blocks of low-motion data at least 60 seconds in duration (Mitra et al., 2014). Head movements often are followed by prolonged signal changes (Power et al., 2018). However, global signal regression (GSR) effectively limits motion artifacts to the epoch of movement (Power et al., 2014; Byrge and Kennedy, 2018; Power et al., 2018), which suggests that a 60-second minimum may be overly conservative when using GSR. Therefore, it is worthwhile to determine the degree to which including shorter blocks can reduce sampling error. To limit the degree to which different points of the CCF have unequal numbers of samples, a reasonable lower limit for block duration would be one that allows for at least one sample per block to contribute to every point of the CCF (i.e., (Δmax + 1) × TR) (Fig. 2A, light green).
Given contiguous data, computing lagged CCFs raises the choice of normalizing the estimate at all lags by a constant (number samples at zero lag, as in Eq. 6) vs. normalizing by the number of samples at each lag. The first option leads to biased but lower variance estimates (Jenkins and Watts, 1968). Given non-contiguous data, as in the present case, the situation is more complicated as the number of samples at each lag may vary widely. Figure 2B illustrates this issue using surrogate data combined with the real temporal mask obtained from moderately censored data. This toy case demonstrates that normalization strategy can lead to markedly different TD estimates.
Finally, if the block approach (see above) is used, a single high-motion time point will result in the loss of several surrounding frames. Because BOLD fluctuations are very slow (<0.1 Hz), it is possible that a reasonably accurate value for a contaminated frame may be estimated from its surrounding frames. Thus, interpolation is another viable strategy for reducing excessive data loss, and hence, sampling error. Alternatively, this strategy assumes that surrounding frames are free of artifact, which is not necessarily true. As with small blocks, determining the utility of interpolation requires quantitative comparisons using real data.
3. METHODS
3.1. Subjects
We used the recently published Midnight Scan Club (MSC) dataset comprising ten 30-minute eyes-open rsfMRI sessions from each of ten individuals (Gordon et al., 2017).
3.2. MRI acquisition
Details for acquisition of the MSC dataset have been described previously (Gordon et al., 2017). All imaging was performed on a Siemens TRIO 3T MRI scanner. For each subject, anatomical scans included four T1-weighted sagittal magnetization-prepared rapid gradient-echo (MP-RAGE) images as well as four T2-weighted sagittal images. Functional, T2*-weighted imaging (gradient-echo, 36 slices, TR = 2.2 s, TE = 27 ms, flip angle = 90°, voxel size = 4 mm isotropic) included 30 contiguous minutes of resting-state fMRI, collected during each of ten sessions performed at midnight, giving each subject five hours of resting-state data. During resting-state data acquisition, subjects fixated a white crosshair against a black background. An EyeLink 1000 eye-tracking system (http://www.sr-research.com) indicated that one subject (MSC08) exhibited prolonged eye closures, likely indicating sleep (Gordon et al., 2017).
3.3. fMRI preprocessing
For each subject a mean of field maps collected over multiple sessions was applied to images from all sessions for distortion correction, as described in detail elsewhere (Laumann et al., 2015; Laumann et al., 2016).
Functional data were next preprocessed to reduce artifact, maximize cross-session registration, and transform to an atlas space. All sessions underwent correction for odd-even slice intensity differences stemming from interleaved acquisition of slices within a volume, correction for within-volume slice-dependent time shifts, intensity normalization to a whole brain mode value of 1000, and within- and between-run rigid body correction for head movement. Transformation to Talairach atlas space (Talairach and Tournoux, 1988) was computed by registering the mean intensity image from a single BOLD session via the average T1-weighted image and average T2-weighted image, and subsequent BOLD sessions were linearly aligned to this first session. This atlas transformation was combined with mean field distortion correction and resampling to 3 mm isotropic atlas space in a single step.
Subsequent processing was performed on the atlas-transformed, volumetric time series to further reduce artifact. First, temporal masks were created to flag motion-contaminated frames. Such frames were identified by outlying values of framewise displacement (FD), a scalar index of instantaneous head motion, computed as the sum of the magnitudes of the differentiated translational (three) and rotational (three) motion parameters (Power et al., 2012). Several subjects exhibited high-frequency peaks in the power spectrum of the y motion parameter, which captured the phase-encoding direction (anterior-to-posterior) (Gordon et al., 2017); because this did not have an obvious influence on the data, nor an obvious relationship to typical head movements, and occurred above frequencies of interest (>.1 Hz), we low-pass filtered the y-motion time course at 0.1 Hz in all subjects prior to computing FD to prevent inflation of FD values and superfluous data loss (Siegel et al., 2017). Frames with FD exceeding 0.2 mm (Power et al., 2014) were replaced via linear interpolation to yield continuous time series that could be filtered while mitigating the spread of motion artifact to surrounding frames (Carp, 2013). Interpolated BOLD time series, as well as motion parameters (Hallquist, Hwang and Luna, 2013), were subsequently passed through a zero-phase second-order Butterworth band-pass filter (0.005 Hz < f < 0.1 Hz) to mitigate scanner drift and high-frequency artifact. Note that the extended duration of MSC scans gives the opportunity to capitalize on lower frequencies than typically analyzed with fMRI.
3.4. Component-based nuisance regression
Next, the filtered BOLD time series underwent a component-based nuisance regression approach incorporating elements of previously published methods (Behzadi et al., 2007; Patriat, Molloy and Birn, 2015). Substantial variance in cerebrospinal fluid (CSF) and white matter corresponds to physiological noise (e.g., CSF pulsations), arterial pCO2-dependent changes in T2*-weighted intensity (Power et al., 2018), and motion artifact. Because such spurious variance is widely shared with regions of interest in gray matter, time series extracted from these regions are often used for nuisance regression. While the mean signals from white matter and CSF are typically regressed from gray matter BOLD time series, regression of multiple components comprising the nuisance signals has the potential to remove additional physiological variance (Behzadi et al., 2007) and motion artifact (Muschelli et al., 2014; Patriat, Molloy and Birn, 2015) that has spatiotemporal structure differing from the mean signal.
Generation of component-based nuisance regressors proceeded as follows. Masks of white matter and ventricles were segmented using FreeSurfer (Fischl, 2012; Dale, Fischl and Sereno, 1999) and spatially resampled in register with the fMRI data. Voxels surrounding the edge of the brain are particularly susceptible to motion artifacts (Satterthwaite et al., 2013; Yan et al., 2013a); hence, a third nuisance mask was created for extra-axial (or “edge” (Patriat, Molloy and Birn, 2015)) voxels by thresholding a temporal standard deviation image (tSD > 2.5%) (Behzadi et al., 2007) that excluded the eyes and a dilated whole brain mask. Voxel-wise nuisance time series were dimensionally reduced as in CompCor (Behzadi et al., 2007), except that the number of retained regressors, rather than being a fixed quantity, was determined independently for each of the three nuisance masks by orthogonalization of the covariance matrix and retaining components ordered by decreasing eigenvalue up to a condition number of 30 (i.e., λmin must satisfy λmax/λmin > 30). The retained components across all compartments formed the columns of a design matrix, X, along with six motion parameter time series.
The columns of X are likely to be substantially collinear. To prevent numerical instability owing to rank-deficiency during nuisance regression, a second-level singular value decomposition was applied to XXT to impose an upper limit of 250 on the condition number. This strategy yielded on average 29.6 ± 8.5 (mean ± standard deviation) regressors per 30 minute session (range = 16–55 regressors), to which the mean signal averaged over the whole brain (global signal), along with its first derivative, were added. Although global signal variance is in part neural in origin (Scholvinck et al., 2010; Wong et al., 2013; Liu et al., 2018; Turchi et al., 2018), global signal regression is a highly effective strategy to reduce spatially distributed artifact from myriad sources (Satterthwaite et al., 2013; Power et al., 2014; Ciric et al., 2017; Power et al., 2017; Power et al., 2018) as well as the temporally extended effects of such artifacts (Byrge and Kennedy, 2018; Satterthwaite et al., 2013; Power et al., 2014; Power et al., 2017), which could lead to spurious time delays.
The final set of regressors was applied in a single step to the filtered, interpolated BOLD time series. Finally, the interpolated time points were re-censored using a temporal mask. Time series were averaged within ROIs, which were either 264 10 mm diameter spheres (Power et al., 2011) for TD and FC distributions or 6 mm gray matter cubes (Mitra et al., 2014) for time delay matrices and lag projections maps (Fig. 1, 5 & 10).
3.5. Surrogate fMRI time series
Determination of TDE accuracy requires knowledge of the true delay between a pair of time series, which is not known in real fMRI data. Therefore, we simulated pairs of fMRI time series with modeled time delays. Characteristics of fMRI signals, such as their 1/f-like behavior (Zarahn, Aguirre and D’Esposito, 1997; He et al., 2010), very low frequencies of interest (< 0.1 Hz), and comparatively small time delays (±1 s), make TDE in fMRI a unique challenge. The creation of time series with these features proceeded as follows: First, two 1/fα Gaussian noise time series of the desired length and temporal sampling rate were generated using a previously published algorithm for the frequency domain generation of power law noise signals (Kasdin, 1995; Kasdin and Walter, 1992), as implemented in MATLAB (Stoyanov, Gunzburger and Burkardt, 2011). We used α = 0.7 for all simulations, which is a typical value for this parameter in fMRI data despite small variations across the brain (He et al., 2010; He, 2011). Next, these time series were put through the same bandpass filter as the BOLD data (i.e., 0.005 < f < 0.1, 2nd order Butterworth). To precisely specify the desired correlation, these time series were standardized (made zero-mean, unit-variance), orthogonalized by projection onto the eigenvectors of the desired 2 × 2 correlation matrix R, standardized once more, and finally multiplied by an upper-triangular matrix U satisfying R = UTU (obtained by the Cholesky factorization of l). This resulted in two zero-mean time series of unit variance that duplicated the spectral content of BOLD time series and had the specified correlation at zero-lag. Finally, one of the time series, x1, was shifted in the frequency domain representation to precisely model the desired time delay, τ. Thus,
| #(10) |
where F(x) and F−1(x) are the Fourier and inverse Fourier transforms of x, Δ is the time shift, f is the equal-length sequence of frequency-domain samples, and multiplication is performed elementwise. TDE was performed between the resulting time domain signal, x1,Δ = τ, and its unshifted signal pair, x2,Δ = 0.
Except where noted, simulated time series were constructed with the following parameters: r = 0.9 (before time shifting), τ = 0.5 s, duration = 60 min. An unrealistically high r was used to visually enhance relationships between TDE error and other factors. Each data point in Figures 3, S1, and S2 represents 2,000 simulations.
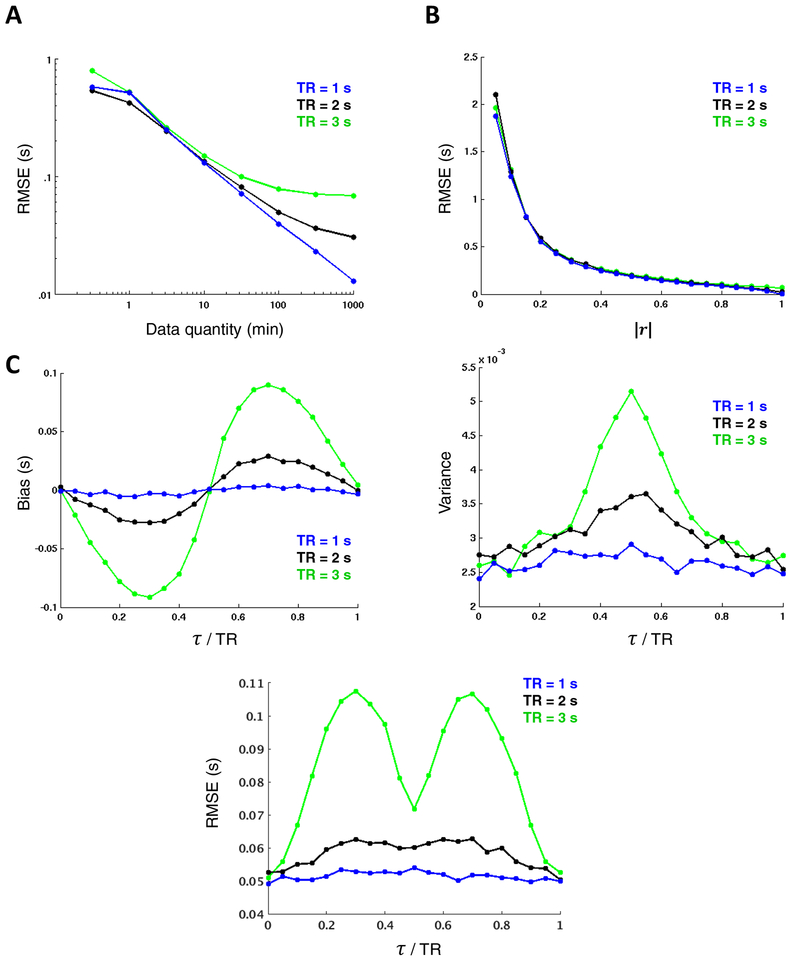
Figure 3. TDE dependence on data quantity, correlation magnitude, and temporal sampling interval.
Surrogate time series (τ = 0.5 s) reveal strong inverse relationships between TDE accuracy and both (A) data quantity (shown for r = 0.9 on a log-log plot spanning several decades) and (B) correlation magnitude (shown for 60 minutes of data). Note that longer TRs asymptote at higher RMSE, limiting their precision relative to shorter TRs. (C) TDE bias (left) reflects parabolic interpolation bias. values tend to cluster at ½ multiples of the TR. The variance pattern (right) is attributable to the subsample TDE that is required in fMRI analysis and thus peaks halfway between samples. Combining these two trends yields a pattern in which RMSE increases with increasing temporal distance between τ and the nearest TR multiple, save for a trough midway between samples owing to the lack of bias in this region. In all cases, lower TRs yield more favorable results; however, TDE dependence on TR is small relative to data quantity and correlation magnitude. Each data point in the Figure represents a mean across 2,000 simulations.
TDE accuracy was evaluated in terms of bias, variance, and root-mean-square error (RMSE). Over n = 2,000 simulations, these were computed as follows:
| #(11) |
| #(12) |
| #(13) |
where τ, and signify the true time delay, the time delay measured on a given simulation i, and the mean time delay over n observations, respectively.
We additionally used zero-lag surrogate time series to evaluate FC accuracy. For these simulations, the “true” correlation r was set in the above manner but for extended duration time series (5,000 minutes). This allowed us to estimate the accuracy of computed over a range of smaller data durations and a range of true correlation (r) values. Accuracy was evaluated in terms of RMSE:
| #(14) |
where z() signifies Fisher z-transformation (Fisher, 1915; Fisher, 1921).
Finally, surrogate data were used to isolate the effects of censoring-induced sampling variability (i.e., variable data quantity) from variable data quality and true intra- and inter-subject variability (Figure 8C–D only). For this analysis, surrogate time series were generated as above but were projected onto the eigenvectors of the real, group average 264 × 264 correlation matrix.
Figure 8. Censoring-induced sampling error in TD, but not FC, remains observable with minimum allowable block duration.
(A) Post-censoring σ:FD scatter plots as in the right panels of Figure 6A–B, but for minimum imposed block duration equivalent to the minimum allowable (rather than 60 seconds, as in Fig. 6). (B) Same distributions as in Figure 6C–D, but only post-censoring and for minimum allowable block duration. Censoring-induced sampling error inflates |TD| even with minimum allowable block duration, but this is less apparent for FC.
MATLAB code for comparing TDE strategies in surrogate time series and computing TD matrices and weighted lag projections as in this paper has been made publicly available at https://github.com/RaichleLab/lag-code.
3.6. Outcome metrics and statistical analysis
TDE strategies (discussed in Section 2) may have opposing impacts on bias and variance, making it difficult to determine whether one strategy is superior to another. However, because the effects on bias and variance disproportionately impact high-motion data, our primary outcome measures were 1) correspondence between low- and high-motion sessions within each subject, and 2) correspondence between each session and the group average. Correspondence was computed over all unique ROI pairs for both TD and FC matrices (i.e., vectorized upper triangular of the 264 × 264 TD or FC matrix). TD pairs corresponding to |FC| <.2 (as determined by the censored group average FC matrix) were excluded in these comparisons to focus reliability analyses on more robust relationships. Correspondence was determined by Spearman’s ρ for TD and Pearson’s r for FC distributions.
Sampling error tends to result in larger magnitude correlations (Power, Schlaggar and Petersen, 2015), which increases the probability of the CCF (erroneously) exhibiting a maximum at some offset from zero-lag. Consequently, sampling error also tends to result in larger time delays. Therefore, we used the width of a given TD or FC distribution as a proxy for sampling error, which we computed as the standard deviation, σ, across the distribution. We also used QC:FC (Power et al., 2012) and QC:TD correlation distributions to visualize the impacts of head motion and sampling error on correlations and time delays, respectively. Each data point in these distributions reflects the correlation between mean FD (quality control metric) and a specific ROI:ROI pair FC (or TD) value, across all 100 MSC sessions. We use the FC or TD absolute value (|FC| and |TD|) in order to focus on the impact of sampling error on the magnitude of these statistics. While mean FD reflects the degree of head motion prior to censoring, it also provides an approximation for the relative amount of data loss following censoring (i.e., subjects with higher mean FD will generally lose more data due to censoring). Thus, because we are primarily interested in the effects of sampling variability due to data loss, we use mean FD computed prior to censoring throughout the paper. This is favorable to FD computed after censoring, which will be less correlated with data loss, and the actual quantity of data loss, which will differ depending on the strategy used for TDE. Nonetheless, FD computed before and after censoring correlated well (r = .71). Moreover, across different strategies, FD computed prior to censoring correlated well with the number of frames used for TDE (r > −.75 in all cases; r = −.92 with minimum allowable block duration). Further information related to motion and censoring can be found in Supplementary Tables 1–4.
Statistical significance of differences between TDE methods was assessed with Student’s paired t-tests performed on the Fisher-z transformed ρ or r values, or σ values corresponding to the TD or FC distributions.
4. RESULTS
4.1. Factors influencing TDE (and FC) accuracy: insights from surrogate time series
We used data simulations to explore the dependence of BOLD TDE accuracy on data quantity, correlation magnitude, and temporal sampling interval (Fig. 3). Figure 3A shows a roughly linear relationship between data quantity and RMSE extending over multiple decades on a log-log plot, underscoring the sensitivity of TDE accuracy to the quantity of data. Note that an unrealistically high correlation (r = 0.9) was used to make the pattern clear; as is evident in Figure 3B, TD RMSE exhibits a strong dependence on correlation magnitude. In particular, as correlation magnitude falls below ~0.2, RMSE markedly increases. An algebraic model of this effect is given below in section 4.4. Thus, in real (GSR) data, where the mean pairwise correlation magnitude may be as low as ~0.1 (as in the present study), the pattern in Figure 3A would be substantially shifted rightward (see Fig. S1 for RMSE plots at weaker correlation magnitudes). Note that Figure 3B explores TD RMSE as function of correlation magnitude in 60-minute time series; see Figure S1 for this dependence in typical session- (10 minutes) and group-level (250 minutes) data quantities.
In comparison to data quantity and correlation magnitude, the effect of TR is relatively minor but is most apparent given large quantities of data, where higher TRs (lower sampling rate) asymptote at greater RSME (Fig. 3A & S1). Thus, coarse sampling leads to poorer TDE resolution, even after parabolic interpolation. The improved detection of directionality in fMRI with increased sampling rate has previously been demonstrated in real data (Lin et al., 2014).
As pointed out in Equation (13), RMSE can be expressed in terms of bias, which refers to the difference between the expected value of an estimator and the true value of the parameter being estimated, and variance, which reflects the expected (squared) deviation of a single estimate from the mean estimate across a given number of observations. In Figures 3A and B, separate bias and variance plots are not shown because RMSE is largely determined by the latter (i.e., there is no systematic bias in TDE associated with specific data quantities or correlation magnitudes). However, it is useful to visualize all three properties when exploring dependence of TDE accuracy on the true time delay relative to the sampling interval, which is shown in Figure 3C for multiple TRs. The sinusoidal bias pattern (Fig. 3C, left) is a well-known characteristic of parabolic interpolation (Boucher and Hassab, 1981; Céspedes et al., 1995) and effectively biases estimates toward the nearest TR. This bias progressively worsens with increasing temporal distance from (roughly) the nearest half-multiple of the TR. Thus, for time delays in the range of 0 s up to 2 s for TR = 2 s, delays closer to 2 s are overestimated, and there is no bias at exactly 1 s. Bias is most severe when τ/TR ≈0.3 and ≈ 0.7, as reported previously (Boucher and Hassab, 1981; Céspedes et al., 1995). This is yet another instance of a bias-variance tradeoff, as other TDE approaches (e.g., in the frequency domain) are free of this bias but exhibit greater variance.
A complementary pattern is observed for variance, which peaks halfway between samples (Boucher and Hassab, 1981; Céspedes et al., 1995) (Fig. 3C, right). Combining these bias and variance effects yields an RMSE pattern that exhibits peaks around the quarter-interval marks and a local trough halfway between samples (Fig. 3C, lower). Note also that RMSE in seconds scales with TR without change in pattern (Céspedes et al., 1995).
Like TDE, FC accuracy is highly dependent on data quantity and continues to decrease linearly on a log-log plot up to the maximum measured duration (1000 minutes). However, FC sampling variability is not obviously sensitive to the true correlation of a given time series pair, nor the temporal sampling rate, making it a simple reflection of data quantity measured in units of time (Fig. S2).
4.2. Manifestations of bias and variance in real data (prior to censoring)
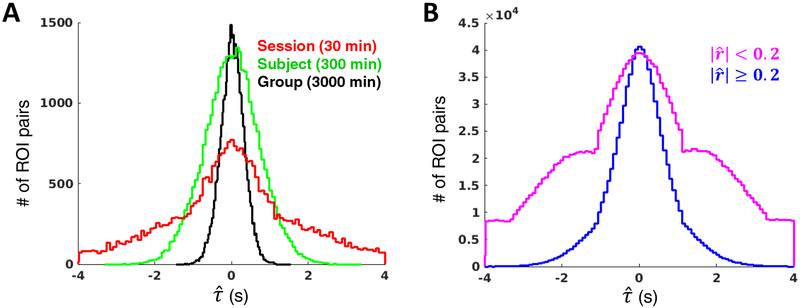
We next sought to determine whether the above relationships are apparent in real data. Figure 4A displays histograms of all possible pairwise time delay estimates among 264 ROIs (Power et al., 2011) using our published approach for TDE (Mitra et al., 2014): data is from either one session (MSC01 session 1; red), one subject (MSC01, time delays averaged over all 10 sessions; green), or all 10 subjects (MSC01-MSC10, time delays averaged across sessions within subject and subsequently across subjects; black). Decreasing variance associated with increasing data quantity is apparent in the widths of the distributions.
Figure 4. Manifestations of sampling error in real rsfMRI data without censoring.
(A) Distributions of pairwise time delays among 264 ROIs (upper triangular of TD matrix) at the session (red), subject (green) and group (black) levels in the MSC dataset Increasing data quantity reduces sampling error, as indicated by the width of the TD distributions. (B) Distributions of all MSC session-level pairwise time delays corresponding to zero-lag correlation magnitudes < .2 (pink) or ≥ .2 (blue), as determined by the MSC average correlation matrix. The increased width of the pink distribution results from sampling error associated with weaker correlations. The wide distribution also makes the bias of parabolic interpolation readily observable: time delay estimates cluster around the TR (here, 2.2 s) and slope discontinuities appear at every ½ TR.
Figure 4B displays histograms of all unique pairwise time delays from all 100 MSC sessions. The blue trace reflects only those time delays corresponding to ROI pairs with zero-lag correlation magnitude ≥ 0.2, while pairs with correlation < 0.2 are represented by the pink trace. Several inferences can be made from these histograms. First, there are far more pairwise correlations below rather than above 0.2. Second, parabolic interpolation bias is much more apparent for weaker as opposed to stronger correlations. Structure in the pink trace (slope discontinuity at ±1.1 sec in data acquired at TR = 2.2 sec) reflects bias associated with parabolic interpolation (Moddemeijer, 1991) (Fig. 3C, left). The pattern is less obvious (but nonetheless present) for more strongly correlated pairs (blue) because they exhibit less sampling error, hence, relatively few delays far from zero.
We next consider how TD error can obscure spatiotemporal patterns of interest. Figure 1D shows the MSC-average TD matrix, masked to include only cortical (6 mm)3 cubes with high-probability (≥ 90%) affiliation with one of seven functional networks (Hacker et al., 2013). The rows and columns of this matrix have been sorted from early-to-late by their mean values, and by functional network, to demonstrate delays on the order of ~1 s in both on- and off-diagonal blocks. Note that the well-ordered, early-to-late progression within each block, as well as the consistency with which certain voxels appear as early or late across rows/columns, is not imposed; rather, this latency structure suggests that infra-slow activity is well-organized both within and between networks. Importantly, this matrix represents 3000 minutes of data and recapitulates prior findings obtained from similarly large data quantities (Mitra et al., 2014). In contrast, Figure 5A shows a TD matrix from one MSC subject (MSC01, averaged across all 10 sessions; 300 minutes) following the same sorting procedure as in Figure 1D, along with the zero-lag, absolute value FC matrix from the same subject. Structure in the off-diagonal blocks is less evident in Figure 5A in comparison to Figure 1D. In general, the degree to which a block in the TD matrix of Figure 5A is structured appears to correspond to the strength of absolute value FC within the block.
To quantify the relationship between TD matrix structure and correlation magnitude, we first created a measure that approximately reflects temporal structure. Specifically, because well-structured blocks of the sorted TD matrix appear to comprise roughly iso-latent diagonals, we defined “error” in the latency structure of each block as the RMSE of all time delays in the block relative to the mean delay of their respective diagonals (Fig. 5B). Next, we averaged |FC| within each of the blocks (Fig. 5C). These procedures resulted in block-wise values of both error and mean |FC| (Fig. 5D), which we correlated with each other using session-, subject-, and group-level matrices. As expected, error in latency structure decreased with increasing data. Moreover, there was a strong inverse correlation between error and mean |FC| at the session (r = −.87, p < .0001) and subject (r = −.81, p < .0001) levels, but not at the group level (r = .26, p = .18) (N = 28 blocks for each correlation) (Fig. 5E). This pattern is understandable as a consequence of Figure 3A–B: while data quantity at the group-level was sufficient for a majority of ROI pairs (e.g., Fig. 1D), data quantity contributing to session- and subject-level TD matrices was sufficient for only those ROI pairs with relatively strong FC. Once sampling error is largely mitigated, there is little dependence of latency structure on the underlying correlations.
4.3. Sampling error incurred from motion censoring
As TDE sampling error can be readily observed prior to censoring, removing time points necessarily increases this source of error, even while mitigating error stemming from artifact. Accordingly, we sought to determine how censoring contributes to sampling error. Because sampling error tends to increase the magnitude of correlations (Yan et al., 2013a; Power, Schlaggar and Petersen, 2015), and thus, cross-correlation derived time delays (e.g., Fig. 4), we focused on TD and FC magnitudes and distribution widths in relation to head motion and data loss.
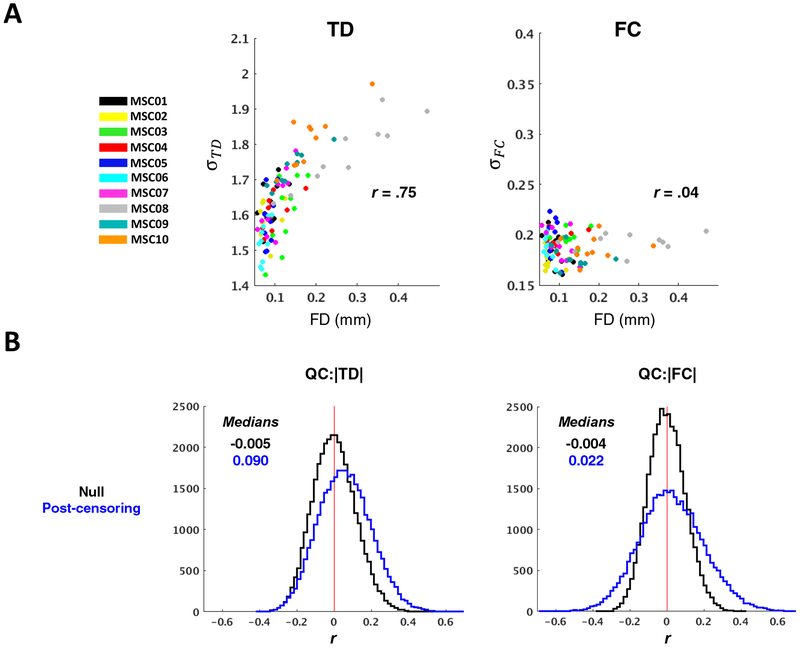
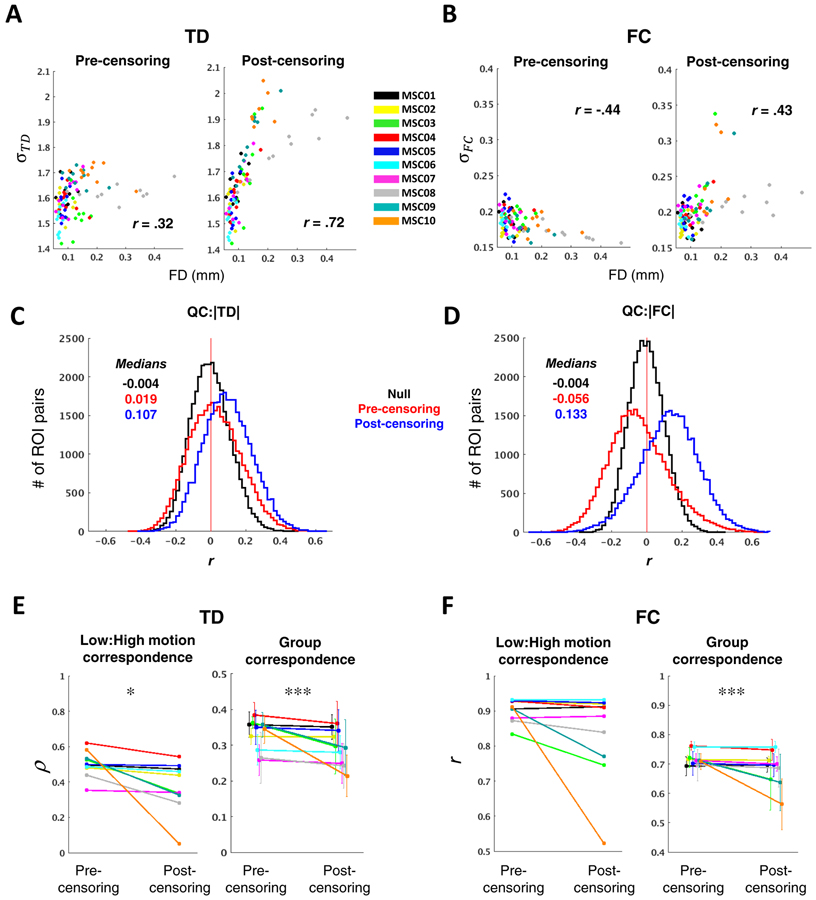
Results pertaining to head motion artifact and data loss are shown in Figure 6. Prior to motion censoring, the standard deviation of a single session’s TD distribution was positively correlated with mean FD across all 100 MSC sessions (r = .32, p < .001) (Fig. 6A left). This result implies that head motion introduces spurious time delays that tend to be longer than those arising from neurophysiology (Byrge and Kennedy, 2018). After censoring FD > 0.2 mm frames (Power et al., 2014) and using our original strategy of discarding segments of data < 60 s in duration (Mitra et al., 2014), the mean distribution width (as measured by the standard deviation) across all sessions was greatly increased (σpre = 1.60 ± 0.07, σpost = 1.67 ± 0.15; ppost-pre < .0001) and the correlation between TD distribution width and mean FD increased to .72 (p < .0001) (Fig. 6A right). Although the standard deviation of the FC distribution was inversely correlated with mean FD prior to censoring (r = −.44, p < .0001), perhaps owing largely to stronger negative correlations in low-motion sessions, FC σ, like TD σ, also became strongly correlated with mean FD after censoring (r = .43, p < .0001) σpre = 0.18 ± 0.01, σpost = 0.20 ± 0.03; ppost-pre < .0001) (Fig. 6B).
Figure 6. Sampling error arising from aggressive data exclusion.
(A) Scatter plots illustrating the relationship between TD distribution width, as measured by the standard deviation (σTD), and head motion/data loss, as measured by mean FD. Each point represents one MSC session, color-coded by subject. Pre-censoring plots reflect a relationship with head motion, while post-censoring plots predominantly reflect sampling error. Censoring exacerbates an already positive relationship between mean FD and σTD. (B) Same as in (A), but for FC. Following censoring, the relationship between σFC and mean FD changes from significantly negative to significantly positive. (C) Distribution of correlations between |TD| and mean FD, across all 100 sessions. Each data point included in the QC:|TD| histogram corresponds to a single ROI pair. Null distributions, computed by randomly permuting mean FD values, are centered near zero (black). Higher motion sessions show modestly greater magnitude time delays (left) before censoring (red); this effect is exacerbated after data exclusion (blue) due to increased sampling error in higher-motion sessions. (D) Same as in (C), but for |FC|. Censoring leads to inflated |FC| (blue). (E) The left panel shows intra-subject correspondence (Spearman’s rho) of the vectorized TD matrix averaged across the five lowest- and highest-motion sessions for each subject. The right panel shows, for each subject, mean correspondence between each session’s TD matrix and the censored group average. Error bars denote standard deviation. (F) Same as in (E), but for FC, and correspondence is measured as Pearson’s r. In both (D) and (E), stringent motion criteria adversely impact reliability (*p <.05; **p < .01; ***p < .001; N = 10 for Low:High motion correspondence, N = 100 for Group correspondence).
Relating distribution widths to FD before versus after censoring, as above, permits quantification of the influence of head motion and data loss, respectively, on TD (and FC) at the session level. These relationships can be further examined at the level of individual ROI pairs. Accordingly, a histogram may be constructed in which each observation reflects one ROI pair, and its value corresponds to the correlation, across 100 sessions, between mean FD and the TD of that ROI pair. A similar histogram can be constructed for FC for all ROI pairs. Such “QC:FC” (quality control:functional connectivity) correlation distributions have previously been used to visualize the impact of head motion on FC, where head motion generally shifts the QC:FC distribution rightward (Power et al., 2014; Ciric et al., 2017). Here, we extend this strategy to studying how head motion (and data loss) impacts TD as well as FC. We computed QC:TD (QC:FC) by taking the absolute value of the TD (FC). pair to focus specifically on sampling error. A null model was generated by randomly permuting mean FD over sessions. Prior to censoring, the QC:|TD| distribution was shifted slightly rightward compared to the null model (Fig. 6C) while the QC:|FC| distribution was shifted leftward (Fig. 6D). Thus, as observed at the session level (Fig. 6A–B), head motion leads to inflated estimates of TD while tending to reduce FC magnitude. After censoring, both QC:|TD| and QC:|FC| distributions were shifted rightward, suggesting, once again, that increased data loss leads to inflated TD and FC estimates. Altogether, these findings point to a strong increase in sampling error associated with censoring under the 60-second block requirement.
We next explored the ramifications of censoring-induced sampling error. Because high-motion sessions are more severely impacted, we assessed correspondence between the five lowest- and highest-motion sessions within each of the 10 MSC subjects, as well as the correspondence of each session to the group average. Importantly, the latter metric is also sensitive to head motion and is significantly inversely correlated with mean FD across all 100 sessions before motion censoring (r = −.39, p < 0.0001 for TD; r = −0.39, p < 0.0001 for FC). Comparing TDE results with and without motion censoring, using an FD threshold of 0.2 mm with the 60 second block requirement, resulted in greater divergence between low- versus high-motion sessions (N = 10 subjects, p < .05) and consistently decreased session-to-group correspondence (N = 100, p < .001) (Fig. 6D). This was true of FC as well (low:high-motion, p < 0.1; session:group, p < 0.001) (Fig. 6E). Thus, an overly stringent approach to motion censoring (FD < 0.2mm and 60 sec blocks) yields poorer results for both TD and FC than simply retaining the high-motion time points.
4.3. Comparing strategies for TDE among discontinuous time series
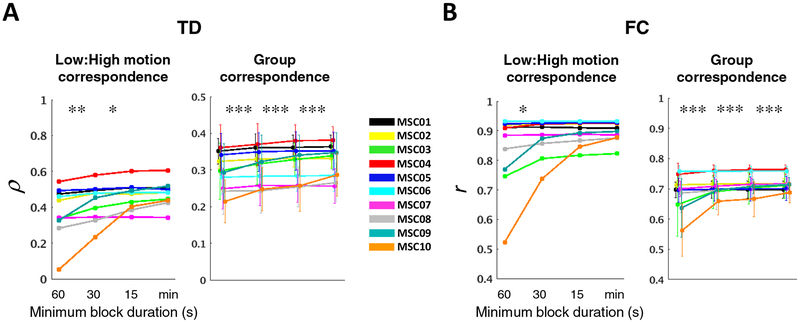
The 60-second block duration was originally adopted to avoid TDE errors generated by temporally extended artifact associated with head motion. However, it has since been shown that GSR (which we use) effectively reduces such artifacts (Power et al., 2014; Byrge and Kennedy, 2018), Accordingly, we next determined how including relatively short epochs impacts our outcome metrics. Outcome was again assessed as the correlation between vectorized TD and FC matrices (correspondence). We found that low:high-motion correspondence as well as session:group correspondence monotonically increased as the imposed minimum block duration was reduced down to the limit consistent with at least one data point from each block contributing to each CCF lag (“minimum allowable” block duration) (Fig. 7A). Similar results were observed for FC (Fig. 7B).
Figure 7. Including small blocks of clean data improves intra- and inter-subject reliability of TD and FC.
(A) Same plots as in Figure 6E–F, but for different minimum imposed block durations. The minimum allowable block duration (min) is 8.8 s ((Δmax + 1) × TR). (B) Same as in (A), but for FC.
Results so far have been reported for the unbiased CCF estimator, i.e., normalized by the number of sampled frames at each lag. Since the minimum allowable block approach (“min”) proved optimal, we compared it against three alternatives: (i) biased CCF estimator (i.e., normalized by the number of sampled frames at zero-lag) with the minimum allowable block duration (“biased”), (ii) enforcing equal samples at each time point in an unbiased CCF estimator (as in Figure 2A, light green; “equal”), and (iii) unbiased estimator using all valid frames at a given time shift (as in Figure 2A, black; “all”). Of these 4 approaches, the unbiased CCF estimator with minimum allowable block requirement performed best (Fig. S3). However, the differences between these approaches were minimal in comparison to relaxing the imposed minimum block duration requirement.
We additionally investigated whether interpolating over censored frames could further improve the unbiased, minimum allowable block approach. Given the degree of sampling error present at the single-session level, even with 30-minute sessions, it might be expected that interpolation would improve outcome metrics by salvaging data, even if that data is of poor quality. Accordingly, the effects of linear interpolation were compared against an approach in which interpolated frames were replaced with the original (post-regression), potentially contaminated values. Although both of these approaches improved group correspondence for both TD and FC, interpolation did not outperform the alternative for FC and, for TDE, performed significantly worse (Fig. S4).
Finally, because the minimum allowable block duration approach is far more lenient than the imposed 60-second minimum and is comparable with conventional FC data constraints (e.g., (Power et al., 2014)), we repeated the analyses in Figure 6A–D using the minimum allowable block duration approach. We found that both TD distribution widths and magnitudes remained positively correlated with mean FD, though these relationships were no longer apparent for FC (Fig. 8). In order to aid interpretation of this result, we repeated these analyses in surrogate time series; doing so enabled us to isolate potential consequences of censoring-induced sampling error, when using the minimum allowable block duration, from effects related to data quality or biology. We generated a single set of 264 surrogate time series based on the real group average correlation matrix (and assumption of zero lag among all time series). Next, we censored these time series according to the real temporal censoring masks (FD > 0.2) from each of the 100 MSC sessions. Hence, any differences in correlation or lag structure computed from these time series would be attributable to censored-induced sampling error.
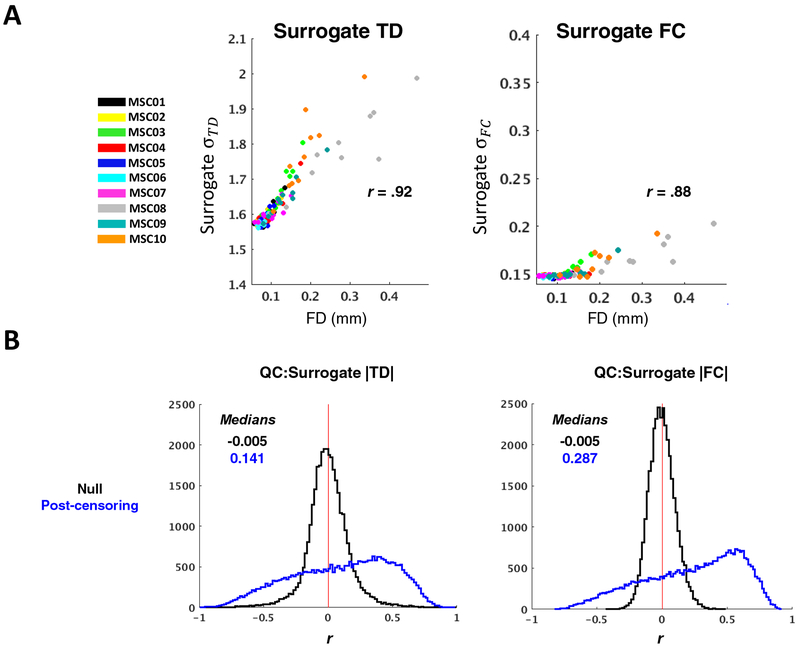
We found TD and FC relationships with FD to be outstanding in the surrogate data (Fig. 9), demonstrating that censoring-induced sampling variability remains a significant source of error for both TD and FC when using the minimum allowable block duration approach, despite 30-minute sessions. Taking these findings into account, it can be concluded from the real data (Fig. 8) that 1) sampling variability still has a considerable influence on observed time delays when using minimum allowable block duration, and 2) absence of a prominent FC:FD relationship when using the minimum block approach does not indicate the absence of sampling error, but rather that the influence of sampling error is less salient in comparison to other factors (e.g., data quality and inter-session or inter-subject variability). Thus, sampling error remains an issue for TD and FC when using 30-minute sessions.
Figure 9. Censoring-induced sampling error in TD and FC computed from surrogate data remains substantial with minimum allowable block duration.
(A) Post-censoring σ:FD scatter plots as in Figure 8A, but for TD and FC distributions computed from surrogate data. The 100 real, session-specific temporal censoring masks were applied to a single set of surrogate time series, which was constructed from the MSC average 264 × 264 FC matrix (no lags were built in). Note that the group average correlation distribution is narrower than that obtained from single sessions; thus σTD values are somewhat larger than in Figure 8A (more sampling error) and σFC values are generally smaller than in Figure 8A. (B) Same distributions as in Figure 8B, but for TD and FC computed from surrogated data as described above. Effects of censoring- induced sampling error are still present with minimum allowable block duration.
4.4. Weighting lag projections against sampling error
We use “lag projections” to visualize each region’s mean temporal relationship with the rest of the brain (Fig. 1E). Lag projections are computed by averaging a region’s temporal lag with respect to all other regions (columns of TD matrices; Eq. 9). Given the dependence of TDE accuracy on correlation, we asked whether this relation could be used to obtain more reliable lag projections. Inspection of the relation between RMSE and |r| (e.g., Fig. 3B) suggested the following functional form:
| #(15) |
which accurately describes TD RMSE in surrogate time series with β fit by conventional regression (Fig. 10A). This expression explains >.99 of the variance in data quantities that are typical in group-level analyses.
Equation (15) can be used to reduce the sampling error of lag projections by down-weighting high-variance lag estimates. Thus, weighted lag projections, (wTDP) are computed by inversely weighting TD pairs in proportion to modeled squared error. Thus,
| #(16) |
In Equation (16), the correlation used to compute wi,j is the conventional zero-lag FC metric . In principle, the peak correlation at could have been used instead. However, this measure is more susceptible to spurious inflation (Bright, Tench and Murphy, 2017). Given the predominance of frequencies below 0.1 Hz in BOLD signals, zero-lag correlation differs only slightly from peak correlations obtained within the range of lags studied here.
The effect of weighting in real data is examined in Figure 10B–D. Panel B shown voxel-wise lag projections at the session-, subject- and group-levels. Weighting generally increases the magnitude of projection values. This effect is quantitatively demonstrated in panel C as an increase in session-level lag projection distribution widths. Weighting disproportionately impacts sessions with less data (i.e., those with the higher mean FD), which manifests as greater correlation between lag projection σ and FD (unweighted r = .75, weighted r = .37). Despite this effect, weighting drastically improved individual correspondence with the group average unweighted lag projection (panel D). Thus, weighting effectively reduces the impact of sampling error on the spatiotemporal patterns reflected in lag projections.
5. DISCUSSION
Here we have investigated factors contributing to sampling variability in fMRI time delay estimation (TDE). The overarching result is that sampling error is a critical issue in both TDE and zero-lag functional connectivity (FC) analyses. Below we discuss the implications of these findings for rsfMRI research.
5.1. Motion censoring and TDE
We compared multiple strategies for TDE in the presence of discontinuities introduced from motion censoring (Fig. 2). Several of these strategies involve tradeoffs between bias and variance that more strongly impact high-motion sessions, i.e., sessions with less useable data. Therefore, to examine bias-variance tradeoffs, we used correspondence between low- and high-motion sessions as well as session-level correspondence with the motion-censored group data as outcome measures.
We found that including small blocks of contiguous data greatly reduces sampling error, down to the minimum allowable duration at which each block still contributes at least one temporal sample to all CCF lags (Fig. 7). Hence, in order to minimize data loss, the smallest possible number of time shifts should be used to estimate the CCF. Because the spectral content of BOLD signals is weighted towards very low frequencies, CCF peaks on the order ~10 sec or more may be expected. However, we currently exclude delays longer than four seconds as, in our experience, such latencies seem to reflect sampling error or artifact. Thus, in the MSC data, we were able to compute each CCF over just seven time shifts (Δmax = 3), making the minimum allowable block duration (Δmax + 1) × TR = 8.8 s (see Section 2.2 and Fig. 2A).
Including all valid frames at a given time shift makes maximal use of data, hence minimized sampling error. However, this approach did not improve outcome measures, possibly owing to artifact in extremely short segments of data (i.e., here, < 5 frames) that are surrounded by high-motion epochs, or spurious time delays associated with data samples on opposite sides of high-motion epochs. Because the “all” valid frames approach yields results comparable to the minimum allowable block approach (“min”), we favor the latter to avoid large disparities in the number of frames contributing to (and thus, the variance of) each lag of the CCF. Using a block approach, temporal interpolation also salvages substantial data, that is, frames surrounding the censored artifact. However, interpolation failed to improve outcome metrics beyond simply including the original high-motion time points. Therefore, replacing potentially contaminated frames with interpolated data is not advisable. However, we did not account for the level of head motion in the frames that were interpolated. It remains possible that interpolation is useful in specific situations, for example, when a long block of data is interrupted by a single large head movement. Nonetheless, because we find that the minimum imposed block duration can be brief, interpolation, even if effective, has only limited potential to salvage data. Finally, we found that, while the biased CCF is associated with reduced variance, in our case, the unbiased CCF estimator yielded more favorable outcome metrics, although these differences were small. Based on these findings, the unbiased, minimum allowable block approach with no interpolation was the most effective of the examined TDE strategies.
We note that the purpose of these comparisons is primarily to outline the nuances of motion censoring in the context of TDE and to assess the involved bias-variance tradeoffs. In practice, the nature of the dataset (e.g., TR, degree and pattern of head motion, pre-processing strategies) will likely affect which approaches appear “optimal.” For example, interpolation may be more useful in datasets with shorter TR. Further, even micro-movements (i.e., FD below 0.2) can still have a detectable influence on rsfMRI data (Power et al., 2014), and are likely to be more prevalent in temporal proximity to larger movements. Therefore, in very large datasets in which sampling error has been minimized, more aggressive data exclusion (e.g., stricter criteria for censoring and/or minimum block duration) may prove beneficial. Our findings may provide a useful guideline but are not guaranteed to be optimal in all cases. To aid in the evaluation and application of TDE in diverse fMRI datasets, we have made publicly available MATLAB code for lag computation in real and surrogate data as described here (https://github.com/RaichleLab/lag-code).
5.2. Using correlation to inform lag analysis
The accuracy of TDE between two signals is highly dependent on the strength of correlation between them (Walker and Trahey, 1995; Céspedes, Ophir and Alam, 1997) (Fig. 3B). TD matrices comprise both intra- (on-diagonal) and inter-network (off-diagonal) relationships (e.g., Fig. 5), the latter of which correspond (by definition) to comparatively weak correlations prone to sampling error. Even so, large quantities of data reveal structure in off-diagonal blocks (Fig. 1D), suggesting that the activity shared between networks, albeit comparatively minor, is well-organized and may be biologically important (Mitra and Raichle, 2016; Mitra and Raichle, 2018). Indeed, inter-network lag relationships may reflect integrative aspects of spontaneous brain activity complementary to the segregated functional networks revealed by zero-lag FC. Unfortunately, inter-network lag relationships require large quantities of data to estimate accurately (Fig. 5). Nonetheless, informative lag analyses can be performed with data quantities that may not be sufficient to stabilize the full TD matrix. For example, time delays among highly correlated ROI pairs can be estimated to reasonable accuracy with far less data than that required to study brain-wide propagation. Correlations may also be used to threshold seed lag maps, providing a more reliable visualization of the seed’s temporal relationships with regions exhibiting closely shared activity.
TD matrices exhibit significant transitivity (Mitra et al., 2014), as defined by the high proportion of all possible triples whose time delays sum to 0 (Nikolić, 2007), despite high dimensionality (Mitra et al., 2015a). Thus, one-dimensional lag projections provide a useful spatiotemporal representation of propagation structure. Moreover, unlike full TD matrices, stable lag projections can be computed with relatively limited quantities of data (Fig. 10D). Further, statistical testing performed between lag projections from different groups or conditions is a useful low-dimensional approach to identifying regions whose spatiotemporal relationships may be altered (Mitra et al., 2015b; Mitra et al., 2017). By using correlation magnitude to give weight to stronger pairwise relationships, weighted lag projections offer increased reliability and may prove more sensitive to group differences in spatiotemporal patterns.
We show above that sampling error increases the distribution widths of both measured TDs and correlations. Perhaps counterintuitively, weighting also increased the distribution width of lag projection values (Fig. 10C). Weighting likely increases sampling error by reducing the effective number of ROIs over which the mean temporal delay is computed, which leads to increased correlation between distribution width and data loss. However, this effect appears to be less important than down-weighting sampling error from weak correlations. Accordingly, the overall effect of weighting is improved reliability. We conclude that weighting usefully mitigates the adverse impact of sampling error on observed spatiotemporal topographies.
Finally, in addition to their statistical relation, TD and FC are phenomenologically related. Therefore, statistical differences in TD cannot be properly interpreted without comparison of underlying correlation structure. Likewise, interpretation of a given TD is greatly informed by knowledge of FC. Statistical significance of TD may be established by comparison with TD computed from appropriate null data: surrogate time series matching the quantity, correlation magnitude(s), TR, and auto- and cross-spectral content of the real data, but with peak correlation at zero-lag (i.e., devoid of latencies). This can be achieved, for example, by destroying phase information from the original time series (Hindriks et al., 2018). Null data may also be used to construct confidence intervals for empirical TD. Nonetheless, the biological interpretation of a significant TD or significant between-group difference in TD may differ widely depending on the underlying FC, or the presence and/or nature of a change in FC.
5.3. Motion censoring and sampling error in rsfMRI
Limited data quantity is among the most significant challenges in rsfMRI research. The slow nature of fMRI signals (<0.1 Hz) necessitates large quantities of data to obtain sufficient independent temporal samples. Even after reducing the minimum imposed block duration to that of conventional FC analysis (e.g., (Power et al., 2014)), across 100 scans, the width of both the TD (in real and simulated data) and zero-lag FC (in simulated data) distributions following censoring remained positively correlated with head motion (i.e., data loss) (Fig. 8–9). Yan et al. previously demonstrated an increase in observed FC magnitude with excessive censoring (Yan et al., 2013a); we show that this manifestation of FC sampling error is observable even in atypically long (30 minutes before censoring) rsfMRI time series.
We additionally found that QC:|TD| (in real and simulated data) and QC:|FC| (primarily in simulated data) distributions were shifted rightward after censoring, again reflecting the tendency of sampling error to inflate TD and FC estimates (Fig. 6C–D, Fig. 8B & Fig. 9B). Why have these patterns not been apparent in prior studies? One reason is that the range of data quantities in the present study is larger than typical. Thus, if 10 minutes typically are acquired, and censoring removes as much as half, the range of retained data quantities in a given dataset remains relatively limited. This potential for censoring to introduce large discrepancies in retained data quantity among long scans was previously discussed by Satterthwaite et al. (Satterthwaite et al., 2013). Computing QC:|FC| rather than QC:FC, as in prior work, also is crucial. In our analysis, the QC:|FC| distribution was left-shifted (relative to the null) prior to censoring and right shifted after censoring (Fig. 6D). In contrast, the QC:FC distribution was zero-centered and minimally impacted by censoring (Fig. S5), which is typical of GSR data (Power et al., 2014; Ciric et al., 2017).
How does unequal sampling error impact statistical comparisons across groups? Welch’s t-test and non-parametric tests for group differences in mean value take sampling variability into account. Thus, unequal sampling error is not a significant barrier in most group comparisons when group differences in mean value is at issue. The possibility of adjusting censoring (or discarding data) to ensure uniform number of frames in all subjects has been discussed (Ciric et al., 2017; Power et al., 2014). However, we see no reason to deliberately introduce sampling error in this manner except when unequal variance biases outcomes, as in analyses based on machine learning (Power et al., 2014). Of greater consequence is that sampling error is not fully eliminated in 30-minute rsfMRI sessions, let alone conventional five-minute sessions. This point is evident in recent reports on highly-sampled individuals, in which it is shown that single-subject FC matrix reliability plateaus only after more than an hour of data is analyzed (Laumann et al., 2015; Gordon et al., 2017).
Corruption of FC by head motion artifact and denoising strategies (e.g., nuisance regression, filtering) for reducing this motion-related bias have been well-described (Power, Schlaggar and Petersen, 2015; Satterthwaite et al., 2017). However, these strategies currently fall short of completely removing motion artifact; hence, excluding high-motion time points further improves data quality (Power et al., 2012; Power et al., 2014; Satterthwaite et al., 2013; Yan et al., 2013a; Yan et al., 2013b; Burgess et al., 2016; Ciric et al., 2017; Siegel et al., 2017). But, motion censoring exacerbates sampling error (Ciric et al., 2017). Although in principle sampling error (variance) is preferable to a systematic bias, sampling error increases the likelihood of spurious findings, reduces statistical power for detecting true effects, and produces artificially inflated estimates of TD and FC under the limited data conditions typical of most fMRI studies. Thus, censoring necessarily involves a bias-variance tradeoff, both sides of which should be considered when determining censoring criteria and when interpreting reported outcomes.
We used reliability to assess the tradeoff between bias reduction versus increased variance associated with censoring. Theoretically, reliability as an outcome measure can be confounded by reliable artifact. However, this is unlikely a significant concern in the present study for the following reasons: (1) We examined reliability following extensive nuisance regression. (2) Reliability was assessed as correspondence between low- and high-motion sessions. (3) Reliability additionally was assessed as correspondence between individual sessions and the censored group average, and this measure inversely correlated with head motion. Thus, these measures were unlikely to have reflected reliability of artifact.
That said, we observed only modest and mixed effects of censoring on TD and FC reliability, provided that the analyses used the minimum allowable block duration strategy (compare Fig. 7 with Fig. 6E–F). The small magnitude of these effects may be attributable to effective denoising, including component-based regression (Behzadi et al., 2007; Patriat, Molloy and Birn, 2015) and GSR (Power et al., 2014), and to the present dataset being relatively low-motion (Tables S1–4). The impact of censoring on reliability likely depends on both data quantity and quality, including the efficacy of pre-processing and the type and pattern of motion artifact (e.g., small vs. large, sparse vs. frequent; see Supplementary Tables 1–4 for session-specific information related to motion and censoring from the present dataset). More work is needed to better define these dependencies.
More generally, while many of the analyses herein suggest that maneuvers increasing data quantity are preferable, this was not always the case. As described above, neither the “all” condition nor temporal interpolation improved outcome measures despite increased data quantity. It is likely that an increase in bias associated with these approaches counteracted any benefits of decreased variance. Moreover, the present results focus on single sessions (albeit 30 minutes); in larger group analyses, researchers can afford to sacrifice more potentially-biased data without substantially increased variance. Our analyses bring attention to the perhaps underappreciated influence of sampling error. In all cases, both artifact-related bias (Power et al., 2012; Satterthwaite et al., 2012; Van Dijk, Sabuncu and Buckner, 2012; Siegel et al., 2017) and sampling variability warrant careful consideration in fMRI analyses.
6. CONCLUSIONS
TDE is a useful complement to zero-lag FC for studying the spatiotemporal organization of spontaneous infra-slow brain activity, as manifest in rsfMRI signals. However, sampling error presents a significant hurdle to TDE in fMRI and, as we show here, is an underappreciated challenge to FC analysis as well. Different research questions will warrant different tolerances for artifact-related bias and for sampling variability, each of which can often be reduced at the cost of increasing the other. In general, more data is needed for TDE as compared to zero-lag FC analysis, which itself requires more data than task-based fMRI analyses. Nonetheless, while large datasets will permit the most informative studies of propagation throughout the brain, useful lag projection comparisons and time delays between strongly-correlated time series can be computed with more limited quantities of data. Surrogate time series may be useful to gauge the data requirements for a specific question given the nature of the data.
Supplementary Material
ACKNOWLEDGEMENTS
This work was supported by the NIH via NS080675 to M.E.R. and A.Z.S. and MH106253 to A.M., and by the NSF via DGE-1745038 to R.V.R. We thank Nico Dosenbach for access to the MSC dataset (Gordon et al., 2017).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Amemiya S, Takao H, Hanaoka S and Ohtomo K (2016) ‘Global and structured waves of rs-fMRI signal identified as putative propagation of spontaneous neural activity’, Neuroimage, 133, pp. 331–340. [DOI] [PubMed] [Google Scholar]
- Behzadi Y, Restom K, Liau J and Liu TT (2007) ‘A component based noise correction method (CompCor) for BOLD and perfusion based fMRI’, Neuroimage, 37(1), pp. 90–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM and Hyde JS (1995) ‘Functional connectivity in the motor cortex of resting human brain using echo-planar MRI’, Magn Reson Med, 34(4), pp. 537–41. [DOI] [PubMed] [Google Scholar]
- Boucher RE and Hassab JC (1981) ‘Analysis of discrete implementation of generalized cross correlator’, IEEE T Acoust Speech, ASSP-29(3), pp. 609–611. [Google Scholar]
- Bright MG, Tench CR and Murphy K (2017) ‘Potential pitfalls when denoising resting state fMRI data using nuisance regression’, Neuroimage, 154, pp. 159–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess GC, Kandala S, Nolan D, Laumann TO, Power JD, Adeyemo B, Harms MP, Petersen SE and Barch DM (2016) ‘Evaluation of Denoising Strategies to Address Motion-Correlated Artifacts in Resting-State Functional Magnetic Resonance Imaging Data from the Human Connectome Project’, Brain Connect, 6(9), pp. 669–680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrge L and Kennedy DP (2018) ‘Identifying and characterizing systematic temporally lagged BOLD artifacts’, Neuroimage, 171, pp. 376–392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caballero-Gaudes C and Reynolds RC (2017) ‘Methods for cleaning the BOLD fMRI signal’, Neuroimage, 154, pp. 128–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carp J (2013) ‘Optimizing the order of operations for movement scrubbing: Comment on Power et al. ’, Neuroimage, 76, pp. 436–8. [DOI] [PubMed] [Google Scholar]
- Ciric R, Wolf DH, Power JD, Roalf DR, Baum GL, Ruparel K, Shinohara RT, Elliott MA, Eickhoff SB, Davatzikos C, Gur RC, Gur RE, Bassett DS and Satterthwaite TD (2017) ‘Benchmarking of participant-level confound regression strategies for the control of motion artifact in studies of functional connectivity’, Neuroimage, 154, pp. 174–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Céspedes I, Huang Y, Ophir J and Spratt S (1995) ‘Methods for estimation of subsample time delays of digitized echo signals’, Ultrason Imaging, 17(2), pp. 142–71. [DOI] [PubMed] [Google Scholar]
- Céspedes I, Ophir J and Alam SK (1997) ‘The combined effect of signal decorrelation and random noise on the variance of time delay estimation’, IEEE T Ultrason Ferr, 44(1), pp. 220–225. [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B and Sereno MI (1999) ‘Cortical surface-based analysis. I. Segmentation and surface reconstruction’, Neuroimage, 9(2), pp. 179–94. [DOI] [PubMed] [Google Scholar]
- Damoiseaux JS, Rombouts SA, Barkhof F, Scheltens P, Stam CJ, Smith SM and Beckmann CF (2006) ‘Consistent resting-state networks across healthy subjects’, Proc Natl Acad Sci U S A, 103(37), pp. 13848–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B (2012) ‘FreeSurfer’, Neuroimage, 62(2), pp. 774–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher RA (1915) ‘Frequency distribution of the values of the correlation coefficient in samples from an indefinitely large population’, Biometrika, 10(4), pp. 507–521. [Google Scholar]
- Fisher RA (1921) ‘On the “probable error” of a coefficient of correlation deduced from a small sample’, Metron, 1, pp. 3–32. [Google Scholar]
- Fox MD and Raichle ME (2007) ‘Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging’, Nat Rev Neurosci, 8(9), pp. 700–11. [DOI] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC and Raichle ME (2005) ‘The human brain is intrinsically organized into dynamic, anticorrelated functional networks’, Proc Natl Acad Sci U S A, 102(27), pp. 9673–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K, Moran R and Seth AK (2013) ‘Analysing connectivity with Granger causality and dynamic causal modelling’, Curr Opin Neurobio, 23(2), pp. 172–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Kahan J, Biswal B and Razi A (2014) ‘A DCM for resting state fMRI’, Neuroimage, 94, pp. 396–407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garg R, Cecchi GA and Rao AR (2011) ‘Full-brain auto-regressive modeling (FARM) using fMRI’, Neuroimage, 58(2), pp. 416–41. [DOI] [PubMed] [Google Scholar]
- Gilson M, Moreno-Bote R, Ponce-Alvarez A, Ritter P and Deco G (2016) ‘Estimation of Directed Effective Connectivity from fMRI Functional Connectivity Hints at Asymmetries of Cortical Connectome’, PLoS Comput Biol, 12(3), pp. e1004762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goebel R, Roebroeck A, Kim DS and Formisano E (2003) ‘Investigating directed cortical interactions in time-resolved fMRI data using vector autoregressive modeling and Granger causality mapping’, Magn Reson Imaging, 21(10), pp. 1251–61. [DOI] [PubMed] [Google Scholar]
- Gordon EM, Laumann TO, Gilmore AW, Newbold DJ, Greene DJ, Berg JJ, Ortega M, Hoyt-Drazen C, Gratton C, Sun H, Hampton JM, Coalson RS, Nguyen AL, McDermott KB, Shimony JS, Snyder AZ, Schlaggar BL, Petersen SE, Nelson SM and Dosenbach NUF (2017) ‘Precision Functional Mapping of Individual Human Brains’, Neuron, 95(4), pp. 791–807.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hacker CD, Laumann TO, Szrama NP, Baldassarre A, Snyder AZ, Leuthardt EC and Corbetta M (2013) ‘Resting state network estimation in individual subjects’, Neuroimage, 82, pp. 616–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallquist MN, Hwang K and Luna B (2013) ‘The nuisance of nuisance regression: spectral misspecification in a common approach to resting-state fMRI preprocessing reintroduces noise and obscures functional connectivity’, Neuroimage, 82, pp. 208–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He BJ (2011) ‘Scale-free properties of the functional magnetic resonance imaging signal during rest and task’, J Neurosci, 31(39), pp. 13786–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He BJ, Zempel JM, Snyder AZ and Raichle ME (2010) ‘The temporal structures and functional significance of scale-free brain activity’, Neuron, 66(3), pp. 353–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hiltunen T, Kantola J, Abou Elseoud A, Lepola P, Suominen K, Starck T, Nikkinen J, Remes J, Tervonen O, Palva S, Kiviniemi V and Palva JM (2014) ‘Infra-slow EEG fluctuations are correlated with resting-state network dynamics in fMRI’, J Neurosci, 34(2), pp. 356–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hindriks R, Adhikari MH, Murayama Y, Ganzetti M, Mantini D, Logothetis NK and Deco G (2016) ‘Can sliding-window correlations reveal dynamic functional connectivity in resting-state fMRI?’, Neuroimage, 127, pp. 242–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hindriks R, Micheli C, Bosman CA, Oostenveld R, Lewis C, Mantini D, Fries P and Deco G (2018) ‘Source-reconstruction of the sensorimotor network from resting-state macaque electrocorticography’, Neuroimage, 181, pp. 347–358. [DOI] [PubMed] [Google Scholar]
- Hlinka J and Hadrava M (2015) ‘On the danger of detecting network states in white noise’, Front Comput Neurosci, 9, pp. 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkins GM and Watts DG (1968) Spectral Analysis and Its Applications. San Francisco, CA: Holden-Day. [Google Scholar]
- Kasdin NJ (1995) ‘Discrete simulation of colored noise and stochastic processes and 1/fa power law noise generation’, Proceedings of the IEEE, 83(5), pp. 802–827. [Google Scholar]
- Kasdin NJ and Walter T (1992) ‘Discrete simulation of power law noise’, IEEE Freq Control Symp, pp. 274–283. [Google Scholar]
- Kendall MG (1954) ‘Note on bias in the estimation of autocorrelation’, Biometrika, 41(3/4), pp. 403–404. [Google Scholar]
- Laumann TO, Gordon EM, Adeyemo B, Snyder AZ, Joo SJ, Chen MY, Gilmore AW, McDermott KB, Nelson SM, Dosenbach NU, Schlaggar BL, Mumford JA, Poldrack RA and Petersen SE (2015) ‘Functional System and Areal Organization of a Highly Sampled Individual Human Brain’, Neuron, 87(3), pp. 657–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laumann TO, Snyder AZ, Mitra A, Gordon EM, Gratton C, Adeyemo B, Gilmore AW, Nelson SM, Berg JJ, Greene DJ, McCarthy JE, Tagliazucchi E, Laufs H, Schlaggar BL, Dosenbach NU and Petersen SE (2016) ‘On the Stability of BOLD fMRI Correlations’, Cereb Cortex. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin FH, Ahveninen J, Raij T, Witzel T, Chu YH, Jaaskelainen IP, Tsai KW, Kuo WJ and Belliveau JW (2014) ‘Increasing fMRI sampling rate improves Granger causality estimates’, PLoS One, 9(6), pp. e100319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu TT (2016) ‘Noise contributions to the fMRI signal: An overview’, Neuroimage, 143, pp. 141–151. [DOI] [PubMed] [Google Scholar]
- Liu X, de Zwart JA, Scholvinck ML, Chang C, Ye FQ, Leopold DA and Duyn JH (2018) ‘Subcortical evidence for a contribution of arousal to fMRI studies of brain activity’, Nat Commun, 9(1), pp. 395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liegeois R, Laumann TO, Snyder AZ, Zhou J and Yeo BTT (2017) ‘Interpreting temporal fluctuations in resting-state functional connectivity MRI’, Neuroimage, 163, pp. 437–455. [DOI] [PubMed] [Google Scholar]
- Majeed W, Magnuson M, Hasenkamp W, Schwarb H, Schumacher EH, Barsalou L and Keilholz SD (2011) ‘Spatiotemporal dynamics of low frequency BOLD fluctuations in rats and humans’, Neuroimage, 54(2), pp. 1140–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marriott FHC and Pope JA (1954) ‘Bias in the estimation of autocorrelations’, Biometrika, 41(3/4), pp. 390–402. [Google Scholar]
- Matsui T, Murakami T and Ohki K (2016) ‘Transient neuronal coactivations embedded in globally propagating waves underlie resting-state functional connectivity’, Proc Natl Acad Sci U S A, 113(23), pp. 6556–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra A, Kraft A, Wright P, Acland B, Snyder AZ, Rosenthal Z, Czerniewski L, Bauer A, Snyder L, Culver J, Lee JM and Raichle ME (2018) ‘Spontaneous Infra-slow Brain Activity Has Unique Spatiotemporal Dynamics and Laminar Structure’, Neuron, 98(2), pp. 297–305.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra A and Raichle ME (2016) ‘How networks communicate: propagation patterns in spontaneous brain activity’, Philos Trans R Soc Lond B Biol Sci, 371(1705). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra A and Raichle ME (2018) ‘Principles of cross-network communication in human resting state fMRI’, Scand J Psychol, 59(1), pp. 83–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra A, Snyder AZ, Blazey T and Raichle ME (2015a) ‘Lag threads organize the brain’s intrinsic activity’, Proc Natl Acad Sci U S A, 112(17), pp. E2235–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra A, Snyder AZ, Constantino JN and Raichle ME (2017) ‘The Lag Structure of Intrinsic Activity is Focally Altered in High Functioning Adults with Autism’, Cereb Cortex, 27(2), pp. 1083–1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra A, Snyder AZ, Hacker CD, Pahwa M, Tagliazucchi E, Laufs H, Leuthardt EC and Raichle ME (2016) ‘Human cortical-hippocampal dialogue in wake and slow-wave sleep’, Proc Natl Acad Sci U S A, 113(44), pp. E6868–E6876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra A, Snyder AZ, Hacker CD and Raichle ME (2014) ‘Lag structure in resting-state fMRI’, J Neurophysiol, 111(11), pp. 2374–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra A, Snyder AZ, Tagliazucchi E, Laufs H and Raichle ME (2015b) ‘Propagated infra-slow intrinsic brain activity reorganizes across wake and slow wave sleep’, Elife, 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moddemeijer R (1991) ‘On the determination of the position of extrema of sampled correlators’, IEEE TSignal Proces, 39(1), pp. 216–219. [Google Scholar]
- Muschelli J, Nebel MB, Caffo BS, Barber AD, Pekar JJ and Mostofsky SH (2014) ‘Reduction of motion-related artifacts in resting state fMRI using aCompCor’, Neuroimage, 96, pp. 22–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikolić D (2007) ‘Non-parametric detection of temporal order across pairwise measurements of time delays’, J Comput Neurosci, 22(1), pp. 5–19. [DOI] [PubMed] [Google Scholar]
- Palva JM and Palva S (2012) ‘Infra-slow fluctuations in electrophysiological recordings, blood-oxygenation-level-dependent signals, and psychophysical time series’, Neuroimage, 62(4), pp. 2201–11. [DOI] [PubMed] [Google Scholar]
- Pan WJ, Thompson GJ, Magnuson ME, Jaeger D and Keilholz S (2013) ‘Infraslow LFP correlates to resting-state fMRI BOLD signals’, Neuroimage, 74, pp. 288–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patriat R, Molloy EK and Birn RM (2015) ‘Using Edge Voxel Information to Improve Motion Regression for rs-fMRI Connectivity Studies’, Brain Connect, 5(9), pp. 582–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Barnes KA, Snyder AZ, Schlaggar BL and Petersen SE (2012) ‘Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion’, Neuroimage, 59(3), pp. 2142–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Cohen AL, Nelson SM, Wig GS, Barnes KA, Church JA, Vogel A Laumann TO, Miezin FM, Schlaggar BL and Petersen SE (2011) ‘Functional organization of the human brain’, Neuron, 72(4), pp. 665–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Mitra A, Laumann TO, Snyder AZ, Schlaggar BL and Petersen SE (2014) ‘Methods to detect, characterize, and remove motion artifact in resting state fMRI’, Neuroimage, 84, pp. 320–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Plitt M, Gotts SJ, Kundu P, Voon V, Bandettini PA and Martin A (2018) ‘Ridding fMRI data of motion-related influences: Removal of signals with distinct spatial and physical bases in multiecho data’, Proc Natl Acad Sci U S A, 115(9), pp. E2105–E2114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Plitt M, Laumann TO and Martin A (2017) ‘Sources and implications of whole-brain fMRI signals in humans’, Neuroimage, 146, pp. 609–625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Schlaggar BL and Petersen SE (2015) ‘Recent progress and outstanding issues in motion correction in resting state fMRI’, Neuroimage, 105, pp. 536–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raatikainen V, Huotari N, Korhonen V, Rasila A, Kananen J, Raitamaa L, Keinanen T, Kantola J, Tervonen O and Kiviniemi V (2017) ‘Combined spatiotemporal ICA (stICA) for continuous and dynamic lag structure analysis of MREG data’, Neuroimage, 148, pp. 352–363. [DOI] [PubMed] [Google Scholar]
- Satterthwaite TD, Ciric R, Roalf DR, Davatzikos C, Bassett DS and Wolf DH (2017) ‘Motion artifact in studies of functional connectivity: Characteristics and mitigation strategies’, Hum Brain Mapp. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Elliott MA, Gerraty RT, Ruparel K, Loughead J, Calkins ME, Eickhoff SB, Hakonarson H, Gur RC, Gur RE and Wolf DH (2013) ‘An improved framework for confound regression and filtering for control of motion artifact in the preprocessing of resting-state functional connectivity data’, Neuroimage, 64, pp. 240–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Wolf DH, Loughead J, Ruparel K, Elliott MA, Hakonarson H, Gur RC and Gur RE (2012) ‘Impact of in-scanner head motion on multiple measures of functional connectivity: relevance for studies of neurodevelopment in youth’, Neuroimage, 60(1), pp. 623–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scargle JD (1989) ‘Studies in astronomical time series analysis. III. Fourier transforms, autocorrelation functions, and cross-correlation functions of unevenly spaced data’, Astrophys J, 343, pp. 874–887. [Google Scholar]
- Schneider G, Havenith MN and Nikolić D (2006) ‘Spatiotemporal structure in large neuronal networks detected from cross-correlation’, Neural Comput, 18(10), pp. 2387–413. [DOI] [PubMed] [Google Scholar]
- Scholvinck ML, Maier A, Ye FQ, Duyn JH and Leopold DA (2010) ‘Neural basis of global resting-state fMRI activity’, Proc Natl Acad Sci U S A, 107(22), pp. 10238–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel JS, Mitra A, Laumann TO, Seitzman BA, Raichle M, Corbetta M and Snyder AZ (2017) ‘Data Quality Influences Observed Links Between Functional Connectivity and Behavior’, Cereb Cortex, 27(9), pp. 4492–4502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Salimi-Khorshidi G, Webster M, Beckmann CF, Nichols TE, Ramsey JD and Woolrich MW (2011) ‘Network modelling methods for FMRI’, Neuroimage, 54(2), pp. 875–91. [DOI] [PubMed] [Google Scholar]
- Snyder AZ and Raichle ME (2012) ‘A brief history of the resting state: the Washington University perspective’, Neuroimage, 62(2), pp. 902–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoyanov M, Gunzburger M and Burkardt J (2011) ‘Pink noise, 1/fa noise, and their effect on solutions of differential equations’, Int J Uncertain Quantification, 1(3), pp. 257–278. [Google Scholar]
- Sun FT, Miller LM and D’Esposito M (2005) ‘Measuring temporal dynamics of functional networks using phase spectrum of fMRI data’, Neuroimage, 28(1), pp. 227–37. [DOI] [PubMed] [Google Scholar]
- Talairach J and Tournoux P 1988. Co-planar stereotaxic atlas of the human brain. Thieme Medical Publishers, New York. [Google Scholar]
- Turchi J, Chang C, Ye FQ, Russ BE, Yu DK, Cortes CR, Monosov IE, Duyn JH and Leopold DA (2018) ‘The Basal Forebrain Regulates Global Resting-State fMRI Fluctuations’, Neuron, 97(4), pp. 940–952.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dijk KR, Sabuncu MR and Buckner RL (2012) ‘The influence of head motion on intrinsic functional connectivity MRI’, Neuroimage, 59(1), pp. 431–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker WF and Trahey GE (1995) ‘A fundamental limit on delay estimation using partially correlated speckle signals’, IEEE T Ultrason Ferr, 42(2), pp. 301–308. [Google Scholar]
- Wong CW, Olafsson V, Tal O and Liu TT (2013) ‘The amplitude of the resting-state fMRI global signal is related to EEG vigilance measures’, Neuroimage, 83, pp. 983–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan CG, Cheung B, Kelly C, Colcombe S, Craddock RC, Di Martino A, Li Q, Zuo XN, Castellanos FX and Milham MP (2013a) ‘A comprehensive assessment of regional variation in the impact of head micromovements on functional connectomics’, Neuroimage, 76, pp. 183–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan CG, Craddock RC, He Y and Milham MP (2013b) ‘Addressing head motion dependencies for small-world topologies in functional connectomics’, Front Hum Neurosci, 7, pp. 910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo BT, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, Roffman JL, Smoller JW, Zollei L, Polimeni JR, Fischl B, Liu H and Buckner RL (2011) ‘The organization of the human cerebral cortex estimated by intrinsic functional connectivity’, J Neurophysiol, 106(3), pp. 1125–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zarahn E, Aguirre GK and D’Esposito M (1997) ‘Empirical analyses of BOLD fMRI statistics. I. Spatially unsmoothed data collected under null-hypothesis conditions’, Neuroimage, 5(3), pp. 179–97. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.