Censoring Unbiased Regression Trees and Ensembles

Abstract

This paper proposes a novel paradigm for building regression trees and ensemble learning in survival analysis. Generalizations of the CART and Random Forests algorithms for general loss functions, and in the latter case more general bootstrap procedures, are both introduced. These results, in combination with an extension of the theory of censoring unbiased transformations applicable to loss functions, underpin the development of two new classes of algorithms for constructing survival trees and survival forests: Censoring Unbiased Regression Trees and Censoring Unbiased Regression Ensembles. For a certain “doubly robust” censoring unbiased transformation of squared error loss, we further show how these new algorithms can be implemented using existing software (e.g., CART, random forests). Comparisons of these methods to existing ensemble procedures for predicting survival probabilities are provided in both simulated settings and through applications to four datasets. It is shown that these new methods either improve upon, or remain competitive with, existing implementations of random survival forests, conditional inference forests, and recursively imputed survival trees.

1. Introduction

Recursive partitioning methods for regression problems provide a useful nonparametric alternative to parametric and semiparametric methods. Methods based on the Classification and Regression Trees (CART; Breiman et al., 1984) algorithm are the most popular recursive partitioning procedures in use today. One of the most attractive features of CART is its focus on building a simple, interpretable tree-structured prediction model. In the original formulation of CART for regression, the resulting hierarchically structured predictor is determined by maximizing within-node homogeneity through loss minimization. However, a common criticism of CART is that the final predictor can suffer from instability, a phenomenon that usually occurs in settings where a small change in the loss can induce a large change in the form of the predictor (Breiman, 1996).

Bagging is a general method for variance reduction that averages several prediction models derived from bootstrapping the original data. Bagging has been shown to work well with models with low bias and high variance (e.g., fully grown CART trees); see Breiman (1996). Breiman (2001) proposed the Random Forests (RF) algorithm as a way to further improve prediction accuracy, this being achieved by de-correlating the individual regression trees (i.e., built under squared error loss) using random feature selection at each split-point.

A survival tree (survival forest) is built when a suitably modified version of the CART (RF) algorithm is applied to data involving an outcome that can be right-censored. For building single trees, several variations of CART have been proposed and can be divided into two general categories: maximizing within-node homogeneity (e.g., Gordon and Olshen, 1985; Davis and Anderson, 1989; LeBlanc and Crowley, 1992; Molinaro et al., 2004; Steingrimsson et al., 2016) or maximizing between-node heterogeneity (e.g., Segal, 1988; Leblanc and Crowley, 1993). Ishwaran et al. (2008) proposed the Random Survival Forests (RSF) algorithm, modifying the RF algorithm for survival data through building the individual trees in the forest via maximizing the between-node log-rank statistic. Zhu and Kosorok (2012) proposed the recursively imputed survival trees (RIST) algorithm. Similarly to the RSF algorithm, RIST makes splitting decisions by maximizing a log-rank test statistic, but differs from RSF in several ways. In particular, in place of bagging, the RIST algorithm generates an ensemble of predictors by recursively imputing censored observations; second, it makes use of extremely randomized trees, replacing the search for optimal split points with a value that “is chosen fully at random” (i.e., splitting decisions are made on the basis of K randomly selected pairs of covariates and possible split points).

With the exception of Molinaro et al. (2004) and Steingrimsson et al. (2016), the afore-cited methods for survival trees and forests all use splitting rules specifically constructed to deal with the presence of censored outcome data. Such methods commonly share two features: (i) most use decision rules derived under a proportional hazards assumption; and, (ii) none reduce to a loss- based method that might ordinarily be used with “full data” (i.e., no censoring). For single trees, Molinaro et al. (2004) closed this gap between tree-based regression methods used for censored and uncensored data by using an inverse probability censoring weighted (IPCW) loss function that (i) reduces to the full data loss function that would be used by CART in the absence of right-censored outcome data and (ii) is an unbiased estimator of the corresponding risk. Based on similar principles, Hothorn et al. (2006a) proposed a RF-type algorithm. Steingrimsson et al. (2016) proposed doubly robust survival trees, generalizing the methods of Molinaro et al. (2004) by using augmentation to construct doubly robust loss functions that use more of the available information, thereby improving the efficiency and stability of the tree building process. However, they did not generalize these ideas to the problem of constructing an appropriate ensemble procedure.

The focus of this paper is on developing a new class of ensemble algorithms for building survival forests when outcomes can be censored (i.e., right censored). Section 2 first lays out the CART algorithm of Breiman et al. (1984) in the case where a general loss function is used for the purposes of making splitting and pruning decisions. We then propose a novel and general class of ensemble algorithms that extends the RF algorithm for use with an arbitrary loss function and permits the use of more general weighted bootstrap procedures, such as the exchangeably weighted bootstrap (Prmstgaard and Wellner, 1993). Both of these algorithms are initially developed in the full data setting. Section 3 then introduces the framework needed for extending these two classes of algorithms for censored outcomes, respectively leading to the development of the Censoring Unbiased Regression Trees (CURT) and Censoring Unbiased Regression Ensembles (CURE) algorithms. These developments rely directly on an extension of the theory of censoring unbiased transformations (CUTs; e.g., Fan and Gijbels, 1996) that can be applied to loss functions. CUTs have long been of importance to survival analysis; notable examples include Buckley and James (1979), Koul et al. (1981), Leurgans (1987), Fan and Gijbels (1994), and Rubin and van der Laan (2007). The use of a CUT for a given full data loss function ensures that both CURT and CURE directly generalize an algorithm that would ordinarily be used if censoring were absent. The IPCW and the “doubly robust” survival tree methods respectively considered in Molinaro et al. (2004) and Steingrimsson et al. (2016) both have this property, and each is a special case of the class of CURT algorithms introduced here. CURE subsequently extends these methods to building ensemble predictors. Section 4 provides a detailed development of CURT and CURE in the special case of squared error loss and shows, in particular, how response imputation can be used to implement each one using existing software for CART and RF (i.e., for uncensored outcomes). Simulation studies and applications to several datasets are respectively presented in Section 5 and 6. Section 7 contains a discussion and some general remarks on topics for future research. A Supplementary Web Appendix contains proofs, additional developments and further results.

2. Regression Trees and Ensembles for General Loss Functions

Regression procedures typically rely on the specification of a loss function (or related objective function) that quantifies performance. This includes, but is not limited to, algorithms like CART and RF, where the loss function plays a key role in all aspects of the model fitting process. In this section, we first review the basics of the CART algorithm, developing it for use with a general loss function in Section 2.1. Section 2.2 then introduces a new related class of ensemble learning algorithms that contains the algorithms of Breiman (1996) and Breiman (2001) for squared error loss as special cases. The algorithms in these two subsections are developed without reference to censoring or survival data.

As shown in Breiman et al. (1984), the use of a loss function in building a regression tree implies focusing on a prediction model that minimizes a corresponding measure of risk (i.e., expected loss). This correspondence between loss and risk will be especially important in the developments of Section 3, where it is shown how the algorithms of Sections 2.1 and 2.2 can be extended to censored outcomes through a generalization of the theory of CUTs.

Throughout, we will let (Z, W’)’ represent a vector of data on a given subject, where the outcome Z is scalar-valued with support on some subset of the real line R, $W\in \mathcal{S}\subset R^p$ is a bounded p-dimensional vector of covariates, and (Z, W’)’ has some non-degenerate joint probability distribution. Define $\mathcal{F}=\{{(Z_i,W_i^{\prime })}^{\prime },i=1\dots n\}$ to be the corresponding data for an i.i.d. sample of data from this joint distribution.

2.1. Regression Tree Algorithms for General Loss Functions

Let W = (W⁽¹⁾,..., W^(p))’, where each W^(j),j = 1,... ,p, is either continuous or ordinal; a modification of the methods to be described below is needed for any categorical covariate having at least 3 unordered levels. Define ψ: $\mathcal{S}\to R$ to be a real-valued function of W, where ψ ∈ Ψ. A loss function L(Z,ψ(W)) defines a nonnegative measure of the distance between Z and its prediction ψ(Ψ’). A popular choice for continuous Z is the squared error loss L₂(Z,ψ(W)) = (Z — ψ(W))²; the absolute deviation loss L₁_(Z ψ(W)) = |Z — ψ(W)| is another possibility. In the case where Z is binary or a count, L(Z,ψ(W)) might correspond to the negative loglikelihood under a generalized linear model. When Z is binary, squared error loss is also a possible choice (e.g., Brier, 1950).

Suppose that $\mathcal{F}$ is observed. In the case of a regression tree, the relevant prediction function ψ(·) can be viewed as a piecewise constant function on $\mathcal{S}$. Specifically, we may write $\psi (w)={\sum }_{k=1}^K{\beta }_{k}I\{w\in {\mathcal{N}}_k\}$ for any $w\in \mathcal{S}$, where ${\mathcal{N}}_1,\dots ,{\mathcal{N}}_K$ form some finite partition of $\mathcal{S}$. The CART algorithm of Breiman et al. (1984) is one of the most well-known statistical learning methods for estimating ψ(·) in this context. This predictive modeling method employs recursive binary partitioning, cost complexity pruning and cross validation in combination with squared error loss to estimate ψ(·), and in particular, adaptively determines $\{K,{\mathcal{N}}_1,\dots ,{\mathcal{N}}_K\}$. The corresponding partition structure may be graphically represented as a hierarchically-structured tree, with each branch being formed on the basis of a binary split for some W^(j).

In developing CART for regression, Breiman et al. (1984) focused on squared error loss as a homogeneity measure for a continuous response Z. However, as becomes quickly evident, the basic CART algorithm is agnostic to both the choice of loss function and continuity of Z. Algorithm 1 below provides pseudocode that summarizes the CART modeling process in the case of a general univariate response Z and a specified loss function L(Z,ψ(W)). To describe this algorithm, the notions of cost complexity and cross validation and their respective dependence on the loss function need to be formalized. Specifically, for a given tree ψ, define the cost complexity as ${\mathcal{K}}_{\alpha }(\psi )={\sum }_{i=1}^{n}L(Z_i,\psi (W_i))+\alpha |\psi |$, where α is a tuning parameter that penalizes the estimated loss by the size of the tree (i.e., by |ψ|, the number of terminal nodes). To describe cross-validation using a general loss function, assume that $\mathcal{F}$ is split into V mutually exclusive subsets D₁, ..., D_V. For simplicity, suppose all of these subsets also contain the same number of observations and let ρ be the proportion of $\mathcal{F}$ that falls into each subset D₁,..., D_V. For a given υ ∈ {1,..., V} let S_i,υ be the indicator if observation i is in the subset D_υ. Let ${\psi }_{t{r}_v}$ be any tree built using only the data in the v^th training set $\mathcal{F}\backslash D_v$ and define the cross-validated estimator of risk for ${\psi }_{t{r}_v}$ (e.g., Molinaro et al., 2004) as $\widehat{\theta }={(n\rho V)}^{-1}{\sum }_{v=1}^V{\sum }_{i=1}^{n}I(S_i{}_{,v}=1)L(Z_i,{\psi }_{t{r}_v}(W_i))$, where ${\psi }_{t{r}_v}(W_i),{(Z_i,W_i^{\prime })}^{\prime }\in D_v$ are the predictions obtained from the tree ${\psi }_{t{r}_v}$ for subjects in D_υ.

Algorithm 1.

CART Algorithm For General Loss Functions

1: Generate a maximal tree ${\widehat{\psi }}_{max}$

(a) Define the root node of the tree ${\widehat{\psi }}_{max}$ as consisting of all observations in $\mathcal{F}$.

(b) In the current node, identify all possible binary splits of the form W(j) ≤c versus W(j) > c for j = 1,...,p.

(c) Considering all such possible splits in (b), select the (covariate, split) combination that leads to the largest reduction in ∑i∈node L(Ziψ(Wi)) (i.e., the loss in the current, or parent, node) and divide it into two mutually exclusive subsets (i.e., daughter nodes).

(d) Check predetermined stopping criterion; if met, exit, otherwise apply Step 1.(b)-(c) to subset of observations falling into each daughter node that hasn’t met stopping criterion.

2: Using cost-complexity pruning, generate a sequence of candidate trees from the (unpruned) tree ${\widehat{\psi }}_{max}$. Specifically, setting $\psi ={\widehat{\psi }}_{max}$ in ${\mathcal{K}}_{\alpha }(\psi )$, let a vary from 0 to ∞ and define ${\widehat{\psi }}^{(\alpha )}$ as the corresponding subtree of ${\widehat{\psi }}_{max}$ that minimizes ${\mathcal{K}}_{\alpha }(\psi )$. This generates a finite sequence of optimal subtrees ${\widehat{\psi }}^{({\alpha }_1)},\dots ,{\widehat{\psi }}^{({\alpha }_l)}$, each of which represents a candidate for the best tree.

3: Use cross-validation to select the “best” tree from ${\widehat{\psi }}^{({\alpha }_1)},\dots ,{\widehat{\psi }}^{({\alpha }_l)}$.

(a) Re-run Step 1 using only the data in training set $\mathcal{F}\backslash D_v$, υ = 1,..., V.

(b) For each of the V maximal trees obtained in Step 3.(a), employ cost complexity pruning with α1, ..., αl from Step 2 to find the subtrees ${\widehat{\psi }}_{t{r}_v}^{({\alpha }_{\mathcal{l}})},\mathcal{l}=1\dots l$.

(c) For $\mathcal{l}=1\dots l$, calculate $\widehat{\theta }$ for the tree ${\widehat{\psi }}_{t{r}_v}^{({\alpha }_{\mathcal{l}})}$ and denote the value as $\widehat{\theta }(\mathcal{l})$.

(d) Select the final tree (i.e., best candidate tree) from ${\widehat{\psi }}_{max}$ as the subtree ${\widehat{\psi }}^{({\alpha }_{\widehat{\mathcal{l}}})}$, where $\widehat{\mathcal{l}}$ is the value of $\mathcal{l}$ that minimizes $\widehat{\theta }(\mathcal{l}),\mathcal{l}\in \{1,\dots ,l\}$.

Algorithm 1 with L(Z,ψ(W)) = L₂(Z,ψ(W)), hereafter referred to as CART-L₂, corresponds to that developed in detail in Breiman et al. (1984).

2.2. Regression Ensemble Algorithms for General Loss Functions

Prediction accuracy is usually improved by averaging multiple bootstrapped trees. Breiman (1996) proposed bagging, which averages fully grown CART–L₂ trees (i.e., see Step 1 of Algorithm 1) derived from many independent nonparametric bootstrap samples. These boostrapped trees, though conditionally independent of each other, are marginally correlated. Breiman (2001) proposed to reduce this correlation by additionally making use of random feature selection; that is, the original RF algorithm using squared error loss modifies the tree growing procedure so that only mtry ≤ p randomly selected covariates are considered for splitting at any given stage. The use of bootstrapping and/or random feature selection does not modify the loss-based decision making process that lies at the core of the RF algorithm. Therefore, it is possible to extend the RF algorithm to the case of more general bootstrap schemes, such as the exchangeably weighted bootstrap; see Prmstgaard and Wellner (1993). An extensive literature search revealed no examples of RF algorithms that use bootstrap procedures other than the nonparametric bootstrap.

To develop this extension, consider a given full data loss L(Z,ψ(W)) for use with data $\mathcal{F}$ and define ω₁,... ,ω_n to be a set of exchangeable, non-negative random variables such that E[ω_i] = 1 and $\mathrm{Var}({\omega }_i)={\sigma }^2<\infty$ for i = 1,…,n, ${\sum }_{i=1}^n{\omega }_i=n$, and ω₁,... ,ω_η are completely independent of $\mathcal{F}$. Define the weighted loss function

$$L_{\omega }(\mathcal{F},\psi )={\displaystyle \sum _{i=1}^n}{\omega }_{i}L(Z_i,\psi (W_i)).$$ (1)

The loss (1) evidently reduces to the empirical loss ${\sum }_{i=1}^{n}L(Z_i,\psi (W_i))$ if P(ω₁ = · · · = ω_n = 1) = 1; more generally, $E[L_{\omega }(\mathcal{F},\psi )|\mathcal{F}]=L_{\omega }(\mathcal{F},\psi )$, implying that the weighted and empirical loss functions have the same marginal expectation. Replacing ${\sum }_{i\in \mathrm{node}}L(Z_i,\psi (W_i))$ in Step 1.(c) of Algorithm 1 with ${\sum }_{i\in \mathrm{node}}{\omega }_{i}L(Z_i,\psi (W_i))$ (i.e., its counterpart under (1)) leads to a general class of case-weighted CART algorithms that can be used to build ensemble predictors. Algorithm 2 below summarizes this procedure for a general set of bootstrap weights. The base learners used in Algorithm 2 are modified versions of fully grown CART trees that incorporate random feature selection.

The use of nonparametric bootstrap sampling (i.e., resampling observations with replacement) is equivalent to the multinomial sampling scheme (ω₁,..., ω_η) ~ Multinomial(n, (n⁻¹,..., n⁻¹)), with positive weights being placed on approximately 63% of the observations in any given bootstrap sample. In this case, Algorithm 2 with L(Z_i, ψ(W_i)) = L₂(Z_i,ψ(W_i)), i = 1,..., n is just the RF algorithm of Breiman (2001) (hereafter, RF-L₂); the bagging procedure of Breiman (1996) is obtained when mtry = p. The extension of these algorithms to the exchangeable bootstrap avoids generating additional ties in the data when P(∪_i{ω_i = 0}) = 0; each observation then appears in every bootstrap sample (i.e., for every set of bootstrap weights) with a strictly positive weight.

Algorithm 2.

Exchangeably Weighted Regression Ensembles

1: Generate M independent sets of exchangeable bootstrap weights ω1,... ,ωn.

2: For each set of bootstrap weights, build a fully grown CART tree using Step 1 of Algorithm 1 with the loss function ${\sum }_{i\in \mathrm{node}}{\omega }_{i}L(Z_i,\psi (W_i))$ where, at each stage of splitting, mtry covariates are randomly selected from the p available covariates for candidate splits.

3: For each tree in the forest, calculate an estimator at each terminal node and average over the results obtained for the M sets of bootstrap weights to get the final ensemble predictor.

3. Censoring Unbiased Regression Trees and Ensembles

When $\mathcal{F}$ is observed, the use of a given loss function in Algorithms 1 or 2 results in a prediction model that intends to minimize the corresponding risk (i.e., expected loss). However, when outcomes can be censored, $\mathcal{F}$ is not fully observed and the desired loss function must be modified in order to preserve one’s focus on the same measure of risk.

As noted in the Introduction, several contributions to the problem of building regression trees for right-censored outcomes that focus on maximizing within-node homogeneity have been made over the past 30 years. Each one of these contributions can be viewed as a modified implementation of Algorithm 1, differing mainly in the type of loss function. In almost all cases, the loss function used has been adapted from methods specifically developed for right-censored outcomes. Related generalizations of RF have also been proposed for censored outcomes. These too can be viewed as a modified version of Algorithm 2, where unpruned versions of the censoring-modified CART trees are combined with nonparametric bootstrapping to construct ensemble predictors.

The goal of this section is to develop a framework that allows us to directly generalize Algorithms 1 and 2 for censored outcomes. To accomplish these extensions, we first extend the existing theory of censoring unbiased transformations for right-censored outcomes in a substantial way; we then show how this theory can be applied to construct loss functions for censored data that have several desirable properties. These developments allow us to directly generalize Algorithms 1 and 2 to the case of censored data, resulting in two new classes of statistical learning methods, respectively referred to as the CURT and CURE algorithms.

3.1. Full and Observed Data Structures

Our interest lies in modeling time-to-event (i.e., survival time) data. Let T > 0 denote the survival time of interest. In the notation of Section 2, let Z = h(T) where T is continuous and h(·) is a specified continuous, monotone increasing function (e.g., h(u) = u or h(u) = logu) that maps R⁺ to R* ⊆ R. Suppose (T, W’)’ have a joint distribution, where S₀(t\w) = P(T > t\W = w) denotes the conditional survivor function for T given W = w and ${\vartheta }_{S_0}=\inf \{t:S_0(t|w)=0\}$ is assumed to be independent of $w\in \mathcal{S}$. Then $\mathcal{F}$ represents an i.i.d. sample of survival data in which the outcome of interest is the h—transformed survival time and all survival times are completely observed.

In follow-up studies, T may not be fully observed, and most commonly, may be censored as a result of loss to follow-up. Let the observed data on a given subject be denoted by $O=(\tilde{Z},\mathrm{\Delta },W\prime )\prime$, where $\tilde{Z}=h(\tilde{T})$, $\tilde{T}=\min (T,C)$ for a continuous censoring time C,and Δ = I(T≤ C) indicates whether T or C is observed. It is assumed that C is conditionally independent of T given W. Let G₀(t\w) = P(C > t\W = w) be the conditional survivor function for C given W = w, where ${\vartheta }_{G_0}=\inf \{t:G_0(t|w)=0\}$ is assumed to be independent of $w\in \mathcal{S}$. Finally, let $\mathcal{O}=\{{({\tilde{Z}}_i,{\mathrm{\Delta }}_i,W_i^{\prime })}^{\prime },i=1\dots n\}$ denote the censored data observed on an i.i.d. sample. In this case, $\mathcal{F}$ represents the full data that one would have observed had no censoring occurred.

3.2. Censoring Unbiased Transformations: Review and Generalization

Let Y be a scalar function of (Z, W’)’ (i.e., the full data) and let Y^*(O) be a function of ${(\tilde{Z},\mathrm{\Delta },W^{\prime })}^{\prime }$ (i.e., the observed data). Then, we define Y*(O) to be a censoring unbiased transformation (CUT) for Y if E[Y*(O)|W = w] = E[Y|W = w] for every $w\in \mathcal{S}$. The transformation

$$Y*(O)=\mathrm{\Delta }T+(1-\mathrm{\Delta })E[T|T>t,W=w]$$ (2)

is one of the earliest examples of a CUT (Buckley and James, 1979). Several other examples of CUTs in the case where Y = h(T) = Z are described in Fan and Gijbels (1996, Sec. 5.2.2). Motivated by the need to correctly specify the conditional expectation function in (2), Rubin and van der Laan (2007) later proposed a “doubly robust” version of the Buckley-James transformation (2). Below, we develop a substantial generalization of the doubly robust CUT introduced Rubin and van der Laan (2007) and establish a new result on the variance of this transformation function.

Let $\varphi (r,w),(r,w)\in R*\times \mathcal{S}$ be any known scalar function that is continuous for r ∈ R* except possibly at a finite number of points. Assume |ϕ(r,w)| <∞ to whenever max{|r|, ||w||} < ∞, and suppose that E[ϕ(Ζ,W )| W = w] exists for each $w\in \mathcal{S}$. In addition, let G(t |w) and S (t |w) be two functions on R⁺ × $\mathcal{S}$. For every $w\in \mathcal{S}$, we assume throughout this section that G(0|w) = S(0|w) = 1 and that G(u|w) ≥ 0 and S(u|w) ≥ 0 are continuous, non-increasing functions for u ≥ 0 (e.g., proper survivor functions). Define ${\mathrm{\Lambda }}_G(t|w)=-{\int }_0^t{[G(u|w)]}^{-1}dG(u|w)$; note that Λ_G(t\w) is just the cumulative hazard function corresponding to G(·|·) when G(·|·) is a proper survivor function. Finally, define $m_{\varphi }(t,w;S)={[S(t|w)]}^{-1}{\int }_t^{\infty }\varphi (h(u),w)dF(u|w)$ where F(u|w) = 1 — S(u|w) for any u ≥ 0; note that mϕ(t,w; S) is continuous as a function of t. When S(·|·) is a proper survivor function and t is such that mp(t, w; S) exists, mϕ(t, w; S) reduces to E_S[ϕ(Ζ, W)|T > t, W = w], calculated assuming S(·|·) is the conditional survivor function for T.

With the above in place, consider the transformation

$$Y_d^{*}(O;G,S)=\frac{\mathrm{\Delta }\varphi (\tilde{Z},W)}{G(\tilde{T}|W)}+\frac{1-\mathrm{\Delta }}{G(\tilde{T}|W)}{m}_{\varphi }(\tilde{T},W;S)-{\displaystyle {\int }_0^{\tilde{T}}\frac{m_{\varphi }(u,W;S)}{G(u|W)}}d{\mathrm{\Lambda }}_G(u|W).$$ (3)

Suppose first that G(t|w) = 1 for all (t,w) ∈ R⁺ × $\mathcal{S}$. Then, (3) reduces to

$$Y_b^{*}(O;S)=\mathrm{\Delta }\varphi (\tilde{Z},W)+(1-\mathrm{\Delta })m_{\varphi }(\tilde{T},W;S);$$ (4)

setting ϕ(h(u),w) = u in (4) now gives (2). Hence, (3) with G(t|w) = 1 for all (t,w) ∈ R⁺ × $\mathcal{S}$ generates a class of Buckley-James-type transformations that generalizes (2), and is necessarily a CUT when ϕ(h(u), w) = u and S(u|w) = S₀(u|w) for (u,w) ∈ R⁺ × $\mathcal{S}$. Now, suppose instead that no restrictions on G(·|·) or S(·|·) beyond those noted earlier are imposed. Then, setting ϕ(h(u), w) = u (i.e., $\varphi (\tilde{Z},W)=\tilde{T}$) in (3) once again, we obtain the doubly robust CUT first studied in Rubin and van der Laan (2007, Eqn. 7). “Double robustness” in this specific context refers to the fact that (3) is a CUT for T if either S(t|w) = S₀(t|w) for all (t,w) ∈ R⁺ × $\mathcal{S}$ or G(t|w) = G₀(t|w) for all (t,w) ∈ R⁺ × $\mathcal{S}$, but not necessarily both.

The transformation (3) generalizes that in Rubin and van der Laan (2007, Eqn. 7) to a much wider class of functions. Two examples of particular relevance to the developments of this paper include ϕ(h(u),w) = h(u) and ϕ(h(u),w) = L(h(u), ψ(w)), where L(h(u),ψ(w)) is a specified loss function that measures the distance between h(u) and some corresponding prediction ψ(w) (e.g., L(h(u),ψ(w)) = (h(u) — ψ(w))²). Under certain conditions, Theorem 3.1 below shows that the transformation (3) yields a CUT for Y = ϕ(Ζ, W) if either S(t|w) = S₀(t|w) or G(t|w) = G_o(t|w) for all (t,w) ∈ R⁺ × $\mathcal{S}$. Moreover, if both of these functions are correctly specified, then it shows that $Y_d^{*}(O;G_0,S_0)$ minimizes the variance among all transformations of the form $Y_d^{*}(O;G_0,S)$.

Theorem 3.1. Let φ(Λ,(·), ·), S(·|·) and G(·|·) be functions on (t,w) ∈ R⁺ × $\mathcal{S}$ satisfying the regularity conditions given in Appendix S.5. Then, the transformations $Y_d^{*}(O;G,S_0)$, $Y_d^{*}(O;G_0,S)$ and $Y_d^{*}(O;G_0,S_0)$ are each CUTs for Y; furthermore, $\mathit{Var}(Y_d^{*}(O;G_0,S)|W)\ge \mathit{Var}(Y_d^{*}(O;G_0,S_0)\left|W\right)$.

Theorem 3.1 is proved in Section S.5 of the Supplementary Web Appendix. This result shows $\mathit{Var}(Y_d^{*}(O;G_0,S)|W)\ge \mathit{Var}(Y_d^{*}(O;G_0,S_0)\left|W\right)$ for any suitable proper survivor function. One may also ask whether $\mathit{Var}(Y_d^{*}(O;G,S_0)|W)\ge \mathit{Var}(Y_d^{*}(O;G_0,S_0)\left|W\right)$ holds for all suitable choices of G(·|·). However, a general result in this direction is not available even for the interesting case where G(·|·) = 1 (i.e., for (4)). The challenge in establishling such a domination result reflects more general open questions surrounding the development of efficiency properties for doubly robust estimators under misspecification of the missing data mechanism; see Rotnitzky and Vansteelandt (2014, Sec. 9.6) for further discussion. However, for the specific case of G(·|·) = 1, a different type of optimality result can be established. In particular, provided mφ(t, w; S) exists with S(t|w) = S₀(t|w), (t,w) ∈ R⁺ × $\mathcal{S}$, it can be shown that $Y_b^{*}(O;S_0)$ is the best predictor of Y in the sense that it minimizes E[(Y*(O) — Y)²|W = w] among all possible CUTs Y*(O) (e.g., Fan and Gijbels, 1996).

The transformation (3) has other notable properties. First, it reduces to $\mathrm{\Delta }\varphi (\tilde{Z},W)/G\left(\tilde{T}\right|W)$ if mφ(t,w; S) = 0 for all (t,w) ∈ R⁺ × $\mathcal{S}$; this IPCW estimator is a CUT when G(t|w) = G₀(t|w) for all (t, w) £ R+ x $\mathcal{S}$. Second, it reduces to Y = φ(Ζ, W) regardless of £(·|·) when Δ = 1 and G₀(t|W) = 1 for $t\le \tilde{T}$ (i.e., with probability one); that is, when censoring cannot occur on $[0,\tilde{T}]$.

3.3. Using CUTs to Derive Unbiased Estimates of Risk with Censored Data

Let L(Z,ψ(W)) denote a given loss function for the full data (Z,W); the corresponding risk is then $\mathcal{R}(\psi )=E\left[L\right(Z,\psi \left(W\right)\left)\right]$. A ψ ∈ Ψ that minimizes $\mathcal{R}(\psi )$, say ψ₀, defines a target parameter of interest that is ideally uniquely specified. For example, the risk under the loss function L₂(Z,ψ(W)) is $\mathcal{R}(\psi )=E\left[\right(Z-\psi \left(W\right){)}^2]$ and is minimized at the target parameter ψ₀(W) = E[Z|W]. Thus, in the context of Section 3.1, selecting h(s) = log s yields Z = logT and results in a (full data) L₂ loss function whose corresponding risk is minimized at ψ₀(W) = E[log T|W]. Alternatively, for a given t > 0, selecting h(s) = I(s > t) yields Z = I(T > t). The resulting full data L₂, or Brier, loss function leads to a risk function that is instead minimized at ψ_0t(W) = S₀(t|W).

In the case where Z can be censored, it is not generally true that $E\left[L\right(\tilde{Z},\psi \left(W\right)\left)\right]=\mathcal{R}(\psi )$ and hence one cannot simply use $L(\tilde{Z},\psi (W\left)\right)$ in place of L(Z,ψ(W)). However, as shown in Molinaro et al. (2004), it is still possible to construct an observed data loss function that has the same risk $\mathcal{R}(\psi )$. Specifically, assuming $\mathcal{R}(\psi )$ exists and that P(G(T|W) > ϵ) = 1 for some ϵ > 0, the inverse probability of censoring weighted (IPCW) loss function

$$L_{ipcw}(O,\psi ;G)=\frac{\mathrm{\Delta }L(\tilde{Z},\psi (W))}{G(\tilde{T}|W)}=\frac{\mathrm{\Delta }L(Z,\psi (W))}{G(T|W)}$$ (5)

satisfies E[L_ipcw(O,ψ;G₀)] = E[L(Z,ψ(W))] = $\mathcal{R}(\psi )$. That is, L_ipcw(O,ψ; G₀) is an unbiased estimator of the desired risk $\mathcal{R}(\psi )$ when G(t|w) = G₀(t|w) for all (t,w) ∈ R⁺ × $\mathcal{S}$. In fact, given any ψ(·), E[L_ipcw(Ο,ψ; G₀)|W] = E[L(Z,ψ(W))|W] under the same regularity conditions. Consequently, L_ipcw (Ο,ψ; G₀) is also a CUT for θ(Z,W) = L(Z,”(W)); see Section 3.2. By applying the theory for augmented estimators in missing data problems as developed in Tsiatis (2007, Ch. 9 & 10), Steingrimsson et al. (2016) derived a doubly robust estimator for $\mathcal{R}(\psi )$. Specifically, the observed data estimator used in Steingrimsson et al. (2016) is given by

$$L_d(O,\psi ;G,S)=\frac{\mathrm{\Delta }L(\tilde{Z},\psi (W))}{G(\tilde{T}|W)}=\frac{1-\mathrm{\Delta }}{G(\tilde{T}|W)}{m}_L(\tilde{T},W;S)-{\displaystyle {\int }_0^{\tilde{T}}}\frac{m_L(u,W;S)}{G(u|W)}d{\mathrm{\Lambda }}_G(u|W),$$ (6)

where m_L (u, w; S) = E_S [L(h(u), ψ(w))|T > u,W = w] for any u > 0 and $w\in \mathcal{S}$ and the expectation is calculated assuming T|W = w has survivor function S(-|w). Under certain regularity conditions (e.g., boundedness), the double robustness property of (6) as an augmented estimator implies that the marginal expectation of (6) is $\mathcal{R}(\psi )$ if either G(·|·) = Go(·|·) or S(·|·) = So(·|·). For a fixed ψ(·), (6) can evidently be obtained directly from (3) upon setting φ(Ζ, W) = L(Z,ψ(W)), where m_L(⋅,w;S) depends on ψ(·). Under regularity conditions that permit the application of Theorem 3.1, the observed data estimator (6) satisfies E[L_d(O, ψ; G₀,S₀)|W] = E[L_d(O,ψ; G₀,S)|W] = E[L_d(Oψ; G,S₀)|W] = E[L(Z, ■0(W))|W]. Hence, (6) is a doubly robust CUT for L(Zψ(W)) that estimates $\mathcal{R}(\psi )$. Following Section 3.2, the observed data loss function

$$L_b(O,\psi ;S)=\mathrm{\Delta }L(\tilde{Z},\psi (W))+(1-\mathrm{\Delta })m_L(\tilde{T},W;S)$$ (7)

is also obtained as a special case of (6) upon setting G(t|w) = 1 for all (t, w) ∈ R⁺ × $\mathcal{S}$. This observed data estimator, hereafter referred to as the Buckley-James loss function, is a CUT of the form (4) for L(Z,ψ(W)) when S(t|w) = S₀(t|w) for all (t,w) ∈ R⁺ × $\mathcal{S}$.

By Theorem 3.1, for any fixed ψ(·) and under sufficient regularity conditions, L_d(O, ψ; G₀, S₀) has a smaller conditional variance for estimating $\mathcal{R}\left(\psi \right)$ in comparison to L_ipcw(O,ψ; G₀). Estimators derived under L_d(O, ψ; G₀,S₀) are expected to be more efficient than those derived under L_ipcw(O, ψ; G₀). However, it does not seem possible to determine in general whether the conditional variance of L_b(O, ψ; S₀) exceeds that of L_d(O, ψ; G₀, S₀); hence, estimators derived under these two loss functions can be expected to exhibit different efficiencies in different settings.

3.4. The CURT and CURE Algorithms

The developments of Sections 3.2 and 3.3, combined with Algorithms 1 or 2, can be used to devise new statistical learning methods for censored outcomes. An extension of Algorithm 1 to the case where Z is censored is immediately obtained by replacing any desired full data loss L(Z,ψ(W)) with an observed data estimator for $\mathcal{R}\left(\psi \right)$, where ψ(w) = ${\sum }_{k=1}^K{\beta }_{k}I\{w\in {\mathcal{N}}_k\}$ is a piecewise constant function on $\mathcal{S}$. For example, one can replace L(Z,ψ(W)) with either (5) or (6); the Buckley-James CUT L_b(O,ψ;S) could instead be used in place of L_d(O,ψ;G,S). Each generates a new example of a Censoring Unbiased Regression Tree (CURT) algorithm, the desired (but unobservable) full data loss function used in Algorithm 1 being replaced with a corresponding CUT of the form (6) (i.e., see Section 3.3). For a specified general full data loss function, any CURT algorithm can be implemented using the customization capabilities provided through rpart (Therneau et al., 2014).

Algorithm 2 extends Algorithm 1 to the construction of ensemble predictors. One can therefore extend the CURT algorithm by replacing the full data loss function in Algorithm 2 with an estimated CUT of the form (6), each time generating a new example of a Censoring Unbiased Regression Ensemble (CURE) algorithm. However, unlike CURT, the implementation of CURE for a general observed data loss function that employs random feature selection is not as straightforward because the prevailing RF software packages lack the customization capabilities of rpart. In the important special case L(Z,ψ(W)) = L₂(Z,ψ(W)), existing software for CART-L₂ and RF-L₂ can be used in combination with response imputation to implement both CURT and CURE using (6) for making decisions; detailed developments are provided in the next section.

Hereafter, CURT and CURE will respectively be used to describe any implementation of Algorithms 1 or 2 that employ a CUT of the form (6) for a given full data loss L(Z,ψ(W)). The restriction to CUTs of the form (6) ensures that the resulting CURT and CURE algorithms reduce to their corresponding full data versions when censoring is absent. As written, (6) depends on the functions G(·|·) and S(·|·). In practice, both must typically be estimated from the observed data $\mathcal{O}$, and the indicated algorithms will employ estimated CUTs. We discuss these algorithms further in Section 4. The double robustness property suggests that an estimated CUT for the loss function should behave as a CUT in large samples if at least one of the plug-in estimators $\widehat{G}(·|·)$ and/or $\widehat{S}(·|·)$ are respectively consistent for G₀(·|·) and S₀(·|·). Theorem 3.1 further implies that a doubly robust CUT for the full data loss calculated for one observation will reduce variance compared to the corresponding IPCW CUT for the same full data loss. However, the implication for variance reduction using estimated CUTs is less clear cut. Theorem 3.1 is developed for a transformation calculated at the level of an individual observation (e.g., as opposed to an average) and it is challenging to characterize the effects on efficiency when substituting in an arbitrary consistent estimator $\widehat{G}(·|·)$ and/or $\widehat{S}(·|·)$ into either (3) or (6).

4. Implementing CURT and CURE With Squared Error Loss

Specific examples of both CURT and CURE that employ a CUT of the form (6) for the full data loss function L(Z,ψ(W)) = L₂(Z,ψ(W)) already exist in the literature. For example, as suggested in Molinaro et al. (2004), one can replace the loss function L₂(Z,ψ(W)) with L_2,ipcw(Ο,ψ;Ĝ) throughout Algorithm 1; here, L_2,ipcw(Ο,ψ;Ĝ) is (5), calculated by replacing L(Z,ψ(W)) with L₂(Z,ψ(W)) for Z = logT and substituting Ĝ(·|·), an estimator for G₀(·|·), in for G(·|·). This algorithm is easily implemented via the rpart package using the case weights ${\mathrm{\Delta }}_i/\widehat{G}\left({\tilde{T}}_i\right|W_i)$, i = 1,... ,n. The doubly robust survival trees algorithm of Steingrimsson et al. (2016) is another example of CURT. In this algorithm, one can replace the general full data loss function L(Z, ψ(W)) throughout Algorithm 1 with L_d(O, ψ; Ĝ, Ŝ) in (6); here, estimators Ĝ(·|·) and Ŝ(·|·) for both G₀(·|·) and S₀(·|·) respectively replace G(·|·) and S(·|·) in (6). Implementation for a specified full data loss L(Z, ψ(W)) is again possible using rpart, though requires that one takes advantage of its ability to incorporate customized decision and evaluation functions (Therneau et al., 2014). Similarly to Molinaro et al. (2004), Steingrimsson et al. (2016) implemented this algorithm for L(Z,(ψ(W)) = L₂(Z,ψ(W)) for Z = log T. Consistent with expectations, their extensive simulation study demonstrates important performance gains compared to the IPCW loss L_2,ipcw(O,ψ; Ĝ), despite the fact that (possibly inconsistent) estimates for both G₀(·|·) and S₀(·|·) are used. We refer the reader to Steingrimsson et al. (2016) for additional details on this particular implementation of CURT, including methods used to construct the estimators Ĝ(·|·) and S(·|·). Although not specifically considered in the literature, the Buckley-James CUT L_b(O,ψ;Ŝ) could be similarly implemented.

For the case of $L_{2,ipcw}(O,\psi ;\widehat{G})$, Hothorn et al. (2006a, Sec. 3.1, p. 359) proposed an example of CURE that used a multinomial bootstrap with sampling weights $w_i/{\sum }_{j=1}^n{w}_j$, i = 1,...,n where $w_i={\mathrm{\Delta }}_i{[\widehat{G}({\tilde{T}}_i|W_i)]}^{-1}$. This ensemble algorithm resamples only uncensored observations and uses fully grown CART trees combined with random feature selection to estimate E[Z|W]. Implementation of this algorithm is possible using rfsrc (Ishwaran and Kogalur, 2016) because this R function accepts general multinomial sampling weights.

Below, we introduce an easy way to implement both CURT and CURE when using a CUT of the form (6) for the full data loss function L(Z, ψ(W)) = L₂(Z, ψ(W)). In particular, Section 4.1 shows how response imputation can be used to implement this special case of CURT, hereafter referred to as CURT-L₂, given some implementation of CART-L₂ (e.g., rpart). These results allow, for example, the methods of Steingrimsson et al. (2016) to instead be implemented using response imputation, resulting in an algorithm that is both easy to implement and fast. Importantly, these developments also provide the necessary framework for implementing the corresponding CURE-L2 algorithm using any implementation of RF-L₂,such as the R functions randomForest(Liaw and Wiener, 2002) and rfsrc (Ishwaran and Kogalur, 2016). These extensions are summarized in Section 4.2, where it is further shown how to generalize CURE-L₂ to more general weighted bootstrap schemes provided that one has available an implementation of RF that incorporates case weights directly into the loss function calculation. For reasons that will be explained more fully in the next section, versions of these algorithms that use the loss function (5) are not covered by these results. However, in general, such algorithms are easily implemented using other approaches.

CART–L₂ and RF–L₂ respectively denote specific implementations of Algorithms 1 or 2 because the loss function and bootstrapping scheme are both fully specified. The CURT–L₂ and CURE–L₂ algorithms considered here specify the form of the CUT to be (6). Specific implementations of CURT–L₂ and CURE–L₂ are obtained by specifying/estimating both G(·|·) and S(·|·) and, in the case of CURE–L₂, the particular bootstrap scheme. The results to be developed in the next two sections assume both G(·|·) and S(·|·) are given; thus, when estimated from O, it is explicitly assumed that such calculations are done outside of the CURT and CURE algorithms (i.e., these estimates are not updated dynamically).

4.1. Implementing a CURT-L₂ Algorithm using Response Imputation

Define L₂,_d(O, ψ;G,S) as (6) calculated using the full data loss L(Z,ψ(W)) = L₂(Z,ψ(W)). In this section, we establish how an existing implementation of CART-L₂ can be used to implement a CURT-L₂ algorithm, that is, Algorithm 1 implemented using L₂,_d(O, ψ; G, S) in place of L₂(Z,ψ(W)). As noted previously, the algorithm developed in Steingrimsson et al. (2016) for squared error loss is an important example; a second important example is obtained using the Buckley-James loss $L_b(O,\psi ;\widehat{S})$, this immediately being seen upon recalling that L_b(O,ψ; S) = L_d(Oψ;1,S) for any choice of S(·|·) satisfying the conditions of Section 3.2. Below, we demonstrate the desired equivalence for L_2,d(O, ψ; G, S) for general choices of G(·|·) and S(·|·). For reasons to be explained later, the results to be developed below do not extend to L₂,_ipcw(O,ψ; G), despite the fact that it can also be recovered as a special case of L₂,_d(O_i, ψ; G, S).

The CURT-L₂, _d algorithm substitutes L₂,_d (O_i, ψ; G, S) in for L₂(Z_i, ψ(W_i)), i = 1,…, n throughout Algorithm 1. As shown below, this same algorithm can also be implemented using the original CART-L₂ algorithm by employing a related CUT of the form (3) for the response variable. We begin by establishing an equivalent representation for L₂,_d(O_i, ψ; G,S). Let

$$A_{ki}(G)=\frac{{\mathrm{\Delta }}_i{\tilde{Z}}_i^k}{G({\tilde{T}}_i|W_i)},B_{ki}(G,S)=\frac{(1-{\mathrm{\Delta }}_i)m_k({\tilde{T}}_i,W_i;S)}{G({\tilde{T}}_i|W_i)},C_{ki}(G,S)={\displaystyle {\int }_0^{{\tilde{T}}_i}}\frac{m_k(u,W_i;S)d{\mathrm{\Lambda }}_G(u|W_i)}{G(u|W_i)},$$

for k = 0,1,2, where $m_k(t,w;S)={[S(t|w)]}^{-1}{\int }_t^{\infty }{[h(u)]}^{k}dF(u|w)$, k = 1, 2 and we have defined m₀(t,w; S) = 1 for each (t, w) ϵ R⁺ × $\mathcal{S}$. Straightforward algebra gives

$$L_{2,d}(O_i,\psi ;G,S)=Q^{(1)}(O_i;G,S)-2\widehat{Z}(O_i;G,S)\psi (W_i)+K(O_i;G){\psi }^2(W_i),$$ (8)

where K(O_i;G) = A_0i(G) + B_0i(G) − C_0i(G), $\widehat{Z}(O_i;G,S)$ = A_1i(G) + B_1i(G,S) − C_1i(G,S), and Q⁽¹⁾(O_i;G,S)=A_2i(G)+B_2i(G,S)-C_2i(G,S)for every i.That K(O_i;G)does not depend on S(·|·)follows from (i) the definition of A_0i(G); and, (ii) the assumption m₀(t,w; S) — 1, which implies B_0i(G,S) and C_0i(G,S) are each independent of S(·|·) for every i. In fact, we have for every i under weak conditions on G(·|·) that K(O_i; G) = 1; this follows immediately from TheoremS.6.1, presented and proved in the Supplementary Web Appendix (Section S.6).

The observed data quantity $\widehat{Z}(O_i;G,S)$ is an example of (3), hence a CUT. Define the modified loss function $L_{2,d}^{*}(O_i,\psi ;G,S)=(\widehat{Z}(O_i;G,S)-\psi (W_i){)}^2$; then, expanding the square in $L_{2,d}^{*}(O_i,\psi ;G,S)$ and simplifying the resulting expression gives

$$L_{2,d}^{*}(O_i,\psi ;G,S)=Q^{(2)}(O_i,G,S)-2\widehat{Z}(O_i;G,S)\psi (W_i)+{\psi }^2(W_i),$$ (9)

where $Q^{(2)}(O_i,G,S)={[\widehat{Z}(O_i;G,S)]}^2$ for each i. For any G(·|·) satisfying the regularity conditions of Theorem S.6.1, we have K(O_i; G) = 1 for every i in (8); as a result, (8) and (9) are identical up to a term that does not involve ψ(·).

The arguments above show that each of L₂,_d(O_i-ψ; G, S) and $L_{2,d}^{*}(O_i,\psi ;G,S)$ takes the form L₂(O_i,ψ; G,S,Q) = ψ(W_i)² + H(O_i; G,S)ψ(W_i) + Q(O_i; G,S) and the losses differ only in the specification of Q(O_i; G,S). Theorem 4.1, given below and proved in the Supplementary Web Appendix (Section S.7), demonstrates that the decisions made by the CART algorithm on the basis of L₂(O_i, ψ; G,S,Q),i = 1,..., n do not depend on Q(O_i; G,S),i = 1,..., n.

Theorem 4.1. For each i = l,...,n, define the loss function L₂(O_i, ψ;G,S,Q) = ψ(W_i)² + H(O_i; G,S)ψ(W_i+ Q(O_i; G,S) and assume max_i=1,...,_n{|H(O_i; G,S)|, |Q(O_i; G,S)|} < ∞. Then, the CART algorithm that uses the loss L₂(O, ψ; G,S, Q) does not depend on Q(O; G,S).

Theorem 4.1 implies that one can implement CURT-L₂ with loss function (8) by applying any (full data) CART-L₂ algorithm to the imputed dataset $\{\widehat{Z}(O_i;G,S),W_i;i=1,\dots ,n\}$. This works because all decisions made by the algorithm depend on either changes in loss or loss minimization, neither of which is affected by terms in the loss function that are independent of ψ(·). This equivalence result does not depend on the specific nature of Z (i.e., except that it is univariate).

As remarked earlier, the equivalences just established do not extend to the loss function (5), that is, where L₂,_ipcw(O_i, ψ; G) is used in place of L₂,_d(O_i, ψ; G, S), i = l,..., n. The equivalence results for L₂,_d(O_i, ψ; G,S) and L₂,_b(O_i, ψ; G,S) rely heavily on the fact that m₀(t,w; S) = l for every (t, w) and hence that K(O_i; G) = l for every i. These identities fail in the case of L₂,_ipcw(O_i, ψ; G) because this loss function can only be treated as a special case of L₂,_d(O_i, ψ; G, S) in the event that m₀(t,w; S) = 0 for every (t, w). Under this assumption, the loss function (8) is still appropriate; however, because $K(O_i;G)={\mathrm{\Delta }}_i/G({\tilde{T}}_i|W_i)\ne 1$ for any i, equations (8) and (9) are no longer equivalent up to terms that do not depend on ψ(W).

4.2. Implementing a CURE-L₂ Algorithm using Response Imputation

Algorithm 2 implemented using nonparametric bootstrap sampling in combination with one of L₂,_ipcw(O, ψ; G), L₂,_d(O,ψ; G,S), or L₂,_b(O,ψ; G,S) generalizes Breiman’s original RF algorithm to the case of censored outcomes. The nonparametric bootstrap is a particular example of the multinomial bootstrap, where observations are sampled with replacement with possibly unequal probability weights (e.g., Hothorn et al., 2006a). In Algorithm 2, the loss function only comes into consideration in Step 2, where it governs the process of growing the unpruned regression trees used to create the ensemble predictor. Hence, in view of the equivalences established in Section

4.l, Theorem 4.l implies that CURE-L₂ using either L₂,_d(O, ψ; G,S), or L₂,_b(O,ψ; G, S) can be implemented for a general multinomial bootstrap scheme by (i) constructing the relevant imputed dataset $\{{(\widehat{Z}(O_i;G,S),W_i^{\prime })}^{\prime };i=1,\dots ,n\}$ (ii) resampling observations with replacement using the desired multinomial bootstrap method; and, (iii) applying RF-L₂ (e.g., randomForest or rfsrc) to build a single unpruned tree using random feature selection for each such bootstrap sample. The resulting trees are then processed as desired to construct the desired ensemble predictor. The use of random feature selection in growing each unpruned tree in the forest does not affect the applicability of Theorem 4.1 in justifying the needed equivalence. Imputation also continues to work because a multinomial bootstrap allows for sampling weights that are exactly zero: each set of boostrap weights merely modifies the input dataset and not the actual decision process used for building trees. Implicit here is the assumption that G(·|·) and S(·|·) are held fixed; hence, when estimated from the observed data, neither is recalculated for each bootstrap sample. Importantly, in the case of the nonparametric bootstrap, steps (ii) and (iii) are combined and carried out by default as part of the RF-L₂ algorithm, further simplifying implementation.

As an example of a more general exchangeably weighted bootstrap scheme satisfying the conditions needed to use Algorithm 2, let A₁, ..., A_n be i.i.d. positive random variables with finite variance that are completely independent of the observed data and define the weights ${\omega }_i=A_i/{\sum }_{j=1}^n{A}_j$ for i = 1,…,n. In contrast to the nonparametric or multinomial bootstrap, this i.i.d. weighted bootstrap (Prmstgaard and Wellner, 1993) puts a positive weight on every observation in every bootstrap sample. The Bayesian bootstrap (Rubin, 1981) is obtained when A₁,...,A_n are standard exponential; in this case (ω₁,... ,ω_i) follow a uniform Dirichlet distribution, having the same expected value and correlation as the nonparametric bootstrap weights but a variance that is smaller by a factor of n/(n + 1). In contrast to the multinomial boostrap, it is not possible to implement CURE-L₂ using a simple resampling scheme when P(ω_i> 0, i = 1,...,n) = 1, that is, when all case weights are strictly positive. In this case, the resulting decision making processes need to incorporate these case weights directly. The corresponding version of CURE-L₂ is therefore easily implemented given an implementation of RF-L₂ that allows for case weights when calculating the loss function. Specifically, consider

$$L_{2,d,w}(O_i,\psi ;G,S)={\omega }_i[Q^{(1)}(O_i;G,S)-2\widehat{Z}\left(O_i;G,S\right)\psi (W_i)+{\psi }^2(W_i)],$$ (10)

the case-weighted version of (8), for i = 1,..., n. Because ω₁,..., ω_n are generated independently of the observed data and each has unit mean, (8) and (10) have the same expectation. Now, consider the comparably weighted version of loss function (9), that is,

$$L_{2,d}^{*}(O_i,\psi ;G,S)={\omega }_i[Q^{(2)}(O_i;G,S)-2\widehat{Z}\left(O_i;G,S\right)\psi (W_i)+{\psi }^2(W_i)],$$ (11)

where $Q^{(2)}(O_i;G,S)={[\widehat{Z}(O_i;G,S)]}^2$. It follows that (9) and (11) also have the same expectation and, in addition, that the weighted losses (10) and (11) are equal up to terms that do not involve ψ(·). These results hold as stated even when G(·|·) and/or S(·|·) are estimated, provided neither depends on ωι,...,ω_η. An easy generalization of the arguments in Section 4.1 now shows that CURE-L₂ can be implemented using the imputed dataset $\{{(\widehat{Z}(O_i;G,S),W_i^{\prime })}^{\prime };i=1,\dots ,n\}$ with case weights ωι,..., ω_η. We are not currently aware of an implementation of the RF-L₂ algorithm that accepts case weights in the manner required above. For the simulation study of Section 5, we have therefore extended the randomForest package to permit case weights in the calculation of the loss function (and associated estimators). This modified algorithm is used to implement CURE-L₂ for the weighted bootstrap for the loss functions L₂,_b(O, ψ; S) and L₂,_d(O, ψ; G, S) when G(·|·) and/or S(·|·) are estimated from the data $\mathcal{O}$.

5. Simulations

In this section, we use simulation to compare the performance of two CURE-L₂ algorithms to that of several available implementations of survival forests. The following subsections describe the simulation settings used (Section 5.1) and the choices made for implementing each CURE-L₂ algorithm (Sections 5.2 and 5.3). Section 5.4 summarizes the results; further results for other censoring rates and different covariate dimensions are provided in the Supplementary Web Appendix, where we also revisit the simulation study conducted in Steingrimsson et al. (2016) and compare the performance of the CURT-L₂ algorithms respectively using the doubly robust and Buckley-James loss functions, with both implemented using the imputation approach described in Section 4.1.

5.1. Simulation Parameters

The simulation settings reported here are very similar to Settings 1 — 4 in Zhu and Kosorok (2012). The four settings considered are respectively described below:

1. Each simulated dataset is created using 300 independent observations where the covariate vector (W₁..., W₂₅) is multivariate normal with mean zero and a covariance matrix having elements (i, j) equal to 0.9^|j-j|. Survival times are simulated from an exponential distribution with mean $\mu =e^{0.1{\sum }_{i=11}^{20}{W}_i}$ (i.e., a proportional hazards model) and the censoring distribution is exponential with mean chosen to get approximately 30% censoring.

2. Each simulated dataset is created using 200 independent observations where the covariate vector (W₁,..., W25) consists of 25 i.i.d. uniform random variables on the interval [0,1]. The survival times follow an exponential distribution with mean $\mu =\sin (W_1\pi )+2|W_2-0.5|+W_3^3$. Censoring is uniform on [0, 6] which results in approximately 24% censoring. Here, the proportional hazards assumption is mildly violated.

3. Each simulated dataset is created using 300 independent observations where the covariates (W₁,..., W₂₅) are multivariate normal with mean zero and a covariance matrix having elements (i, j) equal to 0.75^|i-j|. Survival times are gamma distributed with shape parameter $\mu =0.5+0.3\left|{\sum }_{i=11}^{15}{W}_i\right|$ and scale parameter 2. Censoring times are uniform on [0,15] which results in approximately 20% censoring. Here, the proportional hazards assumption is strongly violated.

4. Each simulated dataset is created using 300 independent observations where the covariates (W₁,..., W₂₅) are multivariate normal with mean zero and a covariance matrix having elements (i,j) equal to 0.75^|j-j|. Survival times are simulated according to a log-normal distribution with mean $\mu =0.1\left|{\sum }_{i=1}^5{W}_i\right|+0.1\left|{\sum }_{i=21}^{25}{W}_i\right|$. Censoring times are log-normal with mean μ + 0.5 and scale parameter one, and the censoring rate is approximately 32%. Here, the underlying censoring distribution depends on covariates.

Simulations for other settings, respectively considering variations on the above in which the total covariate dimension is increased to 50 or 100 and also when the censoring rate is increased, are summarized in the Supplementary Web Appendix.

5.2. Squared Error Loss Functions

With uncensored data and a continuous outcome, the most common loss function used in connection with the CART and RF algorithms is the L₂ loss. With Z = log T, the relevant full data loss function is L₂(Z, ψ(W))=(log T – ψ(W))² and the nominal estimation focus becomes ψ₀(W) = E[log T|W] whether CURT—L₂ or CURE—L₂ is used. Equation (8) gives the corresponding doubly robust loss L₂,_d(O, ψ; G,S) for suitable choices of G(·|·) and S(·|·); the Buckley-James loss is given by L₂,_d(O,-ψ; G,S). Further details on the calculation of L₂,_d(O,−0; G,S) for Z = logT in the case of building a single CART tree may be found in Steingrimsson et al. (2016).

With time-to-event data, a survival probability of the form S₀(t|W) = P(T = t\W) is typically of interest. The output from any CURT or CURE algorithm can be post-processed to generate estimators for S₀(t|W) derived from $\mathcal{O}$. For example, rather than computing a restricted mean (log) lifetime, one can instead estimate S₀(t|W) by using Kaplan-Meier estimators in each terminal node. This flexibility will be used in constructing an ensemble estimator for S₀(t|W) using Algorithm 2 in Section 5.4.

Alternatively, the loss function used by the CURE—L₂ algorithm can be chosen to focus on directly estimating S₀(t|W) for a fixed t >, 0 e.g., using the Brier loss function. Algorithm 2 calculated using (8) with Z = I(T > t) is referred to as the doubly robust Brier CURE—L₂ algorithm, and Algorithm 2 calculated using (8) with G(t|w) = 1 and Z = I(T > t) is referred to as the Buckley-James Brier CURE—L₂ algorithm. Supplementary Web Appendix S.1 gives further details on development and implementation of these two algorithms.

5.3. Specifying S(·|·) and G(·|·)

Algorithms that use the loss function (6) or (8) require specifying the functions S(·|·) and G(·|·). In general, this requires using estimators $\widehat{S}(t|w)$ and/or $\widehat{G}(t|w)$ derived from the observed data. These estimators are also needed for deriving the imputed dataset $\{{(\widehat{Z}(O_i;\widehat{G},\widehat{S}),W_i^{\prime })}^{\prime };i=1,\dots ,n\}$.

Many methods are available for estimating a conditional survivor function. Preserving the spirit of double robustness suggests avoidance of IPCW estimators. In building survival trees using a special case of the CURT algorithm based on (8), Steingrimsson et al. (2016) considered estimators $\widehat{S}(t|w)$ respectively derived from Cox regression, survival regression tree models, random survival forests, and parametric accelerated failure time (AFT) models for calculating the augmented loss function. Although the performance of the doubly robust methods gave noticeable improvement over those using IPCW loss, the choice of estimator $\widehat{S}(t|w)$ used in calculating the doubly robust loss generally made little difference in the chosen performance measures. Consequently, in this study, we use $m_1(u,w;\widehat{S})$ with $\widehat{S}(t|W_i),i=1,\dots ,n$ estimated using the random survival forests (RSF) procedure as proposed by Ishwaran et al. (2008) and implemented in rfsrc.

For all four simulation settings, we calculate $\widehat{G}(t|w)$ using the survival tree algorithm proposed by LeBlanc and Crowley (1992), with the minimum number of observations in each terminal node set to 30. In practice, use of (8), equivalently (9), requires that the empirical positivity condition $G({\tilde{T}}_i|W_i)\ge ϵ>0$ holds. To ensure that the estimated (possibly covariate dependent) censoring probabilities remain bounded away from zero, within each terminal node a sample-dependent truncation time $\widehat{\vartheta }$ is set such that the proportion of observed times in the terminal node exceeding $\widehat{\vartheta }$ is 10%; “Method 2” truncation as described in Steingrimsson et al. (2016) is then used. In short, times ${\tilde{T}}_i$ exceeding $\widehat{\vartheta }$ are designated as failures and $\widehat{G}({\tilde{T}}_i|W_i)$ and $\widehat{G}(u|W_i)$ are respectively replaced by $\widehat{G}(\widehat{\vartheta }\wedge {\tilde{T}}_i|W_i)$ and $\widehat{G}(\widehat{\vartheta }\wedge u|W_i)$ in calculating $\widehat{Z}(O_i;\widehat{G},\widehat{S})$ above, but survival times are not otherwise modified in the remainder of the calculations. As shown in Steingrimsson et al. (2016), this typically performs better than the standard approach to truncation (i.e., truncating all follow-up times that exceed $\widehat{\vartheta }$ and treating each as uncensored).

5.4. Simulation Results

In what follows, we focus on estimating S₀ (t|W) for a given fixed time-point t. Settings 1 — 4 are used to compare the performance of two CURE—L₂ algorithms to other implementations of survival forests. Both CURE—L₂ algorithms are a version of Algorithm 2 implemented using response imputation as described in Sections 4.1 and 4.2. To be more specific, we use L₂ to denote the CURE-L₂ algorithm that uses the loss (8) with Z = logT and estimates S₀ (t|W) by calculating Kaplan-Meier estimators in each terminal node (see Step 3 of Algorithm 2). Here, G(·|·) and S(·|·) are replaced by the estimates described in Section 5.3. Similarly, we use L2 BJ to denote this same CURE-L₂ algorithm, but where G(t|w) = 1 everywhere. We focus on versions of these two algorithms that use the nonparametric bootstrap as these have the advantage of being easily implemented using existing RF-L₂ software with uncensored outcomes. Results for other bootstrap schemes and also two additional CURE-L₂ algorithms derived from the loss (8) with Z = I(T > t) (i.e., the Brier loss) are discussed at the end of this section.

We will compare the results of L₂, and L₂ BJ to three available ensemble algorithms for survivor function estimation: the default method for censored data in the party package (CI; Hothorn et al., 2010); the default method for censored data in the randomForestSRC package (RSF; Ishwaran and Kogalur, 2016); and, recursively imputed survival trees (RIST; Zhu and Kosorok, 2012). The CI algorithm constructs a survival ensemble where conditional inference trees based on the two sample log-rank statistic are used in place of CART trees as the base learner (Hothorn et al., 2006b). The RSF algorithm in the randomForestSRC package implements that proposed in Ishwaran et al. (2008) and relies on the log-rank statistic for splitting decisions. The RIST algorithm is currently available from https://sites.google.com/site/teazrq/software.

All of these algorithms require specifying several tuning parameters. The tuning parameters for the RIST algorithm are chosen as in the example code provided by the authors with the exception that the length of the study parameter is chosen larger than the largest survival time. This includes using two-fold recursively imputed survival trees with 50 trees in each fold, $mtry=[\sqrt{p}]$, and a minimum of 6 cases in each terminal node. To make the tuning parameters more comparable to the rfsrc function, we also include a version of RIST that sets the minimum number of cases in each terminal node to 3. For all other methods, including the CURE-L₂ algorithms, $mtry=[\sqrt{p}]$ and the number of trees used in the ensemble is set to 1000. The remaining tuning parameters are respectively selected as the default in the corresponding R functions. At the request of a referee, we also implement and include a version of the RSF algorithm where the number of cases in each terminal node (nodesize parameter in the rfsrc function) is tuned rather than set at the default value of 3. In particular, for each of the four simulation settings, the RSF algorithm is fit using the default value along with three different values of nodesize, respectively corresponding to 1%, 5%, and 10% of the expected number of events rounded up to the nearest integer. The final (i.e., tuned) value of nodesize is set as the value which gives the smallest out-of-bag (OOB) error rate reported from the rfsrc function, calculated using the C-index (e.g., Mogensen et al., 2012).

Each survival forest procedure predicts S₀(t|W) on an independent test set consisting of 1000 observations simulated from the full data distribution with t respectively chosen as the 25th, 50th and 75th quantile of the marginal failure time distribution. For all four simulation settings the mean squared estimation error (MSE) is calculated as $0.001\times {\sum }_{i=1}^{1000}{(\widehat{S}(t|W_i)-S_0(T|W_i))}^2$, where $\widehat{S}(t|W)$ is the prediction from the algorithm and S₀(t|W) is the true conditional survival curve. Boxplots from 1000 simulations for t equal to the median of the marginal survival distribution for the four different simulation settings are shown in Figure 1. The corresponding plots for t equal to the 25 and 75th quantile of the marginal survival distributions are given in Figures S-1 and S-3 in Supplementary Web Appendix S.2. The labels used in all plots correspond to the methods as described above. The main results from Figure 1 are summarized below:

Figure 1:

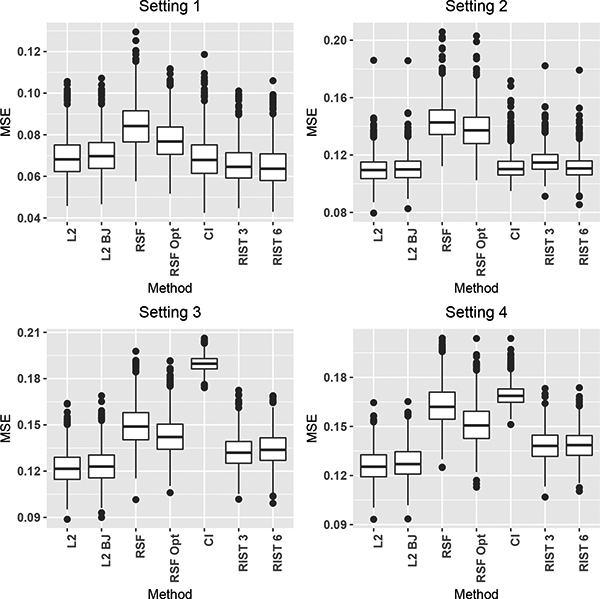
Boxplots of MSE estimated at the 50th quantile of the marginal failure time distribution for the four simulation settings described in Section 5.1. L2 and L2 BJ are the CURE-L₂ algorithms, with BJ referring to the use of the Buckley-James CUT. RSF and CI are the default methods for rfsrc and cforest functions. RSF Opt is the default method for rfsrc with the nodesize parameter tuned. RIST is the recursively imputed survival trees algorithm, and 3 and 6 stand for the minimum number of observed failure times in a terminal node.

• Overall, the CURE—L₂ algorithms L2 and L2 BJ show the best performance. The RIST algorithm is also a strong performer, doing the best in Setting 1 and remaining competitive in all others. Using currently available software, the CURE—L₂ algorithms run considerably faster when compared to RIST, even when accounting for the calculations needed to compute the augmentation terms needed for the Buckley-James and doubly robust loss functions.

• Settings 1 — 3 are used to illustrate the performance under different degrees of misspecification of the proportional hazards assumption (correctly specified, mildly misspecified, and severely misspecified). Figure 1 shows that as the severity of the misspecification increases the relative performance of the methods not utilizing log-rank based splitting statistics (i.e., the CURE—L2 algorithms) becomes better compared to the algorithms where splitting decisions utilize such statistics (i.e., RSF, CI, RIST 3, RIST 6, RSF Opt).

The Supplementary Web Appendix contains several additional results that follow the four main settings considered in this section. We respectively review these results below.

1. All of the results presented in Figures S-1 through S-14 in Supplementary Web Appendix S.2 include comparisons to the doubly robust and Buckley-James Brier CURE algorithms described earlier and presented in greater detail in Supplementary Web Appendix S.1. The results show that the CURE algorithms based on the Brier loss perform either similarly or worse than the CURE algorithms implemented using the L₂ loss. We conjecture that this occurs because the L₂ loss function for Z = log T can be viewed as making use of information across time (i.e., a type of composite loss for the survivor function), whereas the Brier loss that uses Z = I(T > t) makes more limited use of the available data. The use of a composite Brier loss function incorporating information for estimating S₀(t\W) using several different choices for t is likely to improve performance further. However, it is unclear whether one can use imputation methods like those introduced earlier in combination with existing software to implement such methods; we intend to explore this in future work.

2. Section S.2.2 presents comparisons of the CURE-L₂ algorithms that use the non-parametric bootstrap to CURE-L₂ algorithms that respectively use the Bayesian bootstrap and the i.i.d. weighted bootstrap with weights A₁,... ,A_n simulated from a Gamma(4,1) distribution. The Bayesian and Gamma(4,1) bootstrap CURE-L₂ procedures are fit by extending the capabilities of randomForest (Liaw and Wiener, 2002) to handle arbitrary nonnegative case weights in calculating the loss function; the code for implementing these methods can be obtained from the first author. Figures S-4 - S-9 in Supplementary Web Appendix S.2.2 demonstrate comparable performance between the three bootstraps in all settings at all quantiles for all combinations of loss functions and CUTs.

3. Section S.2.3 shows results both when $\widehat{S}(\cdot |\cdot )$ is calculated using a parametric accelerated failure time model with error distribution that is assumed to follow an Weibull distribution and also when $\widehat{G}(\cdot |\cdot )$ is obtained using a Kaplan-Meier estimator. Section S.2.4 summarizes results when the total covariate dimension is respectively increased to 50 and 100 and Section S.2.5 summarizes results when the censoring rate is increased to 50%. In these sections, and in view of the similar performance of bootstrap methods observed in Section S.2.2, only CURE-L₂ algorithms that use the nonparametric bootstrap are considered in these simulations, and all results show similar trends to those seen in Figure 1.

A disadvantage of the nonparametric bootstrap is the tendency of this methodology to create heavy ties (i.e., on average, only 63% of any given bootstrap sample consists of distinct observations). An advantage of using the nonparametric bootstrap is the existence of an OOB sample. The OOB sample consists of observations that are not selected into a given bootstrap sample and it is commonly used to evaluate prediction accuracy and the importance of variables in the RF algorithm; see Section 6 for more detailed discussion on variable importance measures. The lack of an OOB sample for the exchangeably weighted bootstraps with positive weights on all observations, combined with the comparative ease of implementation for the nonparametric bootstrap and the absence of significant differences in prediction error suggested by our simulation results, suggest that the nonparametric bootstrap may be preferred when implementing a CURE-L₂ algorithm.

6. Applications to Public-Use Datasets

In this section we evaluate the performance of the CURE-L₂ algorithms on two datasets; results for two additional datasets, the Netherlands and R-Chop data, are provided in Section S.4.1 in the Supplementary Web Appendix. The two datasets analyzed in this section are:

1. TRACE Study Group Data: This dataset consists of 1878 subjects that were randomly sampled from 6600 patients and is included in the R package timereg. The event of interest is death from acute myocardial infarction (AMI). Subjects that died from other causes or were alive when they left the study were considered censored. Information on gender, age, diabetes status, if clinical heart pump failure (CHF) was present, and if the patient had ventricular fibrillation are used here. As in Steingrimsson et al. (2016), who analyzed the dataset using doubly robust survival trees (i.e., an example of CURT-L₂), we focus on the subset of patients surviving past 30 days. Two such observations having an undefined censoring status were removed from the dataset, leaving 1689 patients and a 53.8% censoring rate.

2. Copenhagen Stroke Study: This dataset consists of 518 patients admitted to hospital with stroke. The event of interest is time from admission to death and the censoring rate is 22%. There are 13 covariates, which are listed in Table S-2 in Supplementary Web Appendix S.4. These publicly available data are available from the R package pec.

3. We first compare the prediction performance of the CURE-L₂ algorithms (i.e., using the nonparametric bootstrap and for Z = log T) to the default methods in the randomForestSRC and party package as well as the two versions of the RIST method described in Section 5. A tuned version of the RSF algorithm, with the node size chosen in the same way as described in Section 5, is also included at a request from a referee. We also include tuned versions of the CURE-L₂ algorithm. Each tuned CURE-L₂ algorithm first fits four corresponding CURE-L₂ algorithms with the node size respectively chosen as the default value, 1%, 5%, and 10% of the number of observations. The final node size is chosen as that which minimizes the OOB prediction error calculated using the $L_{2,d}^{*}(O,\psi ;\widehat{G},\widehat{S})$ loss; see (11). Because the CURE-L₂ algorithms that use the Brier loss function were observed to be somewhat inferior to the CURE-L₂ implemented using Z = log T in our simulation study, we do not include the former in our comparisons.

All algorithms are used to predict S₀(t|W), where t is set equal to 3 years; respectively, the corresponding marginal survival probabilities (i.e., estimated using a Kaplan Meier curve) are 0.73 and 0.65 for the TRACE and Copenhagen datasets. The estimator $\widehat{S}(\cdot |\cdot )$ used in calculating the augmentation terms in the CURE-L₂ algorithms is obtained using the RSF procedure; the doubly robust methods use the Kaplan-Meier estimator $\widehat{G}(\cdot )$ and Method 2 truncation as described in Section 5.3. Prediction performance is evaluated using a cross-validated version of the censored data Brier score of Graf et al. (1999, Sec. 6); this MSE-type measure is calculated using a 10-fold cross-validation procedure that approximately balances censoring rates in the training and test sets.

Figure 2 shows boxplots of the censored data Brier score for 200 different splits into test and training sets for the two datasets; lower values indicate better performance. Figure S-17 in Supplementary Web Appendix S.4.1 shows the corresponding results for the Netherlands and R-Chop data. Figures S-19 and S-20 in Supplementary Web Appendix S.4.3 show results for six other time points. Overall, the results show that L2 and L2 BJ have the best performance, performing either similarly to or better than all other methods for all datasets and time points.

Figure 2:

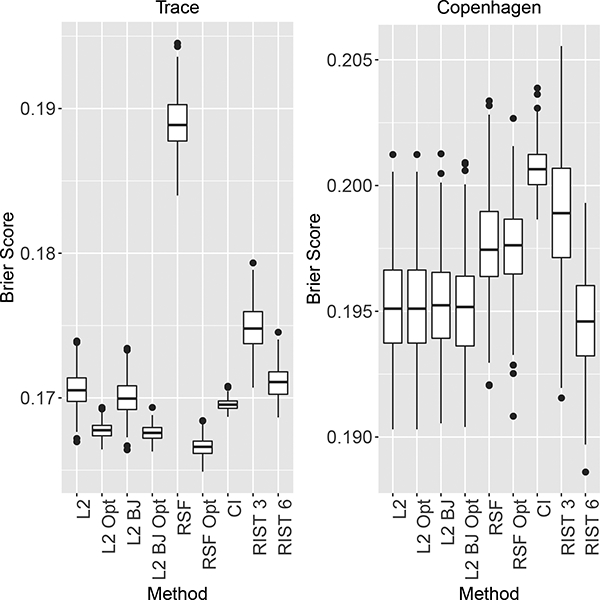
Censored data Brier Score at t = 3 years for the TRACE and Copenhagen Stroke studies; lower values indicate better prediction accuracy. L2 and L2 BJ are the CURE-L₂ algorithms, with BJ referring to the use of the Buckley-James CUT. Opt refers to tuning the nodesize parameter. RSF and CI are the default methods for the rfsrc and cforest functions in R. RIST is the recursively imputed survival trees algorithm, where 3 and 6 denote the minimum number of cases in a terminal node.

Variable importance measures (VIMPs) are commonly used to evaluate the importance of each variable in the predictions generated by an ensemble algorithm. The method of Breiman (2001) (see also Ishwaran et al., 2008) involves permuting the observed values of covariate j in each OOB sample and then evaluating the associated increase in prediction error compared to that for the original forest; see Section S.3 for further details on the calculation of this OOB prediction error measure for the case of L₂ loss and the corresponding VIMP. Theorem S.3.1 in Supplementary Web Appendix S.3 shows that calculating the VIMP of Breiman (2001) using $\{{(\widehat{Z}(O_i;G,S),W_i^{\prime })}^{\prime };i=1,\dots ,n\}$ is identical to the version that would be calculated if the (unobserved full data) L₂ loss were replaced by the CUT for this loss function that corresponds to $\widehat{Z}(O_i;G,S),$ i = 1,…,n.

Ishwaran et al. (2010) proposed an alternative VIMP measure based on the intuitively sensible idea that splits made earlier in the individual trees in the forest are more likely to be important predictors. In particular, if the depth of a given node in a given tree is defined as the number of splits that are made between this node and the root node, then one can determine the minimal observed depth for any given variable by calculating the depth for all nodes that split on this particular variable. This calculation can be done for each variable in each tree in the ensemble; the resulting minimal depth VIMP for each variable is then calculated as the average of the minimal observed depths for that variable over all trees. Variables with lower average minimal depth are considered more influential. Because the minimal depth VIMPs do not require the presence of an OOB sample, such measures can be calculated for CURE-L₂ algorithms using more general bootstrap schemes, such as the i.i.d.-weighted or Bayesian bootstrap.

Below, we illustrate the use of the minimal depth VIMP measure for the TRACE data. Table 1 shows these measures calculated using the L2 and L2 BJ algorithms and the RSF method. One of the main findings in Jensen et al. (1997) was that the effect of ventricular fibrillation (VF), an acute emergency condition, vanished when analyzing the data consisting of subjects surviving beyond 30 days. The results in Table 1 support this conclusion as VF has the highest minimal depth VIMP of all variables for all algorithms (i.e., judged as the least important). Age and CHF have the two lowest VIMP measures for all methods, a result consistent with those in Steingrimsson et al. (2016), where all trees are observed to split on age and (with one exception) also on CHF. The corresponding results for the OOB prediction error VIMPs are presented in Supplementary Web Appendix S.4 and lead to the same conclusions. VIMPs for the Copenhagen study are also presented in Supplementary Web Appendix S.4, Tables S-2 and S-3 show that well-known risk factors for the overall survival of stroke patients are identified as being the most influential.

Table 1:

Minimal depth variable importance measures for the TRACE data; lower values indicate more influential variables. BJ refers to the Buckley-James transformation. RSF is the default method in the randomForestSRC package.

	L2	L2 BJ	RSF
Age	0.90	1.13	0.82
Clinical Heart Pump Failure	1.02	0.96	1.11
Diabetes	1.67	2.04	1.45
Gender	1.99	1.15	2.02
Ventricular Fibrillation	2.14	2.17	2.43

7. Discussion

This paper makes several contributions to the literature. We extend the theory of censoring unbiased transformations in a substantial way and establish some useful efficiency results. This theory is applied to the problem of risk estimation, resulting in a class of censoring unbiased loss functions. These results are subsequently used to extend versions of the CART and RF algorithms for general (full data) loss functions to the case of censored outcomes by replacing the full data loss with a CUT. For the special case of the L₂ loss function, we show that a certain form of response imputation can be used to implement these new algorithms using standard software for uncensored responses. The proposed methods are shown to perform well compared to several existing ensemble methods both in simulations and when predicting risk using several public-use datasets.

The use of the L₂ loss function for predicting E(log T| W) may have certain advantages over methods that focus on survival differences. For example, in the absence of censoring, Ishwaran (2015) studied the effect of different splitting statistics used in the RF algorithm. The author showed that using reduction in L₂ loss as a splitting criteria results in splitting rules that split near the edges for noise variables and split in a region where the curvature of the underlying regression function is the steepest for signal variables. This property of simultaneously adapting to both signal and noise may contribute to the strong MSE performance of the CURE-L₂ algorithms considered here (i.e., L2 and L2 BJ).

Potentially interesting future research directions include: extensions to more complex data- structures such as multivariate outcomes, competing risks, missing covariate data and more complex sampling schemes (i.e. case-cohort or nested case-control designs); studying the performance of iterated versions of this algorithm, where the conditional expectations required for computing the doubly robust and Buckley James loss functions are updated using the latest ensemble predictor (or possibly updated dynamically in batches); and, deriving asymptotic properties of the CURE algorithm (or certain special cases, such as CURE-L₂), possibly by extending the consistency results in Scornet et al. (2015) or developing methods to calculate asymptotically valid confidence intervals for the predictions from the CURE algorithm (e.g. Mentch and Hooker, 2016).

As discussed in Section 5, the CURE-L₂ algorithms that used the non-parametric bootstrap showed similar prediction accuracy to those using two versions of the exchangeable weighted bootstrap. This similarity is interesting since it is not known whether Breiman’s original RF-L₂ algorithm, which uses the nonparametric bootstrap, is consistent. Scornet et al. (2015) proves consistency for a RF algorithm that uses subsampling without replacement in place of the nonparametric bootstrap. The main role of subsampling is to preserve independence among the observations in each subsample. A weighted bootstrap that uses strictly positive weights also preserves the independence of the observations within each bootstrap sample. Although outside the scope of this work, it would be interesting to investigate whether a weighted bootstrap sampling with continuous, strictly positive weights would permit one to use arguments similar to those in Scornet et al. (2015) to prove consistency.

The theory justifying the use of censoring unbiased loss functions is not restricted to the CART algorithm or to ensemble methods that use CART trees as building blocks. For example, it is possible to use the results in this paper in connection with other recursive partitioning methods (e.g., the partDSA algorithm; see Lostritto et al., 2012), which builds a predictor by recursively partitioning the covariate space using both ‘and’ and ‘or’ statements. Implementation using imputed response data as done here in the case of L₂ loss remains possible more generally in cases where model building decisions do not depend on the absolute level of loss (e.g., relative change, loss minimization, etcetera).