Abstract
Position-specific denatured-state thermodynamics were determined for a database of human proteins by use of an ensemble-based model of protein structure. The results of modeling denatured protein in this manner reveal important sequence-dependent thermodynamic properties in the denatured ensembles as well as fundamental differences between the denatured and native ensembles in overall thermodynamic character. The generality and robustness of these results were validated by performing fold-recognition experiments, whereby sequences were matched with their respective folds based on amino acid propensities for the different energetic environments in the protein, as determined through cluster analysis. Correlation analysis between structure and energetic information revealed that sequence segments destined for β-sheet in the final native fold are energetically more predisposed to a broader repertoire of states than are sequence segments destined for α-helix. These results suggest that within the subensemble of mostly unstructured states, the energy landscapes are dominated by states in which parts of helices adopt structure, whereas structure formation for sequences destined for β-strand is far less probable. These results support a framework model of folding, which suggests that, in general, the denatured state has evolutionarily evolved to avoid low-energy conformations in sequences that ultimately adopt β-strand. Instead, the denatured state evolved so that sequence segments that ultimately adopt α-helix and coil will have a high intrinsic structure formation capability, thus serving as potential nucleation sites.
Keywords: denatured states, fold recognition, thermodynamic environments, framework model, energy landscape
Introduction
Characterization of the denatured states of proteins has long been recognized as important for understanding protein folding, stability, transport across membranes, and turnover rates.1,2 More recently, the denatured state has gained significant prominence with the observation that many proteins are intrinsically disordered (ID) or contain ID regions, even under normal physiological conditions,3 which suggests that many proteins may have evolved to use the denatured state for functions previously associated with folded, native proteins. Indeed, disorder has been found to be a conserved feature,4–6 and its importance has already been established to processes such as catalysis7,8 and molecular recognition.9–11 In addition, the biological advantages of coupling allosteric control to the folding of ID regions have recently been developed.12
Although the relationship between ID regions and the denatured states of folded proteins has been the subject of intensive study,3,5,13–19 the ability of osmolytes to induce the folding of ID regions, such as the N-terminal domain of the glucocorticoid receptor,20 suggests that ID regions may share common structural and thermodynamic characteristics. The observation that ID regions can be folded by osmolytes indicates that while the conformational ensemble under physiological conditions is dominated by unstructured states for these proteins, there exists a restricted conformational manifold of folded and compact structures that are important for functional interactions, similar to what is observed for natively folded proteins. As such, the study of the denatured states of proteins may help to illuminate the common thermodynamic organizing principles governing the relationships between sequence, structure, and function in both folded and ID proteins.
Our approach here is to study the denatured states of a database of proteins and to identify common thermodynamic architecture across all proteins. Previously, we showed that the native states of proteins share common thermodynamic properties, and that these properties are independent of, and even transcend, structural similarities.21–23 This was done by developing a position-specific energetic description of each protein and determining the amino acid propensities for the different thermodynamic environments. The utility of our energetic representation was established by matching (with an 84% success rate) a protein’s sequence to a one-dimensional representation of that protein’s energy landscape. That result conclusively demonstrated that the organizing principles for native proteins can be represented in purely energetic terms and that the specific thermodynamic descriptors developed in that work were sufficient to quantitatively characterize a diverse database of human protein structures.
Here, the thermodynamics of the denatured states of that same database of proteins was examined in order to determine (1) if organizing principles exist for denatured proteins similar to those that were observed for natively folded proteins, (2) the nature of the organizing principles under unfolding conditions, (3) the relationship of this organizing scheme with both sequence and structure, and (4) the quantitative similarity between the native and unfolded state energetics.
Results and Discussion
Ensemble-based thermodynamic characterization of the denatured state
Much in the same way that structural similarities across multiple proteins can be used as the basis for establishing organizing principles, thermodynamic organization and hierarchy can be identified via similarities in the position-specific thermodynamics of different protein folds. To facilitate a thermodynamic description, a COREX/BEST analysis was performed on a database of nonhomologous Homo sapiens protein structures (Fig. 1).21,23 Briefly, the COREX/BEST algorithm starts with the high-resolution structure of a protein and generates a statistical thermodynamic ensemble of states by alternatively folding and unfolding a fixed number of residues of the sequence (in this case, five) in all possible combinations. This strategy produces a large ensemble of states, each containing different amounts of folded and unfolded segments. Application of an experimentally trained surface-area-based energy function provides the relative energy of each state from which the probabilities can be calculated.24,25 Although conceptually simple, the COREX/BEST energy function has been tested extensively by comparing calculated with experimentally determined protection factors from hydrogen–deuterium exchange.24,26 The utility of the COREX/BEST algorithm has also been validated through a number of other experimental comparisons examining a range of biophysical and functional phenomena, such as residue cooperativity,27–29 pH-dependent stability,30 and cold denaturation.31,32
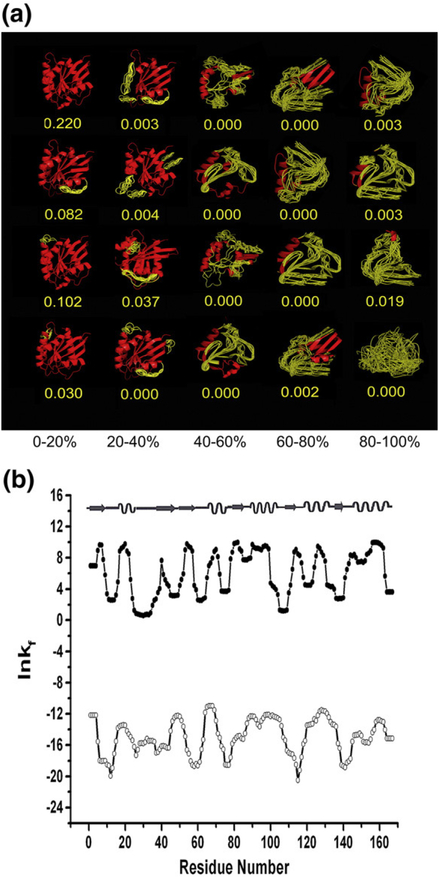
Fig. 1.
Example of the COREX ensemble and position-specific stability constants under native and denaturing conditions for G protein 1KAO. (a) The COREX ensemble: each column represents a different percentage of unfolding. Red regions in each state are portions that were modeled as native-like. Yellow regions were modeled as denatured-like (for schematic purposes only). The calculated state probabilities (values in yellow) are given below each state. (b) The position-specific stability constant, ln κf,J, calculated for the native (filled circles) and denatured ensembles (open circles). The positions of native secondary structure are shown at the top.
Position-specific thermodynamic descriptors for each protein were calculated by determining the energetic differences between the folded and unfolded (i.e., conformationally fluctuating) subensembles for each position (see Materials and Methods). As such, these descriptors report the energetics of the whole ensemble, but are obtained on a position-specific basis.21–23 Because our previous analysis was determined under native conditions, the Boltzmann- weighted thermodynamic values reported at each position were dominated by contributions from structured states, as they have the highest probability under native conditions (See Fig. 1a). In other words, for a database of proteins, we generated an energetic representation of native state conformational fluctuations, and this representation provided a thermodynamic picture of each native fold.
To determine whether fold-encoding information (and thus common organizing principles) is also contained within any other subset of states in the full ensemble (i.e., vertical columns in Fig. 1a), the previously computed ensembles were systematically perturbed by increasing the stability of each state in a manner proportional to the amount of unfolded structure, as described in Materials and Methods. The net effect of such a perturbation strategy preserves the relative stability of the different states within a particular column in Fig. 1a, but redistributes the ensemble so that the more unfolded states (column 1 in Fig. 1a) are more probable. These conditions can be referred to as denaturing because the ensemble probabilities are dominated by states wherein the folded regions account for less than 20% of the residues in any given state. We note that according to this model, the denatured ensemble is composed solely of states that have isolated segments of native structure in an otherwise disordered protein, and that alternative folded conformations are not considered explicitly. Although such a treatment may seem at first to bias the results, we show below that this treatment does not impact the conclusions of this work.
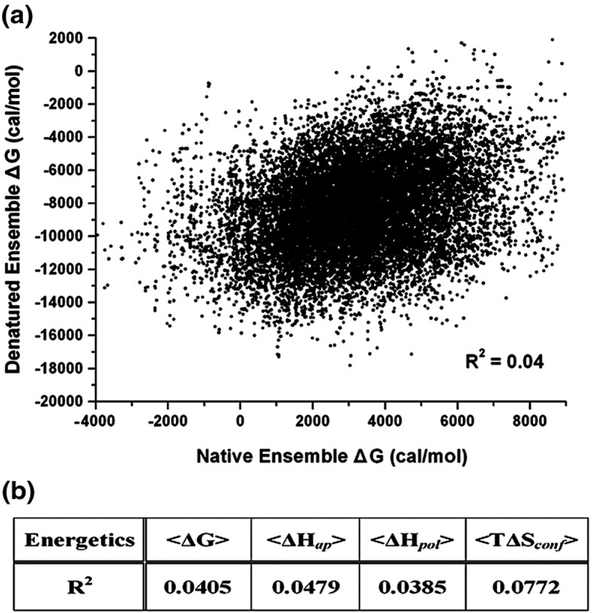
Interestingly, the Boltzmann-weighted descriptors determined here for the ensemble under denaturing conditions differ considerably from the values determined previously under native conditions. This is highlighted in Fig. 1b, where it is clear that regions of high stability under native conditions often correspond to regions of low stability under denaturing conditions, and vice versa. Quantitative comparison of the position specific free energies under native and denatured conditions, for example (Fig. 2), show no correlation (R2 = 0.04). In fact, all four position-specific thermodynamic variables (i.e., the position-specific free energy [ΔG]j, conformational entropy [TΔS]conf,j, and apolar [ΔH]apol,j and polar [ΔH]pol,j enthalpy), show no correlation between native and denaturing conditions (Fig. 2b), indicating that the calculations for the native and denatured ensembles are monitoring different physical properties. This point becomes clear upon inspection of the generalized expressions used to calculate the position-specific energetics. Each position-specific thermodynamic parameter, [ΔX]j, is determined from the difference in the average values for two different subensembles as revealed by the expression;
| (1) |
where the first term in Eq. (1) is a summation over the subensemble in which residue j is folded and can be represented as:
| (2) |
where Ki and Pi are the statistical weight and probability of each state i, Nfolded is the number of states in the folded subensemble, and Q is the partition function. The second term of Eq. (1), 〈ΔXnonfolded,j〉, was calculated in an analogous manner, except the summation was over the subensemble in which residue j is unfolded.
Fig. 2.
Calculated energetics using native and denatured ensembles show no correlation. (a) The position-specific free-energy (stability) values, [ΔG]j, calculated from denatured and native ensembles. Each point of the scatter plot corresponds to a residue in the H. sapiens protein database; all 122 proteins of the database were represented. The ordinate is the positional free energies calculated from denatured ensembles; the abscissa is from native ensembles. The correlation coefficient (R2) between the native and denatured [ΔG]j values were ~ 0.04, indicating no correlation. (b) Correlation statistics between the thermodynamic descriptors calculated under native and denaturing conditions are summarized, demonstrating that no correlations were observed.
Under denaturing conditions, the energetics at each position are largely reporting on the stability of isolated pieces of the native structure in the absence of the stabilization effects from tertiary interactions. This is because only highly denatured states have appreciable probability under these modeled conditions. The energetics under native conditions, in contrast, are reporting on the stability of each region in the context of those stabilizing interactions with neighboring segments. For example, the loop at position 105 to 111 in G protein (Fig. 1b; PDB ID 1KAO) is a moderately stable element of structure under denaturing conditions, yet under native conditions it is among the least stable regions. The stability of this loop region originates from local interactions; the folding of the remainder of the molecule adds comparatively little to the stability of this region. Conversely, many positions involved in the β-sheet (e.g., residues 55–57 and 78–81) have relatively low stability under denaturing conditions, owing to the dearth of short-range stabilizing interactions, but acquire significant stability under native conditions because those regions come together from distal parts of the protein to form the stable core.
Identification and characterization of thermodynamic environments within denatured ensembles
Identification of the thermodynamic organization within the denatured state of the database was facilitated through the use of the partitioning around medoids clustering method applied to the position-specific thermodynamic descriptors for the entire database. This was followed by an indirect determination of the information content through fold-recognition experiments. The strategy was to establish amino acid propensity scales for different energetic environments (similar to the propensity scales for structural environments)33 and to determine the generality of these preferences by successfully matching sequences to their respective fold (defined in energetic terms).21,23 This strategy will establish whether a common set of thermodynamic rules applies across the entire database.
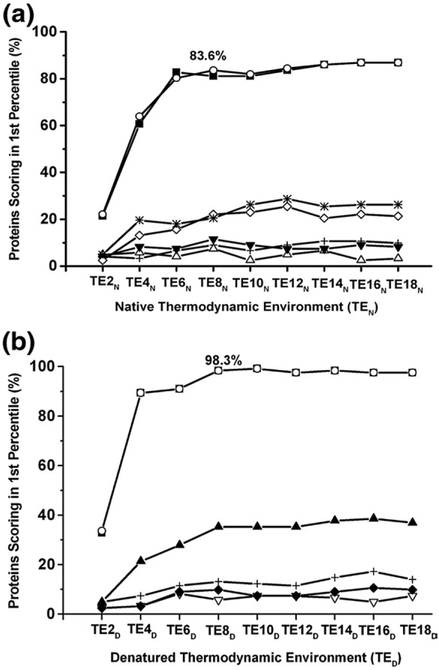
Fold-recognition success was defined as cases where the target sequence scored higher than 99% of the sequences in the decoy library. Because the decoy library that was used contained 431 sequences,21 to be successful, the target sequence had to score among the top 4 sequences. As described previously, grouping the position-specific thermodynamics calculated from the database of natively folded proteins into eight thermodynamic environments (TEN) yielded a success rate of 83.6% (i.e., more than 80% of the sequences were matched successfully to their fold21; see Fig. 3a). Confirming that the residue-specific information at each position originated from native-like states, identical results were obtained when the thermodynamic environments were derived instead by clustering data calculated solely from the subensemble of states that contain 80–100% folded structure. Fold-recognition success was not achieved for control calculations where the subensembles that contain 20–40%, 40–60%, or 60–80% of the folded native structure were used. The inability of the states with between 20% and 80% folded structure to show common organizing principle by this method suggests that these folding intermediates play little to no role in determining which native fold a particular sequence will adopt. It should be noted that a success rate of 28% was observed in fold-recognition experiments that used the subensemble of states that contained 10 folded residues or less (a success rate higher than that of the control calculations), suggesting that a denatured ensemble may contain some folding information even under native conditions.
Fig. 3.
Fold-recognition performance using thermodynamic environments identified with native and denatured ensembles. Fold recognition successes as a function of the number of thermodynamic environments. The fold-recognition experiments used scoring matrices composed of the log-odds probability of the amino acids for each thermodynamic environment. Fold recognition was defined as successful when the target protein was among the top 4 (1%) out of 431 sequences. Both native ensembles (a) and denatured ensembles (b) were divided into five subensembles (0–20% folded, 20–40% folded, 40–60% folded, 60–80% folded, and 80–100% folded) to determine the subensemble contributions to fold recognition. (a) Fold-recognition success as a function of TENs. Each line represents a different subensemble (from top to bottom): full ensemble (open circle), 80–100% folded subensemble (filled square), the subensemble of states that contained 10 residues or less folded (star), 60–80% folded subensemble (open diamond), 0–20% folded subensemble (cross), 40–60% folded sub- ensemble (filled down triangle), 20–40% folded subensemble (open up triangle). (b) Fold-recognition success as a function of TEDs. Each line represents a different subensemble (from top to bottom): full ensemble (open circle), 0–20% folded subensemble (filled square), 80–100% folded subensemble (filled up triangle), 20–40% folded subensemble (cross), 60–80% folded subensemble (filled diamond), and 40–60% folded subensemble (open down triangle).
To evaluate fold determinants in the denatured state, fold-recognition experiments were conducted using thermodynamic descriptors calculated under denaturing conditions (TED). Interestingly, for the denatured ensembles, fold-recognition success was found to plateau at 98.3%, using eight environments, a substantial improvement over the same calculation performed with ensembles under native conditions (Fig. 3b). Partitioning the denatured ensembles to investigate the contribution of the different subensembles revealed that under denaturing conditions, the information content of the subensemble containing 80–100% structure (i.e., 0–20% unfolded regions) was sufficient to produce fold-recognition success at a rate of only 35%.
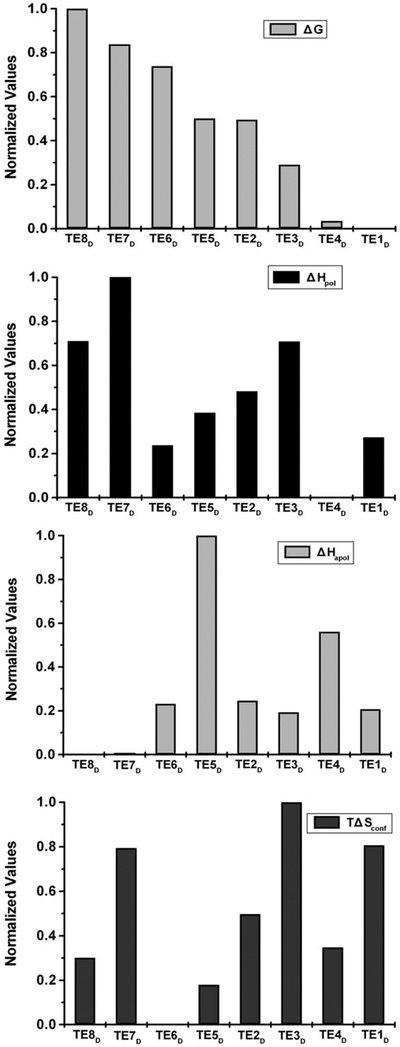
Within the context of this analysis, the eight clusters identified from the partitioning correspond to different thermodynamic environments. This is shown in Fig. 4, where the normalized average thermodynamic properties (i.e., the numerical mean of all positions) of each cluster are shown for the four position-specific descriptors, where TE8D is the least stable and TE1D is the most stable environment. Similar to the previous analysis using the native-state thermodynamic environments,21 the eight denatured-state thermodynamic environments (TED) represent a segmenting of the space (Fig. 4), where the different environments correspond to different free energies of stabilization as well as the different thermodynamic contributions (i.e., polar and apolar enthalpy and entropy differences) for achieving that stability. Thus, cluster analysis can be readily applied to the ensemble under native or denaturing conditions, and the clusters obtained in each case can be used for fold-recognition experiments. Nonetheless, as Fig. 1b reveals, the range of thermodynamic values for the ensemble under native and denaturing conditions is significantly different (i.e., under native conditions, the stability constants, ln κf,j, are generally positive, meaning the states in which each residue is folded are more probable than states in which each residue is unfolded, and under denaturing conditions that trend is reversed). This indicates that the environment clusters identified in each case are different.
Fig. 4.
Comparison of the eight thermodynamic environments in denatured ensembles. The thermodynamic environments were defined based on the clustering of four thermodynamic descriptors. The mean values for the four thermodynamic descriptors within each cluster are plotted: free energy ΔG, apolar enthalpy ΔHapol, polar enthalpy ΔHpol, and conformational entropy TΔSconf. The TEDs are listed in order of increasing stability along the abscissa. Thus, TED7 and TED8 are the least stable, and TED1 and TED4 are the most stable. The normalized mean values of the thermodynamic descriptors are presented along the ordinate.
Identifying the source of denatured-state fold-recognition success
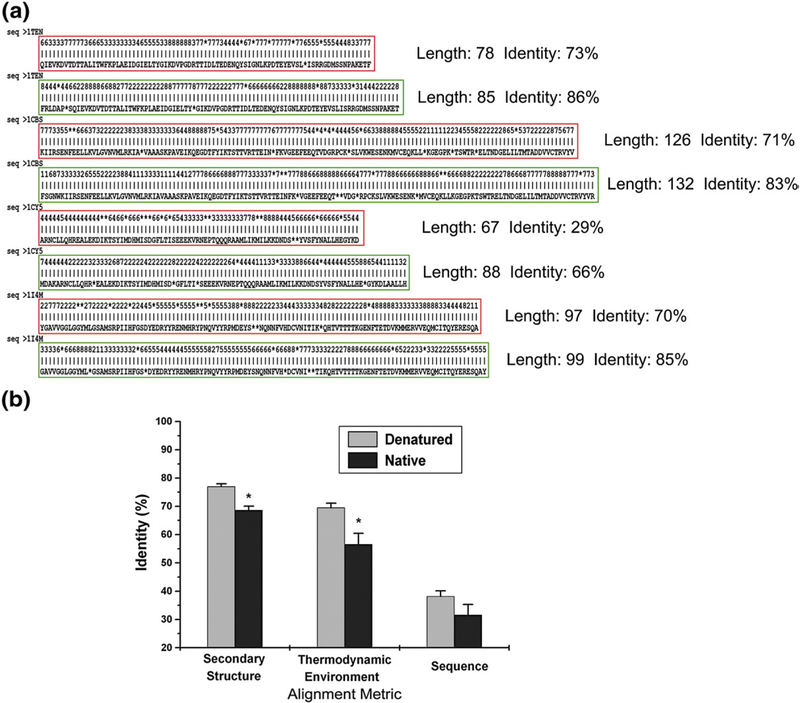
To identify the source of the improved fold-recognition success when using the denatured-state thermodynamics, the target sequences that scored well using TED, but poorly when using TEN, were examined. Improved alignments were observed (Fig. 5a), resulting in a 15% increase in the success rates for the fold-recognition experiments. To assess quantitatively the improvements in the alignments obtained from the denatured-state energetics, we compared the average identities for structural, energetic, and sequence information obtained from native and denatured fold-recognition experiments (Fig. 5b). For example, the mean identity of the thermodynamic environments between the actual and the aligned structures is 69.5% using denatured-state energetics for fold recognition, compared to just 56.6% (P = 0.02) when using native thermodynamic environments. Similarly, secondary-structure identities display a statistically significant improvement (+8%) when denatured-state energetics, rather than native-state energetics, were used as the basis for alignment. As the alignment statistics reveal, both the length and the quality of the alignments were increased when derived from denatured-state energetics.
Fig. 5.
Comparison of alignments generated from the fold-recognition experiments using native and denatured thermodynamic environments. Alignments were generated using the Smith–Waterman local alignment algorithm to score proteins for fold recognition based on the identified thermodynamic descriptors. (a) Alignments using TEN are boxed in red, while alignments using TED are boxed in green (gaps are represented as asterisks). Local alignment length and identity are shown next to the alignment and show clearly that alignments based on the denatured ensemble thermodynamic environments are matched over longer stretches and have higher identities. (b) The mean of calculated identities for all alignments of the target sequence matched to the fold is compared between the native (gray bar) and denatured (black bar) ensembles. Identities calculated based on (1) secondary structure, (2) thermodynamic environments, (3) and amino acid assignments are shown. Calculated identities using thermodynamic environments and secondary-structure assignments show a statistically significant difference between the two ensembles (P < 0.05).
The relationship between denatured-state thermodynamic environments and secondary structure
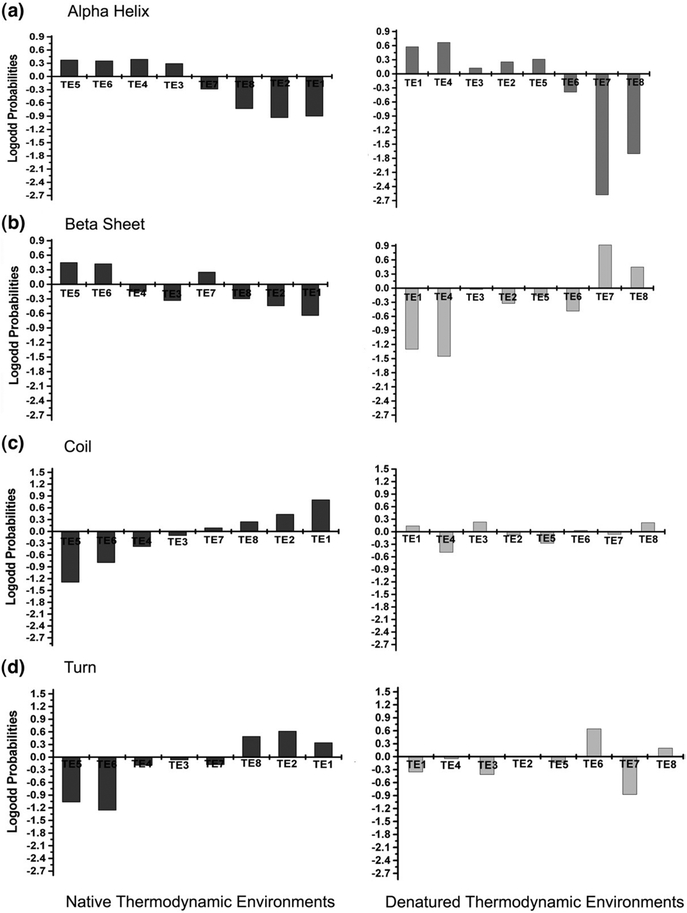
The high level of alignment identity for secondary structure using denatured-state energetics suggests that the algorithm may be capturing local energetics that are specific to different structure types. To address this question, the propensity of each secondary-structure type for each thermodynamic environment was calculated (see Fig. 6), and four important observations can be made from the calculated propensities. First, the propensity of each secondary structure for different thermodynamic environments is nonrandom in both the native and the denatured states, resulting in “thermodynamic signatures” for different secondary structural elements. Second, within the native state, there appear to be only two general signatures, one that is shared by regular secondary structures (i.e., α-helix and β-strand) and one that is shared by irregular structures (coil and turn). Positions that adopt either α-helices or β-strands have positive propensities for environments TEN 5 and 6, which correspond to the most stable regions in the proteins, and negative propensities for TEN 1, 2, and 8, which correspond to the least stable regions of the proteins. On the other hand, positions that adopt either coil or turn have positive propensities for environments TEN 1, 2, and 8 and negative propensities for TEN 4,5, and 6. Third, unlike the native-state signatures, the thermodynamic signatures for regular secondary structures (i.e., α-helix and β-strand) within the denatured-state thermodynamic environments show clear differences. Positions that adopt α-helix in the folded protein show preferences to be in TED 1,2,3,4, and 5 (i.e., the most stable environments in the denatured ensemble), whereas positions that adopt β-strand prefer TED 7 and 8 (i.e., the least stable regions). Fourth, although the signatures for α-helix and β-strand (and to a lesser extent, turn) contain strong propensities, there are no significant propensities for coil when compared to the magnitude of the propensities in the native thermodynamic environments. In summary, the propensities in Fig. 6 show clearly that while the thermodynamics of the native state can discriminate between regular and nonregular structure, the denatured-state thermodynamics appear to discriminate between different types of regular structure.
Fig. 6.
Secondary-structure propensities for TENs and TEDs. In each plot, the eight environments are aligned on the ordinate and the log-odds probabilities of the secondary structure are plotted against the abscissa. The log-odds probabilities of (a) α-helices, (b) β-strands, (c) coils, and (d) turns were calculated for both TEN (black bar) and TED (gray bar). In each panel, the eight thermodynamic environments appear in order of decreasing stability, with the highest stability environment on the left and the lowest stability environment on the right.
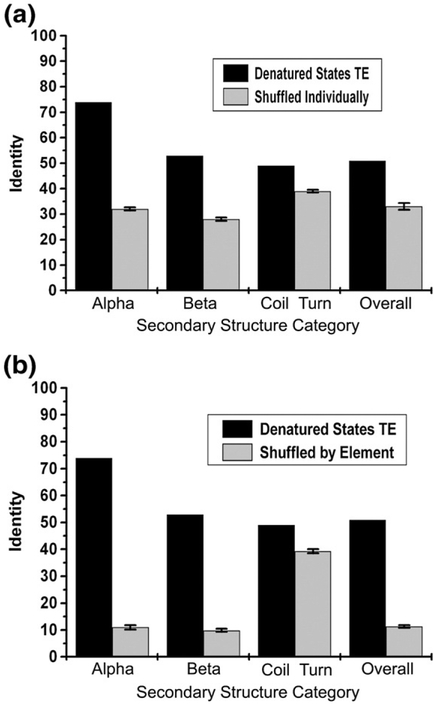
The clear separation of thermodynamic propensities (Fig. 6) based on the secondary structure adopted by that position in the final fold opens the possibility that calculations using TED may be useful for making inferences about secondary structure. To challenge this hypothesis, the thermodynamic environment of each position (from the TEDs) was assigned to a secondary structure based on the propensity of observing the structure in that environment (taken from Fig. 6). For example, because α- helix has a high propensity (i.e., >0.2) for TED 1, 2, 4, and 5, any positions with TED 1, 2, 4, or 5 were assigned to α-helix. That assignment was then compared to the secondary structure observed in the native fold. The fraction of matches for each secondary structure using this approximation is shown in Fig. 7 (black bar). For comparison, the number of matches obtained by assigning secondary structure randomly from a fixed number of counts for each secondary-structure type (i.e., controlling for the composition of each secondary structure in the database; Fig. 7a) reveals that the predictions are significant in all cases, but especially for α-helix and β-strand. Similarly, when the results were compared to the number of matches obtained by randomly assigning entire elements to consecutive stretches of positions (i.e., controlling for composition and continuity of each secondary structural element in the database; Fig. 7b), it is clear that in successfully matching sequence to fold, the denatured-state thermodynamic information performs disproportionately well with regular secondary structure, and only marginally well in turns and coils.
Fig. 7.
Comparison of secondary-structure assignments using thermodynamic environment information to the random assignment of secondary structure. The overall identity and those reported for each subcategory (α, β, and coil) using thermodynamic environment information (black bar) was compared to identities calculated using the random assignment of secondary structure (gray bar). (a) Secondary structures were randomly shuffled individually and reassigned to each position. (b) Randomly assigned secondary-structure segments within database. Irregular structures (including coil and turn) were categorized as coil. The identities calculated with the null model were the average of 100 repetitions.
The results presented in Figs. 6 and 7 indicate that the thermodynamic properties of denatured states contain significant fold-encoding information, and that the majority of the positions that are correctly aligned in the fold-recognition experiments are found to be in regions of high α-helix and β-strand content. To investigate whether those results are due simply to our modeling of the denatured ensembles (i.e., that they are composed of states with isolated segments of native-like structure), we next explored the importance of nonnative conformations in modeling the denatured states.
The role of nonnative structures in the denatured-state ensemble
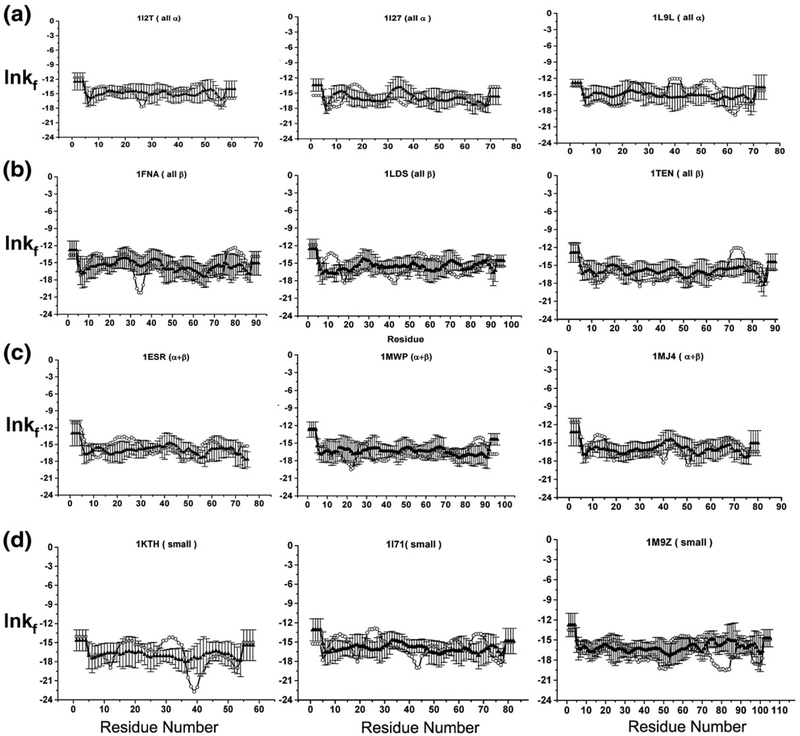
To investigate the importance of the local structural features to the position-specific energetics of the denatured ensemble, the hard-sphere collision model34 was used to generate self-avoiding conformations through random sampling of backbone and side-chain dihedral angles, as described elsewhere.35 For this analysis, 12 proteins from the database were selected (DATASET1) such that each structural class [i.e., all alpha (all-α), all beta (all-β), alpha and beta (α + β), and small proteins (small)] had three representative members. Fifty random structures were generated for each sequence using the hard-sphere collision model (RAND_3D) and the denatured position-specific thermodynamics were calculated in separate experiments for each random structure using the same ensemble-based method that was applied to the original structures (see Materials and Methods).
Although the notion of calculating stability constants for a random conformation appears at first to be paradoxical, the unique computational strategy employed by the COREX/BEST algorithm24–26 allows this calculation to be made in a straightforward manner. Just as with a structured protein, any randomly generated conformation can be defined by a set of atomic coordinates. Of course, in the case of the randomly generated conformation, the resultant chain will not form a compact tertiary structure. There will nonetheless be regions that, due to local structural constraints caused by neighboring residues, will bury surface area, even in a randomly generated chain. We are interested in determining how much surface area is being buried along the sequence in each randomly generated conformation, and we are interested in calculating the energetic cost of burying that surface by comparing the measured value to nominal unfolded-state values for near completely exposed amino acids.24–26,36 In other words, what is the difference between an extended conformation and the randomly generated conformation for an amino acid sequence? By generating multiple conformations for a given sequence and calculating the energetics of local structure formation (i.e., only 5 or 10 residues) with COREX/BEST for each case, we can ascertain (1) whether there is a consistent deviation from the extended conformation, (2) where in the sequence these deviations occur, and (3) what the energetic consequences of these deviation are.
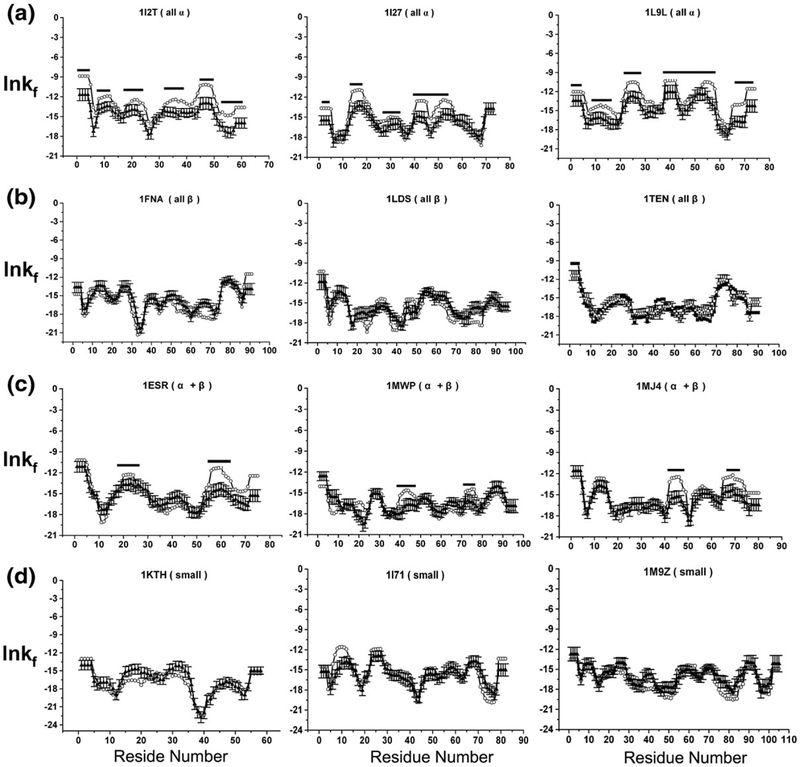
Shown in Fig. 8 for each of the 12 sample sequences (DATASET1) are the position-specific stabilities, ln κf,j, calculated under denaturing conditions and averaged over the 50 random structures. Interestingly, the stability profiles determined under denaturing conditions for the high-resolution structures were practically identical to the averaged stabilities determined for the random structures (with the exception of regions known to adopt α-helix in the native fold, as discussed below). Inspection of Eq. (8) (see Materials and Methods) reveals the origin of this behavior. Because the thermodynamics of the unfolded subensemble for each residue j, 〈ΔGnf,j〉, is dominated by the probability of the completely unfolded state, PU, it is determined from the additive contribution of the individual unfolded state values for each amino acid (Table 1).24,25,37–39 As such, 〈ΔGnf,j〉 for each amino acid is independent of conformation, and the variation in the magnitude of ln κf,j for each conformation, taken at each position, is reporting on the variability of 〈ΔGf,j〉. The similarities in the ln κf,j pattern for each conformation calculated from different denatured-state structures (Fig. 8) indicates that the differences in stability between the different regions of the sequence are far greater than the stability variation between each alternative conformation for a specific region. In other words, the peaks and valleys that are visible in each sequence provide an ensemble-averaged “foldability” metric (i.e., the probability of finding that residue in the context of its sequence neighbors in a unique conformation, relative to being disordered). We distinguish foldability from stability because stability refers to the energy of a particular structure, relative to the unfolded state, whereas the foldability describes the average stability of multiple conformations and is surprisingly insensitive to the structure. The foldability is instead determined primarily by the sequence.
Fig. 8.
Examining the effect of native structure to calculated position-specific stability ([ΔG]j) in denatured ensembles. Twelve proteins, three from each structural class [(a) all α, (b) all β, (c) α + β (d) small] were randomly selected (DATASET1, open circles). The [ΔG]j values calculated for each of the 12 proteins were compared to the null model where the protein structures were generated randomly (RAND_3D, filled triangles with error bars). Regions of α helices are highlighted with a black bar.
Table 1.
Amino acid denatured-state properties
| Ala | Arg | Asn | Asp | Cys | Gin | Glu | Gly | His | He | |
|---|---|---|---|---|---|---|---|---|---|---|
| ASAex,apol (Å2)a | 70.0 | 87.1 | 38.1 | 42.1 | 30.3 | 65.0 | 71.1 | 26.2 | 90.0 | 110.7 |
| ASAex,pol (Å2)a | 36.1 | 126.1 | 104.0 | 95.0 | 75.1 | 121.6 | 94.3 | 43.1 | 68.0 | 10.9 |
| ΔSSC (cal·mol−1·KT−1)b | 0.00 | −0.84 | 2.24 | 2.16 | 0.61 | 2.12 | 2.27 | 0.00 | 0.79 | 0.67 |
| ΔSbb (cal·mol−1·K−1)c | 4.10 | 3.40 | 3.40 | 3.40 | 3.40 | 3.40 | 3.40 | 6.50 | 3.40 | 2.18 |
| ASAex,apol(Å2)a | 122.3 | 101.3 | 104.6 | 186.8 | 100.8 | 55.1 | 79.5 | 184.5 | 175.8 | 88.7 |
| ASAex,pol (Å2)a | 27.5 | 79.0 | 64.0 | 36.5 | 15.6 | 81.9 | 41.1 | 52.3 | 71.1 | 17.8 |
| ΔSSC (cal·mol−1·KT−1)b | 0.25 | 1.02 | 0.58 | 1.51 | 0.00 | 0.55 | 0.48 | 1.15 | 1.74 | 1.29 |
| ΔSbb (cal·mol−1·K−1)c | 3.40 | 3.40 | 3.40 | 3.40 | 3.40 | 3.40 | 3.40 | 3.40 | 3.40 | 2.18 |
Solvent-accessible apolar (ASAex,apol) and polar (ASAex,pol) surface area for each amino acid in the denatured state.24,25,39
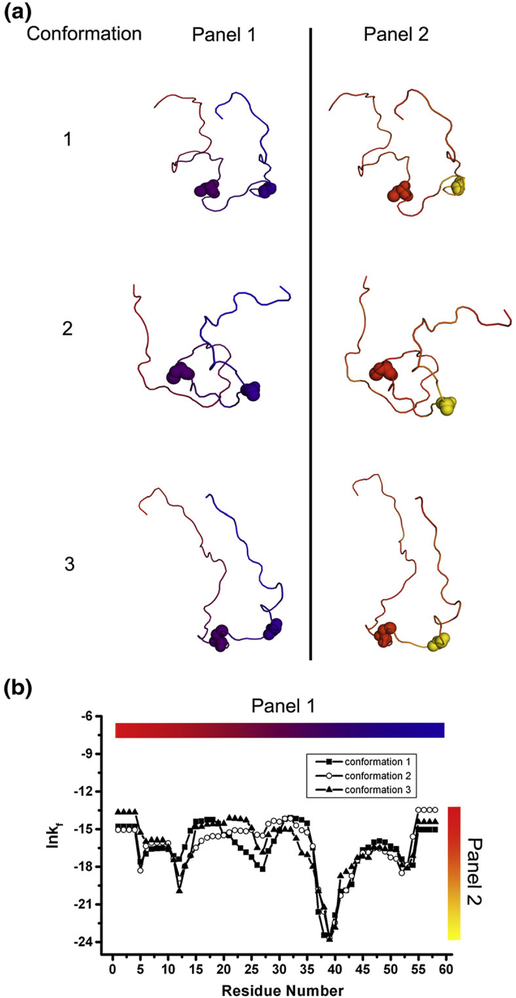
Although the negative sign for ln κf,j in Fig. 8 indicates that the denatured ensemble is dominated by a broad conformational repertoire at every position, there are, nonetheless, significant position-specific differences in the foldability metric. For example, the difference between the denatured-state foldability at positions 33 and 40 of the protein 1KTH (Fig. 9) reveals that regardless of the specific conformation, position 40 is 20,000 times less likely to adopt a unique conformation than position 33, and will instead populate a broader ensemble. In other words, the combined probability for the ensemble of alternative conformations at position 40 is far greater than at position 33 and ensures that the ensemble will be distributed among many states.
Fig. 9.
Three structures of the small Kunitz-type inhibitor protein (PDB ID 1KTH) generated randomly and the position-specific stability ([ΔG]j) calculated under denatured conditions for each of these structures. (a) The three randomly generated structures. Panel 1 shows conformations colored by residues. Panel 2 shows conformations colored by the position-specific stability. Two residues, 33 (left) and 40 (right), are rendered in spacefill in each structure. The three random structures are clearly different. (b) The position-specific stabilities for the three structures under denatured conditions. Clearly, the structures generated randomly show similar denatured state stability profiles.
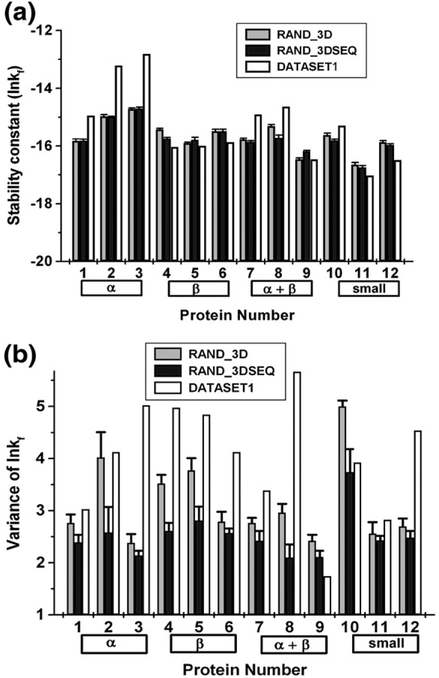
The sequence contributions to the observed stabilities in Fig. 8 were investigated further by comparing the denatured stability profiles from the actual sequences to those calculated in an identical manner with sequences that were randomly shuffled (RAND_3DSEQ, Fig. 10). Several observations can be made from these comparisons. First, the sequence composition determines the mean stability for each protein with little deviation from this mean, even when the sequence has been shuffled several times (Fig. 11a). The difference between the mean value when only the native structure was randomized and the case where both the sequence was shuffled and the structure was randomized is not statistically significant (P = 0.77). Second, the ordering of amino acids within a sequence impacts the variance of residue stabilities (P = 0.03), indicating that neighboring residues have significant stabilizing and destabilizing contributions (Fig. 11b) and that the thermodynamics that are calculated at each position are not simply reporting on the properties of the individual amino acids.
Fig. 10.
Examination of sequence contribution to the position-specific stability values in 12 proteins. Changes in position-specific stability were investigated between proteins with randomly generated structures (RAND_3D, open circles) and randomly generated structures plus randomly shuffled sequences serving as a second null model (RAND_3DSEQ, filled triangles with error bars). The same proteins from DATASET1 were used.
Fig. 11.
Sequence composition affects the mean observed stability, while sequence order effects the observed variance. (a) The mean position-specific stability ([ΔG]j) and (b) observed variance for each protein of DATASET1 (white), RAND_3D (gray), and RAND_3DSEQ (black) were calculated.
Is the denatured state poised to minimize unfavorable folding?
A significant observation from Fig. 8 is that segments of protein that ultimately adopt α-helix in the native structure are more stable under denaturing conditions using the denatured state that consists of only native-like conformations. The origin of this increase in stability is that the helical structure is significantly more compact and stable than randomly selected conformations and represents a very narrow region of the conformational space sampled in the random generation of states. Nonetheless, it is note-worthy that in spite of this built-in bias, sequence segments destined for α-helix show peaks in structure-forming propensity (i.e., in the foldability of the sequence), even when randomly generated structures were used, indicating that these segments of protein have a comparatively low energetic cost associated with constraining the ensemble to a unique structure. In fact, reinspection of Figs. 4 and 6 reveal that the positive propensities that were found in the most stable environments (i.e., TE1D and TE4D) are only those segments destined for α-helix. Sequences destined for all other secondary structures have low intrinsic structure-forming capability (i.e., they are represented by troughs in Fig. 8). Likewise, sequence segments with high intrinsic structure-forming capability (i.e., peaks in Fig. 8) have among the highest negative propensities for β-sheet. In other words, relative to all other secondary structure, β-forming sequences characteristically favor high conformational degeneracy when in isolation.
The presence of residual structure in denatured proteins has been the subject of intensive study40–44 because of the perceived importance of residual structure in determining the folding pathway. The structural thermodynamic characterization of the denatured state described here reveals interesting and previously unreported trends that support a framework model of protein folding.45,46 Specifically, the denatured state is predicted to be macroscopically heterogeneous, with the propensity for any single structure being highly improbable across the entire sequence. Within this background, many regions, particularly those destined for α-helix or coil, will flicker (in the context of small isolated segments) into the folded conformation far more often than those regions destined for other secondary structures (Fig. 12). Indeed, the existence of residual structure in the denatured state as well as regional difference in the propensity to form structure has been observed experimentally.42,44 More important, however, is that our results provide a statistical picture, which reveals that regions destined for β-sheet will form unique local structure much less often than random. In effect, the denatured-state thermodynamics (particularly with regard to β and α-helical structures) are characterized by strong negative propensities (Fig. 6).
Fig. 12.
Schematic representation of the denatured-state energy landscape. Shown is a hypothetical unfolded protein (top), which is depicted as having no structural propensity. The strong negative bias for β-structure formation coupled to the modest propensity for α-helix and coil structure formation suggests that the subpartition function for states involving isolated folded segments of helix and coil (Qα/C, left) is significantly higher than the subpartition function for states where isolated segments of β-strand (Qβ/T, right) are folded. By minimizing the Qβ/T subensemble, the probability is decreased for misfolding events (pathways 3 and 4), and the folding flux25 through potentially hazardous pathways is decreased (pathway 2). We note that the precollapse equilibrium does not obligatorily signify that nucleation between different parts of the structure and subsequent folding occurs only through helix and coil, only that those segments in isolation have high folding probabilities.
Although our studies do not establish the underlying reasons why protein denatured states have evolved with these propensities, there is at least one plausible hypothesis. Because β-strands interact with other β-strands through backbone hydrogen bonding, the potential for partnering through incorrect strand formation is relatively high. α-Helices, however, presumably exclude potential nonspecific backbone interactions through the formation of local i to i + 4 hydrogen bonds of the helix. As a consequence, most of the favorable (and unfavorable) interactions between helical regions can, in principle, be controlled or modulated through individual site mutations, as they will involve mostly side-chain interactions. Controlling for incorrect β-strand pairing, on the other hand, will be less amenable to modulation through single-site mutation and would presumably require a more global solution. Our results provide insight into such a solution. The thermodynamic architecture of the denatured state indicates that the denatured ensemble is biased in a way that minimizes the probability of equilibrium states that could promote folding to non-productive end states (Fig. 12). It is interesting that protein misfolding into amyloid fibrils has been associated with β structure formation, indicating that nonspecific β structure is indeed a potential problem.47,48 The fact that our results suggest that the denatured states evolved to minimize this problem raises the possibility that the determinants of amyloid propensity for a sequence may be found in the denatured-state thermodynamics, rather than in the properties of the native state. Whether this is indeed the case awaits further study.
Equally as important as the strong negative preference for structure formation in sequences that adopt β structure in the final fold are the positive propensities for structure formation in sequences that adopt α-helix. For function, molecular recognition features were identified in ID regions involved in protein–protein interactions.49,50 Interestingly, sequence analysis of those ID regions predicted α-helical structure, which was ultimately verified when high-resolution structural data of the bound complexes became available. It has been postulated that the presence of preformed structural elements in the ID regions may help to facilitate molecular recognition and transient binding.19 Although we cannot rule out the possibility that α-helices may be especially useful for facilitating the recognition process in these ID proteins, the observed abundance of helix in ID regions is consistent with the need to minimize non-specific interactions. For proteins that utilize disorder for function, a strong negative preference for β structure would minimize the probability of amyloid formation47,48 when the sequence is unfolded and most vulnerable to nonspecific β structure.
Finally, the high negative preference for structure formation in sequences that adopt β in the native fold could have significant implications for fold prediction. Specifically, numerous efforts have sought to understand β-sheet specificity by elucidating the determinants of β formation and establishing propensity scales.51–56 Our results, however, would suggest that those regions that adopt β structure are “less committed” to a particular conformation and that the determinants would be largely context dependent. Based only on our energetic considerations, folding into β could be viewed more as the consequence of other regions adopting a specific fold, as opposed to being a determinant of a particular fold. Indeed, our results are consistent with the studies of Minor and Kim,57 who conclude that β-sheet propensities, unlike helical propensities, are largely determined by the tertiary context.
Conclusions
The results presented here reveal that the overall fold that a sequence will adopt is not simply determined by the energetics of the final structure, but can also be determined by energetics in the denatured state. Under denaturing conditions, the energy landscape of the protein ensemble contains significant protein fold-encoding information, and this information is distinctly different from the information derived under native conditions. The fact that the denatured-state thermodynamic information is sufficient to match sequence to the thermodynamic signature almost 100% of the time within a database of structures suggests that the properties are robustly encoded. Information in denatured states is also found to correlate with secondary-structure elements in the folded native protein and appears to support a framework model of protein folding. Namely, the denatured ensemble strongly disfavors structure formation in most regions, especially those forming β-strands in the final fold. Somewhat positive propensities for structure in coil and helices promote “flickering” structure formation, which would presumably allow productive nucleation and intermediate folding. The high negative propensities for folding of β and turn, on the other hand, would prevent nonspecific structure accretion. Equally as important is the observation that the correlations between structure and energy in the denatured state are described by negative propensities, suggesting that the evolution of protein folds has been driven to a considerable extent by negative selection. Finally, because the partitioning of the energetic landscape can be successfully correlated to the structural features in the native state, it suggests that the denatured-state thermodynamics may also contain functional clues. Although this is an intriguing possibility, the validity of this hypothesis awaits further study.
Materials and Methods
Data sets used for analysis
Nonredundant data set of H. sapiens proteins
A data set of nonredundant H. sapiens proteins with protein structures in the Protein Data Bank (PDB) was curated for this analysis. This data set contained 122 proteins with a total of 17,802 residues. The selection criteria for this data set are as follows: (1) proteins containing 50–250 amino acids with a maximum of 50% sequence identity within the set; (2) only X-ray structures having a resolution better than 2.5 Å. These criteria were set with consideration for computational demands and structure quality. The PDB IDs for the data set are 1A17, 1A3K, 1AD6, 1ALY, 1B56, 1B9O, 1BD8, 1BIK, 1BKF, 1BKR, 1BR9, 1BUO, 1BY2, 1BYQ, 1CBS, 1CDY, 1CLL, 1CTQ, 1CY5, 1CZT, 1D7P, 1DV8, 1E21, 1E87, 1EAZ, 1ESR, 1FAO, 1FIL, 1FL0, 1FNA, 1FNL, 1FP5, 1FW1, 1G1T, 1G96, 1GEN, 1GGZ, 1GH2, 1GLO, 1GNU, 1GP0, 1GQV, 1GR3, 1GSM, 1H6H, 1HDO, 1HDR, 1HMT, 1HNA, 1HUP, 1HZI, 1I1N, 1I27, 1I2T, 1I4M, 1I71, 1I76, 1IAM, 1IAP, 1IFR, 1IHK, 1IJR, 1IJT, 1IKT, 1IMJ, 1J74, 1JHJ, 1JK3, 1JSF, 1JSG, 1JWF, 1JWO, 1K04, 1K1B, 1K59, 1KAO, 1KCQ, 1KEX, 1KMV, 1KPF, 1KTH, 1L8J, 1L9L, 1LCL, 1LDS, 1LN1, 1LPJ, 1LSL, 1M7B, 1M9Z, 1MFM, 1MH1, 1MH9, 1MJ4, 1MWP, 1N6H, 1NKR, 1PBK, 1PBV, 1PHT, 1POD, 1QB0, 1QDD, 1QKT, 1QUU, 1RBP, 1RLW, 1SRA, 1TEN, 1TN3, 1ZON, 1ZXQ, 2ABL, 2CPL, 2FCB, 2FHA, 2ILK, 2PSR, 2TGI, 3FIB, 3IL8, and 5PNT.
DATASET1
This data set contains 12 randomly selected proteins from the nonredundant data set described above for a more in-depth analysis of sequence and structural contributions to the observed stability. Three proteins were selected from four diverse Structural Classification of Proteins (SCOP) categories [all α (PDB IDs 1I2T, 1I27, 1L9L), all β (PDB IDs 1FNA, 1LDS, 1TEN), α + β (PDB IDs 1ESR, 1MWP, 1MJ4), and small (PDB IDs 1KTH, 1I71, 1M9Z) to construct a representative data set.
RAND_3D (NULL MODEL1)
The null model used to investigate the structural contribution to the calculated energetics that were generated for DATASET1 was called RAND_3D. Random structures were generated for each protein of DATASET1 using an algorithm based on the hard-sphere collision model, MPMOD, as described elsewhere.35 Fifty random structures were generated for each protein. Position-specific energetics were then calculated for each of the random structures generated using COREX/BEST, as described below. Because the ensemble under denaturing conditions is dominated by states that have 5 or 10 residues folded, there are no tertiary interactions in any of the most probable states. As such, all of the interactions are local, arising from buried surface associated with small groups of residues that are contiguous in sequence. When random structures are generated with MPMOD, the fact that they are random means they will not have native interactions like a folded globular protein. They will however, have local structure that can be compared to the local native-like structure under denatured conditions. Thus, while the MPMOD-generated structures cannot be used to compare alternative native folds, they can be used to compare the stability of native structural elements (taken in isolation) with local structure observed in the MPMOD calculations.
RAND_3DSEQ (NULL MODEL2)
The null model used to investigate the sequence contributions to the calculated energetics that were generated for DATASET1 was called RAND_3DSEQ. The sequence from each protein in DATASET1 was first shuffled randomly and then structures were generated randomly in the same manner as for RAND_3D (see above). Sequences were shuffled randomly 10 times with 50 random structures generated for each of the shuffled sequences. Position-specific energetics were then calculated for each of the random structures generated using COREX/BEST, as described below.
The COREX/BEST algorithm
The COREX/BEST algorithm is a statistical thermodynamic model in which a native protein is depicted as an ensemble of states rather than as a single static structure.24,25 The thermodynamic properties of each of the 122 proteins in the H. sapiens data set was calculated using this algorithm. For proteins larger than 80 residues, due to computational intractability, Monte Carlo sampling was used to generate ensembles.29 For proteins less than 80 residues, all states in an ensemble were fully enumerated.
We describe the COREX/BEST algorithm briefly here and ask readers to refer to references for additional detail.25 Under equilibrium conditions, the probability of any given microstate, i, in the ensemble is given by:
| (3) |
where Ki = e(−ΔGi/RT) is the statistical weight of each microstate and the summation in the denominator is the partition function, Q, for the system. The Gibbs free energy for each microstate, ΔGi, is calculated as:
| (4) |
where W is an entropy weighting factor used to control the contributions of unfolded states.
Perturbing the ensemble to favor native or denatured subensembles
This entropy weighting factor enables us to perturb the ensemble to favor denatured or natively folded states, allowing us to investigate thermodynamic properties calculated under natively folded or denaturing conditions. For the calculation of the position-specific thermodynamic properties, an entropy weighting factor of W = 0.5 was used to increase the population of natively folded states in an ensemble, while W = 1.5 was used to favor the unfolded ensemble states. It should be noted that changes in W have very little impact on the relative distribution of states within a particular subensemble (e.g., fraction unfolded = 80–100%) because the ΔSconf values are generally proportional to fraction unfolded. Thus, changes in W provide a means of alternately studying the energetics of the native and denatured subensembles without interference from the other subensemble.
The COREX/BEST energy function
The solvation terms of Eq. (4) were separated into their component apolar and polar contributions using accessible surface area (ASA)-based parameterized equations:24,37,39,58
| (5) |
| (6) |
The conformational entropy term of Eq. (4), ΔSconf, was determined as described previously.37,38 Simulation temperature was set at 25 °C and the window size for local unfolding was five residues with a minimum window size set at four residues.
An important statistical descriptor of the equilibrium can be evaluated for each residue in the protein, which is defined as the residue stability constant, κf,j.24 This quantity is the ratio of the summed probability of all states in the ensemble in which a particular residue j is in a folded conformation (∑Pf,j) to the summed probability of all states in which j is in an unfolded conformation (∑Pnf,j):
| (7) |
From the stability constant, the position-specific free energy can be written as:
| (8) |
The importance of the stability constant is that it has been shown to closely match hydrogen–deuterium exchange protection factors24 and thus represents an experimentally verifiable description of the energy landscape.
The COREX/BEST analysis of random conformations
COREX/BEST models states as being combinations of folded and unfolded regions. According to the algorithm, folded regions utilize the atomic coordinates to determine ASAs, while unfolded regions have their surface areas computed from the table of unfolded state surface areas (Table 1). COREX/BEST generates an ensemble by using a binomial expansion to systematically treat all folding units (i.e., five residue segments) of the protein as being either folded or unfolded in all possible combinations. For instance, for a 50-amino-acid protein, there will be 10 folding units. In the first state, residues 1–5 will be treated as folded, and 6–50 will be treated as unfolded. The total surface area for that state will be the sum of the computed solvent-accessible surface area39 for the random structure for residues 1–5 and the unfolded state values for residues 6–50. Because we are interested in the energetics of local structure formation, the denatured ensemble only includes those states that have two or less folding units folded.
Position-specific thermodynamic descriptors
Parsing Eq. (4) into its component parts allowed for the calculation of four position-specific thermodynamic descriptors, which were then calculated by taking the difference in the weighted sum between those ensemble states in which a particular residue j was folded relative to the states that were unfolded. This was done for the free energy, [ΔG]j the apolar and polar enthalpies, [ΔH]apol,j and [ΔH]pol,j, respectively, and the conformational entropy, [ΔS]confj
| (9) |
| (10 |
| (11) |
Quantities in the folded and unfolded subensembles were calculated as described previously:21,23
| (12) |
| (13) |
Defining thermodynamic environments
The partitioning around medoids clustering method was used to cluster all 17,802 residues in the H. sapiens data set based on the four position-specific thermodynamic descriptors ([ΔG]j, [ΔH]apol,j, [ΔH]pol,j, and T[ΔS]conf,j) to identify in separate experiments 2, 4, 6, 8, 10, 12, 14, 16, and 18 medoids. Thermodynamic environments were labeled according to clustering of medoids. Manhattan distance was used to measure dissimilarity between medoids. The clustering analyses were performed using the S-Plus 6.0 professional software. TENs were defined by clustering all residues using the four position-specific thermodynamic descriptors for ensembles under native conditions. TEDs were defined by clustering all residues using the four position-specific thermodynamic descriptors for ensembles under denaturing conditions.
Log-odds probability calculations for each residue in each thermodynamic environment
Double-normalized log-odds probabilities (LOP) of each amino acid in thermodynamic environments were calculated21 as:
| (14) |
where AATE is the number of a particular amino acid in a specific thermodynamic environment (TE), TotalAA is the total number of a particular amino acid, TotalTE is the number of residues in the database in a particular TE, and Totalresidues is the total of all residues in the database.
Log-odds probability calculations for secondary structures in each thermodynamic environment
Secondary structures were assigned to each residue in the database using the program STRIDE.59 Log-odds probabilities of four secondary-structure categories (alpha, beta, coil, and turn) for each thermodynamic environment were calculated as:
| (15) |
where SSTE is the number of a particular secondary structure (SS) type in a specific thermodynamic environment (TE), TotalSS is the total number of a particular SS, TotalTE is the number of residues in the database in a particular TE, and Totalresidues is the total of all residues in the database.
Fold-recognition experiments
Fold-recognition experiments were performed using PROFILESEARCH of Bowie et al.33 as described previously.21 Based on the clustering results, each protein (profile) in the database was represented as a one-dimensional string with each residue assigned to a thermodynamic environment. There were 431 decoy sequences,21 including the 122 native sequences in our data set from which correct fold recognition was tested. PROFILE-SEARCH implements the Smith-Waterman local alignment algorithm60 that was used to align each profile to each sequence in the database. Log-odds probabilities of amino acids in thermodynamic environments [Eq. (15)] were used to construct a scoring matrix for alignment. Gaps were allowed with open and extension penalties set at the PROFILESEARCH defaults. A successful fold-recognition experiment was one in which the native sequence had an alignment Z score among the top 4 (1%) scores out of the total 431 sequences that were scored.
Alignment identity calculations
Alignments between TEs and sequence were obtained based on PROFILESEARCH output. With these alignments, identities based on thermodynamic environment, secondary structure, and residue identities were calculated. Identity was calculated as the percentage of matched positions divided by total length of alignment. To test secondary structural alignment, each residue in the aligned sequence was assigned according to the log-odds probabilities of secondary structures in thermodynamic environments. For example, if α-helices have a positive log-odds probability in thermodynamic environment 1, residues in this environment were classified as α-helical. Secondary-structure assignment for residues in target sequences, the template structure used for fold recognition, was assigned using the program STRIDE.59 The alignment identities between these two assignments were then calculated.
Statistical tests
All statistical tests were performed using the open statistics software, R†. The simple t test was used to compare (1) the mean identity between the denatured ensemble alignment and the native ensemble alignment, (2) the mean of the stability profiles between DATASET1 and RAND_3D, (3) the mean of the stability profiles between RAND_3D and RAND_3DSEQ and (4) the variance of the stability profiles between RAND_3D and RAND_3DSEQ. The threshold for significance was set at α = 0.05.
Acknowlegements
This study was supported by National Science Foundation grant MCB-0406050 and the Robert A. Welch Foundation grant H-1461. We thank Dr. Jamie Wrabl for helpful discussions and thoughtful critiques of this work.
Abbreviations used:
- ID
intrinsically disordered
- TEN
native-state thermodynamic environment
- TED
denatured-state thermodynamic environment
- ASA
accessible surface area
References
- 1.Dill KA & Shortle D (1991). Denatured states of proteins. Annu. Rev. Biochem 60, 795–825. [DOI] [PubMed] [Google Scholar]
- 2.Tompa P (2003). The functional benefits of protein disorder. J. Mol. Struct.: THEOCHEM, 666, 361–371. [Google Scholar]
- 3.Wright PE & Dyson HJ (1999). Intrinsically unstructured proteins: re-assessing the protein structure-function paradigm. J. Mol. Biol 293, 321–331. [DOI] [PubMed] [Google Scholar]
- 4.Ross CA & Poirier MA (2004). Protein aggregation and neurodegenerative disease. Nat. Med 10 (Suppl.), S10–S17. [DOI] [PubMed] [Google Scholar]
- 5.Romero P, Obradovic Z & Dunker AK (2004). Natively disordered proteins: functions and predictions. Appl. Bioinf 3, 105–113. [DOI] [PubMed] [Google Scholar]
- 6.Chen JW, Romero P, Uversky VN & Dunker AK (2006). Conservation of intrinsic disorder in protein domains and families: II. Functions of conserved disorder. J. Proteome Res 5, 888–898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kukreja R & Singh B (2005). Biologically active novel conformational state of botulinum, the most poisonous poison. J. Biol. Chem 280, 39346–39352. [DOI] [PubMed] [Google Scholar]
- 8.Bledsoe RK, Montana VG, Stanley TB, Delves CJ, Apolito CJ, McKee DD et al. (2002). Crystal structure of the glucocorticoid receptor ligand binding domain reveals a novel mode of receptor dimerization and coactivator recognition. Cell, 110, 93–105. [DOI] [PubMed] [Google Scholar]
- 9.Dunker AK & Obradovic Z (2001). The protein trinity–linking function and disorder. Nat. Biotechnol 19, 805–806. [DOI] [PubMed] [Google Scholar]
- 10.Meszaros B, Tompa P, Simon I & Dosztanyi Z (2007). Molecular principles of the interactions of disordered proteins. J. Mol. Biol 372, 549–561. [DOI] [PubMed] [Google Scholar]
- 11.Iakoucheva LM, Kimzey AL, Masselon CD, Bruce JE, Garner EC, Brown CJ et al. (2001). Identification of intrinsic order and disorder in the DNA repair protein XPA. Protein Sci. 10, 560–571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hilser VJ & Thompson EB (2007). Intrinsic disorder as a mechanism to optimize allosteric coupling in proteins. Proc. Natl Acad. Sci. USA, 104, 8311–8315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Uversky VN (2002). What does it mean to be natively unfolded? Eur. J. Biochem 269, 2–12. [DOI] [PubMed] [Google Scholar]
- 14.Blow DM (1977). Flexibility and rigidity in protein crystals. Ciba Found. Symp 60, 55–61. [DOI] [PubMed] [Google Scholar]
- 15.Ringe D & Petsko GA (1986). Study of protein dynamics by X-ray diffraction. Methods Enzymol. 131, 389–433. [DOI] [PubMed] [Google Scholar]
- 16.Peng K, Radivojac P, Vucetic S, Dunker AK & Obradovic Z (2006). Length-dependent prediction of protein intrinsic disorder. BMC Bioinf. 7, 208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tompa P (2002). Intrinsically unstructured proteins. Trends Biochem. Sci 27, 527–533. [DOI] [PubMed] [Google Scholar]
- 18.Hennig M, Bermel W, Spencer A, Dobson CM, Smith LJ & Schwalbe H (1999). Side-chain conformations in an unfolded protein: chi1 distributions in denatured hen lysozyme determined by heteronuclear 13C, 15N NMR spectroscopy. J. Mol. Biol 288, 705–723. [DOI] [PubMed] [Google Scholar]
- 19.Fuxreiter M, Simon I, Friedrich P & Tompa P (2004). Preformed structural elements feature in partner recognition by intrinsically unstructured proteins. J. Mol. Biol 338, 1015–1026. [DOI] [PubMed] [Google Scholar]
- 20.Kumar R, Baskakov IV, Srinivasan G, Bolen DW, Lee JC & Thompson EB (1999). Interdomain signaling in a two-domain fragment of the human gluco-corticoid receptor. J. Biol. Chem 274, 24737–24741. [DOI] [PubMed] [Google Scholar]
- 21.Larson SA & Hilser VJ (2004). Analysis of the “thermodynamic information content” of a Homo sapiens structural database reveals hierarchical thermodynamic organization. Protein Sci. 13, 1787–1801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wrabl JO, Larson SA & Hilser VJ (2001). Thermodynamic propensities of amino acids in the native state ensemble: implications for fold recognition. Protein Sci. 10, 1032–1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wrabl JO, Larson SA & Hilser VJ (2002). Thermodynamic environments in proteins: fundamental determinants of fold specificity. Protein Sci. 11, 1945–1957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hilser VJ & Freire E (1996). Structure-based calculation of the equilibrium folding pathway of proteins. Correlation with hydrogen exchange protection factors. J. Mol. Biol 262, 756–772. [DOI] [PubMed] [Google Scholar]
- 25.Hilser VJ, Garcia-Moreno EB, Oas TG, Kapp G & Whitten ST (2006). A statistical thermodynamic model of the protein ensemble. Chem. Rev 106, 1545–1558. [DOI] [PubMed] [Google Scholar]
- 26.Hilser VJ & Freire E (1997). Predicting the equilibrium protein folding pathway: structure-based analysis of staphylococcal nuclease. Proteins, 27, 171–183. [DOI] [PubMed] [Google Scholar]
- 27.Hilser VJ, Dowdy D, Oas TG & Freire E (1998). The structural distribution of cooperative interactions in proteins: analysis of the native state ensemble. Proc. Natl Acad. Sci. USA, 95, 9903–9908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Liu T, Whitten ST & Hilser VJ (2006). Ensemble-based signatures of energy propagation in proteins: a new view of an old phenomenon. Proteins, 62, 728–738. [DOI] [PubMed] [Google Scholar]
- 29.Pan H, Lee JC & Hilser VJ (2000). Binding sites in Escherichia coli dihydrofolate reductase communicate by modulating the conformational ensemble. Proc. Natl Acad. Sci. USA, 97, 12020–12025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Whitten ST, Garcia-Moreno EB & Hilser VJ (2005). Local conformational fluctuations can modulate the coupling between proton binding and global structural transitions in proteins. Proc. Natl Acad. Sci. USA, 102, 4282–4287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Babu CR, Hilser VJ & Wand AJ (2004). Direct access to the cooperative substructure of proteins and the protein ensemble via cold denaturation. Nat. Struct. Mol. Biol 11, 352–357. [DOI] [PubMed] [Google Scholar]
- 32.Whitten ST, Kurtz AJ, Pometun MS, Wand AJ & Hilser VJ (2006). Revealing the nature of the native state ensemble through cold denaturation. Biochemistry, 45, 10163–10174. [DOI] [PubMed] [Google Scholar]
- 33.Bowie JU, Luthy R & Eisenberg D (1991). A method to identify protein sequences that fold into a known three-dimensional structure. Science, 253, 164–170. [DOI] [PubMed] [Google Scholar]
- 34.Richards FM (1977). Areas, volumes, packing and protein structure. Annu. Rev. Biophys. Bioeng 6, 151–176. [DOI] [PubMed] [Google Scholar]
- 35.Whitten ST, Yang H-W, Fox RO & Hilser VJ (2008). Exploring the effect of conformational bias on the binding of peptides to the SEM5 C-SH3 domain. Protein Sci. 17, 1200–1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Luque I, Mayorga OL & Freire E (1996). Structure-based thermodynamic scale of alpha-helix propensities in amino acids. Biochemistry, 35, 13681–13688. [DOI] [PubMed] [Google Scholar]
- 37.D’Aquino JA, Gomez J, Hilser VJ, Lee KH, Amzel LM & Freire E (1996). The magnitude of the backbone conformational entropy change in protein folding. Proteins, 25, 143–156. [DOI] [PubMed] [Google Scholar]
- 38.Lee KH, Xie D, Freire E & Amzel LM (1994). Estimation of changes in side chain configurational entropy in binding and folding: general methods and application to helix formation. Proteins, 20, 68–84. [DOI] [PubMed] [Google Scholar]
- 39.Murphy KP & Freire E (1992). Thermodynamics of structural stability and cooperative folding behavior in proteins. Adv. Protein Chem 43, 313–361. [DOI] [PubMed] [Google Scholar]
- 40.Baldwin RL (2002). A new perspective on unfolded proteins. Adv. Protein Chem 62, 361–367. [DOI] [PubMed] [Google Scholar]
- 41.Bierzynski A & Baldwin RL (1982). Local secondary structure in ribonuclease A denatured by guanidine·HCl near 1 degree C. J. Mol. Biol 162, 173–186. [DOI] [PubMed] [Google Scholar]
- 42.Kohn JE, Millett IS, Jacob J, Zagrovic B, Dillon TM, Cingel N et al. (2004). Random-coil behavior and the dimensions of chemically unfolded proteins. Proc. Natl Acad. Sci. USA, 101, 12491–12496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lindorff-Larsen K, Kristjansdottir S, Teilum K, Fieber W, Dobson CM, Poulsen FM & Vendruscolo M (2004). Determination of an ensemble of structures representing the denatured state of the bovine acyl-coenzyme a binding protein. J. Am. Chem. Soc 126, 3291–3299. [DOI] [PubMed] [Google Scholar]
- 44.Shortle D (2002). The expanded denatured state: an ensemble of conformations trapped in a locally encoded topological space. Adv. Protein Chem 62, 1–23. [DOI] [PubMed] [Google Scholar]
- 45.Udgaonkar JB & Baldwin RL (1988). NMR evidence for an early framework intermediate on the folding pathway of ribonuclease A. Nature, 335, 694–699. [DOI] [PubMed] [Google Scholar]
- 46.White GW, Gianni S, Grossmann JG, Jemth P, Fersht AR & Daggett V (2005). Simulation and experiment conspire to reveal cryptic intermediates and a slide from the nucleation-condensation to frame-work mechanism of folding. J. Mol. Biol 350, 757–775. [DOI] [PubMed] [Google Scholar]
- 47.Booth DR, Sunde M, Bellotti V, Robinson CV, Hutchinson WL, Fraser PE et al. (1997). Instability, unfolding and aggregation of human lysozyme variants underlying amyloid fibrillogenesis. Nature, 385, 787–793. [DOI] [PubMed] [Google Scholar]
- 48.Dobson CM (2001). The structural basis of protein folding and its links with human disease. Philos. Trans. R. Soc. London, Ser. B, 356, 133–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Mohan A, Oldfield CJ, Radivojac P, Vacic V, Cortese MS, Dunker AK & Uversky VN (2006). Analysis of molecular recognition features (MoRFs). J. Mol. Biol 362, 1043–1059. [DOI] [PubMed] [Google Scholar]
- 50.Vacic V, Oldfield CJ, Mohan A, Radivojac P, Cortese MS, Uversky VN & Dunker AK (2007). Characterization of molecular recognition features, MoRFs, and their binding partners. J. Proteome Res 6, 2351–2366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Chen PY, Lin CK, Lee CT, Jan H & Chan SI (2001). Effects of turn residues in directing the formation of the beta-sheet and in the stability of the beta-sheet. Protein Sci. 10, 1794–1800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kim CA & Berg JM (1993). Thermodynamic beta-sheet propensities measured using a zinc-finger host peptide. Nature, 362, 267–270. [DOI] [PubMed] [Google Scholar]
- 53.Minor DL Jr & Kim PS (1994). Measurement of the beta-sheet-forming propensities of amino acids. Nature, 367, 660–663. [DOI] [PubMed] [Google Scholar]
- 54.Otzen DE & Fersht AR (1995). Side-chain determinants of beta-sheet stability. Biochemistry, 34, 5718–5724. [DOI] [PubMed] [Google Scholar]
- 55.Pal D & Chakrabarti P (2000). beta-sheet propensity and its correlation with parameters based on conformation. Acta Crystallogr., Sect. D: Biol. Crystallogr 56, 589–594. [DOI] [PubMed] [Google Scholar]
- 56.Zaremba SM & Gregoret LM (1999). Context-dependence of amino acid residue pairing in antiparallel beta-sheets. J. Mol. Biol 291, 463–479. [DOI] [PubMed] [Google Scholar]
- 57.Minor DL Jr & Kim PS (1994). Context is a major determinant of beta-sheet propensity. Nature, 371, 264–267. [DOI] [PubMed] [Google Scholar]
- 58.Gomez J, Hilser VJ, Xie D & Freire E (1995). The heat capacity of proteins. Proteins, 22, 404–412. [DOI] [PubMed] [Google Scholar]
- 59.Frishman D & Argos P (1995). Knowledge-based protein secondary structure assignment. Proteins, 23, 566–579. [DOI] [PubMed] [Google Scholar]
- 60.Smith TF & Waterman MS (1981). Identification of common molecular subsequences. J. Mol. Biol 147, 195–197. [DOI] [PubMed] [Google Scholar]