Abstract
Metformin is an important antidiabetic drug and often used as a probe for drug–drug interactions (DDIs) mediated by renal transporters. Despite evidence supporting the inhibition of multidrug and toxin extrusion proteins as the likely DDI mechanism, the previously reported physiologically‐based pharmacokinetic (PBPK) model required the substantial lowering of the inhibition constant values of cimetidine for multidrug and toxin extrusion proteins from those obtained in vitro to capture the clinical DDI data between metformin and cimetidine.1 We constructed new PBPK models in which the transporter‐mediated uptake of metformin is driven by a constant membrane potential. Our models successfully captured the clinical DDI data using in vitro inhibition constant values and supported the inhibition of multidrug and toxin extrusion proteins by cimetidine as the DDI mechanism upon sensitivity analysis and data fitting. Our refined PBPK models may facilitate prediction approaches for DDI involving metformin using in vitro inhibition constant values.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
☑ Metformin is an important antidiabetic drug and a probe drug to predict drug–drug interactions (DDI) mediated by renal transporters. The previously reported physiologically‐based pharmacokinetic (PBPK) models required a substantial lowering of in vitro inhibition constant values to reproduce the observed DDI data, necessitating the development of PBPK models suitable for the bottom‐up prediction of the DDI potential.
WHAT QUESTION DID THIS STUDY ADDRESS?
☑ This study aimed to develop a new PBPK model of metformin and to quantitatively predict DDI between metformin and cimetidine (an inhibitor of organic cation transporter 1/2 and multidrug and toxin extrusion proteins) using in vitro inhibition constant values.
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
☑ The constructed PBPK model incorporated the metformin transport process driven by the membrane potential kept constant and achieved the quantitative prediction of DDI incurred by cimetidine using in vitro inhibition constant values. The simulation results also supported the inhibition of multidrug and toxin extrusion proteins by cimetidine as the DDI mechanism.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
☑ This metformin PBPK model represents an important advancement in quantitatively capturing the DDI mediated by renal transporters using middle‐out approaches.
Metformin is a first‐line therapy for type 2 diabetes, but its response varies substantially, with about 30% of patients failing to achieve glycemic control2, 3 and the rare incidence of severe events of lactic acidosis.4 As such, it is important to understand the factors contributing to interindividual variation in metformin response and to quantitatively predict the potential for drug–drug interactions (DDIs) involving metformin.
The pharmacokinetics of metformin has been well characterized. The oral bioavailability of metformin is 50–60%.5, 6, 7, 8 Metformin undergoes negligible hepatic metabolism, but it is mainly excreted intact into the urine; its renal clearance exceeds the glomerular filtration rate, indicating tubular secretion. With negligible plasma protein binding, metformin slowly distributes to erythrocytes.6, 9 Metformin exists ionized at physiological pHs, relying on transporters for its translocation across cell membranes. Metformin is transported by the organic cation transporters (OCTs), particularly OCT1 in the liver10 and OCT2 in the kidney.11 Multidrug and toxin extrusion proteins (MATEs), namely MATE1 and MATE2‐K are also shown to mediate the extrusion of metformin from proximal renal tubular cells to urine.12 These transporters harbor genetic variations, some of which can impact the pharmacokinetics and pharmacodynamics of metformin.13, 14, 15
Cimetidine is an inhibitor of OCT2 and MATEs and incurs DDIs with metformin; the coadministration of cimetidine increased the systemic exposure of metformin in plasma by ~ 50%, whereas it decreased the renal clearance of metformin by ~ 30%.16, 17 The inhibition of OCT2 by cimetidine had been initially suspected as the DDI mechanism, but it was deemed unlikely as the reported values of the OCT2 inhibition constant (Ki) for cimetidine (ranging from 72.6–510 μM10, 11) are much higher than the maximal unbound plasma concentrations of cimetidine (Cmax; ranging from 7.67–9.48 μM after the oral administration of 400 mg cimetidine).18, 19 The reported Ki values of cimetidine for MATEs range from 1.21–13.5 μM.20, 21, 22 The results from the mouse study (in vitro and in vivo) also supported the inhibition of MATEs as a likely mechanism for the DDI between cimetidine and metformin.21
Physiologically‐based pharmacokinetic (PBPK) modeling analysis allows for quantitative prediction of drug concentration‐time profiles and enhances our mechanistic understanding of DDI.1, 23, 24 For metformin, a minimal PBPK model was previously reported but with no consideration of transporter‐mediated processes.9 Later, whole‐body PBPK models were developed with the mechanistic components reflecting transporter‐mediated processes (by OCT1, OCT2, and MATEs), namely, the conventional model and the “electrochemical model” driven by dynamically changing electrochemical modulation.1 To reproduce clinical DDI data, these models required a substantial lowering of the Ki values of cimetidine for transporters from the in vitro reported values: for the conventional model, the lowering of the Ki values for OCT1 and OCT2 nearly by 500‐fold, and for the electrochemical model, the lowering of the Ki values for OCT1, OCT2, and MATEs by 8~18‐fold.1 Thus, there is a clear need to develop a PBPK model that can quantitatively predict DDIs involving metformin using Ki values obtained in vitro.
We developed a new metformin PBPK model by incorporating hepatic and renal transporter–mediated processes driven by the membrane potential, which is kept constant. Our PBPK model achieved quantitative prediction of DDIs between metformin and cimetidine using in vitro data, supporting the inhibition of MATEs by cimetidine as the major DDI mechanism.
Materials and Methods
Development of the metformin PBPK model
We modified the previously reported model1, 25 by adding erythrocyte compartments and implementing changes in the kidney and the liver (Figure 1 a). The physicochemical and pharmacokinetic parameters of metformin are summarized in Table S1 , and relevant physiological parameters are summarized in Tables S2 and S3 . Adipose, muscle, and skin are incorporated considering their contribution to the distribution volume. Rapid equilibrium was assumed using the tissue‐to‐plasma concentration ratios predicted in silico 26 by physicochemical properties.
Figure 1.
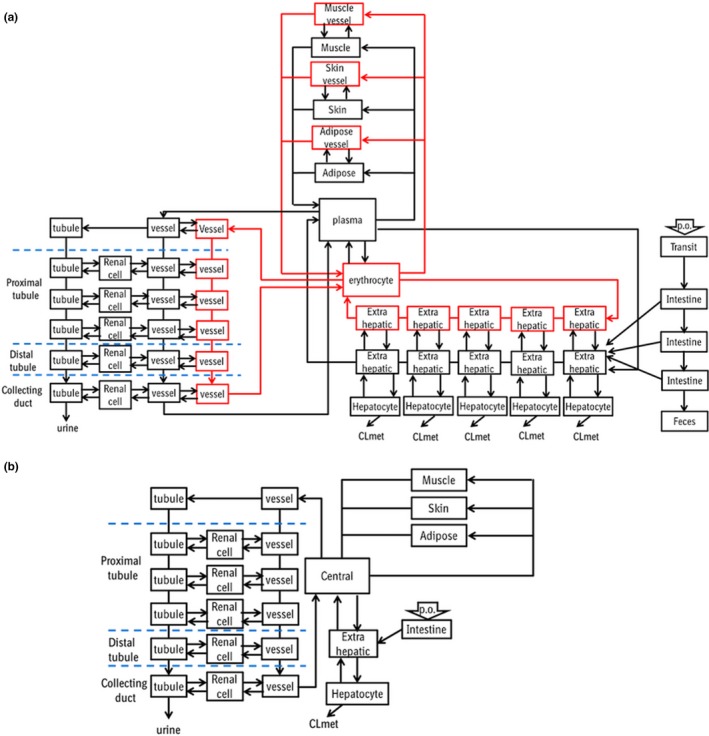
Structures of the physiologically‐based pharmacokinetic models for metformin (a) and cimetidine (b). Erythrocyte compartments were incorporated into all the tissues in the metformin model (red boxes). CL met, metabolic clearance; p.o., per os.
Erythrocyte compartments
Considering its slow distribution to erythrocytes and time‐dependent changes in blood‐to‐plasma concentration ratios,6 the systemic circulation and capillary vessels in all tissues were divided into plasma and erythrocyte compartments. The distribution processes between plasma and erythrocytes are defined in Eqs. (1) and (2).
| (1) |
| (2) |
where X erythro and X plasma are the amount of metformin in the erythrocyte and plasma compartment, respectively, and k in,RBC and k out,RBC are the partitioning rate constants of metformin from plasma to erythrocytes and from erythrocytes to plasma, respectively, and obtained in vitro by measuring time‐dependent blood cell distribution of metformin using human blood9 (Table S1 ).
Liver model
A five‐compartment liver model was used as similar to our previous report.24 Biliary excretion was not included in the model as clinical data indicated that metformin is not excreted into bile. Considering that OCT1 is a bidirectional transporter driven by the membrane potential, the OCT1‐mediated transport is defined using Eq. (3),27 the Michaelis–Menten constant (K m,OCT1), and the maximum rate (Vmax,OCT1).
| (3) |
| (4) |
where PSOCT1,inf and PSOCT1,eff are the intrinsic OCT1‐mediated clearance via influx into and efflux out of hepatocytes, respectively; C HC and C EH are the metformin concentrations inside and outside hepatocytes, respectively; R OCT1,inf/eff is the OCT1‐mediated influx‐to‐efflux ratio; z, Φ, F, R, and T are the valence, the membrane potential, Faraday's constant, the gas constant, and the absolute temperature, respectively. The definitions for the other parameters are provided in the Supplemental Text .
Kidney model
The kidney model comprised the glomerulus, the proximal tubule (further divided into the S1, S2, and S3 regions), the distal tubule, and the collecting duct. The proximal tubule, the distal tubule, and the collecting duct were further divided into the three subcompartments representing the blood vessels, cells, and the urinary lumen, similar to the previous report.1 The active transport of metformin was assumed to occur only in the proximal tubule by OCT2 and MATEs at the basolateral and luminal sides, respectively. Reabsorption of metformin from the urinary lumen was assumed to be mediated by passive diffusion. Considering that OCT2 is a bidirectional transporter driven by the membrane potential, the transport process by OCT2 is defined using Eq. (5), the Michaelis–Menten constant (K m,OCT2) and the maximum rate (Vmax,OCT2).
| (5) |
where PSOCT2,inf and PSOCT2,eff are the OCT2‐mediated intrinsic clearance via influx into and efflux out of renal cells, respectively; R OCT2,inf/eff is the influx‐to‐efflux ratio of OCT2; and C r and C rcell are the metformin concentrations in the blood vessels and renal cells, respectively.
As shown in Eq. (5), our model defined that the OCT2‐mediated transport process is driven by a constant membrane potential, different from the previously reported PBPK model where the membrane potential changed in response to time‐dependent changes in metformin concentrations.1 The transporter‐mediated processes in the liver were similarly defined using the membrane potential kept constant. Intrinsic clearance by MATEs was defined using Eq. (6), the Michaelis–Menten constant (K m,MATE) and the maximum rate (Vmax,MATE).
| (6) |
In the proximal tubule, based on the extended clearance concept,28 the parameters CLint,sec, βkidney, R MATE/dif, γr, and γurine were defined using Eqs. (7), (8), (9), (10), (11), (12), (13), (14):
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
where CLint,sec is the intrinsic urinary secretion clearance; PSr,inf and PSr,eff are the intrinsic renal clearance via influx into and efflux out of renal cells, respectively; PSurine is the intrinsic efflux clearance from renal cells to the urinary lumen; PSr,dif,inf and PSr,dif,eff are the intrinsic passive clearance via influx into and efflux out of renal cells, respectively; PSurine,dif,inf and PSurine,dif,eff are the intrinsic passive clearance via influx into cells from the urinary lumen and efflux out of cells to the urinary lumen; RMATE/dif is the ratio of the intrinsic clearance of MATEs to the intrinsic passive diffusion clearance via efflux out of cells to the urinary lumen; γr and γurine are the passive influx‐to‐efflux ratio on the basolateral and luminal sides, respectively; λ is the ratio of passive diffusion for the ionized form to that for the unionized form; f o,union and f o,ion are the extracellular fractions of the unionized and ionized forms, respectively; f i,union and f i,ion are the intracellular fractions of the unionized and ionized forms, respectively; βkidney is a hybrid parameter reflective of the major rate‐limiting steps of CLint,sec
Metformin (pKa of 12.3) exists mainly ionized at physiological pHs (thus, f o,union = f i,union = 0 and f o,ion = f i,ion = 1), and γr and γurine were calculated using the Nernst equation.29 Passive diffusion clearances of each compartment in the kidney were calculated using permeability measured in a parallel artificial membrane permeability assay system,30 surface area, γr, and γurine (Table S3 ).29, 31
Optimization of model parameters
Other unknown parameters (absorption rate constant, k a; transit rate constant from the transit compartment to the intestinal compartment, k trans; and R MATE/dif) were optimized by fitting to the two clinical data sets obtained after oral administration of metformin at 1,500 mg (time profiles of plasma and blood concentrations and urinary excretion)6 or 250 mg (DDI data between metformin and cimetidine).16 Because reliable βkidney was not estimated from the observed metformin pharmacokinetic data, four different βkidney values (0.1, 0.3, 0.5, and 0.8) were used to cover a wide range of rate‐determining step situations. Unknown parameters were optimized with βkidney fixed (Table 1 ) and used as fixed values for DDI simulation. Under DDI conditions, the βkidney value was not fixed and allowed to change as the renal transport processes became inhibited. Upon oral dosing, metformin showed a less than dose‐proportional increase of area under the curve (AUC), suggesting saturable intestinal absorption processes.32 To reflect such saturation, our PBPK model assumed that metformin is absorbed via first‐order kinetics with the intestinal availability set as 0.57 and 0.84 for the metformin oral doses of 1,500 and 250 mg, respectively (back‐calculated from the bioavailability data, Table S1 ). Between the two data sets (metformin oral doses of 250 mg and 1,500 mg),6, 16 time of maximum concentration (Tmax) values varied (3.3 and 1.5 hours, respectively). The reported Tmax values vary substantially even with the same doses,5, 14, 17 and the adjustment of Tmax was deemed necessary in analyzing the two data sets together. As the same formulation was used in the two clinical studies,6, 16 the data of the 1,500 mg dose were used to obtain the optimized k a value, which was then used for the data of the 250 mg dose. The k trans and R MATE/dif values were optimized by fitting to the observed data after oral dosing of 250 mg metformin16 using varying βkidney values (0.1, 0.3, 0.5, and 0.8).
Table 1.
Optimized physiologically‐based pharmacokinetic model parameters (k a, k trans, and R MATE/dif) after fitting to the oral metformin doses of 1,500 and 250 mg using differing βkidney values
| 1,500 mg metformin | |||||
|---|---|---|---|---|---|
| Observed6 | βkidney | ||||
| 0.1 | 0.3 | 0.5 | 0.8 | ||
| R MATE/dif | – | 153 ± 18.1 | 213 ± 25.5 | 325 ± 39.2 | 814 ± 111 |
| k a (/hour) | – | 0.21 ± 0.013 | 0.21 ± 0.013 | 0.21 ± 0.013 | 0.21 ± 0.013 |
| k trans (/hour) | – | 2.4 ± 0.36 | 2.4 ± 0.36 | 2.4 ± 0.36 | 2.4 ± 0.36 |
| AUC0–24 (mg•h/L) | 21.4 ± 3.18 | 20.1 | 20.1 | 20.2 | 20.2 |
| CLr (L/hour) | 23.0 ± 3.87 | 29.8 | 29.8 | 30 | 30 |
| 250 mg metformin | |||||
|---|---|---|---|---|---|
| Observed16 | βkidney | ||||
| 0.1 | 0.3 | 0.5 | 0.8 | ||
| RMATE/dif | – | 183 ± 30.1 | 261 ± 43.3 | 402 ± 66.3 | 1,143 ± 186 |
| k a (/hour) | – | 0.21 | 0.21 | 0.21 | 0.21 |
| k trans (/hour) | – | 0.61 ± 0.044 | 0.61 ± 0.044 | 0.61 ± 0.044 | 0.61 ± 0.044 |
| AUC0–12 (mg•hour/L) | 3.75 ± 1.43 | 4.12 | 4.12 | 4.12 | 4.12 |
| CLr (L/hour) | 31.6 ± 9.90 | 28.5 | 28.6 | 28.6 | 28.6 |
| Cmax (μg/L) | 590 ± 240 | 502 | 502 | 502 | 502 |
| Tmax (hour) | 3.3 ± 0.8 | 3.72 | 3.72 | 3.72 | 3.72 |
AUC0–24, area under the curve from 0–24 hours; AUC0–12, area under the curve from 0–12 hours; CLr, renal clearance; Cmax, maximum plasma concentration; Tmax, time of maximum concentration; ka,absorption rate; ktrans, the rate from transit compartment to intestine compartment; RMATE/dif, the ratio of the intrinsic clearance of MATEs to the intrinsic passive diffusion clearance via efflux out of cells to the urinary lumen.
Development of the cimetidine PBPK model
The cimetidine PBPK model was developed by implementing several modifications to the metformin PBPK model (Figure 1 b, Supplemental Text ). At physiological pHs, cimetidine (pKa of 6.9) can exist as both ionized and unionized, and their fractions were calculated using the Henderson–Hasselbalch equation (Table S3 ).24, 33 To calculate γh, γr, and γurine of cimetidine using Eq. (10), λ was set to be 0.1 as described previously.29
DDI simulation
DDI simulation was performed by combining the developed metformin and cimetidine PBPK models. Cimetidine was assumed to be a competitive inhibitor in the transport of metformin by OCT1, OCT2, or MATEs, as shown in Eq. (15):
| (15) |
where PSact(control) and PSact(+I) are the intrinsic active clearance of metformin in the absence and the presence of an inhibitor, respectively, and I is the inhibitor concentration.
In vitro Ki (or half maximal inhibitory concentration (IC50)) values of cimetidine were obtained from the reports where the metformin concentration was sufficiently lower than its Km value (Table 2 ).
Table 2.
Sensitivity analysis for AUC, Cmax, and CLr ratios between control and drug–drug interaction conditions using different Ki values for OCT2 and MATEs
| Sensitivity analysis of three different Ki values for OCT2 (72.6, 509, and 159 represent the lowest and highest values and the geometric mean of in vitro Ki values, respectively) and differing βkidney values. The Ki value for MATEs was fixed at the geometric mean value. | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Observed16 | βkidney = 0.1 | βkidney = 0.3 | βkidney = 0.5 | βkidney = 0.8 | |||||||||
| Ki for OCT2 (μM) | Ki for OCT2 (μM) | Ki for OCT2 (μM) | Ki for OCT2 (μM) | ||||||||||
| 72.6 | 159 | 509 | 72.6 | 159 | 509 | 72.6 | 159 | 509 | 72.6 | 159 | 509 | ||
| AUC ratio | 1.47 ± 0.75 | 1.23 | 1.23 | 1.23 | 1.19 | 1.19 | 1.19 | 1.14 | 1.14 | 1.14 | 1.07 | 1.07 | 1.07 |
| Cmax ratio | 1.72 ± 0.97 | 1.32 | 1.32 | 1.32 | 1.26 | 1.26 | 1.26 | 1.19 | 1.19 | 1.19 | 1.08 | 1.08 | 1.08 |
| CLr ratio | 0.72 ± 0.32 | 0.75 | 0.75 | 0.75 | 0.80 | 0.80 | 0.80 | 0.84 | 0.84 | 0.84 | 0.90 | 0.90 | 0.90 |
| Sensitivity analysis of three different Ki values for MATEs (1.22, 13.5, and 3.93 represent the lowest and highest values and the geometric mean of in vitro Ki values, respectively) and differing βkidney values. The Ki value for OCT2 was fixed at the geometric mean value. | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Observed16 | βkidney = 0.1 | βkidney = 0.3 | βkidney = 0.5 | βkidney = 0.8 | |||||||||
| Ki for MATEs (μM) | Ki for MATEs (μM) | Ki for MATEs (μM) | Ki for MATEs (μM) | ||||||||||
| 1.22 | 3.93 | 13.5 | 1.22 | 3.93 | 13.5 | 1.22 | 3.93 | 13.5 | 1.22 | 3.93 | 13.5 | ||
| AUC ratio | 1.47 ± 0.75 | 1.44 | 1.23 | 1.10 | 1.40 | 1.19 | 1.07 | 1.30 | 1.14 | 1.05 | 1.15 | 1.07 | 1.03 |
| Cmax ratio | 1.72 ± 0.97 | 1.57 | 1.32 | 1.13 | 1.52 | 1.26 | 1.09 | 1.41 | 1.19 | 1.07 | 1.21 | 1.08 | 1.03 |
| CLr ratio | 0.72 ± 0.32 | 0.59 | 0.75 | 0.89 | 0.63 | 0.80 | 0.92 | 0.70 | 0.84 | 0.94 | 0.82 | 0.90 | 0.97 |
The geometric mean and the ranges of the reported in vitro Ki (μM) values of cimetidine were as follows: OCT1, 10411; OCT2, 159, 72.6–50910, 11, 20, 21, 34, 35; MATEs, 3.93, 1.22–13.520, 21, 22, 41 .
AUC, area under the curve; Ki, inhibition constant; Cmax, maximum plasma concentration; CLr, renal clearance; βkidney = PSurine/(PSr,eff+PSurine); OCT2, organic cation transporter 2; MATEs, multidrug and toxin extrusion proteins.
The Numeric Analysis Program for Pharmacokinetics (version 2.31)34 was used for simulation and optimization of parameters using the nonlinear least‐squares method. The weight for the calculation was set as 1 (the square root of the value).
Results
Metformin PBPK model
The k a, k trans, and R MATE/dif were optimized by fitting the model to the time profiles of plasma and blood concentrations and urinary excretion of metformin after a single oral dose of 1,500 mg metformin6 at varying βkidney values (Table 1 ). Although the optimized R MATE/dif varied from 150–800 at different βkidney values, the optimized k a and k trans were 0.21 ± 0.01 hour−1 and 2.4 ± 0.4 hour−1, respectively, regardless of βkidney values. The use of these optimized parameters well reproduced the observed data, including the increase of blood‐to‐plasma ratios over time (likely from slow distribution of metformin to erythrocytes; Figure 2 a–d, Figure S1 ). Next, the k trans and R MATE/dif were optimized by fitting the model to the plasma concentration‐time profile after oral metformin dosing of 250 mg16 (intestinal availability adjusted to 0.84 as described in the Methods section) using differing βkidney values (Figure 2 e–h, Table 1 ). The use of the optimized parameters yielded simulated Tmax (3.72 hours) and AUC0–12 (4.12 mg•h/L) comparable with the observed values (3.3 ± 0.8 hours and 3.75 ± 1.43 mg•h/L, respectively) at all four βkidney values.
Figure 2.
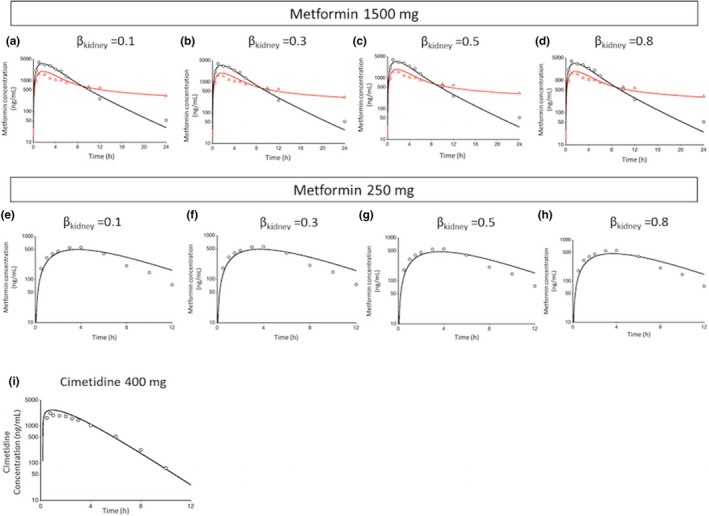
Fitted and observed metformin plasma and blood concentration‐time profiles after single oral administration of 1,500 mg metformin (a–d), fitted and observed plasma concentration‐time profiles after a single oral administration of 250 mg metformin (e–h) and after a single oral administration of 400 mg cimetidine (i). The black circles and red triangles represent the observed concentration‐time profiles in plasma and blood, respectively. The black and red lines represent the fitted concentration‐time profiles in plasma and blood, respectively. Simulations were performed using differing βkidney values; βkidney = PSurine/(PSr,eff+PSurine).
Cimetidine PBPK model
Parameters for the cimetidine PBPK model were from the reported data (Table S4 )1, 10, 27, 30 and used with no further optimization. Our PBPK model yielded the simulation results that well reproduced the observed data after a single oral administration of 400 mg cimetidine (Figure 2 i).18 The simulated AUC (9.10 mg•h/L) was comparable with the observed value (10.4 ± 2 mg•h/L).
DDI simulation
The pharmacokinetic profiles under DDI conditions were simulated using the developed PBPK models for metformin and cimetidine and in vitro Ki values (geometric mean) of cimetidine for OCT1, OCT2, and MATEs at differing βkidney values. The simulated plasma concentrations of metformin were increased with coadministration of cimetidine at all βkidney values, but the extent of the changes showed some discrepancies between the simulated and observed values; the fold changes of AUC, Cmax, and CLr in the simulations were 1.07–1.23, 1.08–1.32, and 0.75–0.90, respectively, whereas the observed fold changes were 1.47, 1.72, and 0.72, respectively (Table 2 , Figure S2 ).
Sensitivity analysis for in vitro Ki values of cimetidine for OCT2 and MATEs
As the reported in vitro Ki values of cimetidine for OCT2 and MATEs vary widely (Table 2 ),10, 11, 20, 21, 22, 35, 36, 37 we conducted sensitivity analyses for Ki values. DDI simulations were initially conducted with three in vitro Ki values for OCT2 (72.6, 509, and 159 μM, corresponding to the smallest and largest values and the geometric mean of the reported values, respectively), whereas the Ki values for OCT1 and MATEs were fixed to the geometric means of 104 μM and 3.93 μM, respectively. The fold changes of AUC, Cmax, and CLr were not impacted by the Ki values for OCT2 regardless of βkidney values (Table 2 ). DDI simulations were also conducted with three in vitro Ki values for MATEs (1.22, 13.5, and 3.93 μM, corresponding to the smallest and largest values and the geometric mean of the reported values, respectively), whereas the Ki values of cimetidine for OCT1 and OCT2 were fixed to 104 μM and 159 μM, respectively. The fold changes in AUC, Cmax, and CLr were impacted by the Ki values for MATEs (Table 2 ).
Estimation of the in vivo Ki value of cimetidine for MATEs
The in vivo Ki value of cimetidine for MATEs was estimated by fitting to clinical DDI data with k trans and R MATE/dif fixed to their optimized values at varying βkidney values. Simulation using the estimated in vivo Ki values for MATEs at all four βkidney values reproduced the observed fold changes in AUC, CLr, and Cmax with less than 15% differences (Figure 3 , Table 3 ). The good agreement between the simulated and observed profiles regardless of βkidney values appears to be consistent with our initial trial on reliable βkidney estimation by fitting to the clinical metformin pharmacokinetic data. The estimated in vivo Ki values for MATEs were in the range of the in vitro reported Ki values with βkidney values of 0.1 and 0.3 but not with 0.5 and 0.8 (corresponding to 0.52‐ and 0.18‐fold of the smallest in vitro reported Ki value (1.22 μM), respectively).
Figure 3.
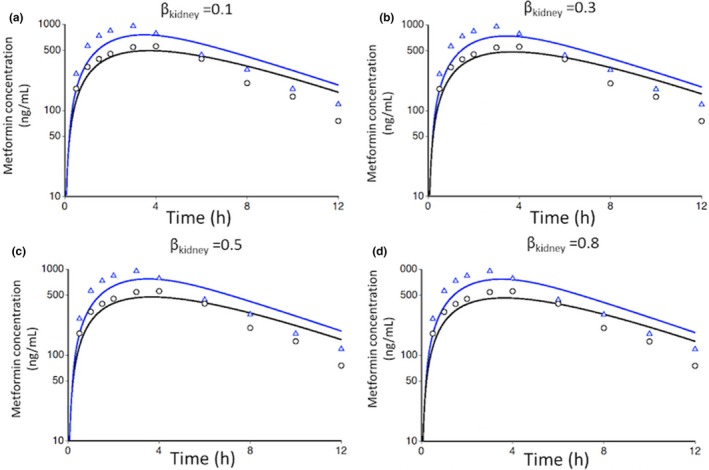
Metformin plasma concentration‐time profiles under control and drug–drug interaction conditions using fitted in vivo inhibition constant values for multidrug and toxin extrusion proteins after oral administration of 250 mg metformin and 400 mg cimetidine. For the control condition, the optimized parameters shown in Table 1 for βkidney value of 0.1 (a), 0.3 (b), 0.5 (c), or 0.8 (d) were used. For drug–drug interaction conditions, the optimized parameters were fixed, but the βkidney value was not fixed and allowed to change as the renal transport processes became inhibited. The black circles and blue triangles represent the observed plasma concentrations under control and drug–drug interaction conditions, respectively, and the black and blue lines represent the corresponding simulation results; βkidney = PSurine/(PSr,eff+PSurine).
Table 3.
Observed and simulated AUC, Cmax, and CLr ratios of metformin between control and drug–drug interaction conditions with fitted in vivo Ki value for MATEs at various βkidney values
| βkidney a | Fitted in vivo Ki value for MATEs (μM) | Fold changes from simulations | ||
|---|---|---|---|---|
| AUC (1.47 ± 0.75)16 | Cmax (1.72 ± 0.97)16 | CLr (0.72 ± 0.32)16 | ||
| 0.1 | 1.71 ± 0.74 | 1.40 | 1.52 | 0.63 |
| 0.3 | 1.34 ± 0.60 | 1.39 | 1.50 | 0.64 |
| 0.5 | 0.64 ± 0.34 | 1.42 | 1.54 | 0.61 |
| 0.8 | 0.23 ± 0.12 | 1.42 | 1.54 | 0.61 |
AUC, area under the curve; Cmax, the maximum plasma concentration; CLr, renal clearance; Ki, inhibition constant; MATEs, multidrug and toxin extrusion proteins.
For the control condition, the βkidney value was set to 0.1, 0.3, 0.5, or 0.8, and the optimized parameters shown in Table 1 were used. For the drug–drug interaction conditions, the optimized parameters were fixed, but the βkidney value was not fixed and allowed to change as the renal transport processes became inhibited.
Sensitivity analysis of Ki values of cimetidine for MATEs
For comparison with the previously reported model,1 we examined the impact of changing Ki values for MATEs on the fold changes in plasma AUC, CLr, or AUC in the proximal tubule cell segment 1 under DDI conditions. Initially, the sensitivity analysis of our PBPK model (βkidney of 0.1) was compared with that of the conventional and electrochemical models reported previously (Figure 4 a–c).1 In our model, βkidney values reflect the rate‐determining step of renal secretion in proximal tubule cells. Upon additional sensitivity analysis using varying βkidney values (Figure 4 d–f), the sensitivity to changing Ki values for MATEs on plasma AUC, CLr, and AUC in proximal tubule segment 1 in our model tended to be greater than the previously reported model1 except for the extreme ends of the βkidney ranges tested. For the plasma AUC of metformin, the observed fold change (1.47) under DDI conditions was recovered by lowering the Ki values for MATEs by ~ 1.5, 2.5, and 6‐fold from the smallest in vitro Ki value with βkidney values of 0.3, 0.5, and 0.8, respectively (Figure 4 d). With a βkidney of 0.1, the lowest reported Ki value (1.22 μM) yielded the observed 1.44‐fold change in the plasma AUC, close to the observed value. For the CLr, the observed fold change (0.72) was recovered using the Ki values for MATEs that fell within the range of the reported in vitro Ki values except for a βkidney of 0.8; for a βkidney of 0.8, the Ki for MATEs had to be lowered to 0.40 μM (approximately threefold lower than the smallest in vitro Ki value; Figure 4 e). For the AUC in proximal tubule segment 1, the fold change under DDI conditions was not available, but as βkidney values increased, so did the sensitivity to changing Ki values for MATEs increase (Figure 4 f). Overall, the observed fold changes in the plasma AUC or CLr were reproduced using the Ki values for MATEs near and within the range of those obtained in vitro with βkidney values of 0.1, 0.3, or 0.5 but not 0.8.
Figure 4.
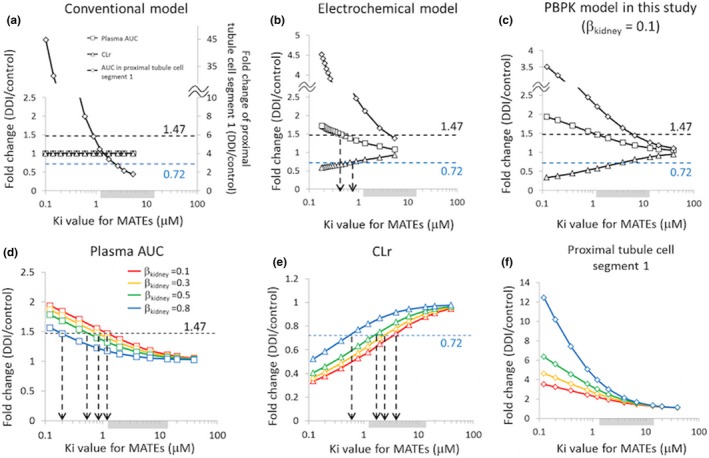
Sensitivity analysis to examine the impact of changing Ki values for MATEs on the fold changes in plasma AUC (□), CLr (△), or AUC in the proximal tubule cell segment 1 (♢). For comparison, the initial analysis was performed using the conventional model (a) and the electrochemical model (b) reported by Burt et al.1 and our current PBPK model (c) using βkidney = 0.1. For our current PBPK model, the impact of changing βkidney values was examined on plasma AUC (d), CLr (e), and AUC in the proximal tubule cell segment 1 (f). The shaded area near the x‐axis indicates the range of in vitro Ki values for MATEs reported in the literature (geometric mean: 3.93 μM (1.22–13.5 μM)). The dotted horizontal lines indicate the observed fold changes in plasma AUC (1.47, black) or CLr (0.72, blue). (d–f) Red, orange, green, and blue symbols and lines represent the simulation results using optimized values shown in Table 1 for βkidney values of 0.1, 0.3, 0.5, and 0.8, respectively. DDI, drug–drug interaction; Ki, inhibition constant; MATEs, multidrug and toxin extrusion proteins; PBPK, physiologically‐based pharmacokinetic. AUC, area under the curve; CLr, renal clearance; βkidney = PSurine/(PSr,eff+PSurine).
Discussion
Metformin is a clinically important antidiabetic drug and often used as a probe drug to examine the potential DDI mediated by renal transporters. Thus, there is a clear need to establish and refine PBPK models that can accurately and quantitatively predict the DDI potential between metformin and other drugs using in vitro data. To this end, the previous metformin PBPK model (“electrochemical model”)1 incorporated the transport process by OCTs driven by dynamically changing membrane potential in response to metformin levels. This electrochemical model reproduced the plasma concentration profile of metformin alone, but the extent of the fold changes in the plasma AUC under DDI conditions was recovered only when the Ki value for MATEs was set at 8.7‐fold lower values than the geometric mean value of the reported in vitro Ki values (3.93 μM). Although in vitro Ki values can substantially vary, the 8.7‐fold difference is rather substantial. To reconcile these differences, our model considered the electrogenic property of OCTs but kept the membrane potential constant. In the living cells and organisms, the electrochemical potential is regulated by concentration and permeability of multiple ions (e.g., potassium ion, sodium ion, chloride ion, typically at 100–200 mM) present at much higher concentrations.38 Thus, a reasonable assumption may be that drug‐induced changes in the electrochemical potential at the therapeutically relevant level to be modest extent. Our current PBPK model yielded in vivo simulated Ki values within the reported in vitro Ki values when βkidney was 0.1 or 0.3 (Table 3 ). In the sensitivity analysis, the observed plasma AUC change was reproduced within 15% difference (Table 2 ) with the lowest in vitro Ki values and observed CLr change was reproduced in the range of in vitro Ki values (1.22–5 μM) except for a βkidney of 0.8 (Figure 4 e). Overall, our model reproduced the clinical DDI data of metformin and cimetidine with in vitro Ki values when βkidney was 0.3 or less. In addition, the results from sensitivity analysis were comparable between the previous electrochemical model and our model with a βkidney of 0.8 (Figure 4 b,d,e). These results suggest that the rate‐determining step in the electrochemical model is likely the renal uptake, requiring one to greatly lower the Ki value for MATEs or OCT2 from in vitro Ki values to reproduce the observed DDI data. Thus, a βkidney of 0.3 or less is recommended for future efforts to predict the potential DDI using in vitro Ki values. Of note, we could not obtain reliable βkidney estimates by fitting to clinical metformin data (under control conditions). Our approach was to use a wide range of fixed βkidney values (to cover situations with differing rate‐determining steps) under control conditions and to deduce optimal βkidney ranges from sensitivity analysis. This approach may represent another strategy to indirectly estimate βkidney.
In understanding how our model was capable of reproducing the clinical DDI data using in vitro Ki values and small βkidney values, a mechanistic interpretation of the βkidney values may shed some light on possible reasons. The extended clearance concept takes all intrinsic processes into account when assessing the overall elimination process. Incorporating the extended clearance concept, CLint,sec is described as PSr,inf·βkidney (Eq. (7)). By converting the parameters with Eqs. (5) and (8), (9), (10), (11), (12), (13), (14), CLint,sec can be transformed to Eq. (16).
| (16) |
When βkidney is 0.1, the values for individual parameters in Eq. (16) are as follows: PSOCT2,inf, 732 L/hour; PSr,dif,inf, 0.043 L/hour; PSr,dif,eff, 0.0031 L/hour; PSMATE, 4.47 L/hour; PSurine,dif,eff, 0.024 L/hour; e N/R OCT2,inf/eff, 0.055. When the transport of metformin by MATEs becomes inhibited to 20% in the presence of cimetidine (i.e., PSMATE decreased to 0.89 L/hour), the βkidney is changed from 0.1 to 0.022, and CLint,sec is decreased from 73.5 to 16.3 L/hour, by ~ 4.5‐fold when compared with the control condition. A similar calculation can be performed when βkidney is 0.8. The values for individual parameters in Eq. (16) are as follows: PSOCT2,inf, 126 L/hour; PSr,dif,inf, 0.043 L/hour; PSr,dif,eff, 0.0031 L/hour; PSMATE, 27.9 L/hour; PSurine,dif,eff, 0.024 L/hour; e N/R OCT2,inf/eff, 0.055. When the transport of metformin by MATEs becomes inhibited to 20% in the presence of cimetidine (i.e., PSMATE decreased to 5.6 L/hour), βkidney is changed from 0.8 to 0.45, and CLint,sec is decreased from 101 to 56.4 L/hour, by ~ 1.8‐fold when compared with the control condition. These calculation results indicate that as βkidney values become smaller, the inhibition of MATEs has a much greater impact on CLint,sec.
A number of DDI cases have been reported between metformin and other drugs that can inhibit both OCT2 and MATEs (e.g., pyrimethamine,39, 40 dolutegravir,41 trimethoprim,37, 42 and vandetanib43). For pyrimethamine, in vitro Ki values for MATEs (0.059–0.15 μM) are much lower than those for OCT2 (4.1–23 μM).22, 38, 44 The observed Cmax values of unbound pyrimethamine in plasma range from 0.30–0.40 μM after a 50 mg oral pyrimethamine dose,35, 45 suggesting the inhibition of MATEs as the likely DDI mechanism. In the case of dolutegravir, its in vitro Ki values for OCT2 and MATE1 are 1.9 and 6.3 μM,41 respectively. In a clinical DDI study, the coadministration of dolutegravir increased the plasma AUC of metformin by 79% and 145% when dolutegravir was coadministered as a single daily dose of 50 mg and two daily doses of 50 mg with a 12‐hour interval.41 With its unbound Cmax values being much lower than the in vitro Ki values for OCT2 and MATE1, the inhibitions of OCT2 and MATE1 were deemed unlikely to explain the observed DDI, and the exact mechanism remains unknown. Our current PBPK model may aid the efforts to quantitatively predict the DDI and gain mechanistic insights into complex DDI cases between metformin and other drugs.
Our PBPK model for metformin may also have some utility in understanding the source of variable response and toxicity to metformin therapy. Drug concentrations in plasma or blood are often assumed to be associated with drug efficacy and toxicity. It is, however, increasingly recognized that it may not be the case if a drug is actively taken up into tissues or metabolized in the tissues.46 Although one third of patients did not respond to metformin,2, 3 the metformin levels in plasma are not predictive of blood lactate concentrations and the risk for lactic acidosis.4, 15, 47 In addition, the diabetic patients carrying the MATE1 promoter variant (g.‐66T→C) exhibit a greater response to metformin than those carrying the wildtype.15 By incorporating variables consistent with biologically plausible mechanisms (especially variables for transport processes by OCT1/2 and MATEs), it might be possible to gain mechanistic insights into interindividual variations in metformin response and side effects and to predict the pharmacokinetic profiles and clinical outcomes using the virtual clinical study method.48
In conclusion, we developed a refined PBPK model for metformin that successfully reproduced the DDI between metformin and cimetidine with in vitro Ki values. Our results supported the fact that the DDI between metformin and cimetidine is likely mediated by the inhibition of MATEs by cimetidine rather than by OCT2 inhibition.
Funding
No funding was received for this work.
Conflict of Interest
The authors declared no competing interests for this work.
Author Contributions
K.N., K.T., W.L., N.I., B.B., and Y.S. wrote the manuscript. K.N., K.T., and Y.S. designed the research. K.N., K.T., and Y.S. performed the research. K.N., K.T., and Y.S. analyzed the data.
Supporting information
Figure S1. Simulated (lines) and observed (open circles) time profiles of metformin urinary excretion after a single oral administration of 1,500 mg metformin using various βkidney values.
Figure S2. Metformin plasma concentration time profiles of control and drug–drug interaction conditions using the lowest and geometric mean of inhibition constant values of cimetidine at differing βkidney values after the administration of 250 mg metformin and 400 mg cimetidine.
Table S1. Various parameters used in the metformin physiologically‐based pharmacokinetic model and reported in vitro Km values for transporters of metformin parameters used in the metformin physiologically‐based pharmacokinetic model.
Table S2. Physiological parameters of blood volume, tissue volumes, hematocrit value, and blood flows.
Table S3. Physiological parameters, membrane potential, blood flow, and urinary flow in the kidney model.
Table S4. Parameters used in the cimetidine physiologically‐based pharmacokinetic model.
Supplementary Material S1. Model code file.
Supplementary Material S2. Model equations for metformin.
References
- 1. Burt, H.J. et al Metformin and cimetidine: physiologically based pharmacokinetic modelling to investigate transporter mediated drug‐drug interactions. Eur. J. Pharm. Sci. 88, 70–82 (2016). [DOI] [PubMed] [Google Scholar]
- 2. Graham, G.G. et al Clinical pharmacokinetics of metformin. Clin. Pharmacokinet. 50, 81–98 (2011). [DOI] [PubMed] [Google Scholar]
- 3. Shikata, E. et al Human organic cation transporter (OCT1 and OCT2) gene polymorphisms and therapeutic effects of metformin. J. Hum. Genet. 52, 117–122 (2007). [DOI] [PubMed] [Google Scholar]
- 4. Lalau, J.D. & Race, J.M. Lactic acidosis in metformin‐treated patients. Prognostic value of arterial lactate levels and plasma metformin concentrations. Drug Saf. 20, 377–384 (1999). [DOI] [PubMed] [Google Scholar]
- 5. Pentikainen, P.J. , Neuvonen, P.J. & Penttila, A. Pharmacokinetics of metformin after intravenous and oral administration to man. Eur. J. Clin. Pharmacol. 16, 195–202 (1979). [DOI] [PubMed] [Google Scholar]
- 6. Tucker, G.T. , Casey, C. , Phillips, P.J. , Connor, H. , Ward, J.D. & Woods, H.F. Metformin kinetics in healthy subjects and in patients with diabetes mellitus. Br. J. Clin. Pharmacol. 12, 235–246 (1981). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Rena, G. , Pearson, E.R. & Sakamoto, K. Molecular mechanism of action of metformin: old or new insights? Diabetologia 56, 1898–1906 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Stage, T.B. , Brøsen, K. & Christensen, M.M. A comprehensive review of drug–drug interactions with metformin. Clin. Pharmacokinet. 54, 811–824 (2015). [DOI] [PubMed] [Google Scholar]
- 9. Xie, F. , Ke, A.B. , Bowers, G.D. & Zamek‐Gliszczynski, M.J. Metformin's intrinsic blood‐to‐plasma partition ratio (B/P): reconciling the perceived high in vivo B/P > 10 with the in vitro equilibrium value of unity. J. Pharmacol. Exp. Ther. 354, 225–229 (2015). [DOI] [PubMed] [Google Scholar]
- 10. Umehara, K.I. , Iwatsubo, T. , Noguchi, K. & Kamimura, H. Functional involvement of organic cation transporter1 (OCT1/Oct1) in the hepatic uptake of organic cations in humans and rats. Xenobiotica 37, 818–831 (2007). [DOI] [PubMed] [Google Scholar]
- 11. Kimura, N. , Okuda, M. & Inui, K. Metformin transport by renal basolateral organic cation transporter hOCT2. Pharm. Res. 22, 255–259 (2005). [DOI] [PubMed] [Google Scholar]
- 12. Tanihara, Y. , Masuda, S. , Sato, T. , Katsura, T. , Ogawa, O. & Inui, K. Substrate specificity of MATE1 and MATE2‐K, human multidrug and toxin extrusions/H(+)‐organic cation antiporters. Biochem. Pharmacol. 74, 359–371 (2007). [DOI] [PubMed] [Google Scholar]
- 13. Christensen, M.M. et al The pharmacogenetics of metformin and its impact on plasma metformin steady‐state levels and glycosylated hemoglobin A1c. Pharmacogenet. Genomics 21, 837–850 (2011). [DOI] [PubMed] [Google Scholar]
- 14. Christensen, M.M. et al A gene‐gene interaction between polymorphisms in the OCT2 and MATE1 genes influences the renal clearance of metformin. Pharmacogenet. Genomics 23, 526–534 (2013). [DOI] [PubMed] [Google Scholar]
- 15. Stocker, S.L. et al The effect of novel promoter variants in MATE1 and MATE2 on the pharmacokinetics and pharmacodynamics of metformin. Clin. Pharmacol. Ther. 93, 186–194 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Somogyi, A. , Stockley, C. , Keal, J. , Rolan, P. & Bochner, F. Reduction of metformin renal tubular secretion by cimetidine in man. Br. J. Clin. Pharmacol. 23, 545–551 (1987). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Wang, Z.J. , Yin, O.Q. , Tomlinson, B. & Chow, M.S. OCT2 polymorphisms and in‐vivo renal functional consequence: studies with metformin and cimetidine. Pharmacogenet. Genomics 18, 637–645 (2008). [DOI] [PubMed] [Google Scholar]
- 18. Grahnén, A. , von Bahr, C. , Lindström, B. & Rosén, A. Bioavailability and pharmacokinetics of cimetidine. Eur. J. Clin. Pharmacol. 16, 335–340 (1979). [DOI] [PubMed] [Google Scholar]
- 19. Somogyi, A. , Thielscher, S. & Gugler, R. Influence of phenobarbital treatment on cimetidine kinetics. Eur. J. Clin. Pharmacol. 19, 343–347 (1981). [DOI] [PubMed] [Google Scholar]
- 20. Elsby, R. et al Mechanistic in vitro studies confirm that inhibition of the renal apical efflux transporter multidrug and toxin extrusion (MATE) 1, and not altered absorption, underlies the increased metformin exposure observed in clinical interactions with cimetidine, trimethoprim or pyrimethamine. Pharmacol. Res. Perspect. 5 (2017). 10.1002/prp2.357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Ito, S. et al Competitive inhibition of the luminal efflux by multidrug and toxin extrusions, but not basolateral uptake by organic cation transporter 2, is the likely mechanism underlying the pharmacokinetic drug‐drug interactions caused by cimetidine in the kidney. J. Pharmacol. Exp. Ther. 340, 393–403 (2012). [DOI] [PubMed] [Google Scholar]
- 22. Shen, H. et al Characterization of organic anion transporter 2 (SLC22A7): a highly efficient transporter for creatinine and species‐dependent renal tubular expression. Drug Metab. Dispos. 43, 984–993 (2015). [DOI] [PubMed] [Google Scholar]
- 23. Watanabe, T. , Kusuhara, H. , Maeda, K. , Shitara, Y. & Sugiyama, Y. Physiologically based pharmacokinetic modeling to predict transporter‐mediated clearance and distribution of pravastatin in humans. J. Pharmacol. Exp. Ther. 328, 652–662 (2009). [DOI] [PubMed] [Google Scholar]
- 24. Yoshikado, T. et al Quantitative analyses of hepatic OATP‐mediated interactions between statins and inhibitors using PBPK modeling with a parameter optimization method. Clin. Pharmacol. Ther. 100, 513–523 (2016). [DOI] [PubMed] [Google Scholar]
- 25. Futatsugi, A. , Toshimoto, K. , Yoshikado, T. , Sugiyama, Y. & Kato, Y. Evaluation of alteration in hepatic and intestinal BCRP function in vivo from ABCG2 c.421C>a polymorphism based on PBPK analysis of Rosuvastatin. Drug Metab. Dispos. 46, 749–757 (2018). [DOI] [PubMed] [Google Scholar]
- 26. Rodgers, T. , Leahy, D. & Rowland, M. Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate‐to‐strong bases. J. Pharm. Sci. 94, 1259–1276 (2005). [DOI] [PubMed] [Google Scholar]
- 27. Chien, H.C. et al Rapid method to determine intracellular drug concentrations in cellular uptake assays: application to metformin in organic cation transporter 1‐transfected human embryonic kidney 293 cells. Drug Metab. Dispos. 44, 356–364 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Yoshida, K. , Maeda, K. & Sugiyama, Y. Hepatic and intestinal drug transporters: prediction of pharmacokinetic effects caused by drug‐drug interactions and genetic polymorphisms. Annu. Rev. Pharmacol. Toxicol. 53, 581–612 (2013). [DOI] [PubMed] [Google Scholar]
- 29. Yoshikado, T. et al Comparison of methods for estimating unbound intracellular‐to‐medium concentration ratios in rat and human hepatocytes using statins. Drug Metab. Dispos. 45, 779–789 (2017). [DOI] [PubMed] [Google Scholar]
- 30. Balimane, P.V. & Chong, S . Evaluation of permeability and P‐glycoprotein interactions: industry outlook In Biopharmaceutics Applications in Drug Development (eds. Krishna R. and Yu L.) 101–138 (Springer, New York, 2008). [Google Scholar]
- 31. Min, K.A. , Zhang, X. , Yu, J.Y. & Rosania, G.R. Computational approaches to analyse and predict small molecule transport and distribution at cellular and subcellular levels. Biopharm. Drug Dispos. 35, 15–32 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Scheen, A.J. Clinical pharmacokinetics of metformin. Clin. Pharmacokinet. 30, 359–371 (1996). [DOI] [PubMed] [Google Scholar]
- 33. Siener, R. , Jahnen, A. & Hesse, A. Influence of a mineral water rich in calcium, magnesium and bicarbonate on urine composition and the risk of calcium oxalate crystallization. Eur. J. Clin. Nutr. 58, 270–276 (2004). [DOI] [PubMed] [Google Scholar]
- 34. Hisaka, A. & Sugiyama, Y. Analysis of nonlinear and nonsteady state hepatic extraction with the dispersion model using the finite difference method. J. Pharmacokinet. Biopharm. 26, 495–519 (1998). [DOI] [PubMed] [Google Scholar]
- 35. Masuda, S. et al Identification and functional characterization of a new human kidney‐specific H+/organic cation antiporter, kidney‐specific multidrug and toxin extrusion 2. J. Am. Soc. Nephrol. 17, 2127–2135 (2006). [DOI] [PubMed] [Google Scholar]
- 36. Tsuda, M. , Terada, T. , Mizuno, T. , Katsura, T. , Shimakura, J. & Inui, K. Targeted disruption of the multidrug and toxin extrusion 1 (mate1) gene in mice reduces renal secretion of metformin. Mol. Pharmacol. 75, 1280–1286 (2009). [DOI] [PubMed] [Google Scholar]
- 37. Müller, F. et al N(1)‐methylnicotinamide as an endogenous probe for drug interactions by renal cation transporters: studies on the metformin‐trimethoprim interaction. Eur. J. Clin. Pharmacol. 71, 85–94 (2015). [DOI] [PubMed] [Google Scholar]
- 38. Hodgkin, A.L. & Katz, B. The effect of sodium ions on the electrical activity of giant axon of the squid. J. Physiol. 108, 37–77 (1949). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Kusuhara, H. et al Effects of a MATE protein inhibitor, pyrimethamine, on the renal elimination of metformin at oral microdose and at therapeutic dose in healthy subjects. Clin. Pharmacol. Ther. 89, 837–844 (2011). [DOI] [PubMed] [Google Scholar]
- 40. Oh, J. et al Inhibition of the multidrug and toxin extrusion (MATE) transporter by pyrimethamine increases the plasma concentration of metformin but does not increase antihyperglycaemic activity in humans. Diabetes Obes. Metab. 18, 104–108 (2016). [DOI] [PubMed] [Google Scholar]
- 41. Song, et al The effect of dolutegravir on the pharmacokinetics of metformin in healthy subjects. J. Acquir. Immune Defic. Syndr. 72, 400–407 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Grün, B. et al Trimethoprim‐metformin interaction and its genetic modulation by OCT2 and MATE1 transporters. Br. J. Clin. Pharmacol. 76, 787–796 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Johansson, S. et al Pharmacokinetic evaluations of the co‐administrations of vandetanib and metformin, digoxin, midazolam, omeprazole or ranitidine. Clin. Pharmacokinet. 53, 837–847 (2014). [DOI] [PubMed] [Google Scholar]
- 44. Yin, J. , Duan, H. & Wang, J. Impact of substrate‐dependent inhibition on renal organic cation transporters hOCT2 and hMATE1/2‐K‐mediated drug transport and intracellular accumulation. J. Pharmacol. Exp. Ther. 359, 401–410 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Mansor, S.M. et al Single dose kinetic study of the triple combination mefloquine/sulphadoxine/pyrimethamine (Fansimef) in healthy male volunteers. Br. J. Clin. Pharmacol. 27, 381–386 (1989). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Chu, X. et al Intracellular drug concentrations and transporters: measurement, modeling, and implications for the liver. Clin. Pharmacol. Ther. 94, 126–141 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Hermann, L.S. , Scherstén, B. , Bitzén, P.O. , Kjellström, T. , Lindgärde, F. & Melander, A. Therapeutic comparison of metformin and sulfonylurea, alone and in various combinations. A double‐blind controlled study. Diabetes Care 17, 1100–1109 (1994). [DOI] [PubMed] [Google Scholar]
- 48. Toshimoto, K. , Tomaru, A. , Hosokawa, M. & Sugiyama, Y. Virtual clinical studies to examine the probability distribution of the AUC at target tissues using physiologically‐based pharmacokinetic modeling: application to analyses of the effect of genetic polymorphism of enzymes and transporters on irinotecan induced side effects. Pharm. Res. 34, 1584–1600 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. Simulated (lines) and observed (open circles) time profiles of metformin urinary excretion after a single oral administration of 1,500 mg metformin using various βkidney values.
Figure S2. Metformin plasma concentration time profiles of control and drug–drug interaction conditions using the lowest and geometric mean of inhibition constant values of cimetidine at differing βkidney values after the administration of 250 mg metformin and 400 mg cimetidine.
Table S1. Various parameters used in the metformin physiologically‐based pharmacokinetic model and reported in vitro Km values for transporters of metformin parameters used in the metformin physiologically‐based pharmacokinetic model.
Table S2. Physiological parameters of blood volume, tissue volumes, hematocrit value, and blood flows.
Table S3. Physiological parameters, membrane potential, blood flow, and urinary flow in the kidney model.
Table S4. Parameters used in the cimetidine physiologically‐based pharmacokinetic model.
Supplementary Material S1. Model code file.
Supplementary Material S2. Model equations for metformin.


