BraggNet: integrating Bragg peaks using neural networks

It is shown that artificial neural networks can be used to predict the location and shape of neutron Bragg peaks, resulting in increased integration accuracy.

Abstract

Neutron crystallography offers enormous potential to complement structures from X-ray crystallography by clarifying the positions of low-Z elements, namely hydrogen. Macromolecular neutron crystallography, however, remains limited, in part owing to the challenge of integrating peak shapes from pulsed-source experiments. To advance existing software, this article demonstrates the use of machine learning to refine peak locations, predict peak shapes and yield more accurate integrated intensities when applied to whole data sets from a protein crystal. The artificial neural network, based on the U-Net architecture commonly used for image segmentation, is trained using about 100 000 simulated training peaks derived from strong peaks. After 100 training epochs (a round of training over the whole data set broken into smaller batches), training converges and achieves a Dice coefficient of around 65%, in contrast to just 15% for negative control data sets. Integrating whole peak sets using the neural network yields improved intensity statistics compared with other integration methods, including k-nearest neighbours. These results demonstrate, for the first time, that neural networks can learn peak shapes and be used to integrate Bragg peaks. It is expected that integration using neural networks can be further developed to increase the quality of neutron, electron and X-ray crystallography data.

1. Introduction  

Crystallography has served as a workhorse for atomic and molecular structural studies (Groom et al., 2016 ▸; Berman et al., 2000 ▸). The primary data resulting from these experiments are integrated Bragg peak intensities from which structure factors can be calculated and used to refine structural models. Accordingly, conclusions drawn from crystallographic experiments rely critically on accurately integrated intensities. For X-ray crystallography studies, which comprise the vast majority of reported macromolecular structures, peaks are typically integrated using one of a few common software packages (Kabsch, 2010 ▸; Leslie, 2006 ▸; Pflugrath, 1999 ▸; Winter et al., 2018 ▸; Minor et al., 2006 ▸). Since its introduction in 1979 (Rossmann, 1979 ▸), profile fitting has been embraced to the extent that all of these packages rely on profile fitting to some degree, be it through fitting intensities to analytical forms or applying profiles from strong peaks. These packages have been developed over many decades into robust programs that have, in no small way, been essential to the recent growth in macromolecular X-ray crystallography. While some neutron crystallography beamlines have been able to adapt these packages for their use (Langan & Greene, 2004 ▸; Blakeley et al., 2010 ▸; Meilleur et al., 2013 ▸), the most recent generation of time-of-flight (TOF) neutron diffractometers (Coates et al., 2015 ▸; Chapon et al., 2011 ▸; Tanaka et al., 2010 ▸; Langan et al., 2008 ▸) rely on in-house packages. Namely, SXD2001 (Gutmann, 2005 ▸), Mantid (Arnold et al., 2014 ▸) and STARGazer (Yano et al., 2018 ▸) are used. While these packages have enabled routine analysis for these beamlines, they have not achieved the level of maturity of their X-ray counterparts. As a first step towards addressing this, we recently developed and implemented a profile fitting algorithm for TOF data that more accurately integrates peaks than previously used peak-minus-background integration techniques (Sullivan et al., 2018 ▸). Aside from reducing sensitivity to noise, profile fitting naturally accommodates varying peak sizes, inaccurate peak location prediction and nearby overlapping peaks, all of which cause simple peak-minus-background integration schemes to fail. In essence, profile fitting’s ability to precisely separate the peak from the background is critical to its success.

Computationally, identifying a peak in the presence of background and nearby peaks can be posed as an image segmentation problem. The simplest segmentation approaches rely on intensity-based thresholding in which bright pixels (or voxels in three dimensions) are separated from dark pixels on the basis of intensity (Pal & Pal, 1993 ▸). While these approaches have proven useful in automating data analysis across many fields of science, they are fundamentally unable to identify features which are barely distinguishable from background. As a result, threshold-based segmentation is not suitable for peak detection. Recently, the computer vision community has made significant progress in solving the image segmentation problem using machine learning techniques. Machine learning techniques rely on training and using models that map inputs to outputs. The model is ‘trained’ by setting the model’s parameters based on generating outputs which best match known answers. Deep learning (machine learning using models with multiple connected computational layers) was first applied to image segmentation in 2014 by using fully convolutional neural networks (Long et al., 2015 ▸). Artificial neural networks are deep learning constructs which use neurons – simple input/output units – as the base computational unit. A neuron outputs some activation function (f _A, typically valued between 0 and 1) based on a weighted sum of all of its inputs plus some bias and can be used as input to the next layer in the network. In other words, the output value of the jth neuron in a layer, p_j, with n inputs from the previous layer is given by

where x_i represents the inputs, w_ij represent the weights and b_j is the layer’s bias. The act of training a neural network updates these weights and biases to minimize a loss function describing the differences between the model’s predictions and known test functions. A convolutional neural network is such a network that includes convolution operators from the input image. Since then, a number of improvements have been demonstrated, including encoder–decoder architectures (U-Nets) (Ronneberger et al., 2015 ▸), dilation (Yu & Koltun, 2015 ▸) and advanced pooling (down-sampling) schemes (Zhao et al., 2017 ▸).

Given that peak integration can be posed as an image segmentation problem to identify the peak followed by quantitation, it is sensible to expect that integration algorithms can benefit from these advances in computer vision. In posing integration as a machine learning problem, the scaled number of detected events around each peak serves as the input to a model which returns the set of voxels that compose a peak. For the model to effectively integrate whole data sets, it needs to be trained against a set of peaks which reflect all the potential peak shapes the model will be expected to predict. Macromolecular data sets are ideal for developing machine learning techniques as they have many peaks; some of these peaks are strong and can be used to generate a training data set that can identify weaker peaks, allowing them to be accurately integrated.

Here, we present a complete data set integrated using locations and shapes predicted from a neural network. The intensities and resulting structure factors are compared with common peak-minus-background integration, profile fitted integration and a k-NN integration model (defined below), representing the simplest possible machine learning model for integration. By analysing the resulting intensity statistics, it is shown that using even a simple neural network results in improved integration when compared with other commonly used integration schemes. These results are the first time it has been demonstrated that a neural network can indeed learn peak shapes. Given the simplicity of this proof-of-concept model, it is easy to envision that machine learning techniques could enhance X-ray, electron and neutron integration schemes.

2. Materials and methods  

2.1. Sample preparation and neutron data collection  

A crystal of perdeuterated Ser70Ala/Arg274Asn/Arg276Asn Toho-1 β-lactamase was grown as previously described (Tomanicek et al., 2010 ▸, 2013 ▸; Langan et al., 2018 ▸). Data were collected at the MaNDi beamline (Coates et al., 2010 ▸, 2015 ▸, 2018 ▸) at the Spallation Neutron Source at Oak Ridge National Laboratory (Oak Ridge, TN, USA). Five orientations separated by Δφ = 20° were collected for 14 h per orientation. The crystal size was 1 mm³.

2.2. X-ray data collection and processing  

X-ray data from the Toho-1 β-lactamase crystal were recorded to 1.57 Å resolution at 296 K (Table S3). Diffraction data were collected using a Rigaku FR-E SuperBright Cu Kα rotating-anode generator at 45 kV and 45 mA equipped with an R-AXIS IV⁺⁺ detector. The crystal formed in the space group P3₂21 with unit-cell dimensions of a = b = 73.40, c = 99.43 Å. Reflections were processed using HKL-3000 for indexing, integration and scaling (Minor et al., 2006 ▸).

2.3. Neutron data pre-processing  

Initial analysis was done using the Mantid framework (Arnold et al., 2014 ▸), which allows for rapid manipulation of data and conversion to reciprocal space. Each run was converted to reciprocal space and indexed, and the location of each peak was predicted from the resulting orientation (UB) matrix. The crystal was determined to have unit-cell dimensions of a = b = 73.30, c = 99.0 Å using the neutron data set. Each peak was integrated using spherical integration to allow comparison of the machine learning models with peak-minus-background integration. A peak radius of 0.017 Å⁻¹ was used for peaks, while the background shell was taken to be between 0.018 and 0.019 Å⁻¹. To allow comparison of machine learning models with profile fitting, peaks were fitted using the IntegratePeaksProfileFitting algorithm within the Mantid package (Sullivan et al., 2018 ▸).

2.4. Generating training data sets for machine learning  

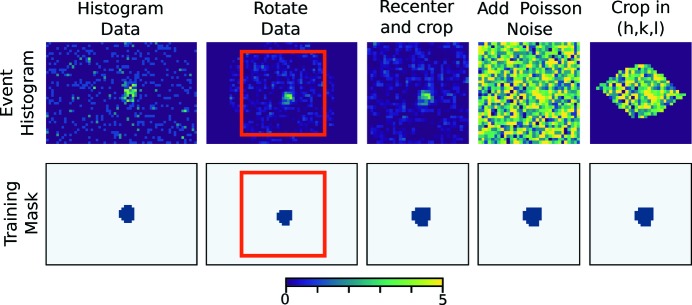
The success of machine learning lies in the generation of an appropriate training data set. The data sets must be robust enough to expose the model to any effects it may encounter. The training data set for this work is composed of 11 720 peaks simulated from profile fitted peaks: 10 499 peaks for training and 1221 peaks for testing. Testing peaks are a randomly selected subset of the generated peaks that are never exposed to the model during training and serve as an unbiased test that the network can predict beyond training data. Training peaks are generated from strong peaks, defined as peaks with an intensity greater than 200 counts according to spherical integration. First, each peak is fitted in Mantid using the recently developed 3D profile fitting algorithm (IntegratePeaks­Profile­Fitting). Voxels with a fitted intensity greater than 2.5% of the maximum of the fitted intensity were considered to be in the peak (see Fig. 1 ▸, left, for an example). With a 50% probability, the peaks are rotated by a random angle from −180 to 180° around the q_x, q_y and q_z axes (a different random angle was chosen for each axis). This rotation allows different peak orientations to be learned. Simulated Poisson noise with an expected intensity of λ, randomly selected between 0 and half the maximum number of events in the peak, is then added. Adding noise simulates weak peaks from strong peaks. Finally, each peak is translated along q_x, q_y and q_z by a maximum of 6 voxels in either direction (again, a different value is chosen for each direction). This allows the machine to learn when a peak location is slightly mis-predicted, which can be due to imperfect orientation (UB) matrix determination or instrument calibration. Finally, for peak hkl, data outside the range (h − 1/4, k − 1/4, l − 1/4) through (h + 1/4, k + 1/4, l + 1/4) were set to zero. This cropping ensures that only one peak is present in each training image; in principle, this is not necessary but simplifies the learning process. This process is shown for an example peak in Fig. 1 ▸. For learning and predicting, data are scaled to have zero mean and unit standard deviation.

Figure 1.

Example of a generated training peak. Raw event data are histogrammed, rotated and cropped slightly off centre. Poisson noise is added before cropping to a box of length 0.5 in h, k, l space so that exactly one peak is present in the box. These data are then normalized to have zero mean and unit variance before being used for training. The top row shows the event data while the bottom row shows the peak mask. The plane shown is a slice in the q_xq_y plane centred at the predicted peak location along q_z.

2.5. Machine learning models  

Here we implement and compare two different machine learning models. The first is a k-nearest neighbour (k-NN) algorithm. k-NN algorithms make predictions for a given input by finding the most similar training input for each peak and assuming the most similar training peak’s profile is appropriate for the input. Here, the term ‘nearest neighbour’ will be used to refer to the most similar input for a k-NN model, which is not to be confused with neighbouring peaks in reciprocale space (‘nearest peaks’). The k-NN algorithm here was implemented using Euclidian distance to determine the nearest neighbour, with the input being scaled to have zero mean and unit variance and being cropped in (h, k, l) like training data.

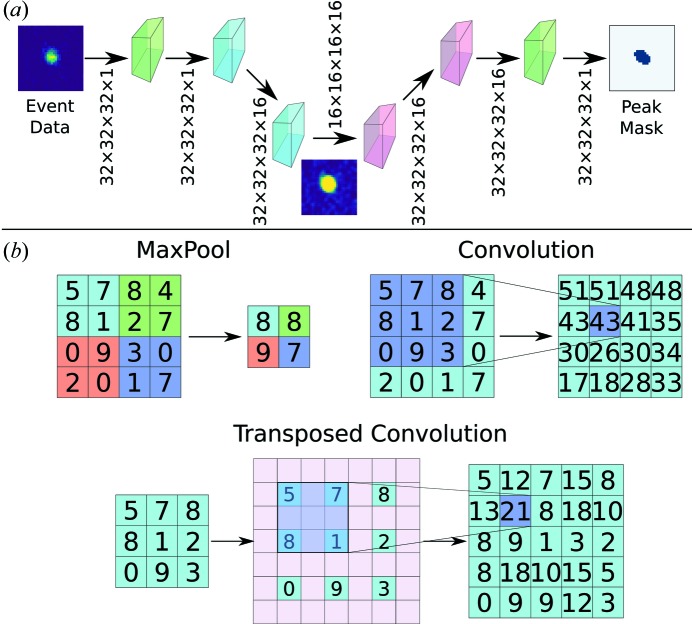
The second machine learning model, a convolutional neural network, was implemented in Keras using a TensorFlow backend (Chollet, 2015 ▸; Abadi et al., 2016 ▸). A schematic of the network, based on the commonly used U-Net (Ronneberger et al., 2015 ▸), is shown in Figs. 2 ▸(a) and S1. The network is based on convolution, deconvolution (transposed convolution) and maximum pooling layers; each of these operations is illustrated in Fig. 2 ▸(b). Additionally, the network incorporates dropout layers with a dropout rate of 0.5 to avoid overfitting; these layers randomly ‘disconnect’ half of the neurons by setting the connectivity weights to zero (Srivastava et al., 2014 ▸). Batch normalization layers are also used to expedite training (Ioffe & Szegedy, 2015 ▸). In total, the model has 103 873 trainable variables and 320 non-trainable variables. The trainable parameters are the weights and biases between layers that are updated during the training process (see Introduction ), while the non-trainable variables are temporary means and variances used for batch normalization. Training was done for 100 epochs using an ADAM optimizer with a learning rate of 0.0005, β₁ = 0.9 and β₂ = 0.999 (Kingma & Ba, 2014 ▸). Of the generated training peaks, 80% were used for training, 10% for validation and 10% for testing. Testing and validation peaks do not influence the learning process but instead are used to ensure that the model is learning to predict peak shapes generally rather than just for the training set. Testing and validation peaks fill a role in machine learning comparable to the peaks set aside to calculate R _free in structural refinement.

Figure 2.

(a) Schematic of the network used to learn peak shapes. Green layers represent input and output, blue layers represent down-sampling layers, and red boxes represent up-sampling layers. A complete description of the network is shown in Fig. S1. (b) A summary of operations for the neural network for 2D images. MaxPool layers allow down-sampling by taking the highest-valued pixel in the given regions. Convolutions compute local averages and allow projection into higher dimensions. Up-sampling is done by transposed convolution in which the original image is padded with zeros (shown in pink) and convoluted.

2.6. Metrics for machine learning  

While accuracy is a common, intuitive metric for assessing machine learning models, the Dice coefficient (Dice, 1945 ▸; Sørensen, 1948 ▸) and intersection over union (IoU) are commonly used for image segmentation because they emphasize correctly identifying features rather than identifying that most of the image is background. As an example, with these data, if the peak is 6³ voxels and we are evaluating a volume of 32³ voxels, trivially predicting false for all voxels gives an accuracy of 1 − (6/32)³ = 99.3%. For binary predictions, if prediction X is being compared with a known answer (known as the ground truth) Y, the Dice coefficient, D, is defined as

while the IoU is defined as

Both the Dice coefficient and IoU range from 0 to 1 in the cases of no overlap and perfect overlap, respectively. For the work here, the loss function being minimized is the Dice loss function L _D:

These were implemented as losses or metrics in Tensorflow for evaluation by the training function. Table 1 ▸ shows these training results for 12 different models. Each of these 12 models had the same layers present as described in Section 2.5 and illustrated Fig. S1 and was trained against the same data sets. The models differed only in the values used to initialize each model’s weights and biases before starting training. As a result, these data sets can be used to assess the dependence of the training procedure on initial conditions.

Table 1. Summary of learning and intensity statistics from 12 identical network architectures trained against the same data sets.

Intensity statistics for I and F are for acentric data. Means are presented as mean ± standard deviation. Values in bold are theoretical values for ideal crystals.

	Dice coefficient		Mean IoU		〈I 2〉/〈I〉2	〈F〉2/〈F 2〉	〈L〉	〈L 2〉
Model	Train	Test	Train	Test	2.0	0.785	0.518	0.333
1	0.633	0.627	0.462	0.456	1.859	0.83	0.431	0.254
2	0.641	0.638	0.471	0.469	1.954	0.808	0.464	0.29
3	0.640	0.635	0.470	0.465	1.943	0.812	0.462	0.287
4	0.653	0.647	0.484	0.479	1.892	0.826	0.435	0.258
5	0.661	0.654	0.494	0.486	2.006	0.799	0.475	0.302
6	0.650	0.646	0.481	0.478	1.929	0.817	0.447	0.271
7	0.641	0.636	0.470	0.465	2.007	0.798	0.48	0.307
8	0.661	0.662	0.499	0.494	1.96	0.809	0.46	0.284
9	0.665	0.659	0.498	0.491	1.898	0.818	0.452	0.277
10	0.661	0.656	0.494	0.497	2.031	0.794	0.476	0.305
11	0.653	0.648	0.484	0.479	1.933	0.817	0.45	0.274
12	0.656	0.650	0.488	0.481	1.942	0.813	0.46	0.285
Mean	0.652±0.011	0.647±0.010	0.483±0.012	0.477±0.011	1.946±0.050	0.812±0.011	0.457±0.015	0.282±0.017

2.7. Peak integration using predicted peak shapes  

For each predicted peak location, a 32 × 32 × 32 voxel intensity profile was constructed and scaled to have zero mean and unit variance. To scale data, the mean intensity is first subtracted from the voxel and then the intensities are divided by the standard deviation of intensities. Scaling each peak in this way means that the model can learn peak shapes independently of the actual number of counts in the peak. These scaled intensities are used as input to the trained network. The output of the neural network is a score related to the probability that each voxel is a part of the peak; for most peaks, this results in most voxels being nearly 0 or 1 (Fig. 3 ▸). For this work, voxels with a score above 0.15 are placed into 8-connected groups. The largest blob is assumed to be the one that represents the peak. In practice, this step eliminates isolated voxels that may be misclassified as belonging to a peak. Examples of these probability maps are shown in Fig. 3 ▸. If each voxel contains N_i counts and the peak volume is n voxels large, then the peak intensity, I, is determined by

where λ_BG is the average background around the peak. Here we take λ_BG to be constant throughout the volume of the peak. The variance of the intensity, σ²(I), is the sum of the total counts in the peak plus the total counts in the background:

After integration, wavelength normalization was carried out using LAUENORM from the Lauegen package (Campbell, 1995 ▸; Helliwell et al., 1989 ▸).

Figure 3.

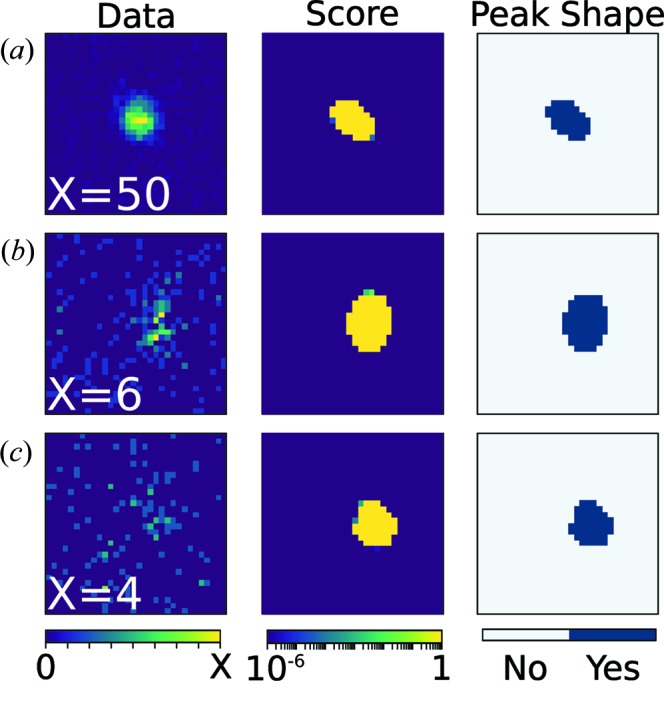
Example of peak predictions for strong (a), medium (b) and weak (c) peaks using a neural network. The column on the left shows a 2D slice of the peak centred around the predicted peak location from the UB matrix. Slices are shown with display ranges from 0 to X. The middle column shows the output of the neural network – a score given to each pixel for being classified as a peak – for the same slice. The right column shows the final binarized peak shape used for integration. The planes shown are slices in the q_xq_y plane centred at the predicted peak locations along q_z.

2.8. Calculation of statistics  

All statistics were calculated from wavelength-normalized intensities or structure factors using PHENIX (Adams et al., 2010 ▸). Expectation values of intensity ratios and cumulative distribution functions (CDFs) were originally presented by Wilson (1949 ▸) and are also reviewed in International Tables for Crystallography, Vol. B (Hahn et al., 1993 ▸) and in the supporting information of this paper. The L test was introduced by Padilla & Yeates (2003 ▸). CDFs are presented in terms of resolution-normalized intensity, Z. These statistical tests are commonly used to diagnose irregularities in crystallographic data, including twinning and non-crystallographic symmetries. Given the robustness of X-ray crystallography instrumentation and integration packages, these metrics are usually used to infer crystal symmetry and irregularities in the crystal itself (e.g. twinning) (Evans, 2011 ▸; Rees, 1980 ▸; Lebedev et al., 2006 ▸). However, applied to a near-ideal crystal they can be used to assess the accuracy of an analysis routine, as this work does.

2.9. Model refinement against integrated intensities  

Refinement was carried out in PHENIX using phenix.refine (Adams et al., 2010 ▸; Afonine et al., 2012 ▸). Refinement was done using peaks for which I/σ > 1 for integration by neural network, k-NN and profile fitting (i.e. the peaks in Table 1 ▸, solid lines in Fig. 4 ▸). The same peaks were selected for calculating R _work and R _free. PDB entry 6c78 (Langan et al., 2018 ▸) was used as a starting point, with the initial model for refinement being made using phaser and phenix.readyset (McCoy et al., 2007 ▸). Refinement was done for nine cycles, refining atomic coordinates, occupancies and atomic B factors. The results of refinement are given in Table 3 and map comparisons are shown in Fig. 5 (see Section 3).

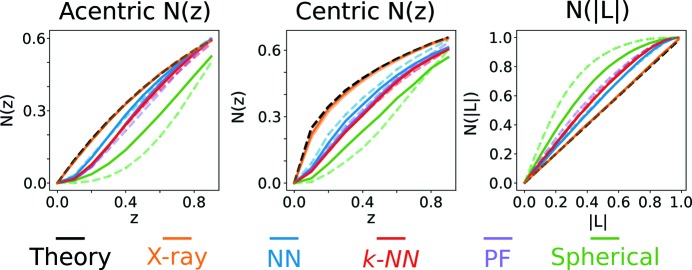
Figure 4.

Cumulative distribution functions N(z) and N(|L|). The theory curve is for an ideal crystal (see supporting information). X-ray includes peaks with I/σ > 1 to 1.8 Å (solid) or 1.65 Å (dashed). Neutron integration peak sets include peaks for which all integration methods determined I/σ > 1 to 1.8 Å (solid) or all peaks for which the individual integration method determined I/σ > 1 to 1.65 Å (dashed). Neutron data are from model 1 in Table 1 ▸.

3. Results  

The first issue to address was if machine learning algorithms are capable of learning peak shapes. Here the Dice coefficient and mean IoU (see Section 2.6) are used to assess machine performance. The generated training data set consisted of around 10 000 peaks. Twelve of the same networks were trained on these data and their metrics are shown in Table 1 ▸. Overall, the networks yielded consistent performance, with Dice coefficients of around 65% and mean IoUs of around 48%. The networks also yield consistent intensity statistics (Table 1 ▸), which are near the predicted values for an ideal crystal. As a negative control, a model was trained with inputs matched to random peak shapes from the training set. In this control experiment, the network achieved a Dice coefficient of 15% and a mean IoU of 8%. For brevity, the results from model 1 in Table 1 ▸ are presented throughout the rest of the manuscript.

It is prudent to compare the resulting intensity statistics with those from other integration methods. First, consider the X-ray statistics from the same crystal. X-ray data collection, which induces radiation damage into the sample (Garman & Schneider, 1997 ▸), was performed after neutron data collection, which is a non-ionizing probe. Comparing the resulting intensity statistics (Table 2 ▸) and CDFs (Fig. 4 ▸) recorded with predicted profiles for ideal crystals demonstrates that the Toho-1 β-lactamase crystal being analysed is nearly ideal. Having established the crystal quality, we can attribute any deviations in neutron intensity statistics to either the experiment or the data analysis (in particular, the integration method). Table 2 ▸ also shows a summary of intensity statistics for neutron data, which vary only by the integration method: either the neural network, profile fitting or the k-NN algorithm. These data are composed of the same peak sets for peaks in the range 13.97–1.80 Å with I/σ > 1 for all three integration methods. This resolution was chosen as it has greater than 75% completeness in the high-resolution shell. Table 2 ▸ shows that the neural network yields intensities that better reproduce the intensity statistics from X-ray measurements and ideal crystal predictions. Table 3 ▸ shows merging statistics for the same peak set. These statistics show that the overall R factors are lower and the correlation coefficient CC_1/2 (Karplus & Diederichs, 2012 ▸) is higher for peaks integrated using the neural network, demonstrating a more consistent integration across the data set. Note, however, that in the outer shell the profile fitting has slightly lower R values and higher CC_1/2. By all metrics, integration by the k-NN model produces statistics that are worse than neural network integration and comparable to profile fitting. Finally, spherical integration results in statistics comparable to the k-NN model, with the exception that CC_1/2 is nearly zero at 1.8 Å. Taken with the resulting intensity statistics, it is likely that spherical integration yields relatively consistent, though inaccurate, intensities.

Table 2. Summary of intensity statistics from using different integration methods.

X-ray data include all peaks recorded during X-ray collection with I/σ > 1 to a resolution of 1.80 Å. Neutron data sets are taken from peaks with I/σ > 1.0 for the neural network (NN), profile fitting (PF) and the k-NN integration schemes to 1.80 Å. These statistics are from model 1 in Table 1 ▸.

	Acentric reflections			Centric reflections
	〈I 2〉/〈I〉2	〈F〉2/〈F 2〉	〈|E 2− 1|〉	〈I 2〉/〈I〉2	〈F〉2/〈F 2〉	〈|E 2 − 1|〉	〈L〉	〈L 2〉	Z score
Theory	2.000	0.785	0.736	3.0	0.637	0.968	0.500	0.333	n/a
X-ray	2.000	0.785	0.736	2.996	0.645	0.942	0.487	0.317	1.490
NN	1.859	0.830	0.672	2.336	0.759	0.848	0.431	0.254	4.484
k-NN	1.772	0.850	0.627	2.244	0.783	0.795	0.402	0.226	8.035
PF	1.773	0.850	0.633	2.249	0.775	0.825	0.400	0.225	8.267
Spherical	1.452	0.903	0.48	1.755	0.852	0.605	0.328	0.161	22.654

Table 3. Merging and refinement statistics for each integration method.

Numbers in parentheses represent the value in the highest-resolution shell. Peaks included are integrated using model 1 in Table 1 ▸ considering only peaks with I/σ > 1 for the neural network, profile fitting and k-NN to 1.80 Å.

Neutron unit-cell parameters (Å, °)	a = b = 73.3, c = 99.0, α = β = 90, γ = 120
Space group	P3221
No. of orientations	5
No. of unique reflections	25 910 (2169)
Resolution range (Å)	13.97–1.80 (1.86–1.80)
Multiplicity	3.42 (2.29)
Completeness (%)	88.65 (75.31)

	Neural network	Profile fitting	k-NN	Spherical
Mean I/σ	11.5 (4.0)	13.3 (3.7)	9.2 (3.1)	8.4 (3.0)
R merge (%)	12.9 (26.5)	13.7 (22.2)	21.7 (31.2)	25.4 (52.2)
R pim (%)	7.1 (17.0)	7.5 (14.3)	12.0 (20.4)	14.0 (34.6)
CC1/2	0.976 (0.745)	0.974 (0.754)	0.923 (0.505)	0.928 (0.089)
Refinement statistics
R work	0.1666	0.1654	0.1801	0.2013
R free	0.2008	0.2029	0.2230	0.2605

A convenient way to visualize the effect of integration on intensity statistics is to look at the CDFs of resolution-normalized intensities, N(z). Fig. 4 ▸ shows the CDFs for the peak set in Tables 2 ▸ and 3 ▸. Spherical integration is also shown for comparison. Consistent with the ratios of moments in Table 2 ▸, the X-ray CDFs agree almost perfectly with the ideal crystal prediction. For the acentric N(z), integration using the neural network shows better agreement with the X-ray and ideal crystal prediction distributions. Similarly, the centric CDF shows that the neural network yields the best statistics, though no integration technique reproduces the distribution exactly. Finally, the CDF for |L| is best matched again by the neural network. We note that, of the presented integration methods, the neural network is the only approach to yield a linear CDF as expected [N(|L|) = |L|; see supporting information].

Imposing I/σ > 1 for the three integration methods (not spherical) is convenient to directly compare integration methods using the exact same peaks. It may, however, dampen the improvements neural network integration can provide by removing peaks that the neural network can successfully integrate and other techniques cannot. The same statistics are presented in Fig. 4 ▸ (dashed lines) and Tables S1 and S2 for peak sets for which I/σ > 1 for a single integration method. These data are presented to 1.65 Å since the completeness for each integration method is above 75%. Overall, the acentric CDF for the neural network and k-NN integration do not change with the inclusion of more peaks, while profile fitting and spherical integration agree less with the expected distributions. Furthermore, the centric CDF for the neural network improves with the inclusion of all peaks with I/σ > 1 to 1.65 Å. Finally, the CDF for |L| is unchanged for the machine learning methods, while it shows worse agreement for spherical integration and profile fitting. Intensity moment ratios and L statistics are not affected much by the peak selection scheme (Table S2). The notable exception is the CDF for centric peaks using neural network integration, which shows much better agreement with the X-ray and predicted CDFs. Note also that there are more peaks with I/σ > 1 using neural network integration than for the profile fitted data sets or k-NN integration (Table S1), demonstrating the potential for machine learning to increase the completeness of neutron data sets. Spherical integration results in the highest data completeness, but those peaks demonstrate poor intensity and merging statistics, suggesting that they are not accurately integrated.

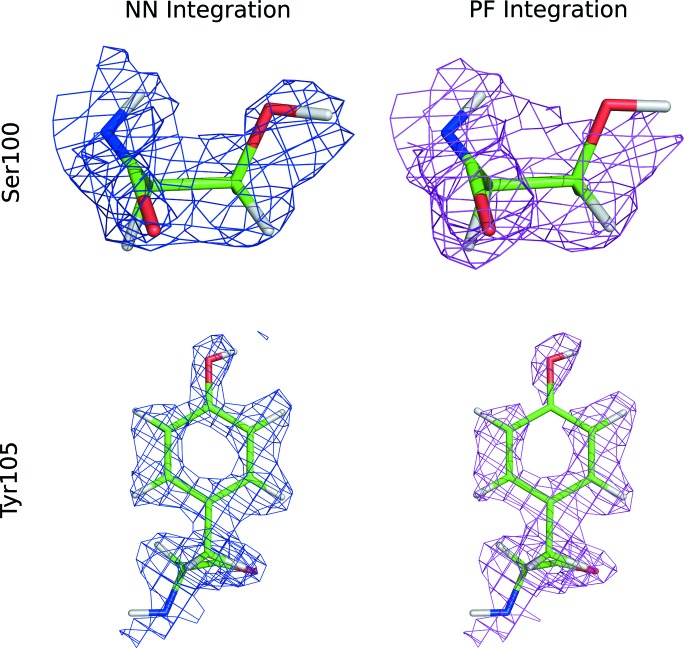
To determine the effect of the integration technique on the resulting nuclear density maps, we refined a structural model against the structure factors derived from integrated intensities. Neural-network-based integration and profile fitting refine to very similar R values. Neural-network-based integration ultimately yielded the lowest R _free values when comparing the same peaks and the same free peak sets. While the differences are small, some residues on the protein surface show appreciable differences between NN integration and profile fitting integration (Fig. 5 ▸). On Ser100, profile fitting fails to recover density for the hydroxyl group, while for Tyr105 profile fitting does not provide a continuous density for the amino acid side chain.

Figure 5.

2mFo–Fc maps for neural network (NN) and profile fitting (PF) integration for two amino acid side chains located on the surface of the protein. The 2mFo–Fc maps are contoured at 1.1σ for Tyr105 and 0.8σ for Ser100.

4. Discussion  

In this work, a relatively simple neural network based on a U-Net was tasked with a 3D image segmentation problem to identify Bragg peaks in reciprocal space. The training set was composed of ∼10 000 examples generated from strong peaks to replicate weak peaks. Remarkably, the network can determine peak locations and shapes. One straightforward way to assess the performance of the network is to visually inspect peaks. Fig. 3 ▸ shows three peaks of varying intensity and the corresponding prediction which visually matches the peak. Quantifiable metrics also demonstrate that the network can correctly segment peaks. Over the ∼10 000 training peaks, networks consistently train to an average Dice coefficient of around 65% and an average IoU of around 48% (Table 1 ▸). As a negative control, training peaks were matched with random solutions, which achieved a Dice coefficient of 15% and a mean IoU of 8%. Since each training example is centred around a peak location predicted from the UB matrix, this important control demonstrates that the network is learning peaks rather than just summing around the predicted peak location (which is effectively what spherical integration does). In terms of magnitude, the Dice coefficient and IoU are relatively low for machine learning experiments. It is important to remember, however, that the ‘ground truth’ comes from peak fitting, which may not be a perfect model of the peaks. Also, while both of these metrics are intuitive in two dimensions, segmenting small features in three dimensions causes both metrics to quickly fall to zero, even when visually the feature has been segmented well.

Machine learning techniques have been used previously for crystal screening (Liu et al., 2008 ▸; Bruno et al., 2018 ▸), to inform experiment design in protein–drug interaction (Zhang et al., 2017 ▸; Ding et al., 2014 ▸) and to detect the presence of crystals in single X-ray free-electron laser (XFEL) pulses (Ke et al., 2018 ▸), but rarely to actually analyse crystallographic data. One notable exception is the work of Pokrić et al. (2000 ▸), who first demonstrated that networks could learn peak shapes. These authors used radial basis function (RBF) networks to predict peak shapes by training against profiles of strong peaks. RBF networks are a subset of neural networks that use activation functions that depend only on the distance from their centre. One major difference between the two studies is the use of training sets augmented by simulated peaks. Pokrić et al. (2000 ▸) demonstrated the feasibility of using networks to predict peak shape but only reported integration for a handful of strong peaks (I/σ > 50). The present work uses strong peaks to simulate weak peaks, allowing machine learning models to identify even weak peaks [e.g. Fig. 3 ▸(c)] and ultimately enable improvements in density maps (Fig. 5 ▸).

Given the ability to determine peak location and shape, we sought to determine if the neural network can be used to increase the accuracy of peak integration. Previously, we have used trial refinements starting from the same initial model to compare integration schemes quantitatively (Sullivan et al., 2018 ▸). This worked well to compare profile fitting with spherical integration because the differences sharply contrasted. The improvements between profile fitting and the presented machine learning integration schemes, however, are not as drastic and so any differences could be an artefact of structural modelling. Intensity statistics allow integration schemes to be compared without having to involve structural modelling, which is somewhat dependent on the person performing the modelling. The intensity statistics from the X-ray data, which were collected after the non-ionizing neutron data collection, show distributions in agreement with ideal distributions (Fig. 4 ▸ and Table 2 ▸). These results confirm that data are measured from a high-quality crystal with no detectable twinning or pseudo-centring. It must be the case, then, that any deviation in intensity statistics from the neutron data set is a result of either experiment quality or the peak integration scheme.

A summary of intensity statistics for the same peak set for neutron data varying only by integration scheme is presented in Table 2 ▸, while the CDFs of resolution-normalized intensities, N(z), are shown in Fig. 4 ▸ (solid lines). Looking at acentric peaks, spherical integration deviates considerably from the ideal distribution, particularly at low Z where the slope of N(z) is nearly zero. Such a discrepancy in the CDFs demonstrates that spherical integration fails to provide accurate intensities and variances for low-intensity peaks. Furthermore, this deviation from accuracy persists when considering only peaks with I/σ > 1 for spherical integration (dashed line) and explains why spherical integration results in higher data completeness despite poor accuracy (Table S1). Profile fitting, which has been shown to more accurately integrate high-resolution low-intensity peaks (Sullivan et al., 2018 ▸), yields a CDF with much better agreement with the predicted and X-ray CDFs, especially at low z. The k-NN algorithm, which applies the profile of the most similar peak in the training set, yields nearly the same intensity statistics as profile fitting. This is an important control experiment result as it demonstrates that the training set used to train the neural network provides enough coverage for the peaks the neural network is expected to predict. Finally, the neural network results in intensity statistics that most resemble the expected and X-ray distributions. This result demonstrates unequivocally that neural networks can be used to integrate Bragg peaks. Profile fitting, k-NN and the neural network yield similar merging statistics (Table 3 ▸), with the neural network showing slightly decreased overall R factors and an increased CC_1/2 in the outermost shell (Karplus & Diederichs, 2012 ▸). Similar distributions are seen for centric peaks. Analysis of the L statistics, which do not rely on shell normalization, confirm the performance of each integration method. Furthermore, to explore the full potential of each integration method, results are presented for which I/σ > 1 for each integration method (Tables S1 and S2, and Fig. 4 ▸, dashed lines.)

Another interesting feature to consider is the variation of peak shapes across the detector sphere. Through profile fitting, the principal dimensions of the peak shapes were found to be effectively constant with the azimuthal angle but decreased gradually with increasing scattering angle (Sullivan et al., 2018 ▸). Profile fitting exploited this when integrating weak peaks by assuming they had the same functional form as nearby strong peaks. Similarly, neural-network-based integration can learn different peak sizes provided that the training set includes peaks of varying size. In this work, the peaks used to generate training data were the same as those used as a template for weak peaks. Given that both techniques are based on the same strong peaks, there is no reason to suspect that the training process cannot encode peak-shape variation. Indeed, the observed accuracy confirms that variations in peak shape are being correctly incorporated into the learned model at least as well as for profile fitting.

It should be explicitly noted that we are not claiming integration by machine learning is unambiguously more accurate than every other integration scheme. The current work is limited to integration schemes currently available to the MaNDi user community plus the two machine learning models presented. In particular, this work does not make comparisons with the minimum σ(I)/I method (Wilkinson et al., 1988 ▸; Wilkinson & Schultz, 1989 ▸) or the 1D profile fitting integration technique (Schultz et al., 2014 ▸), both of which have been successful in improving data quality but are not currently optimized for MaNDi data. Rather, the intention here is to demonstrate that neural networks are capable of learning peak shapes and can yield accurate intensities.

Given the vast parameter space that needs to be sampled in optimizing a neural network, even one as small as the ∼100 000 parameter network used here, it is reasonable to question the reproducibility of such a model. To determine the robustness of neural networks’ ability to predict peak shapes, we have trained the same model against the same data set 12 different times, varying only the initial weights used for training. A summary of the learning and intensity statistics is given in Table 1 ▸. These results show that, while training over 100 epochs does not necessarily reach a global minimum, neural networks can consistently outperform profile fitting in yielding correct intensity statistics.

The final product of a successful crystallography experiment is a structural model. So that integration methods may be compared directly with respect to map quality, we refined the same model against the same set of peaks, varying only the integration method. Profile fitting and NN integration resulted in the lowest refinement R values, followed by k-NN and spherical integration (Table 3 ▸). Consistent with the similar R _work and R _free values, the maps for profile fitting and NN integration are remarkably similar, with modest improvements for NN integration (Table 3 ▸). These data sets diffract to beyond 1.8 Å; however, we limit our refinement to this resolution as it has sufficient completeness when comparing all integration techniques. Moving forward, it will be interesting to see how these two techniques compare for more challenging data sets such as samples that are not perdeuterated and thus have higher backgrounds.

A major contributor to the recent success of deep learning techniques is that they are readily parallelized using graphical processing units (GPUs), which permits timely processing of the massive data sets required to train networks and rapid evaluation on an already trained network. Similarly, peak integration using networks can be performed remarkably faster than other methods. As detailed by Sullivan et al. (2018 ▸), profile fitting tries every possible background level and determines which yields a TOF profile most consistent with the known moderator emission. This process is computationally intensive and ∼700 ms are required to fit each peak in the data set reported here. By contrast, evaluating the neural network on a standard, commercially available video card (NVidia Quadro P4000) takes ∼7 ms per peak. While a single peak can be integrated around 100× faster using a neural network, directly comparing the start-to-finish analysis time of each integration technique is challenging as network training times depend critically on the hardware used and a number of hyperparameters that define the training procedure. One important extension of this work will be determining how to train a model that can integrate peaks from an arbitrary sample. Such a model would allow the training process, and therefore any profile fitting, to be skipped. Conventional wisdom in machine learning notes that if we can generate a sufficiently diverse data set then this should be possible. Given that strong peaks from a variety of samples can be modelled (Sullivan et al., 2018 ▸), generating such a data set should be possible. Once such a model is available, we expect that such increases in performance will be critical in designing data reduction streams for future instruments which will have higher flux and thus higher data rates.

5. Conclusions  

Here we demonstrated that a simple neural network can identify even weak peaks in TOF neutron crystallography data and, by using the predicted peaks, result in more accurate integration. Furthermore, the use of the neural network increased the completeness of the data sets. Low completeness in high-resolution shells is a common artefact in neutron crystallography data. More sophisticated and better-optimized neural networks could further extend the capabilities of neutron macromolecular crystallography. It will also be interesting to see if X-ray crystallography can benefit from machine-learning-based integration. While software for synchrotron and table top sources is already well established, software for serial crystallography remains under development. Such software is especially motivated by data recorded at XFELs (Winter et al., 2018 ▸; Kabsch, 2014 ▸; White et al., 2016 ▸; Barty et al., 2014 ▸). Given the increased repetition rate of new and planned XFELs (e.g. Emma et al., 2014 ▸; Altarelli, 2011 ▸; Milne et al., 2007 ▸) and the demand for larger higher-resolution detectors, data rates of 100 GB s⁻¹ are anticipated. The remarkable parallelization of neural networks running on graphical processing units (GPUs) suggests that using a neural network to integrate data may be appropriate to provide users with near-real-time feedback when faced with such an incredible amount of data.

Funding Statement

This work was funded by National Institutes of Health, National Institute of General Medical Sciences grant R01-GM071939. U.S. Department of Energy, Basic Energy Sciences grant DE-AC05-00OR22725. U.S. Department of Energy, Office of Science grant .