Intracortical smoothing of small-voxel fMRI data can provide increased detection power without spatial resolution losses compared to conventional large-voxel fMRI data

Abstract

Continued improvement in MRI acquisition technology has made functional MRI (fMRI) with small isotropic voxel sizes down to 1 mm and below more commonly available. Although many conventional fMRI studies seek to investigate regional patterns of cortical activation for which conventional voxel sizes of 3 mm and larger provide sufficient spatial resolution, smaller voxels can help avoid contamination from adjacent white matter (WM) and cerebrospinal fluid (CSF), and thereby increase the specificity of fMRI to signal changes within the gray matter. Unfortunately, temporal signal-to-noise ratio (tSNR), a metric of fMRI sensitivity, is reduced in high-resolution acquisitions, which offsets the benefits of small voxels. Here we introduce a framework that combines small, isotropic fMRI voxels acquired at 7 Tesla field strength with a novel anatomically-informed, surface mesh-navigated spatial smoothing that can provide both higher detection power and higher resolution than conventional voxel sizes. Our smoothing approach uses a family of intracortical surface meshes and allows for kernels of various shapes and sizes, including curved 3D kernels that adapt to and track the cortical folding pattern. Our goal is to restrict smoothing to the cortical gray matter ribbon and avoid noise contamination from CSF and signal dilution from WM via partial volume effects. We found that the intracortical kernel that maximizes tSNR does not maximize percent signal change (ΔS/S), and therefore the kernel configuration that optimizes detection power cannot be determined from tSNR considerations alone. However, several kernel configurations provided a favorable balance between boosting tSNR and ΔS/S, and allowed a 1.1-mm isotropic fMRI acquisition to have higher performance after smoothing (in terms of both detection power and spatial resolution) compared to an unsmoothed 3.0-mm isotropic fMRI acquisition. Overall, the results of this study support the strategy of acquiring voxels smaller than the cortical thickness, even for studies not requiring high spatial resolution, and smoothing them down within the cortical ribbon with a kernel of an appropriate shape to achieve the best performance—thus decoupling the choice of fMRI voxel size from the spatial resolution requirements of the particular study. The improvement of this new intracortical smoothing approach over conventional surface-based smoothing is expected to be modest for conventional resolutions, however the improvement is expected to increase with higher resolutions. This framework can also be applied to anatomically-informed intracortical smoothing of higher-resolution data (e.g. along columns and layers) in studies with prior information about the spatial structure of activation.

Introduction

Spatial smoothing of functional MRI (fMRI) data is a standard pre-processing step used to increase signal-to-noise ratio (SNR) through noise averaging, to assist with cross-subject registration, and to help ensure that statistical assumptions regarding the smoothness of the images are met. Typically, spatial smoothing is performed using a 3D smoothing kernel (such as a Gaussian function), which substitutes the image intensity of each voxel with a weighted average of the intensities of its neighbors. However, this standard volumetric smoothing of fMRI data has been shown to induce mislocalization errors such as cortical gray matter activation being incorrectly assigned to an adjacent gyral fold (Andrade et al., 2001) or even to nearby white matter regions (Stelzer et al., 2014).

Anatomically-constrained smoothing can help contain detected activation within tissue boundaries to avoid these errors. This is specifically appropriate in those cases in which some prior information is available—e.g., when activation is expected only within the cortical gray matter. Cortical surface-based smoothing approaches, by respecting the anatomical boundary of the cortex, have been shown to achieve both higher sensitivity and higher specificity, including less crosstalk between adjacent gyri (Jo et al., 2009, 2007; Kiebel et al., 2000).

Many existing surface-based smoothing approaches approximate the cortical ribbon as a 2D sheet, and enact the smoothing by first generating a mesh reconstruction of the cortical surface, projecting the fMRI data onto this surface reconstruction, and then smoothing along the surface, to provide a convenient anatomically-constrained smoothing within and along the cortex. However, with the growing availability of receive coil arrays and high-magnetic-field MRI scanners (3T and higher), fMRI voxel sizes well below 2 mm are increasingly available; with these smaller voxels, it becomes possible to treat the cortical gray matter as a 3D volume rather than a simple 2D sheet. Not only does this enable intracortical analyses of the columnar and laminar architecture of the cortical gray matter (Polimeni et al., 2018), but, for studies investigating large-scale organization over the brain, the question arises of how to appropriately smooth fMRI data when there are multiple voxels spanning the cortical thickness. Furthermore, for conventional fMRI studies where the expected spatial scale of activation is on the order of centimeters, it is unclear whether there would be any benefit to acquiring such small voxels because increased spatial resolution comes with the cost of decreased SNR, and hence decreased sensitivity to detecting functional activation. Taking into consideration the SNR efficiency, it is usually advantageous to acquire larger voxels than to smooth smaller voxels to the equivalent resolution (Buxton, 2009), however voxel volume is not the sole determinant of SNR in fMRI data.

It has been shown that fMRI data acquired at a higher spatial resolution than required and then spatially smoothed to a lower resolution are less affected by physiological noise than data natively acquired at the required resolution, and can provide higher temporal SNR (tSNR) (Triantafyllou et al., 2006). Smaller voxels combined with anatomically-informed sampling can also improve spatial accuracy and thereby improve spatial specificity. The spatial specificity of fMRI activation has been shown to increase in voxels sampled deep within the cortical gray matter (GM) ribbon away from the pial vasculature (Nasr et al., 2016; Polimeni et al., 2010), and fMRI analysis approaches that exclude those voxels intersecting the pial surface (i.e., “no-pial” sampling) have been proposed to improve spatial fidelity within individual subjects as well as the agreement of spatial maps across subjects (Ahveninen et al., 2016). However, including deep cortical voxels that contain subjacent white matter (WM) through partial volume effects should also be avoided, because no fMRI activations are expected within the WM. Therefore, acquiring fMRI data with a resolution higher than what is seemingly required may be beneficial, as it allows to spatially redistribute the small voxels and perform smoothing restricted to the cortical ribbon to avoid both noise contamination from cerebrospinal fluid (CSF) and signal dilution from WM, shown diagrammatically in Fig. 1. This diagram illustrates conceptually how one can view a given 3-mm isotropic voxel as pooling or averaging signal across a fixed set of 1-mm isotropic sub-voxels contained within it (Fig. 1a), and how acquiring 1-mm voxels provides flexibility to pool signal from a collection of voxels that are spatially redistributed to better respect the curved boundaries of the folded gray matter tissue (Fig. 1b). In both cases, a set of weighted 1-mm voxels is averaged (shown in a 2D cross-section in Fig. 1), but by selecting only 1-mm voxels that are contained within the GM one can average groups of contiguous small voxels while avoiding signal contamination/dilution from surrounding CSF and WM. Furthermore, a weighted average of the smaller, 1-mm voxels can provide additional control over the shape and extent of the smoothing, which can be tailored based on prior information about the expected spatial pattern of activation.

Fig. 1.

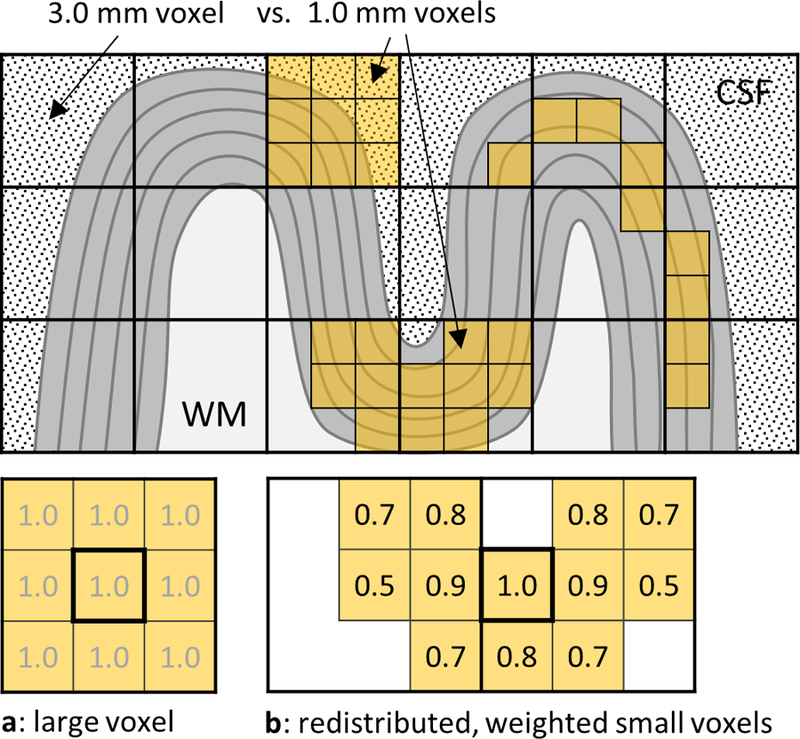
A diagram demonstrating the redistribution of small voxels and the weighting of their signals in the process of surface mesh-navigated anatomically-informed smoothing, which allows avoiding CSF and WM influences that commonly affect the signal within large voxels. (a) A large 3×3×3 mm³ voxel effectively smooths (averages) signal from 27 small 1×1×1 mm³ voxels contained within it, using an equal weight of 1.0 for each; here we show the 2D cross-section only, which includes 9 small 1×1×1 mm³ voxels. (b) With smaller voxels, the same volume can be achieved while distributing the voxels such that they are restricted to the cortical ribbon and conform to its shape. Furthermore, the weights can be adapted to provide more flexibility in defining the shape and extent of the kernel.

In this study, we developed and applied a fully automated surface mesh-navigated smoothing framework using “steerable” smoothing kernels, of varying tangential and radial extent, adapted and restricted to the cortical ribbon. The combination of fMRI acquisitions with small isotropic voxels with our intracortical smoothing framework can help avoid noise contributions from superficial CSF to provide higher sensitivity (i.e., tSNR) as well as minimize partial volume effects from activation-free WM to provide higher GM-specificity and thus higher functional contrast (i.e., percent signal change). Different kernel designs can be employed to achieve a desired smoothing strategy aimed at maximizing either only tSNR or percent signal change, or a balance between the two. Both resting-state and task-driven fMRI data were acquired at 7T with different native voxel sizes to investigate the potential advantages of the proposed approach, and to test whether appropriately smoothed high-resolution data can substitute for data acquired natively at the required lower resolution. Multiple smoothing kernel shapes and sizes were analyzed to determine their effect on sensitivity and GM-specificity, i.e., tSNR and percent signal change, two determinants of fMRI detection power. Resting-state fMRI data were obtained to quantify tSNR and task-driven data were used to quantify percent signal change as well as functional contrast-to-noise ratio (fCNR). We demonstrate that intracortical surface-based smoothing kernels designed within the proposed framework and applied to small-voxel fMRI data yield two advantages: (i) higher sensitivity and GM-specificity than conventional 3D volume-based smoothing applied to the same small-voxel data, and (ii) higher sensitivity, GM-specificity, and resolution than native large-voxel fMRI data. The improvement of our 3D intracortical smoothing technique, which allows for smoothing both tangentially and radially to the cortical surface, is expected to increase with higher resolution fMRI data in which more voxels are contained within the gray matter ribbon, allowing for more noise cancelation by smoothing along the radial direction.

Methods

Subjects and data acquisition

Ten healthy volunteers (6F/4M, 28 ± 5 y.o. (mean ± S.D.)) participated in this study. Written informed consent was obtained from all participants, and the study protocol was approved by the Institutional Review Board of Massachusetts General Hospital.

Each subject was scanned on a whole-body 7T scanner (Siemens Healthineers, Erlangen, Germany) equipped with a home-built 32-channel receive array head coil and birdcage transmit coil system (Keil et al., 2010), and a body gradient coil (SC72) using four single-shot gradient-echo EPI BOLD-weighted fMRI protocols with isotropic spatial resolutions 1.1×1.1×1.1 mm³, 1.5×1.5×1.5 mm³, 2.0×2.0×2.0 mm³ and 3.0×3.0×3.0 mm³ (for details of the scanning parameters, see Table 1). The protocols were each separately optimized in order to represent realistic fMRI protocols used in fMRI studies at 7T, including high-(1.1 mm isotropic) and low-resolution (3.0 mm isotropic), and two intermediate-resolution protocols. Resting-state fMRI data consisting of one run of each of these four protocols were acquired on five subjects (3F/2M, 27±6 y.o.) with eyes open or closed with no visual fixation task and used for tSNR analysis. Task-driven fMRI data also consisting of one run of each of the four protocols were acquired on the remaining five subjects (3F/2M, 28±5 y.o.), including breath-hold (BH) and visual stimulus (VIS) tasks. An additional run of high-resolution 1.1 mm data was acquired to define the ROI functionally—i.e., a separate “functional localizer” was acquired, to avoid any potential circularity involved with defining the ROI using data to be analyzed within that ROI (Saxe et al., 2006)—for task-driven fMRI experiments with the VIS task (see fMRI analysis section below for details). Same-session structural data were acquired at 7T for each subject with a two-echo T₁-weighted ME-MPRAGE sequence equipped with a TR-FOCI inversion pulse (Hurley et al., 2010; van der Kouwe et al., 2008) at 0.75×0.75×0.75 mm³ isotropic resolution (Zaretskaya et al., 2018).

Table 1.

Summary of the scanning parameters: matrix size = image encoding matrix (number of readout lines × number of phase encoding lines × number of slices), R = acceleration factor, MB = multi-band factor, TR = repetition time, TE = echo time, TI = inversion time, α = flip angle, ESP = nominal EPI echo spacing, BW = bandwidth. N_REST represents the number of time points used in the tSNR analysis of resting-state data; N_BH, and N_VIS correspond to the numbers of time points acquired in breath-hold and visual task runs, respectively.

pulse sequence	resolution [mm3]	matrix size [Px]	R	MB	TR [ms]	TE [ms]	TI [ms]	α [°]	ESP [ms]	BW [Hz/Px]	BW number of timepoints
											NREST	NBH	NVIS
EPI	1.10 × 1.10 × 1.10	174 × 174 × 99	4	3	2000	26	--	74	0.79	1512	60	122	96
EPI	1.50 × 1.50 × 1.50	128 × 128 × 75	3	3	1500	26	--	68	0.80	1446	80	162	128
EPI	2.00 × 2.00 × 2.00	96 × 96 × 57	2	3	1040	26	--	60	0.57	2170	115	234	184
EPI	3.00 × 3.00 × 3.00	64 × 64 × 39	1	3	745	26	--	52	0.53	2368	161	326	257
EPI	0.80 × 0.80 × 0.80	200 × 200 × 32	5	--	2000	28	--	74	1.00	1190	80	--	110
ME-MPRAGE	0.75 × 0.75 × 0.75	320 × 320 × 224	2	--	2530	1.76, 3.7	1100	7	6.2	615	--	--	--

Task-driven fMRI paradigms

Subjects viewed breath-hold cues and visual stimuli through a rear-projection screen mounted to the end of the magnet bore with a mirror mounted on the interior of the volume transmit coil. Each run of BH task experiment consisted of four 15-s long breath-holds preceded by paced breathing (three cycles of 3 s breathe-in followed by 3 s breathe-out) and expiration. The timed breathing cues were presented to ensure consistent timing across subjects, and subject compliance was monitored using respiration measurements recorded with respiratory bellows. The VIS task consisted of four 16-s long blocks of a full-field-of-view black-and-white ‘scaled noise’ pattern counter phase flickering at 8 Hz, alternated with 24-s long blocks of neutral gray as a baseline condition (whose duration was chosen to ensure BOLD signal recovery to baseline before the next stimulation). To ensure subject attention and accurate eye fixation, an additional fixation task was provided during both stimulation and baseline conditions, which consisted of a small red dot located in the center of the visual field that changed luminance between two states randomly over time (drawn from a uniform distribution between 0 and 3 s). Subjects were instructed to press a button on an MRI-compatible button box immediately after each occurrence of the luminance change, and their performance and reaction time were monitored on-line and recorded. Any runs where performance dropped below 60% accuracy were to be discarded, although this did not occur for any subjects in this study.

Pre-processing

For each subject, high-resolution structural data were bias corrected and used to generate cortical surface reconstructions with FreeSurfer (Fischl, 2012) (https://surfer.nmr.mgh.harvard.edu/) automatically, with a submillimeter voxel size to provide increased accuracy of automatic WM/GM and GM/CSF surface placement without manual intervention (Zaretskaya et al., 2018). The accuracy of the reconstructed meshes was inspected visually. The “laminar” cortical depth analysis scheme was employed (Polimeni et al., 2018, 2010) to generate a family of 11 surfaces within the cortical gray matter spaced every 10% (0–100%) of the cortical thickness, where 0% corresponds to the WM-GM interface and 100% corresponds to the GM-CSF interface. All fMRI data were motion corrected using AFNI (https://afni.nimh.nih.gov/) to the middle frame of each run, then linearly detrended (higher-order temporal trends were not observed in our data). Each run of EPI data was registered to the anatomical reference data (the T₁-weighted ME-MPRAGE volume) using Boundary-Based Registration (via the command bbregister from the FreeSurfer package), which aligns the WM-GM surface reconstruction with the WM-GM tissue boundary within the fMRI data (Greve and Fischl, 2009). Brain regions known to be affected by EPI geometric distortion (i.e., those cortical regions near to the frontal sinuses and ear canals) were identified using the automatic atlas-based cortical parcellation generated by FreeSurfer, similar to previous approaches (Greve and Fischl, 2009), then masked out and excluded from all further analysis. The resulting transformations were used to align the cortical surface reconstructions to the fMRI volumes, and, finally, the fMRI data were projected onto the cortical surface meshes by assigning to each vertex in the surface mesh the data of the nearest voxel, equivalent to nearest-neighbor interpolation. Because the spacing between adjacent surface vertices may vary with cortical depths and cortical curvature (Kay et al., 2018), which may lead to regional differences in the effective smoothing levels in the data after performing surface-based smoothing, we measured the vertex spacing at the white matter surface and pial surface separately for vertices within sulci, gyri and banks of the cortex defined based on the local mean curvature as computed via FreeSurfer (i.e. sulci were defined as vertices where curvature was greater than 0.25, gryi as vertices where curvature was less than −0.25, and banks as vertices where curvature was between −0.25 and 0.25).

fMRI analysis

While tSNR provides a useful metric for assessing the sensitivity of a particular fMRI acquisition, both tSNR and percent signal change (∆S/S) are determinants of detection power and are components of fCNR. Because the fMRI signal may be diluted through partial volume effects with nearby WM or CSF, causing a reduction in task-driven percent signal change, here we quantified the effects of anatomically-constrained smoothing on both tSNR and fCNR. While tSNR values were calculated directly from the resting-state fMRI data, fCNR was quantified from the task-driven fMRI data using the z-statistic, which measures the contrast or signal difference between two conditions (task and baseline) compared against an estimate of noise (based on the temporal variance of the residuals).

To calculate tSNR for a given run, the resting-state fMRI data were first pre-processed as described above, then for each voxel the temporal mean was divided by the temporal standard deviation to produce a tSNR map. To ensure that the level of accuracy of the tSNR estimates across protocols with different repetition times (TRs) were not affected by varying amount of the subject motion occurring during the scans of different durations, the number of time points of resting-state data (N_REST) used for the tSNR calculation was adjusted for each protocol such that a total time (TR × N_REST) was equal to approximately 120 s (see Table 1). Since N_REST for each protocol was equal or larger than 60, the differences in tSNR estimation accuracy due to the varying numbers of time points across the protocols were considered negligible.

General linear model (GLM) analyses of the task-driven fMRI data were performed using FSL Feat (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki) (Woolrich et al., 2001) and the resulting z-statistic, ∆S/S and noise standard deviation (i.e., the noise standard deviation of the contrast, stdcon, defined as √varcon) were calculated. Visual cues presented during the BH task in the form of small text shown in the center of the screen were not expected to cause activation synchronized with the activation induced by the task, nevertheless we conservatively excluded the primary visual cortex (V1) from the analysis using a V1 label generated automatically by FreeSurfer during the cortical surface reconstruction (Fischl et al., 2008; Hinds et al., 2008). A delay of the breath-hold response was assumed to be subject specific and was estimated directly from the time series of the non-smoothed 3.0-mm isotropic resolution data based on the timing of the observed change of the signal averaged across the cortex. For VIS task data, a region of interest (ROI) was created for each subject by intersecting the V1 label provided by FreeSurfer with a mask generated from the thresholded z-statistic map (after conventional volume-smoothing with a 5-mm FWHM kernel) obtained from the 1.1-mm functional localizer.

Surface mesh-navigated smoothing

A new surface mesh-navigated smoothing framework was developed to define smoothing kernels of different radial and tangential extents, as illustrated in Fig. 2. Radial extent of the smoothing kernel is defined by the number of adjacent cortical depths included in the kernel; so, for example, a radial extent of 3 indicates that the smoothing kernel averages data across three neighboring surfaces. Because there is a natural vertex correspondence across the family of 11 intracortical surface meshes (Polimeni et al., 2010), radial smoothing simply averages fMRI data projected onto these corresponding vertices across the cortical depths, with a uniform (constant) weighting applied in the radial direction. Tangential extent is parameterized by a vertex neighborhood (NB), which indicates the radius of the smoothing along the surface, and values of the contributing neighbors are weighted by their neighborhood distance from the central vertex of the kernel (an approximation of the geodesic distance from the central vertex). Therefore, a NB=1 tangential extent indicates a given vertex and its first-order neighborhood, a NB=2 tangential extent indicates a given vertex plus its first- and second-order neighborhoods (i.e., the union of the vertex, its neighbors, and their neighbors), and so on. The average vertex spacing of the cortical meshes (measured to be 0.66 mm on average across all subjects) was used to convert vertex NB sizes to millimeters. We considered various kernel shapes and extents including: (i) radial kernels (which are 1D), extending across all cortical depths with NB=1; (ii) tangential kernels (which are 2D), each smoothing within one cortical depth, extending from NB=1 to NB=6, and applied separately to each of the 11 depths; (iii) intracortical (IC) kernels (which are 3D), which extend in both the radial and tangential directions. Here we explored two types of intracortical kernels: one type is anchored on the WM/GM boundary and extends towards the pial surface, called intracortical-WM or “IC-wm”, and the other type is anchored on the midgray depth (i.e., the 50% depth surface) and extends symmetrically both towards the WM and the pial surface, called intracortical-midgray or “IC-mid”. The IC-mid kernels are attractive because they allow for a 3D intracortical smoothing that removes voxels from the top and bottom boundaries of the GM (i.e., those that exhibit partial volume effects with the surrounding WM and CSF) to provide a smoothing that maximizes the contribution from voxels within the GM. Note that conventional surface-based smoothing is a special case of our framework: conventional surface-based smoothing of fMRI data is purely 2D tangential smoothing typically performed along the WM surface (recommended for lower-resolution fMRI data) and in our nomenclature is equivalent to smoothing with an IC-wm kernel, however we also consider purely 2D tangential smoothing along the midgray surface (recommended for moderate-resolution fMRI data) equivalent to smoothing with an IC-mid kernel. A third category, which can be considered to be anchored on the WM/GM boundary or on the midgray depth, includes all depths and is therefore called intracortical-all or “IC-all”. For comparison, conventional isotropic volume-based smoothing using 3D Gaussian kernels were employed, and their smoothing extent was parameterized by the full-width-half-maximum (FWHM) of the Gaussian, ranging from 1.5 to 5.0 mm in steps of 0.5 mm.

Fig. 2.

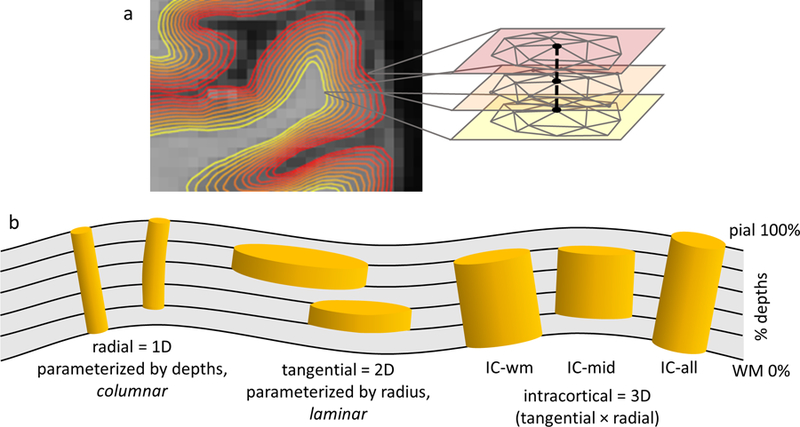
(a) A diagram presenting a family of intracortical surface meshes, where the heat scale represents the cortical depth; the mesh topology (i.e., both the numbers of vertices and edges and the connections between the vertices) is the same for all depths, so that a given vertex index in one mesh corresponds to the same vertex index across all the meshes. (b) A schematic illustration of steerable smoothing kernels tracking the cortical GM folds: 1D radial or “columnar”, 2D tangential or “laminar”, and 3D or “intracortical” (IC) extending from WM surface (IC-wm) and from midgray depth (IC-mid), and over all cortical depths (IC-all); columnar smoothing is enacted by an average of the data across the corresponding vertices.

Evaluation of anatomically-informed surface smoothing

Because the spatial extents of the various surface-smoothing kernels are quantized in both the radial and tangential directions (based on the numbers of cortical depths and the numbers of neighboring vertices), the smoothing capacity, or the effective amount of smoothing imparted by the kernel, was calculated for each kernel size and shape to enable comparison between surface-and volume-based smoothing. To estimate the smoothing capacity, each surface- and volume-smoothing kernel was applied to synthetic noise data consisting of 100 time-frames of statistically independent (i.e., spatially and temporally uncorrelated, i.i.d.) zero-mean/unit-variance Gaussian white noise. The temporal standard deviations (tSTDEV) of the smoothed noise data were then calculated voxel-wise to estimate the effective smoothing capacity of each applied kernel. To identify the set of surface-smoothing kernel sizes and shapes applied to 1.1-mm isotropic resolution data that provided equivalent smoothing capacity to a volume-based kernel with 2.0-mm FWHM applied to the same data, we simply identified those surface-based kernels that when applied to the 1.1-mm synthetic noise data yielded a tSTDEV that was less than or equal to the tSTDEV value generated by this volume-based kernel, as illustrated in Supplementary Fig. 1. Because the synthetic noise has similar statistical characteristics to thermal noise, these surface-based kernels identified in this fashion are expected to have the same impact on tSNR for the thermal noise dominated data (such as 1.1-mm resolution), regardless of the kernel shape. This procedure was employed to provide a direct, easily interpretable measure of smoothing capacity, and was therefore favored over an analytic approach based on estimating kernel volume. Note that, because the sizes of the intracortical smoothing kernels are quantized by their tangential and radial neighborhoods, smoothing capacities were not exactly matched in all cases, but for each comparison the set of kernel sizes with as similar as possible smoothing capacities was chosen.

To evaluate the overall impact of smoothing on both tSNR and fCNR across our group of subjects, the group-level analysis had to account for cross-subject differences in tSNR and fCNR values. Therefore, for each group-level analysis the tSNR or z-statistic values for each subject were first normalized to the values of the reference 3.0-mm resolution dataset from that subject and then the resulting normalized tSNR or z-statistic values were averaged across subjects. The tSNR and z-statistic values (for BH and VIS) of smoothed and non-smoothed data were plotted across cortical depth for all data resolutions to investigate a depth-dependence of the effect of smoothing on tSNR. The effect of the size of the radial, tangential and IC-all kernels on tSNR was also investigated across all data resolutions. A direct comparison of the effect of the kernel sizes for volume-based and tangential surface-based smoothing on z-statistic values obtained for these kernels applied to 1.1 mm isotropic resolution data for all cortical depths was also analyzed. To visualize the effects of the anatomically-informed smoothing, and to assess the spatial distribution of tSNR over the brain, the tSNR maps across subjects were averaged together in a common atlas space. To achieve this, tSNR maps of both the original (non-smoothed) and smoothed data of each subject were first normalized using the average tSNR of the non-smoothed 3.0-mm isotropic resolution reference data (using the mean value of the tSNR sampled at midgray depth), then the normalized values were projected onto each subject’s native white matter surface reconstruction and aligned across subjects via surface-based atlasing (using the “CVS_avg35” atlas (Postelnicu et al., 2009) distributed with FreeSurfer), and finally averaged across all subjects in this common space. In addition to the tSNR maps, “tSNR gain maps”, defined as the ratio of tSNR between the smoothed and non-smoothed data, were calculated for high-resolution (1.1 mm isotropic) data to assess the relative tSNR improvement provided by smoothing the high-resolution data.

Validation and application of the smoothing framework on ultra-high-resolution fMRI data

In order to demonstrate benefits of the proposed smoothing framework on submillimeter resolution data, two additional datasets were acquired on a whole-body 7T scanner (Siemens Healthineers, Erlangen, Germany) using a 2D single-shot gradient-echo EPI acquisition with 0.8 mm isotropic resolution (see Table 1 for acquisition details). For one subject (M, 28 y.o.) BOLD-weighted resting-state fMRI data (80 time points) was acquired in an oblique-coronal slice orientation with acquisition centered on the occipital lobe. For the second subject (F, 40 y.o.) BOLD-weighted task-driven fMRI data were acquired with similar oblique-coronal slice prescription and placement; here the subject was presented with a retinotopic “test pattern” visual stimulus consisting of two orthogonal stimulus conditions (A: ‘foreground’ and B: ‘background’) designed to elicit a desired spatial pattern of activation in the visual cortex, in this case ‘diamond-shaped’ spatial activation pattern within V1. To generate the stimulus pattern, the intended activation pattern was warped according to a standard visuotopic mapping model (shown in Supplementary Fig. 9a), following the procedure described previously (Polimeni et al., 2010). Fourteen runs (110 time-points each) were acquired, with two repetitions of 8-s stimulus blocks with 38–46-s inter-stimulus-intervals (ISI). Same-session structural data were also obtained for each of these two subjects with the protocol described above for FreeSurfer surface mesh reconstruction. Data preprocessing followed the steps of surface-based analysis described above. Resting-state data were smoothed with several intracortical surface-based smoothing kernels and tSNR values were calculated for each kernel. Task-driven data were smoothed with two example 3D intracortical smoothing kernels with equivalent smoothing capacity and with a narrow tangential extent (both with NB=1) and radial extent (either 00–04 or 03–07). A standard GLM analysis was applied to both the original unsmoothed and the smoothed data to detect activation in response to the stimulus, and resulting z-statistic values were projected onto the inflated representation of the cortical surface reconstruction for visual comparison. This provided means to test the ability of the method to improve fCNR while preserving spatial specificity, as assessed qualitatively here by how well the spatial pattern of activation resembled the intended “test pattern”.

Results

As it can be seen in Supplementary Fig. 2, while a handful of small, localized errors can be seen in the vicinity of the temporal pole and the orbitofrontal cortex, as previously reported for similar 7T MEMPRAGE data (Zaretskaya et al., 2018), overall the quality of these automatic reconstructions, generated without any manual corrections, was deemed to be sufficient. However, because the regions located near to susceptibility gradients and therefore affected by EPI geometric distortion are also prone to surface reconstruction errors, fMRI data from these regions of the brain were automatically masked out and excluded from all analyses as described above in the Methods section. To quantify potential differences in surface mesh vertex spacing that vary systematically with cortical depth and cortical curvature, we computed histograms of vertex spacing, equivalent to the length of the edges in the surface mesh, separately for sulci, gyri and banks for white matter (WM/GM) and pial (GM/CSF) surface meshes, with the results shown in Supplementary Fig. 3. While the vertex spacing was not strongly dependent on cortical surface curvature within the white matter surface, within the pial surface vertices found within sulci exhibited an average vertex spacing that was approximately 20% lower than vertices within the gyri or banks, indicating that smoothing based on neighborhood distances alone will cause small differences in the degree of smoothing in units of mm for some locations along the pial surface (see Discussion), however there is a large degree of overlap seen in these distributions of vertex spacing.

Effects of anatomically-informed smoothing on tSNR

The tSNR maps of Fig. 3a demonstrate that the tSNR values calculated for resting-state fMRI data increased with increasing voxel size, as expected. These example tSNR maps corresponding to different spatial resolutions also qualitatively highlight varying levels of physiological noise contribution to the total fMRI time-series noise across voxel sizes. The tSNR maps at 1.1-mm resolution exhibit a spatial pattern that is expected for thermal noise dominated data, in which tSNR is the highest around the periphery of the brain, near the coil elements, and decreases steadily towards the center of the brain, whereas the tSNR maps at 3.0-mm resolution exhibit a spatial pattern that is expected for physiological noise dominated data, based on the known difference in physiological noise levels across tissue types (Bodurka et al., 2007), in which tSNR is the highest in WM (where physiological noise is lowest), tSNR is the lowest in CSF (where physiological noise is highest), and tSNR is intermediate in GM (Wald and Polimeni, 2017).

Fig. 3.

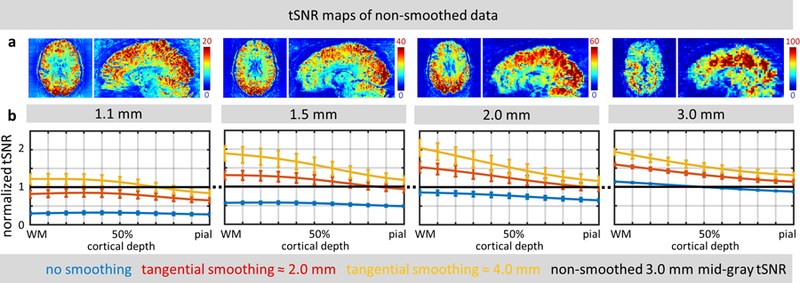
(a) Example axial slices and sagittal reformats of tSNR maps calculated for all four spatial resolutions (1.1, 1.5, 2.0, 3.0 mm isotropic) of resting-state fMRI data for a representative subject. (Note that different color scales were used across resolutions to better visualize spatial distribution of tSNR.) (b) The effect of tangential smoothing on tSNR values across cortical surfaces, normalized to tSNR of 3.0-mm isotropic resolution non-smoothed data (represented by the black horizontal line), for all four spatial resolutions, averaged across five subjects. Error bars indicate standard error across subjects.

The tSNR trends across cortical depth and their changes with spatial smoothing, shown in Fig. 3b, also reflect the varying levels of physiological noise contribution to each voxel size. In the unsmoothed data (represented by the blue traces), there is no discernable trend of tSNR across cortical depths in the small-voxel (1.1-mm and 1.5-mm) data, indicating that there is no systematic relationship between spatial gradients in tSNR and the radial direction of the cortex, as expected for thermal-noise-dominated data (provided that the tSNR trend across depth is plotted for a sufficiently large region of cortex). For the large-voxel (2.0-mm and 3.0-mm) data, a clear trend begins to emerge in which the tSNR of the unsmoothed data steadily decreases from the WM to the CSF.

As the data is smoothed tangentially within the cortex—which, unlike conventional 3D volumetric smoothing, minimizes contamination of signal originating in GM from signal originating in WM or CSF, and minimizes any signal mixing across cortical depths—the tSNR trends across depths seen in Fig. 3b become more pronounced, even in the small-voxel (1.1-mm) data. This is likely due to cancellation of the spatially uncorrelated thermal noise by spatial smoothing, as has been shown previously (Triantafyllou et al., 2006), and consequently the increased dominance of physiological noise, which is spatially correlated and therefore is not cancelled by moderate levels of spatial smoothing.

The effects of surface-smoothing on tSNR calculated from resting-state fMRI data using different kernel sizes and shapes are summarized in Fig. 4. For all analyzed kernels, smoothing improved tSNR values, and a trend can be observed where greater improvement is seen for larger kernel sizes applied to higher-resolution data, with a consistently larger tSNR increase seen from data sampled at the midgray cortical depth than at the pial surface. As described in the Methods section, the tSNR values of each subject were normalized to a reference tSNR—taken as the mean tSNR of the non-smoothed 3.0-mm resting-state fMRI data sampled at the midgray surface (50% of cortical depth)—for each subject.

Fig. 4.

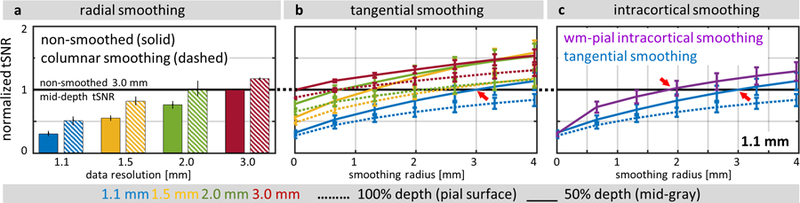
The effect of radial (columnar), tangential (laminar), and intracortical smoothing on tSNR values of resting-state fMRI data. For comparison, tSNR values were normalized to a reference tSNR of non-smoothed 3.0-mm isotropic resolution data sampled at midgray depth (represented by the black horizontal line), then averaged across five subjects. (a) The results of radial smoothing (dashed bars) are compared with the tSNR of the original data (solid bars) for all four spatial resolutions (1.1, 1.5, 2.0 and 3.0 mm isotropic) and averaged across all cortical depths. (b) The results of tangential smoothing plotted as a function of tangential smoothing radius, for all four spatial resolutions; line colors indicate different spatial resolutions (as in panel a). (c) The results of intracortical smoothing across all depths (IC-all: 00– 10, extending from WM to pial surface) plotted as a function of tangential smoothing radius, for 1.1-mm isotropic resolution data only. For comparison, the tSNR plot of tangential smoothing (blue curve) is reproduced from panel b. In (b) and (c), dashed lines represent data at 100% depth (i.e., at the pial surface), and solid lines represent data at 50% depth (i.e., at the midgray surface); see legend below panel. Red arrows indicate transitions where smoothing of 1.1-mm data produces tSNR that exceeds the tSNR level of the reference non-smoothed 3.0-mm data. Error bars indicate standard error across subjects.

The effects of radial (1D) smoothing across all cortical depths (i.e., “columnar” smoothing) are shown in Fig. 4a. Radial smoothing of the 1.1-mm isotropic resolution data led to a 67% increase of the resulting tSNR compared to non-smoothed data, and reached the level of just over 50% of tSNR of non-smoothed 3.0-mm data. As expected, the effect of columnar smoothing on tSNR was less pronounced for lower-resolution data, with a 50% increase in tSNR seen in the 1.5-mm data, a 30% increase seen in the 2.0-mm data, and a 18% increase seen in the 3.0-mm data.

The effects of tangential (2D) smoothing for each cortical depth (i.e., “laminar” smoothing) are shown in Fig. 4b. For all resolutions, tangential smoothing resulted in a monotonic increase in tSNR with larger smoothing kernel radius, however the rate of tSNR increase was greater for data sampled from the midgray surface (50% depth) versus the pial surface (100% depth), which can be explained by the proximity and possible contamination of the pial surface signal by physiological noise from CSF through partial volume effects. Tangential smoothing of the 1.1-mm data using a 2D kernel with NB=5 corresponding to a tangential radius of approximately 3.0 mm (the equivalent smoothing capacity to a volume-based 3D smoothing kernel with 1.88-mm FWHM, therefore yielding an effective resolution after smoothing of approximately 2.18 mm isotropic) at the midgray depth of the cortex increased tSNR to the level of non-smoothed 3.0 mm isotropic data. Note that, although smoothing the 1.1-mm isotropic data to an effective resolution of 2.18 mm isotropic yields a higher tSNR than non-smoothed 3.0-mm isotropic data, because the 1.1-mm isotropic acquisition and the 3.0-mm isotropic acquisition utilized differing levels of parallel imaging acceleration (R=4 vs. R=1, respectively) and have differing levels of physiological noise, it is difficult to assess the expected gains of tSNR achieved by increasing the effective voxel size (see Discussion).

The effects of intracortical (3D) smoothing across all cortical depths (00–10) are shown in Fig. 4c. The intracortical smoothing provided further increase of tSNR in the 1.1-mm data, allowing a smaller tangential radius of approximately 1.8 mm (the equivalent smoothing capacity to a volume-based 3D smoothing kernel with 1.93-mm FWHM, therefore yielding an effective resolution after smoothing of approximately 2.22 mm isotropic) to be used to reach the level of non-smoothed 3.0-mm data tSNR. This radius represents the minimal tangential extent needed for an intracortical smoothing kernel that is maximally extended in the radial direction (00–10) to achieve the tSNR of the original 3.0-mm data. The rate of tSNR increase with increasing tangential smoothing radius for this 3D intracortical smoothing was comparable to that observed for the purely 2D tangential smoothing.

The tSNR values of 1.1-mm resolution data smoothed with a selected set of kernels with different shapes but with equivalent smoothing capacity, including both strictly 2D tangential kernels and 3D intracortical kernels, are summarized in Fig. 5. To aid the comparison, and to help remove the expected variation of tSNR across subjects and sessions, tSNR values for each subject were first normalized to the midgray tSNR resulting from the conventional volume-based 3D smoothing with the 2.0-mm FWHM kernel. Importantly, the normalized tSNR values resulting from surface-based smoothing across all of the kernels from this chosen set were higher than that of the volume-based kernel of the same smoothing capacity. The selected 3D intracortical kernels performed slightly better than the average across depths of the strictly 2D tangential kernels with radius NB=5. Note that the normalized tSNR values corresponding to the non-smoothed, volume-smoothed and 2D (tangential) surface-smoothed data were first calculated for each depth separately and then averaged across the depths, while the normalized tSNR values corresponding to smoothing with 3D (intracortical) kernels were not. Results from all smoothing kernels with equivalent smoothing capacity (including the subset presented in Fig. 5) are presented in Supplementary Fig. 4.

Fig. 5.

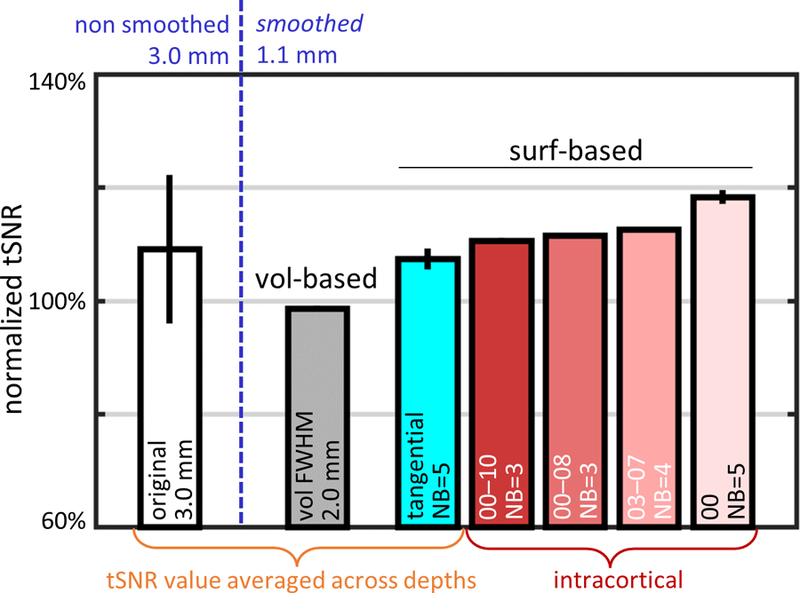
tSNR values (averaged across 5 subjects) calculated for 1.1-mm isotropic resting-state fMRI data after smoothing with a set of kernels with equivalent smoothing capacities. For comparison, the resulting tSNR was normalized to the reference tSNR of conventional volume-based smoothed data using a 3D kernel with FWHM=2.0 mm sampled at midgray depth. The reference tSNR of the volume-smoothed data, represented by the gray bar, is compared with the tSNR after applying a set of surface-based smoothing kernels with smoothing capacity matched to the FWHM=2.0 mm volume-smoothing kernel: a purely tangential kernel with NB=5 (radius≈3.3 mm, cyan bar) where the resulting tSNR values were averaged across depths, and with intracortical kernels with varying tangential neighborhoods (red-scale bars) including: one extending across all depths (IC-all: 00–10), one extending from the WM to an intermediate depth (IC-wm: 00–08), one centered at midgray depth and extending symmetrically in both directions (IC-mid: 03–07), and one consisting only of the WM surface (IC-wm: 00). Normalized tSNR of non-smoothed 3.0-mm isotropic data was plotted for comparison (white bar). Error bars indicate standard error across subjects.

Comparing the tSNR resulting from the various kernels with similar smoothing capacity but different shapes and sizes suggests that some kernels may be more effective at avoiding physiological noise contamination. The normalized tSNR seen after smoothing with the intracortical kernel 00–10/NB=3 (extending across all 11 cortical depths) was comparable (111%) to that for the similar intracortical kernel 00–08/NB=3 (112%, extending across the lower 9 cortical depths), even though the latter kernel is smaller in size, suggesting that avoiding cortical depths close to the pial surface, where there is physiological noise from downstream BOLD signals pooled in the pial vessels and from nearby CSF, can improve tSNR. Avoiding cortical depths near the white matter appears to have the opposite effect, which can be seen in the reduced normalized tSNR after intracortical smoothing with the 02–08/NB=3 kernel (104%, see Supplementary Fig. 4). In order to achieve the same tSNR level, the reduced radial extent is balanced by the increase of the tangential extent as it can be seen comparing the 00–08/NB=3 kernel with the 03–07/NB=4 kernel, which reached similar tSNR levels (112% and 113%). Also included in Supplementary Fig. 4 are the tSNR levels resulting from conventional 2D tangential smoothing (i.e., a special case equivalent to smoothing with the 00/NB=5 kernel) and from 2D tangential smoothing along the midgray surface (i.e., another special case, equivalent to smoothing with the 05/NB=5 kernel); here it can be seen that, by virtue of avoiding noise contributions from the pial surface, conventional 2D smoothing outperforms both 2D tangential midgray smoothing and 3D intracortical smoothing in terms of tSNR (by about 10%), however as is shown below this conventional 2D tangential smoothing dramatically underperforms in terms of fCNR.

Similar trends in tSNR values after smoothing can be seen in the results of applying this smoothing framework to our ultra-high-resolution 0.8 mm isotropic resting-state BOLD fMRI data, where the 3D intracortical smoothing with the 03–07/NB=4 kernel outperformed conventional 2D tangential smoothing (i.e., smoothing with the 00/NB=5 kernel) by 25% and mid-gray 2D tangential smoothing (i.e., smoothing with the 05/NB=5 kernel) by about 10% (shown in Supplementary Fig. 8). This illustrates how, as expected, when going to smaller voxel sizes our 3D intracortical kernel can outperform conventional 2D smoothing in terms of tSNR because of the larger numbers of independent intracortical voxels available along the radial direction. As an aside, comparing the two purely 2D tangential smoothing methods—the conventional 2D tangential smoothing and midgray 2D tangential smoothing—we see that in these 0.8 mm iso. data the tSNR resulting from smoothing along the white matter surface is now lower than the tSNR resulting from smoothing along the midgray surface (cf. Fig. 3). This may be attributable to the thermal-noise dominance in these ultra-high-resolution data even after spatial smoothing (see Discussion).

Fig. 6 presents the group-averaged tSNR maps generated from all subjects to assess both the spatial distribution of tSNR and the tSNR gain over the cortical hemispheres. Fig. 6a shows the normalized tSNR maps calculated from the original (non-smoothed) 3.0-mm isotropic resolution data and from the 1.1-mm data smoothed with the IC-mid 03–07/NB=4 kernel highlighted above, which demonstrates that the tSNR of the smoothed 1.1-mm isotropic data is higher than the tSNR of the unsmoothed 3.0-mm data in almost every cortical region, although the benefit of the smoothed high-resolution data varies spatially across the brain. In addition, the tSNR gain maps presented in Fig. 6b for the 1.1-mm isotropic resolution data better demonstrate the regional variation in tSNR gain due to the intracortical smoothing, showing that some brain regions naturally benefit more from this smoothing than others. Similar maps generated to assess the spatial distribution of fCNR before and after smoothing and the associated fCNR gain provided by smoothing are presented in Supplementary Fig. 7.

Fig. 6.

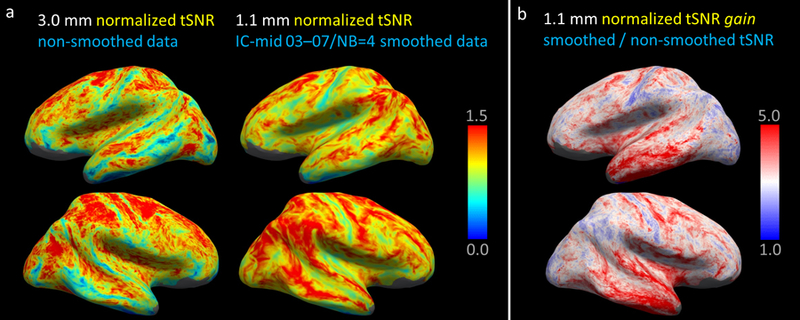
Visualization of the spatial distribution of tSNR averaged across subjects using the FreeSurfer CVS avg35 atlas space, shown on the inflated surface representation. (a) Normalized tSNR of the non-smoothed 3.0-mm isotropic resolution data and the 1.1-mm isotropic resolution data after smoothing with surface-based kernel IC-mid 03–07 NB=4. Regional differences in the tSNR maps are seen, however the tSNR of the smoothed 1.1 mm isotropic data is higher than the unsmoothed 3.0-mm isotropic data in nearly every region of the cortical hemispheres. (b) tSNR gain maps showing the tSNR increase, the ratio of 1.1-mm isotropic resolution data smoothed using the kernel from panel (a) by the same non-smoothed 1.1-mm data. For this example acquisition and this example kernel, some brain regions naturally benefit more from smoothing than others.

Effects of anatomically-informed smoothing on fCNR

Task-driven fMRI data were used to investigate the effects of different smoothing kernels on fCNR by potentially avoiding partial volume effects with WM voxels (where fMRI activation is not expected).

For each subject, ∆S/S, stdcon and z-statistic values were normalized using the corresponding values obtained for the reference non-smoothed 3.0-mm resolution data, in order to remove across-subject variations. To assess how the smoothing impacted fCNR as a function of cortical depth, the results for non-smoothed and surface-smoothed data with a single tangential (2D) kernel extending over a moderate radius, NB=3 (≈2.0 mm), across all five subjects are plotted against cortical depth in Fig. 7 for BH and VIS task conditions, and for all data resolutions (1.1, 1.5, 2.0, 3.0 mm).

Fig. 7.

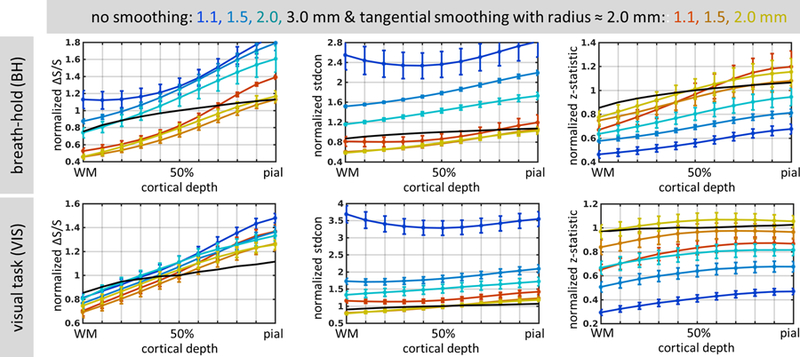
Normalized percent signal change (ΔS/S), contrast standard deviation (stdcon), and z-statistic values, averaged across 5 subjects and plotted as a function of cortical depth, for breath-hold (BH, top) and visual task (VIS, bottom), for all spatial resolutions: 1.1, 1.5, 2.0 and 3.0 mm isotropic. Blue-to-cyan lines represent original, non-smoothed data at 1.1, 1.5, and 2.0-mm isotropic resolution, while red-to-yellow lines correspond to data smoothed tangentially with radius of about 2.0 mm (NB=3) at 1.1, 1.5, and 2.0-mm isotropic resolution. Black line represents the values of the non-smoothed 3.0-mm isotropic data for comparison. Error bars indicate standard error across subjects.

While the normalized ∆S/S values were similar across the data resolutions, the decreases in normalized stdcon and corresponding increases in normalized z-statistic values with increasing voxel size were more pronounced, as expected. Trends for all three measures to increase across the cortical depth from WM boundary towards the pial surface were observed for both non-smoothed and smoothed data, and similar trends were seen for the BH and VIS task conditions. Smoothing decreased ∆S/S and stdcon, due to the expected averaging of both signal and noise across multiple vertices, but the slope of ∆S/S over depths was steeper than the slope of stdcon; and because, by definition, the z-statistic increases with ∆S/S and decreases with stdcon, the relatively steeper increases of ∆S/S with depth caused both an overall increase of z-statistic and an increase of z-statistic with depth in the surface-smoothed data. We observed less decrease of ∆S/S due to smoothing in the VIS data than the BH data, which may reflect both higher levels of spatial heterogeneity in the BH data over the whole-brain ROI and the use of a restricted ROI in the VIS data including only voxels with strong visual responses. In both the BH and the VIS data, tangential smoothing lead to a largely uniform increase in z-statistics across all voxel sizes. The roughly U-shaped curves representing stdcon in both VIS and BH plots for 1.1-mm data show that variability of the BOLD signal was greater close to the WM surface and the pial surface than in the middle depths of the cortex.

Fig. 8 provides comparisons of normalized z-statistic values obtained for the task-driven fMRI data after volume-smoothing with kernels of FWHM ranging from 1.5 to 4 mm and after surface-smoothing with strictly tangential (2D) kernels of the extents ranging from NB=1 to 6, over 11 cortical depths for 1.1-mm isotropic resolution BH task data and across all five subjects. Indicated in these plots for reference are one volume-based kernel and one surface-based kernel with equivalent smoothing capacity: the volume-smoothing kernel with FWHM=2.0 mm and the surface-smoothing kernel with NB=5. For these two kernels, it is apparent that there is a broader range of z-statistic values across depths in the surface-smoothed data compared to the volume-smoothed data, indicating that that tangential smoothing causes less mixing of the signals across the cortical depths than volume smoothing. Also, in both plots it appears that the z-statistic value reaches an asymptote with progressively larger kernel sizes; similar asymptotic behavior has been previously seen in tSNR with increased smoothing (Krüger et al., 2001; Triantafyllou et al., 2006). The asymptotic value seems to be reached sooner in the data sampled from the pial surface compared to the data sampled from the white matter surface, which suggests that data that is more physiological noise dominated achieves the maximal z-statistic value with a narrower smoothing kernel compared to data that is more thermal noise dominated.

Fig. 8.

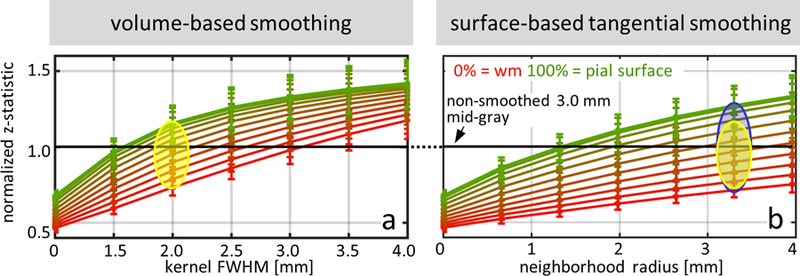
Normalized z-statistic values, averaged across 5 subjects, calculated for 1.1-mm isotropic breath-hold fMRI data, plotted as a function of smoothing kernel size, for all cortical depths (red to green, with red representing data sampled at the WM surface, and green representing data sampled at the pial surface). (a) Conventional 3D volume-based smoothing with various kernel sizes up to 4-mm FWHM. The yellow oval highlights the spread of z-statistic values for a specific kernel size (2-mm FWHM). (b) Proposed 2D tangential surface-based smoothing with radius up to 4 mm. The yellow oval from panel (a) is reproduced here, and is placed at the surface-smoothing radius corresponding to the kernel with smoothing capacity equivalent to the 2.0-mm FWHM 3D volume-smoothing kernel, with the blue oval outlining spread of the z-statistic values across cortical depths (NB=5, radius≈3.3 mm). The blue oval highlights how, at this same smoothing capacity, the surface-based tangential smoothing achieves a broader range of resulting z-statistic values across depths. In both panels the black line represents the reference non-smoothed 3.0-mm isotropic data, and error bars represent standard error across subjects.

The shape of the smoothing kernel had a strong effect not only on tSNR, as seen in Fig. 5, but also on fCNR quantified by the z-statistic. The same set of selected kernels shown in Fig. 5, each having a different shape but with equivalent smoothing capacity, were applied to the BH task data. Shown for comparison are the z-statistics of unsmoothed 3.0-mm task-driven fMRI data and the z-statistics resulting from smoothing the 1.1-mm task-driven fMRI data with a conventional volume-based 3D smoothing kernel set to 2.0-mm FWHM to achieve equivalent smoothing capacity to the surface-based smoothing kernels. Again, to help remove the expected variation of fCNR across subjects and sessions, z-statistic values for each subject were first normalized to a fixed reference, the average value sampled at the mid-gray depth resulting from the conventional volume-based 3D smoothing with the 2.0-mm FWHM kernel. The results are shown in Fig. 9. The z-statistic value obtained using the reference volume-smoothing kernel (98%) was slightly lower than the value obtained for non-smoothed 3.0-mm data, however the surface-smoothing kernels performed better than the reference kernel, with the IC-wm 00–10/NB=3 kernel (which included all cortical depths) producing the highest z-statistic value (109%), and the IC-mid 03–07/NB=4 kernel producing the next-highest value (105%). Notably, the only exception was the IC-wm 00/NB=5 kernel (i.e., smoothing along at the WM/GM boundary), which produced the lowest fCNR of all kernels (72%), although this same kernel yielded the highest tSNR when applied to the resting-state fMRI data (118%, see Fig. 5). Comparison of Figs. 5 and 9 also shows that two particular kernels, IC-wm 00–10/NB=3 and IC-mid 03–07/NB=4, provided the best overall balance between tSNR and fCNR (109% and 11%, 105% and 113%, respectively) within this set of kernels, and achieved both improved sensitivity and GM-specificity when applied to the 1.1-mm isotropic data compared to the unsmoothed 3.0-mm data. Bar plots presenting z-statistic for all kernels of equivalent smoothing capacity (including a subset presented in Fig. 9) are shown in Supplementary Fig. 5. Again, included in Supplementary Fig. 5 are the fCNR levels resulting from conventional 2D tangential smoothing (i.e., 00/NB=5 kernel) and from 2D tangential smoothing along the midgray surface (i.e., 05/NB=5 kernel); in contrast to the results seen with respect to tSNR, here it can be seen that, conventional 2D smoothing dramatically underperforms both 2D tangential midgray smoothing and 3D intracortical smoothing in terms of fCNR.

Fig. 9.

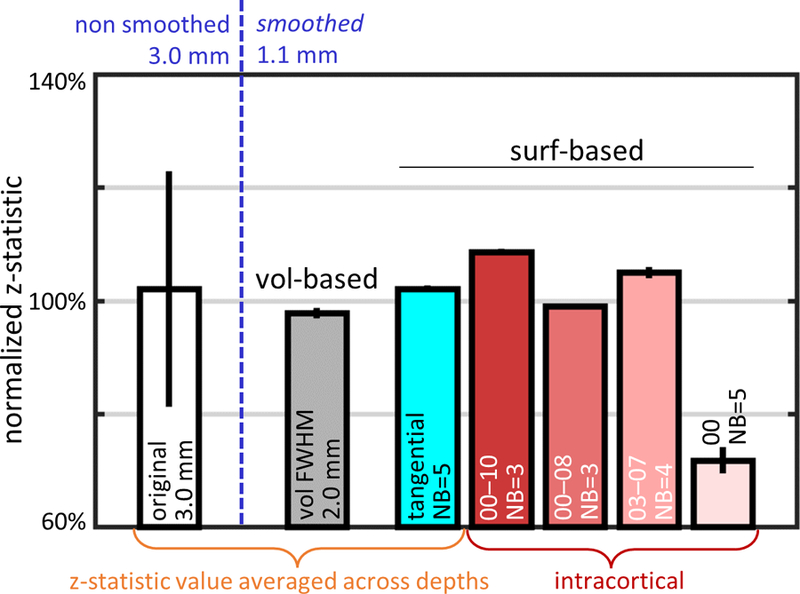
Normalized z-statistic values (averaged across 5 subjects) calculated for 1.1-mm isotropic BH task fMRI data after smoothing with a set of kernels with equivalent smoothing capacities, just as in Fig. 5. The z-statistic values in each subject were first normalized to the z-statistic resulting from conventional volume-based smoothed data using a 3D kernel with FWHM=2.0 mm sampled at midgray depth, then averaged across subjects. The z-statistic of the reference volume-smoothed data, represented by the gray bar, is compared with the z-statistic after applying a set of surface-based smoothing kernels with equivalent smoothing capacity including: a purely tangential kernel with NB=5 (radius≈3.3 mm, cyan bar) where the resulting z-statistic values were averaged across depths, and with intracortical kernels with varying tangential neighborhoods (red-scale bars) including: one extending across all depths (IC-all: 00–10), one extending from the WM to an intermediate depth (IC-wm: 00–08), one centered at midgray depth and extending symmetrically in both directions (IC-mid: 03–07), and one consisting only of the WM surface (IC-wm: 00). Normalized z-statistic of non-smoothed 3.0-mm isotropic data was plotted for comparison (white bar). Error bars indicate standard error across subjects. Unlike the tSNR results shown in Fig. 5, here the normalized z-statistic value of the NB=5 smoothed data at the WM surface is the lowest value of all cases shown.

To demonstrate the ability of our approach to preserve fine-scale details of fMRI activation patterns while smoothing in 3D within the cortex, an example of our smoothing applied to a retinotopic activation pattern measured at 0.8 mm isotropic resolution at 7T is shown in Supplementary Fig. 9. The original unsmoothed data as well as the data smoothed with the IC-mid 03–07/NB=1 or with the IC-mid 00–04/NB=1 smoothing kernels, which have equivalent smoothing capacities, are shown projected onto the inflated surface representation. While both 3D intracortical smoothing kernels succeed in increasing the fCNR of the “diamond-shaped” activation pattern as can be seen in the overall increase in z-statistic values within the foreground and background regions of the activation pattern, in this case the spatial fidelity of the pattern is improved after smoothing with the IC-mid 03–07/NB=1 kernel, presumably due to the reduced partial volume effects with subjacent white matter than may be present after smoothing with the IC-mid 00–04/NB=1 kernel. While the exact kernel size and shape that is appropriate for any given application will depend on the fMRI resolution and the optimal trade-off between sensitivity and spatial specificity for the question at hand, this example demonstrates how the 3D intracortical smoothing can preserve the spatial pattern of activation in 2D along the cortical surface while smoothing both within and across the cortex to improve fCNR.

Discussion

In this work, we have proposed a fully-automated framework for designing surface mesh-navigated smoothing kernels with varying tangential and radial extents within the cortical ribbon. After evaluating these kernels on resting-state and task-driven fMRI data, we found that surface-smoothing kernels of particular shapes can provide both higher tSNR and higher fCNR than either the conventional volume-smoothing approach or natively lower resolution data, by avoiding noise contributions from CSF and signal dilution from WM via partial volume effects. Our comparison of the performance of various kernels of equivalent smoothing capacity, which therefore achieve similar final spatial resolution in the smoothed data, showed that surface-smoothing kernels of different shapes and sizes have different and potentially opposite impacts on tSNR and fCNR—a kernel that performs well with respect to tSNR may perform poorly with respect to fCNR. For example, based on tSNR considerations alone, when smoothing within GM it may be advantageous to utilize a kernel that includes a portion of WM into the voxel, since physiological noise is lower in the WM than in the GM; however, based on fCNR considerations, because functional activation is not expected from the WM, this same kernel would cause a reduction in detected activation. (While a small number of recent fMRI studies have reported subtle fMRI activation in WM, these activation levels are far smaller than activation in GM due to the relatively low blood volume in WM, and these studies used paradigms specifically designed to induce brain activity in WM (Courtemanche et al., 2018; Gawryluk et al., 2014); the tasks used in our study (BH and VIS) are not expected to appreciably activate WM, and our results are consistent with low activation from the WM subjacent to GM.) Therefore, the specific kernel design to maximize sensitivity may not maximize fMRI detection power.

The patterns of tSNR changes with smoothing in the resting-state fMRI data (Fig. 3) were consistent with the known thermal noise dominance in high-resolution data and physiological noise dominance in low-resolution data (Krüger et al., 2001; Triantafyllou et al., 2005; Wald and Polimeni, 2017). The cancellation of spatially uncorrelated thermal noise via surface-based tangential smoothing led to an increase in tSNR for all cortical depths, causing the smoothed high-resolution data (1.1 mm and 1.5 mm) to be dominated by physiological noise. This manifested as a positive slope across depths and tSNR depth profiles with a maximum cancellation at the pial surface (Fig. 3b), as expected based on previous work (Triantafyllou et al., 2006). The same effect could also be seen in the faster increase in tSNR values with kernel size observed in data sampled from the midgray cortical depths compared to the slower increase in tSNR values in data sampled close to the pial surface (Fig. 4), indicating that the well-known spatial correlations in physiological noise resulted in a less pronounced tSNR increase for those fMRI data voxels with more physiological noise contribution via partial volume effects. It has been previously demonstrated that physiological noise levels are tissue specific, with the strongest physiological noise within the CSF and on the cortical surface due to the pulsatile flow effects and presence of large pial vessels (Bodurka et al., 2007; Polimeni et al., 2015; Triantafyllou et al., 2016). Therefore, voxels closer to the pial surface have far higher noise levels then those located deeper within the cortex, closer to the WM/GM interface.

While tSNR was observed to monotonically decrease from the WM/GM interface to the GM/CSF interface, the opposite trend was observed for ΔS/S in the task-driven fMRI data, in which ΔS/S was maximal at the pial surface (Fig. 7). This can be explained by the fact that the BOLD signal is dominated by changes in deoxyhemoglobin in the venous side of the vasculature and these signal changes increase within the downstream pooling of deoxygenated blood in the large draining vessels on the pial surface, which imposes a systematic increase of ΔS/S with proximity to the pial vasculature (Polimeni et al., 2010; Poplawsky et al., 2017; Uludağ and Blinder, 2016). In addition, similar partial volume effects can also reduce the measured signal change in voxels intersecting the WM/GM boundary, since little or no fMRI activation is expected in the WM. Therefore, due to these opposing effects of both low noise and low signal change originating from the WM, surface-smoothing kernel including only voxels at the WM/GM boundary produced largest increase of tSNR and at the same time the largest decrease of fCNR values (seen in Fig. 5 for tSNR and in Fig. 9 for fCNR). However, a different trend across cortical depths can be seen in the results of smoothing applied to our ultra-high-resolution data. As noted above in the Results section, the trend in tSNR across depths after smoothing differs between the 1.1 mm iso. data and the 0.8 mm iso. data—after smoothing, the tSNR is higher near to the white matter than near to the midgray surface in the 1.1 mm data whereas the opposite is true and the tSNR is lower near to the white matter than near to the midgray surface in the 0.8 mm data. With these small 0.8 mm iso. voxels even after smoothing the data may be thermal-noise dominated. Therefore, in this case tSNR is highest around the periphery of the brain—near to the surface coil array detectors—and lowest in the center of the head (Wald and Polimeni, 2017), which explains why in this ultra-high-resolution data the tSNR after smoothing is lower near to the white matter surface.

Tangential smoothing of the fMRI data caused a small decrease in ΔS/S but a large decrease in stdcon, leading to an increase of z-statistic (Fig. 7). Tangential smoothing also resulted in a broader range of z-statistic values across depths, providing an indirect indication of better separability of the fMRI activation originating at different cortical depths (Fig. 8), which is relevant for laminar fMRI studies seeking to discriminate distinct activation across cortical depths or cortical layers. This observed broader range of z-statistic values across depths is consistent with the expected degree of spatial independence of the values across cortical depths. Similar intracortical tangential smoothing within cortical depths has recently been applied in this context and was shown to increase the visibility of intracortical functional activation in both standard EPI-based BOLD measurements and VASO-based CBV measurements (Huber et al., 2017; Polimeni et al., 2015).

The two smoothing kernels which provided the best overall performance in terms of both tSNR (Fig. 5) and fCNR (Fig. 9) were intracortical kernels IC-wm 00–10/NB=3 and IC-mid 03–07/NB=4. The first of these kernels extends across all cortical depths including WM/GM interface and the GM/CSF interface, and produces the same tSNR level (Fig. 5) and about 10% lower z-statistic (Fig. 9) than the somewhat smaller IC-wm 00–08/NB=3 kernel, which excludes 20% of the cortical depth adjacent to the GM/CSF interface. This illustrates that the “no-pial” smoothing approach leads to a loss of signal accompanied by a reduction of noise, ultimately resulting in a similar level of tSNR compared to the kernel that encompasses 100% of the cortical depth. This finding is consistent with a previous study recommending a “no pial” approach to decrease spatial variability of the fMRI activation while retaining tSNR (Ahveninen et al., 2016; Polimeni et al., 2010). Further reduction of the radial extent of smoothing was achieved in the IC-mid 03–07/NB=4 kernel that excluded 30% of the cortical depth adjacent to the WM/GM interface as well as 30% of the cortical depth adjacent to the GM/CSF interface, and in this configuration a small increase in tangential smoothing radius (NB) was required to compensate for the decrease of the kernel size in the radial direction. This kernel provided increases in both tSNR and fCNR, and it represents a new “no-pial and no-wm” strategy to achieve the optimal tSNR/fCNR balance. Although spatial specificity was not investigated in this study, it is known to degrade at the pial surface due to similar downstream venous effects (Ahveninen et al., 2016; Nasr et al., 2016; Polimeni et al., 2010). Therefore, studies seeking to simultaneously achieve high fCNR and high spatial specificity should take this prior knowledge into account and avoid kernels that intersect the pial surface.

Our resting-state and whole-brain task-driven fMRI data allowed us to quantify the impact of intracortical smoothing on both tSNR and fCNR over the entire cortex, which provide quantitative measures of detection sensitivity. These generic data and quantitative measures were utilized to obtain an account of the expected gains provided by our smoothing framework that would generalize to a wide range of fMRI experiments. Although tSNR is still the most commonly used metric to quantify sensitivity in a way that is agnostic to effect size, making it a useful metric to assess the acquisition that is independent of the details of any specific study, recent work has argued that the relationship between tSNR and detection power may however be complicated in fast TR data due to potentially increased levels of temporal autocorrelations apparent in these data (Corbin et al., 2018). Nevertheless, here we use tSNR and fCNR as standard metrics, and, although the absolute tSNR and fCNR values will vary with the specifics of the acquisition, here we report the relative changes and trends in these metrics with different forms of intracortical smoothing.

Since the choice of the most appropriate kernel for a specific study would likely depend on the acquisition details, including not only the nominal voxel size but also other factors that impact SNR such as the amount of parallel imaging acceleration and the degree of T₂* blurring in the EPI data, as well as temporal sampling rate and flip angle, the above recommendations for a specific kernel size and shape should be treated as a general guideline. In addition, studies focusing on specific brain areas should take into account that tSNR gain due to any form of smoothing, including the proposed intracortical smoothing, will not be spatially uniform across the cortex. An example of regional variability is provided for one kernel and one acquisition in Fig. 6b, but the details of this pattern will likely depend on several factors including the transmit and receive coil layout, the ratio of thermal to physiological noise for the particular fMRI protocol (which is also field strength-dependent), and the spatially varying partial volume effects that depend both on fMRI voxel size and on cortical thickness.

As reported above, after applying two forms of anatomically-informed smoothing (both 2D tangential and 3D intracortical smoothing) to fMRI data acquired at 1.1-mm isotropic resolution to achieve an equivalent voxel size of approximately 2.2 mm isotropic, the resulting tSNR exceeded that of unsmoothed 3.0-mm isotropic data. Not only did the 1.1-mm isotropic acquisition and the 3.0-mm isotropic acquisition differ in their voxel volumes, but to achieve proper BOLD weighting these acquisitions also differed in their parallel imaging acceleration as summarized in Table 1, e.g., the 1.1-mm isotropic protocol used a high level of acceleration (R=4), further increasing thermal noise dominance (Triantafyllou et al., 2011), whereas the 3.0-mm isotropic protocol used no acceleration (R=1). Therefore, the SNR in the 1.1-mm isotropic acquisition is expected to be far lower than that of the 3.0-mm isotropic acquisition. Counteracting this large expected gap in tSNR is the clear physiological noise dominance of the 3.0-mm isotropic acquisition, seen in Fig. 3, which leads to a smaller tSNR in the 3.0-mm data than expected based on considerations of voxels size and acceleration alone (Krüger and Glover, 2001; Triantafyllou et al., 2005). Nevertheless, the observed gains in tSNR seen in the smoothed 1.1-mm isotropic data is a result of a smoothing operation that averages and cancels spatially uncorrelated thermal noise without adding physiological noise, as explained previously (Triantafyllou et al., 2006). In general, the performance of smoothing high-resolution data will therefore depend on the ratio of thermal noise to physiological noise, i.e., the degree of physiological noise dominance, which will depend on the specifics of the data acquisition.

The framework that we have used to generate these surface mesh-guided kernels and to evaluate kernel performance can be repeated to determine the appropriate kernel size and shape for a given acquisition and a given spatial pattern of activation, which will affect tSNR and ΔS/S, respectively. In addition, local cortical anatomy of the region of interest (curvature and thickness of the surface) and local vascular anatomy (proximity of the pial vessels) may also be taken into account while designing a smoothing kernel to optimize performance. Prior information about the expected pattern of underlying neuronal activity (e.g., uniform activation over the entire area versus columnar or laminar) could also be helpful to decide the smoothing kernel shape and size, as a kernel that is too large may suppress activation, according to the matched-filter theorem. It is also worth noting that in the case where the goal is to maximize tSNR, not only can the inadvertent decrease of fCNR arise, but naturally there is a risk of introducing smoothing artifacts and spatial bias (Stelzer et al., 2014).

Several surface-based smoothing methods have been proposed, including those based on the heat equation (Chung et al., 2005), on defining a coordinate system on the cortical surface (Joshi et al., 2009) or on applying sophisticated edge-preserving techniques (Grady and Polimeni, 2010). These methods usually require a surface mesh representation, project the fMRI time-series data onto the mesh vertices, and use the mesh to restrict smoothing to the cortex (Polimeni et al., 2018). These techniques all seek to smooth while avoiding mixing together signals originating from cortical regions which are nearby with respect to the 3D embedding space due to cortical folding but are far with respect to geodesic distance. Existing 2D surface-based smoothing methods typically project fMRI voxels onto a given cortical surface mesh (most often the WM/GM surface) and perform smoothing along this mesh allowing to avoid the signals originating from CSF, but may not remove the signal dilution due to the partial volume with WM; an example smoothing kernel from our study that represents the conventional surface-based smoothing approach is the 2D intracortical smoothing kernel 00/NB=5 which includes only voxels intersecting the WM/GM boundary. In our comparisons of smoothing performance (Figs. 5 and 9 and Supplementary Figs. 1 and 2) the cyan bar represents the average results of this conventional 2D tangential smoothing but applied to each cortical depth and averaged across depths; it can be seen that this kernel performed relatively well in terms of tSNR values (Fig. 5 and Supplementary Fig. 4) due to the decreased noise contamination from CSF and in terms of fCNR (Fig. 9 and Supplementary Fig. 5) due to decreased signal dilution from WM, however in our data it did not outperform the non-smoothed low-resolution data or the 03–07/NB=4 intracortical kernel. These findings are expected because CSF exhibits stronger levels of physiological noise compared to GM and WM, and therefore the primary cause for this observation is likely noise contamination from CSF, whereas WM exhibits far weaker levels of physiological noise and very little BOLD fluctuations at all, so the primary cause is likely signal reduction from diluting the GM signal via partial volume effects with WM. Insofar as there is noise in the WM, sampling away from WM will also reduce that source of physiological noise but this is likely a secondary effect. Our results demonstrate that the performance of 2D tangential smoothing varies as a function of the cortical depth chosen and that smoothing both in the tangential and radial directions—i.e. in 3D but restricted to the cortical ribbon—can yield improved performance.

The novelty of the approach presented here is that, motivated by the availability of small fMRI voxels, we treat the cortical ribbon not as a 2D surface but as a 3D structure. Furthermore, our anatomically-informed smoothing kernels enabled by the cortical surface representation can be viewed as a form of 3D ‘steerable’ smoothing kernels, which are widely known in the image processing field (Freeman and Adelson, 1991). Unlike the existing approaches, this framework provides the capability to flexibly adjust the kernel size and shape, taking into account considerations such as the voxel size used (and so the expected scale of partial volume effects), prior knowledge about the ‘shape’ of the activation pattern (e.g., columnar or laminar patterns), and the desired tradeoff between sensitivity and specificity. While the additional flexibility afforded by this framework has the potential downside of allowing for a more diverse set of possible smoothing approaches (in terms of kernel shapes and sizes) used across different laboratories and studies, which could lead to greater heterogeneity of preprocessing pipelines used in practice, here we demonstrate how these kernels can be evaluated and compared based on how different kernels affect tSNR and fCNR distributions across the cortex, informing the process of selecting the appropriate kernel and providing quantifiable justification for the kernel used for a particular study. Future studies using this framework should not only report the kernel size and shape used during the analysis but are also able to justify their choice through similar quantitative comparisons based on the specific acquisition and design used in their study, which can help to avoid erroneous/inappropriate kernel selections.

The framework was implemented as a part of the FreeSurfer software package and uses 11 cortical surface meshes (one every 10% of cortical depth between WM/GM boundary and the pial surface) to allow for precise control of not only the tangential but also the radial extents of the smoothing kernels. Several improvements and extensions of this approach could be considered. The family of cortical surface meshes used as a basis to design the smoothing kernels could be extended above the current number of 11 to allow more precise definition of radial extent of the kernel, and the surface meshes could be refined or up-sampled to allow more precise definition of tangential extent, however this would increase computational and storage cost. Different data interpolation schemes, such as nearest-neighbor versus linear or higher-order interpolation, used to project the fMRI voxel data onto the surface mesh should also be compared and re-evaluated when the data is to be explicitly smoothed using our framework. Furthermore, in this study we adopted a simple weighting approach where the weights were set to the inverse of the vertex’s approximate geodesic distance from the central vertex of the kernel. Additional weighting shapes (e.g., a Gaussian function, etc.) could be added to allow more flexibility in kernel design to achieve a desired smoothing capacity. More sophisticated methods for defining the width of the smoothing kernel based on iteratively estimating the smoothness of the resulting data could also be incorporated (Hagler et al., 2006; Saad and Reynolds, 2012), as well as weighting strategies that take into account spatially-varying vertex density and spacing seen in Supplementary Fig. 3 to reduce the dependence of the smoothing on the surface mesh topology to yield a more “mesh-independent” solution (Balasubramanian et al., 2010). Identifying kernels with equivalent smoothing capacity in this study was somewhat challenging due to the simple weighting scheme we employed, which quantizes the tangential extent of the kernel due to our parameterization of the width by the integer number of vertex neighborhoods. As an additional feature of our framework, it may also be possible to develop an automatic kernel shape/size optimization procedure which would be able to determine a kernel (or a set of kernels) providing the most favorable trade-off between tSNR, fCNR and resolution for a given dataset. Also, our kernel size parameterization along the radial direction is currently in terms of relative cortical thickness, which means that even with a fixed kernel extent in the radial direction, regions with thicker cortex will be smoothed to a coarser resolution than regions with thinner cortex; to demonstrate this effect, we computed a 2D histogram of the normalized tSNR gain between the non-smoothed and smoothed 1.1 mm data shown in Fig. 6 as a function of cortical thickness (see Supplementary Fig. 6), and while no strict relationship was found indeed trend can be seen in which thicker cortex results in a larger tSNR can through 3D intracortical smoothing, as expected. This can be addressed in the future by appropriately weighting the kernel in the radial direction by distance, . An option to assign different tangential extents and/or weightings to different cortical depths (to impose e.g. cone-shaped kernels or hourglass-shaped kernels) could allow incorporating additional prior knowledge about the expected spatial pattern of the activation (smaller/larger on specific depths), correction for partial volume fraction of different tissue types (Shafee et al., 2015) or even partial volume fractions of different cortical depths or layers (Polimeni et al., 2018) into the kernel design. Care must be taken in including this prior information, as it has the potential to bias results, nevertheless our framework provides this additional flexibility. This also highlights how the performance of our 3D intracortical smoothing technique, compared to conventional 2D tangential smoothing, is expected to increase with higher resolution, since smaller fMRI voxels will allow for more independent voxels contained within the cortical gray matter thickness providing more flexibility in smoothing along the radial direction. Indeed, for the results presented in Supplementary Fig. 8 we see that for ultra-high-resolution 0.8 mm isotropic fMRI data the tSNR from 3D intracortical smoothing is about 10% higher than the mid-gray 2D tangential smoothing, whereas the same two kernels yielded almost the same tSNR when applied to 1.1 mm isotropic data. Therefore, as spatial resolutions continue to increase, more benefits from this approach based on treating the cortical ribbon as a 3D structure is expected, while for moderate resolutions the improvement compared to conventional 2D tangential smoothing.

The intracortical coordinate system created by the cortical meshes could be easily adjusted for the specific applications to become “anatomically inspired” (Polimeni et al., 2018). The proposed framework extends the commonly employed concept of anatomically-informed smoothing that respects the boundaries of the cortical gray matter to finer-scale anatomically-informed smoothing that respects intracortical features such as cortical columns and cortical layers. Cortical columns run roughly perpendicularly to the cortical boundary surfaces, and cortical layers run roughly parallel to the cortical boundary surfaces, therefore given a cortical reconstruction the anatomical configuration of these intracortical features can be estimated. The surfaces could then be placed along the expected laminar boundaries for the particular cortical regions (Hinds et al., 2015; Waehnert et al., 2014) and vertices along expected columnar structures (Leprince et al., 2015). Since the microanatomical geometry of cortical columns and layers changes systematically across the cortex and can change abruptly at cortical area boundaries (Bok, 1959; Nieuwenhuys, 2013), validity of smoothing across the area boundaries could be questionable and care must be taken. However, new tools are becoming available that provide a more accurate prediction of the locations and geometry of these features within cortical areas (Kleinnijenhuis et al., 2015; Leprince et al., 2015; Waehnert et al., 2014) and with some additional information, a curvilinear anatomy-matched intracortical coordinate system could possibly be established. The proposed smoothing framework could also be potentially useful for studies of the subcortical gray matter structures, where precisely shaped and weighed anatomically-informed smoothing kernels can also provide some advantage.

One limitation of the presented work is not accounting for the possible changes in temporal autocorrelation of the BOLD signal as a function of cortical depth and physiological noise contribution, which could affect the effective degrees of freedom (DOFs) at each depth and thus influence the z-statistic values (as discussed previously (Blazejewska et al., 2017)). Since estimating DOFs is non-trivial, for the purpose of this work, we adopted a common assumption that DOFs were the same over the entire brain, but this assumption should be revisited (Eklund et al., 2016; Wald and Polimeni, 2017).

Another potential limitation of the presented framework is its strong dependence on the accuracy of the surface reconstruction and on the alignment of the functional data onto the surface meshes given the differing levels of geometric distortion between conventional functional and anatomical data. Recent improvements in surface reconstruction accuracy have been provided by increasing resolution and quality of anatomical data (see Supplementary Fig. 2), which partially addresses this limitation (Bazin et al., 2014; Glasser et al., 2013; Zaretskaya et al., 2018). The concern related to the well-known geometric distortion in EPI data impacting the alignment can also be mitigated through a recently proposed strategy of using EPI data themselves as the anatomical reference and generating cortical surface reconstructions directly from EPI data that are distortion-matched to the functional data (Huber et al., 2017; Kashyap et al., 2017; Renvall et al., 2016).

Our results show that the strategy of acquiring small, isotropic voxels that can adequately sample the cortex might be preferable to the common strategies of using either large voxels or anisotropic voxels with high in-plane resolution and thicker slices tailored to one small cortical region. In our approach, the same high-resolution acquisition could be used in multiple studies across multiple brain regions, since many spatial scales of interest could be investigated through different smoothing kernel sizes and shapes. This strategy, as previously proposed (Triantafyllou et al., 2006), nicely decouples the details of the acquisition from the anatomical region of interest and the spatial scale of the expected activation. A potential drawback of acquiring whole-brain coverage fMRI with small voxels is loss of the temporal resolution, however newly available techniques such as SMS-EPI (Barth et al., 2016) used in this study help to compensate for this, making our recommended strategy more practically feasible even on clinical MRI scanners.

Conclusions

Here we propose a new framework for surface mesh-navigated smoothing of the cortical ribbon viewed as a 3D structure with the use of small isotropic voxels, which allows smoothing within the folded cortical gray matter while avoiding noise contamination and signal dilution from surrounding CSF and WM, resulting in activation that is specific to GM. This framework can be applied in both high-resolution fMRI studies investigating intracortical features aligned relative to the cortical GM boundaries, such as cortical columns and layers, as well as in conventional fMRI studies investigating regional patterns of activation. Appropriately smoothed small voxels achieved higher tSNR and fCNR than conventional large voxels while also avoiding contamination from pial vasculature known to reduce spatial specificity. Voxels smaller than the cortical thickness, such as 1 mm isotropic voxels, should therefore be collected to adequately sample cortical gray matter, and subsequently smoothed with a kernel specifically designed for the particular study to maximize fMRI detection power while preserving spatial resolution.

Highlights:

• We introduce an anatomically-informed intracortical spatial smoothing method

• Smoothing fMRI data while avoiding white matter and CSF has advantages

• Different smoothing kernels maximize SNR and percent signal change

• Smoothing small-voxel data can provide improved detection and comparable resolution

• This smoothing framework can also benefit laminar and columnar activation patterns