Alteration of Visual Input Results in a Coordinated Reorganization of Multiple Visual Cortex Maps

Abstract

In the adult visual cortex, multiple feature maps exist and have characteristic spatial relationships with one another. The relationships can be reproduced by “dimension-reduction” computational models, suggesting that the principles of continuity and coverage may underlie cortical map organization. However, the mechanisms responsible for establishing these relationships are unknown. We explored whether removing one feature map during development causes a coordinated reorganization of the remaining maps or whether the remaining maps are unaffected. We removed the ocular dominance map by monocular enucleation in newborn ferrets, so that single eye stimulation drove the cortex in a more spatially uniform manner in adult monocular animals compared with normal animals. Maps of orientation, spatial frequency, and retinotopy formed in monocular ferrets, but their structures and spatial relationships differed from those in normal ferrets. The wavelength of the orientation map increased, so that the average orientation gradient across the cortex decreased. The decrease in the orientation gradient in monocular animals was most prominent in the high gradient regions of the spatial frequency map, indicating a coordinated reorganization between these two maps. In monocular animals, the orthogonal relationship between the orientation and spatial frequency maps was preserved, and the orthogonal relationship between the orientation and retinotopic maps became more pronounced. These results were consistent with detailed predictions of a dimension-reduction model of cortical organization. Thus, the number of feature maps in a cortical area influences the relationships between them, and inputs to the cortex have a significant role in generating these relationships.

Introduction

The response properties of neurons are mapped in a strikingly ordered manner across the surface dimension of sensory cortex. Although the layouts of the maps have been well described, the mechanisms responsible for their development are not understood. Intrinsic mechanisms may establish certain feature maps (Crowley and Katz, 2000). Conversely, mechanisms dependent on the patterns of spontaneous or visually driven input to the system can also account for map development (Sharma et al., 2000). Finally, these mechanisms could act in combination, in which each is responsible for certain aspects of the map layouts (Katz and Crowley, 2002; McLaughlin and O'Leary, 2005; Sur and Rubenstein, 2005).

Cortical feature maps have characteristic spatial relationships with each other that are similar across species, and mechanisms proposed to account for map development must be able to explain these relationships. For example, in primary visual cortex (V1) of Old World monkeys, cats, and ferrets, pinwheel regions of the orientation map tend to locate to ocular dominance column centers, and contours of orientation and ocular dominance maps tend to cross at near-orthogonal angles (Blasdel and Salama, 1986; Bartfeld and Grinvald, 1992; Crair et al., 1997b; Hubener et al., 1997; Yu et al., 2005). Similar relationships exist between orientation and spatial frequency maps (Hubener et al., 1997; Issa et al., 2000; Yu et al., 2005). Finally, distortions in the retinotopic map are related to the direction of elongation of ocular dominance, orientation, and spatial frequency domains (Blasdel and Campbell, 2001; Yu et al., 2005).

Computational models of cortical organization can reproduce cortical map structures and spatial relationships (Durbin and Mitchison, 1990; Goodhill and Willshaw, 1990; Obermayer et al., 1990; Chklovskii and Koulakov, 2004). Although implemented by different algorithms, the successful models are of the “dimension-reduction” type and are driven by two competing constraints: continuity, or achieving a smoothly varying representation of each feature across the cortex, and uniform coverage, or having an equal representation of each feature combination (Erwin et al., 1995; Swindale, 1996). The similarities between experimental maps and those produced by these models support the hypothesis that continuity and coverage principles underlie the structures of cortical maps and their spatial relationships.

However, the mechanisms that encode these principles and give rise to map relationships are not understood. We reasoned that if map relationships are regulated by inputs, then removal of a feature map during development should cause concomitant changes to the layouts of the remaining maps. Furthermore, these changes may be in line with recent predictions of dimension-reduction models, which have been used to explore how the number of features represented within an area might affect the layouts of maps (Swindale, 2000, 2004; Carreira-Perpinan et al., 2005; Yu et al., 2005). Conversely, if map relationships are encoded rigidly, then altering one feature map early in development should not affect the layouts of other maps.

Performing neonatal monocular enucleation may allow one to test these predictions experimentally, because this manipulation has significant potential (as shown by anatomical methods) to alter or remove the ocular dominance map (Rakic, 1981; Guillery et al., 1985), particularly in a species such as the ferret whose visual system is very immature at this developmental stage (Johnson and Casagrande, 1993; Herrmann et al., 1994). Furthermore, monocular enucleation leaves cortical cell responses to other stimulus parameters relatively intact, although it is unknown how it affects the two-dimensional maps of these parameters (Fregnac et al., 1981; Shook et al., 1985; Bisti and Trimarchi, 1993; Bisti et al., 1995). Here, we show that early monocular enucleation leads to a loss of the ocular dominance map and causes changes in the remaining maps that are consistent with a dimension-reduction model of map organization.

Materials and Methods

Computational model.

We used the Kohonen self-organizing feature map (SOM) algorithm (Kohonen, 1982), as modified by Obermayer (Obermayer et al., 1992), to simulate the mapping of multiple features across a two-dimensional surface. This model was used because it can closely reproduce the structures of, and spatial relationships between, feature maps measured from the adult ferret visual cortex (Yu et al., 2005). The details of the model have been described previously (Yu et al., 2005). A multidimensional stimulus feature space is defined in which each stimulus is represented as a multicomponent vector V _s = (x_s, y_s, q_scos(2φ_s),q_ssin(2φ_s), z_s, f_s) within this space. Here x and y correspond to azimuth and elevation retinotopic position, respectively, q and φ are orientation magnitude and angle, z is ocular dominance, and f is spatial frequency. The feature x ranges from (0, X), y from (0, Y), q from (0, Q), φ from (0, π), z from (0, Z), and f from (0, F). The stimuli are mapped onto a cortical surface, which is represented as a two-dimensional grid of N × N cortical points. Each cortical point r = (i, j) has preferred features (i.e., a “receptive field”) defined as W _r = (x_r, y_r, q_rcos(2φ_r),q_rsin(2φ_r), z_r, f_r).

The maps are formed through iterations (1.5 million) of three steps. (1) A stimulus V _s is chosen one at a time randomly from the complete feature space, assuming uniform distributions of each feature. (2) The cortical point r _c = (i_c, j_c), whose preferred features are closest to those of the stimulus, is identified as the “winner.” The closeness of the feature is measured with the Euclidian distance between the vectors |V _s − W _r|². (3) The preferred features of the cortical points are updated according to the equation ΔW _r = αh(r)(V − W _r). Here α is the learning rate, r is the cortical distance between a given cortical point (i, j) and the winner r _c, and h(r) = exp(−r ²/σ²) is the neighborhood function. The neighborhood function restricts the changes in receptive fields to those cortical points nearby, in cortical distance, to the winner.

To model the normal adult ferret visual cortex, we ran “four-feature” simulations, in which the four maps of retinotopy, ocular dominance, orientation, and spatial frequency were formed. The free parameters were set to the following values: N = 513, Y = N, X = ρN, ρ = 4, Q = 40, Z = 60, F = 60, σ = 5, α = 0.02. Here ρ is the elevation to azimuth magnification ratio of the retinotopic map and was chosen to match the magnification anisotropy that exists in the region of ferret visual cortex that was studied. The parameters for the four-feature simulations were the same as those described previously (Yu et al., 2005) and were chosen so that the individual maps formed in the simulations, and the relative wavelengths of the different maps, resemble those found in normal ferret visual cortex.

To simulate the effects of removing the ocular dominance map (as a result of early monocular enucleation) on cortical organization, we also ran “three-feature” simulations. In this case, the model parameters were identical to those used in the four-feature case, except that the ocular dominance input values were completely uniform (i.e., Z = 0, so that no “ocular dominance” map formed). Although additional changes to cortex may result from monocular enucleation and could be modeled by additional parameter changes, we reasoned that the range of ocular dominance input is the most likely parameter to change. We also ran simulations with five and six total features, to determine whether the effects of removing a feature map change based on how many feature maps are present to begin with. The additional features, n ₁ and n ₂, were scalar features with uniform distributions ranging from (0, 60) (i.e., analogous to the ocular dominance and spatial frequency features described above).

Neonatal monocular enucleations.

All experimental procedures were approved by the Massachusetts Institute of Technology Animal Care and Use Committee and conformed to National Institutes of Health guidelines. Timed-pregnant ferrets were purchased from a commercial supplier (Marshall Farms, North Rose, NY). Monocular enucleations were performed on kits at postnatal day 0 (P0) (within 24 h of birth). The ferrets were anesthetized by deep hypothermia, and the analgesics proparacaine and lidocaine were applied locally to the eye to be enucleated. The eyelids were separated, the rectus muscles were separated from the sclera, and the optic nerve was tied off and severed with suture. The antibiotic cephalothin was applied to the eye orbital, and the orbital was then packed with sterile Gelfoam. The eyelids were closed with 6-0 sutures. After recovery from surgery, the animals were returned to their mother in their home cage. Animals were allowed to grow to adulthood (>4 months) before physiological experiments were performed.

Preparation for acute intrinsic signal optical imaging.

Ten normal adult ferrets and 12 monocularly enucleated adult ferrets were used in these experiments (animals from each group came from more than four different mothers). Anesthesia was induced with ketamine (25 mg/kg) and xylazine (1.5 mg/kg) and maintained with isoflurane (1.0–1.5% in 70:30 mixture of N₂O/O₂) delivered through a tracheal cannula using artificial respiration. Fluid maintenance was achieved with a 50:50 mixture of 5% dextrose and lactated Ringer's solution and, after completion of surgery, was supplemented with Norcuron (0.25 mg · kg⁻¹ · h⁻¹) for muscle relaxation. Expired CO₂ was maintained at 4%, and the anesthesia level was monitored continuously by EEG and electrocardiogram. Body temperature was maintained at 37.5°C. A craniotomy and durotomy were performed to expose the primary visual cortex. A chamber was mounted on the skull around the exposed region and filled with agarose (1.5% in saline). This was covered by a cover glass and silicone oil. Zero-power contact lenses were used to protect the corneas from drying.

Optical imaging acquisition and stimuli.

The details of optical imaging have been described previously (Dragoi et al., 2000). The cortex was illuminated with 630 nm light. Images of cortical reflectance were obtained using a video camera consisting of a 748 × 480 array of pixels (9.4 × 6.9 mm) equipped with a tandem macro-lens arrangement and then digitized and fed into a computer (Imager 3001; Optical Imaging, Mountainside, NJ). The camera was focused 500 μm below the cortical surface. Stimuli were generated using a computer-controlled system (Cambridge Research Systems, Rochester, Kent, UK) on a cathode ray tube monitor that was placed at 57 cm from the eyes and covered 40° (horizontal) × 30° (vertical) of the visual field.

Optical imaging of orientation and spatial frequency maps.

For orientation and spatial frequency maps, stimuli were presented binocularly and consisted of full-field square-wave gratings having one of four orientations (separated by 45°) and one of four fundamental spatial frequencies (0.08, 0.125, 0.225, or 0.375 cycles/°). A stimulus having a particular orientation/spatial frequency combination was presented without moving for 10 s and then drifted (at a temporal frequency of 2 Hz) for 4 s. Cortical images were captured at 1 Hz during the 4 s of the drifting phase, and these four images were averaged together, representing the cortical activation pattern in response to that orientation/spatial frequency combination for one trial. Stimuli were presented in pseudorandom order, and the results of 24–40 trials of each stimulus were averaged together. The differential orientation maps displayed in the figures were obtained by subtracting the response to a 90° stimulus from the response to a 0° stimulus; no spatial filtering was performed. Single-condition orientation maps were obtained by subtracting the response to all orientations combined (“cocktail blank”) from the response to each single orientation. To produce orientation angle maps, high-pass (Gaussian filter, σ = 0.1 mm) and low-pass (uniform filter, 1 mm) filtered single-condition orientation maps were vector summed at each pixel. The angle of the resultant vector is an estimate of the average preferred orientation at that pixel. The spatial frequency map was calculated by subtracting the cortical response to high spatial frequency (0.375 or 0.225 cycles/°) stimuli (averaged over all orientations) from the response to low-frequency (0.125 or 0.08 cycles/°) stimuli; no spatial filtering was performed on the differential spatial frequency maps displayed in the figures.

Optical imaging of monocular and binocular response maps.

For monocular response maps, stimuli of four orientations (at 0.125 cycles/°) were presented to the contralateral eye. The response to the drifting phase of the stimulus was subtracted from the response to the final 3 s of the stationary phase of the stimulus. The resulting spatial activation pattern, summed over the different orientation conditions, was termed the “monocular response map” and represents the cortical spatial activation pattern attributable to stimulation of one eye. For the “binocular response map,” the same procedure was performed, except that stimuli were presented binocularly.

Optical imaging of retinotopic maps.

To generate retinotopic maps, we used a periodic visual stimulation paradigm (presented to the contralateral eye) combined with continuous data acquisition intrinsic signal optical imaging (Kalatsky and Stryker, 2003). To measure the azimuth dimension of the retinotopic map, we designed drifting oriented vertical “aperture” stimuli that contain multiple orientations. In preliminary studies, we found that drifting vertical bars preferentially stimulate tissue preferring the orientation of the bar and that this can lead to minor local distortions in the retinotopic map (our unpublished observations). The aperture stimuli were designed to activate the tissue more uniformly across orientations. The stimuli consisted of oriented black–white gratings visible through a vertical aperture and masked by a background of uniform intermediate contrast. Along the horizontal center of the vertical aperture, the contrast of the gratings was 100%, and, in moving away from the center, the contrast of the gratings decreased with a Gaussian falloff until they reached 0% contrast. The gratings had a spatial frequency of 0.175 cycles/° and cycled randomly through four different orientations at 4 Hz. Each vertical aperture was separated by 24° in the azimuth dimension. The aperture drifted along the azimuth dimension of space at 1.6°/s, such that an aperture passed by any given visual field location on the monitor every 15 s. These aperture stimuli were highly effective in eliciting cortical responses. Light-reflectance images were captured at 3 Hz. Each retinotopic stimulus trial consisted of 30 cycles of stimulation, after which a blank screen was shown for 25 s, and each experiment consisted of three to four such trials. The light-reflectance data were averaged in-phase over all trials and cycles. Each frame of the averaged response thus represents the activation pattern during a restricted phase of the stimulus cycle. To determine the preferred receptive field position of each pixel, we calculated the phase of the fast Fourier transform at the stimulation frequency, on the time course response of each pixel (Kalatsky and Stryker, 2003). Because the optical imaging signals follow the stimulation with an unknown lag time, this method provides maps of relative rather than absolute retinotopy. All of our analyses rely only on relative retinotopy values.

Wavelength analysis of orientation and spatial frequency maps.

We used identical procedures for analyzing our computational and experimental data. To measure the wavelength of the orientation angle maps and the differential spatial frequency maps, the spatially filtered maps were first rotated such that the domains within the maps were elongated horizontally. These rotated maps were then embedded within a rectangular region, and individual image pixels outside of the valid map regions were set to random values. We next applied a two-dimensional fast Fourier transform. To calculate the wavelength of the x (horizontal, or anteroposterior) dimension of the maps, we averaged together the Fourier magnitude values over all vertical positions of the transformed map. We then calculated the centroid frequency of the resultant power spectrum for the x dimension (taking into account a range of frequencies that included the majority of power) and took this as the average frequency with maximum power. Similarly, to calculate the wavelength of the y (vertical, or mediolateral) dimension of the map, we averaged together the Fourier magnitude values over all horizontal positions of the transformed map and then calculated the centroid frequency of the resultant power spectrum for the y dimension. The power spectrums typically elicited a single peak for the y dimension but not for the x dimension; thus, we reasoned that a centroid was the most reasonable estimate of the average map wavelength.

Calculation of orientation, spatial frequency, and retinotopic gradient vectors.

Gradient maps were computed from spatially high- and low-pass-filtered maps of retinotopy, orientation, or spatial frequency as the two-dimensional spatial derivative at each pixel. Specifically, let A(x,y) be the value at a pixel (x,y), dx = (A(x + 1, y) − A(x,y)) and dy = (A(x,y + 1) − A(x,y)). Then the gradient vector magnitude at (x,y) is (dx ² + dy ²)^1/2, and the gradient vector angle is (180/π)a tan(dy/dx) and ranges from −90 to 90. The gradient magnitude describes how much a feature changes around a given pixel in the map, and the gradient angle indicates the axis of cortex along which the feature changes maximally (and is orthogonal to the map contour at that pixel). To calculate gradient intersection angles for pairs of maps, we computed the angle between the gradient vectors at the corresponding pixel of the two maps and mapped it to [0°,90°]. The gradient intersection angle is equivalent to the angle between the contours of the two maps at that pixel. We performed this calculation for all pixels within the region of interest, except when stated (supplemental Fig. 3, available at www.jneurosci.org as supplemental material).

Results

Computational model predictions: effects of removing a feature map on cortical organization

We used a dimension-reduction computational model, based on the Kohonen SOM algorithm (Kohonen, 1982; Obermayer et al., 1990, 1992), to simulate the mapping of either four or three features onto a two-dimensional model cortical surface. The parameters of the four-feature simulation were chosen such that the maps that it produced closely resemble the same four maps (retinotopy, orientation, ocular dominance, and spatial frequency) found in the normal adult ferret visual cortex (Yu et al., 2005). We used identical parameters for the four- and three-feature simulations, except for the exclusion of the ocular dominance map in the three-feature case (see Materials and Methods). The model attempts to represent each feature smoothly across the surface (i.e., continuity), while also ensuring that each combination of features has a relatively uniform cortical representation (i.e., uniform coverage). Comparing the results of the four- and three-feature simulations allows us to determine the predicted effects of removing a feature map on the layouts of the remaining maps in the real cortex, if the principles of continuity and uniform coverage are driving principles of representation. Although the effects of mapping different numbers of features have been explored previously with computational models (Swindale, 2000, 2004; Carreira-Perpinan et al., 2005), we wanted to run simulations with parameters that would allow us to directly compare the model predictions with experimental measurements in the ferret.

The overall structures of the individual maps produced by the model were similar for the four- and three-feature simulations (Fig. 1 A–D and E–H, respectively), but quantitative differences existed. The wavelengths of the orientation and spatial frequency maps, measured by two-dimensional Fourier analysis, were larger in the three-feature than in the four-feature simulation (Fig. 1 I,J). The increase in the wavelengths was significant along the horizontal (x) dimensions of the maps (orientation, p < 0.01; spatial frequency, p < 0.01; t test, two-tailed) but not the vertical (y) dimensions (Fig. 1 I,J), indicating that the domains in the maps became less fragmented along the x-dimension in the three-feature case. Consistent with a less fragmented orientation map, there were significantly less high rate-of-change (i.e., high gradient) regions in the orientation map in the three-feature simulation (t test, two-tailed, p < 0.001) (Fig. 1 K,N,R). Thus, removing a feature map is predicted to alter the structures of the orientation and spatial frequency maps. These results are in agreement with previous simulations run with the elastic net algorithm or with the Kohonen algorithm using a different parameter regimen (Swindale, 2004; Carreira-Perpinan et al., 2005).

Figure 1.

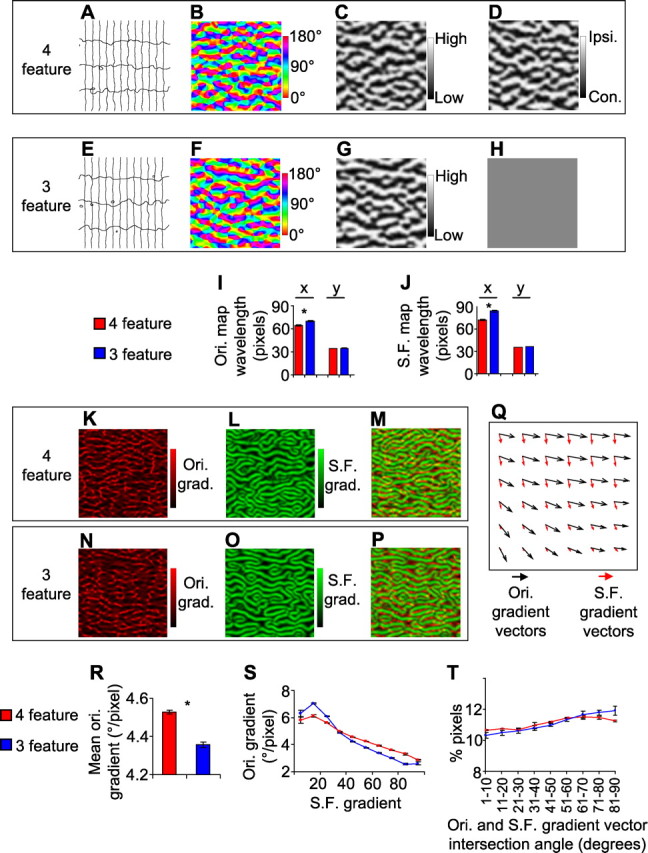
Differences in cortical maps predicted by a dimension-reduction model when either four or three feature maps are to be represented on a two-dimensional surface. A–H, Feature maps produced by the model. Each represents a 250 × 250 pixel region of the model cortex. The maps in A–D come from the four-feature simulation; each is derived from the same region of the model cortex. The maps in E–H come from the three-feature simulation. A, E, The retinotopic map is illustrated by iso-elevation (horizontal in figure) and iso-azimuth (vertical in figure) contours; all contour intervals are identical. Vertical contour lines are more widely spaced than horizontal contour lines, indicating anisotropy in the visual map magnification factor. This simulates the anisotropy found in ferret visual cortex. B, F, The orientation preference map, denoted by color coding each pixel according to its preferred orientation. C, G, The spatial frequency preference map. D, H, The ocular dominance map. The ocular dominance value of all image pixels was uniform in the three-feature case, to simulate the results of removing the ocular dominance map. I, The orientation map wavelength, measured using Fourier analysis along the x (horizontal) dimension and the y (vertical) dimension. J, The spatial frequency map wavelength. K, N, The orientation gradient magnitude map, from the same region of model cortex as the corresponding orientation map shown above. L, O, The spatial frequency gradient magnitude map. M, P, Superimposition of the orientation and spatial frequency gradient magnitude maps. Q, Superimposition of the orientation and spatial frequency gradient vectors from a 7 × 7 pixel region of the model cortex from the four-feature simulation, showing their intersection angles. R, The mean orientation gradient magnitude over the entire model cortex. S, Image pixels from the entire model cortex were grouped into 10 bins according to their spatial frequency gradient (bin 1, 0–10% of maximum gradient; bin 2, 10–20% of maximum; …), and the mean orientation gradient for each group was calculated. T, The intersection angle between the orientation gradient and spatial frequency gradient at each pixel of the model cortex was calculated; the percentage of image pixels that had intersection angles that were in nine different ranges (0–10°, 10–20°, …, 80–90°) is indicated. Error bars denote SEM over data obtained from three separate simulations for both the four- and three-feature cases. Ipsi., Ipsilateral; Con., contralateral; Ori., orientation; S.F., spatial frequency.

We next determined how the removal of the ocular dominance map is predicted to alter the spatial relationships between the remaining maps. We first examined the relationships between the orientation and spatial frequency gradient magnitudes at corresponding pixels of the model cortex. By superimposing the orientation gradient magnitude map (Fig. 1 K) and the spatial frequency gradient magnitude map (Fig. 1 L) in the four-feature model, a clear relationship between them can be seen (Fig. 1 M). Specifically, the regions of cortex that have the highest orientation gradient (red) generally do not overlap with regions of cortex that have the highest spatial frequency gradient (green). Interestingly, we found that this relationship becomes more pronounced in the three-feature simulation (Fig. 1 N–P). These relationships are quantified in Figure 1 S, which shows that there is an inverse relationship between the spatial frequency gradient and the orientation gradient in the four-feature simulation, and that this relationship is even more pronounced in the three-feature simulation. Thus, removing the ocular dominance map increases the strength of the relationship between the orientation and spatial frequency maps. To examine the spatial relationships between these maps in an additional way, we calculated the intersection angles between the orientation and spatial frequency gradient vectors (Fig. 1 Q; example is from four-feature model). The intersection angles can range from 0° to 90°. In the four-feature simulation, there was a weak preponderance of near-perpendicular intersection angles between these two maps across the entire model cortex (Fig. 1 T). For the three-feature simulation, this preponderance became slightly more pronounced (Fig. 1 T). Together, these results predict specific quantitative effects of removing the ocular dominance map on the structures of, and spatial relationships between, the orientation and spatial frequency maps.

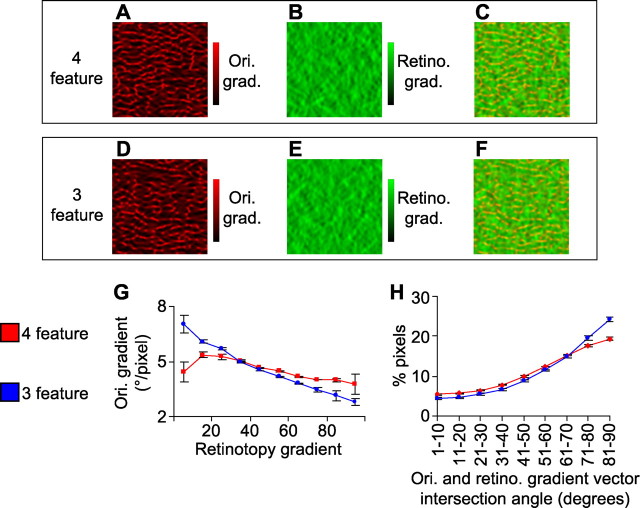
We also explored how removing the ocular dominance map is predicted to alter the relationships between the orientation and retinotopic maps (we focused on the azimuth dimension of the retinotopic map). We first examined how the orientation gradient magnitudes (Fig. 2 A,D) and retinotopy gradient magnitudes (Fig. 2 B,E) relate at corresponding pixels of the cortex (Fig. 2 C,F). The model predicts that, for the four-feature simulation, there is only a weak correlation between the gradient magnitudes of orientation and retinotopy (Fig. 2 C and red line in G). For the three-feature simulation, in contrast, a clear overall negative correlation is predicted between the gradient maps (Fig. 2 F and blue line in G). The model also predicts a slight increase, in the three-feature simulation compared with the four-feature simulation, in the amount of near-orthogonal intersection angles between the retinotopic and orientation gradients (Fig. 2 H). Thus, removing the ocular dominance map is predicted by the model to also alter in a specific way the relationship between the orientation and retinotopic maps. These results are qualitatively consistent with previous simulation results, which have explored the effects of mapping different numbers of features onto a two-dimensional surface (Swindale, 2004; Carreira-Perpinan et al., 2005).

Figure 2.

Differences in relationships between orientation and retinotopic maps predicted by a dimension-reduction model when either four or three feature maps are to be represented on a two-dimensional surface. The maps in A–C come from the four-feature simulation; each is derived from the same region of the model cortex as the maps in Figure 1. The maps in D–F come from the three-feature simulation. A, D, The orientation gradient (Ori. grad.) magnitude map. B, E, The gradient map for the azimuth dimension of retinotopy (Retino. grad.). C, F, Superimposition of the orientation and retinotopic gradient magnitude maps. G, Image pixels from the entire model cortex were grouped into 10 bins according to their azimuth retinotopic gradient (bin 1, 0–10% of maximum gradient; bin 2, 10–20% of maximum; …), and the mean orientation gradient for each group was calculated. H, The intersection angle between the orientation gradient and the retinotopic gradient at each pixel of the model cortex was calculated; the percentage of image pixels that had intersection angles that were in nine different ranges (0–10°, 10–20°, …, 80–90°) is indicated. Error bars denote SEM over data obtained from three separate simulations for both the four- and three-feature cases.

The reason we chose to simulate the mapping of four and three features in our model is that we can consistently reveal four feature maps in normal ferret visual cortex, and three would be the number of maps expected to exist in cortex after the ocular dominance map is removed. Although another group has reported the existence of an additional map (of direction selectivity) in the ferret visual cortex (Weliky et al., 1996; Li et al., 2006), the general effect of removing a feature map holds when starting with six, five, or four features; differences exist only in the magnitude of the effects (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). We next tested whether the ocular dominance map can be removed experimentally and whether its removal impacts the spatial relationships between the remaining feature maps in the manner predicted by the model. This would allow us to critically test whether interactions between these maps in the brain are governed by the same principles as govern the dimension-reduction model, i.e., continuity and uniform coverage.

Neonatal monocular enucleation alters the expression of the ocular dominance map

To attempt to remove the map of ocular dominance, monocular enucleations were performed in postnatal day 0 ferrets. We found that, in enucleated animals reared to adulthood, the optic nerve from the enucleated eye had degenerated completely such that the optic chiasm received input from only one eye (data not shown). Thus, the removal of input from one eye to the brain was complete.

To test whether this manipulation successfully ablated the ocular dominance map (that is, caused spatially uniform activation of cortex by the remaining eye), we used intrinsic signal optical imaging to compare, between normal and monocular ferrets, the cortical spatial activation pattern resulting from monocular stimulation. The presence of an ocular dominance map should be reflected in a patchy response pattern across cortex after monocular stimulation. In normal animals, we measured the cortical spatial activation pattern resulting from stimulation of the contralateral eye (the responses to grating stimuli of four different orientations were summed) (Fig. 3 B). As expected, the spatial pattern in this map was non-uniform, indicating that, in a normal animal, the contralateral eye activates V1 in a patchy manner. The overall pattern elicited by contralateral stimulation was similar to the pattern obtained by comparing the cortical response to contralateral and ipsilateral eye stimulation, the typical way in which an ocular dominance map is obtained (Fig. 3 A; same animal as in B). In contrast, in monocular ferrets the spatial activation pattern in response to contralateral eye stimulation was less patchy, indicating a more uniform cortical activation (Fig. 3 C).

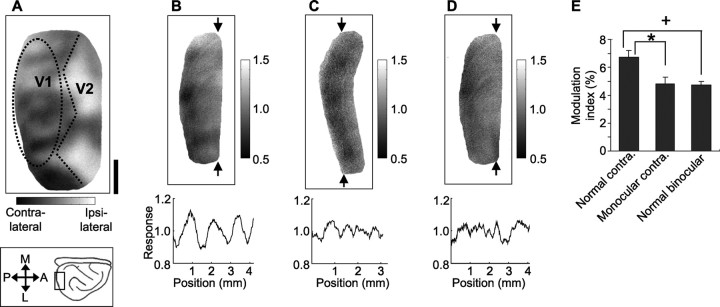
Figure 3.

The cortical spatial activation pattern resulting from monocular stimulation is more uniform in monocular than in normal ferrets. A, The functional map of ocular dominance from a normal ferret, comparing the cortical response to contralateral and ipsilateral eye stimulation. Straight dotted lines indicate the approximate location of the V1/secondary visual cortex (V2) border. B, C, Monocular maps, produced by summing the cortical response to contralateral eye presentation of grating stimuli of four different orientations. The data in B come from the same normal ferret (see the oval-shaped outlined region) from which the ocular dominance map in A was derived; the data in C come from a monocular ferret. The plots below represent the light-reflectance pattern along a vertical line through the corresponding map at the position indicated. The SD of this line, averaged over multiple positions covering the imaged region, is termed the spatial modulation index for that animal. D, Map produced by summing the cortical response to binocular presentation of grating stimuli (from same ferret as in A and B). E, The mean modulation index for the three groups shown. Error bars denote the SEM over eight, seven, and five ferrets, respectively. Scale bar: (in A) A–D, 1 mm. M, Medial; A, anterior; L, lateral; P, posterior.

To quantify the patchiness, we plotted the light-reflectance signal as a function of distance along the mediolateral axis of cortex (across which ocular dominance columns run in this region of ferret visual cortex) and calculated the SD of this line (Fig. 3, B for normal ferret, C for monocular ferret). This was done separately for lines at each anteroposterior position within the imaged portion of V1. The average value for all positions was termed the “modulation index” for that animal. A higher modulation index indicates a more patchy activation of cortex. The average monocular modulation index was significantly lower in the monocular animals compared with normal animals [p < 0.05, Fisher's protected t test (Fig. 3 E, *)]. As expected, the modulation index resulting from binocular stimulation in a normal ferret (Fig. 3 D) was also significantly lower than that resulting from monocular stimulation in a normal ferret [p < 0.05, Fisher's protected t test (Fig. 3 E, +)]. Finally, although the modulation index did not go to zero in monocular animals, it did go as low as, and was not different from, the degree of modulation resulting from binocular stimulation in normal animals (p > 0.05, Fisher's protected t test) (Fig. 3 E).

The results indicate that single-eye stimulation in a monocular ferret activates the cortex more uniformly than single-eye stimulation in a normal ferret and as uniformly as binocular stimulation in a normal ferret. This suggests that monocular enucleation at postnatal day 0 in the ferret removes the expression of the functional ocular dominance map in the adult cortex.

Structures of orientation and spatial frequency maps in monocular ferrets

Given that the ocular dominance map was removed in monocular ferrets, we next tested whether the remaining three feature maps still formed in these animals and, if so, whether their structures were altered in the manner predicted by the dimension-reduction model. In the binocular region of normal ferret V1, orientation preference is mapped smoothly in orientation “domains” and breaks sharply at “pinwheels” and “fractures” (Fig. 4 A,B). In monocular ferrets, in the cortex contralateral to the remaining eye, orientation maps appeared normal (Fig. 4 D,E). Spatial frequency preference is also mapped in the binocular region of normal ferret V1, in alternating high and low domains (Fig. 4 C). In monocular ferrets, in the cortex contralateral to the remaining eye, we also found a map of spatial frequency preference (Fig. 4 F). Our results indicate that both the orientation and spatial frequency maps form in the cortex contralateral to the remaining eye in monocular ferrets, so that visual input from the contralateral eye alone is sufficient to form these maps. [In the cortex ipsilateral to the remaining eye in monocular ferrets, we found a systematic map of orientation preference (supplemental Fig. 2, available at www.jneurosci.org as supplemental material) but not of spatial frequency (data not shown). It is unclear whether the spatial frequency map did not form in the ipsilateral hemisphere or was too weak to detect with intrinsic signal optical imaging.]

Figure 4.

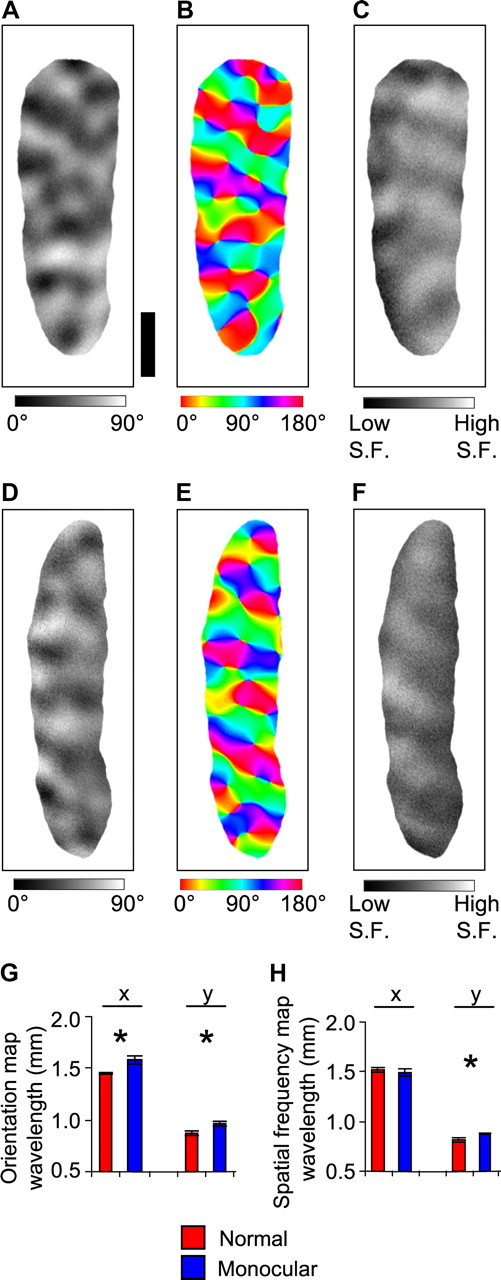
Maps of orientation and spatial frequency in normal and monocular ferrets. A, D, Differential orientation maps from a normal ferret (A) and from the cortex contralateral to the remaining eye in a monocular ferret (D), comparing the cortical response to 0° and 90° grating stimulation. B, E, Orientation angle maps from a normal ferret (B) and from a monocular ferret (E). Each pixel is color coded according to its preferred orientation. C, F, Differential spatial frequency (S.F.) maps in V1 from a normal ferret (C) and from a monocular ferret (F), comparing the cortical response to 0.08 and 0.225 cycle/° stimulation. G, The orientation map wavelength, measured using Fourier analysis along the x (horizontal, anteroposterior) dimension and the y (vertical, mediolateral) dimension of cortex. Error bars denote SEM over 10 normal ferrets and 12 monocular ferrets. H, The spatial frequency map wavelength, measured using Fourier analysis along the x (horizontal) dimension and the y (vertical) dimension of cortex. Error bars denote SEM over five normal ferrets and seven monocular ferrets. Scale bar: (in A) A–F, 1 mm.

Given that the orientation and spatial frequency maps can form in monocular animals without an ocular dominance map, we can determine whether the layouts of the maps change in the manner predicted by the dimension-reduction model after the removal of a feature map. The model predicted that the removal of a feature map should result in a higher wavelength of the orientation and spatial frequency maps (Fig. 1). Consistent with the model predictions, we found that the orientation map wavelength was greater in monocular ferrets than in normal ferrets. The increase occurred along both the x (horizontal, anteroposterior) dimension (p < 0.01, t test, one-tailed) and y (vertical, mediolateral) dimension (p < 0.05, t test, one-tailed) of the map, although the increase was most pronounced along the x dimension (Fig. 4 G). For the spatial frequency map, the wavelength increased significantly along the y dimension (p < 0.01, t test, one-tailed) but did not change for the x dimension (p > 0.05, t test, one-tailed) (Fig. 4 H).

Consistent with the change in the orientation map wavelength, we also found a significant difference between normal and monocular ferrets in the gradient, or rate of change, of the orientation map. In a normal ferret, most of V1 is covered by iso-orientation domains, in which the orientation gradient is low. These regions are punctuated by orientation pinwheels and fractures, which have a high orientation gradient (Fig. 5 A). A similar layout was observed for the orientation gradient map in monocular ferrets (Fig. 5 D), but a pronounced difference was that the mean orientation gradient in V1 was significantly lower for monocular ferrets than for normal ferrets (p < 0.01, t test, one-tailed) (Fig. 5 G). This may relate to the increased wavelength of the orientation map in monocular ferrets: a higher orientation map wavelength would be expected to cause an increase in the spacing of adjacent high orientation gradient regions (i.e., orientation pinwheels and fractures) and thus to result in a lower average orientation gradient. These results are consistent with the model (Fig. 1 R), which predicted that removal of the ocular dominance map should result in a lower mean orientation gradient.

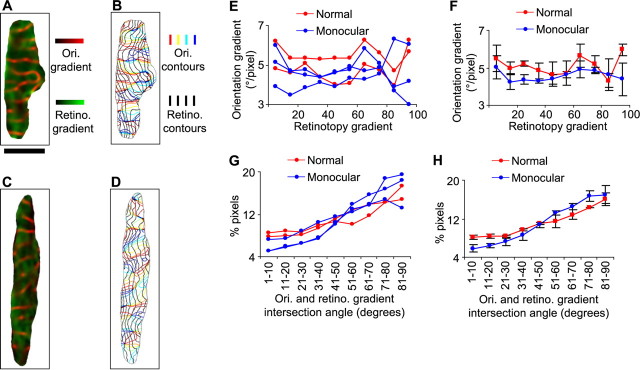
Figure 5.

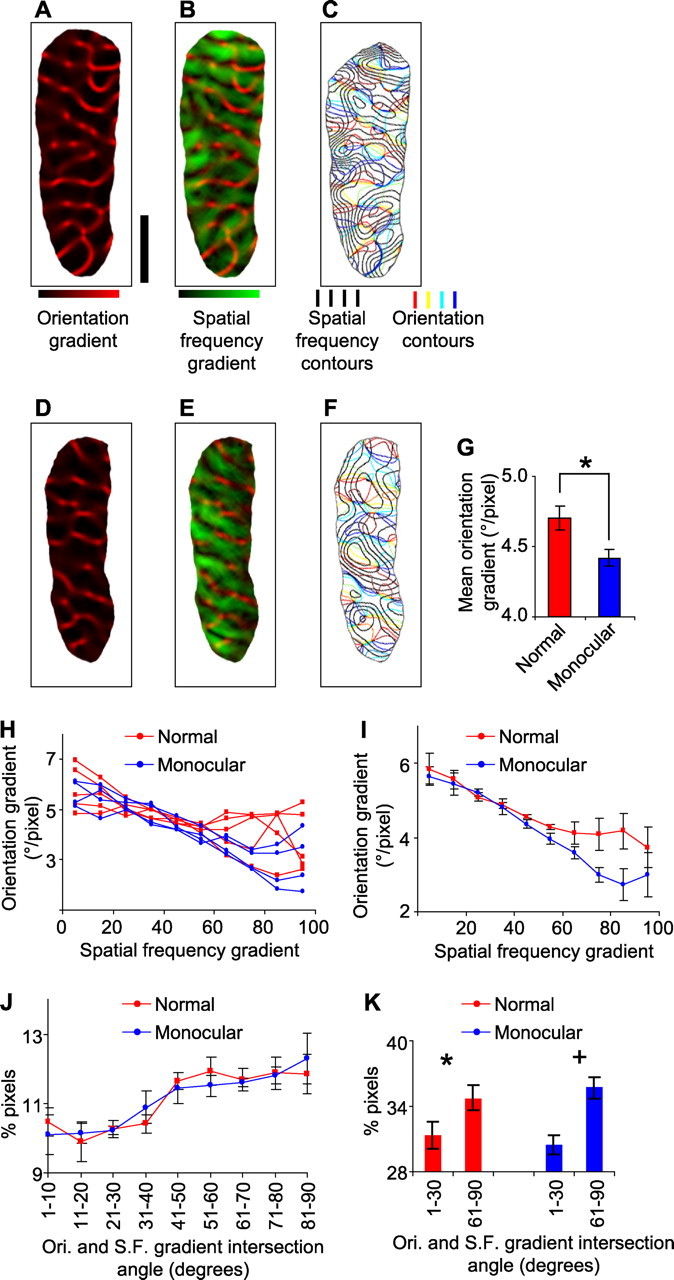
Spatial relationships between orientation and spatial frequency maps in normal and monocular ferrets. A, D, The orientation gradient map from a normal (A) or monocular (D) ferret, produced by calculating the two-dimensional orientation preference gradient at each pixel. B, E, The orientation gradient map (red) is superimposed on the spatial frequency gradient map (green). Results are from a normal (B) or monocular (E) ferret. C, F, Iso-orientation contours are superimposed on iso-spatial frequency contours. Results are from a normal (C) or monocular (F) ferret. G, The mean orientation gradient magnitude over all image pixels of the imaged portion of V1. Error bars denote SEM over 10 normal ferrets and 12 monocular ferrets. H, The correlation between the orientation and spatial frequency gradient magnitudes. For each individual animal, image pixels from V1 are grouped into 10 bins according to their spatial frequency gradient (bin 1, 0–10% of maximum; bin 2, 10–20% of maximum; …), and the mean orientation gradient for each group is indicated. I, Same as in H, except that each point represents the average over the individual cases within the group. Error bars denote SEM over five normal ferrets and four monocular ferrets. J, The percentage of image pixels in V1 having intersection angles, between the orientation (Ori.) and spatial frequency (S.F.) gradient vectors, within the nine ranges indicated. Pixels were obtained from five normal ferrets and four monocular ferrets. K, The percentage of image pixels in V1 having intersection angles, between the orientation and spatial frequency gradient vectors, between 1 and 30° or between 61 and 90°. Scale bar: (in A) A–F, 1 mm.

Alterations in relationships between orientation and spatial frequency maps

A central prediction of dimension-reduction models is that the number of features that are mapped within a cortical area should determine the spatial relationships between the maps. Specifically, the model we used predicts that, as fewer features are mapped to the cortex, the high gradient regions of the remaining maps will overlap with one another less often and the remaining features will be mapped more orthogonally to one another (Figs. 1, 2). We next asked whether the experimental removal of the ocular dominance map, caused by monocular enucleation, altered the relationships between the remaining feature maps.

We first analyzed the relationships between the gradient magnitudes of the orientation and spatial frequency maps. In normal ferrets, regions of high orientation gradient (Fig. 5 B, bright red) generally do not overlap with regions of high spatial frequency gradient (Fig. 5 B, bright green). This relationship can be illustrated quantitatively by plotting the orientation gradient as a function of the spatial frequency gradient. For each normal animal tested, it can be seen that, as the spatial frequency gradient increases, the average orientation gradient decreases (Fig. 5 H, red lines). The same overall tendency holds for monocular ferrets (Fig. 5 E and blue lines in 5H), but on average the slopes of the relationship are steeper in monocular ferrets than in normal ferrets (p < 0.05, Mann–Whitney U test, one-tailed). Pooling the data within normal and monocular ferrets also reveals a difference between the slope of the relationship (normal, r = 0.96, slope of −0.22°/pixel per group; monocular, r = 0.99, slope of −0.35°/pixel per group) (Fig. 5 I). Together our results indicate that the mean orientation gradient is lower in monocular ferrets than in normal ferrets (Fig. 5 G) and that the decrease in the orientation gradient does not occur uniformly across the cortex but rather is most pronounced in the high spatial frequency gradient regions (Fig. 5 I). This result is consistent with the dimension-reduction model, which predicts that removal of a feature map should result in an overall decrease in the orientation gradient and that the change in the orientation gradient should be non-uniform across the spatial frequency map (Fig. 1).

A related prediction of the dimension-reduction model is that the removal of a feature map should result in a slight increase in the amount of near-orthogonal intersection angles between the contours (i.e., gradient vectors) of the orientation and spatial frequency maps, i.e., greater “orthogonality” between these two maps (Fig. 1 T). To illustrate the contour relationships, we superimposed the orientation and spatial frequency contour maps from a normal ferret (Fig. 5 C) or monocular ferret (Fig. 5 F). For both groups, we then quantified the distribution of intersection angles between the gradient vectors of the two maps. In both normal and monocular ferrets, a significantly larger proportion of image pixels had near-perpendicular intersection angles (61–90°) than near-parallel intersections (1–30°) between orientation and spatial frequency gradients [normal ferrets, p < 0.05 (Fig. 5 K, *); monocular ferrets, p < 0.01 (Fig. 5 K, +); t test, one-tailed]. In normal ferrets, there was a positive slope between the intersection angle and the proportion of pixels with that angle (r = 0.87, slope of 0.27%/group) (Fig. 5 J, red line), indicating a preponderance of near-orthogonal intersection angles. This positive slope was also present in monocular ferrets (r = 0.97, slope of 0.29%/group) (Fig. 5 J, blue line). However, the results do not indicate a difference, between normal and monocular ferrets, in the distribution of intersection angles. It is possible that the noise associated with experimental measurements may obscure the slight difference predicted by the model (Fig. 1 T). [We showed in a previous study that, in normal ferrets, the tendency for orthogonal crossings between orientation and spatial frequency gradients is most pronounced in those regions of the cortex in which high gradient magnitude regions of these two maps coincide (Yu et al., 2005). This tendency also holds for monocular ferrets (supplemental Fig. 3, available at www.jneurosci.org as supplemental material).]

Together, the differences between normal and monocular ferrets in the structures of the orientation and spatial frequency maps are similar to the differences predicted between four- and three-feature simulations (Fig. 1). Thus, removing a map experimentally produces similar effects as mapping one less feature with a dimension-reduction model. Specifically, the wavelength of the orientation map is higher in monocular animals, leading to a decrease in the mean orientation gradient in V1. The decrease in the orientation gradient occurs preferentially in the high gradient regions of the spatial frequency map, indicating a coordinated reorganization of these two maps.

Alterations in relationships between orientation and retinotopic maps

We also measured the map of the azimuth dimension of retinotopy in monocular animals and examined the relationships between this map and that of orientation. The model predicts that, as less features are mapped to the cortex, the high gradient regions of the retinotopic and orientation maps should avoid each other more strongly and that these two features should be mapped more orthogonally (Fig. 2). We found previously that, in normal ferrets, the relationship between the gradient magnitude of retinotopy and the gradient magnitude of orientation is weak when measured with intrinsic signal optical imaging (Yu et al., 2005). This may be attributable to a difficulty in measuring the local structure of the retinotopic map using this technique: in contrast to the orientation map, in which nearby domains have opposite orientation preferences, the preferred retinotopic position in space changes gradually across the entire extent of visual cortex. Thus, local gradients in retinotopy may be less pronounced and more difficult to detect than orientation gradients. In Figure 6, we superimpose the orientation gradient map and the azimuth retinotopic gradient map from a normal ferret (Fig. 6 A) or from a monocular ferret (Fig. 6 C). We do not find a consistent relationship between the gradient magnitudes of retinotopy and orientation in either normal or monocular ferrets (Fig. 6 E,F). However, given the above considerations, it is unclear whether a relationship does not exist or whether we are unable to detect a relationship using optical imaging.

Figure 6.

Spatial relationships between orientation and retinotopic maps in normal and monocular ferrets. A, C, The orientation (Ori.) gradient map (red) is superimposed with the azimuth retinotopy (Retino.) gradient map (green). Maps are from a normal (A) or monocular (C) ferret. B, D, Iso-orientation contours are superimposed on iso-azimuth retinotopic contours. Results are from a normal (B) or monocular (D) ferret. E, The correlation between the orientation and retinotopic gradient magnitudes. For each individual animal, pixels from V1 were grouped into 10 bins according to their azimuth retinotopy gradient (bin 1, 0–10% of maximum; bin 2, 10–20% of maximum; …) and the mean orientation gradient for each group was calculated. F, Same as in E, except that each point represents the average over the individual cases within the group. Error bars denote SEM over two normal ferrets and three monocular ferrets. G, The percentage of pixels in V1 having intersection angles, between the orientation gradient and the azimuth retinotopy gradient vectors, within the nine ranges indicated. H, Same as in G, except that each point represents the average over the individual cases within the group. Error bars denote SEM over two normal ferrets and three monocular ferrets. Scale bar: (in A) A–D, 1 mm.

In contrast, because retinotopy contours run approximately parallel to one another over small scales of cortex, intrinsic signal imaging can be used to measure their average direction in local regions of cortex. Indeed, optical imaging can detect a nonrandom relationship between contours of the retinotopic and orientation maps in normal ferrets (Yu et al., 2005). In visual cortex of both normal and monocular ferrets, iso-azimuth lines run approximately mediolaterally across the cortex (Fig. 6 B,D) (for orientation of the maps relative to the brain, see Fig. 3), and it can be seen that, on average, iso-orientation contours run approximately perpendicularly to the iso-azimuth contours. This indicates a strong overall spatial relationship between these two maps. The relationship can be quantified by calculating the percentage of image pixels having intersection angles of various ranges between the retinotopic and orientation map gradient vectors. In both normal and monocular ferrets, a significantly larger proportion of image pixels have near-perpendicular intersection angles (61–90°) than near-parallel intersections (1–30°) between orientation and retinotopic gradients (normal ferrets, p < 0.05; monocular ferrets, p < 0.01; t test, one-tailed). There is a strong correlation between intersection angle and the percentage of pixels with that angle for both normal ferrets and monocular animals (Fig. 6 G,H). However, this tendency is enhanced on average in monocular ferrets (normal, r = 0.97, slope of 1.0%/group; monocular, r = 0.98, slope of 1.6%/group) (Fig. 6 H). There is a significant difference in the intersection angle cumulative distributions between normal and monocular ferrets (p < 0.01, Kolmogorov–Smirnov test). The enhanced tendency, in monocular compared with normal ferrets, for orthogonal crossings between retinotopic and orientation contours, is consistent with the predictions of the dimension-reduction model for removing a feature map (Fig. 2).

Discussion

We show that neonatal monocular enucleation in the ferret results in spatially uniform activation of visual cortex following monocular stimulation and hence the absence of a functional ocular dominance map. As a consequence, the spatial relationships between the remaining feature maps in visual cortex are altered in a manner that is in agreement with the predictions of a dimension-reduction model of cortical organization. These results suggest that the relationships between feature maps are not intrinsically determined. Rather, altered input can cause maps to reorganize in a coordinated manner that is consistent with satisfying mapping principles for the number of feature maps that are represented in a given area.

Inputs play a role in guiding the development of map relationships

Although the effects of altered input on individual cortical maps have been well studied, little is known about the effects on multiple maps and their spatial relationships. Previous studies that have examined the structures of multiple maps after sensory manipulations have provided some evidence for altered map relationships. For example, after several days of monocular deprivation, the ocular dominance domains belonging to the deprived eye shrink. In these animals, orientation pinwheels are found to be preferentially located in the centers of ocular dominance domains (Crair et al., 1997a) to a degree that is enhanced compared with that in normal animals (Crair et al., 1997b; Hubener et al., 1997). Because the orientation map does not appear to change after monocular deprivation of a similar duration (Kim and Bonhoeffer, 1994), these data suggest a reorganization of the ocular dominance map that is coordinated with a fixed orientation map. Similarly, inducing strabismus results in a sharpening of ocular dominance column borders but no detectable change in the orientation map (Lowel et al., 1998). In these animals, there exists a bias toward orthogonal intersection angles between ocular dominance and orientation contours, similar to what is found in normal animals. These studies therefore indicate that altered input can cause a rearrangement of the ocular dominance map that preserves or enhances its spatial relationship with an unaltered orientation map.

Our results extend these findings by showing that, after changes to input from the two eyes, maps in addition to ocular dominance rearrange. Furthermore, we show that spatial relationships between orientation, spatial frequency, and retinotopic maps are altered. One reason that we see changes to multiple maps might be that monocular enucleation represents a more severe disruption of input than monocular deprivation or strabismus. In addition, we perform our manipulation at an earlier developmental stage than in the previous studies (Kim and Bonhoeffer, 1994; Crair et al., 1997a; Lowel et al., 1998).

Our findings indicate that the mechanisms that set up the relationships between maps are not entirely intrinsic but rather can respond to changes in inputs. This suggests that one role for inputs is to coordinate the response properties of adjacent neurons and therefore to modify the detailed spatial relationships between feature maps. Several possible mechanisms could mediate input-driven coordinated map reorganization. Alterations in one map could change the cortical expression pattern of a set of molecules, which individually or in combination set up the multiple maps (McLaughlin and O'Leary, 2005; Sur and Rubenstein, 2005; Rash and Grove, 2006). Alternatively, activity-dependent synaptic modification rules, similar in principle to those that underlie dimension-reduction algorithms (Kohonen, 1993; Kohonen and Hari, 1999), might be responsible for map relationships and be affected by altered input activity patterns. For example, correlated activity between the two eyes in normal animals may have an instructive role in shaping certain map relationships, and its absence in monocular animals could signal changes to these relationships.

Does altered input affect the initial formation of map relationships or cause a later reorganization?

There are two alternatives regarding how maps may come to obtain their altered spatial relationships after monocular enucleation. First, the initial establishment of maps may take a normal course, but the maps reorganize at some later developmental stage. Consistent with this alternative, most visual cortical maps, with the exception of the direction map (Li et al., 2006), arise before visual experience and early manipulations of input including monocular and binocular enucleation do not affect their initial formation (Crair et al., 1998; Crowley and Katz, 1999, 2000; Li et al., 2006). Furthermore, spontaneous LGN firing patterns measured before eye opening are not disrupted by enucleation of the ipsilateral eye (Weliky and Katz, 1999). In contrast, manipulations that alter input after eye opening, i.e., after most maps are initially established, can change the structures of maps (Wiesel and Hubel, 1963; Crair et al., 1998; Sengpiel et al., 1999; White et al., 2001; Li et al., 2006). In a similar manner, our enucleation paradigm may not affect the initial layout of individual maps or their spatial relationships but rather may cause reorganization at a later time, such as during the critical period.

However, the second alternative, that our monocular enucleation paradigm affects the initial formation of maps and their relationships, is also a valid possibility. In the study cited above, which showed no effect of monocular enucleation on the initial formation of ocular dominance columns, the enucleations were performed between P7 and P14 (Crowley and Katz, 2000). Although enucleation performed during this age range may not affect the initial establishment of ocular dominance columns, our earlier manipulations performed at P0 might. Indeed, there are important developmental milestones between these stages, including the formation of cytoarchitectonic eye-specific layers in the LGN and the ingrowth of thalamocortical axons to layer IV of cortex (Linden et al., 1981; Johnson and Casagrande, 1993; Herrmann et al., 1994).

The developmental window within which our P0 enucleations exert their effect on map relationships could be narrowed down by measuring the resulting map relationships at an age earlier than adulthood, e.g., at the beginning of the critical period. It would also be instructive to test whether monocular enucleation performed at ages later than P0 has the potential to result in altered map relationships.

Computational models of cortical organization

A number of studies have recently used computational models, based on either the Kohonen algorithm (Swindale, 2000, 2004; Yu et al., 2005) or the elastic net algorithm (Carreira-Perpinan et al., 2005), to explore the consequences of mapping different numbers of features on the resulting map wavelengths and map relationships. Although differing in detail, each of these algorithms makes qualitatively similar predictions.

The first studies that addressed this issue used the Kohonen algorithm to map retinotopy along with additional abstract features, such binary features, scalar features, or circular features (Swindale, 2000, 2004). The effects of mapping additional features were to cause a gradual decrease in the wavelengths of the existing feature maps, except in the case of binary features in which the trend was less clear (Swindale, 2000, 2004). More recently, the effects of mapping a variable number of more realistic feature maps were explored using the elastic-net algorithm (Carreira-Perpinan et al., 2005). Specifically, retinotopy and orientation were mapped either alone or with the successive addition of direction, ocular dominance, and spatial frequency. The mapping of additional features again caused a decrease in the wavelengths of the existing maps. Similar to the latter study, we explored the effects of mapping a variable number of realistic feature maps. However, our algorithm differed in a number of ways. Most notably, we used the Kohonen algorithm instead of the elastic-net algorithm. Second, we did not include a map of direction preference. Finally, we modeled a strong anisotropy in the retinotopic map (to mimic the anisotropy found in the ferret visual cortex). Despite these differences, our study also predicted that the wavelengths of existing maps would decrease with the mapping of additional features.

The algorithms mentioned above have also been used to explore the effects of mapping additional features on the spatial relationships between maps. The most extensive exploration was performed in the elastic-net study, in which it was shown that, as more features were mapped, the relationships between the existing maps became weaker (Carreira-Perpinan et al., 2005). Studies using the Kohonen model also showed that the gradient correlations between retinotopy and other feature maps became weaker as additional features were mapped (Swindale, 2004; Yu et al., 2005). In the current study, we show a similar effect of mapping additional features on the relationships between the orientation and spatial frequency maps.

The present study provides the first experimental evidence that removing a map alters the individual maps and their relationships in a manner consistent with the predictions of these computational modeling studies. It is notable that the Kohonen and elastic-net algorithms make similar qualitative predictions, in agreement with our experimental results, regarding the effects of mapping different numbers of features. Each of these two algorithms is also relatively successful in reproducing the spatial relationships found among maps in the adult primary visual cortex (Erwin et al., 1995; Swindale, 1996; Carreira-Perpinan and Goodhill, 2002). Thus, characteristics that are shared between the algorithms appear to be the key that leads to their success in reproducing the experimental data. A central idea is that of balancing feature map continuity and coverage uniformity, which each of the algorithms implement although in different ways (Erwin et al., 1995; Swindale, 1996).