Significance
F1-ATPase is a small motor protein, composed of 3 α- and 3 β-subunits that surround a central γ-subunit. The β-subunits alternate cyclically between 2 major conformational states to produce the rotation of the γ-subunit. Although the rotation on the microsecond timescale is powered by the differential binding of ATP and its hydrolysis products ADP and HPO42−, there is near-100% conversion efficiency of the free energy of ATP hydrolysis, which occurs on the picosecond timescale. The free-energy profile constructed for the 360° rotation cycle shows that F1-ATPase achieves its high energy-conversion efficiency by elegantly separating fast catalytic events, which involve small local conformational changes, from the slow binding/release of ligands involved in the large conformational change.
Keywords: F1-ATPase, chemo–mechanical coupling, energy-conversion efficiency, free-energy profile
Abstract
Our understanding of the rotary-coupling mechanism of F1-ATPase has been greatly enhanced in the last decade by advances in X-ray crystallography, single-molecular imaging, and theoretical models. Recently, Volkán-Kacsó and Marcus [S. Volkán-Kacsó, R. A. Marcus, Proc. Natl. Acad. Sci. U.S.A. 112, 14230 (2015)] presented an insightful thermodynamic model based on the Marcus reaction theory coupled with an elastic structural deformation term to explain the observed γ-rotation angle dependence of the adenosine triphosphate (ATP)/adenosine diphosphate (ADP) exchange rates of F1-ATPase. Although the model is successful in correlating single-molecule data, it is not in agreement with the available theoretical results. We describe a revision of the model, which leads to consistency with the simulation results and other experimental data on the F1-ATPase rotor compliance. Although the free energy liberated on ATP hydrolysis by F1-ATPase is rapidly dissipated as heat and so cannot contribute directly to the rotation, we show how, nevertheless, F1-ATPase functions near the maximum possible efficiency. This surprising result is a consequence of the differential binding of ATP and its hydrolysis products ADP and Pi along a well-defined pathway.
F1-ATPase is one of the smallest motor proteins; only some kinesins are smaller (1). It consists of 3 α- and 3 β subunits, which are arranged alternatively to form a ring around the γ-subunit. The motor drives the rotation of the central γ-stalk of the enzyme by harnessing the differential binding free energies of adenosine triphosphate (ATP) and its hydrolysis products, adenosine diphosphate (ADP) and Pi (2, 3). The energy-conversion efficiency, measured in terms of the hydrolysis energy of ATP, is near 100% (2, 4–7). X-ray crystallography has established that the 3 β-subunits adopt 2 significantly different conformations that depend on the ligands in the active sites, and cyclically alternate through a sequence of conformational transitions between the two. The 3 α-subunits contribute residues for the catalysis but their conformational changes are small (8). In the conformational cycle, only 1 site is catalytically active for hydrolysis of ATP at a given time.
The γ-subunit rotation in 120° steps was demonstrated early by single-molecule imaging experiments (9, 10). This result was subsequently refined to show that the rotation occurs in 40° and 80° substeps (11–13). [In this work, we use the 40° and 80° notation following Adachi et al. (12), although the choice is somewhat arbitrary and other papers use other values (11, 14–19).] Through these studies, as well as others (20, 21), in conjunction with simulations (16, 22–24), a detailed molecular description of each of the 2 substeps in the γ-subunit rotation cycle was established (Fig. 1A). Based on the chemical events in each substep, the 40° substep is referred to as the catalytic step and the 80° substep as the ATP binding step. A conformation first trapped by a molecular dynamics simulation (23), which is consistent with the structural changes suggested by single-molecule experiments (25, 26), as well as a more recent simulation (27), is associated with the ATP binding “dwell.” The open βE-conformation binds substrate ATP; the subsequent closing of βE induces a conformational change in an adjacent β-subunit to release the hydrolysis products of a previous ATP binding event, and together leads to the 80° substep of the γ-subunit. Once this substep reaches the catalytic dwell, the hydrolysis of 1 ATP and release of 1 inorganic phosphate (Pi) result in the 40° substep rotation. This rotation is followed by release from the βHO-subunit [precisely, βHO––like in Nam et al. (23)] of 1 ADP, which was formed from the ATP hydrolyzed during the 40° substep. In these 2 substeps, the interfaces of the β-subunits with the 3 α-subunits change in response to alterations in the β-subunits. The resulting change in contacts is likely to play an important role, as suggested in our previous publication (23). Recent simultaneous single-molecule fluorescence resonance energy transfer (FRET) and rotation measurements (26) support this picture of the rotation cycle, as does the paper by Martin et al. (19). In human F1-ATPase, on the other hand, it has recently been shown that the rotation takes place in 3 substeps: 0° → 65° during ATP binding/ADP release, 65° → 90° with Pi release, and 90° → 120° with ATP hydrolysis (28). However, the mechanistic origin of the difference of the Pi release/ATP hydrolysis steps between human and other F1-ATPases is not fully understood (18, 28). In what follows, the results in Fig. 1 are used in a model that suggests a basis for the nearly 100% efficiency of F1ATPase. This occurs despite the fact that the hydrolysis energy, per se, is thermalized too rapidly (in picoseconds to nanoseconds) (3, 29) to contribute to the rotation, which is on a timescale of microseconds.
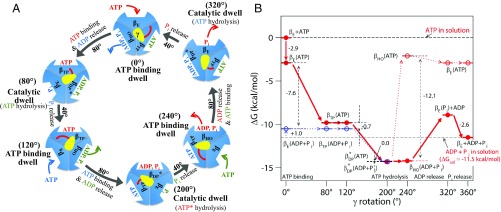
Fig. 1.
(A) Proposed 360° rotation cycle of F1-ATPase showing each β-subunit conformation based on ref. 23. In brief, an ATP bound at 0° (ATP binding dwell) is hydrolyzed at 200° (catalytic dwell), and the hydrolysis product ADP and Pi are released at 240° and 320°, respectively. The changes of the β-subunits’ conformation, γ-subunit orientation, and ligands occupancy at each subunit associated with the ATP/ADP exchange and catalytic events are indicated at each step. (B) FE (kcal/mol) profile for ATP hydrolysis based on the model presented in A. In each γ-rotation angle, the FE of β-subunit is shown for the state with bound ATP (red) and the hydrolysis product ADP + Pi (blue), whose FEs are determined using the reaction FE of ATP hydrolysis in solution with the cellular concentrations of ATP, ADP, and Pi (i.e., [ATP] = 3 mM, [ADP] = 0.4 mM, and [Pi] = 6 mM) and their binding FEs shown in SI Appendix, Table S1. For the state at 320°, the subunit with bound Pi and free ADP represents the state after the departure of ADP from βHO(ADP + Pi). The lines shown with solid arrow represent the changes of β-subunit with the rotation of γ. The dotted black lines show the FE of ATP hydrolysis in each β-subunit at different γ-angles, and the dotted red and blue lines are for the transitions with bound ATP versus ADP + Pi.
Fig. 1A shows the proposed full 360° rotation cycle. It is essential to use the full cycle for a correct description because the ATP bound at 0° (ATP binding dwell) is hydrolyzed only after a 200° rotation (catalytic dwell) and the hydrolysis products, ADP and Pi, are released at 240° (ATP binding dwell) and 320° (catalytic dwell), respectively. We note that the 3 β-subunits of each F1-ATPase vary their conformation between βE, βTP, βDP*, and βHO relative to γ. An updated version of the thermodynamics involved in the rotational steps is shown in Fig. 1B and is discussed below. Given this microscopic description of the F1-ATPase cycle, there remains the challenge of developing consistent theoretical models that simultaneously explain the single-molecule measurements, as does the above description, and the ensemble experiments (30–32). In this regard, we focus on 2 recent papers by Volkán-Kacsó and Marcus (33, 34) (referred to as V-K&M in what follows), who have developed a thermodynamic model based on the classic 2-state reaction rate theory of Marcus and Sutin (35), augmented with the introduction of the elastic structural deformation that occurs in F1-ATPase. Their model is consistent with the exponential dependence on the γ-rotation angle of the ATP/ADP exchange rates observed in both recent stalled- (36) and controlled-rotation single-molecule experiments (37). We show here that a revision of the V-K&M model for the molecular coupled rotary-binding change mechanism, and the thermodynamic diagram of the enzyme cycle (Fig. 1B) based on the atomistic simulation results (14, 16, 23, 27, 38), yield deeper insights into how F1-ATPase works.
Free-Energy Profile for ATP Hydrolysis along 360° Rotation Cycle
Fig. 1B shows the free-energy (FE) diagram for the entire 360° cycle of ATP hydrolysis. This diagram is constructed based on the 360° rotation model proposed recently (23) and the binding FE data of ATP, ADP, and Pi in different β-conformations (SI Appendix, Table S1) (14). The data are based on the physiologically relevant concentrations of ATP, ADP, and Pi [i.e., [ATP] = 3 mM, [ADP] = 0.4 mM and [Pi] = 6 mM (14, 38, 39)], which give −11.5 kcal/mol as the total FE of ATP hydrolysis in water.
Starting from an unoccupied βE at 0°, whose FE is defined to be zero, ATP binding lowers its FE to −2.9 kcal/mol. This value is the sum of −6.3 kcal/mol for ATP binding in βE (SI Appendix, Table S1) and 3.4 kcal/mol for [ATP] = 3 mM. By the rotation of γ to 80° with a binding FE of −9.8 kcal/mol, βE changes to βTP. This value corresponds to an FE change of −6.9 kcal/mol, a value very close to −6.7 kcal/mol determined by Czub et al. (27) for the corresponding transition of an isolated αβ-dimer. The binding FE of ATP decreases further to −14.3 kcal/mol when βDP* is reached at 200°, where the catalytic dwell takes place and the bound ATP is hydrolyzed, as mentioned above. The estimate of the FE change in the βTP (ATP) → βDP*(ATP) transition (indicated with the red arrow between 120° and 200° in Fig. 1B) is based on 2 results: first, that the FE of ATP hydrolysis in βDP* is zero. This conclusion is supported by the similar rates of ATP hydrolysis and synthesis measured in the stalled rotation experiments (13, 36); and second, that the conformation of βDP*(ADP + Pi) is very similar to that of βDP, which is the conformation found in many X-ray structures with ADP and Pi analogs (40). Thus, its affinities for ADP and Pi are expected to be essentially the same as those of βDP (SI Appendix, Table S1). The β-subunit then is transformed to βHO at 240°. In this step, we have assumed that the binding affinities of ATP, ADP, and Pi in this β-subunit are intermediate between their corresponding values in βHC and βDP, since the βHO-conformation is approximately intermediate between βDP and βHC [as presented in SI Appendix, figure S2 of Nam et al. (23)]. Subsequently, ADP exits from βHO, producing βE(Pi) and free ADP, whose FE is higher by 5.3 kcal/mol than βDP*(ADP + Pi). Finally, Pi is released from βE to complete the ATP hydrolysis cycle.
The FE diagram (Fig. 1B) indicates that the 80° rotation produces a total −9.0-kcal/mol change in FE. This is mainly contributed by the change of an empty βE to βTP with ATP binding (−9.8 kcal/mol), whereas the FEs of the other 2 β-subunits approximately compensate each other; i.e., the values are −4.5 kcal/mol for the βTP(ATP) → βDP*(ATP) transition and 5.3 kcal/mol for the βHO(ADP + Pi) → βE(Pi) + ADP transition, respectively. The 40° substep rotation yields only −2.6 kcal/mol, which arises from the Pi release by βE, while the other 2 β-subunits contribute nothing to the overall FE change. This finding and the conclusion by Gao et al. (14, 38) are different from those of Mukherjee and Warshel (41), who suggested that a larger FE change occurs during the 40° substep (SI Appendix, section SI1).
Origin of High Energy-Conversion Efficiency of F1-ATPase
The analysis based on Fig. 1B shows how F1-ATPase utilizes the differential binding affinities of ATP versus ADP and Pi to achieve a highly efficient energy conversion; i.e., the motor is essentially 100% efficient, as measured by the FE of ATP hydrolysis (4, 5). This is a surprising result given that the hydrolysis occurs on the picosecond timescale, while the γ-rotation occurs on the microsecond timescale. For this high efficiency, 2 conditions must be met. First, the enzyme should follow a well-defined sequence of events, which is that presented in Fig. 1 (23). Any event that deviates from that pathway would lower the energy-conversion efficiency (i.e., such “off-path” event could lead to an α3β3-conformational change without inducing γ-rotation). Astumian et al. (42) suggested that such off-path events can be avoided by their having high kinetic barriers in comparison with those of the on-path events. Nevertheless, from time to time, the enzyme deviates from the path, for example, by a backward rotation as observed in the single-molecule experiment (12), which may result in a reduced energy-conversion efficiency. Similarly, ADP inhibition (43) may reduce the efficiency if the long pause caused by ADP inhibition results in the change of ligands in different β-subunits as in the 4ASU ADP-inhibited structure (44). Second, F1-ATPase has to function by separating the overall chemical reaction into 2 substeps: 1) binding and release, which are coupled with large protein conformational changes, and 2) breaking/making of chemical bonds, which involve zero FE changes and are associated only with localized conformational changes. As a result of this separation, the FE of ATP hydrolysis is not used directly in the function of F1-ATPase, but is mirrored by the differential binding affinities of ATP and ADP/Pi and the associated changes in the α3β3-conformation (Fig. 1) (3, 15, 45).
The remaining question is how the enzyme ensures a correct rotation of γ in each substep (46). To this end, the analysis presented in Rotor Stiffness Versus γ-Rotation FE suggests that one part, such as the coiled-coil portion of γ, is tightly coupled to the α3β3-conformational change, which occurs with ATP/ADP exchange, and a second part, such as the globular portion of γ, is relatively weakly coupled for effective transduction of forces between the F1-ATPase moiety and the c-ring of the full F0F1-ATPsynthase during both ATP synthesis and hydrolysis. Given that, the tightly coupled region of γ (the coiled-coil part) changes its conformation together with α3β3 in each substep, and the remaining part of γ (the globular portion) rotates spontaneously to complete the rotation. Previously, Karplus and Gao (3) suggested that for γ to couple tightly with the α3β3 hexamer, the FE should change linearly along the γ-rotation reaction coordinate in both the 80° and 40° rotation steps. The model of V-K&M (i.e., equation 5 of ref. 33) indeed shows that the ATP/ADP exchange FE at a rotation angle θ, ΔGo (θ), as defined in SI Appendix, Eq. S1, changes linearly with the γ-rotation angle. This result, in turn, is consistent with the exponential angle dependence of the ATP/ADP exchange equilibrium constants (36). Another prediction (3) deals with the FE ΔG available for γ-rotation under an external bias W, where and is the FE of ATP hydrolysis in solution. If is a linear function of the reaction coordinate (i.e., γ-rotation angle), the rate for γ-rotation should be a linear function of W. This result was observed in the single-molecule measurements under external torque (5).
In summary, the present analysis, in conjunction with the recent single-molecule experiments (7, 26, 36, 37, 47) and simulations (14, 16, 22, 23, 48), provides a confirmation of the predictions of Karplus and Gao (3), and leads to a better understanding of the connection between the thermodynamics of ATP hydrolysis by F1-ATPase and the molecular mechanism underlying the generation of the torque (the “power stroke”) that drives the γ-rotation with high energy-conversion efficiency.
Fig. 2B, together with Fig. 3 and SI Appendix, Fig. S2, propose a particular sequence of events for the F1-ATPase cycle. The rotation angle of γ fluctuates between −40° and 40° in the reactant state before the ATP/ADP exchange, with the associated work term (i.e., the energetic penalty to rotate γ from its 0° resting state) varying by less than 1/2 . The α3β3-conformational change then occurs with the ATP/ADP exchange with the minimum barrier being at 38°, followed by the completion of γ-rotation to the subsequent catalytic dwell state; see also Martin et al. (19). Further discussion of the detailed sequence of events is provided in Proposed Sequence of Events Between ATP Binding and ADP Release in ATP Binding Dwell. In this process, the completion of γ-rotation is driven by the change of the FE minimum to favor the rotated conformation in the product state (i.e., after the ATP/ADP exchange and α3β3-conformational change); i.e., with delayed ATP/ADP exchange or delayed ADP release, γ-rotation is delayed (17). This sequence of events is that described in our recent simulation (23) which showed that the rotation angle of γ first fluctuates in the catalytic dwell and only after the α3β3-conformational change does it change spontaneously, via a power stroke, to the subsequent ATP binding dwell. This suggests that the 40° rotation of γ from the catalytic dwell is also driven by the change in the FE minimum as a result of the conformational change of α3β3 after ATP hydrolysis and Pi release.
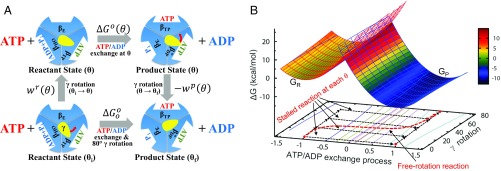
Fig. 2.
(A) Thermodynamic cycle connecting the stalled/controlled rotation at the γ-rotation angle (Upper) and freely rotating systems (Lower) for the 80° rotation step. In the freely rotating system, and refer to the γ-rotation angles at the resting reactant and product states, respectively. (B) FE diagram of the ATP/ADP exchange process for the stalled- and free-rotation systems determined based on the reorganization energy and values with = 16 pN·nm. value is a function of and the 2 work functions (see also SI Appendix, Fig. S2). For the ATP/ADP exchange process, “−1” denotes the reaction coordinate (RC) value at the reactant state and “1” at the product state, respectively. In the Marcus theory FE diagram (upper surface), the parabola shown in red mesh is the FE surface of the reactant state and the blue mesh is for the product-state FE surface . The transition state is where the 2 parabolas intersect. In the reactant state, the FE value of (at RC = −1) increases by the term with the increase of θ from 0° to 80°; the FE also increases similarly for the angle less than 0°. In contrast, the FE of (at RC = 1) decreases by in the product state as increases. The free-rotation reaction, i.e., the ATP/ADP exchange process in the freely rotating system (shown in red dashed line), is indicated by following the minimum FE values in the FE surface. In this diagram, the barrier height relative to (i.e., the FE of the resting reactant state) is relatively insensitive to the change of , whereas [i.e., the barrier relative to ] decreases as increases (SI Appendix, Fig. S2).
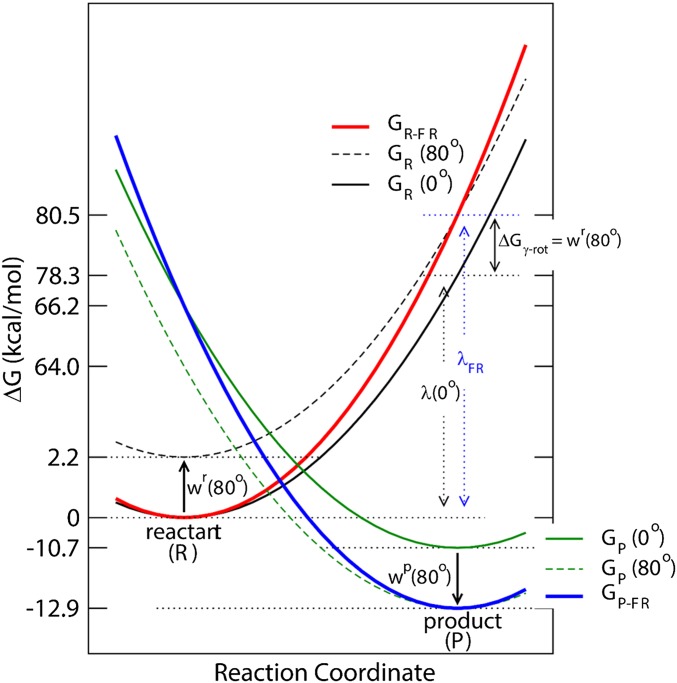
Fig. 3.
Schematic FE diagram of the stalled rotation and freely rotating systems based on Fig. 2. For each system, the 2 parabolas represent the FE surfaces of the reactant and product states , respectively. Two FE surfaces are shown for the stalled rotation system, one at 0° [ with a black solid line and with a green solid line] and the other at 80° [ with a black dashed line and with green dashed line]. The shift from one surface to the other is represented by the work terms (i.e., and ). The X axis represents the progress of the reaction, i.e., the ATP/ADP exchange in the stalled rotation system and the ATP/ADP exchange plus 80° γ-rotation in the freely rotating system. Red solid line represents the reactant-state FE surface of the freely rotating system and blue solid line that for the product state . In the freely rotating system, the FE minimum of the reactant state is set equal to that of the 0° reactant state of the stalled rotation system, and the FE value at the product-state RC to that of the 80° rotated reactant state to include the contribution of the γ-subunit rotation to the reactant state, i.e., . Similarly, the FE minimum of the product state is set to that of the 80° rotated product state of the stalled rotation system, and the product-state FE at the reactant-state RC to that of the 0° product state, respectively.
Estimation of FEs of ATP/ADP Exchange and 80° γ-Rotation
In the model of V-K&M (33), the ATP/ADP exchange reaction was described in both the stalled rotation and the freely rotating systems by the 2-state Marcus-type reaction theory, as follows:
| [1] |
where and are the activation barriers in the stalled rotation and freely rotating systems, respectively, and are their associated standard FE changes, is the work term to bring ATP from water solvent to the binding site of the enzyme, and is the reorganization energy. Each of these terms is discussed further in subsequent portions of the article. The work involved in the rotation of γ and any associated changes of the α3β3-conformation (hereafter, simply denoted as the γ-rotation) from the conformations of the reactant state, wr(θ), and the product state, wP(θ), of the freely rotating system were modeled as an elastic deformation as in V-K&M, i.e.,
| [2] |
where is the effective stiffness constant of the elastic deformation, and and the γ-rotation angles at the ATP binding state and the subsequent catalytic dwell state in the F1-ATPase hydrolysis direction, respectively; see also Sielaff et al. (47) and Wächter et al. (49).
Although the V-K&M model explains the rotational angle dependence of the measured ATP/ADP exchange rates and equilibrium constants in the stalled (36) and controlled rotation systems (37), it does not make clear certain important differences in the treatment of the exchange process between the stalled/controlled rotation systems (hereafter, simply stalled rotation) and the freely rotating systems.
First, whereas the γ-stalk rotation was separated out explicitly as the 2 work terms in the stalled rotation system, it was treated as a part of the process in the freely rotating system (Fig. 2A). Consequently, the analysis assumes implicitly that the terms associated with the 80° γ-rotation in the freely rotating system are included in the 2-state model, i.e., in the term in Eq. 1. To obtain a consistent treatment of the γ-rotation in the 2 systems under different conditions, the standard FE of the entire process in the freely rotating system can be written as a sum of the reaction FE at and the FE of γ-rotation
| [3] |
where , , and correspond to the definitions given in scheme 1 of ref. 33, as represented schematically in Fig. 3. is the FE of the ATP/ADP exchange process and associated conformational change of the α3β3-hexamer, including closure of βE and opening of βHO (Fig. 2A), at (i.e., at the reactant state). This decomposition is exact in terms of the thermodynamics of the conformational change. However, in terms of the kinetics, it assumes a particular sequence of events; i.e., the γ-rotation follows the ATP/ADP exchange and α3β3-conformational change at . In Eq. 3, refers to the FE change of the 80° γ-rotation. It may involve only the rotation of the globular portion of γ, while the changes in the coiled-coil portion of γ may occur with the α3β3-conformational change, caused by the contact interactions proposed by Pu and Karplus (16) and others (27, 48, 50).
Second, the FE change associated with the ATP/ADP exchange [i.e., ] should include the contributions for both the ATP binding and ADP release processes. More specifically, whereas only the ATP binding was considered in the V-K&M model (33), our analysis suggests that ADP release (equivalently, ADP binding in the reverse direction) should be included in the definition of ; see the difference between SI Appendix, Eq. S1 and equation 10 in ref. 33. A detailed analysis of this modification of the V-K&M model is provided in SI Appendix, section SI3, along with the effect of the revision on the values of and organization energy .
Using the expression for the 2 work terms (i.e., and given in Eq. 2), the term in Eq. 3 can be expressed as at . Since , we have
| [4] |
Since and , the FE change associated with the 80° γ-rotation is −2.2 kcal/mol with = 16 pN·nm (33, 34) and −2.8 kcal/mol with = 20 pN·nm (49); we write the spring constant as pN·nm, following the usual convention, although the actual units are pN·nm·rad−2. The value of = 20 pN·nm given in ref. 49 was determined with a thermal fluctuation correction to the stiffness value ( = 68 pN·nm) measured by Sielaff et al. (47). In fact, this value is associated with the most compliant region of F0F1-ATPsynthase, which consists of the globular portion of γ, subunit ε, and c-ring of F0-ATPsynthase. Other regions of the enzyme showed a large variation in their stiffness; e.g., = 50 pN·nm for the DELSEED motif of the β-subunits, = 750 pN·nm for the coiled-coil helix and the C-terminal helix of γ (medium stiffness) and = 1,500 pN·nm for the α3β3-hexamer and the eccentric region of the stator (47); the large values result from the eccentric stator and the c-ring of F0F1-ATPsynthase. Large variations of the stiffness were also observed in the all-atom molecular dynamics simulations (48). As discussed in the paper by Sielaff et al. (47) and also in Rotor Stiffness Versus γ-Rotation FE below, the different compliances suggest a possible sequence of events during ATP synthesis. When the c-ring rotates, it first induces rotation (or twisting) of the globular portion of γ relative to the rest of α3β3 and the coiled-coil region of γ, during which a restoring energy, similar to the work term in Eq. 2, accumulates. This accumulated energy then forces the rotation of the coiled-coil region of γ and concomitant changes in α3β3. In this model, the regions with the medium stiffness mediate the transfer of energy from the c-ring to the α3β3-hexamer and the eccentric region of the stator (largest stiffness). The V-K&M model is different from this proposal but becomes consistent with it after the revision introduced in SI Appendix, section SI3 and the analysis that follows.
Rotor Stiffness Versus γ-Rotation FE
If the same stiffness constant , as for the 80° rotation, is assumed for the stator–rotor complex during the 40° rotation, based on the observation that torque variation is similar for the 80° and 40° rotations (7), Eq. 3 can be used to estimate the total FE of the 120° γ-rotation as the sum of the 40°- and 80°-rotation FE values. The resulting value is −2.8 kcal/mol with = 16 pN·nm and −3.5 kcal/mol with = 20 pN·nm, in which the 40° rotation contributes −0.6 kcal/mol and −0.7 kcal/mol, respectively. Given −11.5 kcal/mol as the FE of ATP hydrolysis in water under the cellular concentrations of ATP, ADP, and Pi (i.e., [ATP] = 3 mM, [ADP] = 0.4 mM and [Pi] = 6 mM, respectively) (14), the 120° γ-rotation would account for only 24 ∼ 30% of the total FE of ATP hydrolysis.
Clearly, the above estimate of the FE associated with 120° γ-rotation is not consistent with experiments showing near-100% energy-conversion efficiency (4, 5). For example, there is a large difference between −11.5 kcal/mol for the FE of ATP hydrolysis and the −2.8 kcal/mol for the γ-rotation contribution determined above with = 16 pN·nm; with = 20 pN·nm (49), −3.5 kcal/mol of 120° γ-rotation FE. This suggests that the rotor stiffness value of the V-K&M model and the value by Wächter et al. are underestimates. If the value of 68 pN·nm measured by Sielaff et al. (47), which is the value before the correction by Wächter et al. (49), is used, the total contribution to the γ-rotation increases to −11.9 kcal/mol and with the value of 30 pN·nm of the ATP binding dwell (47), the rotation FE is −5.3 kcal/mol. Similarly, with the 80-pN·nm effective spring constant, which was estimated on the basis of the torque oscillation of F1-ATPase (7), the FE of γ-rotation is −14.0 kcal/mol. These larger values are in much better agreement with the hydrolysis FE of −11.5 kcal/mol.
It is also possible that the stalled/controlled rotations of γ measured in the single-molecule experiments (36, 37) account for only a part of the total γ-rotation in F1-ATPase. As noted above, F1-ATPase showed different stiffness values for different regions (47, 48). In particular, the region where the coiled-coil of γ interacts with the α3β3-hexamer showed a much larger -value than the value for the globular portion of γ (47). This suggests that, whereas the globular portion of γ has rotated in the single-molecule experiments of Watanabe et al. (36) and Adachi et al. (37), the rest of F1-ATPase, including the coiled-coil and c-terminal region of γ and the α3β3-hexamer, has remained in the unrotated (0°) conformation before ATP/ADP exchange. Such an interrelation is consistent with the possibility that the stiffness constant (16 pN·nm) estimated by fitting the V-K&M model to the single-molecule experimental rates (33) is an underestimate, as noted above. This analysis is supported by the simulation results of Pu and Karplus (16) in which a steric clash between γ and α3β3 blocks the rotation of γ without the conformational change in α3β3.
Proposed Sequence of Events between ATP Binding and ADP Release in ATP Binding Dwell
In Fig. 1A, we do not specify whether ATP binding and ADP release occur simultaneously or sequentially. However, given the time required for βE-closure and βHO-opening, we propose that ADP release occurs in a separate step from ATP binding. This is consistent with the angle delay between ATP binding and ADP release observed by Martin et al. (19) as well as with the rotary catalysis model proposed by Suzuki et al. (28). Our results suggest that the γ-rotation (or, better, fluctuation) in the ATP binding dwell is independent of the ATP/ADP exchange. Specifically, ATP binding induces βE-closure, which triggers the opening of βHO to allow ADP release. During these events, because of the time required for each conformational change, the globular portion of γ fluctuates between −40° and 40°. Indeed, Adachi et al. (12) showed a similarly large fluctuation of γ in the ATP binding dwell. Once the conformational change of α3β3 and the release of ADP have taken place, γ completes its rotation to the 80° state, which is thermodynamically favored. The separation of the pre-ATP/ADP exchange γ-fluctuation from the postexchange rotation (the power stroke) is consistent with Pu and Karplus (16). For example, figure 3b of ref. 16 showed that a torque for γ-rotation was generated in several stages. In the first stage, i.e., at the beginning of the 80° γ-rotation, no high torque was generated on γ. With the further rotation of γ, βE came into contact with the residues between 20 and 25 of γ and produced a torque on it. Then, when γ reached ∼40°, βE began to close and generated a high torque on the 232 to 238 residues of γ to complete the 80° rotation [85° in the Pu and Karplus paper (16)]. Interestingly, this high-torque region corresponded to the angle of the phase 2 power stroke observed by Martin et al. (19). In the stalled rotation experiment, by contrast, γ-rotation was enforced by magnetic tweezers (36). The delay between ATP binding and ADP release then depends on the rates of the α3β3-conformational change and ADP release, which are assumed to be fast and independent of γ-rotation. Thus, when γ is constrained to rotate at a constant speed, the ADP release can appear to occur in concert with the γ-rotation.
Concluding Remarks
The FE profile constructed for the entire 360° rotation cycle provides a basis for understanding the high energy-conversion efficiency of F1-ATPase. It is achieved by elegantly separating fast catalytic events (i.e., hydrolysis of ATP) from slow binding/release of ligands (i.e., ATP, ADP, and Pi) and conformational changes. A revision of the model of Volkán-Kacsó and Marcus provides an explanation of the differences in rotor stiffness reported for the different regions of the enzyme, and leads to a deeper understanding of the events that occur during the ATP binding dwell and the underlying chemo–mechanical coupling mechanism. The V-K&M model, as well as recent experiments, confirms the early prediction that the FE changes linearly along the rotation coordinate. From the viewpoint of the molecule, the ATP/ADP exchange in the ATP binding dwell and the ATP hydrolysis/Pi release in the catalytic dwell induce the correlated conformational changes in the α3β3-hexamer. These conformational changes produce the torques (power strokes) involved in the rotation of γ by 80° and 40°, respectively. From an alternative perspective, the α3β3-conformational change and γ-rotation result from the change in the underlying FE surface, which is controlled by the differential binding affinities of ATP and ADP/Pi in the different β-subunit conformations.
Supplementary Material
Acknowledgments
We acknowledge the financial support from the University of Texas at Arlington (K.N.), Swedish Research Council (VR 2015-04114 to K.N.), and the Chemistry at Harvard Molecular Mechanics (CHARMM) Development Project at Harvard (M.K.).
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1906816116/-/DCSupplemental.
References
- 1.Junge W., ATP synthase and other motor proteins. Proc. Natl. Acad. Sci. U.S.A. 96, 4735–4737 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Boyer P. D., The ATP synthase–A splendid molecular machine. Annu. Rev. Biochem. 66, 717–749 (1997). [DOI] [PubMed] [Google Scholar]
- 3.Karplus M., Gao Y. Q., Biomolecular motors: The F1-ATPase paradigm. Curr. Opin. Struct. Biol. 14, 250–259 (2004). [DOI] [PubMed] [Google Scholar]
- 4.Junge W., Sielaff H., Engelbrecht S., Torque generation and elastic power transmission in the rotary F0F1-ATPase. Nature 459, 364–370 (2009). [DOI] [PubMed] [Google Scholar]
- 5.Toyabe S., Watanabe-Nakayama T., Okamoto T., Kudo S., Muneyuki E., Thermodynamic efficiency and mechanochemical coupling of F1-ATPase. Proc. Natl. Acad. Sci. U.S.A. 108, 17951–17956 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Walker J. E., The ATP synthase: The understood, the uncertain and the unknown. Biochem. Soc. Trans. 41, 1–16 (2013). [DOI] [PubMed] [Google Scholar]
- 7.Saita E., Suzuki T., Kinosita K. Jr, Yoshida M., Simple mechanism whereby the F1-ATPase motor rotates with near-perfect chemomechanical energy conversion. Proc. Natl. Acad. Sci. U.S.A. 112, 9626–9631 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Abrahams J. P., Leslie A. G. W., Lutter R., Walker J. E., Structure at 2.8 Å resolution of F1-ATPase from bovine heart mitochondria. Nature 370, 621–628 (1994). [DOI] [PubMed] [Google Scholar]
- 9.Noji H., Yasuda R., Yoshida M., Kinosita K. Jr, Direct observation of the rotation of F1-ATPase. Nature 386, 299–302 (1997). [DOI] [PubMed] [Google Scholar]
- 10.Itoh H., et al. , Mechanically driven ATP synthesis by F1-ATPase. Nature 427, 465–468 (2004). [DOI] [PubMed] [Google Scholar]
- 11.Yasuda R., Noji H., Yoshida M., Kinosita K. Jr, Itoh H., Resolution of distinct rotational substeps by submillisecond kinetic analysis of F1-ATPase. Nature 410, 898–904 (2001). [DOI] [PubMed] [Google Scholar]
- 12.Adachi K., et al. , Coupling of rotation and catalysis in F1-ATPase revealed by single-molecule imaging and manipulation. Cell 130, 309–321 (2007). [DOI] [PubMed] [Google Scholar]
- 13.Watanabe R., Iino R., Noji H., Phosphate release in F1-ATPase catalytic cycle follows ADP release. Nat. Chem. Biol. 6, 814–820 (2010). [DOI] [PubMed] [Google Scholar]
- 14.Gao Y. Q., Yang W., Marcus R. A., Karplus M., A model for the cooperative free energy transduction and kinetics of ATP hydrolysis by F1-ATPase. Proc. Natl. Acad. Sci. U.S.A. 100, 11339–11344 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kinosita K. Jr, Adachi K., Itoh H., Rotation of F1-ATPase: How an ATP-driven molecular machine may work. Annu. Rev. Biophys. Biomol. Struct. 33, 245–268 (2004). [DOI] [PubMed] [Google Scholar]
- 16.Pu J., Karplus M., How subunit coupling produces the γ-subunit rotary motion in F1-ATPase. Proc. Natl. Acad. Sci. U.S.A. 105, 1192–1197 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Martin J. L., Ishmukhametov R., Hornung T., Ahmad Z., Frasch W. D., Anatomy of F1-ATPase powered rotation. Proc. Natl. Acad. Sci. U.S.A. 111, 3715–3720 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Okazaki K., Hummer G., Elasticity, friction, and pathway of γ-subunit rotation in F0F1-ATP synthase. Proc. Natl. Acad. Sci. U.S.A. 112, 10720–10725 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Martin J. L., Ishmukhametov R., Spetzler D., Hornung T., Frasch W. D., Elastic coupling power stroke mechanism of the F1-ATPase molecular motor. Proc. Natl. Acad. Sci. U.S.A. 115, 5750–5755 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Shimabukuro K., et al. , Catalysis and rotation of F1 motor: Cleavage of ATP at the catalytic site occurs in 1 ms before 40° substep rotation. Proc. Natl. Acad. Sci. U.S.A. 100, 14731–14736 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nishizaka T., et al. , Chemomechanical coupling in F1-ATPase revealed by simultaneous observation of nucleotide kinetics and rotation. Nat. Struct. Mol. Biol. 11, 142–148 (2004). [DOI] [PubMed] [Google Scholar]
- 22.Okazaki K., Hummer G., Phosphate release coupled to rotary motion of F1-ATPase. Proc. Natl. Acad. Sci. U.S.A. 110, 16468–16473 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nam K., Pu J., Karplus M., Trapping the ATP binding state leads to a detailed understanding of the F1-ATPase mechanism. Proc. Natl. Acad. Sci. U.S.A. 111, 17851–17856 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mukherjee S., Bora R. P., Warshel A., Torque, chemistry and efficiency in molecular motors: A study of the rotary-chemical coupling in F1-ATPase. Q. Rev. Biophys. 48, 395–403 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Masaike T., Koyama-Horibe F., Oiwa K., Yoshida M., Nishizaka T., Cooperative three-step motions in catalytic subunits of F1-ATPase correlate with 80° and 40° substep rotations. Nat. Struct. Mol. Biol. 15, 1326–1333 (2008). [DOI] [PubMed] [Google Scholar]
- 26.Sugawa M., et al. , F1-ATPase conformational cycle from simultaneous single-molecule FRET and rotation measurements. Proc. Natl. Acad. Sci. U.S.A. 113, E2916–E2924 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Czub J., Wieczór M., Prokopowicz B., Grubmüller H., Mechanochemical energy transduction during the main rotary step in the synthesis cycle of F1-ATPase. J. Am. Chem. Soc. 139, 4025–4034 (2017). [DOI] [PubMed] [Google Scholar]
- 28.Suzuki T., Tanaka K., Wakabayashi C., Saita E., Yoshida M., Chemomechanical coupling of human mitochondrial F1-ATPase motor. Nat. Chem. Biol. 10, 930–936 (2014). [DOI] [PubMed] [Google Scholar]
- 29.Henry E. R., Eaton W. A., Hochstrasser R. M., Molecular dynamics simulations of cooling in laser-excited heme proteins. Proc. Natl. Acad. Sci. U.S.A. 83, 8982–8986 (1986). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Weber J., Senior A. E., Catalytic mechanism of F1-ATPase. Biochim. Biophys. Acta 1319, 19–58 (1997). [DOI] [PubMed] [Google Scholar]
- 31.Weber J., Senior A. E., ATP synthase: What we know about ATP hydrolysis and what we do not know about ATP synthesis. Biochim. Biophys. Acta 1458, 300–309 (2000). [DOI] [PubMed] [Google Scholar]
- 32.Nakamoto R. K., Ketchum C. J., Kuo P. H., Peskova Y. B., Al-Shawi M. K., Molecular mechanisms of rotational catalysis in the F0F1 ATP synthase. Biochim. Biophys. Acta 1458, 289–299 (2000). [DOI] [PubMed] [Google Scholar]
- 33.Volkán-Kacsó S., Marcus R. A., Theory for rates, equilibrium constants, and Brønsted slopes in F1-ATPase single molecule imaging experiments. Proc. Natl. Acad. Sci. U.S.A. 112, 14230–14235 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Volkán-Kacsó S., Marcus R. A., Theory of single-molecule controlled rotation experiments, predictions, tests, and comparison with stalling experiments in F1-ATPase. Proc. Natl. Acad. Sci. U.S.A. 113, 12029–12034 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Marcus R. A., Sutin N., Electron transfers in chemistry and biology. Biochim. Biophys. Acta 811, 265–322 (1985). [Google Scholar]
- 36.Watanabe R., et al. , Mechanical modulation of catalytic power on F1-ATPase. Nat. Chem. Biol. 8, 86–92 (2012). [DOI] [PubMed] [Google Scholar]
- 37.Adachi K., Oiwa K., Yoshida M., Nishizaka T., Kinosita K. Jr, Controlled rotation of the F1-ATPase reveals differential and continuous binding changes for ATP synthesis. Nat. Commun. 3, 1022 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gao Y. Q., Yang W., Karplus M., A structure-based model for the synthesis and hydrolysis of ATP by F1-ATPase. Cell 123, 195–205 (2005). [DOI] [PubMed] [Google Scholar]
- 39.Kashket E. R., Stoichiometry of the H+-ATPase of growing and resting, aerobic Escherichia coli. Biochemistry 21, 5534–5538 (1982). [DOI] [PubMed] [Google Scholar]
- 40.Okazaki K., Takada S., Structural comparison of F1-ATPase: Interplay among enzyme structures, catalysis, and rotations. Structure 19, 588–598 (2011). [DOI] [PubMed] [Google Scholar]
- 41.Mukherjee S., Warshel A., Electrostatic origin of the mechanochemical rotary mechanism and the catalytic dwell of F1-ATPase. Proc. Natl. Acad. Sci. U.S.A. 108, 20550–20555 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Astumian R. D., Mukherjee S., Warshel A., The physics and physical chemistry of molecular machines. ChemPhysChem 17, 1719–1741 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hirono-Hara Y., et al. , Pause and rotation of F1-ATPase during catalysis. Proc. Natl. Acad. Sci. U.S.A. 98, 13649–13654 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Rees D. M., Montgomery M. G., Leslie A. G. W., Walker J. E., Structural evidence of a new catalytic intermediate in the pathway of ATP hydrolysis by F1-ATPase from bovine heart mitochondria. Proc. Natl. Acad. Sci. U.S.A. 109, 11139–11143 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.O’Neal C. C., Boyer P. D., Assessment of the rate of bound substrate interconversion and of ATP acceleration of product release during catalysis by mitochondrial adenosine triphosphatase. J. Biol. Chem. 259, 5761–5767 (1984). [PubMed] [Google Scholar]
- 46.Wang H., Oster G., Energy transduction in the F1 motor of ATP synthase. Nature 396, 279–282 (1998). [DOI] [PubMed] [Google Scholar]
- 47.Sielaff H., et al. , Domain compliance and elastic power transmission in rotary F0F1-ATPase. Proc. Natl. Acad. Sci. U.S.A. 105, 17760–17765 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Czub J., Grubmüller H., Torsional elasticity and energetics of F1-ATPase. Proc. Natl. Acad. Sci. U.S.A. 108, 7408–7413 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wächter A., et al. , Two rotary motors in F-ATP synthase are elastically coupled by a flexible rotor and a stiff stator stalk. Proc. Natl. Acad. Sci. U.S.A. 108, 3924–3929 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Böckmann R. A., Grubmüller H., Nanoseconds molecular dynamics simulation of primary mechanical energy transfer steps in F1-ATP synthase. Nat. Struct. Biol. 9, 198–202 (2002). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.