Plastic Deformation and Fragmentation of Strained Actin Filaments

Abstract

The assembly of actin filaments and filament networks generate forces that drive cell and vesicle movement. These structures and the comprising actin filaments must be mechanically stable to sustain these forces and maintain their structural integrity. Filaments in these dynamic structures must also be disassembled to recycle and replenish the pool of actin monomers available for polymerization. Actin-severing proteins such as cofilin and contractile myosin motor proteins fragment these nominally stable structures. We developed a mesoscopic-length-scale actin filament model to investigate force-induced filament fragmentation. We show that fragmentation in our model occurs at curvatures similar to previous measurements of fragmentation within (cofil)actin and actin-cofilactin boundaries. Boundaries between bare and cofilin-decorated segments are brittle and fragment at small bending and twisting deformations. Extending filaments disperses strain uniformly over subunit interfaces, and filaments fragment with no detectable partial rupture or plastic deformation. In contrast, bending or twisting filaments imposes nonuniform interface strain and leads to partial interface rupture, accelerating filament fragmentation. As a result, the rupture force under compressive loads is an order of magnitude lower than under tensile loads. Partial interface rupture may be a primary mechanism of accelerating actin filament fragmentation by other actin-destabilizing proteins.

Significance

Computational models have been useful for describing actin filament fragmentation, but these simulations require compromises between accuracy and speed. Here, we develop a coarse-grained actin filament model that captures spatially localized strain within protein interfaces while allowing simulated deformations of biologically relevant filament lengths. We show the limits of elasticity in describing actin filaments as a continuum material, and we show the importance of plastic deformations in bent filaments. Although we have limited our scope to the effects of cofilin in this study, one can use the approach and methods described to gain a more accurate understanding of other force-accelerated protein rupture processes or to improve existing continuum-mechanical models for actin networks.

Introduction

When actin polymerizes, it can generate forces to move cell structures and boundaries, e.g., at the leading edge of a migrating cell (1, 2, 3). Filaments must be mechanically stable and resist fragmentation to generate and sustain the forces that drive movement, but they must also be capable of continuous remodeling. Various families of regulatory proteins that fragment actin filaments (e.g., severin, Inf2, gelsolin, twinfilin, and ADF-cofilin (4, 5, 6, 7, 8, 9)) act to accelerate this process by increasing the concentration of free filament ends (3). Contractile proteins can act synergistically with actin-severing proteins to accelerate network turnover (10, 11). Fragmentation is necessary for the steady-state actin dynamics found in biology (12).

Members of the ADF-cofilin family of severing proteins accelerate filament rupture (13). Cofilin changes the average helical pitch of actin filaments and renders them more compliant in bending and twisting (14, 15, 16). Cofilin binding is cooperative, and clusters of bound cofilin form along filaments (6). Severing occurs at or near the junctions between bare and cofilin-decorated regions (i.e., boundaries), where there is a change in filament structure and mechanical properties (17, 18, 19, 20). The cofilin N-terminus plays a critical role in binding, alteration of filament mechanics, and fragmentation (21).

Computational and mathematical studies of bare and cofilin-decorated actin (cofilactin) filament fragmentation span broad force regimes and length- and timescales and have been valuable for understanding filament dynamics, mechanics, stability, and fragmentation by regulatory proteins (22, 23, 24). Molecular dynamics (MD) simulations of actin and cofilactin filaments explain why cofilin binding alters filament bending and twisting mechanics (25, 26, 27, 28, 29) but are restricted to relatively short filaments and timescales that do not allow for the application of forces of a physiologically relevant magnitude (30). Continuum mechanics treatments allow the simulation of (relatively) large-scale filament deformations of long filaments (multiple helical pitches). These simulations show that heterogenous filament bending mechanics localizes filament strain energy and accelerates boundary severing (17). However, continuum modeling provides little molecular insight into the process.

Mesoscopic filament modeling fills the gap between MD and continuum mechanics. This scale of simulation has uncovered twist-bend coupling in actin filaments and described how strain distributes along the length of actin and cofilactin filaments (31, 32). The latter study’s underlying predictions of how strain affects filament severing presupposes a two-state system (fragmented and intact). However, this is unlikely to be true for a filament of appreciable width, for which strain distributes unevenly over the filament cross section. The nonuniform strain suggests filaments are likely to fragment in multiple, distinguishable phases, as opposed to the simultaneous rupture of all protein-protein interfaces comprising the filament cross section. Accordingly, the pathway of strained filament fragmentation remains an open question.

Here, we develop a model to show how deformation affects the spatial distribution of strain across interfaces. We show that partial interface rupture and remodeling is a necessary precursor to complete fragmentation of bent and twisted (but not extended) bare and fully cofilin-decorated filaments. Actin-cofilactin boundaries are brittle and fragment at small deformations and without partial interface rupture. Comparing the effects of deformation on fragmentation to the available experimental data suggests that high filament curvature destabilizes actin D-loop docking, which may kinetically favor localized cofilin binding (33). Partial interface rupture, resulting from the uneven application of load or other means (e.g., cofilin binding), may be a generally applicable mechanism for destabilizing otherwise stable macromolecule interfaces.

Materials and Methods

Details of mesoscopic model

The work presented here builds on our previous mesoscale filament modeling (32), which is implemented using the software MATLAB 2018b (The MathWorks, Natick, MA). Proteins are represented as rigid ellipsoids. Protein subunit size and filament geometry are measured from Protein Data Bank (PDB): 3J8I (actin) and 3J0S (cofilactin) (34, 35). Protein interface areas are estimated by the buried solvent-accessible surface area between adjacent molecules in the structural models. Filaments are 100 nm in length to balance between physiologically relevant lengths and computational simplicity. The boundary conditions for each type of deformation were chosen so that the result should apply for a small segment within a longer filament. The (minor) effects of this choice are explored further in Figs. S1–S3. The parameters used to generate the model are summarized in Table S1.

Protein interactions are approximated by a random placement of harmonic bonds at protein interfaces. Bonds for all interfaces are placed uniformly with identical area density (12 links/nm²). This choice of density had only minor effects on the results (Fig. S4). Because of the contour (roundness) of the modeled subunits, the initial bond lengths differ. Individual bonds resist extension and compression but are free to bend or rotate axially. The overall stiffness of each protein-protein interface is measured by MD model parameters, as previously described (see Supporting Materials and Methods; (31, 32)). The stiffness of each bond (S_bond) is equal to S_Int/N, where S_int is the total interface stiffness and N is the number of bonds within each interface. For filaments with cofilin, all interfaces of any actin molecule that is contacted by cofilin have cofilactin properties. In practice, this means the geometry and parameters of cofilactin extend two subunits into bare actin regions (i.e., the nearest neighbor on each strand) (Video S1. Bare Actin Filament Compression, Video S3. Actin-Cofilactin Boundary Filament Compression, Video S4. Bare Actin Filament Extension, Video S5. Actin-Cofilactin Boundary Filament Extension, Video S6. Bare Actin Filament Overtwisting, Video S7. Bare Actin Filament Undertwisting, Video S8. Actin-Cofilactin Boundary Filament Overtwisting, Video S9. Actin-Cofilactin Boundary Filament Undertwisting, Document S2. Article plus Supporting Material A). We decided to build our filament this way because of recent structural work that shows the twist of cofilactin propagates two to three subunits into the undecorated region of the filament (18).

Deformations are applied by applying translational (or rotational) movement to one or two subunits on one end of the filament while holding the other end. Compressive deformations are applied by fixing a subunit on one end in space and incrementally moving the subunit on the other filament end directly toward the first along the initial filament axis. Twisting simulations are applied similarly, but with applied rotation instead of translation (Fig. S6). Stretching simulations are performed by fixing two proteins on the end of the filament and moving two subunits on the other end directly away along the filament axis.

Deformations are applied in a series of short steps, allowing for equilibration between each step. Filament compression and extension were applied at speeds comparable to that of nonmuscle myosin II-B (60 and 10 nm s⁻¹, respectively (36, 37)). Filament rotation was applied at 720° s⁻¹, which is comparable to the rotation rate associated with incorporation of actin subunits to formin-capped filaments under unloaded conditions (37). Equilibration positions are calculated as previously described (32) and detailed in the Supporting Materials and Methods.

Determination of severing parameters and transition state energies

The filament fragmentation rate constant (k_frag) varies with experimental conditions (e.g., salt concentration). Here, we assume a k_frag value of 5 × 10⁻⁷ s⁻¹ subunit⁻¹, near the average measured for bare actin in vitro under physiological solution conditions (12, 38). We assume the fragmentation rate constant of cofilactin is comparable to that of bare actin (19).

Using the Arrhenius equation of transition state theory (Eq. 1),

$$k_{frag\left(native\right)}=\kappa \frac{k_{B}T}{h}{e}^{-\mathit{\Delta }{G}_{fil}^{‡}/k_{B}T},$$ (1)

we can relate k_frag to the activation energy for filament fragmentation (ΔG^‡_fil), Planck’s constant (h), Boltzmann’s constant (k_B), and the temperature (T). This equation, assuming the transmission coefficient (κ) is unity, yields a fragmentation activation energy of 44 k_BT. Note that ΔG^‡_fil reflects a kinetic barrier (activation energy) and thus is distinct from estimations of equilibrium binding energy (39).

We assume that the sum of interface activation energies (ΔG^‡_int) across the filament cross section (3 for actin and actin-cofilactin boundaries, 5 for cofilactin; Video S1. Bare Actin Filament Compression, Video S2. Cofilactin Filament Compression, Video S3. Actin-Cofilactin Boundary Filament Compression, Video S5. Actin-Cofilactin Boundary Filament Extension, Video S8. Actin-Cofilactin Boundary Filament Overtwisting, Video S9. Actin-Cofilactin Boundary Filament Undertwisting) is equal to the total filament fragmentation activation energy (Eq. 2),

$$\mathit{\Delta }{G}_{fil}^{‡}=\sum _i\mathit{\Delta }{G}_{int,i}^{‡},$$ (2)

and that interface activation energies (ΔG^‡_int) are proportional to their MD-derived stiffness (S_int), such that

$$\frac{\mathit{\Delta }{G}_{int,1}^{‡}}{\mathit{\Delta }{G}_{int,2}^{‡}}=\frac{S_{int,1}}{S_{int,2}}$$ (3)

for any given interfaces 1 and 2. The activation energy of each interface is divided equally among that interface’s N total bonds:

$$\mathit{\Delta }{G}_{int}^{‡}/N=\mathit{\Delta }{G}_{bond}^{‡}.$$ (4)

Implementation of filament fragmentation

In our model, protein-protein contacts and interfaces rupture at two different scales: individual harmonic bonds rupture when extended beyond a critical distance, and the filament spontaneously fragments (because of thermal energy), as dictated by the rate constant and subunit interface strain. For clarity, we refer to the breaking of individual harmonic bonds as “bond rupture” and the breaking of the filament as “filament fragmentation,” or just fragmentation. These two levels of fragmentation together tend to accelerate fragmentation. Bond rupture alone eventually leads to very flexible interfaces (because the few remaining bonds are free to rotate) that break very slowly when filaments and their interfaces are bent. Spontaneous fragmentation alone would be slightly slower, as well, because bond rupture lowers the activation energy of fragmentation more than elastic strain would on its own.

We have chosen to implement stochastic filament fragmentation (as opposed to a purely deterministic process) to avoid overanalyzing short-lived, low-stability intermediates. Filaments in vitro (or in vivo) are constantly experiencing thermally induced deformations. In this case, there exists an intrinsic rate constant for filament fragmentation of fluctuating filaments. If forces drive changes in filament shape, as we have modeled here, the strain energy within filament interfaces increases, and the stability of these interfaces is compromised. Interfaces that are highly strained or mostly ruptured will fragment rapidly. Because these strained interfaces have relatively short lifetimes, we implemented a stochastic fragmentation that limits our analysis to a subset of intermediates with partially ruptured interfaces. This approach allows us to estimate the extent of interface disruption required for fragmentation.

Individual interface bonds rupture when stretched to their critical bond distance R_bond (Table S1). The critical bond distance for a given interface, i.e., the distance to which all bonds of an interface must be stretched to reach the fragmentation transition state energy (ΔG^‡_int), is defined by Eq. 5 (following Hooke’s law):

$$R_{bond}=\sqrt{2\mathit{\Delta }{G}_{bond}^{‡}/S_{bond}}=\sqrt{2\frac{\mathit{\Delta }{G}_{bond}^{‡}\ast N}{S_{bond}\ast N}}=\sqrt{2\mathit{\Delta }{G}_{int}^{‡}/S_{int}},$$ (5)

where N is the number of bonds in an interface. Individual bonds only rupture when they are extended, not compressed. Ruptured bonds retain a small resistivity (0.05% of original stiffness) to assist with energy minimization in subsequent deformation steps.

The total strain energy within each interface (E_{strain, int}) is the sum of all elastic (E_{elastic, bond}) and ruptured (E_{rupture, bond}) bond energies across each interface:

$$E_{strain,int}=\sum _j{E}_{elastic,bond,j}+\sum _j{E}_{rupture,bond,j}.$$ (6)

We assume that the elastic strain energy of the interface (E_{strain, int}) destabilizes the ground state and increases the filament fragmentation rate constant by lowering the transition state energy barrier (Fig. 1). The elastic energy of any given bond (E_{elastic, bond}) is reduced to 0 upon rupture, and its initial resting energy (ΔG^‡_bond; Eq. 4), assumed to destabilize the ground state because contacts are lost, is expressed as E_{rupture, bond} to indicate that it has been ruptured. An alternative description of this process is that the ruptured bonds do not contribute to the strain energy but instead lower the transition state energy barrier. Both approaches yield identical results because we monitor energy changes.

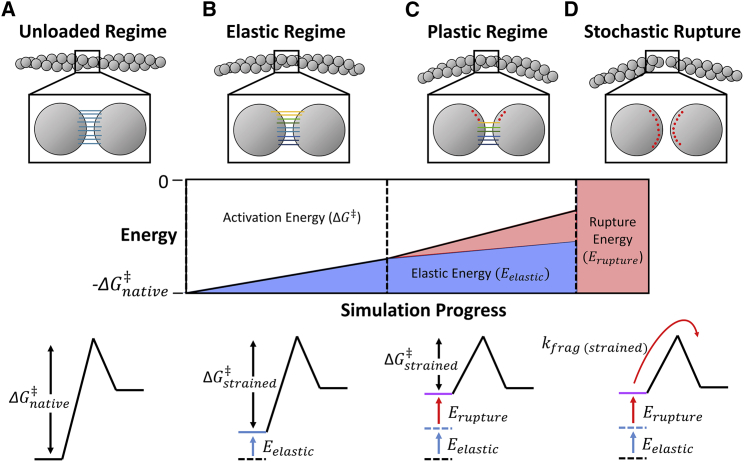
Figure 1.

Schematic of compressed filament fragmentation. (A) The interface of a filament under no external load. (B) The elastic regime, in which bonds within interfaces are strained, decreasing the activation energy of fragmentation (ΔG^‡). (C) The plastic regime, in which bonds rupture and further decrease the activation energy. (D) The stochastic fragmentation, which occurs at the rate k_frag. Fragmentation can occur at any point during the simulation, but the rate constant increases with reductions in ΔG^‡, according to Eq. 8. The energies shown in the bottom two rows refer to the total energy across the filament cross section. These cross-sectional energies are used to calculate the rate of filament fragmentation at each time step (Eq. 9). The actual values shown in the energy diagrams here are illustrative and not equal to the actual simulation values. To see this figure in color, go online.

The strain energy across each filament cross section (shown in Video S1. Bare Actin Filament Compression, Video S3. Actin-Cofilactin Boundary Filament Compression, Video S4. Bare Actin Filament Extension, Video S5. Actin-Cofilactin Boundary Filament Extension, Video S6. Bare Actin Filament Overtwisting, Video S7. Bare Actin Filament Undertwisting, Video S8. Actin-Cofilactin Boundary Filament Overtwisting, Video S9. Actin-Cofilactin Boundary Filament Undertwisting, Document S2. Article plus Supporting Material A) is the sum of the comprising interface strain energies:

$$E_{strain,fil}=\sum _i{E}_{strain,int,i}.$$ (7)

Filament fragmentation does not require that E_strain,fil reach the level of ΔG^‡_fil for filament fragmentation. Fragmentation possibly occurs for each interface after every simulation step, according to Kramer’s theory:

$$k_{frag\left(strained\right)}=\frac{k_{B}T}{h}{e}^{-\mathit{\Delta }{G}_{fil}^{‡}/k_{B}T+E_{strain,fil}/k_{B}T}=k_{frag\left(native\right)}{e}^{E_{strain,fil}/k_{B}T}.$$ (8)

We convert this rate to a probability of filament fragmentation after each step (Eq. 9), according to the cumulative distribution function of an exponential process:

$$P_{filfragment}=1-e^{-k_{frag\left(strained\right)}\ast \mathit{\Delta }t}.$$ (9)

After each small deformation, we check every filament-severing interface for fragmentation according to the strain energy (E_{strain, fil}) and the corresponding fragmentation rate constant. The time step Δt is determined by the rate of deformation (described above) and the distance of that deformation step.

Summary of simulation flow

Simulations are initiated by building a helical filament according to an input filament length and cofilin distribution. After an initial equilibration of the filament in its resting position, a small translation or rotation was applied to a subset of proteins (Fig. S6, blue subunits), after which the position and rotation of all other subunits (Fig. S6, gray subunits) were iteratively adjusted until force-balance equilibrium was achieved for all proteins in the filament. Bond rupture was assessed after each iteration (Eq. 5). Each filament interface was checked for fragmentation according to the probability defined by Eqs. 8 and 9. If fragmentation did not occur, the simulation resumed with additional translation and/or rotation of boundary subunits. If the filament fragmented, the simulation was concluded.

Results

Fragmentation of compressed or bent filaments

We simulated the compressive fragmentation of bare actin, cofilactin, and boundary-containing filaments. Filaments (100 nm) with freely rotating ends were compressed (Fig. S6). During these simulations, the filament ends are brought closer together until filament fragmentation occurs (at which point the simulation is stopped). Cofilin occupancy affects the magnitude and location of strain (Fig. 2) and thus the deformation at which rupture occurs.

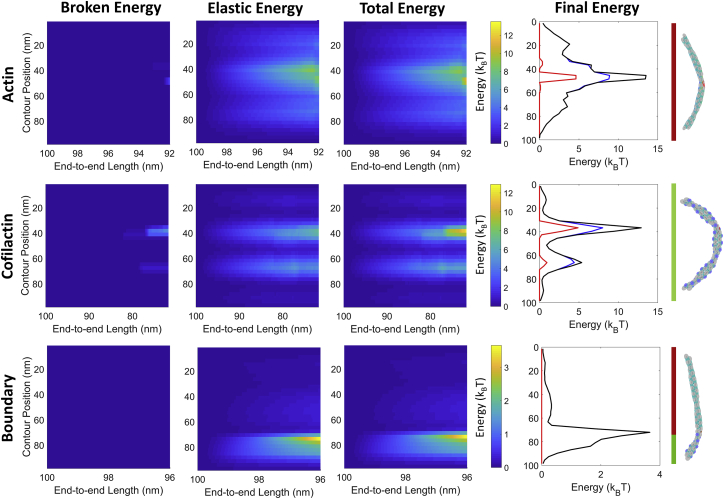
Figure 2.

Filament energy (ruptured, elastic, and total) of compressed filaments. 100 nm filaments are compressed with freely rotating ends. The first row shows a simulation of bare actin; the second, cofilactin; and the third, a boundary. Lines on the right edge of the figure show the location of actin (red) and cofilactin (green) for each distribution. Final energy corresponds to the energy immediately before rupture (and the rightmost column of the kymographs). E_ruptured,fil, red; E_elastic,fil, blue; E_strain,fil, black. These traces show a single rupture event. Note that the x axis and energies for each row are a different scale. To see this figure in color, go online.

At low curvature, elastic energy accumulates primarily in longitudinal (long-axis) actin-actin interfaces (32). Further compression leads to the partial interface rupture of highly strained areas of the filament, again, primarily in longitudinal bonds (Table S2). The periodic elastic energy along the filament seen in actin and cofilactin filaments corresponds to the half-helical pitch of actin or cofilactin and can be explained by changes of the bending moment for different helical orientations (32). The strain-energy profile for these simulations differs slightly from our previous work because of differences in filament length and boundary conditions (freely rotating instead of clamped ends) that are meant to mimic a bent region within a longer filament.

Compression of bare actin filaments unevenly strains longitudinal interfaces, leading to partial interface rupture before complete fragmentation (red bonds/bars Fig. 3, A–C; Video S1). As the bonds at the “edges” of longitudinal interfaces begin to rupture, some of the remaining bonds in that interface compensate by stretching to the level of the recently ruptured bonds. The resulting weakness in the longitudinal interfaces after bond rupture (due to loss of stiffness and interface area) further localizes strain energy at those sites, akin to strain localization at boundaries (17, 32). This accelerates energy accumulation after the initial onset of bond rupture. In all cases of bare actin fragmentation, a significant fraction of the interface is ruptured before complete fragmentation occurs (Table S3).

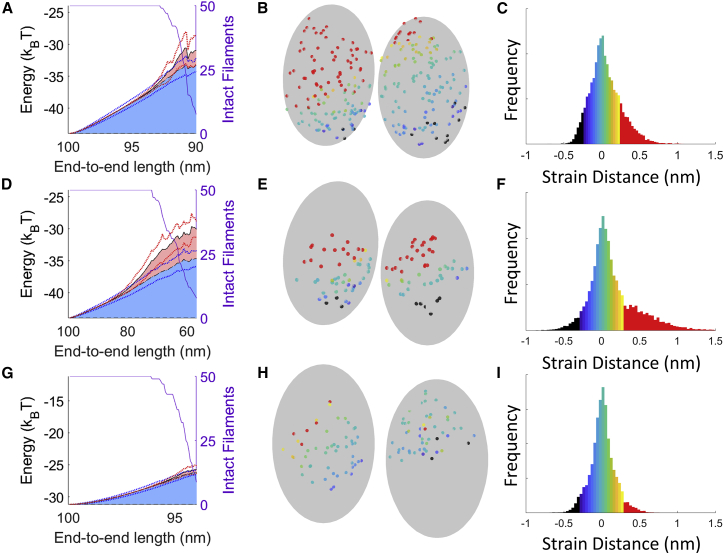
Figure 3.

Strained interfaces of compressed filaments immediately before filament fragmentation. (A) Elastic (blue) and ruptured bond (red) energy of the eventually fragmented interface within a compressed actin filament with freely rotating ends are shown. Blue and red shaded regions correspond to the average elastic energy and ruptured energy of interface bonds, respectively. Blue and red dotted lines show the SD of elastic and total energy. 50 filaments are simulated, but at larger deformations (smaller end-to-end lengths), only a subset of the overall population still exists (purple line). The energy shown is relative to the activation energy of fragmentation (where 0 k_BT is the energy of rupture). (B) A snapshot of the longitudinal interfaces immediately before fragmentation is shown. Red dots correspond to ruptured bonds. (C) Histogram of the strain distance for all 50 simulations. The colors shown in the histogram follow the same color scale as in (B). Stretched bonds are positive, and compressed bonds are negative (i.e., green bonds are at their resting length, yellow bonds are stretched, and blue bonds are compressed). Red bars show ruptured bonds. (D–F) The same as above is shown for cofilactin. Cofilin molecules and other interfaces are present but not drawn for ease of viewing. (G–I) The same as above is shown for boundaries. Note that the scale for the x axes in (A), (D), and (G) differ. The offset for the y axes in these panels differs, but the scale is the same. To see this figure in color, go online.

Like bare actin filaments, compressed cofilactin filaments most often fragment after significant partial interface rupture (red bonds/bars Fig. 3, D–F; Table S3; Video S2). The greater flexibility of cofilactin means the strain energy for a given filament deformation is lower than an equally deformed actin filament. This leads to more gradual fragmentation, both in terms of the amount of deformation required for severing (i.e., a higher critical fragmentation angle) and the length of time the interfaces across the fragmentation interface are partially ruptured.

Compressive loads fragment boundaries before any significant bond rupture occurs (Fig. 3, G–I; Video S3), in contrast to bare or fully decorated filaments. For these simulations, the boundary is placed off-center to maximize curvature (and severing) at the boundary (because placing it in the center yields maximal curvature within cofilactin), but a filament with a centrally placed boundary will still preferentially fragment at the boundary (Fig. S7). The activation energy of fragmentation is considerably lower at boundaries because the longitudinal actin-actin contacts are weaker (like cofilactin), but they lack the stabilizing cofilin-actin contacts seen in fully decorated filaments (40). Consequently, few bonds rupture before complete filament fragmentation because a small increase in elastic strain energy at this site is sufficient to promote severing at small deflections. In other words, the boundaries are more brittle than bare or cofilactin filaments.

Fragmentation of extended and twisted filaments

We next studied the effect of extension on bare actin filaments (Video S4) and actin-cofilactin boundaries (Video S5). Filaments (100 nm) were stretched by fixing the positions of the molecules on one end of the filament and moving the other end away while not allowing rotation (Fig. S6). The strain energy across extended filaments is uniform, aside from a small spike in elastic strain energy at the boundary (Fig. S8). The rupture location is random for bare actin but always occurs at the boundary of partially decorated filaments. Very few, if any, individual links rupture before fragmentation because the bonds are all evenly strained under filament extension (Fig. 4; Table S3).

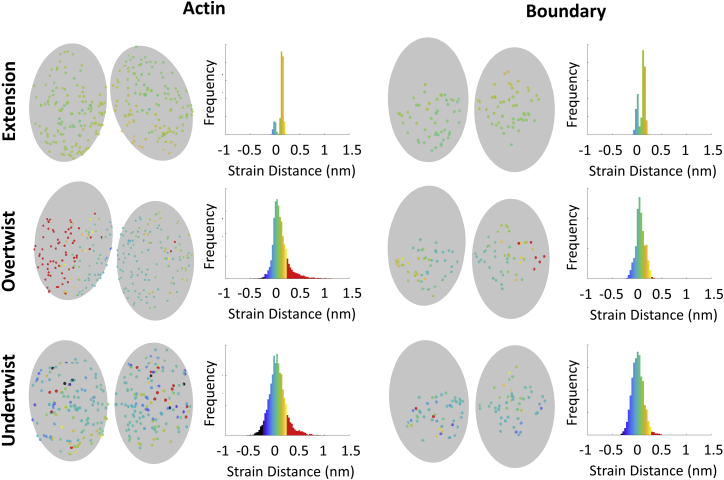
Figure 4.

Strain distribution of extended and twisted filaments (rows) within longitudinal interfaces of the rupture cross section. The histograms show the distribution of strain distance for all bonds in the fragmentation interfaces of actin and actin-cofilactin boundaries (columns, 20 simulations for each). The colors on the histogram correspond to the strain distances for the longitudinal interfaces shown to the left of each histogram (one example simulation). Red bonds are ruptured, and histogram bars depict ruptured bonds. To see this figure in color, go online.

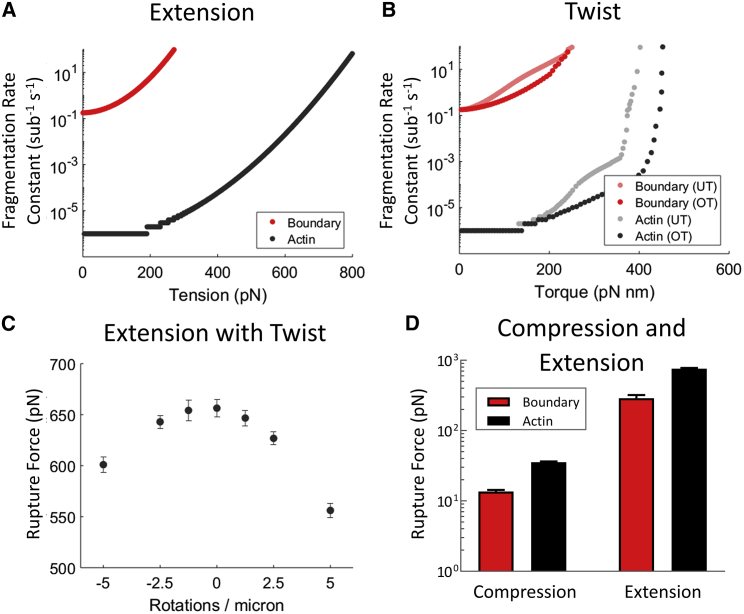
Actin-cofilactin boundaries fragment more rapidly than bare actin and are more sensitive to tension (Fig. 5 A). Fragmentation rates were calculated for a center (or boundary) interface during twist (Eq. 8). Low tension (less than 100 pN) has minor effects on fragmentation (less than 10-fold), as seen in wet-lab experiments (41). This holds for both bare actin interfaces and boundary interfaces, though boundaries are more affected by tension above this threshold.

Figure 5.

Comparison of rupture properties between actin and actin-cofilactin boundaries. (A) Individual simulation trace of the severing rate constant of a bare actin filament and filament boundary interface under tension (without individual bond rupture) is shown. (B) Individual simulation trace of the severing rate constant of an interface within a twisted bare actin filament and at a filament boundary, allowing individual bond rupture, is shown. Data are shown for both undertwisted (UT) and overtwisted (OT) filaments. (C) The effect of twist on extensional rupture force is shown. Positive values refer to overtwist. The rupture force is defined as the force at which the rupture rate constant is 0.1 s⁻¹. Uncertainty bars show the SD of extensional rupture force for each twist (N = 10). (D) Compression and extensional rupture forces are shown. Uncertainty bars show the SD of rupture force for compression (N = 50) and extension (N = 20). Rupture forces are the maximal force before rupture for deformations applied as outlined in the main text. Note that the y axis is on a logarithmic scale. To see this figure in color, go online.

We then twisted 100 nm filaments by fixing the positions of both ends and rotating the two actin molecules on each end (Fig. S6). The strain energy across twisted filaments is uniform, save for a small spike in elastic strain energy at boundaries (Fig. S9). The fragmentation site for twisted filaments is random in bare actin (Videos S6 and S7) but consistently occurs at an actin-cofilactin boundary, if present (Videos S8 and S9).

Boundaries are also more susceptible to fragmentation by torsion than bare actin, as when under extensional stress. Undertwisting (i.e., left-handed rotation against actin’s natural right-handed twist) filaments promote fragmentation more than overtwisting (right-handed rotation) by the same number of turns for both bare actin and boundaries (Fig. 5 B). Fragmentation rate constants were calculated for a center (or boundary) interface during extension using Eq. 8. Small torques are predicted to have little effect on bare actin or boundaries.

We also evaluated the effects of simultaneous twist and extension (Fig. 5 C). Overtwisting has a slightly higher effect on filament stability under tension (∼15% decrease vs. ∼8% for undertwisting 5 rotations/μm). Our model suggests that bare-actin-filament stability under tensile loads is only modestly affected by twist, contrary to previous reports that report a large effect from smaller twists (42). The reasons for the discrepancy between the results from this study and those presented here are not clear. However, such a high sensitivity to twist is surprising given the actin filament torsional stiffness, which the authors state is 8 × 10⁻²⁶ Nm². A twist of one rotation (2π) on a 10 μm filament (as used in the study) adds ∼1.6 × 10⁻¹⁹ J, or ∼38 k_BT (at 298 K), of energy throughout the entire filament ($E=\left(1/2\right)\left(C/L\right){\theta }^2$, where C is the torsional rigidity, L is the length of the filament, and θ is the twist in radians). If this energy distributes uniformly among the >7000 filament interfaces (longitudinal and lateral) in a 10 μm filament, each would experience <0.01 k_BT of strain energy from this twist, which is much smaller than thermal energy. Additionally, this would only add an additional 0.1° twist per subunit rise, far less than the estimated 2.9° deviation per subunit for even straightened (and less heterogenous) filaments visualized by cryo-electron microscopy (34).

Critical bending angle of filament fragmentation

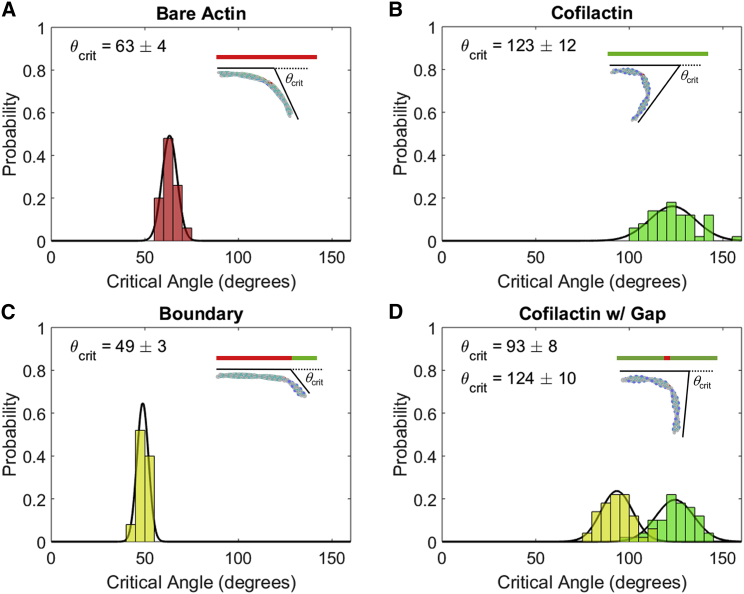
We measured the critical angle of fragmentation for compressed filaments to compare our simulations to previous experiments (19). In these simulations, the critical angle was measured by measuring the angle between the ends of a compressed 100 nm filament immediately before filament fragmentation (Fig. 6). The relationship between critical angles is similar to that previously measured (θ_{crit,cofilactin} > θ_crit,actin > θ_{crit,boundary}), though the curvature required for rupture is ∼50–100% greater for boundaries and cofilactin (Fig. 6). As previously discussed (19), cofilactin filaments are more compliant in bending than bare actin and thus require larger bending deformations for an equal amount of strain energy to accumulate and accelerate fragmentation.

Figure 6.

Critical severing angle distributions of actin and cofilactin filaments. Histograms are shown of the angle between the ends of 100 nm filaments of (A) bare, (B) fully decorated, (C) 25% decorated filaments, and (D) fully decorated filaments with a single missing cofilin. Colors in (D) show severing events at the cofilin gap (yellow) and within cofilactin (green). Insets are illustrative of cofilin distribution (green) relative to bare actin (red). Insets also show an example filament at the critical angle (at the gap for D). Each distribution is sampled from 50 independent simulations (100 for cofilactin with gap), and critical angles are calculated by a fit to a normal distribution (black lines). To see this figure in color, go online.

Discussion

Filament fragmentation angles

Measuring the critical fragmentation angle gives us insight into the bimodal distribution of cofilactin rupture angles found in the experiments by McCullough et al. (19). Experiments performed at saturating cofilin concentrations are not truly saturating but are instead at 90–95% occupancy (6). This leaves small gaps in the cofilin distribution along the filament undetectable by fluorescence microscopy. We found that one missing cofilin molecule in the center of an otherwise decorated filament recovered a bimodal distribution (Fig. 6 D). The cofilin gap was the most frequent point of fragmentation and involved in nearly 50% of the total fragmentation events (yellow). The other 50% occurred somewhere else on the filament, most often near the center, similar to cofilactin (green). The relative shift between these peaks is similar in magnitude to the shift between critical fragmentation angles of actin and boundaries. This suggests that the gap resembles a boundary, but the higher flexibility of cofilactin means a larger overall deformation must be applied to reach a similar local strain and fragmentation rate. This effect was originally attributed to an alternate binding mode in which cofilactin adopts actin-like mechanical properties and thus severs at a similar angle to bare actin. Although this potential explanation cannot rule out the previous interpretation, it serves as an additional explanation for the observed behavior.

The difference in absolute angles may arise for multiple reasons. Cofilactin filaments may be slightly less stable than actin filaments (we assumed the rate constant of fragmentation was the same), which would lead to a higher critical fragmentation angle in our experiments. In addition, the distance over which the angle is measured for a given radius of curvature affects the value of the critical angle. This value is difficult to determine for optical microscopy, so the 100 nm used here should be considered a rough estimate. Lastly, the previously measured critical angle is for freely fluctuating filaments, meaning that the results are convoluted with the probability of reaching a given angle.

Actin-cofilactin boundaries are brittle and fragment at low bending angles

Strained filament boundaries fragment immediately adjacent to sites of cofilin clusters before significant interface rupture. The boundary is characterized by a brittleness that leads to quick rupture at a lower bending angle and less interface remodeling than either bare or fully cofilin-decorated actin filaments. This observation is not unexpected because the parameters used in constructing the model, which are based on experimental observations, indicate boundary interfaces fragment more rapidly (lower ΔG^‡) than fully decorated or bare actin interfaces (19, 20, 41, 43). Not predicted by model parameters, however, is that short-range propagation of cofilactin structural changes, just a single subunit on each strand, into bare actin (Video S1. Bare Actin Filament Compression, Video S3. Actin-Cofilactin Boundary Filament Compression, Video S4. Bare Actin Filament Extension, Video S5. Actin-Cofilactin Boundary Filament Extension, Video S6. Bare Actin Filament Overtwisting, Video S7. Bare Actin Filament Undertwisting, Video S8. Actin-Cofilactin Boundary Filament Overtwisting, Video S9. Actin-Cofilactin Boundary Filament Undertwisting, Document S2. Article plus Supporting Material A) is sufficient to capture the observed enhancement of fragmentation at bare and fully decorated boundaries. The loss of the D-loop interactions in actin adjacent to cofilin clusters is a likely contributor to boundary weakness, both in stiffness and stability (33, 44, 45). This is implemented in our model with the smaller longitudinal interface area and weaker spring stiffness in cofilactin. Although the interface energies of barbed- and pointed-end boundaries are identical in our model, the effect shown here may more closely resemble the weaker, pointed-end boundary (43).

Plastic deformations regime precedes fragmentation of compressed filaments

For small deformations, the interface is stressed elastically (elastic regime, Fig. 1 B). In this regime, we do not expect any large-scale structural rearrangements, although there may be a shift in the equilibrium between energetically similar configurations (e.g., the D-loop of an actin subunit docking and undocking with the adjacent subunit). For larger deformations, some regions of the protein interface are ruptured (plastic regime, Fig. 1 C). This is likely the point of irreversibility for network compression.

Partial interface rupture is also likely to occur because of thermal fluctuations even in the absence of external load, but the ruptured bonds would reform as the filament relaxes. Under constant load, as applied in this study, these filaments are not allowed to relax (i.e., “heal”).

High filament curvature partially disrupts long-axis actin subunit contacts and can potentially enhance cofilin binding kinetics

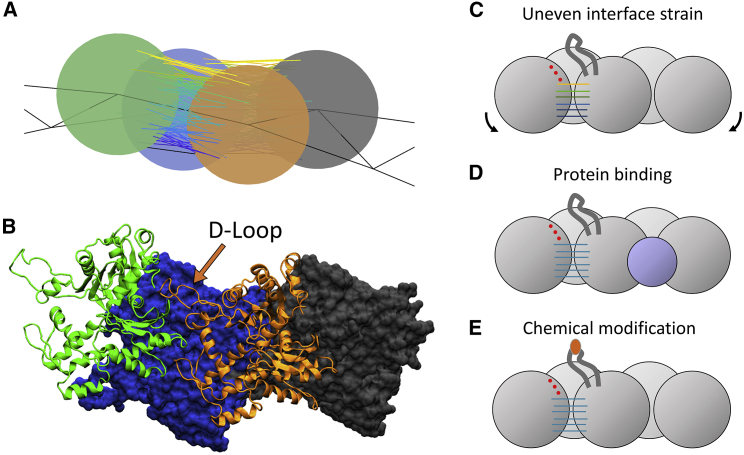
Our results show that bending filaments localizes strain both along the filament (because of the filament helicity) and within the interface because of the orientation of proteins in a given point along the helix. The two contributions combine to specifically enhance strain in a region that spatially corresponds to contacts between subdomain 1 and subdomain 2 of the adjacent filament subunit (Fig. 7, A and B). That is, these bonds are at the convex edge of the most strained filament regions (Fig. 2).

Figure 7.

Strain localization predicts the importance of the D-loop for bare-actin-filament bending rupture. (A) A snapshot is given of the most strained longitudinal interfaces of a compressed actin filament and (B) the corresponding structure of the actin filament (PDB: 2ZWH) oriented with the pointed end to the left. The highest strain in bent filaments is between subdomain 2 and subdomain 1 of the adjacent monomers. This region spatially corresponds to the location of the D-loop. Interface disruption can be caused by (C) uneven application of force on an interface; (D) protein (cofilin) binding, leading to a structural change; or (E) chemical modification of amino acids (as by MICAL). To see this figure in color, go online.

This localized strain likely destabilizes contacts in the D-loop region, shifting the equilibrium to more D-loop undocking even before bond rupture in this model (Fig. 3 D). Consequently, we predict that high curvature may accelerate cofilin association kinetics because of the linkage between cofilin binding and D-loop destabilization (29, 33, 44, 45). In contrast, filament tension uniformly strains actin-actin interfaces, so we do not predict that filament tension affects cofilin affinity, as reported for low tensile loads (41). Additionally, this observation provides a link between the observed bias for Arp2/3 binding on curved filaments and structural observations of the complex on actin filaments (46, 47).

Partial rupture of protein interfaces may be a general mechanism to disrupt stable protein-protein interactions

For any stable protein-protein interaction, uneven interface strain and partial bond rupture may be necessary to facilitate interface fragmentation at reasonable timescales and forces. This observation is exemplified by actin, for which the disruption of a portion of the interface is used to enhance fragmentation in multiple ways. As described above, filament compression strains the filament interface unevenly, which leads to partial interface rupture (Figs. 3 and 7 C). In contrast, tension strains the longitudinal interfaces uniformly, which effectively means the entire interface must be stretched nearly to the point of failure before fragmentation (Fig. 4). Because of the difference in how load is applied to interfaces, the extensional rupture force is over an order of magnitude higher than the force required to fragment compressed filaments (Fig. 5 D; Table S3; (10, 11, 23, 42)).

Proteins that sever actin filaments also act by weakening long-axis contacts. Cofilin is thought to accelerate fragmentation of actin filaments by disrupting D-loop contacts of a filament subunit with its long-axis neighbor, weakening the interface energy at actin-cofilactin boundaries (Fig. 7 D; (48)). Similarly, the actin-destabilizing enzyme MICAL acts by reversibly oxidizing methionine residues in the D-loop of F actin monomers to inhibit these contacts (Fig. 7 E; (45, 49, 50)). The similarities between these distinct mechanisms of fragmentation suggest that a similar partial rupture pathway may apply to other actin-related fragmentation events (e.g., forces on the Arp2/3 complex causing debranching) and that this theme is likely ubiquitous in biology for interactions that require large modulations of stability.

Author Contributions

A.C.S., J.-L.M., and E.M.D.L.C. conceived the project. A.C.S., J.-L.M., and E.M.D.L.C. designed the simulations. A.C.S. performed model simulations. G.M.H. performed MD simulations and analysis. A.C.S., G.M.H., G.A.V., J.-L.M., and E.M.D.L.C. contributed analytical tools. A.C.S., J.-L.M., and E.M.D.L.C. analyzed data. A.C.S. and E.M.D.L.C. wrote the article. G.M.H., G.A.V., and J.-L.M. edited the article.

Editor: Dimitrios Vavylonis.