A Polymer Physics Framework for the Entropy of Arbitrary Pseudoknots

Abstract

The accurate prediction of RNA secondary structure from primary sequence has had enormous impact on research from the past 40 years. Although many algorithms are available to make these predictions, the inclusion of non-nested loops, termed pseudoknots, still poses challenges arising from two main factors: 1) no physical model exists to estimate the loop entropies of complex intramolecular pseudoknots, and 2) their NP-complete enumeration has impeded their study. Here, we address both challenges. First, we develop a polymer physics model that can address arbitrarily complex pseudoknots using only two parameters corresponding to concrete physical quantities—over an order of magnitude fewer than the sparsest state-of-the-art phenomenological methods. Second, by coupling this model to exhaustive enumeration of the set of possible structures, we compute the entire free energy landscape of secondary structures resulting from a primary RNA sequence. We demonstrate that for RNA structures of ∼80 nucleotides, with minimal heuristics, the complete enumeration of possible secondary structures can be accomplished quickly despite the NP-complete nature of the problem. We further show that despite our loop entropy model’s parametric sparsity, it performs better than or on par with previously published methods in predicting both pseudoknotted and non-pseudoknotted structures on a benchmark data set of RNA structures of ≤80 nucleotides. We suggest ways in which the accuracy of the model can be further improved.

Significance

The functions and properties of RNA molecules are closely tied to the set of structures they can fold into and their free energies. However, complex structures termed pseudoknots are not well predicted by current tools despite their prevalence. Here, we describe a method to analytically calculate the entropies of arbitrarily complex pseudoknots using only two parameters corresponding to concrete physical quantities. This approach represents an order-of-magnitude reduction in parameters compared to even the sparsest state-of-the-art tools. We employ this method alongside an exhaustive enumeration of the set of possible structures to predict the entire free energy landscape of short RNA molecules, given their sequence. Finally, we show that despite its parametric sparsity, our algorithm outperforms current state-of-the-art methods in pseudoknot prediction.

Introduction

RNA molecules play physiological roles that extend far beyond translation. In human cells, most RNA molecules are not translated (1). Noncoding RNAs interact functionally with messenger RNA (2), DNA (3), and proteins (4) and can be as large as thousands of nucleotides (nts) (5, 6). However, a substantial fraction are <40 nts in length, including microRNAs and small interfering RNAs, which serve as regulators for the translation of messenger RNA (2, 7), and piwi-interacting RNAs, which form RNA-protein complexes to regulate the germlines of mammals (8). The in vitro evolution of RNA, especially through systematic evolution of ligands by exponential enrichment (9, 10, 11), has led to an explosion of applications for short RNA molecules because of their ability to tightly and specifically bind to a remarkable range of target ligands (12).

Overwhelmingly, the properties of short noncoding RNA molecules are tied to their structures (13, 14, 15). Such structures are formed because of the energetic favorability of bonds between complementary nts (primarily A to U, C to G, and the wobble pair G to U). However, these bonds impose an entropic cost. Therefore, the conformations most frequently adopted balance the energetic gain of maximal basepairing with the entropic cost of structural constraints. In equilibrium, the RNA adopts each possible structure with Boltzmann weighted probabilities.

Because of the relevance of RNA structure to function (16, 17), current research aims to predict the minimum free energy (MFE) structures given the sequence. Algorithms typically predict “secondary structure,” a list of the basepairings (18, 19). The early Pipas-McMahon RNA structure prediction algorithm sought to completely enumerate and evaluate the free energy of all possible secondary structures, thereby constructing the entire energy landscape (20). More recent algorithms have made progress in making similar enumerations less computationally intensive (21), the most successful of which are the TT2NE algorithm and its stochastic version, McGenus (22, 23). The complete landscape enumeration approach including all secondary structures has so far been limited to short (<30 nt) RNA molecules (24, 25), and the field has instead almost entirely been dominated by dynamic programming approaches (26, 27, 28, 29, 30). Such algorithms efficiently consider an enormous number of structures without explicitly generating them by iteratively finding the optimal structure for subsequences (18).

Despite the substantial success of dynamic programming, these algorithms have difficulty predicting RNA secondary structures that include pseudoknots (i.e., structural elements with at least two non-nested basepairs) (see Fig. S1 A for an example) that make up roughly 1.4% of basepairs (18) and are overrepresented in functionally important regions of RNA (31). Pseudoknots are disallowed from the most popular RNA structure prediction algorithms (32, 33) because of computational cost; indeed, enumerating all pseudoknotted structures a given RNA molecule can fold into has been shown to be NP-complete (34, 35, 36). Significant advances have been made with heuristics, which do not guarantee finding the MFE structure (23, 37, 38, 39, 40, 41, 42, 43), and by disallowing all but a limited class of pseudoknots (44, 45, 46, 47, 48, 49, 50, 51).

A further major challenge for predicting pseudoknotted structures is the relative lack of experimental data or physical models to estimate their entropies (52, 53). An important caveat is the simple “H-type” pseudoknot for which both experimental data (54, 55, 56, 57) and physical models (37, 50, 51, 58, 59, 60) are available. However, for more complex single-molecule pseudoknots, even those which can be enumerated by current dynamic programming algorithms (47), entropy estimates have been limited to phenomenological extensions of the non-pseudoknotted and H-type pseudoknot models (43, 44, 61), and few experimental studies are available (62). A recent strategy uses machine learning of large experimental data sets (50, 63); although these approaches can be useful, they come with the disadvantages of compounding possible experimental errors and often using an enormous number of parameters, which can impact generalizability. A sketch of a theoretical description of simple pseudoknot entropies based on polymer physics was developed by Isambert and Siggia (37, 60); however, their derivations have not been published. Given the relative lack of experimental data to validate current simple phenomenological approaches on complex pseudoknots, the lack of a physical model for such structures is a pressing concern.

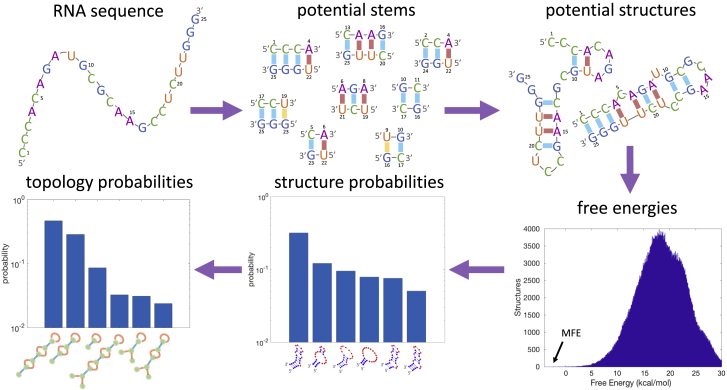
In this study, we develop a physical model to calculate the entropies of arbitrarily complex pseudoknots. We combine our model with complete enumeration of the secondary structure landscape, demonstrating that we can exactly solve for the probabilities of the RNA folding into each of the possible structures, including those with pseudoknots (Fig. 1). We demonstrate that this approach is feasible, not only for short RNA molecules of ∼25 nts that have been examined in previous studies (25) but even for biologically relevant RNA sequences of ∼80 nts in length.

Figure 1.

Schematic overview of the algorithm. Given an RNA sequence, the algorithm first enumerates all potential stems (sequences of consecutive basepairs) that can form. It then searches for all possible combinations of stems such that no nt is paired with more than one other, thus forming all possible secondary structures. For each structure, it calculates the free energy, which is comprised of a bond free energy term and a loop entropy term. In this work, we describe a polymer physics model to calculate this loop entropy term for arbitrarily complex pseudoknotted structures using only two parameters. The histogram of free energies for the sequence shown is plotted with an arrow pointing to the minimum free energy (MFE). Given the entire free energy landscape, the algorithm calculates the probability of any arbitrary secondary structure of forming in equilibrium. Finally, we coarse grain over similar structures described by the same topology, arriving at a probability distribution for every possible topology forming in equilibrium. To see this figure in color, go online.

Our approach combines a method based on the work of Isambert and Siggia with a, to our knowledge, novel graph-theoretical depiction of the RNA, allowing us to calculate the entropy of any arbitrary RNA structure. We demonstrate the generality of our formalism using the H-type and kissing hairpin pseudoknots as examples. Despite this generality, our loop entropy model uses only two parameters corresponding to experimentally derived physical quantities: the persistence length of single-stranded RNA, and the volume within which two RNA nts are considered bound. This represents an enormous parameter reduction compared to state-of-the-art algorithms; for example, the phenomenological Dirks-Pierce model has 11 parameters for the loop entropy of pseudoknots and ∼18 parameters for non-pseudoknotted loops (63).

We test our model predictions on molecules from the RNA STRAND (64), PseudoBase++ (65), and CompaRNA (66) databases and find good agreement with experimental results. We find that a significant heterogeneity in pseudoknot types exists even for sequences ≤80 nts in length, based on the polymer model representing their entropies. This heterogeneity is found to result in systematic errors of heuristic models’ estimates of the entropies of complex pseudoknots, motivating the generality of the entropic model derived here, which can correct such errors. Although we fit our entropy model only to data from non-pseudoknotted structures, we find that our model performs as well or better than previously published methods in predicting pseudoknots while performing on par with current methods in the prediction of non-pseudoknotted structures. Given the success of the model alongside its parametric sparsity, future work should build upon it to include further biological considerations neglected in the current treatment, and we give suggestions for where such improvements can be made.

Methods

Calculating free energies

The probability of the RNA sequence folding into a given equilibrium structure σ is given by the Boltzmann factor:

$$p\left(\sigma \right)=\text{exp}\left(-\beta G_{\sigma }\right)/Z,$$ (1)

where β = 1/k_BT (T is the temperature, and k_B is Boltzmann’s constant), and the partition function, Z, is defined such that the probability distribution is normalized: $\sum _{\sigma }p\left(\sigma \right)=1$. Here G_σ, the Gibbs free energy of structure σ, is a function of the enthalpy H_σ and entropy S_σ of the structure:

$$\mathit{\Delta }{G}^{\text{o}}=\mathit{\Delta }{H}^{\text{o}}-T\mathit{\Delta }{S}^{\text{o}},$$ (2)

where we drop the subscripts for notational convenience and introduce Δ to signify that free energies are measured with respect to the free chain. The superscripts implying standard conditions will be dropped from here on.

We separate the free energy calculation into two independent components: the free energy of consecutive basepairs (stems) and the free energy of loops. We make the simplifying assumption that ΔH is determined solely by the basepairs in the structure, ignoring higher order corrections, such that ΔH = ΔH_stems. For the entropy, we make no such assumption, and ΔS = ΔS_stems + ΔS_loops, where the entropy of stems represents the entropy lost by basepaired nts, and the entropy of loops represents the entropy lost by the constraints those basepairs place on the rest of the molecule. To calculate the terms ΔH_stems and ΔS_stems, we consider nearest-neighbor interactions among basepairs following the Nearest Neighbor Database (67), assuming (with few exceptions tabulated in the database) independence of the free energy contributions of each stem. See further details in Supporting Materials and Methods.

Calculating loop entropies

The goal of this and the next section is to build up a theoretical framework to estimate the loop entropies of arbitrarily complex RNA pseudoknots. This calculation has a significant effect on the prediction results. In fact, the magnitude of the loop entropy is on average equal to that of the overall free energy at physiological temperatures (see Fig. S7). This is as expected intuitively; the difficulty in RNA structure prediction lies precisely in predicting the balance between the energy gain from basepair constraints and the entropy gain from unpaired nts.

Because the following calculation is somewhat involved, we will begin by clarifying explicitly the nature of the loop entropy. A free RNA chain has a large number of conformations available to it, which we will call Ω. The loop entropy is the quantification of the reduction in conformations available to the RNA molecule upon introducing constraints on the structure, such as that certain nts are paired (68).

Ω depends on the length x of the RNA, such that Ω(x₁)Ω(x₂) = Ω(x₁ + x₂); in other words, we assume (for the free chain) independence of the various subsections of the RNA. This is in principle only true in the limit x₁, $x_2\gg b$, where b ≈ 2.4 nts is the Kuhn length of single-stranded RNA, and further neglects self-avoidance of the RNA molecule. Throughout, we will consider regions of single-stranded RNA long enough such that $x\gg b$ but short enough such that we assume self-avoidance has negligible probability. We discuss how to systematically consider shorter RNA loops in Supporting Materials and Methods and will make some notes regarding self-avoidance later in this section. We will also make the approximation that Ω is independent of sequence.

When a loop is formed in RNA, that loop constrains the number of conformations available to the RNA. For example, an RNA molecule that has its first nts bonded to its last only has available to it a fraction of the conformations available to the free chain—namely, all those that have the first and last nts close enough to bind. We are interested not in absolute values of the entropy S, but in ΔS, where the free chain is our reference state with $\mathit{\Delta }{S}_{\text{loops}}^{\text{free}}=0$. The entropy of a structured RNA of length x with ω_struct conformations available to it is given by ΔS_loops = k_Blog(ω_struct/Ω(x)) < 0, where we have written the difference of logs as the log of the ratio. We can simplify this formula by writing ω_struct = Ω(x) × p, where p is the fraction of conformations available to the free chain that are consistent with the structure being considered. We therefore have

$$\mathit{\Delta }{S}_{\text{loops}}=k_B\log p.$$ (3)

It is worth reiterating that the entropy of stems themselves was already taken into account in the term ΔS_stems and that ΔS_loops only measures the entropy lost because of loop closures (69). To avoid overcounting the entropy lost because of the constraints placed on basepaired nts, stems do not directly contribute to ΔS_loops. Therefore, a stem comprised of l basepairs (or 2l nts) should be treated—for the purposes of the ΔS_loops calculation—as if it has Ω(2l) available conformations; that it in reality has far fewer has already been quantitatively accounted for in the ΔS_stems term. Because of this, factors of Ω cancel out entirely in calculations of ΔS_loops.

We now turn to polymer physics to quantitatively describe how loop closure constraints affect p, the fraction of configurational space available to the molecule. We model a single-stranded region comprised of x unpaired nts as a random walk of (x + 1)/b steps, whereas before b is the Kuhn length of single-stranded RNA. We denote by $P_s\left(\overrightarrow{R}\right)d\overrightarrow{R}$ the probability of a random walk of length s to have end-to-end vector $\overrightarrow{R}$:

$$P_s\left(\overrightarrow{R}\right)={\left(\frac{3}{2\pi sb}\right)}^{3/2}\text{exp}\left(-\frac{3R^2}{2sb}\right).$$ (4)

We have assumed $s\gg b$ to arrive at the Gaussian formula above through the central limit theorem. The mean of the Gaussian is zero by symmetry. To find the variance we first consider a single step of length b in three dimensions, which has variance in the $\hat{i}$, $\hat{j}$, and $\hat{k}$ coordinates of b²/3 by symmetry. For a random walk of N = s/b steps, by independence of subsequent steps, the total variance is equal to Nb²/3 = sb/3, leading to Eq. 4.

Eq. 4 is accurate for non-self-avoiding random walks; self-avoiding random walks cannot be treated analytically in this way. However, for sufficiently short walks, the probability of self-interaction is low. As described in Supporting Materials and Methods, we can systematically consider higher order corrections to Eq. 4 while maintaining its Gaussian nature. Whereas the accuracy of the assumption $s\gg b$ does not always hold in the problems considered, we ultimately find very good agreement between results using Eq. 4 and experiment and that corrections to Eq. 4 as described in Supporting Materials and Methods, are negligible.

For a structure with n single-stranded regions of lengths s_i (1 ≤ i ≤ n), the fraction of conformations consistent with the structure is given by the following:

$$p=\int \prod _i{P}_{s_i}\left(\overrightarrow{R_i}\right)d\overrightarrow{R_i},$$ (5)

where $\overrightarrow{R_i}$ is the end-to-end distance vector of the i^th single-stranded region, and the primed integral is taken only over those $\overrightarrow{R_i}$ consistent with the overall structure. We will describe how to address these integrals via a Feynman diagram-like approach in the next section.

To demonstrate how Eqs. 3, 4, and 5 are applied, we first consider the simple hairpin loop. We will call its entropy ΔS_closed-net-0, neglecting the subscript of “loops” from here on. The notation follows (37, 60), and the subscript references the number of stems enclosed by the loop (zero in this case; see Fig. S2 for other examples). Following Jacobson and Stockmayer (70), we allow that basepairing can occur as long as the two nts are within a small volume v_s of one another. We assume that the bond length r_s is small enough that for all $\left|\overrightarrow{R}\right|\le r_s$, $P_s\left(\overrightarrow{R}\right)\approx P_s\left(\overrightarrow{0}\right)$. Therefore, $p=v_s{P}_s\left(\overrightarrow{0}\right)$, and Eqs. 3, 4, and 5 yield

$$\mathit{\Delta }{S}_{\text{closed}-\text{net}-0}=k_B\left[\text{log}\left(v_s\right)+\frac{3}{2}\text{log}\left(\frac{3}{2\pi sb}\right)\right].$$ (6)

We emphasize that within our model, this formula is applicable to hairpin loops, bulge loops, internal loops, and multiloops. We discuss in a later section how our model can be extended to break this equivalency.

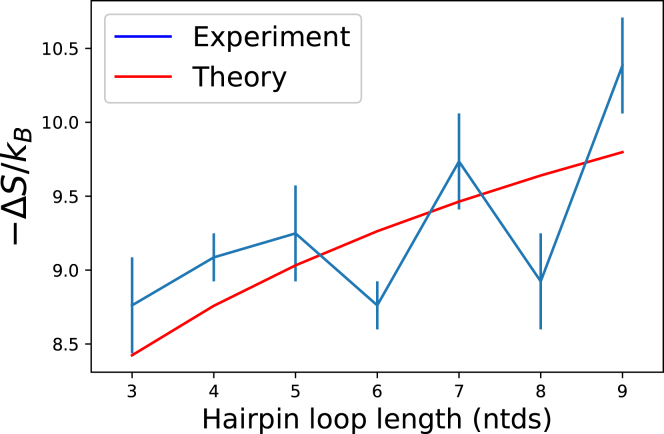
We estimate v_s by fitting experimental measurements of the entropy of hairpin loops of variable lengths to Eq. 6. Although Eq. 6 implies that the entropy of a hairpin should increase monotonically as a function of its length, the experimental measurements are nonmonotonic, and their nonmonotonicity exceeds the error bars (71). This nonmonotonicity may be due to enthalpic effects (72), which were neglected in our analysis following (30). Nevertheless, Fig. 2 shows that Eq. 6 gives a reasonable fit to the experimental data with v_s = 0.0201 ± 0.0036 nts³. A more precise definition of v_s might include a dependence on the closing basepairs of the hairpin loop; we expect that the penalties placed on specific closing basepairs and first mismatches in (30, 71) play a similar role, though such penalties were not included here. If one ignores all angular dependences of bond formation, our estimate of v_s leads to a naive underestimate of the length of a hydrogen bond of 0.56 Å, which nonetheless is well within an order of magnitude of the true length of hydrogen bonds.

Figure 2.

v_s estimated from experimental data. Experimental estimates for the free energy of hairpin loops of length s from Table 1 of (71) were converted to entropy estimates (blue points and error bars) by assuming ΔH = 0 as in (30). These data were fit to Eq. 6, yielding an estimate of v_s = 0.0201 ± 0.0036 nts³. To see this figure in color, go online.

Because we find b using previous experimental results and fit v_s based on data from non-pseudoknotted structures, our model is in truth a zero-parameter model when it comes to pseudoknots. No data from pseudoknotted structures were used to fit our model.

Pseudoknot loop entropies: RNA Feynman diagrams

Our goal in this section is to find Eq. 5 for arbitrary pseudoknots. In Eq. 5, the P_s(R) terms are given by the single-stranded segments, whereas stems appear through the constraint on the integral. The persistence length of double-stranded RNA is extremely long (∼200 nts (73)) compared to both single-stranded RNA and the length of any stem we will actually consider. Therefore, we will model stems as rigid rods with a fixed end-to-end distance given by the length of the stem. In other words, a stem in which nts i through i + k are bound to j through j − k constrains nts i and i + k (as well as j and j − k) to be a fixed distance apart. As we will see, such constraints end up only affecting the value of the integral for pseudoknotted structures, as exemplified by Fig. 3 c.

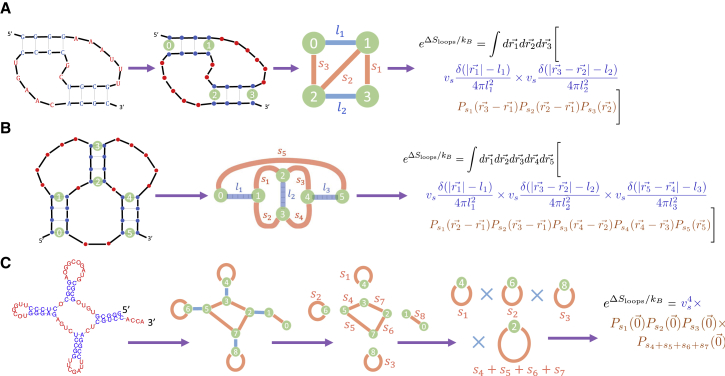
Figure 3.

RNA Feynman diagrams. (a) An instance of the canonical H-type pseudoknot is shown (the first panel). Bold lines represent the RNA backbone; thin lines represent hydrogen bonds. The loop entropy of this structure can be calculated by first assuming sequence independence of the loop entropy (second panel) and then converting the structure to a graph (third panel). The nodes of the graph represent the first and last basepairs of each stem, and two types of edges represent single- and double-stranded RNA. The graph directly represents the integral in Eq. 7, reprinted in the fourth panel. The nodes are integrated over three-dimensional space, subject to constraints specified by the rigid double-stranded edges (blue), which correspond to delta functions. The integrand is given by the flexible single-stranded edges (red), which correspond to a $P_s\left(\overrightarrow{R}\right)$ term. (b) The intramolecular kissing hairpin pseudoknot (first panel) is converted to a graph (second panel), representing the integrals necessary to compute its loop entropy (third panel). Although for this structure, the integrals are in general not analytically solvable, we numerically solve them (see Supporting Materials and Methods) as well as solve them analytically for the case s₁/s₃ = s₂/s₄ (Eq. 8). (c) The process of calculating the loop entropy of an RNA structure by converting it to a graph representing the entropy in integral form can be applied to any arbitrary structure. Separable integrals are represented by graphs which can be disconnected by the removal of any one edge. Thus, once appropriate factors of v_s are included (one for each stem in the original structure), the loop entropy of the example structure in question is simple to calculate and is given by four closed-nets-0 (originating from the three hairpins and multiloop). The four closed-net-0 loops contribute multiplicatively to the exponential of the loop entropy, meaning additively to the loop entropy itself. For non-pseudoknotted structures, all double-stranded edges (blue) can be removed in this way. To see this figure in color, go online.

To calculate the entropy of a pseudoknot of arbitrary complexity, we invent a, to our knowledge, novel graph formulation inspired by Feynman diagrams from quantum field theory. We build on previous work by Rivas and Eddy (44) and later by Orland and Zee (74) who developed innovative graphical decomposition methods for RNA structures for the purposes of pseudoknot enumeration; here, we use a related diagrammatic approach for the entropy calculation instead. First, the RNA structure being considered is translated into a graph. Nodes are used to represent the two end points of a stem, and two types of edges represent single- and double-stranded RNA.

Defined in this way, the graph of the RNA structure directly represents the integrals necessary to compute its entropy. The positions of the nodes, ${\overrightarrow{r}}_i$, are integrated over all of space, while the constraints of the structure are included in the integrand: a double-stranded edge of length l between nodes i and j leads to a term $v_s\delta \left(|{\overrightarrow{r}}_i-{\overrightarrow{r}}_j|-l\right)/4\pi l^2$ (because of the rigid rod approximation of the stem), and a single-stranded edge of length s between these nodes leads to a term $P_s\left({\overrightarrow{r}}_i-{\overrightarrow{r}}_j\right)$ in the integrand (as in Eq. 5). Note that two bonded nts in isolation are considered a stem of length l → 0.

As a concrete example, we consider the canonical H-type pseudoknot, an instance of which is shown in Fig. 3 a (first panel). The loop entropy is sequence independent (second panel) and can be calculated by translating the structure into a graph (third panel) in which each node represents the edge of a stem, blue edges represent regions of double-stranded RNA of length l_i, and red edges represent regions of single-stranded RNA of length s_i. For the example in Fig. 3 a, s₃ = 6 nts, and l₁ = 3 nts. We set the origin of our coordinate system to node 0 and call the distance vector between node i and the origin $\overrightarrow{r_i}$. Integrating over the possible placements of nodes 1–3 (while including the constraints of the structure in the integrand as described previously) we obtain the following Gaussian integral formulation of the entropy:

$$e^{\text{Δ}{S}_{\text{H}-\text{type}}/k_B}=v_s^2\int d\overrightarrow{r_1}\int d\overrightarrow{r_2}\int d\overrightarrow{r_3}\frac{\delta \left(\left|\overrightarrow{r_1}\right|-l_1\right)}{4\pi l_1^2}\frac{\delta \left(|\overrightarrow{r_3}-\overrightarrow{r_2}|-l_2\right)}{4\pi l_2^2}{P}_{s_1}\left(\overrightarrow{r_3}-\overrightarrow{r_1}\right)P_{s_2}\left(\overrightarrow{r_2}-\overrightarrow{r_1}\right)P_{s_3}\left(\overrightarrow{r_2}\right),$$ (7)

where using the assumption $s\gg b$, we allow the integrals to extend over all of space. A more comprehensive derivation of this formula, including the origin of the v_s terms, can be found in Supporting Materials and Methods. This integral can be calculated analytically (Supporting Materials and Methods; (37)).

A complex pseudoknot involved in biological processes ranging from viral replication to antisense regulation is the intramolecular kissing hairpin pseudoknot (Fig. 3 b; (43, 75, 76, 77, 78, 79)). Despite its biological prevalence, its entropy cannot be estimated using existing formalisms, necessitating the use of simple heuristic energy models (43). Our formalism on the other hand can readily address this pseudoknot by translating the structure to integrals as in Eq. 7. Although the integrals representing the entropy of the kissing hairpin are not in general analytically solvable, they are for the special case of s₁/s₃ = s₂/s₄. Rescaling the s to be s/γ with γ = 3/2b, we define the variables s_c = s₅(s₁ + s₂)(s₃ + s₄) and s_d = s₁s₂(s₃ + s₄) + s₃s₄(s₁ + s₂) along with 

$$s_A=\frac{s_5\left(s_c+s_d\right)}{s_c};s_B=\frac{s_3{s}_4{\left(s_1+s_2\right)}^2}{s_d};s_v=\sqrt{s_c+s_d}$$

to arrive at

$$e^{\mathit{\Delta }{S}_{\text{KH}}/k_B}=\frac{{\left(v_s/s_v\right)}^3}{2{\pi }^{9/2}}\frac{s_A}{l_1{l}_3}{e}^{-\left(\frac{l_1^2+l_3^2}{s_A}\right)-\frac{l_2^2}{s_B}}\text{sinh}\left(\frac{2l_1{l}_3}{s_A}\right),$$ (8)

where sinh is the hyperbolic sin function.

The complete derivation of Eq. 8, along with a derivation of the numerically solvable general case, can be found in Supporting Materials and Methods. We have also provided an eight-dimensional table of the results of the numerical integration for different combinations of the s and l as Supporting Materials and Methods (Table S2).

We note that the intermolecular kissing hairpin complex, for which physical models have previously been developed (80), is simpler than the intramolecular structure in the context of our formalism, and its entropy calculation is shown in Fig. S2.

Our Feynman diagram-like graphical formalism allows intuitive manipulation of the integrals. Graphs that can be disconnected by the removal of any one edge correspond to separable integrals and thus to distinct motifs in the RNA structure. The decomposition of a structure into its component graphs is depicted in Fig. 3 c for a classical cloverleaf RNA (a second example, this one of a pseudoknotted RNA, is provided in Supporting Materials and Methods, Section 10). The RNA in question decomposes into four instances of closed-net-0 (originating from the three hairpins and multiloop) and one instance of an open-net-0, or free chain (which by definition does not affect the entropy). For non-pseudoknotted structures, once appropriate factors of v_s are included in the integrals (one for each double-stranded edge of the graph), all double-stranded edges can be removed through this graphical decomposition process. As shown in the figure, nodes that can be removed without changing the topology can be removed in the graph decomposition process. This is made possible by the property of $P_s\left(\overrightarrow{r}\right)$ that $\int P_x\left(\overrightarrow{r_1}\right)P_y\left(\overrightarrow{r_2}-\overrightarrow{r_1}\right)d\overrightarrow{r_1}=P_{x+y}\left(\overrightarrow{r_2}\right)$ (see Supporting Materials and Methods for further discussion).

In Fig. S2, we display all possible graphs of up to two stems and their respective RNA structures. As in Fig. 3, single-stranded edges are displayed with red, and double-stranded are displayed with blue. For each graph, the integral formulation of its entropy is displayed in the figure alongside what it evaluates. RNA sequences, even those of length ≤80 nts, form a wide array of pseudoknots more complex than those discussed in that figure, such as H-type pseudoknots with internal loops. Heuristics for treating such pseudoknots make systematic errors that our model can correct. See Supporting Materials and Methods for further discussion.

In Supporting Materials and Methods, we provide a full sample calculation for the free energy of a pseudoknotted structure.

Comparison of methodology to other physics-based pseudoknot entropy models

Although our model is able to address arbitrarily complex pseudoknots, prior physical models have been developed to address H-type pseudoknots in particular. The parametric sparsity of the model described above necessitates a neglect of several biological considerations, which have been considered by these previous models. Here, we will discuss how the framework developed above can be modified to include several factors considered in such models. The rationale for building atop our framework is provided in the next section. We demonstrate that despite the loop entropy model’s apparent physical simplicity—it uses an order of magnitude fewer parameters than current tools while being general enough to apply to arbitrarily complex pseudoknots—it performs on par with state-of-the-art prediction software and therefore appears to succinctly capture the essential physics at play (see Results and Discussion).

An early model for the loop entropy of pseudoknots was developed by Gultyaev et al. (81). That model was based in large part on Jacobson and Stockmayer’s derivation of the loop entropy of hairpins, which is rederived (Eq. 6) and then significantly extended by our formalism. To account for excluded volume, Gultyaev et al. replaced the factor of 3/2 in Eq. 4 with 1.75 (82). Such a change does not accurately account for excluded volume for the case of pseudoknots; we therefore did not make this replacement in our own article (in an effort for self-consistency), though it can easily be made. A more systematic treatment of how to include self-avoidance for the case of complex pseudoknots is still lacking.

The first pseudoknot models such as Gultyaev’s did not consider interhelix loops for the H-type pseudoknot (i.e., they only considered those structures for which s₂ = 1 in the language of Fig. 3 a). The approximation made in our own work is in fact the opposite limit—that of $s_2\gg b$—and our results should be most appropriate for long single-stranded regions. More precise treatment of short loops would forgo the simple ideal chain approximation of Eq. 4 in favor of the worm-like chain approximation. Although it would preclude analytic solutions of the integrals, numeric integration can easily be employed to make an effective look-up table as we demonstrated for the intramolecular kissing hairpin pseudoknot.

A similar complication is dealt with in Cao and Chen’s Vfold model, which considers bond geometries explicitly using the diamond lattice (50). Although the enumeration procedure employed on the lattice is not computationally feasible for very large or complex pseudoknots, it is expected to capture the atomistic geometries more precisely than our own continuous three-dimensional space theory. Modifications can still be made within our framework, most directly by integrating only over a specific range of angles determined by the geometry. Such geometric considerations may also affect our treatment of non-pseudoknotted structures and, in particular, our equivalent treatment of hairpin, internal, bulge, and multiloops (83).

Perhaps most importantly, our model neglects the twists of the RNA helix. These twists may play a role in the nonmonotonicity of the experimental data in Fig. 2 and are likely significant. Isambert’s KineFold model claims to effectively consider such twists by modification of the value of the double-stranded stem lengths l inputted to the pseudoknot formulae (60); however, as for the pseudoknot formulae themselves, the derivations of these modifications have not been published, and no physical basis for them was given. Finally, although we do not distinguish between the major and minor grooves of the RNA, accounting for the different grooves can explain asymmetries in physiological H-type pseudoknots (58). Aalberts and Nandagopal demonstrated that with the addition of a single experimentally measured parameter, $P_s\left(\overrightarrow{R}\right)$ can be modified to account for this factor (84, 85).

Enumerating RNA structures

In this section, we describe the process by which we exhaustively enumerate the secondary structures, including pseudoknots, into which an arbitrary given sequence can fold. This process was developed by Pipas and McMahon (20). The Pipas-McMahon algorithm first enumerates all possible secondary structures for a given sequence (sans pseudoknots) and then evaluates the free energy for each to construct the entire free energy landscape for non-pseudoknotted structures. A major shortcoming is the significant computer time required for long sequences. However, the exponential increase in computer power over the past 40 years, coupled with increased appreciation for the physiological and engineering relevance of short RNA strands, suggests revisiting this approach. This process is also employed by the TT2NE algorithm, with the caveat that rather than stems, that algorithm uses helipoints—defined as sets of stems separated by a bulge loop of size one or a 1 × 1 internal loop—as the backbone of the enumeration procedure, thus coarse graining over many similar structures (22).

We first number the nts in the RNA sequence from 1 to N from the 5′ end. We define an N × N symmetric matrix B, which describes which nts can bind to each other: B_i,j = 1 if nts i and j can bind to form a basepair (i.e., they belong to the set {(A,U)(C,G)(G,U)}) and 0 otherwise.

Next, we search for all possible stems (strings of consecutive basepairs) that could form. We define a parameter m to be the minimal allowed stem length (m ≥ 1; we set m = 1 throughout unless otherwise specified). We also impose the physical constraint that hairpins (single-stranded region connecting one end of a stem) have a minimal length of three nts. We include not only the longest possible stems that can form but all contiguous subsets of those stems (86, 87). We denote the number of stems found by N_stems.

We next define the N_stems × N_stems symmetric compatibility matrix C, where C_p,q = 1 if a structure could be made with both stems p and q ac$\left(C_{q,q}=1\forall q\right)$. We impose the constraint that each nt may be paired with, at most, one other nt by setting C_p,q = 0 if stems p and q share at least one nt.

Finally, we explicitly enumerate the remaining possible secondary structures by identifying all compatible combinations of stems. Starting from a single stem s₁, we consider stems s₂ where 1 ≤ s₁ ≤ s₂ ≤ N_stems and add the first stem for which C_s1,s2 = 1. Then, we repeat the process, adding the first stem s₃ > s₂ compatible with both s₁ and s₂ and so forth, continuing until we can add no more stems. We add the resulting structure, composed of M stems, to the list of possible structures, remove the last stem added (to obtain the structure composed of stems s₁, s₂, …, s_M–1), and continue the process. This algorithm returns all possible secondary structures resulting from the primary sequence.

The algorithm described here was implemented in MATLAB (The MathWorks, Natick, MA), and all code is available on the GitHub repository (https://github.com/ofer-kimchi/RNA-FE-Landscape). The repository also includes a Python version of the code.

Once we completely enumerate the possible secondary structures, we calculate the probabilities that the RNA will fold into each of them by calculating their free energies as described in the previous sections.

Results and Discussion

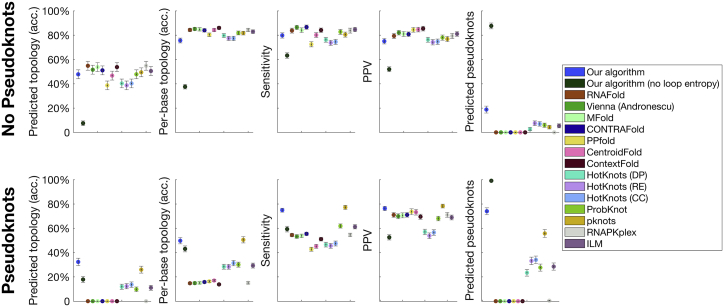
We use experimentally determined structures to compare the predictions of our model with other current methods; results are shown in Fig. 4. For sequences of length $\le 80$ nts from the RNA STRAND (64), PseudoBase++ (65), and CompaRNA (66) databases (186 non-pseudoknotted structures with 58 different topologies; 235 pseudoknotted structures with 52 different topologies), which had a sequence dissimilarity ≥0.2 (using Jukes-Cantor), we measured the number of basepairs correctly predicted by our algorithm’s MFE structure compared to 14 other current algorithms. Seven of these cannot predict pseudoknots and serve as useful benchmarks for the non-pseudoknotted results (detailed methods in Supporting Materials and Methods; we have included the entire benchmark data set in Table S1). We also tested whether our algorithm’s predictions are dependent on the accuracy of our loop entropy model by setting all loop entropies to zero (dark green). The poor performance of our algorithm in this case compared to the case in which loop entropies are considered demonstrates the success of the loop entropy model.

Figure 4.

Summary statistics for comparison to other prediction tools. To assess the relative success of our algorithm, we compare its performance in predicting experimentally determined RNA structures to that of 14 other current prediction tools: RNAFold (33, 118), ViennaRNA (Andronescu parameters) (119), Mfold (32), CONTRAfold (120), PPfold (121), CentroidFold (122), Context Fold (123), HotKnots (Dirks-Pierce parameters), HotKnots (Rivas-Eddy parameters), HotKnots (Cao-Chen parameters) (63), ProbKnot (40), PKNOTS (44), RNAPKplex (33, 118), and iterated loop matching (ILM) (38). We measure sensitivity, PPV, the fraction of topologies predicted correctly by the MFE structure, the average per-base topology accuracy (defined in the main text), and the fraction of MFE structures containing a pseudoknot. We separate the results into sequences that experimentally form pseudoknots and those that do not. Error bars show the standard error. Despite the fact that our algorithm requires only two parameters to describe the entropy of any arbitrary secondary structure (at least an order of magnitude–and often several–fewer than the other algorithms tested against) and that the parameters were trained on non-pseudoknotted structures, our algorithm outperforms the other algorithms tested in predicting pseudoknotted structures and performs on par with them in predicting non-pseudoknotted structures. We also demonstrate that our algorithm’s success is dependent on the accuracy of our loop entropy model because setting all loop entropies to zero (dark green) leads to poor performance (see main text for further discussion). To see this figure in color, go online.

Although the entropy model presented here can give an integral expression for arbitrarily complex pseudoknots, the integral may need to be solved numerically for sufficiently complex structures. For this large-scale comparison, we disallowed pseudoknots more complex than those displayed in Fig. S2, and our algorithm therefore did not require any numerical integration. Fig. S6 demonstrates that even without this practical constraint, the complete enumeration of secondary structures including all possible pseudoknots is nonprohibitive. We similarly disallowed parallel stems, which can be stable in neutral and acidic pH conditions (88). We also set the minimal stem length for each sequence (m) to the minimal value it could take such that the total number of possible stems is less than $N_{\text{stems}}^{\text{max}}=150$. These choices were all made to speed up computation time; each sequence took between several seconds and an hour to run. Details of the computation time of our algorithm can be found in Figs. S4–S6.

Although these practical constraints were chosen to speed up the computation time, they also led to errors in the algorithm’s predictions. Of the tested pseudoknots, 64 were topologically more complex than any of those presented in Fig. S2. Furthermore, 33 of the non-pseudoknotted sequences tested (and eight of the pseudoknotted) include basepairs outside of those allowed by the algorithm (AU, GC, and GU). Removing such structures from our comparison analysis leads to our algorithm performing even better compared to current tools (see Fig. S3).

Further errors were due to our choice of m, which was not optimized and was too high compared to the length of the shortest stem in the experimental structure for 58 non-pseudoknotted cases and 54 pseudoknotted cases. By changing $N_{\text{stems}}^{\text{max}}$ from 150 to 200, these numbers decreased to 46 for both pseudoknotted and non-pseudoknotted sequences, but the results for $N_{\text{stems}}^{\text{max}}=200$ were practically identical to the results of Fig. 4 (see full results in Table S1). For $N_{\text{stems}}^{\text{max}}=200$, the computation time was increased significantly (to several hours in the worst cases, though the majority of the computation time is spent on the Feynman diagram decomposition process, which has not been optimized in the current code). In addition to these sources of error, the nearest-neighbor parameters may need to be re-examined to be used most effectively with the loop entropy model presented here.

We considered the basepairs present in the experimental structure and in each algorithm’s MFE structure. Basepairs present in both were labeled as true positives (TP), those present only in the predicted algorithm were labeled as false positives (FP), and those present in the experimental structure but not the predicted MFE structure were labeled as false negatives (FN). The sensitivity (TP/TP + FN) and the positive predictive value (PPV; TP/TP + FP) of our algorithm were measured to be 0.80 and 0.75 for the non-pseudoknotted cases and 0.75 and 0.76 for the pseudoknotted cases, respectively. Our algorithm performed better than or as well as all other prediction tools tested for the prediction of pseudoknots and on par with other tools in the prediction of non-pseudoknotted sequences. The full results can be found in Table S1.

Although sensitivity and PPV are the most common metrics used to establish the success of an RNA prediction algorithm (89), we sought to develop a test that measures success on the scale of the full RNA rather than on the scale of individual basepairs. To this end, we measured how frequently each algorithm was able to correctly predict the topology of the experimentally measured structure, in which the topology of a structure is defined by its graph. We found for our algorithm that the experimental topology is within the top 1, 5, and 10 topologies at frequencies of 49, 65, and 70% for non-pseudoknotted structures, and 34, 59, and 62% for pseudoknotted, demonstrating a sharp increase between top 1 and top 5 and a plateau between top 5 and top 10.

Considering whether an algorithm correctly predicts the full topology can lead to errors arising from small variations in structure. For example, the opening of a single bond on the edge of a stem can lead to a different topology as we have defined it, if that stem includes one of the ends of the molecule. To arrive at a per-base measure of topology, we consider for each bond along the RNA backbone to which of the minimal graphs of Fig. S2 it belongs. For example, the bond between the second and third nts of Fig. 3 a belong to a stem of an open-net-2a graph. We then measure for each sequence the fraction of correct per-base topology predictions made by each algorithm’s predicted MFE structure. We find that our algorithm averages an 76% per-base topology prediction accuracy for non-pseudoknotted sequences and a 49% accuracy for pseudoknotted.

Finally, we compare how frequently each algorithm predicts an MFE structure containing a pseudoknot. Our algorithm correctly predicted 174/235 pseudoknots among the pseudoknotted cases, far more than any other algorithm tested. However, it also erroneously predicted 35/186 incorrect pseudoknots among the non-pseudoknotted cases.

For each of these metrics, the success of our algorithm is dependent on the loop entropy model. If we set all loop entropies to zero, our algorithm’s predictive power plummets (see Fig. 4, dark green). This is especially true for the prediction of non-pseudoknotted structures because removing the loop entropy term leads the algorithm to erroneously predict that 88% of these would form pseudoknots.

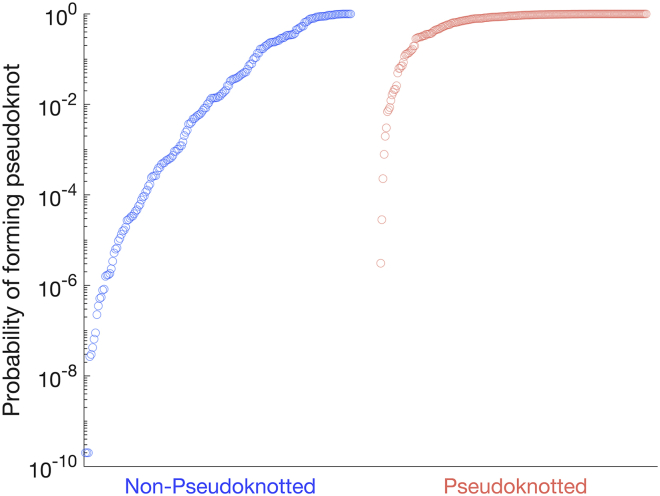
Our algorithm also provides the probability of folding into a pseudoknotted structure for each sequence. These data for the 421 sequences tested are presented in Fig. 5. Each data point represents a different sequence and the total probability calculated of that sequence folding into a pseudoknotted structure. For figure clarity, a lower bound of pseudoknot probability was set at 2 × 10⁻¹⁰.

Figure 5.

Probability of folding into a pseudoknot. The predicted probability of each of the 421 sequences tested folding into a pseudoknot is presented. Of these sequences, 186 were experimentally found not to form pseudoknots (blue) and 235 were found to form pseudoknots (red). Our algorithm successfully predicts pseudoknots forming in the latter category far more frequently than in the former. For figure clarity, a lower bound of pseudoknot probability was set at 2 × 10⁻¹⁰. To see this figure in color, go online.

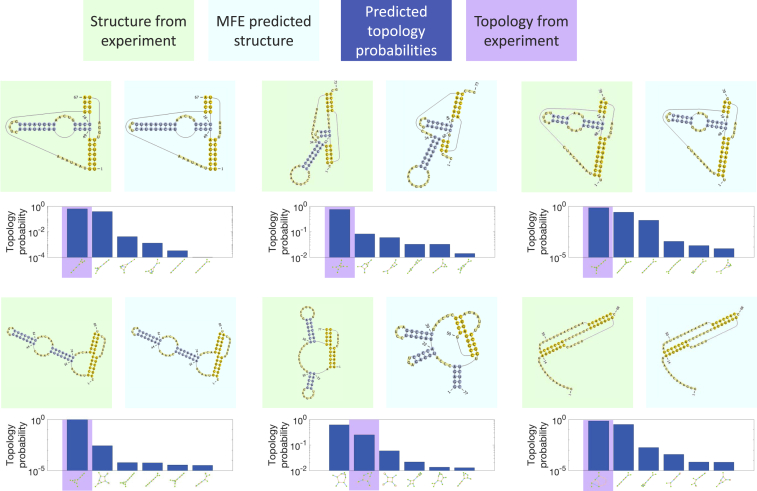
The algorithm’s predictions for the six longest RNA sequences less than 89 nts in length from the PseudoBase++ database are presented in Fig. 6. We considered only those sequences whose structure was directly supported by experiments and which could be decomposed into the minimal topologies shown in Fig. S2. We display the experimental structure (green background) alongside the MFE predicted structure (light blue background) and the top six predicted topologies (out of several hundred, depending on the sequence; dark blue) in which the experimental topology is highlighted (purple). RNA secondary structure was plotted using the PseudoViewer package (90). Our results demonstrate successful predictions even for long pseudoknotted sequences, especially in terms of the predicted topology. Detailed methods are provided in Supporting Materials and Methods.

Figure 6.

Comparison to experiments for long sequences. Six long sequences were chosen from the PseudoBase++ database as described in the main text. The sequences are fragments derived from the following (starting from the top left and moving across): tobacco mosaic virus (124, 125, 126), Bacillus subtilis (127), tobacco mild green mosaic virus (125, 128), Bacillus subtilis (129), Giardiavirus (130), and Visna-Maedi virus (131). The experimental structures are supported by (numbering the sequences in the same order) sequence comparison (1–4,6), structure probing (1,3,5,6), mutagenesis (2,4–6), three-dimensional modeling (1), and NMR (6). We show the experimental structure (green background) and the MFE-predicted structure (light blue background) plotted using the PseudoViewer software (90). We also display the top six topologies (out of several hundred, depending on the particular sequence) and their respective predicted probabilities, with the topology corresponding to the experimental structure highlighted in purple. Overall, our results demonstrate successful predictions even for these long pseudoknotted sequences, especially in terms of the predicted topology. To see this figure in color, go online.

Conclusions

The accurate prediction of the ensemble of secondary structures explored by an RNA or DNA molecule has played a major role in shaping modern molecular biology and DNA nanotechnology over the past several decades. In this work, we showed that the modern ubiquity of extremely powerful computers can be used alongside novel polymer physics techniques to completely enumerate and solve for the free energy landscape of an RNA molecule including complex pseudoknots. This exponential time algorithm can be used to tackle even relatively long (∼80 nts) RNA sequences and, aside from the enumeration procedure (which is relatively fast compared to the free energy calculation for long sequences; see Figs. S4 and S6), is easily parallelizable.

Remarkably, the entropy model discussed in this work requires only two parameters—orders of magnitude fewer than other current algorithms—corresponding to clearly measurable physical quantities. Despite this and despite the fact that all parameters used in our model were derived using experiments on non-pseudoknotted RNA, our algorithm is more successful in predicting pseudoknotted structures than any of the other algorithms tested and on par with all predictors tested in predicting non-pseudoknotted structures on a benchmark data set of sequences of length ≤80 nts. The success of our algorithm is particularly notable given that the entropy model developed in this work can be used to address any RNA secondary structure, regardless of complexity. Given these results, we expect that more accurate entropy models can be formulated by building atop the framework presented here and have highlighted several avenues for improvement.

Although we have not done so in this work, we expect that our results can be further improved by optimizing the nearest-neighbor parameters, given the entropy model presented here.

The algorithm presented here can also be easily generalized to probe multiple interacting strands (see discussion in Supporting Materials and Methods). The sequences considered can be any combination of DNA and RNA; their identities affect the nearest-neighbor parameters of the model that have been previously tabulated (91) and to a lesser extent, the two entropy parameters (b and v_s).

Our finding that the integral formulation of the entropy of arbitrary complex RNA secondary structures can be represented graphically is reminiscent of Feynman diagrams in quantum field theory. The topologies defined by these graphs can also serve as useful biological constructs to group similar RNA structures together. The depiction of RNA structure as a graph has played an important role in the prediction of RNA secondary structure (22, 74, 92, 93) as well as in the search for novel RNAs (94, 95) and the description of similarity between RNA structures (96, 97, 98, 99), which is especially useful in the study of the effects of mutations (100, 101). A common approach among these graphical depictions of RNA has been to represent loops (e.g., hairpins, internal loops, etc.) as vertices and stems as edges (94, 98, 99). However, this depiction of RNA does not always distinguish between pseudoknotted and non-pseudoknotted structures (94). Our approach has a similar coarse-graining effect of grouping similar structures as the same graph but explicitly distinguishes between different topologies of secondary structure and may therefore be useful in the contexts described previously. Although our approach is in many ways similar to the planar digraphs of (94), it is able to address the ambiguity present in those graphs, particularly with regards to parallel stems (see Fig. 2 of (94)).

We expect that the complete free energy landscape prediction described in this work will be useful in understanding the kinetics of RNA and DNA structure transitions, including the interactions of multiple strands (24, 25, 102, 103, 104, 105, 106, 107, 108). In addition to the complete energy and entropy landscapes, a complete kinetics model only needs a definition of the transition state matrix. Such a matrix can be derived from the energy and entropy landscapes directly. For example, by defining neighboring states as secondary structures differing by the opening or closing of a single basepair, the transition rate of opening a basepair is expected to be exponential in the energy difference of the two states, whereas the rate of closing a basepair is exponential in the entropy difference (24, 102, 109). Even for transitions between two non-pseudoknotted structures, pseudoknots often play a significant role in the transition pathway (108, 110, 111, 112, 113). Predicting the kinetics of structure transitions using this framework and determining whether such kinetics can be accurately predicted for RNA molecules of the lengths considered here, using only secondary structure considerations, will be a subject for future work.

Author Contributions

All the authors designed research. O.K. carried out theoretical calculations and wrote the code. O.K. and T.C. analyzed data. All the authors wrote the article.

Editor: Tamar Schlick.

Supporting Citations

References (114, 115, 116, 117) appear in the Supporting Material.