R-Type Calcium Channels Contribute to Afterdepolarization and Bursting in Hippocampal CA1 Pyramidal Neurons

Abstract

Action potentials in pyramidal neurons are typically followed by an afterdepolarization (ADP), which in many cells contributes to intrinsic burst firing. Despite the ubiquity of this common excitable property, the responsible ion channels have not been identified. Using current-clamp recordings in hippocampal slices, we find that the ADP in CA1 pyramidal neurons is mediated by an Ni²⁺-sensitive calcium tail current. Voltage-clamp experiments indicate that the Ni²⁺-sensitive current has a pharmacological and biophysical profile consistent with R-type calcium channels. These channels are available at the resting potential, are activated by the action potential, and remain open long enough to drive the ADP. Because the ADP correlates directly with burst firing in CA1 neurons, R-type calcium channels are crucial to this important cellular behavior, which is known to encode hippocampal place fields and enhance synaptic plasticity.

Introduction

In most textbook depictions, action potentials are followed by an afterhyperpolarization. In principal cells of the CNS, however, single action potentials are often followed by an afterdepolarization (ADP). The ADP is particularly prominent in pyramidal neurons of the CA1 region of the hippocampus (Schwartzkroin, 1975; Storm, 1987), in which it has been associated with action potential bursting (Azouz et al., 1996; Jensen et al., 1996; Magee and Carruth, 1999), a distinguishing feature of in vivo recordings in this region (Kandel and Spencer, 1961; Ranck, 1973; Fox and Ranck, 1975; Suzuki and Smith, 1985a,b). Reports of bursting in vivo show correlations with specific behaviors, including goal identification and approach, as well as with rest and sleep (Ranck, 1973; Suzuki and Smith, 1985a; Otto et al., 1991). Furthermore, action potential firing of CA1 place cells codes for an animal's position in space (O'Keefe, 1976; Muller et al., 1987), and receptive field size is spatially restricted when only bursting is taken into consideration (Otto et al., 1991; Harris et al., 2001). Bursting has also been shown to enhance synaptic plasticity at the Schaffer collateral to CA1 synapse (Thomas et al., 1998; Pike et al., 1999; Fortin and Bronzino, 2001).

The identity of the currents that underlie the ADP and drive bursting in CA1 pyramidal neurons remains unresolved. In studies in which extracellular calcium is low to absent, persistent sodium current has been suggested to play a role (Azouz et al., 1996; Su et al., 2001), but when potassium channels are blocked, contributions from calcium currents are enhanced (Magee and Carruth, 1999; Sanabria et al., 2001; Su et al., 2002).

Our aim is to identify the ionic currents contributing to the ADP and bursting in CA1 pyramidal neurons in physiological ionic conditions. In voltage clamp, we isolate a current that reflects the voltage dependence and pharmacological characteristics of the action potential ADP observed in current-clamp experiments. The properties of the isolated current compare favorably with those reported for R-type calcium current (Randall and Tsien, 1995, 1997). Previously reported functions for R-type current include the control of neurotransmitter release (Wu et al., 1998; Gasparini et al., 2001), the enhancement of presynaptic plasticity (Dietrich et al., 2003), and calcium entry into dendrites (Christie et al., 1995; Magee and Johnston, 1995a,b; Magee et al., 1995; Isomura et al., 2002; Yasuda et al., 2003). Our results, demonstrating that R-type current is a critical component in generating the ADP and bursting, identify a novel role of this current in cellular excitability.

Materials and Methods

Tissue preparation. Artificial CSF (ACSF) and sucrose solution were always bubbled with 95% O₂/5% CO₂. See below for concentrations. Male Wistar rats were used for the preparation of transverse hippocampal slices according to standard procedures (Golding et al., 1999). Slices were transferred to a suspended mesh within a chamber of fresh ACSF (current-clamp recordings) or sucrose solution (voltage-clamp recordings), incubated at 35°C for 20-35 min, and held at room temperature thereafter. For recording, individual slices were held in a small chamber perfused with fresh ACSF at 1-3 ml/min and visualized with an upright, fixed-stage microscope (Axioskop FS or FS2; Zeiss, Oberkochen, Germany) using differential interference contrast infrared videomicroscopy at 60-160× magnification. CA1 pyramidal somata were chosen for their smooth, flat appearance.

Current-clamp recordings. Whole-cell recordings were performed at 35°C in slices from rats aged postnatal day 14 (P14) to P20 (although in Fig. 1, 3 of 132 animals were P21-P24) and P30-P35 (where noted). Current-clamp recordings were performed using bridge balance and capacitance compensation with BVC-700 amplifiers (Dagan, Minneapolis, MN). Data were filtered at 5 kHz and sampled at 100 kHz. Patch electrodes (3-6 MΩ) were made from thick-walled borosilicate glass (EN-1; Garner Glass, Claremont, CA) and filled with K-gluconate internal solution. Only cells with membrane potentials negative to -55 mV were used for experiments. Except where noted, membrane potential was maintained at -67 mV with DC injection as needed. Recordings used for analysis were obtained in the presence of blockers of excitatory, inhibitory, and muscarinic synaptic input including 2.5 mm kynurenic acid, 2 μm SR95531 [2-(3-carboxypropyl)-3-amino-6-(4-methoxyphenyl)-pyridazinium bromide], and 1 μm atropine, respectively.

Figure 1.

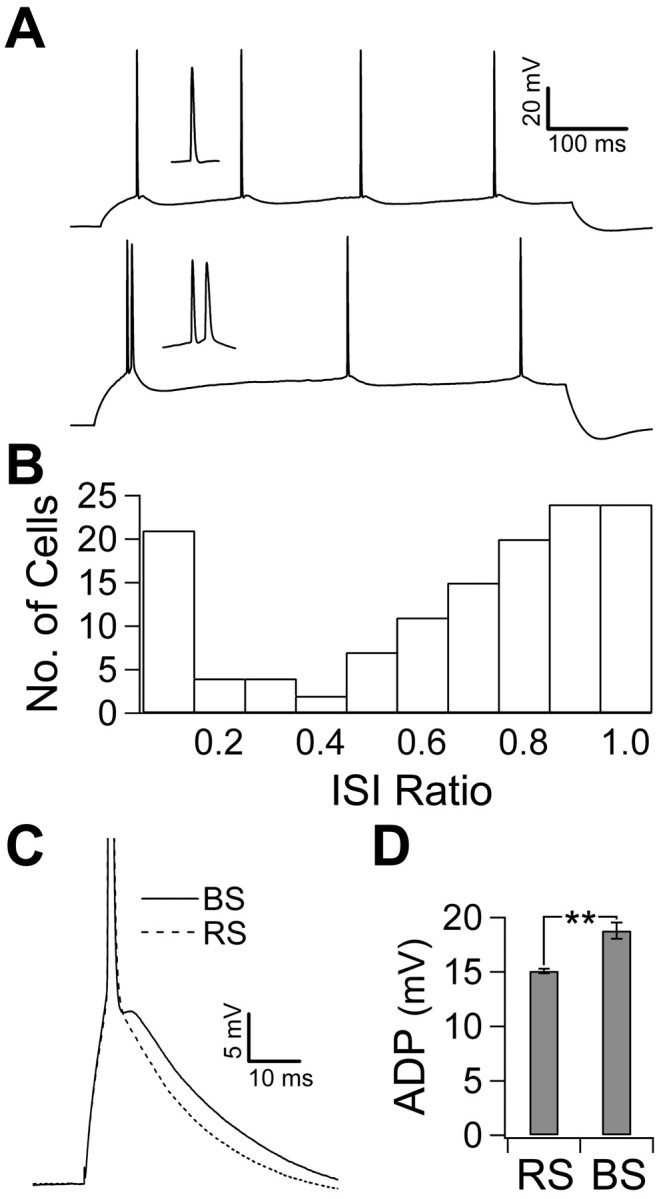
Action potential firing mode and the ADP. A, The response to a 600 ms current injection just above rheobase in a representative regular-spiking cell (top trace) and a representative burst-spiking cell (bottom trace) recorded in the presence of synaptic blockers. Insets show the single spike and burst. B, The ISI ratio (shortest ISI/mean ISI) was calculated by taking the shortest ISI in the train of action potentials evoked by the stimulus in A over the mean ISI. The histogram shows the distribution of the ISI ratio in 132 recorded cells. Note the distinct peak at the lowest bin representing bursting cells. C, A single spike was evoked using a 5 ms current injection just above rheobase. Traces show the ADP in a representative RS cell (dashed trace) and a representative BS cell (solid trace). The ADP is the depolarizing crest that follows the fast repolarization of an action potential. D, The amplitude of the ADP, relative to the resting potential before the spike, was calculated by averaging the membrane potential for 10 ms after the fast repolarization. Burst-spiking cells (21 of 132) had a larger ADP than regular-spiking cells (^** p < 0.01). Error bars represent SEM.

Voltage-clamp recordings. Voltage-clamp recordings were performed in nucleated patches, which allow almost ideal voltage clamp, even for fast current (Martina and Jonas, 1997). Recordings were done at room temperature (24-26°C) from slices of P12-P19 animals using a patch-clamp amplifier (Axopatch 200B; Molecular Devices, Union City, CA). Data were filtered at 10 kHz and sampled at 20 kHz. Patch pipettes of 2.5-4 MΩ were pulled from Corning #0010 lead glass (World Precision Instruments, Sarasota, FL) or borosilicate 0.5 mm walled glass (Hilgenberg, Malsfield, Germany) and contained a CsCl internal solution. Pipettes were wrapped in Parafilm (Pechiney Plastic Packaging, Chicago, IL) to minimize capacitive transients, the remainder of which was maximally cancelled using the fast compensation circuitry of the amplifier. The whole-cell configuration was obtained, and the pyramidal identity of cells was confirmed by presence of sag in the membrane potential in response to a hyperpolarizing current injection. Then the nucleus was slowly withdrawn while applying -75 to -250 mbar suction as the membrane wrapped around it. After detachment, patches were held at -90 mV. Leakage and capacitive currents were subtracted using a P/-4 protocol (four negative correction pulses, each with an amplitude one-fourth of the test pulse). Stimuli were repeated 5-15 times, and results were averaged. When pipette capacitance was not fully canceled by the amplifier circuitry, the duration of the capacitive transient at the onset of voltage step was measured, and analysis of the peak of the tail current was taken after the same duration following the end of the voltage step.

Solutions and drugs. Unless indicated otherwise, chemicals were obtained from Sigma (St. Louis, MO). ACSF contained the following (in mm): 125 NaCl, 25 NaHCO₃, 2.5 KCl, 1.25 NaH₂PO₄, 25 glucose, 2 CaCl₂, and 1 MgCl₂. Sucrose solution contained the following (in mm): 87 NaCl, 25 NaHCO₃, 25 glucose, 75 sucrose, 2.5 KCl, 1.25 NaH₂PO₄, 0.5 CaCl₂, and 7 MgCl₂. K-gluconate internal solution, pH 7.3, contained the following (in mm): 115 K-gluconate, 20 KCl, 10 Na-phosphocreatine, 10 HEPES, 2 Mg-ATP, 0.3 Na-GTP, and 0.1% w/v biocytin for later histological processing. CsCl internal solution, pH 7.3, contained the following (in mm): 138 CsCl, 2 MgCl₂, 2 Na₂-ATP, 0.2 Na-GTP, 10 EGTA, 10 HEPES, 2 Tris-phosphocreatine, and 2 NaCl. Voltage-clamp recordings were performed in HEPES-buffered ACSF, pH 7.3 (not bubbled) containing the following (in mm): 138 NaCl, 2.5 KCl, 10 HEPES, 25 glucose, 2 CaCl₂, 1 MgCl₂, or 40 NaCl, 10 HEPES, 10 glucose, 1 MgCl₂, 1 CsCl, 5 BaCl₂, 5 4-AP, and 80-150 tetraethylammonium (TEA)-Cl (osmolarity, 325 mOsm), as indicated. For most current-clamp recordings, drugs were delivered via bath application added to the perfusate. Current-clamp experiments with ω-conotoxin MVIIC used a solution buffered with a combination of NaHCO₃ and 6 mm HEPES to maintain pH, because perfusion was stopped, and the drug was applied directly to the bath. Focal application of nickel (NiCl₂, 2 mm) and SNX-482 (1 μm; a peptide toxin from the venom of the African tarantula Hysterocrates gigas; Peptides International, Louisville, KY) was achieved by light, positive pressure to the back of a large-bore patch pipette positioned directly over the soma. The location of the cloud of perfusate was confirmed in three of nine recordings via two-photon laser-scanning fluorescent microscopy: 200 μm Fluo4 (Molecular Probes, Eugene, OR) was included in the intracellular solution, and 10 μm Alexa 594 (Molecular Probes) was included in the perfusion pipette. The dyes were excited with a laser-scanning device at 806 nm. Emission was detected with separate, tuned photomultiplier tubes. The drug was limited to the somatic region and washed away in the direction of the basal dendrites and above the plane of the cell. In one cell, direct application of Ni²⁺ at the basal dendrites produced no effect. For voltage-clamp recordings, nucleated patches were held in the mouth of capillary tubes with syringe pump-driven streams of solution at 30 μl/min. Nimodipine was prepared in a concentrated stock (100 mm) with dimethylsulfoxide or methanol and added to solution on the day of use. Light levels were kept low for nimodipine experiments. Calcium channel toxins were purchased from Alomone Labs (Jerusalem, Israel) and dissolved in solution containing 0.05% bovine serum albumin when used at nanomolar concentrations. Pharmacological effects were measured at steady state and demonstrated reversibility (see Figs. 4 B, 7A), with the exception of bath-applied Ni²⁺ in whole-cell current-clamp experiments.

Figure 4.

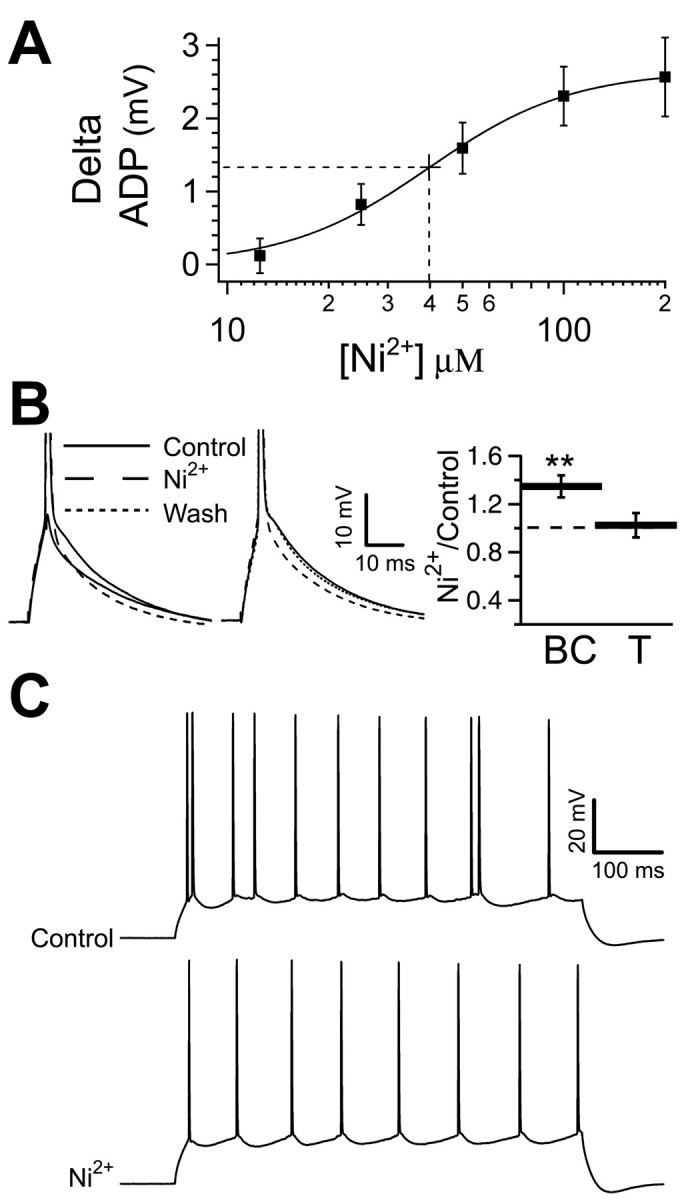
Blocking calcium currents reduces the ADP and stops bursting. A, The size of the ADP is decreased in a concentration-dependent manner by concentrations of Ni²⁺ between 12.5 and 200 μm; higher doses produce a saturated response. The half-maximal block occurs at 40 ± 4 μm (dashed line). Ni²⁺ (200 μm) REDUCED THE ADP BY 2.7 ± 0.1 MV. B, LEFT, THE ADP AND SUBTHRESHOLD RESPONSE IN A REPRESENTATIVE CELL (SOLID TRACES). THE ADP IS REDUCED BY 200 Mm Ni²⁺ (roughly dashed trace). Center, The ADP is reversibly decreased by Ni²⁺ applied locally to the soma (washout represented by finely dashed trace). Right, Bar chart (n = 15) of the burst current (BC; ^**p < 0.01) and the action potential threshold (T; p > 0.05) in 200 μm Ni²⁺ relative to control. C, The response to a 600 ms current injection in a representative cell in the elevated potassium condition (3.5 mm K⁺; top trace) and with subsequent application of 200 μm Ni²⁺ (bottom trace). The increased potassium induced the bursting, which was then blocked by Ni²⁺.

Figure 7.

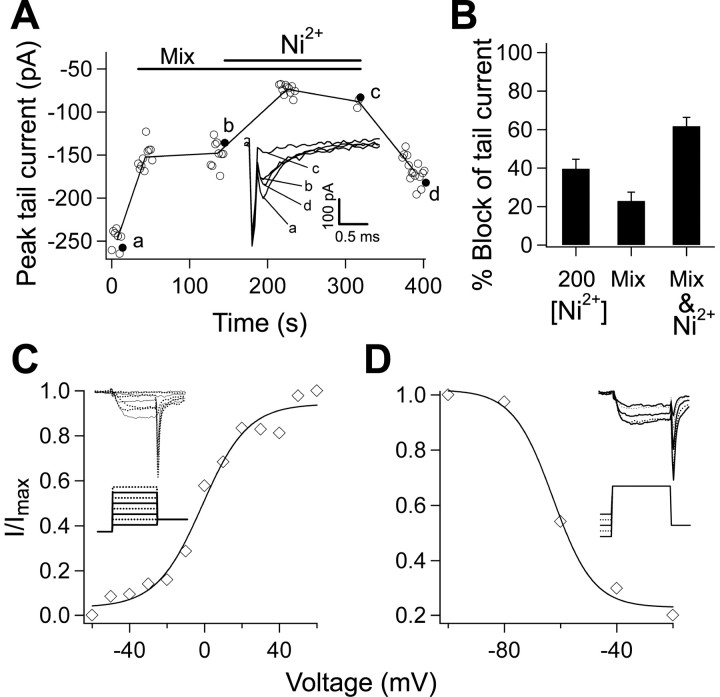
The component of the tail current that underlies the ADP is R-type current. A, A representative experiment demonstrating steady state and partial reversibility of the effect of drug application on the peak of the barium-mediated tail current. The open circles represent repeated measures with time, and the filled circles (labeled a-d) are the data points represented in the inset. The line connects the averages at each point. The inset shows single traces taken at the indicated time points. Note that the capacitive transient is easily distinguished from the tail current. B, Bar chart of the percentage block of the tail current by the pharmacological agents used. Ni²⁺ (200 μm) reduced the tail current (n = 14; p < 0.01). A mixture of calcium channel antagonists (Mix) 10 μm nimodipine with either 100 μm ω-conotoxin GVIA and 100 nm ω-agatoxin IVA (n = 7) or 10 μm ω-conotoxin MVIIC (n = 7) reduced the tail current. There was no difference between the two; therefore, the results were pooled (n = 14; p < 0.01). Additive application of 200 μm Ni²⁺ reduced the current to 38 ± 3% of its control value, indicating a summation of the two effects (n = 4; p < 0.01). C, The voltage dependence of activation of the Ni²⁺-sensitive component was studied by varying the level of the 5 ms voltage step (inset). The tail current was normalized to the maximum and plotted against the voltage of the step. The result was fit with a Boltzmann equation, yielding an average V_1/2 = 2.5 ± 9.6, k = 11 ± 7.6 (n = 6). A representative example is shown. D, The test pulse was preceded by a 1 s prepulse varying from -90 to -20 mV to study voltage-dependent inactivation of the Ni²⁺-sensitive tail current (inset). After normalizing to the maximum value, the tail current amplitude was plotted against the voltage of the prepulse and fit with a Boltzmann equation, where the average V_1/2 = -60.9 ± 3.1, and k = 7.9 ± 3.0 (n = 6). A representative example is shown.

Data acquisition and analysis. Data were transferred to a computer during experiments by either an ITC-18 digital-to-analog converter (InstruTech, Port Washington, NY) or a Digidata 1322A (Molecular Devices). Both IgorPro (WaveMetrics, Lake Oswego, OR) and pClamp (Molecular Devices) software were used for acquisition and analysis. Statistical tests were performed using Excel software (Microsoft, Redmond, WA) or GB-STAT (Dynamic Microsystems, Silver Spring, MD). All results are reported as mean ± SE, and significance was determined by paired two-tailed t tests, unless otherwise indicated.

The ADP is reported as the average membrane potential, relative to the resting membrane potential (for 50 ms before the spike), in the first 10 ms after the fast phase of action potential repolarization (the point at which the change in voltage with time reached a minimum as detected in the derivative of the waveform). In each cell, between 3 and 12 current injection-evoked ADPs were used for analysis in a given experimental condition. Threshold was defined as the point at which the change in voltage with time met or exceeded 28 mV/ms using the derivative of the waveform and was confirmed by eye as being the inflection point at which an action potential began. Threshold values are reported relative to the resting membrane potential (for 50 ms before the spike). Input resistance was determined from the slope of the steady-state voltage versus current plot that resulted from giving 600 ms current injections ranging from -150 to 50 pA. The concentration-response relationship of the block of the ADP by Ni²⁺ was determined by fitting the data with a Hill equation in the form of V = V_max/(1 + ([Ni²⁺]/K_d)ⁿ), where V is the voltage amplitude of the ADP relative to control, V_max is the control amplitude, [Ni²⁺] is the concentration of Ni²⁺, K_d is the half-maximal concentration, and n is the Hill coefficient.

Voltage dependence of activation was determined after normalizing to the maximum current. The resulting values were fit with a Boltzmann equation with the form f(V) = I/(1 + exp((V - V_1/2)/k), where I is the normalized current, V_1/2 is the voltage at which the activation is half-maximal, and k is the slope factor. The voltage dependence of inactivation was similarly determined using a Boltzmann equation: f(V) = I/(1 + exp((V_1/2 - V)/k)). The time course of current deactivation was determined by fitting control currents with a biexponential equation, f(t) = A₁exp(-t/τ₁) + A₂exp(-t/τ₂), yielding two time constants (τ₁ and τ₂) and their amplitudes (A₁ and A₂). When time constant measurements were performed first in control conditions and then during the application of pharmacological agents, a four-variable (fast and slow time constants and their relative amplitudes) best fitting was performed only in control conditions. In the presence of the drug(s), the time constants were constrained to their values in control, and only the relative amplitudes were left as free parameters. This assumes that the effect of the drugs on current decay was negligible compared with their ability to selectively block some current components.

Results

Action potential bursting and the ADP

To characterize the action potential firing mode of CA1 pyramidal neurons, we assessed the response of 132 cells to 600-1000 ms current injections through the somatic recording electrode during whole-cell current-clamp recordings in hippocampal slices. The intensity of the current injection was 10% above rheobase for spiking. This stimulus evoked a consistent response across trials. The majority of cells responded with a train of regularly spaced action potentials (Fig. 1A, top trace). The remaining cells demonstrated action potential bursting, in which a pair of action potentials in the train, usually the first two, occurred in a burst (Fig. 1A, bottom trace). The distinction between these two types of responses was captured by comparing the shortest interspike interval (ISI) with the mean ISI of the response in each cell (ISI ratio). In regular spiking (RS), this produces a ratio of ∼1; however, in bursting, it gives a much smaller value. A histogram of this ratio shows that burst-spiking (BS) cells represent a distinct population with an ISI ratio of ≤0.1 (Fig. 1B). In the 21 of 132 (16%) neurons that demonstrated action potential bursting in this manner, the frequency of firing within a burst was 142 ± 10 Hz.

Because these recordings were obtained in the presence of synaptic blockers, the ability to burst reflects an intrinsic property of the neurons. Shortening the current injection to 5 ms removed the sustained depolarization caused by the longer current injection, revealing the time course of intrinsic repolarization after a single action potential. All cells, regardless of their action potential firing mode, demonstrated a prominent ADP (Fig. 1C). We investigated whether the size of the ADP correlates with firing mode. To quantify the ADP, we averaged the membrane potential in the first 10 ms after the fast phase of repolarization and compared this with the resting membrane potential before the spike. This measure reflects the amount of depolarization toward threshold throughout the time window in which the second spike occurs in bursting. Burst-spiking cells had significantly larger ADPs than RS cells (15.1 ± 0.2 mV in RS cells, n = 111; 18.8 ± 0.7 mV in BS cells, n = 21; p < 0.01) (Fig. 1C,D). In burst-spiking responses, it appeared that the second spike in a burst was driven by the ADP. To test this, we determined whether the size of the ADP correlated with the ease with which a second action potential could be evoked. After the first spike was elicited with a 5 ms current injection (5% above rheobase), we injected a transient current during the ADP. The amplitude of the second current injection was increased until it was large enough to produce a second spike. We then took the ratio of the second injection to the first and called this the “burst current” (Fig. 2A). The burst current is therefore larger in cells that required more current to evoke the second spike. This allowed us to assay the propensity for burst spiking in all cells regardless of their response to a 600 ms current injection. In keeping with our hypothesis, cells with larger ADPs tended to have a lower burst current (n = 97; r² = 0.56; p < 0.01) (Fig. 2B). Another factor that may have influenced the burst current is the threshold for the second action potential. It may have been that bursting cells have a lower threshold for the second action potential, indicating that they have higher sodium channel availability, or conversely, that the prolonged depolarization the ADP provides increases inactivation and raises the threshold for the second spike in cells that spike regularly. Neither was the case, however, because the burst current did not correlate with the threshold, measured relative to the resting potential, for the second spike (n = 97; r² = 0.0029; p > 0.05) (Fig. 2C). Other action potential characteristics did not differ between regular-spiking and burst-spiking cells, including spike amplitude and half-width (data not shown). Higher input resistance could also have accounted for the propensity to burst; however, the burst current was positively correlated with input resistance (n = 77; r² = 0.1134; p < 0.05) (Fig. 2D), suggesting that passive properties do not determine the propensity to burst but rather that an active component enhances the ADP.

Figure 2.

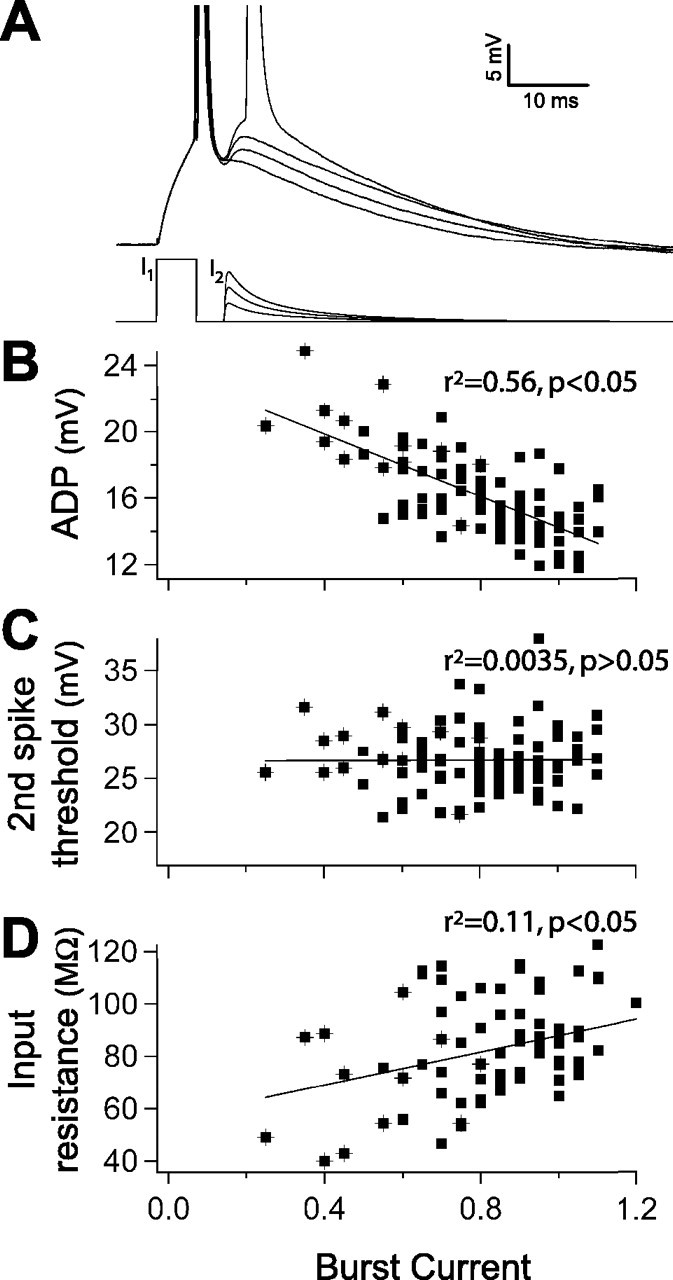
ADP size determines burst current. A, The burst current. A biexponential current was injected during the peak of the ADP (bottom traces). The amplitude of this current was increased until a second spike was evoked (top traces, representative cell). The burst current was calculated as the amplitude ratio of the second current injection (I₂) to the first current injection (I₁). B, Inverse relationship between the size of the ADP and the burst current (n = 97). C, The threshold for the second spike does not influence the burst current (n = 97). D, Burst current varies directly with input resistance (n = 77). B-D, Symbols marked with crosshairs indicate burst-spiking cells.

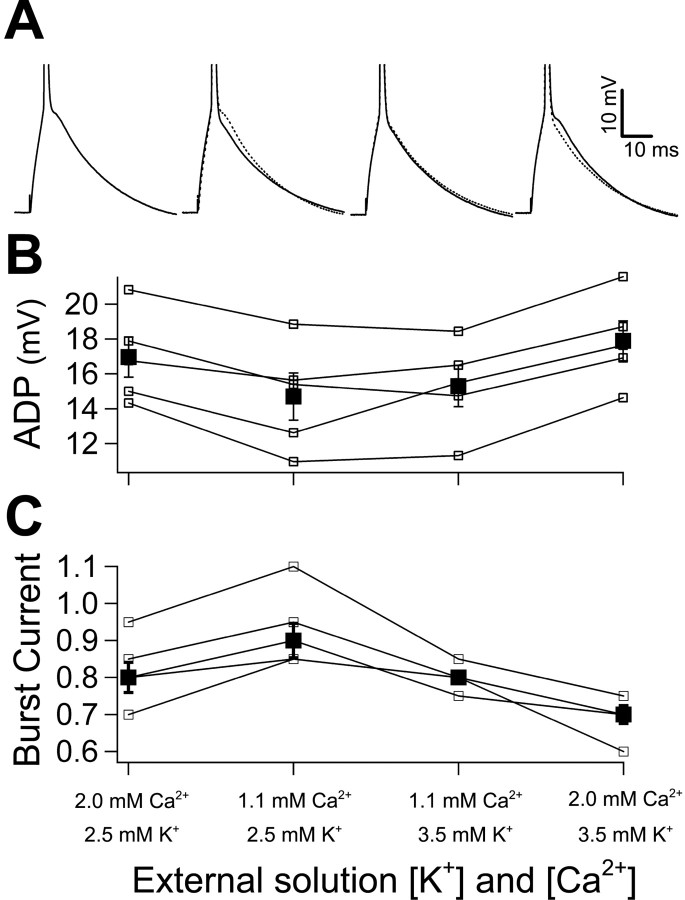
Having established that the ADP correlates with bursting, we studied its ionic mechanism. We varied the concentrations of calcium and potassium in the extracellular solution in a stepwise manner (n = 5) (Fig. 3) and observed the changes in the size of the ADP and burst current to infer which ionic currents contribute to the mechanism underlying bursting. Previous studies provide conflicting reports regarding the role of calcium in CA1 bursting. Magee and Carruth (1999) suggest that bursting is calcium dependent, whereas Azouz et al. (1996) and Su et al. (2001) propose that lowering or removing calcium results in an upregulation of a persistent sodium current that is essential for bursting. We attempted to differentiate between these possibilities by lowering, but not eliminating, calcium with equimolar substitution of magnesium. This led to a reduction in the ADP (17 ± 1.2 mV in 2.0 mm Ca²⁺; 14.7 ± 1.4 mV in 1.1 mm Ca²⁺) with a corresponding increase in the burst current (0.82 ± 0.04 in 2.0 mm Ca²⁺; 0.93 ± 0.05 in 1.1 mm Ca²⁺). This lends support to the hypothesis that the mechanism underlying bursting is dependent on extracellular calcium. We also investigated whether potassium currents act to inhibit bursting. We increased the concentration of potassium from 2.5 to 3.5 mm, which is closer to the value measured in the CSF of rats (Manthie at al., 1973). Membrane potential was maintained at -67 mV, with DC injection as needed. With the change in external potassium, the ADP increased in size (15.3 ± 1.2 mV in 2.0 mm Ca²⁺/3.5 mm K⁺), and the burst current decreased (0.80 ± 0.02 in 3.5 mm K⁺). This points to a role for potassium in resisting bursting. Finally, when we restored the concentration of calcium to 2.0 mm, the size of the ADP increased to its largest value (17.9 ± 1.1 mV in 2.0 mm Ca²⁺/3.5 mm K⁺), and the burst current was at its lowest value in this condition (0.69 ± 0.02 in 2.0 mm Ca²⁺/3.5 mm K⁺). The patterns of change in the ADP and burst current during this series of ionic changes were found to be significant (p < 0.01) when evaluated using an ANOVA, suggesting that calcium currents underlie the ADP and propensity to burst, whereas potassium currents act to oppose this active mechanism for bursting. In a larger population of cells (n = 32), the increase in the size of the ADP in the elevated potassium condition was accompanied by a parallel increase in the percentage of burst-spiking cells (25% compared with 16% in our control condition).

Figure 3.

Changing ionic conditions reveals that calcium currents contribute to the ADP, whereas potassium currents inhibit the ADP. A, The ADP in the same representative cell as the ionic concentrations was changed in a stepwise manner. Solid traces were recorded in the condition indicated in the graph, and dashed traces are from the previous condition. Equimolar magnesium was substituted for calcium. B, Open, connected symbols represent the size of the ADP in each cell across ionic conditions (n = 5). Filled symbols represent the average. Decreasing calcium reduces the size of the ADP. An additive increase in potassium results in a larger ADP. Restoration of calcium yields the largest ADP. C, The burst current in each cell (open, connected symbols; n = 5) and the average (filled symbols) in each ionic condition. Changes in the burst current are consistently opposite to the change in the size of the ADP. The patterns of change in the ADP and burst current during this series of ionic changes shown in B and C were found to be significant (p < 0.01) when evaluated using an ANOVA.

To test for the role of voltage-gated calcium currents in mediating the ADP, we began by using the calcium channel blocker Ni²⁺, which decreased the size of the ADP in a concentration-dependent manner. Reduction was observed at concentrations as low as 12.5 μm and saturated at 200 μm Ni²⁺ (Fig. 4A,B), where the ADP was 12.6 ± 0.8 mV compared with 15.3 ± 0.9 mV in control (n = 9; p < 0.01). The decrease in the size of the ADP in Ni²⁺ was accompanied by a parallel increase in the burst current (0.71 ± 0.06 in control; 1.02 ± 0.11 in 200 μm Ni²⁺; n = 7; p < 0.05) (Fig. 4B, right, BC). The data were fit with a Hill equation yielding a half-maximal block at 40 ± 4 μm Ni²⁺. Local application of Ni²⁺ (at 2 mm to allow for 10-fold dilution) to the soma produced an equivalent decrease in the size of the ADP (15.7 ± 1.4 mV in control; 12.8 ± 1.3 mV with Ni²⁺; n = 4; p < 0.01) (Fig. 4B, center), indicating that the relevant channels are located in or near the soma. With 200 μm Ni²⁺ being maximally effective in reducing the ADP, we investigated whether it would also block bursting. To increase the incidence of bursting, we raised external potassium from 2.5 to 3.5 mm. In the cells that exhibited bursting under this condition (n = 4 of 15), 200 μm Ni²⁺ blocked bursting (n = 4 of 4) (Fig. 4C). In this high-K⁺ condition, 200 μm Ni²⁺ continued to be effective in reducing the ADP (17.1 ± 1.0 mV in control; 15.0 ± 0.8 mV in 200 μm Ni²⁺; n = 15; p < 0.01) and increasing the burst current (0.75 ± 0.04 in 3.5 mm K⁺; 1.02 ± 0.1 in 200 μm Ni²⁺/3.5 mm K⁺; n = 10; p < 0.01). Ni²⁺ has been shown to also partly block sodium currents (Jung et al., 2001); however, 200 μm Ni²⁺ did not affect action potential threshold measured relative to the resting potential (19.3 ± 1.0 mV in control; 19.6 ± 2.0 mV in 200 μm Ni²⁺; n = 15; p > 0.05) (Fig. 4B, right, T). The ADP was resistant to the selective calcium channel antagonists nimodipine (16.1 ± 0.9 mV in control; 16.9 ± 1.2 mV in 10 μm nimodipine; n = 7; p > 0.05) and ω-conotoxin MVIIC (15.0 ± 0.90 mV in control; 16.3 ± 0.8 mV in 10 μm ω-conotoxin MVIIC; n = 4; p > 0.05), which block L-type and N/P/Q-types, respectively. In each experiment, the potency of the ω-conotoxin MVIIC was tested by observing the complete and maintained block of EPSPs evoked via stimulation in stratum radiatum. Ca_V2.3 subunits have been shown to contribute to R-type current in CA1 pyramidal neurons (Sochivko et al., 2002); however, the Ca_V2.3 (α_1e) blocker SNX-482 (1 μm), when applied locally to the soma, did not decrease the size of the ADP (14.7 ± 0.8 mV in control; 15.0 ± 0.8 mV with SNX-482; n = 5; p > 0.05). The potency of SNX-482 was ensured in a parallel experiment, in which the application of SNX to subicular neurons actually increased the ADP (data not shown), possibly by indirectly reducing a Ca²⁺-activated K⁺ current (Jung et al., 2001).

We wanted to test the possibility that persistent sodium current contributes to the ADP, as has been suggested previously (Azouz et al., 1996; Su et al., 2001). Again, increasing the extracellular potassium concentration to 3.5 mm induced bursting (5 of 11 cells). A 10 nm concentration of TTX stopped bursting in five of eight cells (Fig. 5A); however, when testing the effects of 10 nm TTX in standard ionic conditions, the depolarization achieved by the ADP was not decreased (14.6 ± 0.5 mV in control; 14.4 ± 0.5 mV in 10 nm TTX; n = 8; p > 0.05) (Fig. 5B, left, top traces, C, ADP). The burst current did increase (0.85 ± 0.04 in control; 1.05 ± 0.05 in 10 nm TTX; n = 8; p < 0.01) (Fig. 5C, BC), but this likely reflects the increase in threshold, which increased (21.2 ± 0.5 mV in control; 22.8 ± 1.1 mV in 10 nm TTX; n = 8; p < 0.01) (Fig. 5C, T). In addition to increased threshold, a decrease in spike amplitude (67 ± 2 mV from threshold in control; 61 ± 3 m V in 10 nm TTX; n = 8; p < 0.05) (Fig. 5C, SA) is additional evidence of the effectiveness of 10 nm TTX in blocking a fraction of the transient sodium current. We verified the efficacy with which we blocked persistent sodium current by examining the effect of 10 nm TTX on subthreshold voltage amplification, a phenomenon attributed to persistent sodium current. Stuart and Sakmann (1995) reported TTX-sensitive (0.5-1 μm) amplification of EPSPs at depolarized potentials and suggested that this “boosting” is attributable to persistent sodium current because of the slow time course of the EPSPs. We gave a 200 pA, 5 ms current injection at two holding potentials (-65 and -55 mV) in control solution, in 10 nm TTX, and subsequently, in 250 nm TTX. We compared the change in the size of the response by calculating the integral of the decaying phase (peak-to-rest). At -65 mV, there was no amplification of the subthreshold response, because it was the same in control and in 250 nm TTX (Fig. 5B, left, bottom traces). At -55 mV, the subthreshold response was amplified 29 ± 1%, as determined by comparing the control condition with 250 nm TTX. A 10 nm concentration of TTX reduced this amplification by 28 ± 1% (n = 3; p < 0.01) (Fig. 5B, right, bottom traces). At this same potential, 10 nm TTX continued to have no effect on the ADP (Fig. 5B, right, top traces). We therefore infer that we effectively reduced persistent sodium current without affecting the ADP. These results suggest that sodium current is essential in determining action potential firing mode and spike characteristics but does not contribute measurably to the ADP under these ionic conditions. To quantify the effect of this concentration of TTX in blocking sodium currents, we tested it on nucleated patches. We isolated sodium currents by blocking potassium currents with cesium-based internal solution, external TEA (10 mm), and 4-AP (5 mm), by blocking calcium currents with external cadmium (100 μm), and by blocking I_h with external CsCl (1 mm). From a holding potential of -90 mV, patches were stepped to +30 mV. The peak sodium current activated quickly and demonstrated typical fast inactivation. A 10 nm concentration of TTX reduced the peak transient current by 49 ± 7% (n = 6; p < 0.01) (Fig. 5D), in good agreement with the findings of Madeja (2000). Thus, blocking nearly one-half of the sodium current stops bursting by raising the action potential threshold but does not reduce the size of the ADP.

Figure 5.

Sodium current contributes to bursting but not the ADP. A, The response to a 600 ms current injection in a representative cell in the elevated potassium condition (3.5 mm K⁺; left trace) and with subsequent application of 10 nm TTX (right trace). The increased potassium induced the bursting, which was then blocked by TTX. B, Left, Top traces, The ADP in a representative cell (solid trace) is not reduced by 10 nm TTX at -65 mV. Right, Top traces, The ADP is not reduced by 10 nm TTX when evoked from -55 mV. Left, Bottom traces, The subthreshold response is not amplified in a TTX-sensitive manner at -65 mV. Right, Bottom traces, At -55 mV, the subthreshold response is amplified 29 ± 1% (compare control with 250 nm TTX), and 10 nm TTX reduces this amplification (28 ± 3%; n = 3; p < 0.01). C, Bar chart (n = 8) of the size of the ADP (^* p > 0.05), burst current (BC; ^**p < 0.01), spike amplitude (SA; ^**p < 0.05), and threshold (T; ^**p < 0.01) in 10 nm TTX relative to control for the population of cells. D, Averaged fast, transient current in control (thin trace) and 10 nm TTX (thick trace) in a representative nucleated patch stepped to +30 mV from a holding potential of -90 mV (inset). This concentration of TTX blocked 49 ± 7% of the peak current (n = 6; p < 0.01).

Bursting has been shown to increase with age (Smith et al., 2000); however, the relationship of the ADP to bursting and its mechanism was conserved when tested in a group of slightly older animals (P30-P35; n = 13). The size of the ADP correlated inversely with the burst current (r² = 0.59). Similar to young animals, 200 μm Ni²⁺ reduced the size of the ADP (14.3 ± 0.9 mV in control; 13.2 ± 0.8 mV in 200 μm Ni²⁺; p < 0.05) and increased the burst current (0.86 ± 0.1 in control; 1.1 ± 0.1 in 200 μm Ni²⁺; p < 0.01; experiments in the 3.5 mm K⁺ condition to maximize ADP). In the raised potassium condition, one cell exhibited bursting, which was blocked by Ni²⁺.

Calcium currents in nucleated patches

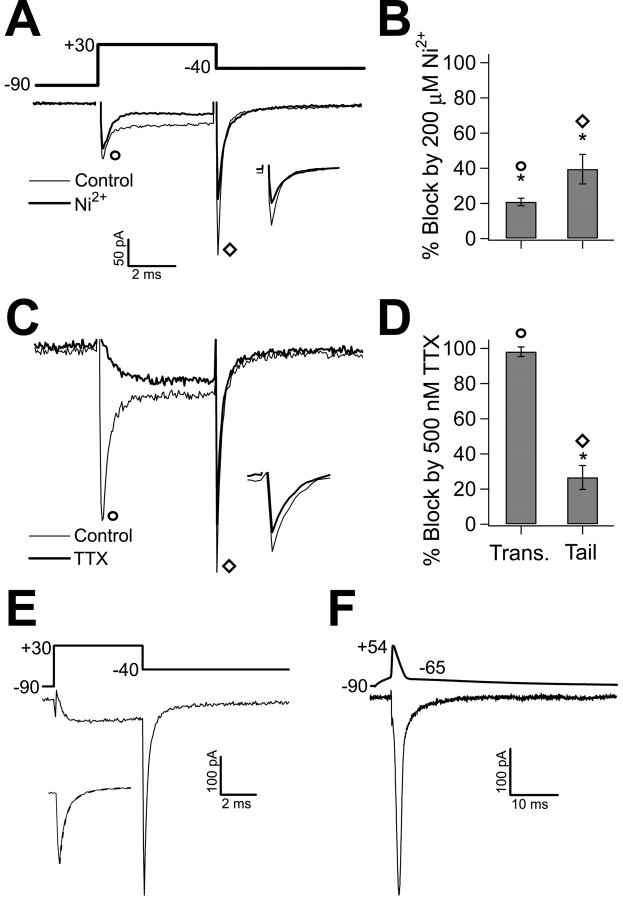
We next investigated the ionic currents that could contribute to the ADP. With a cesium-based internal solution and an external solution containing TEA (>80 mm), 4-AP (5 mm), and CsCl (1 mm), we stepped nucleated patches from -90 to +30 mV for 5 ms, followed by repolarization to -40 mV. This produced fast transient inward current during the step and, after repolarization, an inward tail current with a duration determined by the time course of deactivation (Fig. 6A). The peak amplitude of the tail current was -261 ± 64 pA (n = 6). As a first step in identifying the current, we applied the maximally effective concentration of Ni²⁺ (200 μm) to the patches. The fast transient evoked during the step was decreased by 21 ± 2% (n = 6; p < 0.01) (Fig. 6A,B), and the tail current was reduced 40 ± 8% (n = 6; p < 0.01) (Fig. 6A,B). Although the isolated sodium current did inactivate during the 5 ms step (98 ± 2%; n = 6), we cannot rule out a contribution of sodium current to the tail current. We therefore completely blocked the fast transient current with 500 nm TTX, decreasing the tail current by 27 ± 7% (n = 9; p < 0.01) (Fig. 6C,D). The current that remained in the presence of 500 nm TTX demonstrated slower activation, such that, at the time point at which the sodium current peaked, the TTX-resistant current was only just appearing (Fig. 6C). This allows us to conclude that the Ni²⁺ block of the fast transient current (21 ± 2%) (Fig. 6A,B) was attributable to an effect on sodium currents, as seen previously in the subiculum (Jung et al., 2001). Because Ni²⁺ reduced the sodium current by 21% and a component of the tail current was sensitive to 500 nm TTX (27%), we can infer that the reduction of the tail current by Ni²⁺ is only minimally attributable to block of sodium current (21% of 27% = 5.7%). The largest component of the tail current was resistant to TTX, indicating involvement of calcium currents.

Figure 6.

The inward tail current mostly consists of calcium current. A, In nucleated patches, 5 ms steps to +30 mV from a holding potential of -90 mV evoked inward current with a fast transient peak, moderate inactivation, and a prominent tail after the return step to -40 mV. The thin trace is averaged current recorded in a representative cell in the control condition. Ni²⁺ (200 μm) reduced both the transient current and the tail current (thick trace). Inset, The tail current on an enlarged scale in control and Ni²⁺. B, Bar chart (n = 6) of transient (circle; ^*p < 0.01) and tail (diamond; ^*p < 0.01) current block by 200 μm Ni²⁺. C, Application of 500 nm TTX produces a small block of the tail current and eliminates the fast transient current. The averaged control current is shown by the thin trace for a representative cell, the current resistant to 500 nm TTX is shown by the thick trace, and the inset shows the tail current on an enlarged scale in control and TTX. Calibration bar in A also applies to C. D, Bar chart of transient (Trans.; circle; n = 7; p < 0.01) and tail (diamond; n = 5; ^*p = 0.01) current block by 500 nm TTX. E, From a holding potential of -90 mV, a 5 ms step to + 30 mV evokes a slowly activating current. The tail current produced by the subsequent step to -40 mV demonstrates fast deactivation resembling that evoked by the action potential/ADP voltage command. Inset, The tail current fit with a double exponential (dashed line), the slow component (34% of the total tail current) had a τ of 5.0 ms, and the fast component had a τ of 141 μs. Averaged recording from a representative nucleated patch in calcium current isolating conditions [5 mm Ba, 300 nm TTX, 1 mm CsCl, 5 mm 4-AP, and >100 mm TEA (and CsCl internal solution) is shown. F, Averaged recording in the same conditions as E. Using a prerecorded action potential with an ADP as a voltage command evokes an inward current that activates at the peak of the spike and peaks at the beginning of the ADP. Error bars represent SEM.

To better isolate currents carried by calcium channels, we replaced calcium with 5 mm barium as a charge carrier, which further blocks potassium currents and prevents activation of calcium-activated potassium current, and continued to block sodium currents with 300 nm TTX. The resulting currents were completely blocked with 200 μm Cd²⁺, indicating that we successfully isolated calcium channels. Under these conditions, the peak amplitude of the tail current from a holding potential of -90 mV was -323 ± 32 pA (n = 34) (Fig. 6E). There could be two explanations for the increase in the size of the tail current. First, we may have obtained better isolation of inward currents, because barium will not activate calcium-dependent potassium conductances, and it blocks potassium currents. Second, many calcium channels are known to be more permeable to barium than calcium (Bean, 1989; Williams et al., 1994; Bourinet et al., 1996; Tottene et al., 2000). To determine whether an action potential evokes the isolated current that could contribute to the ADP, we used an action potential recorded from an intact cell as the voltage command. An inward current appeared at the peak of the action potential voltage command and reached its maximum value during the repolarization just before the ADP. This current decayed before the potential returned to rest (Fig. 6F) and closely resembled the current evoked by the square-pulse waveform (Fig. 6E); therefore, we used square-pulse protocols for additional characterization of the tail current.

We proceeded to compare the pharmacological profile of the tail current with that of the ADP. A 200 μm concentration of Ni²⁺ reduced the barium-mediated tail current by 38 ± 8% (n = 14; p < 0.01) (Fig. 7B), similar to the reduction seen when both calcium and sodium currents were present (40 ± 8%). We then applied mixtures of the selective calcium channel toxins including the L-type blocker nimodipine (10 μm) in combination with either N/P- and Q-type blockers (100 μm ω-conotoxin GVIA and 100 nm ω-agatoxin IVA; n = 7) or an N/P/Q-type blocker (10 μm ω-conotoxin MVIIC; n = 7). Because the reduction produced by the two approaches was similar (p > 0.05), we pooled the data, resulting in a 23 ± 5% reduction of the tail current (n = 14; p < 0.01) (Fig. 7A,B, Mix). When the depolarizing step was extended to 200 ms, the mixtures blocked 50 ± 9% of the steady-state current (data not shown) in accordance with literature reports (Sochivko et al., 2002, 2003). The mixture-resistant tail current was further reduced by subsequent application of 200 μm Ni²⁺ (55 ± 0%; n = 4; p > 0.05). A representative example of this experiment is shown in Figure 7A. The combination of mixture and Ni²⁺ reduced the tail current by 62 ± 3% (n = 4; p < 0.01) (Fig. 7B), near the linear sum of the block produced by each applied separately. These data indicate that 200 μm Ni²⁺ is selective in blocking a component of the tail current that is resistant to selective antagonists.

To further characterize the calcium tail current, we analyzed its time course of deactivation (Table 1). The total calcium tail current, in control conditions, demonstrated biexponential decay with a fast component (τ_fast = 340 μs) constituting the majority (92%) of the current and a slower component (τ_slow = 5.8 ms) contributing the remainder of the current (n = 31) (see fit in Fig. 6F). The Ni²⁺-sensitive component, obtained by digital subtraction after application of 200 μm Ni²⁺ either in control conditions or in the presence of specific calcium channel blockers, exhibited nearly identical biexponential decay. The current resistant to both specific blockers and Ni²⁺ also exhibited biexponential decay, although the slow component was slightly larger (Table 1).

Table 1.

Deactivation time constants of calcium tail currents

	Slowly deactivating component (% of total tail current)	Slow τ (ms)	Rapidly deactivating component (% of total tail current)	Fast τ (μs)
Control (n = 31)	8 ± 1	5.8 ± 0.3	92 ± 1	340 ± 31
Ni2+ sensitive (n = 13)	3 ± 1	5.5 ± 0.6	97 ± 1	311 ± 18
Mix resistant (n = 15)	8 ± 2	5.6 ± 0.4	92 ± 2	343 ± 31
Ni2+ sensitive, Mix resistant (n = 5)	4 ± 3	6.5 ± 0.9	96 ± 3	344 ± 68
Mix resistant, Ni2+ resistant (n = 5)	15 ± 5	5.5 ± 0.7	85 ± 5	357 ± 57

Finally, to examine voltage-dependent activation of the Ni²⁺-sensitive component of the tail current, the 5 ms test pulse was increased in 10 mV increments from -70 to +70 mV from the holding potential of -90 mV (Fig. 7C, inset). Fitting of the normalized tail current with a Boltzmann equation gave a half-activation value of 2.5 ± 7.6 mV (n = 6) (Fig. 7C). The mixture-resistant, Ni²⁺-sensitive current had a half-activation voltage of -3.0 ± 6.9 mV (n = 3; data not shown), not significantly different from the activation of the Ni²⁺-only sensitive current (p > 0.05). This is consistent with the notion that the Ni²⁺-senstive currents are the same, regardless of whether specific channel blockers are applied first. We also examined the availability of the Ni²⁺-sensitive tail current from different holding potentials. The test pulse was given after holding for 1 s at potentials varying from -90 to -20 mV, in 20 mV increments (Fig. 7D, inset). The tail current exhibited voltage-dependent inactivation that reached one-half of its maximal value at -60.9 ± 3.0 mV (n = 6) (Fig. 7D).

Discussion

Our findings support the conclusion that an active component of the ADP is mediated by an Ni²⁺-sensitive, high-threshold current, most consistent with R-type calcium current. The conductance is activated by the action potential, and the current increases with the enhanced driving force as the action potential repolarizes. The resulting ADP can trigger a second action potential, thus leading to intrinsic burst firing.

R-type versus T-type calcium current

Both T- and R-type calcium currents are sensitive to Ni²⁺ and resistant to selective antagonists (Bean, 1989; Tsien et al., 1991; Soong et al., 1993; Zhang et al., 1993; Eliot and Johnston, 1994; Tottene et al., 1996, 2000; Zamponi et al., 1996; Yu and Shinnick-Gallagher, 1997; Lee et al., 1999; Foehring et al., 2000; Sochivko et al., 2002, 2003); however, the majority of the blocker-resistant calcium current in CA1 pyramidal neurons has been attributed to R-type current (Sochivko et al., 2002, 2003). In voltage clamp, the high half-activation voltage and rapid deactivation of the calcium tail current are more consistent with R-type current than T-type current (Bean, 1989; Takahashi et al., 1991; Tsien, 1991; Ellinor et al., 1993; Randall and Tsien, 1995, 1997; Hilaire et al., 1997; Yu and Shinnick-Gallagher, 1997; Nakashima et al., 1998; Piedras-Renteria and Tsien, 1998; Foehring et al., 2000; Magistretti et al., 2000; Tottene et al., 2000; Wilson et al., 2000; Lee et al., 2002). Furthermore, nimodipine, which has been shown to block T-type but not R-type calcium channels (Randall and Tsien, 1997), had no effect on the ADP. Other properties of the ADP and bursting in CA1 are unlike bursts driven by T-type current. In the thalamocortical neurons, bursts are driven by a low-threshold calcium spike, which inactivates at depolarized holding potentials (Deschenes et al., 1982; Llinas and Jahnsen, 1982; McCormick and Huguenard, 1992). In contrast, we observed no indication of subthreshold calcium channel activation (i.e., subthreshold responses lacked a depolarizing shoulder) or voltage-dependent inactivation of the ADP or bursting. These characteristics suggest that T-type calcium current is not a major contributor to the ADP or bursting in CA1 and are more consistent with a contribution from the R-type calcium current.

A novel role for R-type calcium current

In CA1 pyramidal neurons, R-type calcium current has been shown to be the source of calcium entry during backpropagating action potentials (Christie et al., 1995), local synaptic input (Magee and Johnston, 1995b; Magee et al., 1995), and synaptic plasticity (Isomura et al., 2002). R-type calcium channels are also modulated by LTP-inducing stimuli, resulting in increased calcium entry into dendritic spines (Yasuda et al., 2003), and they play a role in apoptosis associated with juvenile myoclonic epilepsy (Suzuki et al., 2004). In other cell types, R-type current contributes to neurotransmitter release (Wu et al., 1998; Gasparini et al., 2001) and presynaptic plasticity (Dietrich et al., 2003). Our study is the first to identify R-type currents as an important contributor to intrinsic burst firing. We were not able to identify the molecular identity of the channel underlying the R-type current. Although the ADP was not blocked by the Ca_V2.3 (α_1E) blocker SNX-482, it remains possible that the current underlying the ADP is mediated by an SNX-resistant isoform of Ca_V2.3 (Tottene et al., 2000). In addition, mice lacking Ca_V2.3 subunits still contain blocker-resistant calcium current (Wilson et al., 2000; Lee et al., 2002; Sochivko et al., 2002), so other molecular components may contribute to R-type current.

Somatic and dendritic currents contribute to different kinds of bursting

We estimate that the amount of depolarization caused by the contribution of R-type current is on the order of a few millivolts. A substantial fraction of the R-type current responsible for this component of the ADP appears to be generated near the soma, as indicated by reduction of the ADP during perisomatic application of Ni²⁺ (Fig. 4B) and the presence of an Ni²⁺-sensitive calcium tail current in nucleated patches (Figs. 6, 7) (Magee and Johnston, 1995b; Kavalali et al., 1997). Thus, much of the current that drives intrinsic burst firing may be located perisomatically, where it could exert a strong influence over the spike initiation zone in the axon (Colbert and Johnston, 1996; Colbert and Pan, 2002).

Because R-type current is also present in CA1 dendrites (Christie et al., 1995; Magee and Johnston, 1995b; Magee et al., 1995; Isomura et al., 2002; Yasuda et al., 2003), it may be important during strong synaptic activation, which can lead to bursts driven by dendritic calcium spikes in CA1 pyramidal neurons (Wong and Stewart, 1992; Golding et al., 1999). The role of dendritic R-type current may be especially relevant to bursting after downregulation of dendritic K⁺ currents, which would normally counteract the effects of dendritic R-type current (Hoffman et al., 1997; Magee and Carruth, 1999). Under these conditions, calcium currents in the dendrites can be activated by backpropagating action potentials and feed back into the soma to create the ADP (Mainen and Sejnowski, 1996; Williams and Stuart, 1999; Lemon and Turner, 2000), or they may contribute directly to dendritic spike initiation.

Other factors contributing to the ADP

Blocking the R-type current with Ni²⁺ reduces the ADP substantially and eliminates the “bump” that is most prominent on the ADP of bursting cells (Fig. 1C); however, the terminal decay of the remaining action potential is slow, approximately mirroring the decay of a subthreshold voltage response (Fig. 4B). Despite the passive appearance of this terminal decay, a number of voltage-activated conductances are likely to shape the ADP, including slowly deactivating K⁺ currents (such as M current) (Yue and Yaari, 2004), the hyperpolarization-activated H current, and possibly small T-type Ca²⁺ and Na⁺ currents (see below). The R-type Ca²⁺ current serves to provide additional inward current near the end of the action potential, during a time window that is critical for high-frequency bursting. Although the R-type current deactivates rapidly, its effects are sustained, because the extra charge leaves the cell slowly. Our preliminary attempts to simulate the ADP in a reconstructed CA1 pyramidal neuron model suggest that a rapidly deactivating Ca²⁺ current can indeed produce a sustained effect on the ADP (V. Menon and W. L. Kath, personal communication).

The importance of K⁺ currents in regulating the ADP and bursting is indicated by several observations: first, reducing K⁺ current by raising external K⁺ increases the size of the ADP (Fig. 3) (Jensen and Yaari, 1994); second, blocking voltage-gated K⁺ currents enhances the ADP and bursting (Hoffman et al., 1997; Magee and Carruth, 1999; Yue and Yaari, 2004); third, blocking Ca²⁺-activated potassium currents enhances bursting in subicular pyramidal neurons (Jung et al., 2001). This may also be the case in CA1 (Yue and Yaari, 2004) and is a particularly interesting idea in light of the contribution of N-, P-, Q-, and possibly L-type channel contributions to the calcium tail current during the ADP. The fact that blocking these channels does not reduce the ADP suggests that their activation may be coupled specifically to calcium-activated K⁺ currents. Finally, a substantial component of the calcium tail current is resistant to both specific blockers and Ni²⁺. This “really resistant” calcium current may also contribute to the ADP.

Calcium and sodium currents partner to create bursting

We show that TTX-sensitive voltage-gated sodium current does not contribute directly to the ADP (Fig. 5), which differs from some previous reports (Tian et al., 1995; Alkadhi and Tian, 1996; Azouz et al., 1996; Su et al., 2001). This difference may be attributable to extracellular calcium concentration. We limited our manipulations to a narrow range reflecting physiologically relevant conditions (Manthie et al., 1973). Sodium current plays a more predominant role in creating the ADP under conditions of lower-to-absent calcium, which causes upregulation of persistent sodium current and changes in channel gating (Armstrong and Cota, 1991, 1999; Azouz et al., 1996; Su et al., 2001). Nevertheless, the voltage dependence of sodium channels dictates that at least some sodium current is likely to flow during the ADP. Furthermore, sodium channel inactivation could limit bursting by raising the threshold for the second spike in a manner similar to the effects we show using 10 nm TTX. Thus, we suggest that bursting results from a dynamic partnership between sodium currents, which are responsible for the action potentials and may contribute to the ADP under some conditions, and calcium currents, which contribute directly to the ADP.

Comparison with subicular pyramidal cells

Calcium tail currents also generate the ADP and drive bursting in pyramidal neurons in the subiculum (Jung et al., 2001). As much as 78% of subicular cells burst (Staff et al., 2000), in contrast to the 10% of CA1 cells shown here. This difference is likely attributable to the larger and slower calcium tail current in the subiculum (Jung et al., 2001). Thus, these two populations of hippocampal pyramidal neurons appear to employ similar, calcium-dependent mechanisms of bursting, but with differences in channel composition or regulation determining their markedly different bursting properties. Given the importance ascribed to bursting in the spatial and cognitive functions of the hippocampus, clear identification of the intrinsic currents contributing to bursting is an important step toward understanding the cellular basis of hippocampal function.