NONPARAMETRIC INFERENCE FOR MARKOV PROCESSES WITH MISSING ABSORBING STATE

Abstract

This paper deals with the issue of nonparametric estimation of the transition probability matrix of a non-homogeneous Markov process with finite state space and partially observed absorbing state. We impose a missing at random assumption and propose a computationally efficient nonparametric maximum pseudolikelihood estimator (NPMPLE). The estimator depends on a parametric model that is used to estimate the probability of each absorbing state for the missing observations based, potentially, on auxiliary data. For the latter model we propose a formal goodness-of-fit test based on a residual process. Using modern empirical process theory we show that the estimator is uniformly consistent and converges weakly to a tight mean-zero Gaussian random field. We also provide methodology for simultaneous confidence band construction. Simulation studies show that the NPMPLE works well with small sample sizes and that it is robust against some degree of misspecification of the parametric model for the missing absorbing states. The method is illustrated using HIV data from sub-Saharan Africa to estimate the transition probabilities of death and disengagement from HIV care.

1. Introduction

Continuous time non-homogeneous Markov processes with finite state space and absorbing states play an important role in medicine, epidemiology and public health. Modern medical decision making is frequently based on estimates of the transition probability matrix of an absorbing continuous time Markov process with the ultimate goal to evaluate the cost-effectiveness of different medical strategies. Additionally, absorbing Markov processes are crucial in studies of natural history and prognosis of disease, for the evaluation of the health needs of various populations, and for the monitoring and evaluation of public health programs.

A quite common problem in studies involving absorbing Markov processes is that absorbing state ascertainment is incomplete due to the usual nonresponse or by the study design. A design with planned missing observations on absorbing states can be used to reduce the total cost of the study, in case of expensive absorbing state diagnostic procedures. Moreover, such a design can be used to provide the necessary information to deal with absorbing state misclassification in studies that by default use imperfect diagnostics, such as studies that use electronic health record data (Ladha and Eikermann, 2015; Kolek et al., 2016). In such cases, a gold standard diagnostic procedure is used in a small sample of cases in an absorbing state due to financial or other constraints, while for the remaining cases in an absorbing state gold standard diagnosis is missing. The study design with planned missing observations in the absorbing state can be regarded as a special case of a double-sampling design. Double-sampling designs have been used in the past to deal with misclassification in simpler settings (Tenenbein, 1970; Rahardja and Young, 2011; Rahardja and Yang, 2015).

The issue of nonparametric estimation with missing absorbing state in the competing risks model, which is the simplest Markov process with multiple absorbing states, under a missing at random (MAR) assumption, has recently received some attention. Effraimidis and Dahl (2014) proposed a fully nonparametric estimation approach that does not utilize auxiliary information. This estimator was shown to converge at a rate slower than the usual $\sqrt{n}$ rate. Lee et al. (2014) proposed a $\sqrt{n}$ consistent estimator based on parametric multiple-imputation (Wang and Robins, 1998; Lu and Tsiatis, 2001). Recently, Gouskova et al. (2017) proposed a fully nonparametric estimator which is $\sqrt{n}$ consistent. It is worth noting that none of the aforementioned works developed methodology for simultaneous confidence band construction for the transition probabilities, also known as cumulative incidence functions (CIF) in the competing risks setting. Moreover, Effraimidis and Dahl (2014) and Gouskova et al. (2017) established only pointwise asymptotic normality for their CIF estimators. Finally, the latter fully nonparametric estimation approaches do not utilize auxiliary information, which may be needed in order to make the MAR assumption plausible in practice (Lu and Tsiatis, 2001).

In this work, we address the issue of nonparametric inference for general continuous time non-homogeneous Markov processes with finite state space and missing absorbing state with right-censored and/or left-truncated data, under MAR. We use auxiliary variables in a parametric model for the true absorbing state probabilities and derive a closed-form nonparametric maximum pseudolikelihood estimator (NPMPLE) of the transition probability matrix. The basic idea is to replace the missing absorbing state-specific counting processes by the expected state-specific processes according to the fitted parametric model. This approach was similarly developed by Cook and Kosorok (2004) for the analysis of time to the first event of interest in clinical trials where event ascertainment is delayed. Our method can be regarded as an extension of the modified Kaplan-Meier estimator proposed by Cook and Kosorok (2004) in the sense that we provide an estimator of a general Markov process that describes the complete event history of the population under study, where some absorbing states are missing or their ascertainment is delayed. Using modern empirical process theory we study the asymptotic properties of the NPMPLE for the transition probability matrix and evaluate its performance with finite samples through simulation studies. We show that the estimator is $\sqrt{n}$ consistent and converges weakly to a tight zero mean Gaussian random field. We also develop a methodology for the construction of simultaneous confidence bands. The performance of our NPMPLE with small to moderate samples is satisfactory and, in particular, the NPMPLE seems to be robust against some degree of misspecification of the parametric model for the true absorbing state probabilities. We also propose a formal goodness-of-fit approach for evaluating the parametric assumption regarding this model. As an illustration, the NPMPLE is used to estimate the transition probabilities of disengagement from HIV care and death while in care, using data from the East Africa Regional International Epidemiologic Databases to Evaluate AIDS (IeDEA) Consortium, where death status is incompletely ascertained due to a double-sampling design.

The rest of this article is organized as follows. Section 2 provides an overview of non-homogeneous Markov processes, presents our nonparametric estimation approach and describes a formal goodness-of-fit procedure for the model of the absorbing state probabilities; Section 3 states the asymptotic theory for the NPMPLE and the goodness-of-fit procedure; Sections 4 and 5 present simulation studies and data analysis for the motivating HIV study, respectively. Finally, Section 6 concludes the paper with some remarks. Proofs of the asymptotic theorems and additional simulation results are provided in the Supplementary Materials.

2. Data and Method

Let {X(t) : t ≥ 0} be a continuous time non-homogeneous Markov process with a finite state space ℐ = {0, 1, …, q}. The stochastic behaviour of X can be described by the (q + 1) × (q + 1) transition probability matrix P₀(s, t) = (P_hj(s, t)) with elements

$$P_{\mathit{\text{hj}}}(s,t)=\text{Pr}(X(t)=j|X(s)=h,{𝒳}_{s^{-}})=\text{Pr}(X(t)=j|X(s)=h),h,j\in ℐ,$$

where 𝒳_t = σ〈{N_hj(u) : 0 ≤ u ≤ t, h, j ∈ ℐ}〉 is the σ-algebra generated by the counting processes N_hj(t), which count the direct transitions from state h ∈ ℐ to state j ∈ ℐ, with h ≠ j, in [0, t]. The conditional independence of the transition probabilities from the past history of the process is the so-called Markov property. An absorbing state h is a state for which P_hj(s, t) = 0 for all j ≠ h, and t ∈ (s, τ], while a transient state is a state that is not absorbing. Let 𝒯 = {h₁, …, h_k} ⊂ ℐ denote the absorbing state subspace. The transition probability matrix for Markov processes with absorbing states can be expressed as

$$\mathbf{P}=\left(\begin{array}{cc}\hfill {\mathbf{P}}_{{𝒯}^c}\hfill & \hfill {\mathbf{P}}_{𝒯}\hfill \\ \hfill {\mathbf{0}}_{k\times (q-k+1)}\hfill & \hfill I_k\hfill \end{array}\right),$$

where P_𝒯^c and P_𝒯 are the transition probability submatrices for the transitions from the transient states to the transient states and the absorbing states, respectively, 0_k×(q−k+1) is a k × (q − k + 1) matrix containing zeros and I_k is the k × k identity matrix. The transition intensities are defined as

$${\alpha }_{\mathit{\text{hj}}}(t)=\underset{u\downarrow 0}{\text{lim}}\frac{1}{u}{P}_{\mathit{\text{hj}}}(t,t+u),h\ne j,h,j\in ℐ.$$

Additionally, define the (q + 1) × (q + 1) integrated transition intensity matrix A(t) with elements

$$A_{\mathit{\text{hj}}}(t)={\int }_0^t{\alpha }_{\mathit{\text{hj}}}(u)\mathit{\text{du}},h,j\in ℐ,$$

where α_hh ≡ − Σ_j≠h α_hj due to the fact that Σ_j P_hj(s, t) ≡ 1 for all s, t ∈ [0, τ] by the definition of a stochastic matrix. Then, the transition probability matrix can be defined as the product integral of the cumulative transition intensity matrix (Andersen et al., 1993)

The observations from n i.i.d. subjects that are followed over the interval [0, τ] with τ < ∞, are the counting processes N_ihj(t), which count the observed direct transitions from h to j of subject i = 1, …, n on [0, t], and the at-risk processes Y_ih(t), which are the indicator processes that the ith subject is at state h ∈ ℐ just before t. Note that N_ihj(t) can be > 1 for transient states, although we restrict our discussion to the case where the counting processes are uniformly bounded by some finite constant. Right censoring and/or left truncation can be directly incorporated in the at-risk process Y_ih(t), which is no longer a monotonic function due to both left truncation and the fact that subjects may visit a transient state more than 1 times. The counting processes N_ihj(t) are governed by the transition intensities of the form λ_hj(t) = α_hj(t)Y_h(t), with h ≠ j and t ∈ [0, τ].

One can estimate the elements of the integrated transition intensity matrix using the Nelson-Aalen estimator

$${\hat{A}}_{\mathit{\text{hj}}}^{\mathit{\text{N A}}}(t)={\int }_0^t\frac{{\mathit{\text{dN}}}_{·\mathit{\text{hj}}}(u)}{Y_{·h}(u)},h\ne j$$ (2.2)

where $Y_{·h}(t)={\sum }_{i=1}^n{Y}_{\mathit{\text{ih}}}(t)$ and $N_{·\mathit{\text{hj}}}(t)={\sum }_{i=1}^n{N}_{\mathit{\text{ihj}}}(t)$, and the transition probability matrix by the Aalen-Johansen estimator (Aalen and Johansen, 1978)

(2.3)

where ${\hat{\mathbf{A}}}_n^{\mathit{\text{NA}}}$ is the matrix with elements ${\hat{A}}_{\mathit{\text{hj}}}^{\mathit{\text{NA}}}(t)$, h, j ∈ ℐ. As a matter of fact, ${\hat{\mathbf{A}}}_n^{\mathit{\text{NA}}}$ is the nonparametric maximum likelihood estimator (NPMLE) of A₀, the true transition intensity matrix, based on the likelihood for discrete-time Markov chains under the assumption of independent and noninformative right censoring and left truncation (Andersen et al., 1993):

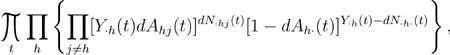(2.4)

where A_h·(t) = Σ_j≠h A_hj(t) and N_·h·(t) = Σ_j≠h N_·hj(t). Since the Aalen Johansen estimator (2.3) is a 1-1 function of the NPMLE ${\hat{\mathbf{A}}}_n^{\mathit{\text{NA}}}$, it is also a NPMLE of P₀, the true transition probability matrix (Andersen et al., 1993).

2.1 Inference with Missing Absorbing States

In this paper we assume that the absoring states are MAR. In cases with incomplete absorbing state ascertainment let R_i to be the “response” indicator, with R_i = 1 if the absorbing state has been observed and R_i = 0 otherwise. Additionally, let Z_i ∈ 𝒵 ⊂ ℝ^p be an auxiliary covariate vector that may contain information about the true unobserved absorbing state, such as a diagnosis obtained by an imperfect absorbing state ascertainment procedure and the last state visited prior to the arrival at an the absorbing state. Such information is critical in practice to make the MAR assumption plausible (Lu and Tsiatis, 2001) and to potentially increase the efficiency of the estimator. Next, let δ_ij and ${\delta }_i={\sum }_{j=1}^k{\delta }_{\mathit{\text{ij}}}$ be the indicators that the ith subject has reached the absorbing state j ∈ 𝒯 and any absorbing state, respectively. The observed data for the ith subject are

$$D_i=\{\begin{array}{cc}({\mathbf{N}}_i,{\mathbf{Y}}_i,{\delta }_i,R_i,{\mathbf{Z}}_i)\hfill & \text{if }{\delta }_i=0\hfill \\ ({\mathbf{N}}_i,{\mathbf{Y}}_i,{\mathit{\delta }}_i,R_i,{\mathbf{Z}}_i)\hfill & \text{if }{\delta }_i=1\text{ and }{R}_i=1\hfill \\ ({\mathbf{N}}_i^{\star },{\mathbf{Y}}_i,{\delta }_i,R_i,{\mathbf{Z}}_i)\hfill & \text{if }{\delta }_i=1\text{ and }{R}_i=0,\hfill \end{array}$$

where N_i = (N_ihj : h ≠ j), ${\mathbf{N}}_i^{\star }$ is equal to N_i with N_ihj(t) being replaced by N_ih·(t) = Σ_j∈𝒯 N_ihj(t) for all j ∈ 𝒯 which is a one-jump counting process, Y_i = (Y_i0, …, Y_iq)^T, and δ_i = (δ_i1, …, δ_ik)^T. The absorbing state-specific counting processes can be expressed as N_ihj(t) = δ_ijN_ih·(t), h ∉ 𝒯, j ∈ 𝒯. We propose replacing the missing dN_·hj(t), j ∈ 𝒯, in the logarithm of the likelihood (2.4) which is linear in the missing data dN_·hj(t), by

$$E[{\mathit{\text{dN}}}_{·\mathit{\text{hj}}}(t)|\mathbf{D}]\equiv d{\stackrel{\sim }{N}}_{·\mathit{\text{hj}}}(t)=\sum _{i=1}^n[R_i{\delta }_{\mathit{\text{ij}}}+(1-R_i)E({\delta }_{\mathit{\text{ij}}}|\mathbf{D})]{\mathit{\text{dN}}}_{\mathit{\text{ih}}·}(t),$$ (2.5)

where D denotes the observed data D_i for all i = 1, …, n. Following Cook and Kosorok (2004), we propose replacing E(δ_ij|D) by an estimate π_j(Z_i, β̂_n) based on maximum likelihood under a parametric “working” model (such as the multinomial logit model), using the subjects in any absorbing state with known δ_ij and utilizing the auxiliary information Z_i. This approach is valid under the MAR assumption since:

$$\text{Pr}({\delta }_{\mathit{\text{ij}}}=1|R_i=1,{\mathbf{Z}}_i)=\text{Pr}({\delta }_{\mathit{\text{ij}}}=1|R_i=0,{\mathbf{Z}}_i)\equiv {\pi }_j({\mathbf{Z}}_i,{\mathit{\beta }}_0),$$

where β₀ is the true parameter value. Maximizing the resulting pseudolikelihood, which involves π_j(Z_i, β̂_n), gives the NPMPLEs

$${\hat{A}}_{n,\mathit{\text{hj}}}(t)={\int }_0^t\frac{d{\stackrel{\sim }{N}}_{·\mathit{\text{hj}}}(u;{\hat{\mathit{\beta }}}_n)}{Y_{·h}(u)},h\notin 𝒯,j\in 𝒯,t\in [0,\tau ]$$

and ${\hat{A}}_{n,\mathit{\text{hj}}}(t)={\hat{A}}_{\mathit{\text{hj}}}^{\mathit{\text{NA}}}(t)$ if j ∉ 𝒯, with h ≠ j, of the integrated transition intensities. Now, the NPMPLE of the transition probability matrix is given by the plug-in estimator

(2.6)

where the components of Â_n are Â_n,hj which were given above. Methodology for constructing 1 − α pointwise confidence intervals and simultaneous confidence bands for the components of P₀(s, t) is presented in Section 3 of this paper.

2.2 Goodness-of-Fit Procedure

To simultaneously evaluate the parametric model assumption for π_j(Z_i, β₀), j ∈ 𝒯, we provide a goodness-of-fit procedure. First, we define the (estimated) residual processes $L_j(t;{\hat{\mathit{\beta }}}_n)=n^{-1}{\sum }_{i=1}^n{L}_{\mathit{\text{ij}}}(t;{\hat{\mathit{\beta }}}_n)$, where

$$L_{\mathit{\text{ij}}}(t;{\hat{\mathit{\beta }}}_n)=R_i[N_{i·j}(t)-{\pi }_j({\mathbf{Z}}_i,{\hat{\mathit{\beta }}}_n)N_{i··}(t)],j\in {𝒯}^{(-1)},t\in [0,\tau ],$$

with N_i·j(t) = Σ_h∉𝒯 N_ihj(t) and N_i··(t) = Σ_h∉𝒯 Σ_j∈𝒯 N_ihj(t) being the counting processes that count the transitions to the absorbing state j and to any absorbing state by time t ∈ [0, τ], respectively. Also, 𝒯⁽⁻¹⁾ ⊂ 𝒯 denotes the absorbing state subspace that includes k − 1 absorbing states. Note that only k−1 residual processes are considered since the model for one absorbing state is completely determined by the models for the remaining k − 1 absorbing states. To construct a formal statistical test for goodness of fit and a diagnostic plot for the parametric absorbing state probability model, we follow a procedure similar to that developed by Pan and Lin (2005). First, it can be shown (Supplementary Material) that under the null hypothesis E[L_j(t; β₀)] = 0 we have

$$V_{\mathit{\text{nj}}}(t)\equiv \sqrt{n}{L}_j(t;{\hat{\mathit{\beta }}}_n)=n^{-1/2}\sum _{i=1}^n{\psi }_{\mathit{\text{ij}}}^L(t)+o_p(1)$$

where ${\psi }_{\mathit{\text{ij}}}^L(t)=L_{\mathit{\text{ij}}}(t;{\mathit{\beta }}_0)-{\mathit{\omega }}_i^{T}E[{\dot{\pi }}_j({\mathbf{Z}}_i,{\mathit{\beta }}_0)R_i{N}_{i··}(t)]$, in which ω_i is the ith individual influence function for β̂_n, given by ω_i = I⁻¹(β₀)U_i(β₀) where I(β₀) is the Fisher information about β₀, U_i(β₀) is the individual score function for the ith subject, and π̇_j(Z_i, β₀) = ∂π_j(Z_i, β)/∂β|_β=β0. The influence functions ${\psi }_{\mathit{\text{ij}}}^L(t)$ can be estimated by replacing the unknown components with the corresponding estimated components and the expectation with the sample average, that is

$${\hat{\psi }}_{\mathit{\text{ij}}}^L(t)=L_{\mathit{\text{ij}}}(t;{\hat{\mathit{\beta }}}_n)-{\hat{\mathit{\omega }}}_i^T{n}^{-1}\sum _{i=1}^n[{\dot{\pi }}_j({\mathbf{Z}}_i,{\hat{\mathit{\beta }}}_n)R_i{N}_{i··}(t)],$$

with ω̂_i = Î⁻¹(β̂_n)U_i(β̂_n). Now define ${\hat{V}}_{\mathit{\text{nj}}}(t)=n^{-1/2}{\sum }_{i=1}^n{\hat{\psi }}_{\mathit{\text{ij}}}^L(t){\xi }_{\mathit{\text{ij}}}$, with ξ_ij, i = 1, …, n randomly drawn from N(0, 1). The goodness of fit for the parametric model can be evaluated as follows:

1. Simulate many {ξ_ij}_{i∈{1,…,n},j∈𝒯⁽⁻¹⁾} sets of values from N(0, 1).

2. For each simulated set {ξ_ij}_{i∈{1,…,n},j∈𝒯⁽⁻¹⁾} calculate, given ${\hat{\psi }}_{\mathit{\text{ij}}}^L(t)$, the quantity sup_t∈[0,τ] max_{j∈𝒯⁽⁻¹⁾} |V̂_nj(t)|.

3. Calculate the 1−α percentile of the distribution of sup_t∈[0,τ] max_{j∈𝒯⁽⁻¹⁾} |V̂_nj(t)| values that is denoted by c_1−α.

4. Calculate the simultaneous confidence band for E[L_j(t; β₀)] = 0 as ±n^−1/2ĉ_1−α, and plot it along with the residual processes L_j(t; β̂_n), j ∈ 𝒯⁽⁻¹⁾ and t ∈ [0, τ].

5. Calculate the p-value for the null hypothesis of overall goodness of fit as the proportion of sup_t∈[0,τ] max_{j∈𝒯⁽⁻¹⁾} |V̂_nj(t)| values that are larger than or equal to sup_t∈[0,τ] max_{j∈𝒯⁽⁻¹⁾} |υ_nj(t)|, where υ_nj(t) is the observed value of the V_nj(t) statistic based on the data.

Lack of fit for the parametric model π_j(Z_i, β₀)N_i··(t), j ∈ 𝒯, is indicated with a type I error α if the residual process for at least one j ∈ 𝒯⁽⁻¹⁾ is not contained in the confidence band for E[L_j(t; β₀)] = 0. Equivalently, a p-value less than α provides evidence for lack of fit for at least one absorbing state model. The validity of this approach is ensured by Theorem 3 that is stated in Section 3.

3. Asymptotic Theory

Assume that the following regularity conditions hold:

• C1The follow-up interval is [0, τ], with τ < ∞.
• C2Pr(N_hj(τ) ≤ C) = 1 for some constant C ∈ (0, ∞), for all h, j ∈ ℐ. Also, inf_t∈[0,τ] E[Y_h(t)] > 0, for all h ∉ 𝒯, which implies that the expected number of observations at all transient states is positive for any time t ∈ [0, τ].
• C3C3A₀ is a (q + 1) × (q + 1) matrix-valued function with elements that are continuous functions of bounded variation on [0, τ].
• C4The inverse of the link function for the model of the absorbing state vector δ, has a continuous derivative on compact sets. Also, the corresponding parameter space ℬ is a bounded subset of ℝ^p.
• C5The estimator β̂_n for the true model parameter β₀ for the absorbing states δ is strongly consistent and asymptotically linear, i.e. $\sqrt{n}({\hat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)=n^{-1/2}{\sum }_{i=1}^n{\mathit{\omega }}_i+o_p(1)$, with ω_i being i.i.d., Eω_i = 0 and E‖ω_i‖² < ∞. Additionally, the plug-in estimators of ω_i, ω̂_i for i = 1, …, n satisfy $n^{-1}{\sum }_{i=1}^n{\Vert {\hat{\mathit{\omega }}}_i-{\mathit{\omega }}_i\Vert }^2=o_p(1)$.
• C6The auxiliary covariate vector Z is bounded in the sense that there exists a constant K ∈ (0, ∞) such that Pr(‖Z‖ ≤ K) = 1.

It has to be noted that estimating β₀ using maximum likelihood under a correctly specified generalized linear model and assuming that the proportion of missing data is independent of the sample size implies C5. Before stating the asymptotic theory results we introduce some further notation. First, the NPMPLE can be expressed as

$${\hat{\mathbf{P}}}_n(s,t)=\left(\begin{array}{cc}{\hat{\mathbf{P}}}_{n,{𝒯}^c}(s,t)\hfill & \hfill {\hat{\mathbf{P}}}_{n,𝒯}(s,t)\hfill \\ {\mathbf{0}}_{k\times (q-k+1)}\hfill & \hfill I_k\hfill \end{array}\right).$$

Next, define the influence functions

$${\gamma }_{\mathit{\text{ihj}}}(s,t)=\sum _{l\notin 𝒯}\sum _{m\in ℐ}{\int }_s^t{P}_{0,\mathit{\text{hl}}}(s,u-)P_{0,\mathit{\text{mj}}}(u,t)d{\psi }_{\mathit{\text{ilm}}}(u),$$

for h ∉ 𝒯, j ∈ ℐ, and i = 1, …, n, where

$${\psi }_{\mathit{\text{ilm}}}(t)=\{\begin{array}{c}{\int }_0^t\frac{d{\stackrel{\sim }{N}}_{\mathit{\text{ilm}}}(u;{\mathit{\beta }}_0)}{{\mathit{\text{EY}}}_l(u)}-{\int }_0^t\frac{Y_{\mathit{\text{il}}}(u)}{{\mathit{\text{EY}}}_l(u)}{\mathit{\text{dA}}}_{0,\mathit{\text{lm}}}(u)+{\mathit{\omega }}_i^T{\mathbf{R}}_{\mathit{\text{lm}}}(t)\text{ if }m\in 𝒯\hfill \\ {\int }_0^t\frac{{\mathit{\text{dN}}}_{\mathit{\text{ilm}}}(u)}{{\mathit{\text{EY}}}_l(u)}-{\int }_0^t\frac{Y_{\mathit{\text{il}}}(u)}{{\mathit{\text{EY}}}_l(u)}{\mathit{\text{dA}}}_{0,\mathit{\text{lm}}}(u)\text{ if }m\notin 𝒯\hfill \end{array}$$

for l ≠ m, where ${\mathbf{R}}_{\mathit{\text{lm}}}(t)=E\{(1-R){\dot{\pi }}_m(\mathbf{Z},{\mathit{\beta }}_0){\int }_0^t{[{\mathit{\text{EY}}}_l(u)]}^{-1}{\mathit{\text{dN}}}_{l·}(u)\}$. If l = m then ψ_ill(t) = − Σ_h≠l ψ_ilh(t). Moreover, define

$${\hat{W}}_{n,\mathit{\text{hj}}}(s,t)=\frac{1}{\sqrt{n}}\sum _{i=1}^n{\hat{\gamma }}_{\mathit{\text{ihj}}}(s,t){\xi }_i,0\le s<t\le \tau$$

where γ̂_ihj(s, t) are the estimated influence functions where the unknown quantities have been replaced by their consistent estimators and the expectations by sample averages, and ξ_i are independent draws from N(0, 1). Given regularity conditions C1–C6 the following theorems hold:

Theorem 1

The NPMPLE is uniformly consistent in the sense that

$$\underset{t\in (s,\tau ]}{\text{sup}}\Vert {\hat{\mathbf{P}}}_n(s,t)-{\mathbf{P}}_0(s,t)\Vert \stackrel{\mathit{\text{as}}\ast }{\to }0,$$

for any s ∈ [0, τ), where the norm ‖A‖ stands for sup_h Σ_l|a_hl| for the matrix A = [a_hl].

Theorem 2

The NPMPLE is an asymptotically linear estimator with

$$\sqrt{n}[{\hat{\mathbf{P}}}_n(s,t)-{\mathbf{P}}_0(s,t)]=\frac{1}{\sqrt{n}}\sum _{i=1}^n{\mathit{\gamma }}_i(s,t)+\mathit{\epsilon },$$

where γ_i(s, t) is a matrix-valued function with elements γ_ihj(s, t) that belong to Donsker classes and ε is a (q+1) × (q+1) matrix with elements that are o_p(1). Moreover, Ŵ_n,hj(s, ·) converges weakly conditional on the observed data D to the same limiting process as that of $\sqrt{n}[{\hat{P}}_{n,\mathit{\text{hj}}}(s,·)-P_{0,\mathit{\text{hj}}}(s,·)]$ (unconditionally) for any s ∈ [0, τ), h ∉ 𝒯, and j ∈ ℐ.

Theorem 3

The goodness-of-fit statistic sup_t∈[0,τ] max_{j∈𝒯⁽⁻¹⁾} |V̂_nj(t)| converges weakly conditional on the data D to the same limiting process as that of sup_t∈[0,τ] max_{j∈𝒯⁽⁻¹⁾} |V_nj(t)| (unconditionally).

The proofs for the theorems are outlined in the Supplementary Materials.

Remarks

The asymptotic result of Theorem 2 can be also expressed in a conventional vector form as $\sqrt{n}[{\widehat{𝒫}}_n(s,t)-{𝒫}_0(s,t)]$, where 𝒫̂_n = (vec^TP̂_n,𝒯^c, vec^TP̂_n,𝒯)^T and 𝒫₀ = (vec^TP_0,𝒯^c, vec^TP_0,𝒯)^T with vecA being the column vector formed by concatenating the columns of the matrix A and vec^T A the transpose of vecA. As a consequence of Theorem 2 and an application of the Cramer-Wold device, $\sqrt{n}[{\widehat{𝒫}}_n(s,·)-{𝒫}_0(s,·)]$ converges weakly to a Gaussian random field with each of its elements being a tight mean-zero Gaussian processes in the space D[s, τ] of cadlag functions on [s, τ]. Due to the asymptotic linearity of the NPMPLE, the corresponding asymptotic variance-covariance matrix-valued function, given the starting time point s, is equal to Σ(t, w; s) = E [vecγ_i(s, t)vec^Tγ_i(s, w)], 0 ≤ s < t, w ≤ τ, where Σ(t, w; s) is a (q − k + 1) (q + 1) × (q − k + 1) (q + 1) matrix-valued process. Using this asymptotic variance-covariance matrix-valued function and after some algebra it can be shown that the asymptotic variance of

$$\sqrt{n}[{\hat{P}}_{n,\mathit{\text{hj}}}(s,t)-P_{0,\mathit{\text{hj}}}(s,t)],t\in (s,\tau ],$$

the hj-element of the transition probability matrix, for given s ≥ 0, can be decomposed as

$$E{[{\gamma }_{\mathit{\text{ihj}}}^F(s,t)]}^2+E{[{\gamma }_{\mathit{\text{ihj}}}^M(s,t)]}^2+2E[{\gamma }_{\mathit{\text{ihj}}}^F(s,t){\gamma }_{\mathit{\text{ihj}}}^M(s,t)],$$ (3.3)

where

$${\gamma }_{\mathit{\text{ihj}}}^F(s,t)=\sum _{l\notin 𝒯}\sum _{m\in ℐ}{\int }_s^t{P}_{0,\mathit{\text{hl}}}(s,u-)P_{0,\mathit{\text{mj}}}(u,t)d{\psi }_{\mathit{\text{ilm}}}^F(u),$$

with

$${\psi }_{\mathit{\text{ilm}}}^F(t)={\int }_0^t\frac{{\mathit{\text{dN}}}_{\mathit{\text{ilm}}}(u)}{{\mathit{\text{EY}}}_l(u)}-{\int }_0^t\frac{Y_{\mathit{\text{il}}}(u)}{{\mathit{\text{EY}}}_l(u)}{\mathit{\text{dA}}}_{0,\mathit{\text{lm}}}(u),$$

and where

$${\gamma }_{\mathit{\text{ihj}}}^M(s,t)=\{\begin{array}{c}{\sum }_{l\notin 𝒯}{\int }_s^t{P}_{0,\mathit{\text{hl}}}(s,u-)d{\psi }_{\mathit{\text{ilj}}}^M(u)\text{ if }j\in 𝒯\hfill \\ 0\text{ if }j\notin 𝒯\hfill \end{array}$$

with

$${\psi }_{\mathit{\text{ilj}}}^M(t)=(1-R_i){\int }_0^t\frac{d[{\pi }_j({\mathbf{Z}}_i,{\mathit{\beta }}_0)N_{\mathit{\text{il}}·}(u)-N_{\mathit{\text{ilj}}}(u)]}{{\mathit{\text{EY}}}_l(u)}+{\mathit{\omega }}_i^T{\mathbf{R}}_{\mathit{\text{lj}}}(t),$$

for j ∈ 𝒯. The influence function ${\gamma }_{\mathit{\text{ihj}}}^F(s,t)$ is the influence of the ith observation on the estimator in the ideal situation without missing absorbing states, while ${\gamma }_{\mathit{\text{ihj}}}^M(s,t)$ is the influence associated with missingness and the fact that we impute the unobserved jumps dN_ilj(t) with π_j(Z_i, β̂_n)dN_il·(t), for j ∈ 𝒯. Therefore, based on decomposition (3.3) it is obvious that the asymptotic variance of the transition probability estimator to an absorbing state is equal to the variance of this estimator in the absence of missing data $E{[{\gamma }_{\mathit{\text{ihj}}}^F(s,t)]}^2$, plus the additional variability due to missingness $E{[{\gamma }_{\mathit{\text{ihj}}}^M(s,t)]}^2$ and 2 times the covariance between the influence function of the estimator without missingness and the influence function related to missingness $E[{\gamma }_{\mathit{\text{ihj}}}^F(s,t){\gamma }_{\mathit{\text{ihj}}}^M(s,t)]$. It is also obvious that the variability $E{[{\gamma }_{\mathit{\text{ihj}}}^M(s,t)]}^2$ due to missingness depends on the variability of β̂_n, through its influence function ω_i, weighted by the fixed quantity R_lj(t) which is proportional to the percent of missingness, and also the difference between the imputed expected jump π_j(Z_i, β₀)dN_il·(t) and the actual unobserved jump dN_ilj(t) for the missing cases. Hence the variability of our proposed estimator for incorporating missing absorbing states is influenced by the missing rate in addition to the total sample size.

Using regularity conditions C1–C6 and Theorems 1 and 2 it can be shown that the asymptotic variance-covariance function of the transition probability matrix estimator can be uniformly consistently (in probability) estimated by ${\hat{\sum }}_n(t,w;s)=n^{-1}{\sum }_{i=1}^n[\text{vec}{\hat{\mathit{\gamma }}}_i(s,t){\text{vec}}^T{\hat{\mathit{\gamma }}}_i(s,w)]$, with the components of γ̂_i(s, ·) being γ̂_ihj(s, ·), defined above, for h ∉ 𝒯 and j ∈ ℐ and 0 otherwise. These results along with the functional delta method can be used for the construction of 1 − α pointwise confidence intervals for P_0,hj(s, t), under a known and differentiable transformation g (for example g(x) = log[−log(x)]) that ensures that the corresponding limits of the interval lie in (0, 1). For the construction of simultaneous confidence bands consider the process $\sqrt{n}{q}_{\mathit{\text{hj}}}(s,t)\{g[{\hat{P}}_{n,\mathit{\text{hj}}}(s,t)]-g[P_{0,\mathit{\text{hj}}}(s,t)]\}$, where q_hj(s, t) is a time-dependent weight that converges uniformly in probability to a nonnegative bounded function on [t₁, t₂] with 0 ≤ s ≤ t₁ ≤ t₂ < τ. This weight function can be set equal to P̂_n,hj(s, t)/σ̂_hj(s, t), where ${\hat{\sigma }}_{\mathit{\text{hj}}}(s,t)={[n^{-1}{\sum }_{i=1}^n{\hat{\gamma }}_{\mathit{\text{ihj}}}^2(s,t)]}^{1/2}$ is the estimated standard error of $W_{n,\mathit{\text{hj}}}(s,t)=n^{-1/2}{\sum }_{i=1}^n{\gamma }_{\mathit{\text{ihj}}}(s,t)$, or to ${\hat{P}}_{n,\mathit{\text{hj}}}(s,t)/[1+{\hat{\sigma }}_{\mathit{\text{hj}}}^2(s,t)]$. The first weight is equivalent to an equal precision weight (Nair, 1984) and the second to a Hall-Wellner weight (Hall and Wellner, 1980). Using Theorem 2 and the functional delta method it can be easily shown that the process $\sqrt{n}{q}_{\mathit{\text{hj}}}(s,t)\{g[{\hat{P}}_{n,\mathit{\text{hj}}}(s,t)]-g[P_{0,\mathit{\text{hj}}}(s,t)]\}$ is asymptotically equivalent to the process B̂_n,hj(s, t) = q_hj(s, t) ġ [P̂_n,hj(s, t)]Ŵ_n,hj(s, t). Next, similarly to Spiekerman and Lin (1998), define c_α to be the 1 − α percentile from a large number of realizations of sup_t∈[t1,t2] |B̂_n,hj(s, t)| generated by repeated simulations of ${\{{\xi }_i\}}_{i=1}^n$. Now, the 1 − α confidence band is

$$g^{-1}\{g[{\hat{P}}_{n,\mathit{\text{hj}}}(s,t)]\pm \frac{c_a}{\sqrt{n}{q}_{\mathit{\text{hj}}}(s,t)}\},t\in [t_1,t_2],$$

for a given s ∈ [0, t₁]. In general, the confidence band can be unstable in the tails of the observable time domain (Yin and Cai, 2004). To deal with this issue we can restrict the domain of the confidence band to [u₁, u₂], where these limits can be set equal to the solutions of $c_l={\hat{\sigma }}_{\mathit{\text{hj}}}^2(s,u_l)/[1+{\hat{\sigma }}_{\mathit{\text{hj}}}^2(s,u_l)]$, l = 1, 2, with {c₁, c₂} = {0.1, 0.9} or {c₁, c₂} = {0.05, 0.95} (Nair, 1984; Yin and Cai, 2004).

4. Simulation Study

To evaluate the performance of the proposed estimator with finite samples and to study its robustness against misspecification of the parametric model for the probability of the absorbing states, we conducted extensive simulation studies. We considered a non-homogeneous Markov process with two absorbing states, denoted by 1 and 2, and one initial transient state denoted by 0. This model is equivalent to the competing risks model with two causes of failure. The transition probabilities for the two absorbing states were P₀₁(0, t) = 0.4 {1 − exp [−(t/λ₁)^ν₁]} and P₀₂(0, t) = 0.6 {1 − exp [−(t/λ₂)^ν₂]}. The probability of remaining in the transient state was $P_{00}(0,t)=1-{\sum }_{j=1}^2{P}_{0j}(0,t)$. Four scenarios were considered: 1) (λ₁, ν₁, λ₂, ν₂)^T = (1, 1, 0.5, 1)^T; 2) (λ₁, ν₁, λ₂, ν₂)^T = (1, 0.8, 0.5, 1)^T; 3) (λ₁, ν₁, λ₂, ν₂)^T = (1, 0.4, 0.5, 1)^T; and 4) (λ₁, ν₁, λ₂, ν₂)^T = (1, 0.2, 0.5, 1)^T. Right censoring times were simulated based on the uniform distribution U(0, 5). Under these simulation settings, the average proportion of right-censored observations was 15% and the proportion of non-censored observations in the absorbing state 1 was 37%. The probability of a missing absorbing state was set equal to 0.8 or 0.6. To mimic a setting with planned missingness due to a double-sampling design, such as the design in our motivating HIV study presented in Section 5, we considered the auxiliary covariate Z = (T, C^⋆)^T, where T is the arrival time at an absorbing state and C^⋆ is the absorbing state according to an imperfect diagnostic procedure. Let C denote the true, but incompletely observed absorbing state. C^⋆ was simulated conditional on C from the Bernoulli distribution with probabilities ${\pi }_{11}^{\star }=\text{Pr}(C^{\star }=1|C=1)=0.9$ and ${\pi }_{22}^{\star }=\text{Pr}(C^{\star }=2|C=2)=0.7$. Therefore, the misclassification probabilities of the imperfect diagnostic were 0.1 and 0.3 for absorbing states 1 and 2, respectively. It is noted that C^⋆ was completely observed. We considered the sample sizes of n = 200 and n = 400.

In this simulation study we evaluated the usual Aalen-Johansen estimator for the observed data by only using the misclassified absorbing state C^⋆ and ignoring the non-missing C values (Naïve), the Aalen-Johansen estimator under a complete-case analysis where the observations with a missing C were discarded from the analysis (CC), and the proposed estimator. For the proposed estimator we considered a “working” logistic model with logit[π₁(Z, β)] = β₀ + β₁T + β₂I_{C^⋆=1}. Note that the true probability of the absorbing state 1 under the four simulation scenarios is given by

$$\text{logit}[{\pi }_1(T,C^{\star };\mathit{\beta })]={\beta }_0+f(T;{\lambda }_1,{\nu }_1,{\lambda }_2,{\nu }_2)+{\beta }_2{I}_{\{C^{\star }=1\}}$$

where

$$f(T;{\lambda }_1,{\nu }_1,{\lambda }_2,{\nu }_2)=-{\lambda }_1^{-{\nu }_1}{T}^{{\nu }_1}-{\lambda }_2^{-{\nu }_2}{T}^{{\nu }_2}+({\nu }_1-{\nu }_2)\text{ log}(T).$$

Setting ν₁ = ν₂ = 1 in Scenario 1 implied a linear logit model for the where probability of the absorbing state 1 in T, of the form logit[π₁(Z, β₀)] = β₀ + β₁T + β₂I_{C^⋆=1}, while Scenarios 2–4 implied nonlinear logit models in T. Therefore, our “working” linear logit model was correctly specified in Scenario 1 and was misspecified in Scenarios 2–4. The nonlinear dependence of logit[π₁(Z, β₀)] on T in Scenarios 2–4, that corresponds to misspecification of our “working” model, is depicted in Figure S1 in the Supplementary Materials. Based on this Figure it is clear that the degree of nonlinearity on T, and thus the degree of linear logit model misspecification, increases as ν₁ decreases. For constructing 95% simultaneous confidence bands we performed 1,000 simulations of sets ${\{{\xi }_i\}}_{i=1}^n$ of i.i.d. random variables from N(0, 1) and considered both equal-precision and Hall–Wellner-type weights.

Pointwise simulation results for absorbing state 1 under Scenario 1 are presented in Table 1. In all cases, the naïve approach gave highly biased estimates. The CC analysis also provided biased estimates and lower than the nominal 95% level coverage probabilities. In contrast, the proposed NPMPLE provided virtually unbiased estimates. Furthermore, the estimated standard errors (ASE) were close to the Monte Carlo standard deviations (MCSD) of the estimates and the coverage probabilities close to the nominal 95% level even with 80% missing absorbing states and n = 200. Interestingly, the MCSD of our estimator was larger compared to that from the CC analysis at the time points t₁ and t₂ with 80% missingness and n = 200. This is attributed to: i) the large variability of β̂_n, the estimated parameter of the model for the probability of the absorbing state 1, as a consequence of the fact that it was estimated using only 34 observations on average, and ii) the fact that β̂_n was used in imputing the missing counting process jumps in a relatively large number of cases (i.e. 136 on average or 80% of the non-right-censored cases). When sample size was 400 or the missing rate was 60%, this phenomenon was almost gone and our estimator was more efficient than the CC analysis, except at time point t₁ for the case of n = 400 with missing rate of 80%. Although the proposed estimator may have slightly larger standard error in some cases compared to the CC analysis when sample size is not large and the missing rate is high, our estimator still outperforms the CC estimator in terms of the mean squared error due to fact that the CC analysis usually yields biased estimates.

Table 1.

Pointwise simulation results for estimating the transition probability of absorbing state 1 at t₁ = 0.4, t₂ = 0.8 and t₃ = 1.2, under the naïve approach, the complete case analysis (CC) and the proposed method, under Scenario 1.

	Bias×102			MCSD×103			ASE×103			CP×102
Method (missing)	t1	t2	t3	t1	t2	t3	t1	t2	t3	t1	t2	t3
n = 200
Naïve	8.5	12.2	13.4	29.4	35.0	36.8	29.8	35.0	36.9	15.6	4.6	3.7
CC (80%)	−3.9	−5.5	−5.6	39.4	53.8	64.7	38.6	53.6	65.0	74.4	75.7	80.7
CC (60%)	−1.9	−2.5	−2.5	33.7	44.7	50.7	33.5	44.0	50.6	86.2	88.5	89.0
Proposed (80%)	−0.2	0.0	0.0	42.2	56.4	62.7	40.0	53.9	60.1	92.9	93.4	92.4
Proposed (60%)	−0.1	−0.1	−0.1	30.4	40.0	44.7	30.8	40.8	45.5	93.8	95.0	95.4
n = 400
Naïve	8.7	12.2	13.6	21.3	24.6	26.0	21.1	24.7	26.1	0.8	0.1	0.0
CC (80%)	−3.9	−5.2	−5.4	28.4	39.0	46.8	27.5	38.2	45.8	65.1	69.2	74.3
CC (60%)	−1.8	−2.3	−2.2	23.9	31.6	37.0	23.7	31.1	35.6	84.1	85.4	88.0
Proposed (80%)	−0.1	−0.1	−0.1	28.6	38.6	42.9	27.9	37.9	42.5	92.2	92.8	93.3
Proposed (60%)	−0.1	−0.1	−0.1	21.7	28.6	31.3	21.6	28.7	32.0	94.4	94.8	94.8

MCSD, Monte Carlo standard deviation; ASE, average standard error; CP, coverage probability

Simulation results under Scenario 2, where the proposed method was evaluated under a misspecified parametric model π₁(Z, β), are presented in Table 2. Again, the naïve approach and the CC analysis provided biased estimates. The proposed approach performed well, as in Scenario 1. Simulation results about the performance of the simultaneous confidence bands are presented in Table 3. The coverage probabilities for the 95% simultaneous confidence bands were close to the nominal level even with 80% missing absorbing states, n = 200, and a misspecified parametric model π₁(Z, β). Simulation results for more pronounced misspecification of the probability model of absorbing state 1 (Scenarios 3 and 4) are reported in Tables S1–S3, and Figure S2 in the Supplementary Materials. The pointwise results in Tables S1 and S2 reveal that more pronounced misspecification of π₁(Z, β) led to more pronounced bias in the transition probability estimates. However, the degree of bias under the misspecified models was still much smaller than that in the naïve and CC analyses, and was almost negligible compared to the corresponding true values (Figure S2). Moreover, the ASE were close to the corresponding MCSD and the coverage probabilities close to the nominal level in all cases. When considering the whole estimated transition probability functions (Figure S2), it appears that the bias levels were in general small even under a severely misspecified model π₁(Z, β) (Scenario 4). Thus, it is evident that the proposed estimator is robust against some degree of misspecification of the “working” model π₁(Z, β). Nevertheless, the impact of misspecification was more pronounced with respect to the coverage of the simultaneous confidence bands, especially under Scenario 4 (Table S3 in the Supplementary Materials).

Table 2.

Pointwise simulation results for estimating the transition probability of absorbing state 1 at t₁ = 0.4, t₂ = 0.8 and t₃ = 1.2, under the naïve approach, the complete case analysis (CC) and the proposed method, under Scenario 2.

	Bias×102			MCSD×103			ASE×103			CP×102
Method (missing)	t1	t2	t3	t1	t2	t3	t1	t2	t3	t1	t2	t3
n = 200
Naïve	8.3	12.1	13.5	30.7	35.2	36.6	30.6	35.0	36.7	20.6	5.4	3.8
CC (80%)	−4.9	−6.5	−6.9	41.2	51.6	59.9	39.8	51.5	60.2	68.0	67.0	73.6
CC (60%)	−2.4	−3.0	−3.2	35.8	43.8	48.7	35.1	43.4	48.7	84.2	85.8	85.4
Proposed (80%)	−0.4	0.2	0.3	44.7	57.1	62.6	42.6	54.8	60.2	93.2	93.4	93.1
Proposed (60%)	−0.3	0.0	0.1	32.5	40.7	44.4	32.8	41.3	45.3	93.8	95.2	95.2
n = 400
Naïve	8.5	12.1	13.6	21.9	24.8	26.1	21.7	24.7	25.9	1.8	0.1	0.0
CC (80%)	−4.9	−6.3	−6.7	28.7	37.7	43.5	28.5	36.6	42.6	55.9	58.3	61.4
CC (60%)	−2.3	−2.9	−2.9	24.8	31.6	35.6	24.8	30.7	34.3	81.3	80.3	83.0
Proposed (80%)	−0.4	0.0	0.2	29.8	38.9	43.0	29.7	38.5	42.5	92.7	93.0	93.3
Proposed (60%)	−0.4	0.0	0.1	22.5	28.6	31.3	23.0	29.0	31.9	94.5	95.7	95.0

MCSD, Monte Carlo standard deviation; ASE, average standard error; CP, coverage probability

Table 3.

Simulation results on the coverage probability of the proposed 95% simultaneous confidence bands based on equal-precision (EP) and Hall–Wellner-type (HW) weights, under Scenarios 1 and 2.

		Scenario 1		Scenario 2
n	missing	EP	HW	EP	HW
200	80%	93.6	92.9	94.3	93.2
	60%	95.3	96.1	95.6	96.2
400	80%	93.6	93.3	94.2	93.8
	60%	94.7	95.5	96.3	95.6

The efficiency of our estimator is expected to depend on the missing rate and the accuracy of the auxiliary variable C^⋆. To evaluate numerically this efficiency dependence we performed further simulation experiments by varying the missing rate from 0% to 80% while keeping ${\pi }_{11}^{\star }$ and ${\pi }_{22}^{\star }$ fixed at 0.9 and 0.7, respectively, as well as by varying ${\pi }_{11}^{\star }$ from 0.5 to 0.9, while setting ${\pi }_{22}^{\star }={\pi }_{11}^{\star }$ and the missing rate at 80%. The simulation results on the MCSD of the estimated transition probability at t = 0.4, 0.8 and 1.2, based on 1,000 simulations, are presented in Figure S3 and Table S4 in the Supplementary Materials. As expected, higher missing rate led to larger estimation standard error and higher accuracy of C^⋆ lead to smaller estimation standard error. Interestingly, the effect of the accuracy of C^⋆ on standard error was not pronounced.

We also compared our method to that proposed by Gouskova et al. (2017) (GLF) for the competing risks model, which does not incorporate auxiliary covariates, by considering Scenarios 1–3 with n = 400. In this simulation study we did not consider Scenario 4 because the GLF estimator was highly unstable under this Scenario. In these simulations, we generated missingness according to the following two scenarios: i) missing completely at random (MCAR) where the probability of missingness did not depend on the auxiliary variable C^⋆ with Pr(R = 0) = 0.6, and ii) MAR where the probability of missingness depended on the auxiliary variable C^⋆ with Pr(R = 0|C^⋆) = 0.5 + 0.2I_{C^⋆=1}. These simulation results, which are presented in Tables S5 and S6 in the Supplementary Materials, revealed that the GLF estimator had always larger mean squared error compared to our proposed method, even in cases where our parametric model π₁(Z, β) was misspecified (Scenarios 2 and 3). Moreover, the GLF estimator was severely biased when the probability of missingness depended on the auxiliary variM able C^⋆.

To illustrate the computational efficiency of our estimator we present the average computation times in seconds and the corresponding standard deviations, based on 100 simulations, in Table S7 in the Supplementary Materials. These figures correspond to the time needed to compute the transition probability estimates and the associated standard errors, with and without the construction of simultaneous confidence bands, for sample sizes n = 200 to n = 1, 500, under Scenario 1. The computation times under the Scenarios 2–4 were similar. Finally, we investigated the performance of the naïve approach according to the diagnostic accuracy of C^⋆ under Scenario 1. These results are presented in Table S8 in the Supplementary Materials. As expected, a lower accuracy of C^⋆ was associated with a larger bias in the naïve approach as a result of the higher misclassification rate of C^⋆.

To sum up, our extensive simulation studies provided sufficient evidence to numerically justify the superior statistical and computational efficiency properties of our proposed method for estimating the transition probabilities of non-homogeneous Markov processes with partially observed absorbing states.

5. HIV Data Analysis

From an implementation science perspective, the primary outcome of interest in HIV care is how adhesive to care are the HIV patients and this was the main objective in our motivating study. In the light of this, the proposed method was applied to estimate the transition probabilities of disengagement from care and death while in care based on data from the East Africa IeDEA study. A major issue in this ongoing study is the significant death under-reporting, where unreported deaths are incorrectly classified as disengagements from care since deceased patients do not return to care. To deal with this issue, a double-sampling design was applied in the IeDEA study, where a small sample of patients lost to clinic was intensively pursued in the community by outreach workers, and, subsequently, the corresponding vital statuses were actively ascertained. The database consisted of 58,876 HIV-infected individuals who initiated antiretroviral therapy (ART) with a CD4 count below 350 cells/µl. Throughout the study, 3,338 (5.7%) patients were (passively) recorded as dead and 27,034 (45.9%) were lost to clinic. The remaining patients were alive and in care at the data closure date, and their arrival times at an absorbing state were considered administratively right-censored. In this dataset, 4,020 (14.9%) patients, out of the 27,034 who were lost, were doubly-sampled and outreached within a short period after the time they were agged as disengagers by the clinicians. Among these doubly-sampled patients, 917 (22.8%) were actually dead indicating a significant death under-reporting issue. The vital status was missing for the remaining 85.1% of the lost patients who were not doubly-sampled.

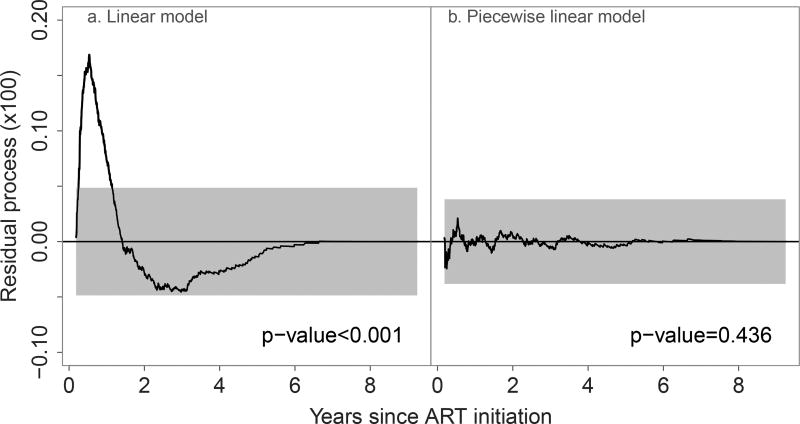
At the first stage of the analysis we considered a logistic regression model for the probability of death among those who were agged as disengagers, with a linear effect of time from ART initiation. We evaluated the goodness of fit of this model using the residual process presented in Section 2. The left panel of Figure 1 clearly indicates the lack of fit of this model. More specifically, the model seems to overestimate the true probability of death during the first year after ART initiation. We then considered a model with piecewise linear effect of time with a change in slope at 12 months post ART initiation. The residual process for this model (right panel of Figure 1) was close to 0 at all time points and remained within the 95% goodness-of-fit band (p-value=0.436). This was the model used in our proposed NPMPLE for this analysis.

Figure 1.

Residual process for the parametric model π₁(Z, β) based on the IeDEA HIV data along with the 95% goodness-of-fit band (grey area) and the corresponding p-value.

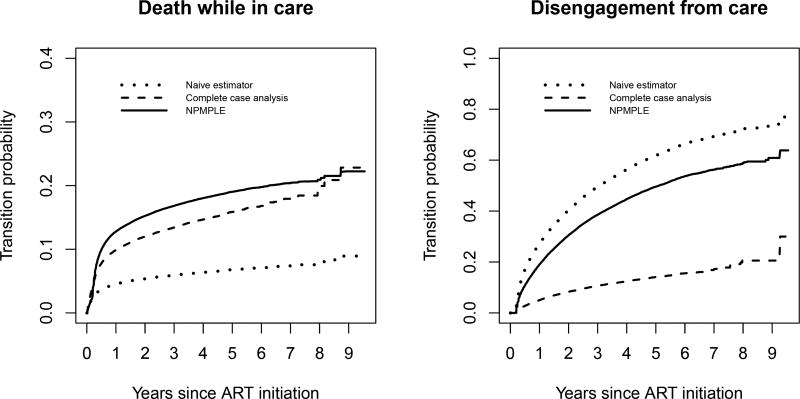
The estimates of the transition probabilities of death while in HIV care and disengagement from care are presented in Figure 2. The naïve analysis, which ignores the information from double-sampling, significantly underestimated mortality while in HIV care (left panel of Figure 2) and, also, overestimated disengagement from HIV care (right panel of Figure 2), compared to the proposed NPMPLE method. The CC analysis underestimated both probabilities of death and disengagement from care, compared to the proposed estimator. Note that the findings from the CC analysis were in accordance to the findings from the simulation study. However, the results from the naïve analysis were not in accordance to the results from the simulation study since in the HIV data example Pr(C^⋆ = 2|C = 2) = 1, that is the imperfect state classification was always correct when the true state was “disengagement”. On the contrary, in the simulation study we considered the more general case with Pr(C^⋆ = 2|C = 2) < 1. The computing time for estimating the transition probabilities over the whole study period using our motivating dataset of 58,876 observations was only 15 seconds in a modern i7 processor.

Figure 2.

Transition probability estimates in the HIV study based on the naïve approach, the complete case analysis (CC) and the proposed NPM-PLE method.

6. Concluding Remarks

In this paper we proposed a computationally efficient nonparametric estimation approach for the transition probability matrix of a non-homogeneous Markov process with missing absorbing state, allowing for both right censoring and left truncation. Additionally, we derived a covariance function estimator based on the estimated influence functions and proposed a methodology for simultaneous confidence band construction. The validity of our methodology was studied both theoretically and numerically. Even though our approach uses the parametric model π_j(Z, β) to estimate the probabilities of each absorbing state for the missing cases, it seems, based on our simulation studies, to be robust against some degree of misspecification of this model. Moreover, we proposed a formal goodness-of-fit approach for evaluating the “working” model for π_j(Z, β).

Alternative approaches for the competing risks model, which is a special case of an absorbing Markov process with a single transient state, are the estimators proposed by Effraimidis and Dahl (2014) and Gouskova et al. (2017). These methods estimate nonparametrically the probabilities of the absorbing states π_j(t) as functions of time. However, unlike our approach, these methods do not incorporate auxiliary variables and thus impose stronger missing at random assumptions. Therefore, these estimators can be biased in cases where the probability of missingness depends on variables other than time, as it was illustrated in the simulation study.

While the proposed method is computationally efficient and has superior statistical properties compared to the existing methods, it is not clear if it is fully statistically efficient. Therefore, it would be interesting to study the efficiency of our pseudolikelihood estimator theoretically. For this, one could consider either the full class of nonparametric estimators of the transition probability matrix of a Markov process that utilize a parametric model for the probabilities of the absorbing states, or the subclass of the union of pseudolikelihood estimators considered in this article and potential augmented inverse probability estimators. The latter approach is very useful in cases where derivation of the efficient influence function is very challenging. The study of efficiency within a restricted class of estimators has been considered by Kulich and Lin (2004) and Breslow et al. (2009) for the class of augmented inverse probability weighting estimators for the Cox proportional hazards model under case-cohort study designs. Such efficiency considerations in the framework of the method proposed in this article are technically challenging, but constitute an interesting topic for future research.