Exploring the power of Bayesian birth‐death skyline models to detect mass extinction events from phylogenies with only extant taxa

Abstract

Mass extinction events (MEEs), defined as significant losses of species diversity in significantly short time periods, have attracted the attention of biologists because of their link to major environmental change. MEEs have traditionally been studied through the fossil record, but the development of birth‐death models has made it possible to detect their signature based on extant‐taxa phylogenies. Most birth‐death models consider MEEs as instantaneous events where a high proportion of species are simultaneously removed from the tree (“single pulse” approach), in contrast to the paleontological record, where MEEs have a time duration. Here, we explore the power of a Bayesian Birth‐Death Skyline (BDSKY) model to detect the signature of MEEs through changes in extinction rates under a “time‐slice” approach. In this approach, MEEs are time intervals where the extinction rate is greater than the speciation rate. Results showed BDSKY can detect and locate MEEs but that precision and accuracy depend on the phylogeny's size and MEE intensity. Comparisons of BDSKY with the single‐pulse Bayesian model, CoMET, showed a similar frequency of Type II error and neither model exhibited Type I error. However, while CoMET performed better in detecting and locating MEEs for smaller phylogenies, BDSKY showed higher accuracy in estimating extinction and speciation rates.

Introduction

Mass extinction events (MEE) are distinguished in the paleontological records as widespread, higher taxonomic group extinctions (e.g., up to 96% of marine invertebrate species became extinct during the largest, late Permian MEE; Raup 1979). An MEE is defined as a period where (i) the ratio of the extinction rate μ over the speciation rate λ, aka the turnover rate or background extinction, $\epsilon =\frac{\mu }{\lambda }$, is larger than 1; and (ii) this period is less than one million up to about 15 million years duration, dependent on the magnitude or intensity of the MEE (Sepkoski 1982). This often results in an ecosystem's speedy decline and reordering (Gould 1994). MEEs are monocyclic (irregularly cycling) and are generally recognized as a resultant of abiotic changes (Sepkoski 1982; Jablonski 2008), which are often compared to current‐day greenhouse‐induced climate change (IPCC 2001). MEEs have been usually studied from paleontological evidence (Raup 1979; Sepkoski 1982; Jablonski 2008). High extinction rates, as those associated with MEEs, can also leave an imprint on the timing and structuring of cladogenetic events in phylogenetic trees containing only extant taxa (Harvey et al. 1994). This has permitted a burgeoning of method development in the context of macroevolutionary birth–death models for detecting the phylogenetic signature of MEEs. Methodologically—within the birth–death model framework—an MEE detecting model can be defined as either: (i) a “single‐pulse” model, in which a significant number or percentage of species are instantaneously and simultaneously removed from the phylogenetic tree at a specific point in time t (Stadler 2011a; Fig. 1A); or (ii) a “time‐slice” model, in which there is a significant increase in the extinction rate μ for a short time interval, with turnover rate ε > 1, followed by a decrease in μ that returns ε < 1 in the next time interval (Fig. 1B). The first definition, the single‐pulse model, is the one used more often in mathematical birth–death modeling (Harvey et al. 1994; Stadler 2011b; Laurent et al. 2015; May et al. 2016).

Figure 1.

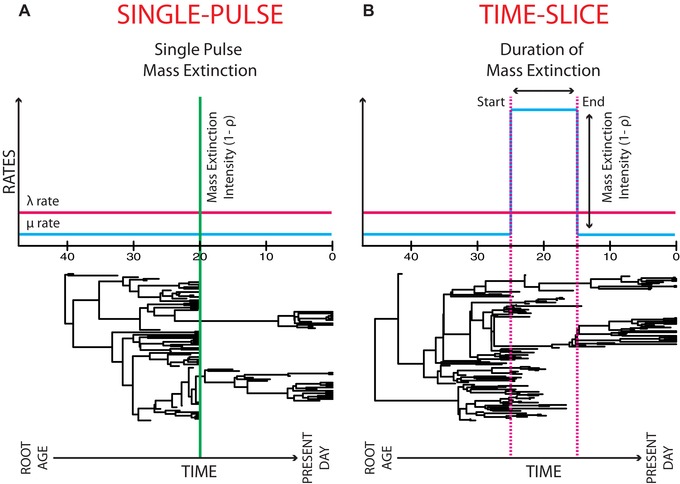
Two examples of full (extant and extinct taxa) phylogenetic trees that contain 20 taxa at time t = 0 and have similar root ages. The first tree has been affected by a MEE that is defined under the “single‐pulse” scenario, and the second tree has been affected by a MEE, defined under the “time‐slice” scenario. Within these scenarios speciation rate, λ is assumed to be unchanged. In the “single‐pulse” scenario, the MEE is caused by a significant percentage of species being simultaneously and instantaneously removed from the tree, at a specified time. In the “time‐slice” scenario, the MEE is defined as a significant increase in the extinction rate, μ for a specific period of time, where the turnover or background extinction rate, ε = $\frac{\mu }{\lambda }$ > 1, followed with a decrease in μ that results in a return to ε < 1. In the two trees, the “pre‐MEE" μ is equal to “post‐MEE" μ but this is not necessary.

If a clade is associated with a sufficient fossil record, then this record can be used to quantify the most probable number of MEEs within the specific time period that spans the fossil data (Raup 1979). However, most clades either possess an incomplete fossil record or lack a fossil record entirely. Phylogenetic trees of extant species can also be incomplete as a result of incomplete extant species sampling, roughly defined as either: (i) a random fraction of missing species in the phylogeny; or (ii) clades in the phylogeny are collapsed to single tips due to higher taxonomic sampling level. Constant‐rate birth–death models can accommodate for such incomplete extant taxon sampling through the introduction of a sampling parameter (Höhna et al. 2011; Stadler and Bokma 2012). These constant‐rate birth‐death models have been expanded to estimate speciation and extinction rate shifts through time and search for the presence of possible MEEs in the past (Stadler 2011c; Höhna 2014).

Stadler (2011b) introduced a birth–death model that is able to detect the presence of rate shifts based on phylogenetic trees containing extant taxa only. This model assumes discrete time intervals during which the speciation and extinction rate is constant, and the rates may change arbitrary between intervals (Stadler 2011b). Such changes may be due to time‐slice MEEs or other non‐mass‐extinction rate changes. The model can also be used to detect instantaneous MEEs following the single‐pulse model defined above—points in time in which the standing diversity is reduced by a significant fraction that is controlled by the magnitude of the MEE, with the magnitude being defined as 1 minus the survival probability of each species at the MEE (ρ). Stadler's birth–death model was implemented within a maximum likelihood (ML) framework in the R package TreePar (Stadler 2011b), and used successfully to detect the timing of MEEs in phylogenies that have a large to moderate number of terminals (e.g., N > 200–500 taxa; Beaulieu and O'Meara 2015; Laurent et al. 2015). Sanmartín and Meseguer (2016) found that this model underperforms with relatively small phylogenies (N < 50 taxa).

For phylogenetic trees that span millions of years, it is likely they have been affected by rate shifts and single‐pulse MEEs, perhaps caused by global (climatic or geological) events (Laurent et al. 2015). However, although Stadler (2011b)’s model can be used in principle to estimate the timing and magnitude of single‐pulse MEEs from extant‐only taxa, it remains difficult to simultaneously estimate the frequency of tree‐wide rate shifts in diversification and single‐pulse MEEs due to issues of parameter non‐identifiability, i.e., when different combinations of parameter values yield flat likelihood surfaces for part of the parameter space (Rannala 2002). In fact, under a ML framework, it remains impossible to distinguish between a constant birth–death process with single‐pulse MEEs and a process in which diversification rates vary discretely over time because both types of processes generate identical phylogenetic signatures and have comparable likelihood functions (Stadler 2011b; Sanmartín and Meseguer 2016). Hence, in TreePar, one of these parameters must be fixed, for example, by assuming that μ and λ have remained constant before and after the single‐pulse MEE event, or by fixing the intensity of the MEE before inferring the timing and number of rate shifts (Stadler 2011b). Also, the algorithm cannot estimate multiple rate shifts simultaneously; instead, it uses a greedy approach where the time of one rate shift is estimated and fixed before estimating the time of the next rate shift (Stadler 2011b).

To overcome this overparameterization issue, May et al. 2016 introduced a Bayesian statistical inference approach to the single‐pulse MEE model, the Compound Poisson Process (CPP) on Mass Extinction Times (CoMET), implemented in the R package TESS (Höhna et al. 2015). Bayesian inference is less problematic under overparameterization than equivalent likelihood‐based approaches due to the integration of parameter uncertainty through estimation of marginal likelihoods. CoMET implements a stochastic branching process model in which rates of speciation and extinction are constant between rate shifts, and single‐pulse MEEs are modeled as tree‐wide instantaneous extinction events. Specifically, the method considers three types of events: instantaneous tree‐wide shifts in speciation rate, instantaneous tree‐wide shifts in extinction rates, and instantaneous tree‐wide single‐pulse MEEs. Each of them is modeled through a separate CPP, with waiting times distributed exponentially according to event‐specific rate parameters (May et al. 2016). To address the problem of parameter non‐identifiability in single‐pulse models, CoMET implements a hierarchical Bayesian approach in which rate shifts in speciation and extinction are considered as “nuisance” parameters that are integrated over in the estimation of the marginal posterior probabilities of the focal parameters: the time, number, and the intensity (magnitude) of single‐pulse MEEs. CPP models themselves are sensitive to the choice of priors, which means that in practice some parameters of the model, such as the magnitude of the single‐pulse MEE, are assigned informative empirical priors (May et al. 2016).

Here, we examine a different type of approach, the “Bayesian birth‐death skyline” (BDSKY) model, first introduced by Stadler and collaborators to trace temporal changes of epidemic spread in an infectious disease (Stadler et al. 2013; Boskova et al. 2014). Stadler and collaborators (2013) used simulations to explore the power of the BDSKY model to detect changes in the rate of becoming non‐infectious, akin to time‐slice MEEs in an epidemiological context. In this study, we explore the power of the BDSKY model to detect MEEs from species phylogenies under a “time‐slice” (paleontological) approach, that is, through sequential changes in extinction rates, where a shift to negative diversification rates and background extinction ɛ > 1 is followed—after a (geologically) short time interval—by a return to positive diversification rates (Fig. 1B; Condamine et al. 2013, cf. Fig. 4; May et al. 2016). Unlike in Stadler et al. 2013’s phylogenies, which included serial sampling (tips of different age) and were simulated under the BDSKY model, our reconstructed species phylogenies included only contemporaneous tips and mass extinction events were simulated under the single‐pulse model. The aim was to assess the ability of BDSKY as a statistical phylogenetic method for detecting and estimating the timing of MEEs through changes in the extinction rate (“time‐slice” approach), even when mass extinction is modeled as an instantaneous event in the same manner as in TreePar and CoMET.

Figure 4.

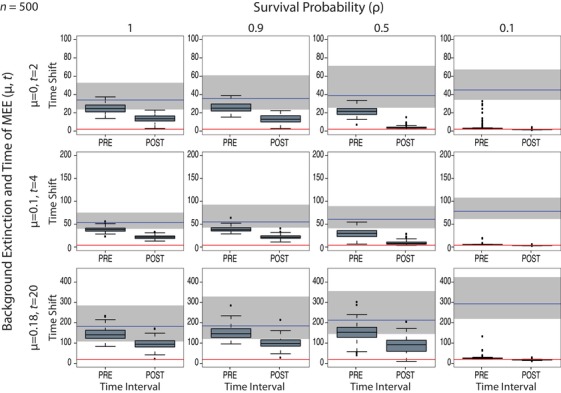
Estimates of the pre‐MEE and post‐MEE rate shift times bounding the second time interval, for Model C and under varying levels of μ and mass extinction survival probability, ρ. The red line indicates the value of the true (simulated) time of the MEE, t. The time is shown from present to past: left boxplot (post‐MEE) corresponds to the rate shift between time intervals “MEE” and “post‐MEE,” after which diversity is expected to recover; right boxplot (pre‐MEE) corresponds to the rate shift between time intervals “pre‐MEE” and “MEE,” after which the MEE is expected to have occurred. The grey bar indicates the variance in root ages across tree simulations, while the blue line shows the mean of this range. Notice the low variance and the small difference between the two boxplots (pre‐ and post‐MEE rate shifts), indicating that the time‐slice model is able to locate the MEE even when modeled as a nearly single‐pulse (instantaneous) event. See Figure S6 for the results with varying values of N (100, 200, and 500). Figures S7 and S8 show the equivalent results of this analysis for Model A.

We set up an extensive simulation study in which phylogenies were generated under a constant‐rate birth–death process with one single‐pulse MEE with intensity or magnitude 1– ρ. In these simulations, we sequentially varied different parameters to explore their influence on the power of BDSKY to detect and estimate the timing of MEEs: the survival probability of a species at the time of the MEE (ρ); the number of tips or extant taxa in the phylogeny (N); and the magnitude of μ relative to λ or background extinction (ε). We then compared the simulated values with the marginal posterior probability distributions of the model parameters estimated under the BDSKY model by Bayesian MCMC. Specifically, we aimed to answer the following questions: (i) Can we detect the phylogenetic signal of a MEE in the extant phylogenetic tree through changes in the diversification rate? (ii) If we are able to identify the presence of a MEE, can we accurately estimate the timing of that MEE? (iii) If we can identify and locate the MEE, can we provide reasonable estimates for λ and μ pre‐ and post‐MEE?

In addition, we compared the performance of BDSKY against CoMET (May et al. 2016), implemented in TESS (Höhna et al. 2015). We analyzed a subset of the simulated phylogenies above and then compared the behavior of the two models in terms of their frequency of Type I and Type II errors and their accuracy in estimating the magnitude of speciation and extinction rates and the timing of MEEs. Finally, we applied BDSKY to the conifer phylogeny of Leslie et al. 2012, which was also analyzed under CoMET by May et al. 2016, and therefore, provides a test study to investigate the robustness of the two models with an empirical dataset.

Material and Methods

SIMULATION DESIGN

The phylogenetic trees were simulated using the backward algorithm implemented by the function sim.rateshift.taxa from the TreeSim R package (Stadler 2011a). This algorithm simulates birth–death trees with speciation rate λ, extinction rate μ, an MEE at time t before the present, and survival probability of a species at the MEE, ρ. Simulated trees were conditioned on a fixed number of extant taxa (Stadler, 2011a).

All trees were simulated to include a single‐pulse MEE at time t, and assuming equal and constant rates of μ and λ before and after the MEEs and across all clades in the phylogeny. Although the assumption of constant rates and rate homogeneity across clades is empirically unsound (Rabosky 2014), using this constant birth–death process provides insights into the ability to infer MEEs in the simplest scenarios, and facilitates the comparison with other studies that examined the power of episodic birth–death models for MEE estimation (Laurent et al. 2015; May et al. 2016). Since we are interested here in the power to detect MEEs through changes in extinction rates, λ was fixed to 0.2, whereas the rate of extinction was allowed to vary across simulation scenarios. One hundred trees were simulated for each of the following scenarios and (10) parameter combinations: varying background extinction rate ε (μ = 0, 0.1, 0.18) with fixed number of extant taxa (N = 500) but under different survival probability scenarios (ρ = 0.9, 0.5, 0.1), and varying number of extant taxa (N = 100, 200, 500) and background extinction rate ε (μ = 0, 0.1, 0.18) but with fixed (low) survival probability (ρ = 0.1).

We considered that all present‐day species were included in the phylogeny (i.e., taxon sampling was complete at present). The MEE was simulated under a “field of bullets” scenario, where all taxa have the same probability of becoming extinct (1– ρ), which is often considered as the null model for mass extinction scenarios (Raup 1979; Harvey et al. 1994; Laurent et al. 2015). For each parameter combination, we set up a control or null model corresponding to a scenario where there is no MEE (ρ = 1 at time t); again we simulated 100 trees for each parameter combination with ρ = 1. In all, our simulation study included 2400 trees.

We selected varying values of t (the time of the single‐pulse MEE) for the varying values of μ, such that we could get a comparable number of lineages at the time of the MEE in all simulations (∼4000 lineages; Fig. S1 and S2); in particular, we chose $t=\frac{0.4}{(\lambda -\mu )}$. The final simulations were done with μ = 0.18, t = 20; μ = 0.1, t = 4; and μ = 0, t = 2.

PARAMETER ESTIMATION UNDER THE BDSKY MODEL

We used the BDSKY model implemented in BEAST v2.2.1 (Bouckaert et al. 2014) (http://beast2.org) to estimate the marginal posterior probability distribution of the model parameters using Bayesian MCMC for all simulated trees under the scenarios described above and their corresponding controls. Some parameters in the BDSKY model were set to fixed values: the simulated trees were fixed (i.e., not estimated from sequence data); sampling before present was fixed to 0, as we have no serial sampling through time (i.e., only the extant reconstructed tree is considered); and extant species sampling was set to 1 as in the simulations. We set the number of rate shifts to two, defining three time intervals (pre‐MEE, MEE, and post‐MEE), and estimated the speciation and extinction rates in each time interval, as well as the two rate‐shift times bounding the MEE time interval (i.e., the time interval assumed to contain the MEE). We compared this full BDSKY model, in which all free parameters are estimated, against constrained BDSKY models, where some parameters are fixed:

• (1)Full model: All eight parameters were estimated: the two rate‐shift times bounding the MEE time interval and the values of λ and μ in the pre‐MEE, MEE, and post‐MEE time intervals.
• (2)Constrained‐time model: The rate shift times were fixed to ±5% around the MEE (i.e., t ± 0.05 t), but μ and λ were allowed to vary and estimated for each of the three time intervals: [0, t − 0.05t), [t − 0.05t, t + 0.05t], (t + 0.05t, root age]. For example, for t = 20, these time intervals would be [0, 19), [19, 21], (21, root age]; for t = 4, they are [0, 3.8], [3.8,4.2], [4.2, root age)].
• (3)Constrained‐speciation model: The time interval around the MEE was estimated (i.e., the rate‐shift times bounding the MEE interval) and μ was allowed to vary across time intervals, but the speciation rate λ was estimated and assumed constant (i.e., no speciation rate shifts allowed).

Priors

We explored through initial analyses different prior distribution choices available in BEAST2. These were set eventually to the following: the extinction and speciation rates, μ and λ, were each modeled with an “exponential” distribution (Exponential (0.25)). The rate shift times for μ and λ in Models A and C were modeled with a “uniform” prior distribution, with the lower boundary being (root age of the tree) × 0.05 and the upper boundary equal to (root age of the tree) × 0.95. In Model B, the parameters birth Rate Change Times and death Rate Change Times were assigned fixed values (see above). We used the forward‐in‐time approach (reverseTimeArrays set to FALSE) for defining the time intervals between the two rate shifts (Stadler et al. 2013). Thus, the first time interval is the oldest interval in the phylogeny (pre‐MEE); the second interval is the time interval assumed to contain the MEE; and the third interval is the youngest time interval (post‐MEE). The complete xml files used in the three analysis settings (models A–C) are provided in Supporting Information SCRIPTS a. To aid in the implementation of these analyses in BEAST2, we also provide a new R function (that uses R packages TreeSim, picante, and their dependents) to write the xml code necessary to run a full or constrained BDSKY model for species trees, and example code for running this function; see Supporting Information SCRIPTS b–e.

Analysis

Each model was run to convergence, when the effective sample size (ESS) for each estimated parameter reached a value equal or larger than 200. MCMC runs that were unable to converge after 1000 million generations were discarded but not replaced, so the final number of analyzed simulated trees differed between prior settings, although this was never lower than 86% (Supporting Information Table S1). We compared the performance of the three BDSKY model settings (Models A–C) in terms of Type I error or the percentage of false positives—detecting the presence of a MEE when none was simulated—and Type II error or false negatives—failing to detect the simulated MEE; the latter is equivalent to 1 minus “power,” i.e., the proportion of trees analyzed for which the method correctly detected the MEE. We defined the detection of a MEE as the 95% High Posterior Density (HPD) credibility interval for the diversification rate estimate (r = λ – μ) being negative in the MEE time interval (and not containing 0), followed by a return to positive diversification rates (and potentially containing 0) in the third time interval. Hence, we defined a new statistic to measure performance: HPDn is the percentage of simulated trees for which all values within the 95% HPD for the diversification rate are lower than 0 (and the 95% HPD for ε is fully above 1) in the MEE interval, and the 95% HPD for diversification rate is fully above or containing 0 in the post‐MEE time interval. We also estimated the robustness of BDSKY under each model setting in the estimation of the nonfixed parameters. For each simulation scenario (with and without a MEE), we measured: the accuracy, the true (simulated) parameter value minus the mean of the estimated parameter means for each tree; the precision, the mean of the width of the 95% HPD interval across all analyzed trees; and the coverage, the percentage of simulated trees where the 95% HPD contained the true parameter value. In particular, we focused on the ability of the BDSKY model to estimate the posterior distributions of the parameters: diversification rate (r), speciation rate (λ), and extinction rate (μ) in each time interval, as well as the two rate‐shift times bounding the MEE time interval. For this interval, the true diversification rate can be calculated with respect to the true mass extinction intensity and the rates of λ and μ as:

$$\begin{array}{ccc}\hfill \mathit{True}\mathit{Diversification}\mathit{Rate}\mathit{in}\mathit{MEE}\mathit{interval}& =& \\ \hfill \lambda -\mu -\frac{1-\rho }{\mathit{length}\mathit{of}\mathit{time}\mathit{interval}}\end{array}$$

The mass extinction rate s = $\frac{(1-\rho )}{lengthoftimeinterval}$ summarizes the instantaneous mass extinction intensity. The rate s is obtained by recalling that the probability for mass extinction is s × (length of time interval) = (1−ρ) given that the time interval is short.

For those analyses in which rate shift times were not fixed but estimated (Models A and C), we do not have a corresponding true value. Instead, the MEE occurred at time t while we estimate a time interval (t ₁, t ₂) during which the extinction rate exceeded the speciation rate, signaling the presence of the MEE. In these two models, precision was measured as the mean of the 95% HPD interval of the time length (t ₁ – t ₂) across trees. Similarly, coverage was measured as the percentage of simulations in which the 95% HPD of the estimated time interval length (t ₁ – t ₂) contained the true (simulated) time of the single‐pulse MEE, t.

COMPARISON WITH THE SINGLE‐PULSE COMET MODEL

Simulation study

Because each analysis was time consuming, we made a random selection of ten extant trees for each of the 10 parameter‐combinations, totaling 240 simulated trees. We conditioned the CoMET model on taxa survival, and used the function tess.analysis from TESS (Höhna et al. 2015) to estimate the number and magnitude of rate shifts in μ and λ and the number of MEEs from the phylogeny (estimate Number Mass Extinctions, estimate Mass Extinction Times = TRUE). We used default parameter settings for the priors of the three independent CPP processes: num Expected Mass Extinctions and num Expected Rate changes for λ and μ were set to equal to two; this assigns a 50% probability to zero MEEs and zero rate changes (Höhna et al. 2015). A Beta (α = 5, β = 95) distribution was used as the prior for the mass extinction survival probability, which assigns an expected value of ρ = 0.1 (an MEE with 0.9 intensity). The prior distributions for the speciation and extinction rates were estimated using an empirical Bayesian approach with the function empiricalHyperPriors = TRUE. In this approach, a short preliminary analysis is performed in CoMET under a constrained, constant birth–death model to estimate reasonable values for the hyperprior distributions of λ and μ, which are then used in a longer unconstrained CoMET analysis to estimate the marginal posterior distributions of all parameters (May et al. 2016). As with BDSKY above, we assumed complete taxon sampling at present (ρ = 1). For each tree, the model was run until the ESS for every parameter reached a value of 500. Bayes Factor comparisons were employed to evaluate the marginal likelihoods of competing models for the timing of the MEEs, with significance values following Kass and Raftery (1995): BF > 2 (positive support), and BF > 6 (strong support).

Empirical study

To compare the robustness of BDSKY and CoMET against a real empirical dataset, we analyzed the conifer time tree of Leslie et al. (2012: 342 taxa, 78% taxon sampling), which was also used in May et al.’s 2016 study. For BDSKY, we ran models B and C, setting the number of rate shifts to vary between two and five to emulate CoMET in allowing for multiple sequential MEEs. We also cut off (“masked”) part of the tree length by instructing the model to start searching for a MEE after ∼6%, ∼11%, and ∼18% of the tree root age (340 million years ago): 320, 300, and 280 million years ago; this was done in order to remove parts of the tree with very little information regarding MEEs. The initial rate shift values were set to be equally spaced across the tree length. Prior distributions for μ and λ rates followed May et al. (2016, cf. Supporting Information S14): a lognormal distribution with an SD of 0.02 and mean = 0.09 for μ and 0.16 for λ. Analyses were run until the ESS value reached 200 for each parameter; analyses that did not converge after 1000 million iterations were discarded. All data results from this study are deposited in the public repository dryad, https://doi.org/10.5061/dryad.qv10c62.

Results

IMPACT OF PARAMETER SETTINGS IN SIMULATED PHYLOGENIES

Figures S1 and S2 show the simulated trees—full (including extinct and extant taxa) and reconstructed (extant taxa only)—under the different parameter‐combination settings. Comparison of the lineage‐through‐time (LTT) plots among scenarios reveals several aspects that we expect from analytical considerations (e.g., Gernhard 2008). The background extinction (ratio of a varying μ over constant λ) has a large influence over: the root age: as μ increases, the root age in the full and reconstructed trees increases; the root age variation: as μ increases, the variation increases; and on the variation of the root age between the full and reconstructed trees: as μ increases, this difference also increases.

PARAMETER ESTIMATION UNDER THE BDSKY MODEL

We compare below the performance of the three BDSKY analyses (Models A–C) in terms of how well they answer the questions posited in the Introduction:

• (1)Can we detect the phylogenetic signal of a MEE in the extant phylogenetic tree through changes in the diversification rate?

Results from the control scenario (with no mass extinction, ρ = 1) showed that the percentage of false positives or Type I error was very low in the three models: HPDn values were 0 for all models (Model C: Fig. 2, Model A: Fig. S3, Model B: Fig. S4). Precision and accuracy for estimates of the diversification rate were best for Model C, followed by Model A (Table S2; Fig. 2, Fig. S3); both models were also able to capture the true simulated value within the 95% HPD interval in 100% trees (full coverage, Table S2). The time‐constrained Model B showed the lowest values for accuracy, precision, and coverage, especially in the first (pre‐MEE) and second (MEE) intervals (Fig. S4 and Table S2). The MEE interval is most likely too short, containing a very low number of nodes, and thus the method cannot detect any significant result for that time interval.

Figure 2.

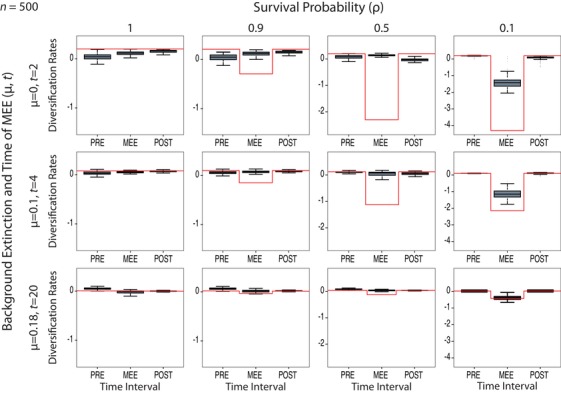
Detection of MEEs under the BDSKY Model C through sequential changes in the magnitude of the diversification rate (diversification = λ – μ) under varying levels of μ and mass extinction survival probability, ρ. The red line represents the true (simulated) value; this has been adjusted for ρ = 0.1 in the MEE time interval to reflect the effect of the MEE (see text). The boxplots show the variance in the estimated value across simulated trees, depicting the mean of the means of all trees (thicker dark line), the 75–24% interquartile ranges (shaded box) and the post extreme data points (whiskers). Notice that in the high‐extinction scenario (ρ = 0.1), the diversification rate becomes negative in the second time interval, followed by recovery to positive values in the next interval, signaling the presence of the MEE (μ > λ), but that this change is not observed in the control scenario (with no mass extinction, ρ = 1). Figures S3 and S4 show the same results for Models A and B, respectively.

The percentage of false negatives or Type II error in trees simulated under varying levels of MEE survival probability (ρ) was highest for Model B, which showed no significant decrease in diversification rate in the MEE time interval (i.e., HPDn was always 0, Table S2), irrespective of the value of extinction μ (Fig. S4). Accuracy, precision, and coverage for Model B were also the lowest among the three models when ρ < 1 (Table S2). Because of this failure to detect the MEE under varying settings, Model B was discarded and will not be further commented upon. Between the other two models and for the high‐intensity mass extinction scenario (ρ = 0.1) and N = 500, Model C (constrained‐speciation) showed the highest power in detecting the MEE irrespective of the value of μ: it returned negative values for the diversification rate in the MEE time interval, with a rebound to positive values in the third interval (Fig. 2), an indication of the ability of this model to detect the MEE. Even when the coverage was 0 (the true value was not contained within the 95% HPD interval), as in the case of μ = 0, the model returned a negative value for the diversification rate in the MEE time interval in 84% of the trees that did converge (HPDn = 0.84, Table S2), and this percentage became higher with increasing values of μ (93%, 97%). Accuracy, precision, and coverage also increased with higher values of μ, and were the highest for μ = 0.18 (Fig. 2, Table 1).

Table 1.

Summary statistics for the parameters in the Birth–Death Skyline Model C (N = 500; see text for more detailed description)

		ρ = 1						ρ = 0.9						ρ = 0.5						ρ = 0.1
		λ			μ			λ			μ			λ			μ			λ			μ
	Time interval	Acc	Prec	Cov	Acc	Prec	Cov	Acc	Prec	Cov	Acc	Prec	Cov	Acc	Prec	Cov	Acc	Prec	Cov	Acc	Prec	Cov	Acc	Prec	Cov
μ = 0.0	Pre	−0.02	0.07	0.91	−0.03	0.59	0	−0.02	0.07	0.95	−0.03	0.58	0	−0.03	0.1	0.8	−0.08	0.49	0	−0.03	0.08	0.77	−0.19	0.1	0
	MEE	–	–	–	−0.11	0.4	0	–	–	–	−0.11	0.38	0	–	–	–	−0.14	0.37	0	–	–	–	5.84	1.72	0
	Post	–	–	–	−0.14	0.27	0	–	–	–	−0.13	0.26	0	–	–	–	0.03	0.4	0	–	–	–	−0.05	0.39	0
μ = 0.1	Pre	0	0.07	0.96	0.05	0.46	1	0	0.08	0.99	0.05	0.44	1	−0.01	0.09	0.96	0.02	0.31	1	0	0.08	0.97	0	0.09	0.97
	MEE	–	–	–	0.03	0.33	1	–	–	–	0.03	0.33	1	–	–	–	0.09	0.49	1	–	–	–	3.49	1.41	0.24
	Post	–	–	–	0.01	0.19	0.99	–	–	–	0.02	0.21	1	–	–	–	0.07	0.27	0.84	–	–	–	0	0.22	0.99
μ = 0.18	Pre	0	0.07	0.97	0.12	0.32	0.99	0	0.07	0.95	0.11	0.32	0.98	0	0.07	0.97	0.12	0.28	0.99	0	0.07	0.94	0.16	0.08	0.93
	MEE	–	–	.	0.18	0.42	1	–	–	–	0.17	0.4	1	–	–	–	0.17	0.35	1	–	–	–	1.02	0.77	0.94
	Post	–	–	–	0.16	0.14	0.99	–	–	–	0.16	0.14	0.99	–	–	–	0.17	0.15	0.97	–	–	–	0.16	0.12	0.94

Abbreviations: “μ,” value of extinction rate in simulations; “ρ,” survival probability in simulations; mass extinction intensity = (1− ρ). “Acc,” the mean of the means of the estimated parameters across trees; “Prec,” the mean of the width of the 95% high posterior density (HPD) credibility interval across trees; “Cov,” coverage, percentage of simulated trees where the 95% HPD credibility interval contained the true parameter value.

As expected, the percentage of false negatives (i.e., failing to detect the MEE) increased as the mass extinction intensity (1 – ρ) decreases (Fig. 2), with HPDn values generally close to zero for ρ = 0.5 and ρ = 0.9 (Table 1). Accuracy, precision, and coverage were lower for ρ = 0.5 than for ρ = 0.1 (except for the MEE interval with μ = 0), whereas ρ = 0.9 showed values very similar to the null model (Table 1). Similarly, a lower number of extant taxa in the reconstructed phylogeny (N) translates into a decrease in the power to detect the MEE, especially for μ = 0 (Fig. 3).

Figure 3.

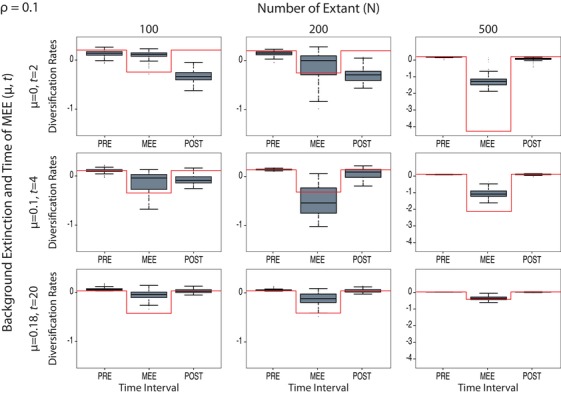
Detection of MEEs through interoperating changes in the magnitude of the diversification rate in Model C under varying levels of N (number of taxa). All other conventions follow Figure 2.

The full parameterized Model A (Fig. S3) performed worse than Model C, showing HPDn values close to zero (Table S2). A trend toward negative values can be observed for the scenario with the lowest MEE survival probability (ρ = 0.1) and N = 500, signaling the presence of a MEE (Fig. S3). But precision and coverage were considerably worse than in Model C (broader 95% HPD intervals, Table S2), and accuracy was also lower (Table S2). The ability of the model to detect the MEE was similarly low for higher values of ρ (0.9, 0.5, Fig. S3) and smaller values of N (100, 200; Fig. S5).

• (2) Can we accurately estimate the time interval of the MEE from an extant phylogenetic tree? Figure 4 shows that Model C performed well in estimating the time of the rate shifts bounding the MEE interval within which the MEE was expected to occur, for the high‐intensity scenario (ρ = 0.1) and varying values of μ. Coverage was always equal to 1, and 95% HPD intervals (precision) were narrow, especially for μ = 0 and 0.1 (Table 1). However, this power notably decreases with higher values of MEE survival probability: the variance in the two rate shift estimates pre‐ and post‐MEE overlaps across age values for ρ = 0.9 and ρ = 0.5 (Fig. 4), indicating the failure of the model to capture the rate shift times under low‐intensity MEE scenarios. Likewise, for N < 500, the model is unable to estimate the MEE time interval with any accuracy or precision (Fig. S6). For the null model (ρ = 1), the time length covered by the variance in these estimates (boxplots in Fig. 4) spans the entire range of root ages across simulated trees, as can be expected in the absence of a MEE. The full Model A (Figs. S7 and S8) again performed worse than Model C in terms of precision and coverage (Table S2): it failed to estimate the rate shift times bounding the MEE for any parameter combination of μ and ρ (Fig. S7), as well as for the low values of N (100, 200; Fig. S8).
• (3) Can we provide reasonable estimations for λ and μ pre‐ and post‐MEE? Since Model C was the only model that could successfully detect and estimate the time interval of the MEE (for N = 500 and ρ = 0.1), we focus here on this model to evaluate the performance in parameter estimation of μ and λ.

Figure 5 shows the variance in the estimates of λ and changes in the magnitude of μ across the three time intervals, for different simulation scenarios. Estimates of λ were good across varying settings of μ and ρ, especially regarding accuracy and precision (Table 1); coverage was lower for low values of extinction (Table 1). Estimates of λ were also good for the control scenario in terms of accuracy, precision, and coverage (Table 1).

Figure 5.

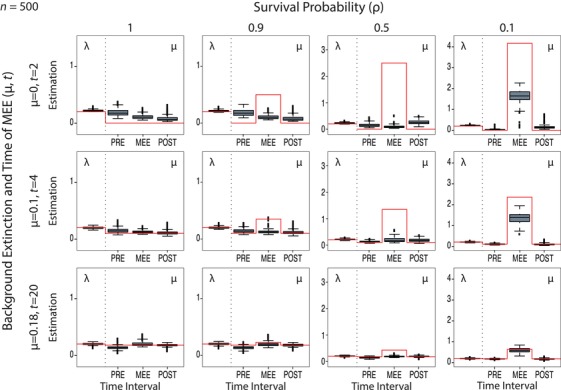
Estimation of changes in magnitude of μ across time intervals for Model C under different values of background extinction and MEE survival probability, ρ. In this model, λ is estimated but assumed constant over time; that is, MEEs are only detected through changes in the magnitude of μ. The red line represents the true simulated value; this has been adjusted for ρ = 0.1 in the MEE time interval to reflect the effect of the MEE (see text). Notice the large increase of μ (>1) in the MEE time interval for ρ = 0.1, indicating the presence of the MEE, while this effect is not seen in the control scenario (ρ = 1). See Figure S9 for the results with varying values of N (100, 200, and 500).

For estimates of μ, in general, the best results were obtained with the low mass extinction survival probability scenario (ρ = 0.1), especially for the pre‐ and post‐MEE time intervals, and for scenarios with moderate (μ = 0.1) or high (μ = 0.18) background extinction. For μ = 0, the coverage (95% HPD containing the true value) was very low (Table 1; true value is red line in Fig. 5, ρ = 0.1), and precision and accuracy were generally worse. However, the model was able to recover the signal of an increase in background extinction in the MEE time interval for the majority of trees (see Fig. 5, ρ = 0.1).

As the mass extinction survival probability, ρ, increases, the power to accurately measure changes in μ also decreases; no significant differences in variance were observed with respect to the null model (ρ = 1), with the rate of μ over‐ or underestimated across time intervals (Fig. 5, ρ ≠ 0.1). Lowering the number of extant taxa also resulted in a lower ability to detect changes in magnitude in μ (Fig. S9). Yet, for N = 200 and moderate/high background extinction, Model C was still able to capture the increase in the extinction rate for the MEE time interval, and estimates of λ and of μ for the post‐ and pre‐MEE time intervals were relatively accurate (Fig. S9).

COMPARISON AGAINST SINGLE‐PULSE COMET

Simulation study

Table 2 summarizes the differences and similarities between the BDSKY and CoMET models in terms of performance with the set of simulated trees (see Figs. S10–S15 for CoMET). The two models have a similar frequency of Type II error as defined here, failing to detect the MEE through changes in the diversification rate (HPDn), and they exhibit no Type I error, i.e., false detection of a MEE where none was simulated, ρ = 1 (Table 2). The BDSKY model performed slightly better in detecting the MEE under the high‐intensity mass extinction scenario (ρ = 0.1) and N = 500, whereas CoMET did the same for the moderate‐intensity scenario (ρ = 0.5); CoMET also performed better for smaller phylogenies with N = 100 and N = 200. The same pattern can be observed in the location of the MEE, that is, estimating the timing of the MEE: both models succeeded with large phylogenies (N = 500) under the high‐intensity scenario (ρ = 0.1), but CoMET performed better under moderate/low‐intensity mass extinction scenarios (ρ = 0.5, 0.9) and with smaller phylogenies (N = 100, 200). There is one interesting difference, however. Whereas in BDSKY, the timing of the MEE was identified through the rate shift times of μ—in accordance with the time‐slice model—in CoMET, MEEs were often located through the timing of rate shifts for λ (i.e., as a significant decrease in speciation rates) rather than through the specific parameter used in CoMET to detect MEEs, mass extinction times. If the mass extinction times parameter succeeded to locate the MEE, the Bayes Factor comparisons were often not significant (2 < BF < 6, Table 2). In general, BDSKY showed better accuracy than the CoMET model in the estimation of μ and λ, irrespective of the MEE intensity (1 – ρ) and the size of the phylogeny (N). CoMET performed worse in scenarios with no extinction (μ = 0), systematically overestimating μ or over/underestimating λ. Both BDSKY and CoMET showed the best behavior under scenarios with moderate extinction (μ = 0.1, Table 2).

Table 2.

Table summarizing the performance of the time‐slice BDSKY Model C, and the single‐pulse CoMET model (May et al. 2016) for the simulated set of phylogenies that converged in BEAST2 (see Table S1). Color code: “White” indicates the success of the model in estimating the parameter value or detecting the MEE event; “green” indicates the failure of the model; “yellow” indicates mixed results. See footnotes for an explanation (the corresponding Figure numbers illustrating these results are given under each header; posterior probability estimates and accuracy values for each parameter are given in Table S3)

	λ estimation		μ estimation		MEE detection		MEE time estimation
Model Settings (N, ρ, μ, t)	BDSKY (5, S9)	CoMET (S14, S15)	BDSKY (5, S9)	CoMET (S14, S15)	BDSKY (2, 3)	CoMET (S10, S11)	BDSKY (4, S6)	CoMET (S11, S13)
(500, 0.1, 0, 2)	a	a1	a2	a1	b*	b1	c	c – λ
(500, 0.1, 0.1, 4)	a	a1*	a	a1*	b	b	c	c – λ
(500, 0.1, 0.18, 20)	a	a	a	a	b	b	c	c – λ
								c2 – μ
								c2 – MEE
(500, 0.5, 0, 2)	a	a	a1	a1	b2	b2	c2	c1 – λ
(500, 0.5, 0.1, 4)	a	a*	a	a*	b2	b1	c2	c – λ
(500, 0.5, 0.18, 20)	a	a	a	a	b2	b2	c2	c2
(500, 0.9, 0, 2)	a	a	a1	a1	b2	b2	c2	c2
(500, 0.9, 0.1, 4)	a	a	a	a*	b2	b2	c2	c2
(500, 0.9, 0.18, 20)	a	a	a	a*	b2	b2	c2	c2
(500, 1, 0, 2)	a	a	a2	a1	d	d	d	d
(500, 1, 0.1, 4)	a	a	a	a*	d	d	d	d
(500, 1, 0.18, 20)	a	a	a	a	d	d	d	d
(100, 0.1, 0, 2)	a1*	a2	a1	a1	b2	b1	c2	c – λ
(100, 0.1, 0.1, 4)	a*	a*	a2	a*	b2	b2	c2	c1‐λ
								c2–  MEE
(100, 0.1, 0.18, 20)	a	a	a**	a*	b2	b2	c2	c2– MEE
(200, 0.1, 0, 2)	a1	a1*	a1	a1	b2	b1*	c2	c – λ
(200, 0.1, 0.1, 4)	a	a1	a**	a1*	b2	b	c2	c – λ
(200, 0.1, 0.18, 20)	a	a	a**	a	b1*	b2	c2	c– MEE
(100, 1, 0, 2)	a	a1	a1	a1	d	d	d	d
(100, 1, 0.1, 4)	a	a*	a*	a*	d	d	d	d
(100, 1, 0.18, 20)	a	a*	a*	a*	d	d	d	d
(200, 1, 0, 2)	a	a1	a2	a2	d	d	d	d
(200, 1, 0.1, 4)	a	a	a*	a*	d	d	d	d
(200, 1, 0.18, 20)	a	a*	a	a*	d	d	d	d

a: Simulated (true) value falls within 95% HPD (BDSKY) or Credible Interval (CoMET). (*) Large 95% HPD interval width (≥0.05 between lower and upper boundary). (**) Large only for post−MEE interval.

a¹: Under/Overestimation of true value (falls outside the 95% HPD or Credible Interval). (*) Mean overestimated but the true value falls within 95% HPD (BDSKY); under/overestimation only observed in part of the tree length (CoMET).

a²: True value falls within 95% HPD (BDSKY) or Credible Interval (CoMET), but only in either the pre‐ or post‐MEE interval.

b: Success in detecting MEE: Mean and 95% HPD (BDSKY)/Credible Interval (CoMET) of the diversification rate estimate fall below 0 (r < 0) at MEEE (“MEE interval” in BDSKY) and goes back to simulated values after MEE (“post‐MEE interval”). (*) Only 84% of HPDn <0 for the percentage of simulated phylogenies that converged.

b¹: Weak detection of MEE: Diversification rate decreases in pre‐MEE interval (BDSKY) or at MEE (CoMET), but mean and/or 95% HPD/Credible Interval of the diversification rate is not negative. (*) Only part of the HPD falls below 0.

b²: Type II error: Failure to detect the MEE through the diversification rate.

c: Good estimation. MEE time correctly bounded by rate shift times in μ (BDSKY). MEE time correctly identified by significant Bayes Factor comparisons (BF > 6) of λ shift times (c – λ) or single‐pulse MEE times (c‐MEE) (CoMET).

c¹: Weak estimation (CoMET): MEE time correctly identified by non‐significant BF tests (2< BF < 6) of rate shift times in λ (c¹‐λ), or in (c¹‐μ), or single‐pulse MEE times (c¹‐MEE).

c²: Failed estimation. MEE time incorrectly identified by rate shift times in μ (BDSKY) or by non‐significant BF tests of μ shift times (c²‐μ) or single‐pulse MEE times (c²‐MEE) (CoMET).

d: No Type I error. No MEE is detected in the control scenario (ρ = 1).

Abbreviations: λ estimation, power to estimate speciation rate; μ estimation, power to estimate extinction rate; MEE detection, power to detect the MEE through interoperating changes in the diversification rate; MEE time estimation, timing of MEE detected through successive shifts in extinction rate estimates (BDSKY) or through shifts in speciation rate (CoMET).

Empirical study

Figure 6 shows the results of the BDSKY and CoMET models with the empirical conifer dataset of Leslie et al. 2012. CoMET detected a significant MEE (BF > 10) at about 23 million years ago, as in May et al. 2016. BDSKY located a drop in net diversification to r < 0 at 43 (78–23) million years ago and an increase in net diversification to r > 0 at 3 (10–0) million years ago, given we allow for three rate shifts. If we allow for five rate shifts, the drop happens within roughly the same HPD interval (70–20 million years ago) with the median being at 30 million years ago (instead of 43 million years ago). Thus, the estimated period of negative diversification spans several decades of millions of years. The instantaneous MEE of May et al. 2016 is estimated to be at 23 Ma, and thus falls within the period of negative net diversification that we estimate. In contrast, the other, “potential” mass extinction events reported by May et al. 2016 at 173 and 77 million years ago (2 < BF < 6) are not recovered by BDSKY as true MEEs according to our definition (r < 0, ε > 1), but as low‐magnitude rate‐shifts in μ.

Figure 6.

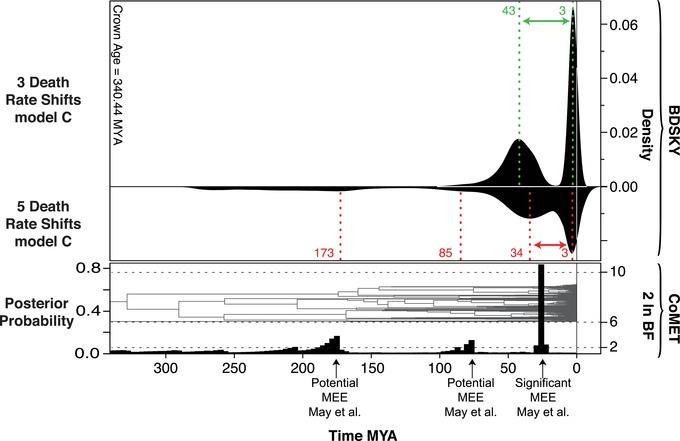
Comparison of the BDSKY and CoMET model performance with the empirical conifer dataset (Leslie et al. 2012): BDSKY was run under Model C. We explored models with one and multiple rate shifts (shown here are the best models with three and five rate shifts). CoMET was run under the same settings used by May et al. 2016. CoMET detected a major event of mass extinction at about 23 million years ago. BDSKY indicated a drop in the net diversification to r < 0 at about 43 or 34 million years ago, dependent on the number of rate shifts, and an increase in net diversification to r > 0 at 3 million years ago. BDSKY, suggests that the two nonsignificant MEEs (2 < BF < 6) detected by CoMET at 173 and 77 million years ago (May et al. 2016), are not true MEEs (ε > 1), but rather low‐magnitude rate‐shifts in μ.

Discussion

TIME‐SLICE VERSUS SINGLE‐PULSE APPROACH TO DETECT MASS EXTINCTION EVENTS

Evolutionary episodes of hyperdiversification—that is defined as speciation rates within a lineage that are significantly higher than those expected under the background diversification rate of their encompassing clade—have long attracted the attention of biologists (Hughes and Eastwood 2006; Valente et al. 2010) and analytical systematists (Rabosky 2006; Alfaro et al. 2009; Rabosky 2014) because of their potential links to “key innovations” (morphological novelties) or the colonization of novel environments leading to increased species fitness, “key opportunities” (Wiens et al. 2010; Donoghue and Sanderson 2015).

By contrast, episodes of high extinction rates such as mass extinction events (MEE), have traditionally received less attention in the phylogenetic literature because of the difficulty of measuring a process that removes rather than generates diversity (Pyron and Burbrink 2012; Sanmartín and Meseguer 2016). However, these MEEs form a key element of the paleontological record as responsible for major ecosystem reordering and change (Raup 1979; Sepkosky 1982; Purvis 2008; Benton 2009), and recently have regained importance in the context of human‐induced biodiversity loss (Barnosky et al. 2011a, b).

Unlike speciation or background extinction rates, which are assumed to depend on species biotic traits or a clade's ecology (Purvis 2008; Ezard et al. 2011), MEEs are often linked to abiotic factors, i.e., long‐term environmental changes or catastrophic, geological events whose effects are felt across multiple lineages (Pyron and Burbrink 2012; Sanmartín and Meseguer 2016). Because of this, MEEs are often modeled in the phylogenetic literature as tree‐wide events that act simultaneously across clades in contrast to events that are clade‐specific (Stadler 2011c, b). Indeed, most macroevolutionary approaches model MEEs as random instantaneous extinction events, in which the standing diversity is reduced by a fraction equal to the magnitude or intensity of the mass extinction, 1– ρ (Harvey et al. 1994; Stadler 2011b; May et al. 2016).

Modeling MEEs under this single‐pulse approach (i.e., through the parameter ρ)—as in the birth–death models implemented in TreePar and TESS—has the advantage that one can estimate the magnitude or intensity of MEEs, and that it allows for the statistical testing of time‐specific MEE hypotheses (Stadler 2011c; May et al. 2016; Sanmartín and Meseguer 2016). Yet, the single‐pulse approach stands in contrast with the paleontological literature, where MEEs are defined in terms of intensity and duration, where unusually high background extinction rates take place over a (geologically) short time period, followed by a recovery or a return to positive net diversification rates (Raup 1979). We showed here that the BDSKY model (Stadler et al. 2013)—developed initially to trace the spread of viral or bacterial infections over time—can be used to detect MEEs under the “time‐slice” approach: MEEs are identified and located through a combination of negative diversification rates and two sequential rate shifts in the extinction rate occurring in a significantly short period of time (Fig. 2; Table 1).

A second advantage of the time‐slice approach relates to the issue of parameter non‐identifiability. Joint estimation of instantaneous tree‐wide changes in dispersal and extinction rates (i.e., rate shifts in λ and μ) and MEE single‐pulse events (ρ) is not possible because the three parameters are modeled with the same likelihood function, and in fact the model becomes non‐unidentifiable. This applies to TreePar when allowing for both single‐pulse and time‐slice MEEs, that is, through diversification rate changes (this option is not recommended in the R package documentation due to parameter correlations). To escape from this paradox, CoMET, which can also be used to model both types of MEEs, uses a hierarchical Bayesian approach in which MEEs are estimated by marginalizing over other nuisance parameters such as all possible instantaneous shifts in speciation and extinction rates (May et al. 2016). Therefore, CoMET may be seen as a more general and powerful tool than BDSKY. While CoMET solely returns single‐pulse MEEs, it additionally also outputs changes in speciation and extinction rates, which may be regarded as equivalent to returning time‐slice MEEs. However, the risk of diluting the signal of the MEE by explaining it partially as single‐pulse and partially as a time‐slice exists. This can be observed in our results for the simulation data in CoMET, where we setup the MEE model to be a single‐pulse (i.e., recover the MEE through the parameter mass extinction times); however, we mainly recovered MEEs under the time‐slice approach, that is, as speciation rate changes (Figs. S12 and S13; Table 2).

In BDSKY, we investigate the posterior distribution of the extinction rate through time and thus detect the presence of MEEs in the phylogeny as time periods with elevated extinction rates. There is no need to mathematically disentangle MEEs from background extinction and speciation rate shifts (Stadler 2011a; May et al. 2016) because we estimate rate shifts in background extinction and MEEs within the same continuous‐time framework (Fig. 1B). This can be directly seen with the example of the conifer dataset (Fig. 6): BDSKY identifies the increase in extinction rates detected by CoMET at about 23 million years ago as a genuine MEE (ε > 1), whereas the other low‐magnitude events (173 and 77 million years ago in CoMET) are identified as periods of high background extinction rates with ε < 1. These changes in extinction rate were picked up only when the BDSKY model was allowed to explore multiple rate shifts, indicating that as the number of rate shifts increases, BDSKY becomes more sensitive to the influence of low‐magnitude changes in μ. Yet, parameter identifiability issues can also affect the BDSKY model. Our simulations were generated under the single‐pulse approach to MEEs, as instantaneous events, and then estimated under the MEE time‐slice approach in BDSKY; notice the low variance and the small difference between the pre‐MEE and post‐MEE values of rate shifts in Figure 4. Since pulses can be seen as the limit of time‐slice models, then, at least for extremely short time slices with very high extinction (which would be well approximated by a pulse model), BDSKY could get into the same problems of parameter non‐identifiability as CoMET or TreePar. In future studies, it would be interesting to test the performance of the BDSKY model for longer‐duration MEEs scenarios.

It is important to emphasize that all three methods, CoMET, TreePar, and BDSKY, rely on the same likelihood function for estimating speciation, extinction, and MEEs, and therefore conceptually allow for both types of MEEs, namely single‐pulse and time‐slice scenarios. However, they differ in their statistical framework and the type of prior distributions used for detecting MEEs, which conditions their performance. CoMET (Bayesian) and TreePar (ML) were specifically designed to identify single‐pulse MEEs (also termed explicit MEEs in May et al. 2016); the time‐slice MEEs would not be reported as MEEs but as “regular” changes in extinction and speciation rates. Instead, BDSKY was developed to detect rate changes (Stadler et al. 2013) and is thus better tuned to detect MEEs under the time‐slice approach. In particular, CoMET focuses on the detection of instantaneous events, while BDSKY focuses on the time interval during which MEEs occur.

COMPARING THE PERFORMANCE OF BDSKY AND COMET

Our simulation study reveals that BDSKY and CoMET performed well and suffered from similar low rates of Type I (false discovery rate) and Type II error (failing to detect the MEE) for the control (ρ = 1) and high‐intensity MEE (ρ = 0.1) scenarios. For the small (N = 100) and medium‐sized (N = 200) phylogenies, CoMET was more robust to Type I and Type II errors in the detection and location (timing) of the MEE than BDSKY. On the other hand, BDSKY performed better than CoMET in the estimation of the rate of speciation (λ) and of changes in the magnitude of extinction (μ) across time intervals, in particular for N = 500 and ρ = 0.1.

Overall, CoMET has a larger number of parameters than BDSKY because it models the frequency of MEEs and speciation and extinction rate shifts through three independent CPP processes, and also includes the survival probability parameter ρ (May et al. 2016). CPP models are known to be sensitive to the choice of priors and suffer from parameter identifiability issues (Rannala 2002). Because of this, May et al. 2016 advocated the use of strongly informative (biologically grounded) priors on some parameters such as the frequency or the intensity of MEEs to increase the power of CoMET in detecting these events. For example, one can use the paleontological record (Benton 2009) to inform the MEE intensity (1 – ρ), which should be about 90%, or the expected number of MEEs (λ_M) in the CPP prior, as in the conifer example (Höhna et al. 2015; May et al. 2016). A prior expectation on the number of rate shifts in speciation and extinction (λ_B and λ_D) is more difficult to justify on biological grounds, and are often given the same value as the one given to the expected number of MEEs (number Expected rate changes = number Expected Mass Extinctions = 2; Höhna et al. 2015). For the speciation and extinction rates, an empirical Bayesian approach is used to parameterize the hyperpriors. May et al. 2016 argued that the use of Bayes factor comparisons cancels out these prior assumptions, which are only used to speed up the convergence of the MCMC search but should not have an effect on the eventual conclusions (Höhna et al. 2015). Yet, due to the issues of parameter non‐identifiability (above), the results from CoMET may still be dependent on the choice of hyperprior being used in the analysis. Moreover, because MEEs in CoMET are estimated by integrating over speciation and extinction rate shifts, which are considered as nuisance parameters in the model, May et al. 2015 originally warned that researchers should be cautious not to over‐rely on the values of these parameters (tree‐wide diversification rate shifts), for which we have also less biological information compared to MEEs. This could explain the poor performance of CoMET in estimating the magnitude of rate changes in λ and μ (Table 1). In contrast, BDSKY is unaffected by this issue because MEEs are estimated through changes in the background extinction rate, and therefore MEEs and temporal changes in extinction rates are treated in the same way (Condamine et al. 2013; cf. Fig. 4).

It is important to notice, however, that we are referring here to the BDSKY Model C, in which we constrained the speciation rate (λ) to be constant across time intervals; Model A, allowing speciation and extinction rates to vary, as CoMET does, performed significantly worse. The assumption of constant speciation rates might seem unrealistic and hard to justify on biological grounds. Yet, in an often‐cited study, Ezard et al. 2011 found that speciation rates in the fossil record were mostly shaped by biotic factors such as diversity dependence, whereas fossil‐based extinction rates responded mainly to abrupt abiotic perturbations, such as major geological or climatic changes. Therefore, it might be appropriate to detect time‐slice MEEs through the extinction rate parameter, which is (potentially) more sensitive to these environmental changes than the speciation rate.

In all, both BDSKY and CoMET have their strengths and drawbacks and could be used side‐by‐side. CoMET performs best as a method for testing time‐specific hypotheses on MEEs, when we have some prior information on their presence, while BDSKY can be seen as an exploratory model to search for the signal of potential MEEs in a phylogeny in the absence of such data. This can be exemplified again in the conifer phylogeny. CoMET detected a major episode of mass extinction at about 23 million years ago, as well as the weak signal of other increases in extinction rate in the distant past. Although May et al. 2016 regarded this MEE as a possible artifact of biased divergence time estimates, it is temporally congruent with the Late Oligocene Warming Event (LOWE, 26.7–23.5 million years ago, Zachos et al. 2001), a widespread major warming pulse that accompanied the closing of the eastern arm of the ancient Mesozoic Tethyan Seaway (Liu et al. 2018). In the southern Palearctic, this event was followed by high extinction rates and the gradual replacement of a former subtropical flora by continental xerophytic and Mediterranean lineages (Manafzadeh et al. 2017). The result from BDSKY is more ambiguous, pointing to a longer period of negative diversification rates, which spans several tens of millions of years, starting at 43 or 34 million years ago. The start of this period corresponds to the global cooling event at the Late Eocene–Early Oligocene boundary, the Terminal Eocene event (TEE) or Late Eocene–Oligocene Cooling event (Zachos et al. 2001), which in the Northern Hemisphere led to widespread extinction and the replacement of a boreotropical flora by temperate elements (Meseguer et al. 2018). The fact that BDSKY cannot narrow down the time interval of negative diversification rates can be considered a weakness of the method. However, as Leslie et al. 2012 noted, the major families in the conifer tree exhibit different diversification trajectories, which seem to be related to their geographic distribution. Thus, Southern Hemisphere families Podocarpaceae and Araucariaceae comprise on average older (Miocene) clades, and their LTT plots show plateaus (interpreted as signaling an MEE, Harvey et al. 1994), extending between 50 and about 30–25 million years ago (cf. Fig. 2A in Leslie et al. 2012). This signal could correspond with the TEE, which restricted evergreen plant lineages to the equatorial latitudes of the Northern and Southern Hemispheres (Meseguer et al. 2018). In contrast, major clades within the Northern Hemisphere Pinaceae and Cupressoideae are mainly of Late Neogene age (<20 million years ago), with the species‐rich conifer genera Pinus, Juniperus, and Cupressus diversifying within the last 5–3 million years ago (cf. Fig. 1D, Leslie et al. 2012). The recovery phase detected by BDSKY, with a return to positive diversification rates at about 3 million years ago, could well correspond to this period of rapid diversification reported by Leslie et al. 2012. Overall, the ambiguity in the BDSKY results could actually reflect the different diversification trajectories, and their reaction to these sequential MEEs, taken by the conifer families depending on their geographic distribution. Northern Hemisphere conifers in Pinaceae and Cupressoideae were probably as affected by the TEE as the Southern Araucariaceae or Podocarpaceae, but later major climatic events such as the Late Oligocene Warming Event could have obscured the signal of these more ancient events.

Finally, both CoMET and BDSKY (and TreePar) assume that changes in speciation and extinction rates occur simultaneously across all branches in the phylogeny (“tree‐wide rate shifts”). There is, however, increasing evidence that speciation and extinction rates vary across clades, dependent on biotic factors such as the appearance of key innovations or the colonization of a new ecological niche (Donoghue and Sanderson 2015). Laurent et al. 2015 found that TreePar suffers from a higher frequency of Type I error under scenarios with substantial clade‐rate heterogeneity, whereas CoMET is relatively insensitive to this bias (May et al. 2016). It would be interesting to test the behavior of BDSKY under such scenarios. Another limitation of CoMET or BDSKY is that they model mass extinction events as a non‐selective (statistically random) “field of bullets” scenario, in which all lineages in the tree have the same probability of being affected by the mass extinction event (Raup 1982; Harvey et al. 1994). Some authors conceive mass extinction as a “fair game” (Darwin‐like) scenario, in which the best‐adapted species would have the highest survival probability (Raup 1982; Pyron and Burbrink 2012). The geographic distribution of a clade might also condition the impact of the MEE. This could be the case of the conifers, that is, the older southern lineages exhibit lower turnover rates than the northern lineages, and might have survived the climatic shifts of the Late Cenozoic in the relatively warm or wet oceanic climates of the austral landmasses (Leslie et al. 2012). Future method development should consider allowing the magnitude or survival probability to the mass extinction event to vary across clades within the phylogeny.

Conclusions

Here, we demonstrate that estimating changes in extinction rates through time as in the BDSKY model allows detecting the signature of mass extinction events from phylogenies with only extant taxa. The advantages of a time‐slice approach are its closer resemblance to the paleontological record and the possibility to cover a broader range of MEEs, from nearly instantaneous events to a longer time period of elevated extinction rates. However, further simulations are needed to understand the limits of this approach.

Associate Editor: S. Smith

Handling Editor: P. Tiffin

Supporting information

Table S1. Percentage of simulated phylogenies that converged in BEAST2 for each of the three model settings (A, B, and C) of the birth‐death skyline model parameter (BDSKY).

Table S2. Summary statistics for the Birth‐Death Skyline model parameters. Models A to C refer to different BEAST2 settings with varying constraints (see text for a detailed description). Abbreviations: “N” = Number of taxa; “m” = value of extinction rate in simulations; “r” = survival probability in simulations; mass extinction intensity = (1 ‐ r). Posterior probability estimates and accuracy for the Diversification Rate: “Acc”: the mean of the means of the estimated parameters across trees; “Prec”: the mean of the width of the 95% High Posterior Density (HPD) credibility interval across trees; “Cov”: Coverage, percentage of simulated trees where the 95% HPD credibility interval contained the true parameter value; “HPDn” is defined as the percentage of simulated trees where the 95% HPD for the diversification rate falls entirely below 0. r). Posterior probability estimates and accuracy for the Rate Shift Times: “Prec”; the width of the 95% HPD of the estimated MEE time interval; “Cover”: the percentage of simulations where at least 95% of the estimated MEE time interval contains the true time t.

Figure S1. LTT plots of simulated phylogenies under different scenarios with varying values of µ and ρ. Black lines represent the LTT plot of the full (extinct and extant taxa) tree; the red lines show the reconstructed, extant‐only tree LTT plot. Horizontal boxplots represent the variation in the age of the root for the full (grey) and reconstructed (red) trees. Vertical boxplots represent the variation in the number of pre‐MEE lineages in the models with low mass extinction survival probability, ρ.

Figure S2. LTT plots of simulated phylogenies under different values of µ and number of extant taxa in reconstructed phylogeny (N). Black lines represent the LTT plot of the full (extinct and extant taxa) tree; the red lines show the reconstructed, extant‐only tree LTT plot. All other conventions as in Figure S1.

Figure S3. Detection of MEEs through interoperating changes in the magnitude of the diversification rate in Model A under varying levels of µ and mass extinction survival probability, ρ. All other conventions follow Figure 2.

Figure S4. Detection of MEEs through interoperating changes in the magnitude of the diversification rate in Model B under varying levels of µ and mass extinction survival probability, ρ. All other conventions follow Figure 2.

Figure S5. Detection of MEEs through interoperating changes in the magnitude of the diversification rate in Model A under varying levels of N (number of taxa). All other conventions follow Figure 2.

Figure S6. Location of MEEs (as accurate estimation of time intervals for rate changes in µ that contain the MEE) for Model C under varying levels of background extinction and N (number of extant taxa). All other conventions follow Figure 4.

Figure S7. Location of MEEs (as accurate estimation of time intervals for rate changes in µ that contain the MEE) for Model A under varying levels of background extinction and mass extinction survival probability, ρ. All other conventions follow Figure 4.

Figure S8. Location of MEEs (as accurate estimation of time intervals for rate changes in µ that contain the MEE) for Model A under varying levels of background extinction and number of extant taxa (N). All other conventions follow Figure 4.

Figure S9. Estimation of changes in magnitude of µ across time intervals for Model C under different values of background extinction and number of extant taxa (N). All other conventions follow Figure 5.

Figure S10. Detection of MEEs through interoperating changes in the magnitude of the diversification rate (diversification = λ ‐ µ) in CoMET under varying levels of µ and mass extinction survival probability, ρ.

Figure S11. Detection of MEEs through interoperating changes in the magnitude of the diversification rate (diversification = λ ‐ µ) in CoMET under different values of background extinction and number of extant taxa (N).

Figure S12. Location of MEEs indicated in the rate changes times in λ (purple) and/or µ (red) and/or mass extinction time (green) if returned by CoMET under varying levels of background extinction and mass extinction survival probability, ρ.

Figure S13. Location of MEEs indicated in the rate changes times in λ (purple) and/or µ (red) and/or mass extinction time (green) if returned by CoMET under different values of background extinction and number of extant taxa (N).

Figure S14. Estimation of changes in magnitude of µ and λ across time intervals for CoMET under different values of background extinction and MEE survival probability, ρ.

Figure S15. Estimation of changes in magnitude of µ and λ across time intervals for CoMET under different values of background extinction and number of extant taxa (N).

SI16. The scripts used to run the simulation and empirical studies for the BDSKY model. “a” shows example .xml file that can be run in BEAST2; “b” gives the RScript used to create all of the simulation data; “c” gives the R function «createBDSKYbeast2Code» used to write all of the BEAST2 xml files; “d” gives the RScript that uses the R function «createBDSKYbeast2Code» to create all of the xml files for the simulation data; and “e” gives the RScript to create the xml files for the empirical tree data.