Merely changing the linkage of yeast GAL genes without altering the expression level of any gene toxifies the cell.
Abstract
Functionally related genes tend to be chromosomally clustered in eukaryotic genomes even after the exclusion of tandem duplicates, but the biological significance of this widespread phenomenon is unclear. We propose that stochastic expression fluctuations of neighboring genes resulting from chromatin dynamics are more or less synchronized such that their expression ratio is more stable than that for unlinked genes. Consequently, chromosomal clustering could be advantageous when the expression ratio of the clustered genes needs to stay constant, for example, because of the accumulation of toxic compounds when this ratio is altered. Evidence from manipulative experiments on the yeast GAL cluster, comprising three chromosomally adjacent genes encoding enzymes catalyzing consecutive reactions in galactose catabolism, unequivocally supports this hypothesis and elucidates how disorder in one biological phenomenon—gene expression noise—could prompt the emergence of order in another—genome organization.
INTRODUCTION
Genomes are not random assemblies of constituent genes; there is mounting evidence that functionally related genes tend to be chromosomally clustered in eukaryotic genomes even after the removal of tandem duplicates (1–5). Several hypotheses have been proposed to explain this phenomenon (1–8). For example, one hypothesis posits that such clustering minimizes recombination between coadapted alleles of functionally related genes and so is selectively favored (1). Another hypothesis argues that functionally related genes are easier to be simultaneously horizontally transferred when they are clustered than when they are not, causing the spread of gene clusters (5, 7). But, none of the proposed benefits of gene clustering have been experimentally validated (1–8), rendering the cause of this phenomenon elusive. In this study, we propose that the benefit of chromosomal clustering of functionally related genes is to reduce the stochastic fluctuations of the relative expression levels of these genes, which, under certain circumstances, can raise fitness. We then test this hypothesis using manipulative experiments on a metabolic gene cluster in the budding yeast Saccharomyces cerevisiae.
RESULTS
The expression cofluctuation hypothesis
Like most cellular processes, gene expression has substantial stochastic variation or biological noise, because the substrates of transcription and translation typically have only one to several molecules per cell (9). In eukaryotes, gene expression noise arises primarily from the pulse-like transcriptional initiations due to the stochastic on/off switches of promoters as a result of random opening and closing of chromatin domains (9–11). Many biological functions require the cooperation of multiple proteins with a strict stoichiometry (12–14), but the expression noise poses a challenge (15), because even if the promoters of the genes encoding these proteins are identical, each promoter is randomly switched on and off independently. As a result, the between-gene ratio in mRNA concentration fluctuates substantially (Fig. 1A). Because neighboring genes on a chromosome are likely controlled by the same chromatin domain, the transcriptional pulses of neighboring genes are synchronized (16) such that their relative mRNA and, consequently, protein concentrations are more or less constant even though the expression noise of individual genes is inevitable (Fig. 1B). Therefore, chromosomal clustering of functionally related genes is advantageous if a relatively constant expression ratio among these genes is favored. An analysis of 100 fungal genomes (8) revealed that gene pairs that are both chromosomal neighbors and metabolic neighbors (i.e., encoding enzymes catalyzing successive reactions in a metabolic pathway) tend to have a toxic intermediate metabolite when compared with gene pairs that are metabolic neighbors but not chromosomal neighbors, suggesting that chromosomal clustering of metabolic genes is an adaptation against the accumulation of toxic intermediates. It is known in bacteria that suboptimal relative enzyme concentrations resulting from gene expression noise could lead to the accumulation of toxic metabolites and growth arrest (17). Furthermore, fungal metabolic gene clusters are often regulated by chromatin-based mechanisms (18). Given the above observations and considerations, we propose that it is the synchronization of stochastic expressions of neighboring genes that ensures a stable stoichiometry of their products, which minimizes the accumulation of toxic intermediates in metabolic pathways (Fig. 1B); consequently, chromosomal clustering of metabolic genes is selectively favored.
Fig. 1. Schematics explaining the hypothesis that coordination of stochastic expressions drives the clustering of functionally related genes.
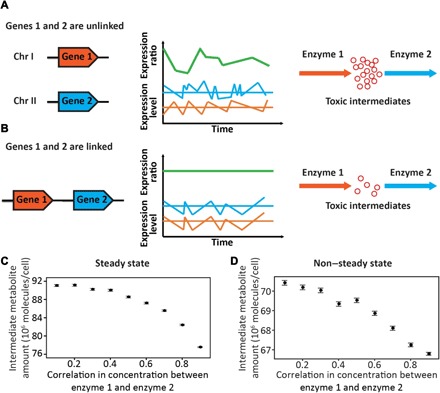
Genes 1 and 2 encode two enzymes catalyzing successive reactions in a metabolic pathway, where the intermediate metabolic of the two reactions is toxic. (A) When the two genes are unlinked, their stochastic expressions are uncoordinated, leading to a high variation of their expression ratio that causes the accumulation of the toxic intermediate. (B) When the two genes are closely linked, their common chromatin environment coordinates their stochastic expressions, stabilizing their expression ratio, which lessens the accumulation of the toxic intermediate. (C and D) Expected concentrations of the intermediate metabolite under different levels of correlation between the concentrations of enzyme 1 and enzyme 2, determined by numerical simulations under steady states (C) or non–steady states (D). Each circle shows the average from 100,000 simulations in (C) or 10,000 simulations in (D). Error bars show SEs.
To theoretically verify our model, we analyzed a linear pathway consisting of two reactions with an intermediate metabolite. It can be shown analytically that, under steady states, the expected concentration of the intermediate metabolite decreases with the correlation between the concentrations of the enzymes respectively catalyzing the two reactions, due to nonlinear relationships between enzyme concentrations and metabolic fluxes (see Materials and Methods). Numerical simulations confirmed this result (Fig. 1C) and suggested that the trend also holds under non–steady states (Fig. 1D). While multiple additional factors can influence the relative concentrations of enzymes and the accumulation of intermediate metabolites in relation to gene expression noise (15, 17, 19–22), our model is tenable, at least in principle.
The yeast GAL cluster as a case study
To experimentally test our hypothesis, we used S. cerevisiae, a model eukaryote where metabolic gene clusters have been extensively surveyed (3, 4). Among the 20 clusters reported in this species (4), we focused on the GAL cluster because of its better-understood function and regulation (23). The S. cerevisiae GAL cluster comprises three chromosomally adjacent genes: GAL1, GAL7, and GAL10 (Fig. 2A). They encode enzymes catalyzing three consecutive reactions in galactose catabolism, with a cytotoxic intermediate, galactose-1-phosphate (galactose-1-P) (24) (Fig. 2B). Using numerical simulations, we confirmed that expression cofluctuations among the three GAL genes are expected to reduce the galactose-1-P concentration (Fig. 2C and fig. S1). The S. cerevisiae GAL cluster emerged through relocations of initially unlinked genes in evolution (25). Similar events occurred independently in Cryptococcus fungi, resulting in another GAL cluster with different order and different orientations of the three genes (25). These observations suggest that it is the chromosomal proximity instead of the order or orientation of the GAL genes that has potentially been selected for. The yeast galactose catabolism pathway has been a model for understanding gene regulation (23) and its evolution (26). When glucose is present in the medium, GAL gene expressions are repressed; when glucose is absent and galactose is present, GAL gene expressions can be up-regulated by as much as 1000-fold (23). This strong induction depends on the binding of the transcriptional activator Gal4 on the specific upstream activating sequence (UAS) present in GAL gene promoters. Given that the GAL genes are already coregulated by Gal4, it is fascinating to investigate whether chromosomal clustering provides yet another layer of coregulation in the face of expression noise.
Fig. 2. Testing advantageous coordination of stochastic expressions of GAL1 and GAL10 in the GAL gene cluster.
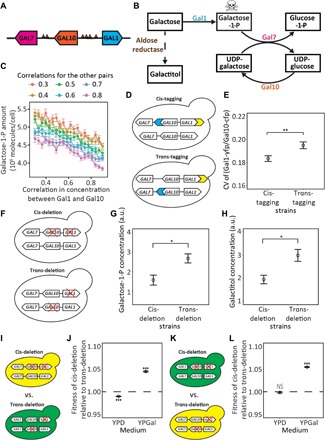
(A) Chromosomal locations of GAL cluster genes in yeast. Arrows indicate transcriptional directions. Each small triangle indicates a UAS. (B) Yeast galactose catabolism pathway, showing metabolic reactions catalyzed by enzymes encoded by the GAL gene cluster (solid arrows) and a reaction catalyzed by aldose reductase (dashed arrow). The skull-and-crossbones symbol indicates toxicity. Galactitol is probably toxic (28, 29). (C) Expected concentrations of galactose-1-P under different levels of correlation between the concentrations of Gal1 and Gal10, determined by non–steady-state numerical simulations. The correlation coefficients in the concentration between Gal1 and Gal7 and that between Gal7 and Gal10 are fixed at various levels indicated on the top of the figure. Each circle indicates the average from 2000 simulations. (D) Schematics showing cis- and trans-tagging strains. Blue and yellow arrows, respectively, represent the cyan (CFP) and yellow (YFP) fluorescence protein genes. (E) The CV of the Gal1-yfp/Gal10-cfp protein level ratio among cells is significantly lower for the cis- than trans-tagging strains. Each circle indicates the mean from eight biological replicates, each with 5000 cells. (F) Schematics showing cis- and trans-deletion strains. A red cross indicates gene deletion. (G and H) Cellular concentrations of galactose-1-P (G) and galactitol (H) are significantly lower in the cis- than in the trans-deletion strains. In (G) and (H), each circle represents the mean from four biological replicates, each having three technical repeats. a.u., arbitrary units. (I) Schematics showing cis- and trans-deletion strains used for fitness estimation via strain competition. Green and yellow cells, respectively, indicate cells that express a green fluorescence protein gene (GFP) and a YFP gene at the HO locus. (J) The fitness of the cis-deletion strain relative to the trans-deleting strain in (I) is substantially greater than 1 in a galactose medium (YPGal) but is slightly below 1 in a glucose medium (YPD). (K) Schematics showing cis- and trans-deletion strains with reciprocal fluorescence markers used for fitness estimation. (L) The fitness of the cis-deletion strain relative to the trans-deleting strain in (K) is substantially greater than 1 in YPGal but is not different from 1 in YPD. In (J) and (L), each circle represents the mean from eight biological replicates, and statistical tests of the null hypothesis that the relative fitness equals 1 are performed. In all panels, error bars show SEs. Significance levels are indicated as follows: NS, P ≥ 0.05; *P < 0.05; **P < 0.01, ***P < 0.001.
Test of the hypothesis for GAL1 and GAL10
We started by examining the pair of GAL1 and GAL10 (Fig. 2A). Our hypothesis predicts that the expression ratio between the two genes should have smaller variations when they are linked than when they are unlinked. Without relocating the genes, which could have unintended consequences such as disrupting regulatory sequences or encountering position effects (27), we created a diploid that has one GAL1 allele tagged with a yellow fluorescence protein gene (YFP) and one GAL10 allele from either the same or homologous chromosome tagged with a cyan fluorescence protein gene (CFP), yielding a cis-tagging strain and a trans-tagging strain, respectively (Fig. 2D). Thus, the Yfp/Cfp expression ratio in the cis- and trans-tagging strains respectively measures the Gal1/Gal10 expression ratio for the linked and unlinked GAL genes. We grew each strain in YPGal, a rich medium with galactose as the carbon source, until the mid-log phase, and simultaneously quantified the two fluorescence signals of individual cells by flow cytometry. We calculated the Yfp/Cfp signal ratio for each cell and used the coefficient of variation (CV) of this ratio among 5000 cells as a measure of the variation of the Gal1/Gal10 expression ratio.
The among-cell mean protein level of Gal1-yfp is not significantly different between the cis- and trans-tagging strains (P = 0.41, t test; fig. S2A), nor is the mean level of Gal10-cfp (P = 0.20, t test; fig. S2B). However, the CV of the ratio of the Gal1-yfp to Gal10-cfp levels is significantly lower for the cis- than for the trans-tagging strains (P = 0.0092, t test; Fig. 2E). Consistently, the partial correlation between the Gal1-yfp and Gal10-cfp levels among cells upon the control of cell morphology is greater for the cis- than trans-tagging strains (P = 0.045, t test; fig. S2C). These results support our hypothesis that gene clustering reduces the stochastic variation of the expression ratio of the clustered genes.
Our hypothesis further predicts that the enhanced expression cofluctuation of GAL1 and GAL10 lowers the cellular concentration of the toxic intermediate in galactose catabolism and increases the fitness. To verify these predictions without relocating any gene in the genome, we used CRISPR-Cas9 to create a cis-deletion diploid with only one intact GAL1 allele and one intact GAL10 allele, both located on the same chromosome, and a trans-deletion diploid with only one intact GAL1 allele and one intact GAL10 allele, respectively located on the two homologous chromosomes (Fig. 2F and fig. S3); these two strains are otherwise genetically identical. To be noted, using the scarless and markerless CRISPR-Cas9 technology here is vital because traditional gene deletion methods typically introduce selection markers and scars, which could reduce the detectability of fitness effects of gene linkage (6).
The accumulation of galactose-1-P is cytotoxic in yeast (24) and causes galactosemia in humans (28). Additionally, because intracellular galactose could be reduced to galactitol by aldose reductase when the galactose catabolism is inefficient (Fig. 2B), galactitol is accumulated in patients with galactosemia (28) and is believed to contribute to galactosemia (29). We used gas chromatography–mass spectrometry (GC-MS) to quantify the cellular concentrations of galactose-1-P and galactitol in the cis- and trans-deletion strains cultured in YPGal. Supporting our prediction, both galactose-1-P (P = 0.018, t test; Fig. 2G) and galactitol (P = 0.016; Fig. 2H) concentrations are significantly lower in the cis- than in the trans-deletion strains.
We respectively inserted at the HO locus of the cis- and trans-deletion strains YFP and GFP (green fluorescence protein gene) to allow the use of flow cytometry to differentiate between the two deletion strains in a coculture (Fig. 2I). The two strains competed in YPGal and YPD (yeast extract, peptone, and dextrose), a rich medium with glucose as the carbon source. By cell counting of the two genotypes in the coculture at multiple time points during the competition, we estimated that the fitness of the cis-deletion strain is ~6% higher than that of the trans-deletion strain in YPGal, but this disparity diminished when they competed in YPD (Fig. 2J), as one would expect from the fact that galactose catabolism is turned off in glucose. Swapping the fluorescence markers between the two deletion strains (Fig. 2K) did not change the results (Fig. 2L), indicating that our results are not attributable to any potential difference in the fitness effect of the two fluorescent protein genes.
Test of the hypothesis for GAL7 and GAL10
GAL1 and GAL10 are divergently oriented with only 668 nucleotides between their translation start sites, and they share UASs that are bound by Gal4 (23) (Fig. 2A). To test if our hypothesis holds beyond such circumstances, we similarly investigated the pair of GAL7 and GAL10, which are concordantly oriented without shared UASs (Fig. 3A). As in the case of GAL1 and GAL10, the mean protein levels of Gal7-yfp (P = 0.87; fig. S2D) and Gal10-cfp (P = 0.92; fig. S2E) are not significantly different between the cis- and trans-tagging strains. By contrast, the Gal7-yfp/Gal10-cfp protein level ratio has a smaller CV in the cis- than in the trans-tagging strains (P = 0.039; Fig. 3B), and the partial correlation between the Gal7-yfp and Gal10-cfp levels upon the control of cell morphology is higher in the cis- than in the trans-tagging strains (P = 0.015; fig. S2F). Thus, the chromosomal clustering of GAL7 and GAL10 promotes their expression cofluctuation even though they do not share cis-regulatory elements. GC-MS revealed lower concentrations of galactose-1-P (P = 0.0002; Fig. 3C) and galactitol (P = 0.0057; Fig. 3D) in the cis- than in the trans-deletion strains. Consistently, competition assays showed that the cis-deletion strain is significantly fitter than the trans-deletion strain in YPGal but not YPD, regardless of whether the cis-deletion strain has YFP (Fig. 3E) or GFP (Fig. 3F). Therefore, our hypothesis also holds for the pair of GAL7 and GAL10.
Fig. 3. Testing advantageous coordination of stochastic expressions of GAL7 and GAL10 in the GAL gene cluster.
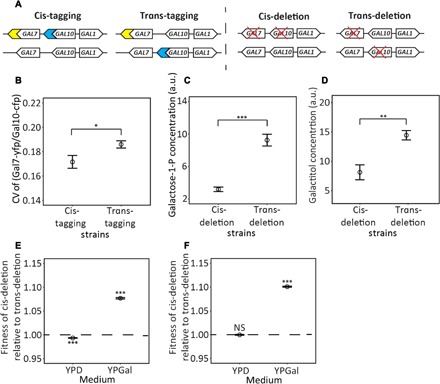
(A) Schematics showing cis- and trans-tagging strains and cis- and trans-deletion strains. Blue and yellow symbols, respectively, represent the CFP and YFP genes. A red cross indicates gene deletion. (B) The CV of the Gal7-yfp/Gal10-cfp protein level ratio among cells is significantly lower for the cis- than for the trans-tagging strains. Each circle is the average from six replicates, each with 5000 cells. (C and D) Cellular concentrations of galactose-1-P (C) and galactitol (D) are significantly lower in the cis- than in the trans-deletion strains. In (C) and (D), each circle represents the average from four biological replicates, each having three technical repeats. (E) The fitness of the YFP-marked cis-deletion strain relative to the GFP-marked trans-deletion strain is substantially greater than 1 in a galactose medium (YPGal) but is slightly below 1 in a glucose medium (YPD). (F) The fitness of the GFP-marked cis-deletion strain relative to the YFP-marked trans-deletion strain is substantially greater than 1 in YPGal but is not different from 1 in YPD. In (E) and (F), each circle represents the average from eight biological replicates, and statistical tests of the null hypothesis that the relative fitness equals 1 are performed. In all panels, error bars show SEs. Significance levels are indicated as follows: NS, P ≥ 0.05; *P < 0.05; **P < 0.01, ***P < 0.001.
DISCUSSION
In this study, we proposed a potential benefit for chromosomal clustering of functionally related genes in eukaryotic genomes and tested this hypothesis using the yeast GAL cluster as a case study. Although our comparison between cis- and trans-deletion strains allows assessment of the consequences of gene linkage without relocating genes, there is a caveat. When constructing these strains for the pair of GAL1 and GAL10, for example, we deleted one allele each of GAL1 and GAL10 but left both alleles of GAL7 intact, creating dose imbalance between GAL7 and the other two GAL genes. Notwithstanding, the imbalance is the same in the cis- and trans-deletion strains, so it does not invalidate our comparison between them. However, the dose imbalance might modulate the effect of disrupting the linkage between GAL1 and GAL10. Greater differences between the cis- and trans-deletion strains were observed for the pair of GAL7 and GAL10 (Fig. 3) than the pair of GAL1 and GAL10 (Fig. 2) in terms of toxic intermediate concentrations and fitness, despite that the difference in the CV of expression ratio is similar for the two gene pairs. This is probably because having one allele each of GAL7 and GAL10 but two alleles of GAL1 slows the use of galactose-1-P relative to its production (Fig. 2B), raising the concentration of galactose-1-P. By contrast, having one allele each of GAL1 and GAL10 but two alleles of GAL7 may have reduced the impact of disrupting the linkage between GAL1 and GAL10 because of a slower production than the use of galactose-1-P (Fig. 2B). One might think that it is better to compare cis- and trans-deletion strains with only one copy of each of GAL1, GAL7, and GAL10 to avoid gene dose imbalance. However, dosage balance for the GAL pathway likely also involves GAL regulatory proteins and the galactose transporter. So, maintaining only one copy of each of GAL1, GAL7, and GAL10 would not solve the dosage imbalance problem. Furthermore, such a design would have two pairs of genes in the trans configuration, complicating the interpretation of any observation.
A recent study reported that the genomic region between GAL1 and GAL10 encodes a long noncoding RNA (GAL10-ncRNA) that can repress the stochastic expression of GAL1 (30). Nevertheless, this suppression diminishes upon cell preculture in galactose (30). Because we precultured cells in galactose before the competition between cis- and trans-deletion strains, the impact of GAL10-ncRNA should be minimal. Additionally, both the promoter and poly(A) signal of GAL10 are known to influence GAL7 expression (31). But, because our gene deletions removed only the coding regions of the GAL genes, the comparison between the corresponding cis- and trans-deletion strains remains valid.
In summary, our experiments provide direct evidence that chromosomal clustering of genes encoding enzymes of the same metabolic pathway minimizes the random fluctuation of their relative expressions, which reduces the accumulation of toxic intermediates and promotes growth. Our finding echoes reports of molecular and genomic features that are shaped by various cellular noises/errors as well as natural selections that lower the impacts of these imprecisions (32–34). It illustrates how disorder in one biological phenomenon—stochasticity of gene expression—could prompt the emergence of order in another, genome organization, and argues for the value of systemic analysis in understanding biology. Our finding can also help design optimal synthetic genomes.
Although our experiments focused on metabolic genes, our hypothesis is general and can be applied to any cluster as long as fluctuations of relative expression levels of its constituent genes are selectively disfavored. For example, multiple lines of evidence support the view that dosage imbalance among subunits of stable protein complexes is deleterious (13, 35, 36). Hence, our hypothesis can explain why these genes tend to be located within 10 to 30 kb of each other in yeast (37). Our hypothesis probably also holds in other eukaryotes, because the primary role of stochastic opening and closing of chromatin domains in generating gene expression noise is likely universal among eukaryotes. A recent analysis of mammalian single-cell RNA sequencing data revealed a genome-wide feature of stronger among-cell expression correlations between linked alleles than unlinked alleles (38). This said, we caution that only one gene cluster has thus far been shown to support our hypothesis, and many more studies are required to establish its potential generality. It is also worth stressing that the experimental validation of our hypothesis does not refute other evolutionary hypotheses (1–8) on the chromosomal clustering of functionally related genes. In the future, it will be important to experimentally test these other hypotheses and evaluate the relative merits and applicability of various hypotheses.
MATERIALS AND METHODS
Concentration of the intermediate metabolite in a two-reaction linear pathway
Let x and y be two random variables with expectations of μx and μy and variances of Var(x) and Var(y), respectively. Let f(x, y) be a function of x and y. Using the Taylor expansion of the function at θ(μx, μy), we have
Thus, the expectation of f(x, y) is
when . Hence
| (1) |
Now, let us consider the following two metabolic reactions that form a linear pathway.
In the above, E1 and E2 are two enzymes that respectively catalyze the two reactions, whereas M1 is the substrate for the pathway, M2 is the intermediate metabolite, and M3 is the product of the pathway, respectively. [] stands for the concentration of the chemical inside the brackets. Km1 and Km2 are the Michaelis constants, and kcat1 and kcat2 are the catalytic rate constants of the two reactions, respectively.
At the steady state, . Hence, . Let . We then have [E1]L1(Km2 + [M2]) = kcat2[M2][E2].
Thus
| (2) |
Let x=[E1] and y = kcat2[E2] − L1[E1]. Let . So, , and .
According to Eq. 2, because [M2] > 0, kcat2μ2 – L1μ1 > 0. Thus, E([M2]) decreases with ρ. In other words, increasing ρ, the correlation in concentration between the two enzymes, causes a reduction in E([M2]), the expected concentration of the intermediate metabolite.
Numerical simulation of the two-reaction linear pathway
We first simulated the above-described linear pathway with two reactions. [M1] and the kinetic parameters in the simulation were assigned with biologically relevant values (table S1). [M1] was kept constant throughout the simulation. Under the steady-state assumption, equilibrium is reached instantly, and [M2] is given by Eq. 2. Because [M2] > 0, kcat2[E2] must exceed L1[E1]. Enzyme concentrations were randomly sampled from a truncated bivariate Gaussian distribution with means of 10,000 molecules per cell for both enzymes. The CV of enzyme concentration was set at 0.5 for both enzymes, and the correlation coefficient between the concentrations of the two enzymes was set at 0.1, 0.2, 0.3, ..., or 0.9. Given that, in reality, enzyme concentrations cannot be negative or too large and that the steady-state assumption puts a constraint on the [E1]/[E2] ratio, we applied an upper bound of 13,500 molecules per cell and a lower bound of 6500 molecules per cell for both [E1] and [E2] in the simulation. Under each set of parameters, we simulated 100,000 pairs of enzyme concentrations and computed 100,000 [M2] values and the average [M2].
Under non–steady states, we first calculated the steady-state [M2] when both enzymes are at the concentration of 10,000 molecules per cell and used that value as the starting [M2]. We simulated the enzyme concentrations at time zero and used them for the next 30 min of simulation, because protein concentrations fluctuate over a time scale that is on the order of a cell cycle (39). Every minute, [M2] is calculated by [M2] at the previous minute plus , where substrate concentrations are from the previous minute. We estimated the mean [M2] of each simulation by averaging [M2] of the 30 time points. We replicated the simulation 10,000 times and estimated the overall mean [M2] across replicates. In total, nine scenarios were simulated, with the correlation coefficient between the enzyme concentrations being 0.1, 0.2, 0.3, ..., or 0.9. Qualitatively similar results were obtained when enzyme concentrations were sampled every 20 or 100 min.
Numerical simulation of the GAL pathway
The relevant part of the GAL pathway can be described as follows.
| (3) |
| (4) |
| (5) |
where G1, G7, and G10, respectively, refer to Gal1, Gal7, and Gal10 enzymes, while Gal, G1P, Gl1P, UGl, and UGa, respectively, stand for galactose, galactose-1-P, glucose-1-P, uridine diphosphate (UDP)–glucose, and UDP-galactose. Km and kcat refer to the Michaelis constant and catalytic rate constant of the corresponding substrate and reaction (table S2), whereas Keq is the equilibrium constant of the reaction in Eq. 5. The values of these parameters used in the numerical simulation are provided in table S2. The galactose concentration was maintained constant throughout the simulation. Given that we have three reactions with multiple parameters, the steady-state assumption would lead to too many constraints. So, we only performed non–steady-state simulations. We similarly started with all metabolite concentrations at the equilibrium, sampled the enzyme concentrations at the beginning of the simulation, and used them for a 30-min simulation. The concentrations of Gal1, Gal7, and Gal10 were sampled from a truncated trivariate Gaussian distribution with identical means of 1000 molecules per cell for all enzymes. The CV of enzyme concentration was set at 0.33 for all enzymes. To avoid extreme protein concentrations, we set an upper limit of 4000 molecules per cell and a lower limit of 10 molecules per cell. We calculated metabolite concentrations every 0.1 min because the kcat values of the Gal enzymes are large, and computed the mean G1P concentration across the 300 time points. We examined one pair of enzymes at a time while fixing the correlation coefficients in enzyme concentration of the other two pairs at one of six different levels: 0.3, 0.4, 0.5, ..., and 0.8. The correlation coefficient in enzyme concentration for the focal pair varied from 0.3 to 0.9 in the simulation. Under each parameter set, we repeated the simulation 2000 times and estimated the overall mean G1P concentration by averaging the mean concentration of G1P from each simulation. For the focal pair of Gal7 and Gal10, we increased the simulation to 10,000 times because of the large stochasticity.
Strain constructions
Here, we use the pair of GAL1 and GAL10 genes as an example to describe strain constructions, because strains involving the pair of GAL7 and GAL10 were similarly constructed. All primers used in this study are provided (table S3), and so are all guide RNA (gRNA) target sequences (table S4).
To construct cis- and trans-tagging strains, we generated a linker-YFP-CYC1T-TEF1P- KanMX4-TEF1T cassette with a region homologous to the C terminus of GAL1 and a linker-CFP-CYC1T-TEF1P-NatMX-TEF1T cassette with a region homologous to the C terminus of GAL10 by polymerase chain reaction (PCR) from plasmids pRS416-HO-YFP-Kan and pRS416-FIT2-CFP-Nat, respectively. Here, the gene name followed by a subscript T refers to the source of the terminator, whereas the gene name followed by a subscript P refers to the source of the promoter. Each cassette was separately introduced into yeast cells by high-efficiency transformation (40). KanMX4 and NatMX respectively provide yeast with resistance to geneticin and nourseothricin, allowing selection for correct genotypes after yeast transformations. Via homologous recombination, GAL1 of the laboratory strain BY4741 was fused with the cassette of linker-YFP-CYC1T -TEF1P-KanMX4-TEF1T, yielding the BY4741 GAL1-YFP strain. Similarly, GAL10 of the laboratory strain BY4742 and that of the BY4741 GAL1-YFP strain were fused with the cassette of linker-CFP-CYC1T-TEF1P-NatMX-TEF1T to yield the BY4742 GAL10-CFP strain and the BY4741 GAL1-YFP GAL10-CFP strain. Because GAL10 is adjacent to both GAL1 and GAL7, we deleted NatMX together with its promoter and terminator by CRISPR-Cas9–based technology to prevent its potential influence on the expressions of its neighboring genes. The gRNA was constructed by annealing two primers and ligating the product to a backbone plasmid with a Cas9 expression module, following a previous protocol (41). The resulting plasmid was confirmed by Sanger sequencing. The donor for CRISPR-Cas9 deletion was generated by annealing and extending two primers. The colonies were picked from the selection plates, checked by PCR, and subsequently confirmed by Sanger sequencing. Last, the BY4741 GAL1-YFP strain was mated with the BY4742 GAL10-CFP strain to create the trans-tagging diploid strain, while the BY4741 GAL1-YFP GAL10-CFP strain was mated with BY4742 to create the cis-tagging diploid strain.
To construct cis- and trans-deletion strains, we generated a TDH3P-GFP-CYC1T cassette and a TDH3P-YFP-CYC1T cassette by PCR from plasmids pRS416-HO-GFP-Kan and pRS416-HO-YFP-Kan, respectively, and integrated them into the HO locus of the BY4742 strain by CRISPR-Cas9, yielding the BY4742 hoΔ::YFP strain and the BY4742 hoΔ::GFP strain (fig. S3). Next, we used CRISPR-Cas9 to delete the coding sequence of GAL1, GAL10, or both of them in BY4741, BY4742 hoΔ::YFP, and BY4742 hoΔ::GFP, yielding the strains of BY4741 gal1Δ, BY4742 hoΔ::YFP gal10Δ, BY4742 hoΔ::GFP gal10Δ, and BY4741 gal1Δgal10Δ (fig. S3). Genome editing was confirmed by the correct fragment size upon PCR, followed by Sanger sequencing. The Cas9 plasmids for all these mutants were lost by serial transfer per 12 hours in YPD (1% yeast extract, 2% peptone, 2% glucose, and 2% agar) for a total of 36 hours. The final culture was diluted and plated on YPD plates. The colonies without Cas9 plasmids were screened by replica plating onto an YPD plate with selective drugs corresponding to the resistant genes on the Cas9 plasmids. Then, BY4741 gal1Δ was respectively mated with BY4742 hoΔ::YFP gal10Δ and BY4742 hoΔ::GFP gal10Δ to yield the trans-deletion diploid strains (fig. S3). BY4741 gal1Δgal10Δ was mated respectively with BY4742 hoΔ::YFP and BY4742 hoΔ::GFP to yield the cis-deletion diploid strains (fig. S3).
Although we confirmed the DNA sequences in regions subject to CRISPR-Cas9 editing, off-target mutations outside the sequenced regions are possible. We conducted a control experiment of competitions in the glucose medium (see below). It is extremely unlikely that such off-target mutations occurred and affected fitness in the galactose, but not glucose, media.
Quantifying GAL gene expressions
We precultured all the cis- and trans-tagging strains in 5 ml of the YPGal medium (1% yeast extract, 2% peptone, and 2% galactose) for 24 hours at 30°C. We then measured cell density at optical density at a wavelength of 660 nm (OD660) using a Genesys 5 spectrophotometer (Thermo Fisher Scientific). In a 96-well plate, we diluted cells into fresh YPGal with a starting cell density of ~2 × 104 cells/ml, with 10 replicates per strain. After 18 hours of growth at 30°C on a roller drum, we measured cell density using a plate reader (Tecan Sunrise). Next, we diluted cells to ~1.5 × 106 cells/ml in 30 μl of phosphate-buffered saline in a 96-well plate before examining them using the iQue Screener PLUS–VBR flow cytometer (IntelliCyt). The violet laser (405 nm) channel with a 530/30 optical filter was used for capturing the Cfp signal, while the blue laser (488 nm) channel with a 572/28 optical filter was used for capturing the Yfp signal. Fluorescence data were analyzed with custom R scripts. First, we used the forward scatter area (FSCA) and side scatter area with a clustering package to remove noncell particles. Second, we used the FSCA and forward scatter height to remove doublets. Third, we used cluster analysis to remove cells with fluorescence outside the 99% quantile region. Fourth, we randomly picked 5000 cells from the remaining cells. Last, because the two fluorescent proteins have overlapped spectra, we eliminated the cross-talk following a previously described method (42).
Fitness estimation by competition
Following a published protocol (43), we competed cis- and trans-deletion strains to measure their relative fitness. The cis- and trans-deletion strains with different fluorescent markers were first cultured in 5 ml of either YPD or YPGal for 36 hours to reach saturation. We then measured the cell density, diluted cells, and mixed approximately equal numbers of cis- and trans-deletion cells in the same culture (of either YPD or YPGal) with eight replicates for each competition in a 96-well plate. Cells were grown at 30°C on a roller drum for 12 hours of acclimation, at which point we considered time t = 0 in our fitness estimation. Cells were diluted at t = 0, 12, 23, and 41 hours, transferred to fresh media, and grown at the above condition. At t = 0, 12, 23, and 41 hours, cell density was counted using an Accuri C6 flow cytometer (BD Biosciences). When each genotype grows exponentially at a fixed rate, the logarithm of the relative cell number of the two genotypes in a competition is a linear function of t (44). This linear relationship was indeed observed in our experiment (fig. S4). The fitness of the cis-deletion strain relative to the trans-deletion strain was estimated using the following equation
| (6) |
Here, and are cell numbers of the cis-deletion strain at time 0 and t, respectively, and are cell numbers of the trans-deletion strain at time 0 and t, respectively, and rcis and rtrans are the growth rates of the cis- and trans-deletion strains, respectively. We plotted ln() against t across multiple time points, allowing the estimation of the slope, which is rcis − rtrans. Fitness of the cis-deletion strain relative to the trans-deletion strain was estimated by f = e(rcis − rtrans)T, where T is the doubling time of the trans-deletion strain (table S5).
The competition data presented in Fig. 2 were from the same batch of experiments, and the replicates were from the same transformants. Nevertheless, these competitions were repeated multiple times, and the conclusion did not change from batch to batch. The same can be said for Fig. 3.
Doubling time estimation using bioscreen C
Each trans-deletion strain was precultured in 5 ml of either YPD or YPGal for 36 hours to reach saturation. We then measured cell density, diluted cells, and transferred cells into honeycomb plates (Growth Curves USA) with a final volume of 150 μl and an initial cell density of ~1 × 106 cells/ml per well. The honeycomb plates were put into a Bioscreen C (Oy Growth Curves Ab) for culturing at 30°C. Optical density was monitored with a 600-nm filter, measurements were taken every 20 min, and the shaking model was set to continuous shaking with maximal amplitude and fast speed. The doubling time was calculated according to a previous protocol (45).
Quantifying galactose-1-P and galactitol using GC-MS
Yeast cells were precultured overnight in YPGal and then transferred to fresh YPGal at an initial OD600 of 0.1. Cell culture (0.5 ml) grown to the mid-log phase was vacuum filtered using Vac-Man Laboratory Vacuum Manifold (Promega) assembled with a nylon membrane filter (pore size, 0.45 μm; diameter, 13 mm; Whatman) and a filter holder (Millipore). The filtered cell culture was then washed with 2.5 ml of prechilled distilled water. The entire process of fast filtration was completed within 1 min. The filter membrane containing the washed cells was quickly mixed with 1 ml of cold 90% (v/v) methanol and 100 μl of glass beads. The mixture was vortexed for 3 min to disrupt cell membranes, allowing extraction of intracellular metabolites. The extraction mixture was then centrifuged at 16,100 relative centrifugal force for 3 min at 4°C. Supernatant (0.6 ml) containing the intracellular metabolites was dried for 4 hours using a speed vacuum concentrator. Prior to GC-MS, intracellular metabolites were derivatized by trimethylsilylation. Specifically, the intracellular metabolites were trimethylsilylated by adding 50 μl of N-methyl-N-trimethylsilyltrifluoroacetamide (Sigma-Aldrich) and 50 μl of pyridine (Sigma-Aldrich) at 90°C for 30 min. The derivatized metabolite samples were analyzed by GC-MS by an Agilent 7890A GC/5975C mass-selective detection system (Agilent Technologies) equipped with an RTX-5Sil MS capillary column (30 m by 0.25 mm; film thickness, 0.25 μm; Restek) and an additional 10-m-long integrated guard column. One microliter of the derivatized sample was injected into the GC in a splitless mode. The oven temperature of the GC was initially set at 150°C for 1 min, after which the temperature was raised to 330°C at 20°C per minute, where it was held for 5 min. The mass spectra were recorded in a scan range of 85 to 500 mass/charge ratio at 70 eV of electron impact, and the temperatures of the ion source and transfer line were 230° and 280°C, respectively. The raw data obtained from the GC-MS analysis were processed using an automated mass spectral deconvolution and identification system (AMDIS) software for peak detection and deconvolution of mass spectra. The processed data were uploaded to SpectConnect (http://spectconnect.mit.edu) for peak alignment and generation of the data matrix with Golm Metabolome Database mass spectral reference library. Galactitol intensity was shown after the data analysis. Galactose-1-P in the samples was identified by comparing with a galactose-1-P standard (Sigma-Aldrich) and manually analyzed by the height of the peak.
Supplementary Material
Acknowledgments
We thank W. Qian and members of the Zhang laboratory for valuable comments. Funding: This work was supported by the U.S. National Institutes of Health grant GM120093 to J.Z. and funding from the Energy Biosciences Institute to Y.-S.J. Author contributions: J.Z. conceived the study. H.X. and J.Z. designed the experiments. H.X., J.-J.L., Z.L., and Y.L. performed the experiments. H.X. analyzed the data. Y.-S.J. and J.Z. acquired funding and provided resources. H.X. and J.Z. wrote the paper with input from all authors. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/10/eaax6525/DC1
Fig. S1. Simulation of the GAL pathway.
Fig. S2. Comparison of protein expression levels of GAL genes between cis- and trans-tagging strains.
Fig. S3. Flowchart showing the construction of cis- and trans-deletion strains for the pair of GAL1 and GAL10 genes.
Fig. S4. Ln(cell number ratio between the cis- and trans-deletion strains) as a function of competition time.
Table S1. Parameter values used in the simulation of the linear pathway with two reactions.
Table S2. Parameter values used in the simulation of the GAL pathway.
Table S3. Primers for strain construction.
Table S4. gRNA target sequences.
Table S5. Doubling times for various trans-deletion strains.
REFERENCES AND NOTES
- 1.Hurst L. D., Pal C., Lercher M. J., The evolutionary dynamics of eukaryotic gene order. Nat. Rev. Genet. 5, 299–310 (2004). [DOI] [PubMed] [Google Scholar]
- 2.Lee J. M., Sonnhammer E. L., Genomic gene clustering analysis of pathways in eukaryotes. Genome Res. 13, 875–882 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wong S., Wolfe K. H., Birth of a metabolic gene cluster in yeast by adaptive gene relocation. Nat. Genet. 37, 777–782 (2005). [DOI] [PubMed] [Google Scholar]
- 4.Rokas A., Wisecaver J. H., Lind A. L., The birth, evolution and death of metabolic gene clusters in fungi. Nat. Rev. Microbiol. 16, 731–744 (2018). [DOI] [PubMed] [Google Scholar]
- 5.Lawrence J. G., Shared strategies in gene organization among prokaryotes and eukaryotes. Cell 110, 407–413 (2002). [DOI] [PubMed] [Google Scholar]
- 6.Lang G. I., Botstein D., A test of the coordinated expression hypothesis for the origin and maintenance of the GAL cluster in yeast. PLOS ONE 6, e25290 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Walton J. D., Horizontal gene transfer and the evolution of secondary metabolite gene clusters in fungi: An hypothesis. Fungal Genet. Biol. 30, 167–171 (2000). [DOI] [PubMed] [Google Scholar]
- 8.McGary K. L., Slot J. C., Rokas A., Physical linkage of metabolic genes in fungi is an adaptation against the accumulation of toxic intermediate compounds. Proc. Natl. Acad. Sci. U.S.A. 110, 11481–11486 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Raj A., van Oudenaarden A., Nature, nurture, or chance: Stochastic gene expression and its consequences. Cell 135, 216–226 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sanchez A., Choubey S., Kondev J., Regulation of noise in gene expression. Annu. Rev. Biophys. 42, 469–491 (2013). [DOI] [PubMed] [Google Scholar]
- 11.Brown C. R., Mao C., Falkovskaia E., Jurica M. S., Boeger H., Linking stochastic fluctuations in chromatin structure and gene expression. PLOS Biol. 11, e1001621 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Birchler J. A., Riddle N. C., Auger D. L., Veitia R. A., Dosage balance in gene regulation: Biological implications. Trends Genet. 21, 219–226 (2005). [DOI] [PubMed] [Google Scholar]
- 13.Papp B., Pál C., Hurst L. D., Dosage sensitivity and the evolution of gene families in yeast. Nature 424, 194–197 (2003). [DOI] [PubMed] [Google Scholar]
- 14.Veitia R. A., Exploring the etiology of haploinsufficiency. Bioessays 24, 175–184 (2002). [DOI] [PubMed] [Google Scholar]
- 15.Wang Z., Zhang J., Impact of gene expression noise on organismal fitness and the efficacy of natural selection. Proc. Natl. Acad. Sci. U.S.A. 108, E67–E76 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Raj A., Peskin C. S., Tranchina D., Vargas D. Y., Tyagi S., Stochastic mRNA synthesis in mammalian cells. PLOS Biol. 4, e309 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ray J. C. J., Wickersheim M. L., Jalihal A. P., Adeshina Y. O., Cooper T. F., Balázsi G., Cellular growth arrest and persistence from enzyme saturation. PLOS Comput. Biol. 12, e1004825 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gacek A., Strauss J., The chromatin code of fungal secondary metabolite gene clusters. Appl. Microbiol. Biotechnol. 95, 1389–1404 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Acar M., Pando B. F., Arnold F. H., Elowitz M. B., van Oudenaarden A., A general mechanism for network-dosage compensation in gene circuits. Science 329, 1656–1660 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Peng W. L., Song R. J., Acar M., Noise reduction facilitated by dosage compensation in gene networks. Nat. Commun. 7, 12959 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cookson N. A., Mather W. H., Danino T., Mondragón-Palomino O., Williams R. J., Tsimring L. S., Hasty J., Queueing up for enzymatic processing: Correlated signaling through coupled degradation. Mol. Syst. Biol. 7, 561 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Steiner P. J., Williams R. J., Hasty J., Tsimring L. S., Criticality and adaptivity in enzymatic networks. Biophys. J. 111, 1078–1087 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Johnston M., A model fungal gene regulatory mechanism: The GAL genes of Saccharomyces cerevisiae. Microbiol. Rev. 51, 458–476 (1987). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Slepak T., Tang M., Addo F., Lai K., Intracellular galactose-1-phosphate accumulation leads to environmental stress response in yeast model. Mol. Genet. Metab. 86, 360–371 (2005). [DOI] [PubMed] [Google Scholar]
- 25.Slot J. C., Rokas A., Multiple GAL pathway gene clusters evolved independently and by different mechanisms in fungi. Proc. Natl. Acad. Sci. U.S.A. 107, 10136–10141 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hittinger C. T., Carroll S. B., Gene duplication and the adaptive evolution of a classic genetic switch. Nature 449, 677–681 (2007). [DOI] [PubMed] [Google Scholar]
- 27.Chen X., Zhang J., The genomic landscape of position effects on protein expression level and noise in yeast. Cell Syst. 2, 347–354 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Coelho A. I., Rubio-Gozalbo M. E., Vicente J. B., Rivera I., Sweet and sour: An update on classic galactosemia. J. Inherit. Metab. Dis. 40, 325–342 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.de Jongh W. A., Bro C., Ostergaard S., Regenberg B., Olsson L., Nielsen J., The roles of galactitol, galactose-1-phosphate, and phosphoglucomutase in galactose-induced toxicity in Saccharomyces cerevisiae. Biotechnol. Bioeng. 101, 317–326 (2008). [DOI] [PubMed] [Google Scholar]
- 30.Zacharioudakis I., Tzamarias D., Bimodal expression of yeast GAL genes is controlled by a long non-coding RNA and a bifunctional galactokinase. Biochem. Biophys. Res. Commun. 486, 63–69 (2017). [DOI] [PubMed] [Google Scholar]
- 31.Greger I. H., Proudfoot N. J., Poly(A) signals control both transcriptional termination and initiation between the tandem GAL10 and GAL7 genes of Saccharomyces cerevisiae. EMBO J. 17, 4771–4779 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Warnecke T., Hurst L. D., Error prevention and mitigation as forces in the evolution of genes and genomes. Nat. Rev. Genet. 12, 875–881 (2011). [DOI] [PubMed] [Google Scholar]
- 33.Zhang J., Yang J. R., Determinants of the rate of protein sequence evolution. Nat. Rev. Genet. 16, 409–420 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lynch M., Field M. C., Goodson H. V., Malik H. S., Pereira-Leal J. B., Roos D. S., Turkewitz A. P., Sazer S., Evolutionary cell biology: Two origins, one objective. Proc. Natl. Acad. Sci. U.S.A. 111, 16990–16994 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pessia E., Makino T., Bailly-Bechet M., McLysaght A., Marais G. A., Mammalian X chromosome inactivation evolved as a dosage-compensation mechanism for dosage-sensitive genes on the X chromosome. Proc. Natl. Acad. Sci. U.S.A. 109, 5346–5351 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lehner B., Selection to minimise noise in living systems and its implications for the evolution of gene expression. Mol. Syst. Biol. 4, 170 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Teichmann S. A., Veitia R. A., Genes encoding subunits of stable complexes are clustered on the yeast chromosomes: An interpretation from a dosage balance perspective. Genetics 167, 2121–2125 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sun M., Zhang J., Chromosome-wide co-fluctuation of stochastic gene expression in mammalian cells. PLOS Genet. 15, e1008389 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rosenfeld N., Young J. W., Alon U., Swain P. S., Elowitz M. B., Gene regulation at the single-cell level. Science 307, 1962–1965 (2005). [DOI] [PubMed] [Google Scholar]
- 40.Gietz R. D., Schiestl R. H., High-efficiency yeast transformation using the LiAc/SS carrier DNA/PEG method. Nat. Protoc. 2, 31–34 (2007). [DOI] [PubMed] [Google Scholar]
- 41.Laughery M. F., Hunter T., Brown A., Hoopes J., Ostbye T., Shumaker T., Wyrick J. J., New vectors for simple and streamlined CRISPR-Cas9 genome editing in Saccharomyces cerevisiae. Yeast 32, 711–720 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Yan C., Wu S., Pocetti C., Bai L., Regulation of cell-to-cell variability in divergent gene expression. Nat. Commun. 7, 11099 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Duveau F., Toubiana W., Wittkopp P. J., Fitness effects of cis-regulatory variants in the Saccharomyces cerevisiae TDH3 promoter. Mol. Biol. Evol. 34, 2908–2912 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.He X., Qian W., Wang Z., Li Y., Zhang J., Prevalent positive epistasis in Escherichia coli and Saccharomyces cerevisiae metabolic networks. Nat. Genet. 42, 272–276 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Warringer J., Ericson E., Fernandez L., Nerman O., Blomberg A., High-resolution yeast phenomics resolves different physiological features in the saline response. Proc. Natl. Acad. Sci. U.S.A. 100, 15724–15729 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Teusink B., Diderich J. A., Westerhoff H. V., van Dam K., Walsh M. C., Intracellular glucose concentration in derepressed yeast cells consuming glucose is high enough to reduce the glucose transport rate by 50%. J. Bacteriol. 180, 556–562 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Demir O., Aksan Kurnaz I., An integrated model of glucose and galactose metabolism regulated by the GAL genetic switch. Comput. Biol. Chem. 30, 179–192 (2006). [DOI] [PubMed] [Google Scholar]
- 48.Ostergaard S., Olsson L., Nielsen J., In vivo dynamics of galactose metabolism in Saccharomyces cerevisiae: Metabolic fluxes and metabolite levels. Biotechnol. Bioeng. 73, 412–425 (2001). [DOI] [PubMed] [Google Scholar]
- 49.Guthrie C., Fink G., Guide to yeast genetics and molecular biology. Methods Enzymol. 194, 3–933 (1991). [PubMed] [Google Scholar]
- 50.Ross K. L., Davis C. N., Fridovich-Keil J. L., Differential roles of the Leloir pathway enzymes and metabolites in defining galactose sensitivity in yeast. Mol. Genet. Metab. 83, 103–116 (2004). [DOI] [PubMed] [Google Scholar]
- 51.de Atauri P., Orrell D., Ramsey S., Bolouri H., Evolution of ‘design’ principles in biochemical networks. Syst. Biol. 1, 28–40 (2004). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/10/eaax6525/DC1
Fig. S1. Simulation of the GAL pathway.
Fig. S2. Comparison of protein expression levels of GAL genes between cis- and trans-tagging strains.
Fig. S3. Flowchart showing the construction of cis- and trans-deletion strains for the pair of GAL1 and GAL10 genes.
Fig. S4. Ln(cell number ratio between the cis- and trans-deletion strains) as a function of competition time.
Table S1. Parameter values used in the simulation of the linear pathway with two reactions.
Table S2. Parameter values used in the simulation of the GAL pathway.
Table S3. Primers for strain construction.
Table S4. gRNA target sequences.
Table S5. Doubling times for various trans-deletion strains.


