THE GRAPHICAL STRUCTURE OF RESPONDENT-DRIVEN SAMPLING

Abstract

Respondent-driven sampling (RDS) is a chain-referral method for sampling members of hidden or hard-to-reach populations, such as sex workers, homeless people, or drug users, via their social networks. Most methodological work on RDS has focused on inference of population means under the assumption that subjects’ network degree determines their probability of being sampled. Criticism of existing estimators is usually focused on missing data: the underlying network is only partially observed, so it is difficult to determine correct sampling probabilities. In this article, the author shows that data collected in ordinary RDS studies contain information about the structure of the respondents’ social network. The author constructs a continuous-time model of RDS recruitment that incorporates the time series of recruitment events, the pattern of coupon use, and the network degrees of sampled subjects. Together, the observed data and the recruitment model place a well-defined probability distribution on the recruitment-induced subgraph of respondents. The author shows that this distribution can be interpreted as an exponential random graph model and develops a computationally efficient method for estimating the hidden graph. The author validates the method using simulated data and applies the technique to an RDS study of injection drug users in St. Petersburg, Russia.

1. INTRODUCTION

Hidden populations, such as drug users, men who have sex with men, sex workers, or homeless people, are often subjected to social stigma or criminalization. Learning about these populations can be challenging for sociologists, epidemiologists, and public health researchers, because potential subjects may fear exposure or prosecution. Several survey techniques have been developed for sampling from hidden populations, including social link tracing and snowball designs (Goodman 1961; Thompson and Frank 2000). Respondent-driven sampling (RDS) is a common survey method for hidden or hard-to-reach populations for which no convenient sampling frame exists (Broadhead et al. 1998; Heckathorn 1997). In RDS, study participants recruit members of their social network who are also members of the hidden population. Starting with a set of “seeds,” participants are given a fixed number of coupons tagged with a unique code. Participants then recruit members of their social network by giving them coupons. The recipient of the coupon redeems it at the study site (or over the phone, online, etc.), is interviewed, and receives coupons to recruit others. A dual incentive encourages recruitment: subjects receive a small reward for participating in the study and for each new subject they recruit. Subjects cannot be recruited more than once, and only a small number of coupons are given to new participants, to prevent the local network from being saturated with coupons or the emergence of a secondary market for coupons. To safeguard the privacy of subjects not participating in the study, subjects do not reveal the identities of their social contacts to researchers. The only network information typically reported by subjects is their network degree, the number of social contacts who are also members of the study population.

Although RDS is an effective procedure for recruiting members of a hidden population, estimation of population characteristics from data obtained by RDS is controversial. Most methodological work on RDS assumes that the recruitment process takes place in a hidden social network connecting members of the study population. With the understanding that the structure of this hidden network likely affects individual subjects’ likelihood of being recruited, many researchers have sought to determine sampling probabilities for design-based estimation of population means (e.g., human immunodeficiency virus [HIV] infection prevalence). Salganik and Heckathorn (2004) constructed a model of the recruitment process in which subjects receive only one coupon and can be recruited infinitely many times. They modeled the recruitment as a random walk with replacement on the hidden population social network. When this walk is at “equilibrium,” they argued that the probability that a given subject is sampled is proportional to his or her network degree. Salganik and Heckathorn and Volz and Heckathorn (2008) proposed a Horvitz-Thompson type estimator for the population mean, in which observations are weighted by the inverse of the subject’s degree. Aronow and Crawford (2015) clarified the conditions under which this estimator has good statistical properties, and Gile (2011) derived a related estimator whereby sampling is without replacement.

Unfortunately, the characterization of the RDS recruitment process as a sampling design, whereby sampling probability is a function of network degree alone, suffers from some fundamental flaws. First, RDS recruitment is always without replacement, because subjects cannot be recruited more than once; second, a without-replacement random walk on a network is never at equilibrium with respect to its probability of sampling particular subjects—once a subject is recruited, he or she can never be visited by the recruitment process again; and third, if the recruitment process operates on the social network connecting the sampled individuals and seeds are not chosen at random, the network structure itself determines the probability that a given person will be reached by the recruitment chain. Indeed, for a given sample size n on a fixed population network, any potential subject whose minimum path length to a seed is greater than n has sampling probability 0, regardless of his or her network degree. The random walk characterization of RDS also neglects the fundamental role of coupon depletion in the dynamics of recruitment. Depletion of certain recruiters’ coupons can block paths to isolated parts of the network, providing no way for the recruitment chain to reach some members of the population. Researchers have raised serious concerns about the empirical properties of population estimates from data obtained by RDS and the Volz and Heckathorn (2008) estimator in particular (Gile and Handcock 2010; Goel and Salganik 2010; Johnston et al. 2010; Mills et al. 2014; Salganik 2012; White et al. 2012). Studies comparing RDS with traditional sampling or census of the same population have highlighted serious bias in estimates (McCreesh et al. 2012) or problems with variance estimation (Wejnert 2009).

It is difficult to determine the correct sampling probabilities for recruited subjects under RDS because the underlying social network is only partially observed (Gile and Handcock 2010, 2015). The unobserved links between recruited subjects, and between recruited and unrecruited population members, constitute missing data in RDS studies. Characterization of the network on which the sampling process takes place is therefore a major methodological frontier in research on estimation from RDS (Handcock and Gile 2010). Remarkably, a typical RDS study reveals a great deal of information about the network of respondents: the observed degrees, recruitment chain, and patterns of coupon allocation and depletion are all readily available and provide valuable information about the local structure of the population network. Insight into the information content of data from RDS studies would clarify exactly which network and population properties researchers can hope to estimate, and which they cannot, in real-world studies. In particular, a better understanding of the network on which RDS recruitment operates could facilitate computation of marginal sampling probabilities similar to those calculated by Gile and Handcock (2015) for use in Horvitz-Thompson-type estimators for population means (e.g., Volz and Heckathorn 2008). Alternatively, specification of a probability model for dependence between trait values of vertices that share an edge in G may allow regression approaches to population estimation and adjustment for dependence in outcomes induced by the network structure (e.g., Bastos et al. 2012). An estimate of the subnetwork of respondents in an RDS study could also be used to estimate the size of the target population in a manner analogous to the “network scale-up” population size estimator (Bernard et al. 2010; Feehan and Salganik 2014; Killworth et al. 1998).

In addition to its statistical uses for population-level inference, the subnetwork of respondents is of inherent sociological and epidemiological interest. The network connecting sampled subjects reveals social links between participants and possible avenues for transmission of ideas, behaviors, practices, or infectious agents. Comprehensive socio-metric mapping can be difficult and costly in hidden populations, and many researchers have attempted to estimate epidemiological properties of recruited individuals’ networks from recruitment data obtained by RDS (e.g., Cepeda et al. 2011; Li et al. 2011; Liu et al. 2009; Stein, Steenbergen, Buskens, et al. 2014; Stein, Steenbergen, Chanyasanha, et al. 2014). The ability to estimate features of the subnetwork of respondents in an RDS study would place sociological and epidemiological inquiries about the local network onto firmer theoretical and methodological ground.

In other areas of network theory, researchers have made progress in reconstructing networks from partial observation. When links are missing, some techniques assume that subjects with similar traits are likely to be connected (Atchade 2011; Leskovec, Huttenlocher, and Kleinberg 2010; Lü and Zhou 2011; Koskinen et al. 2013). When vertices, edges, or egocentric networks are sampled, several authors have proposed ways of estimating global network properties (Bliss, Danforth, and Dodds 2014; Goyal, Blitzstein, and de Gruttola 2014; Smith 2012) or when vertices can be observed more than once (Frank and Snijders 1994; Yan and Gregory 2013). Sometimes dynamic or random processes can reveal structural information about networks (Kramer et al. 2009; Shandilya and Timme 2011; Linderman and Adams 2014). Gile (2011) and Gile and Handcock (2015) presented methods for random graph model-assisted inference of the degree distribution from RDS, but they still assume that sampling probability is a function of network degree alone.

In this article, we show how to use data from RDS studies to probabilistically reconstruct the social network of respondents. We first define the observed data under RDS and construct a realistic continuous-time model of the RDS recruitment process on a graph. The model is a simple and natural formalization of the RDS recruitment procedure initially defined by Heckathorn (1997). Interrecruitment waiting times carry information about the network edges linking recruiters to unsampled individuals at each moment in time. We combine this timing information, knowledge of who recruited whom, who had coupons at which times, and the network degrees of recruited subjects to place a well-defined probability distribution on the structure of the recruitment-induced subgraph. A fundamental result of this article is that under simple and realistic assumptions, the likelihood of the recruitment process on a hidden graph can be interpreted as an exponential random graph model (ERGM). We describe a technique for jointly estimating the recruitment-induced subgraph and recruitment rate. An important feature of the algorithm is a computationally efficient method to calculate the likelihood of the recruitment-induced subgraph. We validate the proposed technique using simulated and real networks and apply it to an RDS study of injection drug users in St. Petersburg, Russia. We conclude with a new perspective on the information content of data from RDS studies.

2. DEFINITIONS AND ASSUMPTIONS

We begin by stating definitions and assumptions to ensure that the graph inference problem is well posed. (We use the terms graph and network interchangeably.) The first is implicit in the foundational work on RDS and guarantees that the objects under study exist (Heckathorn 1997; Salganik and Heckathorn 2004; Volz and Heckathorn 2008).

• Assumption (A-1): The hidden population exists and has finite size N. The social network connecting members of the hidden population is an undirected graph G = (V, E) with |V| = N and no parallel edges or self-loops.

Members of the hidden population are vertices in V. A vertex is recruited if it is known to the study. A vertex is a recruiter if it has at least one coupon and at least one unrecruited neighbor; a susceptible vertex is unrecruited and has at least one neighbor who is a recruiter. A susceptible edge connects a recruiter and a susceptible vertex, and recruitments can take place only across susceptible edges. A recruited vertex cannot be recruited again. At the moment it is recruited, a vertex is endowed with a non-negative number of coupons it may use to recruit its susceptible neighbors. Every recruitment reduces the number of coupons held by the recruiter by one. When all the coupons belonging to a recruiter vertex are depleted, the vertex is no longer a recruiter, and any edges incident to it are no longer susceptible. Seeds are recruited vertices chosen from the entire population of vertices by some mechanism, not necessarily random, usually at the beginning of the study. Seeds are not considered to have been recruited by any other vertex.

• Definition 1 (Recruitment-induced Subgraph): The recruitment-induced subgraph is G_S = (V_S, E_S), where V_S ⊆ V consists of n = |V_S| sampled vertices (including seeds), and {i, j} ∈ E_S if and only if i ∈ V_S, j ∈ V_S, and {i, j} ∈ E.

• Definition 2 (Recruitment Graph): The directed recruitment graph is G_R = (V_R, E_R), where V_R = V_S is the set of n sampled vertices and (i, j) ∈ E_R means i recruited j.

Because subjects cannot be recruited more than once, G_R is acyclic. Assumption (A-1) does not require that G be connected, nor that the RDS sample take place in the largest connected component, or even a single component. Therefore the recruitment-induced subgraph G_S may not be connected. Let d be the n×1 vector of recruited subjects’ degrees (in the order of their recruitment into the study) and let t = (t₁, …,t_n) be the n×1 vector of recruitment times, where t₁<⋯<t_n.

• Definition 3 (Coupon Matrix): Let C be the n×n coupon matrix whose element C_ij is 1 if subject i has at least one coupon just before the jth recruitment event, and zero otherwise. The rows and columns of C are ordered by subjects’ recruitment time.

The RDS recruitment process reveals only some of this information to researchers.

• Assumption (A-2): The observed data consist of Y = (G_R, d, t, C).

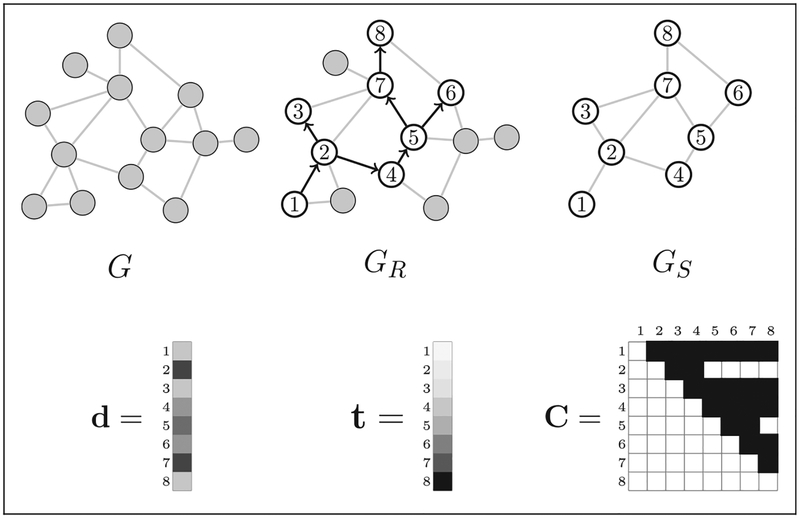
In particular, researchers do not observe the recruitment-induced subgraph G_S of the sampled vertices. Figure 1 shows an example graph G and a realization of the RDS recruitment process on G. The recruitment graph G_R, recruitment-induced subgraph G_S, degree vector d, recruitment times t, and coupon matrix C are also shown.

Figure 1.

Example of unobserved and observed data in respondent-driven sampling (RDS). The true hidden population network is G. One seed is chosen (the vertex marked 1), and the RDS recruitment proceeds with each recruited vertex receiving two coupons. The directed recruitment graph G_R is shown superimposed on G. The recruitment-induced subgraph G_S is the subgraph of the recruited vertices. The degrees d = (d₁, …,d₈) of each recruited vertex are observed, along with the recruitment times t = (t₁, …,t₈). The coupon matrix C shows which recruiters had at least one coupon just before each recruitment event. In RDS, researchers observe neither G nor G_S; the observed data consist of Y = (G_R, d, t, C).

We now state three assumptions about the behavior of recruiters and their knowledge of the recruitment status of their neighbors.

• Assumption (A-3): Vertices become recruiters immediately upon entering the study and receiving one or more coupons. They remain recruiters until their coupons or susceptible neighbors are depleted, whichever happens first.

• Assumption (A-4): When a susceptible neighbor j of a recruiter i is recruited by any recruiter, the edge connecting i and j is immediately no longer susceptible.

By assumption (A-4), recruitment is competitive: the first recruiter to recruit a given susceptible vertex immediately removes it from the pool of susceptibles. Finally, we specify a parametric waiting time distribution for the time it takes for a recruiter to recruit a susceptible neighbor.

• Assumption (A-5): The time to recruitment along an edge connecting a recruiter to a susceptible neighbor has exponential distribution with rate λ, independent of the identity of the recruiter, neighbor, and all other waiting times.

By assumption (A-5), waiting times to recruitment along susceptible edges are independent and elapse concurrently in continuous time, so recruitment is simultaneous. Together, assumptions (A-3), (A-4), and (A-5) place a well-defined probability distribution on the recruitment-induced subgraph of respondents.

2.1. Consequences of the Waiting Time Assumption

The results below follow directly from assumption (A-5). Let R be the set of recruiters with coupons and let S be the set of susceptible vertices at a certain moment in the recruitment process. Let S_u be the set of susceptible vertices that are neighbors of the recruiter u ∈ R. Likewise, let R_v be the set of possible recruiters of a susceptible vertex v ∈ S. Clearly, v ∈ S_u if and only if u ∈ R_v.

• Proposition 1: Given that the recruiter u recruits one of its susceptible neighbors v ∈ S_u before any other recruiter, the waiting time to this recruitment event is distributed as Exponential (λ|S_u|). The probability that the susceptible vertex v ∈ S_u is the next recruit is uniform 1/|S_u| and independent of the waiting time to the recruitment event.

• Proposition 2: The waiting time to the next recruitment of any susceptible vertex is distributed as Exponential $\left(\lambda {\sum }_{u\in R}\left|S_u\right|\right)$. The probability that the susceptible vertex v ∈ S is the next recruit is $\left|R_v\right|/{\sum }_{k\in S}\left|R_k\right|$ independent of the waiting time.

Proofs of propositions 1 and 2 are given in the online Appendix. Intuitively, proposition 2 means that the new recruited vertex is chosen with probability proportional to the number of edges along which it can be recruited. These results formalize the consequences of simultaneous and competitive recruitment in continuous time.

Interestingly, assumptions (A-3) to (A-5) and the resulting recruitment probability differ starkly from the recruitment dynamics used in simulations by other researchers to test the performance of estimators for RDS. Gile and Handcock (2010) simulated the RDS recruitment process by first choosing seeds, after which “subsequent sample waves were selected without-replacement by sampling up to two nodes at random from among the unsampled alters of each sampled node” (p. 303). This leads to a brief corollary establishing the difference between these approaches.

• Corollary 1: Assumptions (A-3) to (A-5) (simultaneous and competitive recruitment) result in different conditional recruitment probabilities than the RDS recruitment implementation of Gile and Handcock (2010).

A proof is given in the online Appendix. The process defined by Gile and Handcock (2010) requires that recruiters “take turns.” This approach implicitly requires that recruiters have knowledge about the behavior of other recruiters—even those to whom they are not connected in the network. This process induces a different distribution on the susceptible degree, and hence on the overall degree, of the new recruit than the model described in assumptions (A-3) to (A-5) of this article. Most existing methods for population inference from RDS data depend intimately on the degree distribution of recruited vertices (e.g., Gile 2011; Salganik and Heckathorn 2004; Volz and Heckathorn 2008), so it is important to highlight scenarios when methods for simulation of recruitment dynamics differ.

3. LIKELIHOOD OF THE RECRUITMENT TIME SERIES

Proposition 2 shows that under assumptions (A-3) to (A-5), the rate of recruitment is proportional to the number of susceptible edges. Given a realization of the recruitment-induced subgraph G_S, it is not immediately obvious how to determine quickly the number of susceptible edges just before each recruitment. When a given susceptible vertex is recruited, all susceptible edges incident to it disappear from the set of susceptible edges (assumption A-4). Furthermore, the newly recruited vertex now has coupons, so there may be new susceptible edges connected to it. Finally, if the new vertex is not a seed, its recruiter has used one coupon; if its coupons are now depleted, any other susceptible edges incident to the recruiter are no longer susceptible. Clearly, the number of susceptible edges can increase, decrease, or stay the same from one recruitment to the next. In this section, we derive a computationally efficient representation of the likelihood of the recruitment time series using matrix algebra. This approach obviates costly enumeration of all |E_S| edges to determine whether they are susceptible at each step in the recruitment process. A preliminary definition will assist in this task. Let 1{X} be the indicator of an event X, which takes value 1 when X is true and zero otherwise.

• Definition 4 (Compatibility): An estimated subgraph ${\widehat{G}}_S=\left({\widehat{V}}_S,{\widehat{E}}_S\right)$ is compatible with the observed data Y = (G_R, d, t, C) if the following conditions are met:

  1. The vertices in the estimated subgraph are identical to the set of recruited vertices: $v\in {\widehat{V}}_S$ if and only if v ∈ V_R.
  2. All directed recruitment edges are represented as undirected edges: for each $\left(i,j\right)\in E_R,\left\{i,j\right\}\in {\widehat{E}}_S$.
  3. The number edges in G_S belonging to each sampled vertex does not exceed the vertex’s degree: for all $v\in V_R,{\sum }_{u\in V_R\backslash v}1\left\{\left\{u,v\right\}\in {\widehat{E}}_S\right\}\le d_v$ where d_v is the degree of vertex v.

Let $\mathcal{C}\left(G_R,d\right)$ denote the set of all compatible subgraphs. These compatibility conditions provide topological constraints on the structure of G_S. Combining these with the likelihood of the recruitment time series allows probabilistic reconstruction of G_S.

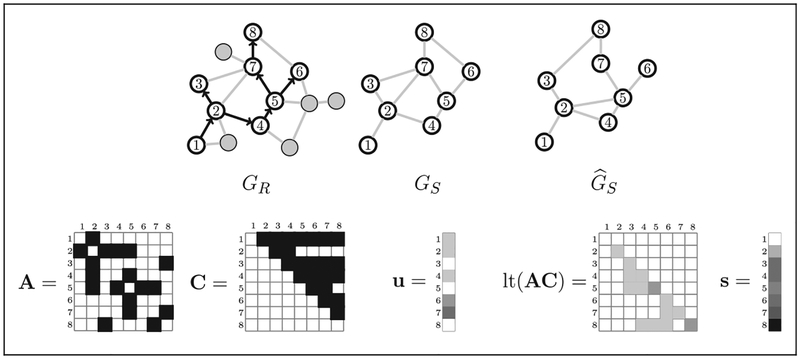
Let A be the n×n adjacency matrix (sociomatrix) of a compatible estimate G_S, where the rows and columns of A correspond to subjects in the order of their recruitment. The product of A and the coupon matrix C gives an n×n matrix whose elements describe the number of recruiters connected to each vertex in G_S over time. Let w = (0, t₂ − t₁, …,t_n − t_n−1) be the n×1 vector of waiting times between recruitments. Let u be the n×1 vector of the number of edge ends belonging to each vertex (in the order of recruitment) that are not connected to any other sampled vertex. When j ≤ i, {AC}_ij is the number of recruiters connected to i just before the time t_j of the jth recruitment. Then lt(AC), the lower triangle of AC, is the number of recruiters connected to each vertex at each time before recruitment of that vertex. Likewise, the jth element of C′u is the number of susceptible edges connecting sampled vertices to unsampled vertices at time t_j. Figure 2 shows examples of these matrices. Finally, let M be the set of seeds.

Figure 2.

Examples of matrices used to calculate the recruitment time series likelihood. At top left is the recruitment graph G_R overlaid on the population graph G, with recruited vertices numbered and other vertices and edges in gray. The true recruitment-induced subgraph G_S is not directly observed. We estimate G_S by ${\widehat{G}}_S$ and let A be the adjacency matrix of ${\widehat{G}}_S$. The coupon matrix C and the number of pendant edges attached to each recruited vertex is u. Pendant edges connect recruited vertices to unknown/unsampled vertices. The i, jth element of lt(AC) is the number of recruiters connected to i just before the jth recruitment event.

• Proposition 3: Under assumptions (A-1) to (A-5), the likelihood of the recruitment time series is

  $$L(w|G_S,\lambda )=\left(\prod _{k\notin M}\lambda s_k\right)\text{exp}\left[-\lambda s\prime w\right],$$ (1)

  where

  $$s=\text{lt}\left(AC\right)\prime 1+C\prime u$$ (2)

  is a vector whose elements are the number of susceptible edges just before each recruitment event.

A proof is given in the online Appendix. As before, the rate of recruitment is proportional to the number of susceptible edges, and proposition 3 generalizes proposition 2 by providing an explicit expression for the number of susceptible edges at each step, taking coupons into account and allowing for seeds to be added at any time.

Although equation (1) is the likelihood of the recruitment time series w, we can also view it as a function of the recruitment-induced subgraph adjacency matrix A with λ and w held fixed. Consider the statistic T(A) = − λs, where s is defined by equation (2), θ = w, and $B\left(A\right)={\sum }_{k\notin M}\text{log}\left(\lambda s_k\right)$. Then we can renormalize the likelihood (equation 1) to form the probability $\text{Pr}\left(A|\theta \right)=\text{exp}\left[T\left(A\right)\prime \theta +B\left(A\right)\right]/\kappa \left(\theta \right)$, where κ(θ) is a normalizing constant that does not depend on A. It is clear that Pr (A|θ) is a member of the exponential family of distributions. In particular, it can be interpreted as an ERGM, also known as a p* graph (Frank and Strauss 1986; Wasserman and Pattison 1996). Regardless of whether we view equation (1) as the likelihood of the random waiting times w or as the probability of the random graph G_S, the inference procedure we develop below benefits from Markov chain Monte Carlo algorithms developed for sampling edges in ERGMs (see Snijders and Van Duijn 2002 for an example).

4. RECONSTRUCTING THE RECRUITMENT-INDUCED SUBGRAPH G_S

Together, the compatibility conditions (definition 4) and proposition 3 make possible simultaneous estimation of the recruitment-induced subgraph G_S and the waiting time parameter λ under the recruitment model. Because proposition 3 implies a probability model for $G_S\in \mathcal{C}\left(G_R,d\right)$, we can learn about this distribution by drawing samples from joint posterior

$$p\left(G_S,\lambda |Y\right)\propto L\left(w|G_S,\lambda \right)Pr\left(G_S\right)\pi \left(\lambda \right),$$ (3)

where Y = (G_R, C, d, t) is the observed data, and Pr (G_S) and π(λ) are prior distributions. We take the uniform prior distribution over the recruitment-induced subgraph: $\text{Pr}\left(G_S\right)=1/\left|\mathcal{C}\left(G_R,d\right)\right|$ for every $G_S\in \mathcal{C}\left(G_R,d\right)$. To draw pairs (G_S, λ) from p(G_S, λ|Y), we use a Metropolis-within-Gibbs sampling scheme. To sample G_S conditional on λ, suppose λ is fixed and we have a compatible subgraph G_S. We generate a new compatible subgraph $G_S^{*}=\left(V_S,E_S^{*}\right)$ using a proposal algorithm given in the online Appendix. To sample λ conditional on G_S, we use a Metropolis-Hastings step based on an approximation of the conditional distribution of λ given in the online Appendix. By alternating these steps, we define a reversible Markov chain whose equilibrium distribution is the given by equation (3).

Computationally efficient Monte Carlo sampling of G_S via the Metropolis-Hastings algorithm depends on rapid evaluation of the likelihood ratio $L\left(w|G_S^{*},\lambda \right)/L\left(w|G_S,\lambda \right)$, where $G_S^{*}$ is a new proposed subgraph. The online Appendix presents simple expressions for these likelihood ratios that depend only on a simple change statistic and do not require evaluation of the matrix products required in the likelihood equation (1). More generally, the computational burden of the procedure scales with the sample size n and is not affected by the total size N = |V| of the target population.

When only a single “most likely” subgraph G_S is desired, a faster algorithm is available for maximum likelihood (or maximum a posteriori [MAP]) estimate of G_S and λ. This Monte Carlo optimization approach is called “simulated annealing” (e.g., see Robert and Casella 2004 for details) and produces a sequence of estimates (G_S, λ) that tend toward the most likely values under the likelihood or posterior distribution. The simulated annealing procedure is outlined in the online Appendix.

5. VALIDATION BY SIMULATION

In simulation studies, reasonably accurate reconstruction of the recruitment-induced subgraph G_S can be achieved using the proposed recruitment model (equation 1). In the online Appendix, we analyze the performance of reconstruction in simulated networks and a real-world social network. Conditional on the population network, we simulate the RDS recruitment process with n subjects, |M| seeds, and recruitment rate λ, under assumptions (A-3) to (A-5). From the simulated recruitment data, we extract the observed data Y = (G_R, t, d, C) in accordance with assumption (A-2). We place a gamma prior distribution on the waiting time parameter, $\pi \left(\lambda \right)\propto {\lambda }^{\eta -1}{e}^{-\xi \lambda }$, where η>0 and ξ>0. We assess the accuracy of reconstruction over 100 repetitions of simulated RDS recruitment over different networks, and for each simulated data set, we find the joint MAP estimate of G_S and λ using the procedure outlined in Section 4. MAP estimates represent the mode of the posterior distribution over (G_S, λ) and provide a convenient point estimate for comparing results over many repetitions of the simulation. We also assess the accuracy of reconstruction under a misspecified waiting time model in which assumption (A-5) is violated; reconstruction remains robust, with corresponding bias in estimates of λ.

6. APPLICATION

The HIV epidemic in St. Petersburg, Russia, is concentrated in people who inject drugs (PWID). At least 12,000 people are registered as drug users, but the number of current PWID is likely much higher (Heimer and White 2010). Injection drug use is highly stigmatized in the Russian Federation, and criminal penalties for drug possession can be severe. PWID suffer from high rates of HIV infection and may lack access to treatment and health-related educational resources (Niccolai et al. 2010, 2011).

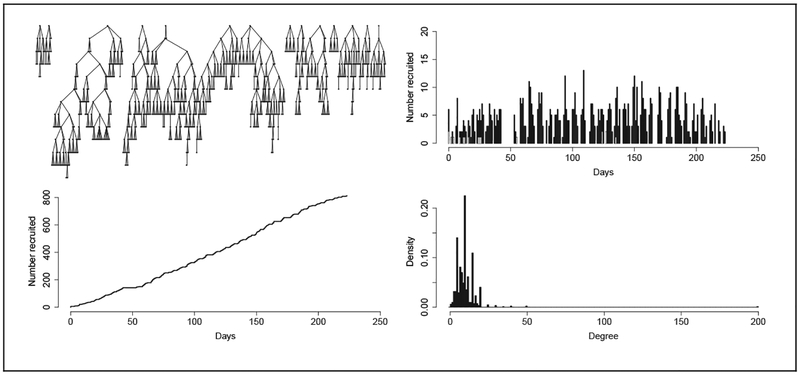
As part of a study to assess perceived barriers to use of HIV prevention and treatment services, n = 813 PWID were recruited using RDS in St. Petersburg during 2012 and 2013. Outreach workers identified 17 seed subjects using venue-based sampling in six city districts. Interviews collected demographic information, injection practices, sex practices, mental health measures, and knowledge of HIV/AIDS and tuberculosis resources, but we focus solely on network structure in this analysis. Figure 3 shows the raw RDS data: the recruitment trees, number of new recruits per day, cumulative number of recruits, and reported network degrees.

Figure 3.

Raw data from a respondent-drivien sampling (RDS) sample of n = 813 people who inject drugs in St. Petersburg, Russia. In the top left panel, 14 RDS recruitment chains originating from different seeds are shown. Recruited subjects are organized into “waves” along the vertical axis. The top right panel shows the number of subjects interviewed on each day of the study, with seeds indicated by gray bars. The bottom left panel shows the cumulative number of recruits over the course of the study, and the bottom right panel shows a histogram of the reported degrees of subjects, with bin size 1.

Participation in the study was limited to current injection drug users over the age of 21 years who had injected within the previous four weeks. Subjects’ status as PWID was verified either by inspection of arms for injection marks or explanation of drug preparation. Subjects received a voucher with a value of about US$20 for being interviewed and a secondary reward with value about US$10 for recruiting another eligible subject. Following their interview, each subject received three coupons, and no subject could be recruited more than once. Informed consent was obtained from all participants, and the study was approved by the Yale University and Stellit (St. Petersburg) institutional review boards.

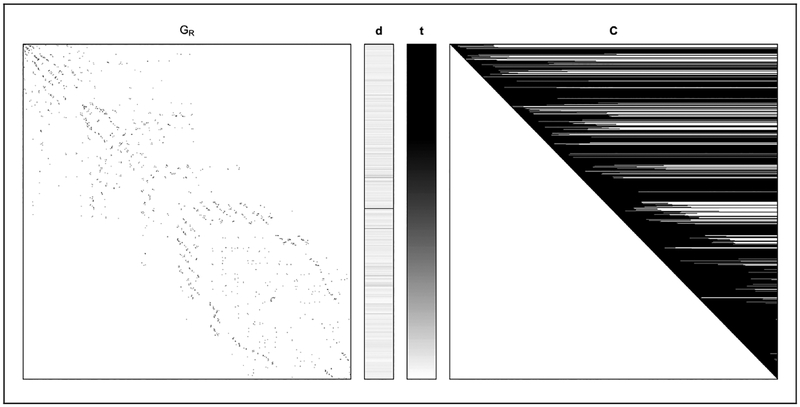
Figure 4 shows the observed data Y = (G_R, d, t, C) from this study. The recruitment graph G_R was constructed by matching participants’ coupon ID with the IDs of coupons given to their recruiter. The coupon matrix C was constructed by calculating the number of coupons held by each subject just before each recruitment event. Interviews assessed network degree by asking, “How many people do you know (you know one another’s names) who you have seen within the last 4 weeks who inject drugs?”

Figure 4.

Raw respondent-driven sampling data Y = (G_R, d, t, C) extracted from study recruitment information.

A subject’s minimum degree was defined as the number of undirected edges incident to that subject in the recruitment graph G_R. We assumed a subject’s network degree was accurately reported, except when a subject’s reported degree was less than his or her minimum degree. In these cases, we replaced the reported degree by the minimum degree. The average reported degree of subjects was 10.3. Interview dates and times were recorded for each subject; the elapsed time between a subject’s interview and the next interview (in days) was treated as the interrecruitment waiting time. To estimate the edgewise recruitment rate λ more reliably, we removed weekends and other breaks during which no interviews were scheduled. This slightly changed the units of λ but allowed better estimation of the true waiting time distribution. The online Appendix describes the prior specification for l. In a few cases, the interview times for a subject and his or her recruit were the same, presumably because both individuals came to the interview site together. In these cases, we resolved the tie by jittering the recruiter’s interview time to be slightly earlier than the recruitee’s interview time.

Construction of G_R and C revealed a minor violation of the RDS recruitment specification: we found seven recruits whose coupon IDs matched the IDs of already redeemed coupons. The financial reward for recruiting another eligible subject may provide a strong incentive for participants to fraudulently inflate the number of coupons they hold by creating a facsimile of the original coupon and giving it to another potential subject to redeem. This appears to be what happened: the recruiter photocopied the original coupon, this reproduction was not detected by the interviewer, and both the new recruit and recruiter received their corresponding rewards. Rather than breaking the recruitment chain by omitting data from the seven subjects with duplicated coupon IDs, we instead artificially increased the number of coupons held by the apparent recruiter to be equal to the number of subjects who redeemed coupons bearing the ID of the recruiter.

Overall recruitment of participants in this study was rapid: the mean time between interviews was 0.28±0.74 days. However, the mean time between a particular subject’s interview and his or her recruiter’s interview was 23.4±18.0 days, indicating that the per edge waiting times for recruited subjects were substantially longer (the maximum waiting time from interview to recruitment was 112 days). Indeed, this calculation is conditional on the subject’s actually being recruited within the study time frame, so any longer waiting times are censored by the end of the study. We evaluated the posterior mode with η ranging from 0.1 to 10, and in every case the estimate ranged from 0.0050 to 0.0053. The rate of recruitment across susceptible edges is estimated to be approximately 1/λ = 199 days with posterior quantiles (186, 215), nearly as long as the study duration of 223 days. The apparent discrepancy between the high frequency of interviews and very slow recruitment across susceptible edges is explained by the fact that researchers observe the minimum waiting time to recruitment across all susceptible edges at each step in the recruitment process.

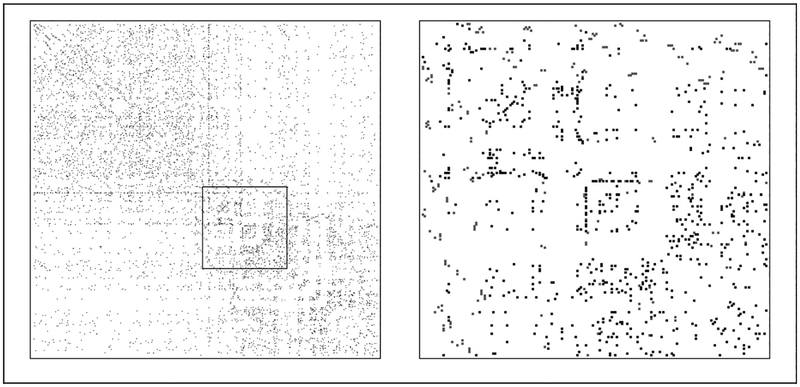
Figure 5 shows the MAP estimate of the adjacency matrix for all 813 sampled subjects (left) and inset submatrix (right). Recruitment edges appear in gray. The apparent bands in the adjacency matrix represent high-degree individuals with many nonrecruitment edges. Probabilistic assignment of these edge ends to other recruited individuals depends on the timing of recruitments of other subjects. The blocklike structure evident in this adjacency matrix may indicate subnetworks of highly connected individuals. Subjects recruited nearby in time may be more likely to know one another, even if they are not linked by a recruitment edge.

Figure 5.

Maximum a posteriori (MAP) estimate of G_S for the St. Petersburg respondent-driven sampling study. The left panel shows the MAP estimate of the adjacency matrix of G_S, and the right panel shows the inset submatrix in detail. Edges in the recruitment graph are shown in gray.

7. DISCUSSION

Nearly every paper on statistical methods for RDS data states or assumes a version of assumption (A-1): the social network connecting members of the hidden population exists and determines the sampling probabilities. But because this network is only partially observed in real-world RDS studies, assumption (A-1) is usually disregarded in the formulation of statistical estimators. Instead, researchers usually make the simplifying assumption that sampling probability is proportional to degree and does not otherwise depend on subjects’ location in the network. This simplification is justified by a thought experiment in which the rules of the game are altered: subjects can be recruited infinitely many times, each subject receives only one coupon, and this process continues for an infinitely long time (Goel and Salganik 2009; Salganik and Heckathorn 2004; Volz and Heckathorn 2008).

In this paper, we have embraced assumption (A-1) and its natural consequence: RDS recruitment happens across edges in the network connecting members of the hidden population. This point of view emphasizes that RDS is more like a stochastic spreading process on a hidden network than a survey sampling method. We define a simple continuous-time model for RDS recruitment on a hidden population graph using the kind of data obtained by every RDS study. The model results in sensible nonuniform conditional recruitment probabilities: the next subject is recruited with probability proportional to the number of edges he or she shares with recruiters (proposition 2), not their total network degree. Combining this model with the observed data from an RDS study allows joint estimation of the recruitment-induced subgraph G_S and the waiting time parameter λ. Most important, the model directly connects the observed data to the recruitment process on the underlying network.

This approach yields two computational benefits. First, the time required to evaluate the likelihood via proposition 3 is a function of the sample size n alone, and it does not depend on the population size N, which is likely to be much larger. In particular, we never simulate unobserved portions of the population network G; the ERGM (equation 1) specifies a probability model for the recruitment-induced subgraph G_S only. In contrast, some researchers dealing with partially observed network data marginalize over the entire unsampled portion of the graph, which may be burdensome or impossible for large N (Gile and Handcock 2015). Second, the likelihood (outlined in the online Appendix) does not require computation of the matrix products implied by equation (2). Instead, efficient update expressions given in the online Appendix depend only on a change statistic that can be efficiently updated.

Our approach is unique because it uses all the available data Y = (G_R, d, t, C) from real-world RDS studies. Several researchers have attempted to estimate the population degree distribution but they use only G_R and d (and sometimes d alone), ignoring t and C (Gile 2011; Gile and Handcock 2015; Handcock, Gile, and Mar 2015; Salganik and Heckathorn 2004; Volz and Heckathorn 2008). Berchenko, Rosenblatt, and Frost (2013) gave a formulation of recruitment event intensity similar to assumption (A-2) by using a multitype epidemic model in which active recruiters correspond to infective individuals. In their model, the rate of recruitment of a new subject with degree k is proportional to the product of the number of active recruiters and the number of susceptible subjects with degree k. However, they use only d, t, and C but do not take advantage of the topological information contained in G_R.

Historically, there have been two major statistical objections to RDS as a survey design for inference of population quantities. First, sampling probabilities cannot be computed directly from the observed data without additional assumptions (Gile 2011; Gile and Handcock 2010). Second, there may be statistical dependence between the traits of a given subject and his or her neighbors (particularly their recruiter) in the network (Fisher and Merli 2014; Heckathorn 1997, 2002; Tomas and Gile 2011). This dependency might be due to homophily—the tendency for people to form social ties with others similar to themselves—or preferential recruitment of certain types of people, conditional on existing social ties. Clearly, the network structure local to the seeds and recruitment chain encodes the sampling probabilities and the statistical dependencies between subjects’ attributes. This leads us to the conclusion that a fundamental obstacle to principled statistical inference for RDS is missing data: in RDS, not all network neighbors of a vertex i are observed, either because they remain unsampled, or because the recruitment graph G_R does not reveal a tie between i and the sampled vertices to which it is connected. Objections to RDS typically under-state the information about this network contained in the recruitment graph G_R and the time series of interviews. Our results—revealing the graphical structure of data obtained by RDS—raise the possibility that researchers can account for both of these sources of missing data without imposing strong prior assumptions about the network.

Although the network may be of interest for sociological reasons, it can also be viewed as a nuisance parameter when population attributes are of primary interest. Marginalizing (integrating) over the recruitment-induced subgraph G_S can be understood as multiple imputation, repeatedly filling in the missing data in accordance with its distribution under the model (Little and Rubin 1986; Huisman 2009; Koskinen, Robins, and Pattison 2010; Koskinen et al. 2013). In the absence of any other information, we could marginalize over compatible graphs in $\mathcal{C}\left(G_R,d\right)$ with respect to the uniform distribution. However, the reconstructed graph would be subject to two types of reconstruction inaccuracy. First, for three sampled vertices i, j, and k with at least one pendant edge each, the uniform distribution provides no basis to distinguish an edge {i, j} from an edge {i, k} unless a recruitment event took place along one of those edges. For any given pendant edge, there are usually many more incorrect ways to connect it to sampled vertices than there are correct ways. Second, marginalization with respect to the uniform distribution usually results in inclusion of too many or too few edges overall in G_S. The waiting time model developed in this paper provides a coherent basis for adding edges to the recruitment subgraph G_R and helps ensure that estimates of G_S have approximately the same number of edges as the true underlying graph.

In conclusion, we offer a mixed message about the prospect for statistically rigorous analysis of data from real-world RDS studies. First, current estimators for population characteristics depend on assumptions that bear little similarity to RDS recruitment processes on social networks, and they do not use all the available data. This may account for their poor performance in empirical studies. Second, and more optimistically, data from RDS studies contain far more information about the social network connecting respondents than has been acknowledged. Estimation of population-level characteristics should therefore proceed from knowledge about the network of sampled subjects: The subgraph G_S is the maximal network object that can be estimated directly from the observed data without further assumptions. Extrapolation to the population network requires stronger assumptions than those given in this article. By introducing a simple technique for probabilistic reconstruction of the recruitment-induced subgraph, we hope to offer researchers a new tool for sociological inquiry: a social network sampling method that delivers the network.

Author Biography

Forrest W. Crawford is an assistant professor in the Department of Biostatistics at the Yale School of Public Health. He is affiliated with the Department of Ecology and Evolutionary Biology, the Center for Interdisciplinary Research on AIDS, the Institute for Network Science, the Computational Biology and Bioinformatics program, and the Operations doctoral program at the Yale School of Management. He received his PhD in biomathematics from the University of California, Los Angeles, in 2012. His interests include network analysis, stochastic processes, and missing data.