Theory and simulations for RNA folding in mixtures of monovalent and divalent cations

Significance

RNA molecules require ions to fold. The problem of how ions of differing sizes and valences drive the folding of RNA molecules is unsolved. Here, we take a major step in its solution by creating a method, based on the theory of polyatomic liquids, to calculate the potential between divalent ions and the phosphate groups. The resulting model, accounting for inner and outer sphere coordination of Mg²⁺ and Ca²⁺ to phosphates, when used in coarse-grained molecular simulations, predicts folding free energies for a number of RNA molecules in the presence of both divalent and monovalent ions that are in excellent agreement with experiments. This work sets the stage for probing sequence and ion effects on DNA and synthetic polyelectrolytes.

Abstract

RNA molecules cannot fold in the absence of counterions. Experiments are typically performed in the presence of monovalent and divalent cations. How to treat the impact of a solution containing a mixture of both ion types on RNA folding has remained a challenging problem for decades. By exploiting the large concentration difference between divalent and monovalent ions used in experiments, we develop a theory based on the reference interaction site model (RISM), which allows us to treat divalent cations explicitly while keeping the implicit screening effect due to monovalent ions. Our theory captures both the inner shell and outer shell coordination of divalent cations to phosphate groups, which we demonstrate is crucial for an accurate calculation of RNA folding thermodynamics. The RISM theory for ion–phosphate interactions when combined with simulations based on a transferable coarse-grained model allows us to predict accurately the folding of several RNA molecules in a mixture containing monovalent and divalent ions. The calculated folding free energies and ion-preferential coefficients for RNA molecules (pseudoknots, a fragment of the rRNA, and the aptamer domain of the adenine riboswitch) are in excellent agreement with experiments over a wide range of monovalent and divalent ion concentrations. Because the theory is general, it can be readily used to investigate ion and sequence effects on DNA properties.

The lack of a rigorous and thermodynamically consistent treatment of interactions between counterions and RNA has impeded a quantitative description of the self-assembly of RNA molecules (1). Although many factors contribute to the stability of a folded RNA molecule, the interplay between monovalent and divalent cations and the highly correlated nature of ion–RNA interactions make it challenging to develop an accurate and tractable theory for RNA folding thermodynamics and kinetics. The effects of monovalent ions could be accurately accounted for by using the Debye–Hückel theory (2–4). However, theoretical and computationally tractable treatments of the effects of divalent cations, such as Mg²⁺, which play an essential role in RNA structure, folding, and function (5–8), have not been fully developed. Accounting for the effects of divalent ions on RNA folding requires an approach that goes beyond the use of the Poisson–Boltzmann equation (9–11) to account for the ion size, ion–ion correlations, and the complex coordination with the phosphate groups. The simultaneous presence of monovalent and divalent ions introduces additional complexity that has to be dealt with to arrive at a reasonable predictive theory of RNA folding.

How ions modulate the RNA energy landscape has also been the subject of extensive experimental and theoretical studies (1, 9, 12–20). From the chemistry perspective, binding of divalent ions to the negatively charged phosphate groups could be conceptually classified into 2 categories: direct (or inner-sphere) contact where an atom (or more) of the RNA is part of the divalent ion coordination sphere and indirect (or outer-sphere) contact where the interaction is mediated by a water molecule (5). Recent surveys of the RNA structures in the Protein Data Bank (PDB) reported the frequencies of both inner and outer spheres Mg²⁺ binding to RNA atoms (21, 22), which suggests that a theoretical model must take these interactions into account to describe RNA folding. However, a complete knowledge of the distribution of ions around RNA in solution is still lacking although initial insights have been provided in a recent study (23).

To arrive at an accurate model, which reliably predicts the thermodynamic properties of large RNA molecules, we first began with a sequence-dependent three-interaction site (TIS) coarse-grained (CG) model for nucleic acids (24), which has been adopted to study a range of problems related to RNA folding (2, 10, 25–32). Even with this simplification, the inclusion of both monovalent ions (present in excess concentration relative to divalent cations) and divalent ions explicitly is computationally demanding, although folding simulations of a 195-nt Azoarcus ribozyme and pseudoknots have been carried out successfully (10, 33). Here, we report the folding thermodynamics of RNA molecules using simulations performed with a hybrid model in which monovalent ions are implicitly treated but divalent cations are explicitly included. To develop such a model, we resort to the reference interaction site model (RISM) theory (34–40) to obtain the potential of mean force (PMF) between divalent cations and phosphate groups. We show that this treatment is necessary to obtain accurate results for RNA thermodynamics, especially for Mg²⁺ ions, which are involved in both the inner and outer shell coordination with the negatively charged phosphate groups. Using our model and simulations, we calculate, with high accuracy, the thermodynamics of RNA folding in the presence of divalent and monovalent cations for several RNA molecules in the folded, intermediate, and unfolded states. In the process, we establish that divalent ions interact strongly with RNA molecules in the intermediate structures (41), which provides a structural interpretation of site-specific interactions between RNA and ions. Our work also shows that accounting for both inner- and outer-sphere coordination of divalent cations with RNA is necessary to faithfully reproduce divalent cation–RNA interaction thermodynamics. The general framework, which integrates liquid-state theories with molecular simulations, is applicable to investigate folding of large RNA molecules over a broad range of salt concentrations, thus vastly expanding the scope of simulations to a variety of problems in RNA biology.

Theory

RNA Model.

We adopt the TIS model, in which each nucleotide is modeled using three interaction sites located at the center of geometry of phosphate (P), sugar (S), and base (B) (2, 3, 10, 24, 31). The energy function, $U=U_{\mathrm{B}\mathrm{A}}+U_{\mathrm{E}\mathrm{V}}+U_{\mathrm{S}\mathrm{T}}+U_{\mathrm{H}\mathrm{B}}+U_{\mathrm{E}\mathrm{L}}$, takes into account the bond length and angle constraints, excluded volume interactions, secondary stacking between consecutive bases and tertiary stacking (stacking between bases that are not consecutive in the structure), and both nonnative and native hydrogen bond interactions. Details of the force field are given in SI Appendix.

Previously (10), we treated all of the ions (including monovalent ions) explicitly, and therefore the phosphate charge was fixed at $Q=-e$. Here, we employ the Debye–Hückel (DH) equation to approximate the screening effect of monovalent ions. Thus, the electrostatic interactions between the P–P and the divalent cations are written as

$$U_e\left(r\right)\hspace{0.17em}=\hspace{0.17em}\frac{1}{2ϵ}\sum _{i,j}\frac{Q_i{Q}_j\exp \left(-\frac{r}{\lambda }\right)}{r},$$ [1]

where $\lambda ={\left(8\pi l_B{\rho }_1\right)}^{-\frac{1}{2}}$ is the DH screening length that depends on the number density of monovalent ions, ${\rho }_1$, and $l_B=\frac{e^2}{4\pi \epsilon k_{B}T}$ is the Bjerrum length. For divalent cations $Q_i=+2e$. The renormalized charge on the phosphate $Q_{\mathrm{P}}\left(T,C_1,C_2\right)$ depends on the concentrations of both the monovalent ($C_1$) and divalent ions ($C_2$), which is calculated using the counterion condensation (CIC) theory (42–44). The electrostatic interaction between the divalent ions and phosphate groups is treated precisely to account for water-mediated outer- and inner-shell interactions (below). Because the X²⁺–P potential (X is Mg or Ca) includes the excluded volume interactions, we do not explicitly account for such interactions in the coarse-grained TIS force field (SI Appendix).

Phosphate Charge Renormalization.

A consequence of CIC is that the effective charge on the phosphate is reduced from $-1e$, thus softening the overall electrostatic interactions enabling the compaction and folding of the RNA. Following our earlier studies (2, 3), we include ion condensation effects for the implicitly treated monovalent ion. Since we treat divalent ions explicitly and monovalent ions implicitly, a thermodynamically consistent treatment of ion effects is needed. As the divalent ion concentration increases, the condensed divalent ions outcompete monovalent ions for the phosphate groups. This occurs because for each condensed divalent ion, approximately 2 monovalent ions are released, which is favored because the overall entropy of the system is increased.

In the mixed ion system, we assume that 1 divalent ion replaces exactly 2 monovalent ions, and the total RNA charge neutralized in the process is equal to those in the monovalent salt alone. In other words, if ${\theta }_1$ and ${\theta }_2$ are the numbers of condensed monovalent and divalent ions per phosphate group, respectively, then

$${\theta }_1+2{\theta }_2=\theta =1-\frac{b}{l_B\left(T\right)},$$ [2]

with the mean spacing between phosphate charges, $b=4.4$ Å, a value used in our previous studies (2, 31). Although a more complicated treatment based on the balance between the interaction energy of ion–phosphate and entropic effects is possible (45), we find that this simple approximation works well for a broad range of ion concentrations.

A relation between ${\theta }_1$ and ${\theta }_2$ can be derived by considering the entropic cost of localizing 1 divalent ion vs. 2 monovalent ions. By neglecting ion–ion correlation effects, we obtain

$$\ln \left(\frac{e{\theta }_2}{C_2{V}_2}\right)=2\ln \left(\frac{e{\theta }_1}{C_1{V}_1}\right),$$ [3]

where e is Euler’s number, and $C_i$ and $V_i$ are, respectively, the bulk concentration and the effective condensation volume of ion i. We calculated $V_i$ using (43, 45)

$$V_i=4\pi e{b}^3\left(1+Z_i\right)\left(\xi -\frac{1}{Z_i}\right),$$ [4]

where $Z_i$ is the bare charge of the ions ($Z_1=+1$, $Z_2=+2$), and the Manning parameter, $\xi =\frac{l_B}{b}$. From Eqs. 2 and 3, one can determine both ${\theta }_1$ and ${\theta }_2$. Thus, the effective charge on the phosphate is $Q_{\mathrm{P}}\left(T,C_1,C_2\right)=1-{\theta }_1$, considering only the monovalent ion condensation. We account for the contributions from the divalent cations, ${\theta }_2$, by treating them explicitly in the simulations. The electrostatic interactions involving the P groups are calculated using $Q_{\mathrm{P}}\left(T,C_1,C_2\right)$, as the effective charge on the phosphate.

Mg²⁺–P Effective Potential.

To compute the Mg²⁺–P effective potential, V_Mg-P (r), the PMF between Mg²⁺–P derived from the RISM theory has to be modified because it is dependent on temperature and concentrations of both the monovalent and divalent ions. A number of studies have shown that it is difficult to capture the short-ranged electrostatic interactions, which has prompted others to propose several ways of separating the Coulomb potential into short- and long-ranged components (46–49). The short-ranged interactions are usually determined using molecular simulations. Our approach, which is closest in spirit to a more rigorous treatment by Weeks and coworkers (50, 51), is implemented as follows. The short-ranged part of the V_Mg-P is taken to be identical to the PMF, while the long-ranged part is corrected based on the temperature and salt concentrations. We write the effective potential V_Mg-P (r) as

$$V_{\text{Mg}-\text{P}}\left(r\right)\hspace{0.17em}=\hspace{0.17em}W\left(r\right)\hspace{0.17em}+\hspace{0.17em}\left[U_{\mathrm{D}\mathrm{H}}\left(r\right)\hspace{0.17em}-\hspace{0.17em}W\left(r\right)\right]\hspace{0.17em}\exp \left(-\frac{a^2}{r^2}\right),$$ [5]

where $W\left(r\right)$is the PMF calculated using the RISM theory (details are in SI Appendix), and $U_{\mathrm{D}\mathrm{H}}\left(r\right)$is the DH potential between Mg²⁺–P, accounting for the screening effect of monovalent ions. (We tried other functional forms to combine W and $U_{\mathrm{D}\mathrm{H}}$ and found that Eq. 5 served our purposes in both maintaining the direct-contact interaction and smoothly merging V to $U_{\mathrm{D}\mathrm{H}}$ at $r\gg a$.) The constant, $a=5.0$ Å, was chosen to preserve the Mg²⁺–P direct-interaction energy. Thus, at short distances a Mg²⁺ ion (or more generally, any spherical divalent cation) in proximity to the phosphate group would interact according to the PMF calculated theoretically using RISM. At large values of $r$, the Mg²⁺ ion would experience a screened phosphate charge due to the presence of monovalent ions. An advantage of our approach is that we calculate the fully equilibrated PMF between the Mg²⁺ cation and phosphate using numerical solution of the RISM equations instead of relying on MD simulations (46–49). This is particularly important for divalent ions that have slow ion–water exchange rate and cannot be reliably implemented using conventional all-atom MD simulations (52–57).

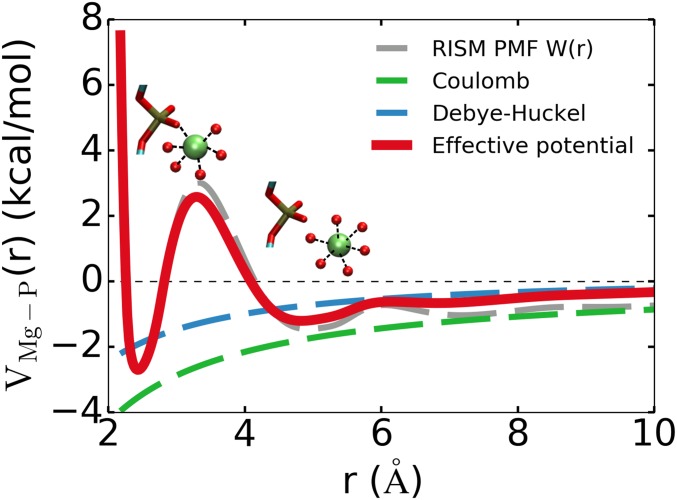
The calculated PMF between Mg²⁺–P is shown in Fig. 1 for a solution containing 1.0 mM magnesium monophosphate. It is worth pointing out that $V_{\text{Mg}-\text{P}}\left(r\right)$(the red curve in Fig. 1) has 2 minima, one corresponding to the inner-sphere Mg²⁺ coordination to P, and the other is the outer-sphere coordination. Accounting for both the direct contact and water-mediated Mg²⁺–P interactions using Eq. 5 is necessary to calculate Mg²⁺-induced RNA folding accurately since the folding of most large RNA molecules requires both tightly bound and screening due to Mg²⁺ ions (5, 7, 10, 21). We used a similar procedure to obtain interactions for calcium V_Ca-P (r).

Fig. 1.

Effective (Eq. 5) Mg²⁺–P potential (red) constructed by combining the short-ranged part of the PMF (gray dashed line) with the long-ranged Debye–Hückel potential (blue dashed line). Calculations of the PMF were performed at 1.0 mM magnesium monophosphate and 25 ^○C using the RISM theory (for details see SI Appendix). The first minimum represents the inner-shell interaction, where Mg²⁺ interacts directly with the phosphate groups. The second minimum at $r\approx 5$ Å represents the outer-shell interaction, where Mg²⁺ retains its first hydration shell.

Results

Determination of the Parameters in the TIS RNA Model.

The 2 adjustable parameters in our RNA force field are $U_{hb}^0$ that determines the strength of hydrogen bonds and $\mathrm{\Delta }{G}_0$ that dictates the balance between stacking and hydrogen bonding (details described in SI Appendix). Following our previous study (2), we determined the values of the 2 parameters by reproducing the experimental heat capacity curves of human telomerase RNA hairpin and a viral pseudoknot. The melting temperatures of the 2 RNA motifs are reproduced well by simulations using the model (largest deviation is <5 ^○C) (SI Appendix, Fig. S2). In the rest of this paper, we use this set of parameters, coupled with our treatment of divalent ion–phosphate interactions, to investigate the effects of a mixture of divalent and monovalent ions on folding of 3 RNA molecules. It is worth emphasizing that the same set of parameters is used for all RNA molecules over a wide range of ion concentrations.

Preferential Interaction Coefficient as a Function of Mg²⁺ Concentration.

We first performed CG simulations to probe the binding of divalent cations to the RNA, expressed in terms of the experimentally measurable ion-preferential interaction coefficient, ${\mathrm{\Gamma }}_X$ (where X is Mg or Ca). In the simulations, a single RNA molecule was placed in a cubic simulation box in the presence of explicitly modeled divalent cations. After equilibration, we calculated ${\mathrm{\Gamma }}_X$ using the Kirkwood–Buff integral (58–63),

$${\mathrm{\Gamma }}_X=C_2\int \left[g_X\left(\mathbf{r}\right)\hspace{0.17em}-\hspace{0.17em}1\right]d\mathbf{r},$$ [6]

where $g_X\left(\mathbf{r}\right)$is the 3D distribution function of the divalent cations, reflecting the excess (or deficit) of X²⁺ relative to the bulk ion concentration, $C_2$, in the presence of the RNA.

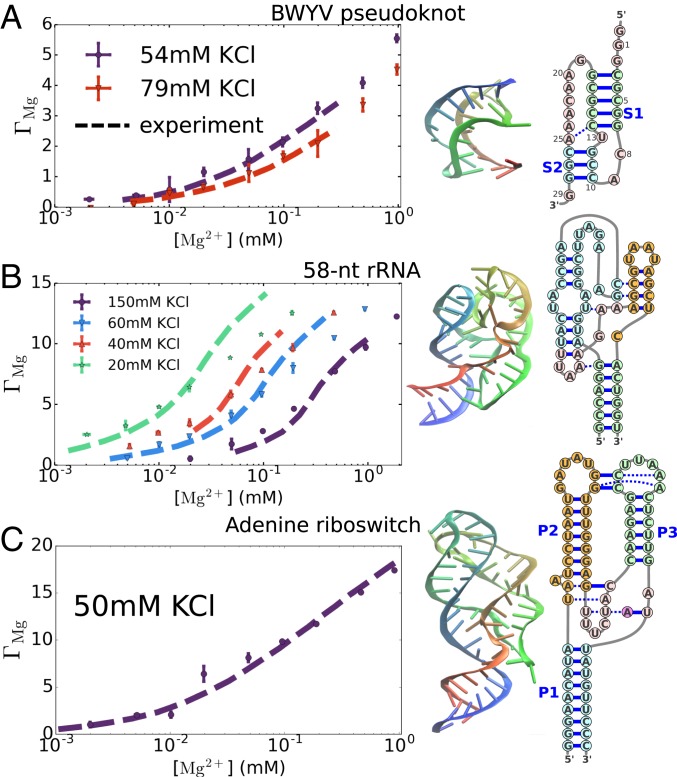
In Fig. 2, we show ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ for beet western yellow virus pseudoknot (BWYV PK), a 58-nt fragment of the ribosomal RNA (rRNA), and the aptamer domain of adenine riboswitch at different concentrations of monovalent and magnesium ions. The BWYV PK folds in the presence of monovalent ions without Mg²⁺. Our simulations show that if the divalent ion concentration is increased, more of them are attracted to the PK, which is in quantitative agreement with experimental data. We also capture a more subtle experimental finding that there is a decrease of ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ if the monovalent ion concentration is increased from 54 mM to 79 mM, thereby effectively enhancing the competition with Mg²⁺ binding.

Fig. 2.

(A–C) Comparison of the calculated and measured values of the preferential interaction coefficient ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ for (A) BWYV pseudoknot (64), (B) the 58-nt fragment of the large subunit ribosomal RNA (65), and (C) the aptamer domain of adenine riboswitch (66) at various monovalent salt concentrations. Experimental data are taken from refs. 67–69. The results of simulations are given by colored symbols with standard errors, and the dashed lines are data from experiments. In most cases, the error bars from the simulations are smaller than the symbol sizes. Only BWYV remains folded at all values of the concentrations of Mg²⁺. The riboswitch and rRNA partially unfold at low Mg²⁺ concentrations. At high Mg²⁺ concentrations (up to ∼1 mM) the RNA molecules are in the folded states, whose structures are shown in A–C, Center. Nucleotides are colored from 5′ to 3′ as red to blue. Secondary structures are shown in A–C, Right, displaying the sequences.

For the rRNA and the riboswitch, the situation is more complicated. Both of them partially unfold at low Mg²⁺ concentrations because tertiary interactions are disrupted. For these 2 RNA molecules, in addition to Mg²⁺ ion concentration, ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ also strongly depends on the state of the RNA. At low Mg²⁺ concentrations, the equilibrium shifts to extended states, which further decreases ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$. Interestingly, our simulations quantitatively reproduce ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ (Fig. 2) over a broad range of monovalent and divalent ion concentrations, for both the rRNA and riboswitch (see below for additional results for rRNA).

Divalent Ion-Dependent Folding Free Energy of BWYV Pseudoknot.

In a typical titration experiment, one often measures ${\mathrm{\Gamma }}_X$ as a function of divalent ion concentrations in the presence of excess monovalent ions ($C_2\ll C_1$) (41, 67, 70–73). If the RNA remains in a single state S (F, folded; I, intermediate; or U, unfolded) during the titration process, the free energy change due to the accumulation of divalent ions around RNA in state S is directly related to ${\mathrm{\Gamma }}_{X,S}$. For concreteness, consider the following equilibrium reaction $RN{A}_S+n{X}^{2+}\rightleftarrows RN{A}_S.n{X}^{2+}$, showing that there is an uptake of n (need not be an integer) divalent cations by the RNA in the S state. Provided $C_2\ll C_1$, the free energy change associated with the equilibrium reaction given above, $\mathrm{\Delta }{G}_{X,S}$, is related to ${\mathrm{\Gamma }}_{X,S}$ as

$$\mathrm{\Delta }{G}_{X,S}=-k_{B}T{\int }_o^{C_2}{\mathrm{\Gamma }}_{X,S}d\ln C.$$ [7]

Note that Eq. 7 would not be valid if the RNA simultaneously populates different states during the titration process. For instance, if the RNA remains folded at high $C_2$ but unfolds at low $C_2$ (as in the rRNA and riboswitch cases), there is no obvious way to relate ${\mathrm{\Gamma }}_X$ and $\mathrm{\Delta }{G}_{X,S}$, because ${\mathrm{\Gamma }}_X$ reflects the binding affinity to 2 (or more) states.

To calculate the free energy change upon folding, it is necessary to calculate $\mathrm{\Delta }{G}_{X,S}$ for each state of the RNA separately, which can be done if the ensemble of RNA conformations is restricted to S. We choose BWYV PK for illustrative purposes because its (un)folding can be used to clearly distinguish between the F, I, and U states. Furthermore, the availability of experimental data allows us to compare directly with our simulations (67, 74).

The folded structure of the BWYV PK (Fig. 2A) has 2 Watson–Crick stems (S1 and S2) that are connected by 2 small loops. The F state is stabilized by tertiary interactions between the 2 loops and the 2 stems. The stem S1 has 5 G-C base pairs, while S2 has only 3 G-C base pairs. Therefore, we anticipate that S2 should unfold first upon increasing the temperature or lowering the salt concentration, as predicted by the stability hypothesis (75). Both experiments (74) and our previous simulations (31) have shown that BWYV does unfold by 3 sequential equilibrium transitions as temperature is increased, thus populating 2 intermediates. In one of them, there is a loss of tertiary interactions but the stems are intact. However, the probability of formation of such a state is small. Thus, for practical purposes, the overall transition to the unfolded state occurs by populating one intermediate, F → I → U.

To calculate the free energies of the folding and unfolding transitions, we first generated an ensemble of unfolded structures. We performed simulations of the I state by disallowing interactions between base pairs in S2, while preserving the full interaction for S1, as shown in previous studies (31, 74). The ensemble of such structures coincides with what we observed in our thermal unfolding simulations (SI Appendix, Fig. S2). We surmise that the simulated ensemble is the one probed in the experiments (67), where all of the nine 3′-terminal nucleotides were mutated to uracil, thus preventing the formation of S2. In the U state, both the stems are unfolded, which can be mimicked by disrupting all of the specific interactions within the PK. This renders the PK essentially a polyelectrolyte dominated by Coulomb repulsions between the phosphate charges and secondary stackings between consecutive bases.

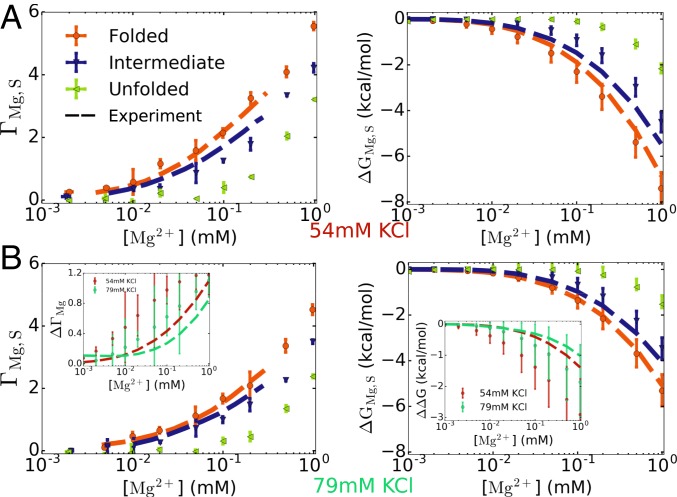
With the simulated ensemble of U and I structures, we calculated ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g},I}$ and ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g},U}$. The results are shown in Fig. 3 at two different KCl concentrations. The uptake of Mg²⁺ in the I and U states is less compared to the F state because they adopt more expanded conformations with spatially separated phosphate groups, thus weakening the electrostatic attraction. The calculations of ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g},S}$ are in quantitative agreement with the experimental data. The difference $\mathrm{\Delta }{\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}={\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g},F}-{\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g},I}$ between the 2 states is the number of Mg²⁺ uptake in the I → F transition, which is shown in Fig. 3B, Insets at 2 monovalent concentrations. We find a slight increase in $\mathrm{\Delta }{\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ as the Mg²⁺ concentration increases, in agreement with the direct measurement of $\mathrm{\Delta }{\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ from the fluorescence dye method (67). This is in accord with other experiments, which have shown that $\mathrm{\Delta }\mathrm{\Gamma }$ for monovalent ions also exhibits a dependence on the salt concentration (44, 76). Our calculations, therefore, do not support the Wyman linkage analysis used to determine $\mathrm{\Delta }{\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$, as this method yields a constant value for $\mathrm{\Delta }{\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ over the Mg²⁺ concentration range (67).

Fig. 3.

(A and B) Ion preferential interaction coefficient ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g},S}$ (Left) and free energy of Mg²⁺–pseudoknot interaction $\mathrm{\Delta }{G}_{\mathrm{M}\mathrm{g},S}$ (Right) for BWYV in 54 mM KCl (A) and 79 mM KCl (B), at $T=$ 25 °C. The calculations were performed for the folded, intermediate, and unfolded states (S = F, I, or U) (see main text and Fig. 4 for definition of the states). Experimental data for the F and I states are plotted as dashed lines (67). The results for the U state serve as a prediction of the simulations. The differences between the F and I states, $\mathrm{\Delta }{\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}={\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g},F}-{\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g},I}$ and $\mathrm{\Delta }\mathrm{\Delta }{G}_{I-F}=\mathrm{\Delta }{G}_{\mathrm{M}\mathrm{g},F}-\mathrm{\Delta }{G}_{\mathrm{M}\mathrm{g},I}$, are plotted in B, Insets. $\mathrm{\Delta }{\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ (Left Inset) represents the number of Mg²⁺ ions released when BWYV transitions from the F to the I state. $\mathrm{\Delta }\mathrm{\Delta }{G}_{I-F}$ (Right Inset) is the change in the free energy of the F state relative to the I state upon addition of Mg²⁺ ions. The error bars in Insets are relatively large. However, it is clear that $\mathrm{\Delta }{\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ and $\mathrm{\Delta }\mathrm{\Delta }{G}_{I-F}$ are not constant in the range of [Mg²⁺] here.

We then calculated the free energy changes for all of the states using Eq. 7, and the results are shown in Fig. 3. Interestingly, Mg²⁺ ions are also localized near the U and I states, albeit to a lesser extent, demonstrating that it is important to characterize Mg²⁺–RNA interactions not only in the F state but also in other relevant states along the folding pathway. For example, at 1 mM Mg²⁺ and 54 mM KCl, $\mathrm{\Delta }{G}_{\mathrm{M}\mathrm{g},U}\sim -2$ kcal/mol, $\mathrm{\Delta }{G}_{\mathrm{M}\mathrm{g},I}\sim -4$ kcal/mol, while $\mathrm{\Delta }{G}_{\mathrm{M}\mathrm{g},F}\sim -7$ kcal/mol. One way to quantify the effect of Mg²⁺ addition on the folding process is to compute $\mathrm{\Delta }\mathrm{\Delta }G$. For instance, for the I → F transition, $\mathrm{\Delta }\mathrm{\Delta }{G}_{I-F}=\mathrm{\Delta }{G}_{\mathrm{M}\mathrm{g},F}-\mathrm{\Delta }{G}_{\mathrm{M}\mathrm{g},I}$. The stabilization of the F state relative to the I state or U state caused by Mg²⁺ addition ($\mathrm{\Delta }\mathrm{\Delta }{G}_{I-F}$ or $\mathrm{\Delta }\mathrm{\Delta }{G}_{U-F}$) is therefore ∼ −3 and −5 kcal/mol, respectively. The relatively small value of the Mg²⁺ dependence on the folding free energy is likely due to the small size of this PK, whose folded state is stable even in the absence of Mg²⁺ (SI Appendix, Figs. S2B and S5).

Free Energy of BWYV Pseudoknot Using Thermodynamic Cycle.

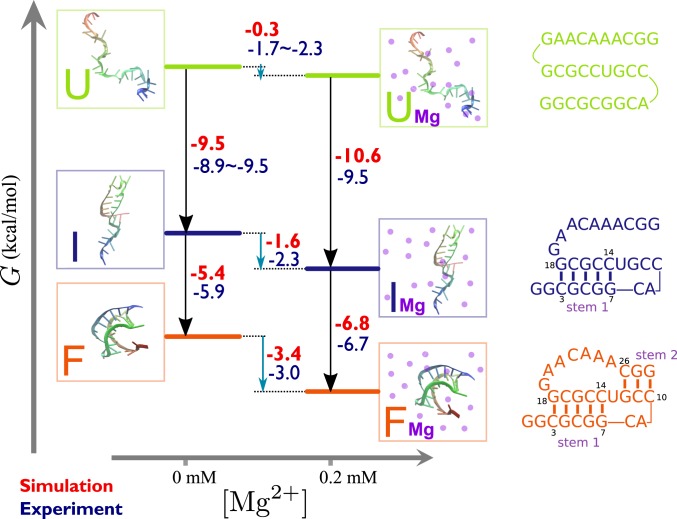
In Fig. 4, we illustrate how the free energy data shown in Fig. 3 in conjunction with the RNA folding free energy data obtained by varying the temperature could be used to construct a folding free energy diagram for BWYV at 0.2 mM Mg²⁺. Similar diagrams at arbitrary concentration of Mg²⁺ can be generated. The vertical free energy differences (Fig. 4) are from WHAM analysis of multiple-temperature simulations with or without Mg²⁺ (see SI Appendix for additional details). The horizontal free energy differences are Mg²⁺–RNA free energies as in Fig. 3. The Mg²⁺-dependent free energy of stabilization is evaluated by 2 ways using the thermodynamic cycle,

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{I-F}=\mathrm{\Delta }{G}_{\text{Mg},F}-\mathrm{\Delta }{G}_{\text{Mg},I}=\mathrm{\Delta }{G}_{I-F,\text{Mg}}-\mathrm{\Delta }{G}_{I-F}$$ [8]

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{U-I}=\mathrm{\Delta }{G}_{\text{Mg},I}-\mathrm{\Delta }{G}_{\text{Mg},U}=\mathrm{\Delta }{G}_{U-I,\text{Mg}}-\mathrm{\Delta }{G}_{U-I},$$

where $\mathrm{\Delta }{G}_{\alpha -\beta ,\mathrm{M}\mathrm{g}}$ and $\mathrm{\Delta }{G}_{\alpha -\beta }$ are, respectively, the free energy difference between the $\alpha$ and $\beta$ states ($\alpha ,\beta$ is F, I, or U) in the presence and absence of Mg²⁺. The calculated free energies are in remarkable agreement with experiments and are consistent with each other ($\mathrm{\Delta }\mathrm{\Delta }G$ values estimated by 2 different methods give similar values, with the errors $\pm 0.4$ kcal/mol). Given that they are independently determined, it shows that our theory can be reliably used to study thermodynamics of Mg²⁺-induced RNA folding.

Fig. 4.

Folding free energy (kcal/mol, 25 °C) diagram of BWYV pseudoknot at 54 mM KCl in the absence (Left) or presence (Right) of 0.2 mM Mg²⁺. Theoretical values are in red and experimental values are in blue. Experimental data for $\mathrm{\Delta }{G}_{\text{U}-\text{I}}$ (no Mg²⁺) and $\mathrm{\Delta }{G}_{\mathrm{M}\mathrm{g},U}$ are not available. For $\mathrm{\Delta }{G}_{\text{U}-\text{I}}$, data for 40 mM and 74 mM KCl are reported with the hope that they should bracket the 54 mM KCl data. $\mathrm{\Delta }{G}_{\mathrm{M}\mathrm{g},U}$ for experiment is then evaluated based on the other free energies in the cycle. Folding free energies (black arrows) are calculated from thermal denaturation simulations. Mg²⁺–RNA free energies (blue arrows) are taken for each state at 0.2 mM Mg²⁺ from Fig. 3.

Mg²⁺-Induced Folding of the 58-nt rRNA.

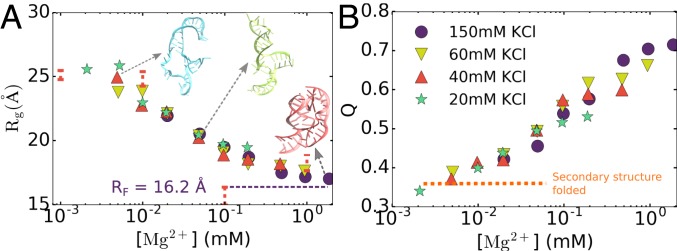
We investigated the folding of the 58-nt rRNA, which, although folds at high (∼1.6 M) monovalent ion concentrations, requires Mg²⁺ (68). We carried out simulations of the 58-nt rRNA as a function of different combinations of monovalent and divalent ion concentrations. Fig. 2B already shows that we can quantitatively account for the dependence of ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ as a function of both monovalent and divalent ion concentrations. To fully characterize the folding of the rRNA fragment, we calculated the radius of gyration, $R_g$, as a function of Mg²⁺ concentration at 4 concentrations of KCl. Fig. 5A shows that $R_g$ values decrease continuously from ∼25 Å at [Mg²⁺] $\sim$2 $\mathrm{\mu }$M to ∼16 Å at high Mg²⁺ concentrations, which is consistent with experimental measurements at 40 mM KCl (shown as red bars in Fig. 5) (68). Interestingly, our calculations show that the concentration of KCl has minimal effect on the dependence of $R_g$ on Mg²⁺, even at low Mg²⁺ concentrations at which the RNA is partially unfolded. This is because at these KCl concentrations, the secondary structure of the rRNA is fully formed (Fig. 5B). Therefore, adjusting the monovalent ion concentration does not considerably assist folding since it requires Mg²⁺ for tertiary structure formation. Fig. 5B shows the average fraction of native contacts for the rRNA, Q, as a function of Mg²⁺ concentrations. In accord with the $R_g$ analysis, the Q values at low [Mg²⁺] are small, fluctuating around ∼0.35. At these Mg²⁺ concentrations, the secondary structure of the rRNA is completely stabilized without forming tertiary interactions. At high [Mg²⁺], Q increases and reaches ∼0.7. Just as found for $R_g$, we also observe a negligible dependence of Q on monovalent ion concentration. Thus, both the order parameters ($R_g$ and Q) show that rRNA formation, which does not depend much on KCl concentrations, is only moderately cooperative.

Fig. 5.

Mg²⁺-induced folding of the 58-nt fragment of ribosomal RNA. (A) Compaction of rRNA as the Mg²⁺ concentration increases. The colors correspond to 4 monovalent ion concentrations (shown in B). $R_F$ is the value of $R_g$ for the F state, calculated from the PDB structure (PDB ID 1HC8). Experimental measurements of $R_g$ in 40 mM KCl are plotted as vertical red error bars (68). Some representative structures from the simulations are also shown. (B) Average fraction of native contacts vs. Mg²⁺ concentration. The horizontal dashed line at around $Q\approx 0.35$ indicates complete secondary structure formation with no tertiary interactions.

Free Energy Changes upon Folding.

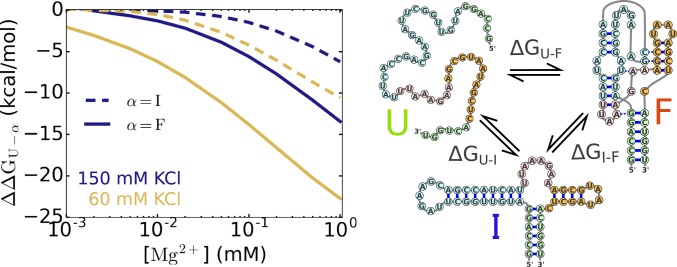
To obtain the folding thermodynamics of rRNA we calculated $\mathrm{\Delta }{G}_{\mathrm{M}\mathrm{g},S}$ for each state of the 58-nt rRNA by assuming that the folding transition occurs sequentially, U → I → F, where the I state is composed only of secondary structure of 3 stems connected by small loops (Fig. 6). It is possible that for such a complex RNA, more than one intermediate state could be populated during the (un)folding process. However, we chose only one intermediate state to separate the effect of divalent cations on secondary and tertiary interaction formation. The transition U → I involves only secondary structure formation, while I → F requires the formation of only tertiary interactions. As before, we performed simulations for each state by constraining the ensemble of RNA structures in such state. We emphasize that these simulations are completely different from the simulations above (from which we calculated ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$, $R_g$, and Q), which were performed using all of the sampled conformations. The constrained simulations were used only to calculate ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g},S}$, Mg²⁺–RNA free energies, $\mathrm{\Delta }{G}_{\mathrm{M}\mathrm{g},S}$, and $\mathrm{\Delta }\mathrm{\Delta }{G}_{\alpha -\beta }$ (where S, $\alpha$, and $\beta$ are F, I, and U).

Fig. 6.

Stabilization free energies, $\mathrm{\Delta }\mathrm{\Delta }G$ (defined in Eq. 8), of the intermediate state (dashed lines) or the folded state (solid lines) relative to the unfolded state upon addition of Mg²⁺ ions for rRNA. $\mathrm{\Delta }\mathrm{\Delta }{G}_{I-F}$ is the difference between these 2 free energies $\mathrm{\Delta }\mathrm{\Delta }{G}_{I-F}=\mathrm{\Delta }\mathrm{\Delta }{G}_{U-F}-\mathrm{\Delta }\mathrm{\Delta }{G}_{U-I}$. In the I state, secondary structures are formed. Therefore, $\mathrm{\Delta }\mathrm{\Delta }{G}_{U-I}$ and $\mathrm{\Delta }\mathrm{\Delta }{G}_{I-F}$ are, respectively, the stabilization free energies of Mg²⁺ on secondary and tertiary structure formation.

In Fig. 6, we show the results for the stabilization free energies of the folding transitions upon addition of Mg²⁺ ions, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\alpha -\beta }$, calculated using Eq. 8. Data for ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g},S}$ and $\mathrm{\Delta }{G}_{\mathrm{M}\mathrm{g},S}$, which were used to compute $\mathrm{\Delta }\mathrm{\Delta }{G}_{\alpha -\beta }$, can be found in SI Appendix, Fig. S7. $\mathrm{\Delta }\mathrm{\Delta }{G}_{\alpha -\beta }$ shows the change of the relative stability of the 2 states $\alpha$ and $\beta$ upon addition of Mg²⁺ on the $\alpha \leftrightarrow \beta$ transition. We explicitly show only $\mathrm{\Delta }\mathrm{\Delta }{G}_{U-I}$ and $\mathrm{\Delta }\mathrm{\Delta }{G}_{U-F}$ curves, but $\mathrm{\Delta }\mathrm{\Delta }{G}_{I-F}$ can be calculated as the difference between these 2 curves, as $\mathrm{\Delta }\mathrm{\Delta }{G}_{I-F}=\mathrm{\Delta }\mathrm{\Delta }{G}_{U-F}-\mathrm{\Delta }\mathrm{\Delta }{G}_{U-I}$. It is obvious that the higher the [Mg²⁺] is, larger is the effect of Mg²⁺ ions on all 3 transitions since all $\mathrm{\Delta }\mathrm{\Delta }G$ values decrease (increase in magnitude) as [Mg²⁺] rises. Therefore, higher [Mg²⁺] induces a shift in the equilibrium toward more compact states (U → I → F). The magnitude of $\mathrm{\Delta }\mathrm{\Delta }G$ for rRNA is quite large compared to BWYV, indicating the dramatic dependence of the rRNA folding on Mg²⁺. For rRNA in 60 mM KCl, adding 0.1 mM Mg²⁺ leads to $\mathrm{\Delta }\mathrm{\Delta }{G}_{I-F}\approx -8$ kcal/mol and $\mathrm{\Delta }\mathrm{\Delta }{G}_{U-F}\approx -13$ kcal/mol. In comparison, for BWYV at 54 mM KCl, those values are $\mathrm{\Delta }\mathrm{\Delta }{G}_{I-F}\approx -1.4$ kcal/mol and $\mathrm{\Delta }\mathrm{\Delta }{G}_{U-F}\approx -2.2$ kcal/mol, respectively. On the other hand, if one instead increases the concentration of monovalent ions, the values of $\mathrm{\Delta }\mathrm{\Delta }G$ become smaller (Fig. 6), which also happens in the BWYV PK (shown in Fig. 3B, Insets). At 150 mM KCl, adding 0.1 mM Mg²⁺ into the solution of rRNA leads only to $\mathrm{\Delta }\mathrm{\Delta }{G}_{I-F}\approx -4$ kcal/mol and $\mathrm{\Delta }\mathrm{\Delta }{G}_{U-F}\approx -6$ kcal/mol, respectively.

Comparison between Mg²⁺ and Ca²⁺ Ions.

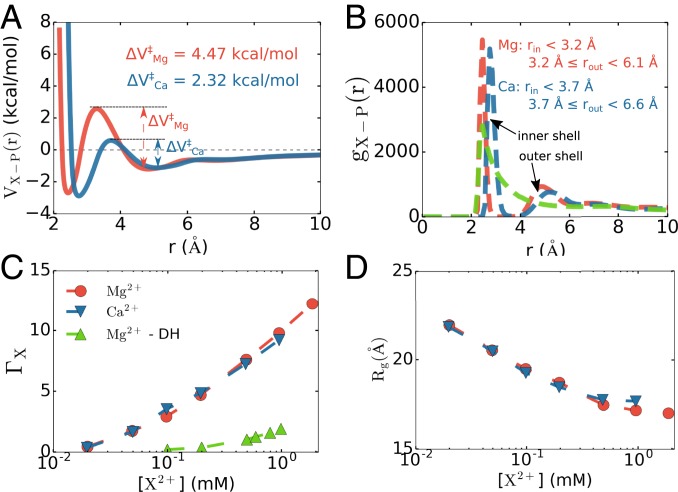
We also studied the effect of the cation size (Mg²⁺ vs. Ca²⁺) on RNA folding. We computed the Ca²⁺–P effective potential, $V_{\text{Ca}-\text{P}}\left(r\right)$, using the same procedure used to obtain V_Mg-P (r). Fig. 7A compares the effective potentials of the 2 ions. A major difference between $V_{\text{Ca}-\text{P}}\left(r\right)$and $V_{\text{Mg}-\text{P}}\left(r\right)$is that the barrier separating the inner-shell and outer-shell binding in Ca²⁺ is much lower than in Mg²⁺. This difference arises because the charge density of Mg²⁺ is much higher than that of Ca²⁺, which results in orders of magnitude difference in the water exchange kinetics between Mg²⁺ and Ca²⁺ (77). It is also in accord with the observation that the interaction of Mg²⁺ with water in the first hydration shell is stronger than in Ca²⁺ (SI Appendix, Fig. S10).

Fig. 7.

Comparison between Mg²⁺ and Ca²⁺ binding to phosphate groups and RNA. (A) Effective potentials for Mg²⁺ and Ca²⁺ with the phosphate group show that the transition barrier between inner-shell–outer-shell coordination for Ca²⁺ is considerably lower than for Mg²⁺. However, the depths of the inner- and outer-shell minima are comparable. (B) Radial distribution function between the ions and phosphate groups in BWYV. Also shown are the results for Mg²⁺ ions in which Mg²⁺–phosphate interactions are modeled using the Debye–Hückel potential (green). (C and D) Preferential interaction coefficient ${\mathrm{\Gamma }}_X$ (C) and radius of gyration $R_g$ (D) computed for 58-nt rRNA. Only data for 150 mM KCl are presented here; data for other KCl concentrations can be found in SI Appendix, Fig. S6. The rRNA reaches its native states at high divalent ion concentrations using our model, but does not easily fold at any Mg²⁺ concentration should the Debye–Hückel potential be used.

Fig. 7B shows the radial distribution function, _gX-P (r), between the divalent ions and phosphate groups in BWYV PK. It is obvious that our model accounts for both types of binding. The presence of inner- and outer-shell binding of Mg²⁺ to P is indicated by 2 visible peaks in _gMg-P (r). The first peak is located at r ∼ 2.4 Å and the second one is at r ∼ 4.8 Å. The slow decay of _gMg-P (r) toward 1 is due to the presence of other phosphates in the RNA. The peaks for Ca²⁺ are very similar and are shifted slightly upward toward longer distance (2.7 Å and 5.1 Å), indicating that Ca²⁺ has a comparable affinity for the phosphate groups.

We also investigated the folding of the rRNA in the presence of Ca²⁺ ions. Due to the similar affinity of the 2 ions toward phosphate groups, there is little difference in the folding behavior of rRNA between Ca²⁺ and Mg²⁺ in terms of ion accumulation, fraction of native contacts, and global size (Fig. 7 C and D). It is possible that the difference between the 2 ions is apparent only in the case of more complex RNAs, such as group I intron ribozyme (10), where the folded state is highly compact and there is not sufficient room in the core of the RNA to accommodate larger ions, and therefore replacing Mg²⁺ by Ca²⁺ in these cases would destabilize the folded state. Nonetheless, we find an interesting difference in the nature of binding of the 2 ions: Ca²⁺ dehydrates readily due to its lower charge density and binds the phosphate groups directly in the inner shell, while Mg²⁺ coordination, with a higher charge density, is roughly similar between the inner and outer shells. A more detailed study will be reported in a subsequent publication.

In addition, we also show in Fig. 7 data for Mg²⁺ assuming that the Mg²⁺–P interaction is given by the DH potential (green curves). In the $g_{\text{Mg}-\text{P}}\left(r\right)$plot (Fig. 7B), the DH potential completely misses the second peak and the first peak is also much lower compared to our model. This leads to lower affinity with the phosphate groups, resulting in fewer ions accumulated around the RNA. When applying the DH potential to rRNA folding, we find that the RNA does not fold, but rather adopts much more extended conformations, which is directly related to the small uptake of ions, at all Mg²⁺ concentrations (Fig. 7 C and D). Our model thus reveals the importance of treating Mg²⁺–P interaction accurately to faithfully capture both structural and thermodynamic features of Mg²⁺-assisted RNA folding.

Importance of Outer-Sphere Mg²⁺-P Coordination.

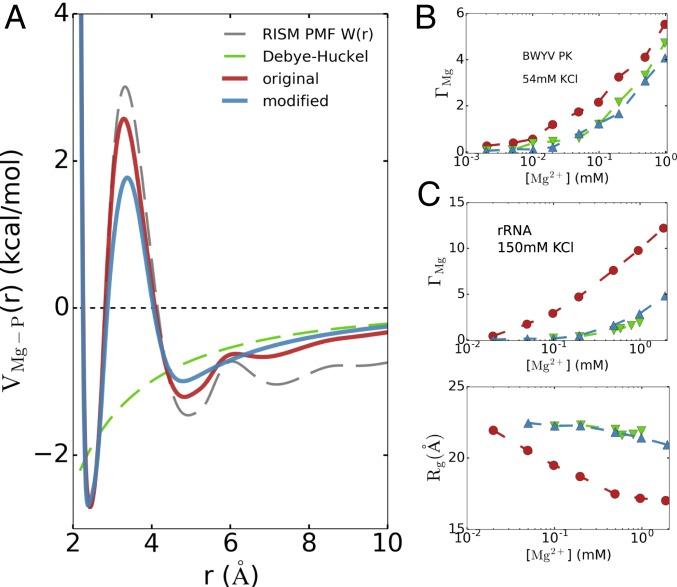
One of the key predictions of this work is that accurate predictions of RNA folding thermodynamics require a consistent description of both the inner- and outer-sphere coordination of divalent cations to phosphate groups. To assess the importance of the outer-sphere coordination, we created a potential that retains the inner-shell interaction between Mg²⁺–P, while smoothly joining the outer-shell interaction with the DH potential (Fig. 8A). In so doing all of the outer-shell interactions between Mg²⁺–P are eliminated. The barrier between inner sphere and outer sphere in the modified potential is lower than in the original potential. We believe that the smaller barrier would only alter the kinetics of water and ion exchange around Mg²⁺ and should not affect the folding thermodynamics quantities. The outer-sphere coordination interaction is only weakened ∼0.2 kcal/mol in the modified potential.

Fig. 8.

Importance of treating both inner- and outer-sphere coordination. (A) Modified effective potential for Mg²⁺ with softened outer-sphere coordination interaction, while keeping the inner-sphere coordination interaction intact. (B and C) Comparison of (B) preferential interaction coefficient ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ for BWYV PK at 54 mM KCl and (C) ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ and $R_{\mathrm{\text{g}}}$ for 58-nt rRNA at 150 mM KCl using the modified potential. Despite a tiny difference in the outer-sphere coordination ($\sim$0.2 kcal/mol), the values of ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ decrease significantly from those of the original model. In rRNA, the modified potential even cannot fold the rRNA at relevant Mg²⁺ concentrations, as can be seen in the high values of $R_{\mathrm{\text{g}}}$.

The simulations using the modified potential reveal a large impact on Mg²⁺–RNA interactions and RNA folding. The substantial changes are illustrated in Fig. 8B, comparing the values of ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$ for BWYV in 54 mM KCl. A seemingly small softening of the outer-sphere coordination interaction leads to a significant decrease in ${\mathrm{\Gamma }}_{\mathrm{M}\mathrm{g}}$. This shows, rather vividly, that the Mg²⁺–RNA interaction, and therefore the Mg²⁺–RNA free energy, is extremely sensitive to the Mg²⁺–P interaction. In rRNA, the situation is even more pronounced (Fig. 8C). Because the folding of the rRNA depends dramatically on Mg²⁺, weakening the outer-sphere coordination interaction modestly prevents the folding of rRNA even at high [Mg²⁺] due to an insufficient number of condensed Mg²⁺. Interestingly, the use of the modified potential results in insignificant compaction of rRNA even at the highest Mg²⁺ concentration (Fig. 8C, Lower). Surprisingly, there is negligible difference in the predictions for $R_g$ between the predictions using the DH potential and the modified potential. The results in Fig. 8 B and C show that accurate predictions for RNA folding thermodynamics require accounting for both inner- and outer-sphere coordination of Mg²⁺ with phosphates.

Discussion

In this study, we have introduced a method to capture the impact of a solution containing a mixture of monovalent and divalent cations on RNA folding. In our model, based in part on liquid-state theory, divalent cations are treated explicitly while the screening effect of monovalent salt is treated implicitly. We reasoned that since the DH theory works well at long range (in fact, the DH theory gives asymptotically correct results at long distances), we could improve the divalent cation interactions by using theory to describe the short-ranged interactions. To obtain the short-ranged interactions, we used RISM theory to compute the PMF between the divalent cation–phosphate group and combined it with the long-ranged part of the DH potential to obtain the effective potential $V_{\text{X}-\text{P}}\left(r\right)$. Applications to 3 RNA molecules, with different sequences and structures, illustrate that our theory quantitatively reproduces the Mg²⁺ preferential interaction coefficients and Mg²⁺–RNA free energies for different combinations of ion concentrations. The transition free energies, as the RNA traverses along the folding pathway, are also in remarkable agreement with experimental data. The simulations not only reproduce the thermodynamics of divalent cation binding to RNA but also recapitulate the correlation between divalent cation concentration and RNA folding. In addition, we presented the effects of divalent cations on secondary and tertiary structure formations for an RNA construct and its dependence on monovalent concentrations.

The difference in the divalent cation–RNA interactions between our model and the DH theory occurs only in the short-ranged part, $r_{\mathrm{X}-\mathrm{P}}\le 10$ Å (little difference exists from $r\sim 6-10$ Å in Fig. 1). Nonetheless, such a difference proves to be very crucial in obtaining the correct divalent cation binding free energies, as it translates to at least ∼2.0 kcal/mol deviation of $\mathrm{\Delta }{G}_{\mathrm{M}\mathrm{g},F}$ for BWYV (SI Appendix, Fig. S9). We also show that to obtain the correct divalent ion–RNA binding free energies, it is important to take into account both inner- and outer-shell interaction accurately. A deviation of only 0.2 kcal/mol in the divalent cation–P potential could lead to a substantial decrease in the number of bound ions. In complex RNAs whose folding depends on divalent ions, loss of bound ions could even cause the RNAs to be thermodynamically unstable even at elevated ion concentrations. It is also worth stating that since our model treats monovalent ions implicitly, it has a large advantage over fully explicit ion models in terms of simulation performance and could be used to study much larger RNA molecules including RNA–protein interactions. Indeed, our theory is sufficiently general that it can be applied to calculate ion (with arbitrary valence and size) effects on DNA as well as synthetic polyelectrolytes and polyampholytes.

Although no other existing computational model can be used to calculate ion-dependent folding thermodynamic properties of RNA of arbitrary size and sequence accurately, as we have done here, our theory is not without limitations. For example, we considered only the divalent ion–phosphate interaction and neglected interactions with the bases, which might be important as the size of RNA molecules increases. It is suspected that the Mg²⁺ ion interacts with electronegative atoms in the base moiety (both inner shell and outer shell) (21, 22). However, it is unknown whether such interactions are relevant for RNA folding thermodynamics. In addition, our RNA force field includes nonnative interactions only in a limited manner. Nevertheless, the remarkable agreement between the theoretical predictions and experiments opens entirely different ways to quantitatively probe ion-induced folding of RNAs regardless of their sizes and sequences.

Conclusions

We have proposed a theory of divalent ion–phosphate interactions, based on concepts in liquid-state physics, for use in coarse-grained simulations of RNA folding in the presence of explicit divalent cations while the screening effect of monovalent salt is treated implicitly. Because our model accounts for both the inner- and outer-sphere coordination of divalent cations with the RNAs using RISM, the theory quantitatively reproduces divalent cation-dependent free energies for folding transitions and the correlation between the divalent cation binding and RNA folding. The success of our general method, which integrates liquid-state theories and a coarse-grained TIS model for RNA, is widely applicable to a variety of problems in RNA biology in which divalent cations play an important role. Finally, the theory could also be used to treat the effects of spherical and nonspherical ions on the conformations of RNA as well as DNA.

Materials and Methods

Full details of RISM theory, the calculation of divalent cation–phosphate potential, the RNA coarse-grained force field, and simulation details are provided in SI Appendix.