Quantifying Dynamics in Phase-Separated Condensates Using Fluorescence Recovery after Photobleaching

Abstract

Cells contain numerous membraneless organelles that assemble by intracellular liquid-liquid phase separation. The viscous properties and associated biomolecular mobility within these condensed phase droplets, or condensates, are increasingly recognized as important for cellular function and also dysfunction, for example, in protein aggregation pathologies. Fluorescence recovery after photobleaching (FRAP) is widely used to assess condensate fluidity and to estimate protein diffusion coefficients. However, the models and assumptions utilized in FRAP analysis of protein condensates are often not carefully considered. Here, we combine FRAP experiments on both in vitro reconstituted droplets and intracellular condensates with systematic examination of different models that can be used to fit the data and evaluate the impact of model choice on measured values. A key finding is that model boundary conditions can give rise to widely divergent measured values. This has important implications, for example, in experiments that bleach subregions versus the entire condensate, two commonly employed experimental approaches. We suggest guidelines for determining the appropriate modeling framework and highlight emerging questions about the molecular dynamics at the droplet interface. The ability to accurately determine biomolecular mobility both in the condensate interior and at the interface is important for obtaining quantitative insights into condensate function, a key area for future research.

Significance

Phase transitions play a key role in the formation of dynamic, often liquid-like condensates within living cells. The mobility of biomolecules within these condensates is increasingly recognized as being important for cellular function and dysfunction and is widely determined using fluorescence recovery after photobleaching (FRAP). However, the assumptions behind the models commonly used to fit FRAP data are often not carefully considered. This work reveals that model choice and boundary effects in experiments have a strong impact on measured values. The results presented here also have implications for interpreting commonly used techniques in FRAP of condensates: bleaching subregions versus the entire condensate. Finally, this work reveals emerging questions about the molecular mobility at the droplet interface.

Introduction

The interior of cells is highly structured into numerous organelles, which help to localize biomolecules and organize thousands of reactions for proper function. Many of these organelles, including the nucleus and endoplasmic reticulum, are membrane-bound structures that partition molecules via a selectively permeable membrane. However, most organelles are not actually enclosed by membranes but still form compositionally well-defined compartments (1, 2). In many cases, these organelles are enriched in RNA and protein and are therefore referred to as ribonucleoprotein bodies or, increasingly, as condensates. These include structures in the nucleus, such as nucleoli and Cajal bodies, and in the cytoplasm, such as stress granules and P granules.

In some cases, condensates such as the nucleolus are highly dynamic, with components freely exchanging within and with the surrounding nucleoplasm. This exchange was demonstrated using fluorescence recovery after photobleaching (FRAP) of GFP-fibrillarin, a nucleolar protein (3). In a typical FRAP experiment, a defined region of the sample is bleached irreversibly (Fig. 1 A), and the recovery of the fluorescent signal in the bleached area results from the exchange of bleached and nonbleached protein. The kinetics of recovery give an indication of the protein mobility, with faster recovery suggesting a higher effective diffusion coefficient (Fig. 1 B). Dynamic exchange of nucleolar proteins is likely important for allowing condensates to function as microreactors, for which increased concentration and mobility of biomolecules are expected to enhance reaction rates. Conversely, some condensates, such as Balbiani bodies, may function to slow down reactions, whereby molecular interactions are reduced or even inhibited by sequestration into the body (4). For example, FRAP experiments of an abundant Balbiani body component, Xvelo-GFP, show incomplete exchange with the cytoplasm, with an apparent plateau in fluorescence recovery of roughly 20% after 1 h (4). Furthermore, condensates are increasingly recognized as being linked to protein aggregation pathologies, in which molecular dynamics may be dramatically slowed (5).

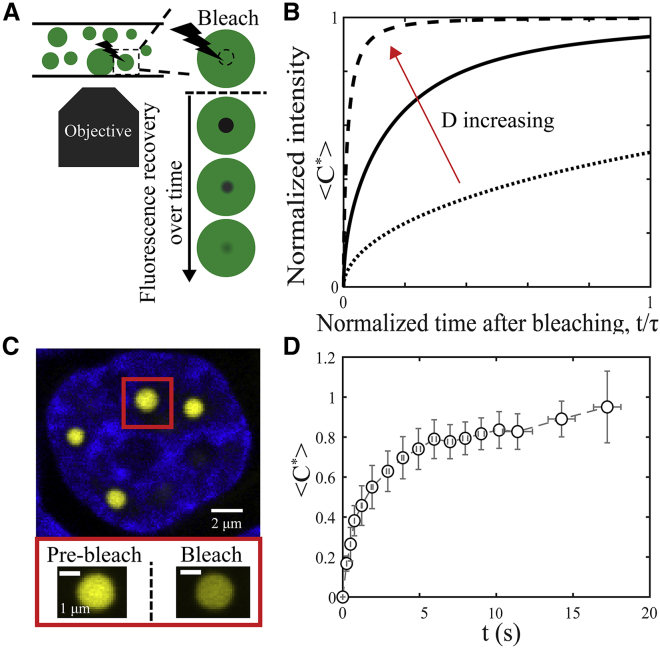
Figure 1.

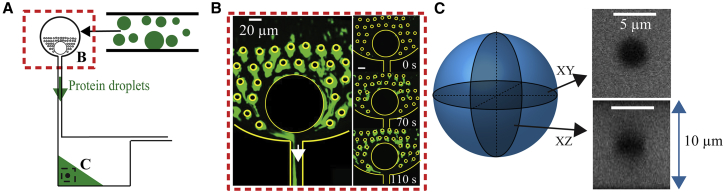
(A) Schematic of a FRAP experiment performed within spherical drops (green). (B) Predicted FRAP recovery curves show that a larger diffusion coefficient, D (i.e., from dotted to solid to dashed lines), leads to a higher average normalized intensity inside the bleach spot, <C^∗>, at a given time after bleaching. The curves are calculated using a 3D infinite model, described in the results section. (C) Image of Ddx4-YFP droplets in the nucleus of a Hek293 cell, double-stranded DNA labeled with Hoechst 33342, are shown. (Bottom panel) Zoomed-in image of a Ddx4-YFP droplet before and immediately after bleaching is shown. (D) Fluorescence recovery curve of Ddx4-YFP droplets 2.2 ± 0.2 μm in diameter is shown. Typical error bars represent SD of measurements on eight cells. To see this figure in color, go online.

Despite their biological importance, a biophysical mechanism underlying the assembly and rapid biomolecular dynamics of condensates has only recently begun to emerge. Key insights into condensate assembly stem from experiments on Caenorhabditis elegans embryos, where germline P granules are implicated in specifying the fate of germ cells. Under shear flow, P granules were observed to flow, drip, and fuse into spherical shapes upon contact, which are examples of classic liquid-like phenomena (6). P granules also dissolve throughout the entire embryo and condense only in the posterior above a saturating component concentration, defined by gradients in polarity proteins (6, 7). These features were hypothesized to arise via liquid-liquid phase separation, a mechanism by which P-granule segregation is now understood in significant molecular detail (8, 9, 10). A wide array of other membraneless condensates, including nucleoli (11, 12), stress granules (13), postsynaptic density (14), signaling clusters (15), and many others, were subsequently shown to exhibit similar liquid-like properties and concentration-dependent formation and are also thought to assemble via liquid-liquid phase separation (1, 16). Thus, phase transitions appear to play a universal role in assembling condensates and organizing the cell into coherent bodies, which nevertheless exhibit rapid biomolecular exchange.

Many condensates are highly enriched with proteins that are unstructured or have unstructured regions and exhibit conformational heterogeneity (17, 18). These intrinsically disordered regions (IDRs) and proteins, which are closely related to so-called low complexity sequences and prion-like domains, are strongly implicated in promoting ribonucleoprotein assembly. For example, the IDR of Ddx4, a key RNA helicase in nuage bodies, forms droplets in the nuclei of HeLa cells when fused to YFP and expressed at high concentrations (19). Furthermore, a closely related P-granule RNA helicase, LAF-1, forms droplets in vitro in an IDR-dependent manner (10) and is implicated in P-granule assembly along with other disordered proteins (20). Similarly, the nucleolar protein, fibrillarin, also forms in vitro droplets dependent on protein concentration and the presence of an IDR (21). Recently, an abundance of IDRs has been demonstrated to form droplets in vitro, including stress granule proteins hnRNPA1 (13, 22), FUS (22, 23, 24), and TDP-43 (25) and the Q-rich fungal protein Whi3 (26). Together with oligomerizing self-interaction domains and other forms of valency amplification (unpublished data), IDRs are a central driving force for phase separation.

In addition to protein concentration, the presence of salt and RNA are two additional parameters strongly affecting the formation and resulting properties of droplets (10, 21, 24, 26, 27, 28). For example, LAF-1 droplets at a lower salt concentration are more viscous because of an increase in both the droplet protein concentration and protein-protein interactions (27). The time after phase separation also appears to play a role in droplet properties, with proteins such as FUS, hnRNPA1, Whi3, and fibrillarin initially forming liquid-like droplets that transition to more solid-like behavior over the course of several hours (13, 21, 23, 26, 28, 29). Changes in bulk viscosity may also impact the mesh size inside droplets (i.e., the average distance between polymer chains), which would have consequences for the diffusion and partitioning of proteins that are this size scale (27). Importantly, because protein diffusion coefficients are expected to impact reaction rates, these microstructural characteristics could have important implications for condensate function. For example, higher diffusion coefficients may be advantageous for transcribing ribosomal RNA in the nucleolus, whereas low diffusion coefficients associated with solid-like assemblies such as the Balbiani body may facilitate quiescence during biomolecular storage (4). Quantitatively measuring protein diffusion coefficients would enable direct comparison of condensates and in vitro proteins, potentially facilitating new insights into condensate function.

Although many studies use FRAP to assess whether the dynamics within condensates are more qualitatively fluid or solid-like, few use these measurements to extract precise quantitative information. Because of the liquid-like properties of many condensates, full recovery of the fluorescence signal after photobleaching primary components is often observed (30), allowing for extraction of diffusion coefficients by fitting the data to a diffusion model. Even within intracellular condensates with a solid-like scaffold, components that are not part of the solid scaffold may still be highly mobile and exhibit significant and quantifiable FRAP recovery; care must clearly be taken in interpreting rapid molecular dynamics as reflective of an underlying liquid state (31). The large number of components in cells complicates analysis because the network of potential binding partners is expected to impact fluorescence recovery (32). Thus, many studies make use of bottom-up approaches, using purified proteins and fitted fluorescence recovery data to estimate diffusion coefficients.

Despite a multitude of FRAP models that currently exist (32, 33, 34, 35, 36, 37, 38, 39, 40), only two are typically used in the literature to interpret FRAP data for biomolecular condensates: a simple exponential model or a two-dimensional (2D) infinite model (Table 1). Often, the simple exponential is used to make qualitative comparisons between proteins or experimental conditions by comparing τ, the (e.g., exponential) timescale for recovery; t_1/2, the time at which half of the fluorescence recovers; or D, the diffusion coefficient. Importantly, fitting the same data set with both models can result in a different estimated D; diffusion coefficients are seen to vary by a factor of roughly five when applied to LAF-1 protein droplets at 80 mM NaCl (Fig. 2). This finding raises questions about what assumptions give rise to these models and whether they are met in experiments. For example, when is quasi-2D, radial diffusion expected, or do quasi-three-dimensional (3D) or one-dimensional (1D) models better describe the physics? Additionally, when can droplets be considered large enough to use an infinite model, and what model best describes bleaching an entire droplet? Interpretation of results from such model fitting should thus be done with care, not only for accurate diffusion coefficient measurements but also for comparison to reported measurements.

Table 1.

Summary of Primary Models Used in the Literature to Fit FRAP Data Inside Phase-Separated Protein Condensates

Model Used	Protein Marker	Calculate	References
Simple exponential	NPM-1 in vitro and in vivo	τ	Feric et al. (21)
	hnRNPA1 in vitro		Molliex et al. (13)
	FUS in vitro		Banerjee et al. (58)
	SH34 in vitro		Li et al. (59)
Simple exponential	LAF-1 in vitro	D	Elbaum-Garfinkle et al. (10)
	Whi3 in vitro		Zhang et al. (26)
	PGL-1 in vivo C. elegans		Brangwynne et al. (6)
	SIM and polySUMO in vitro		Banani et al. (60)
Simple exponential	PUB, Lsm, Tia1, FUS in vitro	t1/2	Lin et al. (28)
	FUS in vitro		Patel et al. (23)
	G3BP in vivo cell culture		Jain et al. (61)
	LSM4 in vivo cell culture		Kroschwald et al. (62)
	CPEB4 in vivo cell culture		Guillen-Boixet et al. (63)
2D infinite	TDP-43 in vivo rodent neurons	D	Gopal et al. (64)
	RNA (pA15, pN15, pU15) in vitro		Aumiller et al. (65)
	IBB in vivo cell culture		Schmidt and Rohatgi (66)
	FUS LC in vitro		Burke et al. (24)
	CAR-1 in vivo oocytes		Hubstenberger et al. (67)
	FUS in vitro		Kaur et al. (68)

The third column denotes whether τ, D, or half time to recovery, t_1/2, was calculated by fitting data to either model.

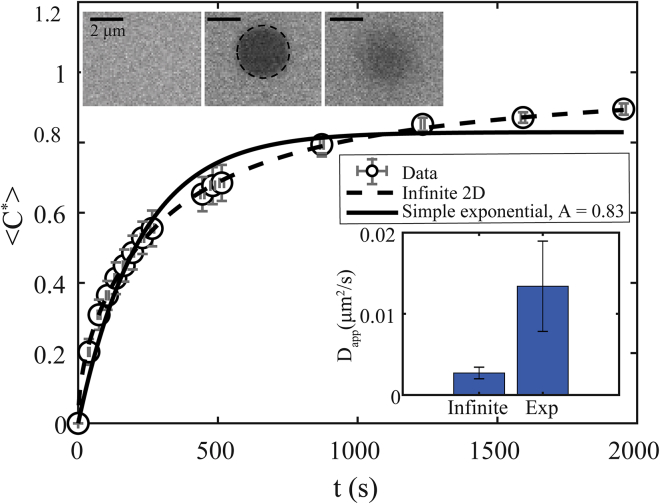
Figure 2.

FRAP data for LAF-1 at 80 mM NaCl (open black circles) fitted using a simple exponential model (solid black line) and 2D infinite model (dashed black line); see Table 2 and Table S2. (Upper inset) Representative large droplet phases in which ≈ 5% of LAF-1 is labeled with Dylight 488 are shown: prebleach (left), postbleach (center), and t = 104 ± 5 s (right). (Lower inset) Fitting to a simple exponential model results in a factor-of-five-higher apparent D compared to a 2D infinite model (i.e., 13.4 ± 5.6 × 10⁻³, R² = 0.97 vs. 2.7 ± 0.7 × 10⁻³μm²/s, R² = 0.99). Typical error bars are shown and represent SD of eight replicates. To see this figure in color, go online.

Here, we address these issues by highlighting physical assumptions that give rise to these two widely used models and evaluate differences in predicted fluorescence profiles and dynamics of average fluorescent recovery. Furthermore, we utilize a previously published microfluidic device (41) to create effectively infinite in vitro droplet phases and evaluate whether experimentally measured conditions resemble model assumptions. We address how changes in experimental conditions, such as the bleach spot size and the ratio of bleach spot to drop size, can influence the apparent measured diffusion coefficient and demonstrate how to overcome this by choosing an appropriate model. Finally, we develop a model to describe FRAP of entire in vitro and in vivo droplets and compare measured diffusion coefficients. These experiments reveal the possible presence of interfacial resistance to mass transfer for in vitro droplets, which may have important biological implications.

Materials and Methods

Protein purification and preparation

Full-length LAF-1 was tagged with 6×-His and expressed in Escherichia coli BL21 (DE3) using standard procedures. LAF-1 purification was performed following Elbaum-Garfinkle et al. (10). Briefly, LAF-1 was purified on Ni-NTA agarose resin (Qiagen, Hilden, Germany) followed by a HiTrap Heparin column (General Electric Healthcare, Uppsala, Sweden) and stored in Heparin elution buffer. Glycerol was added to 10% (vol/vol) before flash freezing in liquid nitrogen and storing at −80°C. For FRAP experiments, individual LAF-1 frozen aliquots were handled as described previously (10, 27). Briefly, to prepare unlabeled LAF-1, aliquots were thawed at room temperature, centrifuged at 14,000 × g for 2 min, and buffer exchanged (Merck Millipore, Tullagreen, Carrigtohill, Cork, Ireland; 0.5 mL volume, 10 KDa molecular weight cutoff) into high salt buffer (20 mM Tris (pH 7.4), 1M NaCl, and 1 mM DTT) to inhibit droplet formation. Separately, Dylight488 N-hydroxysuccinimide ester (Thermo Fisher Scientific, Rockford, IL) was conjugated to LAF-1 according to manufacturer protocols, and fluorophore-labeled LAF-1 was buffer exchanged into high salt buffer. Then, protein solutions containing ≈ 5% fluorophore-labeled LAF-1 were mixed with no salt buffer (20 mM Tris (pH 7.4) and 1 mM DTT) to achieve a final salt concentration of 80 mM NaCl.

Mammalian cell culture

Human embryonic kidney (Hek)293 cells were cultured in growth media containing high glucose Dulbecco’s modified Eagle’s medium (Gibco, Thermo Fisher Scientific, Rockford, IL), 10% fetal bovine serum (Atlanta Biologicals, Flowery Branch, GA), and 10 U/mL penicillin-streptomycin (Gibco, Thermo Fisher Scientific) and incubated at 37°C and 5% CO₂ in a humidified incubator. Cells were grown on 35 mm glass-bottomed MatTek dishes (MatTek, Ashland, MA) coated with 0.25 mg/mL Fibronectin (Sigma-Aldrich, Saint Louis, MO) to ∼70% confluency before being transfected with plasmid DNA using Lipofectamine 3000 (Invitrogen, Thermo Fisher Scientific, Rockford, IL) using manufacturer protocols. Briefly, a transfection mixture of 250 μL containing 2.5 μg of plasmid DNA was added to a single 35 mm dish and removed 24 h post-transfection. Transfected cells were imaged 24–48 h post-transfection. The plasmid DNA used was Ddx4-YFP, where the DEAD-box domain in Ddx4 was previously replaced with YFP (kind gift from Timothy Nott lab, University of Oxford). In Fig. 1, cells were fixed with 3.7% formaldehyde aqueous solution (Sigma-Aldrich) and permeabilized with 0.5% Triton X-100 (Promega, Madison, WI), and double-stranded DNA was labeled with Hoechst 33342 (Invitrogen, Thermo Fisher Scientific).

Device design and microfabrication

As described previously in Taylor et al. (41), the microfluidic device was designed using AutoCAD and fabricated using standard photolithography and soft lithography techniques. The device had a square geometry (Fig. 6 A) and was 10 μm high.

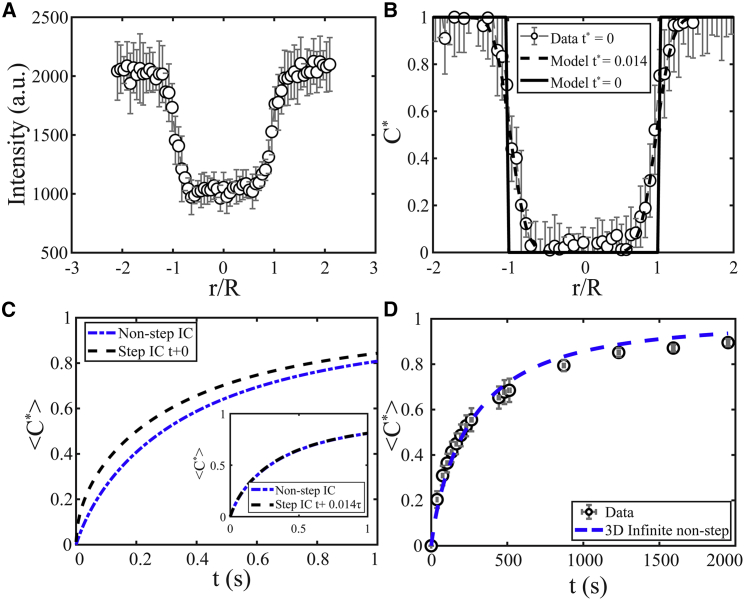
Figure 6.

(A) Measured concentration profile profiles for bleach spots within in vitro LAF-1 droplets in the xy plane immediately after bleaching, using an ROI = 3 μm. (B) Fitting the 3D infinite model (black dashed line) to the measured initial normalized profile results in a nonzero normalized time, t_s^∗ = t_s/τ = 0.014. Model initial profile, t_s^∗ = 0, is shown as a black solid line. (C) Solution for <C^∗> using C^∗(r, t_s^∗) as the initial condition (blue dash-dotted line) is shifted to the right compared to using a step initial condition. (Inset) Using t_s^∗ as an offset time in the 3D infinite model with a step initial condition results in an equivalent solution. (D) Measured <C^∗> vs. t (black open circles) are fitted to the 3D infinite model with non-step-initial condition (blue dashed line), resulting in D = 0.0017 ± 0.0005 μm²/s. Typical error bars are shown and represent SD of eight replicates. To see this figure in color, go online.

Device operation and protein droplet formation

To achieve on-chip coalescence of LAF-1 droplets, microfluidic devices were surface treated overnight by flushing with 1 wt% PF127 (Pluronic F-127; Sigma-Aldrich) at 0.01 mL/h using a syringe pump (Chemyx, Stafford, TX) as described previously (41) and soaked overnight in water to prevent evaporation through the polydimethylsiloxane (PDMS) device. After phase separation, a protein droplet solution was inserted into the top channel at roughly 50 μL/h, and flow was stopped for image analysis. For experiments on smaller LAF-1 droplets (i.e., <40 μm diameter), protein droplet solutions were added to a chambered cover glass (Grace Bio-Labs, Bend, OR), pretreated with 1 wt% PF127 to minimize droplet wetting and/or surface interactions.

FRAP

FRAP was performed using an inverted Nikon laser scanning confocal microscope with a 60× oil immersion objective with numerical aperture (NA) equal to 1.4 (Apo oil immersion; Nikon, Melville, NY). Bleaching was performed inside large protein droplets inside microfluidic devices, on smaller protein droplets in chambered cover glass wells, in Hek293 cells expressing Ddx4-YFP, and on 20 nm in diameter red fluorescent beads in a 90% glycerol solution. For experiments in microfluidic devices, a circular region of interest (ROI) is bleached using a laser with 488 nm wavelength at distances >10 μm from the edge of the droplet phase and in the midplane of the device using a scanning speed (i.e., bleaching time) equal to 63 ms and 500 ms and bleaching power equal to ≈ 60 and ≈ 500 μW for an ROI diameter equal to 3 and 1 or 50 μm, respectively. Experiments were conducted in separate microfluidic devices on different droplets to determine the SD. For experiments in chambered cover glass wells, a 3 μm ROI (488 nm wavelength) was bleached with 63 ms bleaching time and ≈ 60 μW bleaching power in the center (in the xy plane) of LAF-1 droplets, roughly 1–3 μm above the cover glass surface depending on the droplet size. Experiments were conducted in separate wells on different droplets to determine the SD. For both sets of experiments, a z-stack was acquired immediately after bleaching, and then images were collected at the midplane of bleaching initially every 30 s, then every 3 min, and then every 6 min to reduce photobleaching during acquisition. FRAP experiments of Ddx4-YFP droplets were performed using 63 ms bleaching time and ≈13 μW bleaching power, and images at the midplane of bleaching were acquired immediately after bleaching (514 nm wavelength) initially every 0.3 s, then every 1 s, and then every 3 s to reduce photobleaching during acquisition. For FRAP experiments of 20 nm beads, a 125 ms bleaching time and ≈ 640 μW bleaching power was used; images were also acquired immediately after bleaching at the midplane of bleaching, then every 1 s, then every 3 s and 5 s, and finally every 10 s to reduce photobleaching during acquisition. Experiments were conducted in separate cells on different droplets to determine SD. Laser power was measured after the 60× objective (Apo oil immersion, NA = 1.4; Nikon) using a handheld digital power meter (PM100D; Thorlabs, Newton, NJ) in scanning mode for a 64 × 64 field of view.

Image analysis for FRAP

The center of the bleach spot was found by applying MATLAB (The MathWorks, Natick, MA) code for an automated image thresholding and identification of centroids. The time-dependent concentration is denoted C(r, t). We define the normalized concentration, C^∗(r, t), as

$$C^{\ast }\left(r,t\right)=\left(C\left(r,t\right)-C\left(\mathrm{0,0}\right)\right)/\left(\langle C_{ref}\rangle -C\left(\mathrm{0,0}\right)\right),$$ (1)

where C(0, 0) is the minimal fluorescence intensity immediately after bleaching (i.e., at the bleach spot center) and <C_ref> is the average fluorescent intensity far from the bleach spot; C^∗(r, t) should be close to zero in the middle of the bleach spot and, for full FRAP recovery, would uniformly then approach a value of 1 at longer times. We use C^∗(r, t) to determine the bleach spot radius, perform fits of the initial concentration profile, and to display concentration profiles. The radius, R, of the bleach spot was defined experimentally to be the half-width of where the normalized initial concentration C^∗(r, 0) is equal to 0.75 (i.e., C^∗(R, 0) = 0.75). The average of the integrated fluorescent intensity, <C>, within the bleach spot of radius R was next measured over time. We normalized <C> according to

$$\langle C^{\ast }\rangle \left(t\right)=\left(\langle C\left(r,t\right)\rangle -\langle C\left(r,0\right)\rangle \right)/\left(\langle C_{ref}\rangle -\langle C\left(r,0\right)\rangle \right),$$ (2)

where <C(r, 0)> is the average of the initial fluorescent intensity inside the bleach spot (i.e., the first image acquired after bleaching); we note that this is not the same as the average of Eq. 1 because the pixel values within the bleach spot vary. We use this normalized average concentration <C^∗>(t) to perform fits of average fluorescence recovery data to a variety of models. In our analysis, we assume that the measured fluorescence intensity is linearly proportional to the fluorophore concentration. Bleaching is commonly accomplished by either using a stationary beam or a line scanning beam. The latter is used here. For a stationary Gaussian laser beam, Axelrod et al. (33) described the initial concentration profile as an exponential of the stationary laser intensity distribution, represented by a Gaussian function. Moreover, they describe the measured average fluorescence in the bleach spot as the convolution integral of the laser intensity distribution and the concentration within the spot. They also compare to the result in which a uniform circular laser beam is used for bleaching, which is equivalent to the 2D infinite model discussed here. Because of the mostly uniform bleach profile achieved in our experiments (see Results), using our non-step-initial condition model (see Results) and Axelrod’s solution for a Gaussian laser beam result in similar measured diffusivities., see Supporting Materials and Methods for more details. We note that for less uniform initial profiles, introducing a convolution integral may increase accuracy.

Fluorescence correlation spectroscopy

Fluorescence correlation spectroscopy (FCS) experiments were performed using an inverted Nikon A1 laser scanning confocal microscope with a 60× oil immersion objective with NA = 1.4 (Apo oil immersion; Nikon). Measurements and data analysis were performed using the SymPhoTime Software (Picoquant, Berlin, Germany) on free dye solutions, including Alexa 488 (succinimidyl ester; Thermo Fisher Scientific) and Dylight 488 (N-hydroxysuccinimide ester; Thermo Fisher Scientific), inside the protein-lean phase of a LAF-1 droplet solution, and in the nucleus of Hek293 cells expressing Ddx4-YFP. For each sample, experiments were performed with a 30 s measurement time and an oil immersion objective either 1 or 4 μm above the surface. Autocorrelation curves are then fitted to Eq. S29 to obtain diffusivity and concentration; see Supporting Materials and Methods for more details. For experiments on LAF-1 samples, protein droplet solutions were added to a chambered cover glass (Grace Bio-Labs), pretreated with 1 wt% PF127 to minimize droplet wetting and/or surface interactions.

Partition coefficient measurements

The ratio of concentration inside the droplet to that in the protein-lean phase (i.e., the partition coefficient) is determined for LAF-1 and Ddx4-YFP samples. For LAF-1, the partition coefficient is calculated from the ratio of concentrations inside/outside of the droplet, and for Ddx4-YFP, from the ratio of fluorescent intensities; see Supporting Materials and Methods for more details. For experiments on LAF-1 samples, protein droplet solutions were added to a chambered cover glass (Grace Bio-Labs), pretreated with 1 wt% PF127 to minimize droplet wetting and/or surface interactions.

Results

Simple exponential recovery results from fixed boundary and reaction-dominant models

Given the large number of studies that use a simple exponential to fit average fluorescence recovery data and extract diffusion coefficients, we sought to examine the underlying transport models that yield this functional form. One model that results in an exponential assumes reaction-dominated transport (Table S2), in which motion is limited by the kinetics of binding and unbinding rather than diffusion (32). However, although binding kinetics are likely relevant in many cases in living cells, we expect that these binding effects are negligible in single-component purified protein droplets, commonly employed in the field (10, 13, 21, 22, 26, 28). Here, we focus on such simplified in vitro systems and examine models with only pure diffusion. A second model that yields a single exponential assumes that the concentration of fluorescent molecules at the bleach spot boundary is fixed during the entire recovery process and that the initial bleach profile resembles a step. More detailed equations and boundary conditions are given in the Supporting Materials and Methods. The resulting solutions for the concentration profiles are well-known from the literature (42) (Table S1) and can be integrated to obtain the average normalized concentration, <C^∗>(t) (Table S2), which is only a function of time and the characteristic timescale τ.

In addition to the question of choosing appropriate model boundary conditions, a second key element is the dimensionality of the model. Often, one must determine whether diffusion occurs effectively in one dimension, two dimensions, or three dimensions, and for each dimension, the equations describing the concentration distribution—and so the average normalized concentration—have a different form. Equations for one dimension (Cartesian coordinates), two dimensions (cylindrical coordinates), and three dimensions (spherical coordinates) diffusion are shown in Table S2 for comparison. Nevertheless, in each case, taking only the first term in the summation results in a single exponential. However, each fixed boundary and simple exponential model has different factors preceding the exponential and in the argument of the exponential. These factors are expected to result in different dynamics of the equations for a given diffusion time, τ. Moreover, because τ = R²/D for all models, using the same initial bleach spot radius (e.g., R = 1 μm) and diffusion coefficient (e.g., D = 1 μm²/s) will result in different dynamics of <C^∗>(t). Alternatively, fitting the same data with these different time-dependent equations would yield different values for τ and hence D.

We show a graphical comparison of the equations from Table S2 in Fig. 3, which underscores several salient features. First, close agreement for t/τ > 0.1 between the leading-order exponentials (dashed lines) and full series solution (solid lines) indicates a good description of the dynamics is provided by the first term in the summation. Each increase in dimension from one dimension (red line) to two dimensions (black line) to three dimensions (blue line) results in a faster recovery of <C^∗>(t), which makes sense physically because diffusion can occur from more directions. Of the fixed boundary models, the 1D model is most similar to the simple exponential model (pink dashed line), which has the slowest dynamics. Finally, the reaction-dominated model is most similar to the simple exponential model when k_off = 1/τ and C_eq = 1, the latter resulting from the effective binding rate being much faster than unbinding. The inset of Fig. 3 shows the value of τ required to fit each curve to the 1D model. Importantly, τ, and therefore D, can vary by over an order of magnitude between the 3D and simple exponential models. This observation implies that drastically different diffusion coefficients may be obtained from experiments, depending on the model chosen to fit the data.

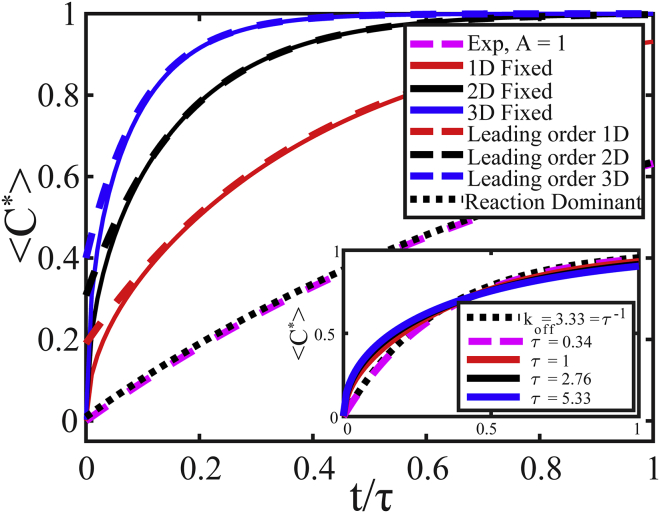
Figure 3.

Calculated <C^∗> vs. normalized time, t/τ, for 3D (blue solid line), 2D (black solid line), and 1D (red solid line) fixed boundary models; simple exponential with A = 1 (pink dashed line); and reaction-dominant model with k_off = 1/τ and C_eq = 1 (black dotted line); see Table S2. τ = R²/D and R = 1 for all diffusion models. Dashed blue, black, and red lines correspond to the first term in the summation of the fixed boundary models and show close agreement to full series solution at later times. (Inset) Fitting all models to the 1D fixed boundary model shows that a different τ, and therefore D, would be calculated using each model. To see this figure in color, go online.

The key assumption in the fixed boundary models is that the concentration of fluorescent molecules at the bleach spot boundary is fixed. For bleach spots much smaller than the droplet size, one would expect that the fluorescent concentration at the bleach spot boundary will change over time because fluorescent and bleached molecules freely exchange within a homogeneous droplet phase. Even for bleach spot sizes comparable to the droplet size, as is typical for experiments in living cells, fluorescent molecules may still exchange with the surrounding reservoir, giving rise to a changing fluorescent concentration. Therefore, the use of an exponential function for the area-averaged concentration, which results from a fixed-boundary model to fit fluorescent recovery data, is often not justified.

Infinite boundary models

Many publications (Table 1) use a model that allows for the boundary concentration to change rather than assume the concentration is fixed at the bleach spot boundary. One such model assumes the droplet is effectively an infinite media, diffusion only occurs in two dimensions radially inwards in the imaging plane with a step-like initial bleach profile, and the prebleach fluorescence concentration is reached infinitely far from the bleach spot. Often, the diffusion coefficient is found from this model by calculating the half time, t_1/2, corresponding to the time at which <C^∗>(t) = 0.5, and using the relationship D = 0.22R²/t_1/2 (34) (Table 2, row 2). Alternatively, one can fit <C^∗>(t) to the equation given in Table 2, row 2 (34). Many publications have utilized this approach instead of an exponential, raising the question of how the dynamics of this 2D infinite model may differ from fixed boundary models. We plot comparisons of these two models (Fig. S1) to build intuition for the difference between the dynamics and assumptions of fixed versus infinite boundary models; see Supporting Materials and Methods for more details. As a result of exchange between bleached molecules and fluorescent molecules over a larger length scale, the infinite boundary model predicts slower recovery within the initial bleach zone, a decrease in normalized concentration outside the initial bleach zone, and a slower recovery of the integrated (average) concentration for the same τ. As with the fixed boundary models, the dimensionality of the infinite boundary model can again strongly impact the resulting rate of recovery, with higher dimension yielding faster recovery with more confined concentration profiles (Fig. S2). See Supporting Materials and Methods for more details. These observations again imply that fitting the same data with these different models would yield different values for τ and therefore yield different diffusion coefficients.

Table 2.

Expressions for the Average Normalized Concentration for Infinite Boundary Models in One Dimension, Two Dimensions, and Three Dimensions

Type	Average Concentration	D ∼ R2/t1/2
1D pure diffusion (infinite boundary)	$\langle {\mathit{C}}^{\ast }\rangle \left(\mathit{t}\right)=1-\mathrm{erf}\left({\left(\mathit{\tau }/\mathit{t}\right)}^{1/2}\right)+{\left(\mathit{t}/\left(\mathit{\pi \tau }\right)\right)}^{1/2}\left[1-\exp \left(-\mathit{\tau }/\mathit{t}\right)\right]$	0.93
2D pure diffusion (infinite boundary)	$\langle {\mathit{C}}^{\ast }\rangle \left(\mathit{t}\right)=\exp \left(-\mathit{\tau }/\left(2\mathit{t}\right)\right)\left[{\mathit{I}}_0\left(\mathit{\tau }/\left(2\mathit{t}\right)\right)+{\mathit{I}}_1\left(\mathit{\tau }/\left(2\mathit{t}\right)\right)\right]$	0.22
3D pure diffusion (infinite boundary)	$\langle {\mathit{C}}^{\ast }\rangle \left(\mathit{t}\right)=1-\mathrm{erf}\left({\left(\frac{\mathit{\tau }}{\text{t}}\right)}^{1/2}\right)+{\left(\frac{\text{t}}{\mathit{\pi \tau }}\right)}^{1/2}\left[3-\exp \left(-\frac{\mathit{\tau }}{\text{t}}\right)\right]+2{\left(\frac{{\text{t}}^3}{\mathit{\pi }{\mathit{\tau }}^3}\right)}^{1/2}\left[\exp \left(-\mathit{\tau }/\mathit{t}\right)-1\right]$	0.1

One dimension, cartesian; two dimensions, cylindrical; three dimensions, spherical. <C^∗> was calculated by averaging the expressions from Table S3. The error function and order zero modified Bessel function are denoted by erf and I₀, respectively. τ = R²/D for all models.

Infinite boundary experiments

An infinite boundary model thus appears to better capture the physics of bleaching within a large droplet and may be applicable not only for large in vitro protein droplets such as those examined here, but also potentially for large in vivo condensates. However, it remains unclear under what experimental conditions diffusion mainly occurs in one dimension, two dimensions, or three dimensions. To examine this question, we sought to set up an effectively infinite droplet phase, determine the shape of the initial bleach spot and apparent dimensionality, and compare the diffusion coefficient measured using the models described above. Previously, we showed that assembling large protein droplets in vitro is readily achieved using a microfluidic device (41) that coalesces many sub-micron-sized droplets to form a single condensed droplet phase (∼50–100 μm wide and ∼10 μm high). As a model in vitro protein droplet system, we utilized LAF-1, a key component of C. elegans P granules. Upon lowering the salt concentration (NaCl), LAF-1 phase separates to form spherical droplets, whose internal dynamics can be examined using FRAP.

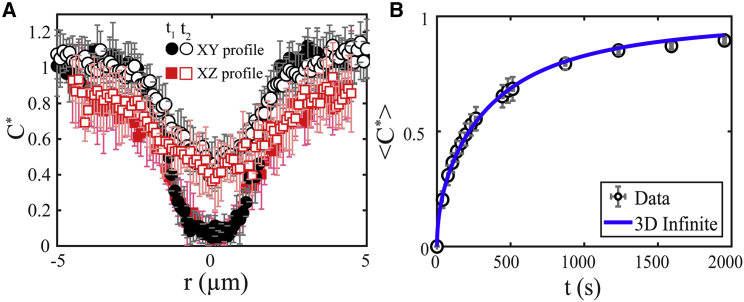
Immediately after phase separation, LAF-1 droplets (shown schematically in green in Fig. 4 A) are introduced into a microfluidic device where the inlet contains PDMS posts: the green arrow in the figure indicates the direction of flow. Briefly, droplets are induced by the PDMS posts to coalesce, forming a stream that is collected as a large bulk phase (Fig. 4 B); for details, see (41). A circular ROI is bleached at distances >10 μm from the edge of the droplet phase (black dashed box in Fig. 4 A) and in the midplane of the device. The 3D initial bleach spot shape is determined by acquiring a z-stack immediately after bleaching (Fig. 4 C). We observe that for an ROI = 3 μm (i.e., radius R = 1.5 μm), a roughly spherical bleach shape is formed in the xz plane, with aspect ratio between the z and x radii, δ = 1.1. Similarly, line scans through the bleach spot center (Fig. 5 A) in the xy (black filled circles) and xz (red filled squares) planes are nearly symmetric at early times. Moreover, negligible decrease in fluorescence intensity is seen at the bottom and top device surfaces (i.e., at r = 5 μm), even after long times, consistent with the assumption of an infinite droplet. Accordingly, we used the 3D spherically symmetric infinite model to fit the normalized average concentration over time (Fig. 5 B), resulting in D = 0.0012 ± 0.0003 μm²/s. Here, we compare the measured average fluorescence in the 2D detection plane (2D average) to that predicted in the 3D detection volume (3D average). We note that there is a small difference in the predicted fluorescence recovery between a 2D and 3D average (Fig. S3 A). Importantly, fitting the data to the 2D average yields no significant change in D (Fig. S3 B) or improvement in the R², whereas the sum of squared residuals gets slightly higher (Table S4). Alternatively, the 3D detection volume can be measured but would lead to greater photobleaching during acquisition, a feature that is not accounted for in these models.

Figure 4.

Setting up of a microfluidic device to mimic a model with boundary conditions at infinity. (A) A schematic showing protein droplets (green) inserted into the inlet containing PDMS posts (red dashed box) is given. Protein droplets coalesce to form a larger droplet phase within which FRAP is performed (black dashed box). (B) Example of protein droplets (e.g., LAF-1) sticking to PDMS posts and coalescing to form a protein-rich stream is shown. Right panel shows time lapse of coalescence; scale bars, 20 μm (adapted from Taylor et al. (41)). (C) 3D volume view acquired immediately after bleaching reveals a symmetric, spherically shaped bleach spot using an ROI = 3 μm. Image contrast is adjusted for clarity. Device height is 10 μm, as indicated, and bleaching is performed >10 μm from the droplet-solution interface. To see this figure in color, go online.

Figure 5.

(A) Measured concentration profiles for bleach spots within in vitro LAF-1 droplets in the xy plane (black circles) and xz plane (red squares) (as indicated in Fig. 4C) for two time points using an ROI = 3 μm. Here, t₁ ≈ 1 min and t₂ ≈ 4 min after bleaching. The average of eight replicates is shown. Error bars represent SD of eight replicates. (B) Measured <C^∗> vs. t (black open circles), obtained by integration of concentration profiles, is fitted to the 3D infinite model (blue solid line), resulting in τ = 1900 s (31 min) and D = 0.0012 μm²/s. Typical error bars are shown and represent SD of eight replicates. To see this figure in color, go online.

The models described thus far assume that the initial bleach profile closely resembles a step. However, the measured initial profile is not a perfect step (Fig. 6, A and B), an effect that arises here because of the roughly Gaussian shape of the laser used for bleaching (33). We sought to address how this assumption might affect the measured diffusion coefficient by using the measured initial profile as the model initial condition. Fitting the 3D infinite model to the initial profile yields a nonzero normalized time, t_s^∗ = t_s/τ = 0.014 (Fig. 6 B). Solving the differential equation with the initial condition defined by C^∗(r, t_s^∗) gives a new solution (blue dash-dotted line), Eqs. S6 and S7, to the 3D infinite model, <C^∗>(t), that is shifted to the right compared to using a step initial condition (black dashed line) (Fig. 6 C). Additionally, an equivalent solution is found (inset, Fig. 6 C) by using t_s^∗ as an offset time in the 3D infinite model with step initial condition equation (i.e., <C^∗>(t + t_s)), where t starts from 0 (Eqs. S7 and S8). Fitting the data (Fig. 6 D) with this updated model results in D = 0.0017 ± 0.0005 μm²/s, a change of roughly 40%.

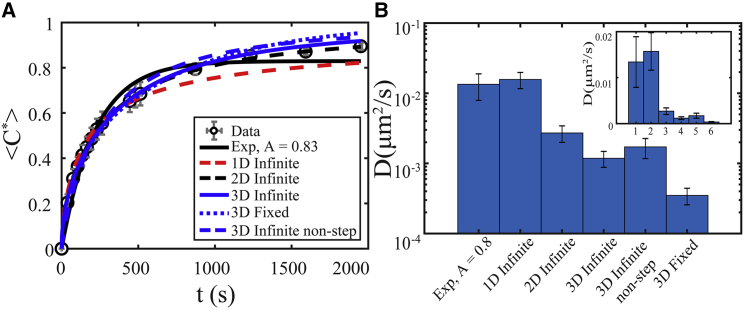
Fitting the same <C^∗>(t) to all 3D models, as well as 1D and 2D infinite models, and to the simple exponential model yields different results. The quality of fit for each model varies significantly (Fig. 7 A; Table S5), and each fit results in a different measured diffusion coefficient (Fig. 7 B). Interestingly, the 3D infinite models (blue solid and dashed lines in Figs. 7 A and S4) appear to fit better than most other models, though the 2D infinite model appears to fit best, and the 3D infinite model fits better than the 3D infinite nonstep model (Table S5). This apparent discrepancy between fit quality and model that should best describe the data could result from many confounding effects (e.g., non-Newtonian behavior of the high concentration protein droplets at long times (21)) and is left for future studies. Moreover, the measured D varies by over an order of magnitude between the simple exponential versus 3D fixed boundary model and by an order of magnitude between the simple exponential and 3D infinite models (Fig. 7 B). Plotting results on a linear scale makes this difference more apparent (inset, Fig. 7 B).

Figure 7.

(A) Measured <C^∗> vs. t (black open circles) inside bleach spots within in vitro LAF-1 droplets using an ROI = 3 μm fit to the 1D (red dashed line), 2D (black dashed line), and 3D (blue solid line) infinite boundary models with a step initial condition; the 3D infinite boundary with a nonstep initial condition (blue dashed line); a simple exponential model (black solid line); and the 3D fixed boundary model (blue dotted line). (B) Measured diffusion coefficient varies by over an order of magnitude depending on the model chosen to fit the data. (Inset) Linear scale. Typical error bars are shown and represent SD of eight replicates. To see this figure in color, go online.

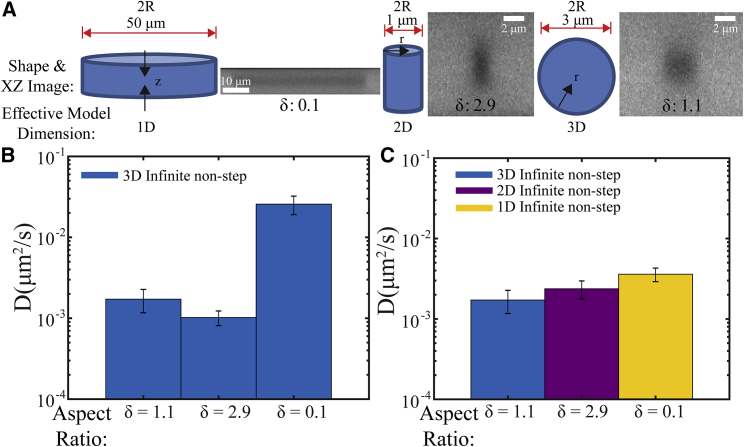
These results suggest that roughly spherical bleach spots are well-described by a 3D infinite model. We examined whether this might break down for nonspherical shapes, for example, using ROI = 50 and 1 μm, which result in disk and elongated cylinder shapes, respectively (Fig. 8 A). We hypothesized that the dominant direction in which diffusion would occur for these ROIs would be in the shorter dimension. In this case, a disk (ROI = 50 μm) would be expected to exhibit quasi-1D diffusion (i.e., along the z axis), whereas an elongated cylinder (ROI = 1 μm) would exhibit quasi-2D, radial diffusion; a 3D infinite cylindrical model confirmed this crossover in effective dimensionality (Fig. S5) (see Supporting Materials and Methods for more details). To examine this, we first determined the diffusion coefficient by fitting the measured <C^∗>(t) versus time for all three ROIs to the 3D infinite model with nonstep initial condition (Fig. 8 B). This resulted in D = 0.0257 ± 0.0066 μm²/s, 0.0010 ± 0.0002 μm²/s, and 0.0017 ± 0.0005 μm²/s for ROI = 50, 1, and 3 μm, respectively. Although D is similar for ROI = 3 and 1 μm, it is over an order of magnitude larger for ROI = 50 μm when using a 3D infinite model and the radius in the xy plane. This difference is remedied when fitting ROI = 50 and 1 μm to the 1D and 2D infinite models with a nonstep initial condition, respectively, and yields corresponding D = 0.0036 ± 0.0007 and 0.0024 ± 0.0006 μm²/s. In both cases, the value is now closer to the mean value obtained using ROI = 3 μm. For ROI = 50 μm, the half-height of the disk is used to calculate D because this is the relevant length scale for quasi-1D diffusion. Importantly, this finding also demonstrates that despite a small amount of increased bleaching in the xz direction (Fig. 5 A) for the roughly spherical bleach shape, a 3D spherically symmetric infinite model measures the same D within error as using a 2D infinite model for an elongated cylindrical bleach spot.

Figure 8.

(A) Bleach spot shape (left drawn shape) and xz image (right) obtained using an ROI diameter equal to 50, 1, and 3 μm (left to right) inside in vitro LAF-1 droplet phases. The measured ratio between z and x radii, δ, is 0.1, 2.9, and 1.1, respectively. Arrows drawn on the shapes indicate the dominant direction in which diffusion occurs and results in effective model dimensions of one dimension, two dimensions, and three dimensions (left to right). (B) Fitting all data sets to the 3D infinite model with a nonstep initial condition results in different D-values. (C) Fitting ROI = 50, 1, and 3 μm data to the 1D, 2D, and 3D infinite models with a nonstep initial condition results in more similar measured diffusion coefficients. Typical error bars are shown and represent SD of at least three replicates. To see this figure in color, go online.

These data imply that FRAP measurements for different bleach shapes are consistent when the appropriate dimensional model is chosen to fit the data. However, one consideration is whether these models give quantitatively accurate diffusion coefficients. We addressed this question by performing a FRAP experiment in which 20 nm red fluorescent beads are bleached as they diffuse within a 90% glycerol solution of known viscosity; bead diffusion coefficient can thus be readily calculated from the Stokes-Einstein equation (see Supporting Materials and Methods for more details). Using the 3D infinite model with nonstep initial condition to fit <C^∗>(t) (Fig. S6) results in an accurate D when compared to the prediction from the Stokes-Einstein relation (i.e., D_{Stokes-Einstein} = 0.094 ± 0.003 μm²/s vs. D = 0.066 ± 0.025 μm²/s). This indicates that the 3D infinite model with nonstep initial condition gives quantitative measurements of D, provided the model assumptions are met.

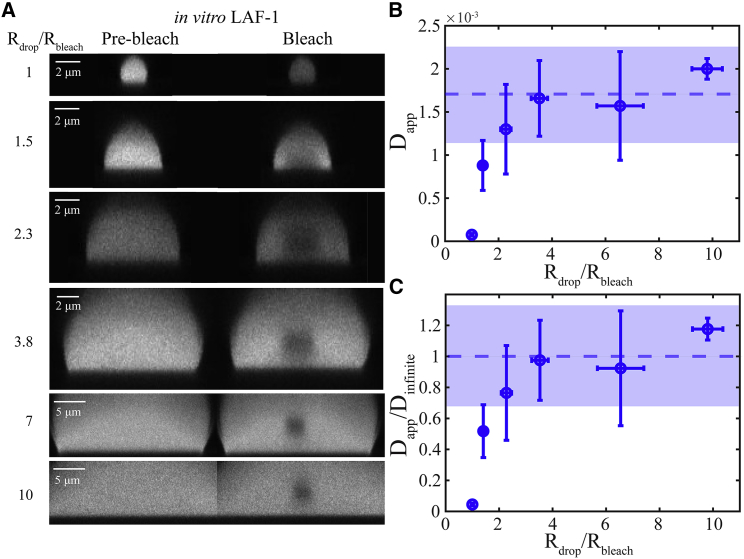
Many in vitro and most in vivo FRAP experiments are performed on small droplets in which a larger fraction of the droplet is bleached, suggesting that infinite models would be inapplicable. We thus sought to determine experimentally how large droplets must be compared to the bleach size to extract similar diffusion coefficients from the same infinite model. We performed a series of FRAP experiments on increasingly large droplets in which we fixed the bleach radius, R_bleach = 1.5 μm, so that R_drop/R_bleach varied from 1 to 10. As expected for this ROI, a roughly spherical bleach shape is formed in the xz plane (Fig. 9 A), and the entire droplet volume is bleached for R_drop/R_bleach = 1. This suggests a 3D spherically symmetric model describes the experimental geometry well. For comparison, we used the 3D infinite model with nonstep initial condition to fit all data. Surprisingly, a value as small as 2.3 for R_drop/R_bleach gave apparent diffusion coefficients, D_app, within error of our previous measurements in much larger droplets (Fig. 9, B and C). However, full bleach of LAF-1 droplets, R_drop/R_bleach = 1, results in D_app that is an order of magnitude smaller than that measured in large droplets.

Figure 9.

(A) xz image of LAF-1 droplets before and immediately after bleaching obtained using an ROI diameter equal to 3 μm, where R_drop/R_bleach varies from 1 to 10. (B) Measured apparent diffusion coefficients for each value of R_drop/R_bleach using the 3D infinite model with a nonstep initial condition are shown. (C) Measured apparent diffusion coefficient scaled by diffusion coefficient measured in large droplets in microfluidic devices, D_infinite = 0.0017 ± 0.0005 μm²/s, is shown. Blue dashed line and shaded blue area indicate average diffusion coefficient and SD, respectively, measured in large droplets in microfluidic devices. Typical error bars are shown and represent SD of at least three replicates. To see this figure in color, go online.

Finite boundary model

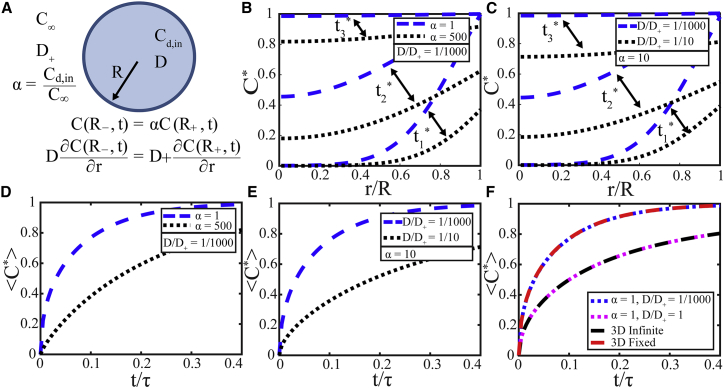
These results indicate that the 3D infinite model does not accurately describe fully bleached finite droplets because it results in a much smaller D_app of LAF-1 inside droplets. This arises from a much slower rate of fluorescence recovery; we hypothesized that this rate is also set by the concentration and diffusivity of fluorescent protein outside of droplets. Accordingly, we derived a 3D spherically symmetric finite model (“3D finite model”) (Eq. S24) with the diffusion coefficient and total protein concentration inside and outside of the droplet defined as D, C_d,in, D₊, and C_∞, respectively (Fig. 10 A). The key assumptions are 1) local equilibrium, C(R₋, t) = αC(R₊, t); 2) continuity of mass flux at the droplet-solution interface, D∂C(R₋, t)/∂r = D₊∂C(R₊, t)/∂r; 3) only fluorescent molecules inside the droplet are bleached; and 4) the protein-lean phase is infinite. Here, α is defined as the partition coefficient, i.e., the ratio of total protein concentration in the condensed phase to that in the protein-lean phase, and R₋ and R₊ represent being just on the inside or outside of the droplet interface, respectively.

Figure 10.

(A) Schematic of spherical model geometry with boundary conditions and parameters labeled. (B) Calculated normalized concentration profiles for 3D finite model with D/D₊ = 1/1000 and α = 1 (blue dashed lines) and α = 500 (black dotted lines) and (C) with α = 10 and D/D₊ = 1/1000 (blue dashed lines) and D/D₊ = 1/10 (black dotted lines) are shown for three time points. Here, t^∗ = t/τ and t₁^∗ = 0.03, t₂^∗ = 0.13, t₃^∗ = 0.5. (D) Calculated <C^∗> vs. t/τ for 3D finite model with D/D₊ = 1/1000 and α = 1 (blue dashed line) and α = 500 (black dotted lines) and (E) with α = 10 and D/D₊ = 1/1000 (blue dashed lines) and D/D₊ = 1/10 (black dotted lines) is shown. (F) Calculated <C^∗> vs. t/τ for 3D fixed (red dashed line), infinite (black dashed line), and finite model with α = 1 and D/D₊ = 1/1000 (blue dotted line) and D/D₊ = 1 (magenta dotted line) is shown. τ = R²/D for all models. To see this figure in color, go online.

The resulting equations (Eqs. S14 and S15) were solved analytically using the Laplace transform method; see Supporting Materials and Methods for more details. We highlight several key observations, which can be seen graphically in Fig. 10. First, for diffusivity ratio D/D₊ = 1/1000, increasing the partition coefficient from 1 to 500 results in slower-evolving and flatter concentration profiles inside droplets (Fig. 10 B). This effect arises from a much lower pool of fluorescent molecules outside of droplets that cannot quickly replace the bleached molecules inside droplets. For partition coefficient, α = 10, increasing the diffusion coefficient outside of droplets, D₊, relative to D from 1/10 to 1/1000 μm²/s speeds up recovery (Fig. 10 C). This arises because of faster mixing outside of droplets and then exchange with bleached molecules inside droplets. Integrated concentration in droplets <C^∗>(t) exhibits similar dynamics (Fig. 10, D and E). The model with α = 1 and D/D₊ = 1 reduces to the 3D infinite model (Fig. 10 F) because fluorescent molecules are evenly partitioned with equal diffusivities in an infinite phase. Finally, if D/D₊ ≪ 1 (e.g., D/D₊ = 1/1000), the dynamics approaches that of the 3D fixed boundary model (Fig. 10 F) because rapid diffusivity outside of droplets maintains a fixed concentration, C^∗ = 1, at the droplet-solution interface.

Finite boundary experiments in vitro

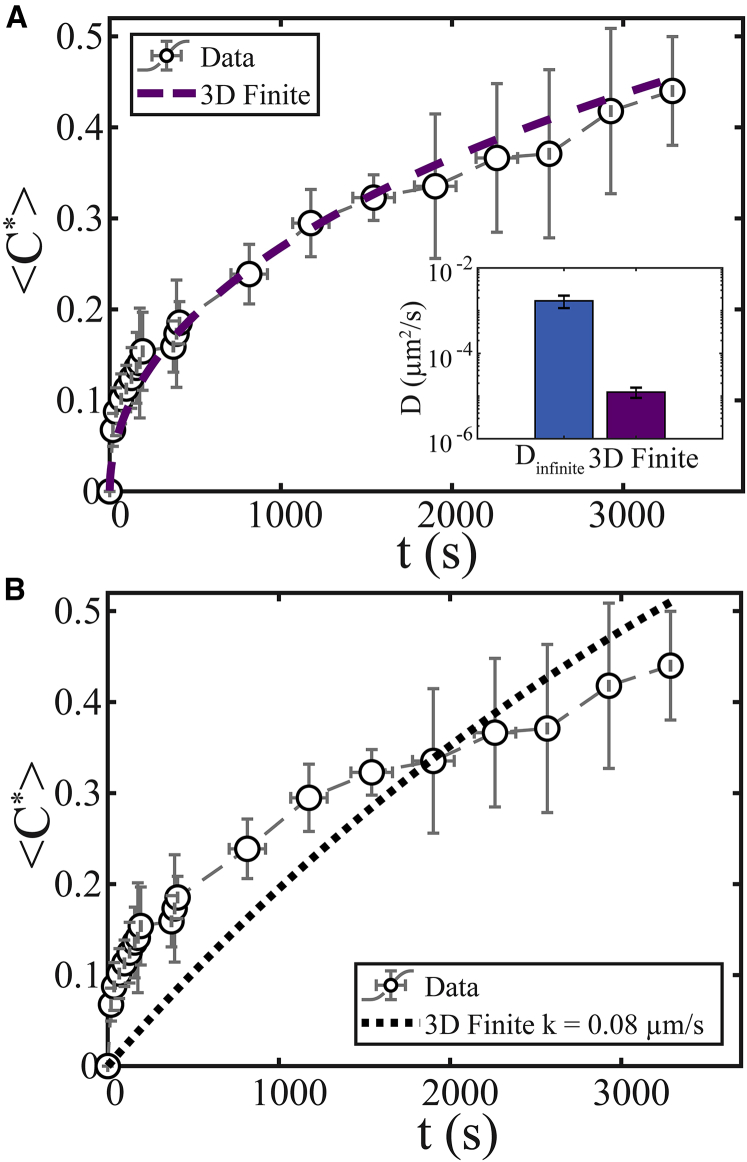
We next sought to determine whether the concentration dynamics <C^∗>(t) in fully bleached finite droplets could be fitted to the 3D finite model and whether it would result in a similar value for diffusion coefficients inside drops, D. For LAF-1 at 80 mM NaCl, we found α = 1190 ± 880, calculated from the ratio of protein concentration inside/outside of drops and D₊ = 94 ± 11 μm²/s from FCS measurements; see Supporting Materials and Methods for more details. Using these parameters, the measured <C^∗>(t) is fitted to Eq. S24 (Fig. 11 A) and results in D = 1.2 ± 0.3 × 10⁻⁵, still two orders of magnitude lower than expected. Here, we use a step initial condition because bleaching results in depletion in fluorescence of the entire droplet, resulting in a flat concentration profile. We note that in our experiments, the bottom surface of the droplet is in contact with a solid surface and not surrounded by an infinite pool of protein-lean phase. However, because this is small compared to the overall droplet surface, we do not expect this feature to lead to a two-orders-of-magnitude decrease in the apparent D.

Figure 11.

(A) FRAP data for LAF-1 at 80 mM NaCl (open black circles) using R_drop/R_bleach = 1 fitted using the 3D finite model (purple dashed line). (Inset) Fitting to the 3D finite model results in a two-orders-of-magnitude-lower apparent D compared to that measured for R_drop/R_bleach ≫1 using the 3D infinite nonstep model (i.e., 1.2 ± 0.3 × 10⁻⁵ and R² = 0.97 vs. 1.7 ± 0.5 × 10⁻³μm²/s). (B) Fitting the data to the 3D finite model with interface resistance (black dotted line) yields k = 0.08 ± 0.01 μm/s, and R² = 0.71. Typical error bars are shown and represent the SD of five replicates. To see this figure in color, go online.

The 3D finite model thus appears to greatly underestimate the diffusion coefficient inside droplets. One key assumption of this model is local equilibrium at the interface, C(R₋, t) = αC(R₊, t), or that there is no interfacial resistance. However, in studies of various nonbiological systems, a number of groups have studied the effect of interfacial resistance on diffusion of a component between two phases (43, 44, 45, 46, 47, 48, 49). We sought to estimate this resistance by using a transfer coefficient, k, and replacing the local equilibrium boundary condition by equating the mass flux on each side of the interface to that at the interface, D∂C(R₋, t)/∂r = D₊∂C(R₊, t)/∂r = −k[C(R₋, t) − αC(R₊, t)]; see also (43). Thus, in the case of no resistance, k approaches infinity, and local equilibrium is established, C(R₋, t) = αC(R₊, t); see Supporting Materials and Methods for more details. The resulting solution (Eq. S28) depends also on k, with higher k indicating less interfacial resistance and leading to faster predicted recovery (Fig. S7). We estimate k for LAF-1 droplets by fitting <C^∗>(t) to Eq. S28 using the parameters D = 0.0017 ± 0.0005 μm²/s, α = 1190 ± 880, and D₊ = 94 ± 11 μm²/s. Fitting results in k = 0.08 ± 0.01 μm/s, indicating significant interfacial resistance (Fig. 11 B). However, we note the best model fit to the data underestimates the early time recovery and overestimates the late time recovery (see Discussion), R² = 0.71.

Finite boundary experiments in vivo

The presence of interfacial resistance (i.e., slower mass transfer at the interface) apparent for in vitro LAF-1 droplets may be relevant in living cells. Indeed, proteins such as fibrillarin and HP1α have been reported to have an order of magnitude slower diffusion coefficient at phase interfaces of the nucleolus and HP1α domains, respectively (50). However, it is unclear whether these measurements indicate the presence of interfacial resistance and how this would affect FRAP experiments with R_drop/R_bleach = 1. Intracellular Ddx4-YFP droplets appear to recover much faster than in vitro LAF-1 droplets (i.e., compare Fig. 1 D with Fig. 2: 50% recovery within 2 versus 3500 s for Ddx4 and LAF-1, respectively), which is consistent with negligible interfacial resistance, but could alternatively simply be a result of a lower α (i.e., 14 ± 6 vs. 1190 ± 880) or higher D. However, applying the 3D finite model with interface resistance to intracellular Ddx4 droplets, we obtained D = 0.023 ± 0.009 μm²/s and k = 648 ± 600 μm/s (Fig. S8 A), suggesting interfacial resistance (1/k) may indeed be negligible for these model intracellular condensates (Fig. S7). But we note that the data can be fitted nearly as well (R² = 0.86 vs. 0.98) with a value for k two orders of magnitude smaller, provided the diffusion coefficient is also significantly larger (Fig. S8 B). In any case, as with the in vitro data (i.e., Fig. 11 A), independent measurements of D will be important for careful analysis of the potential role of interfacial resistance in intracellular protein condensates.

Discussion

In this work, we addressed several key challenges associated with interpretation of FRAP results, utilizing a model in vitro LAF-1 system as well as model intracellular phase separating systems. First, we highlighted assumptions that give rise to two widely used models, explored variations of such models, and evaluated differences in apparent diffusivity obtained when using these models to fit FRAP data. The breakdown in model assumptions was tested by performing FRAP experiments on LAF-1 droplets of decreasing size. We attempted to address the lowest limit, when bleach and droplet sizes were equal, by developing a model accounting for diffusivity and concentration in the protein-lean phase. Using this finite model resulted in a surprisingly lower diffusivity than expected; we hypothesize that this discrepancy results from resistance to mass transfer at the droplet-solution interface, which can be estimated by modifying the finite droplet model.

Two models commonly used to fit FRAP recovery data are a simple exponential and a 2D infinite model. To test assumptions in the 2D infinite model, we used a microfluidic device to set up an effectively infinite droplet phase of the model protein LAF-1. We found that fluorescent concentration far from the bleach spot center (i.e., 5 μm) was constant over time, indicating that the assumption of an infinite phase would be appropriate. However, when bleaching is performed closer to droplet boundaries (i.e., <5 μm) or when a greater percentage of the droplet is bleached, an infinite phase may not be a good assumption. In these cases, recovery will also be influenced by the partitioning of fluorescent molecules into the droplet and does not only reflect reorganization within the phase. Thus, in many experiments, using an infinite model to estimate diffusion coefficients is not justified. Indeed, for values of R_drop/R_bleach lower than ∼3, this model resulted in a decrease in the apparent diffusion coefficient. Values for larger R_drop/R_bleach were consistent with measurements in effectively infinite droplets. However, this threshold value will be system-specific and should be impacted by relative diffusivities and protein concentrations inside and outside droplets. Thus, it is necessary to avoid these confounding size effects to extract meaningful estimates of diffusivity.

When fitting to infinite phase models, quasi-2D diffusion is often assumed. Here, we demonstrated this is not always an accurate assumption and that the dominant direction for diffusion depends on the initial bleach shape. Using a 2D model to fit quasi-3D diffusion data results in roughly a factor of two difference in the diffusion coefficient; an even greater difference was found for 3D model fits to quasi-1D diffusion data. These differences are especially important when comparing different experimental conditions because bleach shape and therefore dimension are affected by ROI size, laser power, and diffusion coefficient (37). If ROI size is changed, this may change the effective model dimension, which, if not corrected for, can lead to apparent differences in measured diffusivity (Fig. S9) and to erroneous conclusions (e.g., the presence of binding and unbinding kinetics (32)). Depending on the appropriate infinite-phase-model dimension, the equations given in column 2 of Table 2 can be used to fit average normalized fluorescent recovery data or the relationships given between t_1/2 and D in column 3. Importantly, these equations should be used for similar shapes as achieved in the Results. More elliptical initial bleach shapes may require a 3D model that is not spherically symmetric (51). Finally, determining the initial 3D photobleached shape by acquiring a z-stack immediately after bleaching may be impossible for faster-diffusing species, as seen for Ddx4-YFP condensates. A possible method is to fix the sample before photobleaching to determine the bleached shape for the chosen experimental parameters. However, for faster-diffusing species, the bleach shape may differ or be larger for nonfixed versus fixed samples (52), and future studies are required to test this approach.

The second model commonly used to fit FRAP data, a simple exponential, is often used to assess qualitative differences in dynamics by determining the characteristic recovery time: either exponential timescale, τ, or half recovery time, t_1/2. Simple exponential recovery can arise from reaction-dominant diffusion (39), which may be particularly relevant in cellular systems, in which the presence of multiple species may increase the likelihood of binding reactions. To test for this, one should demonstrate that bleaching a larger spot results in the same recovery rate because the binding rate, unlike diffusion, does not depend on bleach spot size (32). However, significant changes in spot size may lead to a different reaction-diffusion regime because reaction-dominant diffusion assumes the on rate of binding, k_on^∗, is slow compared to diffusion time, t_d = R²/D, or that the Damkohler number Da = k_on^∗R²/D ≪ 1 (32).

In the absence of binding, a simple exponential recovery can arise for systems exhibiting a fixed concentration at the bleach spot boundary. However, we find that the fluorescent concentration at the bleach spot boundary is not constant when bleaching spots smaller than the droplet (Fig. S10). Assuming a fixed boundary concentration at an interface is nevertheless often an accurate assumption, such as when describing solute diffusion from a large external solution saturated with fluorescent molecules to a separate phase such as a hydrogel (53, 54). For condensed RNA or protein phases, assuming a roughly constant concentration at the droplet boundary may only be strictly accurate for bleaching of an entire droplet in which protein concentration inside and outside of droplets is comparable. However, for many intracellular condensates, the external solution typically has a much lower protein concentration, and proceeding with a fixed boundary concentration assumption may not be justified.

Many of the models presented here, including those in the literature, assume that the initial bleach profile is sharp and step-like. However, for fast diffusion coefficients or for small ROIs, this is not always the case because of both the Gaussian shape of the laser used for bleaching and the finite scan speed of a laser scanning confocal microscope to both bleach and acquire images. Therefore, we suggest two methods to account for nonstep initial profiles. First, experimentally, one can try to minimize the time of bleaching and acquisition by choosing the fastest frame rates and use larger ROIs (i.e., >1 μm), which we found had more step-like initial profiles. Second, one can account for the non-step-like profile in a similar manner as done here: by fitting the appropriate model equation for C^∗(r, t_s^∗) to the initial profile and using t_s^∗ in the appropriate model with a step initial condition equation (i.e., <C^∗>(t + t_s)), where t starts from 0, and fitting to normalized average concentration histories. We suggest implementing both methods to increase accuracy. A different method to account for a nonstep initial condition has been proposed by Kang et al. (37, 52) for 2D geometries and uses both the user-defined ROI radius as well as the measured ROI radius. Future studies may reveal how diffusion coefficients measured using these two methods compare.

A final general experimental consideration for bleaching in “infinite” phases not explored in detail here is the issue of nonspecific photobleaching during acquisition. Here, the time between image acquisitions was increased at later times to reduce the impact of further photobleaching. However, for even slower diffusing species, this can still present an issue. Continued nonspecific photobleaching of the image capture area will result in a net influx of fluorescent molecules from outside the image capture area, a feature that is not accounted for in the models presented here. For more details on this effect and a possible method to correct for this, see Jonsson et al. (55).

Many experiments in living cells utilize bleaching of the entire condensate. Thus, we also explored models to use when the bleach spot is the same size as the droplet. We analyzed FRAP data for Ddx4 in living HEK293 cells, for which we applied the 3D finite model, and interrogated whether local equilibrium is met. Ideally, the diffusivity inside condensates for which R_drop/R_bleach is large would be measured using an infinite model of appropriate dimension and then compared to the finite models fit from bleaching the entire droplet. Indeed, in the case of in vitro LAF-1 droplets under the local equilibrium assumption, this model yielded values of D for LAF-1 that appear much too small compared to values obtained with large droplets analyzed with an infinite model. We speculate that this reflects a breakdown of the local equilibrium condition at the interface due to an additional interfacial resistance, which was estimated using a modified boundary condition of the finite droplet model, accounting for interfacial mass transfer. We note, however, that the quality of the fit was relatively poor (Fig. 11 B). Complementary experiments, for example, performing raster image correlation spectroscopy in the vicinity of the droplet interface as was recently done (50), may yield additional insights. Nonetheless, future work will be required to better understand the origin of these apparent interfacial resistance effects (56); this could potentially shed light on novel biological functions associated with biomolecules that modulate the interfacial properties of intracellular condensates.

Both finite models introduce additional parameters α, D₊, and, for the interfacial resistance model, k. We observed that certain parameter values lead to reduced sensitivity in the predicted <C^∗>(t). For example, a lower α results in reduced sensitivity in the predicted <C^∗>(t) with changes in the parameter D/D₊ (Fig. S11, A–C), and a lower D/D₊ results in reduced sensitivity to the parameter α (Fig. S11, D–F). This suggests that recovery rate for systems that meet these criteria (i.e., small α or D/D₊) is set by either the partition coefficient or diffusivities, respectively. Indeed, we observed that for LAF-1, order of magnitude differences in the input value of α resulted in little difference in the fit D, indicating that LAF-1 was predicted to be limited by diffusivities. Although this was not an issue for fitting D of LAF-1, using the 3D finite model to fit for α using the known values for D/D₊ would result in α-values that are not meaningful. Thus, it is necessary to determine that the model is sensitive to different values of the fit parameter in the regime that is relevant for that system.

Diffusivity values have been widely used to infer viscosity values, assuming bleached components diffuse as dilute, spherical solutes in a manner predicted by the Stokes-Einstein relation. Thus, the accuracy of the measured diffusion coefficient can also greatly affect viscosity estimates. One important consideration is whether conformationally heterogeneous intrinsically disordered proteins diffuse as spherical solutes. Moreover, whether the high concentrations inside condensed phases, from a semidilute (27) to a higher overlap regime (19), allow for Stokes-Einstein predicted scaling of diffusivity to viscosity is not well understood. In some cases, more complicated polymer models such as reptation (57) may better predict the relation between diffusivity and viscosity. Finally, as shown previously, probes below or on the same size scale as the droplet mesh size experience different apparent viscosities (27). We anticipate that such considerations will provide valuable insights into the connection between properties and molecular dynamics, which is likely key to understanding their connection to condensate function.

Conclusion

Because of the simplicity of performing a FRAP experiment, FRAP is widely used to qualitatively assess the material state of condensates and sometimes to estimate diffusion coefficients. However, several confounding effects presented here, including dimensionality and breakdown in infinite boundary and local equilibrium assumptions, may lead to misinterpretation of FRAP data. We have demonstrated here order-of-magnitude differences in the estimated diffusion coefficients depending on the model used. Choosing a model with assumptions that meet experiments will yield meaningful estimates for the diffusion coefficient. These estimates will not only enable better comparison to literature values but will also allow the rapidly growing biomolecular phase-separation field to elucidate the link between diffusivity, material properties, and function of intracellular condensates.

Author Contributions

Conceptualization, N.O.T., C.P.B., and H.A.S.; investigation, N.O.T. and M.T.W.; analysis, N.O.T.; development of mathematical models, N.O.T and H.A.S.; writing, N.O.T., M.T.W., C.P.B., and H.A.S.

Editor: Rohit Pappu.