Abstract
We develop a Bayesian nonparametric framework to analyze single molecule FRET (smFRET) data. This framework, a variation on infinite hidden Markov models, goes beyond traditional hidden Markov analysis, which already treats photon shot noise, in three critical ways: (1) it learns the number of molecular states present in a smFRET time trace (a hallmark of nonparametric approaches), (2) it accounts, simultaneously and self-consistently, for photo-physical features of donor and acceptor fluorophores (blinking kinetics, spectral cross-talk, detector quantum efficiency), and (3) it treats background photons. Point 2 is essential in reducing the tendency of nonparametric approaches to overinterpret noisy single molecule time traces and so to estimate states and transition kinetics robust to photophysical artifacts. As a result, with the proposed framework, we obtain accurate estimates of single molecule properties even when the supplied traces are excessively noisy, subject to photoartifacts, and of short duration. We validate our method using synthetic data sets and demonstrate its applicability to real data sets from single molecule experiments on Holliday junctions labeled with conventional fluorescent dyes.
Graphical Abstract
INTRODUCTION
Single molecule experiments provide information on properties of individual molecules free of bulk averaging.1–3 In a typical smFRET experiment, the molecule under investigation is labeled with a pair or fluorophores selected specifically to allow for Förster resonance. During measurements, upon excitation, one of the fluorophores, designated as donor, may relax radiatively or may transfer energy nonradiatively to the other fluorophore, designated as the acceptor. Following an energy transfer event, the acceptor may subsequently radiatively relax.4–9 Radiative relaxation of either donor or acceptor typically result in the emission of a photon at the appropriate wavelength (determined by the emitting fluorophore) which can be detected and recorded for further analysis.1,3,10
The efficiency of energy transfer depends on the physical separation of the fluorophores,11,12 which can be used to identify distinct conformational molecular states3,10 or gauge intra-molecular distances.13,14 For this reason, since the very first smFRET experiments,15 this technique has become a workhorse across biophysics and biochemistry.
As smFRET measurements employ conventional fluorescence microscopy setups, background photons and shot noise have always presented analysis challenges that, in conjunction with experimental improvements, have motivated the development of an array of sophisticated analysis methods over the years.1,2,16–23 Through careful manipulation of the acquired measurements, under some circumstances these methods denoise the data and robustly resolve dynamics.
Predominant among the existing analysis methods are those based on hidden Markov models (HMM), for example.1,16,17,20,24–35 Typically, such methods model the molecule as undergoing sudden transitions between discrete states of characteristic efficiencies governed by a Markovian (i.e., memoryless) switching process.
The main advantage of HMM formulations is that they robustly cope with the inevitable noise in the supplied data, since, additionally to the stochasticity inherent from the molecule’s state transitions, they also simultaneously and self-consistently account for stochasticity in the generation of the observations themselves (i.e., the “emission” properties). Thus, in the overall HMM picture, dynamics and emission properties are represented by a doubly stochastic process and general purpose statistical methods, e.g., maximum likelihood or Bayesian estimators, are invoked in their training.1
Nevertheless, major limitations of the HMM framework stem from the difficulties involved in the characterization of the molecule’s state space. For example, a molecule with two states requires an HMM containing dynamic and emission parameters for precisely two states, while a molecule with four states requires a HMM that contains parameters appropriate for four states, and so forth. Since most often the size of the molecule’s state space is unknown and needs to be obtained simultaneously with the rest of the estimates, ad hoc or computationally expensive procedures must occur in a preprocessing stage before a HMM is invoked.1 Such weakness has severe implementation consequences and misidentification of the correct state space size in the preprocessing stage may lead to severe under- or overfitting with disastrous effects on the resulting estimates.36
For relatively clear data sets, a specification of the size of the molecule’s state space can be obtained safely in preprocessing or postprocessing, for example, with information theory,16 maximum evidence,17 or even plain thresholding.21 However, for heavily noisy data sets, an independent estimation of the state space size might be difficult or impossible altogether. This is particularly apparent in the analysis of measurements obtained at fast acquisition rates (i.e., short exposure times) in either confocal of widefield setups.37 In such cases, the acquired measurements are produced by a small number of photon detections, typically 10 or less detections per time step, and therefore are contaminated with excessive shot noise. The main disadvantage of HMM is made clear by considering that, for those cases, on one side, it is preferable to use HMM because they cope robustly with excessive noise, but on the other side, excessive noise makes HMM unusable to begin with as the state space required as an input to analysis is unknown.
Recently, infinite hidden Markov models (iHMM) have been proposed to overcome these limitations.38–41 Namely, an iHMM allows denoising in the same manner as a traditional HMM, but unlike HMMs, it also allows simultaneous inference of the size of the state space and the properties of the constitutive states. Similar to any nonparametric method,38,41–43 iHMMs provide global estimates on the measurement generating molecular system without the need to prespecify a certain size for its state space. Instead, an estimate of the size of the state space itself, similar to the properties of each constitutive state, is an output of the very same analysis that needs not be broken into separate preprocessing and postprocessing stages. In the particular case of single molecule data, iHMMs can estimate the entire “spectra” of photoemission rates, kinetic rates, FRET efficiencies, etc. at once irrespectively of the number of peaks contained in each spectrum.38,41,42
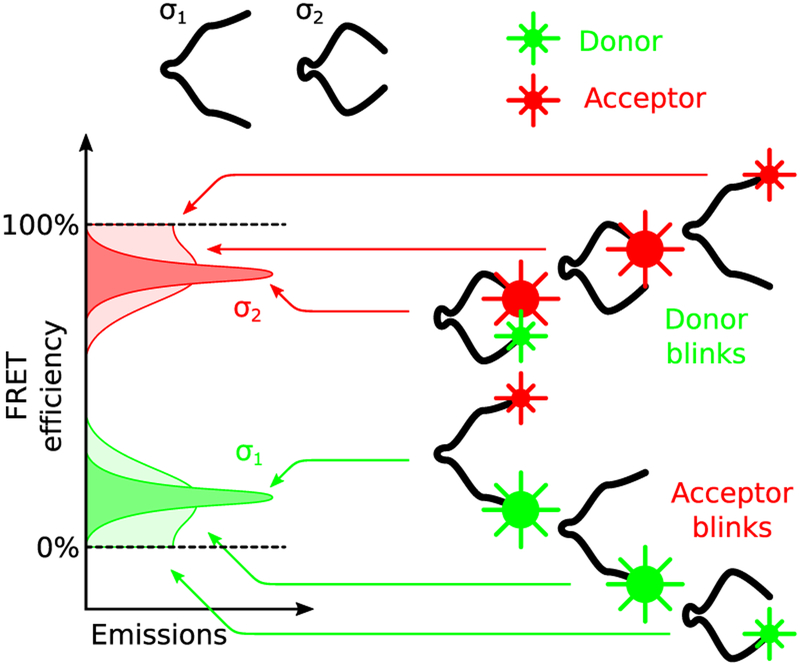
Nevertheless, despite their apparent advantages, iHMM are less robust to model mis-specification than traditional HMM as they are so flexible. Namely, an accurate formulation of the measurement generating molecular system is absolutely necessary to avoid overfitting. In particular, since iHMMs recruit or discard states freely in order to reach agreement between model predictions and the supplied data, they can easily misinterpret fluorophore photoartifacts as additional states. For example, fluorophore blinking, which is particularly pronounced in single molecule assays,44–47 when not explicitly accounted for, is interpreted as sojourns to nonphysical states; for example, see Figure 1. In this case, measurements obtained while donor or acceptor remain dark (i.e., blink), are misinterpreted as artifactual additional states or merged with other states corresponding to totally different conformations.
Figure 1.
Molecule with physical states σ1 and σ2 labeled with a donor/acceptor pair. In the absence of blinking, σ1 is associated with a brighter donor and low FRET efficiency, while σ2 is associated with a brighter acceptor and high FRET efficiency. For well separated distributions, apparent efficiency suffices to distinguish between σ1 and σ2. However, in the presence of blinking, apparent distributions alone may lead to misinterpretation of the molecule’s state since low efficiencies may be observed while the molecule is at σ2 and, vice versa, high efficiencies may be observed while the molecule is at σ1.
In this study we employ, iHMMs and propose a novel formulation to model and analyze smFRET measurements that combine nonparametric statistics1,38,41,42 with an explicit representation of the fluorophore photophysics. Our method uses the denoising advantages of traditional HMM while avoiding the associated state space size restrictions inherent to HMMs. To achieve this, we carefully formulate the measurement process itself accounting for the photophysics on the individual donors and acceptors in addition to other features such as spectral cross-talk and detector quantum efficiency.
METHODS
In this section, we first formulate the experimental system that generates smFRET measurements. Subsequently, we describe the necessary mathematical machinery to obtain estimates, and finally, we describe the acquisition of example data sets that are used in the Results section that follows.
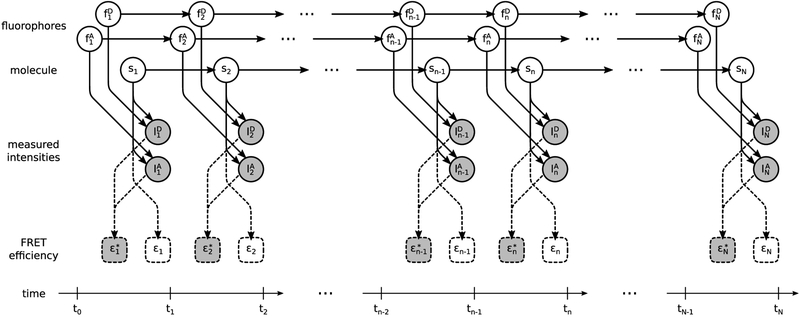
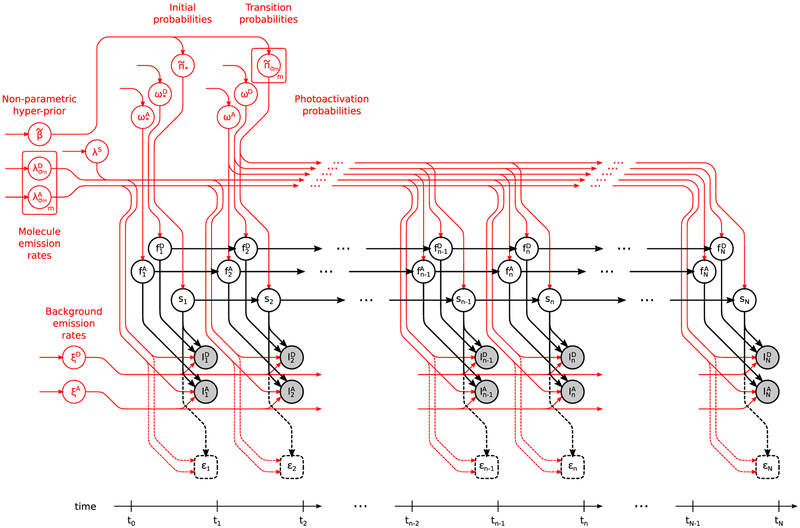
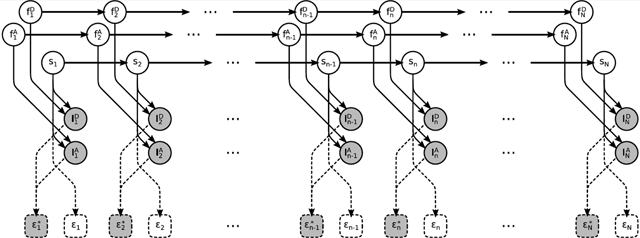
A graphical summary of the formulation employed for the description of the involved physics, described below, is shown in Figure 2, while a more detailed summary, including statistical considerations described next, is shown in Figure 3. We also provide a comprehensive summary of our notation conventions in Appendix A in the Supporting Information.
Figure 2.
Graphical representation of the physical model formulating a smFRET experiment. Fluorophores and molecule , , and sn evolve stochastically through time (left to right). Measured photon intensities and in the donor and acceptor channels are determined by (i) the photoemission rates associated with sn, (ii) the photophysical state of the fluorophores, and (iii) shot noise. FRET efficiency depends exclusively on the molecule state sn. By contrast, apparent FRET efficiency depends on the measured intensities and, due to photoartifacts, need not coincide with . Following common convention, in the schematic, stochastic variables are denoted with circles, deterministic variables are denoted with boxes, measurements are shown shaded, and dependencies among the various variables are indicated by arrows. Dashed lines indicate dependences irrelevant to the generation of the measurements.
Figure 3.
Graphical representation of the statistical model used in the analysis of smFRET measurements. The main model structure is shown in black (for details see Figure 2), while variables on which we place priors are highlighted with red. For clarity, dependencies among the model variables caused by cross-talk are not shown; however, such dependencies are included in the model (see eqs 9 and 10).
Model Formulation.
Suppose a single molecule experiment is initiated at time t0 and, subsequently, measurements are assessed at equidistant times tn, which we index by n = 1, …, N, where tN marks the conclusion of the experiment.
In this study, similarly to existing approaches on smFRET16,22,23 as well as other single molecule sys tems,1,18,20,29,34,38,39,48,49 we assume that the measurement acquisition period δt = tn − tn−1 is much faster than any intrinsic molecular or photophysical rate present in the molecular complex under investigation. As a result, we may safely assume that the physical states of the molecule and the fluorophores remain unchanged between successive assessments and that molecular state transitions coincide with tn.
Molecule and Fluorophore Dynamics.
During the time course of the experiment, the molecule may transition stochastically from one state to another.1,16,18,22,23 Let σm, with m = 1, …, M, denote all possible distinct molecular states that the system has access to (state space). For instance, in this study we use σm to represent conformational states that correspond to different characteristic distances (and, thus, FRET efficiencies). Of course, in practice M and the other parameters that are introduced below are unknown. So, once we present the formulation, which, for the time being, considers parameters as known, we will describe a method appropriate for inferring their values.
Let sn, with n = 1, …, N, denote the state of the molecule between tn−1 and tn. That is, s1→s2→⋯→ sN is the sequence of successive states σm that the molecule follows during the experiment. Also, let denote the probability that the molecule, within one δt, transit from σm to σm′, and, to facilitate the presentation that follows, let gather all transition probabilities departing from σm.
In this study, similarly to the existing approaches,1,16,18,22,23,38,39,48 we assume plain Markovian kinetics
| (1) |
Following the common statistical notation, in this study we use ~ to denote that the random variables on the left-hand side follow, i.e., obey the statistics implied by, the probability distribution on the right-hand side. For instance, eq 1 in other words reads, given that the molecule departs from a state sn−1, its next state sn is chosen from σ1, …, σM according to the probabilities in .
Between tn−1 and tn, while the molecule resides in sn, each fluorophore may be either bright (i.e., capable of emitting photons) or dark (i.e., incapable of emitting photons) independently from the other one.44 To facilitate the description that follows, let and be indicator variables that attain values of 1, when the fluorophores are bright, or 0, when the fluorophores are dark. For simplicity, we also assume plain Markovian kinetics, which in this case take the form
| (2) |
| (3) |
Here, denotes the probability of the donor returning to the bright state given that it departs from the dark one and denotes the probability of the donor remaining at the bright state given that it departs from the bright one. A similar notation is applied for the acceptor’s probabilities and .
Finally, at the very onset of the experiment we assume that molecular and fluorophore states obey
| (4) |
| (5) |
| (6) |
where we have to adopt probabilities and and separately from those introduced earlier, since the states s1, , and driving the very first measurement of the experiment lack predecessors to which we can relate their dynamics.
Measurements Generation.
Suppose and denote the photon intensities recorded in the donor and acceptor channels between tn−1 and tn. Considering that individual photoemissions and photodetections happen stochastically and independently from each other, at least at the time scales relevant to smFRET,10,50,51 we arrive at the following shot-limited formulation
| (7) |
| (8) |
where δτ is the exposure period, which typically is only a fraction of the data acquisition period δt, and qD and qA are the quantum yields52 for photodetection (i.e., detector quantum efficiency) at the donor’s and acceptor’s wavelengths, respectively. In this study, we focus on photon detections. As such, the rates and refer only to those photons that reach the detectors applied on the two channels. In other words, and exclude photons that stray away from the objective or are otherwise blocked by filters and pinholes.
Under FRET, we assume photoemission rates of the fluorophores and unique to each σm; hence, we can relate the molecule’s state sequence to the emission rates driving the recordings in the individual channels. Specifically, as the molecule follows s1→s2→⋯→ sN, the donor’s photoemissions are driven by rates and the acceptor’s photoemissions are driven by rates . Further, assuming separate background rates ξD and ξA in the donor and acceptor channels, respectively, that remain constant throughout the experiment, we arrive at the following photodetection rates for the individual channels
| (9) |
| (10) |
where λS is the donor’s photoemission rate without FRET and other new quantities appearing above are defined shortly.
Accordingly, the donor’s and acceptor’s photoemission rates and , which are linked to the molecule’s state sn, contribute to the recordings in the two channels only when both fluorophores are in their bright photostate, i.e., and , while, when at least one of the fluorophores is in its dark photostate, the recordings are unlinked with the molecule’s state sn. In the latter case, the acceptor does not contribute at all to the recordings, either because it cannot emit photons, e.g., , or because it cannot receive FRET, e.g., ; similarly, the donor either does not contribute to the recordings at all because it resides in its dark photostate, i.e., , or contributes with photorate λS since it cannot transmit FRET, i.e., and . These combinations of fluorophore photostates and photo-emission rates are summarized in Table 1.
Table 1.
Summary of Fluorophore Photostates and Associated Photoemission Rates
| FRET | molecule state sn | donor photostate | acceptor photostate | donor photoemission rate contribution | acceptor photoemission rate contribution |
|---|---|---|---|---|---|
| yes | σm | 1 | 1 | ||
| no | σm | 0 | 1 | none | none |
| no | σm | 1 | 0 | λS | none |
| no | σm | 0 | 0 | none | none |
The cross-talk coefficients cD→D and cD→A in eqs 9 and 10 denote the fraction of photons emitted by the donor that are detected in the donor and acceptor channels, respectively, while cA→A and cA→D denote the fraction of photons emitted by the acceptor that are detected in the acceptor and donor channels, respectively. We emphasize that these coefficients refer only to the photons that reach the detectors on either of the two channels and so consistency requires cD→D + cD→A = 1 and cA→D + cA→A = 1, which reduce the number of cross-talk coefficients that need to be specified to only cD→D and cA→A.
Since cross-talk coefficients cD→D, cA→A can be accurately characterized without using and , for example, through a calibration protocol or after photobleaching,53,54 in this study we consider their values given. Similarly, we also consider as given the values of the quantum efficiencies qD and qA which, typically, can be obtained by the specification chart of the detector’s manufacturer.
FRET Efficiency.
According to the preceding description, the characteristic FRET efficiency4–10 associated with a molecular state σm is given by the ratio
| (11) |
where and are the photoemission rates of the donor and acceptor associated with σm, respectively. Accordingly, in our formulation, depends exclusively on the molecular state11,12 (i.e., separation of the fluorophores) and it is not influenced whatsoever by background, shot noise, blinking, or cross-talk artifacts that, when left unaccounted for, compromise the estimates.10
Just to facilitate the comparison with raw data later on, we also use the following “apparent” photoemission and FRET efficiency definitions
| (12) |
These are the naive estimates that one would obtain by simplistically ignoring photoartifacts.
We emphasize that, , , and generally differ from , , and , since the latter are heavily influenced by photoartifacts while the former are not. We also emphasize that, in this study, we use , , and exclusively for illustrative purposes and we do not imply or suggest that these values offer valid estimates of , , and . In fact, as we describe next, we obtain estimates of , , and through Bayesian principles.
Inference Procedure.
The quantities of typical interest in smFRET, for example, photoemission rates, kinetic rates, etc., are represented by model variables in the preceding formulation. Given measured photon intensity time traces in both donor and acceptor channels, and , we follow the Bayesian paradigm to estimate the unknown variables.1,38,42,43,55 Accordingly, our goal from now on is to describe the choices necessary for the construction of a model posterior probability distribution. This probability distribution ranks all possible choices of the involved variables (i.e., values and combinations thereof) according to their agreement with the observed data and and therefore fully summarizes the output of the analysis.1,38,42,43,55
State Space and Molecule Kinetics.
As our goal is to develop a general model that can be applied universally over measurements that may have been obtained from different molecules of the same species or from the same molecule during different time periods, we need to account for states σm that may be absent from individual traces. That is, we need to allow for states that, although physical, might not be present in every single trace. Additionally, by contrast with the available methods, to account for an a priori unspecified number of different states (i.e., an a priori unknown state space size), we use a nonparametric prior that allows for unboundedly many states, i.e., M = ∞.
Accordingly, the question of estimating the number of different states attained by the molecule during a particular experiment is recast in the sense that we estimate the number of different states that are actually visited during a particular experiment.
To avoid ill conditioning,36 in this case overfitting, at the limit M → ∞, we use a nonparametric hierarchical prior
| (13) |
| (14) |
| (15) |
provided by interlacing a Griffiths-Engen-McCloskey and Dirichlet processes, denoted GEM and DP, respectively. With this choice, depending on the supplied traces and , the employed (nonparametric) state space can recruit or discard states as needed from an infinite pool of potential states that otherwise may remain unvisited.38,41,42,56–58
The rationale of using distributions in eqs 13–15 that are based on the Dirichlet processes is that these distributions allow for dynamical clustering. For example, considering the sequence of states visited by the molecule through time, these distributions ensure that states already visited once will be revisited again. This way, Dirichlet processes help to prevent overfitting. However, distributions based on Griffiths-Engen-McCloskey processes allow for the occasional introduction of states that have not been visited before. This way, Griffiths-Engen-McCloskey processes ensure that our model recruits a sufficient number of states thereby avoiding underfitting. Interleaving Dirichlet and Griffiths-Engen-McCloskey processes, as in eqs 13–15, thus ensures that our formulation neither overfits nor underfits the supplied data.38,58
Fluorophore Kinetics.
To be able to infer fluorophore kinetic rates, i.e., photoswitching probabilities, as well initial fluorophore probabilities, we place independent Beta priors on and and , , , and . These are standard choices and we present fine details in Appendix B in the Supporting Information.
Photoemission Rates.
Since fluorophore and background photoemissions generally depend on the level of applied illumination (i.e., laser power) they most often appear statistically dependent. For example, in most experiments high laser power most likely results in brighter fluorophores and also brighter background, and vice versa for low laser power resulting in dimmer fluorophores and dimmer background.
As a result, to assign priors on ξD, ξA, λS, , and , we use a common reference photoemission rate θ and introduce dimensionless scaling factors ρD, ρA, κS, , and to adjust for the individual rates. In formal terms, we use
| (16) |
| (17) |
for the donor and acceptor photoemission rates, and also λS = κSθ.
Subsequently, we place independent priors on θ and the factors ρD, ρA, κS, , and which allow fine-tuning of the corresponding dependencies. A detailed description of our choices and the induced priors on the actual photorates ξD, ξA, λS, , and is given in Appendices B and C in the Supporting Information.
Estimation.
The model posterior probability distribution that summarizes our analysis method, in its full form, is
where and gather the scaling factors of the photoemission rates of every molecular state, gathers the transition probabilities between every pair of molecular states, and gather the photoswitching probabilities of the two fluorophores, and and gather the phototrajectories of the two fluorophores.
Although this posterior is well-defined mathematically, due to the nonparametric prior in eqs 13–15, an analytic derivation is impossible. For this reason, we develop a specialized computational scheme that can be used to draw pseudorandom posterior samples. In other words, with the developed scheme, we can compute values and combinations thereof to any of the involved variables which, in turn, may be used to obtain any statistic of interest. As we show in the results below, the computed posterior samples can be used to obtain mean values and credible intervals, or even point estimates. For fine details we refer to the existing literature.38,41,43,59
A working implementation of our computational scheme is available through the Supporting Information and algorithmic details are described in Appendix D in the Supporting Information. We term the current implementation bl-ICON as an abbreviation for “blinking ICON” to distinguished it from our earlier implementations that utilize also Baysean nonparametrics39,48 but are not adapted for photoartifacts.
Data Acquisition.
Synthetic Data.
Synthetic data shown in the Results section (see below) are obtained by standard pseudorandom computer simulations60 of the model described in the Methods section, above. For the generation of these data sets, parameters such as photoemission rates are prescribed each time. For all cases we simulated a total of 1000 steps (assuming a data acquisition period of 100 ms, our traces correspond to 1.67 min of total observation time) and we used a kinetic scheme with three moleculur states, σ1, σ2, and σ3. We adjusted the kinetic probabilities to yield mean dwell times of 25 and 12.5 steps for the molecule states, of 50 and 4 steps for the donor’s bright and dark photostates, and of 25 and 6 steps for the acceptor’s bright and dark photostates, respectively. Precise values are listed on Table 2. Under this scheme, we expect roughly 50–60 molecule transitions and roughly 20–40 visits to the dark state for each fluorophore, on each generated data set. Additionally, in accordance with the experimental data (see below), we have used the baseline values cD→D = 0.90, cA→A = 0.75, and qD = 0.85, qA = 0.75, unless specified otherwise.
Table 2.
Summary of Kinetic Scheme Used in the Generation of the Synthetic Data Sets
| transition parameter | transition probability | |
|---|---|---|
| molecule | 0.96 | |
| 0.04 | ||
| 0 | ||
| 0.04 | ||
| 0.92 | ||
| 0.04 | ||
| 0 | ||
| 0.04 | ||
| 0.96 | ||
| 0.50 | ||
| 0.50 | ||
| 0 | ||
| donor | 0.25 | |
| 0.98 | ||
| 0.80 | ||
| acceptor | 0.15 | |
| 0.96 | ||
| 0.90 |
Experimental Data.
Experimental data shown in the Results section are obtained by DNA strands (IDT DNA) for a biotinylated FRET-labeled Holliday junction:
-
Strand 1
5′-ATTO647N-GGGTGCATAGTGGATTGCAGGG
-
Strand 2
5′-Cy3B-CCCTGCAATCCTGAGCACACCC
-
Strand 3
5′-Biotin-TTTTTTTTTTCCCTGATTCGGACTATGCACCC
-
Strand 4
5′-GGGTGTGCTCACCGAATCAGGG
The fluorophores Cy3B (GE Healthcare Bio-Sciences, PA63101) and ATTO647N (Sigma, 18373–1MG-F) were conjugated to amine-labeled strands 1 and 2, respectively, and then purified with high performance liquid chromatography (HPLC). The Holliday junction was made by mixing the four DNA strands at a final equimolar concentration of 200 pmol each in mixing buffer (1× MB) consisting of 40 mM hydrochloride (Tris-HCl) pH 8.0, 20 mM acetic acid, 1 mM ethylenediaminetetraacetic acid (EDTA), and 12.5 mM magnesium chloride (MgCl2) at room temperature for 2 h.
The Holliday junctions (10–50 pM in 1× MB) were immobilized on a streptavidin-coated glass coverslip (Thorlabs, CG15CH). Briefly, the streptavidin-coated glass was prepared by successively applying 1 mg/mL biotinylated Bovine Serum Albumin (BSA, Sigma, A8549) and 0.5 mg/mL streptavidin (Life Technologies, S888) in buffer A (10 mM Tris-HCl, pH8.0, and 50 mM sodium chloride (NaCl)). All measurements are performed in an oxygen scavenger buffer consisting of 2 mM 3,4-dihydroxybenzoic acid (Sigma, P5630) and 50 nM Protocatechuate 3,4-dioxygenase (Sigma, P8279) prepared in 50% glycerol in 50 mM KCl, 1 mM EDTA, and 100 mM Tris-HCl, pH 8.0. For the benchmarking experiment, Trolox-Quinone (TQ) is added at 7500 μM prepared in dimethyl sulfoxide (DMSO) and exposed with a UV light for 5 min.
The Cy3B donor was excited with a 532 nm laser. Data have been acquired with a TIRF setup on the Nanoimager S Mark II from ONI (Oxford Nanoimager) with the lasers 405 nm/150 mW, 473 nm/1 W, 532 nm/1 W, and 640 nm/1 W and dual emission channels split at 640 nm. Cy3B and ATTO647N emissions have been transmitted and lasers have been reflected by a 405/488/532/635 nm beamsplitter (BrightLine quad-edge super-resolution/TIRF dichroic). Time-lapse images of the emissions were acquired at 10 frames/s, i.e., data acquisition time 100 ms, with a Hamamatsu ORCA-Flash4.0 V3 Digital sCMOS camera. From the acquired images, individual FRET pairs have been isolated manually from the donor/acceptor channels after image registration. To recover Poissonian traces and , image values have been transformed to effective photon counts after characterization of the camera’s read-out(i.e., gain and bias offset) through dark and white exposures as described previously.61
RESULTS
In this section, we apply the method developed for the analysis of example data sets. Initially, we use synthetic photon intensity traces for which ground truth for benchmarking is readily available. Subsequently, we use real data sets obtained from single molecule experiments on Holliday junctions assessed through FRET pairs under different photostability regimes. Fine details on the acquisition of each data set can be found above.
Synthetic Data.
To demonstrate the utility of our method, we start with a simple case where we simulate a hypothetical molecule with three states, relatively stable kinetics and somewhat unrealistically low noise, which we achieve by simulating bright fluorophores. Resulting state trajectory and intensity traces are shown in Figure 4. These are generated by assuming a data aquisition period of 100 ms and photoemission rates in the range 500–3000 photons/s, consistent with the brightest fluorescent dyes under typical laser powers used in smFRET.10 Additionally, the traces are contaminated with low background, accounting for 10% and 5% of the smallest photoemission rate in the donor and acceptor channels, respectively, and low cross-talk, accounting for only 1% cross detected photons on each channel.
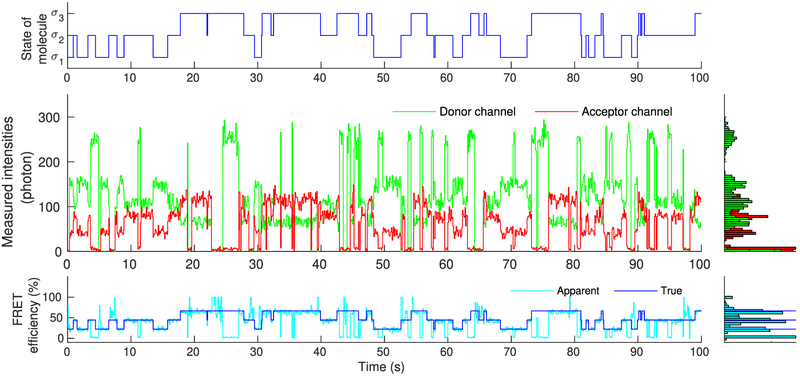
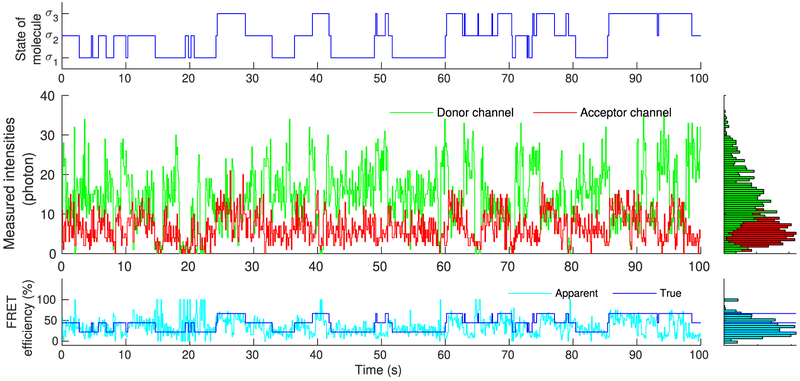
Figure 4.
Simulated molecule, mimicking real single molecule experiments, that transitions stochastically between states σ1, σ2, and σ3 (upper panel). As each of these states is associated with different photoemission rates, recorded intensities change over time (middle panel). Accordingly, FRET efficiency, assessed through the recorded intensities, also changes over time in a manner that reflects the underlying state of the molecule (lower panel). Due to blinking, of either the donor or acceptor, measured intensities occasionally drop to background levels. As a result, near 0% or 100% FRET efficiencies are observed, suggesting dwells to artifactual states beyond σ1, σ2, and σ3.
As a more challenging case, we also consider traces that are generated under less favorable conditions. For example, Figure 5 shows intensity traces produced with photoemission rates in the range 50–300 photons/s and contaminated with background accounting for 25% and 50% of the smallest photoemission rate in the donor and acceptor channels, respectively. In addition, 10% of the donor’s photons leak into the acceptor’s channel and 25% of the acceptor’s photons leak into the donor’s channel.
Figure 5.
Simulated intensity traces that reproduce the conditions of Figure 4. Unlike the earlier example, here photoemission rates are excessively low. As a result, the degrading effect of shot noise is prevalent. In addition, the traces contain a higher background and cross-talk. In summary, the simulated traces are considerably more challenging than those of Figure 4 to analyze.
Indeed, visual inspection of the intensities reveals a strong molecular signature in Figure 4, as it is expected under the favorable conditions simulated. By contrast, due to exaggerated artifacts, visual inspection of the intensities in Figure 5 reveal only a weak signature that is barely distinguishable from background.
As can be seen in Figure 4, despite the low noise, due to the inherent stochasticity in the molecular transitions and photo-detections, some uncertainty concerning the precise instantaneous photoemission rates and FRET efficiencies attained by the molecule remains. Further, donor and acceptor exhibit blinking and they occasionally give rise to near zero recordings (background levels). During such periods, apparent FRET efficiencies approach values near 0% or 100%, which, provided the precise size of the molecule’s state space is unknown, might be misinterpreted as visits to artifactual states of very high or low efficiency additional to the true ones.
The situation becomes even more difficult considering the traces shown in Figure 5. Excessive noise, high background, and cross-talk have a significant impact on the interpretation of the resulting traces, with neither the photoemission rates associated with each molecular state nor even the size of the molecule’s state space visually apparent. In fact, such estimates can be obtained only considering kinetic information through subsequent analysis although fluorophore blinking, in conjunction with high cross-talk and background, eventually degrades the assessment of the kinetics.
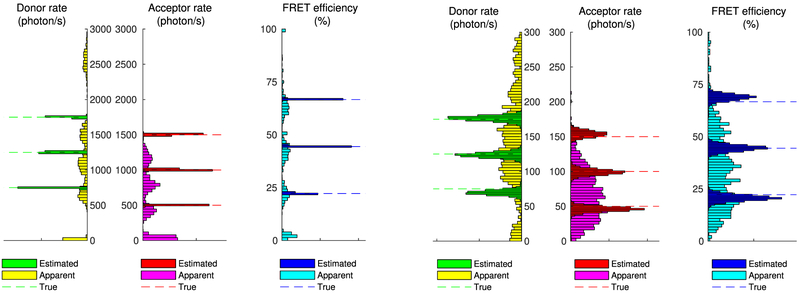
Figure 6 shows estimated photoemission rates and FRET efficiency spectra for the two data sets. As can be seen, concerning the clean traces of Figure 4, our method can identify the three states correctly (despite the occasional fluorophore blinking) and localize them with high certainty in the estimated spectra, as can be deduced from the narrow spread of the peaks. The same remains true even for the heavily corrupted traces of Figure 5; however, as expected, due to increased noise, in the latter case, each one of the estimated states is localized less conclusively than in the clear data set as reflected in the widespread of the estimated peaks.
Figure 6.
Estimated spectra of photoemission rates and FRET efficiency from the intensity traces shown in Figure 4 (left panels) and Figure 5 (right panels). To facilitate comparison, we superimpose estimates (darker boxes), apparent values (lighter boxes), and ground truth values (lines). As can be seen, despite the apparent peaks at low photoemission rates or low/high FRET efficiencies caused by blinking, the estimated spectra correctly identify and localize only the true ones.
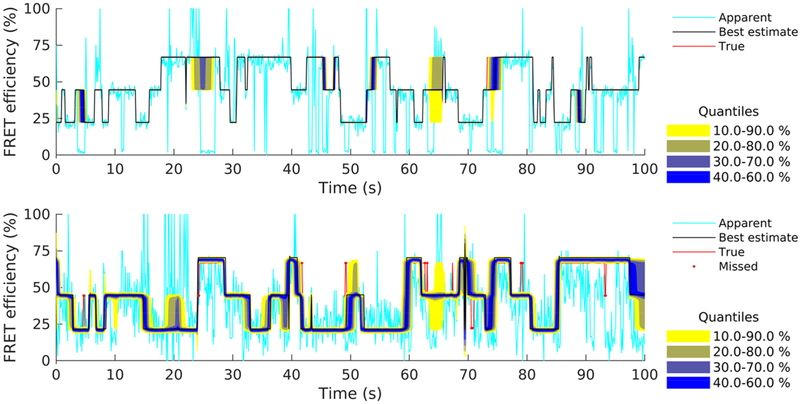
Figure 4 shows estimated FRET efficiency traces corresponding to the two data sets. Both panels show the marginal posteriors for the entire time course of the traces. Given that the method identifies and removes blinking events, it is not surprising that no instantaneous efficiencies are seen approaching 0% or 100% in either case. In particular, for the clear data set (upper panel), the posteriors are sharply peaked (i.e., very conclusive) throughout the trace and, as a result, they can be summarized well by a single representative trace (i.e., best estimated efficiency trace). For example, one characteristic choice for is offered by the efficiency trace nearest to the medians of the marginal that is shown. However, for the corrupted data set (lower panel), the posteriors show large variability over certain time windows, as can be seen from the occasional wide quantiles, for example, near 75 or 100 s. These windows coincide with time periods where at least one of the fluorophores dwells in the dark photostate (i.e., blinking events). As a result, representative traces (i.e., point estimates) during these periods reflect a vague estimate of the true FRET efficiency attained by the molecule, while quantitative conclusions can be drawn only using the entire posterior. At this point, it is worth mentioning, however, that, despite the occasional large variability, from a total of 1000 steps contained in this trace, only 18 fall outside the corresponding 10–90% credible intervals, i.e., less than 2% of all steps are misidentified or identified unreliably.
To assess further the performance of our method on identifying the correct size of the molecule state space, the correct state sequence, and photoblinking events, we have simulated five scenarios of different signal-to-noise ratio (SNR). We have implemented these scenarios by varying the photo-emission rates of both channels by factors as high as 10 to as low as 0.1 and used baseline photoemission rates similar to those used for the traces shown in Figure 5. For each scenario, we generated and analyzed 100 data sets and from each individual analysis we extracted a single best efficiency trace according to the individual marginal posteriors as described above. Following previous work on smFRET analysis,17 we use the number of distinct molecule states in receiving at least 0.05% of the time steps in each data set, as an estimate of the size of the molecule state space. Table 3 summarizes the results. Additionally, we also summarize the fraction of misidentified molecule state and photostate assignments. For this, we have considered a state in as correctly identified when it falls within less than 33.3% of the corresponding one in the ground truth and we have excluded assignments during blinking. As can be seen, our estimates are highly accurate for the higher SNR scenarios, while they become gradually less accurate at the lowest ones. Here, we want to emphasize that as our baseline data sets are similar to those in Figure 5, the lower SNR scenarios utilize traces that are extraordinarily noisy and, therefore, poor performance is expected.
Table 3.
Performance Scores at Different Signal-to-Noise Ratios (SNR)a
| snr | photoemission rates | median state-space size identified | total donor photostates misassigned | total acceptor photostates misassigned | total molecule states misassigned |
|---|---|---|---|---|---|
| high | ×10 | 3 | 0.07% | 1.43% | 0.17% |
| high | ×5 | 3 | 0.16% | 2.40% | 0.91% |
| baseline | ×1 | 3 | 0.20% | 4.38% | 0.47% |
| low | ×0.5 | 3 | 0.56% | 8.97% | 2.52% |
| low | ×0.1 | 1 | 6.79% | 27.50% | 9.80% |
Baseline photoemission rates are set at , , , , , , λS = 3000, ξD = 25, and ξA = 50 photons/s, and varied according to the multipliers shown.
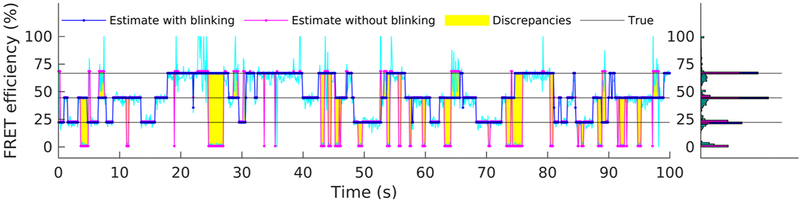
Finally, to highlight the improvements gained by explicitly incorporating blinking into our formulation, in Figure 8 we compare FRET efficiency estimates obtained from the intensities in Figure 4, with and without accounting for blinking. We simulate the latter case by fixing the photostates of both fluorophores and to 1 throughout the trace’s time course; that is, fluorophores are assumed to dwell exclusively in their bright photostate throughout the simulated experiment, see eqs 9 and 10. As mentioned earlier, the full method correctly identifies the size of the molecule state space and also successfully localizes each one of the constitutive states (i.e., total of three states at , , and ; see Figure 7). By contrast, ignoring blinking results in an overpopulation of the molecule’s state space; see Figure 8. Characteristically, at least one additional state is identified and localized at near zero efficiency, coinciding with the periods when at least one of the fluorophores visits its dark state.
Figure 8.
Comparison of estimated FRET efficiency with and without incorporating fluorophore blinking. For both cases, the best estimated FRET efficiency trace (similar to Figure 7) is shown. For these analyses, the intensity traces of Figure 4 have been used.
Figure 7.
Estimated FRET efficiencies from the intensity traces shown in Figure 4 (upper panel) and Figure 5 (lower panel). Estimates are summarized by posterior quantiles (color coded). To facilitate the comparison, we superimpose apparent FRET efficiencies (lighter line), best posterior estimate (black line), and ground truth values (red line). True efficiency values outside the 10–90% credible interval are also highlighted (red dots).
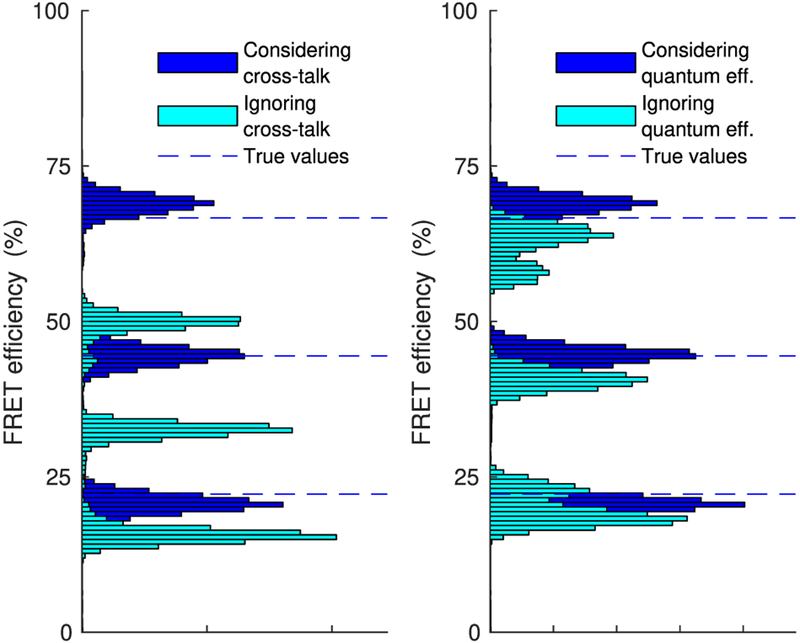
In the same vein, in Figure 9 we show characteristic FRET efficiencies estimated with and without accounting for cross-talk or differences in the detector’s quantum efficiency. For this comparison we have used the corrupted intensity traces shown in Figure 5 and we have implemented the former case by setting both cross-talk coefficients cD→D and cA→A to 100% as compared with the true ones 90% and 75%, respectively, while we have implemented the latter case by setting both detector quantum efficiencies to 100%. As can be seen, while we correctly localize the efficiency peaks when accounting for such features (similar to Figure 7), we are led to underestimation when we do not. The underestimation is particularly pronounced for the higher FRET efficiency, which is now localized significantly below its true value at 70%.
Figure 9.
Comparison of estimated FRET efficiency with and without incorporating cross-talk (left) or differences in detector quantum efficiency (right). For both analyses, the intensity traces of Figure 5 have been used.
Experimental Data.
To assess the performance of our method on experimental smFRET data, we used intensity measurements obtained from Holliday junctions62 labeled with standard fluorophores, Cy3B and ATTO647N. Since Holliday junctions in our setting exhibit stable kinetics (i.e., long dwells on the same molecular state) and also because the applicability of HMM based methods on the identification of state transitions in Holliday junctions has been demonstrated before,62,63 here we focus on benchmarking our method on the characterization of blinking photoartifacts. In the experimental setting described earlier, our FRET pairs probe the transitions between the two junction isomers. The precise transition rates between the isomers probed are sensitive to junction sequences and buffer conditions64 that have been chosen for investigating Holliday junctions that give robust DNA crystals. Since our focus is on characterizing fluorophore induced photoartifacts, we did not assess at the single molecule level the transition rates between the isomers independently.
Trolox-Quinone (TQ) is a nonblinking reagent commonly employed in single molecule assays and its effects have been characterized65,66 independently. More precisely, due to triplet quenching, increased TQ levels have been shown to increase the photostability of the fluorophores.65,66 In other words, it is well established that the higher the concentration of TQ, the longer the dwells of the fluorophores in their respective bright photostate become. As a result, in order to benchmark our method we obtained intensities employing Holliday junctions under TQ concentrations from as low as 0 as high as 7500 μM.
Following our formulation, and specifically eqs 2 and 3, mean dwell times in the bright photostate of the fluorophores are obtained by
| (18) |
where δt denotes the time between successive intensity assessments and and denote the probabilities of the donor and acceptor remaining in their bright photostate between successive assessments. Similar to the other quantities mentioned thus far, in our framework, TD and TA are estimated through the posterior probability distributions and , respectively, where and denote experimentally obtained intensities.
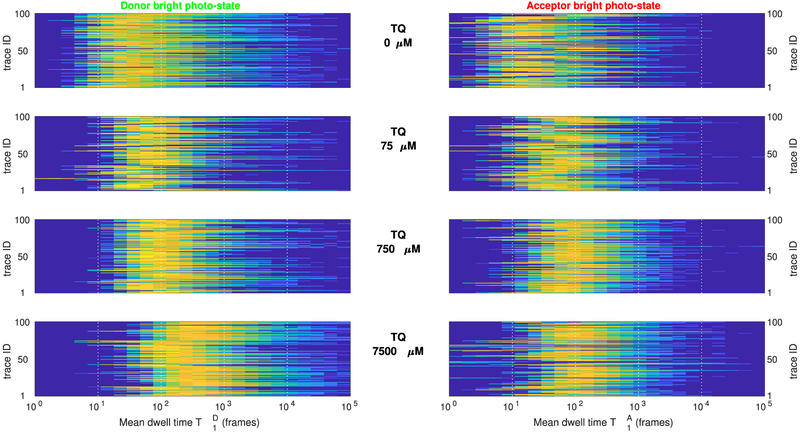
Figure 10 summarizes and obtained from multiple FRET pairs under varying TQ concentrations. Despite the variability of these posteriors found between different FRET pairs at the same concentration, a steady trend of larger TD and TA toward larger concentrations is clearly observed. Indeed, as can be seen from the summary in Figure 11, an approximately 10-fold increase in the estimated mean dwell times is obtained between the measurements at zero and at 7500 μM TQ, in agreement with existing studies.65,66
Figure 10.
Estimated donor and acceptor mean dwell times in the bright photostate from experimental data. Each panel summarizes the posterior probability distributions and (left and right, respectively), obtained from individual intensity traces and , for j = 1, …, 100, under increasing concentrations of the oxygen scavenger Trolox. For clarity, in all panels color encodes and while vertical axes are shown in logarithmic scale. As can be seen, despite the variability found between individual traces, estimated mean dwell times, from ≈102 frames at zero TQ, increase to ≈103 frames at 7500 μM Trolox, indicating an approximately 10-fold increase in the mean duration of the photobright periods for either fluorophore.
Figure 11.
Comparison of the estimated donor and acceptor mean dwell times in the bright photostate from experimental data at 0 and 7500 μM TQ. Each panel shows and , (left and right, respectively), averaged over the traces j = 1, …, 100 shown in Figure 10.
DISCUSSION
Spectroscopic methods based on smFRET rely on distance assessments at the molecular level that are possible through measurements of FRET efficiencies.4–9 In turn, FRET efficiencies are assessed only indirectly through photon intensities.1–3,10 As a result, removal of shot noise, background and cross-talk photons, inherent in intensity measurements, is necessary in learning underlying distances and numbers of molecular states from the data. In addition, equally important is the removal of fluorophore blinking. Characteristically, if blinking is naively ignored, donor/acceptor blinking events over/underestimate the efficiency and accordingly under/overestimate the distances in physical space.
While photoartifacts such as shot noise, background, and cross-talk can be readily addressed by hidden Markov models,1,16,17,20,24–35 blinking imposes a bigger challenge, especially when blinking is encountered by methods meant to estimate the size of the molecule’s state space, such as iHMM and related nonparametric approaches,1,38–41,67,68 as it is typically the case in biochemical or biophysical applications.
Here we have presented a comprehensive method that formulates smFRET measurements and provides a principled method of obtaining estimates that avoids those culprits that render the iHMM difficult to use. We start from the generation of the photon intensities and subsequently we derive a fully Bayesian method of obtaining estimates. In doing so, we specifically account for state spaces of unknown size and this is the very reason, contrary to the available approaches that assume state spaces of known size, we adopt Bayesian nonparametric priors.1,38,39,41,68
Our method operates on photon intensity assessments where individual photon arrivals are binned (i.e., downsampled), usually during the actual experiment, over certain time windows (e.g., exposures) that may be small relative to the total duration of an experiment but still may have significant duration relative to the molecule transitions. As a result, our method may estimate accurately the size of the state space when the involved dynamics are unaffected or affected only minimally by downsampling.69 In other words, our method estimates accurately the size of the state space only when the molecule switches between states slowly relative to the bin size and typical dwell times span or exceed a few time steps such that downsampling artifacts remain inessential.69 By contrast, fast molecule kinetics may give rise to intermediate or aliased states (results not shown) and an overpopulation of the state space similar to the other methods that operate also on intensity assessments.1,17 Overcoming such limitation requires operating on individual photon arrival times directly and requires a fundamentally different nonparametric approach than iHMM that is the focus of future work.
Our formulation extends existing work1,16,17,20,24–35 in at least two unique ways. First, our formulation relaxes the main limitation of the traditional HMM, i.e., that of a restricted or preidentified state space size. Second, our formulation accounts for photokinetics in an explicit way that can be directly interpreted physically.
The resulting method has no need to correct for blinking beforehand and also provides a flexible modeling tool for further development. For example, smFRET time series analysis may be extended to incorporate complex photophysics5–7,70 such as multiple photophysical states with different characteristic times scales (e.g., triplet states) or even multiple photoemission rates (e.g., photoquenched states) that, due to generality, have not been included here. Such extensions require using additional photophysical states for each fluorophore (and the associated number of photoswitching probabilities) instead of only two, such as dark/bright, considered here. The formulation may even be generalized to multicolor smFRET measurements,49,71–76 for example, by the addition of extra fluorophores (and the associated number of photoemission parameters). Both extensions can be readily accommodated in the formulation presented as they involve only minor modifications.
To keep the presentation clear, in this study, we assumed that individual photoemission rates depend on the molecule’s state and the fluorophores’ simplified photostates. Generally, as we explained above, with further extensions, it is possible to account also for photoquenched states, multiple dark states, or photostates with inherent memory. However, since fluorophore photophysics depend largely on the specific FRET pair employed in each experiment as well as other aspects of the experimental protocols used,44 the precise details of such extensions may have to be incorporated on a case-by-case basis not considered here.
CONCLUSIONS
We have presented a novel method that formulates single molecule FRET measurements and can be readily used for the analysis and interpretation of experimental data. Our formulation, which is based on Bayesian nonparametric statistics, relaxes the main limitations of the traditional HMM analysis. Additionally, our formulation explicitly accounts for photokinetics in a way that avoids data misinterpretation, e.g., over- or underfitting. The resulting method is robust to shot noise and has no need to correct the experimental measurements for photoartifacts such as blinking, background, and cross-talk photons, or even differences in the detector’s quantum efficiency, beforehand. Additionally, our method provides a flexible modeling tool that can be used for further development.
Supplementary Material
ACKNOWLEDGMENTS
S.P. acknowledges support from NSF CAREER grant MCB-1719537. R.F.H. was supported by Arizona Biomedical Research Consortium through Grant ADHS18–198867 and National Institutes of Health Director’s New Innovator Award (1DP2AI144247).
Footnotes
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.8b09752.
Software implementation of bl-ICON (ZIP)
Detailed description of the statistical methods developed (PDF)
The authors declare no competing financial interest.
REFERENCES
- (1).Tavakoli M; Taylor J; Li C; Komatsuzaki T; Pressé S Single Molecule Data Analysis: An Introduction. arXiv preprint arXiv:1606.00403, 2016. [Google Scholar]
- (2).Sotomayor M; Schulten K Single-molecule experiments in vitro and in silico. Science 2007, 316, 1144–1148. [DOI] [PubMed] [Google Scholar]
- (3).Ritort F Single-molecule experiments in biological physics: methods and applications. J. Phys.: Condens. Matter 2006, 18, R531. [DOI] [PubMed] [Google Scholar]
- (4).Sekar RB; Periasamy A Fluorescence resonance energy transfer (FRET) microscopy imaging of live cell protein localizations. J. Cell Biol 2003, 160, 629–633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Demchenko AP Introduction to fluorescence sensing; Springer Science & Business Media, 2008. [Google Scholar]
- (6).Gadella TW FRET and FLIM techniques; Elsevier, 2011; Vol. 33. [Google Scholar]
- (7).Periasamy A; Day R Molecular imaging: FRET microscopy and spectroscopy; Elsevier, 2011. [Google Scholar]
- (8).Harris DC Quantitative chemical analysis; Macmillan, 2010. [Google Scholar]
- (9).Helms V Principles of computational cell biology; John Wiley & Sons, 2008. [Google Scholar]
- (10).Roy R; Hohng S; Ha T A practical guide to single-molecule FRET. Nat. Methods 2008, 5, 507–516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Forster T Delocalization excitation and excitation transfer; U.S. Atomic Energy Commission, Institute of Molecular Biophysics, 1965. [Google Scholar]
- (12).Clegg R Fluorescence resonance energy transfer Fluorescence imaging spectroscopy and microscopy; John Wiley & Sons, 1996; Vol. 137, pp 179–251 [Google Scholar]
- (13).dos REMEDIOS CG; Miki M; Barden JA Fluorescence resonance energy transfer measurements of distances in actin and myosin. A critical evaluation. J. Muscle Res. Cell Motil 1987, 8, 97–117. [DOI] [PubMed] [Google Scholar]
- (14).Kilic S; Felekyan S; Doroshenko O; Boichenko I; Dimura M; Vardanyan H; Bryan LC; Arya G; Seidel CA; Fierz B Single-molecule FRET reveals multiscale chromatin dynamics modulated by HP1α. Nat. Commun 2018, 9, 235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Ha T; Enderle T; Ogletree D; Chemla DS; Selvin PR; Weiss S Probing the interaction between two single molecules: fluorescence resonance energy transfer between a single donor and a single acceptor. Proc. Natl. Acad. Sci. U. S. A 1996, 93, 6264–6268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).McKinney SA; Joo C; Ha T Analysis of single-molecule FRET trajectories using hidden Markov modeling. Biophys. J 2006, 91, 1941–1951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Bronson JE; Fei J; Hofman JM; Gonzalez RL Jr; Wiggins CH Learning rates and states from biophysical time series: a Bayesian approach to model selection and single-molecule FRET data. Biophys. J 2009, 97, 3196–3205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Bronson JE; Hofman JM; Fei J; Gonzalez RL; Wiggins CH Graphical models for inferring single molecule dynamics. BMC Bioinf 2010, 11, S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Chodera JD; Noe F Frank Markov state models of biomolecular conformational dynamics. Curr. Opin. Struct. Biol 2014, 25, 135–144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Kelly D; Dillingham M; Hudson A; Wiesner K A new method for inferring hidden Markov models from noisy time sequences. PLoS One 2012, 7, No. e29703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Gopich IV; Szabo A FRET efficiency distributions of multistate single molecules. J. Phys. Chem. B 2010, 114, 15221–15226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Blanco M; Walter NG Methods in enzymology; Elsevier, 2010; Vol. 472, pp 153–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Preus S; Noer SL; Hildebrandt LL; Gudnason D; Birkedal V iSMS: single-molecule FRET microscopy software. Nat. Methods 2015, 12, 593. [DOI] [PubMed] [Google Scholar]
- (24).Keller BG; Kobitski A; Jäschke A; Nienhaus GU; Noe F Complex RNA folding kinetics revealed by single-molecule FRET and hidden Markov models. J. Am. Chem. Soc 2014, 136, 4534–4543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Okamoto K; Sako Y Variational Bayes analysis of a photon-based hidden Markov model for single-molecule FRET trajectories. Biophys. J 2012, 103, 1315–1324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Beausang JF; Zurla C; Manzo C; Dunlap D; Finzi L; Nelson PC DNA looping kinetics analyzed using diffusive hidden Markov model. Biophys. J 2007, 92, L64–L66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Andrec M; Levy RM; Talaga DS Direct determination of kinetic rates from single-molecule photon arrival trajectories using hidden Markov models. J. Phys. Chem. A 2003, 107, 7454–7464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Uphoff S; Gryte K; Evans G; Kapanidis AN Improved Temporal Resolution and Linked Hidden Markov Modeling for Switchable Single-Molecule FRET. ChemPhysChem 2011, 12, 571–579. [DOI] [PubMed] [Google Scholar]
- (29).Noe F; Wu H; Prinz J-H; Plattner N Projected and hidden Markov models for cal- culating kinetics and metastable states of complex molecules. J. Chem. Phys 2013, 139, 184114. [DOI] [PubMed] [Google Scholar]
- (30).Pirchi M; Tsukanov R; Khamis R; Tomov TE; Berger Y; Khara DC; Volkov H; Haran G; Nir E Photon-by-photon hidden Markov model analysis for mi- crosecond single-molecule FRET kinetics. J. Phys. Chem. B 2016, 120, 13065–13075. [DOI] [PubMed] [Google Scholar]
- (31).Müllner FE; Syed S; Selvin PR; Sigworth FJ Improved hidden Markov models for molecular motors, part 1: basic theory. Biophys. J 2010, 99, 3684–3695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).van de Meent J-W; Bronson JE; Wiggins CH; Gonzalez RL Jr Empirical Bayes methods enable advanced population-level analyses of single-molecule FRET experiments. Biophys. J 2014, 106, 1327–1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).van de Meent J-W; Bronson JE; Wood F; Gonzalez RL Jr.; Wiggins CH Hierarchically-coupled hidden Markov models for learning kinetic rates from single- molecule data. arXiv preprint arXiv:1305.3640, 2013. [PMC free article] [PubMed] [Google Scholar]
- (34).Stigler J; Rief M Hidden Markov Analysis of Trajectories in Single-Molecule Experiments and the Effects of Missed Events. ChemPhysChem 2012, 13, 1079–1086. [DOI] [PubMed] [Google Scholar]
- (35).Talaga DS Markov processes in single molecule fluorescence. Curr. Opin. Colloid Interface Sci 2007, 12, 285–296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Lever J; Krzywinski M; Altman N Model selection and overfitting. Nat. Methods 2016, 13, 703–704. [Google Scholar]
- (37).Walt DR Optical methods for single molecule detection and analysis. Anal. Chem 2013, 85, 1258–1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Sgouralis I; Pressé S An Introduction to Infinite HMMs for Single-Molecule Data Analysis. Biophys. J 2017, 112, 2021–2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Sgouralis I; Pressé S ICON: An Adaptation of Infinite HMMs for Time Traces with Drift. Biophys. J 2017, 112, 2117–2126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Hines K; Bankston J; Aldrich R Analyzing single-molecule time series via nonpara-metric Bayesian inference. Biophys. J 2015, 108, 540–556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Lee A; Tsekouras K; Calderon C; Bustamante C; Pressé S Unraveling the Thousand Word Picture: An Introduction to Super-Resolution Data Analysis. Chem. Rev 2017, 117, 7276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Hines K A primer on Bayesian inference for biophysical systems. Biophys. J 2015, 108, 2103–2113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Gelman A; Carlin JB; Stern HS; Dunson DB; Vehtari A; Rubin DB Bayesian data analysis; CRC press: Boca Raton, FL, 2014; Vol. 2. [Google Scholar]
- (44).Ha T; Tinnefeld P Photophysics of fluorescent probes for single-molecule biophysics and super-resolution imaging. Annu. Rev. Phys. Chem 2012, 63, 595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Levitus M; Ranjit S Cyanine dyes in biophysical research: the photophysics of poly- methine fluorescent dyes in biomolecular environments. Q. Rev. Biophys 2011, 44, 123–151. [DOI] [PubMed] [Google Scholar]
- (46).Dickson RM; Cubitt AB; Tsien RY; Moerner W On/off blinking and switching behaviour of single molecules of green fluorescent protein. Nature 1997, 388, 355. [DOI] [PubMed] [Google Scholar]
- (47).Heilemann M; Margeat E; Kasper R; Sauer M; Tinnefeld P Carbocyanine dyes as efficient reversible single-molecule optical switch.J. Am. Chem. Soc 2005, 127, 3801–3806. [DOI] [PubMed] [Google Scholar]
- (48).Sgouralis I; Whitmore M; Lapidus L; Comstock MJ; Pressé S Single molecule force spectroscopy at high data acquisition: A Bayesian nonparametric analysis. J. Chem. Phys 2018, 148, 123320. [DOI] [PubMed] [Google Scholar]
- (49).Lee S; Jang Y; Lee S-J; Hohng S Methods in enzymology; Elsevier, 2016; Vol. 581, pp 461–486. [DOI] [PubMed] [Google Scholar]
- (50).Schuler B Single-molecule FRET of protein structure and dynamics-a primer. J. Nanobiotechnol 2013, 11, S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Hübner CG; Zumofen G; Renn A; Herrmann A; Müllen K; Basché T Pho- ton antibunching and collective effects in the fluorescence of single bichromophoric molecules. Phys. Rev. Lett 2003, 91, No. 093903. [DOI] [PubMed] [Google Scholar]
- (52).Kudryavtsev V; Sikor M; Kalinin S; Mokranjac D; Seidel CA; Lamb DC Combining MFD and PIE for Accurate Single-Pair Förster Resonance Energy Transfer Measurements. ChemPhysChem 2012, 13, 1060–1078. [DOI] [PubMed] [Google Scholar]
- (53).Zal T; Gascoigne NR Photobleaching-corrected FRET efficiency imaging of live cells. Biophys. J 2004, 86, 3923–3939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Bacia K; Petrášek Z; Schwille P Correcting for Spectral Cross-Talk in Dual-Color Fluorescence Cross-Correlation Spectroscopy. ChemPhysChem 2012, 13, 1221–1231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Von Toussaint U Bayesian inference in physics. Rev. Mod. Phys 2011, 83, 943. [Google Scholar]
- (56).MacEachern SN Nonparametric Bayesian methods: a gentle introduction and overview. Communications for Statistical Applications and Methods 2016, 23, 445–466. [Google Scholar]
- (57).Gershman SJ; Blei DM A tutorial on Bayesian nonparametric models. Journal of Mathematical Psychology 2012, 56, 1–12. [Google Scholar]
- (58).Teh Y; Jordan M; Beal M; Blei D Hierarchical Dirichlet processes. J. Am. Stat. Assoc 2012, 101, 1566. [Google Scholar]
- (59).Robert C; Casella G Monte Carlo statistical methods; Springer Science & Business Media, 2013. [Google Scholar]
- (60).Liu JS Monte Carlo strategies in scientific computing; Springer Science & Business Media, 2008. [Google Scholar]
- (61).Huang F; Hartwich TM; Rivera-Molina FE; Lin Y; Duim WC; Long JJ; Uchil PD; Myers JR; Baird MA; Mothes W; et al. Video-rate nanoscopy using sCMOS camera–specific single-molecule localization algorithms. Nat. Methods 2013, 10, 653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (62).McKinney SA; Freeman AD; Lilley DM; Ha T Observing spontaneous branch migration of Holliday junctions one step at a time. Proc. Natl. Acad. Sci. U. S. A 2005, 102, 5715–5720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).Okamoto K; Sako Y State transition analysis of spontaneous branch migration of the Holliday junction by photon-based single-molecule fluorescence resonance energy transfer. Biophys. Chem 2016, 209, 21–27. [DOI] [PubMed] [Google Scholar]
- (64).McKinney SA; Déclais A-C; Lilley DM; Ha T Structural dynamics of individual Holliday junctions. Nat. Struct. Biol 2003, 10, 93. [DOI] [PubMed] [Google Scholar]
- (65).Cordes T; Vogelsang J; Tinnefeld P On the mechanism of Trolox as antiblinking and antibleaching reagent. J. Am. Chem. Soc 2009, 131, 5018–5019. [DOI] [PubMed] [Google Scholar]
- (66).Rasnik I; McKinney SA; Ha T Nonblinking and long-lasting single-molecule fluorescence imaging. Nat. Methods 2006, 3, 891. [DOI] [PubMed] [Google Scholar]
- (67).Calderon CP; Bloom K Inferring latent states and refining force estimates via hierarchical dirichlet process modeling in single particle tracking experiments. PLoS One 2015, 10, No. e0137633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (68).Sgouralis I; Whitmore M; Lapidus L; Comstock MJ; Pressé S Single molecule force spectroscopy at high data acquisition: A Bayesian nonparametric analysis. J. Chem. Phys 2018, 148, 123320. [DOI] [PubMed] [Google Scholar]
- (69).Hamilton JD Time series analysis; Princeton university press: Princeton, NJ, 1994; Vol. 2. [Google Scholar]
- (70).Uphoff S; Holden SJ; Le Reste L; Periz J; Van De Linde S; Heilemann M; Ka- panidis AN Monitoring multiple distances within a single molecule using switchable FRET. Nat. Methods 2010, 7, 831. [DOI] [PubMed] [Google Scholar]
- (71).Hohng S; Joo C; Ha T Single-molecule three-color FRET. Biophys. J 2004, 87, 1328–1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (72).Wang L; Tan W Multicolor FRET silica nanoparticles by single wavelength excita- tion. Nano Lett 2006, 6, 84–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (73).Gambin Y; Deniz AA Multicolor single-molecule FRET to explore protein folding and binding. Mol. BioSyst 2010, 6, 1540–1547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (74).Lee S; Lee J; Hohng S Single-molecule three-color FRET with both negligible spec- tral overlap and long observation time. PLoS One 2010, 5, No. e12270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (75).Lee J; Lee S; Ragunathan K; Joo C; Ha T; Hohng S Single-molecule four-color FRET. Angew. Chem., Int. Ed 2010, 49, 9922–9925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (76).Sobhy M; Elshenawy M; Takahashi M; Whitman B; Walter N; Hamdan S Versatile single-molecule multi-color excitation and detection fluorescence setup for studying biomolecular dynamics. Rev. Sci. Instrum 2011, 82, 113702. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.