Abstract
The liver performs critical physiological functions, including metabolizing and removing substances, such as toxins and drugs, from the bloodstream. Hepatotoxicity itself is intimately linked to abnormal hepatic transport, and hepatotoxicity remains the primary reason drugs in development fail and approved drugs are withdrawn from the market. For this reason, we propose to analyze, across liver compartments, the transport kinetics of fluorescein—a fluorescent marker used as a proxy for drug molecules—using intravital microscopy data. To resolve the transport kinetics quantitatively from fluorescence data, we account for the effect that different liver compartments (with different chemical properties) have on fluorescein’s emission rate. To do so, we develop ordinary differential equation transport models from the data where the kinetics is related to the observable fluorescence levels by “measurement parameters” that vary across different liver compartments. On account of the steep non-linearities in the kinetics and stochasticity inherent to the model, we infer kinetic and measurement parameters by generalizing the method of parameter cascades. For this application, the method of parameter cascades ensures fast and precise parameter estimates from noisy time traces.
Graphical Abstract
INTRODUCTION
Physiological Context of Hepatotoxicity.
Liver transport is a fundamental physiological process whose significance to human health has increased with the proliferation of pharmaceuticals and environmental toxins.1–3 Since the liver is a primary venue for the clearance of xenobiotics, it is particularly susceptible to drug-induced injury in a process known as hepatotoxicity.4–6 Drug hepatotoxicity is associated with inhibition of hepatic transport7–9 through the inhibition of transporters.10,11 Drug effects on hepatic transporters are also a major cause of drug-drug interactions, compromising drug safety and complicating drug dosing.12 Although hepatic side effects are a primary focus of preclinical drug evaluations, drug-induced liver injury affects an estimated several millions of people each year globally and is the most common cause for withdrawal of drugs from the market.13,14
Typically, the effects of a drug on hepatic transport are first evaluated outside animal models such as in studies of vesicle preparations or cultured cells.15 While these simplified systems yield accurate kinetic transport parameters, they also have key limitations: (1) they do not recapitulate the complexity of typical clinical situations, which may include one or more pathological conditions in an individual taking a combination of drugs;16 and (2) they lack the pharmacokinetic processes that determine drug distributions, confounding prediction of in vivo drug effects from in vitro dose-response curves.17,18 In other words, they lack the full complexity of in vivo transport, a non-vectorial process mediated by the simultaneous activity of multiple transporters.19,20
By contrast, laboratory animals, combined with the tools of intravital microscopy (IVM) data,21 provide the necessary physiological context.22 The failure to predict drug transport inside the liver from IVM data, however, highlights fundamental shortcomings in how we exploit the data. In principle, the data contains information on the mechanism of vectorial drug transport involving different transporters, often with overlapping specificities. Imaging methods also, simultaneously, are poised to provide spatial and temporal resolution on how drugs might impact liver transport from their point of uptake into hepatocytes through secretion into the bile, with secretion back into the blood, or flow in the biliary tract.23,24
Recently, some studies have used IVM21,25,26 to monitor transport kinetics of sodium fluorescein27,28 and identify the effects of chronic kidney disease on organic anion transport.29 While rich in structure, the IVM data also presents important challenges toward achieving a complete picture of fluorescein’s transport kinetics as it evolves from the liver capillaries (sinusoids) into the cytosol of the hepatocytes (uptake) and then into the bile canaliculi (canalicular secretion), from which they are cleared into the bile. However, fluorescein’s emission is deeply dependent on its local chemical environment. That is, the fluorescence signal from these probes is sensitive to environmental quenching,30,31 and fluorescein itself may exist in multiple forms, for example, the glucuronidated form,30 across liver compartments.
Thus, in this study, we combine experiments and theory to develop a quantitative method to analyze hepatic transport from fluorescence time measurements using IVM data. In particular, we model the kinetics of hepatic transport, in other words, the kinetics of transport of fluorescent species, using a set of ordinary differential equations (ODEs).32–37 We treat the units of fluorescing species in a particular compartment and their kinetics between liver compartments as hidden (latent) variables and introduce measurement parameters to describe the relationship between the absolute concentrations and fluorescence intensity in different observed regions. We calibrate our ODE model, that is, infer kinetic and measurement parameters, from noisy fluorescence time traces obtained from IVM using the method of parameter cascades.38
Mathematical Methods of ODE Parameter Estimation.
A number of parameter estimation methods exist,39–50 some of which we have recently reviewed.51,52 Here, we adapt the method of parameter cascades,38 which is computationally efficient, maintains good numerical efficiency for estimation of ODE parameters from data,53 works for linear or nonlinear dynamics, straightforwardly estimates measurement parameters, and takes simultaneous advantage of all points in a time trace to perform parameter inference.54 Using this method, ODE solutions are approximated using spline coefficients. These coefficients are estimated with penalized smoothing splines with a roughness penalty term.
MATERIALS AND METHODS
Experimental Methods.
Here, we used quantitative IVM data for transport in the liver of rats with 5/6th nephrectomy (5/6N)55,56 where hepatic drug transport is impacted by chronic kidney disease.29,56 This data was previously published, and information on 5/6N rat models and IVM data collection is given in refs 29 and 21.
ODE Model and Parameter Estimation.
We begin with a set of ODEs describing the evolution in time, t, of a species vector, x, of length m whose elements are units of fluorescence in a particular compartment
| (1) |
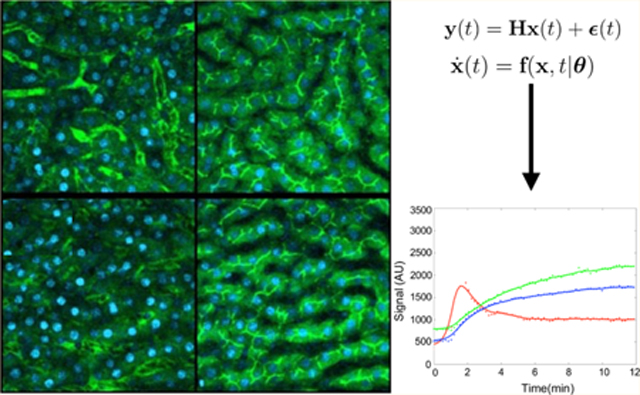
In particular, the species coincide with different chemical forms of fluorescein, that is, modified by being glucuronidated,30 and unmodified forms in each compartment. The vector θ contains parameters (kinetic rates describing transport parameters between liver compartments) whose values are a priori unknown. The vector, x, itself is not directly observed. Rather, we supplement the dynamical above with the following measurement model
| (2) |
where y(t) is a noisy vector of length r describing total units of fluorescence measurements in each compartment at time t and ϵ describes the noise associated with the measurement assuming white noise with zero mean and finite variance (σ2). H is an m × n measurement matrix in the measurement equation (eq 2), which relates the state to the measurement output similar to an equivalent matrix appearing in Kalman filtering.57 Each element of H is called a measurement parameter. For example, a measurement parameter of 0.15 indicates that only 15% of the substrate is observed, while the remaining 0.85 is unobserved. It naturally follows that all measurement parameters take values between [0, 1]. We define a vector of all measurement and kinetic parameters, called structural parameters (θ′ = {θ, H}), and assume that the variances associated with the noise are, a priori, known.
Next, we use the method of parameter cascades38 to learn the parameters from the data. To do so, we first approximate the solution, x(t), of the ODE (eq 1) with a linear combination of K basis functions, as follows
| (3) |
where is the approximation of the curve x in terms of our linear expansion. We use i to iterate over the m species in our model and call the expansion coefficients cik nuisance parameters. The basis functions must themselves approximate the ODE solutions. We selected B-splines as these basis functions allow us to appropriately control solution smoothness across time as warranted by the data, which serves as input.41,53 The number of basis functions must be large enough to adequately represent x,58 and the function must be learned by optimizing a global objective function that, at once, satisfies the ODE and adequately fits the noisy data.59 We then iterate between two optimization routines until a pre-specified criterion for the global optimum is met. In the first optimization step, the nuisance parameters, c, are estimated using a smoothing ODE-penalized criterion in a process known as inner optimization. Within the inner optimization, the structural parameters are kept fixed, and the nuisance parameters are fitted to data by minimizing the following penalized sum of squares.
| (4) |
In the inner optimization, the regularization parameter, λ, controls the tradeoff between fitting the data and fidelity to the ODEs for each xi. Intuitively, for larger noise, as defined by eq 2, we need larger λ as the data themselves become less reliable.
In the outer optimization step, the structural parameters, θ′, are updated by minimizing the following sum of squared errors between the data yi and our estimates
| (5) |
Here, Jout(θ′ | λ, y) is minimized with respect to θ′ by using the Newton–Raphson method. The following pseudo-code (further detailed in Supplementary Information, Appendix A) sketches this procedure.
Algorithm 1
| procedure |
| Set a value for λ |
| Pick initial values for |
| Inner optimization loop: |
| Estimate by minimizing |
| given by Eq. (4) |
| Outer optimization loop: |
| Estimate by minimizing |
| given by Eq. (5) |
| if are changed (to within some preset precision), is reoptimized with respect to then goto Inner optimization. |
| else |
| close; |
To be clear, we explicitly include measurement parameters among the structural parameters. The ability to incorporate measurement parameters constitutes an important generalization of the method of cascades to deal with noisy data that was previously suggested.38 We highlight here that the method of cascades is an important, fast, and general alternative to extended Kalman filters or other Kalman filter variants.60–62 Kalman filters may solve similar problems to that above but may suffer in the case of pronounced non-linearities in the dynamics, that is, eq 1. This is especially relevant to us here as we would like our method to hold for a broad range of non-linear dynamics.63,64
In Supplementary Information, Appendix B, we describe in greater detail how confidence intervals of parameter estimates are determined. Briefly, here, we mention that if the data are poor or data sets are too small for the number of parameters to be estimated, the global objective function maybe flat around its maximum and unable to sharply discriminate between different parameter values (a problem known as “weak identifiability”65,66). By contrast, “structural unidentifiability” arises when model parameters are not independent and different parameter choices result in equally good fits.67
In our case, by using a method drawn from ref 68, we identified which structural parameter(s) is unidentifiable and input their values from other sources before estimating other parameters. To do this, we used an approach proposed in ref 69 detailed in Supplementary Information, Appendix B.
Method Validation.
To test our method, we validate its performance on systems of increasing complexity using sets of simulated (i.e., synthetic) data where the ground truth is known.
Two-State System.
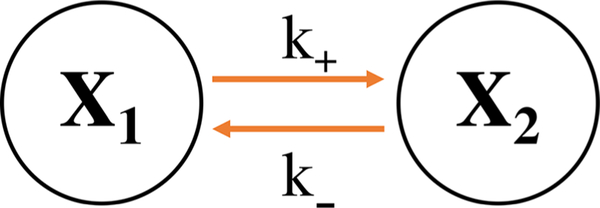
In the simplest example, we have started with a two-state (compartments or pixels) model whose (Markov) kinetics is determined by two transition rates. Figure 1 illustrates this simple two-state Markov model.
Figure 1.
Schematic of two-state Markov model. Here, we have two rates, k+ and k−, corresponding to these two states.
The linear ODEs describing this system are
| (6) |
With measurements
| (7) |
where θ′ = [k+, k−, α, β] is the unknown structural parameter vector. The mean of both ϵ1 and ϵ2 is zero, and the variance of both is assumed to be known; that is, the measurement noise assumed to be Gaussian is fixed in a pre-calibration step. To resolve structural unidentifiability (see Supplementary Information, Appendix B), we must specify either α or β. For concreteness, we presume that from other experiments, it is known that α = 0.5 and thus we are left with three unknown parameters.
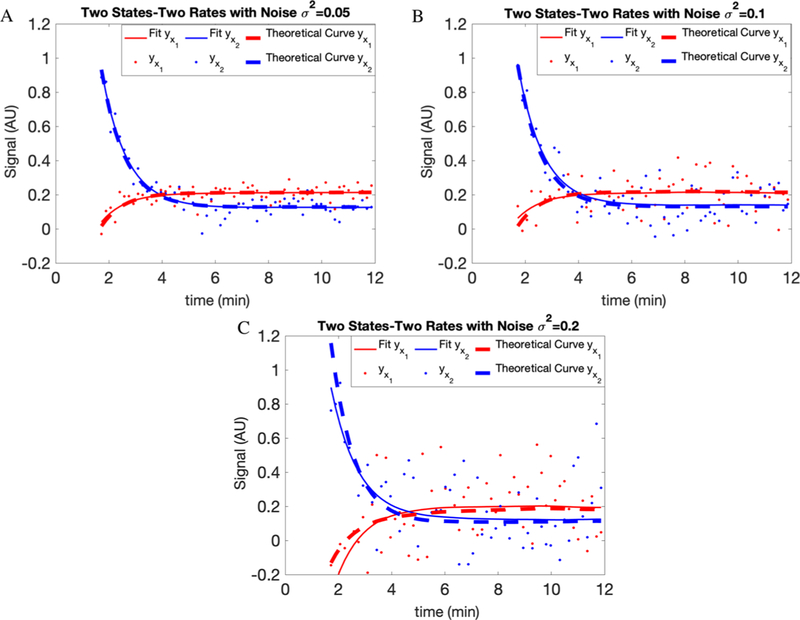
The solutions to eqs 6 and 7 are plotted in Figure 2 for parameter values [0.5, 2, 0.5, 0.3] and known initial conditions
Figure 2.
Fits for the synthetic model shown in Figure 1. For each compartment, the results are shown after adding white noise with variances of (A) 0.05, (B) 0.1, and (C) 0.2. The dots are generated data points, the dashed lines are theoretical curves, and the solid lines are the fits on our data. AU here stands for arbitrary units.
We also tested the accuracy of our approach by adding white noise with different variances, namely 0.05, 0.1, and 0.2, to our simulated data. In Figure 2 and Table 1, we show the results of our fitting and parameter estimation.
Table 1.
Two-State Resultsa
| parameter | k+ | k− | β |
|---|---|---|---|
| Without noise | |||
| true values | 0.5 | 2.0 | 0.3 |
| estimated values | 0.5000 | 2.0000 | 0.3000 |
| standard deviation | 0.0001 | 0.0002 | 0.0001 |
| σ2 = 0.05 for the noise | |||
| true values | 0.5 | 2.0 | 0.3 |
| estimated values | 0.4555 | 1.9854 | 0.3120 |
| standard deviation | 0.0466 | 0.2809 | 0.0206 |
| σ2 = 0.1 for the noise | |||
| true values | 0.5 | 2.0 | 0.3 |
| estimated values | 0.5202 | 2.2808 | 0.3185 |
| standard deviation | 0.0180 | 0.1434 | 0.0650 |
| σ2 = 0.2 for the noise | |||
| true values | 0.5 | 2.0 | 0.3 |
| estimated values | 0.5582 | 1.7767 | 0.3381 |
| standard deviation | 0.1134 | 0.3351 | 0.1266 |
Results of parameter estimation for the two-state system captured in Figure 1 with and without considering noise (the rates are in units of min−1). The standard deviations reported for the structural parameters are taken from one representative run after determining these parameters over multiple runs of a given synthetic data set.
Generalized Two-State System.
We continue testing our approach by generalizing the previous example. That is, we have two decoupled sets of ODEs for the dynamics whose outputs are coupled by measurement. That is, we have
| (8) |
| (9) |
and
| (10) |
The above reflects, for example, two different fluorescent species (the primed and unprimed) hopping between two compartments (subscripted one and two). Measurements on both compartments reveal the total amount of fluorescent material in each compartment but do not discriminate between the primed and unprimed.
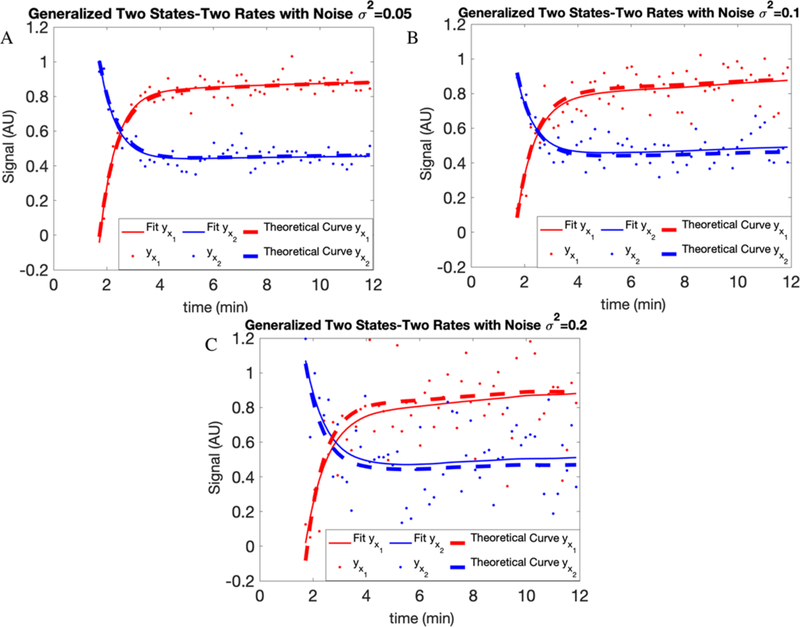
The structural parameter vector here is To eliminate structural unidentifiability, using the procedure highlighted earlier, we specify α = 0.5 and α′ = 0.25. The solutions to eqs 8–10 are plotted in Figure 3 for parameter values [0.3, 0.5, 2.0, 4.0, 0.5, 0.5, 0.25, 0.15] and initial conditions [yX1 (0), yX2 (0)] = [0,1]. The noise, ϵ1 and ϵ2, is treated as we did earlier.
Figure 3.
Fits for generalized two-state systems. For each compartment, the results of adding white noise with variances of (A) 0.05, (B) 0.1, and (C) 0.2 have been shown. The dots are generated data points, dashed lines are theoretical curves, and the solid lines are the fits on our data.
We test the accuracy of our approach by considering white noise with different variances (0.05, 0.1, and 0.2) added to our simulated data. In Figure 3 and Table 2, we show the results of our fitting and parameter estimation with and without noise.
Table 2.
Generalized Two-State Resultsa
| parameter | k+ | k− | β | β′ | ||
|---|---|---|---|---|---|---|
| Without noise | ||||||
| true values | 0.3 | 0.5 | 2.0 | 4.0 | 0.5 | 0.15 |
| estimated values | 0.2991 | 0.5000 | 2.0012 | 4.0001 | 0.5000 | 0.1501 |
| standard deviation | 0.0023 | 0.0001 | 0.0016 | 0.0004 | 0.0008 | 0.0005 |
| σ2 = 0.05 for the noise | ||||||
| true values | 0.3 | 0.5 | 2.0 | 4.0 | 0.5 | 0.15 |
| estimated values | 0.3055 | 0.5101 | 2.0192 | 4.0501 | 0.4938 | 0.1471 |
| standard deviation | 0.0234 | 0.0005 | 0.0737 | 0.0403 | 0.0062 | 0.0043 |
| σ2 = 0.1 for the noise | ||||||
| true values | 0.3 | 0.5 | 2.0 | 4.0 | 0.5 | 0.15 |
| estimated values | 0.2795 | 0.4316 | 1.7738 | 4.2755 | 0.5729 | 0.1421 |
| standard deviation | 0.1064 | 0.1884 | 0.1348 | 0.1229 | 0.1261 | 0.1087 |
| σ2 = 0.2 for the noise | ||||||
| true values | 0.3 | 0.5 | 2.0 | 4.0 | 0.5 | 0.15 |
| estimated values | 0.1993 | 0.6909 | 1.7047 | 3.2478 | 0.4247 | 0.1967 |
| standard deviation | 0.1231 | 0.1983 | 0.1801 | 0.1293 | 0.1129 | 0.0915 |
Results of parameter estimation for the generalized two-state system with and without considering noise (the rates are in units of min −1). See Table 1 for details on the standard deviation.
FitzHugh–Nagumo Model.
Finally, we tested our method with one of the best known models, developed by FitzHugh70 and Nagumo et al. to examine the behavior of spike potentials in the giant axon of squid neurons. While this model is dissimilar in structure to our hepatic transport model, the FitzHugh–Nagumo model, shown below, is often used as a benchmark in ODE parameter estimation problems38,72
| (11) |
This system describes the mutual dependency between voltage across an axon membrane, V, and a recovery variable R summarizing outward currents. In this case, we set up simulated data for parameter values [a, b, c] = [0.2, 0.2, 3] and initial conditions [V(0), R(0)] = [ − 1,1].
In addition to the above, we supplement the dynamical model with a measurement model
| (12) |
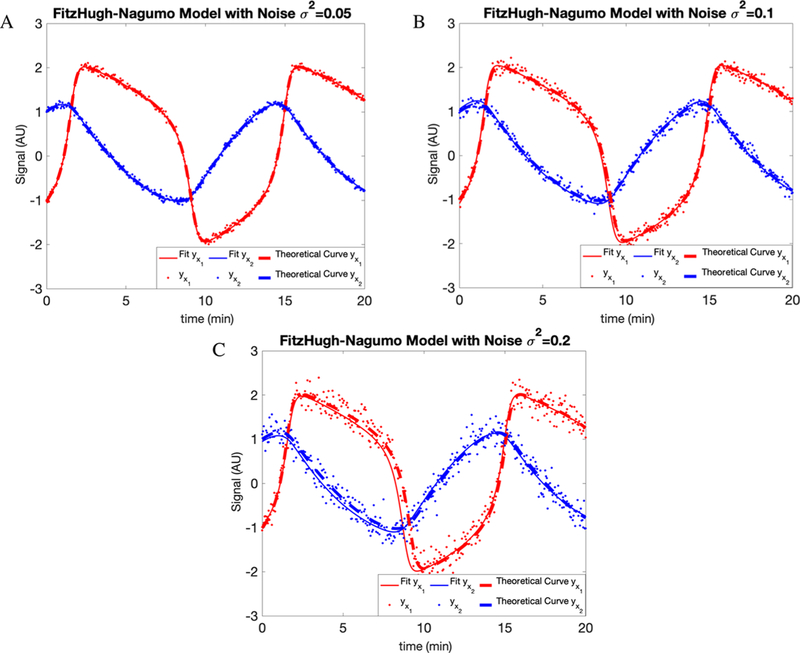
Thus, the parameters to be determined are now θ′ = [a, b, c, α, β]. Identifiability demands that we specify either α or β. For this reason, here, we set α = 0.5. For synthetic data generated using [0.2, 0.2, 3.0, 0.5, 0.75] and initial conditions [V(0), R(0)] = [ − 1, 1], the results are shown in Figure 4 and Table 3.
Figure 4.
Fit to the FitzHugh-Nagumo model supplemented by a measurement model. As before, we consider the following different noise variance levels: (A) 0.05, (B) 0.1, and (C) 0.2. Details in text.
Table 3.
FitzHugh–Nagumo Model Resultsa
| parameter | a | b | c | β |
|---|---|---|---|---|
| Without noise | ||||
| true values | 0.2 | 0.2 | 3 | 0.75 |
| estimated values | 0.2001 | 0.1999 | 3.0001 | 0.7500 |
| standard deviation | 0.0001 | 0.0013 | 0.0032 | 0.0001 |
| σ2 = 0.05 for the noise | ||||
| true values | 0.2 | 0.2 | 3 | 0.75 |
| estimated values | 0.2005 | 0.1995 | 3.0020 | 0.7498 |
| standard deviation | 0.0012 | 0.0016 | 0.0160 | 0.0018 |
| σ2 = 0.1 for the noise | ||||
| true values | 0.2 | 0.2 | 3 | 0.75 |
| estimated values | 0.1895 | 0.1841 | 3.046 | 0.7702 |
| standard deviation | 0.0114 | 0.0280 | 0.0243 | 0.0124 |
| σ2 = 0.2 for the noise | ||||
| true values | 0.2 | 0.2 | 3 | 0.75 |
| estimated values | 0.1543 | 0.2317 | 2.9056 | 0.6924 |
| standard deviation | 0.0189 | 0.0372 | 0.0662 | 0.0726 |
Results of parameter estimation for the FitzHugh–Nagumo model obtained by considering increasing noise as before (the rates are in units of min−1). See Table 1 for details on the standard deviation.
As expected across all models, increasing the noise variance level decreases our parameter estimation accuracy and robustness (i.e., error bar). The amount by which increased noise reduces the accuracy and robustness of our estimates depends on the model under consideration. So much is clear by comparing, with a variance of 0.2 for the white noise, the results from Figure 1 to those of Figure 4.
RESULTS
Full Hepatic Transport Model.
We now construct a model of hepatic transport. Transport in the liver consists of fluorescein transport between and through sinusoid blood vessels into the hepatocytes and then into the canaliculi.21 The data we have collected consists of fluorescence intensity from fluorescein in all three compartments.
To construct our model, we (1) assume no direct transport between sinusoid and canaliculus and (2) assume only three compartments (sinusoid, hepatocyte, and canaliculus). In this case, we designate fluorescein species in the sinusoid, hepatocyte, and canaliculus as S(t), H(t), and C(t), respectively. In full generality, we also consider back flow from the hepatocyte back into the sinusoid.
We treat fluorescein in each compartment as a different species with a different measurement parameter since each compartment presents variable quencher species and concentrations (e.g., binding proteins reducing fluorescein net emission).21 What is more, we consider two forms of fluorescein, both unmodified and glucuronidated as it is known that the majority of fluorescein is glucuronidated within 30 min of intravenous injection.30
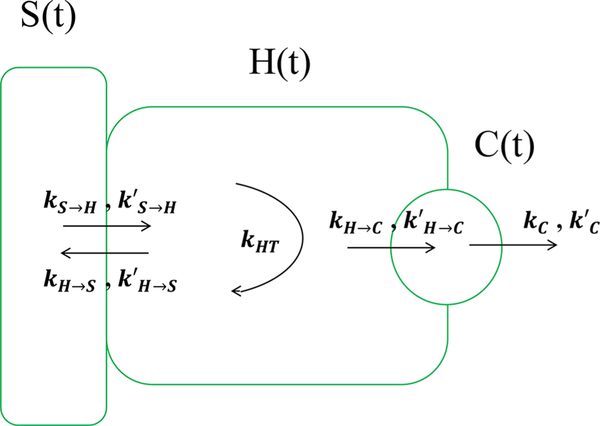
A schematic of the model is provided in Figure 5. In our model, the species vector, previously written as x in eq 1, includes the unit of measurement for unmodified and modified (glucuronidated) fluorescein in each compartment. The quantities are given by S, H, and C for fluorescein and S, H′, and C′ for glucuronidated fluorescein in each compartment. Finally, while we have six species, glucuronidated and unmodified fluorescein in three compartments, we only have three measurements, namely the fluorescence intensity in each compartment.
Figure 5.
Schematic of hepatic transport model used. We consider five transport rates for fluorescein: kS → H for the transport from the sinusoid to the hepatocyte, kH → S from the hepatocyte back to the sinusoid, kH → C from the hepatocyte to the canaliculus, and a loss rate kC from the canaliculus. We also assume glucuronidated fluorescein is transported via the same mechanisms, albeit with rates that have different values, designated by the primed symbols above. Finally, kHT represents the transformation of fluorescein into its glucuronidated form within the hepatocyte. The arrows show the direction of flow.
Based on the model schematic provided in Figure 5, after prespecifying the input rate into the sinusoid thereby setting initial conditions, the dynamical model is given by
| (13) |
and
| (14) |
The measurement model is now
| (15) |
The parameters α, β, and γ and their primes are our measurement parameters for unmodified and glucuronidated fluorescein in each compartment. We note that in this case, the measurement matrix H is no longer square or diagonal; at any given time, we have fewer measurements than number of species in our model.
Furthermore, just as we did with simulated data, we used the identifiability problem procedure (detailed in Supplementary Information, Appendix B) and, on this basis, pre-specified the values for the measurement parameters of both fluorescein and glucuronidated fluorescein in the sinusoid, α = 0.5 and α′ = 0.25, and also the conversion rate between them in the hepatocyte, kHT = 0.5 min−1.
Study on Sham Control and 5/6N Rat Model of Chronic Kidney Disease.
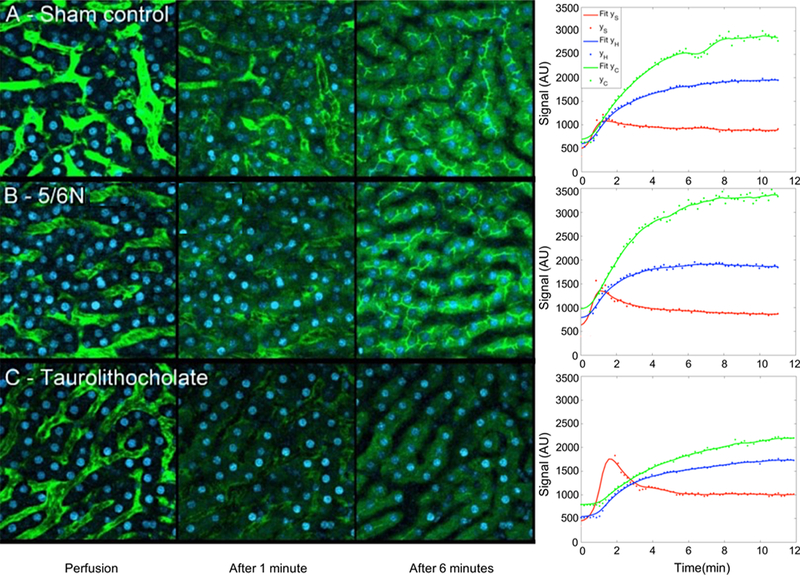
Here, we used IVM data from 5/ 6N rat models as these are often used as models for the study of chronic kidney disease.73 To evaluate the functional outcomes of the 5/6N model on hepatic transport, we collected IVM data29 in the liver of sham control-operated rats Figure 6A. In this case, sham control-operated rats were treated with the same anesthetic and surgical procedures without kidney removal (as opposed to 5/6N with kidneys removed).
Figure 6.
Results of studies of fluorescein transport in rat model sham control, 5/6N, and taurolithocholate (TLC)-treated Livers. (A) We have sample images from a set of collected images from the liver of a rat as the sham control (without removing the kidneys) during intravenous injection of sodium fluorescein. On the right-hand side, we see our method’s fit to the data with kinetic parameters responsible for the fit reported in Table 4. (B) We show results for a 5/6N rat model in which the kidneys were removed. The main difference between (A) and (B) is the change in the rate of hepatic uptake of fluorescein as quantified by the rates from the sinusoid to the hepatocyte between the sham control and 5/6N rats for both glucuronidated and unglucuronidated forms of fluorescein. More details on the rat model are provided in ref 29. (C)We show example images collected from a rat treated by the agent TLC obtained after intravenous injection. The TLC highly reduces the rate of fluorescein uptake into the canaliculus.
The results for these studies are shown in Tables 4 and 5. Similar to previously published work,29 our results also show a meaningful change in hepatic transport in 5/6N as compared to the sham control. Concretely, our analysis reveals that the 5/6N rats, when compared to the sham control-operated rats, exhibited a decrease rate of hepatic uptake of fluorescein. Put differently, we anticipate differences in and between these two cases as hepatic transport is impaired in the 5/6N rat.
Table 4.
Experimental Results Using Sham Control-Operated Ratsa
| parameter | kS → H | kH → S | kH → C | kC | β | γ | β′ | γ′ | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mean values | 2.2440 | 2.1501 | 0.1726 | 0.3802 | 0.6744 | 2.5368 | 1.5433 | 0.9639 | 0.4731 | 0.1393 | 0.1340 | 0.3763 |
| standard deviation | 0.1678 | 0.1082 | 0.1007 | 0.0963 | 0.1324 | 0.0751 | 0.1035 | 0.2076 | 0.0995 | 0.1179 | 0.0514 | 0.0985 |
Parameter estimates for the experimental data in Figure 6A (the rates are in units of min−1).
Table 5.
Experimental Results Using 5/6N Rat Models of Chronic Kidney Diseasea
| parameter | kS → H | kH → S | kH → C | kC | β | γ | β′ | γ′ | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| estimated values | 2.0661 | 2.2067 | 0.1580 | 0.2753 | 0.5385 | 2.1169 | 1.4519 | 0.6943 | 0.6285 | 0.2305 | 0.5092 | 0.2564 |
| standard deviation | 0.1558 | 0.0592 | 0.0347 | 0.0997 | 0.1527 | 0.0372 | 0.2725 | 0.2617 | 0.0590 | 0.0218 | 0.0334 | 0.0125 |
Parameter estimates for the experimental data in Figure 6B (the rates are in units of min−1).
To resolve model unidentifiability, we pre-specify kHT as well as the measurement parameters α and α′ in our model. We chose kHT and those two parameters as their values are the easiest to determine via physiological experiments74–76 or via fluorescence lifetime imaging.77 Our quantitative conclusions are insensitive to exact parameter estimates used initially for kHT, α, and α′.
Effect of Taurolithocholate.
In the previous subsection, we devised a control to assess the functional consequences of the 5/6N model and recovered a change in transport rates from the sinusoid to the hepatocyte. Now, we look at different treatment controls using taurolithocholate (TLC)-treated rats.29 TLC is a pharmaceutical agent that inhibits transport from the hepatocyte to the canaliculus and out from the canaliculus, so we expect these relevant rates to decrease.
TLC-induced cholestasis is a common experimental model for drug-induced cholestasis.78–80 According to previous work, TLC impairs hepatic transport81 and also significantly blocks hepatocyte uptake of sodium fluorescein.80 Thus, by using TLC-treated rat models, we could evaluate our method to see how well it works in estimating transport rates from the hepatocyte to the canaliculus and transport rates from canaliculus out.
The result of blocking hepatocyte uptake of sodium fluorescein using TLC-treated rats on the hepatocyte is shown in Figure 6C. The estimated ODE parameter values for this data set appear in Table 6 where we note that the blocking effect TLC has on secretions to and from the canaliculus recovered by our model as measured by the small values for the rates kH → C and kC.
Table 6.
Experimental Results Using TLCa
| parameter | kS → H | kH → S | kH → C | kC | β | γ | β′ | γ′ | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| estimated values | 1.6657 | 0.9180 | 0.0032 | 0.0026 | 3.3125 | 1.8065 | 1.0885 | 0.8773 | 0.2158 | 0.7079 | 0.1042 | 0.7474 |
| standard deviation | 0.0212 | 0.0332 | 0.0008 | 0.0005 | 0.0695 | 0.0800 | 0.0158 | 0.0286 | 0.0172 | 0.0502 | 0.0112 | 0.0407 |
Results of parameter estimation for the experimental data Figure 6C (the rates are in units of min−1).
kHT, α, and β′ were pre-specified for the same reasons as for the sham control and 5/6N Rat cases above.
DISCUSSION AND CONCLUSIONS
Drug development is a long and costly endeavor; the average drug costs nearly a billion dollars and takes roughly 15 years to bring to market.82,83 Given these costs and timescales, it is critical to identify the efficacy and risks associated with a candidate drug early in the development process. Clearly improving the prediction of drug failures could substantially reduce development costs.83,84 The need for improved tools for preclinical evaluation of drugs is the central focus of the FDA’s Critical Path Initiative.85 Although new drugs are scrutinized for effects on liver function, adverse effects on the liver comprise the most common biological reason for drug failure in the development of new pharmaceuticals86,87 and the most common cause for withdrawal of drugs from the market.12 The failure to predict these problems reflects fundamental shortcomings in the methods that are used in preclinical drug studies.
Our long-term goal is to combine mathematical modeling with IVM experimental data to determine the effects of drugs on hepatic transport. The theoretical framework we develop here provides more accurate and reproducible measures of transport, including pathways that cannot be observed by other methods, supporting more powerful studies of in vivo liver function. By specifically addressing problems tied to fluorescence measurement, our approach could increase the physiological relevance of in vivo studies in ways that could impact preclinical evaluations of the hepatic drug effects thereby extending the predictive power of in vitro drug development studies, minimizing the numbers of animals needed for in vivo studies, and reducing the number of drug failures. As a first step toward developing new methods for the estimation of in vivo transport rate parameters, we have presented an implementation of the known method of parameter cascades for ODE parameter estimation, one that we tailored to IVM experimental data on hepatic transport.
In the context of biophysics, parameter inference methods have a comparatively long history.88–96 The goal of parameter estimation is to find unknown parameters of the model that give the best fit to a set of experimental data.97 While a number of methods tailored to learning parameters from ODEs exist, many of them require that the ODEs be numerically solved,39,40 which entails expensive computation and requires knowing the initial values of the ODE variables. However, efficient computational methods exist that do not require actually solving the ODEs numerically.41–43 A drawback for many of these methods is that they do not take into account error approximation when making parameter inferences, which causes the well-known bias problem.44 On the other hand, we deal with these problems through parameter cascades by defining two nested levels of optimization in our adaptation. In the inner optimization loop, we estimated nuisance parameters (coefficients of basis function). Then, structural parameters are estimated in the outer optimization loop.
Disadvantages of our method include the fact that weight assigned to the penalty term (the regularization parameter) can impact overall inference if unreasonable values are selected.98 This is also true for any Bayesian inference problem if unusual hyperparameters are selected.57 Furthermore, we only determine point estimates rather than full posterior distributions over the unknown parameter values.99–106
Regarding other approaches that focus on parameter estimation such as maximum likelihood and Bayesian mehods,107,108 naive implementations demand that ODEs be solved first.101,104,109 Here, with parameter cascades, this step is unnecessary even for highly non-linear dynamics (as exemplified by the FitzHugh–Nagamo results). On account of its ability to deal with non-linear dynamics as well as measurement parameters, our method should be general enough to deal with non-linearities introduced, say, by having kinetics dictated by Michaelis–Menten ODE forms for all reactions. The latter would be especially relevant to capturing transporter saturation if such information is discernible from the data.
Supplementary Material
ACKNOWLEDGMENTS
We acknowledge IU Collaborative Research Grants (IUCRG) for partial financial support. S.P. also acknowledges support from the NIH NIGMS (R01GM130745-01). We also thank the Indiana Center for Biological Microscopy for providing experimental data for the study.
Footnotes
ASSOCIATED CONTENT
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.9b04729.
Detailed description of the methods developed (PDF)
The authors declare no competing financial interest.
REFERENCES
- (1).Veldhoen M; Hirota K; Westendorf AM; Buer J; Dumoutier L; Renauld J-C; Stockinger B. The Aryl Hydrocarbon Receptor Links TH17-Cell-Mediated Autoimmunity to Environmental Toxins. Nature 2008, 453, 106–109. [DOI] [PubMed] [Google Scholar]
- (2).Brent JA; Rumack BH Role of Free Radicals in Toxic Hepatic Injury II. Are Free Radicals the Cause of Toxin-Induced Liver Injury? J. Toxicol. Clin. Toxicol 2008, 31, 173–196. [DOI] [PubMed] [Google Scholar]
- (3).Osburn WO; Kensler TW Nrf2 Signaling: An Adaptive Response Pathway for Protection Against Environmental Toxic Insults. Mutat. Res., Rev. Mutat. Res 2008, 659, 31–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Sturgill MG; Lambert GH Xenobiotic-induced Hepatotoxicity: Mechanisms of Liver Injury and Methods of Monitoring Hepatic Function. Clin. Chem 1997, 43, 1512–1526. [PubMed] [Google Scholar]
- (5).Holt MP; Ju C. Mechanisms of Drug-induced Liver Injury. AAPSJ. 2006, 8, E48–E54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Navarro VJ; Senior JR Drug-related Hepatotoxicity. N. Engl. J. Med 2006, 354, 731–739. [DOI] [PubMed] [Google Scholar]
- (7).Russmann S; Kullak-Ublick GA; Grattagliano I. Current Concepts of Mechanisms in Drug-induced Hepatotoxicity. Curr. Med. Chem 2009, 16, 3041–3053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Bissell DM; Gores GJ; Laskin DL; Hoofnagle JH Drug-induced Liver Injury: Mechanisms and Test Systems. Hepatology 2001, 33, 1009–1013. [DOI] [PubMed] [Google Scholar]
- (9).Stieger B; Fattinger K; Madon J; Kullak-Ublick GA; Meier PJ Drug- and Estrogen-induced Cholestasis Through Inhibition of the Hepatocellular Bile Salt Export Pump (Bsep) of Rat Liver. Gastroenterology 2000, 118, 422–430. [DOI] [PubMed] [Google Scholar]
- (10).Dawson S; Stahl S; Paul N; Barber J; Kenna JG In vitro Inhibition of the Bile Salt Export Pump Correlates with Risk of Cholestatic Drug-induced Liver Injury in Humans. Drug Metab. Dispos 2011, 40, 130–138. [DOI] [PubMed] [Google Scholar]
- (11).Morgan RE; Trauner M; van Staden CJ; Lee PH; Ramachandran B; Eschenberg M; Afshari C; Qualls CW Jr.; Lightfoot-Dunn R; Hamadeh HK Interference with Bile Salt Export Pump Function is a Susceptibility Factor for Human Liver Injury in Drug Development. Toxicol. Sci 2010, 485–500. [DOI] [PubMed] [Google Scholar]
- (12).Giacomini KM; Huang S-M; Tweedie DJ; Benet LZ; Brouwer KL; Chu X; Dahlin A; Evers R; Fischer V; Hillgren KM; Hoffmaster KA; Ishikawa T; Keppler D; Kim RB; Lee CA; Niemi M; Polli JW; Sugiyama Y; Swaan PW; Ware JA; Wright SH; Yee SW; Zamek-Gliszczyncski MJ; Zhang L. Membrane Transporters in Drug Development. Nat. Rev. Drug Discovery 2010, 9, 215–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Temple RJ; Himmel MH Safety of Newly Approved Drugs: Implications for PrescribingDrugs. JAMA 2002, 287, 2273–2275. [DOI] [PubMed] [Google Scholar]
- (14).Lee WM Drug-induced Hepatotoxicity. N. Engl. J. Med 2003, 349, 474–485. [DOI] [PubMed] [Google Scholar]
- (15).Kostrubsky VE; Strom SC; Hanson J; Urda E; Rose K; Burliegh J; Zocharski P; Cai H; Sinclair JF; Sahi J. Evaluation of Hepatotoxic Potential of Drugs by Inhibition of Bile-acid Transport in Cultured Primary Human Hepatocytes and Intact Rats. Toxicol. Sci 2003. 76, 220–228. [DOI] [PubMed] [Google Scholar]
- (16).Zimmerman HJ Hepatotoxicity: The Adverse Effects of Drugs and other Chemicals on the Liver; Lippincott Williams & Wilkins: Philadelphia, PA, USA,, 1999. [Google Scholar]
- (17).Bjornsson TD; Callaghan JT; Einolf HJ; Fischer V; Gan L; Grimm S; Kao J; King SP; Miwa G; Ni L. The Conduct of in Vitro and In Vivo DrugDrug Interaction Studies: A Pharmaceutical Research and Manufacturers of America (PhRMA) Perspective. Drug Metab. Dispos 2003, 31, 815–832. [DOI] [PubMed] [Google Scholar]
- (18).Wu C-Y; Benet LZ Predicting Drug Disposition via Application of BCS: Transport/Absorption/Elimination Interplay and Development of a Biopharmaceutics Drug Disposition Classification System. Pharm. Res 2005, 22, 11–23. [DOI] [PubMed] [Google Scholar]
- (19).van de Steeg E; Wagenaar E; van der Kruijssen CMM; Burggraaff JEC; de Waart DR; Elferink RPJO; Kenworthy KE; Schinkel AH Organic Anion Transporting Polypeptide 1a/1b-knockout Mice Provide Insights into Hepatic Handling of Bilirubin, Bile Acids, and Drugs. J. Clin. Invest 2010, 120, 2942–2952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).van de Steeg E; Stránecký V; Hartmannová H; Nosková L; Hřebíček M; Wagenaar E; van Esch A; de Waart DR; Elferink RPJO; Kenworthy KE; Sticová E; al-Edreesi M; Knisely AS; Kmoch S; Jirsa M; Schinkel AH Complete OATP1B1 and OATP1B3 Deficiency Causes Human Rotor Syndrome by Interrupting Conjugated Bilirubin Reuptake into the Liver. J. Clin. Invest 2012, 122, 519–528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Babbey CM; Ryan JC; Gill EM; Ghabril MS; Burch CR; Paulman A; Dunn KW Quantitative Intravital Microscopy of Hepatic Transport. IntraVital 2014, 1, 44–53. [Google Scholar]
- (22).Marx U; Walles H; Hoffmann S; Lindner G; Horland R; Sonntag F; Klotzbach U; Sakharov D; Tonevitsky A; Lauster R. ‘Human-on-a-chip’ Developments: A Translational Cutting-edge Alternative to Systemic Safety Assessment and Efficiency Evaluation of Substances in Laboratory Animals and Man? ATLA, Altern. Lab. Anim 2019, 40, 235–257. [DOI] [PubMed] [Google Scholar]
- (23).Chan LMS; Lowes S; Hirst BH The ABCs of Drug Transport in Intestine and Liver: Efflux Proteins Limiting Drug Absorption and Bioavailability. Eur. J. Pharm. Sci 2004, 21, 25–51. [DOI] [PubMed] [Google Scholar]
- (24).Sherlock S; Dooley J. Diseases of the Liver and Biliary System; John Wiley & Sons: New, York, NY, USA, 2008. [Google Scholar]
- (25).Presson RG Jr.; Brown MB; Fisher AJ; Sandoval RM; Dunn KW; Lorenz KS; Delp EJ; Salama P; Molitoris BA; Petrache I. Two-photon Imaging within the Murine Thorax without Respiratory and Cardiac Motion Artifact. Am. J. Pathol 2011,179,75–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Lorenz KS; Salama P; Dunn KW; Delp EJ Digital Correction of Motion Artefacts in Microscopy Image Sequences Collected from Living Animals using Rigid and Nonrigid Registration. J. Microsc 2012, 245, 148–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).De Bruyn T; Fattah S; Stieger B; Augustijns P; Annaert P. Sodium Fluorescein is a Probe Substrate for Hepatic Drug Transport Mediated by OATP1B1 and OATP1B3. J. Pharm. Sci 2011, 100, 5018–5030. [DOI] [PubMed] [Google Scholar]
- (28).Mor-Cohen R; Zivelin A; Rosenberg N; Shani M; Muallem S; Seligsohn U. Identification and Functional Analysis of Two Novel Mutations in the Multidrug Resistance Protein 2 Gene in Israeli Patients with Dubin-Johnson syndrome. J. Biol. Chem 2001, 276, 36923–36930. [DOI] [PubMed] [Google Scholar]
- (29).Ryan JC; Dunn KW; Decker BS Effects of Chronic Kidney Disease on Liver Transport: Quantitative Intravital Microscopy of Fluorescein Transport in the Rat Liver. Am. J. Physiol. Regul Integr. Comp. Physiol 2014, 307, R1488–R1492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Blair NP; Evans MA; Lesar T; Zeimer RC Fluorescein and Fluorescein Glucuronide Pharmacokinetics After Intravenous Injection. Invest. Ophthalmol. Visual Sci 1986, 27, 1107–1114. [PubMed] [Google Scholar]
- (31).Chahal P; Neal M; Kohner E. Metabolism of Fluorescein After Intravenous Administration. Invest. Ophthalmol. Visual Sci 1985, 26, 764–768. [PubMed] [Google Scholar]
- (32).Vanlier J; Tiemann CA; Hilbers PAJ; van Riel NAW Parameter Uncertainty in Biochemical Models Described by Ordinary Differential Equations. Math. Biosci 2013, 246, 305–314. [DOI] [PubMed] [Google Scholar]
- (33).Kwang-Hyun C; Sung-Young S; Hyun-Woo K; Wolkenhauer O; McFerran B; Kolch W. Mathematical Modeling of the Influence of RKIP on the ERK Signaling Pathway. International Conference on Computational Methods in Systems Biology; Springer: Berlin, Heidelberg, 2003, pp 127–141. [Google Scholar]
- (34).Cho K-H; Shin S-Y; Lee H-W; Wolkenhauer O. Investigations into the Analysis and Modeling of the TNF -Mediated NF-B-Signaling Pathway. Genome Res. 2003, 13, 2413–2422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Swat M; Kel A; Herzel H. Bifurcation Analysis of the Regulatory Modules of the Mammalian G1/S Transition. Bioinformatics 2004, 20, 1506–1511. [DOI] [PubMed] [Google Scholar]
- (36).Tyson JJ; Chen K; Novak B. Network Dynamics and Cell Physiology. Nat. Rev. Mol. Cell Biol 2001, 2, 908–916. [DOI] [PubMed] [Google Scholar]
- (37).Voit EO Computational Analysis of Biochemical Systems: A Practical Guide for Biochemists and Molecular Biologists; Cambridge University Press: Cambridge, U.K, 2000. [Google Scholar]
- (38).Ramsay JO; Hooker G; Campbell D; Cao J. Parameter Estimation for Differential Equations: A Generalized Smoothing Approach. J. R. Stat. Soc. Series B Stat. Methodol 2007, 69, 741–796. [Google Scholar]
- (39).Bard Y. Nonlinear Parameter Estimation; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- (40).Biegler LT; Damiano JJ; Blau GE Nonlinear Parameter Estimation: A Case Study Comparison. AIChE J. 1986, 32, 29–45. [Google Scholar]
- (41).Ramsay JO Functional data analysis. Encycl. Stat. Sci 2006, 4, 37–111. [Google Scholar]
- (42).Brunel NJ-B Parameter Estimation of ODEs via Non-parametric Estimators. Electron. J. Statist 2008, 2, 1242–1267. [Google Scholar]
- (43).Chen J; Wu H. Efficient Local Estimation for Time-varying Coefficients in Deterministic Dynamic Models with Applications to HIV-1 Dynamics. J. Am. Stat. Assoc 2008, 103, 369–384. [Google Scholar]
- (44).Conrad PR; Girolami M; Sarkka S; Stuart A; Zygalakis K. Probability Measures for Numerical Solutions of Differential Equations. arXiv preprint arXiv:1506.04592, 2015, [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Rosales RA. MCMC for Hidden Markov Models Incorporating Aggregation of States and Filtering. Bull. Math. Biol 2004, 66, 1173–1199. [DOI] [PubMed] [Google Scholar]
- (46).Siekmann I; Wagner LE II; Yule D; Fox C; Bryant D; Crampin EJ; Sneyd J. MCMC Estimation of Markov Models for Ion Channels. Biophys. J 2011, 100, 1919–1929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Girolami M; Calderhead B. Riemann Manifold Langevin and Hamiltonian Monte Carlo Methods. J. R. Stat. Soc. Series B Stat. Methodol 2011, 73, 123–214. [Google Scholar]
- (48).Dondelinger F; Husmeier D; Rogers S; Filippone M. ODE Parameter Inference using Adaptive Gradient Matching with Gaussian Processes. AISTATS 2013, 216–228. [Google Scholar]
- (49).Calderhead B; Girolami M; Lawrence ND Accelerating Bayesian Inference Over Nonlinear Differential Equations with Gaussian Processes. Advances in neural information processing systems. 2009, pp 217–224. [Google Scholar]
- (50).Gupta S; Kihara Y; Maurya MR; Norris PC; Dennis EA; Subramaniam S. Computational Modeling of Competitive Metabolism Between ω3-and ω6-polyunsaturated Fatty Acids in Inflammatory Macrophages. J. Phys. Chem. B 2016, 120, 8346–8353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Tavakoli M; Taylor JN; Li C-B; Komatsuzaki T; Pressé S. Single Molecule Data Analysis: An Introduction. Adv. Chem. Phys 2017, 162, 205–305. [Google Scholar]
- (52).Lee A; Tsekouras K; Calderon C; Bustamante C; Pressé S. Unraveling the Thousand Word Picture: An Introduction to Super Resolution Data Analysis. Chem. Rev 2017, 117, 7276–7330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Cao J; Fussmann GF; Ramsay JO Estimating a Predator-Prey Dynamical Model with the Parameter Cascades Method. Biometrics 2008, 64, 959–967. [DOI] [PubMed] [Google Scholar]
- (54).Wang L; Cao J; Ramsay JO; Burger DM; Laporte CJL; Rockstroh JK Estimating Mixed-effects Differential Equation Models. Stat. Comput 2014, 24, 111–121. [Google Scholar]
- (55).Laouari D; Yang R; Veau C; Blanke I; Friedlander G. Two Apical Multidrug Transporters, P-gp and MRP2, Are Differently Altered in Chronic Renal Failure. Am. J. Physiol. Renal. Physiol 2001, 280, F636–F645. [DOI] [PubMed] [Google Scholar]
- (56).Naud J; Michaud J; Leblond FA; Lefrancois S; Bonnardeaux A; Pichette V. Effects of Chronic Renal Failure on Liver Drug Transporters. Drug Metab. Dispos 2007, 36, 124–128. [DOI] [PubMed] [Google Scholar]
- (57).Welch G; Bishop G. An Introduction to the Kalman Filter. University of North Carolina at Chapel Hill: ACM, Inc; 1995, [Google Scholar]
- (58).Zhang X; Cao J; Carroll RJ On the Selection of Ordinary Differential Equation Models with Application to Predator-prey Dynamical Models. Biometrics 2015, 71, 131–138. [DOI] [PubMed] [Google Scholar]
- (59).Cao J; Qi X; Zhao H. Next Generation Microarray Bioinformatics; Springer, 2012; pp 185–197 [Google Scholar]
- (60).Mobed P; Munusamy S; Bhattacharyya D; Rengaswamy R. State and Parameter Estimation in Distributed Constrained Systems. 1. Extended Kalman Filtering of a Special Class of Differential-algebraic Equation Systems. Ind. Eng. Chem. Res 2016, 56, 206–215. [Google Scholar]
- (61).Jazani S; Sgouralis I; Presse S. A Method for Single Molecule Tracking Using a Conventional Single-focus Confocal Setup. J. Chem. Phys 2019, 150, 114108. [DOI] [PubMed] [Google Scholar]
- (62).Jazani S; Sgouralis I; Shafraz OM; Sivasankar S; Presse S. An Alternative Framework for Fluorescence Correlation Spectroscopy. Biophys J. 2019, 116,282a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).Lillacci G; Khammash M. Parameter Estimation and Model Selection in Computational Biology. PLoS Comput. Biol 2010, 6, No. e1000696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Lillacci G; Khammash M. A distribution-matching method for parameter estimation and model selection in computational biology. Int. J. Robust Nonlinear Control 2012, 22, 1065–1081. [Google Scholar]
- (65).Raue A; Kreutz C; Theis FJ; Timmer J. Joining Forces of Bayesian and Frequentist Methodology: A Study for Inference in the Presence of Non-identifiability. Phil. Trans. R. Soc. A 2012, 371, 20110544. [DOI] [PubMed] [Google Scholar]
- (66).Vanlier J; Tiemann CA; Hilbers PAJ; van Riel NAW An Integrated Strategy for Prediction Uncertainty Analysis. Bioinformatics 2012, 28, 1130–1135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (67).Chis O-T; Banga JR; Balsa-Canto E. Structural Identifiability of Systems Biology Models: A Critical Comparison of Methods. PLoS One 2011, 6, No. e27755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (68).Walter E; Pronzato L; Norton J. Identification of Parametric Models from Experimental Data; Springer: Berlin, 1997. [Google Scholar]
- (69).Bellman R; Åström KJ On Structural Identifiability. Math. Biosci 1970, 7, 329–339. [Google Scholar]
- (70).FitzHugh R. Impulses and Physiological States in Theoretical Models of Nerve Membrane. Biophys. J 1961, 1, 445–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (71).Nagumo J; Arimoto S; Yoshizawa S. An Active Pulse Transmission Line Simulating Nerve Axon. Proc. IRE 1962, 50, 2061–2070. [Google Scholar]
- (72).Cao J; Wang L; Xu J. Robust Estimation for Ordinary Differential Equation Models. Biometrics 2011, 67, 1305–1313. [DOI] [PubMed] [Google Scholar]
- (73).Leblond F; Guevin C; Demers C; Pellerin I; Gascon-Barré MG; Pichette V. Downregulation of Hepatic Cytochrome P450 in Chronic Renal Failure. J. Am. Soc. Nephrol 2001, 12, 326–332. [DOI] [PubMed] [Google Scholar]
- (74).Grotte D; Mattox V; Brubaker R. Fluorescent, physiological and pharmacokinetic properties of fluorescein glucuronide. Exp. Eye Res 1985, 40, 23–33. [DOI] [PubMed] [Google Scholar]
- (75).Lee H; Blaufox M. Blood Volume in the Rat. J. Nucl. Med 1985, 26, 72–76. [PubMed] [Google Scholar]
- (76).Bijsterbosch MK; Duursma AM; Bouma JMW; Gruber M. The Plasma Volume of the Wistar Rat in Relation to the Body Weight. Experientia 1981, 37, 381–382. [DOI] [PubMed] [Google Scholar]
- (77).Hato T; Winfree S; Day R; Sandoval RM; Molitoris BA; Yoder MC; Wiggins RC; Zheng Y; Dunn KW; Dagher PC Two-photon intravital fluorescence lifetime imaging of the kidney reveals cell-type specific metabolic signatures. JASN 2017, 28, 2420–2430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (78).Javitt NB; Emerman S. Effect of Sodium Taurolithocholate on Bile Flow and Bile Acid Excretion. J. Clin. Invest 1968, 47, 1002–1014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (79).Layden TJ; Boyer JL Taurolithocholate-induced Cholestasis: Taurocholate but not Dehydrocholate, Reverses Cholestasis and Bile Canalicular Membrane Injury. Gastroenterology 1977, 73, 120. [PubMed] [Google Scholar]
- (80).Roma MG; Peñalva GL; Agüero RM; Rodríguez Garay EA Hepatic Transport of Organic Anions in Taurolithocholate-induced Cholestasis in Rats. J. Hepatol 1994, 20, 603–610. [DOI] [PubMed] [Google Scholar]
- (81).Petzinger E. Transport of Organic Anions in the Liver. An Update on Bile Acid, Fatty Acid, Monocarboxylate, Anionic Amino Acid, Cholephilic Organic Anion, and Anionic Drug Transport. Rev. Physiol., Biochem. Pharmacol 1994, 94, 47–211. [DOI] [PubMed] [Google Scholar]
- (82).Chong CR; Sullivan DJ New Uses for Old Drugs. Nature 2007, 448, 645–646. [DOI] [PubMed] [Google Scholar]
- (83).DiMasi JA; Hansen RW; Grabowski HG The Price of Innovation: New Estimates of Drug Development Costs. J. Health Econ 2003, 22, 151–185. [DOI] [PubMed] [Google Scholar]
- (84).Paul SM; Mytelka DS; Dunwiddie CT; Persinger CC; Munos BH; Lindborg SR; Schacht AL How to Improve R&D Productivity: The Pharmaceutical Industry’s Grand Challenge. Nat. Rev. Drug Discov 2010, 9, 203–214. [DOI] [PubMed] [Google Scholar]
- (85).Karsdal MA; Henriksen K; Leeming DJ; Mitchell P; Duffin K; Barascuk N; Klickstein L; Aggarwal P; Nemirovskiy O; Byrjalsen I; Qvist P; Bay-Jensen AC; Dam EB; Madsen SH; Christiansen C. Biochemical Markers and the FDA Critical Path: How Biomarkers May Contribute to the Understanding of Pathophysiology and Provide Unique and Necessary Tools for Drug Development. Biomarkers 2009, 14, 181–202. [DOI] [PubMed] [Google Scholar]
- (86).Larrey D. Epidemiology and Individual Susceptibility to Adverse Drug Reactions Affecting the Liver. Semin. Liver Dis 2002, 22, 145–156. [DOI] [PubMed] [Google Scholar]
- (87).Larrey D. Drug-induced Liver Diseases. J. Hepatol 2000, 32, 77–88. [DOI] [PubMed] [Google Scholar]
- (88).Sun J; Garibaldi JM; Hodgman C. Parameter Estimation Using Metaheuristics in Systems Biology: A Comprehensive Review. IEEE/ACM Trans. Comput. Biol. Bioinf 2012, 9, 185–202. [DOI] [PubMed] [Google Scholar]
- (89).Chen Z. Bayesian Filtering: From Kalman Filters to Particle Filters, and Beyond. Statistics 2003, 182, 1–69. [Google Scholar]
- (90).Pressé S; Lee J; Dill KA Extracting Conformational Memory from Single-Molecule Kinetic Data. J. Phys. Chem. B 2013, 117, 495–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (91).Pressé S; Ghosh K; Dill KA Modeling Stochastic Dynamics in Biochemical Systems with Feedback Using Maximum Caliber. J. Phys. Chem. B 2011, 115, 6202–6212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (92).Lee J; Pressé S. A Derivation of the Master Equation from Path Entropy Maximization. J. Chem. Phys 2012, 137, No. 074103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (93).Castillo-Hair SM; Sexton JT; Landry BP; Olson EJ; Igoshin OA; Tabor JJ FlowCal: A User-friendly, Open Source Software Tool for Automatically Converting Flow Cytometry Data from Arbitrary to Calibrated Units. ACS Synth. Biol 2016, 5, 774–780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (94).Hebisch E; Knebel J; Landsberg J; Frey E; Leisner M. High Variation of Fluorescence Protein Maturation Times in Closely Related Escherichia Coli Strains. PLoS One 2013, 8, No. e75991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (95).Firman T; Balázsi G; Ghosh K. Building Predictive Models of Genetic Circuits Using the Principle of Maximum Caliber. Biophys. J 2017, 113,2121–2130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (96).Firman T; Wedekind S; McMorrow TJ; Ghosh K. Maximum Caliber Can Characterize Genetic Switches with Multiple Hidden Species. J. Phys. Chem. B 2018, 122, 5666–5677. [DOI] [PubMed] [Google Scholar]
- (97).Gábor A; Banga JR Robust and Efficient Parameter Estimation in Dynamic Models of Biological Systems. BMC Syst. Biol 2015, 9, 74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (98).Cao J; Ramsay JO Generalized Profiling Estimation for Global and Adaptive Penalized Spline Smoothing. Comput. Stat. Data Anal 2009, 53, 2550–2562. [Google Scholar]
- (99).Hines KE A Primer on Bayesian Inference for Biophysical Systems. Biophys. J 2015, 108, 2103–2113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (100).Hines KE; Middendorf TR; Aldrich RW Determination of Parameter Identifiability in Nonlinear Biophysical Models: A Bayesian Approach. J. Gen. Physiol 2014, 143, 401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (101).Epstein M; Calderhead B; Girolami MA; Sivilotti LG Bayesian Statistical Inference in Ion-channel Models With Exact Missed Event Correction. Biophys. J 2016, 111, 333–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (102).Barenco M; Tomescu D; Brewer D; Callard R; Stark J; Hubank M. Ranked Prediction of p53 Targets using Hidden Variable Dynamic Modeling. Genome Biol. 2006, 7, R25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (103).Brown KS; Sethna JP Statistical Mechanical Approaches to Models with Many Poorly Known Parameters. Phys. Rev. E 2003, 68, No. 021904. [DOI] [PubMed] [Google Scholar]
- (104).Vyshemirsky V; Girolami MA Bayesian Ranking of Biochemical System Models. Bioinformatics 2008, 24, 833–839. [DOI] [PubMed] [Google Scholar]
- (105).Sgouralis I; Madaan S; Djutanta F; Kha R; Hariadi RF; Pressé S. A Bayesian Nonparametric Approach to Single Molecule Forster Resonance Energy Transfer. J. Phys. Chem. B 2018, 123, 675–688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (106).Sgouralis I; Pressé S. An Introduction to Infinite HMMS for Single-molecule Data Analysis. Biophys. J 2017, 112, 2021–2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (107).Tsekouras K; Custer TC; Jashnsaz H; Walter NG; Pressé S. A Novel Method to Accurately Locate and Count Large Numbers of Steps by Photobleaching. Mol Biol. Cell 2016, 27, 3601–3615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (108).Chen Y; Deffenbaugh NC; Anderson CT; Hancock WO Molecular Counting by Photobleaching in Protein Complexes with Many Subunits: Best Practices and Application to the Cellulose Synthesis Complex. Mol. Biol. Cell 2014, 25, 3630–3642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (109).Chkrebtii OA; Campbell DA; Calderhead B; Girolami MA Bayesian Solution Uncertainty Quantification for Differential Equations. Bayesian Anal. 2016, 11, 1239–1267. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.