Significance
Pathogens interact with the human microbiome and are often a part of the microbiome themselves. This nestedness permits a great amount of genetic exchange, including resistance for antibiotics. To date, most studies have focused on either resistance evolution itself or the dynamics of the microbiome. In this study, we merge both lines of research and build a composite model to have a full understanding of the resistance evolution in the microbiome. Using this model, we quantify the connection between prior antibiotic use and risk of carrying resistance for a single individual. We identify the relevant characteristics of the treatment history determining the prevalence of resistance, which may help clinicians to make more personalized and precise decisions on the choice of future treatments.
Keywords: plasmid-mediated resistance, gut microbiota, prior treatment, risk factor
Abstract
To understand how antibiotic use affects the risk of a resistant infection, we present a computational model of the population dynamics of gut microbiota including antibiotic resistance-conferring plasmids. We then describe how this model is parameterized based on published microbiota data. Finally, we investigate how treatment history affects the prevalence of resistance among opportunistic enterobacterial pathogens. We simulate treatment histories and identify which properties of prior antibiotic exposure are most influential in determining the prevalence of resistance. We find that resistance prevalence can be predicted by 3 properties, namely the total days of drug exposure, the duration of the drug-free period after last treatment, and the center of mass of the treatment pattern. Overall this work provides a framework for capturing the role of the microbiome in the selection of antibiotic resistance and highlights the role of treatment history for the prevalence of resistance.
Pathogenic bacterial species interact with the microbiome and are often part of the microbiome themselves (1), which makes the problem of antibiotic resistance more challenging both in terms of understanding the drivers of resistance and in terms of management and prevention of resistance. The former challenge arises because the pathogen–microbiome interactions imply that a full understanding of the dynamics of resistance necessitates also a quantitative understanding of the microbial ecosystem inhabiting an individual host. The latter challenge results from the effects of collateral selection and cross-species exchange of resistance that this interaction enables. The grave resistance crisis in enterobacterial infections (2–6) is a case in point for these challenges, as arguably the interactions with the highly diverse microflora and the horizontal genetic transfer of resistance by conjugative plasmids are a major driver of the high level of resistance observed in Enterobacteriaceae.
In recent years, metagenomic studies have generated an unprecedented wealth of data on the composition and dynamics of microbial communities (7–13). However, translating this knowledge into predictions on the impact of the microbiome on resistance evolution is difficult. One way to move from a description of the microbiome to a mechanistic understanding and predicting its effect on antibiotic resistance is mathematical models that integrate both the rich data on microbiome compositions and the processes of resistance evolution. Although there are numerous studies on modeling plasmid-mediated resistance evolution (14–19) and dynamics of the microbiome (20–26), a composite mathematical model which includes both does not exist to our knowledge. The distinctiveness of our model lies in the integration of these 2 independently investigated lines of research, namely the dynamics of microbial communities and resistance evolution via horizontal gene transfer.
Antibiotic use is one of the major drivers of antibiotic resistance and this effect is at least partially mediated by the microbiome. Therefore, one important application of such models is to investigate the expected association between antibiotic use and antibiotic resistance at the level of individual patients. On the epidemiological level, antibiotic consumption is known to correlate with prevalence of resistance (27). Similarly, on the level of the individual treated patient, past antibiotic exposure is associated with increased risk of treatment failure (28–38). Specifically for plasmid-conferred resistance, prior antibiotic use is an independent risk factor for AmpC- and extended spectrum beta-lactamase (ESBL)-producing Escherichia coli and Klebsiella pneumoniae infections (39–41). The use of antimicrobial agents generates a selection pressure that allows resistant enterobacteria to become effective intestinal colonizers and potentially cause infections which are hard to treat. To prescribe more effective empirical antimicrobial therapy, clinicians need to have an increased awareness of the factors affecting the prevalence of resistance among enterobacteria, including which patients are at risk for infection (42) and what aspects of past antibiotic consumption drive an individual’s risk of carrying and spreading resistance. A recent study identified a strong association of antibiotic resistance with the history of drug purchases of the patients and showed that the use of information on treatment history can greatly reduce the risk of mismatched treatment compared with the current standard of care (43).
To address the effect of treatment history on the prevalence of resistance for an enterobacterial infection with plasmid-conferred resistance, we first develop a computational framework that describes the within-patient population dynamics of the gut microbial community and its plasmids and parameterize it based on published data. Next, we use the model to simulate treatment histories, where the initiation, duration, and number of treatments are randomized. We then identify the most important characteristics of the random treatment histories in determining the prevalence of resistance. By doing so, we show that the impact of prior antibiotic exposure can be captured by focusing on 3 properties of the treatment history, which are the total days of drug exposure, the duration of the drug-free period after last treatment, and the center of mass of the treatment pattern. Furthermore, we demonstrate that the most relevant information on the prevalence of resistance is contained in the most recent treatments of the patient.
Results
Model.
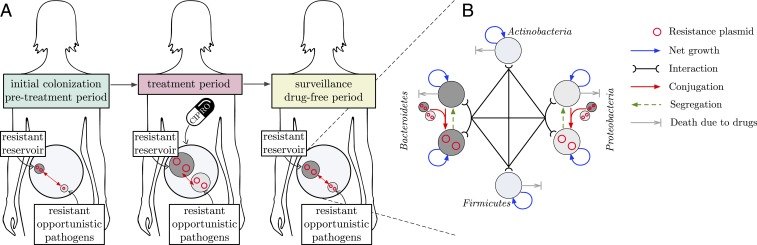
Our mathematical model describes the following general scenario: A patient is colonized with a microbial gut community harboring an opportunistic pathogen belonging to phyla Proteobacteria, which may cause an infection by translocating to the blood stream, by migrating to other organs, or via fecal contamination of skin and other body sites (44–47). We assume that the community also harbors a harmless commensal Bacteroidetes population, bearing conjugative plasmids conferring resistance to quinolones, forming a reservoir of plasmid-mediated quinolone resistance (PMQR) genes in the gut microbiome. These genes are horizontally transferred between the harmless and the pathogenic commensals and maintained in the gut microbiome for a certain amount of time even in the absence of treatment. We assume that the patient occasionally received antibiotic treatment(s) in the past, which we refer as the treatment history. Due to the selection pressure imposed during this treatment period, prevalence of resistance among the gut community increases, thus increasing the possibility of a resistant infection to occur. An illustration of the model scenario and the summary of the dynamical model of the gut microbiome are given in Fig. 1 A and B, respectively. We use this model to investigate how past antibiotic treatment affects the prevalence of resistance—a proxy for the risk of treatment failure—measured by the frequency of resistance within the opportunistic pathogen population in the gut. Specifically we focus on treatment with ciprofloxacin (CIP) and PMQR.
Fig. 1.
(A) Illustration of the model scenario. (B) Summary of the dynamical model of the gut microbiome.
We first develop a system of ordinary differential equations describing the rate of change of the population size of each phylum over time (Fig. 1B). We then estimate the interaction and growth parameters using the operational taxonomic unit (OTU) reads of gut microbiome provided in ref. 11. Conjugation frequencies, resistance costs, and missegregation fraction are jointly assigned to achieve a plausible decay rate for the plasmid, which is assumed to be 2 y (720 d). Bacterial death rates are obtained based on the quantitative and qualitative results published in the literature (see Table 3). Details on the estimation methods are provided in Materials and Methods. Statistics on the growth and interaction parameter estimates are provided in SI Appendix, Table S1 and Fig. S1, and the corresponding time series estimations of the phylum-level abundances are provided in SI Appendix, Fig. S2. Statistics on death rates, conjugation frequencies, resistance costs, and missegregation fraction are given in SI Appendix, Table S2, and the corresponding parameter distributions are provided in SI Appendix, Figs. S5 and S6. A hybrid stochastic–deterministic simulation method (48) is adopted to simulate the model to capture the stochastic extinction of the plasmid-bearing bacteria. Briefly, this method approximates the fast reactions associated with species with high abundance as continuous processes, whereas all other reactions are still realized as discrete stochastic processes, thus decreasing the computational cost.
Table 3.
Summary of the literature on gut microbiota response after short-term antibiotic treatment
| Study | Exclusion criteria | Treatment | Observations |
| (49) | Antibiotic use within previous 2 mo or hospitalization within previous 30 d. | 10 d 1 course 500 mg CIP twice, daily | Decreased relative abundance of Firmicutes, increased relative abundance of Bacteroidetes, recovery in 4 wk. |
| (50) | Significant medical problems. | 3 d 1 course 500 mg CIP twice, daily | Overall diversity of the gut microbiota was largely restored 28 d after treatment. |
| (51) | Antibiotic use within previous 12 mo. | 5 d 1 course 500 mg CIP twice, daily | Community composition 4 wk after treatment is within the range of temporal variability of pretreatment. |
| (52) | Antibiotic use within previous 12 mo. | 6 d 1 course 500 mg CIP twice, daily | Decreased relative abundance of Proteobacteria. Diversity recovered almost fully 28 d after treatment. |
| (113) | 3 d of vancomycin and imipenem intake | 10-fold decrease in bacterial load right after treatment. |
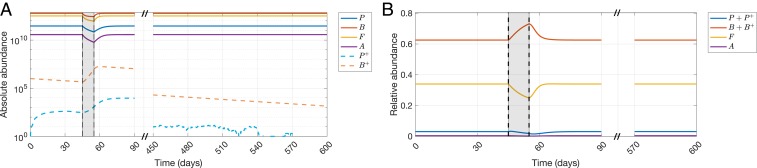
Using the parameterized model, we show a 10-d treatment 45 d after initial colonization with the resistant reservoir in Fig. 2 A and B, where the absolute and relative abundances of phyla are presented, respectively. For the sake of convenience in notation, we denote the phyla Proteobacteria, Bacteroidetes, Firmicutes, and Actinobacteria by , , , and , respectively. Plasmid-bearing counterparts of and are denoted by and , respectively. As seen in Fig. 2A, the resistant reservoir starts to decline in the absence of treatment, while causing an initial increase of the population via conjugation. During the application of treatment, both plasmid-bearing populations and increase, whereas all sensitive phyla decrease in abundance. After the treatment is stopped, sensitive phyla recover back to their pretreatment population sizes, while the plasmid-bearing populations start to decline again due to the absence of drug pressure. The assumptions on relative abundances of phyla during and after CIP treatment (49–52) can be observed in Fig. 2B, where the relative abundances of Proteobacteria and Firmicutes decrease and the relative abundance of Bacteroidetes increases.
Fig. 2.
Demonstration of the model behavior for a 10-d treatment 45 d after initial colonization with the resistant reservoir. , , , and denote the phyla Proteobacteria, Bacteroidetes, Firmicutes, and Actinobacteria, respectively. (A) Absolute abundances of , , , , , and in response to a 10-d CIP treatment. (B) Relative abundances of , , , and in response to a 10-d CIP treatment.
Simulated Treatment Courses.
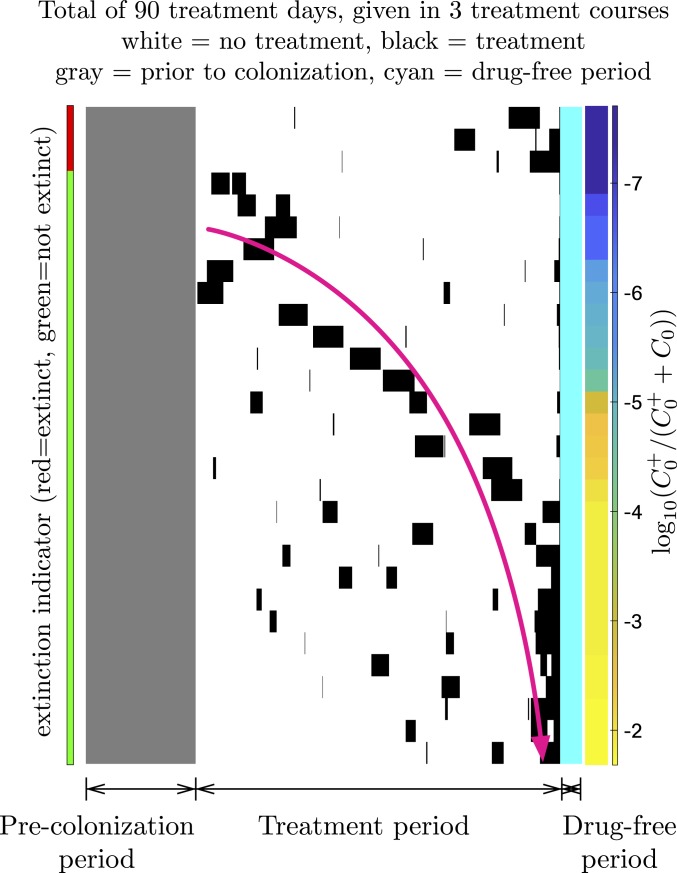
By simulating treatment courses we aim to determine what kind of information on a patient’s past antibiotic treatments should be considered when assessing the risk of treatment failure for an upcoming treatment in the future. We assume that the risk of treatment failure is closely linked to the prevalence of resistance in the opportunistic pathogen. This assumption is based on the fact that the probability of the translocated bacteria containing resistant strains depends on the frequency of resistance in the opportunistic pathogen population in the microbiome. The prevalence of resistance is defined in as the fraction of the opportunistic pathogen population carrying the resistance plasmid; i.e., . To characterize the treatment history of the patient over the time span that the patient was exposed to treatment(s) in the past, we chose a set of intuitively appealing predictors of the overall treatment regimen provided in Table 1. Predictors such as time to first treatment after initial colonization () and the duration of the drug-free period after last treatment () capture the first-order time dynamics of resistance reversal. The number of treatments () and the total duration of all treatments () capture the amount of positive selection applied on the plasmid-bearing population. Although these predictors reveal how strongly and for how long the resistance plasmid is positively selected, they do not contain any information about the pattern of the treatment history. Therefore, we introduce 2 other predictors, namely the coefficient of variation () and the center of mass of the treatment pattern (), which represent the regularity of treatment durations and the time point around which the treatments are centered, respectively. To illustrate the choice of these predictors, we present 30 randomly generated treatment patterns (Fig. 3). This shows that for a fixed amount of total treatment duration, being treated more intensely toward the recent past 1) can lead to extinction of the plasmid-bearing pathogen population since it was not selected strongly enough to persist in the biome after the initial colonization or 2) can lead to high prevalence of resistance given that the plasmid persists in the biome. As a result, center of mass of the treatment pattern relative to the initial colonization and the regularity of treatment durations become the most intuitive 2 predictors related to the treatment pattern. In addition to the parameters related to the treatment regimen, an artificial probe (rnd), which is a random variable independent of the response variable (prevalence of resistance), is also included in the set of predictors. A probe predictor is a metric used for eliminating all of the other predictors that are less relevant than it is in assessing the response variable (53).
Table 1.
List of the predictors used for classification and regression forests with their corresponding descriptions, dependencies, and range of variations
| Predictor | Description | Dependency | Range of variation |
| rnd | The probe predictor. | Randomly sampled from a continuous uniform distribution on the open interval Does not depend on other predictors. | 0–1 |
| No. of treatment courses within the last 1,000 d. | Randomly sampled from the set treatment courses with equal probability. Does not depend on other predictors. | 1–20 treatment courses. | |
| Total duration of all treatments. Represents the total drug pressure (in days). | Depends on the number of treatment courses and the duration of each treatment course. | 3–200 treatment days. | |
| Duration of the most recent treatment. | Randomly sampled from the set d with equal probability. Does not depend on other predictors. | 3–10 treatment days. | |
| Time to first treatment after the initial colonization with the resistant reservoir. | Depends on the total duration of all treatments due to the maximum 1,000-d constraint on the treatment period. | 1–996 drug-free days. | |
| Duration of the drug-free period after the most recent treatment. | Does not depend on other predictors. | 0–360 drug-free days. | |
| Center of mass of the treatment pattern. Represents the time point at which the treatments are centered around relative to the initial colonization. | Depends on the number, initiation, and duration of each treatment course. | 2–998 days | |
| Coefficient of variation for the duration of treatments. Represents the regularity of treatment durations. | Depends on the number of treatment courses and the duration of each treatment course. | 0–0.7615† |
Fig. 3.
Illustration of 30 randomly generated treatment patterns, where the gray pixels represent the time before initial colonization, white pixels represent the days without treatment after the initial colonization, black pixels represent the treatment days, and cyan pixels represent the drug-free time after last treatment. Color bar on the left indicates whether the resistant pathogenic population has gone extinct or not given the treatment pattern, and color bar on the right indicates the prevalence of resistance, sorted in an increasing order from top to bottom. The pink arrow represents how the center of mass of the treatment pattern moves toward the recent past of the patient as the prevalence of resistance increases. To isolate the effects of the treatment pattern only, initial colonization time, drug-free time after last treatment, total duration of all treatments, and number of treatments are fixed to 300 d, 60 d, 90 d, and 3 courses, respectively *.
Predictor Importance Analysis.
To test the relevance of predictors in assessing the prevalence of resistance, first we use classification trees to predict whether the prevalence of resistance within the pathogen population is positive or zero and second we use regression trees to predict the numerical value of the prevalence of resistance within the pathogen population, given that it is above zero. Note that the use of classification trees partitions the prevalence of resistance outcome of each simulation into 2 classes, namely or , which is important to understand the influence of the predictors on the extinction of the resistant pathogen population.
Using an ensemble of these decision trees, we grow random forests to quantify the importance of each predictor on determining the prevalence of resistance, which we refer to as predictor importance analysis. Since our predictors have different scales, and 2 of them are strongly correlated (number of treatments and total duration of all treatments), we use unbiased conditional inference trees (54) and the conditional variable importance method (55) to calculate the variable importances. Combining both methods eliminates potential biases due to the scale difference or the correlation between predictors, but comes at the cost of increased computational time. Therefore, we analyze only randomly subsampled realizations and 200 trees grown for both classification and regression forests.
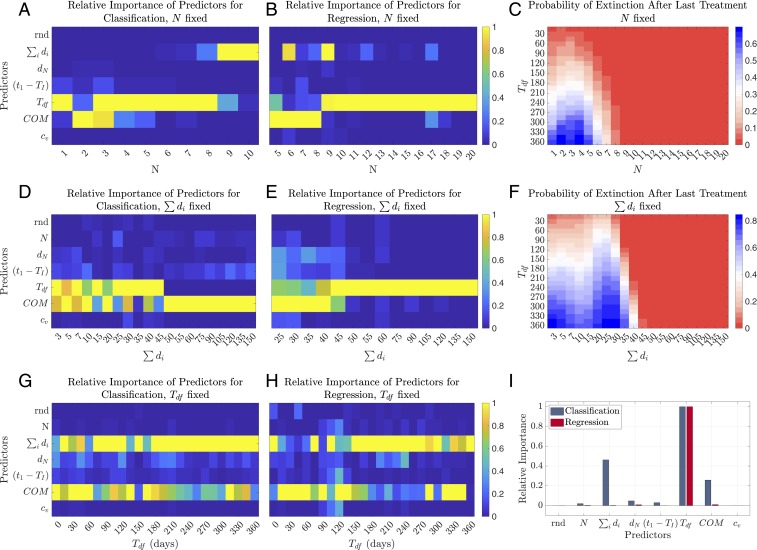
To gain a better understanding of the influence of predictors, we employ the predictor importance analysis via fixing 1) the number of treatment courses (), 2) the total duration of all treatments (), and 3) the duration of the drug-free period after last treatment (). Finally, we employ the predictor importance analysis by randomizing all predictors simultaneously for the case of no a priori information on the treatment history of the patient.
Fixed number of treatment courses.
Fig. 4 A and B shows the predictor importance analysis for each number of treatment courses varying from 1 to 20. As seen in Fig. 4 A and B, the most important predictors in general are the duration of drug-free period after last treatment (), total duration of all treatments (), and the center of mass of the treatment pattern (). The dependence of their relative importances on the number of treatment courses can be understood better from Fig. 4C, where the extinction probability of the resistant pathogen population is presented given the number of treatment courses () and the duration of drug-free period after last treatment (). Note that in our model extinction occurs in 2 different ways: Either the total positive selection applied on the plasmid is not strong enough for it to persist in the pathogenic population during the treatment period or the plasmid persists in the population during the treatment period but becomes extinct during the drug-free period after the last treatment. When the number of treatments exceeds 8 courses per maximum treatment period allowed (1,000 d) in our simulations, the resistant pathogen population increases in abundance to an extent such that the extinction cannot be observed over a drug-free period of 360 d. Therefore, the duration of drug-free period after last treatment becomes unimportant as a predictor of extinction, and the total selection pressure becomes the most important predictor, since it determines whether extinction occurs within the treatment period or not (Fig. 4A).
Fig. 4.
Predictor importance analysis and extinction probabilities of the resistant opportunistic pathogen population. Conditional predictor importance values are calculated over samples and 200 trees and normalized between 0 and 1. Extinction probabilities are calculated using 600,000 randomly subsampled realizations, 1,200 realizations per per value. (A and B) Normalized conditional predictor importance values for (A) classification and (B) regression, for different values of number of treatment courses () varying from 1 to 20. (C) Extinction probability of the resistant pathogen population given the number of treatment courses () and the duration of drug-free period after last treatment (). (D and E) Normalized conditional predictor importance values for (D) classification and (E) regression, for different values of total duration of all treatments () varying from 3 to 150 d. (F) Extinction probability of the resistant pathogen population given the total duration of all treatments () and the duration of drug-free period after last treatment (). (G and H) Normalized conditional predictor importance values for (G) classification and (H) regression, for different values of the duration of drug-free period after last treatment () varying from 0 to 360 d. (I) Normalized conditional predictor importance values for classification and regression when all predictors are randomized.
Predictor importances determining the prevalence of resistance (regression results) depend on how close the resistant pathogenic population is to fixation in the biome. The marginal effect of additional drug pressure on the abundance of the resistant population decreases as the plasmid infects a bigger fraction of the whole population. In this case, resistance prevalence depends more on the factors that lead to its decrease (such as the duration of the drug-free period) rather than its increase (such as additional drug pressure). This phenomenon is observed in Fig. 4B, where the center of mass of the treatment pattern () and the total duration of all treatments () are the most important 2 predictors until the number of treatments exceeds 9 courses, and the duration of drug-free period () becomes the most important predictor afterward.
Fixed total duration of all treatments.
Employing the predictor importance analysis for different values of total duration of all treatments () (Fig. 4 D and E) shows a similar pattern to the predictor importance analysis for a fixed number of treatment courses (Fig. 4 A and B). Influence of the duration of drug-free period () and the center of mass of the treatment pattern () is prominent in Fig. 4 D and E, similar to Fig. 4 A and B. The same logic on extinction and prevalence of the resistant pathogenic population applies here as explained in the previous section on predictor importance analysis for fixed number of treatment courses. The strong influence of the duration of the drug-free period () is observed in determining the extinction up to a total number of 45 treatment days (classification results). The center of mass of the treatment pattern () becomes the most important predictor afterward, in agreement with the extinction probabilities presented in Fig. 4F. The most important predictor for determining the resistance prevalence (regression results) switches to the duration of drug-free period () from the center of mass of the treatment pattern () between total treatment days of 45 to 50 in Fig. 4E, showing a similar behavior to that observed in Fig. 4B. Note that the values at which the most important predictors switch ranking are dependent on the model parameterization and the selection of maximum drug-free period (360 d) observed after the last treatment. Qualitatively, these values are dependent on the chance of extinction during the total treatment period for determining reversal (classification results) and the chance of fixation during the total treatment period for determining the prevalence (regression results).
Fixed drug-free period after last treatment.
The high relative importance of the duration of drug-free period after the last treatment overshadows the influence of other predictors. Therefore, we employed the predictor importance analysis for fixed durations of drug-free period varying from 0 to 360 d (Fig. 4 G and H). This analysis shows that when is kept constant, the most important 2 predictors are the total duration of all treatments () and the center of mass of the treatment pattern () for determining both the extinction and the prevalence of resistance.
When all predictors are randomized.
Finally, we employ the predictor importance analysis by randomizing all of the predictors simultaneously for the case of no a priori information on the treatment history of the patient. The results presented in Fig. 4I suggest that the most important 3 predictors in determining the resistance reversal (classification results) are the duration of the drug-free period after last treatment (), total duration of all treatments (), and the center of mass of the treatment pattern (). The most important predictor for determining the prevalence (regression results) is the drug-free period after last treatment (), emphasizing once again the influence of first-order time dynamics on resistance spread. Duration of the most recent treatment (), time to first treatment after the colonization of the microbiota with resistant commensals (), and the regularity of treatment durations () do not have an important effect relative to the other predictors.
Information Quantification.
Knowing the total number of days that the patient has been exposed to antibiotics () assumes that we have complete information on the patient’s medical history. Unfortunately this detailed information is often not available in practice, and even if there is information regarding the past treatments, the likelihood of containing inaccuracies is substantial (56). Therefore, it is important to quantify how much one can gain by investigating the patient’s records farther back in time and understand whether it is necessary to have complete information to have a good estimate of the prevalence of resistance. To do so, we transformed each realization into a numerical sequence of days, such that the days before the colonization with the resistant reservoir, days without treatment, and days with treatment have zero, negative, and positive impact on the prevalence of resistance, respectively. Using these sequences, we applied linear regression to model the impact of each day on the prevalence of resistance. Detailed information on the methods used for this analysis is provided in SI Appendix.
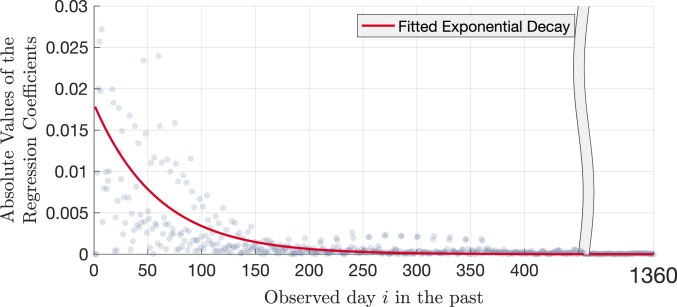
The magnitude of the linear regression coefficients can be interpreted as the weights of each day, i.e., the linear contribution of the activity—being treated or not—at a given day to the prevalence of resistance . As seen in Fig. 5, the largest coefficients in magnitude belong to the most recent days of the patient and decay exponentially as one moves farther back in time. This decay suggests that there is memory in the dynamical system, and most of the information on the prevalence of resistance is contained in the most recent treatments of the patient.
Fig. 5.
Absolute values of the linear regression coefficients given the day index , calculated using 600,000 randomly subsampled realizations, 1,200 realizations per per value. The red curve represents the exponential decay function in the form of , fitted to the magnitude of the linear regression coefficients to demonstrate the exponential decay of contribution of information as one moves farther back in the treatment history of the patient.
Discussion
The development and parameterization of the gut biota model presented here bring different parts of the literature together and provide a framework to explore the interaction, conjugation, and treatment dynamics in the human gut. Moreover, it describes procedures to assign numerical values to conjugation- and treatment-related parameters based on empirical data. Using this model, we show that treatment history has a significant impact on the prevalence of resistance. This impact can be captured by 3 parameters only. The prevalence of resistance in the opportunistic pathogen population is closely linked with the risk of treatment failure once an infection occurs. Thus, our results suggest that future empirical studies on the effect of previous antibiotic consumption on treatment outcomes might be the most informative if they focus on those 3 quantities.
More generally, our results allow us to distinguish relevant from irrelevant characteristics of the treatment history in determining the prevalence of resistance. First, knowing which factors determine the prevalence of resistance allows us to better prevent treatment patterns that lead to high risk of treatment failure. Second, our results suggest what the physician should ask the patient to assess the risk of treatment failure. Considering that the duration of the drug-free period after last treatment () is the most important predictor, the question “When was your last antibiotic treatment?” becomes a critically important one. Additionally, the high relative importance of total drug exposure and the center of mass of the treatment pattern argues that how total selection pressure is distributed in time is as important as how much it is applied.
In most cases clinicians will not have complete access to the patient’s treatment history, and neither will the patients be able to provide absolutely accurate information on previous antibiotic use. Therefore, it is important to quantify how much information one can gain by investigating the patient’s records farther back in time. As seen in Fig. 5, the relevance of information exponentially decays as one goes farther back in the treatment history.
Our predictor importance results are consistent with the reported risk factors on plasmid-mediated resistant infections cause by enterobacteria in the literature. In ref. 39, total prior antibiotic use was found to be the only independent risk factor for ESBL-producing E. coli and K. pneumoniae infections, which confirms the importance of the predictor total duration of all treatments (). In refs. 38, 40, and 41, the authors report that the recent use of antibiotics is found to be an independent risk factor for a resistant infection with plasmid-bearing enterobacteria. These findings support our results on the importance of the duration of drug-free period after last treatment (), as well as the analysis provided in Fig. 5. The agreement of our results with the clinical studies confirms that quantifying the prevalence of resistance for a particular patient with a particular treatment history may help clinicians to make more personalized and precise decisions on the choice of future treatments, rather than relying on the statistical information calculated over regions, sexes, or age groups.
This study has several limitations and strengths. First, the parameterization of our model is based on the current state of the literature, which contains substantial knowledge gaps. Samples used for estimating interaction and growth parameters in ref. 11 were in OTU reads of 2 healthy subjects, but the biomass of the collected samples was not reported. Therefore, we assumed that the total biomass in the subjects’ unperturbed biota is to a good approximation constant, allowing us to estimate the parameters for our absolute abundance-based model from frequency-based OTU reads. When the microbiota are subjected to antibiotics, we assume that the same parameter values hold although the total biomass of the microbiota shrinks in our model. In other words, we assume that the parameters are not density dependent.
It is known that resistance persists in the human gut for a certain amount of time in the absence of antibiotics, but there is not enough evidence to assess the time required to lose plasmid-mediated resistance or to fully understand which properties of the human biome influence this quantification. More importantly, studies on the effects of antibiotics on the human gut microbiota—including the ones referred to in this work—provide conclusions that are more qualitative than quantitative. In vitro time-kill assays provide sufficient data for certain antibiotics applied to certain strains of bacteria, but how these data translate to the in vivo dynamics of the human gut is currently not known. The absence of such information enforces the parameterization of the treatment dynamics to be done via relevant metadata, instead of estimating the corresponding parameters directly.
Second, our model makes several important simplifications. We model the gut biota as it is a closed system, with no immigration or emigration of bacteria. This assumption does not permit the recolonization of the gut microbiome with a plasmid-bearing population, which might contribute to the prevalence of resistance in a similar fashion to that of an additional treatment course. On the other hand, it permits us to isolate the effects of treatment on the prevalence of resistance only. Although gut biota is not a closed system in reality, we believe that the main conclusions of the model would still be valid as long as the relative abundances of phyla or the absolute abundance of plasmid-bearing bacteria do not alter drastically. By modeling the gut microbiome on a phylum level, we neglect the growth, interaction, and conjugation dynamics within each phylum. We further assume that plasmid-bearing variants of Proteobacteria and Bacteroidetes interact with other phyla in the same manner as their sensitive counterparts. Both assumptions permit the model to have low complexity, but they force us to merge parameters related to many different species of the same phylum into one. Finally, we do not consider the emergence of resistance in vivo in the presence of drug pressure. Given that the gut biome already contains a plasmid-bearing resistant population prior to the treatments, we anticipate that the in vivo emergence of chromosomal resistance and its vertical transfer will have a negligible effect compared to the horizontal spread of resistance that is already present.
Given the level of randomization in the simulated treatment courses and the number of dynamical variables that our model outcome (prevalence of resistance) depends on, we focused on simulations only and leave potential analytical approaches for future work.
A key strength of this work is that it simultaneously captures the dynamics of antibiotic resistance in pathogenic bacteria and the microbiome as well as the plasmid-mediated exchange between these populations. It integrates a wealth of in vitro and in vivo measurements on the key drivers of resistance and on the ecological dynamics of the microbiome. Thus, even though there are several important knowledge gaps and simplifications, the presented model represents in our view a very feasible approach incorporating the currently available knowledge of the evolution of resistance in the microbiome. Finally, applying this framework to the question of the impact of previous antibiotic consumption at the level of an individual patient helps to elucidate how complex patterns of antibiotic consumption may drive the prevalence of resistance in an individual.
Materials and Methods
Gut Microbiota Model.
The first step toward building this model is to choose the appropriate level of representation for the human gut microbiota. The gut microbial composition shows substantial interindividual variation, as well as intraindividual temporal fluctuations on a species level. On the level of bacterial phyla, however, the community composition exhibits temporal stability within an individual (57–60). This temporal stability is relevant for the modeling as it allows us to parameterize the model using steady-state solutions. Moreover, using a phylum-level description decreases the number of equations and parameters of the model, thus making parameterization more constrained. Therefore, our model incorporates only the 4 most abundant phyla in the human gut microbiome, which are Proteobacteria, Bacteroidetes, Firmicutes, and Actinobacteria.
We assume that the community harbors a conjugative PMQR plasmid which spreads only among gram-negative bacteria, i.e., Proteobacteria and Bacteroidetes. These 2 assumptions reflect the following observations: 1) PMQR genes have been found in a variety of Enterobacteriaceae, especially E. coli and species belonging to the genera Enterobacter, Klebsiella, and Salmonella (61–65), as well as enteric Bacteroidetes species (66); 2) PMQR genes are usually found on conjugative plasmids (61, 63, 67, 68); and 3) although these genes are found in a variety of gram-positive organisms, they are chromosomal but not plasmid mediated (69, 70). As we are interested in the effect of treatment history on plasmid-mediated resistance, we ignore de novo emergence of resistance. Plasmid-free cells acquire the plasmid only via conjugation, and plasmid-bearing cells might lose the plasmid due to segregation. Bearing the plasmid imposes a fitness cost on the host by reducing the growth rate. We assume that only plasmid-free, i.e., sensitive bacteria are affected by treatment, based on the evidence that the presence of PMQR genes significantly reduces the therapeutic efficacy of CIP in vivo (71–74).
Among gram-negative bacteria, Bacteroidetes play an important role in the in vivo transfer of resistance genes (47, 75, 76) and can serve as a reservoir of resistance determinants to pass onto more virulent bacteria (77–79). Also considering their high abundance in the human colon (80), the resistance reservoir function of the gut microbiota is attributed to the Bacteroidetes phylum in our model. Given that many common human pathogens are found in the Proteobacteria phylum (81), we assume that the opportunistic pathogens in our model are members of Proteobacteria. Since we are interested in modeling a single individual, the gut microbiome is assumed to be a closed system with no influx or efflux of bacteria.
Based on the assumptions above, we build a mathematical model which incorporates growth, interaction, conjugation, and the treatment dynamics, given by Eqs. 1 and 2. Each phylum is denoted by the index , where , , , and represent the phyla Proteobacteria, Bacteroidetes, Firmicutes, and Actinobacteria, respectively. Plasmid-bearing variants of Proteobacteria and Bacteroidetes are denoted by and and assumed to interact with other phyla in the same manner as their sensitive counterparts. Conjugation occurs via mass action kinetics at a rate proportional to the densities of plasmid-bearing and plasmid-free bacteria (14, 16, 82). The term denotes the net growth rate of phylum in the absence of any interaction, and the interaction terms denote the effect of phylum on phylum . The cost imposed on phylum due to plasmid carriage is denoted by and reduces the growth rate of phylum by a factor of . The terms stand for the conjugation frequency between phylum and phylum , and denotes the fraction of plasmid-free cells after plasmid-bearing cell segregation, i.e., the missegregation fraction. A time-dependent binary indicator is included in the system to indicate whether a treatment is being applied or not, denoted by , and is equal to 0 (1) in the absence (presence) of treatment. During treatment, becomes 1 and activates the death rate term of phylum due to drug exposure. Since we assume that conjugation occurs only among gram-negative bacteria, and at any given time:
| [1] |
| [2] |
Parameter Estimation.
Growth and interaction parameters.
After constructing the dynamical system, we proceed with estimating the numerical values of the system parameters. To our knowledge no in vivo study exists that longitudinally monitors composition of phyla and resistance-conferring plasmids in presence and absence of antibiotics. Therefore we obtain numerical values for the growth and interaction parameters by fitting to longitudinal abundance data of bacterial phyla and obtain parameters for conjugation and treatment from other sources.
To estimate the terms and , we utilize the phylum-level time series data obtained from 2 healthy subjects’ gut microbiota (referred as F4 GUT and M3 GUT) provided in ref. 11. Samples presented in ref. 11 were in OTU reads, with an average sampling interval of 1.12 d. To infer parameters invariant to the scale of the data, we normalized the OTU reads across all phyla for each time point and used the resulting quotients for Proteobacteria, Bacteroidetes, Firmicutes, and Actinobacteria as a proxy for their abundance in the gut. The Bayesian variable selection algorithm in MDSINE (83) is adopted for the time series analysis of the data.
Conjugation frequencies, resistance costs, and missegregation fraction.
Persistence of a plasmid is largely driven by the relative magnitude of its fitness cost and missegregation fraction compared to its conjugation efficiency (84). Therefore, the decay rate of plasmid-bearing bacteria in a mixed population is determined by the numerical combination of fitness costs (), conjugation frequencies (), and missegregation fraction (). Merging these 3 parameters into 1, i.e., the decay rate, gives us the opportunity to obtain numerical values for , , and jointly by imposing proper constraints on the temporal stability of the plasmid in our model.
In the absence of antibiotics, as long as the resistance plasmid imposes a fitness cost, plasmid-bearing cells are replaced by their plasmid-free counterparts over a sufficiently long time, effectively reversing resistance (84–90). It has been hypothesized that plasmid-mediated resistance reversal is more likely to happen in in vivo compared to in vitro experiments (91), although it might take longer periods than previously anticipated due to certain adaptation mechanisms. It has been shown that PMQR plasmids were able to persist in the digestive tract of chickens for several weeks (87), and multidrug resistance plasmids persisted in human infant gut microbiota for several months (92). In vivo studies with mice also demonstrated the long-term persistence of plasmid-encoded resistance in the absence of treatment (93) and showed that it is possible to observe the resistant determinants up to 4 y after the drug pressure is removed (94, 95). Furthermore, frequency of a conjugative plasmid that confirms resistance against sulphonamide remained high for 8 y in the United Kingdom despite the national prescribing restriction (96). Additional information specific to human gut suggests that resistant strains—although not necessarily plasmid mediated—persisted for 1 to 3 y after the termination of the treatment (79, 97–99). Considering all of the evidence in the literature, we choose an intermediate value and assume that the PMQR plasmid in our model persists in the gut microbiome for 2 y in the absence of treatment.
Persistence of a plasmid can be associated with different stabilization mechanisms, such as increasing the copy number of the plasmid, active partitioning, and postsegregational killing (88, 100, 101). Among these, reducing the cost of plasmid carriage is the most crucial one, since the main factor determining whether resistant populations can be replaced by their sensitive counterparts is the biological fitness cost of resistance (100). Amelioration of the cost of plasmid carriage and thereby facilitating plasmid stability via compensatory evolution have been demonstrated by a number of in vitro studies (102–105). Therefore, to distinguish the reservoir function of Bacteroidetes, we assume that they acquired compensatory mutations to lower the cost of plasmid carriage, whereas the pathogenic population Proteobacteria bears a larger cost. This is expressed in the model by imposing the constraint .
Conjugative plasmids are highly promiscuous: Donor and recipient cells may belong to different genera or even to different kingdoms (106, 107). Despite their promiscuity, successful conjugation between highly divergent species is expected to occur at significantly reduced frequencies due to bottlenecks in conjugative transfer (108–110). Thus, we assume that intraphyla conjugation occurs at a higher frequency than interphyla conjugation. For the sake of simplicity, we assign a single quantity for the intraphylum and interphyla conjugation frequency for both Bacteroidetes and Proteobacteria, such that and , and impose the constraint .
Taking all constraints, we employ a random sampling scheme to jointly assign numerical values for and such that the total plasmid-bearing population goes extinct after 2 y in the absence of treatment. We assume that the patient is initially colonized with PMQR-plasmid–bearing Bacteroidetes of inoculum size colony-forming units (cfu) (111); i.e., cfu, given that the total abundance of bacteria in the human gut is cfu (112). These values lead to a proportion of at the initial time of colonization. is set to 0 to observe the effects of the reservoir alone. Sampling ranges for the parameters are given in Table 2, with corresponding sampling schemes and constraints imposed on each parameter. To account for the stochasticity in our simulations, we run 1,000 realizations for a given set and calculate the mode of the extinction time distribution for each set. Out of 10,000 randomly sampled sets, we observed only 1 set with a mode of 720 d for plasmid extinction, and this set is used for simulating the treatment courses. Note that more sets can be observed with a larger sampling size with the cost of a longer computational time.
Table 2.
Model parameters given with their descriptions, sampling ranges, sampling schemes, and constraints
| Parameter | Description | Range | Sampling | Constraint |
| Resistance cost for | Linear | |||
| Resistance cost for | Linear | |||
| Intraphyla conjugation frequency | Logarithmic | |||
| Interphyla conjugation frequency | Logarithmic | |||
| Missegregation fraction | Linear |
Death rates due to drug exposure.
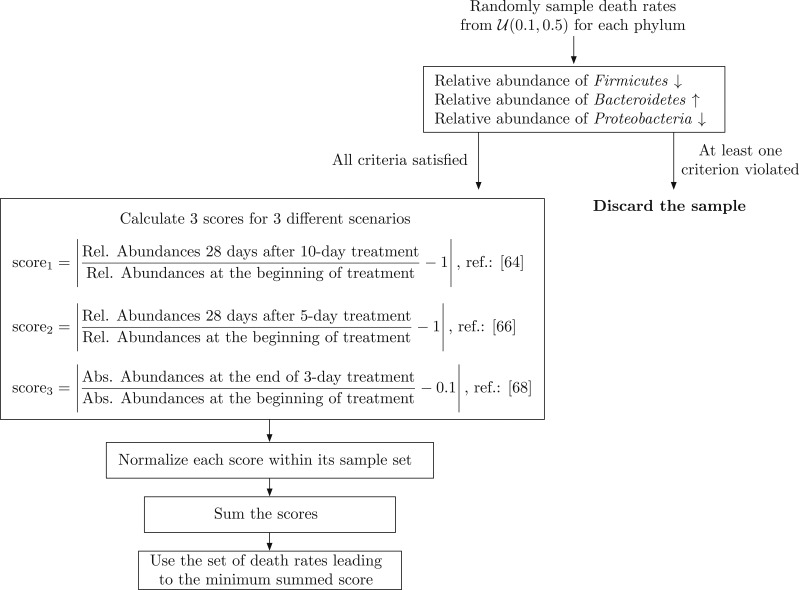
To assign numerical values to death rates of the sensitive bacteria in the presence of treatment, we refer to studies which investigate the effects of short-term antibiotic treatment on the human gut microbiota. These studies provide both qualitative and quantitative information that can be used to determine the values for death rates. Given the data presented in refs. 49–52 for human subjects and in ref. 113 for rats, we assume that 1) relative abundances of phyla recover approximately 28 d after CIP treatment, 2) relative abundance of Bacteroidetes increases in response to CIP treatment, 3) relative abundance of Firmicutes decreases in response to CIP treatment, 4) relative abundance of Proteobacteria decreases in response to CIP treatment, and 5) total bacterial load decreases 10-fold in response to 3-d antibiotic treatment. A summary of the literature on the effects of short-term antibiotic treatment on the gut microbiota is presented in Table 3. Using the information provided in these studies, we use a random sampling scheme to jointly assign numerical values for for , which is presented as a diagram in Fig. 6 to further clarify the process. Since resistance is not considered in the studies mentioned above, we assumed a fully sensitive population without any chromosomal or plasmid-mediated resistance.
Fig. 6.
Random sampling scheme employed for assigning numerical values for death rates .
Simulated Treatment Courses.
To quantify the impact of past treatments on the composition of the gut microbiota, we simulate the parameterized model employing treatment courses that include randomly initiated treatments with randomly chosen durations, which we refer as “random treatment.” We use a hybrid stochastic–deterministic simulation method adapted from ref. 48 to simulate the system of equations given by Eqs. 1 and 2. This method approximates the fast reactions associated with species with high abundance as continuous processes, whereas all other reactions are realized as discrete stochastic processes, thus decreasing the computational cost.
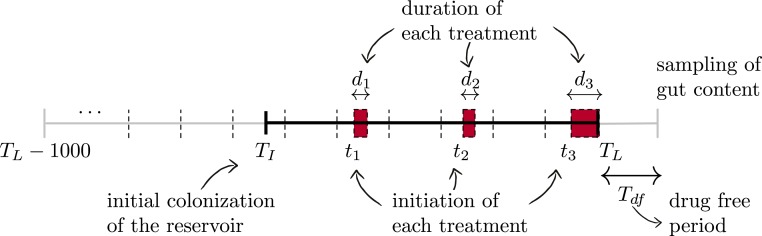
As mentioned in Gut Microbiota Model, we assume that the patient is colonized with PMQR-plasmid–bearing Bacteroidetes prior to the initiation of treatment(s). Time of initial colonization is denoted by the random variable and assumed to occur at most 1,000 d before the termination of the last treatment. The last day of exposure to drugs, i.e., the last day of the last treatment, is denoted by , and the patient receives a number of treatments between and , where is uniformly distributed in the set . We chose to use a uniform distribution on the number of treatment courses () to cover a broad range of treatment frequencies and do not make any a priori assumptions on the treatment frequency. If empirical information on the distribution of the number of treatment courses () is available, one could consider a more realistic distribution on (Poisson, normal, etc.) which might lead to better quantitative predictions of the resistance prevalence. Initiation time and the duration of the treatment are denoted by and , respectively, where is uniformly distributed in the set d. After is chosen, and are sampled together for every treatment in a sequential way, by putting at least 1 drug-free day between 2 consecutive courses of treatment. As a result, is satisfied for each realization. Samples related to the gut microbiome content of the patient are collected days after , where denotes the drug-free days after the termination of the last treatment and varies in the set d. The timeline used in the simulations is demonstrated in Fig. 7.
Fig. 7.
Timeline used for the simulated treatment courses, where , , and denote the initial colonization with the plasmid-bearing commensals, the last day of drug exposure, and drug-free days after the end of the last treatment, respectively. Initial colonization is assumed to occur at most 1,000 d before the termination of the last treatment, and therefore . Every th treatment starts at and lasts for days.
As mentioned in Predictor Importance Analysis, using the methods in refs. 54 and 55 in combination corrects for the scale differences among the predictors. Therefore, the relative importance of a predictor is robust to its range of variation as long as this variation is high enough to induce a change in the response variable (prevalence of resistance). If the given range of values does not permit the predictor to affect the response variable, the predictor becomes practically irrelevant. This can be observed in Fig. 4A where the relative importance of goes down to 0 after the number of treatment courses exceeds 9, simply because no extinction is observed during the drug-free period when the number of treatment courses is 10 or higher (Fig. 4C). Therefore, when applying predictor importance analysis, the best practice is to keep the variation of the independent predictors as high as possible to allow for changes in the response variable.
Source code for this project is available at https://github.com/burcutepekule/gutmicrobiota.
Supplementary Material
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
Data deposition: Source code for this paper has been deposited at https://github.com/burcutepekule/gutmicrobiota.
†Maximum value for is obtained in the case of 2 treatment courses, lasting for 3 and 10 d.
*During randomized simulations, the precolonization and the treatment period add up to 1,000 d, but the lengths of these periods are free to vary.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1912188116/-/DCSupplemental.
References
- 1.Huttenhower C., et al. , Structure, function and diversity of the healthy human microbiome. Nature 486, 207–214 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Neu H. C., The crisis in antibiotic resistance. Science 257, 1064–1073 (1992). [DOI] [PubMed] [Google Scholar]
- 3.French G. L., The continuing crisis in antibiotic resistance. Int. J. Antimicrob. Agents 36 (suppl. 3), S3–S7 (2010). [DOI] [PubMed] [Google Scholar]
- 4.Tanne J. H., Resistance of enterobacteria to carbapenem antibiotics is a global crisis. BMJ 344, e1646 (2012). [DOI] [PubMed] [Google Scholar]
- 5.Tzouvelekis L. S., Markogiannakis A., Psichogiou M., Tassios P. T., Daikos G. L., Carbapenemases in Klebsiella pneumoniae and other Enterobacteriaceae: An evolving crisis of global dimensions. Clin. Microbiol. Rev. 25, 682–707 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hassani M., The crisis of resistant gram-negative bacterial infections: Is there any hope for ESKAPE. Clin. Infect. Dis. 1, 1005 (2014). [Google Scholar]
- 7.Qin J., et al. , A human gut microbial gene catalogue established by metagenomic sequencing. Nature 464, 59–65 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gill S. R., et al. , Metagenomic analysis of the human distal gut microbiome. Science 312, 1355–1359 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kurokawa K., et al. , Comparative metagenomics revealed commonly enriched gene sets in human gut microbiomes. DNA Res. 14, 169–181 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hu Y., et al. , Metagenome-wide analysis of antibiotic resistance genes in a large cohort of human gut microbiota. Nat. Commun. 4, 2151 (2013). [DOI] [PubMed] [Google Scholar]
- 11.Caporaso J. G., et al. , Moving pictures of the human microbiome. Genome Biol. 12, R50 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Walker A. W., Duncan S. H., Louis P., Flint H. J., Phylogeny, culturing, and metagenomics of the human gut microbiota. Trends Microbiol. 22, 267–274 (2014). [DOI] [PubMed] [Google Scholar]
- 13.Qin J., et al. ; MetaHIT Consortium , A human gut microbial gene catalogue established by metagenomic sequencing. Nature 464, 59–65 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Stewart F. M., Levin B. R., The population biology of bacterial plasmids: A priori conditions for the existence of conjugationally transmitted factors. Genetics 87, 209–228 (1977). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Freter R., Freter R. R., Brickner H., Experimental and mathematical models of Escherichia coli plasmid transfer in vitro and in vivo. Infect. Immun. 39, 60–84 (1983). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bergstrom C. T., Lipsitch M., Levin B. R., Natural selection, infectious transfer and the existence conditions for bacterial plasmids. Genetics 155, 1505–1519 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Webb G. F., D’Agata E. M. C., Magal P., Ruan S., A model of antibiotic-resistant bacterial epidemics in hospitals. Proc. Natl. Acad. Sci. U.S.A. 102, 13343–13348 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lili L. N., Britton N. F., Feil E. J., The persistence of parasitic plasmids. Genetics 177, 399–405 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Svara F., Rankin D. J., The evolution of plasmid-carried antibiotic resistance. BMC Evol. Biol. 11, 130 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Trosvik P., et al. , Characterizing mixed microbial population dynamics using time-series analysis. ISME J. 2, 707–715 (2008). [DOI] [PubMed] [Google Scholar]
- 21.Trosvik P., Stenseth N. C., Rudi K., Convergent temporal dynamics of the human infant gut microbiota. ISME J. 4, 151–158 (2010). [DOI] [PubMed] [Google Scholar]
- 22.Stein R. R., et al. , Ecological modeling from time-series inference: Insight into dynamics and stability of intestinal microbiota. PLoS Comput. Biol. 9, e1003388 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gerber G. K., The dynamic microbiome. FEBS Lett. 588, 4131–4139 (2014). [DOI] [PubMed] [Google Scholar]
- 24.Marino S., Baxter N. T., Huffnagle G. B., Petrosino J. F., Schloss P. D., Mathematical modeling of primary succession of murine intestinal microbiota. Proc. Natl. Acad. Sci. U.S.A. 111, 439–444 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Shashkova T., et al. , Agent based modeling of human gut microbiome interactions and perturbations. PLoS One 11, e0148386 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Succurro A., Ebenhöh O., Review and perspective on mathematical modeling of microbial ecosystems. Biochem. Soc. Trans. 46, 403–412 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Goossens H., Ferech M., Stichele R. V., Elseviers M.; ESAC Project Group , Outpatient antibiotic use in Europe and association with resistance: A cross-national database study. Lancet 365, 579–587 (2005). [DOI] [PubMed] [Google Scholar]
- 28.Muder R. R., Brennen C., Drenning S. D., Stout J. E., Wagener M. M., Multiply antibiotic resistant gram-negative bacilli in a long term care facility: A case control study of patient risk factors and prior antibiotic use. Infect. Control Hosp. Epidemiol. 18, 809–813 (1997). [PubMed] [Google Scholar]
- 29.Kollef M. H., Sherman G., Ward S., Fraser V. J., Inadequate antimicrobial treatment of infections: A risk factor for hospital mortality among critically ill patients. Chest 115, 462–474 (1999). [DOI] [PubMed] [Google Scholar]
- 30.Colodner R., et al. , Risk factors for the development of extended-spectrum beta-lactamase-producing bacteria in nonhospitalized patients. Eur. J. Clin. Microbiol. Infect. Dis. 23, 163–167 (2004). [DOI] [PubMed] [Google Scholar]
- 31.Sotto A., et al. , Risk factors for antibiotic-resistant Escherichia coli isolated from hospitalized patients with urinary tract infections: A prospective study. J. Clin. Microbiol. 39, 438–444 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Allen U. D., MacDonald N., Fuite L., Chan F., Stephens D., Risk factors for resistance to “first-line” antimicrobials among urinary tract isolates of Escherichia coli in children. Can. Med. Assoc. J. 160, 1436–1440 (1999). [PMC free article] [PubMed] [Google Scholar]
- 33.Ena J., Amador C., Martinez C., de la Tabla V. O., Kunin C. M., Risk factors for acquisition of urinary tract infections caused by ciprofloxacin resistant Escherichia coli. J. Urol. 153, 117–120 (1995). [DOI] [PubMed] [Google Scholar]
- 34.Garau J., et al. , Emergence and dissemination of quinolone-resistant Escherichia coli in the community. Antimicrob. Agents Chemother. 43, 2736–2741 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pena C., et al. , Relationship between quinolone use and emergence of ciprofloxacin-resistant Escherichia coli in bloodstream infections. Antimicrob. Agents Chemother. 39, 520–524 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Arslan H., Azap Ö. K., Ergönül Ö., Timurkaynak F., Risk factors for ciprofloxacin resistance among Escherichia coli strains isolated from community-acquired urinary tract infections in Turkey. J. Antimicrob. Chemother. 56, 914–918 (2005). [DOI] [PubMed] [Google Scholar]
- 37.Gasink L. B., Zaoutis T. E., Bilker W. B., Lautenbach E., The categorization of prior antibiotic use: Impact on the identification of risk factors for drug resistance in case control studies. Am. J. Infect. Control 35, 638–642 (2007). [DOI] [PubMed] [Google Scholar]
- 38.Hillier S., et al. , Prior antibiotics and risk of antibiotic-resistant community-acquired urinary tract infection: A case–control study. J. Antimicrob. Chemother. 60, 92–99 (2007). [DOI] [PubMed] [Google Scholar]
- 39.Du B., et al. , Extended-spectrum beta-lactamase-producing Escherichia coli and Klebsiella pneumoniae bloodstream infection: Risk factors and clinical outcome. Intensive Care Med. 28, 1718–1723 (2002). [DOI] [PubMed] [Google Scholar]
- 40.Goyal D., Dean N., Neill S., Jones P., Dascomb K., Risk factors for community-acquired extended-spectrum beta-lactamase–producing Enterobacteriaceae infections—A retrospective study of symptomatic urinary tract infections. Open Forum Infect Dis 6, ofy357 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Park Y. S., et al. , Risk factors and clinical features of infections caused by plasmid-mediated ampc -lactamase-producing Enterobacteriaceae. Int. J. Antimicrob. Agents 34, 38–43 (2009). [DOI] [PubMed] [Google Scholar]
- 42.Mathers A. J., Peirano G., Pitout J. D. D., The role of epidemic resistance plasmids and international high-risk clones in the spread of multidrug-resistant Enterobacteriaceae. Clin. Microbiol. Rev. 28, 565–591 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yelin I., et al. , Personal clinical history predicts antibiotic resistance in urinary tract infections. bioRxiv:/10.1101/384842 (9 August 2018). [DOI] [PMC free article] [PubMed]
- 44.Berg R. D., The indigenous gastrointestinal microflora. Trends Microbiol. 4, 430–435 (1996). [DOI] [PubMed] [Google Scholar]
- 45.Mason K. L., et al. , From commensal to pathogen: Translocation of Enterococcus faecalis from the midgut to the hemocoel of Manduca sexta. MBio 2, e00065-11 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Nagarjuna D., et al. , Faecal Escherichia coli isolates show potential to cause endogenous infection in patients admitted to the ICU in a tertiary care hospital. New Microbes New Infect. 7, 57–66 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.van Schaik W., The human gut resistome. Philos. Trans. R. Soc. B 370, 20140087 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Menz S., “Hybrid stochastic-deterministic approaches for simulation and analysis of biochemical reaction networks,” PhD thesis, Freie Universität, Berlin, Germany: (2013). [Google Scholar]
- 49.Stewardson A. J., et al. , Collateral damage from oral ciprofloxacin versus nitrofurantoin in outpatients with urinary tract infections: A culture-free analysis of gut microbiota. Clin. Microbiol. Infect. 21, 344–e1– 344–e11 (2015). [DOI] [PubMed] [Google Scholar]
- 50.Pop M., et al. , Individual-specific changes in the human gut microbiota after challenge with enterotoxigenic Escherichia coli and subsequent ciprofloxacin treatment. BMC Genomics 17, 440 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Dethlefsen L., Huse S., Sogin M. L., Relman D. A., The pervasive effects of an antibiotic on the human gut microbiota, as revealed by deep 16S rRNA sequencing. PLoS Biol. 6, e280 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Willmann M., et al. , Antibiotic selection pressure determination through sequence-based metagenomics. Antimicrob. Agents Chemother. 59, 7335–7345 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Guyon I., Elisseeff A., An introduction to variable and feature selection. J. Mach. Learn. Res. 3, 1157–1182 (2003). [Google Scholar]
- 54.Hothorn T., Hornik K., Zeileis A., Unbiased recursive partitioning: A conditional inference framework. J. Comput. Graph. Stat. 15, 651–674 (2006). [Google Scholar]
- 55.Strobl C., Boulesteix A.-L., Kneib T., Augustin T., Zeileis A., Conditional variable importance for random forests. BMC Bioinf. 9, 307 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Tam V. C., et al. , Frequency, type and clinical importance of medication history errors at admission to hospital: A systematic review. Can. Med. Assoc. J. 173, 510–515 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Coyte K. Z., Schluter J., Foster K. R., The ecology of the microbiome: Networks, competition, and stability. Science 350, 663–666 (2015). [DOI] [PubMed] [Google Scholar]
- 58.Cho I., Blaser M. J., The human microbiome: At the interface of health and disease. Nat. Rev. Genet. 13, 260 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Faith J. J., et al. , The long-term stability of the human gut microbiota. Science 341, 1237439 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Vemuri R., et al. , Gut microbial changes, interactions, and their implications on human lifecycle: An ageing perspective. BioMed Res. Int. 2018, 1–13 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Martínez-Martínez L., Pascual A., Jacoby G. A., Quinolone resistance from a transferable plasmid. Lancet 351, 797–799 (1998). [DOI] [PubMed] [Google Scholar]
- 62.Jacoby G. A., “Plasmid-mediated quinolone resistance” in Antimicrobial Drug Resistance, Mayers D. L., Ed. (Springer, 2017), pp. 265–268. [Google Scholar]
- 63.Chen K., et al. , Identification and characterization of conjugative plasmids that encode ciprofloxacin resistance in Salmonella. Antimicrob. Agents Chemother. 62, e00575-18 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Kim J. H., Cho J. K., Kim K. S., Prevalence and characterization of plasmid-mediated quinolone resistance genes in salmonella isolated from poultry in Korea. Avian Pathol. 42, 221–229 (2013). [DOI] [PubMed] [Google Scholar]
- 65.Pasom W., et al. , Plasmid-mediated quinolone resistance genes, aac (6)-ib-cr, qnrs, qnrb, and qnra, in urinary isolates of Escherichia coli and Klebsiella pneumoniae at a teaching hospital, Thailand. Jpn. J. Infect. Dis. 66, 428–432 (2013). [DOI] [PubMed] [Google Scholar]
- 66.Yan L., et al. , Bacterial plasmid-mediated quinolone resistance genes in aquatic environments in China. Sci. Rep. 7, 40610 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Tomova A., Ivanova L., Buschmann A. H., Godfrey H. P., Cabello F. C., Plasmid-mediated quinolone resistance (pmqr) genes and class 1 integrons in quinolone-resistant marine bacteria and clinical isolates of Escherichia coli from an aquacultural area. Microb. Ecol. 75, 104–112 (2018). [DOI] [PubMed] [Google Scholar]
- 68.Tausova D., et al. , Escherichia coli with extended-spectrum -lactamase and plasmid-mediated quinolone resistance genes in great cormorants and mallards in central Europe. J. Antimicrob. Chemother. 67, 1103–1107 (2012). [DOI] [PubMed] [Google Scholar]
- 69.Jacoby G. A., Hooper D. C., Phylogenetic analysis of chromosomally determined qnr and related proteins. Antimicrob. Agents Chemother. 57, 1930–1934 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Rodríguez-Martínez J. M., et al. , Qnr-like pentapeptide repeat proteins in gram-positive bacteria. J. Antimicrob. Chemother. 61, 1240–1243 (2008). [DOI] [PubMed] [Google Scholar]
- 71.Jakobsen L., et al. , Impact of low-level fluoroquinolone resistance genes qnra1, qnrb19 and qnrs1 on ciprofloxacin treatment of isogenic Escherichia coli strains in a murine urinary tract infection model. J. Antimicrob. Chemother. 67, 2438–2444 (2012). [DOI] [PubMed] [Google Scholar]
- 72.Allou N., Cambau E., Massias L., Chau F., Fantin B., Impact of low-level resistance to fluoroquinolones due to qnra1 and qnrs1 genes or a gyra mutation on ciprofloxacin bactericidal activity in a murine model of Escherichia coli urinary tract infection. Antimicrob. Agents Chemother. 53, 4292–4297 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Domínguez-Herrera J., et al. , Impact of qnra1, qnrb1 and qnrs1 on the efficacy of ciprofloxacin and levofloxacin in an experimental pneumonia model caused by Escherichia coli with or without the gyra mutation ser83leu. J. Antimicrob. Chemother. 68, 1609–1615 (2013). [DOI] [PubMed] [Google Scholar]
- 74.Guillard T., et al. , Ciprofloxacin treatment failure in a murine model of pyelonephritis due to an aac (6’)-ib-cr-producing Escherichia coli strain susceptible in vitro. Antimicrob. Agents Chemother. 57, 5830–5835 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Shoemaker N. B., Vlamakis H., Hayes K., Salyers A. A., Evidence for extensive resistance gene transfer among Bacteroides spp. and among Bacteroides and other genera in the human colon. Appl. Environ. Microbiol. 67, 561–568 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Salyers A. A., Gupta A., Wang Y., Human intestinal bacteria as reservoirs for antibiotic resistance genes. Trends Microbiol. 12, 412–416 (2004). [DOI] [PubMed] [Google Scholar]
- 77.Wexler H. M., Bacteroides: The good, the bad, and the nitty-gritty. Clin. Microbiol. Rev. 20, 593–621 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Sommer M. O. A., Church G. M., Dantas G., The human microbiome harbors a diverse reservoir of antibiotic resistance genes. Virulence 1, 299–303 (2010). [DOI] [PubMed] [Google Scholar]
- 79.Sommer M. O. A., Dantas G., Church G. M., Functional characterization of the antibiotic resistance reservoir in the human microflora. Science 325, 1128–1131 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Salyers A. A., Bacteroides of the human lower intestinal tract. Annu. Rev. Microbiol. 38, 293–313 (1984). [DOI] [PubMed] [Google Scholar]
- 81.Rizzatti G., Lopetuso L. R., Gibiino G., Binda C., Gasbarrini A., Proteobacteria: A common factor in human diseases. BioMed Res. Int. 2017, 1–7 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Levin B. R., Stewart F. M., Rice V. A., The kinetics of conjugative plasmid transmission: Fit of a simple mass action model. Plasmid 2, 247–260 (1979). [DOI] [PubMed] [Google Scholar]
- 83.Bucci V., et al. , Mdsine: Microbial dynamical systems inference engine for microbiome time-series analyses. Genome Biol. 17, 121 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Lopatkin A. J., et al. , Persistence and reversal of plasmid-mediated antibiotic resistance. Nat. Commun. 8, 1689 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Andersson D. I., Hughes D., Antibiotic resistance and its cost: Is it possible to reverse resistance? Nat. Rev. Microbiol. 8, 260–271 (2010). [DOI] [PubMed] [Google Scholar]
- 86.De Gelder L., et al. , Combining mathematical models and statistical methods to understand and predict the dynamics of antibiotic-sensitive mutants in a population of resistant bacteria during experimental evolution. Genetics 168, 1131–1144 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Le Devendec L., Bouder A., Dheilly A., Hellard G., Kempf I., Persistence and spread of qnr, extended-spectrum beta-lactamase, and ampc resistance genes in the digestive tract of chickens. Microb. Drug Resist. 17, 129–134 (2011). [DOI] [PubMed] [Google Scholar]
- 88.Allen R. C., Engelstädter J., Bonhoeffer S., McDonald B. A., Hall A. R., Reversing resistance: Different routes and common themes across pathogens. Proc. R. Soc. B 284, 20171619 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.de Toro M., et al. , Characterisation of plasmids implicated in the mobilisation of extended-spectrum and ampc -lactamase genes in clinical Salmonella enterica isolates and temporal stability of the resistance genotype. Int. J. Antimicrob. Agents 42, 167–172 (2013). [DOI] [PubMed] [Google Scholar]
- 90.Subbiah M., Top E. M., Shah D. H., Call D. R., Selection pressure required for long-term persistence of blacmy-2-positive inca/c plasmids. Appl. Environ. Microbiol. 77, 4486–4493 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.MacLean R. C., Vogwill T., Limits to compensatory adaptation and the persistence of antibiotic resistance in pathogenic bacteria. Evol. Med. Publ. Health 2015, 4–12 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Gumpert H., et al. , Transfer and persistence of a multi-drug resistance plasmid in situ of the infant gut microbiota in the absence of antibiotic treatment. Front. Microbiol. 8, 1852 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Johnsen P. J., Simonsen G. S., Olsvik Ø., Midtvedt T., Sundsfjord A., Stability, persistence, and evolution of plasmid-encoded vana glycopeptide resistance in enterococci in the absence of antibiotic selection in vitro and in gnotobiotic mice. Microb. Drug Resist. 8, 161–170 (2002). [DOI] [PubMed] [Google Scholar]
- 94.Borgen K., et al. , Continuing high prevalence of vana-type vancomycin-resistant enterococci on Norwegian poultry farms three years after avoparcin was banned. J. Appl. Microbiol. 89, 478–485 (2000). [DOI] [PubMed] [Google Scholar]
- 95.Borgen K., Sørum M., Kruse H., Wasteson Y., Persistence of vancomycin-resistant enterococci (vre) on Norwegian broiler farms. FEMS Microbiol. Lett. 191, 255–258 (2000). [DOI] [PubMed] [Google Scholar]
- 96.Enne V. I., Livermore D. M., Stephens P., Hall L. M. C., Persistence of sulphonamide resistance in Escherichia coli in the UK despite national prescribing restriction. Lancet 357, 1325–1328 (2001). [DOI] [PubMed] [Google Scholar]
- 97.Sjlund M., Wreiber K., Andersson D. I., Blaser M. J., Engstrand L., Long-term persistence of resistant enterococcus species after antibiotics to eradicate Helicobacter pylori. Ann. Intern. Med. 139, 483–487 (2003). [DOI] [PubMed] [Google Scholar]
- 98.Löfmark S., Jernberg C., Jansson J. K., Edlund C., Clindamycin-induced enrichment and long-term persistence of resistant bacteroides spp. and resistance genes. J. Antimicrob. Chemother. 58, 1160–1167 (2006). [DOI] [PubMed] [Google Scholar]
- 99.Forslund K., et al. , Country-specific antibiotic use practices impact the human gut resistome. Genome Res. 23, 1163–1169 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Andersson D. I., Hughes D., Persistence of antibiotic resistance in bacterial populations. FEMS Microbiol. Rev. 35, 901–911 (2011). [DOI] [PubMed] [Google Scholar]
- 101.Bahl M. I., Hansen L. H., Sørensen S. J., “Persistence mechanisms of conjugative plasmids” in Horizontal Gene Transfer, Gogarten M. B., Gogarten J. P., Olendzensk L. C., Eds. (Springer, 2009), pp. 73–102. [DOI] [PubMed] [Google Scholar]
- 102.Dahlberg C., Chao L., Amelioration of the cost of conjugative plasmid carriage in Eschericha coli k12. Genetics 165, 1641–1649 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Dionisio F., Conceicao I. C., Marques A. C. R., Fernandes L., Gordo I., The evolution of a conjugative plasmid and its ability to increase bacterial fitness. Biol. Lett. 1, 250–252 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Harrison E., Brockhurst M. A., Plasmid-mediated horizontal gene transfer is a coevolutionary process. Trends Microbiol. 20, 262–267 (2012). [DOI] [PubMed] [Google Scholar]
- 105.Porse A., Schønning K., Munck C., Sommer M. O. A., Survival and evolution of a large multidrug resistance plasmid in new clinical bacterial hosts. Mol. Biol. Evol. 33, 2860–2873 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Dionisio F., Matic I., Radman M., Rodrigues O. R., Taddei F., Plasmids spread very fast in heterogeneous bacterial communities. Genetics 162, 1525–1532 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Dröge M., Pühler A., Selbitschka W., Horizontal gene transfer as a biosafety issue: A natural phenomenon of public concern. J. Biotechnol. 64, 75–90 (1998). [DOI] [PubMed] [Google Scholar]
- 108.Ando T., et al. , Restriction–modification system differences in Helicobacter pylori are a barrier to interstrain plasmid transfer. Mol. Microbiol. 37, 1052–1065 (2000). [DOI] [PubMed] [Google Scholar]
- 109.Matic I., Taddei F., Radman M., Genetic barriers among bacteria. Trends Microbiol. 4, 69–73 (1996). [DOI] [PubMed] [Google Scholar]
- 110.Majewski J., Sexual isolation in bacteria. FEMS Microbiol. Lett. 199, 161–169 (2001). [DOI] [PubMed] [Google Scholar]
- 111.Feng J., et al. , Antibiotic resistome in a large-scale healthy human gut microbiota deciphered by metagenomic and network analyses. Environ. Microbiol. 20, 355–368 (2018). [DOI] [PubMed] [Google Scholar]
- 112.Sender R., Fuchs S., Milo R., Revised estimates for the number of human and bacteria cells in the body. PLoS Biol. 14, e1002533 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Manichanh C., et al. , Reshaping the gut microbiome with bacterial transplantation and antibiotic intake. Genome Res. 20, 1411–1419 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.